1 Introduction

It is widely believed that the introduction of supersymmetry (SUSY) and its local extension – supergravity (SUGRA) – can alleviate the shortcomings of Standard Model (SM) and provide a safe framework for building a variety of inflationary models – see e.g. Refs. [1, 2]. However, we have to accept that there is no direct experimental confirmation of SUSY until now [3]. On the contrary, there is a strong observational evidence in favor of the inflationary paradigm [4, 5]. Consequently, it is worthwhile to build inflationary models compatible with the observations, even without the presence of SUSY.

One of those models – for reviews see Refs. [6, 7] – is undoubtedly Hybrid Inflation (HI) [8, 9] which elegantly combines a period of inflation with a phase transition at its termination. It is termed “hybrid” because the inflationary vacuum energy density is provided by a waterfall field, different from the slowly rolling inflaton field. The model allows for values of the relevant coupling constants larger than those used in chaotic inflation, and can be successfully handled with subplanckian values for the inflaton field. It can be, also, embedded in several Grand Unified Theory (GUT) schemes – mainly in the SUSY framework [10,11,12,13,14,15] – and nicely connects inflationary cosmology with particle physics. A very intriguing possibility of these embeddings is the production of topological defects at its end via the Kibble mechanism [16]. Between them, the metastable cosmic strings are currently of special interest since they may decay generating a stochastic background of gravitational waves [17, 18] and interpreting, thereby, recent results [19, 20] – for other sources of gravitational waves’ production after the end of HI see Refs. [21, 22].

On the other hand, HI suffers from the problem of the enhanced (scalar) spectral index \(n_{\textrm{s}}\) which turns out to be, mostly, well above the present data [23,24,25] – for another point of view see Ref. [26]. Indeed, \(n_{\textrm{s}}\) within tree level HI exceeds unity [8, 9] and only in a minor and tuned region of parameters [27] a reconciliation with data can be achieved. Inclusion of radiative corrections (RCs) [28] due to a possible coupling of the inflaton to fermions [29] or a conveniently selected non-minimal coupling to gravity [27, 30] can reconcile the model’s predictions with observations – for another mechanism possibly applicable in non-SUSY HI see Ref. [31]. However, the situation remains problematic since in both aforementioned cases, HI of hilltop type [32] is obtained and so an unavoidable tuning of the initial conditions emerges. Nonetheless, it is by now well-known [33,34,35,36,37,38,39] that the presence of a pole in the kinetic term of the inflaton facilitates the achievement of observation-friendly chaotic inflation. It would be, therefore, interesting to investigate if this technique can be also applied for HI improving, thereby, its compatibility with the observations – for a similar recent work see Ref. [40].

We find out that two types of HI can be formulated depending on the order p of the inflaton kinetic pole [41, 42]. For \(p=1\) we obtain E-model HI (EHI) whereas for \(p=2\), T-model HI (THI) arises. The terms are coined in analogy to E-model (chaotic) inflation (EMI) [43] (or \(\alpha \)-Starobinsky model [44]) and T-model inflation (TMI) [45]. As in the latter cases [38, 39], EHI and THI can be relied on Kähler potentials and so the relevant particle models can be established as non-linear sigma models with specific geometry of the moduli space. In both cases, the minimal possible RCs [28] to the inflationary potential are considered and subplanckian values for the initial (non-canonically normalized) inflaton field are required. Unfortunately, our scheme is inconsistent with the formation of cosmic strings after HI, since the relevant scale M of the phase transition turns out to be a little lower than the reduced Planck scale, \(m_{\textrm{P}}= 2.44\cdot 10^{18}~{\textrm{GeV}}\), and so the tension of the cosmic strings [17, 18] would be unacceptably large. Therefore, the version of HI with the waterfall field charged under the continuous group U(1) with the lowest possible dimensionality is not a representative working example for our setup. However, if there is a U(1) factor in the initial and the remaining gauge group, with the waterfall field arranged in a convenient representation, then the production of cosmic strings (and monopoles) after HI can be eluded [46]. In our analysis we adopt the simplest possible scenario for reference. Other ways to overcome the obstacle of topological defects within HI are proposed in Refs. [14, 15, 40].

Below, in Sect. 2, we describe how we can formulate these versions of HI. The dynamics of the resulting inflationary models is studied in Sect. 3 and these are tested against observations in Sect. 4. Finally, Sect. 5 summarizes our conclusions. In Appendix A we explore the possibility for generating different moduli kinetic mixings allowed by generic Kähler potentials. Throughout the text, the subscript \(,\chi \) denotes derivation with respect to (w.r.t) the field \(\chi \), charge conjugation is denoted by a star (\(^*\)) and we use units where \(m_{\textrm{P}}= 1\) unless otherwise stated.

2 Models’ setup

Since E and T models are introduced by means of a non-minimal kinetic mixing [38, 39], we find it convenient to establish their combination with HI taking as reference the non-linear sigma models. In these the kinetic mixing is controlled by a metric \(K_{{\alpha }{{\bar{\beta }}}}\) defined on the moduli space. Here we employ two (complex) scalar fields \(Z^{\alpha }\) with \({\alpha }=1,2\) – the inflaton \(Z^1=S\) and the waterfall field \(Z^2=\Phi \). Therefore, the relevant lagrangian terms are written as

$$\begin{aligned} {{\mathcal {L}}} = \sqrt{-{\mathfrak {g}}} \left( K_{{\alpha }{{\bar{\beta }}}}\left( D_\mu Z^{\alpha }\right) ^\dagger D^\mu Z^{{{\bar{\beta }}}} -V(Z^{\alpha })\right) , \end{aligned}$$
(2.1)

where \({\mathfrak {g}}\) is the determinant of the background Friedmann–Robertson–Walker metric \(g^{\mu \nu }\) with signature \((+,-,-,-)\). We further assume that \(K_{{\alpha }{{\bar{\beta }}}}\) originates from a Kähler potential K – as in the context of SUGRA – according to the definition

$$\begin{aligned} K_{{\alpha }{{\bar{\beta }}}}={K_{,Z^{\alpha }Z^{*{{\bar{\beta }}}}}}>0\quad \hbox {with}\ K^{{{\bar{\beta }}}{\alpha }}K_{{\alpha }\bar{\gamma }}=\delta ^{{\bar{\beta }}}_{{\bar{\gamma }}}. \end{aligned}$$
(2.2)

We below, in Sects. 2.1 and 2.2, we respectively specify the kinetic terms and the inflationary potential of our models.

2.1 Kinetic mixing

The adopted K’s include two contributions, one for the inflaton, \(K_{\textrm{I}}\), and one for the waterfall field, \(K_{\textrm{W}}\). Namely, we set

$$\begin{aligned} K= & {} K_{\textrm{I}}+K_{\textrm{W}}\quad \hbox {with}\ K_{\textrm{W}}=|\Phi |^2\ \hbox {and}\ K_{\textrm{I}}\nonumber \\= & {} {\left\{ \begin{array}{ll} -2N\ln (1-(S+S^*)/2) &{}\hbox {for EHI},\\ -(N/2)\ln (1-|S|^2) &{}\hbox {for THI}. \end{array}\right. } \end{aligned}$$
(2.3)

We see that no mixing between the inflaton and waterfall sectors exists and the non-zero elements of the relevant metric are calculated to be

$$\begin{aligned} K_{\Phi \Phi ^*}=1\quad \hbox {and}\quad K_{SS^*}=\frac{N}{2}\cdot {\left\{ \begin{array}{ll} (1-(S+S^*)/2)^{-2} &{}\hbox {for EHI},\\ (1-|S|^2)^{-2} &{}\hbox {for THI}. \end{array}\right. } \end{aligned}$$
(2.4)

For both models, \(K_{\textrm{W}}\) parameterizes flat manifold – contrary to the setting in Refs. [22, 40] – whereas the geometry induced by \(K_{\textrm{I}}\) is hyperbolic, i.e., the curvature of the moduli space is negative. In particular, the scalar curvatures associated with \(K_{\textrm{W}}\) and \(K_{\textrm{I}}\) respectively are

$$\begin{aligned}{} & {} {{\mathcal {R}}}_{\textrm{W}}=0 \quad \hbox {and}\nonumber \\{} & {} {{\mathcal {R}}}_{\textrm{I}}\!=\!-K^{SS^*}\partial _S\partial _{S^*}\ln K_{SS^*}\!=\!-({1}/{N}){\left\{ \begin{array}{ll} 1&{}\hbox {for EHI},\\ 4&{}\hbox {for THI}. \end{array}\right. } \end{aligned}$$
(2.5)

More specifically, \(K_{\textrm{I}}\) parameterizes the coset space SU(1, 1)/U(1) in the case of THI, whereas for EHI the space generated by \(K_{\textrm{I}}\) is invariant under the set of transformations related to the group U(1, 1) – see Ref. [37].

In Eq. (2.1) we include the covariant derivatives for the scalar fields \(D_\mu Z^{\alpha }\) which are given by

$$\begin{aligned} D_\mu Z^{\alpha }=\partial _\mu Z^{\alpha }+ig A^{\textrm{a}}_\mu T^{\textrm{a}}_{{\alpha }{\beta }} Z^{\beta }, \end{aligned}$$
(2.6)

with \(A^{\textrm{a}}_\mu \) being the vector gauge fields, g a gauge coupling constant and \(T^{\textrm{a}}\) with \({\textrm{a}}=1,\ldots ,\mathsf{\small dim}G_{\textrm{GUT}}\) the generators of the gauge group \(G_{\textrm{GUT}}\) with dimensionality \(\mathsf{\small dim}G_{\textrm{GUT}}\). To avoid the production of cosmic defects after the end of HI we have to select \(G_{\textrm{GUT}}\) according to the guidelines of Ref. [46]. For definiteness, we here assume that \(\Phi \) belongs to the \((\textbf{2}, 1)\) representation of the group \(G_{21}=SU(2) \times U(1)\). Interestingly enough, this group may be identified with the \(SU(2)_{\textrm{R}} \times U(1)_{B-L}\) part of a realistic (minimal) version [47, 48] of the GUT based on the group \(G_{\textrm{LR}}=SU(3)_{\textrm{C}}\times SU(2)_{\textrm{L}} \times SU(2)_{\textrm{R}} \times U(1)_{B-L}\).

If we use the following parameterizations for the two fields

$$\begin{aligned} S=\sigma e^{i\theta }\quad \hbox {and}\quad \Phi =\frac{1}{\sqrt{2}}\left\lgroup \begin{matrix} \phi _1+i\varphi _1 \\ \phi _2+i\varphi _2 \end{matrix}\right\rgroup , \end{aligned}$$
(2.7)

we can introduce he canonically normalized (hatted) fields during HI as follows

$$\begin{aligned}{} & {} \langle {K_{{\alpha }{{\bar{\beta }}}}} \rangle _\textrm{HI}\dot{Z}^{\alpha }\dot{Z}^{*{{\bar{\beta }}}} \simeq \frac{1}{2}\left( \dot{{\widehat{\sigma }}}^2+ \dot{\widehat{\theta }}^2+{\dot{\phi _\alpha }}^2+{\dot{\varphi _\alpha }}^2\right) \nonumber \\{} & {} \quad \hbox {for}\ {\alpha }=1,2 \end{aligned}$$
(2.8)

where \(K_{{\alpha }{{\bar{\beta }}}}\) is given by Eq. (2.4) and assures the canonical normalization of \(\phi _\alpha \) and \(\varphi _\alpha \). The symbol “\(\langle {Q} \rangle _\textrm{HI}\)” denotes the value of a quantity Q during HI, where all the fields besides \(\sigma \) are set equal to zero – see below – and dot stands for derivation w.r.t the cosmic time. From Eq. (2.8) the remaining fields \({\widehat{\sigma }}\) and \(\widehat{\theta }\) are identified as

$$\begin{aligned} \frac{d{\widehat{\sigma }}}{d\sigma }= & {} J=\frac{\sqrt{N}}{f_p}~~\Rightarrow ~~{\widehat{\sigma }}\nonumber \\= & {} {\left\{ \begin{array}{ll} -\sqrt{N}\ln (1-\sigma ) &{}\hbox {for}\ p=1,\\ \sqrt{N}\textrm{arctanh}{\sigma } &{}\hbox {for}\ p=2 \end{array}\right. }\quad \hbox {and}\quad \widehat{\theta }\simeq J\sigma \theta ,\nonumber \\ \end{aligned}$$
(2.9)

where \(f_p=1-\sigma ^p\) with \(p=1,2\). Note that \({\widehat{\sigma }}\) gets increased above unity for \(\sigma _{\textrm{c}}\le \sigma <1\), facilitating, thereby, the attainment of HI with sub-Planckian  \(\sigma \) values.

2.2 Inflationary potential

In Eq. (2.1) the inflationary potential for our models is also incorporated. Its form is

$$\begin{aligned}{} & {} V(S,\Phi ) = \kappa ^2\left( |\Phi |^2-M^2\right) ^2\nonumber \\{} & {} \quad +\frac{1}{2} m^2|S|^2+\lambda ^2|\Phi |^2|S|^2+\frac{1}{8}{\widetilde{m}}|S-S^*|^2, \end{aligned}$$
(2.10)

where M, m and \({\widetilde{m}}\) are mass parameters whereas \(\kappa \) and \(\lambda \) are dimensionless coupling constants. The last unusual term is adopted to provide the angular mode of S, \(\theta \), with mass, as we see below. The global minima of V lie at the direction

$$\begin{aligned} \langle {\phi _1} \rangle =\pm \sqrt{2}M\quad \hbox {and}\quad \langle {\sigma } \rangle =\langle {\phi _2} \rangle =\langle {\varphi _\alpha } \rangle =\langle {\theta } \rangle =0 \end{aligned}$$
(2.11)

and ensure a spontaneous breaking of the local symmetry \(G_{21}\) down to a \(U(1)'\). The scalar spectrum of the theory is composed by three real scalars \(\sigma \), \(\delta \phi _1=\phi _1-\langle {\phi _1} \rangle \) and \(\theta \) with masses correspondingly

$$\begin{aligned}{} & {} \widehat{m}_{\sigma }=\sqrt{(m^2+2\lambda ^2 M^2)/N},\quad m_{\delta \phi _1}=2\kappa M\nonumber \\{} & {} \quad \hbox {and}\quad \widehat{m}_{\theta }={\widetilde{m}}/\sqrt{N}. \end{aligned}$$
(2.12)

Thanks to the selected representation of \(\Phi \) in Eq. (2.7) neither cosmic strings nor monopoles are left behind the breakdown of \(G_{21}\) [46]. The truncated form of V with all the fields, but \(\sigma \) and \(\phi _1\), set at the origin reduces to its well-known form [8, 9] within HI, i.e.,

$$\begin{aligned} V \left( \phi _1,\sigma \right) = \kappa ^2 \left( \frac{\phi _1^2}{2}-M^2 \right) ^2+\frac{m^2}{2}\sigma ^2+\frac{\lambda ^2}{2}\phi _1^2 \sigma ^2. \end{aligned}$$
(2.13)

Besides the phase transition above, V in Eq. (2.10) gives rise to HI. This is, because it possesses an almost \(\sigma \)-flat direction at

$$\begin{aligned} \langle {\phi _\alpha } \rangle _\textrm{HI}=\langle {\varphi _\alpha } \rangle _\textrm{HI}=\langle {\theta } \rangle _\textrm{HI}=0\quad \hbox {with}\quad \sigma \ge \sigma _{\textrm{c}}= \sqrt{2}\kappa M/\lambda . \end{aligned}$$
(2.14)

The last inequality here assures the stability of the inflationary path w.r.t the fluctuations of \(\phi _\alpha \) and \(\varphi _\alpha \) during HI. Indeed, as shown in Table 1 – where the mass squared spectrum of the model along the trough in Eq. (2.14) is arranged – the positivity of \(m^2_{\Phi }\) is protected by the last inequality in Eq. (2.14). From Table 1 we can also verify that \(\theta \) acquires mass thanks to the last term of Eq. (2.10) and confirm that \(\widehat{m}^2_{\theta }\gg H_{\textrm{HI}}^2\) and \(\widehat{m}^2_{\Phi }\gg H_{\textrm{HI}}^2\) for \(\sigma _{\textrm{c}}<\sigma \le \sigma _{\star }\). Here we define

(2.15)

the almost constant potential density during HI. Note that no massive gauge bosons exist in the particle spectrum since \(G_{21}\) is unbroken during HI. Using the derived spectrum we can compute the one-loop RCs (to the tree-level potential) \(\Delta V_{\textrm{HI}}\) which can be written as [28]

$$\begin{aligned} \Delta V_{\textrm{HI}}={1\over 64\pi ^2}\left( \widehat{m}_{\theta }^4\ln {{\widehat{m}}_{\theta }^2\over \Lambda ^2} +2\textsf{N}_{\textrm{G}}\widehat{m}_{\phi }^4\ln {{\widehat{m}}_{\phi }^2\over \Lambda ^2} \right) . \end{aligned}$$
(2.16)

Here, \(\textsf{N}_{\textrm{G}}=2\) is the dimensionality of the representation of \(\Phi \) and \(\Lambda \) is a renormalization-mass scale which, is determined by requiring \(\Delta V_{\textrm{HI}}(\sigma _{\star })=0\) or \(\Delta V_{\textrm{HI}}(\sigma _{\textrm{c}})=0\). This determination of \(\Lambda \) renders our results practically independent of \(\Lambda \) in the major parameter space of the models – cf. Ref.  [49]. Indeed, these can be derived exclusively by using the tree level \(V_{\textrm{HI}}=V(S,0)\) with the various quantities evaluated at \(\Lambda \) since the relevant renormalization-group running is expected to be negligible – see Sect. 4. On the other hand, as shown in the same section, \(\Delta V_{\textrm{HI}}\) is capable to ruin the successful inflationary predictions for \(\kappa > rsim 0.003\). This effect may be avoided if extra contributions with opposite sign are included into \(\Delta V_{\textrm{HI}}\) due to possible coupling of S or \(\Phi \) to fermions (such as right-handed neutrinos) – see Ref. [29].

In conclusion, the inflationary potential for EHI and THI is

$$\begin{aligned} V_{\textrm{HI}}=V_{{\textrm{HI}}0}+{1\over 2}m^2\sigma ^2+\Delta V_{\textrm{HI}} \end{aligned}$$
(2.17)

with the canonical normalization of \(\sigma \) in Eq. (2.9) being taken into account and differentiating the models between each other.

Table 1 Mass spectrum for EHI \((p=1)\) and THI \((p=2)\) along the inflationary path in Eq. (2.14)
Full size table

3 Inflation analysis

A period of slow-roll EHI or THI is controlled by the strength of the slow-roll parameters which can be derived by applying the standard formulae – see e.g. Refs. [6, 7]. Note that the derivation can be performed employing \(V_{\textrm{HI}}\) in Eq. (2.17) and J in Eq. (2.9), without express explicitly \(V_{\textrm{HI}}\) in terms of \({\widehat{\sigma }}\) – see e.g. Ref. [27]. Namely, we find

$$\begin{aligned} \epsilon= & {} {1\over 2}\left( \frac{V_{\textrm{HI},{\widehat{\sigma }}}}{V_{\textrm{HI}}}\right) ^2\simeq \frac{m^4f_p^2\sigma ^2}{2NV_{{\textrm{HI}}0}^2} \quad \hbox {and}\quad \nonumber \\ \eta= & {} \frac{V_{\textrm{HI},{\widehat{\sigma }}{\widehat{\sigma }}}}{V_{\textrm{HI}}} \simeq m^2f_p\frac{f_p-p\sigma ^p}{NV_{{\textrm{HI}}0}} \cdot \end{aligned}$$
(3.1a)

In the expressions above we replace \(V_{\textrm{HI}}\) from Eq. (2.15b) whereas \(V_{\textrm{HI},{\widehat{\sigma }}}\) and \(V_{\textrm{HI},{\widehat{\sigma }}{\widehat{\sigma }}}\) are obtained by performing derivations of Eq. (2.17). As m increases beyond \(5\cdot 10^{-6}\) the approximation above becomes less accurate. It can be verified numerically that

$$\begin{aligned} \epsilon (\sigma _{\textrm{c}})\le 1\quad \hbox {and}\quad \eta (\sigma _{\textrm{c}})\le 1 \end{aligned}$$
(3.1b)

and so HI is terminated prematurely – i.e., for \(\sigma _{\textrm{f}}=\sigma _{\textrm{c}}\) – in the major parametric space of our model.

To protect our scenario from the production of extra e-foldings [8, 9, 40, 50, 51] during the waterfall regime, we take into account the behavior of \(\sigma \) and \(\phi _1\) after the time \(H_{\textrm{HI}}^{-1}\) from the moment when \(\sigma =\sigma _{\textrm{c}}\), following the approach in Refs. [8, 9, 40]. The absolute value of the \(\phi _1\) effective mass after this time can be estimated as

$$\begin{aligned} \Delta m_{\phi _1}^2\simeq 2\lambda ^2\Delta \sigma \sigma _{\textrm{c}}\quad \hbox {where}\ \Delta \sigma =3\sqrt{2}{m^2m_{\textrm{P}}^2}/{\lambda \kappa M^3} \end{aligned}$$
(3.2)

is the reduction of the \(\sigma \) value below \(\sigma _{\textrm{c}}\) as can be computed by the inflationary equation of motion. No sizable amount of inflation occurs during the waterfall regime, if

$$\begin{aligned} {\Delta m_{\phi _1}^2}/{H_{\textrm{HI}}^2}\simeq 36{m^2m_{\textrm{P}}^4}/{\kappa ^2 M^6}>1\,\,\Rightarrow \,\,\kappa \lesssim {6mm_{\textrm{P}}^2}/{M^3}, \end{aligned}$$
(3.3)

where \(H_{\textrm{HI}}^2\) is given by Eq. (2.15a). This condition is roughly identical with that obtained in more accurate computations [50, 51] and can be easily met in our scenario – see Sect. 4.

The number of e-foldings \(N_{\star }\) that the pivot scale \(k_{\star }=0.05/\textrm{Mpc}\) experiences during EHI or THI can be calculated through the relation

$$\begin{aligned} N_{\star }= & {} \int _{\widehat{\sigma }_{\textrm{f}}}^{\widehat{\sigma }_*} d{\widehat{\sigma }}\frac{V_{\textrm{HI}}}{V_\mathrm{HI,{\widehat{\sigma }}}}\nonumber \\= & {} \frac{NV_{{\textrm{HI}}0}}{pm^2}\left( \ln \frac{f_{p{\textrm{c}}}}{f_{p\star }} +p\ln \frac{\sigma _{\star }}{\sigma _{\textrm{c}}}+\frac{1}{f_{p\star }}-\frac{1}{f_{p{\textrm{c}}}}\right) , \end{aligned}$$
(3.4)

where \(f_{p\star }=f_p(\sigma _{\star })\) and \(f_{p{\textrm{c}}}=f_p(\sigma _{\textrm{c}})\) with \(\sigma _{\star }~[\widehat{\sigma }_*]\) being the value of \(\sigma ~[{\widehat{\sigma }}]\) when \(k_{\star }\) crosses the inflationary horizon. Taking into account that \(1\simeq \sigma _{\star }\gg \sigma _{\textrm{f}}=\sigma _{\textrm{c}}\), we can find the following approximate version of the exact formula above which can be analytically solved w.r.t \(\sigma _{\star }\) as follows

$$\begin{aligned} N_{\star }\simeq & {} \frac{NV_{{\textrm{HI}}0}}{pm^2}\left( \frac{1}{f_{p\star }}-1-p\ln \sigma _{\textrm{c}}\right) \,\,\Rightarrow \,\,\sigma _{\star }\nonumber \\\simeq & {} \left( 1-\frac{NV_{{\textrm{HI}}0}}{NV_{{\textrm{HI}}0}(1+p\ln \sigma _{\textrm{c}})+N_{\star }pm^2}\right) ^{1/p}. \end{aligned}$$
(3.5)

The elimination of the terms \(p\ln \sigma _{\star }-\ln f_{p\star }\) can be justified by the fact that their contribution to \(N_{\star }\) in Eq. (3.4) is subdominant for the \(\sigma \) values in the range \(0.5\le \sigma _{\star }<1\) encountered in our numerics.

The amplitude \(A_{\textrm{s}}\) of the power spectrum of the curvature perturbations generated by \(\sigma \) at the scale \(k_{\star }\) is estimated as follows

$$\begin{aligned} \sqrt{A_{\textrm{s}}}=\, \frac{1}{2\sqrt{3}\, \pi } \; \frac{V_\textrm{HI}(\widehat{\sigma }_*)^{3/2}}{|V_\mathrm{HI,{\widehat{\sigma }}}(\widehat{\sigma }_*)|}\simeq \frac{\sqrt{N}V_{{\textrm{HI}}0}^{3/2}}{2\sqrt{3}\pi \sigma _{\star }m^2f_{p\star }}\,\cdot \end{aligned}$$
(3.6)

Inserting Eq. (3.5) into the previous equation and expanding the resulting relation in powers of \(N_{\star }\) we can obtain a rough estimation of \(\kappa \) as follows

$$\begin{aligned} \sqrt{A_{\textrm{s}}}\simeq & {} \,\frac{\sqrt{N}V_{{\textrm{HI}}0}^{3/2}}{2\sqrt{3}\pi m^2}\left( 1+\frac{NV_{{\textrm{HI}}0}}{p^2m^2N_{\star }}\right) \,\,\Rightarrow \,\, \kappa \nonumber \\\simeq & {} \left( \frac{2\pi \sqrt{3A_{\textrm{s}}}m^2}{M^6N^{1/2}}\right) ^{1/3}\cdot \end{aligned}$$
(3.7)

We, also, calculate the remaining inflationary observables via the relations

$$\begin{aligned} n_{\textrm{s}}= & {} \, 1-6\epsilon _\star \ +\ 2\eta _\star \simeq 1-\frac{2}{N_{\star }}-\frac{3N}{p^2N_{\star }^2}\nonumber \\{} & {} +\frac{V_{{\textrm{HI}}0}}{m^2N_{\star }^2}\left( {2N\over p^2}+{4N\over p}+N\ln \sigma _{\textrm{c}}^2\right) , \end{aligned}$$
(3.8a)
$$\begin{aligned} \alpha _{\textrm{s}}= & {} \,{2\over 3}\left( 4\eta _\star ^2-(n_\textrm{s}-1)^2\right) -2\xi _\star \simeq -\frac{2}{N_{\star }^2}-\frac{6N}{p^2N_{\star }^3}\nonumber \\{} & {} +\frac{NV_{{\textrm{HI}}0}}{m^2N_{\star }^3}\left( {4\over p^2}+{10\over p}+\ln \sigma _{\textrm{c}}^4\right) , \end{aligned}$$
(3.8b)
$$\begin{aligned} r= & {} 16\epsilon _\star \simeq \frac{8N}{p^2N_{\star }^2}\nonumber \\{} & {} -\frac{16N^2V_{{\textrm{HI}}0}}{p^2m^2N_{\star }^3}\left( {1\over p^2}+{1\over p}+\ln \sigma _{\textrm{c}}\right) , \end{aligned}$$
(3.8c)

where \(\xi ={V_\mathrm{HI,{\widehat{\sigma }}} V_\mathrm{HI,{\widehat{\sigma }}{\widehat{\sigma }}{\widehat{\sigma }}}/V_\textrm{HI}^2}\), the variables with subscript \(\star \) are evaluated at \(\sigma =\sigma _{\star }\) and the approximate expressions are obtained by expanding the exact result in powers of \(1/N_{\star }\). A clear dependence of the observables on the parameters of \(V_{\textrm{HI}}\) in Eq. (2.17) arises which is expected to modify considerably the – dominating at leading order in the expansions above – predictions of the pure E- and T-model inflation [41, 42].

We should, finally, note that the results above can be deliberated from our ignorance about the Planck-scale physics, if we impose two additional theoretical constraints on our models:

(3.9)

As we show below, the first from the inequalities above is easily satisfied in our set-up for \(\kappa \) and M values consistent with Eq. (3.7) – see also Sect. 4. Equation (3.9b) is fulfilled by construction since the K’s in Eq. (2.3) with the parameterizations in Eq. (2.7) induce a kinetic pole for \(\sigma =1\) and so HI takes place for \(\sigma <1\). The introduction of a possible parameter multiplying S in Eq. (2.3) can be absorbed by a reparametrization of the free parameters of the model – see e.g. Refs. [35, 36].

4 Numerical results

The outputs of the analysis above can be refined numerically and employed in order to delineate the available parameter space of the models. In particular, we confront the quantities in Eqs. (3.4) and (3.6) with the observational requirements [4]

(4.1)

In deriving Eq. (4.1a) we assume that HI is followed in turn by a oscillatory phase, with mean equation-of-state parameter \(w_{\textrm{rh}}\simeq 0\), radiation and matter domination. We expect that \(w_{\textrm{rh}}=0\), corresponding to quadratic potential, approximates rather well \(V_{\textrm{HI}}\) for \(\sigma \ll \sigma _{\textrm{c}}\). Motivated by implementations of non-thermal leptogenesis [52, 53], which may follow HI, we set \(T_{{\textrm{rh}}}\simeq 4.1\cdot 10^{-10}\) for the reheat temperature. Also \(g_{{\textrm{rh}}*}=106.75\) is the energy-density effective number of degrees of freedom which corresponds to SM spectrum respectively.

As regards the remaining observables, we take into account the latest data from Planck (release 4) [23], baryon acoustic oscillations, Cosmic Microwave Background (CMB) lensing and BICEP/Keck [24]. Adopting the most updated fitting in Ref. [25] we obtain approximately the following allowed margins

(4.2)

at 95\(\%\) confidence level (c.l.) with \(|\alpha _{\textrm{s}}|\ll 0.01\). The constraint on \(|\alpha _{\textrm{s}}|\) is readily satisfied within the whole parameter space of our models. Enforcing Eq. (4.1a) and (b) we can restrict \(\kappa \) and \(\sigma _{\star }\) and compute the models’ predictions via Eqs. (3.8a), (3.8b) and (3.8c), for any selected N, \(\lambda /\kappa \), m and M – see Eq. (2.10). Note that \({\widetilde{m}}\) is totally irrelevant for the computation and can be fixed at a value (e.g., \({\widetilde{m}}=10m\)) throughout so that \(\widehat{m}_\theta \gg H_{\textrm{HI}}\). With this arrangement, \(\Delta V_{\textrm{HI}}\) in Eq. (2.16) is totally dominated by its second term in the equation above. Given that \(\Lambda \) in Eq. (2.16) can be determined self-consistently as mentioned in Sect. 2.2, \(\Delta V_{\textrm{HI}}\) is calculated using as inputs the free parameters of the tree-level potential in Eq. (2.10). Compared to the original model of HI [8, 9], we here employ one more free parameter, N, related to the non-minimal kinetic terms adopted in Eq. (2.4).

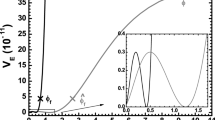
We embark on the presentation of our results by comparatively plotting the variation of \(V_{\textrm{HI}}\) as a function of \(\sigma \) in Fig. 1a and \({\widehat{\sigma }}\) in Fig. 1b for EHI (solid lines) and THI (dashed lines). In both cases we set \(\lambda =\kappa \) and \(M=0.1\) and achieve the central \(n_{\textrm{s}}\) in Eq. (4.2a) by selecting \(m=4.12\cdot 10^{-6}\) [\(m=2.04\cdot 10^{-6}\)] for EHI [THI]. The corresponding values of \(\kappa \), \(N_{\star }\), \(\sigma _{\star }\) and r are listed in the third, fourth, fifth and sixth leftmost column of the Table below the graphs. These results are obtained by our numerical code taking into account exact expressions for \(J, V_{\textrm{HI}}\) and the other observables – i.e., Eqs. (2.9), (2.17), (3.4), and the leftmost equalities in Eqs. (3.8a), (3.8b) and (3.8c). These values can be approximated by those obtained by employing the formulas of Sect. 3 – i.e., Eqs. (3.5), (3.7), and the rightmost equalities in Eqs. (3.8a), (3.8b) and (3.8c). The outputs of this computation are displayed in the five rightmost columns of the Table in Fig. 1. Note that in the case of analytic expressions we prefer to compare \(\sigma _{\star }\) derived by Eq. (3.5) with its numerical value and let m as input parameter. We remark that \(N_{\star }\) is analytically underestimated in both cases. This fact leads to an overestimation of \(\sigma _{\star }\) and \(\kappa \). On the other hand, \(n_{\textrm{s}}\) and r are closer to their numerical values for EHI than for THI. The non-consideration of the second term in Eq. (2.17) in the denominators of Eq. (3.1a) seems to aggravates the error in analytic expressions of THI. Despite their low accuracy, though, the analytical expressions of Sect. 3 assist us in understanding the general behavior of the inflationary dynamics.

In the plots of Fig. 1 we verify the pretty stable mechanism [35,36,37, 45] which establishes EMI and TMI: \(V_{\textrm{HI}}\) expressed in terms of \({\widehat{\sigma }}\) develops a plateau for \({\widehat{\sigma }}\gg 1\) but \(\sigma <1\) – since \({\widehat{\sigma }}\) increases w.r.t \(\sigma \) as inferred from Eq. (2.9). Indeed, the \(\sigma _{\star }\) values depicted in Fig. 1a – and arranged in the Table of Fig. 1 – get enhanced according to Eq. (2.9), i.e., \(\widehat{\sigma }_*=0.99\) [1.66] for EHI [THI] – see Fig. 2b. Contrary to the standard EMI and TMI, though, we here observe that (i) the inflationary path terminates at \(\sigma =\sigma _{\textrm{c}}\) due to the instability in Eq. (2.14) – this is the same for both EHI and THI since M and \(\lambda /\kappa \) are kept fixed in both cases – and (ii) the required \(\sigma _{\star }\) does not lie extremely close to the location of the pole at \(\sigma =1\) and so the relevant tuning of the initial conditions, somehow quantified – cf. Refs. [35,36,37] – by the quantity

$$\begin{aligned} \Delta _{1*}=\left( 1 - \sigma _{\star }\right) , \end{aligned}$$
(4.3)

is less severe here. Namely, we obtain \(\Delta _{1*}=19\%\) [\(\Delta _{1*}=24\%\)] for EHI [THI], whereas \(\Delta _{1*}\le 10\%\) in all the models of chaotic inflation studied in Refs. [35,36,37,38,39]. Also no proximity is needed between \(\sigma _{\star }\) and \(\sigma _{\textrm{c}}\) as in the last paper of Refs. [11,12,13].

Fig. 1
figure 1

Variation of \(V_{\textrm{HI}}\), \(V_{\textrm{HI}}/V_{{\textrm{HI}}0}-1\), as a function of (a) \(\sigma \) for \(\sigma _{\textrm{c}}\le \sigma <1\) and (b) \({\widehat{\sigma }}\) for \({\widehat{\sigma }}(\sigma _{\textrm{c}})\le {\widehat{\sigma }}<{\widehat{\sigma }}(1)\) fixing \(M=0.1\), \(N=1\), \(\lambda =\kappa \) and \(n_{\textrm{s}}=0.965\). We consider EHI (solid lines) or THI (dashed lines). Values corresponding to \(\sigma _{\star }\) and \(\sigma _{\textrm{c}}\) (a) or \(\widehat{\sigma }_*\) and \(\widehat{\sigma }_{\textrm{c}}\) (b) are also depicted. Some of the parameters of our models – derived by employing our numerical and analytic formulae – are displayed in the table

Full size image

Employing data from the two representative cases depicted in Fig. 1, we can analyze further the inflationary mechanism of our models. Namely, (i) the semiclassical approximation, used in our analysis, is perfectly valid avoiding possible corrections from quantum gravity, since \(V_{\textrm{HI}}^{1/4}(\sigma _{\star })=3.3\cdot 10^{-3}\) [\(V_{\textrm{HI}}^{1/4}(\sigma _{\star })=2.9\cdot 10^{-3}\)] for EHI [THI] is less than the ultraviolet cut-off scale, \(m_{\textrm{P}}=1\), of theory – cf. Eq. (3.9); (ii) any possible running of the quantities measured at \(\Lambda \) is negligible, since the scale \(\Lambda \) in Eq. (2.16) is found to be \(\Lambda =1.6\cdot 10^{-3}\) [\(\Lambda =9.5\cdot 10^{-4}\)] for EHI [THI], i.e., quite close to the aforementioned \(V_{\textrm{HI}}^{1/4}(\sigma _{\star })\)’s; (iii) the contribution of \(\Delta V_{\textrm{HI}}\) to \(V_{\textrm{HI}}\) is quite suppressed, since \((\Delta V_{\textrm{HI}}/V_{\textrm{HI}})(\sigma _{\star })=3.6\cdot 10^{-5}\) [\((\Delta V_{\textrm{HI}}/V_{\textrm{HI}})(\sigma _{\star })=10^{-5}\)] for EHI [THI]; (iv) the criterion of Eq. (3.3) is comfortably fulfilled, since \({\Delta m_{\phi _1}^2}/{H_{\textrm{HI}}^2}\simeq 536.5\) [\({\Delta m_{\phi _1}^2}/{H_{\textrm{HI}}^2}\simeq 199.6\)] for EHI [THI] and so no modification of Eq. (4.1a) is necessitated.

A prominent aim of the marriage between E- and T-models and HI is the diminishment of \(n_{\textrm{s}}\) at the acceptable level of Eq. (4.2a). The achievement of this goal is readily demonstrated in Fig. 2 where we display the resulting values of \(n_{\textrm{s}}\) versus m for EHI – see Fig. 2a – and THI– see Fig. 2b – with the constraints of Eq. (4.1) and (4.2b) being fulfilled. We set \(M=0.1\), \(N=1\) and \(\lambda =\kappa \) (solid line), \(\lambda =2\kappa \) (dashed line) and \(\lambda =\kappa /2\) (dot-dashed line). The observational allowed region of Eq. (4.2a) is also limited by thin lines. In both cases m turns out to be of the same order of magnitude (around \(10^{-6}\)) but the allowed region for EHI is wider than that in THI. With fixed M and N, which keep \(\kappa \) roughly unchanged – cf. Eq. (3.7) –, we observe that as m increases (without change order of magnitude) the positive contribution in the approximate part of Eq. (3.8a) decreases together with \(n_{\textrm{s}}\), which enters the observationally favored region of Eq. (4.2a). For even large m values, \(\sigma _{\star }\) in Eq. (3.5) approaches unity – since the second term of the denominator overshadows the first one –, and so Eq. (4.1) ceases to be satisfied and the various lines terminate.

Fig. 2
figure 2

The allowed by Eqs. (4.1) and (4.2b) values of \(n_{\textrm{s}}\) versus m for \(M=0.1\), \(N=1\), several \(\lambda /\kappa \)’s (indicated in the graphs) and (a) EHI or (b) THI. The region of Eq. (4.2a) is also limited by thin lines

Full size image
Fig. 3
figure 3

Allowed curves in the \(m-M\) [\(\kappa -M\)] plane (a and b) [(a\(^\prime \) and b\(^\prime \))] for \(N=1\), \(n_{\textrm{s}}=0.965\) and various \(\lambda /\kappa \)’s indicated in the graphs. We consider EHI (a and a\(^\prime \)) or THI (b and b\(^\prime \)). The allowed ranges of the various parameters for \(\lambda =\kappa \) are listed in the table with units reinstalled

Full size image

Encouraged by the acceptable \(n_{\textrm{s}}\) results above, we proceed to the delineation of the allowed parameter space of our models setting \(N=1\) and \(n_{\textrm{s}}\) equal to its central value in Eq. (4.2a) – possible variation of \(n_{\textrm{s}}\) within its allowed margin yields relatively narrow strips which would be indistinguishable especially in the \(\kappa -M\) plane. We present our findings in Fig. 3 devoting Fig. 3(a) and (a\(^\prime \)) to EHI and Fig. 3(b) and (b\(^\prime \)) to THI. In particular, we display in Fig. 3(a) and (b) the allowed contours in the \(m-M\) plane and in Fig. 3(a\(^\prime \)) and (b\(^\prime \)) the allowed curves in the \(\kappa -M\) plane. The conventions adopted for the various lines are also shown in the right-hand side of each graph. In particular, the solid, dashed and dot-dashed lines correspond to \(\lambda =\kappa \), \(\lambda =2\kappa \) and \(\lambda =\kappa /2\). The various lines terminate at low M (or large \(\kappa \)) values due to the augmentation of the contribution of \(\Delta V_{\textrm{HI}}\) in Eq. (2.16) to \(V_{\textrm{HI}}\) in Eq. (2.17). Indeed, when \(|\Delta V_{\textrm{HI}}/V_{\textrm{HI}}|\) approaches \(8\cdot 10^{-4}\), \(\Delta V_{\textrm{HI}}\) starts influence the predictions of HI. Such a situation is encountered for \(\kappa > rsim 6\cdot 10^{-3}\) [\(\kappa > rsim 3\cdot 10^{-3}\)] in EHI [THI]. On the other side, the almost horizontal part of the various lines stop for large m (low \(\kappa \)) values since \(\sigma _{\star }\) reaches the pole region – see Eq. (3.5) – and the computation related to Eq. (4.1) becomes unstable. At these points we encounter the lowest possible \(\Delta _{1*}\)’s which tend to the ugly amount of \(0.2\%\). For \(\lambda =2\kappa \) the upper bounds of the corresponding lines are obtained for \(M=1\). We adopt this conservative bound which assures meaningful \(\langle {\phi _1} \rangle \) values and comfortable fulfillment of Eq. (3.3).

In the Table of Fig. 3, we accumulate indicatively explicit values of the various parameters (restoring units hereafter) for \(\lambda =\kappa \). From the listed values we notice that the allowed M’s approach mainly the string scale contrary to the SUSY versions of HI where M turns out to be [10,11,12,13] close to the SUSY GUT scale, \(M_\textrm{GUT}\simeq 2.86\cdot 10^{16}~\textrm{GeV}\). This fact, though, neither violates Eq. (3.9a) nor amplifies dangerously \(\Delta V_{\textrm{HI}}\) in Eq. (2.17) since the low enough \(\kappa \) values, which are compatible with Eq. (3.7), keep \(V_{\textrm{HI}}(\sigma _{\star })\) and \(\Delta V_{\textrm{HI}}\) under control. Comparing the data for EHI and THI, we remark that larger m’s and \(\Delta _{1*}\)’s and wider ranges of \(\kappa \) are allowed in EHI whereas both models share similar M’s. For the same inputs of the Table Fig. 3, we can estimate the inflaton mass \(\widehat{m}_{\sigma }\) from Eq. (2.12), with results

$$\begin{aligned} 0.08\lesssim & {} {\widehat{m}_{\sigma }}/{10^{13}~{\textrm{GeV}}}\lesssim 66\quad \hbox {for EHI}; \nonumber \\ 0.27\lesssim & {} {\widehat{m}_{\sigma }}/{10^{13}~{\textrm{GeV}}}\lesssim 44\quad \hbox {for THI}. \end{aligned}$$
(4.4)

These ranges let, in principle, open the possibility of non-thermal leptogenesis [52, 53], if we introduce a suitable coupling between \(\Phi \) and the right-handed neutrinos [29].

Fig. 4
figure 4

Allowed by Eq. (4.1) values of N versus m for \(M=0.1\), \(n_{\textrm{s}}=0.965\) several \(\lambda /\kappa \)’s, indicated in the graphs, and (a) EHI, or (b) THI. Shown is also the variation of r in grey along the lines

Full size image

Varying N beyond unity, we are able to explore another portion of the parameter space of our models as in Fig. 4. We depict there the allowed curves in the \(m-N\) plane for \(M=0.1\), central \(n_{\textrm{s}}\) in Eq. (4.2a) and EHI – see Fig. 4a – or THI – see Fig. 4b. We use the same shape code for the lines as in Fig. 4 with the change that in Fig. 4b the dashed line corresponds to \(\lambda =3\kappa /2\) and not to \(\lambda =2\kappa \) as in all the previous cases. The reason of this replacement is that RCs invalidate almost the whole parameter space of THI for \(\lambda =2\kappa \) and \(N>1\). From our data we see that r increases with N as in the standard EMI and TMI [38, 39, 45] and in agreement with the analytical findings in Eq. (3.8c). The progressive enhancement of r along each line is shown by gray numbers. Note that a segment of the solid and dot-dashed lines in the left graph of Fig. 4 coincide between each other. We display the r’s corresponding to \(\lambda =\kappa /2\) along the common part of these lines. The upper bound on r in Eq. (4.2b) provides an upper bound on N which is related to the geometry of the moduli space via Eq. (2.5). Namely, we find the following maximal N values

$$\begin{aligned} N^\textrm{max}={\left\{ \begin{array}{ll}\begin{matrix} 9.6,&{}13,&{}18\\ 13.1,&{}17.5,&{}33.8\end{matrix}\end{array}\right. }\hbox {for}\,\,\,\lambda /\kappa ={\left\{ \begin{array}{ll}\begin{matrix} 2,&{}1,&{}0.5\,\,\,&{}\hbox {(EHI)}\\ 1.5,&{}1,&{}0.5 \,\,\,&{}\hbox {(THI)} \end{matrix}\end{array}\right. }\!\!. \end{aligned}$$
(4.5)

We observe that the largest \(N^\textrm{max}\) values are obtained for \(\lambda <\kappa \). This can be understood by the observation that \(\ln \sigma _{\textrm{c}}<0\) and dominates the parenthesis in Eq. (3.8c). For \(\lambda <\kappa \), \(|\ln \sigma _{\textrm{c}}|\) is lower than its value for \(\lambda \ge \kappa \) and so, larger N values are needed so as r to reach its bound of Eq. (4.2b). In all, from the data of Fig. 4 we find the following allowed ranges of parameters

$$\begin{aligned} \begin{array}{lllll} 1\lesssim {m/ 10^{13}~{\textrm{GeV}}}\lesssim 10.2,&{}1\lesssim {\kappa }/{10^{-3}}\lesssim 2.8&{}\hbox {and}&{} 1.4\lesssim {\Delta _{1*}/0.1}\lesssim 3.6&{}\hbox {for EHI;}\\ 3.8\lesssim {m/ 10^{12}~{\textrm{GeV}}}\lesssim 84,&{}6.8\lesssim {\kappa }/{10^{-4}}\lesssim 29&{}\hbox {and}&{} 1.8\lesssim {\Delta _{1*}/0.1}\lesssim 3.0&{}\hbox {for THI.}\end{array} \end{aligned}$$
(4.6)

In the ranges above, we obtain \(-6\lesssim \alpha _{\textrm{s}}/10^{-4}\lesssim -1.5\) or \(-2.8\lesssim \alpha _{\textrm{s}}/10^{-4}\lesssim 6\) for EHI or THI respectively. We remark that \(\Delta _{1*}\) increases with N (and r) in both cases.

5 Conclusions

Inspired by the successive data releases on CMB perturbations – which favor the inflationary paradigm – and the negative LHC results regarding SUSY, we focused on the well-known model of non-SUSY HI (i.e. hybrid inflation) [8, 9] attempting to reconcile it with data. Our proposal is based on the non-SUSY potential in Eq. (2.10) and the non-minimal kinetic terms of the inflaton sector with a pole of order \(p=1\) or 2 – see Eqs. (2.1) and (2.4). These terms emerge thanks to the adoption of the logarithmic Kähler potentials in Eq. (2.3) which parameterize hyperbolic moduli manifolds. Therefore, our models although non-SUSY inherit the Kählerian type of moduli geometry from the SUSY context. This assumption restricts considerably the allowed p values as shown in Appendix A. The resulting models are called EHI (for \(p=1\)) and THI (for \(p=2\)) due to the function which relates the initial and the canonically normalized inflaton – see Eq. (2.9).

Selecting the gauge group broken after the end of HI and the representation of the waterfall field we succeeded to evade the formation of any topological defects. We also included the minimal possible one-loop RCs (i.e., radiative corrections) to the inflationary potential and restricted ourselves to the portion of the parameter space where the waterfall regime occurs suddenly. We found ample and natural space of parameters compatible with all the imposed restrictions. E.g., for \(N=1\), \(\lambda =\kappa \) and the observationally central value of \(n_{\textrm{s}}\), we find the allowed ranges shown in the Table of Fig. 3. Increasing N beyond unity, for the same \(n_{\textrm{s}}\) and \(\lambda /\kappa \) values, we verify an enhancement on the r values which reaches its maximal allowed value for \(N=13\) or \(N=17.5\) within EHI or THI, respectively. It is gratifying that no extensive proximity between the values of the inflaton field at the horizon crossing of the pivot scale and the location of the pole is needed – see the \(\Delta _{1*}\) values in the aforementioned Table which increase with N. Therefore, EHI and THI can be characterized as more natural than the original E- and T-model inflation as regards this tuning. On the other hand, EHI and THI are less predictive due to the more parameters which let corridors for larger variation of the inflationary observables. It is also remarkable that the one-loop RCs in Eq. (2.16) do not affect the inflationary solutions for low enough values of the relevant coupling constants \(\kappa \) and \(\lambda \) – see Fig. 3.

Comparing our work with that of Ref. [40], we may remark the following differences-novelties here: (i) We motivated EHI and THI as non-linear sigma models; (ii) we overcome the problem of the topological defect through the consideration of a specific representation of the waterfall field; (iii) we explored not only THI but also EHI; (iv) we considered flat geometry for the waterfall field; (v) we included the minimal one-loop RCs to the inflationary potential; (vi) we delineated the parameter space of the models avoiding any subcritical production of e-foldings. On the other hand, we did not embed our models in SUGRA as done in Ref. [40]. The standard mechanism [54] of embedding is not so effective for HI since the stabilization of the waterfall fields at the origin does not reproduce the non-SUSY potential and a rather different situation may emerge. Moreover, the R symmetry preserved by the superpotential [10] restricts further the possible forms of K, if it is imposed also to it. Modification of the present model in order to generate gravitational waves compatible with the NANOGrav reported signal [19, 20], via a late production of cosmic strings [17, 18] or via a subcritical stage of fast-roll inflation [22] could be another interesting target for future analysis.