Constraints on light leptophilic dark matter mediators from decay experiments

Abstract

We study the influence of leptophilic dark matter interactions on decays of muons and ground state mesons in existing experiments. We consider a secluded dark sector exclusively interacting with leptons via either a (leptophilic) scalar or vector mediator. These interactions will therefore influence leptonic decays and deform the energy spectra. We first study the Michel decay of muons, $\mu ^+\rightarrow e^+\nu _e \bar{\nu }_\mu$, which allow us to constrain the parameter space reasonably well. Secondly, the rare $\pi ^\pm$, $K^\pm$, $D^\pm$ and $D_s^\pm$ decays to $e\nu$ will be considered. Scalar mediators would remove the Standard Model helicity suppression, so that strong constraints can be derived. The resulting bounds on the couplings of the light mediators to electrons and muons still turn out to be somewhat weaker than those from searches at low-energy $e^+e^-$ colliders and the magnetic moment of the muon, respectively. Finally, we show that kaon and pion decays basically exclude a “Co-SIMP” scenario where a scalar dark matter particle has a dimension-5 coupling to electrons.

1 Introduction

Evidence for the existence of substantial non-baryonic mass in the universe, in addition to the baryonic contribution from the known Standard Model (SM) particles, has been piling up for decades [1]. Cosmological observations, from the CMB at the largest scales, the structure of galaxy clusters and gravitational lensing on intermediate scales, down to the rotation of single galaxies, all essentially only probe the gravitational interactions of this dark matter (DM), leaving the properties of the constituents of DM largely obscure. We do know that DM should be “cold”, i.e. non-relativistic well before the CMB decoupled. Moreover, within the minimal cosmological framework, the overall DM density can be determined accurately, $\Omega _\textrm{DM} h^2 =0.120\pm 0.001$ [2]; here $\Omega _\textrm{DM}$ is the scaled DM mass density and h is the rescaled Hubble parameter.

In the absence of data pinning down the properties of DM, a wide range of models has been proposed. In spite of intensive efforts no clear signal for DM particles has yet been found in either direct or indirect detection experiments [1], leading to severe constraints on many models [3]. This is true in particular for models with weakly interacting massive particles (WIMPs), with masses very roughly at the weak scale. This has led to increased interest in sub-GeV masses [4], which for purely kinematic reasons are much less constrained.

Here we consider models that couple the potential dark sector to the Standard Model with light leptophilic mediators, i.e. mediators that couple directly only to leptons. One class of models assumes a gauged lepton-family number; after spontaneous symmetry breaking these models contain a massive vector mediator, sometimes called a “dark photon”, that couples to some leptons of the Standard Model and in the dark sector to Dirac dark matter [5, 6]. This lepton coupling introduces a kinetic mixing term with the ordinary photon, resulting in a small coupling between the dark photon and all electrically charged particles which can also be used to constrain the model. Another class of models assumes a scalar mediator, which again only couples directly to some or all charged leptons. Since this breaks the SU(2) gauge symmetry, models of this kind can at most be an effective theory. Finally, we consider the so-called “Co-SIMP” model [7] containing a light scalar DM particle with a non-renormalizable coupling to electrons.

We present a novel approach to constraining the parameter space using measurements of the decays of muons or ground-state flavored mesons into final states containing an electron. The spectrum of electrons produced in muon decays has been measured accurately; it agrees with SM predictions, which allows us to put upper bounds on the coupling of spin-1 mediators to electrons or muons. However, the resulting bounds turn out to be more than one order of magnitude weaker than the best constraint from $e^+e^-$ colliders. New spin-0 particles coupling to electrons would remove the helicity suppression in charged meson decays into $e \nu _e$ final states; the resulting bounds on the renormalizable couplings of light scalar mediators are tighter than those from muon decay, but still somewhat weaker than those from $e^+e^-$ colliders. However, bounds from pion and kaon decays suffice to exclude a thermal “Co-SIMP” for masses below 0.8 MeV; in the allowed mass range $\chi$ does not behave like a SIMP any more.

The remainder of this article is structured as follows: in Sect. 2 we present the leptophilic models considered here. In Sects. 3 and 4 we describe the method of obtaining limits on the parameter space from the Michel decays of muons and pseudoscalar meson decays respectively. Section 5 presents our results and compares them to existing bounds. Section 6 finishes with some concluding remarks.

2 Models

The strongest bound on many DM models comes from “direct” search experiments, which look for elastic scattering of ambient DM particles off the nuclei in a detector [1]. Leptophilic dark matter models, where the dark matter particles primarily couple to the Standard Model leptons, either directly or via another “mediator” particle, avoid most of these bounds. In such models the DM particles can interact with nucleons only via loop diagrams.

One way of incorporating these ideas is a hidden sector that contains only singlets under the Standard Model gauge group. However, the simplest (thermal) DM production mechanism requires some coupling to SM particles. To this end one may introduce additional fields which mediate interactions between both sectors. These are then fittingly called portals.

2.1 Vector mediator

The extension of the Standard Model by a new vector boson is well motivated both from a bottom up as well as from a top down perspective, e.g. from grand unified theories [8]. Here we consider scenarios where the gauge group is extended by another $U(1)_D$ gauge group which is spontaneously broken such that the associated particles become massive. The new vector boson $A'$ is often called a dark photon. By assumption the Dark Matter particles $\chi$ are charged under $U(1)_D$. In this article we are concerned with the production of a light $A'$ which decays invisibly. The exact nature of $\chi$ therefore is not relevant for us. Assuming it to be a Dirac fermion for simplicity’s sake, the resulting Lagrangian can the be written as

(1)

Here $F_{\mu \nu }$ and $F'_{\mu \nu }$ are the field strength tensors of QED and of $U(1)_D$, respectively. The new coupling constants $g_D$ and $e_l'$ are free parameters of the model, and the term $\propto \epsilon$ describes kinetic mixing between the new gauge boson and the photon. In order to avoid anomalies, one may chose to gauge any combination $X=yB-\sum x_iL_i$ of baryon number B and lepton family number $L_i$, with constraint $3y=x_e+x_\mu +x_\tau$ [9]. Popular choices include gauged $B-L$ or $L_\mu -L_\tau$ [10, 11]. While the former is highly constrained by direct collider searches and other 5th force experiments, the latter still exhibits rather weak constraints with a region that is even favored by the $g_\mu -2$ anomaly [12,13,14].

Fig. 1

Kinetic mixing of $A'$ with the SM photon

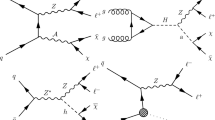
The term proportional to $\epsilon$ has been added to work with the most general renormalizable gauge invariant Lagrangian. Even though this term might be absent at tree level, as is the case for some GUT theories, it can be generated by loop contributions such as the diagram shown in Fig. 1, where the fermion running in the loop is charged both under the Standard Model and dark U(1)-group. In the case at hand this leads to

$$\begin{aligned} \epsilon =\sum _l \frac{ee_l'}{12\pi ^2}\ln \left( \frac{m_l^2}{\mu ^2}\right) \end{aligned}$$

(2)

where the dependence on the renormalization scale $\mu$ cancels in the sum. The term $\propto \epsilon$ in Eq. (1) leads to additional effective interactions of the form

$$\begin{aligned} \mathcal {L}\supset e\epsilon A'_\mu J_\textrm{em}^\mu \,, \end{aligned}$$

(3)

where $J_\textrm{em}^\mu = \sum _\psi Q_\psi \bar{\psi }\gamma ^\mu \psi$ is the electromagnetic current; hence every electrically charged particle interacts with the dark photon as it is now millicharged under $U(1)_D$ [15]. This can be used to put strong constraints on the parameter space.

If $m_{A'}<2m_\chi$ the new gauge boson will mostly decay to the leptons to which it couples directly:

$$\begin{aligned} \Gamma (A' \rightarrow l \bar{l}) = \frac{e_l^{'2}}{12\pi } d_l m_{A'}\left( 1+\frac{2m_l^2}{m_{A'}^2}\right) \sqrt{1-\frac{4m_l^2}{m_{A'}^2}}\,, \end{aligned}$$

(4)

where $d_l = 1$ for charged leptons while $d_l = 1/2$ for left-handed neutrinos. If $m_{A'} > 2 m_{l^\pm }$ one may search for visible $A' \rightarrow l^+l^-$ decays. Here we are instead interested in scenarios with mostly invisible $A'$ decays, either because $m_{A'} < 2 m_{l^\pm }$ for the relevant charged lepton, or because $m_{A'}>2m_\chi$ and $g_D \gg e'_l$. $A' \rightarrow \chi \bar{\chi }$ decays are also described by Eq. (4), with the obvious replacements $e_l \rightarrow g_D, \ m_l \rightarrow m_\chi$ and $d_l \rightarrow 1$.

Within a given cosmological scenario the $\chi$ relic density imposes one constraint on the parameters of the model [4, 14]; even the case $e'_l = 0$, in which case $A'$ couples to SM particles only via Eq. (3), can lead to the correct relic density in minimal cosmology [16]. Here we implicitly assume that this constraint is used to determine the DM mass $m_\chi$, which allows us to vary the mass and couplings of $A'$ freely.

Additional motivation for direct interactions with the muon specifically come from the anomalous magnetic moment of the muon, $a_\mu = (g-2)_\mu /2$. The Standard Model prediction [17] differs from the experimental result [18]: $\Delta a_\mu = a_\mu (\text {Exp}) - a_\mu (\text {SM})= (251\pm 59) \times 10^{-11}$. The additional 1-loop contribution from a vector boson coupling to muons is [19, 20]:

$$\begin{aligned} \Delta a_\mu ^{A'}= \frac{e_\mu '^2}{4\pi ^2} \int _0^1 d z \frac{m_\mu ^2z(1-z)^2}{m_\mu ^2(1-z)^2+m_{A'}^2z}\,. \end{aligned}$$

(5)

For $m_{A'}\ll m_\mu$ this simplifies to

$$\begin{aligned} \Delta a_\mu ^{A'} \approx \frac{e_\mu '^2}{8 \pi ^2} \approx 1.3\times 10^{-10}\left( \frac{e_\mu '}{10^{-4}}\right) ^2\,. \end{aligned}$$

(6)

2.2 Scalar mediator

Another possibility is that a scalar particle mediates interactions between the dark matter and the SM particles. Here we consider a real scalar field $\phi$ with mass $m_\phi$ that is a singlet under the Standard Model gauge group, and again a dark matter Dirac fermion $\chi$. The Lagrangian is:

(7)

This Lagrangian respects QED gauge invariance, but the interactions of the scalar with the leptons break electroweak gauge invariance explicitly. These couplings might originate from gauge invariant (but non-renormalizable) dimension 5 operators [21]:

$$\begin{aligned} \frac{c_l}{\Lambda }\phi \bar{L}_i\Phi e_{iR}+h.c. \,, \end{aligned}$$

(8)

where $\Phi$ is the Standard Model Higgs field. Once $\Phi$ obtains a vacuum expectation value v, the interactions in (8) lead to the scalar couplings in Eq. (7), with

$$\begin{aligned} e'_l=\frac{c_l v}{\Lambda \sqrt{2}}\,. \end{aligned}$$

(9)

Another possibility is to have the light scalar $\phi$ mix with the neutral component of a (second) scalar doublet, which can in principle have renormalizable $\mathcal{O}(1)$ couplings to leptons.¹ Most lepton-specific scalar mediator models considered in the literature assume the effective scalar couplings $c_l$ to be proportional to the charged lepton masses, in which case the $e'_l$ follow the lepton mass hierarchy.

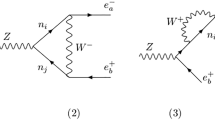
A nonvanishing $e'_l$ leads at 1-loop to an effective coupling of the scalar to two photons, through the diagram shown in Fig. 2. If $m_\phi < 2 m_l$, this decay can be used to search for $\phi$ in the diphoton invariant mass distribution. The decay width to photons is² [24]

$$\begin{aligned} \Gamma (\phi \rightarrow \gamma \gamma )= \frac{\alpha ^2m_\phi ^3}{256\pi ^3} \left|\sum _{l=e,\mu ,\tau } \frac{e'_l}{m_l}F_{1/2}(x_l) \right|^2\,, \end{aligned}$$

(10)

where $x_l = \frac{4m_l^2}{m_\phi ^2}$ and the loop function $F_{1/2}$ reads

$$\begin{aligned} F_{1/2}(x_l)= {\left\{ \begin{array}{ll} -2x_l\left[ 1+(1-x_l)\arcsin ^2(x_l^{-1/2})\right] &{}x_l \ge 1 \\ -2x_l\left[ 1-\frac{1-x_l}{4}\left( -i\pi +\log \frac{1+\sqrt{1-x_l}}{1-\sqrt{1-x_l}}\right) ^2\right] &{}x_l<1 \end{array}\right. } \,. \end{aligned}$$

(11)

For $x_l \gg 1$, the loop function $F_{1/2} \rightarrow -4/3$.

Fig. 2

One loop contribution to the $\phi$-photon coupling

For $g_D > e_l'$ and $2m_\chi < m_\phi$ the scalar mediator decays mostly invisibly to the dark sector. The corresponding decay width is

$$\begin{aligned} \Gamma (\phi \rightarrow \bar{\chi }\chi ) = g_D^2\frac{m_\phi }{8\pi } \left( 1-\frac{4m_\chi ^2}{m_\phi }\right) ^{3/2} \,. \end{aligned}$$

(12)

The main avenue for collider experiments to constrain this model is then missing energy searches. On the other hand, for $2m_\chi> m_\phi > 2 m_l$ the mediator decays mostly visibly to leptons it directly couples to, with decay width

$$\begin{aligned} \Gamma (\phi \rightarrow \bar{l}l)=e_l'^2\frac{m_\phi }{8\pi } \left( 1-\frac{4m_l^2}{m_\phi }\right) ^{3/2}\,. \end{aligned}$$

(13)

We’ll be interested in scenarios where $|e'_l|\gtrsim 10^{-3}$ for $l = e$ or $\mu$. The decay width (13) then corresponds to a lifetime $\tau _\phi \lesssim 1.5\cdot 10^{-14} (1 \ \textrm{MeV}) / m_\phi$ seconds; even accounting for a Lorentz boost, $\phi \rightarrow l^+ l^-$ decays will then usually be “prompt” if the corresponding decay is kinematically allowed.

A light scalar coupling to muons can also explain the $(g-2)_\mu$ results. Its contribution is given by [19, 24]:

$$\begin{aligned} \Delta a_\mu ^\phi = \frac{e_\mu '^2}{8\pi ^2} \int _0^1 d z \frac{m_\mu ^2(1+z)(1-z)^2}{m_\mu ^2(1-z)^2+m_{\phi }^2z}\,. \end{aligned}$$

(14)

For $m_\phi ^2\ll m_\mu ^2$ this simplifies to

$$\begin{aligned} \Delta a_\mu ^\phi \approx \frac{3e_\mu '^2}{16 \pi ^2} \approx 1.9\times 10^{-10}\left( \frac{e_\mu '}{10^{-4}}\right) ^2 . \end{aligned}$$

(15)

2.3 Co-SIMP

Finally, we consider the Co-SIMP mechanism proposed by Smirnov et al. [7]. A real scalar particle $\chi$ with strong self-interactions is assumed as dark matter. An interaction with the Standard Model of the form $\chi \chi e \rightarrow \chi e$ is introduced in order to dissipate entropy from the dark sector whilst a $Z_3$ symmetry stabilizes $\chi$ (Fig. 3).

Fig. 3

Effective operator of the Co-SIMP model we consider

We consider an electrophilic version of this model, in which case the relevant interaction is described by the effective operator

$$\begin{aligned} \mathcal {O}_e = \bar{e}e \frac{\chi ^3}{\Lambda ^2}\,. \end{aligned}$$

(16)

Once again this does not respect the electroweak gauge symmetry; as before gauge invariance can be restored by replacing the dim-5 operator of Eq. (16) by a dim-6 operator $\propto \bar{e} \Phi e \chi ^3 + h.c.$. Observation of cosmological structures imply $m_\chi \gtrsim 5$ keV, while $m_\chi \lesssim m_e$ is required in order to avoid a WIMP-like freeze-out [7]. Note that this model does not contain additional free parameters that allow to tune the relic density independent of the laboratory limits which are the main topic of this work. In order to compute the cosmologically preferred value of $\Lambda$ we therefore solve numerically the Boltzmann equation describing the freeze-out of $\chi$ [7]:

$$\begin{aligned} sH(T) x \frac{dY_\chi }{dx} = -s^3 \langle \sigma _{32} v^2\rangle \left( Y_\chi ^2-Y_\chi Y_\chi ^\textrm{eq}\right) Y_e^\textrm{eq}\,. \end{aligned}$$

(17)

Here $x = m_\chi /T$, T being the temperature, s is the total entropy density, and $Y_\psi = n_\psi /s$ where $n_\psi$ is the number density of $\psi$ particles, with $\psi \in \{\chi , e\}$ in our case; the superscript $\textrm{eq}$ denotes the equilibrium value of the corresponding quantity. The thermally averaged cross section [25] is also obtained numerically from the integral

$$\begin{aligned} \langle \sigma _{32} v^2\rangle= & {} \frac{1}{2n^\textrm{eq}_e n^\textrm{eq}_\chi n^\textrm{eq}_\chi } \int \prod _{i=1}^5\frac{g_i d^3p_i}{(2\pi )^3 2E_i}(2\pi )^4 \nonumber \\{} & {} \cdot \delta ^4(p_1+p_2+p_3-p_4-p_5)f_1f_2f_3\overline{|\mathcal {M} |^2} .\nonumber \\ \end{aligned}$$

(18)

Here $g_i$ denotes the number of internal degrees of freedom of particle i (1 for $\chi$ and 4 for e), $f_i = 1 / (\exp {E_i/T}\pm 1)$ is the phase space distribution function for the i-th particle in the initial state, and $\overline{|\mathcal {M} |^2}$ is the averaged squared matrix element for the relevant process $\chi +\chi +e \rightarrow \chi + e$.

3 Bounds from $\mu ^-$ decays

Having introduced the models we will consider, we turn to a discussion of the decays which we use to derive bounds on the parameters of these models. We begin with a discussion of the muon decay spectrum. Since this has widely been used as a high precision test of the electroweak theory [26], it might provide a good chance to constrain our models. The double differential width for $\mu ^- \rightarrow e^- \nu _\mu \bar{\nu }_e$ decays at rest can be written as [1]:

$$\begin{aligned} \frac{d^2\Gamma }{dxd\cos \theta }= & {} \frac{m_\mu }{2\pi ^3} W_{e\mu }^4 G_F^2 \sqrt{x^2-x_0^2} \nonumber \\ {}{} & {} \cdot \left[ F_{\text {IS}}(x) -P_\mu \cos \theta F_{\text {AS}}(x)\right] . \end{aligned}$$

(19)

Here $W_{e\mu } = (m_\mu ^2+m_e^2)/2m_\mu$ is the maximum electron energy (neglecting possible neutrino masses), $x = E_e / W_{e\mu }$ is the rescaled electron energy, $x_0 = m_e/W_{e\mu }$ is its minimum value, $P_\mu$ is the degree of muon polarization and $\theta$ is the angle between the polarization vector of the muon and the outgoing electron. The functions for the isotropic part $F_\text {IS}(x)$ and the anisotropic part $F_\text {AS}(x)$ are given by [1]:

$$\begin{aligned} F_\text {IS}= & {} x(1-x) + \frac{2}{9} \rho (4x^2-3x-x_0^2) \nonumber \\{} & {} + \eta x_0(1-x) ; \nonumber \\ F_\text {AS}= & {} \frac{1}{3} \xi \sqrt{x^2-x_0^2}\nonumber \\ {}{} & {} \cdot \left[ 1 - x + \frac{2}{3} \delta \left( 4x - 4 + \sqrt{1-x_0^2} \right) \right] . \end{aligned}$$

(20)

Here the Michel parameters $\rho ,\eta ,\xi$ and $\delta$ have Standard Model values 3/4, 0, 1 and 3/4 respectively. Measurements of these parameters have been used to put constraints on the effective parameters of additional four fermions interactions. Here we use precise measurements of the muon decay spectrum to put constraints on four-body decays $\mu ^- \rightarrow e^- \nu _\mu \bar{\nu }_e X$ where X is a light leptophilic mediator. The contributing Feynman diagrams for the case of a vector mediator coupling to electron number are shown in Fig. 4. We assume that X is either long lived or decays invisibly, so that the four-body final state has the same basic signature as the three-body final state. However, the observable electron spectrum of this four-body mode differs from the spectrum predicted by the SM.

The obvious Standard Model background is the radiative muon decay, $\mu ^- \rightarrow e^- \gamma \nu _\mu \bar{\nu }_e$, where the photon escapes detection but nevertheless carries some energy, thereby also altering the electron spectrum.

Fig. 4

Diagrams contributing to $\mu ^- \rightarrow e^- A' \nu _\mu \bar{\nu }_e$ decays for the case that $A'$ couples to electron number

Since our signal involves a four particle final state, this case cannot be mapped directly onto Eqs. (19) and (20). However, when the dark mediator remains invisible the observable final state has the same topology as in the SM, i.e. the combination

$$\begin{aligned} \frac{d\Gamma (\mu \rightarrow e^- \bar{\nu _e} \nu _\mu )}{dx d\cos \theta } + e_l'^2 \frac{d\Gamma (\mu \rightarrow e^- \bar{\nu _e} \nu _\mu X)}{dx d\cos \theta }\big |_{e_l'=1} \end{aligned}$$

(21)

will be observed. In order to derive estimates of possible constraints we studied the sensitivity of fitting procedures similar to those employed in the experimental determination of the spectral parameters.

The four body matrix elements were derived with help of the !Mathematica! package !FeynCalc! [27] followed by the numerical integration over all kinematic parameters except x and $\cos \theta$. The resulting two dimensional distribution is then added to the pure Standard Model spectrum. The Michel parameters that best describe this new distribution were extracted from Eqs. (19) and (20) by means of a $\chi ^2$ fit, using the same binning as in Ref. [26]. This serves as a filter that condenses the spectrum to the parameters that have been measured. More exactly, we minimized

$$\begin{aligned} \chi ^2 = \sum _i \frac{\left[ \Gamma _i(\textrm{Michel}) - \Gamma _i(Z') \right] ^2}{\Gamma _i(Z')} \,. \end{aligned}$$

(22)

Here $\Gamma _i$ is the muon decay width in the $i-$th bin; $\Gamma _i(\textrm{Michel})$ is computed from Eqs. (19) and (20) and depends on the values of the Michel parameters, while $\Gamma _i(Z')$ is computed from Eq. (21) and depends on the mass and coupling of the new $Z'$ boson. Our final estimate for the sensitivity of these measurements to the new coupling is obtained by comparing these fitted Michel parameters to the measured values [1]:

$$\begin{aligned}&\rho = 0.74979 \pm 0.00026 ; \quad \eta = 0.057 \pm 0.034; \ \ \\&\delta = 0.75047 \pm 0.00034 ; \quad \vert P_\mu \xi \vert = 1.0009^{+0.0016}_{-0.0007}. \end{aligned}$$

Whenever a best-fit Michel parameter deviates further than 1.645$\sigma$ from the experimental one, the parameter point is rejected at more than 95% C.L. This conservative approach is taken to justify the simplistic modeling of the experimental setup. We assume muon polarization $P_\mu = 1$, as predicted by the SM for the relevant case of muons produced in meson decays.

A technical subtlety arises because experiments do not fit to the whole spectrum: cuts have to be applied in order to cover detector inefficiencies and blind spots. We modeled the effects of these cuts by restricting our kinematical fit to the fiducial region covered by the TWIST detector [26]: approximately $x \in [0.45, 0.98]$ and $|\cos \theta |\in [0.54,0.96]$. We found that these cuts affect the sensitivity limit on the coupling only by an $\mathcal {O}(1)$ factor, for the mediator masses considered here. Our sensitivity limits should not be confused with experimental bounds; we did not use real data, nor did we include QED corrections when modeling the SM prediction for the decay spectrum. Our procedure should nevertheless give a reasonable estimate of the sensitivity of the measurements of muon decays to the new mediators.

We finally note that the measurement of the muon lifetime cannot be used directly to constrain our models. In the SM this measurement is used to determine the experimental value of $G_F$, which is a free parameter of the theory. A deviation from the SM could therefore only be detected by comparing this measurement with a second, independent determination of $G_F$. Assuming unitarity of the quark mixing (CKM) matrix, the experimental “CKM unitarity test” can be recast as a measurement of $G_F$ – with, however, much poorer precision [1]. Moreover, the emission of collinear mediators can give rise to $\ln (m_\mu / m_X)$ enhanced terms in the decay distribution, which cancel in the total muon decay width by the Kinoshita–Lee–Nauenberg (KLN) theorem [28, 29] once loop diagrams are included. We therefore expect that a comparison of different measurements of $G_F$ has much poorer sensitivity to the light mediators we consider than the measurement of the muon decay spectrum discussed above.

4 Bounds from leptonic decays of charged pseudoscalar mesons

At tree level the total width for the decay of a charged pseudoscalar meson $P^\pm$ to a lepton pair is given by [30]

$$\begin{aligned} \Gamma (P^- \rightarrow l^-\bar{\nu }_l)= & {} \frac{G_F^2 |V_{q_1q_2}|^2}{4\pi } F_P^2 m_P m_l^2 \nonumber \\{} & {} \cdot \left( 1-\frac{m_l^2}{m_P^2}\right) ^2. \end{aligned}$$

(23)

Here $G_F$ is the Fermi constant, $m_P$ and $m_l$ are the meson and lepton mass, respectively, $F_P$ is the P decay constant, and $V_{q_1q_2}$ is a CKM matrix element, $P^+$ being a $(q_1 \bar{q}_2)$ bound state. Owing to the $V-A$ nature of charged current weak interactions, both the charged lepton and the neutrino “like” to be left-handed, which however is forbidden by angular momentum conservation. This leads to the well known helicity suppression represented by the factor $m_l^2$ in Eq. (23). Evidently this factor strongly suppresses the decay to an electron and neutrino. This is often exploited for tests of lepton universality in the ratio of decays to electrons and muons. The SM prediction for the ratio of decay widths is

$$\begin{aligned} R_P^\textrm{SM}\equiv & {} \frac{\Gamma (P\rightarrow e\nu (\gamma ))}{\Gamma (P\rightarrow \mu \nu (\gamma ))} \nonumber \\= & {} \left( \frac{m_e}{m_\mu }\right) ^2 \left( \frac{m_P^2-m_e^2}{m_P^2-m_\mu ^2}\right) ^2 (1+\delta R_\textrm{QED}), \end{aligned}$$

(24)

where $\delta R_\textrm{QED}$ describes the effect of QED corrections, including real photon emission. It is important to note that the emission of a spin-1 boson does not change the helicity structure of the amplitude, and therefore does not lift the helicity suppression. In contrast, if a scalar or pseudoscalar particle couples to the electron, the helicity suppression is removed, which can enhance the electronic decay mode significantly. Since measurements are in agreement with the SM prediction (24), this lifting of the helicity suppression can be used to derive bounds on the couplings of new light spin-0 particles.

In the limit of vanishing electron and neutrino masses, the total width for $P \rightarrow e \nu _e \phi$ decays can easily be computed analytically:³

$$\begin{aligned} \Gamma (P \rightarrow e \nu _e \phi )= & {} \frac{e_e'^2 G_F^2 F_P^2 \vert V_{q_1q_2}\vert ^2 m_P^3}{384\pi ^3}\nonumber \\{} & {} \cdot \left[ 1 - \left( \frac{m_\phi }{m_P}\right) ^6 + \left( \frac{m_\phi }{m_P}\right) ^2\left( 9+6\ln \left( \frac{m_\phi ^2}{m_P^2} \right) \right) \right. \nonumber \\{} & {} \left. -\left( \frac{m_\phi }{m_P}\right) ^4 \left( 9 - 6\ln \left( \frac{m_\phi ^2}{m_P^2}\right) \right) \right] . \end{aligned}$$

(25)

This expression manifestly avoids the $m_e^2$ suppression. In the Co-SIMP model one instead has to emit three scalar $\chi$ particles, leading to a considerably more complicated phase space integral; however, since the new vertex again violates chirality, also in this case the helicity suppression is lifted.

To obtain the decay width numerically the phase space integral is carried out using the Monte Carlo integration routines provided by the GNU Scientific Library.

Whenever the new scalars remain invisible the event will have the same topology as a rare decay into $e+\nu _e$, albeit with a softer electron energy spectrum. This change of the electron spectrum can reduce the sensitivity due to kinematic cuts employed by the experiments. Bounds are then extracted by saturating the maximal allowed difference $\Delta _P$ between the theory prediction $R_p^\textrm{SM}$ and the experimental result $R_p^\textrm{exp}$, i.e.

$$\begin{aligned} \Delta _P\ge \frac{\epsilon \Gamma (e^+\nu _e+ X)}{\Gamma (\mu \nu _\mu (\gamma ))} . \end{aligned}$$

(26)

Here X stands for either a single spin-0 mediator $\phi$ or for the three Co-SIMP scalars $\chi$, and $\epsilon$ is an acceptance correction factor due to the softer electron spectrum. For the most precise measurement of $R_\pi$, by the PIENU Collaboration [34], this factor is computed as follows. This experiment analyses decays of a stopped $\pi ^+$ beam. In order to discriminate between direct $\pi ^+ \rightarrow e^+$ decays and the dominant background from $\pi ^+ \rightarrow \mu ^+ \rightarrow e^+$, an energy cut $E_e \ge {52}\,{\hbox {Me\,V}}$ was used in the experimental definition of $\pi ^+ \rightarrow e^+ \nu _e$ decays, which have a nominal positron energy of $E_e= {69.8}\,{\hbox {Me\,V}}$. If we want to apply this analysis to our $\pi ^+ \rightarrow e^+ \nu \phi$ decay, the same cut on the positron energy should be applied. $10^5$ Monte Carlo pion decays were generated using MadGraph5_aMC@NLO 3.2.0 [35]. The acceptance is then approximated by the efficiency after selecting events with $E_e \ge {52}\,{\hbox {Me\,V}}$ (i.e. the fraction of events passing the cut). The resulting acceptance correction is shown in Fig. 5.

Fig. 5

Acceptance correction for $\pi ^+ \rightarrow e^+ \nu _e \phi$ and $\pi ^+ \rightarrow e^+\nu _e \chi \chi \chi$ decays due to the cut on $E_e$ by the PIENU experiment

For the Co-SIMP model the acceptance is approximately constant in the allowed mass range, with $\epsilon \approx 11\%$. This limitation does not apply to $K^\pm$, $D^\pm$ and $D_s^\pm$ decays, which are studied in flight, so that even the two-body decay mode has a broad energy spectrum. The most precise measurement of $R_K$ comes from the NA62 Collaboration [36]. Here a Kaon beam decays in flight inside the detector. Since the accepted range of electron energies has a width of several ${10}\,\hbox {Ge\,V}$ we simply assume that all decay modes have the same acceptance.

The decay of $D^\pm$ or $D_s^\pm$ mesons to $e \nu$ has not yet been observed, but 90% c.l. upper bounds on the corresponding branching fractions have been set by the CLEO and Belle Collaboration respectively [37, 38]. We use these to derive limits on the couplings of our light spin-0 mediators.

5 Results

Here we show our estimated sensitivity to the new coupling as function of the mass of the postulated new boson, derived from muon and charged meson decays. We also show existing limits found in the literature, where we focus on the strongest bounds for the case at hand.

The relevant current bounds come from:

• BaBar: Dedicated search for the dark photon in $e^+ e^- \rightarrow \gamma A'; A' \rightarrow \text {invisible}$ with CM energies near the $\Upsilon$ resonances. 90% c.l. limits were derived on the dark photon coupling constant $\varepsilon ^2$ for $m_{A'}\le {8}\,\hbox {Ge\,V}$ [39]. This can directly be applied to our model with a vector mediator, with the replacement $e'_e = e \varepsilon$ [6].

• CCFR: Measurement of neutrino trident production events $\nu N \rightarrow \nu N \mu ^- \mu ^+$ using a muon-neutrino beam with average energy $\langle E_\nu \rangle = {160}\,\hbox {Ge\,V}$. The observed $N_\text {CCFR}= 37.0 \pm 12.4$ events agree with the Standard Model prediction $N_\text {SM}=45.3 \pm 2.3$ [40]. This is used to set limits on additional contributions from a vector mediator coupling to the muon-neutrino and to the muon [9].

• Belle II: Search for $e^+ e^- \rightarrow \mu ^+ \mu ^- Z'$ with beam energies of 4 and ${7}\,\hbox {Ge\,V}$ where the $Z'$ is radiated off of one of the muons and decays invisibly with $m_{Z'}<{6}\,\hbox {Ge\,V}$ [41]. The limits can then be recast to muonphilic scalar mediators [42].

• PIENU: Search for the three body decay $\pi ^+ \rightarrow l^+\nu X$ where l is an electron or muon and X an invisible neutral boson. Pions were stopped in a detector and the spectrum of the charged lepton was measured. A search for the smooth signal spectrum was then carried out below the energy of the two body decay. This sets limits on the branching ratio $\Gamma \left( \pi ^+\rightarrow e^+ \nu X\right) /\Gamma \left( \pi ^+\rightarrow \mu ^+ \nu \right)$ for $X-$masses in the range $0< m_X < {120}\,\hbox {Me\,V}$ [43].

Fig. 6

The blue curves indicate our estimated 90% c.l. sensitivity limit on the coupling constant between electron or muon and the spin-1 mediator $A'$ from existing measurements of muon decay. The grey shaded region in the left frame is excluded by the BaBar search for $e^+e^- \rightarrow \gamma A'(A'\rightarrow \text {invisible})$ [39], rescaled to $e'_e=\varepsilon e$, while the red shaded region in the right frame is excluded by an analysis [9] of CCFR data on $\nu N \rightarrow \nu N \mu ^- \mu ^+$. The green band in the right frame indicates parameters that bring the experimental and theoretical values of $(g-2)_\mu$ within $2\sigma$

Our estimated sensitivity of existing muon decay data to the couplings of a new vector mediator are shown in Fig. 6. Unfortunately these estimated sensitivities are considerably weaker than the best existing bounds; the electron coupling is constrained by BaBar, while the muon coupling is constrained by the CCFR trident data. We find a considerably better sensitivity to the electron coupling, since near-collinear $A'$ emission off the electron, which is enhanced by a large logarithm, reduces the energy of the electron and thus leads to an observable effect. In contrast, near-collinear $A'$ emission off the muon neutrino leaves the electron energy essentially unchanged. Below a mediator mass of $\mathcal {O}({10}\,\hbox {Me\,V})$ the bound on the Michel parameter $\delta$ determines the sensitivity limit. For larger mediator masses the sensitivity limit is set by the $\xi$ parameter. Of course, the sensitivity is worse for larger mediator masses due to the closing phase space.

Fig. 7

90% c.l. upper bounds on the coupling constant between electron or muon and the spin 0 mediator $\phi$. The blue curves in both frames indicate the sensitivity derived from muon decay. In the left frame, the dashed black, and solid yellow, red and orange lines indicate limits from additional contributions to $P^+ \rightarrow e^+\nu _e$ decays (dashed black: $P = \pi$; yellow: $P = K$; orange: $P = D$; red: $P = D_s$). The dot-dashed black line represents the limits derived from the result of the search of PIENU for $\pi ^+\rightarrow e\nu X$; the drop of sensitivity at $m_\phi \sim {55}\,\hbox {Me\,V}$ is due to the signal being similar to $\pi ^+ \rightarrow \mu ^+\rightarrow e^+$ [43]. The region shaded in gray in the left frame is excluded by an older BaBar limit recast to scalar mediators [44]. In the right frame the orange shaded region is excluded by a recast of a Belle II search for $e^+e^- \rightarrow \mu ^+\mu ^- A', \ (A'\rightarrow \text {invisible})$ [42], and the green band indicates parameters that bring the experimental and theoretical values of $(g-2)_\mu$ within $2\sigma$

Our projected bounds on the couplings of the scalar mediator $\phi$ are depicted in Fig. 7. Muon decay is much less sensitive to these couplings than to those of a spin-1 mediator shown in Fig. 6, since collinear emission of a soft spin-0 boson off a fermion is suppressed. This also explains why the bounds on $e'_e$ and $e'_\mu$ from muon decay are now quite similar.

However, bounds on $P^+ \rightarrow e^+ \nu _e$ decays, where $P^+$ is a pseudoscalar ground state meson, lead to quite stringent bounds on new scalar couplings of the electron. For $m_\phi \le 400$ MeV the strongest bound originates from Kaon decays; decays of $D^+$ and $D_s$ mesons are considerably weaker, but extend to larger mediator masses. However, even the constraint from $K^+$ decays is somewhat weaker than that from an older BaBar search for $e^+ e^- \rightarrow \phi \gamma$ with invisible $\phi$. We do not show bounds from charged meson decays on the muon coupling. Since the helicity suppression of $P^+ \rightarrow \mu ^+ \nu _\mu$ is much weaker than for the electron mode, the resulting bounds on $e'_\mu$ are considerably less stringent than those on $e'_e$, and are thus not competitive with the constraint from the measurement of $g_\mu - 2$.

Fig. 8

90% c.l. lower bounds on the scale parameter $\Lambda$ of the Co-SIMP model. Again the black dashed and dot-dashed lines indicate limits from pion and kaon decays respectively. The solid blue line indicate parameter pairs that result in $\Omega _\chi h^2 \approx 0.12$ via the freeze-out mechanism in minimal cosmology

In Figs. 6 and 7 we assumed that the mediator couples only to electrons or only to muons. The constraints from $g_\mu - 2$ and from the BaBar and CCFR experiments are sensitive to only one of these couplings, and thus hold in full generality. Since meson decays into scalar mediators constrain the electron coupling much more than the muon coupling, they will remain essentially unchanged in models where both couplings are comparable.

Finally, constraints on the leptonic Co-SIMP scenario are summarized in Fig. 8. The blue curve indicates the value of $\Lambda$ required to obtain the correct relic density via $\chi \chi e \rightarrow \chi e$ reactions, which change the number of $\chi$ particles without changing the number of SM particles; this is the essence of the Co-SIMP scenario of Ref. [7]. The constraint from $K^+ \rightarrow e^+ \nu _e$ decays excludes this value of $\Lambda$ unless $m_\chi > 0.8$ MeV. Note that for $m_\chi > 2 m_e / 3$ another reaction becomes possible, $\chi \chi \chi \rightarrow e^+e^-$; however, this is not a SIMP scenario any more. Meson decays therefore exclude the whole region of parameter space where the correct $\chi$ relic density is determined by the Co-SIMP reaction.⁴

6 Conclusion

In this paper we investigated the influence of leptophilic dark matter models on two well measured decays of Standard Model particles: deviations from the muon decay spectrum due to additional undetected particles and the removal of the helicity suppression in the leptonic decays of charged ground state pseudoscalar mesons. The measured muon decay spectrum proved to be less sensitive to the new couplings than published searches at $e^+e^-$ colliders and from neutrino trident production. Limits on the electrophilic scalar coupling derived from meson decays are an order of magnitude stronger than those from muon decays but still weaker than existing limits by a factor of $\sim 2$. Hence a moderate precision improvement in leptonic kaon decays could probe new regions of parameter space. On the other hand, the measurement of the muon decay spectrum would have to become a lot more accurate to yield competitive limits, which currently looks unlikely. The muonphilic scalar limit at $m_\phi < {1}\,\hbox {Me\,V}$ is competitive with the recast search from Belle II at $e_\mu \sim 5\cdot 10^{-2}$, but lies well above the upper bound from the measurement of the magnetic dipole moment of the muon.

For the purely electrophilic Co-SIMP we showed that the model is ruled out for $m_\chi < {800}{\hbox {ke\,V}}$ by the kaon decay branching ratio because at allowed couplings $\chi$ is overproduced by freeze-out. Above this mass the DM particle $\chi$ doesn’t behave like a SIMP any more, since its relic density is greatly affected by annihilation into SM particles (namely $e^+e^-$ pairs). Our analysis therefore excludes the electrophilic Co-SIMP scenario.