1 Introduction

The inflationary hypothesis [1, 2], which posits that the early Universe underwent exponential expansion, remains the mainstream resolution to the Big Bang’s cosmic conundrums, namely the flatness [3], horizon [4, 5], and monopole [6] problems. This accelerated expansion drove down the initial curvature of spacetime, locked in the uniformity of the Universe, and diluted the density of magnetic monopoles to negligible levels all at once. Although primordial gravitational waves are yet to be detected, cosmic microwave background data strengthens evidence for a scenario that looks a lot like inflation [7]. But despite the phenomenological success of the theory, the usual implementation of inflation via scalar fields called inflatons comes with its own problems [7, 8]. Inflaton models usually violate energy conditions [9, 10], and the fundamental nature of inflatons also remains an open question [11, 12]. These reasons continue to motivate the search for alternative mechanisms [13,14,15,16,17].

One such proposed mechanism is the time-delayed cosmology of Choudhury et al. [18]. In this proposal, the evolution of the energy density of the Universe as expressed in the Friedmann equation is delayed by a constant \(\tau \) relative to expansion (Eq. 4). While ad hoc and seemingly unnatural, the scheme does appear to predict inflation generically without some of the problems of inflaton models. An exploration of its consequences is premised on the possibility of some nonlocal theories effectively generating time-delayed responses in gravitational dynamics [19,20,21], and on the richer dynamics afforded by time-delayed systems [22, 23]. More broadly, it answers a general invitation to explore the potential role of delay differential equations in fundamental physics [24].

However, time-delayed cosmology has received scant attention from the community. This is likely due to its lack of a firm fundamental basis. An important point is that its key parameter, the time delay \(\tau \), is generally just presumed to be of the order of Planck time. One notable attempt to constrain this parameter was made in Ref. [25], where the time delay was found to be only six orders of magnitude larger than the Planck time. This estimate however rests on what appears to be an arbitrarily defined error function of cosmic quantities and an assumption on the number of e-foldings at the end of inflation.

To our knowledge, there is as yet no conclusive estimate of the time delay. But one can reasonably expect that, if it exists at all, it ought to be minuscule – or essentially negligible – in order to avoid resulting in radically different cosmologies from the one we observe.

One of the aims of this work is to empirically test whether this strong – albeit reasonable – expectation comports to constraints given by observational data. Instead of postulating the smallness of the time delay, we let observations settle the value of the delay. In order to do this, we apply time-delayed cosmology to the late Universe where an optically invisible fluid, often dubbed dark energy, supersedes matter and radiation to source the observed late-time cosmic acceleration [26,27,28,29,30]. The substantial evidence for dark energy and the theoretical parallels between primordial inflation and dark energy make the application of time-delayed cosmology to the dark Universe today worth undertaking.

In particular, we consider the effects of the delayed Friedmann equation (Eq. (4)) at late times and determine the background evolution as well as the growth of Newtonian perturbations about this delayed background expansion. We calculate the Hubble expansion rate H(z) as well as two growth observables, the growth rate f(z) and \(f\sigma _8(z)\). We show clear dependence of the predictions on the time delay parameter \(\tau \) and estimate this parameter directly from observational data. While we believe that Solar System and LIGO observations are likely to place significantly tighter constraints on the time-delayed proposal, we emphasize that the proposal, at its core [18], was designed as a phenomenological model for cosmology, where only the Friedmann equation is modified. Lacking a fundamental action, it is not known how a time delay would manifest itself on these local scales. Therefore, we have chosen these two sets of cosmic observables for an initial test of the proposal.

It is not the intent of this paper to defend time-delayed cosmology beyond its original context nor to promote time-delays as a generic feature present in all gravitational phenomena. Our goal is more modest. We wish to empirically check the viability of attributing late-time cosmic acceleration partially to a time delay, and to calculate what our observed cosmology requires the time delay to be. As we shall show, time delays lead to a very distinct feature – i.e. kinks – in our observables that may be used to rule out time delays with future surveys. Our analysis also shows that, in surprising contrast to the expectation that a time delay (should it exist) has to be small in order to mimic standard cosmology, the observational probes we employ require the time delay to be fairly large. This result is of interest especially because it is likely to be strongly discordant with constraints that will come from Solar System and LIGO observations.

In the next section, we briefly introduce important details of time-delayed cosmology. In Sect. 3, we discuss the background evolution. In Sect. 4, we set up the equations for the growth of matter perturbations and discuss the predictions of time-delayed cosmology. In Sect. 5, we perform a Markov chain Monte Carlo sampling and estimate the time delay parameter \(\tau \) directly from the Hubble expansion rate H(z), the growth rate f(z), and \(f\sigma _8(z)\) data. In Sect. 6, we discuss the implications of our time delay estimate. Finally, we conclude our work in Sect. 7. The code for reproducing the figures and calculations in this paper can be freely downloaded at [31].

Conventions We work with the geometrized units \(c = 8 \pi G = 1\) and the mostly plus metric signature \((-,+,+,+)\). A dot over a variable denotes differentiation with respect to the cosmic time t.

2 Time-delayed cosmology

We provide a short introduction to the foundations of time-delayed cosmology (Sect. 2.1) and discuss the method of steps for solving a delay differential equation (Sect. 2.2). We then describe the set-up of time-delayed cosmology at late times (Sect. 2.3).

2.1 Foundations

With the observational support for large-scale statistical homogeneity [32,33,34] and isotropy [35,36,37], the standard description of cosmic evolution is given by the following Friedmann equation:

$$\begin{aligned} \left( \dfrac{\dot{a}(t)}{a(t)}\right) ^2 = \dfrac{1}{3}\rho (t), \end{aligned}$$
(1)

where a(t) is the scale factor which measures the expansion of the cosmos and \(\rho (t)\) is the energy density of the perfect fluid permeating the Universe. Assuming an equation of state of the form \(p(t) = \omega \rho (t)\) (where p is the fluid pressure and \(\omega \) is a constant called the equation of state parameter) and solving the continuity equation,

$$\begin{aligned} \dot{\rho }(t) = -3(\rho (t) + p(t))\dfrac{\dot{a}(t)}{a(t)}, \end{aligned}$$
(2)

the Friedmann equation can be written as

$$\begin{aligned} \left( \dfrac{\dot{a}(t)}{a(t)}\right) ^2 = \dfrac{\rho _{i,x}}{3}a(t)^{-3(1+\omega )}, \end{aligned}$$
(3)

where \(\rho _{i,x}\) is the initial energy density of the fluid denoted by x. A late Universe described by the Friedmann equation and filled with a mixture of cold (i.e. pressureless) dark matter (\(\omega = 0\)) and a cosmological constant \(\varLambda \) (\(\omega = -1\)) is referred to as the standard \(\varLambda \)CDM model.

On the other hand, time-delayed cosmology is based on a delayed Friedmann equation

$$\begin{aligned} \left( \dfrac{\dot{a}(t)}{a(t)}\right) ^2&= \dfrac{\rho _{i,x}}{3}a(t-\tau )^{-3(1+\omega )}, \end{aligned}$$
(4)

where \(\tau \) is some constant that, in the original application in the inflationary era, has units of Planck time \(t_p \sim \mathcal {O}(10^{-44})\) s. The interest for Eq. (4) derives from the fact that in this delayed set-up, inflation appears to be a generic prediction needless of inflatons (shown below). Delaying the energy density term in this way is completely ad hoc and not unique. The time delay parameter \(\tau \) could be introduced in other ways. For example, the left-hand side of the Friedmann equation could have been delayed instead. It is interesting to note however that the original proponents report that Eq. (4) share the same predictions with a couple of time-delayed variants. We choose to study Eq. (4) in particular because this is the proposal studied in Ref. [18]. Furthermore, this is the simplest phenomenological model that admits an analytical accelerated expansion. We believe the simplest model suffices because our goal is merely to study the possible consequences of a (large) time delay.

A fundamental action is yet to be found to support this time-delayed set-up. However, the proposal does draw motivation from fundamental ideas. A nonlocal theory of (quantum) gravity may induce a delayed response on the Universe since nonlocality may imply time-smeared interactions [18]. For example, the Deser–Woodard models [38,39,40], which are inspired by quantum loop corrections, involve cosmological equations with retarded boundary conditions. A more explicit example is Ref. [41] in which nonlocality has resulted to equations of motion that are systems of delay differential equations.

Despite these examples, the limitations of this proposal are clear. Time-delayed cosmology, as originally proposed, is merely phenomenological and primarily designed for cosmology. The fundamental physics behind its predictions is therefore unknown. It is also impossible for us at the moment to assess the ramifications of the proposal in other limits, e.g. Solar system scale; in its current state, effects of a time delay can only be determined on cosmic scales. The original proponents were aware of these issues (and other points such as uniqueness and stability) and have discussed them in Ref. [18]. Nonetheless, even if the proposal is merely phenomenological, it can and must be tested against data, particularly in the context in which it was proposed. The effort undertaken for this work stands on this simple premise.

2.2 The method of steps

Fig. 1
figure 1

The method of steps

Full size image

The delayed Friedmann equation can be solved with the method of steps [22, 23]. The essential idea of the method of steps is to replace the delayed term with a known solution a(t) so that the delay differential equation becomes ordinary within an interval that is then solvable with standard methods. Effectively, the solution to the delayed equation (as with any constant-delay differential equation) is a piecewise function with each composite solution defined on an interval of the size of the delay \(\tau \). The first composite solution, which is to be defined, is called an initial history. This is the equivalent of the initial value in ordinary differential equations.

Figure 1 illustrates the method of steps. Starting with a given delay differential equation, we define an initial history \(\phi (t)\) on an interval at least the size of one delay unit, e.g. \([t_0, t_0 + \tau )\). On the succeeding interval \([t_0 + \tau , t_0 + 2\tau )\), we replace the delayed term with \(\phi (t-\tau )\) and solve the ensuing ordinary differential equation, using \(\phi (t_0 + \tau )\) as an initial value. We label the solution of this ordinary differential equation as \(a_1(t)\). On the following interval \([t_0 + 2\tau , t_0 + 3\tau )\), again with a size of one delay unit, we replace the delayed term with \(a_1(t-\tau )\) and again solve the ensuing ordinary differential equation for \(a_2(t)\), with \(a_1(t_0 + 2\tau )\) as an initial value. We repeat this process for as many intervals as we like, using the previous solution \(a_n(t)\) to replace the delayed term and solve the resulting ordinary differential equation for \(a_{n+1}(t)\). The piecewise function defined by \(a_n(t)\)’s comprise the solution to the delay differential equation.

Fig. 2
figure 2

Some solutions to the delayed Friedmann equation due to a delay \(\tau = 10t_p\), where \(t_p\) is Planck time. The inflationary period lasts for one delay unit (in this figure, from \(t = 10 t_p\) to \(t = 20 t_p\)) before the scale factor transitions to a decelerated evolution

Full size image

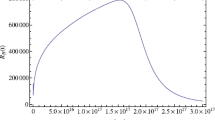
For a power-law initial history \(\phi (t) = t^\alpha \) defined on \(t \in [0, \tau )\), which may be due to a quantum gravity effect or a pre-Big Bang scenario, the delayed Friedmann equation admits inflation in the following interval:

$$\begin{aligned} a(t)&= \phi (\tau )\exp \left( \sqrt{\dfrac{\rho _{i,x}}{3}}\dfrac{(t-\tau )^\gamma }{\gamma }\right) , \ t \in [\tau , 2\tau ), \end{aligned}$$
(5)
$$\begin{aligned} \gamma&= 1-\dfrac{3}{2}(1+\omega )\alpha . \end{aligned}$$
(6)

For succeeding times, the delayed equation has to be solved numerically. In this work, we use the |ddeint| Python package [42] for the numerical solutions. Clearly, in time-delayed cosmology, inflation can be naturally generated for a period of one delay unit. This period also seamlessly ends, thereby avoiding the “graceful exit” problem (see Fig. 2).

2.3 Application to late times

At late times, the phenomenon of interest is cosmic acceleration due to dark energy. Because of the parallels between primordial inflation and late-time cosmic acceleration, the application of the delayed Friedmann equation at late times is worth considering. Furthermore, it will be easier to place constraints on time-delayed cosmology if we can show its impact on the expansion era.

In this application, we phenomenologically regard dark energy as a mixture of a cosmological constant and a time delay. The delayed Friedmann equation is therefore of the form

$$\begin{aligned} H(t)^2 = H_i^2\left( \dfrac{\varOmega _{i,m}}{a^3(t-\tau )}+\varOmega _{i,\varLambda }\right) , \end{aligned}$$
(7)

where \(H(t):= \dot{a}(t)/a(t)\) is the Hubble parameter, \(H_i\) is the initial Hubble parameter value, \(\varOmega _{i,m} := \rho _{i,m}/(3H_i^2)\) is the matter density parameter, and \(\varOmega _{i,\varLambda } := \rho _{i,\varLambda }/(3H_i^2)\) is the cosmological constant density parameter. Equation 7 can be nondimensionalized. Setting \(t \rightarrow \bar{t}t_c\), where \(\bar{t}\) is the dimensionless time and \(t_c\) is the characteristic time scale, Eq. (7) becomes

$$\begin{aligned} H(\bar{t})^2 = H_i^2t_c^2\left( \dfrac{\varOmega _{i,m}}{a^3(\bar{t}-\bar{\tau })}+\varOmega _{i,\varLambda }\right) , \end{aligned}$$
(8)

where \(\bar{\tau }\) is the dimensionless delay. Choosing the time scale \(t_c = 1/H_i\),

$$\begin{aligned} H(\bar{t})^2 = \left( \dfrac{\varOmega _{i,m}}{a^3(\bar{t}-\bar{\tau })}+\varOmega _{i,\varLambda }\right) . \end{aligned}$$
(9)

Figure 3 shows that the delayed Friedmann equation can also accommodate a late-time cosmic acceleration.

Fig. 3
figure 3

Some solutions to the time-delayed Friedmann equation in the presence of a cosmological constant and time delay on the order of \(t_c\), where \(t_c = H_i^{-1} = 0.0175 \pm 0.0001\) Gyr. The integration starts off with an initial history of \(\phi (t) \sim t^{2/3}\) in the matter-dominated era and evolves into the future

Full size image

Because the delay is assumed to be very small as in Ref. [18], it would have no impact on late-time observables, which is why the computed power spectrum in Ref. [25] expectedly appears to be in excellent agreement with observations. In this application, we allow the delay to be large since the relevant time scale \(t_c\) is also large; we will integrate in the matter-dominated era up to the present dark energy-dominated era. We will solve the dimensionless version of Eq. (7) and the relevant time scale would be \(t_c = H_i^{-1}\), with \(H_i\) being the Hubble parameter in the matter-dominated era. We find the value of \(H_i\) using the following relation for a constant dark energy density

$$\begin{aligned} \rho _{i, \varLambda }&= \rho _{0, \varLambda }, \end{aligned}$$
(10)
$$\begin{aligned} \implies 3H_i^2\varOmega _{i,\varLambda }&= 3H_0^2\varOmega _{0,\varLambda }, \end{aligned}$$
(11)

where \(H_0\) and \(\varOmega _{0, \varLambda }\) are the Hubble constant and the present value of the cosmological constant density parameter, respectively. The latest Planck 2018 estimates are \(H_0 = 67.4 \pm 0.5\) km s\(^{-1}\) Mpc\(^{-1}\) and \(\varOmega _{0,\varLambda } = 0.6889 \pm 0.0056\) [30]. Solving for \(H_i\) in Eq. (10), we get

$$\begin{aligned} H_i = H_0\sqrt{\dfrac{\varOmega _{0,\varLambda }}{\varOmega _{i, \varLambda }}}. \end{aligned}$$
(12)

Starting our integrations in the time when \(\varOmega _{i,\varLambda } = 10^{-6}\) (and \(\varOmega _{i,m} = 1 - \varOmega _{i, \varLambda }\)), this results to a time scale of \(t_c = 0.0175 \pm 0.0001 \) Gyr, where here and throughout the paper we have used the |SOAD| package [43] for (asymmetric) error propagation. The units of the time delay will be in terms of this time scale \(t_c\). Note that this assumes the normalization \(a(t_i) = 1 \implies 1 = \varOmega _{i, m} + \varOmega _{i, \varLambda }\) for convenience, where \(t_i\) is the initial integration time. This is different from setting the normalization to \(a(t_0) = 1\) today, where \(t_0\) is the present time. However, once the numerical solution has been obtained, it can be renormalized so that the result matches what we would have obtained if we had taken \(a(t_0) = 1\). The code for reproducing the figures and calculations in this paper can be freely downloaded at [31].

3 Hubble expansion

Fig. 4
figure 4

The evolution of the apparent magnitude m(z) of Type Ia supernovae. Here, we have assumed that the absolute magnitude takes the value \(M = -19.3\) and \(H_0\) is given by the Planck 2018 estimate. Shown on the bottom plot is the relative difference between time-delayed cosmology and \(\varLambda \)CDM, which is used as the reference. Time-delayed cosmology is virtually indistinguishable from \(\varLambda \)CDM

Full size image

To obtain the background evolution from Eq. (7), we must specify an initial history. Throughout this paper, we assume a power-law initial history of the form \(\phi (t) \sim t^\alpha \) for the delayed Friedmann equation. We have checked numerically that the observables we are interested in in this paper do not strongly depend on the parameter \(\alpha \) (see Fig. 12) in redshifts that are currently accessible to us and especially for reasonable values of \(\alpha \) (that is, for \(\alpha \approx 2/3\) which refers to the canonical matter-era solution). Furthermore, although \(\alpha \) gains a stronger effect at very large redshifts in terms of affecting the magnitude of the observables and for very large time delays (\(H_i\tau > 10\)), the general shape of the observables are determined by the time delay parameter and not by \(\alpha \). For these reasons and combined with the fact that an \(\alpha = 2/3\) constitutes a more natural initial history (taking after the canonical \(t^{2/3}\) matter-era solution), we choose to fix the value of \(\alpha \) to 2/3 in the following calculations instead of taking it as a free parameter.

Fig. 5
figure 5

The evolution of the Hubble expansion rate H(z) in units of km s\(^{-1}\) Mpc\(^{-1}\). Shown on the bottom plot is the relative difference between time-delayed cosmology and \(\varLambda \)CDM, which is used as the reference. The predictions have been normalized to have the value of the Planck 2018 estimate of the Hubble constant \(H_0\) at \(z = 0\). A striking feature of time-delayed cosmology is a kink or a point at which its prediction changes sharply. These kinks are encircled in blue above

Full size image

Due to Fig. 3, we can already expect that the background evolution of time-delayed cosmology closely follows that of \(\varLambda \)CDM. Indeed, if we look at the predictions for the apparent magnitude m(z) of supernovae in Fig. 4, we can see that time-delayed cosmological predictions are virtually indistinguishable from the \(\varLambda \)CDM prediction. This is the case even when considering delays on the order of \(H_i\tau \sim 10\) and when considering larger redshifts. The difference between \(\varLambda \)CDM and time-delayed cosmology is revealed when we look at the Hubble expansion rate H(z). Figure 5 shows the evolution of the Hubble expansion rate H(z) for a fixed \(H_0\). The dashed red curve shows the prediction of the standard \(\varLambda \)CDM model and the black curves are the predictions of time-delayed cosmology. Predictions due to delays that are larger than \(H_i\tau = 1\) already notably deviate from the \(\varLambda \)CDM prediction at redshifts \(z > 5\). Notice that the predictions appear to start at different redshifts. This is the case for all the redshift plots in this paper. This happens because different delays affect the scale factor evolution differently, which is then used to obtain the redshift. However, we have made sure that all quantities start out with the same initial condition at the same starting integration time.

A striking observation in Fig. 5 are kinks (encircled in blue) or points at which the predictions of time-delayed cosmology change sharply. In fact, the derivative of H(z) at any of the kinks is undefined. This is an expected feature and an artifact of delay differential equation models. It is well known that discontinuities propagate in the derivatives of the solution to delay differential equations [22, 23]. At the start of integration, the first derivative is discontinuous. One delay unit afterwards, the discontinuity propagates in the second derivative. Since our definition of the Hubble expansion rate involves \(\dot{a}(t)\), we expect to see the discontinuity in the second derivative \(\ddot{a}(t)\) at a certain point (the kinks).

Of course, we do not expect real, physical quantities of the Universe to exhibit these discontinuities. But if our Universe is correctly modeled by a delayed Friedmann equation, the abrupt transitions in H(z) serve as a generic smoking gun that make them empirically interesting. There may be fundamental reasons behind these discontinuities. For example, the improved Deser–Woodard model [38] was shown to have a discontinuous evolution of matter perturbation [44]. A possible cause of the discontinuity is a strong nonlocal effect.

These kinks in the Hubble expansion rate already provide an upper bound on the time delay without further statistical analysis. In Fig. 6, we can see that a time delay with magnitude \(H_i\tau \approx 19\) can already be ruled out due to the presence of a kink that the data clearly does not accommodate. As the value of the time delay is increased, the kinks in the Hubble expansion rate are revealed at smaller and smaller redshifts. This is also true if we consider other observables. Therefore, all time delays \(H_i\tau > 19\) are also ruled out.

Fig. 6
figure 6

The evolution of the Hubble expansion rate H(z) in units of km s\(^{-1}\) Mpc\(^{-1}\) at small and intermediate redshifts. Time-delayed cosmology closely follows \(\varLambda \)CDM even for delays on the order of \(H_i\tau \sim 10\). The Hubble data are taken from the compilation in Ref. [45]

Full size image

For time delays with magnitude \(H_i\tau < 19\), the smoking-gun imprints of time-delayed cosmology on the background evolution are only revealed at large redshifts for which data is still unavailable. When we look at redshifts \(z < 2\) (Fig. 6), we can see that time-delayed cosmology closely follows \(\varLambda \)CDM even for delays on the order of \(H_i\tau \sim 10\). This shows that the key time delay parameter does not have to be of the order of Planck time as originally envisaged in order to fit observational data. Even large cosmic delays appear to be viable. An unfortunate consequence of this is that the Hubble expansion data is unable to distinguish time-delayed cosmology from \(\varLambda \)CDM. To observe the difference, we look to Newtonian perturbations.

4 Newtonian perturbations

In this work, we choose the growth of Newtonian matter perturbations as an additional probe of time-delayed cosmology. In particular, we are interested in the growth rate f(z) and another observable \(f\sigma _8(z)\), where z is the redshift, that are both dependent on the amplitude of perturbations. The former quantity is the speed of growth of perturbations in the Universe with respect to the cosmic expansion, and the latter is essentially the growth rate scaled by the evolving root-mean-square of matter perturbations. These observational probes of large-scale structures have been used to distinguish between modified gravity theories and the standard \(\varLambda \)CDM model [46,47,48,49,50,51,52,53,54]. As we shall see, these will also be useful for obtaining constraints on time-delayed cosmology.

4.1 Set-up

The growth of Newtonian matter perturbations is given by [46, 47]

$$\begin{aligned} \ddot{\delta }(t) + 2H(t)\dot{\delta }(t) - \rho _m(t)\delta (t) = 0, \end{aligned}$$
(13)

where \(\delta (t) := \delta \rho _m(t)/\rho _m(t)\) is the density contrast quantifying the inhomogeneity of the universe and \(\rho _m(t)\) is the background energy density of (dark) matter. This fluctuation equation is valid for sub-horizon perturbations, i.e., \(\lambda / a(t) \ll H(t)^{-1}\), where \(\lambda \) is the co-moving mode wavelength of the density perturbation. It is convenient to rewrite and solve this equation in terms of the scale factor a or the redshift z (using the relation \(z = (1/a) - 1\)). Once \(\delta (a)\) is obtained, the two observables of interest can be easily calculated using the following definitions:

$$\begin{aligned} f(a)&:= \dfrac{d\ln {\delta (a)}}{d\ln {a}}, \end{aligned}$$
(14)
$$\begin{aligned} f\sigma _8(a)&:= \dfrac{\sigma _8}{\delta (a=1)}\delta (a)f(a), \end{aligned}$$
(15)

where \(\sigma _8\) is the present root-mean-square variance in the number of galaxies in spheres of radius 8\(h^{-1}\) Megaparsec (with \(h = H_0/(100\) km s\(^{-1}\) Mpc\(^{-1}\)) being the dimensionless value of the Hubble parameter today). Note that these two observables are fundamentally independent quantities; whereas f(a) carries information on \(d\delta /da\), \(f\sigma _8(a)\) carries information on \(\delta (a)\).

In what follows, we solve the fluctuation equation

$$\begin{aligned} \ddot{\delta }(t) + 2H(t)\dot{\delta }(t) - \dfrac{3}{2}H^2(t)\delta (t) = 0, \end{aligned}$$
(16)

where we have replaced the background matter energy density with its Hubble function equivalent using the (delayed) Friedmann equation. The observables of interest in time are then given by

$$\begin{aligned} f(t)&:= \dfrac{d\ln {\delta (t)}}{d\ln {a(t)}} = \dfrac{1}{H(t)}\dfrac{\dot{\delta }(t)}{\delta (t)}, \end{aligned}$$
(17)
$$\begin{aligned} f\sigma _8(t)&:= \dfrac{\sigma _8}{\delta (t=t_0)}\dfrac{1}{H(t)}\dot{\delta }(t), \end{aligned}$$
(18)

where \(t_0\) denotes the present day. In addition to assuming an initial history of the form \(\phi (t) \sim t^{2/3}\) for reasons we mentioned before, we also set the canonical \(a(t) \sim \delta (t) \sim t^{2/3}\) solution as an initial condition for the perturbation equation. This means that we integrate deep in the matter-dominated era up to the present dark energy-dominated era. In comparing the results with the \(\varLambda \)CDM model, we use the latest value of \(\sigma _8\) given by Planck: \(\sigma _8 = 0.811\pm 0.006\) [30].

We note that we are using the standard (i.e. non-delayed) perturbation equation here instead of a new delayed perturbation equation. We acknowledge that a higher time-delayed theory may not even reduce to a Newtonian limit and therefore the above perturbation equation may need higher order corrections coming from a consistent effective field theory. We argue, however, that on subhorizon scales, \(\lambda \ll 1/H\), and the quasistatic regime, the perturbations should follow Newtonian gravity at the leading order in any viable time-delayed theory, and we shall not be interested in any other time-delayed theory without this Newtonian limit. This view is supported by theory-agnostic constraints coming from large scale structure which show that only small departures from Eq. (13) could even be compatible with cosmic growth data [55, 56]. Absent a fundamental action for time-delayed cosmology, assuming Newtonian perturbations is therefore the most reasonable thing that one can do, short of proposing further ad hoc prescriptions about how the delay directly affects perturbations.

We clarify however that we are not claiming that this limit is generically satisfied by all time-delayed theories. Rather, we anticipate that leading-order effects of viable time-delayed theories may be largely captured by Eq. (13). (Otherwise, they would not be viable if we consider Refs. [55, 56].) We find that this conservative assumption is enough to see interesting consequences of time-delayed cosmology without having to develop an action-based delayed perturbation theory.

4.2 Growth rate f(z)

Fig. 7
figure 7

The evolution of the growth rate f(z). Time-delayed cosmology with intermediate (i.e. \(H_i\tau \sim 10\)) delay parameter values predict markedly different growth rate evolutions. In particular, the predictions for time-delayed cosmology decreases initially before increasing and eventually peaking. There are also kinks (encircled in blue) in the predictions. Note that the non-circled sharp turns on the bottom plot are inflection points produced when taking the absolute value of the relative difference and do not correspond to predicted physical kinks

Full size image

Figure 7 shows the plot of the growth rate f(z). The dashed red curve shows the prediction of the standard \(\varLambda \)CDM model, whereas the black curves are the predictions of time-delayed cosmology at different values of the time delay parameter \(\tau \). Immediately, we can see that time-delayed cosmology makes very different predictions for f(z) for values of the time delay parameter on the order \(H_i\tau \sim 10\). The growth rate of a delayed Universe dips in the matter-dominated era (i.e. \(z > 1\)) and then peaks later on before dark energy finally suppresses it for good (see Fig. 9). On the other hand, if the delays are on the order \(H_i\tau \lesssim 1\), then these dips and peaks are weak or not visible at all and the growth rate is virtually indistinguishable from the prediction of \(\varLambda \)CDM.

The characteristic decreasing of the growth rate predictions earlier on implies that, for a certain period, the delayed Universe was expanding faster than the perturbations were growing. We can see this clearly in Fig. 8a. In Fig. 8b, we can also see that the rate of expansion is initially greater than the rate of growth of the fluctuation. Combined together, these two scenarios suppress the growth rate at early times. But after some time, the growth rate predictions start to increase after decreasing. Notice that the transition to this increasing phase is very abrupt. Since our definition of the growth rate also involves \(\dot{a}(t)\), we expect to see kinks just as we saw in the background evolution. Interestingly, the growth rate becomes greater than unity at a certain point, implying that in the delayed Universe, perturbations will eventually grow faster than the Universe is expanding. This is also clear in Fig. 8a and b. Later on, however, dark energy starts to dominate and the growth rate is eventually driven down.

Fig. 8
figure 8

Comparison of the evolution of the density contrast and the scale factor as well as their time rates of change

Full size image
Fig. 9
figure 9

The evolution of the growth rate f(z) at small and intermediate redshifts. The growth rate data are taken from the compilation in Ref. [57]

Full size image

Figure 9 shows a closer look at the growth rate up to redshift \(z \sim 3\). Here, we can see that the kinks in the growth rate evolution can also provide an upper bound. While the uncertainties of growth rate data at \(z > 2.5\) are very large, it is safe to say that \(H_i\tau \approx 18\) is already very unlikely to be viable. On the other hand, time delays with magnitude \(H_i\tau \lesssim 10\) do appear viable.

4.3 \(f\sigma _8(z)\)

Fig. 10
figure 10

The evolution of \(f\sigma _8(z)\). Time-delayed cosmology with intermediate (i.e. \(H_i\tau \sim 10\)) time delay parameter values predict markedly distinct \(f\sigma _8(z)\) evolutions. It is not as pronounced here, but there are also kinks (encircled in blue) in this plot for the time-delayed cosmology predictions. Note that the non-circled sharp turns on the bottom plot are inflection points produced when taking the absolute value of the relative difference and do not correspond to predicted physical kinks

Full size image

Figure 10 shows the plot of \(f\sigma _8(z)\). Again, the standard \(\varLambda \)CDM prediction is shown in dashed red, and the black curves are the predictions of time-delayed cosmology at different values of the time delay parameter. Similar to the scenario with the growth rate, time-delayed cosmology models with time delay parameter values on the order \(H_i\tau \sim 10\) predict \(f\sigma _8(z)\) evolutions that are different from \(\varLambda \)CDM. The \(f\sigma _8(z)\) of the delayed Universe starts off smaller than but eventually surpasses the standard prediction. When the cosmological constant becomes more important than matter during the dark energy-dominated era, time-delayed cosmology and \(\varLambda \)CDM follow each other in similar evolutions. Naturally, we also find that delays on the order \(H_i\tau \lesssim 1\) lead to \(f\sigma _8(z)\) predictions that are indistinguishable from \(\varLambda \)CDM. As with the growth rate, we also get a kink because the definition of \(f\sigma _8(t)\) also includes \(\dot{a}(t)\). Notice that in Fig. 10 the predictions start out at different magnitudes. Note that all calculations started out with the same initial condition. The differences in the initial value in these plots are due to the normalizing constant \(\delta (t = t_0)\), which is of course different for different models.

Fig. 11
figure 11

The evolution of \(f\sigma _8(z)\) at small and intermediate redshifts. The \(f\sigma _8(z)\) data are taken from the compilation in Ref. [57]

Full size image

Figure 11 is a closer look at \(f\sigma _8(z)\) up to redshift \(z = 2\). In this case, we do not see any kink even for a time delay \(H_i\tau \approx 18\). However, it is clear that a time delay \(H_i\tau \approx 18\) is already unlikely since its predicted evolution already misses plenty of data points. Time delays \(H_i\tau \lesssim 10\) do however lead to predictions that are already distinct from \(\varLambda \)CDM while also appearing viable.

5 Delay estimate

We have already obtained a strict upper bound for the time delay but to achieve a best estimate, we confront our numerical solutions for H(z), f(z), and \(f\sigma _8(z)\) with observational data using a Markov-chain Monte-Carlo (MCMC) analysis. Given data d and parameters p of a model m, Bayes’ theorem states that

$$\begin{aligned} P(p \mid d, m) = \dfrac{P(d \mid p, m)P(p \mid m)}{P(d \mid m)}, \end{aligned}$$
(19)

where \(P(p \mid d, m)\) (the posterior) is the probability distribution of the parameters p given d and m, \(P(d \mid p, m)\) (the likelihood) is the probability of getting the data d given p and m, \(P(p \mid m)\) (the prior) is the probability of the parameters p according to our prior beliefs, and finally \(P(d \mid m)\) (the weight of evidence or marginal likelihood of m) is a normalizing constant that, as we shall see, is important for model comparison.

We consider a likelihood L given by

$$\begin{aligned} \ln L \sim -\sum _i^N\dfrac{(\mu ^\text {obs}_i-\mu ^\text {th}_i)^2}{2\sigma _i^2}, \end{aligned}$$
(20)

where N is the number of data points, \(\mu ^\text {obs}_i\) is an observational data point, \(\mu ^\text {th}_i\) is a predicted value, and \(\sigma _i\) is the observational error. We also take the Hubble constant \(H_0\) and \(\sigma _8\) as nuisance parameters to be estimated. Again, we fix \(\alpha \) to 2/3 because \(\alpha \) has a weak effect on the observables at small redshifts (see Fig. 12) and because this value of \(\alpha \) gives the canonical matter-era solution.

Fig. 12
figure 12

The evolution of different observables for a fixed time delay and at varying initial histories. Here, \(H_i\tau = 5.55\). The effect of \(\alpha \) on observables is not strong at small redshifts and for time delays \(H_i\tau < 10\)

Full size image
Table 1 We choose uniform priors defined over wide ranges for all the parameters
Full size table

Our priors are shown in Table 1. We intentionally choose priors defined over wide ranges so as to avoid inadvertently cutting the posterior short. We note that since our priors are uniform, our arbitrary cutoffs for the priors do not affect the value of the best estimates of the parameters so long as the priors include these best estimates in their ranges. Since each of our prior is defined over a wide range, the best estimate for a parameter is guaranteed to be within the prior for that parameter.

Note that we do not consider negative delays (i.e. \(H_i\tau < 0\)). A negative delay means that the delayed Friedmann equation is advanced in time rather than retarded. In which case, we must provide future information instead of an initial history. The solution then would be the past evolution. Since we are interested in the predictions of time-delayed cosmology in the late Universe, the time delay must be strictly positive.

We use the |PyMultiNest| [58] and |GetDist| [59] Python packages to sample the posteriors via MCMC and post-process the resulting MCMC chains. We consider the Hubble expansion rate data compiled in Table 1 of Ref. [45] as well as the growth rate and \(f\sigma _8(z)\) data compiled in Tables 1 and 2 of Ref. [57], respectively. In what follows, we choose to report the median estimate which is more robust to outliers as compared with the mean. We have checked however that the median estimates below are not too different from the mean estimates with their credible intervals overlapping.

Fig. 13
figure 13

Marginalized posterior distributions of the time delay parameter \(\tau \) and the Hubble constant \(H_0\) using Hubble data. The median estimate is \(H_i\tau = 5.63^{+4.97}_{-3.95}\) or \(\tau = 0.0998^{+0.0890}_{-0.0703}\) Gyr, while the median estimate for the Hubble constant is \(H_0 = 72.67 \pm 1.72\) km s\(^{-1}\) Mpc\(^{-1}\)

Full size image

Figure 13 shows the posterior distributions for the time delay parameter \(\tau \) and the Hubble constant \(H_0\) using Hubble expansion rate data alone. The median estimate for the time delay is \(H_i\tau = 5.63^{+4.97}_{-3.95}\) or \(\tau = 0.0998^{+0.0890}_{-0.0703}\) Gyr. Meanwhile, the median estimate for the Hubble constant is \(H_0 = 72.67 \pm 1.72\) km s\(^{-1}\) Mpc\(^{-1}\). Notably, the credible interval of the time delay estimate is rather large and this is the case for all the data we consider in this work. This may be attributed to two things. Firstly, the uncertainties of the observational data points are themselves large. And secondly, from Fig. 6, we can’t expect a sharply peaked posterior with a narrow credible interval because the predictions of time-delayed cosmology for varying time-delays are very similar.

Fig. 14
figure 14

Posterior distribution of the time delay parameter \(\tau \) using the growth rate data set alone. The median estimate is \(H_i\tau = 7.11^{+4.95}_{-4.62}\) or \(\tau = 0.1232^{+0.0874}_{-0.0806}\) Gyr

Full size image

Figure 14 shows the posterior distribution for the time delay parameter \(\tau \) using the growth rate dataset alone. Upon sampling, we find that the median estimate for the time delay is \(H_i\tau = 7.11^{+4.95}_{-4.62}\) or \(\tau = 0.1232^{+0.0874}_{-0.0806}\) Gyr. The estimate for \(\tau \) has notably increased and we also find that the mass of the posterior distribution has moved to a nonzero time delay. On the other hand, Fig. 15 shows the posterior distributions for the time delay parameter \(\tau \) and \(\sigma _8\) using the \(f\sigma _8(z)\) dataset. The median estimate for the time delay is \(H_i\tau = 7.42^{+4.87}_{-5.09}\) or \(\tau = 0.1277^{+0.0864}_{-0.0885}\) Gyr. The median estimate for \(\sigma _8 = 0.80^{+0.02}_{-0.03}\). Notice in this case that the estimate for the time delay has gotten much larger. Figure 16 shows the posterior distributions when we combine the growth rate and \(f\sigma _8(z)\) datasets. We find that the median estimates for the parameters are \(H_i\tau = 7.12^{+4.60}_{-4.70}\) or \(\tau = 0.1273^{+0.0799}_{-0.0840}\) Gyr and \(\sigma _8 = 0.80 \pm 0.02\). What these results show is that growth observables or perturbations consistently prefer nonzero values of the time delay parameter, especially \(f\sigma _8\) data. We can see this not only in the median estimate but also in the mode.

To arrive at a best estimate, we combine the background and growth datasets. Figure 17 shows the posterior distributions of the time delay parameter, the Hubble constant \(H_0\), and \(\sigma _8\). The median estimates are \(H_i\tau = 5.55^{+4.57}_{-3.76}\) or \(\tau = 0.0993^{+0.0799}_{-0.0664}\) Gyr, \(H_0 = 72.58^{+1.75}_{-1.67}\) km s\(^{-1}\) Mpc\(^{-1}\), and \(\sigma _8 = 0.80 \pm 0.02\). The best estimate for the time delay is expectedly between the background median estimate and growth median estimate. It is clear from the results that growth observables especially prefer higher values of the time delay.

Fig. 15
figure 15

Marginalized posterior distributions of the time delay parameter \(\tau \) and \(\sigma _8\) using the \(f\sigma _8(z)\) data alone. The median estimates are \(H_i\tau = 7.42^{+4.87}_{-5.09}\) or \(\tau = 0.1277^{+0.0864}_{-0.0885}\) Gyr and \(\sigma _8 = 0.80^{+0.02}_{-0.03}\)

Full size image
Fig. 16
figure 16

Marginalized posterior distributions of the time delay parameter \(\tau \) and \(\sigma _8\) using the combined growth rate and \(f\sigma _8(z)\) datasets. The median estimates are \(H_i\tau = 7.12^{+4.60}_{-4.70}\) or \(\tau = 0.1273^{+0.0799}_{-0.0840}\) Gyr and \(\sigma _8 = 0.80 \pm 0.02\)

Full size image
Fig. 17
figure 17

Marginalized posterior distributions of the time delay parameter \(\tau \), the Hubble constant \(H_0\), and \(\sigma _8\) using the combined background and growth datasets. The median estimates are \(H_i\tau = 5.55^{+4.57}_{-3.76}\) or \(\tau = 0.0993^{+0.0799}_{-0.0664}\) Gyr, \(H_0 = 72.58^{+1.75}_{-1.67}\) km s\(^{-1}\) Mpc\(^{-1}\), and \(\sigma _8 = 0.80 \pm 0.02\)

Full size image

To further strengthen our statistical analysis of time-delayed cosmology, we compute the Bayes factor which is roughly the Bayesian equivalent of the p-value used for classical (frequentist) hypothesis testing. Given data d and two models \(m_1\) and \(m_2\), the preference for \(m_1\) over \(m_2\) in light of d is quantified by the Bayes factor \(B_{12}\) defined as

$$\begin{aligned} B_{12} := \dfrac{P(d \mid m_1)}{P(d \mid m_2)}, \end{aligned}$$
(21)

which is simply the ratio of the marginal likelihood of \(m_1\) to the marginal likelihood of \(m_2\). This definition assumes that both models are equally probable before accounting for the data. This is a fair assumption in our case since this is the first time that a time delay is even being considered in late-time cosmology and we do not have prior information whether time-delayed cosmology is preferred over \(\varLambda \)CDM.

Letting \(m_1\) denote \(\varLambda \)CDM and \(m_2\) denote time-delayed cosmology, we compute the Bayes factor based on marginal likelihoods calculated using the Hubble expansion rate data alone (\(\ln B_{12} = 0.629 \pm 0.101\)), the combined growth data (\(\ln B_{12} = 0.286 \pm 0.078\)), and finally the combined background and growth data (\(\ln B_{12} = 0.548 \pm 0.125\)). Following the criteria in Ref. [60], we find that regardless of the data considered, the Bayes factor indicates a statistical preference against time-delayed cosmology in favor of \(\varLambda \)CDM that is not worth more than a bare mention (an odds in favor of \(\varLambda \)CDM less than 3:1). In other words, no conclusion can be drawn as to which model is favored.

6 Discussion

Strictly speaking, we have estimated the dimensionless quantity \(\bar{\tau } := H_i\tau \), not the dimensional \(\tau \) alone. Therefore, provided that \(H_i\) is many orders larger than \(H_0\), the time delay \(\tau \) could still prove to be Planckian in scale. But assuming a constant vacuum energy, we estimated that \(H_i \sim 10^2H_0\) during the matter era at which we started our integration (Eq. 12). This is not even enough to bring the delay down to seconds. In order for the time delay to be Planckian, we must integrate near the inflationary era where we expect the Hubble parameter, which grows backwards in time, to be sufficiently large (i.e. \(H_i \gg 10^2H_0\)). Still however, in that case, we will have to use different observables from which we may get a different value for \(\bar{\tau }\). This means that we may (not necessarily will) find a large estimate for \(\tau \) nevertheless.

To our knowledge, the only previous work done to constrain the delay in the early-universe context is Ref. [25]. In that work the authors estimated the dimensional delay \(\tau \) to be \(\tau \sim 10^6t_p\). Unlike ours, their estimate was not based on data. Rather, it hinges on other estimated quantities (such as the spectral index \(n_s\)), which in turn were the result of minimizing an ad hoc error function. Crucially, these other estimated quantities already assume \(\varLambda \)CDM. Hence, what Ref. [25] actually did is to find the value of \(\tau \) so that the time-delay predictions are as close to \(\varLambda \)CDM as possible as opposed to the value of the time delay that best fits the data. It is no surprise then that their estimate was forced to be astronomically small (since \(\tau \rightarrow 0\) implies \(\varLambda \)CDM).

6.1 Compatibility of a large delay with local observations

The large value of our estimated time delay raises an important concern. Taking off from our intuitive understanding of the usual Friedmann equation, the time-delayed cosmology proposal might be taken to mean that changes in the local energy density result in delayed changes in the local geometry. A large time delay then would be completely incompatible with everything we observe in the Solar System. For instance, if the Sun suddenly disappeared, then the planetary orbits will only change after \(\tau = 0.0993^{+0.0799}_{-0.0664}\) Gyr.

This is clearly troubling, though not without a potential resolution. First off, the time-delayed cosmology proposal is strictly just the delayed Friedmann equation. The naive argument above assumes that a delayed Friedman equation should imply delayed Newtonian gravity. But this is far from obvious. For this reasoning to work, one must first embed time-delayed cosmology within a proper theory and then work out the appropriate Solar System (or Newtonian) limit. It is not clear at all that this should mean delayed effects in the Solar System.

Indeed, it can happen that a large time delay is hidden on Solar System scales. This is precisely how some modern modified gravity theories operate today, evading our very stringent Solar System constraints. With the help of screening mechanisms (e.g. the Vainshtein mechanism [61]), the effects of a potential “fifth force” due to the presence of extra fields are revealed on cosmic scales but hidden in the Solar System. Without an embedding fundamental theory for time-delayed cosmology, this scenario will remain a tantalizing possibility.

Our broader point is that the time-delayed cosmology proposal is entirely phenomenological, and as such must be evaluated in the context in which it was proposed, which is cosmology. Its status is similar to that of modified Newtonian dynamics (or MOND), which in its early days was proposed for galactic scales and no more. Requiring that time-delayed cosmology must touch on Solar System dynamics is analogous to asking MOND to do cosmology. Both represent an overreach for the phenomenological models. They can be done, but not without an embedding theory, which at this point does not exist for time-delayed cosmology.

These matters are open problems and fall outside the scope of our paper, which is largely meant to provide a first empirical grounding of time-delayed cosmology. Further theoretical developments of the model may provide insights into these problems and we expect our work to be informative in these aims.

6.2 Compatibility of a small delay with large scale observations

In all the considerations above, we held the premise, for the sake of discussion, that current cosmic data (at least those that we considered) actually does indicate that the time delay is large. From the marginalized posterior of the dimensionless time delay in Fig. 13 using Hubble data, the mode is actually at the lower bound, \(\bar{\tau } = 0\). We can argue, just from that, that the time delay is indeed small if we take the mode as our “best fit” parameter. But when we start to consider growth data in conjunction with the Hubble data, the mode, median, and mean all clearly shift away from \(\bar{\tau } = 0\). In that case, our “best estimate,” however we define it – mode, median, or mean – will be large. And so we have reported that our best estimate for the time delay is large.

But as we have noted, the Bayes factor actually tells us that there is in fact no conclusive preference for either our best estimate or \(\varLambda \)CDM (which would be indistinguishable from a small delay estimate). This can be expected from our plots in Sects. 3 and 4. Large time delays (at least those around our best estimate) produce predictions close to that of \(\varLambda \)CDM (and therefore, close to those of small time delays). In addition, the uncertainties are much greater than any difference between those predictions.

Therefore, although our marginalized posteriors force us to report a large time delay estimate, it is of course still possible that the time delay is actually small. We can report that the time delay is large with only \(1\sigma \) confidence. Small time delays are already included in the 2\(\sigma \)-contour of the delay posteriors in Fig. 17.

That said, the point of our paper is not to rule out small time delays. These delays trivially satisfy observations. Rather, our point is to show that large time delays, contrary to well-founded expectations, can also satisfy observations. In order to rule out large time delays definitively, we must look to data at larger redshifts where the generic bumps and kinks we have shown are predicted to be present. As we have argued above, we will not be able to impose constraints coming from other scales without a fundamental action prescribing how the time delay appears in those contexts.

7 Conclusion

This paper was motivated by the question of what our cosmological data say about the key parameter of the time-delayed cosmology proposal. One strongly expects that large time delays be disallowed as these lead to a radically different dynamical equation, a delayed Friedmann equation, that we expect would provide discordant predictions. This is fair, but it is an assumption. In this work, we have instead subjected this expectation to a test. Our work is thus meant to be an initial data-driven assessment of time-delayed cosmology.

We applied the delayed Friedmann equation in the late-time Universe and chose the Hubble expansion rate H(z) and Newtonian matter perturbations as our observational probes. We obtained the predictions for the late-time background evolution and the growth data. In calculating the growth observables, we have used the standard perturbation equation and assumed that the effects of time-delayed cosmology enter through the background expansion only. We find that the conservative assumptions we have made are sufficient to reveal smoking-gun imprints of the phenomenological time delay. These imprints can be credited to the propagation of discontinuities inherent in the solutions of delay differential equations. This is the first time that the effects of these discontinuities have been demonstrated in this model.

We unexpectedly find that a significantly large time delay is not ruled out by the probes we considered, in stark contrast to prevailing expectations. This surprising result is one of the main takeaways from our paper. Our best estimate of the key time delay parameter is \(\tau = 0.0993^{+0.0799}_{-0.0664}\) Gyr using the combined Hubble expansion rate and growth datasets. This is clearly many orders of magnitude larger than Planck time. We also calculated the Bayes factor and find no conclusive evidence in favor of \(\varLambda \)CDM against time-delayed cosmology.

Admittedly, the large time delays forced upon us by our data analysis is theoretically quite unpalatable. But we argue that this is precisely what lends the result its significance. It is difficult to imagine that a large time delay in gravitational dynamics can be compatible with Solar System and gravitational wave observations, even though we are unable to check this ourselves because time-delayed cosmology is merely a phenomenological proposal that does not really extend to those scales and still awaits a fundamental action. The consequences of a time delay for smaller scales certainly needs further exploration, but this goes beyond the scope of our work. Here, we have taken time-delayed cosmology at face value – as a phenomenological model meant solely for cosmology – that therefore demands empirical testing. Our work may however be informative in tackling these theoretical problems.

Future large-scale structure surveys [62, 63] and high redshift distance indicators such as proposed standardizable candles (quasars [64] and gamma ray bursts [65]) and standard sirens [66, 67] can be expected to further constrain the time delay. We leave to future work the search for a fundamental action that supports a time-delayed cosmology.