New Hubble parameter data and possibility of more than one deceleration–acceleration transition redshift

Abstract

It is quite believed that Universe has undergone a smooth transition from a decelerated phase to its present accelerated phase of expansion. There exists a wide consensus, based on robust observational indicating transition redshift $z_{tr}$ around the unity. However our analysis on complete collection of reliable Hubble parameter H(z) data at intermediate redshift $0.07<z <2.36$, BAO, Pantheon data, give some hints that the universe may be transit more than one time from deceleration to acceleration phase in course of its evolution. Although we are agree with the results claimed by previous studies state the simplest cosmological models such as $\Lambda CDM$ and XCDM are consistent with Hubble data, but we doubt that they will be the best. We show that the chameleon cosmological model is more favored than the simple models and very well fits with the full Hubble data. Reconstructing the deceleration parameter based on best fitted parameters of the model indicates a new dynamic for the universe in which more than one transition occurs from deceleration to acceleration phase and the last transition occurs at $z_{tr}\simeq .43\pm 0.04$ which is close to that derived by the High-z Supernovae Search (HZSNS) team, $z_{tr}=.43\pm 0.07$ (Riess et al. Astrophys. J. 659, 98–121, 2007).

1 Introduction

It is quite evident that the universe has undergone a smooth transition from a decelerated phase to its present accelerated phase of expansion [1, 2]. Although there exists a wide consensus, based on robust observational indicating transition redshift $z_{tr}$ around the unity [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17]. However, until very recently, this has not been possible to estimate the redshift of the deceleration–acceleration transition with high precision because there has not been much high-quality data at high enough redshift above the transition redshift. The authors of [14] compile and updated list of 38 measurements of the Hubble parameter H(z) between redshifts $0.07<z<2.36$ and use them to place constraints on model parameters. They measured the redshift of the cosmological deceleration–acceleration transition, $z_{tr}$, from these H(z) data. For $H_{0}=68\pm 2.8(73.24\pm 1.74)$ km s$^{-1}$ Mpc$^{-1}$, they have derived $z_{tr}=0.72\pm 0.05 (0.84\pm 0.03)$. The author of [3] have used list of 36 measurements of the Hubble parameter H(z) between redshifts $0.07<z<2.36$ and find the transition redshift varying over $0.33<z_{tr}<1$.

Previous studies have measured transition redshift from these data using well known models such as $\Lambda$CDM, XCDM and $\phi$CDM [3, 14] and [17]. While the consistency of these results are encouraging, our analysis show that chameleon cosmological model is much more consistence with these data. Reconstructing the redshift evolution of the deceleration parameter q(z) in the best fitted model shows that there is more than one transition from deceleration to acceleration phase in course of the evolution of the universe. Interestingly, our result show the last transition occurs at $z_{tr}\simeq .43\pm 0.04$ which is close to that derived by the High-z Supernovae Search (HZSNS)team, $z_{tr}=.43\pm 0.07$ [28] (Table 1).

Table 1 Hubble parameter vs. redshift data

We use Jacobin stability as a robustness tool to demonstrate this behavior in phase space. More analysis show that potential is responsible for the spiral behavior of the Universe. Our stability analyzing simultaneously best fitting the model with observational data show that for the best-fitted $(\alpha ,\beta )$, the universe starts from unstable point in the past, spirally moves towards a stable focus in future. This spiral behavior of the universe in phase plane indicates that deceleration parameter has an oscillating behavior which transits from deceleration to acceleration phase for more than one time. As it is believed dark energy dominates the current cosmological energy budget and is responsible for the currently accelerating cosmological expansion; Hence it is speculated that the universe perhaps has experienced several dark energy epoches in course of its evolution. This dynamic behavior is profoundly different from the standard $\Lambda CDM$ evolution, and may alleviate some conflicts in reconciling the idea of a dark energy-dominated universe with observable in String/M-theory (see [29,30,31,32]).

The universe with two transition indicates that the accepted scenario (inflation followed by radiation, dark matter and dark energy dominated stages) in which only one transition is predicted, need to be improved by the (inflation followed by radiation, dark matter, dark energy,dark mater and dark energy) scenario in which the Universe already had two accelerating stages.

The fact that most previous studies have obtained only one transition redshift may be due to the fact that

• 1. Until very recently there has not been much high-quality data at high enough redshift above the transition, hence it has not been possible to estimate the redshift of the deceleration–acceleration transition with high precision. Hence the recent high redshift data such as compilation of 38 measurements of the Hubble parameter H(z) between redshifts $0.07<z<2.36$ as well as the new “Pantheon” sample of [38], which include 1048 supernovae spanning the redshift range $0.01< z < 2.3$ enable us to estimate the redshift of the deceleration–acceleration transition with high precision.

• 2. Most of the theoretical estimation of transition redshift measurements have been done in $\Lambda CDM$ model in which the transition redshift is obtained as [14]

  $$\begin{aligned} z_{tr}=\left( \frac{2\Omega _{\Lambda }}{\Omega _{m}}\right) ^{\frac{1}{3}}-1 \end{aligned}$$

  (1)

  Where, there is only one solution.The structure of the paper is as follows. Section 2 introduces the chameleon model, while Sect. 3 describes the stability analysis of the model. Section 4 presents observational analysis and results and we conclude the article in Sect. 5.

2 Chameleon field

Chameleon field has been suggested by [33,34,35]. The cosmological value of such a field evolves over Hubble time-scales and could potentially cause the late-time acceleration of our Universe [36]. The crucial feature that these models possess are that the mass of the scalar field depends on the local background matter density. The action of chameleon gravity given by,

$$\begin{aligned} S= & {} \int \left[ \frac{m^{2}_{pl}}{16\pi } R-\frac{1}{2}\phi _{\mu }\phi ^{\mu }+V(\phi )\right] \sqrt{-g}dx^{4}\nonumber \\ {}{} & {} +\int L_{m}(\Psi ^{(i)},g^{i}_{(\mu \nu )})dx^{4} \end{aligned}$$

(2)

where the matter fields $\Psi ^{(i)}$ are coupled to scalar field $\phi$ by the definition $g^{(i)}_{\mu \nu }=e^{\frac{2\beta _i\phi }{m_{pl}}}g_{\mu \nu }$. The $\beta _{i}$ are dimensionless coupling constants, one for each matter species. In the following, we assume a single matter energy density component $\rho _{m}$ with coupling $\beta$. The variation of action (1) with respect to the metric tensor components in a spatially flat FRW cosmology yields the field equations,

$$\begin{aligned} 3H^{2}m^{2}_{pl}= & {} \rho _{m}e^{\frac{\beta \phi }{m_{pl}}}+\frac{1}{2}\phi \dot{}^{2}+V(\phi ), \end{aligned}$$

(3)

$$\begin{aligned} (2\dot{H}+3H^{2})m^{2}_{pl}= & {} -\gamma \rho _{m}e^{\frac{\beta \phi }{m_{pl}}}-\frac{1}{2}\phi \dot{}^{2}+V(\phi ), \end{aligned}$$

(4)

where in deriving the field equations we assumed a perfect fluid for matter field with $p_{m}=\gamma \rho _{m}$. Variation of the action (1) with respect to scalar field $\phi$ provides the wave equation for chameleon field as

$$\begin{aligned} \phi \ddot{}+3H\phi \dot{}=-\frac{dV}{d\phi }-\frac{\beta }{m_{pl}}\rho _{m}e^{\frac{\beta \phi }{m_{pl}}} \end{aligned}$$

(5)

where prime indicated differentiation with respect to $\phi$.

3 Stability

Fig. 1

The constraints at the $68.3\%$, $95.4\%$ and $99.7\%$ confidence levels for parameters $(\alpha ,\beta )$,from H(z)(CC), Pantheon, BAO and combination, Pantheon +CC+ BAO data

In this section, we study the structure of the dynamical system via phase plane analysis. We assume that the universe is filled with cold dark matter, i.e. $\gamma =0$. We introduce the following dimensionless variables,

$$\begin{aligned} \Omega _{ch}=\frac{\rho _{m}e^{\frac{\beta \phi }{m_{pl}}}}{3H^{2}m^{2}_{p}},\Omega _{\phi }=\frac{\phi \dot{}}{\sqrt{6}H m_{pl}},\Omega _{V}=\frac{V}{3H^{2}m^{2}_{pl}} \end{aligned}$$

(6)

We consider the potential $V(\phi )=V_{0}e^{\frac{\alpha \phi }{m_{pl}}}$ where $\alpha$ is dimensionless constants characterizing the slope of potential. Then using Eqs. (3)–(5), the evolution equations of these variables become,

$$\begin{aligned}{} & {} \Omega _{\phi }^{\prime }=-3\Omega _{\phi }+\frac{3}{2}\Omega _{\phi }\Omega _{ch}+3\Omega _{\phi }^{3}-\frac{\sqrt{6}}{2}\beta \Omega _{ch}-\frac{\sqrt{6}}{2}\alpha \Omega _{V} \nonumber \\ \end{aligned}$$

(7)

$$\begin{aligned}{} & {} \Omega _{ch}^{\prime }=-3\Omega _{ch}+3\Omega _{ch}^{2}+\sqrt{6}\beta \Omega _{\phi }\Omega _{ch}+6\Omega _{\phi }^{2}\Omega _{ch} \end{aligned}$$

(8)

$$\begin{aligned}{} & {} \Omega _{V}^{\prime }=\Omega _{V}(\sqrt{6}\alpha \Omega _{\phi }+\Omega _{ch}+6\Omega _{ch}^{2}) \end{aligned}$$

(9)

where prime from now on indicated differentiation with respect to $N = ln a$. The Friedmann constraint equation (3) also becomes

$$\begin{aligned} \Omega _{\phi }^2+\Omega _{ch}+\Omega _{V}=1 \end{aligned}$$

(10)

In term of the new dynamical variable the deceleration parameter will be

$$\begin{aligned} q=-\left( 1+\frac{\dot{H}}{H^{2}}\right) =-1+\frac{3\Omega _{ch}}{2}+3\Omega _{\phi }^{2} \end{aligned}$$

(11)

Using the constraint (10), the Eqs. (7)–(9) are converted to

$$\begin{aligned} \Omega _{\phi }^{'}= & {} -3\Omega _{\phi }+\frac{3}{2}\Omega _{\phi }\Omega _{ch} +3\Omega _{\phi }^{3}-\frac{\sqrt{6}}{2}\beta \Omega _{ch} \nonumber \\{} & {} -\frac{\sqrt{6}}{2}\alpha (1-\Omega _{\phi }^{2}-\Omega _{ch}) , \end{aligned}$$

(12)

$$\begin{aligned} \Omega _{ch}^{'}= & {} -3\Omega _{ch}+3\Omega _{ch}^{2}+\sqrt{6}\beta \Omega _{\phi } \Omega _{ch} +6\Omega _{\phi }^{2}\Omega _{ch}, \end{aligned}$$

(13)

It is more convenient to investigate the properties of the dynamical system Eqs. (12) and (13) than Eqs. (7)–(9). We obtain the fixed points (or critical points) and study the stability of these points. Critical points are always exact constant solutions in the context of autonomous dynamical systems. These points are often the extreme points of the orbits and therefore describe the asymptotic behavior. In the following we find fixed points by simultaneously solving $\frac{d\Omega _{\phi }}{dN}=0$ and $\frac{d\Omega _{ch}}{dN}=0$. Substituting linear perturbations $\Omega _{\phi }'\rightarrow \Omega _{\phi }'+\delta \Omega _{\phi }'$, $\Omega _{ch}'\rightarrow \Omega _{ch}'+\delta \Omega _{ch}'$ about the critical points into the two independent equations (12) and (13), to the first orders in the perturbations, which yield two eigenvalues $\lambda _{i} (i=1,2)$. Stability requires the real part of all eigenvalues to be negative. Solving the above equations we find five fixed points which some of them explicitly depend on $\beta$ and $\alpha$, as illustrated in Table 2.

Table 2 Critical points

Critical points, $A_{\pm }$, corresponding to two kinetic-dominated solutions. These are equivalent to the stiff-fluid-dominated evolution with $a=t^{\frac{1}{3}}$, irrespective of the nature of the potential. The kinetic-dominated solution for $A_{+}$ has two eigenvalues, $\lambda _+=3+\beta \sqrt{6},\lambda _-=6+\sqrt{6} \alpha$,

Critical point, B, corresponding to a potential-kinetic-scaling solution. This solution exists for all kinds of potentials, and has two eigenvalues depending on the slope of the potential and coupling constant $\beta$: $\lambda _+=-3+\frac{\alpha ^2}{2} \,, \qquad \lambda _-=-\beta \alpha +\alpha ^2-3.$

As, the solution is stable for

$$\begin{aligned} \left\{ \begin{array}{ll} \beta<\frac{-3+\alpha ^{2}}{\alpha },&{}\quad -\sqrt{6}<\alpha<0\\ \beta >\frac{-3+\alpha ^{2}}{\alpha },&{}\quad 0<\alpha <\sqrt{6} \end{array} \right. \end{aligned}$$

which means that the potential-kinetic-dominated solution is stable for a sufficiently flat potential ($\alpha ^{2}<6$).

Critical point C , corresponds to the fluid-kinetic-scaling solution. This solution depends on the coupling constant $\beta$ and exists for all potentials. It has two eigenvalues depending on both $\alpha$ and $\beta$: $\lambda _+ = -3/2+\beta ^2$ and $\lambda _- = 3+2 \beta ^2-2 \beta \alpha$. The solution is stable for

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha<\frac{3+2\beta ^2}{2\beta },&{}\quad -\sqrt{\frac{3}{2}}<\beta<0\\ \alpha >\frac{3+2\beta ^2}{2\beta },&{}\quad 0<\beta <\sqrt{\frac{3}{2}} \end{array} \right. \end{aligned}$$

Critical point, D corresponds to a fluid potential-kinetic-scaling solution with eigenvalues

$$\begin{aligned} \lambda _+=\frac{\frac{3}{2}\beta -\frac{3}{4}\alpha +\sqrt{A}}{-\beta +\alpha } \, \qquad \lambda _{-} =\frac{\frac{3}{2}\beta -\frac{3}{4}\alpha -\sqrt{A}}{-\beta +\alpha } \end{aligned}$$

where $A=180\beta ^2-108\beta \alpha -63\alpha ^2-96\beta ^2\alpha ^2+48\beta ^3\alpha +48\beta \alpha ^3+216$.

4 Analysis and results

Table 3 Mean values of free parameters of chameleon model with 1$\sigma$ error bar for different data

Table 4 Mean values of free parameters of various models with 1$\sigma$ error bar for 33 Hubble data

In this section, we report the constraint results of cosmological parameters for the model. The fitting results are listed in Tables 3 and 4.

$\bullet$ Pantheon The use of type Ia supernovae (SNe) as standard candles has been of critical importance to cosmology, leading to the discovery of cosmic acceleration [37, 39]. In this paper, we use the new “Pantheon” sample of Scolnic et al. [38], which adds 276 supernovae from the Pan-STARRS1 Medium Deep Survey at $0.03< z < 0.65$ and various low-redshift and HST samples to give a total of 1048 supernovae spanning the redshift range $0.01< z < 2.3$

The luminosity distance $d_{L}$ can be calculated by

$$\begin{aligned} d_{L} =(1+z)\int \frac{dz}{H(z)} \end{aligned}$$

(14)

In order to incorporate the Eq. (14) with the dynamical system equations of (12)–(13), it can be rewritten in terms of the following differential equations

$$\begin{aligned}&\frac{dd_{L}}{dN}=-d_{L}-\frac{e^{-2N}}{H} \end{aligned}$$

(15)

$$\begin{aligned}&\frac{dH}{dN}=H \left( \frac{\dot{H}}{H^{2}}\right) \end{aligned}$$

(16)

The distance modulus also can be obtained as $\mu _{th}(z)=5\log (d_{L})+42.38$. we can compute the $\chi ^2$-statistics for each case. Therefore, we proceed to define the following quantities:

$$\begin{aligned} \chi ^{2}_{\text {Pantheon}}= \sum _{i}^{N_{\text {Pantheon}} }\frac{ \left( \mu (z_{i})_{\text {obs}}- \mu (z_{i})_{\text {th}} \right) ^{2} }{\sigma (z_{i})_{\text {obs,\; Pantheon}}^{2}}, \end{aligned}$$

(17)

where N is the number of data points, $\sigma _{i}$ is the uncertainty associated with each measurement.

$\bullet$ Baryon acoustic oscillations BAO data

We use the BAO measurements from 6dFGS at $z = 0.106$ [50], SDSS DR7 at $z = 0.15$ [51], BOSS DR12 at $z = 0.38, 0.51$ and 0.61 [52], and the joint constraints from eBOSS DR14 Ly-a autocorrelation at $z = 2.34$ [53] and cross-correlation at $z = 2.35$ [54] While acoustic oscillations were already incorporated in early theoretical calculations of CMB anisotropies [43]. interest in using the BAO feature as a “standard ruler” in galaxy clustering grew after the discovery of cosmic acceleration [44,45,46]. The physics of BAO and contemporary methods of BAO analysis are reviewed at length in Ch. 4 of [47].

In brief, pressure waves in the pre-recombination universe imprint a characteristic scale on late-time matter clustering at the radius of the sound horizon,

$$\begin{aligned} r_{d} = \int _{z_d}^\infty {c_s(z) \over H(z)}dz, \end{aligned}$$

(18)

evaluated at the drag epoch $z_d$, shortly after recombination, when photons and baryons decouple (see [48] for more precise discussion). This scale appears as a localized peak in the correlation function or a damped series of oscillations in the power spectrum. Assuming standard matter and radiation content, the Planck 2015 measurements of the matter and baryon density determine the sound horizon to 0.2%. An anisotropic BAO analysis that measures the BAO feature in the line-of-sight and transverse directions can separately measure H(z) and the comoving angular diameter distance $D_{M}(z)$, which is related to the physical angular diameter distance by $D_{M}(z) = (1+z)D_{A}(z)$, [49] Adjustments in cosmological parameters or changes to the pre-recombination energy density (e.g., from extra relativistic species) can alter $r_{d}$, so BAO measurements really constrain the combinations $D_{M}(z)/r_{d}$, $H(z)r_{d}$. An angle-averaged galaxy BAO measurement constrains a combination that is approximately

$$\begin{aligned} D_{V}(z) = \left[ cz D_{M}^2(z)/H(z)\right] ^{1/3}. \end{aligned}$$

(19)

$\bullet$ CC We use the compilation of 33 H(z) reliable data points, 31 data from Table 2 of [17] and two high redshift data from table I of [3] as reproduced here in Table 1 to constrain the model parameters under consideration by using the Markov Chain Monte Carlo method by minimizing $\chi _{H}^2$,

$$\begin{aligned} \chi _{H}^2 ({\textbf {p}}) = \sum _{i=1}^{N}\frac{[H^\textrm{th} (z_i; {\textbf {p}})-H^\textrm{obs}(z_i)]^2}{\sigma ^2_{\textrm{H},i}}, \end{aligned}$$

(20)

We also used the Bayes Information Criteria

$$\begin{aligned} BIC=\chi ^{2}_{min}+klnN \end{aligned}$$

(21)

and the Akaike Information Criteria

$$\begin{aligned} AIC=\chi ^{2}_{min}+2k \end{aligned}$$

(22)

In these equations $\chi ^{2}_{min}$ is the minimum value of $\chi ^{2}$, k is the number of parameters of the given model, and N is the number of data points. BIC and AIC provide means to compare models with different numbers of parameters; they penalize models with a higher k in favor of those with a lower k , in effect enforcing Occam’s Razor in the model selection process.

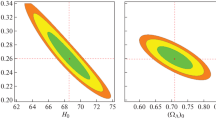
In order to obtain observational constraints on parameter of the model and initial conditions, we perform a Monte Carlo fitting using supernova data, involving the most recent H(z) data data set. The best fitted values for parameters $(\alpha ,\beta )$ and initial conditions $(\Omega _{ch}(0),\Omega _{\dot{\phi }}(0))$ for different data set have been listed in Table 3. For example for CC data , we find the best value for parameters $(\alpha ,\beta )$ as $(\alpha =-4.793,\beta =6.92)$. Figure 1 shows the confidence level for these parameters. We find the best fitted for initial conditions as $(\Omega _{ch}(0)=0.275,\Omega _{\dot{\phi }}(0)=0.4)$. We also performed the analysis for $\Lambda$ CDM and XCDM models

Our results are summarized in Tables 3, 4. As can be seen from these models, chameleon model has the lowest $\chi ^{2}_{min}$ and AIC as $\chi ^{2}_{min}=11.15$ and $AIC=21.15$. For the best fitted parameters $(\alpha ,\beta )$, the nature of the critical pints of system are determined. For example for best fitted values of CC data, the eigenvalues for $A_{\pm }$ are $(\lambda _{+}=3\pm 6.92\sqrt{6},\lambda _{-}=6\mp 4.793\sqrt{6})$ which indicates that both of them are saddle points. The eigenvalues for B and C are $(\lambda _{+}=8.5,\lambda _{-}=53.1)$ and $(\lambda _{+}=165.1,\lambda _{-}=46.4)$ respectively which both are unstable points. The eigenvalues for D is $(\lambda _{+}=-1.1+6.9I, \lambda _{-}=-1.1-6.9I)$ which is stable focus. The phase space around critical point D for best fitted parameters $(\alpha ,\beta )$ have been shown in Fig. 2. The best trajectory which is determined by the best fitted parameters and best fitted initial conditions have been shown in top panel of Fig. 2. Since the elements of the eigenvalue are imaginary with negative real parts, the nature of the critical point is stable focus and the trajectories have spiral behavior around it. Note that behavior of the system for the best fitted parameters of all data set are the same. Figure 3 shows the evolution of deceleration parameter for best fitted , $+1\sigma$ and $-1\sigma$ of best fitted parameters for CC data and Fig. 4 show the evolution of the deceleration parameter against redshift for the best fitted parameters and initial conditions for different data set. It shows that the model allows transition from a decelerating phase (matter dominated era) to an accelerating phase (dark energy epoch) for more than one time.

Fig. 2

The behavior of the dynamical system in the $\Omega _{ch},\Omega _{\phi }$ phase plane for best fitted $\alpha =-4.793$ and $\beta =6.92$. Top panel shows the best trajectory of the phase space for both best fitted parameters $\alpha =-4.793$ and $\beta =6.92$ and initial conditions $(\Omega _{ch}(0)=0.275,\Omega _{\dot{\phi }}(0)=0.4)$

Fig. 3

The plot of deceleration parameters for the best-fitted values of $(\alpha ,\beta )$,$(\alpha =-4.793,\beta =6.92)$ and initial conditions

Fig. 4

The plot of deceleration parameters q for the best-fitted values of parameters of $(\alpha ,\beta )$ using different dataset

Fig. 5

The plot of parameters H for the best-fitted, upper line with $+1\sigma$ and a lower line with $-1\sigma$ values of $(\alpha ,\beta )$ and initial conditions in chameleon model and redshift range $0.07<z<2.36$

Fig. 6

The plot of parameters H for the best-fitted parameters and initial conditions in chameleon model for different data set

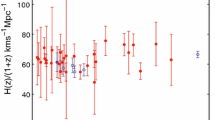
From stability analysis in the previous section, we found that with some parameters in the model, the universe approaches stable points or attractors in its journey. In particular, Figs. 2, 3 and 4 show that by perturbing the dynamical variables in the model, the universe starts from an unstable phase in the past, continue its journey to reach an stable phase in the far future while currently is in an accelerating phase. Figures 3, 4 show the reconstructed parameter q as for best fitted parameters ($\alpha ,\beta$) and initial condition for different data set. As can be seen from Figs. 3, 4, the deceleration parameter q has an oscillating behavior which transits from deceleration to acceleration phase for more than one time. Figures 5, 6 show the plot of H(z) for best fitted of parameters ($\alpha ,\beta$) using different data set.

Fig. 7

The Histogram of parameters $\alpha ,\beta$ and $\chi ^{2}_{min}$ for Bootstrap and original sample

Fig. 8

The plot of H(z) and q(z) for Bootstrap sample

5 Bootstrap procedure

Bootstrapping methods are a numerical approach to generating confidence intervals that use either restamped data or simulated data to estimate the sampling distribution of the maximum likelihood parameter estimates. In particular, bootstrapping can, in principle, generate an estimate of both the bias and standard error for any statistical parameter of interest. Bootstrapping involves drawing a series of random samples from the original sample – with replacement – a very large number of times. The statistic or relationship of interest is then calculated for each of the bootstrap samples. The resulting distribution of the calculated values then provides an estimate of the sampling distribution of the statistic or relationship of interest.

We also use bootstrap procedure to test the validation of our analysis. In this paper we use the Bootstrap method with number of samples $(N_{b})$ and number of data $(n_{b})$. Note that the number of H(z) data are 32. However we can chose random samples with more or less than 32 data. Here we have generated $(N_{b})=800$ sample $(n_{b}=32)$ data randomly from the original sample (32H(z)data) and performed $\chi ^{2}$ analysis for each sample such as what we performed for original sample. The histogram for important parameter of the model $(\alpha ,\beta )$ have been plot and compared with the result with original sample. For original data (32 H(z) data), we have found the best values as $\alpha =-4.695$,$\beta =7.52$ with $\chi ^{2}_{min}=11.106$.

For bootstrap sample, the most probability is for $\alpha =-4.7$ and $\beta =9$ and $\chi ^{2}_{min}=11.11$ which is close to our result. Figures 7, 8 show, the plots of H(z) and q(z) for all bootstrap sample. The plots indicates that the bootstrap are consistence with our results.

6 Conclusion

We have implemented the last list of 33 measurements of the Hubble parameter H(z) in redshifts $0.7<z <2.36$ [17], Pantheon, BAO and combination of the data to examine transition redshift in chameleon cosmology. While the transition redshift using simple models $\Lambda CDM$,XCDM,$\omega CDM$ and $\phi CDM$ model very well fits with these Hubble data, however more analysis show that more favorite than these simple models, chameleon cosmology is consistent with these data. In this paper, we have analyzed chameleon cosmology in presence of an exponential potential $V=V_{0}e^{\frac{\alpha \phi }{m_{pl}}}$. The two parameters $(\alpha ,\beta )$ which are important in chameleon cosmology play also important role in dynamic of the universe and its stability. In order to find the best dynamic for the universe based on the recent H(z) data, we have best fitted these two parameters using $\chi ^{2}_{min}$ method. We have found that the best values of $(\alpha ,\beta )$ and initial condition as $(\alpha =-4.793,\beta =6.92)$ and $(\Omega _{ch}(0)=0.275,\Omega _{\dot{\phi }}(0)=0.4)$, with $\chi ^{2}_{min}=11.27$. Visualization of dynamic of the chameleon model in phase space using Jacobian stability shows that for the best values of $(\alpha ,\beta )$ and initial conditions the chameleon cosmology has attractor behavior around an critical point with nature of stable focus . Interestingly this behavior is equivalent to oscillating behavior of deceleration parameter as shown in Fig. 4. In spite of our expectation that the universe must transits from deceleration to acceleration only one time, the best fitted chameleon cosmology predicts an oscillating behavior for the dynamic of the universe with more than one transition from deceleration to acceleration phase. The question which may arises is that is this behavior related to chameleon model or it is intrinsic property of the universe. Note that although this behavior has been derived from chameleon cosmology, however, distribution of H(z) data in $H-z$ plane (Figs. 5, 6), hints that this behavior is intrinsic property of the universe and a model such as chameleon can interpret it well. The analysis showed that the results of Pantheon, BAO and combination of the data are also consistence with the result of CC data. By looking at the distribution of H(z) data one can deduct that based on the slope of the distribution, the H(z) data can be classified to different slices as $0<z<0.5$, $0.5<z<1$, $1<z<2$ and the two last H(z) data. These slices have different slope. Hence the curve which passes through these four slices in the best way possible, is the best trajectory for H(z). It seems that this condition could not be satisfied by curves which are monotonically increasing functions of z. Because by looking at the distribution of the data, one can see that while some data located in larger redshift, they have lower value of Hubble parameter and the data approximately located on the way to a spiral path. The best fitted of three different models have the same behavior for redshift $0<z<0.5$ (see Fig. 5), but while $\Lambda$ CDM and XCDM have approximately the same behavior for $0.07<z<2.36$, from redshift $z=0.5$, the chameleon model separates its path from the other two models and in the end of the data where the two high z data located, it comes to the other two models again. It is important to note that both $\Lambda$CDM and XCDM models are monotonically increasing function of z. In contrast, the trajectory of H(z) for best fitted chameleon model has the spiral behavior and it can satisfy this condition. In other word the spiral behavior is more than monotonically increasing function of z intimate with the Hubble data. In particular it seems that at first the data between $1<z<2$ pull the trajectory of H(z) downward and deviate it from monotonically increasing form then the two last data upward it again. Hence the curve breaks slowly two times. In addition to chameleon model, we have examined the Brans Dick theory by these data, the same results have been obtained for Brans Dick theory. Note that the alignment between chameleon model and Brans Dick theory may be not surprising, because under appropriate conformal transformation, it is possible to mapping Brans -Dick theory to chameleon gravity .