${\textbf{D}}$-dimensional dyonic AdS black holes with quasi-topological electromagnetism in Einstein Gauss–Bonnet gravity

Abstract

Within Gauss–Bonnet gravity, we construct a solution endowed with dyonic matter fields in a higher dimension. The quasi-topological electromagnetism generates two kinds of contributions; one is the kinetic terms, and the second refers to the interactif terms. This overcomes the invariance topological problem. We investigate the thermodynamical proprieties of the obtained solution, namely, ADM mass, Hawking temperature, and entropy. To inspect the local stability, we examine the associated heat capacity. With regards to optical proprieties, we analyze the null geodesic in terms of the given parameter space. The shadow radius is a generating form with all the physical parameters that govern the shadow behavior. The study restricts only the taking of the effects of the D and $\alpha$ parameters. Finally, we examine the impact of the dimension D, GB coupling constant $\alpha$, the cosmological constant $\Lambda$, the electric $q_e$, the magnetic charge $q_m$ and the coupling constant $\beta$ on the energy emission rate.

1 Introduction

Quasi-topological electromagnetism [1] is considered as an alternative way restoring the dynamic contribution at the level of the equation of motion. The fact that the Maxwell field strength is a topological invariant, as well as the Riemann curvature tensor, all of which are 2-forms.

$$\begin{aligned} \int tr(R\wedge R), \quad \int F\wedge F. \end{aligned}$$

(1.1)

These quantities remain independent of the spacetime metric. To obtain dependancy with the metric, it is necessary to take into consideration another purely magnetic field yielding dyonic objects. The starting point is the introduction of supplemented terms within the corresponding lagrangian, which are related to topological invariants.Indeed, in dimension $D=2k$, any 2k-forms Maxwell field strength is used to build the topological structure, $V_{[2k]}=F_{[2]}\wedge F_{[2]}\wedge \cdots \wedge F_{[2]}$. In order to carry out this treatment, we consider the squared norm combining both electric and magnetic field strengths as follows

$$\begin{aligned} U_{[D]}^{(k)}\sim |V_{[2k]}|^{2}\sim V_{[2k]}\wedge \star V_{[2k]}. \end{aligned}$$

(1.2)

The particular case $k=1$ refers to the Maxwell term. Consequently, these invariants remove the noncontribution to the field equations.

In recent years, the thermodynamics of black holes has attracted a lot of interest in the field of theoretical physics. Since then, several studies have been conducted in favor of constructing a thermodynamic framework using the techniques of classical physics [2,3,4,5]. Kastor, Ray, and Traschen [6] were the first to invent the extended version of phase space thermodynamics, also known as black hole chemistry [7], to focus on this goal. The fundamental idea of this approach requires the consideration that pressure is a negative cosmological constant. Mass has the property of being the enthalpy in this formulation. The equation of state $P-v$ accurately represents the small-large black hole phase transition in AdS black holes from the point of view of the liquid-gas in the Van der Waals (VdW) fluid [8]. To consider AdS black holes as heat engines [9, 10], the variables P and V are used. On the other hand, many contributions have affected the development of gravity models, leading to a new understanding of thermodynamics. By the way, the AdS/CFT duality [11], also known as the holographic principle [12, 13], allows a better understanding of the nature of microscopic degrees of freedom, which contributes to the entropy of the black hole. According to this duality, the dual field theory thermal state is identical to the location of the AdS black hole state in the mass.

Lanczos D. Lovelock [14,15,16] discovered a natural extension framework for Einstein’s theory to higher dimensions. In a special dimension, the Lovelock lagrangian gets different theoretical aspects. More specifically, in three and four dimensions $(D = 3, 4)$, Lovelock’s theory reduces to Einstein’s theory. The second order of the Lovelock theory corresponds to the quadratic tensor of the Gauss–Bonnet term, which turns into a topological surface term and starts being non-trivial in $D=5$ dimensions. On the other hand, there was the most linked investigation concerning the Lovelock gravities in the context of cosmological models [17] and in the cosmological background through string theories. Furthermore, the quadratic Gauss–Bonnet term appropriate to the 2nd order of Lovelock gravities in four dimensions can be derived from the low energy effective action of heterotic string theory [18,19,20,21] and also formed in the six-dimensional Calabi–Yau compactification of M-theory [22, 23], and the theory is free of ghosts of other exactions [24, 25]. After all, a few insights into the quadratic term of Gauss–Bonnet were elaborated in the frame of a spherical black hole by Boulware and Deser in $D > 5$ spacetime [24,25,26,27]. Recent works on Gauss–Bonnet theory have succeeded in interpreting the 4D topological invariant by rescaling the GB coupling constant [28]. As a result, the EGB theory becomes a fruitful sector to explore black hole properties [29,30,31].

The observation of a black hole shadow offers a technique to deal with topological background, in a way that both shape and size are given in terms of the black hole parameters. Generally, the shadow of a Schwarzschild–Tangherlini black hole is perfectly circular [32], but for a Kerr black hole, the shadow is distorted [33]. Recent observations have managed to show, with the help of informatics data, a simulated image with regard to black objects. Roughly speaking, the M87* picture [34, 35], yielded an intensive study of the black hole shadow in different gravity models [36,37,38,39,40,41,42,43].

The outline of this paper is as follows: in Sect. 2, we built a D-dimensional black solution in the frame of EGB gravity with a quasitopological electromagnetism source. Section 3 is devoted to computing the relevant thermodynamic quantities and analyzing the local stability. In Sect. 4, we investigate the optical proprieties of our black hole solution.

2 Einstein Gauss–Bonnet with quasitopological electromagnetism

2.1 The set up

The attempt to have a non-linear electrodynamic field as a source of matter in the context of such a gravity model is governed by the Born–Infeld term [44] as the main and first model. The pursuit of this model opens the way for new models such as Euler–Heisenberg [45], ModMax [46], etc. As inspired by these models, quasitopological electromagnetism is considered to be another non-linear electrodynamic field. Certainly, this model borrows ideas from the topological gravity model [47,48,49,50].

An overview of dyonic fields is dedicated to experiencing the situation of a purely electric source [1] with a part of the magnetic field together in a quasi-topological electromagnetism [51, 52]. However, a convenient choice for the gauges fields should be in the following form

$$\begin{aligned} F_ {\mu \nu }\sim h'(r)\delta ^{x^0x^1}_{\mu \nu },\quad H_{\rho _1\cdots \rho _p}\sim \delta ^{x^2\cdots x^D}_{\rho _1\cdots \rho _p}, \end{aligned}$$

(2.1)

with $p=D-2$, in which $F_{\mu \nu }$ and $H_{\rho _1\cdots \rho _p}$ are the electric and magnetic field strength, respectively. From the gauge field structure, it is worth noting that the only non-vanishing terms are the gauges Kinetic $|{\mathcal {F}}_{[2]}|^2\sim F_{\mu \nu }F^{\mu \nu }$ and $|{\mathcal {H}}_{[p]}|^2$, and an interaction term $|{\mathcal {F}}{\mathcal {H}}_{[D]}|^2$ mentioned above. Indeed, one can consider the following quantities:

$$\begin{aligned} {\mathcal {F}}_{[2k]}= & {} F_{[2]}\wedge F_{[2]}\wedge \cdots \wedge F_{[2]}, \quad k\le \lfloor D/2\rfloor , \end{aligned}$$

(2.2)

$$\begin{aligned} {\mathcal {H}}_{[pk]}= & {} H_{[p]}\wedge H_{[p]}\wedge \cdots \wedge H_{[p]}\quad k\le \lfloor D/p\rfloor , \end{aligned}$$

(2.3)

$$\begin{aligned} {\mathcal {F}}{\mathcal {H}}_{[2k+pl]}= & {} {\mathcal {F}}_{[2k]}\wedge {\mathcal {H}}_{[pl]},\quad \lbrace 2k+p\ell \le D\rbrace . \end{aligned}$$

(2.4)

The present step is devoted to constructing the corresponding physical Lagrangian, where the squared norms $| {\mathcal {F}}_{[2k]}|^2$, $| {\mathcal {H}}_{[pk]}|^2$ and $|{\mathcal {F}}{\mathcal {H}}_{[2k+p\ell ]}|^2$ are given in a component notation after using the Hodge product

$$\begin{aligned}{} & {} |{\mathcal {F}}_{[2k]}|^2\sim \delta ^{\rho _1\cdots \rho _{2k}}_{\sigma _1\cdots \sigma _{2k}}F_{\rho _1\rho _2}F_{\rho _3\rho _4}\cdots \nonumber \\{} & {} F_{\rho _{2k-1}\rho _{2k}}F^{\sigma _1\sigma _2}F^{\sigma _3\sigma _4}\cdots F^{\sigma _{2k-1}\sigma _{2k}}, \end{aligned}$$

(2.5)

$$\begin{aligned}{} & {} \mid {\mathcal {H}}_{[pk]}\mid ^2\sim \delta ^{\rho _1\cdots \rho _{pk}}_{\sigma _1\cdots \sigma _{pk}}H_{\rho _1\cdots \rho _p}\cdots H_{\cdots \rho _{pk}}H^{\sigma _1\cdots \sigma _p}\cdots H^{\cdots \sigma _{pk}}, \nonumber \\ \end{aligned}$$

(2.6)

$$\begin{aligned}{} & {} \mid {\mathcal {F}}{\mathcal {H}}_{2k+p\ell }\mid ^2\sim \delta ^{\rho _1\cdots \rho _{2k+p\ell }}_{\sigma _1\cdots \sigma _{2k+p\ell }}F_{\rho _1\rho _2}H_{\rho _3\cdots \rho _{p+2}}\cdots \nonumber \\{} & {} F_{\cdots } H_{\cdots \rho _{2k+p\ell }}F^{\sigma _1\sigma _2}H^{\sigma _3\cdots \sigma _{p+2}}\cdots F\cdots H^{\cdots \sigma _{2k+p\ell }}, \end{aligned}$$

(2.7)

where $\delta ^{\rho _1\cdots \rho _{2k}}_{\sigma _1\cdots \sigma _{2k}}$ denotes the rank-4k skew-symmetric Kronecker delta. While other quadratic terms can arise differently in a mixed manner between the above quantities, as ${\mathcal {F}}_{[2k]}\wedge *{\mathcal {H}}_{[p\ell ]}$ with $2k=p\ell$ and $k\le \lfloor D/2\rfloor$, ${\mathcal {F}}_{[2k]}\wedge *{\mathcal {F}}{\mathcal {H}}_{[2q+p\ell ]}$ with $p\ell =2(k-q)$ and $k\le \lfloor D/2\rfloor$ where $\lfloor \,\rfloor$ is the floor function, as well as ${\mathcal {H}}_{[pk]}\wedge *{\mathcal {F}}{\mathcal {H}}_{[2q+p\ell ]}$ with $2q=p(k-\ell )$ and $k\le \lfloor D/p\rfloor$. Basically, all these invariant quantities contribute reasonably to the field equations and, therefore, formulate the matter part of the considered action.

Consequently, we consider a D-dimensional action referred to a gravity sector in the essence of the Einstein Gauss–Bonnet theory, and in a part to a matter field labeled by a Quasi-Topological Electromagnetism in the form

$$\begin{aligned}{} & {} S_D\left[ g_{\mu \nu },A_\mu ,B_{\lambda _1\cdots \lambda _{p-1}}\right] \nonumber \\{} & {} \quad =\frac{1}{16\pi }\int d^Dx\sqrt{-g}\left( R-2\Lambda +\alpha {\mathcal {G}}+{\mathcal {L}}_{QTE}\right) , \end{aligned}$$

(2.8)

where the matter field is represented by the following Quasi-Topological Electromagnetism Lagrangian

$$\begin{aligned} {\mathcal {L}}_{QTE}=-\left( \frac{1}{4}F^2+\frac{1}{2p!}H^2+\beta {\mathcal {L}}_{int}\right) \end{aligned}$$

(2.9)

with $F^2=F_{\mu \nu }F^{\mu \nu }$ and $H^2=H_{\rho _1\cdots \rho _p}H^{\rho _1\cdots \rho _p}$, and the interaction term is given by

$$\begin{aligned} {\mathcal {L}}_{int}=\delta _{\gamma _1\cdots \gamma _D}^{\lambda _1\cdots \lambda _D}F_{\lambda _1\lambda _2}H_{\lambda _3\cdots \lambda _D}F^{\gamma _1 \gamma _2}H^{\gamma _3\cdots \gamma _D}. \end{aligned}$$

(2.10)

Here the coupling constant $\beta$ has mass dimension $-2$.

According to Lovelock’s theory of gravity, the computation must be restricted up to second order for the purpose to obtain the Einstein Gauss–Bonnet gravity. The case in which Einstein-Hilbert action arises naturally in a part of the action, in addition to the quadratic Gauss–Bonnet term given as

$$\begin{aligned} {\mathcal {G}}=R^2-4R^{\mu \nu }R_{\mu \nu }+R^{\mu \nu \rho \sigma }R_{\mu \nu \rho \sigma }. \end{aligned}$$

(2.11)

The variation of the considered action given by leads to the following equation of motions

$$\begin{aligned}{} & {} G_{\mu \nu }+g_{\mu \nu }\Lambda +\alpha L_{\mu \nu }=-\frac{1}{2}F_{\mu \rho }F_{\nu }^{\rho }+\frac{1}{8}g_{\mu \nu }F^2\nonumber \\{} & {} \quad -\frac{1}{4}{\mathcal {B}}_{\mu \nu }-\frac{\beta }{2}g_{\mu \nu }{\mathcal {L}}_{int} \end{aligned}$$

(2.12)

$$\begin{aligned}{} & {} \Delta _\nu F^{\nu \mu }-4\beta \,\delta ^{\mu \nu \, \gamma _1\cdots \gamma _p}_{\lambda \cdots \lambda _D} H_{\gamma _1\cdots \gamma _p}\,\nonumber \\{} & {} \quad \Delta _\nu \left( F^{\lambda _1\lambda _2}H^{\gamma _3\cdots \gamma _D}\right) =0 \end{aligned}$$

(2.13)

$$\begin{aligned}{} & {} \Delta H^{\mu \lambda _1\cdots \lambda _{p-1}}+2\alpha \, p!\, \delta ^{\mu \nu \rho \, \lambda _1\cdots \lambda _{p-1}}_{\gamma \cdots \gamma _D}\nonumber \\{} & {} \quad F_{\mu \nu }\Delta _\rho \left( F^{\gamma _1\gamma _2}H^{\gamma \cdots \gamma _D}\right) =0,\nonumber \\ \end{aligned}$$

(2.14)

where $G_{\mu \nu }$ and $L_{\mu \nu }$, respectively, are the Einstein tensor and the Lanczos tensor. They are given by

$$\begin{aligned} G_{\mu \nu }= & {} R_{\mu \nu }-\frac{1}{2}g_{\mu \nu }R, \end{aligned}$$

(2.15)

$$\begin{aligned} L_{\mu \nu }= & {} 2\left( R R_{\mu \nu }-2R_{\mu \rho }R_\nu ^\rho - 2R^{\rho \lambda }R_{\mu \nu \rho \lambda }+R_\mu ^{\rho \lambda \sigma }R_{\nu \rho \lambda \sigma }\right) \nonumber \\{} & {} \quad -\frac{1}{2}g_{\mu \nu }{\mathcal {G}}. \end{aligned}$$

(2.16)

Moreover, ${\mathcal {B}}_{\mu \nu }$ is the energy–momentum tensor for the $B_{[p-1]}$ field. it reads

$$\begin{aligned} {\mathcal {B}}_{\mu \nu }{} & {} =\frac{1}{(p-1)!}H_{\mu \rho _1\cdots \rho _{p-1}}H^{\rho _1\cdots \rho _{p-1}}\nonumber \\{} & {} \quad -\frac{1}{(p!)^2}\delta _{\sigma _1\cdots \sigma _p}^{\rho _1\cdots \rho _p} {^\lambda }(_\mu g_\nu )_\lambda H_{\rho _1\cdots \rho _p}H^{\sigma \cdots \sigma _p}. \end{aligned}$$

(2.17)

An examination is carried out to determine what exactly can result from the variation of the interaction part of the Lagrangian with respect to the metric space-time. Let us now assume the following

$$\begin{aligned} \frac{1}{\sqrt{-g}}\frac{\delta \left( \sqrt{-g}{\mathcal {L}}_{int}\right) }{\delta g^{\mu \nu }}=X_{\mu \nu }-\frac{1}{2}g_{\mu \nu }{\mathcal {L}}_{int}. \end{aligned}$$

(2.18)

Nevertheless these Lagrangians fulfill the identity

$$\begin{aligned}{} & {} \delta ^{\rho _1\cdots \rho _D}_{\sigma _1\cdots \sigma _D} F_{[\rho _1\rho _2}H_{\rho _3\cdots \rho _D}F^{\sigma _1\sigma _2}H^{\sigma _3\cdots \sigma _D}g_{\mu ]\nu }\nonumber \\{} & {} \quad =-X_{\mu \nu }+g_{\mu \nu }{\mathcal {L}}_{int}=0, \end{aligned}$$

(2.19)

where, this allows us to put the result

$$\begin{aligned} \frac{1}{\sqrt{-g}}\frac{\delta \left( \sqrt{-g}{\mathcal {L}}_{int}\right) }{\delta g^{\mu \nu }}=\frac{1}{2}g_{\mu \nu }{\mathcal {L}}_{int}, \end{aligned}$$

(2.20)

of course, this result confirms the validity of the energy–momentum tensor with regards to the interaction Lagrangian. After that, we look for the appropriate solution pertinent to this background.

2.2 Exact solutions

In this part, we are interested in finding a physical solution to model the structure of dyonic charges within the Einstein Gauss–Bonnet theory. For that reason, we consider a static spherically symmetric metric

$$\begin{aligned} ds^2=-f(r)dt^2+\frac{dr^2}{f(r)}+r^2d\Omega ^2_{D-2}, \end{aligned}$$

(2.21)

where one has

$$\begin{aligned} .d\Omega ^2_{D-2}=d\theta _1^2+ \sum _{i=2}^{D-2} \prod _{j=1}^{i-1}\sin ^2\theta _jd\theta ^2_i, \end{aligned}$$

(2.22)

which is the line element of $(D-2)$-dimensional unit sphere. Linking to differential geometry helps to think of a local chart $\lbrace x^i\rbrace$ with $i=1,\ldots , p$, which provides an intrinsic metric $\epsilon _{ij}$ on the manifold $\Omega _{D-2}$, with determinant $\epsilon$. This $(D-2)$-unit sphere involves certain magnetic objects to wrap spherical $(D-2)$-cycles covered the volume form, $H_{[D-2]}\sim \text {Vol}(\Omega )$, namely

$$\begin{aligned} H_{\rho _1\cdots \rho _p}=q_m\sqrt{\epsilon }\delta _{\rho _1\cdots \rho _p}^{x^1\cdots x^p}. \end{aligned}$$

(2.23)

The Maxwell field will be purely electric,

$$\begin{aligned} F_{\mu \nu }=h'(r)\delta _{\mu \nu }^{tr} \end{aligned}$$

(2.24)

where the prime denotes the derivative with respect to r. These quantities give rise to such electric and magnetic charges as

$$\begin{aligned} q_e\sim \int _{\Omega _\infty }\star F_{[2]},\quad q_m\sim \int _{\Omega _\infty } H_{[D-2]}. \end{aligned}$$

(2.25)

At this stage, making use of the Ansatz in Maxwell equations leads to find

$$\begin{aligned}{} & {} r^{2p}\left[ p h'(r)+r h''(r)\right] - 8 \beta (p!)^2 q_m^2\left[ p h'(r)-r h''(r)\right] =0,\nonumber \\{} & {} \quad p=D-2 \end{aligned}$$

(2.26)

which admit a solution in the form

$$\begin{aligned} h'(r)=\frac{q_e r^p}{r^{2p}+8\beta (p!)^2q_m^2}. \end{aligned}$$

(2.27)

A fascinating note from this solution showed that the parameter interaction and magnetic charge have similar behavior in preserving the dyonic structure of the black hole.

The next step focuses on the definition of the metric function f(r). We begin to evaluate the EGB field equations (2.12), reads

$$\begin{aligned} T_{t}^t= & {} \frac{D-2}{2}\Bigg \lbrace \left[ \frac{f'}{r}+\frac{(D-3)f}{r^2}-\frac{D-3}{r^2}\right] \nonumber \\{} & {} -\tilde{\alpha } \left[ \frac{2ff'}{r^3}-\frac{2f'}{r^3}+ \frac{(D-5)f^2}{r^4}-\frac{2(D-5)f}{r^4}+\frac{D-5}{r^4}\right] \Bigg \rbrace , \nonumber \\ T_t^t= & {} T_r^r, \end{aligned}$$

(2.28)

while the energy momentum tensor is given by

$$\begin{aligned} T_t^t\!=\!-\frac{1}{4}\left( \frac{q_m^2}{r^{2(D-2)}}+\frac{q_e^2}{r^{2(D-2)}+8\beta q_m^2 \Gamma (D-1)^2}\right) . \end{aligned}$$

(2.29)

The fact that $\beta$ is positive, results in a way that $T_{tt}$ is a positive quantity. To simplify the computations, we consider the rescaled coupling constant

$$\begin{aligned} \tilde{\alpha }=\alpha (D-3)(D-4). \end{aligned}$$

(2.30)

With these at hand, we can perform such processing to show the explicit form of f(r) which is defined under a differential representation of the (t, t) part of the field equations as follows

$$\begin{aligned}{} & {} \frac{(D-3) f(r)}{r^2}-\frac{D-3}{r^2}+\frac{f'(r)}{r}\nonumber \\{} & {} \quad +\frac{1}{4} \left( \frac{q_e^2}{8 \beta q_m^2 \Gamma (D-1)^2 + r^{2 (D-2)}}+\frac{q_m^2}{r^{2 (D-2)}}\right) \nonumber \\{} & {} \quad + \Lambda -\frac{\alpha }{2} \left( \frac{(D-5) f(r)^2}{r^4}-\frac{2 (D-5) f(r)}{r^4}\right. \nonumber \\{} & {} \quad \left. +\frac{D-5}{r^4}+\frac{2 f(r) f'(r)}{r^3}-\frac{2 f'(r)}{r^3}\right) =0. \end{aligned}$$

(2.31)

This equation provides a pair of distinct solutions referred to by the signs ±. Indeed, these solutions are found to be

$$\begin{aligned} f(r)=1+\frac{r^2}{2\tilde{\alpha }}\left( 1\pm \sqrt{g(r)}\right) , \end{aligned}$$

(2.32)

where

$$\begin{aligned}{} & {} g(r)=1+\frac{4\tilde{\alpha }m}{r^{D-1}}+\frac{8\tilde{\alpha }\Lambda }{(D-2)(D-1)}-\frac{2\tilde{\alpha }}{D-3}\nonumber \\{} & {} \quad \times \left( q_m^2+q_e^2\,{_2}F_1\left[ 1,\frac{D-3}{2 (D-2)};\frac{7-3 D}{4-2 D};\frac{-8 \beta q_m^2 \Gamma (D-1)^2 }{r^{2 D-4}} \right] \right) .\nonumber \\ \end{aligned}$$

(2.33)

Here $_2F_1$ denotes Euler’s hypergeometric function. In fact, the boundary conditions offer the integration constant m, which acts as a mass of the solution in a particular parameter space. Thus, the relevant ADM mass is defined according to [53] by

$$\begin{aligned} M_{ADM}=\frac{(D-2)\omega }{16\pi }m,\quad \text {with } \ \omega =\frac{2\pi ^{\frac{D-1}{2}}}{\Gamma \big [\frac{D-1}{2}\big ]} \end{aligned}$$

(2.34)

where $\omega$ is the volume of the $(D-2)$-dimensional unit sphere.

Henceforth, the physical solution is that of the negative branch, which recovers solutions in EGB theory as well as in general relativity. It is interesting to note that every black hole solution is a given in such a parameter space, uniquely collecting all the physical parameters. Thus, our parameter space takes care of managing the set ${\mathcal {M}}(M,\alpha ,q_e,q_m,\beta ,\Lambda ,D)$. Certain limits across the dynamics of the parameter space, however, are taken into account, from which the cancellation of the GB coupling constant $\alpha$ leads to the exploration of a solution within the framework of general relativity [51]:

$$\begin{aligned} f(r)= & {} 1-\frac{2m}{r^{D-3}}-\frac{2\Lambda r^{2}}{(D-1)(D-2)}\nonumber \\{} & {} +\frac{q_m^2+q_e^2\,{_2}F_1\left[ 1,\frac{D-3}{2 (D-2)};\frac{7-3 D}{4-2 D};\frac{-8 \beta q_m^2 \Gamma (D-1)^2 }{r^{2 D-4}} \right] }{2(D-2)(D-3)r^{2(D-3)}}.\nonumber \\ \end{aligned}$$

(2.35)

Moreover, the disappearance of the electric charge, as well as the magnetic charge, gives rise to the Tangherlini AdS-Schwarzschild solution [54]:

$$\begin{aligned} f(r)=1-\frac{2m}{r^{D-3}}-\frac{2\Lambda r^{2}}{(D-1)(D-2)}. \end{aligned}$$

(2.36)

Fig. 1

The metric function vs radial coordinate r for several values of the parameters space with $D=5$ and $\beta =0.1$

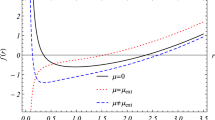
It is shown that Fig. 1 represents the variation of metric function against the radial coordinate. Different cases can be distinguished for the equation $f(r=r-+)=0$, among these cases, on has

• Double roots corresponding to the Cauchy horizon $r_-$ and the event horizon $r_{+}$.

• A degenerated root $r_-=r_+=r_E$ related to an extremal black hole.

• An empty set of solutions.

Thanks to a numerical treatment, we assert unequivocally that the metric function carries at most two horizon radii for such valued parameter space. Moreover, these horizon radii can be degenerated to present one horizon radius, or no black hole system can be found. In particular, for a fixed value of parameters $(q_m=2q_e=0.6,\Lambda =-0.02,\beta =0.1\ \text {and}\ m=1)$, we find the following:

• For $D=5,6,7$ if $\alpha \le 0.3$ $\Rightarrow$ two horizon radius, else no horizon radius.

• For $D=8$ if $\alpha \le 0.4$ $\Rightarrow$ two horizon radius, else no horizon radius.

• For $D=9,10$ if $\alpha \le 0.5$ $\Rightarrow$ two horizon radius, else no horizon radius.

With all this background at hand, one can explore more sides, such as thermodynamic aspects and shadow behavior.

3 Local black hole stability

In this section, we will calculate various thermodynamic quantities for our black hole. More precisely, we compute the mass of the black hole, and then we give the expression for the Hawking temperature, which allows us to calculate the related black hole entropy.

Starting with the mass of the black hole which is obtained in terms of the horizon radius $r_{+}$ by solving the equation $f(r_{+})=0$, taking into account Eq. (2.34) which gives

$$\begin{aligned}{} & {} M_{ADM} =\frac{1}{32\left( 3-4D+D^{2}\right) \pi }r_{+}^{-5-D}\omega \nonumber \\{} & {} \quad \times \left[ \left( D-1\right) q_m^{2}r_{+}^{8}+2\left( D-3\right) r_{+}^{2D}\right. \nonumber \\{} & {} \quad \times \left( \left( 2-3D+D^{2}\right) r_{+}^{2}\right. \nonumber \\{} & {} \quad \left. +\left( 24-50D+35D^{2}-10D^{3}+D^{4}\right) \alpha -2r_{+}^{4}\Lambda \right) \nonumber \\{} & {} \quad +\left( D-1\right) q_e^{2}r_{+}^{8}\ _{2}F_{1}\nonumber \\{} & {} \quad \times \left. \left( 1,\frac{D-3}{ 2\left( D-2\right) },\frac{7-3D}{4-24},-8\beta q_m^{2}r_{+}^{4-2d}\Gamma \left[ D-1 \right] ^{2}\right) \right] . \nonumber \\ \end{aligned}$$

(3.1)

By taking $q_m=q_e=\beta =\Lambda ={\alpha }=0$, Eq. (3.1) goes to the D-dimensional Schwarzschild black hole given by

$$\begin{aligned} M_{ADM}=\frac{(D-2)\omega _{D-2}r^{D-3}}{16\pi }. \end{aligned}$$

(3.2)

The Hawking temperature is defined as follows

$$\begin{aligned} T_{+}(r_{+})=\frac{f^{\prime }(r)}{4\pi }\Bigg |_{r=r_{+}}, \end{aligned}$$

(3.3)

the prime denotes the derivative with respect to r. The computations give

$$\begin{aligned} T_{+}=\frac{t_1}{t_2} \end{aligned}$$

(3.4)

where one has

$$\begin{aligned} t_1&=r_+^{-2 D-1} \big (8 \beta q_m^2 r_+^4 \Gamma (D-1)^2 \big (-2 r_+^{2 D} \big (2 \Lambda r_+^4\nonumber \\&\quad -(D-3) (D-2) \big (\alpha (D-5) (D-4)+r_+^2\big )\big )-q_m^2 r_+^8\big )\nonumber \\&\quad -r_+^{2 D+8} \big (q_e^2+q_m^2\big )-2 r_+^{4 D} \big (2 \Lambda r_+^4\nonumber \\&\quad -(D-3) (D-2) \big (\alpha (D-5) (D-4)+r_+^2\big )\big )\big ) \end{aligned}$$

(3.5)

$$\begin{aligned} t_2&=8 \pi (D-2) \left( 2 \alpha (D-4) (D-3)+r_+^2\right) \nonumber \\&\quad \times \left( 8 \beta q_m^2 r_+^4 \Gamma (D-1)^2+r_+^{2 D}\right) . \end{aligned}$$

(3.6)

In the particular case where $q_m=q_e=\beta =\Lambda =0$, one obtains the following well knowing form of the D-dimensional EGB Hawking temperature

$$\begin{aligned} T_+=\frac{(D-3)\left[ r_{+}^{2}+\alpha (D-5)(D-4)\right] }{4\pi r_{+}\left[ r_{+}^{2}+2\alpha (D-4)(D-3)\right] } \end{aligned}$$

(3.7)

taking $D=5$, one obtains

$$\begin{aligned} T_+=\frac{1}{4\pi }\Big (\frac{2r_+}{r_+^2+4\alpha }\Big ), \end{aligned}$$

(3.8)

which is the 5D Einstein–Gauss–Bonnet black hole temperature [55]. Furthermore, making $\alpha =0$, one recovers the Hawking temperature of the 5D Schwarzschild–Tangherlini black hole given by $T_+=(1/2\pi r)$ [56].

To investigate the behavior of the Hawking temperature, one depicts it on the Fig. 2 below:

Fig. 2

The Hawking temperature vs the event horizon for different values of D and $\alpha$

We can see that the Hawking temperature rises to a maximum value and then drops to a minimum. It turns out that when the dimension D increases, the maximum value of the Hawking temperature also increases. Whereas this maximum is inversely proportional to the GB coupling constant.

This black hole can be regarded as a thermodynamic system only if its associated quantities obey the first-law of thermodynamics given by

$$\begin{aligned} dM=T_+dS+\phi _e dq_e + \phi _m dq_m, \end{aligned}$$

(3.9)

where the associated electric and magnetic potentials are given respectively in the following terms:

$$\begin{aligned} \phi _e&=\frac{\pi ^{\frac{D-3}{2}} q_e r_+^{3-D} \, _2F_1\left( 1,\frac{D-3}{2 (D-2)};\frac{7-3 D}{4-2 D};-8 \beta q_m^2 r_+^{4-2 D} \Gamma (D-1)^2\right) }{8 (D-3) \Gamma \left( \frac{D-1}{2}\right) }, \end{aligned}$$

(3.10)

$$\begin{aligned} \phi _m&= \frac{(D-1) \pi ^{\frac{D-3}{2}} r_+^{3-D} \left( \frac{(D-3) q_e^2 \left( \frac{1}{8 \beta q_m^2 r_+^{4-2 D} \Gamma (D-1)^2+1}-\, _2F_1\left( 1,\frac{D-3}{2 (D-2)};\frac{7-3 D}{4-2 D};-8 \beta q_m^2 r_+^{4-2 D} \Gamma (D-1)^2\right) \right) }{D-2}+2 q_m^2\right) }{32 (D-3) q_m \Gamma \left( \frac{D+1}{2}\right) }. \end{aligned}$$

(3.11)

To construct the black hole entropy, one use the Eq. (3.9) at constant parameters, which yields to

$$\begin{aligned} S=\int \frac{1}{T_+}dM=\int \frac{1}{T_+}\frac{dM}{dr_+}dr_+. \end{aligned}$$

(3.12)

Inserting Eqs. (3.1)–(3.3) into (3.12), the entropy takes the following form

$$\begin{aligned} S=\frac{\omega }{4} r_+^{D-2} \left( 1+\frac{2\tilde{\alpha }}{r_+^2} \frac{D-2}{D-4}\right) . \end{aligned}$$

(3.13)

It is commonly known that the black hole stability is analyzed via the heat capacity sign; the black hole is stable when $C_h$ is positive, or unstable if $C_h$ is negative. The expression of this physical quantity is given by

$$\begin{aligned} C_{h}=\frac{\partial M}{\partial T_+}=\Big (\frac{\partial M}{\partial r_{+}} \Big )\Big (\frac{\partial r_{+}}{\partial T_{+}}\Big ). \end{aligned}$$

(3.14)

By using Eqs. (3.1) and (3.3) we get

$$\begin{aligned} C_{h}=\frac{c_{1}}{c_{2}}, \end{aligned}$$

(3.15)

with

$$\begin{aligned} c_1&=-(D-2)\, \omega \, r_+^D \left( 2 \tilde{\alpha }+r_+^2\right) ^2 \left( 8 \beta r_+^4 \Gamma (D-1)^2 q_m^2+r_+^{2 D}\right) \nonumber \\&\quad \times \left. \Bigg (\left( -2 r_+^{2 D} \left( 2 \Lambda r_+^4-(D-3) (D-2) \left( \tilde{\alpha } \frac{D-5}{D-3}+r_+^2\right) \right) \right. \right. \nonumber \\&\quad \left. -r_+^8 q_m^2\right) \left( 8 \beta r_+^4 \Gamma (D-1)^2 q_m^2+r_+^{2 D}\right) -r_+^{2 D+8} q_e^2\Bigg ), \end{aligned}$$

(3.16)

$$\begin{aligned} c_2&=4 r_+^4 \Bigg (r_+^{2 D+8} q_e^2 \bigg (8 \beta r_+^4 \Gamma (D-1)^2 q_m^2 \big (6 \tilde{\alpha }+r_+^2\big )\nonumber \\&\quad +r_+^{2 D} \bigg ((5-2 D) r^2-2 \tilde{\alpha } (2 D-7)\bigg )\bigg )\nonumber \\&\quad +\bigg (r_+^8 q_m^2 \bigg ((5-2 D) r_+^2-2 \tilde{\alpha } (2 D-7)\bigg )\nonumber \\&\quad +2 r_+^{2 D} \bigg ((D-3) (D-2) \bigg (2 \tilde{\alpha }^2\frac{D-5}{D-3}+\tilde{\alpha }\frac{D-9}{D-3} r_+^2+r_+^4\bigg )\nonumber \\&\quad + 2 \Lambda r_+^4 \big (6 \tilde{\alpha }+r_+^2\big )\bigg )\bigg ) \bigg (8 \beta r_+^4 \Gamma (D-1)^2 q_m^2+r_+^{2 D}\bigg )^2\Bigg ). \end{aligned}$$

(3.17)

It is clear that in the case of $\alpha =q_m=q_e=\Lambda =\beta =0$ the heat capacity (3.15) reduces to

$$\begin{aligned} C_h=-\frac{1}{4}(D-2)r_+^{D-2}\omega , \end{aligned}$$

(3.18)

which is the same result as [57].

Fig. 3

The heat capacity behavior vs $r_+$ for various dimension (a), different GB coupling constant value (b), different values of $\Lambda$ (c) and different values of $q_m$ (d)

The heat capacity behavior against $r_+$ is depicted in Fig. 3 showing the effect of the parameters D, $\alpha$, $\Lambda$ and $q_m$. One observes that the heat capacity $C_+$ is positive for $r_+<r_c$ which means that the black hole is locally stable, whereas the heat capacity is negative for $r_c<r_+$, hence the black hole is locally unstable. Moreover, the heat capacity sign changes at $r_+=r_c$ indicating that the second-order phase transition occurs there. With regards to Fig. 3a, it is remarkable that the $r_c$ is sensitive to the variation of the dimension D. One can see that the $r_c$ increases as the dimension D increases. Likewise, a similar effect is observed from the variation of the GB coupling constant on the changes of $r_c$, Fig. 4a. Whereas the critical radius $r_c$ varies in full agreement with the variation of the cosmological constant $\Lambda$ in such a way that $r_c$ is shifted towards the right when the $\Lambda$ value is increasing (cf. Fig. 3c). In addition to the prior cases, two divergent points $r_{c1}$ and $r_{c2}$ arise regarding the magnetic charge variation, generating three zones (cf. Fig. 3d). Indeed, at small horizon radii, the heat capacity is positive, yielding a stable small black hole. In what follows, the heat capacity becomes negative after crossing the first zone, involving an unstable intermediate black hole. The heat capacity rapidly changes its sign to be positive again, which means that the large black hole is locally stable. It is worth noting that for a certain fixed value of the magnetic charge, the divergent behavior of the heat capacity is completely eliminated. Furthermore, the critical radii $r_{c1}$ and $r_{c2}$ have the opposite behavior when we vary the magnetic charge. Specifically, at a small horizon radius $r_+$, $r_{c1}$ is fully proportional to the $q_m$ variation. In contrast, once $q_m$ increases, the $r_{c2}$ decreases at a large horizon radius. Similarly, the same behavior as in Fig. 3d is shown in Fig. 4 for the electric charge effect.

4 Black hole shadow

In this section,we will study the null geodesics, where the space-time geometry is described by (2.32). We use the Lagrangian and Hamilton–Jacobi equation to obtain the motion equations of the test particle.

We start with Lagrangian, given by

$$\begin{aligned} {\mathcal {L}}=\frac{1}{2}g_{\mu \nu }\dot{x}^{\mu }\dot{x}^{\nu }, \end{aligned}$$

(4.1)

where $g_{\mu \nu }$ is the metric tensor, the dot denotes the derivative with respect to an affine parameter $\lambda$.

The canonically conjugate momentums solution provides,

$$\begin{aligned} P_{t}&=\frac{E}{f(r)}, \end{aligned}$$

(4.2)

$$\begin{aligned} P_{r}&=\frac{1}{f(r)}\dot{r}, \end{aligned}$$

(4.3)

$$\begin{aligned} P_{\theta _{i}}&=r^{2}\sum _{i=1}^{D-3}\prod _{j=1}^{i-1} \sin ^{2}\theta _{j}\,\dot{\theta }_{i}, \end{aligned}$$

(4.4)

$$\begin{aligned} P_{\phi }&=r^{2}\prod _{i=1}^{D-3}\sin ^{2}\theta _{i}=L, \end{aligned}$$

(4.5)

where E and L are the test particle’s energy and angular momentum, respectively. In order to study the photon orbits around the black hole, the geodesics of such a particle must be derived. To achieve such a goal, we employ the Hamilton–Jacobi approach based on the Carter constant separable method in higher dimensions, which is given by

$$\begin{aligned} \frac{\partial S}{\partial \lambda }+\frac{1}{2}g^{\mu \nu }\frac{\partial S}{\partial x^{\mu }}\frac{\partial S}{\partial x^{\nu }}=0, \end{aligned}$$

(4.6)

where S is the Jacobi action. To solve the above equation, we assume the following anzats [32]

$$\begin{aligned} S=\frac{1}{2}m\lambda ^{2}-Et+L\phi +S_{r}(r)+\sum _{i=1}^{D-3}S_{\theta _{i}}(\theta _{i}), \end{aligned}$$

(4.7)

where $S_{r}(r)$, $S_{\theta _{i}}(\theta _{i})$ are functions of r and $\theta _{i}$ respectively, and m is the mass of the test particle, which equals zero as the photon. The substitution of Eq. (4.7) in Eq. (4.6) gives

$$\begin{aligned} -2\frac{\partial S}{\partial \lambda }&=-\frac{1}{f(r)}\left( \frac{\partial S_{t}}{\partial t}\right) ^{2}+f(r)\left( \frac{\partial S_{r}}{\partial r}\right) ^{2}\nonumber \\&\quad +\frac{1}{r^{2} \prod _{i=1}^{D-3}\sin ^{2}\theta _{i}}\left( \frac{\partial S_{\phi }}{\partial \phi }\right) ^{2}\nonumber \\&\quad +\sum _{i=1}^{D-3}\frac{1}{r^{2} \prod _{j=1}^{i-1}\sin ^{2}\theta _{j}}\left( \frac{\partial S_{\theta _{i}}}{\partial \theta _{i}.}\right) ^{2}. \end{aligned}$$

(4.8)

By employing the separability method and introducing the Carter constant ${\mathcal {K}}$, we get

Fig. 4

The heat capacity behavior vs $r_+$ for different values of the electric charge, $q_e$, with $\alpha =0.01$, $q_m=1$, $\Lambda =-0.02$, $\beta =0.1$ and $D=5$

Fig. 5

The effective potential vs the radius coordinate behavior in various dimension for $m=1$, ${\mathcal {K}}=1$, $E=1$ and $L=5$

$$\begin{aligned} 0&=-\frac{1}{f(r)}\left( \frac{\partial S_{t}}{\partial t}\right) ^{2}+f(r)\left( \frac{\partial S_{r}}{\partial r}\right) ^{2}\nonumber \\&\quad +\frac{1}{r^{2}}\Bigg (\frac{1}{ \prod _{i=1}^{D-3}\sin ^{2}\theta _{i}}\left( \frac{\partial S_{\phi }}{\partial \phi }\right) ^{2}+{\mathcal {K}}-\left( \frac{\partial S_{\phi }}{\partial \phi }\right) ^{2}\prod _{i=1}^{D-3}\cot ^{2}\theta _{i}\Bigg )\nonumber \\&\quad +\frac{1}{r^{2}}\Bigg (\sum _{i=1}^{D-3}\frac{1}{ \prod _{j=1}^{i-1}\sin ^{2}\theta _{j}}\left( \frac{\partial S_{\theta _{i}}}{\partial \theta _{i}}\right) ^{2}\nonumber \\&\quad -{\mathcal {K}}+\left( \frac{\partial S_{\phi }}{\partial \phi }\right) ^{2}\prod _{i=1}^{D-3}\cot ^{2}\theta _{i}\Bigg ), \end{aligned}$$

(4.9)

which can be written as follows:

$$\begin{aligned} 0&=-\frac{E^{2}}{f(r)}+f(r)\left( \frac{\partial S_{r}}{\partial r}\right) ^{2}\nonumber \\&\quad +\frac{1}{r^{2}}\Bigg (\frac{L^{2}}{ \prod _{i=1}^{D-3}\sin ^{2}\theta _{i}}+{\mathcal {K}}-\prod _{i=1}^{D-3}L^{2}\cot ^{2}\theta _{i}\Bigg )\nonumber \\&+\frac{1}{r^{2}}\Bigg (\sum _{i=1}^{D-3}\frac{1}{ \prod _{j=1}^{i-1}\sin ^{2}\theta _{j}}\left( \frac{\partial S_{\theta _{i}}}{\partial \theta _{i}}\right) ^{2}-{\mathcal {K}}+\prod _{i=1}^{D-3}L^{2}\cot ^{2}\theta _{i}\Bigg ), \end{aligned}$$

(4.10)

where we have used $\frac{\partial S_{t}}{\partial t}=E$, $\frac{\partial S_{\phi }}{\partial \phi }=L$,

By incorporating Eqs. (4.2)–(4.5) into Eq. (4.10), we can obtain the entire system of equations that govern the photon motion around the black hole, as follows:

$$\begin{aligned}&\dot{t}=\frac{E}{f(r)}, \end{aligned}$$

(4.11)

$$\begin{aligned}&\dot{\phi }=\frac{L}{r^{2}\prod _{i=1}^{D-3}\sin ^{2}\theta _{i}},\end{aligned}$$

(4.12)

$$\begin{aligned}&r^{2}\dot{r}=\pm \sqrt{{\mathcal {R}}(r)},\end{aligned}$$

(4.13)

$$\begin{aligned}&r^{2}\sum _{i=1}^{D-3}\prod _{j=1}^{i-1}\sin ^{2}\theta _{i}\dot{\theta }_{i}=\pm \sqrt{\Theta _{i}(\theta _{i})} \end{aligned}$$

(4.14)

where

$$\begin{aligned} {\mathcal {R}}(r)&=E^{2}r^{4}-r^{2}f(r)\big ({{\mathcal {K}}}+L^{2}\big ), \end{aligned}$$

(4.15)

$$\begin{aligned} \Theta _{i}(\theta _{i})&={\mathcal {K}}-\prod _{i=1}^{D-3}L^{2}\cot ^{2}\theta _{i}. \end{aligned}$$

(4.16)

To obtain the boundary of the black hole shadow, one should study the radial equation. Thus, Eq. (4.13) can be reformulated as

$$\begin{aligned} \dot{r}^{2}+V_{eff}=0 \end{aligned}$$

(4.17)

where $V_{eff}(r)$ is the effective potential for radial motion given by

$$\begin{aligned} V_{eff}(r)=\frac{f(r)}{r^{2}}\big ({\mathcal {K}} +L^{2}\big )-E^{2}. \end{aligned}$$

(4.18)

In Fig. 5, we depict the effective potential as a function of the coordinate r to analyze its behavior as well as to look the effect of the dimension. From such figure, we can see that the potential has a maximum, which corresponds to an unstable orbit, and its value grows with increasing dimension. Furthermore, as we go $r\rightarrow \infty$, effective potential asymptotes to a constant value.

To find the unstable circular orbits that limit the apparent shape of the shadow of a black hole, we maximize the effective potential by setting the following conditions:

(4.19)

where $r_p$ is the photon sphere radius. The radius of the photon sphere is given by the solution of the equation $V(r_p) = 0$. The acquired $r_p$ is then entered into the equation $V'(r_p)=0$ to see if the constraint $V''(r_p)<0$ is satisfied in order to obtain the unstable photon orbits [58].

Now, using the condition $V_{eff}(r)=0\Big {|}_{r=r_{p}}$ yields to

$$\begin{aligned} \frac{r_{p}^{2}}{f(r_{p})}=\frac{L^{2}}{E^2}+\frac{{\mathcal {K}}}{E}=\xi ^{2}+\eta , \end{aligned}$$

(4.20)

where we have adopted the definition of the impact parameters introduced in [59]

$$\begin{aligned} \frac{L}{E}=\xi , \quad \frac{{\mathcal {K}}}{E^{2}}=\eta . \end{aligned}$$

(4.21)

In fact, we use the boundary constraint $\frac{\partial V_{eff}(r)}{\partial r}\Big {|}_{r=r_{p}}=0$, to make the radius $r_{p}$ of the photon sphere accurate. To reach that, we should resolve the following equation

$$\begin{aligned} rf'(r)\big {|}_{r=r_{p}}-2f(r)\big {|}_{r=r_{p}}=0. \end{aligned}$$

(4.22)

However, in our case the above equation can not be solved analytically. So we solve it using a numerical method. The Table 1 outlines the findings

Table 1 The event horizon radius and photon sphere radius for variations in dimension D and the GB parameter $\alpha$ with $q_m=2q_e, \Lambda =-0.02, \beta =0.1$

We now aim to determine the visible shape of the black hole shadow. For a better visualization, we use celestial coordinates X and $Y_{i}$ to determine the location of the shadow. The coordinate X corresponds to the shape’s apparent perpendicular distance as seen from the axis of symmetry, and the coordinate $Y_{i}$ corresponds to the shape’s apparent perpendicular distance as seen from its projection on the equatorial plane.

The celestial coordinates X and Y can be used to illustrate the apparent shape of the black hole shadow for an observer who is far away from the black hole. In accordance with [59] we can write

$$\begin{aligned}{} & {} X=\lim _{r_{0}\rightarrow \infty }\Big (\frac{r_{0}P^{(\phi )}}{P^{(t)}}\Big ), \qquad \nonumber \\{} & {} Y_{i}=\lim _{r_{0}\rightarrow \infty }\Big (\frac{r_{0}P^{(\theta _{i})}}{P^{(t)}}\Big ),\quad i=1,\ldots ,D-3 \end{aligned}$$

(4.23)

Fig. 6

Black hole shadow in celestial plane $(X-Y)$ in different dimension D (left panel), and Gauss–Bonnet parameter $\alpha$ (right panel)

where $r_{0}$ is the distance from the black hole to the far observer. Furthermore, we calculate the above limits by using the canonically conjugate momentum Eqs. (4.2)–(4.5), and the geodesic equation of motion (4.11)–(4.14), we obtains

$$\begin{aligned} X&=\frac{-\xi \prod _{i=1}^{D-3}\csc \theta _{i}}{\sqrt{1-\frac{(\eta +\xi ^{2})(1-\sqrt{1-\frac{8\tilde{\alpha }\Lambda }{(D-1)(D-2)}})}{2\tilde{\alpha }}}}, \end{aligned}$$

(4.24)

$$\begin{aligned} Y_{i}&=\pm \sqrt{\frac{\eta -\xi ^{2}\prod _{i=1}^{D-3}\cot ^{2}\theta _{i}}{\sqrt{1 -\frac{(\eta +\xi ^{2})(1-\sqrt{1-\frac{8\tilde{\alpha }\Lambda }{(D-1)(D-2)}})}{2\tilde{\alpha }}}}}. \end{aligned}$$

(4.25)

We will consider an observer on the equatorial hyperplane $(\theta _{i}=\frac{\pi }{2})$ for the sake of simplicity. The celestial coordinates can be written as

$$\begin{aligned} X&=\frac{-\xi }{\sqrt{1-\frac{(\eta +\xi ^{2})(1-\sqrt{1-\frac{8\tilde{\alpha }\Lambda }{(D-1)(D-2)}})}{2\tilde{\alpha }}}}, \end{aligned}$$

(4.26)

$$\begin{aligned} Y&=\pm \sqrt{\frac{\eta }{\sqrt{1-\frac{(\eta +\xi ^{2})(1-\sqrt{1-\frac{8\tilde{\alpha }\Lambda }{(D-1)(D-2)}})}{2\tilde{\alpha }}}}}. \end{aligned}$$

(4.27)

Fig. 7

The radius shadow behavior with respect to the dimension D for $m=1$

Fig. 8

The energy emission rate variation vs frequency $\varpi$ for different dimension D for $m=1$

Combining the coordinates X and Y yields an equation describing a circle with a radius of $R_s$ in the celestial plane $X-Y$, which is given by

$$\begin{aligned} R_{s}^{2}=X^{2}+Y^{2}=\frac{\xi ^{2}+\eta }{1-\frac{(\eta +\xi ^{2})(1-\sqrt{1-\frac{8\tilde{\alpha }\Lambda }{(D-1)(D-2)}})}{2\tilde{\alpha }}}. \end{aligned}$$

(4.28)

By using Eq. (4.20), the radius shadow $R_{s}$ becomes

$$\begin{aligned} R_{s}^{2}=\frac{\frac{r_{p}^{2}}{f(r_{p})}}{1-\frac{r_{p}^{2}}{f(r_{p})}\Big (\frac{1-\sqrt{1-\frac{8\tilde{\alpha }\Lambda }{(D-1)(D-2)}}}{2\tilde{\alpha }}\Big )}, \end{aligned}$$

(4.29)

which results in

$$\begin{aligned} R_{s}=\sqrt{\frac{\frac{r_{p}^{2}}{f(r_{p})}}{1-\frac{r_{p}^{2}}{f(r_{p})}\Big (\frac{1-\sqrt{1-\frac{8\tilde{\alpha }\Lambda }{(D-1)(D-2)}}}{2\tilde{\alpha }}\Big )}}. \end{aligned}$$

(4.30)

As shown in Fig. 6, we plot black hole shadows for various cases. The size of the black hole’s shadow can be seen to be controlled by the dimension of space-time D and the Gauss–Bonnet parameter $\alpha$. According to Fig. 6a the black hole shadow has a circular shape, and the size of this circle increases as D increases. Furthermore, the same behavior has been noticed with the increase of $\alpha$ in Fig. 6b (Fig. 7).

Fig. 9

The energy emission rate variation vs frequency $\varpi$ for different GB constant $\alpha$ for $m=1$

5 Energy emission rates

In this section, we study the energy emission rate (EER) in the D-dimension. Several studies have demonstrated the analysis of the energy emission rate with respect to the parameter dimension D as well as the coupling constant of the Gauss–Bonnet gravity $\alpha$ [60, 61]. For a faraway observer, it is well known that the shadow is responsible for a high energy absorption cross section due to the black hole. The energy emission rate of a black hole in a higher dimension can be expressed as [62],

$$\begin{aligned} \frac{d^{2}E(\varpi )}{d\varpi dt}=\frac{2\pi ^{2}\sigma _{lim}}{\exp {(\frac{\varpi }{T_{H}})}-1}\varpi ^{(D-1)} \end{aligned}$$

(5.1)

where $\varpi$ is the frequency, $T_H$ is the Hawking temperature given by (3.4), and $\sigma _{lim}$ is the limiting constant value for an absorption cross section oscillating around a spherically symmetric black hole.

Fig. 10

The energy emission rate variation vs frequency $\varpi$ for $\Lambda$ (a), $q_e$ (b) and $q_m$ (c) with $m=1$, $D=5$ and $\beta =0.1$

A D-dimensional black hole’s limiting constant value $\sigma _{lim}$ can be approximated by [63]

$$\begin{aligned} \sigma _{lim}=\frac{\pi ^{(\frac{D-2}{2})}R_{s}^{(D-2)}}{\Gamma (\frac{D}{2})} \end{aligned}$$

(5.2)

where $R_{s}$ is the radius shadow.

Figure 8 shows the energy emission rate against the frequency $\varpi$ in various dimensions D. We can see that there is a peak in the energy emission rate for the black hole. Concretely, this peak becomes greater with an increase in dimension D. Therefore, the evaporation process will be faster in higher-dimensional space-time, Fig. 8a, b. Furthermore, a similar explanation may be given for the effect of the Gauss–Bonnet constant $\alpha$, Fig. 9.

Figure 10 indicates the variation of the energy emission rate as a function of the frequency $\varpi$ for different values of $\Lambda$, $q_e$, and $q_m$. Generally, it is shown that the EER increases until such a peak, then it drops down to vanish. The peak of the EER appears to increase with decreasing $\Lambda$, as shown in Fig. 10a. While both the electric and magnetic charges have a similar effect on peak variation, Fig. 10b, c shows that as the latter parameters increase, the EER peak decreases. Furthermore, It is known that the coupling constant $\beta$ gives rise to dual fields and hence to dyonic objects. The Fig. 10d shows the variation of the EER with respect to different fixed values of the coupling constant $\beta$. It is shown that, contrary to the previous Fig. 10a–c, increasing the coupling constant $\beta$ causes the same variation in the EER peak. In other words, when the electric and magnetic interaction is strong, the evaporation process becomes faster for the dyonic AdS black hole system.

6 Conclusion

In this paper, we have derived a solution for a dyonic quasitopological electromagnetic source in the EGB gravity framework. The obtained solution brings us back to our usual solutions across the cancellation of some parameter space.

We have examined the thermodynamic aspects of the obtained solution, including the relevant ADM mass, Hawking temperature, and entropy. These last quantities have been employed to compute the heat capacity, which gives us the possibility to analyze the local stability. It was discovered that there are two distinct phases, each of which is located near the critical radius $r_c$. In the left region of $r_c$, we have a stable phase, whereas in the right region, we have an unstable phase state. The second phase transition has occurred at the critical radius of $r_c$. The critical radius, $r_c$, is proportionally affected by the parameters D and $\alpha$. Moreover, it has been shown that the variation of $r_c$ is compatible with the negative cosmological constant. In addition, the variations of the electric and magnetic charges have a similar effect on the heat capacity behavior.

Concerning the optical properties of this black hole, the behavior of its shadow has been studied. In brief, the Hamilton–Jacobi method was employed to integrate the geodesic equation of the test particle using Carter’s separation of variables trick. We found that the shadow of this black hole has a circular shape whose radius depends on the value of the different parameters. We limited our study just to the effect of the parameter D and the GB coupling constant. We discovered that the increase in the parameter D and the GB coupling constant reduced the size of the shadow. The energy emission rate was discovered to vary in contrast to the parameters D, GB coupling constant $\alpha$, the cosmological constant $\Lambda$, the electric $q_e$ and the magnetic charge $q_m$.

This work comes up with open questions mainly related to the recent 4D EGB gravity as well as the phase transition study, which will be the next interesting topic.