Moduli stabilization with bulk scalar in nested doubly warped braneworld model

Abstract

We examine the modulus stabilization mechanism of a warped geometry model with nested warping. Such a model with multiple moduli is known to offer a possible resolution of the fermion mass hierarchy problem in the Standard Model. A six dimensional doubly warped braneworld model under consideration admits two distinct moduli, with the associated warp factors dynamically generating different physical mass scales on four 3-branes. In order to address the hierarchy problem related to the Higgs mass, both moduli need to be stabilized around their desired values without any extreme fine tuning of parameters. We show that it is possible to stabilize them simultaneously due to the appearence of an effective 4D moduli potential, which is generated by a single massive bulk scalar field having non-zero VEVs frozen on the 3-branes. This gives rise to two scalar radions, one of which has mass slightly below ${\mathcal {O}}$(TeV) and couplings to SM fields proportional to the inverse of its ${\mathcal {O}}$(TeV) VEV, and the other has nearly ${\mathcal {O}}(M_{Pl})$ mass and interactions with SM fields suppressed by the Planck scale. We also discuss how the entire mechanism can possibly be understood from a purely gravitational point of view, with higher curvature f(R) contributions in the bulk automatically providing a scalar degree of freedom that can serve as the stabilizing field in the Einstein frame.

1 Introduction

The genesis of extra dimensional theories in physics dates back to the early 1920s, marked by Kaluza and Klein’s original attempt to unify classical electrodynamics and Einstein gravity. In recent decades, higher-dimensional braneworld models have attracted fresh interest [1,2,3,4,5,6,7,8,9,10,11,12,13,14], arising as potential candidates for addressing the gauge hierarchy problem which is inherently linked to the problem of the Higgs mass. As the only fundamental scalar in the Standard Model (SM), the Higgs should experience large radiative corrections to its mass due to its self-coupling and couplings to other matter and gauge fields. These corrections are expected to flow up to the ultraviolet cut-off scale of the underlying quantum field theory. Protecting the Higgs mass from such Planck-scale corrections and keeping it safely within the TeV scale requires an extremely precise fine tuning of parameters, which leads to a naturalness problem within the SM. In this sense, the discovery of a Higgs boson as light as $125\,\text {GeV}/c^2$ [15,16,17] has simultaneously validated the last major prediction of the SM and exposed its central conundrum.

The warped braneworld model proposed by Randall and Sundrum [9] offers an elegant explanation of the large mass hierarchy, based on the premise of a non-factorizable warped five-dimensional spacetime geometry. The extra dimension is taken to be an orbifold with topology $S^1/{\mathbb {Z}}_2$. Two 3-branes are located at the opposite boundaries of the bulk, which is a slice of $\text {AdS}_5$. One of these branes (the “TeV brane”) is identified with our visible universe, on which all the SM fields are assumed to be confined to. Gravity alone is assumed to permeate through the bulk. This places the apparent scale of gravity $(M_{Pl})$ on the visible brane very close to the fundamental scale $(M_5)$. In contrast, the energy density in the bulk induces an exponential warping along the extra dimension, which causes the physical mass $m_{H}^{(ph)}$ of the Higgs on the TeV brane to be suppressed from its fundamental mass $m_{H}\sim O(M_5)$ according to $m_{H}^{(ph)}=m_{H}e^{-\pi kr_c}$, where $k\sim M_5$ and $r_c$ is the brane separation (which plays the role of the extra dimensional modulus). For $kr_c\sim 11.54$, the electroweak scale is dynamically generated from the fundamental scale. But the original model contains no mechanism to stabilize the magnitude of $kr_c$ around its desired value. This problem was addressed by Goldberger and Wise [18], who showed that $kr_c$ can be stabilized appropriately by introducing a massive scalar field $\phi$ in the bulk with quartic interactions localized on the branes. Integrating out the extra dimensions results in an effective potential $V_{eff}(r_c)$ which stabilizes the modulus without any excessive fine tuning. This mechanism further allows one to interpret the modulus $r_c$ as the vacuum expectation value (VEV) of a dynamical radion field $\rho (x^\mu )$, i.e., $r_c=\left\langle \rho \right\rangle$, with the effective potential $V_{eff}(\rho )$ driving $\rho$ to settle at its minimum [19]. The mass of the radion and its coupling to matter fields on the visible brane are suggested to be ${\mathcal {O}}(\text {TeV})$, rendering it detectable, in principle, at present generation colliders. Notably, the radion is expected to be lighter than the lowest-lying KK excitations of generic bulk fields, which are typically above ${\mathcal {O}}(\text {TeV})$. This should make the radion the lightest detectable signature of the warped higher dimensional world.

There exists a wealth of work on the dynamics of various bulk fields and KK gravitons in warped spacetime, alongside a variety of generalizations with their own phenomenological and cosmological features (for a small body of examples, see [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36]). The original Goldberger–Wise analysis has also been extended along several avenues, eg. by assuming finite values of the brane coupling constants [37], incorporating back reaction of the bulk scalar on the metric [38,39,40], and dynamical stabilization schemes in cosmological backdrops [41,42,43]. However, in spite of its theoretical appeal, the original 5D RS model has been increasingly challenged by experimental data in recent years. The mass of the first excitation of the graviton KK tower in the 5D setting [23] is suggested to be ${\mathcal {O}}(\text {TeV})$. Moreover, the graviton KK modes are expected to couple to visible brane matter with amplified strength, as the lowest-lying excitations cluster close to the TeV brane. These considerations subsequently inspired several unsuccessful attempts to detect the signatures of the graviton modes through various channels at the LHC [44,45,46,47,48,49]. The absence of any such evidence till date has imposed serious constraints on the parameter space of the model. In particular, a small hierarchy $m_H/M_5\sim 10^{-2}$ is required to explain the null results, indicating the potential appearance of new physics at least two orders of magnitude below the fundamental Planck scale. This is particularly problematic since this hierarchy requires $r_c^{-1}$ (which plays the role of the cut-off above which new physics is expected to appear) to be lowered by two orders of magnitude as well. But the sensitive dependence of the exponential warp factor on $r_c$ severely restricts this possibility, thereby limiting the efficacy of the five-dimensional setup in addressing the gauge hierarchy problem.

2 Review of doubly warped braneworld model

Several higher dimensional extensions of the original RS model have been proposed [50,51,52,53], with most of them introducing additional orbifolds with topology $S^1/{\mathbb {Z}}_2$ besides the first one. Some of these models, generalized to six dimensions, have interesting cosmological features stemming from dynamical stabilization of the extra spacelike dimensions [54, 55]. A particularly interesting extension [56], capable of addressing the aforementioned issues, emerges in the form of a doubly warped braneworld with topology $\left[ {\mathcal {M}}(1,3)\times S^1/{\mathbb {Z}}_2\right] \times S^1/{\mathbb {Z}}_2$. It results in a “brane-box” configuration, with four 4-branes forming the “walls” of the box and four 3-branes located at the “vertices” where adjacent 4-branes intersect. The bulk is a slice of $\text {AdS}_6$ with cosmological constant $\Lambda _6\sim -{{\tilde{M}}}^6$, where ${{\tilde{M}}}$ is the fundamental Planck scale. The complete bulk-brane action (S), comprised of the bulk Einstein–Hilbert action $(S_6)$ and the brane tension terms $(S_5)$, is

$$\begin{aligned}{} & {} S=S_6+S_5\nonumber \\{} & {} S_6=\int d^4xdydz\sqrt{-g_6}\left( \dfrac{1}{2}{{\tilde{M}}}^4R_6-\Lambda _6\right) \nonumber \\{} & {} \begin{aligned} S_5&= \int d^4xdydz\sqrt{-g_5}\left[ V_1(z)\delta (y)+V_2(z)\delta (y-\pi )\right] \\&+ \int d^4xdydz\sqrt{-\bar{g}_5}\left[ V_3(y)\delta (z)+V_4(y)\delta (z-\pi )\right] \end{aligned} \end{aligned}$$

(1)

where $R_6$ is the six dimensional Ricci scalar, and y and z are angular coordinates charting the extra dimensions. For the current purpose, the visible 3-brane has been assumed to be devoid of any matter field, which would have otherwise introduced a further ($S_4$) term as the contribution of the matter Lagrangian. In a multiply warped setting, the brane tensions can, in general, be functions of the bulk coordinates. This is a departure from the 5D case, where the presence of only one extra dimension rules out any such dependence at the very outset. Using an RS-like ansatz to solve the resulting Einstein equations, one obtains the doubly warped metric

$$\begin{aligned} ds^2=\dfrac{\text {cosh}^2(kz)}{\text {cosh}^2(k\pi )}\left( e^{-2c|y|}\eta _{\mu \nu }dx^\mu dx^\nu +R_y^2dy^2\right) +r_z^2dz^2\nonumber \\ \end{aligned}$$

(2)

where $R_y$ and $r_z$ are the radii of the orbifolds, and c and k are constants interconnected through

$$\begin{aligned} c=\dfrac{R_yk}{r_z\text {cosh}(k\pi )};\qquad k=r_z\sqrt{-\dfrac{\Lambda _6}{10{{\tilde{M}}}^4}} \end{aligned}$$

(3)

This peculiar relation makes it clear that in absence of a considerably large hierarchy between $R_y$ and $r_z$, both c and k cannot be simultaneously large. Instead, any one of the two distinct regimes $c>k$ or $c\ll k$ can emerge. It is not entirely possible to get rid of a little hierarchy between $R_y$ and $r_z$, but with suitable choice of c and k, it can be ensured that $R_y/r_z$ does not exceed ${\mathcal {O}}(10)$. The physical mass scale $m_H^{(ph)}$ on the 3-brane located at the vertex $(y_i,z_j)$ is related to the fundamental scale $m_H$ by

$$\begin{aligned} m_H^{(ph)}=m_He^{-cy_i}\dfrac{\text {cosh}(kz_j)}{\text {cosh}(k\pi )} \end{aligned}$$

(4)

In the $c>k$ regime, the choice of $c\sim 10$ and $k\sim 0.1$ yields warp factors which together generate the TeV scale on the two 3-branes at $(\pi ,0)$ and $(\pi ,\pi )$, one of which (preferably the maximally warped one) can be identified with the visible brane. The other pair of 3-branes experiences negligible warping and remains at the Planck scale. This clustering of multiple 3-branes around each of the scales is a salient property of generalized RS models with nested warping, one having important phenomenological implications.

Once the metric is fully solved, the brane tensions can be derived using appropriate junction conditions at the orbifold fixed points; $V_1$ and $V_2$ retain their z-dependence, whereas $V_3$ and $V_4$ turn out to be independent of y.

$$\begin{aligned}{} & {} V_1(z)=-V_2(z)=8\tilde{M}^2\sqrt{-\dfrac{\Lambda _6}{10}}\text {sech}(kz) \end{aligned}$$

(5)

$$\begin{aligned}{} & {} V_3(y)=0;\qquad V_4(y)=-8\tilde{M}^2\sqrt{-\dfrac{\Lambda _6}{10}}\text {sech}(k\pi ) \end{aligned}$$

(6)

The coordinate dependence of the former pair can be shown to emerge from suitable scalar fields confined to the corresponding 4-branes. We summarize the key results here for a quick recap. Considering a scalar field $\varphi (z)$ localized on each $y=y_0$ brane with a corresponding scalar potential ${\mathcal {V}}(\varphi (z))\equiv \rho (z)$, one can extremize the following action $S[\varphi ]$.

$$\begin{aligned} S[\varphi ]=\int d^4x\int \limits _{-\pi }^{+\pi }dz\sqrt{-g_5}\left( g_5^{\alpha \beta }\partial _\alpha \varphi \partial _\beta \varphi +{\mathcal {V}}(\varphi )\right) \end{aligned}$$

(7)

The induced 5D metric $g_5^{\alpha \beta }(y)$ is evaluated at $y=y_0$. Identifying the energy density of this Lagrangian with the brane tension, one obtains the kinetic term $\varphi '^2$ and the potential term $\rho (z)$ explicitly using the equation of motion. For the $y=\pi$ brane, the solutions are

$$\begin{aligned} \rho (z){} & {} =v_0\left[ -\dfrac{7}{6}\text {sech}(kz)+\xi \,\text {sech}^4(kz)\right] , \nonumber \\ \dfrac{\varphi '^2}{r_z^2}{} & {} =v_0\left[ \dfrac{1}{6}\text {sech}(kz)-\xi \,\text {sech}^4(kz)\right] \end{aligned}$$

(8)

where $v_0=8{\tilde{M}}^2\sqrt{-\Lambda _6/10}$, and $\xi$ is an arbitrary constant of integration. Hence, positivity of the kinetic term over the entire domain $z\in [0,\pi ]$ requires $\xi \le 1/6$. On the other hand, for the $y=0$ brane, the analogous solutions are

$$\begin{aligned} \rho (z){} & {} =v_0\left[ \dfrac{7}{6}\text {sech}(kz)+{\tilde{\xi }}\,\text {sech}^4(kz)\right] ,\nonumber \\ \dfrac{\varphi '^2}{r_z^2}{} & {} =v_0\left[ -\dfrac{1}{6}\text {sech}(kz)+{\tilde{\xi }}\,\text {sech}^4(kz)\right] \end{aligned}$$

(9)

where ${\tilde{\xi }}$ is a different constant of integration. The positivity of $\varphi '^2$ over the entirety of this brane requires ${\tilde{\xi }}\ge (1/6)\text {cosh}^3(k\pi )$.

From this pair of constraints on $\xi$ and ${\tilde{\xi }}$, it is evident that if the Planck-TeV scale hierarchy is generated predominantly by warping along z with $c\ll k\sim 10$, then the large value of $\text {cosh}(k\pi )$ implies there must be a similarly large hierarchy between $\xi$ and ${\tilde{\xi }}$. Such a hierarchy between two fundamental parameters on neighbouring branes is unnatural. A radical way out of this problem might be to replace $\varphi$ on the $y=0$ brane with a phantom field having negative kinetic energy, which would necessitate ${\tilde{\xi }}\le 1/6$ just like $\xi$. If the (0, 0) 3-brane is identified with the visible brane, then the phantom could automatically furnish an interesting dark energy candidate with a possibly non-trivial equation of state. Otherwise, the existence of a phantom scalar on the $y=0$ brane does not necessarily have a discernible effect on the SM 3-brane. However, as the energy density of phantom fields is unbounded from below (i.e. violation of classical energy conditions), such fields can cause quantum instability of the vacuum in the ultraviolet regime. To overcome this difficulty, phantom fields are generally deemed admissible only in low energy effective field theories [57,58,59,60,61,62,63,64]. So the emergence of a phantom field is particularly problematic in the present scenario, since the theory is assumed to be valid up to ${\tilde{M}}$. But if one restricts attention to the $c>k$ regime with $c\sim 10$ and $k\sim 0.1$, then $\text {cosh}(k\pi )\sim {\mathcal {O}}(1)$ and there is no unnatural hierarchy between $\xi$ and ${\tilde{\xi }}$ at all. In that case, the very need for introducing a phantom scalar disappears, keeping the theory self-consistent.

The doubly warped model has numerous phenomenological advantages over its singly warped progenitor model. Firstly, owing to the presence of two extra dimensions, the first excited graviton KK mode turns out to be considerably heavier than that of the 5D case. Moreover, coupling between graviton KK modes and SM fields on the visible brane is largely suppressed compared to the 5D model. Taken together, these features can satisfactorily explain the non-detection of KK gravitons at the LHC so far, without recourse to any small hierarchy between $m_H$ and ${{\tilde{M}}}$ [65]. At the same time, significant portions of the parameter space of the extended model remain accessible to the LHC, allowing them to be explored in future runs [66]. Secondly, the doubly warped model can offer an explanation of the mass hierarchy among the SM fermions [56]. In the $c>k$ regime, the ${\mathcal {O}}$(TeV) 4-brane at $y=\pi$ intersects two other 4-branes at $z=0$ and $z=\pi$. Assuming SM fermions to be described by five dimensional fields confined to the $y=\pi$ brane implies natural ${\mathcal {O}}$(TeV) masses for the fermions. In addition to the z-dependent bulk wavefunction on this 4-brane, the fermionic fields can have kinetic terms on the 3-branes at the two intersection points. These boundary terms can modify the fermion-scalar Yukawa coupling on the $(\pi ,0)$ and $(\pi ,\pi )$ 3-branes, thereby causing a splitting among the effective fermion masses. This splitting is arguably small, as the natural mass scales of these 3-branes are already clustered close to each other around the TeV scale.

3 Modulus stabilization in doubly warped model

Like the 5D RS model, the action of the 6D scenario contains no dynamics which can stabilize the extra dimensional moduli around their desired values. In absence of such an underlying stabilizing mechanism, the braneworld model alone cannot be considered adequate. Motivated by the success of the 5D Goldberger–Wise mechanism, it becomes natural to seek a similar approach for the 6D model that might stabilize both c and k (or equivalently, $R_y$ and $r_z$) simultaneously. While other phenomenological aspects of multiply warped spacetimes are well-studied [67,68,69,70], there has been little work in this direction so far, with the notable exception of [71]. The latter study proposes disjoint stabilization mechanisms for c and k with the help of two separate bulk and brane-localized fields in the $c>k$ regime. In the other regime, taking $c\ll k$ makes the metric almost conformally flat, wherefore only $r_z$ needs to be stabilized satisfactorily, with $R_y$ either left unstabilized (which is justified because of the negligibly small value of c) or stabilized with the help of another brane-localized field. Whether stabilization of both moduli can be achieved with the help of a single bulk scalar field, has, however, been an open question so far. In this paper, we attempt to address this very question.

3.1 Dynamics of the bulk field

For our current purpose, we choose to work in the $c>k$ regime, which, as noted already, obviates the need to introduce an unpleasant phantom scalar on the $y=0$ brane to explain the coordinate dependence of its tension, and remove the unnatural hierarchy between the $\xi$ and ${\tilde{\xi }}$ parameters. Additionally, the relative smallness of k allows us to view the entire setup as a not-too-large departure from the 5D model, helping identify the key points of deviation from the latter clearly. A study of the complementary $c\ll k$ domain using tools from supersymmetric quantum mechanics appears in [71].

Analogous to the original Goldberger–Wise scenario, we consider a bulk field propagating freely through the extra dimensional $y-z$ bulk, and interacting only at the locations of the four 3-branes through quartic self-interaction terms. The action $(S_{GW})$ of the bulk field is given by an immediate generalization of the original 5D Goldberger–Wise action.

$$\begin{aligned} S_{GW}= & {} -\dfrac{1}{2}\int d^4x\int \limits _{-\pi }^{+\pi }dy\int \limits _{-\pi }^{+\pi }dz \sqrt{-g_6}\left( g_6^{AB}\partial _A\phi \partial _B\phi +m^2\phi ^2\right) \nonumber \\{} & {} -\sum _{i=1}^4\int d^4x\sqrt{{{\tilde{g}}}_4^{(i)}}\lambda _i\left( \phi ^2-u_i^2\right) ^2 \end{aligned}$$

(10)

Here, ${\tilde{g}}_4^{(i)}$ is the induced metric on the ith 3-brane, with $u_i$ being the VEV of the bulk field (with mass dimension $[u_i]=+2$) and $\lambda _i$ the corresponding coupling constant ($[\lambda _i]=-4$). With its dynamics confined to the higher dimensional space, the bulk field is essentially “frozen” on the corner branes. Defining $a(y)=\text {exp}(-c|y|)$ and $b(z)=\text {sech}(k\pi )\text {cosh}(kz)$, we extremize this action with respect to $\phi$ to obtain the following equation of motion.

$$\begin{aligned} \begin{aligned}&-\dfrac{1}{R_y^2}\partial _y\left( a^4b^3\partial _y\phi \right) -\dfrac{1}{r_z^2}\partial _z\left( a^4b^5\partial _z\phi \right) +m^2a^4b^5\phi \\&\quad +\dfrac{4a^4b^4}{R_yr_z}\left[ \lambda _1\phi \left( \phi ^2-u_1^2\right) \delta (y)\delta (z)\right. \\&\quad \left. +\lambda _2\phi \left( \phi ^2-u_2^2\right) \delta (y-\pi )\delta (z)\right] \\&\quad +\dfrac{4a^4b^4}{R_yr_z}\left[ \lambda _3\phi \left( \phi ^2-u_3^2\right) \delta (y)\delta (z-\pi )\right. \\&\quad \left. +\lambda _4\phi \left( \phi ^2-u_4^2\right) \delta (y-\pi )\delta (z-\pi )\right] =0 \end{aligned} \end{aligned}$$

(11)

Away from the boundaries, the contributions of the interaction terms vanish. Assuming a separable solution of the form $\phi (y,z)=\phi _1(y)\phi _2(z)$, the bulk equation of motion can be reduced to the following pair of uncoupled ODEs, where $-4\alpha ^2$ is the separation constant.

$$\begin{aligned}{} & {} -\dfrac{1}{R_y^2a^4\phi _1}\dfrac{d}{dy}\left( a^4\dfrac{d\phi _1}{dy}\right) =\dfrac{1}{r_z^2b^3\phi _2}\dfrac{d}{dz}\left( b^5\dfrac{d\phi _2}{dz}\right) \nonumber \\{} & {} \quad -m^2b^2=-4\alpha ^2 \end{aligned}$$

(12)

An interesting physical interpretation of $\alpha$ emerges immediately. From the equation for $\phi _1$, it is apparent that $2\alpha$ plays the role of the mass of the $\phi _1$ field. Also, as the $k\rightarrow 0$ (and simultaneously $r_z\rightarrow 0$) limit implies $b(z)\rightarrow 1$ and mathematically reduces the 6D metric to the familiar singly warped form, it must also enforce $2\alpha \rightarrow m$ in order to reduce this equation to the 5D Goldberger–Wise bulk equation of motion. As for the equation for $\phi _2$, it is satisfied trivially in this limit, as $\phi _2(z)\rightarrow 1$ leads merely to $m^2=4\alpha ^2$. However, from a physical standpoint, one cannot of course allow k to be arbitrarily small, as any effective field theory in the semiclassical approach strictly remains valid only for $r_z\ge M^{-1}$, with quantum gravity effects dominating for $r_z< M^{-1}$. In this sense, the $k\rightarrow 0$ limit is not a physically tenable one, but comes with a lower cut-off regulated by $\Lambda _6$. The bottom line is simply that for sufficiently small k, one can expect $\alpha$ to be reasonably close to m, which is a fact that proves useful in due course.

Equation (12) can be solved exactly for the component fields $\phi _1(y)$ and $\phi _2(z)$, leading to the following general solution for the bulk field under the condition of ${\mathbb {Z}}_2$ orbifold symmetry.

$$\begin{aligned}{} & {} \phi (y,z)=e^{2c|y|}\left( Ae^{\nu c|y|}+Be^{-\nu c|y|}\right) \nonumber \\{} & {} \quad \times \left[ DP_n^l(\text {tanh}(k|z|))+EQ_n^l(\text {tanh}(k|z|))\right] \text {sech}^\frac{5}{2}(kz)\nonumber \\ \end{aligned}$$

(13)

where A, B, D and E are four arbitrary constants (arising on account of each equation being a second order ODE), and $P_n^l$ and $Q_n^l$ are associated Legendre functions of the first and second kind respectively. The quantities $\nu$, n and l are defined as

$$\begin{aligned}{} & {} \nu =2\sqrt{1+\dfrac{R_y^2\alpha ^2}{c^2}} \end{aligned}$$

(14)

$$\begin{aligned}{} & {} n=2\sqrt{1+\dfrac{\alpha ^2r_z^2\text {cosh}^2(k\pi )}{k^2}}-\dfrac{1}{2} \end{aligned}$$

(15)

$$\begin{aligned}{} & {} l=\dfrac{1}{2}\sqrt{25+\dfrac{4m^2r_z^2}{k^2}} \end{aligned}$$

(16)

Assuming the magnitudes of the brane coupling constants to be large (i.e. $\lambda _i\rightarrow \infty$) allows the identification of simple energetically favourable configurations to serve as boundary conditions. The very structure of the interaction terms, given by $\lambda _i(\phi ^2-u_i^2)^2\delta (y-y_0)\delta (z-z_0)$, necessitates $\phi (y_0,z_0)\rightarrow u_i$ as such a configuration on the corner brane at $(y_0,z_0)$. This approach leads to the following four equations, where the shorthand $\tau _z=\text {tanh}(k|z|)$ has been introduced for convenience.

$$\begin{aligned}{} & {} \phi _1(0)\phi _2(0)=(A+B)\left[ DP_n^l(0)+EQ_n^l(0)\right] \approx u_1 \end{aligned}$$

(17)

$$\begin{aligned}{} & {} \phi _1(\pi )\phi _2(0)=e^{2c\pi }(Ae^{\nu c\pi }+Be^{-\nu c\pi })\left[ DP_n^l(0)+EQ_n^l(0)\right] \approx u_2 \nonumber \\ \end{aligned}$$

(18)

$$\begin{aligned}{} & {} \phi _1(0)\phi _2(\pi )=(A+B)\left[ DP_n^l(\tau _\pi )+EQ_n^l(\tau _\pi )\right] \nonumber \\{} & {} \quad \times \text {sech}^\frac{5}{2}(k\pi )\approx u_3 \end{aligned}$$

(19)

$$\begin{aligned}{} & {} \phi _1(\pi )\phi _2(\pi )=e^{2c\pi }(Ae^{\nu c\pi }+Be^{-\nu c\pi })\nonumber \\{} & {} \quad \times \left[ DP_n^l(\tau _\pi )+EQ_n^l(\tau _\pi )\right] \text {sech}^\frac{5}{2}(k\pi )\approx u_4 \end{aligned}$$

(20)

Equations (17)–(20) are not all linearly independent, and as such, only allow three of the constants to be solved in terms of the remaining fourth. This poses no problem though, as the forms of the solutions still allow $\phi (y,z)$ to be determined uniquely. In the large c regime, the normalized solutions of the individual component fields are

$$\begin{aligned} \phi _1(y){} & {} =\sqrt{u_1}e^{2c|y|}(c_1e^{\nu c|y|}+c_2e^{-\nu c|y|}) \end{aligned}$$

(21)

$$\begin{aligned} \phi _2(z){} & {} =\sqrt{u_1}\left[ c_3P_n^l(\tau _z)+c_4Q_n^l(\tau _z)\right] \text {sech}^\frac{5}{2}(kz) \end{aligned}$$

(22)

where $c_2=1$, and the other three constants are given by

$$\begin{aligned} c_1{} & {} =e^{-(\nu +2)c\pi }\left[ \dfrac{u_2}{u_1}-e^{-(\nu -2)c\pi }\right] \end{aligned}$$

(23)

$$\begin{aligned} c_3{} & {} =\dfrac{Q_n^l(\tau _\pi )-\left( \frac{u_4}{u_2}\right) Q_n^l(0)\text {cosh}^\frac{5}{2}(k\pi )}{P_n^l(0)Q_n^l(\tau _\pi )-Q_n^l(0)P_n^l(\tau _\pi )} \end{aligned}$$

(24)

$$\begin{aligned} c_4{} & {} =\dfrac{\left( \frac{u_4}{u_2}\right) P_n^l(0)\text {cosh}^\frac{5}{2}(k\pi )-P_n^l(\tau _\pi )}{P_n^l(0)Q_n^l(\tau _\pi )-Q_n^l(0)P_n^l(\tau _\pi )} \end{aligned}$$

(25)

It is interesting to note that, apart from the overall normalization factor of $u_1$, the dynamics of $\phi (y,z)$ is controlled not by the absolute values of the VEVs but only by their ratios. This feature is reminiscent of the 5D mechanism. Further, Eqs. (21)–(25) dictate $u_4/u_2=u_3/u_1$. So the two ratios appearing explicitly in the solution are sufficient to completely specify all the six possible ratios among the four VEVs, thus ruling out any ambiguity.

3.2 The effective potential

Having obtained the solution of the bulk field, one needs to substitute it back in Eq. (10) and integrate over y and z in order to obtain the stabilizing potential $V_{eff}(c,k)$, or equivalently, $V_{eff}(R_y,r_z)$. From the resultant effective 4D action $S_{eff}$, the definition $S_{eff}=-\int d^4xV_{eff}(c,k)$ allows the potential to be read off directly. In the large $\lambda _i$ limit, this amounts to evaluating only the bulk contribution. First, let us define the following dimensionless parameters.

$$\begin{aligned} \mu _1=\dfrac{mr_z}{k};\quad \mu _2=\dfrac{\alpha r_z}{k} \end{aligned}$$

(26)

These quantities roughly estimate the ratios between the mass parameters of the bulk field and the fundamental Planck scale. From the semiclassical standpoint, the admissible range of each ratio should be $0<\mu _i<1$. In terms of these ratios, the parameters from (14)-(16) can be re-expressed as $\nu =2\sqrt{1+\mu _2^2\text {cosh}^2(k\pi )}$, $n=\nu -0.5$, and $l=(5/2)\sqrt{1+4\mu _1^2/25}$. Upon substituting the solution from (13) in the action, the integral over y can be readily evaluated, but the presence of the special functions makes the z-integral analytically intractable. Defining the dimensionless potential ${\tilde{V}}_{eff}=V_{eff}/u_1^2$, and making use of (3) to eliminate $R_y$ and $r_z$ in favour of c and k, the following form emerges for the potential at leading order:

$$\begin{aligned}{} & {} {\tilde{V}}_{eff}(c,k)=\dfrac{1}{2}F(k)+\left[ \dfrac{c_1^2(\nu +2)^2}{2\nu }e^{2\nu c\pi }-2\pi c_1(\nu ^2-4)c\right] \nonumber \\{} & {} \quad \times F_1(k)+\left( \dfrac{c_1^2}{2\nu }e^{2\nu c\pi }+2\pi c_1c\right) \times F_2(k) \end{aligned}$$

(27)

where the k-dependent functions, arising out of the z-integral, are given explicitly by

$$\begin{aligned}{} & {} F_1(k)=k\text {sech}^4(k\pi )\int \limits _{-\pi }^{+\pi }dz\left( c_3P_n^l(\tau _z)\right. \nonumber \\{} & {} \quad \left. +c_4Q_n^l(\tau _z)\right) ^2\text {sech}^2(kz) \end{aligned}$$

(28)

$$\begin{aligned}{} & {} F_2(k)=\dfrac{1}{4}k\text {sech}^4(k\pi )\int \limits _{-\pi }^{+\pi }dz \left[ 2(l-n-1)(c_3P_{n+1}^l(\tau _z)\right. \nonumber \\{} & {} \quad \left. +c_4Q_{n+1}^l(\tau _z))+(2n-3)\tau _z(c_3P_n^l(\tau _z)+c_4Q_n^l(\tau _z))\right] ^2 \nonumber \\{} & {} \quad +k\text {sech}^4(k\pi )\int \limits _{-\pi }^{+\pi }dz\,\mu _1^2(c_3P_n^l(\tau _z)+c_4Q_n^l(\tau _z))^2 \end{aligned}$$

(29)

$$\begin{aligned}{} & {} F(k)=\dfrac{1}{2\sqrt{1+\mu _2^2\text {cosh}^2(k\pi )}}\nonumber \\{} & {} \quad \times \left[ 4\left( \sqrt{1+\mu _2^2\text {cosh}^2(k\pi )}-1\right) ^2F_1(k)+F_2(k)\right] \end{aligned}$$

(30)

There is little choice but to evaluate $F_1(k)$ and $F_2(k)$ numerically for different values of $\mu _1$, $\mu _2$, and $u_4/u_2$, which, by this point, serve as three of the fundamental parameters of the model. The fourth parameter $u_2/u_1$, contained in the coefficient $c_1$, contributes chiefly to the c-dependence of the potential. Equipped with the potential given by (27)–(29), we are in a position to demonstrate the existence of a simultaneous minimum of ${\tilde{V}}_{eff}$ in c and k over some region of the parameter space that doesn’t require excessive fine tuning.

3.3 Stabilizing k

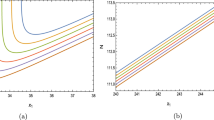
Owing to the explicit form of $c_1$ from (23), both the linear and quadratic terms in $c_1$ appearing in the coefficients of $F_1(k)$ and $F_2(k)$ in (27) are suppressed at least by ${\mathcal {O}}(e^{-4c\pi })$. For $c\sim 10$, this suppression factor is nearly of order $10^{-68}$. The F(k) term, on the other hand, suffers no such suppression. In order to study the k-dependence of the potential, it thus suffices to approximate ${{\tilde{V}}}_{eff}$ by taking only the dominant contributions offered by F(k), and establishing the stabilization of k is tantamount to locating a suitable minimum of F(k). The plots in Fig. 1 show the behaviour of F(k) for various combinations of the parameters.

Fig. 1

Profiles of F(k) vs k for VEV ratios $u_4/u_2=1.3$ (solid blue), $u_4/u_2=1.5$ (dotted green), and $u_4/u_2=1.7$ (dashed red), and a few representative values of $\mu _1$ and $\mu _2$ for each case

For all the choices of parameters, F(k) admits a broad minimum at some $k<0.5$. The location of this minimum is physically important, as the range $0.1\le k\le 0.6$ is of particular interest to scenarios attempting to explain the non-detectability of graviton KK modes at the LHC [65, 66], or exploring the phenomenology of off-brane SM fields that extend into the bulk [69, 70]. As special cases, it can be checked that $\mu _2\rightarrow 0$ produces an asymptotically decaying F(k) with no finite minimum, whereas $u_4=u_2$ admits only $k=0$ as the global minimum. As expected, the most pronounced dependence of the minimum is on the VEV ratio $u_4/u_2$, which governs the potential at the leading order.

3.4 Stabilizing c

The previous plots reveal the existence of a fairly large parameter space which can stabilize k around its desired value. But ${\tilde{V}}_{eff}(c,k)$ also needs to stabilize c, which plays the leading role in determining the degree of warping. To this end, we need to reinstate the previously neglected c-dependence in $\tilde{V}_{eff}(c,k)$ in order to locate a suitable minimum along c. Owing to the form of $c_1$ in (23), one might expect such a minimum to occur at $c_1=0$, which would be close in spirit to the 5D Goldberger–Wise result. Upon closer inspection though, it becomes clear that the existence of such a minimum depends crucially on the value of $\mu _2$. For considerably small values of $\mu _2$ which render $\nu \,\approx \,2+\epsilon _k$, where $\epsilon _k=\mu _2^2\text {cosh}^2(k\pi )$ is small enough so that ${\mathcal {O}}(\epsilon _k^2)$ and higher are negligible compared to unity, the deviation $\delta {{\tilde{V}}}_{eff}$ for any arbitrarily small deviation $c=c_0-\delta$ from the alleged minimum $c_0$ can be estimated as

$$\begin{aligned}{} & {} \delta {{\tilde{V}}}_{eff}|_{c_0}\sim e^{-4\pi (c_0-\delta )-2\epsilon _kc_0\pi }\left[ 25\left( e^{\epsilon _k\delta \pi }-1\right) ^2-8\pi (c_0-\delta )e^{\epsilon _k\delta \pi }\right. \nonumber \\{} & {} \quad \times \left. \left( e^{\epsilon _k\delta \pi }-1\right) \left( 1-6\epsilon _k\right) \right] \end{aligned}$$

(31)

For excessively small $\epsilon _k$ and vanishingly small $\delta$, this quantity is negative. This clearly rules out a minimum at $c_0$. The trouble can be traced to the existence of the ${\mathcal {O}}(c_1)$ terms in ${{\tilde{V}}}_{eff}(c,k)$. While the 5D stabilization mechanism ensured automatic cancellation of the pair of ${\mathcal {O}}(c_1)$ terms in the potential, the current model offers no such way out by default. However, if some particular combination of parameters can result in such cancellation (without excessive fine tuning of course), the issue would be resolved. Once k has been stabilized at some specific $k_{min}$, the condition for the ${\mathcal {O}}(c_1)$ terms to cancel each other translates to

$$\begin{aligned} \left[ \nu (k_{min})^2-4\right] F_1(k_{min})-F_2(k_{min})\simeq 0 \end{aligned}$$

(32)

As $F_1(k)$ and $F_2(k)$ themselves depend on all three parameters in a rather complicated manner, this equation is transcendental and cannot be solved analytically. However, it can be checked numerically that for every choice of $\mu _1$, the allowed parameter space contains approximate solutions to (32), some of which are presented in Table 1.

Table 1 A few examples of critical parameter values approximately satisfying (32), i.e., cancelling the linear $c_1$ terms in (27) at least up to ${\mathcal {O}}(10^{-2})$ compared to the non-negative $c_1^2$ terms, allowing simultaneous stabilization of both moduli around $k_{min}\sim 0.1$ and $c_{min}\sim 10$

Each of the combinations ensures that the non-negative ${\mathcal {O}}(c_1^2)$ terms dominate over the ${\mathcal {O}}(c_1)$ terms by nearly two orders of magnitude, leading to a proper minimum $c_{min}$ (satisfying $c_1=0$) with the following approximate form

$$\begin{aligned} c_{min}\,\approx \,\dfrac{1}{\pi \left[ \nu (k_{min})-2\right] }\text {ln}\left( \dfrac{u_1}{u_2}\right) \end{aligned}$$

(33)

One can immediately estimate the corresponding $u_1/u_2$ ratio which produces the desired value of $c_{min}\sim 11.54$. As given in Table 1, its magnitude depends strongly on $\mu _1$. In order to stabilize k between 0.1 and 0.6, the minimum admissible magnitude of $u_1/u_2$ is ${\mathcal {O}}(10)$, which is slightly larger than the requirement in 5D. For larger values of $\mu _1$, a minor hierarchy between $u_1$ and $u_2$ becomes increasingly prominent. This hierarchy has its physical origin in the fact that we have essentially made the component fields $\phi _1(y)$ and $\phi _2(z)$ yield two distinct warping scales $k\sim 0.1$ and $c\sim 10$ in spite of having chosen their mass parameters (m and $\alpha$) to be of comparable magnitudes! The somewhat large $u_1/u_2$ ratio is precisely the price we need to pay for that. As a reality check, it is instructive to check that choosing $u_1\sim u_2$ in (33) would have resulted in $c_{min}\sim 0.1$, just as this argument suggests.

Due to the huge difference in magnitude between the leading order k-dependent term and the c-dependent terms in the expression of ${\tilde{V}}_{eff}(c,k)$, it is not feasible to demonstrate the minimization directly with a 3D plot. So it might be instructive to convince ourselves analytically one final time that $(c_{min},k_{min})$ indeed gives us a proper minimum. To drive home the point, we consider $c_{min}\rightarrow c_{min}+\delta c$ and $k_{min}\rightarrow k_{min}+\delta k$, where $\delta c$ and $\delta k$ are small deviations which can be either positive or negative. Let us check how the value of ${\tilde{V}}_{eff}(c_{min},k_{min})$ given by (27) changes under these deviations.

• As $F(k_{min})$ is the minimum value of F(k), any such $\delta k$ gives a slightly larger value of F(k). Whatever be the corresponding changes of $F_1(k)$ and $F_2(k)$, the increment of F(k) always dominates over them as $F_1(k)$ and $F_2(k)$ are of similar magnitudes to F(k) over their entire domain but appear with suppression factors of order $e^{-4c\pi }$. On top of that, for the parameter values chosen in Table 1, the ${\mathcal {O}}(c_1)$ terms in the coefficients of $F_1(k)$ and $F_2(k)$ are negligibly small (which has been ensured). So, keeping $c=c_{min}$ fixed, the coefficients of $F_1(k)$ and $F_2(k)$ are practically zero anyway (this condition essentially gives us the location of $c_{min}$ in the first place), which makes the increment of F(k) dominate even more effectively. So $k_{min}$ indeed gives a minimum of ${\tilde{V}}_{eff}(c,k)$ along k.

• Next, keeping $k=k_{min}$ fixed, let us deviate slightly from $c_{min}$ in either direction. For the parameter values in Table 1, (32) holds independently of the value of c and ensures cancellation of the ${\mathcal {O}}(c_1)$ terms. So the coefficients of $F_1(k_{min})$ and $F_2(k_{min})$ contain only the quadratic non-negative ${\mathcal {O}}(c_1^2)$ term, which now assumes a positive value for any $\delta c$. On the other hand, $F_1(k)$ and $F_2(k)$ are strictly positive over their entire domain. Overall, this again gives a slightly positive departure from the value of ${\tilde{V}}_{eff}(c_{min},k_{min})$, which affirms that $c_{min}$ indeed gives a minimum along c.

The mutual cancellation of the ${\mathcal {O}}(c_1)$ terms involves a certain degree of fine tuning among the three parameters which control $F_1(k)$ and $F_2(k)$. While the situation is clearly more delicate than the 5D case, this tuning need not be very extreme. The ${\mathcal {O}}(c_1^2)$ terms can dominate and provide c with a stable minimum if the cancellation of the ${\mathcal {O}}(c_1)$ terms in (32) is accurate roughly up to ${\mathcal {O}}(10^{-2})$, which is sufficient to suppress the latters’ contribution by ${\mathcal {O}}(10^{-2})$. For $c\sim 10$, the critical values of the parameters need to be accurate at most up to ${\mathcal {O}}(10^{-3})$, while larger values of c are somewhat more likely to ameliorate the situation due to increased suppression. This is no worse than the fine tuning associated with the choice of m/M for a given VEV ratio, that is required to generate the TeV scale accurately in the 5D case. Moreover, for some fixed $\nu (k)$, the tuning associated with $u_2/u_1$ can be even more lenient due to the logarithmic dependence of $c_{min}$ on $u_2/u_1$. So simultaneous stabilization of c and k depends on a small degree of fine tuning among the parameters $\mu _1$, $\mu _2$, and $u_4/u_2$, which constitutes a crucial aspect of the extended Goldberger–Wise mechanism in the doubly warped scenario. This feature is not surprising since one should physically expect a two-level tuning for the stabilization of two distinct moduli in a spacetime with nested warping. As the stabilization of k alone requires negligible tuning (as evident from Fig. 1), the stabilization of c justifiably involves both levels. It might be interesting to investigate if incorporating back reaction or quartic self-interaction terms within the bulk can lead to improvements for this tuning requirement.

The minor hierarchy between $u_1$ and $u_2$ (or equivalently between $u_3$ and $u_4$) can be better interpreted if we arrange the magnitudes of the four VEVs in proper order. As the boundary conditions require $u_1/u_2=u_3/u_4$, the VEVs obtained in each case satisfy

$$\begin{aligned} u_3>u_1>u_4>u_2 \end{aligned}$$

(34)

The first two values are very close to each other, as are the last two, with the aforesaid hierarchy pushing the pairs apart. Interestingly, Eq. (34) reflects the order of physical mass scales on the corresponding corner branes (on which these classical values of $\phi$ are defined) for large c and small k, as can be checked using (4) . This can be understood physically as the massive bulk scalar, once frozen on the boundary branes, naturally tends to act against the warping induced by the bulk energy density. Consequently, the resulting mass scales on corner branes associated with larger VEVs can be generally expected to be higher than those with smaller VEVs. This feature is visible in the 5D Goldberger–Wise mechanism as well, albeit in a greatly tempered form. In the present case, it is more pronounced as it also incorporates the clustering effect observed among the physical mass scales.

4 Phenomenology of the stabilized moduli

Due to the presence of two distinct moduli in the model, one should physically expect the appearance of two radions with distinct masses. In the $c>k$ regime, phenomenological features associated with c should be sufficiently similar to those of the 5D model. Owing to the smallness of k, the mass of the second radion should not suffer any significant suppression down from the Planck scale ${\tilde{M}}$. This is hinted at by the form of the stabilizing potential ${{\tilde{V}}}_{eff}(c,k)$ from (27), where the leading order function F(k) and its second derivative are both typically ${\mathcal {O}}(1)$ around the minimum. The individual coupling strengths of the two radions to visible sector matter fields are also of fundamental interest, as they should directly affect radion production mechanisms which can be studied experimentally at the LHC. In the following sections, we estimate these parameters quantitatively based on the stabilizing formalism explored so far.

4.1 Masses of the radions

The starting point is to introduce two scalar modulus fields $T_1(x)$ and $T_2(x)$, whose VEVs determine the extra dimensional radii $R_y$ and $r_z$ respectively, i.e., $\left\langle T_1\right\rangle =R_y$ and $\left\langle T_2\right\rangle =r_z$. Analogous to the 5D case studied in [19], these fields incorporate small fluctuations about the background that are independent of the bulk field $\phi$. Under this modification, the general form of the metric from (2) becomes

$$\begin{aligned} ds^2= & {} b(z,x)^2\left[ a(y,x)^2\eta _{\mu \nu }dx^\mu dx^\nu +T_1(x)^2dy^2\right] \nonumber \\ {}{} & {} +T_2(x)^2dz^2 \end{aligned}$$

(35)

where we can make use of (3) and express the warp factors in terms of the modulus fields as

$$\begin{aligned}{} & {} a(y,x)=\text {exp}\left[ -\dfrac{k'T_1|y|}{\text {cosh}\left( k'T_2\pi \right) }\right] \,,\,\, b(z,x)=\dfrac{\text {cosh}\left( k'T_2z\right) }{\text {cosh}\left( k'T_2\pi \right) }\,,\nonumber \\{} & {} \text {where}\,\,k'=\sqrt{-\dfrac{\Lambda _6}{10{\tilde{M}}^4}} \end{aligned}$$

(36)

We substitute this metric in the following six-dimensional Einstein–Hilbert action

$$\begin{aligned} S_6\,\equiv \,-2{\tilde{M}}^4\int d^4x\int \limits _{-\pi }^{+\pi }dy\int \limits _{-\pi }^{+\pi }dz\sqrt{-{\tilde{g}}}{\tilde{R}} \end{aligned}$$

(37)

Noting $\sqrt{-{\tilde{g}}}=a^4b^5T_1T_2\sqrt{-g}$ (where $\sqrt{-g}=1$ in our presently assumed flat brane scenario), a subsequent Kaluza-Klein reduction of this action leads to the kinetic part

$$\begin{aligned} S_{kin}= & {} -2{\tilde{M}}^4\int d^4x\sqrt{-g}\int \limits _{-\pi }^{+\pi }dy\int \limits _{-\pi }^{+\pi }dz\,[6b^3T_1T_2\partial _\mu a\partial ^\mu a \nonumber \\{} & {} +18ab^2T_1T_2\partial _\mu a \partial ^\mu b+12a^2bT_1T_2\partial _\mu b\partial ^\mu b \nonumber \\{} & {} +6ab^3\partial _\mu a(T_2\partial ^\mu T_1+T_1\partial ^\mu T_2)+2a^2b^2\partial _\mu b(3T_2\partial ^\mu T_1 \nonumber \\{} & {} +4T_1\partial ^\mu T_2)+2a^2b^3\partial _\mu T_1\partial ^\mu T_2] \end{aligned}$$

(38)

It is clear that in the effective 5D limit $T_2\rightarrow {\tilde{M}}^{-1}$ and $b(z,x)\rightarrow 1$ this action indeed reduces to the familiar Goldberger–Wise result from [19]. Substituting (36) in (38) now and integrating over y and z explicitly allows us to obtain $S_{kin}$ entirely in terms of the modulus fields $T_1$ and $T_2$. As an exact treatment of the integrals becomes cumbersome at this point, we reinstate the $c>k$ condition and consider only small fluctuations $T_1=\left\langle T_1\right\rangle +\delta T_1$ and $T_2=\left\langle T_2\right\rangle +\delta T_2$ about the VEVs, which we have earlier shown to satisfy $\left\langle c\right\rangle =k'\left\langle T_1\right\rangle \text {sech}\left( k'\left\langle T_2\right\rangle \pi \right) \sim 10$ and $\left\langle k\right\rangle =k'\left\langle T_2\right\rangle \sim 0.1$. Under this approximation, the 4D effective Lagrangian for (38) simplifies considerably up to leading order and reduces to

$$\begin{aligned} {\mathcal {L}}_{kin}\,{} & {} \simeq \,\,24{\tilde{M}}^4\pi ^2\left( k'T_2\pi \right) e^{-2k'T_1\pi }\partial _\mu T_1\partial ^\mu T_1-\dfrac{2{\tilde{M}}^4\pi }{k'T_1} \nonumber \\{} & {} \quad \times \left[ -2+e^{-2k'T_1\pi }\left( k'T_1\pi \right) ^2\right] \partial _\mu T_1\partial ^\mu T_2 \nonumber \\{} & {} \quad -12{\tilde{M}}^4\pi ^2\left[ 1-2e^{-2k'T_1\pi }\left( k'\pi T_1\right) \right] \partial _\mu T_2\partial ^\mu T_2 \end{aligned}$$

(39)

In order to bring ${\mathcal {L}}_{kin}$ to the canonically normalized form, we need to define two physical fields $\rho _1(T_1,T_2)$ and $\rho _2(T_1,T_2)$ such that

$$\begin{aligned} {\mathcal {L}}_{kin}=\dfrac{1}{2}\partial _\mu \rho _1\partial ^\mu \rho _1+\dfrac{1}{2}\partial _\mu \rho _2\partial ^\mu \rho _2 \end{aligned}$$

(40)

It would then be necessary to solve a system of coupled nonlinear PDEs in order to obtain $\rho _1$ and $\rho _2$ exactly. Even with the leading order approximation of (39) in place, it is evident that obtaining such a set of exact solutions is quite difficult. However, if one assumes $\partial _\mu T_1/T_1\sim \partial _\mu T_2/T_2$ based on naturalness arguments (which we shall refer to as the naturalness assumption), then one can arrive at the following approximate solutions, where once again only small fluctuations around $\left\langle T_1\right\rangle$ and $\left\langle T_2\right\rangle$ have been considered.

$$\begin{aligned} \rho _1(x)\,\simeq \,f_1\sqrt{k'\pi T_2(x)}e^{-k\pi T_1(x)},\quad \rho _2(x)\,\simeq \,f_2\sqrt{k'\pi T_2(x)} \end{aligned}$$

(41)

The constant factors are given by $f_1\sim \sqrt{48{\tilde{M}}^4/k'^2}$ and $f_2\sim \sqrt{8\epsilon {\tilde{M}}^4/k'^2}$, with $\epsilon$ being a small dimensionless parameter of order ${\mathcal {O}}(\delta T_2/\left\langle T_2\right\rangle )$.

A few comments about this parameter and its origin are in order. The precise value of $\epsilon$ is modulated by the naturalness assumption, or more precisely, the extent of cancellation between the two unsuppressed terms of (39) ensured by the aforesaid assumption, which leaves behind a sufficiently small $(\partial _\mu T_2)^2$ term in (39) consistent with $\rho _2$ from (41). As such, it is essentially a tuning parameter connecting the first derivatives of $T_1$ and $T_2$ that allows the following relation to hold.

$$\begin{aligned}{} & {} \dfrac{4{\tilde{M}}^4\pi }{k'T_1}\partial _\mu T_1\partial ^\mu T_2-12{\tilde{M}}^4\pi ^2\partial _\mu T_2\partial ^\mu T_2\nonumber \\{} & {} \quad \simeq \,\dfrac{\epsilon {\tilde{M}}^4\pi }{k'T_2}\partial _\mu T_2\partial ^\mu T_2=\dfrac{1}{2}\partial _\mu \rho _2\partial ^\mu \rho _2 \end{aligned}$$

(42)

To arrive at this equality, we have also assumed small fluctuations about $k'\left\langle T_1\right\rangle \sim 10$ and $k'\left\langle T_2\right\rangle \sim 0.1$, whose values are already fixed from the stabilization mechanism. From a physical standpoint, the importance of $\epsilon$ lies in ensuring $\left\langle \rho _2\right\rangle$ remains bounded by ${\tilde{M}}$ from above. Indeed, it can be readily checked that for $k'\rightarrow {\tilde{M}}$ and $T_2\rightarrow {\tilde{M}}^{-1}$, one requires $\epsilon \lesssim (8\pi )^{-1}$ to ensure $\left\langle \rho _2\right\rangle \lesssim {\tilde{M}}$. On the other hand, it cannot be significantly smaller than this threshold value if we wish to avoid a fine tuning problem involving $\partial _\mu T_1$ and $\partial _\mu T_2$. Based on these considerations, it is important to note that $\epsilon$ is essentially not a new fundamental parameter which has been put in by hand, but merely a by-product of the naturalness assumption. As a final remark, let us also note that mathematically it would be possible to have a tuning which instead resulted in an overall negative unsuppressed term in (39). This would imply $\rho _2$ is a phantom field with a negative kinetic term, a seemingly unphysical mathematical artifact which we discard on physical grounds as we assume both the radions to be real.

It is straightforward to check that $(\partial _\mu \rho _1)^2$ then roughly generates the exponentially suppressed terms present in (39), while the remaining unsuppressed portion is generated by $(\partial _\mu \rho _2)^2$. It must be emphasized that the validity of (41) rests crucially upon both the naturalness assumption (which can be used to estimate the relative magnitudes of the exponentially suppressed terms in (39)) and the consideration of only small oscillations about the field VEVs. Violating either of these assumptions quickly results in a very complicated situation which is analytically intractable and appears to offer no additional physical insight. Upon deeper inspection, it becomes clear that even the precise functional forms of (41) are not of paramount importance. The key takeaway is the fact that in the current scenario, the VEV of one radion suffers very little suppression from the Planck scale, while the other one experiences large exponential suppression. This latter feature is what is of real physical interest.

With the definition of the physical radion fields $\rho _1$ and $\rho _2$, we are now in a position to estimate the corresponding radion masses $m_1$ and $m_2$ from the modulus potential $V_{eff}(\rho _1,\rho _2)$ in (27). First, let us estimate $m_2$, which is given by

$$\begin{aligned} m_2^2\,\equiv \,\dfrac{\partial ^2V_{eff}}{\partial \rho _2^2}\Biggr |_{\begin{array}{c} \rho _1=\left\langle \rho _1\right\rangle \\ \rho _2=\left\langle \rho _2\right\rangle \end{array}}\simeq \quad \left( \dfrac{k'^2u_1^2}{2\pi \epsilon {\tilde{M}}^4}\right) k_{min}\dfrac{\partial ^2{\tilde{V}}_{eff}}{\partial k^2}\Biggr |_{\begin{array}{c} c=c_{min}\\ k=k_{min} \end{array}}\nonumber \\ \end{aligned}$$

(43)

Let us analyze the various quantities appearing here. For the first two sets of values from Table 1 that yield a conservative $u_1/u_2$ ratio, one has $k_{min}\sim 0.1$ and $F''(k_{min})\sim {\mathcal {O}}(1)$. As for the VEV, we have $u_1\sim {\tilde{M}}^2$. Recalling $\Lambda \sim -{\tilde{M}}^6$ in the definition of $k'$ from (36), and assuming a moderate $\epsilon \sim (8\pi )^{-1}$ as argued earlier, one ends up roughly with $m_2\sim {\tilde{M}}$. In other words, the mass of $\rho _2$ suffers very little suppression from the fundamental scale, which is a result consistent with our prior intuition based on small warping along the z direction.

Next for the mass of $\rho _1$, we proceed similarly by taking $c\,\simeq \,k'T_1$ from (36) for simplicity without significant loss of accuracy. Making use of $f_2\rho _1\,\approx \,f_1\rho _2\,e^{-c\pi }$ from (41) and invoking the chain rule, the mass $m_1$ is given by

$$\begin{aligned} m_1^2\,\equiv \,\dfrac{\partial ^2V_{eff}}{\partial \rho _1^2}\Biggr |_{\begin{array}{c} \rho _1=\left\langle \rho _1\right\rangle \\ \rho _2=\left\langle \rho _2\right\rangle \end{array}}\simeq \quad \dfrac{u_1^2}{\pi ^2\rho _1(c,k)^2}\dfrac{\partial ^2{\tilde{V}}_{eff}}{\partial c^2}\Biggr |_{\begin{array}{c} c=c_{min}\\ k=k_{min} \end{array}}\nonumber \\ \end{aligned}$$

(44)

Computing the derivative explicitly and evaluating it at the minimum yields

$$\begin{aligned} m_1^2\,\simeq \,\left( \dfrac{u_2}{f_1}\right) ^2e^{-2c_{min}\pi }\left[ \dfrac{(\nu ^2-4)^2}{\nu k\pi }F_1(k)+\dfrac{(\nu -2)^2}{\nu k\pi }F_2(k)\right] _{k=k_{min}}\nonumber \\ \end{aligned}$$

(45)

where we have made use of (32) to discard the remaining terms of sub-leading magnitude. Let us again study individually the various quantities appearing in (45). For $c_{min}\sim 10$, the exponential term offers large suppression of order $10^{-34}$. For each set of representative values of the parameters from Table 1, the k-dependent term is ${\mathcal {O}}(10^{-2})$. At this point, let us also recall that $f_1\sim \sqrt{48{\tilde{M}}^4/k'^2}$ with $k'\sim {\tilde{M}}$. Further, from Table 1, we have $u_1/u_2 > rsim {\mathcal {O}}(10)$ in each case for simultaneous stabilization of the moduli, with $u_1\sim {\tilde{M}}^2$. Putting everything together, for parameter values which allow $u_1/u_2\sim {\mathcal {O}}(10)$, the RHS of (45) is essentially ${\tilde{M}}^2$ suppressed primarily by $e^{-2c_{min}\pi }$, and additionally by a minor factor of order ${\mathcal {O}}(10^{-6})$. The mass of the radion thus becomes

$$\begin{aligned} m_1\sim \delta \,e^{-c_{min}\pi }{\tilde{M}} \end{aligned}$$

(46)

where the factor $\delta \sim 10^{-3}$ brings the mass somewhat down below the TeV scale. Due to dominant warping along the y-direction, this result is precisely what one physically expects. It strongly resembles the case of the 5D radion, but with $\delta$ apparently being one order of magnitude smaller here. However, it should be noted that we have considered $c_{min}\,\approx \,k'\left\langle T_1\right\rangle$ for simplicity instead of its exact form $c_{min}=k'\left\langle T_1\right\rangle \text {sech}(k'\left\langle T_2\right\rangle \pi )$. While the former is a reasonable leading order approximation due to the smallness of $k'\left\langle T_2\right\rangle$ and leads to no significant change throughout the rest of the analysis, its only noticeable effect lies in rendering the exponential factor in (45) one order of magnitude smaller than what it should really be. Thus, considering the corrected value of $c_{min}$ in (45), $m_1$ can be safely expected to be close to the 5D radion mass obtained by Goldberger and Wise in [19]. This indicates that the exponentially warped radion should be lighter than the lowest-lying KK excitations of bulk fields in the doubly warped model [68] – which is a result analogous to its 5D counterpart.

4.2 Couplings of the radions to visible sector fields

The induced metric on the maximally warped $(\pi ,0)$ visible brane is given by $g^{(ind)}_{\mu \nu }=a(\pi )^2b(0)^2\eta _{\mu \nu }$. As the warp factors are explicit functions of $T_1$ and $T_2$, the radions $\rho _1$ and $\rho _2$ should directly couple to SM fields on the visible brane. As a generic example, we consider a free massive scalar field h(x) on this brane with mass $\mu _0\sim M_{Pl}$. Owing to 4D general covariance, its action is

$$\begin{aligned} S_h=\dfrac{1}{2}\int d^4x\sqrt{-g^{(ind)}}\left( g_{(ind)}^{\mu \nu }\partial _\mu h\partial _\nu h+\mu _0^2h^2\right) \end{aligned}$$

(47)

Keeping the small k assumption and writing the metric explicitly in terms of the radion fields, the scalar-radion interaction terms emerge as follows.

$$\begin{aligned} S_h\simeq & {} \dfrac{1}{2}\int d^4x\left[ \left( \dfrac{f_2\rho _1}{f_1\rho _2}\right) ^2\partial _\mu h\partial ^\mu h-\dfrac{3}{2}\left( \dfrac{\rho _1\rho _2}{f_1f_2}\right) ^2\partial _\mu h\partial ^\mu h\right. \nonumber \\{} & {} \left. +\left( \dfrac{f_2\rho _1}{f_1\rho _2}\right) ^4\mu _0^2h^2-\dfrac{5}{2}\left( \dfrac{\rho _1}{f_1}\right) ^4\mu _0^2h^2\right] \end{aligned}$$

(48)

Rescaling $h(x)\rightarrow \left( \dfrac{f_1\left\langle \rho _2\right\rangle }{f_2\left\langle \rho _1\right\rangle }\right) h(x)$ and defining $\mu =\mu _0\left( \dfrac{\left\langle \rho _1\right\rangle }{f_1}\right) \left( \dfrac{\left\langle \rho _2\right\rangle }{f_2}\right) ^{-1}$, the action becomes

$$\begin{aligned}{} & {} S_h\,\simeq \,\dfrac{1}{2}\int d^4x \Biggl [\left( \dfrac{\rho _1}{\left\langle \rho _1\right\rangle }\right) ^2\left( \dfrac{\rho _2}{\left\langle \rho _2\right\rangle }\right) ^{-2}\partial _\mu h\,\partial ^\mu h\nonumber \\{} & {} \quad +\left( \dfrac{\rho _1}{\left\langle \rho _1\right\rangle }\right) ^4\left( \dfrac{\rho _2}{\left\langle \rho _2\right\rangle }\right) ^{-4}\mu ^2h^2 \nonumber \\{} & {} \quad -\dfrac{3}{2}\left( \dfrac{\rho _1}{\left\langle \rho _1\right\rangle }\right) ^2\left( \dfrac{\rho _2}{\left\langle \rho _2\right\rangle }\right) ^2\left( \dfrac{\left\langle \rho _2\right\rangle }{f_2}\right) ^4\partial _\mu h\,\partial ^\mu h\nonumber \\{} & {} \quad -\dfrac{5}{2}\left( \dfrac{\rho _1}{\left\langle \rho _1\right\rangle }\right) ^4\left( \dfrac{\left\langle \rho _2\right\rangle }{f_2}\right) ^4\mu ^2h^2\Biggr ] \end{aligned}$$

(49)

In this canonically normalized action, the physical mass $\mu$ is close to the electroweak scale as expected. The coupling strengths of the radion fluctuations to ordinary matter are determined by the VEV magnitudes $\left\langle \rho _1\right\rangle$ and $\left\langle \rho _2\right\rangle$. To see it clearly, we expand the fields about their VEVs as $\rho _1=\left\langle \rho _1\right\rangle +\delta \rho _1$ and $\rho _2=\left\langle \rho _2\right\rangle +\delta \rho _2$.

$$\begin{aligned} S_h&\simeq \,\dfrac{1}{2}\int d^4x\Bigg [\left( \partial _\mu h\,\partial ^\mu h+\mu ^2h^2\right) \nonumber \\&\quad +\left( 2-3\dfrac{\,\left\langle \rho _2\right\rangle ^4}{f_2^4}\right) \dfrac{\delta \rho _1}{\left\langle \rho _1\right\rangle }\partial _\mu h\,\partial ^\mu h \nonumber \\&\quad -\left( 2+3\dfrac{\,\left\langle \rho _2\right\rangle ^4}{f_2^4}\right) \dfrac{\delta \rho _2}{\left\langle \rho _2\right\rangle }\partial _\mu h\,\partial ^\mu h \nonumber \\&\quad +\left( 4-10\dfrac{\,\left\langle \rho _2\right\rangle ^4}{f_2^4}\right) \dfrac{\delta \rho _1}{\left\langle \rho _1\right\rangle }\mu ^2h^2\nonumber \\&\quad -\left( 4+6\dfrac{\,\left\langle \rho _2\right\rangle ^4}{f_2^4}\right) \dfrac{\delta \rho _1}{\left\langle \rho _1\right\rangle }\dfrac{\delta \rho _2}{\left\langle \rho _2\right\rangle }\partial _\mu h\,\partial ^\mu h \nonumber \\&\quad -16\dfrac{\delta \rho _1}{\left\langle \rho _1\right\rangle } \dfrac{\delta \rho _2}{\left\langle \rho _2\right\rangle }\mu ^2h^2-\dfrac{5}{2} \dfrac{\,\left\langle \rho _2\right\rangle ^4}{f_2^4}\mu ^2h^2\Biggr ] \end{aligned}$$

(50)

From (41), we recall $\left\langle \rho _2\right\rangle =f_2\sqrt{k'\left\langle T_2\right\rangle \pi }$, which for $k'\left\langle T_2\right\rangle \sim 0.1$ makes $\left\langle \rho _2\right\rangle ^4/f_2^4\sim 0.1$. In other words, all the terms proportional to $\left\langle \rho _2\right\rangle ^4/f_2^4$ in (50) are sub-leading by roughly one order of magnitude, and the numerical coefficients in parentheses are all ${\mathcal {O}}(1)$. Hence, the coupling strength of $\delta \rho _1$ to h is set by $\left\langle \rho _1\right\rangle ^{-1}$, and that of $\delta \rho _2$ by $\left\langle \rho _2\right\rangle ^{-1}$. From (41), it is obvious that the former is a TeV-scale coupling, whereas the latter is of gravitational strength. Further, the cross-coupling of $\delta \rho _1\delta \rho _2$ to h is suppressed by a factor of $\left\langle \rho _2\right\rangle ^{-1}$.

This result can be generalized for any parameter with arbitrary mass dimension d appearing in the matter Lagrangian. Such a parameter needs to be rescaled with $\left( f_1\left\langle \rho _2\right\rangle /f_2\left\langle \rho _1\right\rangle \right) ^d$. On the other hand, operators having n powers of $g_{(ind)}^{\mu \nu }$ carry a factor of $\left( \rho _1\left\langle \rho _2\right\rangle /\rho _2\left\langle \rho _2\right\rangle \right) ^{(4-2n)}$, where inverse vierbeins for fermionic fields further contribute with $n=1/2$. It thus becomes clear that $\delta \rho _1$ and $\delta \rho _2$ couple to visible brane matter through the trace of the energy-momentum tensor $T_{\mu \nu }$ of the Standard Model, but with very distinct coupling strengths.

$$\begin{aligned} {\mathcal {L}}_{int}^{(\rho _1)}{} & {} \simeq \dfrac{\delta \rho _1}{\left\langle \rho _1\right\rangle }T^\mu _{\,\,\mu }\quad , \quad {\mathcal {L}}_{int}^{(\rho _2)} \simeq \dfrac{\delta \rho _2}{\left\langle \rho _2\right\rangle }T^\mu _{\,\,\mu }\quad ,\nonumber \\ {\mathcal {L}}_{int}^{(\rho _1\rho _2)}{} & {} \simeq \dfrac{\delta \rho _1}{\left\langle \rho _1\right\rangle } \dfrac{\delta \rho _2}{\left\langle \rho _2\right\rangle }T^\mu _{\,\,\mu } \end{aligned}$$

(51)

It is only the radion $\rho _1$ which is of direct experimental interest, as it has both ${\mathcal {O}}$(TeV) mass and inverse TeV-scale couplings to SM fields. Its phenomenological features are thus very close in spirit to the single radion phenomenology of the singly warped model studied in [19]. Tracelessness of the tree-level QCD energy-momentum tensor at high energies is expected to suppress certain mechanisms of $\rho _1$ generation. Also, the Higgs-like coupling of the radion to SM fields can be used to derive constraints on radion production relative to Higgs production processes via analogous interactions, as shown in [19]. The other radion $\rho _2$, with its nearly Planck scale mass and inverse Planck strength interactions with visible matter, lies beyond the reach of collider experiments. The cross-couplings among the two radions and visible matter are not of much interest here either, as they are also suppressed by the Planck scale. Although not quite relevant for ground-based colliders, these interactions should, in principle, leave fine detectable signatures in sufficiently high energy events such as extreme astrophysical phenomena (e.g. gamma-ray bursts and compact merger events) and early cosmological features (e.g. next generation CMB observations). Finally, as we have only been interested in estimating the orders of the radion masses and couplings, the precise value of the parameter $\epsilon$ has not been relevant to our leading order analysis. The validity of the underlying tuning assumption connecting $\partial _\mu T_1$ and $\partial _\mu T_2$ can also be probed by constraining $\epsilon$ from such observations, if any. We plan to address these interesting possibilities in future works.

Before concluding this section, it needs to be highlighted that throughout the leading order analysis done so far, we have neglected the back reaction of the bulk field on the background metric. Under certain conditions, this might result in underestimation of the radion mass by a couple of orders of magnitude as shown in [38] and [39]. Furthermore, unlike the 5D model, one can exploit the 6D setup immensely by allowing SM fields to extend into the bulk. This possibility, which constitutes an interesting feature of the doubly warped model, might imply corrections to the radion mass due to interactions of $\phi$ with these fields. There can also be non-negligible mixing between $\phi$ and the scalar degrees of freedom which give rise to coordinate dependent 4-brane tensions in this scenario. However, they are all expected to supply sub-leading corrections to the results derived here. Due to the extremely complicated nature of such a study which can incorporate all these features accurately, we do not consider these prospects here and defer that treatment to a future work.

5 Insight from higher curvature gravity

One of the most compelling advantages of having the size of the extra dimensions set by a single bulk field (as opposed to separate bulk and brane localized fields) is that it allows a purely gravitational interpretation of the stabilizing mechanism. Conventional wisdom suggests that the Einstein–Hilbert action, which provides an effective low energy description of gravity, needs to be amended with additional higher curvature terms respecting diffeomorphism invariance at sufficiently high energy scales. The warped geometry model which is being considered here has a large cosmological constant ( $\sim M_P$ ) in the bulk and as a result the inclusion of higher curvature terms is a natural choice. Two broad classes of such higher curvature theories are the quasi-linear Lanczos–Lovelock models and f(R) models. While Lanczos–Lovelock models enjoy the benefit of being naturally ghost-free [72,73,74], the mathematically simpler f(R) models, equipped with specific conditions to ensure freedom from ghosts, pass some of the cosmological tests [75,76,77,78,79,80]. Furthermore, any given f(R) action typically admits a dual scalar-tensor representation [81,82,83,84,85,86,87,88,89,90,91,92]. In the so-called Einstein frame (related to the Jordan frame through a conformal transformation), the situation is equivalent to that of a scalar field ${{\tilde{\phi }}}$ coupled minimally to gravity, alongside a potential $U({{\tilde{\phi }}})$ whose form is determined by the functional form of f(R). For singularity-free metrics which are not experiencing rapid evolution, this equivalence holds physically [93,94,95,96,97].

5.1 Origin of the scalar mode

In recent works [98] and [99], it has been shown how such a scalar degree of freedom, arising solely from gravity in the 5D RS model, can play the role of the bulk field in the Goldberger–Wise scheme, thus obviating the need to introduce the latter by hand. By choosing $f(R)=R+\gamma _2R^2-|\gamma _4|R^4$ (where $\gamma _2$ and $\gamma _4$ are coupling constants with respective mass dimensions $-2$ and $-6$, and satisfying $\gamma _2>0$ and $\gamma _2>|\gamma _4|$ to ensure freedom from ghosts), the potential can be arranged to contain both quadratic and quartic terms, with the latter encapsulating the effects of back reaction. Although the technique can be readily extended to spacetimes of arbitrary dimensionality, the inclusion of back reaction quickly renders multiply warped settings intractable in their full generality. In the following analysis, we first discuss an extension of the idea to the doubly warped model by retaining only the lowest-order correction term in f(R). To that end, we choose $f(R)=R+\gamma _2R^2$ (akin to the familiar Starobinsky model of inflation [100,101,102]), which provides the action

$$\begin{aligned} {\mathcal {A}}{} & {} =\int d^6x\sqrt{-g}\left[ \dfrac{f(R)}{2\kappa _6^2}-\Lambda _6\right] \nonumber \\{} & {} =\int d^6x\sqrt{-g}\left[ \dfrac{1}{2\kappa _6^2}\left( R+\gamma _2R^2\right) -\Lambda _6\right] \end{aligned}$$

(52)

where $\kappa _6$ is the six-dimensional gravitational constant. In order to arrive at the Einstein frame, one conventionally makes a detour [85] through the intermediate Jordan frame representation

$$\begin{aligned} {\mathcal {A}}{} & {} =\int d^6x\sqrt{-g}\left[ \dfrac{1}{2\kappa _6^2}\{\psi R-V(\psi )\}-\Lambda _6\right] \quad ,\nonumber \\ V(\psi ){} & {} =\chi (\psi )\psi -f(\chi (\psi )) \end{aligned}$$

(53)

where one introduces the auxiliary field $\chi$ and defines $\psi =f'(\chi )$. For $f''(\chi )\ne 0$, the equation of motion for $\chi$ from (53), i.e. the on-shell condition, imposes $\chi =R$. This makes (53) equivalent to the original f(R) action in (52). In order to reduce this to the minimally coupled Einstein frame representation, we apply the conformal transformation

$$\begin{aligned} g_{AB}\rightarrow \tilde{g}_{AB}=\sqrt{\psi }g_{AB},\quad \kappa _6{{\tilde{\phi }}}=\dfrac{\sqrt{5}}{2}\,\text {ln}\,\psi =\dfrac{\sqrt{5}}{2}\,\text {ln}\,f'(R) \end{aligned}$$

(54)

where the last equality follows from the on-shell condition. The action then transforms to

$$\begin{aligned} {\mathcal {A}}{} & {} =\int d^6x\sqrt{-{{\tilde{g}}}}\left[ \left( \dfrac{\tilde{R}}{2\kappa _6^2}-\Lambda _6\right) -\dfrac{1}{2}\partial _A{{\tilde{\phi }}}\partial ^A{{\tilde{\phi }}}-U({{\tilde{\phi }}})\right] \quad ,\nonumber \\ U({{\tilde{\phi }}}){} & {} =\dfrac{Rf'(R)-f(R)}{2\kappa _6^2(f'(R))^\frac{3}{2}} \end{aligned}$$

(55)

Substituting $f(R)=R+\gamma _2R^2$ in (54) and inverting the relation yields $R({{\tilde{\phi }}})$, which can be plugged immediately in (55) to obtain $U({{\tilde{\phi }}})$ as follows.

$$\begin{aligned}{} & {} R=\dfrac{1}{2\gamma _2}\left( e^{\frac{2}{\sqrt{5}}\kappa _6{{\tilde{\phi }}}}-1\right) \nonumber \\{} & {} \quad \implies \quad U({{\tilde{\phi }}})=\dfrac{1}{8\gamma _2\kappa _6^2}\left( e^{\frac{1}{\sqrt{5}}\kappa _6{{\tilde{\phi }}}}-2e^{-\frac{1}{\sqrt{5}}\kappa _6{{\tilde{\phi }}}}+e^{-\frac{3}{\sqrt{5}}\kappa _6{{\tilde{\phi }}}}\right) \nonumber \\ \end{aligned}$$

(56)

The minimum of $U({{\tilde{\phi }}})$ occurs at ${{\tilde{\phi }}}=0$, as evident from $U'(0)=0$ and $U''(0)>0$. Expanding $U({{\tilde{\phi }}})$ about this minimum, the leading order non-vanishing contribution comes from the quadratic term, with all subsequent terms increasingly suppressed by higher powers of $\kappa _6$.

$$\begin{aligned} U({{\tilde{\phi }}})\approx & {} \dfrac{1}{8\gamma _2\kappa _6^2} \left[ \left( 1+\dfrac{\kappa _6{{\tilde{\phi }}}}{\sqrt{5}} +\dfrac{\kappa _6^2{{\tilde{\phi }}}^2}{10}\right) \right. \nonumber \\{} & {} \left. -2\left( 1-\dfrac{\kappa _6{{\tilde{\phi }}}}{\sqrt{5}} +\dfrac{\kappa _6^2{{\tilde{\phi }}}^2}{10}\right) +\left( 1-\dfrac{3\kappa _6{{\tilde{\phi }}}}{\sqrt{5}} +\dfrac{9\kappa _6^2{{\tilde{\phi }}}^2}{10}\right) \right] \nonumber \\= & {} \dfrac{{{\tilde{\phi }}}^2}{10\gamma _2} \end{aligned}$$

(57)

Having identified $(5\gamma _2)^{-1}$ with the mass squared of the scalar mode ${{\tilde{\phi }}}$, the action from (55) reduces precisely to the sum of the Einstein–Hilbert action and the Goldberger–Wise action in the 6D bulk, with ${{\tilde{\phi }}}$ in the Einstein frame remarkably playing the role of the bulk field. Although the higher curvature coupling $\gamma _2$ appears explicitly in the denominator of $U({{\tilde{\phi }}})$, it is easy to show that $U({{\tilde{\phi }}})\rightarrow 0$ in the limit $\gamma _2\rightarrow 0$ as physically expected. One simply needs to re-express ${{\tilde{\phi }}}$ in terms of R using (54), which shows that for small $\gamma _2$ we have $U(R)\,\approx \,(1/2)\gamma _2R^2$, hence the expected result.

In order to justify stopping at the $R^2$ term, let us take a look at the effect of subsequent higher curvature terms on the Einstein frame potential. Starting with $f(R)=R+\gamma _2R^2-|\gamma _4|R^4$ (where $|\gamma _4|\ll \gamma _2$) and proceeding similarly from (54), we obtain, up to the leading order, $R\,\approx \,(1/\sqrt{5}\gamma _2)\kappa _6{\tilde{\phi }}$, for which the potential $U({{\tilde{\phi }}})$ from (55) takes the approximate form:

$$\begin{aligned} U({{\tilde{\phi }}})\,\approx \,\dfrac{\gamma _2R^2-3|\gamma _4|R^4}{2\kappa _6^2} =\dfrac{1}{2}\left( \dfrac{1}{5\gamma _2}\right) {{\tilde{\phi }}}^2-\dfrac{1}{2} \left( \dfrac{3|\gamma _4|\kappa _6^2}{25\gamma _2^4}\right) {{\tilde{\phi }}}^4\nonumber \\ \end{aligned}$$

(58)

which is the quadratic result alongside a quartic correction proportional to the higher order coupling |b|. The latter term corresponds to the nonlinear back-reaction of the bulk field on the background spacetime. Fortunately, for $|\gamma _4|\ll \gamma _2$, suppression by $\kappa _6^2$ renders it negligibly small compared to the leading term. In the same vein, it can be shown that any monomial correction term $\gamma _nR^n$ (with integer $n\ge 2$) in f(R) will roughly contribute to $U({{\tilde{\phi }}})$ a corresponding ${{\tilde{\phi }}}^n$ term, proportional to $\gamma _n$ and suppressed by $k_6^{n-2}$. For the purpose of demonstration, let us consider a generic polynomial form of f(R) as follows:

$$\begin{aligned} f(R){} & {} =R+\sum \limits _{n=2}^N\gamma _nR^n\quad \implies \quad R({{\tilde{\phi }}})\nonumber \\{} & {} \approx \,\dfrac{1}{\sqrt{5}\gamma _2}\kappa _6{{\tilde{\phi }}} \quad \text {(up to leading order)} \end{aligned}$$

(59)

where we have assumed $|\gamma _n|\ll \gamma _2$ for all $n>2$, which is reasonable on physical grounds. The potential from (55) is then given approximately by

$$\begin{aligned} U({{\tilde{\phi }}}){} & {} \approx \,\dfrac{1}{2\kappa _6^2} \sum \limits _{n=2}^N\gamma _n(n-1)R({{\tilde{\phi }}})^n\,\approx \,\dfrac{1}{2}\sum \limits _{n=2}^N\nonumber \\{} & {} \quad \times \Bigg [\dfrac{\gamma _n(n-1)\kappa _6^{n-2}}{(\sqrt{5}\gamma _2)^n}\Bigg ]{{\tilde{\phi }}}^n \end{aligned}$$

(60)

As shown in [98] and [99], such terms beyond $n=2$ usually result in non-trivial modifications of the warp factors themselves. While [99] addresses the full back-reacted problem for the 5D RS model by including the $R^4$ term in the Jordan and Einstein frames separately, such an exact treatment is too complicated to be feasible in the 6D case and falls much beyond the scope of the present work. In any case, as the higher curvature contributions are all sub-leading and highly suppressed compared to $n=2$, they are expected to provide very minor corrections (if any) to our results. As such, they can be safely neglected for the purpose of this work.

5.2 Role in the stabilization scheme

With the necessary $R^2$ contribution from the gravitational sector at hand, one can use heuristic arguments to bridge the gap with the bulk field method from the preceding sections. As the physical origin of the higher curvature correction(s) can be traced to the bulk energy density, it stands to reason that the resulting scalar ${{\tilde{\phi }}}$ should be an explicit function only of the compact coordinates y and z. The solution for the background metric in the Einstein frame is given by (2) (by extremizing (55)). Equipped with the metric, the equation of motion for ${{\tilde{\phi }}}$, as obtained from (55), is formally identical to (11) away from the boundaries:

$$\begin{aligned} -\dfrac{1}{R_y^2}\partial _y\left( a^4b^3\partial _y{{\tilde{\phi }}}\right) -\dfrac{1}{r_z^2}\partial _z\left( a^4b^5\partial _z{{\tilde{\phi }}}\right) +{\tilde{m}}^2a^4b^5{{\tilde{\phi }}}=0\nonumber \\ \end{aligned}$$

(61)

where ${\tilde{m}}^2=(5\gamma _2)^{-1}$ as noted earlier. Note that reducing the value of $\gamma _2$ makes ${{\tilde{\phi }}}$ more and more massive, and in the limit $\gamma _2\rightarrow 0$ the scalar mode becomes infinitely heavy and loses its dynamical behaviour (in addition to ${{\tilde{\phi }}}\rightarrow 0$ itself according to (54)), therefore effectively dropping out of the theory. This is expected, as in absence of the higher curvature correction there can be no scalar potential, hence no stabilizing mechanism in the current picture. (61) can be solved via separation of variables, with the form of the general solution being identical to (13):

$$\begin{aligned}{} & {} {\tilde{\phi }}(y,z)=e^{2c|y|}\left( Ae^{{\tilde{\nu }}c|y|}+Be^{-{\tilde{\nu }}c|y|}\right) \left[ DP_{{\tilde{n}}}^{{\tilde{l}}}\left( \text {tanh}(k|z|)\right) \right. \nonumber \\{} & {} \quad \left. +EQ_{{\tilde{n}}}^{{\tilde{l}}}\left( \text {tanh}(k|z|)\right) \right] \text {sech}^{\frac{5}{2}}(kz) \end{aligned}$$

(62)

where the parameters ${\tilde{\nu }}$ and ${\tilde{n}}$ are defined just as in (14) and (15) (with $-4{\tilde{\alpha }}^2$ being the separation constant of (61) analogous to (12)):

$$\begin{aligned} {\tilde{\nu }}=2\sqrt{1+\dfrac{R_y^2{\tilde{\alpha }}^2}{c^2}}\,\,,\,\,\,{\tilde{n}}=2\sqrt{1+\dfrac{{\tilde{\alpha }}^2r_z^2\text {cosh}^2(k\pi )}{k^2}}-\dfrac{1}{2} \end{aligned}$$

(63)

and ${\tilde{l}}$ (as in (16)) alone contains the information about the higher curvature coupling:

$$\begin{aligned} {\tilde{l}}=\dfrac{5}{2}\sqrt{1+\dfrac{4{\tilde{m}}^2r_z^2}{25k^2}}=\dfrac{5}{2}\sqrt{1+\left( \dfrac{4}{125\gamma _2}\right) \dfrac{r_z^2}{k^2}} \end{aligned}$$

(64)

Now, being a function only of the compact coordinates (as assumed earlier), ${{\tilde{\phi }}}(y,z)$ is forbidden from having any dynamics on the 3-branes. This is qualitatively in agreement with the former bulk field prescription. As an immediate corollary, we obtain four constant values of ${{\tilde{\phi }}}$ (having mass dimension $+2$) serving as fixed boundary values on the four 3-branes.

$$\begin{aligned} {{\tilde{\phi }}}(0,0)={\tilde{u}}_1\,\,,\,\,\,{{\tilde{\phi }}}(0,\pi )={\tilde{u}}_2\,\,,\,\,\,{{\tilde{\phi }}}(\pi ,0)={\tilde{u}}_3\,\,,\,\,\,{{\tilde{\phi }}}(\pi ,\pi )={\tilde{u}}_4\nonumber \\ \end{aligned}$$

(65)

These values can be physically interpreted as the VEVs of ${{\tilde{\phi }}}$ frozen on the corresponding branes. The resulting boundary conditions are completely identical to (17)–(20), with only the various parameters replaced by their tilde counterparts. Note that the current approach renders these boundary conditions exact, whereas in the earlier formulation they were valid only in the large coupling regime. With the full solution for ${{\tilde{\phi }}}$ (which is formally identical to (21)–(25)) at hand, the rest of the analysis can proceed exactly as before, leading to the stabilization of both moduli under appropriate choices of parameters.

In this picture, the set of fundamental parameters turns out to be $\{\gamma _2,\alpha ,{\tilde{u}}_1,{\tilde{u}}_2/{\tilde{u}}_1,{\tilde{u}}_4/{\tilde{u}}_2\}$. The redefinition of the two dimensionless mass parameters $\mu _1$ and $\mu _2$, constructed from m and $\alpha$ respectively, takes the following form:

$$\begin{aligned} {\tilde{\mu }}_1=\dfrac{{\tilde{m}}r_z}{k}=\left( \dfrac{1}{\sqrt{5\gamma _2}}\right) \dfrac{r_z}{k}\,\,,\,\,\,{\tilde{\mu }}_2=\dfrac{{\tilde{\alpha }}r_z}{k} \end{aligned}$$

(66)

It is clear that the effect of $\gamma _2$ enters through the parameter ${\tilde{\mu }}_1$ alone. This relation further allows us to estimate a typical magnitude of $\gamma _2$ which is concordant with the stabilization mechanism dsecribed earlier. First, recall that $|\Lambda _6|\sim {\tilde{M}}^4$ implies $k/r_z\sim {\tilde{M}}$. Combining this with ${\tilde{\mu }}_1\sim 0.1$ (as demonstrated before), one roughly obtains a very small $\gamma _2\sim {\tilde{M}}^{-2}$. This, in turn, explains the closeness of the VEVs of ${\tilde{\phi }}$ to ${\tilde{M}}^2$. Using (54), we have at leading order:

$$\begin{aligned} \langle {{\tilde{\phi }}}\rangle _i={\tilde{u}}_i\sim \dfrac{\sqrt{5}\gamma _2}{\kappa _6}|R|_i\sim |R|_i \end{aligned}$$

(67)

where the subscript denotes the value at the location of the $i^{th}$ 3-brane. With the energy density in the bulk typically rendering $|R|\sim {\tilde{M}}^2$ and making higher curvature contributions significant, it is thus natural for near-Planck scale VEVs to arise in the scalar-tensor picture.

Although ${\tilde{\mu }}_1$ alone is apparently not very sensitive to minor changes in $\gamma _2$, the tuning between ${\tilde{\mu }}_1$ and ${\tilde{\mu }}_2$ necessary for simultaneous stabilization of c and k makes the precise value of the higher curvature coupling play a significant role. However, it is still not possible to constrain $\gamma _2$ accurately from this information alone, as one also needs the value of $\Lambda _6$ to break the degeneracy present in the definition of $\mu _1$. As it is not possible to measure $\Lambda _6$ directly, the current line of argument only allows a rough estimation of the magnitude of $\gamma _2$.

If $\Lambda _6$ and ${\tilde{u}}_2$ can be estimated independently from some other source, e.g. by fitting relevant braneworld-motivated cosmological models with available cosmological data, then experimental measurement of the ${\mathcal {O}}$(TeV) radion mass from (45) might ameliorate the situation and better help constrain the higher curvature coupling(s). The reason is the dependence of the functions $F_1(k)$ and $F_2(k)$ on $\mu _1$ (as seen in Table 1) and their explicit appearance in the expression of $m_1$. Without precise measurement of $\Lambda _6$ however, the degeneracy in $\mu _1$ persists. This is not surprising, as even in the 5D Goldberger–Wise scheme, measurement of the 4D radion mass alone does not help us accurately constrain the mass of the bulk scalar (beyond a rough order of magnitude estimation similar to what has been shown here). In the current picture, the information regarding the bulk scalar’s mass is simply passed on to the higher curvature coupling, preventing any precise estimation of the latter in a similar spirit. In the table below, we show estimates of the radion masses and the corresponding $R^2$ couplings (in terms of the undetermined parameters) for the parameter values listed in Table 1.

Table 2 Estimates of the ${\mathcal {O}}$(TeV) radion masses corresponding to the parameter values from Table 1 (computed using (45)), and the corresponding values of the higher curvature couplings associated with each choice of ${\tilde{\mu }}_1$, expressed in terms of the fundamental parameters of the model which are not expected to be directly measurable in collider experiments

As $f_1\sim \sqrt{48{\tilde{M}}^4/k'^2}$, the values of $m_1$ and $\gamma _2$ are essentially expressed in units involving the two precisely unknown quantities $k'$ and ${\tilde{u}}_2$. This explicitly shows that a measurement of the radion mass alone is not sufficient to constrain $\gamma _2$ accurately unless $k'$ and ${\tilde{u}}_2$ are also known to a sufficiently high degree of accuracy. One expects the latter to lie beyond the scope of collider searches, and alternative avenues like cosmological signatures of the model must be considered. Due to the fundamentally different and involved nature of such an investigation, we leave that treatment to a future work.

6 Discussions

The prospect of stabilizing both moduli of a doubly warped Randall-Sundrum braneworld model using a single bulk scalar field has been studied. Such a mechanism is crucial for a complete resolution of the gauge hierarchy problem in a higher dimensional scenario, and needs to supplement the gravitational part of the action giving rise to the warped metric. While the approach taken here is essentially a direct generalization of the Goldberger–Wise mechanism to six dimensions, the presence of nested warping brings out additional subtleties and constraints on the parameter space. As demonstrated, these constraints do not necessarily involve any extreme fine tuning of the fundamental parameters. In the $c>k$ regime, which is phenomenologically preferred as it requires no brane-localized phantom field to explain the coordinate dependence of the 4-brane tensions, the effective potential admits a true minimum in k around $k_{min}\sim 0.1$ without any significant tuning. The stabilization of c, on the other hand, requires tuning on two different levels: firstly among the parameters $\mu _1$, $\mu _2$, and $u_4/u_2$ (for the appearance of a suitable $c_{min}$), and secondly for $u_1/u_2$ (to ensure $c_{min}\sim 12$). This can be interpreted physically as a consequence of the doubly warped structure of the underlying spacetime. A further departure from the singly warped model is that in order to achieve $0.1\le k_{min}\le 0.6$ and $c_{min}\sim 12$, the minimum admissible magnitude of $u_1/u_2$ is ${\mathcal {O}}(10)$, which is one order of magnitude higher than the analogous requirement in case of the 5D mechanism.

On the phenomenological side, the stabilizing mechanism with a massive bulk scalar gives rise to two scalar radions. One of them has TeV scale mass and couples to SM fields on the visible brane with inverse TeV scale strength. The other one has Planck scale mass and couples to visible matter with inverse Planck strength. The cross-coupling among the two radions and SM fields is also suppressed by the Planck scale. Furthermore, the TeV scale radion is lighter than the lowest-lying KK excitations of bulk scalars in this model. Altogether, these make the TeV scale radion (whose features are expected to be very close to the radion of the singly warped scenario) the first detectable BSM signature of this model in collider experiments. The interactions of the other radion with SM fields, although beyond the scope of ground-based colliders, may leave observable signatures in extreme astrophysical phenomena (e.g. gamma-ray bursts and compact merger events) as well as early cosmological features (e.g. high precision data from next generation CMB missions). Together, ground-based colliders and extra-terrestrial observations may thus probe the validity of the doubly warped model in the near future. The latter prospects are interesting and we intend to explore them in future works.

The bulk scalar approach is especially attractive as it allows room for a purely gravitational interpretation, with higher curvature contributions in the bulk automatically giving rise to the required scalar mode and its potential in the Einstein frame. Since the bulk of such warped geometry model is endowed with large bulk cosmological constant , the contributions from higher curvature terms become natural. This motivates us to include higher curvature terms in the bulk such as in f(R) model. This feature distinguishes it from certain other stabilization schemes, e.g. stabilization of the two moduli with two distinct bulk and brane-localized fields. For appropriate choices of f(R), a variety of bulk scalar potentials can be generated, the simplest of which is the quadratic potential considered here. While the singly warped model could be solved exactly in presence of non-negligible back reaction, the doubly warped model becomes unsolvable as the field equations turn out to be non-linear PDEs. Nevertheless, the well-known $R^2$ correction is sufficient to make contact with the conventional approach on physical grounds. In soothe, at sufficiently high energy scales, gravity alone appears capable of both warping spacetime and determining the degree of warping. This possibility is intriguing, as it may produce observable TeV scale signatures of higher curvature gravity that can be explored in future collider experiments. In principle, foremost among them should be the ${\mathcal {O}}(\text {TeV})$ radion mass associated with the larger modulus, which could be of fundamental importance in constraining the magnitude(s) of the higher curvature coupling(s) alongside independent cosmological probes.

The current study can be extended along various avenues. As pointed out earlier, a more precise study of radion phenomenology in a multiply warped background needs to take interactions of the bulk field with higher dimensional fermionic and gauge fields into account, alongside mixing with the brane-localized scalars responsible for coordinate dependent brane tensions. These effects, which constitute salient features of geometries with nested warping, may introduce a plethora of non-trivial modifications as far as collider signatures are concerned. Theoretically, it is worth investigating how other viable choices of f(R), or other classes of higher curvature theories (e.g. Einstein–Gauss–Bonnet gravity), incorporate higher order phenomena like significant back reaction and affect the stabilization scheme. Such studies would necessarily have to rely on numerical techniques due to the complexity of the model. As plausible alternatives, one can also attempt to explain the origin of the stabilizing potential from quantum and/or thermodynamic perspectives, proceeding along the lines of [103,104,105,106,107]. Finally, it would be interesting to study the role of multiple dynamical radion fields in various cosmological contexts as well, e.g. in the inflationary and bouncing settings, alongside their detectable signature on the Cosmic Microwave Background data from upcoming CMB missions.