1 Introduction

The study of relativistic compact objects has become a significant active research area of stellar astrophysics. In such a sense, these stellar structures can be modelled theoretically as static fluid spheres whose interior is determined through solutions of Einstein’s field equations (EFE). Such solutions have been widely used to model several types of stellar objects such as black holes, gravastars, neutron stars, quark stars, and others. Thus, many models have been developed since Karl Schwarzschild in 1916 [1] found the first exact solution of EFE. These models consider both isotropy and anisotropy pressure on the relativistic fluid which supports the compact object. A large number of isotropic fluid solutions are known, but of all these, only a few satisfy the conditions of physical acceptability for a self-gravitating compact object [2]. Even in the case of the anisotropic fluid solutions, the number of such models that fulfill the physical acceptability conditions for a realistic stellar compact object is limited. Therefore, it is important to build new solutions that help make this number of solutions more significant in order to expand the study of these types of solutions.

Compact stars can be considered spherically symmetric and isotropic, but the anisotropic solutions are very appreciated since the disturbances of the isotropy and fluctuations of the local anisotropy in pressures may be caused by a large variety of physical phenomena of the kind that are expected in compact objects [3]. Examples of such phenomena are the high density regime, the existence of solid stellar cores, the presence of superfluids, phase transitions, rotations, etc [3,4,5,6,7,8,9,10,11,12,13]. In fact, there is a recent result in [14] where it is shown that any realistic physical process of the kind expected in stellar evolution always tends to produce pressure anisotropy by the presence of dissipation, energy density inhomogeneities, and shear. Therefore, any final stage of a dynamical regime in the evolution of a star should exhibit pressure anisotropy. Despite this fact, isotropic solutions remain common assumptions in the study of compact objects since they can perfectly describe phenomena such as realistic stars, or even be used as models of cold fluid planets, or as well as the simple fact of expanding the collection of known isotropic solutions built so far is also valid (see for example, Refs. [15,16,17,18,19,20,21,22,23,24,25,26,27,28]).

On the other hand, it is worth mentioning that the problem of obtaining exact solutions of the EFE for static and spherically symmetric space-times includes solving a robust system of coupled differential equations. In particular, the problem is there are only three independent EFE but five unknown quantities: two metric functions, the energy density, the radial and tangential pressures (matter sector). This problem has been addressed over time using widely successful strategies to obtain exact EFE solutions [29,30,31,32,33,34,35,36,37,38]. However, recently, one framework stands out for its effectiveness when finding new solutions called gravitational decoupling (GD). This framework allows us to use a known isotropic solution as a seed (an anisotropic solution can also be used) in order to obtain new solutions of EFE in the regime of anisotropic pressure. For such purpose the GD through the minimal geometric deformation (MGD) or its extended version (MGDe) uses the seed and extra(s) condition(s) (examples of such conditions are the mimic constraint for the pressure or energy density, barotropic equation of state, regularity of anisotropic pressure, complexity factor, among others) in order to close the entire system of EFE (for the implementation of this framework with the use of several seed solutions and extra conditions see for example the Refs. [39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64]). As well, the GD recently can be used in an effective way in order to study the energy exchange between relativistic fluids that support a static self-gravitating sphere regardless of their nature.

In particular, in this work we use the interpretation of GD through MGDe in order to obtain and study a new isotropic extension of Einstein’s universe solution, which fulfills the acceptability stellar conditions. Thus, the motivation to carry out this work is to show that using the GD through the MGDe a cosmological solution such as the Einstein’s universe can be useful to obtain a physically acceptable isotropic interior solution. It is worth mentioning that, commonly, the GD is used with the aim of extending an isotropic interior solution towards an anisotropic regime, but nevertheless, in the present work we transform a cosmological solution into an isotropic interior solution. Likewise, the found solution in this manuscript has an interesting behaviour from the point of view of the energy exchange between fluids that coexist within a compact stellar object since the two sources that we use are two perfect fluids: one of them is the fluid corresponding to the material sector of Einstein’s universe solution (which is used as the seed solution) and the second one is another perfect fluid (corresponding to the extra source that appears in the GD). In addition, this motivation is reinforced by the fact that such energy exchange between both perfect fluids depends exclusively on how compact the self-gravitating object is that is represented by the new interior solution, and as well, this solution would expand the number of known isotropic interior solutions that are physically acceptable.

Thus, the present paper is organized as follows: In Sect. 2, we review briefly the GD approach applied to a spherically symmetric system containing two generic sources; in Sect. 3, we present the matching conditions for the metrics involved in the model in order to obtain regularity of space-time and matter sector; in Sect. 4, we implement GD through MGDe described in Sect. 2 in order to obtain a new stellar model considering the Einstein’s universe solution as the seed solution and that the extra source is also a perfect fluid. In Sect. 5, we briefly review the fundamental stellar physical acceptability conditions for a realistic stellar compact object; in Sect. 6, we test such conditions for the new obtained stellar model; while in Sect. 7, we are devoted to exploring the energy exchange between the fluids that support the resulting stellar object, and finally, we realize a discussion in Sect. 8.

2 Gravitational decoupling

The GD solves the EFE

$$\begin{aligned} G_{\mu \nu }=R_{\mu \nu }-\frac{1}{2}g_{\mu \nu }R = \kappa T_{\mu \nu }, \end{aligned}$$
(1)

with

$$\begin{aligned} T_{\mu \nu } = T^{s}_{\mu \nu } + \theta _{\mu \nu } , \end{aligned}$$
(2)

where \(\kappa = \frac{8\pi G}{c^4}\)Footnote 1 and \(T^{s}_{\mu \nu }\) represents the matter sector of a known solution of EFE (which can be associated with a already known solution), which is known as the seed sector, and \(\theta _{\mu \nu }\) describes an unknown extra source (see Ref. [65] for more information on this approach via MGDe). In particular, the GD finds the space-time for a spherically symmetric and static self-gravitating compact object corresponding to the complex source (2) given by

$$\begin{aligned} ds^{2}=e^{\nu }dt^{2}-e^{\lambda }dr^{2} -r^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}), \end{aligned}$$
(3)

where the \(\nu \) and \(\lambda \) are functions only of the radial variable r. This space-time surges from the influence of the source \(\theta _{\mu \nu }\) given by

$$\begin{aligned} \theta ^{\mu }_{\nu } = \text {diag}(\theta _{0}^{0},\theta _{1}^{1},\theta _{2}^{2},\theta _{2}^{2}), \end{aligned}$$
(4)

on the known source \(T^{s}_{\mu \nu }\)

$$\begin{aligned} T^{\mu (s)}_{\nu } = \text {diag}(\rho ^{s},-p_{r}^{s},-p^{s}_{t},-p^{s}_{t}). \end{aligned}$$
(5)

Thus, the EFE (1) are explicitly given by

$$\begin{aligned} \kappa \rho= & {} \frac{1}{r^2} + e^{-\lambda }\!\left( \frac{\lambda '}{r} - \frac{1}{r^2}\right) \!,\end{aligned}$$
(6)
$$\begin{aligned} \kappa p_{r}= & {} -\frac{1}{r^2} + e^{-\lambda }\!\left( \frac{\nu '}{r} + \frac{1}{r^2}\right) \!,\end{aligned}$$
(7)
$$\begin{aligned} \kappa p_{t}= & {} \frac{e^{-\lambda }}{4}\!\left( 2\nu '' + {\nu '}^2 - \lambda '\nu ' + 2\frac{\nu '-\lambda '}{r} \right) ,\! \end{aligned}$$
(8)

where

$$\begin{aligned} \rho= & {} \rho ^{s} + \theta _{0}^{0} ,\end{aligned}$$
(9)
$$\begin{aligned} p_{r}= & {} p_r^{s}-\theta _{1}^{1} ,\end{aligned}$$
(10)
$$\begin{aligned} p_{t}= & {} p_{t}^{s} -\theta _{2}^{2} . \end{aligned}$$
(11)

Now, the total energy–momentum tensor \(T_{\mu \nu }\) satisfies the conservation equation

$$\begin{aligned} \nabla _{\mu } T^{\mu \nu } = 0, \end{aligned}$$
(12)

since the Einstein tensor satisfies the Bianchi identities. In fact, the Eq. (12) is given by a linear combination of Eqs. (6)–(8) as

$$\begin{aligned} \left( p_{r}\right) '+\frac{\nu '}{2}\left( \rho + p_{r}\right) +\frac{2}{r}\left( p_{r}-p_{t}\right) = 0. \end{aligned}$$
(13)

Now if one takes the Eq. (13) in terms of the two sources given by Eqs. (4) and (5), it reads as

$$\begin{aligned} (p_r^{s})'{} & {} + \frac{\nu '}{2}\left( \rho ^{s} + p_r^{s}\right) +\frac{2}{r}\left( p_{r}^{s}-p_{t}^{s}\right) \nonumber \\{} & {} \quad - \left( \theta _{1}^{1}\right) '+\frac{\nu '}{2}\left( \theta _{0}^{0}-\theta _{1}^{1}\right) +\frac{2}{r}\left( \theta _{2}^{2}-\theta _{1}^{1}\right) = 0.\nonumber \\ \end{aligned}$$
(14)

The key idea of GD consists of codifying the influence of \(\theta _{\mu \nu }\) on \(T_{\mu \nu }\) through the introduction of a geometric deformation that modifies the space-time corresponding to the seed sector \(T_{\mu \nu }^{s}\) (solution of Eq. (1) when \(T_{\mu \nu } = T_{\mu \nu }^{s}\)) given by

$$\begin{aligned} ds^2 = e^{\xi }dt^2 - e^{\mu }dr^2 -r^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}), \end{aligned}$$
(15)

into the resulting space-time (3) given by

$$\begin{aligned} \nu\longrightarrow & {} \xi + g, \end{aligned}$$
(16)
$$\begin{aligned} e^{-\lambda }\longrightarrow & {} e^{-\mu } + f , \end{aligned}$$
(17)

where \(\{\xi ,\mu \}\) are functions only of radial coordinate r and \(\{f,g\}\) are the so-called decoupling functions.

Then, by inserting (16) and (17) into the system (6)–(8), the entire set of differential equations (6)–(8) can be divided into two subsets: one describing a seed sector sourced by the conserved energy–momentum tensor, \(T_{\mu \nu }^{s}\)

$$\begin{aligned} \kappa \rho ^{s}= & {} \frac{1}{r^2}-e^{-\mu }\left( \frac{1}{r^2}-\frac{\mu '}{r}\right) , \end{aligned}$$
(18)
$$\begin{aligned} \kappa p_r^{s}= & {} -\frac{1}{r^2}+e^{-\mu }\left( \frac{1}{r^2}+\frac{\xi '}{r}\right) ,\end{aligned}$$
(19)
$$\begin{aligned} \kappa p_{t}^{s}= & {} \frac{e^{-\mu }}{4}\left( 2\xi ''+\xi '^2-\mu '\xi '+2\frac{\xi '-\mu '}{r}\right) , \end{aligned}$$
(20)

and the other set corresponding to source \(\theta _{\mu \nu }\)

$$\begin{aligned} \kappa \theta _{0}^{0}= & {} -\frac{f}{r^2}-\frac{f'}{r}\end{aligned}$$
(21)
$$\begin{aligned} \kappa \theta _{1}^{1}= & {} - f\left( \frac{1}{r^2}+\frac{\nu '}{r}\right) - Z_{1}\end{aligned}$$
(22)
$$\begin{aligned} \kappa \theta _{2}^{2}= & {} -\frac{f}{4}\left( 2\nu ''+\nu '^2+\frac{2\nu '}{r}\right) -\frac{f'}{4}\left( \nu '+\frac{2}{r}\right) \nonumber \\{} & {} - Z_{2}, \end{aligned}$$
(23)

where \(Z_{1}=\frac{e^{-\mu }}{r}g'\) and \(Z_{2}=\frac{e^{-\mu }}{4}(2g''+ g'^2+\frac{2g'}{r}+2\xi 'g'-\mu 'g')\).

Now if we insert \(\nu \) in Eq. (14), it becomes into

$$\begin{aligned}{} & {} \bigg [-(p_r^{s})'-\frac{\xi '}{2}\left( \rho ^{s}+p_r^{s}\right) -\frac{2}{r}\left( p_r^{s}-p_t^{s}\right) \bigg ]-\frac{g'}{2}\left( \rho ^{s}+p_r^{s}\right) \nonumber \\{} & {} \quad + (\theta _{1}^{1})'-\frac{\nu '}{2}(\theta _{0}^{0}-\theta _{1}^{1})-\frac{2}{r}(\theta _{2}^{2}-\theta _{1}^{1})=0, \end{aligned}$$
(24)

where the bracket in Eq. (24) represents the divergence of \(T_{\mu \nu }^{s}\) calculated with the metric \(\lbrace \xi ,\mu \rbrace \). Furthermore \(T_{\mu \nu }^{s}\) satisfies

$$\begin{aligned} \nabla _{\sigma }^{(\xi ,\mu )}T_{\nu }^{\sigma (s)} = 0, \end{aligned}$$
(25)

since \(T_{\nu }^{\sigma (s)}\) correspond a known “seed” source that satisfies its respective EFE.

Note that

$$\begin{aligned} \nabla _{\sigma }T_{\nu }^{\sigma (s)}=\nabla _{\sigma }^{(\xi ,\mu )}T_{\nu }^{\sigma (s)}-\frac{g'}{2}(T_{0}^{0 (s)}-T_{1}^{1 (s)})\delta _{\nu }^{1}, \end{aligned}$$
(26)

where the divergence \(\nabla _{\sigma }\) is calculated with the metric \(\lbrace \nu ,\lambda \rbrace \). Explicitly Eq. (25) gives us

$$\begin{aligned} (p_r^{s})'+\frac{\xi '}{2}(\rho ^{s}+p_r^{s})+\frac{2}{r}(p_r^{s}-p_t^{s})=0, \end{aligned}$$
(27)

which is a linear combination of Eqs. (18)–(20). In this way, if one takes into account the Eqs. (25) and (24) results

$$\begin{aligned} \nabla _{\sigma }\theta _{\nu }^{\sigma }=-\nabla _{\sigma } T_{\nu }^{\sigma (s)}=\frac{g'}{2}(T_{0}^{0 (s)}-T_{1}^{1 (s)})\delta _{\nu }^{1}, \end{aligned}$$
(28)

which encodes the information of energy–momentum exchange \(\varDelta \,\textrm{E}\) between the sources, namely

$$\begin{aligned} \varDelta \,\textrm{E}= \frac{g'}{2}\left( \rho +p_r\right) , \end{aligned}$$
(29)

which can also be written as

$$\begin{aligned} \varDelta \,\textrm{E}= \frac{g'}{2\,\kappa }\frac{e^{-\mu }}{r}\left( \xi '+\mu '\right) . \end{aligned}$$
(30)

It is worth noting that the expression (30) produces \(g'>0\), resulting in \(\varDelta \,\textrm{E}>0\). Thus \(\nabla _\sigma \theta ^{\sigma }_{\ \nu }>0\), which is according to the conservation equation (29). In that case, the source \(\theta _{\mu \nu }\) gives energy to the environment. When \(g'<0\), the source \(T_{\mu \nu }\) provides energy to the environment to keep both fluids coexisting inside the stellar compact object (see Refs. [66, 67] for a recent study of the exchange of energy between a perfect fluid and a polytrope).

3 Matching conditions

At the boundary of the stellar compact object (\(r = R\)), the metric components \(e^{\nu }\) and \(e^{-\lambda }\) should match continuously with the Schwarzschild exterior solution, namely

$$\begin{aligned} e^{\nu }|_{r=R} = e^{-\lambda }|_{r=R} = 1 - \frac{2M}{R}, \end{aligned}$$
(31)

where M and R are the total mass and radius of star, respectively.

It is also necessary that

$$\begin{aligned} p_{r}|_{r = R} = 0, \end{aligned}$$
(32)

since the exterior of the star in this case is considered empty.

4 New stellar model

In order to obtain a new stellar model applying the GD by the Extended version of MGD, we consider the Einstein’s universe solution as a seed solution given by [68]

$$\begin{aligned} e^{\xi }= & {} A\end{aligned}$$
(33)
$$\begin{aligned} e^{-\mu }= & {} 1 -\frac{r^2}{C^2}, \end{aligned}$$
(34)

where A and C are constants, and whose matter sector is

$$\begin{aligned} \rho ^{s} = - p^{s} = \frac{3}{\kappa C^2}, \end{aligned}$$
(35)

with the extra consideration that the source \(\theta _{\mu \nu }\) is a perfect fluid, so

$$\begin{aligned} \theta _{0}^{0} = \frac{\varrho }{\kappa }, \end{aligned}$$
(36)

where \(\varrho \) is a constant, and also that

$$\begin{aligned} \varPi _{\theta } = p_{\theta r} - p_{\theta t} = \kappa (\theta _{2}^{2}-\theta _{1}^{1})=0. \end{aligned}$$
(37)

Now, the implicit form of the Eq. (36) is

$$\begin{aligned} \frac{f'}{r} + \frac{f}{r^2} + \varrho = 0, \end{aligned}$$
(38)

whose solution is

$$\begin{aligned} f = -\frac{1}{3}\varrho r^2 + \frac{c_0}{r}, \end{aligned}$$
(39)

where we set \(c_0 = 0\) in order to avoid singularities.

While using (22) and (23) in (37) gives us

$$\begin{aligned}{} & {} 2 r \left( C^2 \left( r^2 \varrho -3\right) +3 r^2\right) g''(r)\nonumber \\{} & {} \quad +\left( C^2 r \left( r^2 \varrho -3\right) +3 r^3\right) g'(r)^2\nonumber \\{} & {} \quad +6 C^2 g'(r) = 0, \end{aligned}$$
(40)

where the seed solution given by (33)–(39) was used. Thus, if one solves Eq. (40), one arrives at

$$\begin{aligned} g= & {} 2 \ln {\left( 2 c_1 \left( C^2 \varrho +3\right) +\sqrt{C^2 \left( r^2 \varrho -3\right) +3 r^2}\right) }\nonumber \\{} & {} \quad + c_2, \end{aligned}$$
(41)

where \(c_1\) and \(c_2\) are integration constants.

Thus, using (16) and (17), we obtain the new metric components

$$\begin{aligned} e^{\nu }= & {} B\left( 2 c_1 \left( C^2 \varrho +3\right) +\sqrt{C^2 \left( r^2 \varrho -3\right) +3 r^2}\right) ^2\end{aligned}$$
(42)
$$\begin{aligned} e^{-\lambda }= & {} 1-\frac{r^2}{C^2}-\frac{r^2 \varrho }{3}, \end{aligned}$$
(43)

where \(B = A e^{c_2}\). Using the EFE (6)–(8), we can now obtain the matter sector

$$\begin{aligned} \rho= & {} \rho ^{s} + \frac{\varrho }{\kappa } = \frac{1}{\kappa }\left( \frac{3}{C^2} + \varrho \right) \end{aligned}$$
(44)
$$\begin{aligned} p_{r}= & {} p_{t} = p\nonumber \\= & {} \frac{-1+e^{-\lambda }\left( 1+\frac{2 r^2}{2 c_1 \sqrt{C^2 \left( r^2 \varrho -3\right) +3 r^2}-\frac{3 C^2}{C^2 \varrho +3}+r^2}\right) }{\kappa r^2}. \end{aligned}$$
(45)

Note that Eq. (44) is according to Eq. (9) as expected; namely, the effective density energy of the new model is the algebraic sum of the energy density of Einstein’s fluid and the energy density \(\theta _{0}^{0} = \frac{\varrho }{\kappa }\). Also, it is worth noticing that p is finite at the center of stellar compact object since \(e^{-\lambda }|_{r=0} = 1\). Furthermore, from Eq. (45), we have that \(\varrho \ne -\frac{3}{C^2}\), \(\varrho r^2\ge 3-\frac{3}{C^2}r^2\) and \(c_{1}^2 \ne \frac{\left( C^2 \varrho r^2-3 C^2+3 r^2\right) ^2}{\left( C^2 \varrho +3\right) ^2 \left( 4 C^2 \varrho r^2-12 C^2+12 r^2\right) }\). Now, the inequality \(\varrho r^2\ge 3-\frac{3}{C^2}r^2\) cannot be true at \(r=0\), which implies that Eqs. (42) and (45) are not defined at \(r=0\), but this inconsistency disappears when the conditions (46)–(48) are used.

Moreover, using the continuity conditions (31) and (32) at the surface of the stellar compact object, we obtain

$$\begin{aligned} c_1= & {} -\frac{3 \sqrt{C^2 \left( R^2 \varrho -3\right) +3 R^2}}{2 C^2 \varrho +6}\end{aligned}$$
(46)
$$\begin{aligned} A= & {} \frac{e^{-c_2} (R-2 M)}{4 \left( C^2 R \left( R^2 \varrho -3\right) +3 R^3\right) }\end{aligned}$$
(47)
$$\begin{aligned} C^2= & {} \frac{3 R^3}{6 M-R^3 \varrho }. \end{aligned}$$
(48)

From the above conditions, we have that \(R > 2M\) which is in accordance with the restriction that any stable configuration should be greater than its Schwarzschild radius and \(\frac{3M}{R} -9< R^2 \varrho < \frac{2M}{R}\).

5 Physical acceptability conditions

The fundamental physical requirements necessary for any interior solution to describe a realistic stellar compact object are (see Ref. [69] for a detailed discussion of these conditions):

  1. C1.

    The metrics \(e^{\nu }\) and \(e^{\lambda }\) should be finite and regular in the interior of any stellar compact object. In addition, \(e^{\nu (0)} = constant\) and \(e^{-\lambda (0)} = 1\).

  2. C2.

    The matter sector given by the energy density \(\rho \), radial pressure \(p_{r}\) and transversal pressure \(p_{t}\) should be positive and regular inside the compact object. They should be decreasing functions of radial coordinate r having their maximum values at the center. Furthermore, the radial pressure should vanish at the boundary, the radial and tangential pressures are equal at the center of the stellar compact object.

  3. C3.

    The dominant energy condition (DEC) \(\rho - p_{r} \ge 0\) and \(\rho - p_{t} \ge 0\) should be fulfilled \(\forall r,\quad r\le R\).

  4. C4.

    The surface redshift \(z(r) = g_{tt}^{-1/2}(r)-1\) should decrease outward, and its value at the surface is less than the universal bound for solutions satisfying the DEC, namely \(z_{bound} = 5.211\) [70].

  5. C5.

    The stability of the stellar object requires that the speed of sound be less than the speed of light, which leads to \(0\le v_{r}^2 = \frac{dp_r}{d\rho }\le 1\) and \(0\le v_{t}^2 = \frac{dp_t}{d\rho }\le 1\) inside of the stellar compact object since we fix \(c =1\) in this work.

Also, there are some physical conditions related to the stability of self-gravitating compact objects, but in this work we do not address these points since they can be tried in greater detail in future works.

6 Physical analysis

In this section, we analyse the physical acceptance of the stellar model obtained in Sect. 4. For the study of these physical conditions, we have checked that the behaviour of the whole model given by Eqs. (42)–(48) is regular with the setting of the compactness factor \(u = \frac{M}{R} < 0.38\) and the density energy \(\varrho = 1\).

6.1 Metrics

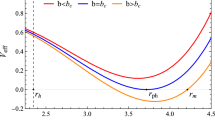
The metrics \(e^{\nu }\) and \(e^{-\lambda }\) are plotted in Figs. 1 and 2. We can observe that these metrics satisfy the condition C1, namely that they behave according to the space-time for the interior of any stellar compact object.

Fig. 1
figure 1

\(e^{\nu }\) for \(u = 0.1\) (blue line), \(u = 0.2\) (black line), \(u = 0.3\) (red line), \(u = 0.37\) (green line) and \(\varrho = 1\)

Full size image
Fig. 2
figure 2

\(e^{-\lambda }\) for \(u = 0.1\) (blue line), \(u = 0.2\) (black line), \(u = 0.3\) (red line), \(u = 0.37\) (green line) and \(\varrho = 1\)

Full size image

6.2 Matter sector

Since the density energy of the new model is a constant given by Eq. (44) is not necessary to plot it. In Fig. 3 the profile of p is plotted. We can observe that the radial pressure is positive and regular inside the compact object. It is a decreasing function of radial coordinate r having its maximum value at the center of the stellar compact object. Notice that p vanishes at the surface of the star since it is rounded by the vacuum.

Fig. 3
figure 3

p for \(u = 0.1\) (blue line), \(u = 0.2\) (black line), \(u = 0.3\) (red line), \(u = 0.37\) (green line) and \(\varrho = 1\)

Full size image

6.3 Energy condition and causality

In Fig. 4 we plot the profile of \(\rho - p\). In this figure, we can observe the DEC is fulfilled by this model.

Fig. 4
figure 4

\(\rho - p\) for \(u = 0.1\) (blue line), \(u = 0.2\) (black line), \(u = 0.3\) (red line), \(u = 0.34\) (green line), \(u = 0.37\) (pink line) and \(\varrho = 1\)

Full size image

Additionally, if one considers the rough approximation of the sound velocity for an incompressible fluid, \(v = \sqrt{\frac{p}{\rho }}\) inside the star, we can show the profile of v in Fig. 5 as a function of radial coordinate. By looking at this figure, we can confirm that the sound velocity inside of the stellar compact object is below the relativistic limit of vacuum light velocity. The sound velocity profile is a monotonously decreasing function that disappears at the surface, as you can see.

Fig. 5
figure 5

v for \(u = 0.1\) (blue line), \(u = 0.2\) (black line), \(u = 0.3\) (red line), \(u = 0.37\) (green line) and \(\varrho = 1\)

Full size image

6.4 Redshift

The redshift function z is presented in Fig. 6. In this figure, we can easily verify that the condition C4 is fulfilled, namely, that the redshift is a monotonously decreasing function of radial coordinate with a maximum value at the center of the star. Additionally, the surface redshift value is below the universal bound of \(z_{bound} = 5.211\).

Fig. 6
figure 6

z for \(u = 0.1\) (blue line), \(u = 0.2\) (black line), \(u = 0.3\) (red line), \(u = 0.37\) (green line) and \(\varrho = 1\)

Full size image

Thus, with everything shown above, we can conclude that the present model obtained in this manuscript fulfills the fundamental physical conditions that are necessary in order to represent a realistic stellar compact object.

7 Energy exchange and nature of extra source

In order to analyse the energy exchange between the fluid given by the Einstein’s solution (seed solution) and the extra source \(\theta _{\mu \nu }\) we have to study the behaviour of the Eq. (30) which is shown in Fig. 7. We observe that \(\varDelta E\) is negative for lower compactness factors, while for the upper compactness factor values \(\varDelta E\) becomes positive, which implies that there is a specie of transition between the situation where \(\varDelta E < 0\) (smaller compactness factor) and \(\varDelta E > 0\) (bigger compactness factor). The above result can be contrasted in Fig. 8, where the energy exchange between the two fluids is shown for different values of the compactness factor; for the lower compactness factor, both fluids increase their energy exchange significantly in the inner shells of the stellar compact object, while such interaction becomes more noticeable on the surface if the stellar object is more compact. Thus, for the coexistence between these fluids, it is necessary that Einstein’s fluid gives energy for the less compact stellar objects, while for the more compact ones the situation is the opposite. Specifically, in the case of the extra source \(\theta _{\mu \nu }\), it is the one that releases the energy in order to maintain the configuration of the stellar compact object.

We also checked for the particular case of \(\varrho = \rho ^{s}=\frac{3}{C^2}\) (density mimic constraint), the new model also fulfils the physical acceptability conditions, but however the exchange of energy between both fluids is positive (\(\varDelta E > 0\)) for the same compactness factor values taken before. As a result, in this case, the extra source \(\theta _{\mu \nu }\) emits energy into the environment (see Figs. 9 and 10).

Fig. 7
figure 7

\(\varDelta E\) for \(u = 0.1\) (blue line), \(u = 0.15\) (black line), \(u = 0.2\) (red line), \(u = 0.3\) (green line), \(u = 0.37\) (yellow line) and \(\varrho = 1\)

Full size image
Fig. 8
figure 8

Density plot of the energy exchange for a \(u = 0.1\), b \(u = 0.15\), c \(u = 0.3\) and d \(u = 0.37\)

Full size image
Fig. 9
figure 9

\(\varDelta E\) for \(u = 0.1\) (blue line), \(u = 0.15\) (black line), \(u = 0.2\) (red line), \(u = 0.3\) (green line), \(u = 0.37\) (yellow line) and \(\varrho = \rho ^{s}=\frac{3}{C^2}\)

Full size image
Fig. 10
figure 10

Density plot of the energy exchange for a \(u = 0.1\) and b \(u = 0.3\) and \(\varrho = \rho ^{s}=\frac{3}{C^2}\)

Full size image

Now the components \(\theta _{1}^{1} = \theta _{2}^{2}=p_{\theta }\) of the extra source \(\theta _{\mu \nu }\) can be seen as the typical interior radial pressure of a stellar compact object since it behaves according to the condition C2, but this radial pressure does not become zero at the star’s surface, which indicates that \(\theta _{\mu \nu }\) also acts outside of the static fluid sphere (see Fig. 11).

Fig. 11
figure 11

\(p_{\theta }\) for \(u = 0.16\) (blue line), \(u = 0.2\) (black line), \(u = 0.3\) (red line), \(u = 0.37\) (green line) and \(\varrho = 1\)

Full size image

So, in this sense, the resulting interior solution given by Eqs. (42)–(48) arises from the interaction between two energy density homogeneous and isotropic fluids; one given by the Einstein’s universe solution and the other given by the source \(\theta _{\mu \nu }\), having as a result a perfect fluid interior that in whose interior there is an interesting exchange of energy of its component fluids that depends exclusively on how compact the resulting stellar object is.

8 Discussion

It is well known that obtaining exact EFE solutions for static and spherically symmetric space-times is difficult due to the non-linear nature of the EFE, which has developed into an active research area in theoretical stellar astrophysics. To solve these difficulties, the GD framework through minimal geometric deformation and its extended version have proven to be one of the most effective techniques when it comes to obtaining new interior solutions.

In this work, we implemented the GD through the MGDe approach, which implies taking into account both geometrical deformations; radial and temporal \(\{f,g\}\) over the metric of seed solution simultaneously as a result of the influence of the extra source \(\theta _{\mu \nu }\) on a known matter sector \(T_{\mu \nu }^{s}\) in order to obtain a new isotropic stellar model. For such purpose, the Einstein’s universe solution as a seed solution and a particular perfect fluid for the extra source \(\theta _{\mu \nu }\) were considered in order to close the system of differential equations. Commonly, the regime to which the new solution is extended is the anisotropic one through the application of GD. However, in this work we have particularly found the isotropic regime, which is due to the analytical simplicity of the seed solution and also to the choice of the extra condition as another perfect fluid. Indeed, such a choice was made with the purpose of studying an interior solution supported by two perfect fluids.

As a result, the radial geometric deformation f was obtained analytically simply by applying the equality of density of energy between both sources, namely \(\rho ^{s}=\theta _{0}^{0} = \varrho \) (a type of mimic density constraint), while the temporal geometric deformation g was obtained by imposition of isotropy pressure of the extra source \(\theta _{\mu \nu }\) (namely \(\varPi _{\theta }=0\)), and thus the EFE was successfully closed. In this way, a new isotropic solution was obtained, which satisfies the fundamental physical acceptability conditions of Sect. 5 (for such purpose, the matching conditions were used also).

In addition, we explored the energy exchange between the two fluids that support the interior of the resulting compact object; one given by the Einstein’s universe solution (\(T_{\mu \nu }^{s}\)) and the other isotropic and constant density fluid (\(\theta _{\mu \nu }\)). Unlike the results reported in previous works [62, 66, 67], the most outstanding result in Sect. 7 is that the energy exchange \(\varDelta E\) depends exclusively on the compactness factor of the gravitational object and not on other parameters in the model. That is, for stellar objects with small compactness factors \(\varDelta E\) becomes negative, while the increase in compactness factor gives a result of the energy exchange that becomes positive. This is easily understood when we consider that, in the first case, Einstein’s fluid gives energy to the environment (the extra source \(\theta _{\mu \nu }\)), whereas in the second case, the opposite occurs.

This behaviour can be seen initially in two ways; one in which one static sphere whose interior is supported by Einstein’s fluid influence by an external source \(\theta _{\mu \nu }\), which can penetrate into the interior of the static sphere according to Fig. 11; and the other one is the opposite case, where the environment created by Einstein’s universe solution modifies the source \(\theta _{\mu \nu }\) which is confined to a finite region of space-time. Then, in order to specify which way describes this situation better, we felt compelled to extend the radial domain of Fig. 11, obtaining Fig. 12. So we can observe that these profiles of \(p_{\theta }\) are finite and have exotic behaviour since they have negative values outside the resulting stellar object surface. Therefore, it permits us to specify that the Einstein’s universe perturbs a finite region of space-time given by the complex source \(\theta _{\mu \nu }\) obtaining a compact stellar object, that is isotropic and incomprehensible, which fulfills the fundamental physical conditions in order to model a realistic stellar compact object.

Fig. 12
figure 12

\(p_{\theta }\) for \(u = 0.16\) (blue line), \(u = 0.2\) (black line), \(u = 0.3\) (red line), \(u = 0.37\) (green line) and \(\varrho = 1\) with a more extended radial domain

Full size image

It is also worth mentioning that the results about energy exchange between the two isotropic fluids in this work, where \(\varDelta E > 0\) (for upper compactness factor), and \(\varDelta E<0\) (for lower compactness factor) is another evidence that it is possible to have scenarios or configurations where both fluids that coexist within the stellar compact object can dominate one over the other in both directions (another evidence is presented in [62]).

Before concluding this work, we have to mention that Einstein’s solution has already been extended to models of static fluid spheres in [27, 71], so in this way, the present work reinforces the idea that this cosmological solution can be used successfully in order to obtain acceptable physical interior solutions.

It should be interesting to explore the behaviour of the model obtained here against small perturbations in the matter sector, in particular with those perturbations in the radial direction (radial pressure), since they can be associated as possible triggers of the star’s quakes or even collapse processes. The obtained solution can also be used as a seed solution in future works within the GD framework to extend the solution to an anisotropic pressure regime.