The possibility of X(4014) as a $D^*{\bar{D}}^*$ molecular state

Abstract

Within the framework of the local hidden gauge approach, we have studied the near-threshold $D^* {\bar{D}}^*$ interaction with quantum numbers $I(J^{PC}) = 0(0^{++})$, $0(2^{++})$, $1(0^{++})$, and $1(2^{++})$, respectively. The contact term and vector meson exchange term in coupled channels are taken into account in this work. One pole, which is found in the case of the quantum numbers $I(J^{PC}) = 0(0^{++})$, could be associated to the X(4014) recently observed by the Belle Collaboration. Thus, we suggest that the X(4014) may be an $D^* {\bar{D}}^*$ molecular state with $I(J^{PC}) = 0(0^{++})$, and more precise information about X(4014), such as resonance parameters and decay properties, could be useful to shed light on its structure.

1 Introduction

In last two decades, a large amount of the charmonium-like states, named XYZ states, have been observed experimentally [1,2,3,4,5]. Many kinds of theoretical interpretations to their structures have been proposed, such as hadro-quarkonia [6, 7], tetraquarks [8, 9], hadronic molecules [10,11,12,13,14,15], kinematic effects [16,17,18,19], and the mixing of different components. Since most of the XYZ states appear at certain hadronic thresholds, hadronic molecule is one of the most promising interpretations among the various exotic states, although there are still many controversies. For instance, the hidden-charm state X(3872) is quite close to the $D{\bar{D}}^*$ threshold [20, 21], $Z_{cs}(3985)$ is close to the ${\bar{D}}_s D^*/{\bar{D}}^*_s D$ threshold [22]. Recently, a $T_{cc}^+$ state reported by the LHCb Collaboration has the mass very close to the $D^{*+}D^0$ threshold [23, 24], and could be interpreted as a $D^*D$ molecular state [25,26,27,28,29,30]. The $Z_c(4025)$ observed by the BESIII Collaboration [31, 32] could be interpreted as the $D^*{\bar{D}}^*$ molecule with $I(J^{P})=1(1^+)$ [33]. In addition, a loosely $D{\bar{D}}$ bound state with $I(J^{PC})=0(0^{++})$ was predicted in Ref. [34], and the authors of Refs. [35, 36] claimed that there were some experimental evidences of such a bound state in the processes $\gamma \gamma \rightarrow D{\bar{D}}$ and $e^+e^-\rightarrow J/\psi D{\bar{D}}$ [37,38,39]. As pointed out in Ref. [40], the molecular structure should appear at any threshold of a pair of heavy-quark and heavy-antiquark hadrons with attractive interaction at threshold, and experimental information about such structures is crucial to deepen our understanding of the interactions between heavy hadrons and the internal structures of the exotic states.

In the year of 2021, the Belle Collaboration has analyzed the two-photon process $\gamma \gamma \rightarrow \gamma \psi (2S)$ from the threshold to 4.2 GeV for the first time [41], and found two structures in the lineshape of the cross sections. The first one with a local significance of $3.1 \sigma$ corresponds to one resonance with a mass and width to be,

$$\begin{aligned} M_1= & {} 3922.4 \pm 6.5 \pm 2.0~\mathrm{MeV}, \nonumber \\ \Gamma _1= & {} 22 \pm 17 \pm 4~\mathrm{MeV}, \end{aligned}$$

(1)

which may be the X(3915), $\chi _{c2}(3930)$, or the mixing of them, and the second one with a local significance of $2.8 \sigma$ corresponds to a new resonance X(4014) with a mass and width to be,

$$\begin{aligned} M_2= & {} 4014.3 \pm 4.0 \pm 1.5~\mathrm{MeV}, \nonumber \\ \Gamma _2= & {} 4 \pm 11 \pm 6~\mathrm{MeV}. \end{aligned}$$

(2)

As discussed in Ref. [41], the X(4014) state has a mass in agreement with the predicted mass 4012 MeV for the $J^{PC}=2^{++}$ $D^*{\bar{D}}^*$ molecule with the assumption of X(3915) as a $J^{PC}=0^{++}$ $D^*{\bar{D}}^*$ molecule [42, 43]. However, the binding energy of $D^*{\bar{D}}^*$ is of the order of 100 MeV if one considers the X(3915) as a $D^*{\bar{D}}$ molecular state, which is much larger than the ones of X(3872), $Z_{cs}(3985)$, $T^+_{cc}$, and $Z_c(4025)$. It should also be pointed out that the molecular explanation of X(3915) is still in debate. For instance, in Refs. [44,45,46,47,48] the X(3915) and $\chi _{c2}(3930)$ could be assigned as the $\chi _{c0}(2P)$ and $\chi _{c2}(2P)$ charmonia, respectively, and in Ref. [49] X(3915) is suggested as an S-wave $D_s^+{D}_s^-$ molecular state. Thus, it implies that the nature of the newly reported X(4014) state is still unclear, and the study on the $D^*{\bar{D}}^*$ interaction is crucial to explore its possible internal structure.

There are many investigations of the $D^*{\bar{D}}^*$ interaction in literatures [33, 50,51,52]. In our previous work, we have analysed the BESIII measurement of $e^+e^-\rightarrow (D^*{\bar{D}}^*)^{\pm ,0} \pi ^{\mp ,0}$ reactions by taking into account the vector-vector $D^* {\bar{D}}^*$, $K^* {\bar{K}}^*$, and $\rho \rho$ interactions within the framework of local hidden gauge formalism, and concluded that the $Z_c(4025)$ structure could be a shallow $D^*{\bar{D}}^*$ bound state [33]. Recently, the interactions between charmed hadrons have been described by constant contact terms, and 229 molecular states were predicted [50]. In Ref. [50], the masses of the $D^*{\bar{D}}^*$ bound states with $I(J^{PC})=0(0^{++})$/$0(1^{+-})$/$0(2^{++})$ are $1.82\sim 36.6$ MeV lower than the $D^*{\bar{D}}^*$ threshold, which favors the $D^*{\bar{D}}^*$ molecular explanation for the X(4014) state. In the present work, we will investigate the S -wave near-threshold $D^* {\bar{D}}^*$ interaction within an alternative framework, i.e. the local hidden gauge approach, and the vector exchanges in the crossed channels in the hidden gauge model provide further insights into the contact interactions explored in Ref. [50]. We also discuss the possibility of the X(4014) as the $D^* {\bar{D}}^*$ molecular state and its favored quantum numbers.

Fig. 1

The sketch diagrams for $D^*{\bar{D}}^*\rightarrow V V$. Diagrams a–d correspond to t-channel, u-channel, s-channel vector meson exchanged interactions, and contact interaction, respectively

This paper is organized as follows. We will show the formalism adopted in the present estimations in Sect. 2, and present the calculated results and related discussions in Sect. 3. Finally, Sect. 4 will be devoted to a short summary.

2 Formalism

In this section, we investigate the $D^* {\bar{D}}^*$ interaction following the approach of Ref. [51]. The Lagrangian is taken from the local hidden gauge formalism describing the interaction of vector mesons, which is [53, 54],

$$\begin{aligned} {\mathcal {L}}=-\frac{1}{4}\langle V_{\mu \nu }V^{\mu \nu }\rangle , \end{aligned}$$

(3)

where the symbol $\langle ~ \rangle$ stands for the trace of SU(4) vector meson matrix, and the tensor $V_{\mu \nu }$ is defined as,

$$\begin{aligned} V_{\mu \nu }=\partial _{\mu }V_{\nu }-\partial _{\nu }V_{\mu }-ig\left[ V_{\mu },V_{\nu }\right] , \end{aligned}$$

(4)

with $V_{\mu }$ to be,

$$\begin{aligned} V_\mu =\left( \begin{array}{cccc} \frac{\omega }{\sqrt{2}}+\frac{\rho ^0}{\sqrt{2}} &{}\quad \rho ^+ &{}\quad K^{*+}&{}\quad {\bar{D}}^{*0}\\ \rho ^- &{}\quad \frac{\omega }{\sqrt{2}}-\frac{\rho ^0}{\sqrt{2}} &{}\quad K^{*0}&{}\quad D^{*-}\\ K^{*-} &{}\quad {\bar{K}}^{*0} &{}\quad \phi &{}\quad D^{*-}_s\\ D^{*0}&{}\quad D^{*+}&{}\quad D^{*+}_s&{}\quad J/\psi \end{array} \right) _\mu . \end{aligned}$$

(5)

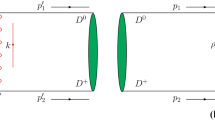
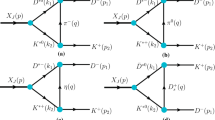
By expanding the effective Lagrangian in Eq. (3), one can obtain two types of $D^*{\bar{D}}^*$ interactions, which are vector-meson exchange interactions (Fig. 1a–c) and contact interaction (Fig. 1d), respectively.

The SU(4) structure of the Lagrangian allows one to take into account all the possible channels with certain quantum numbers. In the present work, the relevant channels are those with zero charmness and strangeness. In the case of $I = 0$, we considered the 10 channels, which are $D^* {\bar{D}}^*$, $D_s^* {\bar{D}}_s^*$, $K^* {\bar{K}}^*$, $\rho \rho$, $\omega \omega$, $\phi \phi$, $J/\psi J/\psi$, $\omega J/\psi$, $\phi J/\psi$, $\omega \phi$ respectively. And we take 6 channels into account for the case of $I = 1$, which are $D^* {\bar{D}}^*$, $K^* {\bar{K}}^*$, $\rho \rho$, $\rho \omega$, $\rho J/\psi$, $\rho \phi$ respectively.

By Expanding the Lagrangian in Eq. (3), one can get the effective Lagrangian of three and four vector mesons interactions. As for the three vector mesons interaction, it reads,

$$\begin{aligned} \mathcal{L}^{(3V)}_{III}= & {} ig\left\langle V^\nu \partial _\mu V_\nu V^\mu -\partial _\nu V_\mu V^\mu V^\nu \right\rangle \nonumber \\= & {} ig\left\langle \left( V^\mu \partial _\nu V_\mu -\partial _\nu V_\mu V^\mu \right) V^\nu \right\rangle . \end{aligned}$$

(6)

With the above effective Lagrangian, one can construct the vector-meson exchange term. The t-channel exchange amplitude corresponding to Fig. 1a is,

$$\begin{aligned} \mathcal{A} (t)= & {} \frac{1}{m_{ex}^2}~g^2~ \epsilon _1 \cdot \epsilon _3^{*} ~\epsilon _2 \cdot \epsilon _4^{*} \nonumber \\&\times ~\left( m_{ex}^2(s-u)+(m_{1}^2-m_{3}^2)(m_{2}^2-m_{4}^2)\right) \nonumber \\&-~4g^2~ \epsilon _1 \cdot \epsilon _3^{*} ~(p_1 \cdot \epsilon _2 ~p_2 \cdot \epsilon _4^{*}+p_1 \cdot \epsilon _4^{*} ~p_4 \cdot \epsilon _2) \nonumber \\&+~4g^2~ p_1 \cdot \epsilon _3^{*} ~(\epsilon _1 \cdot \epsilon _2 ~p_2 \cdot \epsilon _4^{*}+\epsilon _1 \cdot \epsilon _4^{*} ~p_4 \cdot \epsilon _2) \nonumber \\&-~4g^2~ \epsilon _2 \cdot \epsilon _4^{*} ~(p_1 \cdot \epsilon _3^{*} ~p_2 \cdot \epsilon _1+p_2 \cdot \epsilon _3^{*} ~p_3 \cdot \epsilon _1) \nonumber \\&+~4g^2~ p_3 \cdot \epsilon _1 ~(\epsilon _2 \cdot \epsilon _3^{*} ~p_2 \cdot \epsilon _4^{*}+\epsilon _3^{*} \cdot \epsilon _4^{*} ~p_4 \cdot \epsilon _2), \nonumber \\ \end{aligned}$$

(7)

where $m_{ex}$ stands for the mass of the exchange vector meson, the Mandelstam variables are defined as $s=(p_1+p_2)^2$, $t=(p_1-p_3)^2$ and $u=(p_1-p_4)^2$, which satisfy the constraint $s+t+u=\sum _i m_i^2$. Here indices 1, 2, 3, and 4 correspond to the particles with the momenta $p_1$, $p_2$, $p_3$, and $p_4$ in Fig. 1 and the dot indicates the scalar products involving polarization vectors.

As for the u-channel (Fig. 1b), the exchange amplitude $\mathcal{A} (u)$ can be obtained from the expression of $\mathcal{A} (t)$ by exchanging $p_3 \leftrightarrow p_4$ and $\epsilon _3^{*} \leftrightarrow \epsilon _4^{*}$. The s-channel exchange (Fig. 1c) amplitude $\mathcal{A} (s)$ can also be obtained from the expression of $\mathcal{A} (t)$ by performing the exchange $p_2 \leftrightarrow -p_3$ and $\epsilon _2 \leftrightarrow \epsilon _3^{*}$.

As for the four vector mesons interactions, it corresponds to the contact term, which reads,

$$\begin{aligned} {\mathcal {L}}^{(c)}=\frac{g^2}{2}\left\langle V_{\mu }V_{\nu }V^{\mu }V^{\nu }-V_{\nu }V_{\mu }V^{\mu }V^{\nu }\right\rangle \ . \end{aligned}$$

(8)

With the above effective Lagrangian, one can obtain the amplitude corresponding to Fig. 1d, which is,

$$\begin{aligned} {\mathcal {A}}^{(c)}_{D^{*+}D^{*-}\rightarrow D^{*+}D^{*-}}= & {} 2g^2 \left( \epsilon _1 \cdot \epsilon _2 ~\epsilon _3^{*} \cdot \epsilon _4^{*}+\epsilon _1 \cdot \epsilon _3^{*} ~\epsilon _2 \cdot \epsilon _4^{*}\right. \nonumber \\&\left. -2\epsilon _1 \cdot \epsilon _4^{*} ~\epsilon _2 \cdot \epsilon _3^{*} \right) ,\nonumber \\ {\mathcal {A}}^{(c)}_{D^{*+}{D}^{*-} \rightarrow D^{*0}{\bar{D}}^{*0}}= & {} g^2 \left( \epsilon _1 \cdot \epsilon _2 ~\epsilon _3^{*} \cdot \epsilon _4^{*}+\epsilon _1 \cdot \epsilon _3^{*} ~\epsilon _2 \cdot \epsilon _4^{*} \right. \nonumber \\&\left. -2\epsilon _1 \cdot \epsilon _4^{*} ~\epsilon _2 \cdot \epsilon _3^{*} \right) , \end{aligned}$$

(9)

where the superscript ‘c’ stands for the contact term. As indicated in Ref. [55], the gauge coupling constant g can related to the masses of the vector mesons and the decay constants of the corresponding pseudoscalar meson, i.e., $g=m_V/f_P$, for example, considering SU(3) symmetry, one has $g=m_\rho /f_\pi$. However, considering the large violation of SU(4) symmetry, one can adopt different coupling constants for different channels [56], in particular, we take $g_D = M_{D^*}/(2 f_D) = 6.9$ for $D^*{\bar{D}}^*$ channel, $g_{D_s} = M_{D_s^*}/(2 f_{D_s}) = 5.47$ for the $D_s^* {\bar{D}}_s^*$ channel, $g_{\eta _c} = M_{J/\psi }/(2 f_{\eta _c}) = 5.2$ for the $J/\psi J/\psi$ channel and still using $g = M_{\rho }/(2 f_{\pi }) = 4.17$ for the channels that involve light mesons with $f_{\pi } = 93$ MeV, $f_D = 206/ \sqrt{2} = 145.66$ MeV [57], $f_{D_s} = 273/ \sqrt{2} = 193.04$ MeV [57] and $f_{\eta _c} = 420/ \sqrt{2} = 296.98$ MeV [58].

By considering the spin projection operators and the isospin doublets of the charmed and anticharmed mesons as in Refs. [51, 59], we obtain the kernels of $D^*{\bar{D}}^*$ interactions. As for the vector meson exchange processes, one can obtain the total amplitudes with well-defined isospin, where all the possible exchanged mesons have been included. Using the amplitudes for the spin projections we can split the terms into their spin parts, and taking $D^*{\bar{D}}^*\rightarrow D^*{\bar{D}}^*$ as an example, we obtain,

$$\begin{aligned}&V^{(ex,I=0,J=0,2)}_{D^* {\bar{D}}^{*}\rightarrow D^* {\bar{D}}^{*}}\nonumber \\&\quad =\frac{g_D^2 (2\,M^2_\omega M^2_\rho +M^2_{J/\psi } (3\,M^2_\omega +M^2_\rho )) (4\,M^2_{D^*}-3\, s) }{4\, M^2_{J/\psi } M^2_\omega M^2_\rho } \nonumber \\&V^{(ex,I=1,J=0,2)}_{D^* {\bar{D}}^{*}\rightarrow D^* {\bar{D}}^{*}}\nonumber \\&\quad =\frac{g_D^2 (2\,M^2_\omega M^2_\rho +M^2_{J/\psi } (-M^2_\omega +M^2_\rho )) (4\,M^2_{D^*}-3\, s) }{4\, M^2_{J/\psi } M^2_\omega M^2_\rho } \nonumber \\ \end{aligned}$$

(10)

with the superscript ‘ex’ stand for the vector-meson exchange term. As for the contact interactions for different isospin and total angular momentum, the potentials corresponding to $D^*{\bar{D}}^*\rightarrow D^*{\bar{D}}^*$ read,

$$\begin{aligned} V^{(c,I = 0,J = 0)}_{D^*{\bar{D}}^*\rightarrow D^*{\bar{D}}^*}= & {} 6g_{D}^2, \qquad V^{(c,I = 0,J = 2)}_{D^*{\bar{D}}^*\rightarrow D^*{\bar{D}}^*}=-3g_{D}^2, \nonumber \\ V^{(c,I = 1,J = 0)}_{D^*{\bar{D}}^*\rightarrow D^*{\bar{D}}^*}= & {} 2g_{D}^2, \qquad V^{(c,I = 1,J = 2)}_{D^*{\bar{D}}^*\rightarrow D^*{\bar{D}}^*}=-g_{D}^2. \end{aligned}$$

(11)

The potentials of other channels resulted from vector meson exchange and contact interaction can be found in Refs. [51, 60] for details.

Table 1 The approximate total potentials at the threshold of $D^*{\bar{D}}^*$

Moreover, it should be clarified that the mass of X(4014) is very close to the threshold of $D^*{\bar{D}}^*$, and we mainly discuss the energy range around the threshold, thus, $s=(p_1+p_2)^2\simeq 4m_{D^*}^2$, with this approximation, we collected all the relevant potentials in Table 1, which are the sum of the vector meson exchange and contact terms.

With the above potentials, one can search the possible poles by solving the Bethe–Salpeter equation, which is,

$$\begin{aligned} T=[1-VG]^{-1}V, \end{aligned}$$

(12)

where the G is the two-meson loop function given by,

$$\begin{aligned} G=i\int \frac{d^4q}{(2\pi )^4}\frac{1}{q^2-m_1^2+i\epsilon }\frac{1}{(q-P)^2-m_2^2+i\epsilon }\ , \end{aligned}$$

(13)

with $m_1$ and $m_2$ the masses of the two mesons. q is the four-momentum of the meson in the centre of mass frame, and P is the total four-momentum of the meson-meson system.

In the present work, we use the dimensional regularization method as indicated in Refs. [51, 61], and in this scheme, the two-meson loop function G can be expressed as,

$$\begin{aligned} G= & {} \frac{1}{16\pi ^2}\left[ \alpha +\log \frac{m_1^2}{\mu ^2}+\frac{m_2^2-m_1^2+s}{2s}\log \frac{m_2^2}{m_1^2}\right. \nonumber \\&+\frac{|\vec {q}\,|}{\sqrt{s}}\left( \log \frac{s-m_2^2+m_1^2+2|\vec {q}\,|\sqrt{s}}{-s+m_2^2-m_1^2+2|\vec {q}\,|\sqrt{s}}\right. \nonumber \\&+\left. \left. \log \frac{s+m_2^2-m_1^2+2|\vec {q}\,|\sqrt{s}}{-s-m_2^2+m_1^2+2|\vec {q}\,|\sqrt{s}}\right) \right] , \end{aligned}$$

(14)

where $\mu$ and $\alpha$ are model parameter, while $\vec {q}\,$ is the momentum of the meson in the centre of mass frame, which reads,

$$\begin{aligned} |\vec {q}\,|=\frac{\sqrt{\left[ s-(m_1+m_2)^2\right] \left[ s-(m_1-m_2)^2\right] }}{2\sqrt{s}} . \end{aligned}$$

(15)

In the complex plane for a general $\sqrt{s}$, the loop function in the second Riemann sheet can be written as,

$$\begin{aligned} G^{II}(\sqrt{s})=G^{I}(\sqrt{s})+i\frac{|\vec {q}\,|}{4\pi \sqrt{s}},\qquad \mathrm{Im}(|\vec {q}\,|)>0, \end{aligned}$$

(16)

where $G^{II}$ refers to the loop function in the second Riemann sheet, and $G^{I}$ is the one in the first Riemann sheet as given by Eq. (14) for the $D^* {\bar{D}}^*$ channel. When searching for the poles, we use $G^{I}$ for Re$(\sqrt{s}) < m_1+m_2$, and use $G^{II}$ for Re$(\sqrt{s}) > m_1+m_2$.

3 Numerical results and discussions

Before we discuss the numerical results, the values of the relevant parameters should be clarified, which include the parameter $\mu$, and the subtraction constant $\alpha$ introduced by the two-meson loop function. From Eq. (14), one can find,

$$\begin{aligned} G\sim & {} \frac{1}{16\pi ^2} \left[ \alpha +\log \frac{m_1^2}{\mu ^2}+\cdots \right] \nonumber \\= & {} \frac{1}{16\pi ^2} \left[ \alpha -\log {\tilde{\mu }}^2+\log {\tilde{m}}_1^2+\cdots \right] , \end{aligned}$$

(17)

where ${\tilde{\mu }}$ and ${\tilde{m}}_1$ are the values of $\mu$ and $m_1$. Then, in this case, one can define a new model parameter $\alpha ^\prime =\alpha -\log \mu ^2$, which is the only model parameter. When we set $\mu =1$ GeV for all the channels as indicated in Ref. [51], we have $\alpha ^\prime =\alpha$. Then only the $\alpha$ dependences of the results should be carefully checked. As indicate in Ref. [62], the subtraction constant $\alpha$ in the loop function should depend on the mass of involved mesons by,

$$\begin{aligned} \alpha \sim -2 \log \left( 1+\sqrt{1+\frac{m^2}{\mu ^2}} ~\right) . \end{aligned}$$

(18)

In practical estimations, one usually consider $\alpha$ as a parameter around the value determined by Eq. (18). For example, the parameter $\alpha$ in the loop function with light mesons, also named $\alpha _L$, is determined to be − 1.65 [60], which is close to the one obtained by Eq. (18). As for the parameter $\alpha$ in the loop function with heavy-light meson, which is also name as $\alpha _H$, it should be in principle smaller than $\alpha _L$. For example, in Ref. [51] the value of $\alpha _H$ is fixed to be -2.07 in order to get a pole around 3940 MeV in $I=0,\ J=0$ case, which is associated to the X(3915).

As for the discussed X(4014), one can find the experimental data of the cross sections for $\gamma \gamma \rightarrow \gamma \psi (2S)$ are very inaccurate around 4014 MeV [41], thus, it is a bit difficult to fit our results directly with experimental data on this occasion. So in the present work, we mainly focus on the resonance parameters of the X(4014), and vary the subtraction constant $\alpha _H$ in a large range, i.e., $-2.0<\alpha _H<-1.4$, to check whether one can simultaneously reproduce the mass and width of X(4014) in a reasonable parameter range.

Fig. 2

The modulus squared of the amplitude $|T_{D^* {\bar{D}}^* \rightarrow D^* {\bar{D}}^*}|^2$ for the case of $I=0, \ J=0$ depending on the parameter $\alpha _H$

Fig. 3

The mass and width of pole depending on the parameter $\alpha _H$ for the cases of $I(J^{PC}) = 0(0^{++})$, $0(2^{++})$, and $1(2^{++})$ respectively. The grey horizontal line indicates the $D^*{\bar{D}}^*$ threshold and the grey horizontal band indicates the mass and width range of X(4014) measured by Belle collaboration  [41]. The red arrow indicates $\alpha _H=1.65$, which is the same as $\alpha _L$

With the above formalisms, we can estimate the amplitudes for the $D^*{\bar{D}}^*\rightarrow D^*{\bar{D}}^*$ transition with quantum numbers $I(J^{PC})=0(0^{++})$, $0(2^{++})$, $1(0^{++})$, and $1(2^{++})$, respectively. Here, we take the case of $I(J^{PC})=0(0^{++})$ as an example to show the modulus squared of the amplitude $|T_{D^*{\bar{D}}^*\rightarrow D^*{\bar{D}}^*}|$ depending on the subtraction constant $\alpha _H$ in Fig. 2. From the figure, one can find when $\alpha _H$ is very small, such as $\alpha _H=-2.0$, there is a pole around 3964 MeV, by increasing $\alpha _H$, the pole moves to the threshold, then the modulus squared of the amplitude behaves like a cusp when $\alpha _H$ is greater than − 1.65, which will not correspond to any bound state any more.

In Fig. 3, we present the $\alpha _H$ dependences of the estimated masses and widths of poles for the cases of $I(J^{PC}) = 0(0^{++})$, $0(2^{++})$ and $1(2^{++})$, respectively. From the figure, one can find that the pole masses increase with the increasing of $\alpha _H$, and there are overlaps between the theoretical estimations and Belle data. As for the pole widths, they decrease with the increasing of $\alpha _H$ and there are also overlaps between the present estimations and the experimental data. In Table 2, we collect the $\alpha _H$ ranges determined by reproducing the measured mass and width of X(4014). One can find that the resonance parameters of X(4014) can be reproduced by adjusting the subtraction parameter $\alpha _H$ in three possible $I(J^{PC})$ cases. In particular, we can simultaneously reproduce the mass and width of X(4014) with $-1.75<\alpha _H<-1.65$ for $I(J^{PC})=0(0^{++})$ case, while the $\alpha _H$ are determined to be $-1.63\sim -1.40$ and $-1.47\sim -1.40$ for $I(J^{PC})=0(2^{++})$ and $1(2^{++})$ cases, respectively. However, as we have clarified that the value of $\alpha _H$ should be smaller than $\alpha _L$, which is $-1.65$. From our estimations, one can find only the $I(J^{PC})=0(0^{++})$ assignment could fulfill this criteria. Considering the large uncertainties of the experimental data and the lower limit of $\alpha _H$ for $I(J^{PC})=0(2^{++})$ is -1.63, which is very close to $\alpha _L$, we conclude that the $I(J^{PC})=0(2^{++})$ assignment should be weakly favored, while the $\alpha _H$ range for $I(J^{PC})=1(2^{++})$ assignment is much larger than $\alpha _L$ and thus such assignment should be excluded.

Table 2 The parameter ranges determined by reproducing the measured mass and width of X(4014) for different $I(J^{PC})$ assignments

From the above analysis, we conclude that X(4014) can be $D^*{\bar{D}}^*$ molecular state with $I(J^{PC})=0(0^{++})$ and the resonance parameters can be reproduced with $-1.75<\alpha _H<-1.65$. In this parameter range, we also find two bound states with $I(J^{PC})$ quantum numbers to be $0(2^{++})$ and $1(2^{++})$, respectively, as shown in Table 3. By comparing the resonance parameters of $I(J^{PC})=0(0^{++})$ state, one can find the masses of $0(2^{++})$ and $1(2^{++})$ states are about 10 MeV below the one of $0(0^{++})$ state. But the widths of $0(2^{++})$ and $1(2^{++})$ states are larger than the one of $0(0^{++})$ state. In particular, the widths of $0(2^{++})$ and $1(2^{++})$ states are estimated to be $(13\sim 21)$ MeV and $(39\sim 59)$ MeV, respectively. In Ref. [63], the authors argued that the mass of the $D^*{\bar{D}}^*$ molecular state with $I(J^{PC})=0(2^{++})$ was about 4013 MeV, and the upper limit of the width was estimated to be about 10 MeV, which is similar to our present estimations. However, the estimations in Ref. [64] indicated that the $D^*{\bar{D}}^*$ molecular state with $I(J^{PC})=0(2^{++})$ was a deeply bound state with the binding energy to be several tens MeV, and the widths was estimated to be $50 \pm 10$ MeV, which was much different with Ref. [63] and the present estimations.

Besides the above three bound state, we further checked the $\alpha _H$ dependences of modulus square of the amplitude for the case of $I(J^{PC})=1(0^{++})$ in Fig. 4. From the figure one can find that in a very large $\alpha _H$ range, i.e., $-2.0<\alpha _H<-1.0$, there is no pole in the modulus square of the amplitudes, which indicates that the $D^*{\bar{D}}^*$ can not form a bound state with $I(J^{PC})=1(0^{++})$ based on present calculations.

Table 3 The resonance parameters $(m,\Gamma )$ in unit of MeV for the different $I(J^{PC})$ cases depending on the parameter $\alpha _H$

Fig. 4

The modulus squared of the amplitude $|T_{D^* {\bar{D}}^* \rightarrow D^* {\bar{D}}^*}|^2$ for the case of $I(J^{PC})=1(0^{++})$ with different values of parameter $\alpha _H$

4 Summary

Inspired by recent observation of X(4014) in the process $\gamma \gamma \rightarrow \gamma \psi (2S)$, we have studied the hidden-charm $D^* {\bar{D}}^*$ interaction within the framework of the local hidden gauge approach, where the possible $I(J^{PC})$ quantum numbers could be $0(0^{++}), 0(2^{++}), 1(0^{++})$, and $1(2^{++})$ respectively. For the case of $I(J^{PC})=0(0^{++})$, our estimations indicate that in the $\alpha _H$ range of $-1.75 \sim -1.65$ one can reproduce the resonance parameters of X(4014), which satisfy the constraint of $\alpha _H < \alpha _L$. As for the cases of $I(J^{PC})=0(2^{++})$ and $I(J^{PC})=1(2^{++})$, one can also reproduce the measured mass and width of X(4014) with a larger $\alpha _H$. As for the case of $I(J^{PC})=1(0^{++})$, our calculations indicate that there is no pole in the modulus square of the amplitudes in the considered parameter range.

To summarize, in the $D^*{\bar{D}}^*$ molecular scenario, our estimations favor the $I(J^{PC})=0(0^{++})$ assignment for X(4014) comparing to $I(J^{PC})=0(2^{++})$, and the $I(J^{PC})=1(2^{++})$ assignment could be excluded. However, it should be clarified that the local significance of X(4014) is only 2.8$\sigma$, more experimental information about this state is crucial to shed light on its nature. Besides the $I(J^{PC})=0(0^{++})$ state, we also predict two states with $I(J^{PC})=0(2^{++})$ and $I(J^{PC})=1(2^{++})$ with the masses to be about 10 MeV below the one of X(4014).

Before the end of this work, we should mention that there are some hints of X(4014) in the existing experimental data. For instance, the Belle Collaboration has measured the inclusive process $e^+e^-\rightarrow J/\psi X$, and one can observe a peak around 4014 MeV in the $M_\mathrm{rec}(J/\psi )$ distribution, as shown in Fig. 1 of Ref. [65]. Later, the Belle Collaboration reported the study of the processes $e^+e^-\rightarrow J/\psi D^{(*)}{\bar{D}}^{(*)}$, and there is more events in the energy region $4000<M_{D{\bar{D}}^*}<4025$ MeV of the $D{\bar{D}}^*$ invariant mass distribution, as depicted in Fig. 2b of Ref. [66]. In addition, in the cross sections of the process $\gamma \gamma \rightarrow J/\psi \omega$ measured by the Belle Collaboration, one can find the events concentrate in the region $4010\sim 4020$ MeV [67]. All the above hints imply that one state with a mass close to the $D^*{\bar{D}}^*$ threshold and a narrow width may exist, which coincides with the X(4014) observed by the Belle Collaboration [41].

Note added During the review of this work, we prepared another work to estimated hidden charm decay processes of X(4014) in a $D^*{\bar{D}}^*$ molecular scenario with $J^{PC}=0^{++}$ [68], and we found the width of $X(4014) \rightarrow J/\psi \omega$ is sizable and suggested to search X(4014) in the $\gamma \gamma \rightarrow J/\psi \omega$ process, which should be accessible in Belle II.