1 Introduction

Several researchers have studied the nature of gravitational theory at the quantum level in relation to the early evolution of the universe. There is evidence that quantum gravity plays a key role in understanding the very early evolution of the universe, according to the existing literature [1,2,3,4]. The method of revealing quantum gravity is not unique. A variety of approaches have been proposed over the years, including string theory [5], black hole physics [6,7,8], doubly special relativity [9,10,11], and etc. There was a consensus among all of them that there was a minimum length scale close to Planck length. In quantum gravity, this led to what is known as a generalized uncertainty principle (GUP) based on Heisenberg’s uncertainty principle [12]. GUP has many cosmological and astrophysical implications, for example, black hole thermodynamics [13], the origin of the magnetic fields in the Universe sector [14], and etc [15, 16]. It is essential to investigate the effects of GUP on late regime of the universe physics because it plays such a crucial role in early universe physics. Therefore, in order to understand the universe’s complete dynamical picture, GUP should be investigated at both early and late regimes. Several attempts has been performed in the literature, for example see [16, 17].

Several approaches to noncommutative gravity [18,19,20,21] were developed from the initial interest in noncommutative field theory [22, 23]. Noncommutative theories of gravity exhibit a highly nonlinear end result according to all of these formulations. Several aspects of the universe are studied in noncommutative cosmology to determine how noncommutativity affects them [24]. There have been observations in the literature that noncommutative deformations modify noncommutative fields and a full noncommutative theory of gravity would be expected to affect the minisuperspace variables. By introducing the Moyal product of functions into the Wheeler–DeWitt equation, similar to noncommutative quantum mechanics, this is accomplished.

Historically, the noncommutative deformations of the minisuperspace have been analyzed at the quantum level in [24] where a Kantowski–Sachs universe was studied. Nonetheless, classical noncommutative formulations have been suggested utilizing an effective noncommutativity on the minisuperspace. Noncommutativity in classical theory is primarily founded on the assumption that modifying Poisson brackets yields noncommutative equations of motion [24,25,26,27]. As a result, two generally different interpretations are given by phase space deformations, called the “C frame” and the “NC frame”, which, in general, are not physically equivalent [28]. In order to determine the valid range of the deformation parameters, a principle should be adopted [29]: “Deformed phase space models are only valid when the descriptions of C and NC frames are physically equivalent”.

Physicists face a major challenge in explaining the nature and mechanism of our universe’s acceleration. Accelerated expansion of the universe has been confirmed by several astrophysical observations including supernova type Ia [30, 31], CMB studies [32] weak lensing [33], large-scale structure [34], and baryon acoustic oscillations [35]. It contradicts Einstein’s theory of general relativity. The late-time-accelerated expansion has generally been explained by two distinct classes of ideas (solutions). The acceleration that occurs in this process is a consequence of negative pressure; therefore, one way to explain it is that it is caused by an exotic liquid, so-called dark energy, which makes up about \(70\%\) of the universe. Einstein’s cosmological constant was thought to be the most likely solution to dark energy, but it failed to solve the ’fine tuning’ and ’cosmic coincidence’ problems [36]. Hence, other theoretical models such as the phantom field [37, 38], quintessence [39, 40], quintom [41, 42], and tachyon field [43] have been proposed. Another option is that Einstein’s general relativity can be modified so its action is governed by a function of the curvature scalar (\(f(R)\)-gravity) [44, 45]. The approach is not limited to this type of change; various novel gravitational modification theories like scalar-tensor theories, \(f(T)\)-gravity, \(f(T)\)-gravity with an unusual term [46] and etcetera have recently been proposed.

In the current paper, to introduce the deformation we will follow the approach in [47]. Indeed we revisit papers [47] and some parts of [48] to show that both decelerated (matter-dominated era) and accelerated (dark-energy dominated era) epochs of the universe evolution can be obtained by minisuperspace deformation. One can easily compare to find that our solutions are different than these papers.

2 The commutative model

We investigate a flat Friedmann–Robertson–Walker universe with scale factor a(t) and a homogeneous and isotropic scalar field \(\varphi (t)\). Assuming the signature of metric as \((-,+,+,+)\) and dominating the scalar field over other matters degrees of freedom, the action takes the form

$$\begin{aligned} S=\frac{3}{\kappa ^{2}}\int \textrm{d}t\,N \left( \frac{-a {\dot{a}}^{2}}{N^{2}} \right) +\frac{1}{2}\int \textrm{d}t\, N a^{3} \left( \epsilon \frac{{\dot{\varphi }}^{2}}{N^{2}}-2V(\varphi ) \right) ,\nonumber \\ \end{aligned}$$
(1)

where N is the lapse function, and \(\kappa ^{2}=8\pi G\), and the dot represents a differentiation with respect to time. Here, the parameter \(\epsilon \) is a discriminator parameter of ordinary (\(\epsilon =1\)) and phantom (\(\epsilon =-1\)) scalar fields. Let us work in the unit \(\kappa ^{2}=1\) and restrict ourselves to constant potential \(V(\varphi )=-\Lambda \). In order to make our work easy, we perform one of the following equivalent changes of variables:

$$\begin{aligned} \left\{ \begin{array}{ll} x=\lambda ^{-1} (-\epsilon \, a)^{3/2} \sin \left( \sqrt{-\epsilon }\; \lambda \varphi \right) ; \\ y=\lambda ^{-1} a^{3/2} \cos \left( \sqrt{-\epsilon }\; \lambda \varphi \right) , \end{array} \right. \end{aligned}$$

or [49]

$$\begin{aligned} \left\{ \begin{array}{ll} x=\lambda ^{-1} (\epsilon \, a)^{3/2} \sinh \left( \sqrt{\epsilon }\; \lambda \varphi \right) ; \\ y=\lambda ^{-1} a^{3/2} \cosh \left( \sqrt{\epsilon }\; \lambda \varphi \right) , \end{array} \right. \end{aligned}$$

where \(\lambda ^{-1}=\sqrt{8/3}\). Both transformations lead to a conserved equation:

$$\begin{aligned} {\tilde{y}}^2-\epsilon \, {\tilde{x}}^2=1; \quad \left\{ \begin{array}{ll} {\tilde{x}}=\lambda a^{-3/2} x; \\ {\tilde{y}}=\lambda a^{-3/2} y, \end{array} \right. \end{aligned}$$
(2)

meaning that for a phantom scalar field we have Hyperbola (non-periodic) while for a usual scalar field we get circle (periodic). Utilizing one of the above transformations, the canonical Hamiltonian (first class constraint) reads

$$\begin{aligned} {\mathcal {H}}_{c.}=N \left( \frac{1}{2}P_{x}^{2}+\frac{\omega ^{2}}{2} x^2 \right) -\epsilon N \left( \frac{1}{2}P_{y}^{2}+\frac{\omega ^{2}}{2} y^2 \right) , \end{aligned}$$
(3)

in which \(\omega ^{2}=-3 \Lambda /4\). As is observed, for a phantom scalar field, the Hamiltonian is as a sum of two harmonic oscillators while for an ordinary scalar field, the Hamiltonian appeared as a ghost oscillator namely as a difference of two harmonic oscillators. The elements of our new configuration space, \((x\, , \, y)\), and their conjugate momentums fulfill the following commutations based on the Poisson bracket:

$$\begin{aligned} \{ x_{k},x_{j}\}=0, \quad \{ P_{x_{k}}, P_{x_{j}} \}=0, \quad \{ x_{k}, P_{ x_{j}} \}= \delta _{kj}, \end{aligned}$$
(4)

where k and j can take 1 and 2, i.e. \((x_{1},x_{2})=(x,y)\) and \(\delta _{kj}\) is the usual Kronecker delta. The equations of motion declaring the dynamics of our system are

$$\begin{aligned}&{\dot{x}}=P_{x}, \quad {\dot{P}}_{x}=-\omega ^{2}x, \end{aligned}$$
(5)
$$\begin{aligned}&{\dot{y}}=-\epsilon P_{y}, \quad {\dot{P}}_{y}=\epsilon \omega ^{2}y, \end{aligned}$$
(6)

which lead to the following equations for both values of \(\epsilon \):

$$\begin{aligned} \ddot{x}+\omega ^{2} x=0, \end{aligned}$$
(7)
$$\begin{aligned} \ddot{y}+\omega ^{2} y=0. \end{aligned}$$
(8)

Solving this decoupled system yields

$$\begin{aligned} x(t)&=c_{1} \cosh \left( \left| \omega \right| t \right) +c_{2} \sinh \left( \left| \omega \right| t \right) , \end{aligned}$$
(9)
$$\begin{aligned} y(t)&=c_{3} \cosh \left( \left| \omega \right| t \right) +c_{4} \sinh \left( \left| \omega \right| t \right) , \end{aligned}$$
(10)

where \(c_{j}\)s are constants of integration. The cosh-part corresponds to just an accelerated epoch while the sinh-part carries both decelerated and accelerated eras. If we are to preserve both cosh and sinh parts, then transition from a decelerated to an accelerated epoch (late-time-accelerated expansion) is attainable just when the amplitude of cosh is very tiny compared to sinh. As an example, by assuming \(c_{1}\simeq c_{3}\simeq 0\), the scale factor of the universe turns out to be

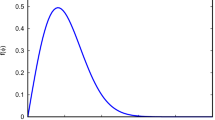
$$\begin{aligned} a(t)\simeq (c_{4}^{2}-\epsilon c_{2}^{2})^{1/3} \left[ \lambda \sinh (|\omega | t)\right] ^{2/3} \end{aligned}$$
(11)

The qualitative behavior of this scale factor has been plotted in Fig. 1. In (11), the amount of cosmological constant (consequently \(\omega \)) is given by observational data (\(\Lambda \sim 10^{-52}\textrm{m}^{-2}\)), hence we have just one degree of freedom (i.e. the amplitude) for matching with observational data which is insufficient because we need three degrees of freedom: one for tuning the present value of the scale factor and consequently the age of the universe; one for tuning the inflection point (the point of shifting from decelerated expansion to accelerated expansion) and the last one for setting the present value of the deceleration parameter.

Fig. 1
figure 1

This figure indicates the qualitative behavior of scale factor (11) for the values \(\lambda (c_{4}^{2}-\epsilon c_{2}^{2})^{1/3}=1\), and \(\omega =1\)

Full size image

3 Deformed minisuperspace

Deformed minisuperspace or so-called deformed phase space was originally conceived in conjunction with noncommutative cosmology [50]. In order to accommodate noncommutativity, they introduce a deformation to the minisuperspace for the purpose of avoiding the complications of a noncommutative theory of gravity. Moyal brackets, which are based on Moyal products, are typically responsible for the deformation. The quantization of deformations provides an alternative method for introducing full phase space deformations [51]. Since quantum cosmology constructs its models in the minisuperspace, studying cosmology in deformed minisuperspace could follow from studying quantum effects in cosmological models [52]. In another construction, symplectic manifolds are employed [53, 54]. It uses the same functional form as the Hamiltonian, but values variables by a modified Poisson algebra. Following the deformation, one is left with a modified Poisson algebra:

$$\begin{aligned} \{x_{i},x_{j}\}_{\alpha }=\theta _{ij}, \quad \{p_{i},p_{j}\}_{\alpha }=\beta _{ij},\quad \{x_{i},p_{j}\}_{\alpha }=\delta _{ij}+\sigma _{ij},\nonumber \\ \end{aligned}$$
(12)

where the Moyal brackets are defined as

$$\begin{aligned} \{f,g\}_{\alpha }=f\star _{\alpha }g - g\star _{\alpha }f, \end{aligned}$$

in which the product between f and g is substituted by Moyal product

$$\begin{aligned} \left( f\star g \right) (x)=\exp \left[ \frac{1}{2}\alpha ^{ab}\partial _{a}^{(1)} \partial _{b}^{(2)} \right] \left. f(x_{1})g(x_{2}) \right| _{x_{1}=x_{2}=x} \end{aligned}$$
(13)

such that

$$\begin{aligned} \alpha = \left( \begin{array}{cc} \theta _{ij} &{} \delta _{ij}+\sigma _{ij} \\ -\delta _{ij}-\sigma _{ij} &{} \beta _{ij} \\ \end{array} \right) \end{aligned}$$

where \(\theta _{ij}\) and \(\beta _{ij}\) are \(2\times 2\) antisymmetric matrices and they indicate the non-commutativity in the coordinates and momenta, respectively. Like Refs. [47, 48], here we study particular expressions for the deformations as \(\theta _{ij}=-\theta \epsilon _{ij}\) and \(\beta _{ij}=\beta \epsilon _{ij}\), where \(\epsilon _{ij}\) is the two dimensional Levi-Civita tensor.

As follows, we can derive an algebra similar to (12). Poisson brackets will differ in two algebras despite there being no difference in the algebra. For Eq. (12), the brackets are the \(\alpha \) deformed ones and are related to the Moyal product, for the other algebra the brackets are the usual Poisson brackets. Taking the classical phase space variables and performing the following transformation

$$\begin{aligned} \left( \begin{array}{c} {\hat{x}} \\ {\hat{y}} \end{array} \right)&= \left( \begin{array}{c} x \\ y \end{array}\right) +\frac{\theta }{2} \left( \begin{array}{c} P_{y} \\ -P_{x} \end{array}\right) , \end{aligned}$$
(14)
$$\begin{aligned} \left( \begin{array}{c} {\hat{P}}_{x} \\ {\hat{P}}_{y} \end{array} \right)&= \frac{\beta }{2}\left( \begin{array}{c} -y \\ x \end{array}\right) + \left( \begin{array}{c} P_{x} \\ P_{y} \end{array}\right) , \end{aligned}$$
(15)

the algebra now reads as follows:

$$\begin{aligned}&\{{\hat{y}},{\hat{x}}\}=\theta ,\quad \{{\hat{p}}_{y},{\hat{p}}_{x}\}=\beta , \end{aligned}$$
(16)
$$\begin{aligned}&\{{\hat{x}},{\hat{p}}_{x}\}=1+\sigma ,\quad \{{\hat{y}},{\hat{p}}_{y}\}=1+\sigma , \end{aligned}$$
(17)

in which \(\sigma =\theta \beta /4\). Consequently, applying the transformation to Hamiltonian (3), one gets

$$\begin{aligned} {\mathcal {H}}_{\mathrm {def.}}= \frac{1}{2}\left[ p_{x}^{2}-\epsilon p_{y}^{2}-\epsilon w_{1}^{2} \left( xp_{y}+\epsilon yp_{x} \right) + w_{2}^{2} \left( x^{2}-\epsilon y^{2} \right) \right] ,\nonumber \\ \end{aligned}$$
(18)

where

$$\begin{aligned} w_{1}^{2}=\frac{4 \beta -4 \epsilon \omega ^{2} \theta }{4-\epsilon \omega ^{2} \theta ^{2}}, \quad w_{2}^{2}= \frac{4\omega ^{2}-\epsilon \beta ^{2}}{4-\epsilon \omega ^{2} \theta ^{2}}. \end{aligned}$$
(19)

Therefore, the equations of motion are obtained as

$$\begin{aligned}&{\dot{x}}=p_{x}-\frac{1}{2}w_{1}^{2}y, \quad {\dot{y}}=-\epsilon p_{y}-\frac{1}{2}\epsilon w_{1}^{2}x, \end{aligned}$$
(20)
$$\begin{aligned}&{\dot{p}}_{x}=\frac{1}{2}\epsilon w_{1}^{2} p_{y}-w_{2}^{2}x, \quad {\dot{p}}_{y}=\frac{1}{2}w_{1}^{2} p_{x}+\epsilon w_{2}^{2}y. \end{aligned}$$
(21)

yielding

$$\begin{aligned} \ddot{x}+w_{1}^{2}{\dot{y}}+w_{3}^{2}x&=0, \end{aligned}$$
(22)
$$\begin{aligned} \ddot{y}+\epsilon w_{1}^{2}{\dot{x}}+w_{3}^{2}y&=0, \end{aligned}$$
(23)

in which \(w_{3}^{2}=\left( 4w_{2}^{2}+\epsilon w_{1}^{2} \right) /4\). In order to solve this system, let us first decouple this coupled system through the transformations:

$$\begin{aligned} \left\{ \begin{array}{ll} X_{1}=\frac{1}{2}\left( x+\sqrt{\epsilon }\, y\right) ; \\ X_{2}=\frac{1}{2}\left( x-\sqrt{\epsilon }\, y\right) , \end{array} \right. \end{aligned}$$
(24)

or put differently

$$\begin{aligned} \left\{ \begin{array}{ll} x=X_{1}+X_{2}; \\ y=\epsilon ^{3/2} \left( X_{1} - X_{2} \right) . \end{array} \right. \end{aligned}$$
(25)

Therefore, (22), (23) become

$$\begin{aligned} {\ddot{X}}_{1}+2 \gamma _{1} {\dot{X}}_{1} +w_{3}^{2} X_{1}&=0, \end{aligned}$$
(26)
$$\begin{aligned} {\ddot{X}}_{2}+2 \gamma _{2} {\dot{X}}_{2} +w_{3}^{2} X_{2}&=0, \end{aligned}$$
(27)

in which \(\gamma _{1}=\epsilon ^{3/2} w_{1}^{2}/2\) and \(\gamma _{2}=-\gamma _{1}\). From classical mechanics, we know that there are three possibilities for these damped oscillators, but since we focused on late-time-accelerated expansion and the phase transition, hence we choose the following solution

$$\begin{aligned} x(t)&=c_{5} \exp \left( -\gamma _{1}t \right) \sinh \left( w_{4}t \right) +c_{6} \exp \left( - \gamma _{1}t \right) \cosh \left( w_{4}t \right) \nonumber \\&\quad +c_{7} \exp \left( \gamma _{1}t \right) \sinh \left( w_{4}t \right) +c_{8} \exp \left( \gamma _{1}t \right) \cosh \left( w_{4}t \right) ,\nonumber \\ \end{aligned}$$
(28)
$$\begin{aligned} y(t)&=c_{5} \exp \left( -\gamma _{1}t \right) \sinh \left( w_{4}t \right) +c_{6} \exp \left( - \gamma _{1}t \right) \cosh \left( w_{4}t \right) \nonumber \\&\quad -c_{7} \exp \left( \gamma _{1}t \right) \sinh \left( w_{4}t \right) -c_{8} \exp \left( \gamma _{1}t \right) \cosh \left( w_{4}t \right) , \end{aligned}$$
(29)

where \(w_{4}=\sqrt{(\beta ^{2}-4\epsilon \omega ^{2})/(4-\epsilon \omega ^{2} \theta ^{2})}\). Again we should desert cosh-parts because of the reason mentioned in the previous section.

Ordinary scalar field: For the ordinary scalar field (\(\epsilon =1\)), the scale factor in the C frame would then be

$$\begin{aligned} a_{\textrm{C}}(t)&=\left\{ -4\lambda c_{5}c_{7} \sinh ^{2}(w_{4}t) \right\} ^{1/3}. \end{aligned}$$
(30)

Now, by tuning

$$\begin{aligned} c_{5}c_{7}=\frac{\Omega _{\textrm{m}}}{-4\lambda \Omega _{\Lambda }}, \quad w_{4}^{2}=\frac{\beta ^{2}-4w^{2}}{4-w^{2}\theta ^{2}} =\frac{9}{4}H_{0}^{2}\Omega _{\Lambda } \end{aligned}$$
(31)

(30) recast in the form

$$\begin{aligned} a_{\textrm{C}}(t)=\left( \frac{\Omega _{\textrm{m}}}{\Omega _{\Lambda }} \right) ^{1/3} \left[ \sinh \left( \frac{3}{2}\sqrt{\Omega _{\Lambda }}H_{0}t\right) \right] ^{2/3} \end{aligned}$$
(32)

where \(\Omega _{\textrm{m}}\) and \({\Omega _{\Lambda }}\) are the critical density of matter and dark energy, respectively, and \(H_{0}\) is the current value of the Hubble parameter. It follows that the present value of the scale factor is one (\(a_{0}=1\)) and the age of the universe is \(t_{0}=13.8 \,\textrm{Gyr}\). Furthermore, the transition from decelerating to accelerating expansion occurred when \(a=(\Omega _{\textrm{m}}/2 \Omega _{\Lambda })^{1/3}\) which evaluates to \(a \simeq 0.6\) or in terms of redshift \(z \simeq 0.66\) for the best-fit parameters estimated from the Planck data. It is also interesting to note two limiting cases:

$$\begin{aligned} a_{\textrm{C}}(t)\simeq \left\{ \begin{array}{ll} \left( \frac{9}{4}\Omega _{\textrm{m}} \right) ^{1/3} \left( H_{0}t \right) ^{2/3} , &{}{H_{0}t\ll 1;} \\ \left( \frac{\Omega _{\textrm{m}}}{4\Omega _{\Lambda }} \right) ^{1/3} \exp \left( \sqrt{\Omega _{\Lambda }}\;H_{0}t \right) , &{} {H_{0}t \gg 1.} \end{array} \right. \end{aligned}$$
(33)

In the case \(H_{0}t \ll 1\), the \(\Lambda \text {-term}\) contributes a tiny fraction to the total density and the Universe expands at a decelerating rate by the law corresponding to matter domination. In the limiting case \(H_{0}t \gg 1\), the contribution of the \(\Lambda \text {-term}\) to the total density becomes dominant, while that of matter significantly decreases. The scale factor at this limit corresponds to the scale factor of a de Sitter expansion. Recall that for the minimal 6-parameter \(\Lambda \text {CDM}\) model, by neglecting the radiation density one also exactly gets (32) [55].

Fig. 2
figure 2

This figure shows the behavior of the scale factor (32). As is observed the present value of it is one and the age of the universe is about \(13.8\,\textrm{Gyr}\). The onset of acceleration has happened at redshift \(z\sim 0.66\) or equivalently \(t=7.3\,\textrm{Gyr}\) which coincides with observational data

Full size image

The behavior of (32) has been plotted in Fig. 2.

The scale factor in the NC frame takes the form

$$\begin{aligned} a_{\textrm{NC}}(t)=\left\{ \lambda c_{5} c_{7} \left[ -4\sinh ^{2}(w_{4}t)+\theta ^{2}w_{4}^{2}\cosh ^{2}(w_{4}t) \right] \right\} ^{1/3}. \end{aligned}$$
(34)

Solutions of this form, have been found before by the use of other ways in some general models in the literature, for example see [56, 57]. In order to determine the valid range of the deformation parameters in Ref. [29], the authors suggest that the following principle should be adopted: “Deformed phase space models are only valid when the descriptions of C and NC frames are physically equivalent.” Therefore, the case \( \{\theta =0 \; \& \; \beta \ne 0\}\) is one of valid ranges. The interpretation of this trivial range is that the coordinates are commutative but the momenta are non-commutative. The case \(\beta =0\) was excluded because it corresponds to a normal commutative case hence by accepting it, non-commutativity would become meaningless. Besides, limpidly, (34) is equivalent to (32) when the value of \(\theta w_{4}\) be sufficiently small. In other words, this equivalence occurs when there is a real inflection point for a selected value of \(\theta w_{4}\). Indeed, despite sinh-part which carries both decelerated and accelerated epochs, cosh-part is responsible for just the accelerated era, hence when we strengthen it, it dominates the decelerated era and even it can remove it. Thus by decreasing its amplitude we can maintain both decelerated and accelerated eras which guarantees existing the inflection point and then the behavior of the two frames would be equivalent. In the limit \(t \rightarrow \infty \), like C frame, the behavior would be de Sitter type:

$$\begin{aligned} a_{\textrm{NC}}(t) \simeq \left( -\lambda c_{5}c_{7}+\frac{\theta ^{2}w_{4}^{2}}{4} \right) \exp \left( \frac{2w_{4}t}{3} \right) . \end{aligned}$$
(35)

Now, like Refs. [47, 48], one can impose some restrictions on parameters by comparing (35) with de Sitter scale factor \(\exp \left( t \sqrt{\Lambda _{\mathrm {eff.}}/3} \right) \) where \(\Lambda _{\mathrm {eff.}}\) is the de Sitter (effective) cosmological constant. However our scale factors are different but the result of comparison would be the same, see:

$$\begin{aligned} \Lambda _{\mathrm {eff.}}=\frac{1}{3}\left( \frac{\beta ^{2}+3\Lambda }{1+\frac{3}{16}\Lambda \theta ^{2}} \right) \end{aligned}$$
(36)

Hence to have a positive effective cosmological constant, two conditions are obtained:

$$\begin{aligned}&\beta ^{2}>-3\Lambda , \nonumber \\&\Lambda \, \theta ^{2}>-\frac{16}{3}. \end{aligned}$$
(37)

The solid curve in Fig. 3 indicates the qualitative behavior of (34).

Fig. 3
figure 3

The solid curve indicates the behavior of scale factor (34) for the values \(c_{5}c_{7}=-1/\sqrt{6}\), \(w_{4}=1\), and \(\theta =0.1\) while the dashed curve demonstrates the plot of (40) for the values \(w_{1}=0.01\) and \(w_{4}=1\)

Full size image

The scale factor (34) (NC frame) is better than (32) (C frame) because of the more degrees of freedom; in (32) one can set only three properties (the present value of the scale factor, the age of the universe, and the redshift of the transition from decelerated to accelerated expansion) while in (34), thanks to cosh-part, we can tune the present value of the deceleration parameter and consequently the value of the equation of state (EoS) parameter as well.

Phantom scalar field: The scale factors of the ‘C’ and ‘NC’ frames for phantom scalar field (\(\epsilon =-1\)) turn out to be

$$\begin{aligned} a_{\textrm{C}}(t)&=\left\{ 2\lambda \sinh ^{2}(w_{4}t) \right. \nonumber \\&\quad \times \left. \left[ c_{5}^{2}\exp (-2\gamma _{1} t)+c_{7}^{2}\exp (2\gamma _{1} t) \right] \right\} ^{1/3}, \end{aligned}$$
(38)
$$\begin{aligned} a_{\textrm{NC}}(t)&=\bigg \{\lambda \left( \frac{c_{5}^{2}}{2} \right) \exp (-2\gamma _{1}t)\left[ 4\sinh ^{2}(w_{4}t)\right. \nonumber \\ {}&\quad + \left. \theta ^{2}w_{4}^{2}\cosh ^{2}(w_{4}t) -2\theta w_{4}\cosh (w_{4}t)\sinh (w_{4}t)\right] \nonumber \\&\quad +\lambda \left( \frac{c_{7}^{2}}{2} \right) \exp (2\gamma _{1}t)\left[ 4\sinh ^{2}(w_{4}t)\right. \nonumber \\ {}&\quad + \left. \theta ^{2}w_{4}^{2}\cosh ^{2}(w_{4}t) +2\theta w_{4}\cosh (w_{4}t)\sinh (w_{4}t)\right] \bigg \}^{1/3} \end{aligned}$$
(39)

To make our discussions easy, let us assume \(c_{5}^{2}=c_{7}^{2}=1/2\). Hence, we get:

$$\begin{aligned} a_{\textrm{C}}(t)&=\left\{ 2\lambda \sinh ^{2}(w_{4}t) \cos \left( w_{1}^{2}t \right) \right\} ^{1/3}, \end{aligned}$$
(40)
$$\begin{aligned} a_{\textrm{NC}}(t)=&\bigg \{2\sinh ^{2}(w_{4}t)\cos \left( w_{1}^{2}t \right) \nonumber \\ {}&\quad + \frac{\lambda }{2}\theta ^{2}w_{4}^{2}\cosh ^{2}(w_{4}t)\cos \left( w_{1}^{2}t \right) \nonumber \\&\quad +i\,\lambda \theta w_{4}\cosh (w_{4}t)\sinh (w_{4}t)\sin \left( w_{1}^{2}t \right) \bigg \}^{1/3}, \end{aligned}$$
(41)

where \(i=\sqrt{-1}\). As is observed, the last term in \(a_{\textrm{NC}}\) has imaginary amplitude, hence we have two possibilities for a valid description of the NC frame: (1) the first possibility is that \(\theta =0\) which leads to \(a_{\textrm{NC}}(t)=a_{\textrm{C}}(t)\). This case has been plotted with a dashed line in Fig. 3. (2) Another option is assuming \(\theta =i\Theta \) in which \(\Theta \) is real, but since this leads to \(\{{\hat{y}}, {\hat{x}}\}=i\Theta \), hence we must leave it aside and proceed with the former one. The limiting cases for the aforementioned scale factors are as

$$\begin{aligned} a_{\textrm{C,NC}}(t)\simeq \left\{ \begin{array}{ll} \left( 2\lambda w_{4} \right) ^{1/3}\;t^{2/3} , &{} {t\ll 1;} \\ \left\{ \frac{\lambda }{2} \cos \left( w_{1}^{2}t \right) \exp \left( 2 w_{4}t \right) \right\} ^{1/3}, &{} {t \gg 1.} \end{array} \right. \end{aligned}$$
(42)

The case \(a_{\textrm{C,NC}}(t)\simeq t^{2/3}\) corresponds to matter dominated era and the expansion is of decelerated nature because the deceleration parameter for such behavior is positive. By assuming a tiny value for \(w_{1}\) so that \(w_{1}^{2}t_{0}\ll 1\), i.e. for example \(w_{1} \sim H_{0} \Longrightarrow \cos \left( w_{1}^{2}t \right) \sim 1\) , the second case in (42) reduces to

$$\begin{aligned} \left( \frac{\lambda }{2} \right) ^{1/3} \exp \left( \frac{2}{3}w_{4}t \right) . \end{aligned}$$
(43)

Hence, the late-time-accelerated expansion is guaranteed by this de Sitter-type expansion behavior. By comparing this scale factor with de Sitter one, we get

$$\begin{aligned} \Lambda _{\mathrm {eff.}}=\frac{1}{3}\left( \beta ^{2}-3\Lambda \right) \end{aligned}$$
(44)

which yields the following bound for having a positive effective cosmological constant

$$\begin{aligned} \beta ^{2} >3\Lambda . \end{aligned}$$
(45)

Therefore, to have phase transition and late-time accelerated expansion we must set

$$ \begin{aligned} \{ \theta =0 \; \& \; \beta ^{2} >3\Lambda \; \& \; \text {Tiny } \beta \}. \end{aligned}$$
(46)

The last condition comes from the condition which was imposed on \(w_{1}\). According to 46, the coordinates are commutative but the momenta are non-commutative.

4 A theorem for valid description of NC frame

In this section, proposing a theorem for a valid description of an NC frame is our objective. In Ref. [29], the following principle has been suggested to be imposed: “Deformed phase space models are only valid when the descriptions of C and NC frames are physically equivalent.” The principle adopted is somewhat a relative sentence. In terms of mathematic, we may propose the following theorem.

\(\bullet \) Valid description theorem

Suppose that \(H_{\textrm{C}}\) and \(H_{\textrm{NC}}\) are the Hubble parameters corresponding to \(a_{\textrm{C}}\) and \(a_{\textrm{NC}}\), respectively. The description of an NC frame is valid if there is a continuous one-to-one correspondence (homeomorphism) that maps trajectories of \(H_{\textrm{NC}}\) on trajectories of \(H_{\textrm{C}}\). This theorem can be “localized” by introducing appropriate regions. It should be emphasized that the homeomorphism need not be differentiable.

Indeed, in this theorem, I first build the corresponding dynamical systems to the scale factors and then use the theorem of equivalence of two dynamical systems. The relative sentence suggested in Ref. [29] may be regarded as weak form of this theorem. However, finding homeomorphism is not an easy task in most cases, such as our case of study.

5 Conclusion

In this paper, we have studied the effects of minisuperspace deformation on the dynamics of Einstein–Hilbert action along with ordinary and phantom scalar fields as the matter contents. It was indicated that in the commutative model, however, the qualitative behavior of the solution shows a transition from decelerated to accelerated expansion, but since it has just one free parameter hence it cannot match with all related observations (the present value of the scale factor; the age of the universe; the present value of the deceleration parameter; the value of the redshift of starting late-time acceleration). After deforming minisuperspace, we found that for the ordinary scalar field, the scale factor in the C frame has an equal form to the scale factor of the minimal 6-parameter \(\Lambda \text {CDM}\) model when one neglects the radiation component. At early time, this scale factor behaves like the scale factor of the matter-dominated era \(a\sim t^{2/3}\) and at latter time it has de Sitter type expansion. Furthermore, this scale factor predicts the onset of the acceleration was around the redshift \(z \sim 0.66\) and the age of the universe is \(13.8\, \textrm{Gyr}\). The scale factor of NC frame for ordinary scalar field for tiny values of \(\theta \) (zero and close to zero such as 0.01) has equivalent behavior to the scale factor of C frame. Such ranges of \(\theta \) indicate that the coordinates must be commutative or close to commutative. The range of \(\beta \) which demonstrate the non-commutativity in momenta was free for this case. By considering the asymptotic behavior, some bounds were found for deformation parameters. For the phantom scalar field, due to the appearance of an imaginary part in the form of the scale factor of NC frame, just zero value of \(\theta \) is acceptable and consequently, the form of the scale factor in both frames becomes equal. Therefore, unlike momenta, the coordinates must be commutative for this case of study. At early time, the scale factor behaves like matter-dominated era while at latter time we get a bouncing universe. By a reasonable assumption, this bouncing behavior changed to de Sitter type scale factor and hence the late-time-accelerated expansion was achieved. Finally, a mathematical theorem for distinguishing valid descriptions of the noncommutative frames was suggested.