1 Introduction

Electrovacuum solutions of the Einstein–Maxwell equations are of considerable interest to the modern theory of gravity and cosmology in connection with their possible applications for describing compact astrophysical objects or early stages of the evolution of the Universe. One of the most interesting types of electrovacuum solutions describes a self-gravitating electromagnetic field configuration without a source, called geon [1].

A cylindrically symmetric static solution of the Einstein–Maxwell equations, describing the geon as a set of purely electric or magnetic field lines connected by their own gravitational interaction, was obtained by Melvin [2]. A number of generalizations for Melvin’s solution are currently known, for instance, in [3] Melvin’s solution was extended to the case of a non-zero cosmological constant, and [4] gives an extension for the string theory. A rather interesting application of Melvin’s solution was found in describing magnetized black holes [5,6,7,8]. In [9] a solution of the Dirac equation in Melvin space-time is obtained, which can be applied to describe fermions in extremely magnetized neutron stars, and [10] presents a non-Abelian solution corresponding to a “hairy” black hole, whose space-time has asymptotics to the Melvin’s background. The paper [11] presents the rotating Melvin-like solution for the perfect fluid with the circular electric current, and [12] gives a multidimensional extension coupled to the scalar fields.

The search for a nonlinear generalization of electrodynamics in vacuum seems to be one of the promising problems of modern field theory. A significant part of the new results in this area is related to the study of effects in empirical models of electrodynamics based on the requirement of regularization of the field energy of point sources. Along with one of the first models leading to such a regularization – Born–Infeld electrodynamics [13], a number of alternative models with a similar property have recently been proposed [14,15,16,17,18]. Some of these models [14] lead to very peculiar solutions, such as charged black points, which are compact objects with an event horizon coinciding with a singularity. Another type of vacuum nonlinear electrodynamics models [19, 20] are based on the principle of maximum correspondence to the group symmetries of Maxwell’s electrodynamics, in particular, such models inherit conformal symmetry and are called conformally invariant models (CNED).

For the listed models, the exact form of the Lagrangian is known, which allows to consider the problem of search a generalization for the Melvin solution to these cases of vacuum nonlinear electrodynamics. In contrast to [21], where a generalization of the Melvin solution to the case of nonlinear electrodynamics was obtained by transforming the Reisner–Nordström solution, this paper proposes integrating combinations that allows to lead the Einstein’s gravity and nonlinear electrodynamics equations to a relatively simple ordinary differential equations. The integration of these equations can be carried out not only with a boundary condition asymptotic to the Melvin solution, which potentially makes it possible to obtain new solutions with a given behavior at spatial infinity. Also, in contrast to [22], we will not require the existence of a regular axis of symmetry and flat or string-like asymptotic at spatial infinity. On contrary, in the context of this paper it seems to be interesting, to consider the singular field configurations in the models of vacuum nonlinear electrodynamics with the regularizing properties.

The paper is organized as follows: In Sect. 2, we discuss equations of vacuum nonlinear electrodynamics and Einstein’s gravitation in the case of cylindrical symmetry. In this section we note some conditions for the existence of solutions to these equations. Section 3 is devoted to Melvin-type solution generalization for an arbitrary conformally invariant vacuum nonlinear electrodynamics (CNED). Section 4 discusses self-sustaining longitudinal, radial, and azimuthal configurations of a pure magnetic field in the models of vacuum nonlinear electrodynamics with the regularizing properties and with the spatial asymptotics to the Melvin solution. In the last section we summarize our results.

For more convenience, we will use geometerized units (\(G=c={\hbar }=1\)) and the metric signature \(\{ +\ , -\ , -\ , -\ \}\).

2 Equations of vacuum non-linear electrodynamics and gravity in the case of cylindrical symmetry

Let us construct equations for the gravitational and electromagnetic fields in the case of an arbitrary Lorentz invariant model of vacuum nonlinear electrodynamics, taking into account the cylindrical symmetry of the field configuration. The action functional for arbitrary vacuum nonlinear electrodynamics (NED) coupled with Einstein’s gravity has the form:

$$\begin{aligned} S=\int \left( {{{\mathcal {L}}}}(J_2,J_4)-\frac{R}{16\pi }\right) \sqrt{-g} \ d^4x, \end{aligned}$$
(1)

where R is the scalar curvature, g is the determinant of the metric tensor, \({{{\mathcal {L}}}}\) is the Lagrangian density, depending on the invariants of the electromagnetic field tensor \(J_2=F_{ik}F^{ki}\) and \(J_4=F_{ik}F^{kl}F_{lm}F^{mi}\). The action (1) leads to Einstein’s gravity equations

$$\begin{aligned} H_{ik}=R_{ik}-\frac{R}{2}g_{ik}=8\pi T_{ik}, \end{aligned}$$
(2)

with the stress-energy tensor for vacuum nonlinear electrodynamics:

$$\begin{aligned} T_{ik}= & {} \frac{2}{\sqrt{-g}}\frac{\delta (\sqrt{-g}{{{\mathcal {L}}}})}{\delta g^{ik}}= 4\left[ \frac{\partial {{{\mathcal {L}}}}}{\partial J_2}+ J_2\frac{\partial {{{\mathcal {L}}}}}{\partial J_4}\right] F_{ik}^{(2)} \nonumber \\{} & {} +\left[ (2J_4-J_2^2)\frac{\partial {{{\mathcal {L}}}}}{\partial J_4}-{{{\mathcal {L}}}}\right] g_{ik}, \end{aligned}$$
(3)

where \(F_{ik}^{(2)}=F_{im}F^{m\cdot }_{\cdot k}\) is the second power of the electromagnetic field tensor. The equations for the electromagnetic field, following from the action (1), in the absence of charges and currents can be expressed with the Bianchi identities and the divergence free equation for an auxiliary tensor \(Q^{kn}\)

$$\begin{aligned} \partial _n F_{ik}+\partial _k F_{ni}+\partial _i F_{kn}=0, \qquad \frac{\partial \sqrt{-g} Q^{kn}}{\partial x^n}=0, \end{aligned}$$
(4)

with can be expressed with the NED model Lagrangian in the form

$$\begin{aligned} Q^{kn}=4\frac{\partial {{{\mathcal {L}}}}}{\partial J_2}F^{kn} +8\frac{\partial {{{\mathcal {L}}}}}{\partial J_4}F_{(3)}^{kn}, \end{aligned}$$
(5)

where \(F^{kn}_{(3)}=F^{kl}F_{lm}F^{mn}\) is the third power of the field strength tensor. In following, we will focus on the study of self-sustained field configurations with cylindrical symmetry, therefore we will take into account that in cylindrical coordinates, static axisymmetric solutions of Einstein’s equations are given by the Weyl metric [23, 24]:

$$\begin{aligned} ds^2=e^{2\alpha }dt^2-e^{2\beta }[d\rho ^2+dz^2]-\rho ^2e^{-2\gamma }d\varphi ^2, \end{aligned}$$
(6)

where in general case the metric functions \(\alpha \), \(\beta \), \(\gamma \) depends on coordinates \(\rho \) and z, however, we restrict ourselves to a particular case, assuming that the metric functions depend only on the radial coordinate \(\rho \). For greater convenience in calculations, we will use the physical representation for the component of the electromagnetic field tensor:

$$\begin{aligned}{} & {} F_{ik}\nonumber \\ {}{} & {} = \begin{pmatrix} 0 &{}\quad E_\rho e^{\alpha +\beta } &{}\quad \rho E_\varphi e^{\alpha -\gamma } &{}\quad E_z e^{\alpha +\beta }\\ -E_\rho e^{\alpha +\beta } &{}\quad 0 &{}\quad -\rho B_z e^{\beta -\gamma } &{}\quad B_\varphi e^{2\beta }\\ -\rho E_\varphi e^{\alpha -\gamma } &{}\quad \rho B_z e^{\beta -\gamma } &{}\quad 0 &{}\quad -\rho B_\rho e^{\beta -\gamma } \\ -E_z e^{\alpha +\beta } &{}\quad -B_\varphi e^{2\beta } &{}\quad \rho B_\rho e^{\beta -\gamma } &{}\quad 0 \end{pmatrix},\nonumber \\ \end{aligned}$$
(7)

where \(E_\rho \),\(E_\varphi \),\(E_z\) and \(B_\rho \),\(B_\varphi \),\(B_z\) are the coordinate components of the electric and magnetic field. In this case, the invariants of the electromagnetic field can be calculated using the Euclidean metric, which greatly simplifies the expressions for them.

For the chosen space-time line-element, the left-hand side of the Einstein equations take a form:

$$\begin{aligned} H_{0\cdot }^{\cdot 0}= & {} e^{-2\beta } \left[ \frac{2\gamma '}{\rho }-\gamma '^2+\gamma ''-\beta ''\right] , \nonumber \\ H_{1\cdot }^{\cdot 1}= & {} e^{-2\beta } \left[ \alpha '\gamma '+\beta '\gamma '-\alpha '\beta '-\frac{\alpha '+\beta '}{\rho }\right] , \nonumber \\ H_{2\cdot }^{\cdot 2}= & {} -e^{-2\beta } \left[ \alpha ''+\beta ''+\alpha '^2\right] , \nonumber \\ H_{3\cdot }^{\cdot 3}= & {} e^{-2\beta } \bigg [\alpha '\beta '-\alpha ''-\alpha '^2+(\alpha '-\beta ')\gamma '+ \gamma ''-\gamma '^2 \nonumber \\{} & {} +\frac{\beta '-\alpha '+2\gamma '}{\rho }\bigg ], \end{aligned}$$
(8)

where the prime denotes the derivative with respect to the radial coordinate.

In what follows, except for the model of conformally invariant vacuum nonlinear electrodynamics (CNED), we will focus on search only pure magnetic solutions (\(\textbf{B}\ne 0\), \(\textbf{E}=0\) and as a consequence \(J_2^2=2J_4\)) of the Eqs. (2) and (4). As follows from [21], the existence of self-consistent solutions of theses equations is possible only for certain field configurations, namely: radial, azimuthal and longitudinal fields.

For radial field configuration \(B_\rho \ne 0\), \(B_\varphi =0\), \(B_z=0\), the stress-energy tensor (3) has additional symmetry, expressed as equality of some components among themselves:

$$\begin{aligned} T_{0 \cdot }^{\cdot 0}=T_{1 \cdot }^{\cdot 1}=Y, \qquad T_{2 \cdot }^{\cdot 2}=T_{3 \cdot }^{\cdot 3}=Y-B_\rho ^2 X, \end{aligned}$$
(9)

where, for brevity, we have introduced the notation for the coefficients

$$\begin{aligned} Y=-{{{\mathcal {L}}}}\left| _{J_2^2=2J_4}, \quad X=4\left[ \frac{\partial {{{\mathcal {L}}}}}{\partial J_2}+ J_2\frac{\partial {{{\mathcal {L}}}}}{\partial J_4}\right] \right| _{J_2^2=2J_4}. \end{aligned}$$
(10)

For an azimuthal magnetic field \(B_\rho =0\), \(B_\varphi \ne 0\), \(B_z=0\), the relation between the stress-energy tensor components is different

$$\begin{aligned} T_{0 \cdot }^{\cdot 0}=T_{2 \cdot }^{\cdot 2}=Y, \qquad T_{1 \cdot }^{\cdot 1}=T_{3 \cdot }^{\cdot 3}=Y-B_\varphi ^2 X. \end{aligned}$$
(11)

And, finally, for the most interesting case of longitudinal field \(B_\rho =0\), \(B_\varphi =0\), \(B_z\ne 0\) the additional symmetry of the stress-energy tensor is the following:

$$\begin{aligned} T_{0 \cdot }^{\cdot 0}=T_{3 \cdot }^{\cdot 3}=Y, \qquad T_{1 \cdot }^{\cdot 1}=T_{2 \cdot }^{\cdot 2}=Y-B_z^2 X. \end{aligned}$$
(12)

To obtain solutions to the equations of nonlinear electrodynamics and gravitation in all three of the above cases, it is necessary to find an integrating combinations for the metric functions \(\alpha \),\(\beta \),\(\gamma \), whose substitution into the Eq. (2) ensures consistency of additional symmetries for the right and left sides of these equations. This means that the symmetry of \(T_{a \cdot }^{\cdot b}\), say, \(T_{1 \cdot }^{\cdot 1}=T_{2 \cdot }^{\cdot 2}\) requires \(H_{1 \cdot }^{\cdot 1} = H_{2 \cdot }^{\cdot 2}\), and to satisfy this condition it is necessary to find some relation between the metric functions. Before proceeding to the search for such relations in the general case, let us consider in more detail the case of a longitudinal magnetic field for a special model of nonlinear electrodynamics, called conformally invariant electrodynamics (CNED), for which an analytical solution similar to the Melvin’s geon can be obtained.

3 Melvin-type solution for CNED

Models of conformally invariant electrodynamics are based on the principle of closest correspondence to a number of properties of Maxwell’s electrodynamics. Like Maxwell’s electrodynamics, CNED models have a zero trace of the stress-energy tensor and are characterized by the same group symmetries as Maxwell’s theory, but unlike it, they predict birefringence in vacuum.

Another advantage of CNED is the lack of a dimensional parameter needed to describe non-linearity in other models, such as Born–Infeld electrodynamics. In the general case, the CNED Lagrangian can be represented as:

$$\begin{aligned} {{{\mathcal {L}}}}= \frac{J_2}{16\pi } W(\eta ), \end{aligned}$$
(13)

where W is an arbitrary function of the dimensionless ratio \(\eta =J_2/\sqrt{2J_4}\), varying from \(\eta =-1\) for a pure magnetic field, to \(\eta =1\), for a pure electric field. When \(W(\eta )\equiv 1\) the CNED corresponds to Maxwell electrodynamics.

Let us consider an electric field with strength E and a magnetic field with inductance B directed along the z axis. For such a longitudinal configuration, the electromagnetic field equations (4) are easily integrated and lead to the expressions:

$$\begin{aligned}{} & {} e^{\alpha +\beta }E=E_0, \nonumber \\{} & {} e^{\alpha +\beta }B\left[ W+\eta W'\left( \frac{E^2(E^2+B^2)}{E^4+B^4}\right) \right] =B_0, \end{aligned}$$
(14)

where \(E_0\) and \(B_0\) are integrating constants, and here and below, the prime on the model function W corresponds to the derivative with respect to its argument \(\eta \). It can be noticed, that the expression in square brackets of the second equation in (14) can be fully expressed in terms of the ratio \(\lambda =B/E\), because of which the ratio of the magnetic field induction to the electric field strength is constant at any point of space. This is easy to verify, if we divide the second equation in (14) by the first equation and use the parameter \(\lambda \) as a new variable

$$\begin{aligned} \lambda \left[ W(\eta )+\frac{1-\lambda ^4}{(1+\lambda ^4)^{3/2}}W'(\eta )\right] =\lambda _0, \end{aligned}$$
(15)

where \(\lambda _0=B_0/E_0\) and the argument of the model function \(W(\eta )\) should be expressed in terms of \(\lambda \) using the expression:

$$\begin{aligned} \eta =\frac{1-\lambda ^2}{\sqrt{1+\lambda ^4}}. \end{aligned}$$
(16)

Equation (15) implies that for each model of conformally invariant nonlinear electrodynamics with a given function W, the ratio \(\lambda \) is determined only by the integration constant \(\lambda _0\) and does not depend on the coordinates.

To determine the explicit form of the electric and magnetic fields, it is necessary to supplement algebraic equations (14) with gravitational equations for metric functions, which can be obtained by using of (2) and (8) and the stress-energy tensor (3). We take into account that for the considered field configuration, additional symmetry for the components of the stress-energy tensor is the same as for the longitudinal case for a pure magnetic field (12), and the components themselves have the form:

$$\begin{aligned} T_{0 \cdot }^{\cdot 0}= & {} T_{3 \cdot }^{\cdot 3}= \frac{E^2}{8\pi }\left[ W+\frac{2\lambda ^2(1-\lambda ^2)}{(1+\lambda ^4)^{3/2}}W'\right] (1+\lambda ^2), \nonumber \\ T_{1 \cdot }^{\cdot 1}= & {} T_{2 \cdot }^{\cdot 2}= -\frac{E^2}{8\pi }\left[ W+\frac{2\lambda ^2(1-\lambda ^2)}{(1+\lambda ^4)^{3/2}}W'\right] (1+\lambda ^2). \end{aligned}$$
(17)

To ensure that the right and left sides of the Einstein equations correspond, it is necessary to introduce additional restrictions on the metric functions. Using, (8), it can be established that the symmetry of the left side of the equations (2), corresponding to the symmetry of the components (17), will be ensured if we accept:

$$\begin{aligned} \alpha =\beta , \qquad \gamma =\text{ ln }(c_0\rho /\alpha '), \end{aligned}$$
(18)

where \(c_0\) is an arbitrary constant that can be used to normalize coordinates, and the prime over metric function \(\alpha \) means the derivative with respect to \(\rho \).

In this case, due to the energy conservation law, there is only one independent Einstein equation, a more convenient form of which is:

$$\begin{aligned} H_{1 \cdot }^{\cdot 1}= & {} -e^{-2\alpha }(2\alpha ''+\alpha '^2)=8\pi T_{1\cdot }^{\cdot 1} \nonumber \\= & {} -E^2\left[ W+\frac{2\lambda ^2(1-\lambda ^2)}{(1+\lambda ^4)^{3/2}}W'\right] (1+\lambda ^2). \end{aligned}$$
(19)

Using the first of the relations (14) for the electric field, the Eq. (19) can be reduced to the form of an autonomous equation:

$$\begin{aligned} 2\alpha ''+\alpha '^2=\frac{4}{R^2}e^{-2\alpha }, \end{aligned}$$
(20)

whose solution \(\alpha =\text{ ln }(1+\rho ^2/R^2)\) differs from the classical Melvin solution only in the choice of the normalization constant R for the radial coordinate

$$\begin{aligned} \frac{1}{R^2}=\frac{1}{4}E_0^2(1+\lambda ^2) \left[ W+\frac{2\lambda ^2(1-\lambda ^2)}{(1+\lambda ^4)^{3/2}}W'\right] . \end{aligned}$$
(21)

Thus, the geon-like solution corresponding to the longitudinal electric and magnetic fields in an arbitrary CNED model coincides in form with the classical Melvin solution, despite the significant nonlinearity of these models. However, for a number of models other than CNED, essentially non-linear properties can manifest themselves differently, and it is interesting to find out how much in this case the solutions will differ from the Melvin geon. Therefore, in the next section, we turn to a description of purely magnetic field configurations in such models.

4 Self-sustaining configurations of a pure magnetic field with cylindrical symmetry in vacuum

4.1 Longitudinal field

Let us consider a longitudinal magnetic field \(B_\rho =B_\varphi =0\), \(B_z\ne 0\), \(\textbf{E}=0\) in an arbitrary model of nonlinear electrodynamics. In this case, it is easy to obtain the first integrals for the equations of the electromagnetic field (4), which have the following form

$$\begin{aligned} e^{\alpha +\beta }B_z\left[ \frac{\partial {{{\mathcal {L}}}}}{\partial J_2} -2B_z^2\frac{\partial {{{\mathcal {L}}}}}{\partial J_4}\right] =\frac{B_0}{16\pi }, \end{aligned}$$
(22)

where \(B_0\) is the constant of integration with the dimension of the magnetic field induction. To ensure the symmetry of the right and left sides of the Einstein equations in the case of a longitudinal magnetic field (12), one should take a relation between the metric functions similar to (18), as a result of which the expressions (2), (8) and (12) leads to only one non-trivial linearly independent equation:

$$\begin{aligned} 2\alpha ''+\alpha '^2=8\pi e^{2\alpha }[B_z^2X-Y]. \end{aligned}$$
(23)

Let us carry out normalization for the magnetic field induction \(b=B_z/B_0\), the coordinate \(r=\rho /R\), where \(R=2/B_0\), and also for the coefficients depending on the choice of the nonlinear electrodynamics model \(U=4\pi X\) and \(V=4\pi Y/B_0^2\), in terms of which the Eqs. (23) and (22) can be represented as:

$$\begin{aligned} 2\alpha ''+\alpha '^2=8e^{2\alpha }[Ub^2-{V}], \qquad e^{2\alpha }U b=1, \end{aligned}$$
(24)

where the prime means the derivative with respect to the normalized coordinate r. It can be easily verified that for Maxwell’s electrodynamics \(U=1, \ V=b^2/2\), and in this case, the general solution of the Eq. (24) can be obtained in the analytical form:

$$\begin{aligned} \alpha= & {} \text{ ln }\left[ \frac{c_1^2(r+c_2)^2+16}{4c_1}\right] ,\quad b = \frac{16c_1^2}{[c_1^2(r+c_2)^2+16]^2}, \nonumber \\ \end{aligned}$$
(25)

where \(c_1\) and \(c_2\) are integration constants, a particular choice for which \(c_1=4\) and \(c_2=0\) leads to classical representation of Melvin’s solution: \(\alpha =\text{ ln }(1+r^2)\) and \(b=1/(1+r^2)^2\).

Let’s start searching for solutions to the Eq. (24) for some models of vacuum nonlinear electrodynamics, which lead to the regularization of the point charge field. For the models such as Born–Infeld electrodynamics [13], logarithmic [14, 15], exponential [16, 17] and rational electrodynamics [18], the coefficients for the Eq. (24) are presented in the Table 1.

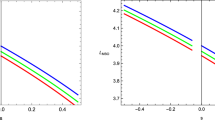
Table 1 Coefficients U and V for some specific models
Full size table

In view of the significant nonlinearity, the Eq. (24) were integrated numerically. The requirement of correspondence between the solutions of these equations in the case of nonlinear electrodynamics and the solution for Maxwell’s electrodynamics (25) for large values of \(r\rightarrow \infty \) was taken as the boundary condition. Figure 1 shows the dependence of the magnetic field induction on the coordinate (solid line), obtained as a result of numerical integration for Born–Infeld electrodynamics at the value of the parameter \(k=1.345\). The dashed line in the figure shows Melvin’s solution (25) with \(c_1=4\) and \(c_2=-3\), which was taken as the boundary condition.

Fig. 1
figure 1

Normalized magnetic field induction as a function of the radial coordinate r

Full size image
Fig. 2
figure 2

Evolution of the solution for the longitudinal electromagnetic field with a change in the parameter k in Born–Infeld electrodynamics

Full size image

Due to the nonlinear features of vacuum electrodynamics, the solution has a pronounced resonant form, corresponding to the concept of geons as particle-like solutions. The Fig. 2 shows the sharpening of the form of the soliton-like solution for magnetic field induction with increasing of the parameter k for Born–Infeld electrodynamics. The plane with the \(k=0\), filled in green, corresponds to Melvin’s solution. With an increase in this parameter, not only a sharp increase in the amplitude occurs, but also a shift of the maximum in the direction of increasing values of the radial coordinate relative to the position of the maximum in the Melvin’s solution.

It is interesting to note that for other models presented in the Table 1, soliton-like nature of the solution for the Eq. (24) is preserved, differing from that shown in Fig. 1 only quantitatively.

Let us pass to the consideration of the radial configuration of the field.

4.2 Radial field

Now suppose that only the radial component of the magnetic field is nonzero: \(B_\rho \ne 0 \), \(B_\varphi =B_z=0\), \(\textbf{E}=0\). In this case, the non-trivial equations for the electromagnetic field are linear (4) and can be easily integrated, which leads to an expression that does not explicitly depend on the choice of the nonlinear electrodynamics model:

$$\begin{aligned} e^{\beta -\gamma }\rho B_\rho =B_0, \end{aligned}$$
(26)

where \(B_0\), as previously, is an integration constant. To ensure additional symmetry of the right and left sides of the Einstein’s equations, which follows from  (9) for the radial field configuration, it is necessary to accept the following relations between metric functions:

$$\begin{aligned} \alpha =\text{ ln }(c_3\beta '),\qquad \gamma =\text{ ln }(c_4\rho )-\beta , \end{aligned}$$
(27)

where the prime denotes the derivative with the respect to the coordinate \(\rho \) and the constants \(c_3\) and \(c_4\) can be used for normalization. For such relations between metric functions, the Einstein equations (2), with the account to the expressions (8) and (9), can be reduced to one non-trivial independent equation:

$$\begin{aligned} 2\beta ''+\beta '^2=-8\pi e^{2\beta }Y. \end{aligned}$$
(28)

It is useful to normalize the values in the Eqs. (26) and (28), similarly the way it was done for the longitudinal magnetic field in the previous section, as a result of which these equations take the form:

$$\begin{aligned} 2\beta ''+\beta '^2=-8e^{2\beta }V, \qquad e^{2\beta }b=1, \end{aligned}$$
(29)

where \(b=B_\rho /B\), the derivatives are taken with respect to the coordinate \(r=\rho /R\) with \(R=2/B_0\), and the coefficients V for various models of vacuum nonlinear electrodynamics are listed in the Table 1.

The solution of the Eq. (29) in the case of Maxwell’s electrodynamics has the form:

$$\begin{aligned} \beta =\text{ ln }\left[ \frac{c_5^2(r+c_6)^2-16}{4c_5}\right] , \qquad b=\frac{16c_5^2}{[c_5^2(r+c_6)^2-16]^2},\nonumber \\ \end{aligned}$$
(30)

where \(c_5\) and \(c_6\) are integration constants, which, in contrast to the longitudinal case (25), can be chosen so that the magnetic field induction will be singular and will tends to infinity for the two values of the radial coordinate \(r_h=-c_6\pm 4/|c_5|\ge 0\).

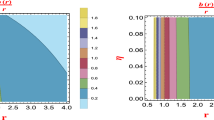
It would be interesting to use such a Maxwellian solution with two singularities as an asymptotic boundary condition at \(r\rightarrow \infty \) for the Eq. (29) in the case when nonlinear models of electrodynamics are considered, and to find out whether it is possible to suppress singularities due to the regularizing properties of these models. The result of numerical integration of the equations (29) for Born–Infeld electrodynamics at \(k=1\), shown in the Fig. 3, indicates that the singularities in the solution are preserved (one should pay attention to the logarithmic scale on the graph).

Fig. 3
figure 3

Normalized magnetic field induction as a function of r. The expressions (30) with the constants \(c_5=4\) and \(c_6=-2.5\) were used as a boundary condition

Full size image

For other models of nonlinear electrodynamics listed in the Table 1, the solution differs from that presented only quantitatively.

4.3 Azimuthal field

Let us consider the last possible configuration corresponding to the azimuthal magnetic field \(B_\rho =B_z=0\), \(B_\varphi \ne 0\), \(\textbf{E}=0\). As previously, we introduce the restrictions on metric functions which allow us to comply the symmetry of the right and left sides of the Einstein equations, which follows from (11)

$$\begin{aligned} \beta =\frac{1}{2}\left( \alpha +\text{ ln }(c_7\alpha ')\right) , \qquad \gamma =\text{ ln }(c_8\rho )-\alpha , \end{aligned}$$
(31)

where \(c_7\) and \(c_8\) are constants and prime denotes the derivative with respect to \(\rho \). The nontrivial equation for the metric function, following from Einstein equations, taking into account of (11) and (31), takes the form

$$\begin{aligned} \alpha ''+2\alpha '^2=8\pi (\alpha ' c_7)e^\alpha (B_\varphi ^2 X-Y), \end{aligned}$$
(32)

while the electromagnetic field equations (4) for the azimuthal case lead to the expression:

$$\begin{aligned} e^{2\alpha }XB_{\varphi }=B_0, \end{aligned}$$
(33)

where \(B_0\) is a constant. As before, it is convenient to normalize the values by taking: \(r=\rho /R\), where \(R=c_7=2/B_0\), and the definitions for b, U, V are the same as for the radial and longitudinal configurations. It is also quite convenient to introduce a new variable for the metric function \(A=e^{\alpha }\), in terms of which the Eqs. (32) and (33) take the form:

$$\begin{aligned} AA''+A'^2=8A^2A'(Ub^2-V), \qquad A^2Ub=1, \end{aligned}$$
(34)

where the prime denotes the derivative with respect to the normalized coordinate r and the coefficients U and V for vacuum nonlinear electrodynamics models are listed in the Table 1.

Obviously, in the general case, one of the trivial solutions of these equations is \(A\equiv const\), which corresponds to a uniform magnetic field. In the case of Maxwell electrodynamics \(U=1\) and \(V=b^2/2\) the first integral of the Eq. (34) is \(A'A+4/A=c_9\), where \(c_9\) is an arbitrary constant. The subsequent solution for A(r) can be obtained analytically, but it has an implicit form, which makes it difficult to analyse its properties. Therefore, we restrict ourselves to the case where \(c_9=0\) for which:

$$\begin{aligned} A=(c_{10}-12r)^{1/3}, \qquad b=\frac{1}{(c_{10}-12r)^{2/3}}, \end{aligned}$$
(35)

where \(c_{10}\) is the integration constant, and when it is positive, the magnetic field induction will be singular. It is interesting to find out whether this singularity can be suppressed in the case of nonlinear electrodynamics. To do this, we use (35) as an asymptotic boundary condition at \(r\rightarrow \infty \) and perform the integration of the Eq. (34) in the case of nonlinear electrodynamics. The result of numerical solution of these equations for Born–Infeld electrodynamics with different values of the parameter k is shown in Fig. 4. As follows from the simulation results, the singularity is not suppressed even with an increase in the parameter k associated with the nonlinearity.

Fig. 4
figure 4

Normalized magnetic field induction as a function of the radial coordinate r. The solution was obtained for Born–Infeld electrodynamics with the boundary condition (35) at \(r\rightarrow \infty \) and the constant \(c_{10}=12\)

Full size image

5 Conclusion

The article considered cylindrically symmetric solutions for self-gravitating electromagnetic systems in various models of nonlinear vacuum electrodynamics in the absence of field sources. For conformally invariant nonlinear electrodynamics, the case of a field configuration with longitudinally directed electric and magnetic fields was described. It was shown that in this case the solution describing the field configuration, up to the rescaling of the radial coordinate, coincides with the Melvin solution for an arbitrary choice of the CNED model.

For non-linear electrodynamics models with regularizing properties, such as Born–Infeld electrodynamics, pure magnetic field configurations depending only on the radial coordinate have been investigated. For an arbitrary Lorentz-invariant model of nonlinear electrodynamics of vacuum, there was obtained equations for the metric functions of cylindrically symmetric space-time and magnetic field induction, in the case of longitudinal, radial, and azimuthal magnetic fields.

For a longitudinal magnetic field, a significant enhancement of the soliton-like properties of the solution in the models of nonlinear electrodynamics was found, which is more consistent with the concept of the geon as a particle-like solution. For the cases of radial and azimuthal magnetic fields, the possibility of regularization of discontinuities in solutions arising in Maxwell’s electrodynamics was considered. It was found that the considered models of nonlinear electrodynamics, despite on the fact that they are based on the condition of regularization of the field of a point charge in the flat space-time, do not lead to the elimination of the magnetic field singularities in the described self-gravitating solutions. This property cannot be attributed to the shortcomings of such models, since in some cases the singularity of solutions can be eliminated by an additional modification of the gravitational sector [25]. The study of the possibility of such a regularization is of considerable interest and will be carried out in the future.