1 Introduction

The term “complexity” is associated with how complex a system is. Often we talk about something being complex but seldom do we think of quantifying it. Moreover, the notion of complexity is very much dependent on the specific matter of study. Scientists have been trying to quantify “complexity” for several years now. So far, several attempts have been made to figure out how to define complexity in various branches of science [1,2,3,4,5,6,7,8,9,10,11,12]. Despite the many efforts, we still lack a pinpointed approach to quantifying complexity. This is more so because the notion of complexity depends on the specificity of the system under investigation. So far, most of the definitions of complexity have been linked to information and disequilibrium or entropy. However, Lopez-Ruiz and colleagues [8,9,10] took a new approach to define complexity, which has been extended to self-gravitating systems [13,14,15,16,17,18]. Due to some drawbacks in using the definition given by Lopez-Ruiz and colleagues for self-gravitating systems, a new definition was proposed by Herrera [19, 20], for static, spherically symmetric systems. This was further extended to the spherically symmetric dynamic cases [21].

In the current paper, we will use the definition of complexity as developed by Herrera [19, 20]. It must be mentioned that this new definition [19, 20] doesn’t involve information and disequilibrium. Rather, it focuses on the “structure” inside the fluid distribution. To define complexity, one must remember the least complex system is the simplest system. So, in this definition, the least complex system is taken as a homogeneous fluid having isotropic pressure. This specific case is taken as the case with vanishing complexity. In this theory, the complexity factor emerges in the splitting of the Riemann tensor. The simplest system, i.e. the locally isotropic fluid with equal principal stresses and homogeneous energy density is assigned a zero value of the complexity factor. The active gravitational mass or Tolman mass [22] is closely associated with the complexity factor in this theory. The Tolman mass is a combination of its value for a zero complexity system along with two other terms, which are associated with the pressure anisotropy and inhomogeneity in energy density respectively. These latter two terms can be represented by a single scalar function, collectively referred to as the “complexity factor”. The complexity factor may vanish in two specific scenarios. In the most trivial one, for isotropic, homogeneous fluid distributions, both these terms become zero and the complexity factor vanishes. In another scenario, the pressure anisotropy and energy inhomogeneity cancel each other leading to the vanishing of the complexity factor. However, for time-dependent systems, we face two different problems. The first being that the concept of complexity has to be generalized in order to incorporate dissipative effects. Secondly, the complexity should be studied in terms of time evolution and one has to determine what qualifies as the simplest dynamical system. It was shown in [21] that for dynamical cases, the complexity factor can be expressed as the same scalar function as the static case while taking into account dissipative variables. It was shown that the simplest mode can be represented by homologous conditions. Later on, it was shown that by considering the quasi-homologous condition, the last condition can be relaxed to increase the number of possible solutions [23]. In a recent study, the contributions from pressure anisotropy, density inhomogeneities and dissipation in the form of radial heat flux to the evolution of complexity in a radiating star have been investigated [24]. Alongside spherically symmetric cases, axially symmetric [25], cylindrically symmetric [26, 27] fluid distributions have also been studied. The definition of complexity in GR [19, 20] has been subsequently extended in several modified gravity theories as well [28,29,30,31,32,33,34,35,36,37,38,39,40]. In this work, we generate a new interior solution for compact stars by demanding the vanishing of the complexity factor at each interior point of the stellar configuration. Before embarking on a quest to solve the field equations, we will shed some light on compact stars and their importance in GR and modified theories.

Compact stars have been very interesting objects to study for researchers as they are the ideal testing conditions for extremely dense nuclear matter. It has been fascinating, what goes inside these objects, and how are the matter distribution and thermodynamical properties. To understand these objects, several researchers have tried to find exact interior solutions, by solving Einstein’s field equations. However, solving these equations is a very tedious task and the physical viability is not guaranteed. In the case of perfect fluid distributions, only a subset of a wide plethora of exact solutions is physically realizable. Due to extremely packed nuclear matter, compact stars in fact are very unlikely to have isotropic matter distribution. Due to strong gravity and extreme internal density, the pressure splits into radial and tangential components with different amplitudes. In this context, it was shown by Ruderman [41] that when densities exceed \(10^{15}\) g/cm\(^3\), the pressure components no longer have the same magnitude and the matter distribution becomes anisotropic in nature. In this connection, Herrera [42] investigated that even if the system is initially considered as an isotropic matter distribution, the stellar model always tends to produce pressure anisotropy due to the internal physical processes within the system. In this regard, Herrera and his collaborators have done several pioneering works for analyzing the role of pressure anisotropy and the processes leading to the generation of anisotropies within fluid spheres [43,44,45,46,47,48,49].

Several novel techniques have been employed to solve the field equations which describe compact stars. Some of these models include considering anisotropy, charge, or a combination of both within the framework of both general relativity and modified theories of gravity. Researchers have incorporated several techniques to solve the field equations in different scenarios. In the present work, we will use two methodologies: the embedding Class I condition and gravitational decoupling to solve the problem. The embedding Class I condition basically deals with embedding a 4-dimensional pseudo-Riemannian spacetime into a 4-dimensional pseudo-Euclidean space. It was first derived by Karmarkar [50] and is known as the Karmarkar condition or the embedding class-I condition. In terms of the curvature components, it takes the form of: \({R_{1212}R_{3030}+R_{1220}R_{1330}}={R_{1010}R_{2323}}\). It was then argued by Pandey and Sharma [51] that this is inadequate for being a class-I condition. There should be another condition alongside, which is \(R_{2323} \ne 0\), that must be fulfilled for it to be a class-I condition. The great utility of the class-I condition is that it gives a relation between the two metric potentials. So if one metric potential is known, the other one can be easily determined by this condition. In recent times, another specific way to solve field equations to obtain interior solutions of compact stars has been very popular amongst scientists. This is named the gravitational decoupling method which was first developed by Ovalle [52, 53] and a systematic and direct approach known as a minimal geometric deformation (MGD) to generate anisotropic solutions for self-gravitating systems from perfect fluid solutions [54]. Later on, the MGD technique has been generalized and its extension is referred to as the complete geometric deformation (CGD) approach [55]. Using the above methodologies, several works have been investigated using the self-gravitating systems in 4D [56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75] as well as in 5D EGB-gravity [76,77,78]. Due to the wide use of the gravitational decoupling approach, it has been used as a powerful tool to investigate exact solutions in the context of the complexity factor and energy exchange in fluid distributions [79,80,81,82,83,84,85,86].

In our current article, we use the CGD technique to solve the system which leads to two sets of equations. The first one is without the generic source, which is the general Einstein’s system and the second one is the quasi-Einstein system coming from the generic source, containing the deformation functions \(f(r)\ne 0\) and \(h(r) \ne 0\). One of the main motivations for this article is to use the vanishing complexity factor condition as well as the (an)isotropization technique to find the deformation function(s). Furthermore, the seed system is solved by using the Class I condition together with a well-defined Kuchowicz metric. The structure of the article is as follows: Sect. 2 represents the field equations under the generic source. The definition of complexity factor and associated scalars are given in Sect. 3. The solution corresponding to the vanishing complexity factor is presented in Sect. 3.1 while the isotropic solution is in Sect. 3.2. The detailed physical analysis for both solutions is given in Sect. 4. The Sect. 5 contains the final concluding remarks for both solutions.

2 Einstein field equations in the framework of gravitationally decoupled system

We take a spherically symmetric static fluid distribution that is locally anisotropic and bounded by a spherical surface \(\Sigma \). The corresponding spacetime is given by the following line element in the Schwarzschild-like coordinate as,

$$\begin{aligned} ds^2 = e^{\nu (r)}dt^{2} - e^{\lambda (r)}dr^{2}-r^{2}(\sin ^{2}\theta d \phi ^{2}+d\theta ^{2}), \end{aligned}$$
(1)

where, \(\nu (r)\) and \(\lambda (r)\) are the metric functions. The gravitationally decoupled Einstein field equations satisfying the metric (1) can be given by,

$$\begin{aligned} G^i_j={\mathcal {R}}^i_j-\frac{1}{2}\,\delta ^i_j\,{\mathcal {R}}= T^i_j, \end{aligned}$$
(2)

where,

$$\begin{aligned} T^i_j= {\hat{T}}^i_j+\beta \Theta ^i_j, \end{aligned}$$
(3)

where \(\Theta ^i_j\) denotes an unknown source introduced by gravitational decoupling constant \(\beta \). To describe the internal structure of the self-gravitating system corresponding to the source \(T^i_j\), we consider the physical content of the spacetime to be filled by anisotropic matter distribution with energy density \(\epsilon \), radial pressure \(P_r\) and tangential pressure \(P_\perp \). Moreover, the energy-momentum tensor \(T^i_j\) is written as,

$$\begin{aligned} T^i_j=\epsilon \,u^i\,u_j-{\mathcal {P}}\,K^i_j+\Pi ^i_j, \end{aligned}$$
(4)

where

$$\begin{aligned}{} & {} {\mathcal {P}}=\frac{P_r+2P_\perp }{3};~~~~\Pi ^i_j=\Pi \left( \xi ^i \xi _j+\frac{1}{3} K^i_j\right) ;\nonumber \\{} & {} \quad \Pi =P_r-P_\perp ; ~~~K^i_j=\delta ^i_j-u^i u_j, \end{aligned}$$
(5)

and \(u^i\) (four-velocity vector) and \(\xi ^i\) (unit space like vector) are given by \(\{i=0,1,2,3\}\),

$$\begin{aligned} u^i=(e^{-\nu /2},~0,~0,~0)~~\text {and}~~\xi ^i=(0,~e^{-\lambda /2},~0,~0), \end{aligned}$$
(6)

such that \(\xi ^i u_i=0\) and \(\xi ^i\xi _i=-1\). Then the components of the energy-momentum tensor for the spherically symmetric line element (1) are,

$$\begin{aligned} T^0_0=\epsilon ,~~~T^1_1=-P_r,~~~~T^2_2=T^3_3=-P_\perp , \end{aligned}$$
(7)

and then Einstein field equations (2) read as,

$$\begin{aligned} \epsilon= & {} \frac{1}{8\pi }\bigg [\frac{1}{r^2}-e^{-\lambda }\left( \frac{1}{r^2}-\frac{\lambda ^{\prime }}{r}\right) \bigg ], \end{aligned}$$
(8)
$$\begin{aligned} {P}_{r}= & {} \frac{1}{8\pi }\bigg [-\frac{1}{r^2}+e^{-\lambda }\left( \frac{1}{r^2}+\frac{\nu ^{\prime }}{r}\right) \bigg ], \end{aligned}$$
(9)
$$\begin{aligned} {P}_{\perp }= & {} \frac{1}{8\pi }\bigg [\frac{e^{-\lambda }}{4}\left( 2\nu ^{\prime \prime } +\nu ^{\prime 2}-\lambda ^{\prime }\nu ^{\prime }+2\frac{\nu ^{\prime }-\lambda ^{\prime }}{r}\right) \bigg ],~~~ \end{aligned}$$
(10)

where primes denote the derivatives with respect to r. From the Eqs. (8)–(10), we easily find the hydrostatic equilibrium equation reads

$$\begin{aligned} \frac{dP_r}{dr}=- \frac{\nu ^\prime }{2} \big ( \epsilon + P_r \big ) + \frac{2 (P_\perp -P_r)}{r}, ~~ \end{aligned}$$
(11)

The above equation is called the generalized Tolman–Oppenheimer–Volkoff equation for anisotropic matter distribution. Furthermore, the mass function m(r) is given by,

$$\begin{aligned} R^3_{232}=1-e^{-\lambda }=\frac{2m}{r}, \end{aligned}$$
(12)

which is equivalent as,

$$\begin{aligned} m(r)=4\pi \int ^r_0 x^2 \epsilon (x) dx, \end{aligned}$$
(13)

Furthermore, we find \(\nu ^\prime \) using Eqs. (6) and (9),

$$\begin{aligned} \nu ^\prime =\frac{2m+8\pi \,r^3 P_r}{(r-2m)}, \end{aligned}$$
(14)

Then TOV equation (11) can be recast as,

$$\begin{aligned} \frac{dP_r}{dr}=- \frac{m+4\pi \,r^3 P_r}{ (r-2m)} \big ( \epsilon + P_r \big ) + \frac{2 (P_\perp -P_r)}{r}, ~~ \end{aligned}$$
(15)

On the other hand, the interior metric should be joined smoothly with the exterior metric on the boundary surface \(r=R\) which means that we require the continuity of the first and the second fundamental forms across the boundary surface. The vacuum Schwarzschild solution describes the exterior spacetime, which is:

$$\begin{aligned} ds^2 {=} \left( 1 {-} \frac{2M}{r}\right) dt^2- \frac{dr^2}{\left( 1 - \frac{2M}{r}\right) } - r^2 (d\theta ^2 + \sin ^2\theta d\phi ^2).\nonumber \\ \end{aligned}$$
(16)

The following junction conditions arise from using the first and second fundamental forms,

$$\begin{aligned} 1-\frac{2M}{R}= & {} e^{\nu (R)},~~~ \end{aligned}$$
(17)
$$\begin{aligned} 1-\frac{2M}{R}= & {} e^{-\lambda (R)},~~~ \end{aligned}$$
(18)
$$\begin{aligned} P_r(R)= & {} 0,~~~ \end{aligned}$$
(19)

The above conditions (17)–(19) are necessary and sufficient for the matching of two spacetime metrics at the boundary surface \(r=R\). Before employing the gravitational decoupling technique, we assume that the matter distributing inside the spacetime for \({\hat{T}}^i_j\) is also anisotropic with energy density \(\rho \), radial pressure \(p_r\) and tangential pressure \(p_t\) depending on spacetime geometry \(\mu \) and \(\eta \). Then,

$$\begin{aligned} {\hat{T}}^i_j=\rho \,\chi ^i\,\chi _j-{\mathcal {P}}_s\,h^i_j+{\hat{\Pi }}^i_j~, \end{aligned}$$
(20)

where

$$\begin{aligned} {\mathcal {P}}_s= & {} \frac{p_r+2p_\perp }{3};~~~~{\hat{\Pi }}^i_j=\Pi _s \left( \zeta ^i \zeta _j+\frac{1}{3} h^i_j\right) ;\nonumber \\ \Pi _s= & {} p_r-p_t; ~~~h^i_j=\delta ^i_j-\chi ^i \chi _j. \end{aligned}$$
(21)

and \(\chi ^i\) (four-velocity vector) and \(\zeta ^i\) are given by,

$$\begin{aligned} \chi ^i=(e^{-\eta /2},~0,~0,~0)\quad \text {and}\quad \zeta ^i=(0,~\sqrt{\mu },~0,~0), \end{aligned}$$
(22)

such that \(\xi ^i \zeta _i=0\) and \(\zeta ^i\zeta _i=-1\). Then,

$$\begin{aligned} \epsilon = \rho +\beta \Theta ^0_0,~~P_r=p_r-\beta \Theta ^1_1,~~P_\perp = p_t-\beta \Theta ^2_2. \end{aligned}$$
(23)

In order to see the general effect of the extra source \(\Theta ^i_j\) on the seed source \(T_{ij}\), we apply the gravitational decoupling using a complete geometric deformation (CGD) methodology. To apply this, we transform the metric functions \(e^{\lambda }\) and \(e^{\nu }\) [55] as,

$$\begin{aligned} \nu (r)= & {} \eta (r) + \beta ~ h ( r ), \end{aligned}$$
(24)
$$\begin{aligned} e^{-\lambda (r)}= & {} \mu (r) + \beta ~ f (r ). \end{aligned}$$
(25)

where, f(r) and h(r) are the geometric deformation functions along radial and temporal metric components, respectively. Due to the CGD, both deformation functions must be non-zero i.e. \(f(r)\ne 0\) and \(h(r)\ne 0\). Then under these transformations, we get the two sets of equations as:

$$\begin{aligned} 8\pi {\rho }= & {} \frac{1-\mu }{r^2} - \frac{\mu ^ \prime }{r} , \end{aligned}$$
(26)
$$\begin{aligned} 8\pi p_r= & {} \frac{\mu -1 }{r^2} - \frac{\mu \,\eta ^\prime }{r}, \end{aligned}$$
(27)
$$\begin{aligned} 8\pi p_t= & {} \mu \bigg ( \frac{\eta ^{\prime \prime }}{2} + \frac{\eta ^{ \prime 2}}{4} + \frac{\eta ^\prime }{2r} \bigg ) + \bigg ( \frac{\eta ^\prime \mu ^\prime }{4} + \frac{\mu ^\prime }{2r}\bigg ),~~~ \end{aligned}$$
(28)

and

$$\begin{aligned} 8\pi \rho ^{\Theta }= & {} - \beta ~~\bigg (\frac{f^\prime }{r} + \frac{f}{r^2}\bigg ), \end{aligned}$$
(29)
$$\begin{aligned} 8\pi p_r^{\Theta }= & {} \beta \bigg [ f ~~\bigg ( \frac{\nu ^\prime }{r} + \frac{1}{r^2} \bigg ) + \frac{\mu \,h^\prime }{r} \bigg ], \end{aligned}$$
(30)
$$\begin{aligned} 8\pi p_t^{\Theta }= & {} \beta \bigg [\frac{ f }{2} ~~\bigg ( \nu ^{\prime \prime } + \frac{\nu ^{\prime 2}}{2} + \frac{\nu ^\prime }{r} \bigg ) + \frac{\beta f^\prime }{2} ~~ \bigg (\frac{\nu ^\prime }{2} + \frac{1}{r}\bigg ) \nonumber \\{} & {} + \frac{\mu }{4}\big (2 h^{\prime \prime } + \beta h^{\prime 2} + \frac{2~h^\prime }{r} + 2 \eta ^\prime h^\prime \big ) + \frac{\mu ^\prime ~h^\prime }{4}\bigg ].~~~~~~ \end{aligned}$$
(31)

where \(\rho ^{\Theta }=\beta \,\Theta ^0_0\), \(p^{\Theta }_r=-\beta \,\Theta ^1_1\), and \(p^{\Theta }_t=-\beta \,\Theta ^2_2\), and the corresponding hydrostatic equilibrium equations read as,

$$\begin{aligned} \frac{dp_r}{dr}=- \frac{m_s+4\pi \,r^3 p_r}{ (r-2m_s)} \big ( \rho + p_r \big ) - \frac{2 \Pi _s}{r}, ~~ \end{aligned}$$
(32)

and

$$\begin{aligned} \frac{dp^{\Theta }_r}{dr}= & {} -\frac{m+4\pi \,r^3 P_r}{ (r-2m)}\big (\rho ^{\Theta }+p^{\Theta }_r\big ) \nonumber \\{} & {} \quad -\frac{\beta h^\prime }{2} \big (p_r + \rho \big )-\frac{2\Pi _{\Theta }}{r}. ~~~~ \end{aligned}$$
(33)

where \(\Pi _{\Theta }=(p^{\Theta }_r-p^{\Theta }_t)\) and mass function \(m_s\) for seed system is defined by,

$$\begin{aligned} m_s(r)=\frac{r}{2} (1-\mu )=4\pi \int ^r_0 x^2\,\rho (x) dx, \end{aligned}$$
(34)

Then

$$\begin{aligned} m=m_s-\frac{\beta \,r}{2}\,f(r). \end{aligned}$$
(35)

Furthermore, it is worth mentioning that both sources \({\hat{T}}_{ij}\) and \(\Theta _{ij}\) can be successfully de-coupled as long as there is an exchange of energy between them, and the corresponding energy exchange \(\Delta E\) between these sources can be given as [55],

$$\begin{aligned} \Delta E=\frac{\beta h^\prime }{2} \big (p_r + \rho \big ), \end{aligned}$$
(36)

According to the definition proposed by Herrera [19, 20], the gravitationally decoupled mass function m(r) can be written in terms of the homogeneous energy density and change induced by density inhomogeneity as,

$$\begin{aligned} m(r)=\frac{4\pi }{3} \epsilon -\frac{4\pi }{3}\,\int ^r_0 {\hat{r}}^3\, \epsilon ^{\prime } d{\hat{r}}, \end{aligned}$$
(37)

Using Eq. (23), we can write

$$\begin{aligned} m(r)=m_s(r)+\beta \,m_{_\Theta } (r), \end{aligned}$$
(38)

where,

$$\begin{aligned} m_s(r)= & {} \frac{4\pi }{3} \rho \,r^3 -\frac{4\pi }{3}\,\int ^r_0 {\hat{r}}^3\, \rho ^{\prime } d{\hat{r}}, \end{aligned}$$
(39)
$$\begin{aligned} m_{_\Theta } (r)= & {} \frac{4\pi }{3} \Theta ^0_0\, r^3- \frac{4\pi }{3}\,\int ^r_0 {\hat{r}}^3\, \left[ \Theta ^0_0\right] ^{\prime } d{\hat{r}}. \end{aligned}$$
(40)

and the solution of the seed system (26)–(28) can be given by the following line element,

$$\begin{aligned} ds^2 = e^{\eta (r)}dt^{2} - \mu ^{-1} (r)\,dr^{2}-r^{2}(\sin ^{2}\theta d \phi ^{2}+d\theta ^{2}), \end{aligned}$$
(41)

Furthermore, Tolman proposed the definition of the mass function for a spherically symmetric static spacetime that describes the energy content of a fluid sphere as,

$$\begin{aligned} m_T=4\pi \,\int ^{r_{_\Sigma }}_0 {\hat{r}}^2\,e^{(\nu +\lambda )/2}\,(T^0_0-T^1_1-2T^2_2)\, d{\hat{r}}, \end{aligned}$$
(42)

which can be written as (see for more details [19, 20])

$$\begin{aligned} m_T= & {} (m_T)_{_\Sigma } \left( \frac{r}{r_{_\Sigma }}\right) ^3-r^3\int ^{r_{_\Sigma }}_r \frac{e^{(\nu +\lambda )/2}}{{\hat{r}}} \nonumber \\{} & {} \times \left[ 8\pi (P_\perp -P_r)+\frac{4\pi }{r^3}\,\int ^r_0 {\hat{r}}^3\, \epsilon ^{\prime } d{\hat{r}}\right] d{\hat{r}}, \end{aligned}$$
(43)

3 Complexity factor and associated scalars in the framework of gravitational decoupling

Herrera recently proposed a definition of complexity in stellar systems which arises from the orthogonal splitting of the Riemann tensor in terms of scalar structures. These scalars usually connect the local anisotropy of the radial and transverse stresses with the density inhomogeneity to the Tolman mass corresponding to a static, bounded stellar structure. These scalars are given,

$$\begin{aligned} X_T= & {} 8\pi \,\epsilon = X^s_T + \beta \,X^{\Theta }_T , \end{aligned}$$
(44)
$$\begin{aligned} X_{TF}= & {} \frac{4\pi }{r^3}\,\int ^r_0 {\hat{r}}^3\, \epsilon ^{\prime } d{\hat{r}} = X^s_{TF}+\beta \,X^{\Theta }_{TF} , \end{aligned}$$
(45)
$$\begin{aligned} Y_T= & {} 4\pi (\epsilon +3P_r-2\Pi )=Y^s_T + \beta \,Y^{\Theta }_T, \end{aligned}$$
(46)
$$\begin{aligned} Y_{TF}= & {} 8\pi \Pi - \frac{4\pi }{r^3}\,\int ^r_0 {\hat{r}}^3\, \epsilon ^{\prime } d{\hat{r}} =Y^s_{TF}+\beta \, Y^{\Theta }_{TF}, \end{aligned}$$
(47)

where,

$$\begin{aligned} X^s_T= & {} 8\pi \rho ,~~~ X^{\Theta }_T=8\pi \Theta ^0_0,~ X^s_{TF}=\frac{4\pi }{r^3}\,\int ^r_0 {\hat{r}}^3\, \rho ^{\prime } d{\hat{r}},\\ X^{\Theta }_{TF}= & {} \frac{4\pi }{r^3}\,\int ^r_0 {\hat{r}}^3\, [\Theta ^0_0]^{\prime } d{\hat{r}},~~ Y^s_T = 4\pi (\rho +3p_r-2\Pi _s),\\ Y^{\Theta }_T= & {} 4\pi \big [\Theta ^0_0-3\Theta ^1_1-2\Pi _{\Theta }\big ], \\{} & {} Y^s_{TF}=8\pi \Pi _s- \frac{4\pi }{r^3}\,\int ^r_0 {\hat{r}}^3\, \rho ^{\prime } d{\hat{r}},\\ Y^{\Theta }_{TF}= & {} 8\pi \Pi _{\Theta } - \frac{4\pi }{r^3}\,\int ^r_0 {\hat{r}}^3\, [\Theta ^0_0]^{\prime } d{\hat{r}}. \end{aligned}$$

Here, the scalar \(Y_{TF}\) is referred to as the complexity factor of the spherically symmetric fluid distribution. The Tolman mass \((m_T)\) can be written in terms of complexity factors,

$$\begin{aligned} m_T= & {} (m_T)_{_\Sigma } \left( \frac{r}{r_{_\Sigma }}\right) ^3+r^3\int ^{r_{_\Sigma }}_r \frac{e^{(\nu +\lambda )/2}}{{\hat{r}}} Y^s_{TF}d{\hat{r}}\nonumber \\{} & {} +\beta \,r^3\int ^{r_{_\Sigma }}_r \frac{e^{(\nu +\lambda )/2}}{{\hat{r}}} Y^{\Theta }_{TF}d{\hat{r}},~~~~~ \end{aligned}$$
(48)

The system of equations (2627)–(28) and (29)–(31) contain 10 unknown parameters and here is the primary motive to solve them for self-gravitating compact objects. In order to get started in solving this system of governing equations, we will first invoke the Embedding Class I condition (Karmarkar condition). Following this, the condition of vanishing complexity factor i.e. \(Y_{TF}=0\) will be used to solve the second system and obtain the expression of the deformation function f(r) Prior to the detailed discussion of the solution, let us briefly shed light on the embedding Class I condition, or the Karmarkar condition, which can be expressed by the following equation containing the Riemannian components,

$$\begin{aligned} R_{1212}R_{3030}+R_{1220}R_{1330} ={R_{1010}R_{2323}}, \end{aligned}$$
(49)

Here, \(R_{2323} \ne 0\). Under the spacetime (41), the above Karmarkar condition (49) gives a differential equation of the form,

$$\begin{aligned}{} & {} (2\eta ''+\xi '\,\eta ^{\prime })\,(\mu \,-\mu ^2)+\mu ^{\prime }\,\eta ^{\prime }=0,~~ \text {where}\nonumber \\{} & {} \quad ~ \mu (r)\ne 1~ \text {for}~ r\ne 0. \end{aligned}$$
(50)

The following relation is derived from the solution of the Eq. (50),

$$\begin{aligned} \mu (r)=1/\big (1+F\,\eta ^{\prime 2} e^{\eta (r)}\big ), \end{aligned}$$
(51)

with F being an arbitrary constant of integration. Now we will use well-defined and known metric functions along with vanishing complexity factor condition to discuss the solution. In our model, we have considered the Kuchowicz metric for \(\eta (r)\) which is discussed in the next section:

3.1 Complete deformed Kuchowicz model in the framework of vanishing complexity factor

We have considered a well-defined Kuchowicz metric function for \(\eta (r)\) which is given by,

$$\begin{aligned} \eta (r)= & {} 2 Ar^2+\ln B, \end{aligned}$$
(52)

with A being a constant having \(length^{-2}\) dimension and B being dimensionless. It must be noted that several researchers have used this form of the metric function for obtaining solutions to Einstein’s field equations for self-gravitating compact stars [88,89,90,91]. The potential \(\mu (r)\) is obtained by plugging Eq. (52) into Eq. (51),

$$\begin{aligned} \mu (r)=\frac{1}{(1+D\,Ar^2\,e^{Ar^2})}, \end{aligned}$$
(53)

with \(D=4\,F\,A\). The physical parameters \(p_r(r)\), \(p_t(r)\), and \(\rho (r)\) are obtained by plugging Eqs. (52) and (53) into the system of equations of motion (26)–(28),

$$\begin{aligned} \rho (r)= & {} \frac{A D e^{A r^2} \left( A r^2 \left( D e^{A r^2}+2\right) +3\right) }{\left( A D r^2 e^{A r^2}+1\right) ^2}, \end{aligned}$$
(54)
$$\begin{aligned} p_r(r)= & {} -\frac{A \left( D e^{A r^2}-4\right) }{A D r^2 e^{A r^2}+1}, \end{aligned}$$
(55)
$$\begin{aligned} p_t(r)= & {} \frac{A \left( A r^2+1\right) \left( D e^{A r^2} \left( 2 A r^2-1\right) +4\right) }{\left( A D r^2 e^{A r^2}+1\right) ^2}.~~~~ \end{aligned}$$
(56)

Now let us focus on the second section where the \(\theta \)-sector depends on the deformation functions f(r) and h(r). Several methodologies can be applied to solve the second system, but our motivation is to use the concept of vanishing complexity factor condition (\(Y_{TF}=0\)) for \(T_{ij}\) system and non-vanishing complexity factor (\({Y}^{s}_{TF}\ne 0\)) for \({T}_{ij}\) system to obtain the solution. In this scenario, we have,

$$\begin{aligned} Y_{TF}= 8\pi \Pi - \frac{4\pi }{r^3}\,\int ^r_0 x^3\, [\epsilon ]^{\prime } dx =Y^s_{TF}+ Y^{\theta }_{TF} =0,~~~ \end{aligned}$$
(57)

where \(\beta =1\)Footnote 1[93]. Here the complexity factors for the seed system and \(\theta \) system are denoted by \(Y^s_{TF}\) and \(Y^{\theta }_{TF}\) respectively. Now, a differential equation in f(r) of the following form is obtained by using the Eqs. (26)–(31) with Eq. (57),

$$\begin{aligned}{} & {} h^{\prime 2} \mu r+2 r (h^{\prime \prime } \mu + (\eta ^{\prime \prime }+h^{\prime \prime }) f-2 Y^{s}_{TF})+(\eta ^{\prime }+h^{\prime }) \nonumber \\{} & {} \quad \times (f^{\prime } r-2 f)+2 h^{\prime } \mu (\eta ^{\prime } r-1)+(\eta ^{\prime }+h^{\prime })^2 f r=0,\nonumber \\ ~~~~ \end{aligned}$$
(58)

As it is seen from Eq. (47), the complexity factor \(Y^s_{TF}\) is dependant on the seed energy density (\(\rho \)) and seed pressure components (\(p_r\) and \(p_t\)). The the expression for \(Y^s_{TF}\) can be cast as,

$$\begin{aligned} Y^s_{TF}=-\frac{2 A^2 r^2 \left( D e^{A r^2} \left( A r^2-1\right) +2\right) }{\left( A D r^2 e^{A r^2}+1\right) ^2}, \end{aligned}$$
(59)

After plugging in \(Y^s_{TF}\) and the metric functions \(\xi (r)\), \(\mu (r)\) into the Eq. (58), we still need to determine the deformation functions f(r) and h(r). Therefore, we must need one more condition to solve this equation. Due to the non-linear nature of Eq. (58), we assume a specific form of temporal deformation function \(h(r)=2 Ar^2\) to solve this equation. Now we obtain f(r) as,

$$\begin{aligned} f(r)= C e^{-4 A r^2}-\frac{1}{A D r^2 e^{A r^2}+1},~~~~~ \end{aligned}$$
(60)

with C being an arbitrary constant of integration. For obtaining the constant F, the physically viable condition of the metric functions is used. According to this, the metric function \(e^{\lambda (r)}=\mu (r)+\beta \,f(r)\) must be unity (\(e^{-\lambda (0)}=1\)) at the center . This condition also requires the deformation function to be zero at the center, i.e. \(f(0)=0\), from which we can find \(C=1\). Then, the expressions for the modified radial components for \(\Theta \)-sector, i.e. \(\rho ^{\Theta }\), \(p_r^{\Theta }\), and \(p_t^{\Theta }\) become,

$$\begin{aligned} e^{\lambda (r)}= & {} \frac{A D r^2 e^{A r^2}+1}{1+\beta \left( A D r^2 e^{-3 A r^2}+e^{-4 A r^2}-1\right) }, \end{aligned}$$
(61)
$$\begin{aligned} e^{\nu (r)}= & {} B e^{2 A (\beta +1) r^2}, \end{aligned}$$
(62)
$$\begin{aligned} \rho ^{\Theta }= & {} \beta \left[ -\frac{2 A^2 D r^2 e^{A r^2}}{\left( A D r^2 e^{A r^2}+1\right) ^2}-\frac{2 A D e^{A r^2}}{\left( A D r^2 e^{A r^2}+1\right) ^2}\right. \nonumber \\{} & {} \left. +\frac{1}{A D r^4 e^{A r^2}+r^2}+8 A e^{-4 A r^2}-\frac{e^{-4 A r^2}}{r^2}\right] , \end{aligned}$$
(63)
$$\begin{aligned} p_r^{\Theta }= & {} \beta \left[ \left( 4 A (\beta +1)+\frac{1}{r^2}\right) \left( e^{-4 A r^2}-\frac{1}{A D r^2 e^{A r^2}+1}\right) \right. \nonumber \\{} & {} \left. +\frac{4 A}{A D r^2 e^{A r^2}+1}\right] , \end{aligned}$$
(64)
$$\begin{aligned} p_t^{\Theta }= & {} -\beta A\Bigg [\frac{2 A D r^2 e^{A r^2} \left( A r^2+1\right) }{\left( A D r^2 e^{A r^2}+1\right) ^2}-\frac{4 \left( A (\beta +2) r^2+1\right) }{A D r^2 e^{A r^2}+1} \nonumber \\{} & {} -\left( \frac{2 A (\beta +1) r+1}{r}\right) \left( \frac{D e^{5 A r^2} \left( A r^2+1\right) }{\left( A D r^2 e^{A r^2}+1\right) ^2}-4\right) \nonumber \\{} & {} \times e^{-4 A r^2} + p^{\Theta }_{t1} \Bigg ],~~ \end{aligned}$$
(65)

where, \( p_{t1}^{\Theta }\) is mentioned in the Appendix. Moreover, the new form of complexity factor \(Y_{TF}\) under the radial metric component (61) is,

$$\begin{aligned} Y_{TF}{=}\frac{2 A^2 \left( \beta ^2-1\right) r^2 e^{-4 A r^2} \left( 2 \beta Y_{TF1}{+}e^{4 A r^2} Y_{TF2}\right) }{\left( ADr^2 e^{A r^2}{+}1\right) ^2}.~~~~~\nonumber \\ \end{aligned}$$
(66)

where \(Y_{TF1}\) and \(Y_{TF2}\) are given in the Appendix. Using the above expression, we can observe the influence of the decoupling constant \(\beta \) on the complexity factor. However \(Y_{TF}\) vanishes at \(\beta =1\). Moreover, the expressions for other scalars are,

$$\begin{aligned} X_{TF}= & {} D \Bigg [\frac{A^2 D e^{2 A r^2} \left( A r^2+1\right) }{\left( ADr^2 e^{A r^2}+1\right) ^2}-\frac{A^2 e^{A r^2}}{ADr^2 e^{A r^2}+1}\Bigg ]\nonumber \\{} & {} \times r^2(\beta -1)+ \frac{\beta e^{-4 A r^2} \left( 4 A r^2+1\right) -\beta }{r^2}, \end{aligned}$$
(67)
$$\begin{aligned} Y_{T}= & {} \frac{1}{\left( ADr^2 e^{A r^2}+1\right) ^2}\Big [2 A (\beta +1) e^{-4 A r^2} Y_{T1}\Big ] , \end{aligned}$$
(68)
$$\begin{aligned} X_{T}= & {} \frac{ADr^2 e^{5 A r^2} \left( A r^2 \left( D e^{A r^2}+2\right) +3\right) +X_{T1}}{\left( ADr^3 e^{A r^2}+r\right) ^2\,e^{4 A r^2} }. \end{aligned}$$
(69)

where the coefficients in the above expressions are highlighted in the Appendix.

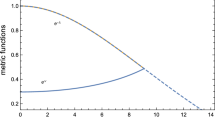
Using the boundary conditions (17)–(19), we find the constant D, \({\mathcal {M}}\), and B for solution (3.1) as

$$\begin{aligned} D= & {} \frac{\beta (e^{4 A R^2}-1)(1+4 A \beta R^2)-4\beta A R^2-4 A R^2 e^{4 A R^2}}{e^{A R^2}\,A R^2 \left( 4 A \beta ^2 R^2+4 A \beta R^2-e^{4 A R^2}+\beta \right) },\nonumber \\ \end{aligned}$$
(70)
$$\begin{aligned} {\mathcal {M}}= & {} \frac{R}{2} \Big [1-\frac{1}{(1+D\,Ar^2\,e^{Ar^2})} -\beta \,{\mathcal {M}}_1(R)\Big ], \end{aligned}$$
(71)
$$\begin{aligned} B= & {} -\frac{\left( -A \beta D R^2 e^{A R^2}+\beta e^{4 A R^2}-e^{4 A R^2}-\beta \right) }{(1+A D R^2 e^{A R^2})\,e^{2 A (\beta +1) R^2+4 A R^2}}, \end{aligned}$$
(72)

where, \({\mathcal {M}}_1(R)=e^{-4 A R^2}-\frac{1}{A D R^2 e^{A R^2}+1}\).

3.2 Isotropic solution for Kuchowicz model via gravitational decoupling

In this section, the novel approach of Casadio et al. [92] will be used to obtain the isotropic gravitationally decoupled solution for the effective energy-momentum tensor \(T_{ij}\) from the corresponding anisotropic system (8)–(10). As the effective system consists of two sub-systems for energy-momentum tensor \({\hat{T}}_{ij}\) and \(\theta _{ij}\). In this context, through source \(\theta _{ij}\), it is possible to transform an anisotropic system (26)–(28) for \({\hat{T}}_{ij}\) with \(\Pi _s \ne 0\) to an isotropic system (8)–(10) given by \(T_{ij}\) with \(\Pi =0\) [92]. It is evident that by setting the value of \(\beta \) to be \(\beta =0\) and \(\beta =1\), the anisotropic system (26)–(28) and isotropic system (8)–(10) can be obtained respectively, and the transformation can be controlled by this setting. In our case, to achieve the isotropization, \(\beta \) is fixed as \(\beta =1\), and for this, \(\Pi =0\) gives,

$$\begin{aligned} \Pi _s=-\,\Pi _{\theta }~~\Longrightarrow ~~ \Pi _s=-(p_r^{\theta }-p_t^{\theta }). \end{aligned}$$
(73)

Now we obtain the following non-linear differential equation by using Eqs. (26)–(31) into Eq. (36) as

$$\begin{aligned}{} & {} 4 + 2 \mu ^{\prime } r + \mu ^{\prime } \eta ^{\prime } r^2 + \beta ^2 h^{\prime 2} \mu r^2 + \mu ( \eta ^{\prime 2} r^2 \nonumber \\{} & {} \quad -4 - 2 \eta ^{\prime } r + 2 \eta ^{\prime \prime } r^2 ) \nonumber \\{} & {} \quad + \beta f (-4 - 2 \nu ^{\prime } r + 2 \nu ^{\prime \prime } r^2 +\nu ^{\prime 2} r^2) \nonumber \\{} & {} \quad + \beta r [2 h^{\prime \prime } \mu r + f^{\prime } (2 + \nu ^{\prime } r)\nonumber \\{} & {} \quad + h^{\prime } (-2 \mu + \mu ^{\prime } r + 2 \eta ^{\prime } \mu r)]=0, \end{aligned}$$
(74)

As we can see that the above equation depends on \(\xi (r)\), \(\mu (r)\), f(r), and h(r). Then using Class I solution from Eq. (51) together with \(h(r)=2Ar^2\) into Eq. (74), we find the deformation function f(r) of the form,

$$\begin{aligned} f(r)= & {} -A r^2 e^{-4 A r^2} \bigg (\frac{4 \textit{ExpIntegralEi}\left( 4 A r^2+1\right) }{e}\nonumber \\{} & {} -\frac{D e^{5 A r^2}}{A D r^2 e^{A r^2}+1}\bigg )+C r^2 e^{-4 A r^2}, \end{aligned}$$
(75)

where, C is a constant of integration. Then the effective energy density and effective pressures are,

$$\begin{aligned} \epsilon (r)= & {} \frac{\Psi _1(r)+A D e^{5 A r^2} \left[ A r^2 \left( D e^{A r^2}+2\right) +3\right] }{\left( 1+A D r^2 e^{A r^2}\right) ^2\,e^{4 A r^2}}, \end{aligned}$$
(76)
$$\begin{aligned} P_r(r)= & {} \frac{1}{1 + A D1 e^{A r^2}) r^2}\Big [b e^{-4 A r^2-1} \left[ 4 A (b+1) r^2+1\right] \nonumber \\{} & {} \times \Psi _{2}(r)+4 A b+A \left( 4-D e^{A r^2}\right) \Big ], \end{aligned}$$
(77)
$$\begin{aligned} P_\perp (r)= & {} \frac{A \left( A r^2+1\right) \left( D e^{A r^2} \left( 2 A r^2-1\right) +4\right) }{\left( A D r^2 e^{A r^2}+1\right) ^2}\nonumber \\{} & {} +\beta \,\Psi _{3}(r). \end{aligned}$$
(78)

Using the boundary conditions (43)–(45), we find the constant D, \({\mathcal {M}}\), and B for solution (3.1) as

$$\begin{aligned} D= & {} \frac{ 4 A b \left( 4 A (\beta +1) R^2+1\right) \text {Ei}\left( 4 A R^2+1\right) - D_1(R)}{A \,e^{A R^2} \left[ e\,D_2(R)-4 A \beta R^2 D_3(R)\right] },\nonumber \\ \end{aligned}$$
(79)
$$\begin{aligned} {\mathcal {M}}= & {} \frac{R}{2} \Big [1-\frac{1}{(1+D\,Ar^2\,e^{Ar^2})} -\beta \,{\mathcal {M}}_2(R)\Big ], \end{aligned}$$
(80)
$$\begin{aligned} B= & {} \frac{e^{-2 A (\beta +1) r^2} \left( \beta A D r^2 e^{A r^2} f(R)+\beta f(R)+1\right) }{(1+D Ar^2 e^{A r^2})}. \end{aligned}$$
(81)

where

$$\begin{aligned} {\mathcal {M}}_2(R)= & {} -A R^2 e^{-4 A R^2} \bigg (\frac{4 \textit{ExpIntegralEi}\left( 4 A R^2+1\right) }{e}\\{} & {} -\frac{D e^{5 A R^2}}{A D R^2 e^{A R^2}+1}\bigg )+C ^2 e^{-4 A R^2}. \end{aligned}$$
Fig. 1
figure 1

Top panels: Left figure shows the behavior of energy density (\(\epsilon (r)\times 10^4 [\text {km}^{-2}]\)) while right figure describe the behavior of radial pressure (\(P_r\times 10^4 [\text {km}^{-2}]\)) versus the radial coordinate r/R for different values of \(\beta \). Bottom panels: The behavior of tangential pressure \((P_\perp \times 10^4 [\text {km}^{-2}])\) and anisotropy \((\Delta \times 10^4 [\text {km}^{-2}])\) versus radial parameter r are shown in left and right panels, respectively. We use \(A = 0.0026~\text {km}^{-2}\) to plot above figures for solution 3.1

Full size image
Fig. 2
figure 2

Top panels: Left figure shows the behavior of energy density (\(\epsilon \times 10^4 [\text {km}^{-2}]\)) while right figure describe the behavior of radial pressure (\(P_r\times 10^4 [\text {km}^{-2}]\)) versus the radial coordinate r/R for different values of \(\beta \). Bottom panels: The behavior of tangential pressure \((P_{\perp }\times 10^4 [\text {km}^{-2}])\) and anisotropy \((\Delta \times 10^4 [\text {km}^{-2}])\) versus radial coordinate r/R are shown in left and right panels, respectively. We use \(A = 0.0021~\text {km}^{-2}\), \(C= 0.0002~\text {km}^{-2}\) to plot above figures for isotropic solution 3.2

Full size image
Fig. 3
figure 3

Left panel: The behavior of complexity factor (\(Y_{TF}\times 10^4 [\text {km}^{-2}]\)) versus radial parameter r for different \(\beta \), and Right panel: The behavior of density inhomogeneity (\(X_{TF}\times 10^4 [\text {km}^{-2}]\)) versus radial parameter r with different \(\beta \). The above figures are plotted for solution 3.1 with the same numerical values as used in Fig. 1

Full size image
Fig. 4
figure 4

Left panel: The behavior of complexity factor (\(Y_{TF}\times 10^4 [\text {km}^{-2}]\)) versus radial parameter r for different \(\beta \), and Right panel: The behavior of density inhomogeneity (\(X_{TF}\times 10^4 [\text {km}^{-2}]\)) versus radial coordinate r/R with different \(\beta \). The above figures are plotted for isotropic solution 3.2. We set the same numerical values as used in Fig. 2

Full size image

4 Physical analysis

4.1 Analyses of basic thermodynamical properties including energy density, pressure components, and anisotropic factor

4.1.1 For solution 3.1

From Fig. 1 it can be seen that the energy density \(\epsilon (r)\) is maximum at the center and it gradually decreases towards the surface. Moreover, as the value of \(\beta \) increases, the energy density increases with it as well. When we look into the radial and tangential pressure components, we observe that both of them are maximum at the center, while keep decreasing towards the surface. It is seen that both radial and tangential pressures increase with an increase in \(\beta \). Furthermore, the radial pressure \(P_r(r)\) for different \(\beta \) values converge at the surface and the tangential pressure \(P_{\perp }(r)\) do not. We note that the anisotropy factor, \(\Delta \) is zero at the center and increases monotonically as one moves towards the surface and is maximum at the surface. Furthermore, an increase in \(\beta \) results in a corresponding increase in \(\Delta \).

4.1.2 For solution 3.2

However, for the second solution, we see some interesting features in the plot of energy density \(\epsilon (r)\). From Fig. 2 it can be seen that although the basic nature of the variation is quite similar to the previous solution, here for \(\beta =0.8\) and \(\beta =1.0\), we see some anomalies in the behavior of the curves. Instead of monotonically decreasing, in these cases, the curves first increase in the range of \(r \simeq 4\) to \(r \simeq 6\) and then decrease. This shows, that as the \(\beta \) approaches 1, the model starts to get unstable, so it can be said that for higher complexity factors, the model has more stability. However, for the second solution as well, the behavior of the radial pressure \(P_r(r)\), tangential pressure \(P_{\perp }(r)\), and the anisotropic factor \(\Delta \) behave as they do in the previous solution. Furthermore, we can see that the magnitude of \(\Delta \) decreases as \(\beta \) increases, and anisotropy totally vanishes at \(\beta =1\), which leads to an isotropic model.

4.2 Complexity factor \(Y_{TF}\) and it’s behaviour

4.2.1 For solution 3.1

The behavior of the complexity factor \(Y_{TF}\) has been studied along with its variation with \(\beta \), and the ensuing trend is plotted in Fig. 3. It is seen that for \(\beta =0\), the complexity factor vanishes, which is the limiting condition of the vanishing complexity factor. Alongside this, it can be seen that the curves of \(Y_{TF}\) for other values of \(\beta \) follow a similar pattern. The complexity factor is zero at the center of the configuration and it gradually increases and reaches its maximum at some point, and then starts decreasing towards the surface. The zero complexity at the center is expected, as it was shown in the previous subsection that the anisotropic factor is also zero at the center. Moreover, it can be seen that the complexity factor increases with the increase in \(\beta \), only except for the \(\beta =0.2\) curve, which leads to the \(\beta =0.0\) curve until it attains its peak. Also, it can be seen that the position of the peaks in the \(Y_{TF}\) curves shift slightly towards the surface as we increase the value of \(\beta \).

4.2.2 For solution 3.2

For the second solution, from Fig. 4 left panel, it can be seen that the complexity factor \(Y_{TF}\) shows markedly different behavior when compared to the first solution. We note that the behavior \(Y_{TF}\) is highly sensitive to \(\beta \). For \(\beta =0.0\), \(\beta =0.2\), and \(\beta =0.4\), the curves start at zero, then increase steadily, and finally near the surface the rate of increase decays. While, for \(\beta =0.6\), the curve keeps on increasing at the same rate near the surface. For \(\beta =0.8\) and \(\beta =1.0\), we see that some part of the \(Y_{TF}\) curves attain negative values, i.e. they start at zero at the center, then go negative up to \(r \simeq 5\) for \(\beta =0.8\) curve and \(r \simeq 7\) for \(\beta =1.0\) curve, and then increase and keep increasing as one moves towards the surface. This negative value of the complexity factor for \(\beta =0.8\) and \(\beta =1.0\) shows, that for these two values of \(\beta =0.8\) and \(\beta \), the solution is quite unstable. This was indicated in the plot of energy density \(\epsilon (r)\) as well, as was discussed in the earlier subsection.

4.3 The density inhomogeneity

4.3.1 For solution 3.1

The behavior of the density inhomogeneity (\(X_{TF}\)) is studied and plotted in the right panel of Fig. 4. It can be seen that while \(X_{TF}\) stays negative throughout the model, it is zero at the center, and its magnitude increases as one moves toward the surface. The vanishing of \(X_{TF}\) at the center of the matter distribution indicates the homogeneity of the density in this region. Moreover, it is also seen that with the increase of the value of \(\beta \), \(X_{TF}\) decreases.

Fig. 5
figure 5

The behavior of scalars (\(Y_T\times 10^4 [\text {km}^{-2}]\))-left panel and (\(X_T\times 10^4 [\text {km}^{-2}]\))-right panel describe the strong energy condition and homogeneous energy density distribution versus r for solution 3.1. We set same numerical values as used in Fig. 1

Full size image
Fig. 6
figure 6

The behavior of scalars (\(Y_T\times 10^4 [\text {km}^{-2}]\))-left panel and (\(X_T\times 10^4 [\text {km}^{-2}]\))-right panel describe the strong energy condition and homogeneous energy density distribution versus r for isotropic solution 3.2. We set same numerical values as used in Fig. 2

Full size image

4.3.2 For isotropic solution 3.2

As we look into the second solution, we can see from the right panel of Fig. 4 that although the basic nature of the curves is the same as the previous solution, for \(\beta =0.8\) and \(\beta =1.0\), we observe anomalies. Here, the density inhomogeneity attains positive values after starting from zero at the center up to \(r \simeq 5\) for \(\beta =0.8\) curve and \(r \simeq 7\) for \(\beta =1.0\) curve, and then steadily decreases and becomes negative. This shows again, that as \(\beta \) approaches 1, the solutions become unstable.

4.4 The strong energy condition

4.4.1 For solution 3.1

In the Fig. 5 left panel, the strong energy condition in terms of the scalar \(Y_{T}\) has been studied. It is seen that \(Y_{T}\) is maximum at the center and decreases monotonically as one moves radially towards the stellar surface. Moreover, with the increase in \(\beta \), its value increases.

4.4.2 For solution 3.2

The variation in \(Y_{T}\) remains similar in the second solution as well, as compared to the first solution as can be seen from the Fig. 6 left panel. This indicates, that for both models, the strong energy condition is satisfied throughout the equilibrium configuration.

4.5 The homogeneous energy density distribution

4.5.1 For solution 3.1

The homogeneous energy density distribution in terms of the scalar \(X_{T}\) has been studied in the Fig. 5 right panel, and it is seen that the homogeneity in energy density is maximum at the center and it gradually decreases as we move radially outwards. Also, with the increase in \(\beta \), the energy homogeneity increases.

4.5.2 For isotropic solution 3.2

From the Fig. 6 right panel, the basic nature of the homogeneous energy density distribution remains the same for the second solution as well, but as seen in the analysis of \(\epsilon (r)\), \(Y_{TF}\), \(X_{TF}\), anomalies are found here as well for \(\beta =0.8\) and \(\beta =1.0\). For these values of \(\beta \), the curves initially increase up to \(r \simeq 5\) and then start decreasing. We expect a monotonically decreasing trend from the centre outwards. This again shows that this solution has some instability as \(\beta \) approaches 1.

4.6 The variation of mass (\(M/M_{\odot }\)) versus the complexity factor \(Y_{TF}\)

4.6.1 For solution 3.1

From Fig. 7 it can be seen that the mass increases as the complexity factor increases. And the relationship between them is linear. In addition, the increase in the value of \(\beta \) is accompanied by a corresponding increase in mass.

Fig. 7
figure 7

The variation of Mass (\(M/M_{\odot }\)) versus complexity factor \(Y_{TF}\) for solution 3.1

Full size image
Fig. 8
figure 8

The variation of Mass (\(M/M_{\odot }\)) versus complexity factor \(Y_{TF}\) for solution 3.2

Full size image

4.6.2 For solution 3.2

For the second solution, it is noticed from Fig. 8 that although the nature of variation of the mass with the complexity factor remains the same, here the variation with \(\beta \) is completely different. Unlike the previous solution, here the mass decreases with the increasing value of \(\beta \).

Fig. 9
figure 9

Left panel: Density plot of the exchange of energy for the solution 3.1 for \(A = 0.0026\). Right panel: Density plot of the exchange of energy for \(A = 0.0021\) and \(C=0.0002\) for the solution 3.2

Full size image

4.7 Energy exchange

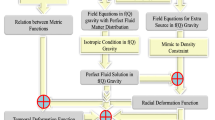
In this section, we will discuss an interesting physical feature of the solution which is the exchange of energy between the generic fluid \(\Theta _{ij}\) and the fluid matter distribution (\({\hat{T}}_{ij}\)) given by Eq. (36). The transfer of energy between fluid distributions can be interpreted according to the positive and negative values of \(\Delta E\) as: (i) if \(\Delta E>0\), then the generic fluid is giving the energy to the environment, (ii) if \(\Delta E<0\), then the perfect/anisotropic fluid is giving the energy. This transition of the energy exchange is shown on the \(\beta -r\) plan via Fig. 9. The left panel of Fig. 9 corresponding to the solution 3.1 shows that \(\Delta E>0\) for all values of \(\beta \le 0.95\) and \(r\in [0,12]\) but when \(\beta >0.951\), then \(\Delta E<0\) near the boundary which means that anisotropic fluid is giving the energy near the boundary in the context of vanishing complexity factor. If we look at the right panel of Fig. 9, the exchange of energy \(\Delta E\) is positive for all values of \(\beta \in (0,1]\) and it is maximum inside the stellar model at \(\beta =1\). This implies that the generic fluid \(\Theta _{ij}\) is giving the maximum energy between \(r\approx 6~ \text {to}~ 10 \) for decoupling constant \(\beta \approx 1\). A systematic approach for the Embedding Class I solution generated by isotropization technique and anisotropic solution in the context of null complexity factor is mentioned in the flow chart (Fig 10).

5 Concluding remarks

After a detailed physical analysis, it was found that for anisotropic solution 3.1, all the thermodynamical properties behave as expected. From Fig. 1, it can be clearly seen, that the energy density, radial, and tangential pressure components are maximum at the center and then decay radially outwards, while the anisotropic factor starts as zero at the center and then increases as one move towards the surface. This shows that the energy density, as well as the pressure, are maximum at the core. Furthermore, near the center, the matter distribution is largely isotropic, but as we move toward the surface, the energy density decreases, as well as the matter density becomes increasingly anisotropic. All of the parameters \(\epsilon \), \(P_r\), \(P_{\perp }\), \(\Delta \) increase with the increase of the value of \(\beta \). While for the isotropic solution 3.2, from Fig. 2 we see some changes compared to the solution 3.1. Firstly, here we see that for the \(\beta =0.8\) and \(\beta =1.0\), the energy density curves act differently. Here, they start with a lower value, then increase to a peak, and then steadily decrease, while they should have started with a maximum value at the center and then decrease steadily. Moreover, unlike the solution 3.1, here the anisotropic factor \(\Delta \) decreases with the increase in \(\beta \).

As we look into the complexity factor (\(Y_{TF}\)), for the solution 3.1, it starts at zero and then increases in the radially outward direction, and after attaining a peak, it decreases (Fig. 3). Also, it must be noted, that \(Y_{TF}\) decreases with the increase in \(\beta \). While for 3.2, all the \(Y_{TF}\) curves start with zero as well, but we see anomalies for \(\beta =0.8\) and \(\beta =1.0\) values, as in those cases, the complexity factor becomes negative for some part and then increases (Fig. 4).

The density inhomogeneity (\(X_{TF}\)) for solution 3.1 is found to be maximum at the center and then gradually decreases as one moves outwards (Fig. 3). It remains negative throughout the model. Moreover, it decreases with the increase in \(\beta \) and the curves tend to diverge at the surface. However, for solution 3.2, anomalies can be seen from \(\beta =0.8\) and \(\beta =1.0\), as the curves for these values of \(\beta \) attain positive values after starting from zero and then go negative and decrease afterward (Fig. 4). However, the other curves behave as expected. Moreover, unlike the previous solution, here the values of \(X_{TF}\) increase with the increase in \(\beta \), and the curves tend to converge at the surface.

Fig. 10
figure 10

The flow chart of the Embedding Class I solution generated by isotropization technique and anisotropic solution in the context of null complexity factor

Full size image

As we analyze the strong energy condition in terms of the scalar \(Y_T\), it can be found that for both the solutions, the nature is similar (Fig. 5 left panel and Fig. 6 left panel). The curves start with a maximum value at the center and then gradually decay in the outward direction. While, for both solutions, \(Y_T\) increases with the increase in the value of \(\beta \).

Shedding light into the homogeneous energy density based on the scalar quantity \(X_T\), it can be found (Fig. 5 right panel) that for the solution 3.1, the curves start at a maximum value at the center and the decrease as we move outward. It shows that the energy is most homogeneous near the center. Also, the value of \(X_T\) increases with the increase in \(\beta \). For the solution  3.2 however, we see that (Fig. 6 right panel) here \(\beta =0.8\) and \(\beta =1.0\) curves behave differently. The curves for these values of \(\beta \) increase initially, then after attaining maximum value, then start decreasing steadily afterward, while they are expected to start at a maximum value at the center. The nature of both the \(Y_T\) curves is similar to the energy density (\(\epsilon \)) curves.

Analyzing the variation of mass (\(M/M_{\odot }\)) with the complexity factor \(Y_{TF}\), it can be ascertained from (Fig. 7) and (Fig. 8) that for both the solutions, the mass varies almost linearly with \(Y_{TF}\). So, with the increase in the complexity factor, mass increases. However, for solution 3.1, the mass increases with the increase in \(\beta \), but, for solution 3.2, the mass decreases with the increase in \(\beta \).

It must be noted that for the isotropic solution 3.2, the anomalies found for the energy density (\(\epsilon \)), complexity factor (\(Y_{TF}\)), density inhomogeneity (\(X_{TF}\)) and the homogeneous energy density \(X_T\) for the higher \(\beta \) values (\(\beta =0.8\) and \(\beta =1.0\)). This indicates that the models become unstable as \(\beta \) approaches 1. We are led to conclude that the presence of anisotropy in self-gravitating systems renders the model stable. In the case of vanishing anisotropy, the model becomes unstable. The instability of the pressure isotropy condition has been demonstrated by Herrera [93] with regard to bounded stellar configurations in GR.