Dynamics and statefinder analysis of a class of sign-changeable interacting dark energy scenarios

Abstract

We revise the dynamical properties of a class of cosmological models where the dark sector interacts through an interacting term that changes sign during evolution. In particular, we obtain the critical points and investigate the existence and stability conditions for cosmological solutions, describing radiation, matter and dark energy dominated eras. We find that all the studied models admit a stable critical point corresponding to an accelerated phase. We use background data to find the best fit parameters for one of the studied models, resulting in an interacting parameter with a definite sign within the $1\sigma$ confidence level, consistent with the results of the dynamical system analysis. We compute the statefinder parameters and plot the $r-q$ and $r-s$ planes, where we observe different evolutionary trajectories for the interacting scenarios, allowing in this sense to discriminate among dark energy models.

1 Introduction

All the available data in cosmology seems to indicate that our current universe consists of $69\%$ of dark energy and $26\%$ of dark matter [1], but to the present understanding of physics, both components have unknown nature [2, 3]. Usually, we consider the standard cosmological scenario $\Lambda$CDM, where the dark components evolve independently. A different approach is to consider that both components interact [4,5,6,7,8,9,10,11,12,13,14,15,16,17]. Interacting scenarios allow to alleviate the coincidence problem [4] and also are useful in addressing the tension in the $H_0$ parameter [18,19,20,21,22]. Among interacting scenarios it is common to consider those models in which the interaction sign remains constant during evolution but there are some less explored scenarios where the interaction sign can change [23,24,25].

In cosmology, dynamical system methods are a very useful technique to investigate the asymptotic behavior of a given cosmological model, especially when analytical solutions are unknown. In Refs. [26] – [28] the authors review the dynamics of a plethora of dark energy models (including interacting models) applying dynamical system methods. In particular, in Ref. [29] the authors study the background and perturbative evolution of some interacting models using dynamical system methods, and they find that interaction can describe the matter and dark energy epochs correctly.

On the other hand, the authors of Ref. [30] introduce the cosmological pair r and s, dubbed statefinder parameters, depending on derivatives of the scale factor up to third order, where the evolution of these parameters allows to differentiate among dark energy models. For instance, in Ref. [31] the authors use the statefinder parameters to characterize interacting quintessence models of dark energy.

In Refs. [32, 33] the authors apply dynamical systems methods and perform a statefinder analysis of interacting dark energy models. Even though the dynamical system analysis shows similar asymptotic behavior for these models, the statefinder diagnosis allows to distinguish among models, when the evolution of the statefinder parameters is studied.

The goal of this work is to revise the dynamics of a class of sign-changeable scenarios which do not have analytical solutions, then it is interesting to characterize the asymptotic behavior of these models through dynamical system analysis and study its performance in fitting the known asymptotic behavior of our universe. The studied models are then compared through the evolution of the statefinder parameters to distinguish their behavior from $\Lambda$CDM.

This work is organized as follows. In Sect. 2 we describe interacting scenarios and the class of sign-changeable interactions to study. Section 3 is devoted to the dynamical system analysis of each of the models described in Sect. 2. In Sect. 4 we use background data to perform the observational contrast for one of the studied models. In Sect. 5 we compute the statefinder parameters and we study the features of the trajectories in the $r-q$ and $r-s$ planes. Finally, in Sect. 6 we present our final remarks on this work.

2 Sign-changeable interacting dark energy models

Let us consider a flat, homogeneous and isotropic universe in the framework of General Relativity and a cosmological scenario containing radiation (r), baryons (b), cold dark matter (c) and dark energy (x). In the context of an interacting dark energy scenario the conservation equation can be separated into the following equations:

$$\begin{aligned} \rho '_b+3\rho _b= & {} 0, \end{aligned}$$

(1)

$$\begin{aligned} \rho '_r+4\rho _r= & {} 0, \end{aligned}$$

(2)

$$\begin{aligned} \rho '_c+3\rho _c= & {} -3\varGamma , \end{aligned}$$

(3)

$$\begin{aligned} \rho '_x= & {} 3\varGamma , \end{aligned}$$

(4)

where by convenience we use $\eta =\ln a$ as time variable and we define $(\,)'= d/d\eta$ (where a is the scale factor). Notice that $\varGamma > 0$ indicates an energy transfer from dark matter to dark energy and $\varGamma < 0$ indicates the opposite.

In this work we study the following sign-changeable linear interactions,

$$\begin{aligned} \varGamma _{1i}= & {} \alpha _{1i}\, q\, \rho _i,\qquad i=T,d,c,x \end{aligned}$$

(5)

$$\begin{aligned} \varGamma _{2j}= & {} \alpha _{2j}\, q\, \rho '_j,\qquad j=T,d,c \end{aligned}$$

(6)

where $\alpha _{1i}$ and $\alpha _{2j}$ are constants, q is the deceleration parameter defined as $q=-1-H'/H$ and H is the Hubble expansion rate. The subscripts T and d denote total energy density, ($\rho _r+\rho _b+\rho _c+\rho _x$), and dark sector energy density, ($\rho _c+\rho _x$), respectively. It was noticed in Ref. [34] that interaction $\varGamma _{1T}$ has analytical solutions for the dark sector energy densities, however, the other scenarios do not, to the authors’ knowledge. We do not include $\varGamma _{2x}$ in our analysis given that this model leads to a constant deceleration parameter in an interacting scenario. Notice that all the studied models reduce to the $\Lambda$CDM scenario when the interacting parameter $\alpha _{1i}$ or $\alpha _{2j}$ is set to zero.

3 Dynamical system analysis

In this section we apply dynamical system methods [26, 27] in order to identify the relevant cosmological eras in the studied models. In this sense, we rewrite the system of Eqs. (1)–(4) in terms of the density parameters $\varOmega _i=\rho _i/3H^2$ (dimensionless) and we use the Friedmann equation as a constraint among parameters, i.e.,

$$\begin{aligned} \varOmega _r+\varOmega _b+\varOmega _c+\varOmega _x=1, \end{aligned}$$

(7)

to reduce the system of equations (1)-(4) to:

$$\begin{aligned} \varOmega _r'= & {} \varOmega _r(-1+\varOmega _r-3\varOmega _x), \end{aligned}$$

(8)

$$\begin{aligned} \varOmega _c'= & {} -\frac{\varGamma }{H^2}+\varOmega _c(\varOmega _r-3\varOmega _x), \end{aligned}$$

(9)

$$\begin{aligned} \varOmega _x'= & {} \frac{\varGamma }{H^2}+\varOmega _x(3+\varOmega _r-3\varOmega _x), \end{aligned}$$

(10)

where interactions (5)–(6) are given in Table 1 in terms of the density parameters and $\alpha$ is the interacting parameter in each case.

Table 1 Revised sign-changeable interactions

The stability of the relevant cosmological epochs is found by calculating the eigenvalues of the linearized system at the critical points. For each cosmological interaction we follow the following scheme. First we consider the set of equations,

$$\begin{aligned} \varOmega _i'=f_i(\varOmega _l), \end{aligned}$$

(11)

where $f_i$ is a function of the density parameters $\varOmega _r$, $\varOmega _c$ and $\varOmega _x$ and $i=r,c,x$. From this we find the critical points $\varOmega _l^*$ of the system (11) by calculating

$$\begin{aligned} f_i(\varOmega _l^*)=0. \end{aligned}$$

Then we linearized the set of equations (11) around the critical points,

$$\begin{aligned} \delta \varOmega _i'=J_i^l(\varOmega _j^*)\varOmega _l, \end{aligned}$$

where $J_i^l=\frac{\partial f_i}{\partial \varOmega _l}$ is the jacobian matrix. By analyzing the jacobian matrix we can find regions in the parameter space where a specific behavior is presented. In particular, we have stable, saddle or unstable points when the real part of the eigenvalues are, all negatives, a mixture of positives and negatives or all positives, respectively.

In the following, we describe in detail each of the models in Table 1. First we present models $\varGamma _{1T}$, $\varGamma _{1x}$ and $\varGamma _{2T}$ which can be reduced to two-dimensional systems, which leads to the same global results as the 3-dimensional analysis. Subsequently we describe models $\varGamma _{1d}$, $\varGamma _{1c}$, $\varGamma _{2d}$ and $\varGamma _{2c}$, which are analysed in terms of three-dimensional systems. We describe each of the critical points with the focus on radiation, matter and dark energy dominance, corresponding to unstable, saddle and stable points, respectively.

3.1 Case A: $\varGamma _{1T}$

For the model $\varGamma _{1T}$ the set of Eqs. (8)–(10) becomes,

$$\begin{aligned} \varOmega _r'= & {} \varOmega _r(-1+\varOmega _r-3\varOmega _x), \end{aligned}$$

(12)

$$\begin{aligned} \varOmega _c'= & {} -\frac{3\alpha }{2} \left( 1+\varOmega _r-3\varOmega _x\right) +\varOmega _c(\varOmega _r-3\varOmega _x), \end{aligned}$$

(13)

$$\begin{aligned} \varOmega _x'= & {} \frac{3\alpha }{2}\left( 1+\varOmega _r-3\varOmega _x\right) +3\varOmega _x(1+\frac{\varOmega _r}{3}-\varOmega _x). \end{aligned}$$

(14)

We notice that the dynamical system analysis can be simplified given that Eqs. (12) and (14) become a closed system, then we can perform a 2-dimensional analysis, which leads in this case to the same results (critical points and existence/stability conditions) as the 3-dimensional analysis. By considering $\varOmega _r'=0$ and $\varOmega _x'=0$ simultaneously we find the critical points of the system, we linearized the system around these points and we analyzed the corresponding eigenvalues in order to obtain the stability conditions.

For the 2-dimensional (or 3-dimensional) analysis of the model $\varGamma _{1T}$ we find the following three critical points $A_i=\{\varOmega _{r},\varOmega _{x}\}$,

$$\begin{aligned} A_1= & {} \{1-\frac{9}{4}\alpha ,-\frac{3}{4}\alpha \},\\ A_2= & {} \left\{ 0,\frac{1}{4}\left( 2-3\alpha -\sqrt{4-\alpha \left( 4-9\alpha \right) }\right) \right\} ,\\ A_3= & {} \left\{ 0,\frac{1}{4}\left( 2-3\alpha +\sqrt{4-\alpha \left( 4-9\alpha \right) }\right) \right\} , \end{aligned}$$

where the matter contribution to the critical points $\varOmega _m=\varOmega _b+\varOmega _c$ is determined by the constraint

$$\begin{aligned} \varOmega _r+\varOmega _m+\varOmega _x=1. \end{aligned}$$

(15)

In the analysis of these points we have considered as physical existence conditions $\varOmega _r\ge 0$ and $\varOmega _m\ge 0$ at the critical points, besides the mathematical existence conditions. On the other hand, notice that the effective state parameter $\omega _{\textrm{eff}}=\frac{p_T}{\rho _T}$ ($p_T$ is the total pressure) is related to the deceleration parameter by $q=\frac{1}{2}(1+3\omega _{\textrm{eff}})$, and in terms of the density parameters q is given by

$$\begin{aligned} q=\frac{1}{2}(1+\varOmega _r-3\varOmega _x). \end{aligned}$$

(16)

Table 2 Description of the critical points for scenario $\varGamma _{1T}$

Table 2 shows the existence and stability conditions on the critical points $A_1-A_3$ (the same conditions for the 2 and 3-dimensional analysis), as well as the $\omega _{\textrm{eff}}$ value. The critical point $A_1$ in Table 2 describes a radiation dominated epoch in which radiation, matter and dark energy coexist for $0<\alpha <\frac{4}{9}$, where this constraint comes from the physical existence condition. The matter contribution to this critical point is given by $\varOmega _m=3\alpha$ and in this case $\varOmega _x$ is always negative given the existence conditions. The signs of the eigenvalues of the linearized system indicate that $A_1$ is an unstable critical point for $\alpha <\frac{4}{9}$.

The critical point $A_2$ has $\omega _{\textrm{eff}}>-\frac{1}{3}$ irrespective of the value of $\alpha$. In the limit $\alpha \rightarrow 0$, this phase can be understood as a phase of matter domination, given that $\omega _{\textrm{eff}}\rightarrow 0$ in this limit. In this phase matter and dark energy coexists. At this critical point the matter component is $\varOmega _m=\frac{1}{4}\left( 2+3\alpha +\sqrt{4-\alpha (4-9\alpha )}\right)$, which is positive irrespective of the $\alpha$ value. On the other hand, we have $\varOmega _x<0$ for $\alpha >0$ and $\varOmega _x>0$ for $\alpha <0$. $A_2$ is a saddle critical point for $\alpha <\frac{4}{9}$ or an unstable critical point for $\alpha >\frac{4}{9}$.

The critical point $A_3$ dynamically corresponds to a phase of dark energy domination ($\omega _{\textrm{eff}}< -\frac{1}{3}$ irrespective of the $\alpha$ value), where matter and dark energy coexist. At this point $\varOmega _m=\frac{1}{4}\left( 2+3\alpha -\sqrt{4-\alpha (4-9\alpha )}\right)$, which is positive for $\alpha >0$, imposing in this sense a physical existence condition for this point. Under this existence condition $\varOmega _x$ is always positive. $A_3$ is a stable critical point for $\alpha >0$.

Fig. 1

Phase plot for model $\varGamma _{1T}$ with $\alpha =0.08$

Figure 1 shows the 2-dimensional phase space $\varOmega _x-\varOmega _r$. The three critical points in Table 2 are shown as red dots, where we can clearly notice the unstable, saddle and stable points, these 3 points can be found in model $\varGamma _{1T}$ for $0\le \alpha <\frac{4}{9}$, nevertheless, in this range $\varOmega _x$ is negative at points $A_1$ and $A_2$. In the figure, the “Present” point is indicated considering $\{\varOmega _b,\varOmega _c,\varOmega _x\}=\{0.0490,0.2621,0.6889\}$ [1].

Finally, notice that the critical points $A_1-A_3$ in Table 2 and their existence and stability conditions reduce to the ones in the $\Lambda$CDM scenario in the limit $\alpha \rightarrow 0$.

3.2 Case B: $\varGamma _{1x}$

For the model $\varGamma _{1x}$ we can reduce the set of Eqs. (8)–(10) to a 2-dimensional set including Eq. (8) and the following equation,

$$\begin{aligned} \varOmega _x'=3\varOmega _x\left( \frac{\alpha }{2}\left( 1+\varOmega _r-3\varOmega _x\right) +1+\frac{\varOmega _r}{3}-\varOmega _x\right) . \end{aligned}$$

For this model, we find three critical points $B_i=\{\varOmega _r,\varOmega _x\}$,

$$\begin{aligned} B_1=\{1,0\},\; B_2=\left\{ 0,0\right\} ,\; B_3=\left\{ 0,\frac{2+\alpha }{2+3\alpha }\right\} , \end{aligned}$$

where the matter contribution to the critical points is determined by the constraint (15).

The existence and stability conditions of the critical points $B_1-B_3$ are shown in Table 3, as well as the $\omega _{\textrm{eff}}$ parameter. In the 3-dimensional analysis we find the same critical points but, the point $B_2$ turns out to be a non-hyperbolic critical point, where we should use the center manifold theorem or rely on numerical inspection in studying its stability. In this scenario, for the sake of simplicity, we perform our analysis in the reduced 2-dimensional system, which includes all the relevant cosmological critical points.

Table 3 Description of the critical points for scenario $\varGamma _{1x}$

The critical points $B_1$ and $B_2$ in Table 3 correspond to a phase of radiation and matter domination, respectively. There are no conditions on the existence of these critical points and the stability analysis indicate that $B_1$ is unstable for $\alpha >-\frac{4}{3}$ and saddle for $\alpha <-\frac{4}{3}$, meanwhile, $B_2$ is saddle for $\alpha >-2$ and stable for $\alpha <-2$.

At the critical point $B_3$ matter and dark energy coexist. At this point $\varOmega _m=\frac{2\alpha }{2+3\alpha }$ which is positive for $\alpha <-\frac{2}{3}$ or $\alpha >0$. On the other hand, for $\alpha >0$, this point corresponds to dark energy domination with $\varOmega _x>0$ as a stable critical point. For $\alpha <-\frac{2}{3}$ we get $\omega _{\textrm{eff}}<-\frac{1}{3}$, $\varOmega _m>\varOmega _x$ and $\varOmega _x>0$ for $\alpha <-2$. The corresponding stability conditions in this case are given in Table 3.

Fig. 2

Phase plot for model $\varGamma _{1x}$ with $\alpha =0.05$

Figure 2 shows the 2-dimensional phase space $\varOmega _x-\varOmega _r$ for the $\varGamma _{1x}$ scenario, where the three critical points in Table 3 are shown as red dots and we can clearly notice the unstable, saddle and stable points. These points can be found in model $\varGamma _{1x}$ for $\alpha \ge 0$, where $\varOmega _x$ is positive at the critical point $B_3$. In the figure, the black dot labeled as “Present” considers the values in Ref. [1].

As well as model $\varGamma _{1T}$, the critical points $B_1-B_3$ reduce to the $\Lambda$CDM critical points in the limit $\alpha \rightarrow 0$.

3.3 Case C: $\varGamma _{2T}$

For the model $\varGamma _{2T}$ we can reduce the set of Eqs. (8)–(10) to a 2-dimensional set including Eq. (8) and the following equation,

$$\begin{aligned} \varOmega _x'=9\left( 1+\frac{\varOmega _r}{3}-\varOmega _x\right) \left( \frac{\varOmega _x}{3} -\frac{\alpha }{2}\left( 1+\varOmega _r-3\varOmega _x\right) \right) . \end{aligned}$$

For this model we find three critical points $C_i=\{\varOmega _r,\varOmega _x\}$,

$$\begin{aligned}{} & {} C_1=\{1+9\alpha ,3\alpha \},\,\quad C_2=\left\{ 0,\frac{3\alpha }{2+9\alpha }\right\} ,\,\\{} & {} C_3=\{0,1\}, \end{aligned}$$

where the matter contribution to the critical points is determined by the constraint (15).

The existence and stability conditions of the critical points are shown in Table 4, which corresponds to the same results as in a 3-dimensional analysis, as well as the $\omega _{\textrm{eff}}$ parameter.

At the critical point $C_1$ coexist radiation, matter and dark energy in a radiation dominated era ($\omega _{\textrm{eff}}=\frac{1}{3}$). For this critical point we have $\varOmega _r=1+9\alpha$ and $\varOmega _m=-12\alpha$, which are positive for $-\frac{1}{9}<\alpha <0$, corresponding to the physical existence condition, but necessarily in this range $\varOmega _x<0$. At the critical point $C_2$ coexists matter and dark energy, $\omega _{\textrm{eff}}\ge -\frac{1}{3}$ for $\alpha >-\frac{2}{9}$. At this point we have $\varOmega _m=\frac{2+6\alpha }{2+9\alpha }$ which is positive for $\alpha <-\frac{1}{3}$ or $\alpha >-\frac{2}{9}$. In the range $\alpha <-\frac{2}{9}$ or $\alpha >0$, the parameter $\varOmega _x$ is also positive. This point corresponds to matter domination in the limit $\alpha \rightarrow 0$.

Fig. 3

Phase plot for model $\varGamma _{2T}$ with $\alpha =-0.02$

The point $C_3$ corresponds to a de-Sitter attractor for $\alpha >-\frac{1}{3}$, where only the dark energy term contributes.

Figure 3 shows the 2-dimensional phase space $\varOmega _x-\varOmega _r$ for the $\varGamma _{2T}$ scenario. The three critical points in Table 4 are shown as red dots, we can clearly notice the unstable, saddle and stable points, which can be found in the model $\varGamma _{2T}$ for $-\frac{1}{9}<\alpha \le 0$. However, in this range, $\varOmega _x$ is negative at the critical points $C_1$ and $C_2$. In the figure the “Present” dot considers the values in Ref. [1].

Table 4 Description of the critical points for scenario $\varGamma _{2T}$

The critical points $C_1-C_3$ corresponding to model $\varGamma _{2T}$ in Table 4 reduce to the $\Lambda$CDM critical points in the limit $\alpha \rightarrow 0$.

3.4 Case D: $\varGamma _{1d}$

For the model $\varGamma _{1d}$ the set of Eqs. (8)–(10) reduces to,

$$\begin{aligned} \varOmega _r'= & {} \varOmega _r(-1+\varOmega _r-3\varOmega _x),\\ \varOmega _c'= & {} \varOmega _c(\varOmega _r-3\varOmega _x)-\frac{3\alpha }{2}\left( 1+\varOmega _r-3\varOmega _x\right) \left( \varOmega _c+\varOmega _x\right) ,\\ \varOmega _x'= & {} \varOmega _x(3+\varOmega _r-3\varOmega _x)+\frac{3\alpha }{2}\left( 1+\varOmega _r-3\varOmega _x\right) \left( \varOmega _c+\varOmega _x\right) . \end{aligned}$$

For this model we find the following critical points $D_i=\{\varOmega _r,\varOmega _b,\varOmega _x\}$,

$$\begin{aligned}{} & {} D_1=\{1,0,0\},\quad D_2=\{0,1,0\},\\{} & {} D_3=\left\{ 0,0,\frac{1}{4}\left( 2-3\alpha -\sqrt{4-\alpha \left( 4-9\alpha \right) }\right) \right\} ,\\{} & {} D_4=\left\{ 0,0,\frac{1}{4}\left( 2-3\alpha +\sqrt{4-\alpha \left( 4-9\alpha \right) }\right) \right\} , \end{aligned}$$

where the $\varOmega _c$ contribution to the critical points is determined by the constraint (7).

In the analysis of these points we have considered as physical existence conditions $\varOmega _r\ge 0$, $\varOmega _b\ge 0$ and $\varOmega _c\ge 0$ at the critical points.

Table 5 Description of the critical points for scenario$\varGamma _{1d}$

The critical points $D_1$ and $D_2$ in Table 5 describe a radiation and a baryon dominated epoch, respectively, irrespective of the $\alpha$ value. The signs of the eigenvalues of the linearized system indicate that $D_1$ is an unstable critical point in the range $-\frac{1}{4}\le \alpha <\frac{4}{9}$. On the other hand, the critical point $D_2$ corresponds to a saddle point in the above range but it represents a non-physical point because there is not a baryon dominated epoch in the actual evolution of our universe.

We notice that scenarios $\varGamma _{1T}$ and $\varGamma _{1d}$ share the same critical points for the dark sector, $D_3$ and $D_4$, with the same existence and stability conditions.

The critical point $D_3$ can be understood as dark matter domination in the limit $\alpha \rightarrow 0$, this point (and its analysis) is equivalent to the point $A_2$ for the scenario $\varGamma _{1T}$. The critical point $D_4$ corresponds to dark energy domination for $\alpha >0$, where we met the physical existence condition $\varOmega _c\ge 0$. This point and its analysis is equivalent to the points $A_3$ in scenario $\varGamma _{1T}$. The existence/stability conditions in Table 5 indicate that these critical points (and the radiation one) can be found for $0\le \alpha <\frac{4}{9}$, but in this range necessarily $\varOmega _x$ becomes negative at the critical point $D_3$. In Fig. 4 we show a projected 2-dimensional phase space $\varOmega _x-\varOmega _c$ where we have fixed $\varOmega _r=0$ to highlight the late-universe evolution. In this figure, we show two critical points (physical) corresponding to the saddle point $D_3$ and the dark energy attractor $D_4$.

Fig. 4

Projected phase plot for model $\varGamma _{1d}$ with $\alpha =0.2$

3.5 Case E: $\varGamma _{1c}$

For the model $\varGamma _{1c}$ the set of Eqs. (8)–(10) reduces to,

$$\begin{aligned} \varOmega _r'= & {} \varOmega _r(-1+\varOmega _r-3\varOmega _x),\\ \varOmega _c'= & {} \varOmega _c(\varOmega _r-3\varOmega _x)-\frac{3}{2}\alpha \left( 1+\varOmega _r-3\varOmega _x\right) \varOmega _c,\\ \varOmega _x'= & {} 3\varOmega _x(1+\frac{\varOmega _r}{3}-\varOmega _x)+\frac{3}{2}\alpha \left( 1+\varOmega _r-3\varOmega _x\right) \varOmega _c. \end{aligned}$$

For this model we find the following critical points $E_i=\{\varOmega _r,\varOmega _b,\varOmega _x\}$,

$$\begin{aligned}{} & {} E_1=\{1,0,0\},\quad E_2=\{0,1,0\},\\{} & {} E_3=\left\{ 0,0,-\frac{\alpha }{2-3\alpha }\right\} ,\quad E_4=\left\{ 0,0,1\right\} , \end{aligned}$$

where given the constraint (7), the contribution $\varOmega _c$ to the critical points is determined to be zero for each point but $E_3$, where $\varOmega _c=\frac{2(1-\alpha )}{2-3\alpha }$.

Table 6 Description of the critical points for scenario $\varGamma _{1c}$

Fig. 5

Projected phase plot for model $\varGamma _{1c}$ with $\alpha =-0.1$

The critical points $E_1$ and $E_2$ in Table 6 describe a radiation and a baryon dominated epoch, respectively. The signs of the eigenvalues of the linearized system indicate that $E_1$ is an unstable critical point for $\alpha <\frac{1}{3}$. On the other hand, the non-physical point $E_2$ (baryon domination) corresponds to a saddle point in the above range. The point $E_3$ represents a phase where the dark fluids coexist with $\varOmega _c>0$ for $\alpha <\frac{2}{3}$ or $\alpha >1$ and $\omega _{\textrm{eff}}>-\frac{1}{3}$ for $\alpha <\frac{2}{3}$, this point corresponds to dark matter domination in the limit $\alpha \rightarrow 0$. The point $E_4$ corresponds to a de-Sitter stage with the dominance of dark energy and this point is stable for $\alpha <1$.

Table 7 Description of the critical points for scenario $\varGamma _{2d}$

From Table 6 we notice that the critical points corresponding to unstable, saddle and stable behavior can be found for $\alpha <\frac{1}{3}$. Considering this range, $\varOmega _x$ remains positive for $\alpha <0$ at the critical point $E_3$. In Fig. 5 we show the projected 2-dimensional phase space $\varOmega _x - \varOmega _c$ where we have fixed $\varOmega _r=0$ to highlight the late-universe evolution. In this figure, we show two critical points (physical) corresponding to the saddle point $E_3$ and the attractor point $E_4$.

3.6 Case F: $\varGamma _{2d}$

For the model $\varGamma _{2d}$ the set of Eqs. (8)–(10) reduces to,

$$\begin{aligned} \varOmega _r'= & {} \varOmega _r(-1+\varOmega _r-3\varOmega _x),\\ \varOmega _c'= & {} \frac{9}{2}\alpha (1+\varOmega _r-3\varOmega _x)\varOmega _c +\varOmega _c(\varOmega _r-3\varOmega _x),\\ \varOmega _x'= & {} -\frac{9}{2}\alpha (1+\varOmega _r-3\varOmega _x)\varOmega _c +\varOmega _x(3+\varOmega _r-3\varOmega _x). \end{aligned}$$

For this model we find the following critical points $F_i=\{\varOmega _r,\varOmega _b,\varOmega _x\}$,

$$\begin{aligned}{} & {} F_1=\{1,0,0\},\quad F_2=\{0,1,0\},\quad \\{} & {} F_3=\left\{ 0,0,\frac{3\alpha }{2+9\alpha }\right\} ,\quad F_4=\left\{ 0,0,1\right\} , \end{aligned}$$

where given the constraint (7), the contribution $\varOmega _c$ to the critical points is determined to be zero at each point but $F_3$, where $\varOmega _c=\frac{2+6\alpha }{2+9\alpha }$.

The critical points $F_1$ and $F_2$ in Table 7 describe a radiation and a baryon dominated era, respectively. The signs of the eigenvalues of the linearized system indicate that $F_1$ is an unstable critical point for $\alpha >-\frac{1}{9}$. On the other hand, the non-physical point $F_2$ (baryon domination) corresponds to a saddle point in the above range. The point $F_3$ represents a phase where the dark fluids coexist with $\varOmega _c>0$ for $\alpha <-\frac{1}{3}$ or $\alpha >-\frac{2}{9}$ and $\omega _{\textrm{eff}}>-\frac{1}{3}$ for $\alpha >-\frac{2}{9}$, this point corresponds to dark matter domination in the limit $\alpha \rightarrow 0$. The point $F_3$ is saddle in the range $\alpha >-\frac{1}{9}$. The point $F_4$ corresponds to a de-Sitter stage with the dominance of dark energy and this point is stable for $\alpha >-\frac{1}{3}$.

From Table 7 we notice that the critical points corresponding to unstable, saddle and stable can be found for $\alpha >-\frac{1}{9}$. Notice that in this range, $\varOmega _x$ remains positive for $\alpha >0$ at the critical point $F_3$. In Fig. 6 we show the projected 2-dimensional phase space $\varOmega _x - \varOmega _c$ where we have fixed $\varOmega _r=0$ to highlight the late-universe evolution. In this figure, we show two critical points (physical) corresponding to the saddle point $F_3$ and the attractor point $F_4$. Notice that the models $\varGamma _{2T}$ and $\varGamma _{2d}$ share the same critical points and existence/stability conditions in the points corresponding to the dark sector, $C_2-C_3$ and $F_3-F_4$.

Fig. 6

Projected phase plot for model $\varGamma _{2d}$ with $\alpha =0.1$

3.7 Case G: $\varGamma _{2c}$

For the model $\varGamma _{2c}$ the set of Eqs. (8)–(10) reduces to,

$$\begin{aligned} \varOmega _r'= & {} \varOmega _r(-1+\varOmega _r-3\varOmega _x),\\ \varOmega _c'= & {} \frac{9\alpha \varOmega _c(1+\varOmega _r-3\varOmega _x)}{2+3\alpha (1+\varOmega _r-3\varOmega _x)} +\varOmega _c(\varOmega _r-3\varOmega _x),\\ \varOmega _x'= & {} -\frac{9\alpha \varOmega _c(1+\varOmega _r-3\varOmega _x)}{2+3\alpha (1+\varOmega _r-3\varOmega _x)} +\varOmega _x(3+\varOmega _r-3\varOmega _x). \end{aligned}$$

For this model we find the following critical points $G_i=\{\varOmega _r,\varOmega _b,\varOmega _x\}$,

$$\begin{aligned}{} & {} G_1=\{1,0,0\},\; G_2=\{0,1,0\},\; G_5=\left\{ 0,0,1\right\} ,\\{} & {} G_3=\left\{ 0,0,\frac{1-\sqrt{1+3\alpha (4+3\alpha )}+6\alpha }{9\alpha }\right\} ,\\{} & {} G_4=\left\{ 0,0,\frac{1+\sqrt{1+3\alpha (4+3\alpha )}+6\alpha }{9\alpha }\right\} , \end{aligned}$$

where given Eq. (7), $\varOmega _c$ is zero at $G_1$, $G_2$ and $G_5$, $\varOmega _c=\frac{-1+\sqrt{1+3\alpha (4+3\alpha )}+3\alpha }{9\alpha }$ at $G_3$, and $\varOmega _c=-\frac{1+\sqrt{1+3\alpha (4+3\alpha )}-3\alpha }{9\alpha }$ at $G_4$.

The critical points $G_1$ and $G_2$ in Table 8 describe a radiation and a baryon dominated epoch, respectively. The signs of the eigenvalues of the linearized system indicate that $G_1$ is an unstable critical point for $\alpha <-\frac{1}{3}$ or $\alpha >-\frac{1}{12}$. The non-physical point $G_2$ (baryon domination) corresponds to a saddle point in the above range.

At the critical point $G_3$ the dark sector coexist in the ranges $\alpha <-\frac{\sqrt{3}+2}{3}$, $\frac{\sqrt{3}-2}{3}<\alpha <0$ or $\alpha >0$. Inside these limits $G_3$ can be unstable for $\frac{\sqrt{3}-2}{3}<\alpha <-\frac{1}{12}$ or saddle for $\alpha <-\frac{\sqrt{3}+2}{3}$ or $\alpha >-\frac{1}{12}$. We notice that $\omega _{\textrm{eff}}>-\frac{1}{3}$ for $\alpha >\frac{\sqrt{3}-2}{3}$ and this point reduces to dark matter domination in the limit $\alpha \rightarrow 0$. Besides, $\varOmega _x>0$ for $\alpha >0$ or $\alpha \le -\frac{\sqrt{3}+2}{3}$. At the point $G_4$ coexists the dark components in the ranges $\frac{\sqrt{3}-2}{3}<\alpha <0$, where this point is saddle and $\alpha \le -\frac{\sqrt{3}+2}{3}$, where it is a stable critical point. In the range where $G_4$ is a saddle point we have $\omega _{\textrm{eff}}>-\frac{1}{3}$, outside this range, in the allowed region, the effective fluid accelerates the universe’s expansion. The $\varOmega _x$ contribution of this point is positive for $\alpha <-\frac{\sqrt{3}+2}{3}$. Notice that the point $G_4$ diverges in the limit $\alpha \rightarrow 0$. The point $G_5$ corresponds to a de-Sitter stage with the dominance of dark energy. This point is stable for $\alpha <\frac{1}{3}$ and unstable outside this range.

We have sketched the behavior of the critical points $G_3-G_5$ in Fig. 8, where we notice that for $\alpha <-\frac{\sqrt{3}+2}{3}$ we have one saddle point and two stable points corresponding to $G_3$ and $G_4$, $G_5$, respectively. In the range $-\frac{\sqrt{3}+2}{3}<\alpha <\frac{\sqrt{3}-2}{3}$, we have no saddle point ($G_3$ and $G_4$ do not exist) and one stable point, $G_5$. For $\frac{\sqrt{3}-2}{3}<\alpha <-\frac{1}{12}$ there is one unstable, one saddle and one stable point, $G_3$, $G_4$ and $G_5$, respectively. In the range $-\frac{1}{12}<\alpha <0$ we have two saddle points, $G_3$ and $G_4$, and one stable point, $G_5$. For $0<\alpha <\frac{1}{3}$ we have one saddle point and one stable point, $G_3$ and $G_5$, respectively. For $\alpha >\frac{1}{3}$ we have two saddle points ($G_3$ and $G_5$) and no stable point.

In Fig. 7 we show the projected 2-dimensional phase space $\varOmega _x - \varOmega _c$ where we have fixed $\varOmega _r=0$ to highlight the late-universe evolution. In this figure, we show two critical points (physical) corresponding to the saddle point $G_3$ and the attractor point $G_5$. The critical point $G_4$ is not present because it violates the physical existence conditions we have imposed at the critical points ($\varOmega _r\ge 0$ and $\varOmega _c\ge 0$).

Fig. 7

Projected phase plots for model $\varGamma _{2c}$ with $\alpha =0.1$

Table 8 Description of the critical points for scenario $\varGamma _{2c}$

In summary, if we search for the models having an unstable, saddle and stable critical points during the evolution we get the following intervals, where existence/stability conditions are jointly met: $\alpha >0$ for $\varGamma _{1x}$, $\alpha <0$ for $\varGamma _{1c}$, $\alpha >0$ for $\varGamma _{2d}$ and $0<\alpha <\frac{1}{3}$ for $\varGamma _{2c}$. For these models, $\varOmega _x>0$ and the sign of the interacting parameter $\alpha$ becomes defined in each case.

On the other hand, the corresponding intervals where existence/stability conditions are jointly met for models where $\varOmega _x<0$ are: $0<\alpha <\frac{4}{9}$ for $\varGamma _{1T}$, $-\frac{1}{9}<\alpha <0$ for $\varGamma _{2T}$ and $0<\alpha <\frac{4}{9}$ for $\varGamma _{1d}$. Models $\varGamma _{1T}$ and $\varGamma _{2T}$ have $\varOmega _x<0$ at radiation and matter domination, nevertheless $\varOmega _x$ changes sign and it becomes positive at dark energy domination. For model $\varGamma _{1d}$ we have $\varOmega _x<0$ for dark matter domination, but it is positive for radiation and dark energy domination, meaning at least two changes of sign of $\varOmega _x$ during evolution.

Finally, notice that the stability conditions of center-type critical points have not been addressed in this work.

Fig. 8

Scheme of the behavior of critical points $G_3-G_5$ in terms of the interacting parameter $\alpha$, for model $\varGamma _{2c}$. The pale blue and gray regions represent a saddle and stable critical point, respectively. The boxed pale yellow regions represent an interval where the existence conditions are not met

4 Observational analysis

In the observational analysis we use background data such as the local measurement of Hubble parameter ($H_0$) [36], cosmic chronometers [37], supernovae type Ia (SNe Ia) [38], baryon acoustic oscillations (BAO) [39], and the angular scale of the sound horizon at the last scattering [40]. In this section we briefly describe the used data, a detailed description can be found in Ref. [35].

4.1 Local determination of $H_0$

We use the $H_0$ value obtained by the SH0ES team using a local distance ladder method based on Cepheids, $h = 0.7402 \pm 0.0142$ [36].

4.2 Cosmic chronometers

We use 24 cosmic chronometers obtained through the differential age method [41]. This procedure provides cosmological-independent direct measurements of the expansion history of the universe up to redshift 1.2 [42], see Table 3 in Ref. [35].

4.3 Supernovae type Ia

We use the Pantheon Sample, a set of 1048 spectroscopically confirmed SNe Ia ranging from redshift 0.01 to 2.3 [38], along with the corresponding covariance matrix. The Pantheon catalog contains measurements of peak magnitudes in the B-band’s rest frame, $m_B$, related to the distance modulus by $\mu =m_B+M_B$. $M_B$ is the absolute B-band magnitude of a fiducial SN Ia, a nuisance parameter. In our analysis the distance modulus at a given redshift is,

$$\begin{aligned} \mu (z)=5\log d_L(z)+25, \end{aligned}$$

(17)

where the luminosity distance $d_L$ is given by,

$$\begin{aligned} d_L=(1+z)\int ^z_0\frac{H_0\, dz'}{H(z')}\, \mathrm{[Mpc]}. \end{aligned}$$

(18)

4.4 BAO data

We use isotropic measurements of the BAO signal from 6dFGS [43], MGS [44] and eBOSS [45]. These measurements are given in terms of the dimensionless ratio,

$$\begin{aligned} d_z(z) = D_V (z)/r_s(z_d), \end{aligned}$$

(19)

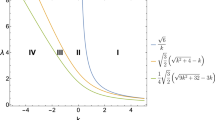
where $z_d$ is the redshift at the drag epoch,

$$\begin{aligned} D_V(z)= & {} \left( (1 + z)^2D_A(z)^2 \frac{c\,z}{H(z)}\right) ^{1/3}, \end{aligned}$$

(20)

$$\begin{aligned} D_A(z)= & {} \frac{c}{(1+z)}\int ^z_0 \frac{dz}{H(z)}, \end{aligned}$$

(21)

$$\begin{aligned} r_s(z)= & {} \int ^{\infty }_z \frac{c}{\sqrt{3(1+R)}}\frac{ dz}{H(z)}, \end{aligned}$$

(22)

with c the speed of light and $R = \frac{3\varOmega _b}{4\varOmega _{\gamma }(1+z)}$ [46].

Furthermore, we use the anisotropic BAO measurements from BOSS DR12 [47] and Ly$\alpha$ forest [48], which are defined in terms of $D_A$ and $D_H=c/H(z)$, as shown in Table 2 of Ref. [49]. We use these data along with the corresponding covariance matrix in Ref. [49].

4.5 Cosmic microwave background data

We consider the angular scale of the sound horizon at the last scattering as the only contribution of CMB data,

$$\begin{aligned} \ell _a =\frac{\pi (1+z_*)D_A(z_*)}{r_s(z_*)}, \end{aligned}$$

(23)

where the comoving size of the sound horizon is evaluated at $z_* = 1089.80$ [1]. We compare the value obtained in our study with the one reported by the Planck collaboration in 2015, $\ell _a=301.63\pm 0.15$ [40].

To compute the maximum likelihood and posterior distributions we use the MultiNest algorithm¹ [50, 51], with a global log-evidence tolerance of 0.01 as a convergence criterion and working with 800 live points to improve the accuracy.

We perform the observational analysis for the only model with an analytical solution, i.e. scenario $\varGamma _{1T}$. The posterior distribution for the parameters h, $\varOmega _c$ and $\alpha$ are shown in Fig. 9 and Table 9.

Fig. 9

Contour plots for the model $\varGamma _{1T}$, $1\sigma$ and $2\sigma$ confidence levels are shown

Table 9 Best fit parameters and $1\sigma$ error for the observational analysis of the $\varGamma _{1T}$ scenario

In this analysis we fix the physical baryon density to $\varOmega _bh^2 = 0.022383$ [1], the physical photon density to $\varOmega _{\gamma }h^2=2.469\times 10^{-5}$ [53], we consider the the radiation density as $\varOmega _{r}=\varOmega _{\gamma }\left( 1+\frac{7}{8}\left( \frac{4}{11}\right) ^{4/3}N_{\textrm{eff}}\right)$, and the effective number of neutrinos $N_{\textrm{eff}}=3.046$ [52]. Notice that we have considered a flat prior for the $\alpha$ parameter consistent with the results of Sect. 3.1, i.e., $0<\alpha <\frac{4}{9}$.

Fig. 10

Evolution of the density parameters for the model $\varGamma _{1T}$ considering the best fit parameters in Table 9

The results in Table 9 are consistent with a small but non-null interaction in the dark sector. Given that the interaction $\varGamma _{1T}$ changes sign during evolution, our results indicate that today dark energy is transferred to dark matter but in the past the transference was the opposite. In Fig. 10 we show the evolution of the density parameters consistent with the best fit parameters shown in Table 9. Here we notice that the dark energy density was negative in the past and around $z=7.2$ it transitioned to a positive dark energy density, as shown in the subplot in Fig. 10. In the limit $z\rightarrow \infty$, the dark energy density tends to $\varOmega _x\rightarrow -0.00675$ instead of 0, as in the $\Lambda$CDM model. Finally, notice that a negative dark energy density in the past is an intrinsic feature of model $\varGamma _{1T}$, which arises from imposing the existence conditions in the dynamical system analysis.

5 Statefinder parameters

The statefinder parameters r and s were first introduced in Ref. [30] in order to compare the plethora of dark energy models available. In the definition of these parameters, derivatives of the scale factor exceed the second-order. In this context, we can explore the phase space by defining:

$$\begin{aligned} r \equiv \frac{\dddot{a}}{a H^3}, \quad s \equiv \frac{r-1}{3\left( q-\frac{1}{2}\right) }. \end{aligned}$$

(24)

In terms of the density parameters, the statefinder parameters are given by:

$$\begin{aligned} r= & {} \left( 2+\varOmega _r-3\varOmega _x\right) q-q', \end{aligned}$$

(25)

$$\begin{aligned} s= & {} \frac{2\left( -1+q(2+\varOmega _r-3\varOmega _x)-q'\right) }{3 (\varOmega _r-3\varOmega _x)}, \end{aligned}$$

(26)

where q is defined in (16). For each model in Table 1 we can obtain the parameters r and s and the $r-q$ and $r-s$ planes can be drawn. In order to do this we have to numerically integrate equations (8)-(10) and we have considered as border conditions the present values of the density parameters as $\{\varOmega _b,\varOmega _c,\varOmega _x\}=\{0.0490,0.2621,0.6889\}$ [1]. The evolutionary trajectories in the planes $r-q$ and $r-s$ can exhibit quite different behaviors, even though the overall behavior of models may appear similar in the dynamical system analysis of Sect. 3. In particular, the $r-q$ and $r-s$ planes for the $\varGamma _{1T}$ model are shown in Fig. 11, where the trajectories correspond to different values of $\alpha$, consistent with the results of Sect. 3. We notice that in both planes the variation in $\alpha$ modifies the trajectories with respect to the $\Lambda$CDM model.

Fig. 11

The figures show the space parameter $r-q$ (left) and $r-s$ (right) for the $\varGamma _{1T}$ model and several values of the $\alpha$ parameter. Black dots indicate current values and gray arrows the evolution’s direction. The solid black line represents $\Lambda$CDM, meanwhile, blue solid, dashed, and dotted lines indicate $\alpha =0.01,0.03,0.08$, respectively

Fig. 12

The figure shows the planes $r-q$ (left) and $r-s$ (right) for the $\varGamma _{1T}$, $\varGamma _{1d}$ and $\varGamma _{1x}$ models in the case $\alpha =0.01$. Black dots indicate current values and gray arrows the evolution’s direction. The solid black line represents $\Lambda$CDM, meanwhile, blue solid, blue dot-dashed and brown lines indicate $\varGamma _{1T}$, $\varGamma _{1d}$ and $\varGamma _{1x}$, respectively

Fig. 13

The figure shows the planes $r-q$ (left) and $r-s$ (right) for the models $\varGamma _{2T}$ and $\varGamma _{1c}$ in the case $\alpha =-0.01$ and models $\varGamma _{2c}$ and $\varGamma _{2d}$ in the case $\alpha =0.01$. Black dots indicate current values and gray arrows the evolution’s direction. The solid black line represents $\Lambda$CDM, meanwhile, purple, red, orange and black dotted lines correspond to models $\varGamma _{2T}$, $\varGamma _{1c}$, $\varGamma _{2d}$ and $\varGamma _{2c}$, respectively

In Fig. 12 we show the $r-q$ and $r-s$ planes for the models $\varGamma _{1T}$, $\varGamma _{1d}$ and $\varGamma _{1x}$ in the case $\alpha =0.01$. From the trajectories we see that all the curves pass through the points $(r,q)=(1,0)$ and $(r,s)=(1,0)$, and they present the same outcomes in the future. Notice that models $\varGamma _{1T}$ and $\varGamma _{1d}$ are very similar in both planes.

Figure 13 shows the $r-q$ and $r-s$ planes for models $\varGamma _{1c}$, $\varGamma _{2T}$, $\varGamma _{2d}$ and $\varGamma _{2c}$, we consider $\alpha =-0.01$ for models $\varGamma _{2T}$ and $\varGamma _{2d}$ and $\alpha =0.01$ for models $\varGamma _{2d}$ and $\varGamma _{2c}$, consistent with the results in Sect. 3. We see that all trajectories in Fig. 13 pass through the points $(r,q)=(1,0)$ and they end at the points $(r,q)=(1,-1)$ and $(r,s)=(1,0)$.

We notice that the fate of the universe can be different from $\Lambda$CDM, the trajectories in Fig. 12 tend to an asymptotic point corresponding to a scaling solution and in Fig. 13 the trajectories evolve towards the de-Sitter point. On the other hand, the evolutionary trajectories of the dark energy models in the (r, s) plane can be classified as quintessence if $r<1$ and $s>0$ or Chaplygin gas if $r>1$ and $s<0$ [54]. In this sense, models $\varGamma _{1T}$, $\varGamma _{1d}$, $\varGamma _{1x}$ and $\varGamma _{2T}$ are now evolving in the quintessence sector, meanwhile, models $\varGamma _{1c}$, $\varGamma _{2d}$ and $\varGamma _{2c}$ are now in the Chaplygin sector.

Besides of comparing the evolutionary trajectories in the statefinder planes with the $\Lambda$CDM behavior, we can compare the trajectories shown in Figs. 12 and 13 among dark energy models in the literature. In particular, similar trajectories to those shown in Fig. 12 for $\varGamma _{1T}$, $\varGamma _{1d}$ and $\varGamma _{1x}$ are found in Ref. [32] for a standard interacting model $\varGamma \propto \rho _x$ without change of sign. On the other hand, the evolutionary trajectory of model $\varGamma _{2T}$ in Fig. 13 is comparable to the trajectory for a standard interacting model $\varGamma \propto \rho _m$ in Ref. [32] and also similar to the trajectories corresponding to a hybrid expansion law in Ref. [55]. Finally, the trajectories for models $\varGamma _{1c}$, $\varGamma _{2d}$, $\varGamma _{2c}$ in Fig. 13 are alike to those in Ref. [56] corresponding to a modified Chaplygin Gas model with interaction.

6 Final remarks

We have performed a dynamical system analysis and a statefinder analysis for a class of sign-changeable interactions in the dark sector [24]. We have shown that the studied models can explain the current acceleration of our universe as a late time attractor in a defined range for the $\alpha$ parameter (see Sect. 3). For the studied models, the evolution of the universe can evolve from a radiation dominated era, through a dark matter dominated era and a final stage of dark energy domination. This kind of evolution is found in each model for a defined range of the interaction parameter $\alpha$ (see Sect. 3). We find that models, $\varGamma _{1T}$, $\varGamma _{2T}$, $\varGamma _{1d}$, need to have $\varOmega _x<0$ at some critical points in order to follow the universe’s evolution, this necessarily implies at least one change of sign of $\varOmega _x$ during evolution, resulting in $\varOmega _x>0$ at the final attractor. Furthermore, the requirement of the existence and stability conditions for the critical points selects in each case a defined sign for the interacting parameter $\alpha$. We notice that some of the sign-changeable interacting scenarios have a negative dark energy density in the past, during radiation or matter domination eras, allowing in this sense to have $\Lambda$-varying model with a negative $\Lambda (t)$ at the beginning of evolution which turns positive near the attractor point. This feature is not present in the standard interacting models, see Refs. [28] and [32].

On the other hand, the observational analysis of model $\varGamma _{1T}$ with background data shows that the posterior distribution of the $\alpha$ parameter is consistent with the result from the dynamical system analysis. Besides, this model includes a change of sign for the dark energy density parameter, which must have been negative in the past.

In order to discriminate the studied interacting models from $\Lambda$CDM and other dark energy scenarios, we apply the statefinder analysis. The statefinder planes indicate that interaction has a significant effect on the evolution of the universe, and the sign-changeable interacting models can be distinguished from the $\Lambda$CDM model by this analysis, nevertheless, there are other dark energy models with similar evolutionary trajectories in the statefinder planes, such as standard interacting scenarios, hybrid expansion law and modified Chaplygin gas with interaction. The statefinder diagrams show that the trajectories of some of the models, $\varGamma _{2T}$, $\varGamma _{1c}$, $\varGamma _{2d}$ and $\varGamma _{2c}$, will eventually approach the $\Lambda$CDM fixed point in the $r-s$ and $r-q$ planes (see Fig. 13), meanwhile, other models asymptotically tend to a scaling state, $\varGamma _{1T}$, $\varGamma _{1d}$ and $\varGamma _{1x}$ (see Fig. 12).