1 Introduction

Nowadays theoretical consistency of any viable model of inflation can be tested against recently proposed Swampland Criteria (SC) [1], and Trans-Planckian Censorship Conjecture (TCC) [2]. Even though the success of Inflationary Cosmology lies in its indigenous ability to solve the puzzles with Standard Big Bang Cosmology and to provide the seeds for Large Scale Structures (LSS) we see today, as well as in its profound consistency with the highly precise Cosmic Microwave Background (CMB) data, the latest being the Planck 2018 data [3], recently it was revealed that the single field, slow roll inflationary paradigm itself is plagued with serious theoretical inconsistency [1]. In brief, in order to embed any model of inflation consistently in a Quantum Gravity theory, it has to satisfy a set of criteria, collectively called the Swampland Criteria, that states that (i) the field excursion by scalar fields in field space is bounded by \(\Delta \phi < \mathcal {O}(1)M_{pl}\); and (ii) the potential of a scalar field which rolls and dominates the energy density of the universe has to satisfy the condition \(V'(\phi )/V(\phi )\sim \sqrt{2\epsilon }M_{pl}^{-1}>c M_{pl}^{-1}\) with \(c\sim \mathcal {O}(1)\) and \(\epsilon \) being the first slow roll parameter and \(M_{pl}\) is the Planck mass. Now if we consider the single field consistency relation \(r = 16 \epsilon = 8 c^2\) with r being the tensor-to-scalar ratio, we can see that the requirement of SC of \(c\sim \mathcal {O}(1)\) can ruin the recent observational bound \(r<0.064\)Footnote 1 [3].

The second constraint on the theory of inflation comes from recently conjectured Trans-Planckian Censorship Conjecture [2]. In order to produce the seeds of perturbations in LSS, the quantum vacuum fluctuations exit the horizon and get frozen during inflation only to re-enter the horizon at a later stage of cosmological evolution. However, one can see that if inflation lasts more than the minimum period required, all the observable modes has to have a length scale smaller than Planck scale, which once again leads to inconsistent theory of Quantum Gravity. This problem is known as Trans-Planckian Problem [6]. The only wayout seems to be coming through a conjecture, called the Trans-Planckian Censorship Conjecture [2], that states that the length scales smaller than Planck scale can never exit the Hubble Horizon. As a consequence this conjecture places a tight theoretical constraint on the tensor-to-scalar ratio \(r<10^{-30}\) and so a constraint on the first slow roll parameter can be written as, \(\epsilon < 10^{-31}\) from the single field consistency relation \(r=16 \epsilon \) [7].

Looking at the constraint on \(\epsilon \) put by the SC and TCC, it may appear that they are in tension with each other, and together they may serve as a no go theorem for a consistent single field slow roll model of inflation. However, it was revealed of late that TCC can be derived from the first SC [8]. Also the second SC can be refined using the first SC and Bousso’s entropy bound [9] and can be restated as, a field theory will not be in Swampland if either \(V'(\phi )/V(\phi )\sim \sqrt{2\epsilon }M_{pl}^{-1}>c M_{pl}^{-1}\) or \(V''(\phi )/V(\phi )\le -c' M_{pl}^{-2}\) with \(c,c'\sim \mathcal {O}(1)\) [10, 11]. Consequently, one can have a valid inflationary scenario consistent with the refined SC if one satisfies the following condition: the second slow roll parameter \(\eta \sim \mathcal {O}(1)\) with the first slow roll parameter still satisfying the observational bound \(\epsilon \ll 1\). The constraint on \(\eta \) from Planck observation [3] is given by \(\eta \sim -0.02\) which can be considered as close to \(\mathcal {O}(1)\) as argued in [12] . As we have already stated, the only requirement from TCC is \(\epsilon \ll 1\). Hence, to summarize the theoretical constraints, any single field slow roll inflationary theory would be consistent with both the refined SC and TCC if one satisfies \(\epsilon \ll 1\) and \(\eta \sim \mathcal {O}(1)\) simultaneously.

Even though one takes care of the theoretical perspective and the possible wayout as discussed above while inflationary model building, on the backdrop this leads to an altogether novel problem from observational point of view, namely, the future prospects of detection of primordial gravitational waves (PGW). As stated earlier TCC requires a very tiny value for \(r<10^{-30}\). This tiny value is beyond the scope of any future observation, let alone the next generation CMB missions like CMB-S4 [13], LiteBIRD [14, 15], COrE [16] etc.

This bound is further tightened to \(r<10^{-47}\) if one assumes that the pre-inflationary era was radiation dominated [17]. Although the bound can slightly be relaxed to \(r<10^{-10}\) if one assumes that the equation of state of inflation changes from \(-1\) to \(-(1/3)\) after a couple of e-folding [18], this is still much below the scope of future CMB missions. Thus, those theoretical constraints put a serious question on the prospects of PGW to act as the smoking gun of inflationary paradigm [19], namely, whether or not it can act as the ‘Holy Grail’ of inflationary cosmology in the light of these theoretical constraints.

However, with further progress of theoretical analysis, it was recently found that one can bypass the SC within the standard single field inflationary framework if one considers the initial states as follows: the tensor modes in Non Bunch Davies state (NBD) and scalar modes in Bunch Davies (BD) state [4, 20]. Subsequently, it was also revealed that if the initial states of both the scalar and tensor modes are NBD, one can relax the TCC bound on r as well, thereby revitalising the possibility of producing a detectable PGW by vacuum fluctuation of inflaton [21] orders close to the range of future CMB missions. Also pre-inflation scenarios suggest that one should set NBD vacuum as the initial states [22]. Thus, the above prescription of considering NBD states for both scalar and tensor modes to obtain a detectable PGW signal from a consistent theoretical framework brings back the relevance of PGW as a probe of inflationary cosmology. The effect of NBD on the scalar perturbations has been studied to a considerable extent [23,24,25,26,27,28,29,30], mostly with theoretical motivation. However, in the light of PGW, the motivation to explore NBD states gets an observational relevance as well. It is important to note that other than initial states modification the upper bound on r can be relaxed by other mechanisms as well e.g in [31] it is shown that by considering a oscillatory stage after inflation the upper bound on r can be significantly relaxed as \(r\le 10^{-8}\).

In this article our primary intention is to develop consistent 3-point statistics with tensor modes with NBD initial states keeping in mind the above discussion on its relevance in the context of SC and TCC. We would primarily focus on TCC to study the properties of 3-point functions and for any possible enhancement in signal strength we would focus on the parameter space where TCC bound is relaxed due to NBD states. To this end, we would bring forth different correlators relevant for the non-Gaussian behavior of PGW followed by the templates for the corresponding nonlinearity parameters \(f_{NL}\) for different relevant shapes considering NBD initial states for both scalar and tensor modes; and study their prospects of detection in future CMB missions. We believe the present analysis is important for couple of reasons. First, the higher order correlation functions can be very sensitive to the choice of initial state (BD/NBD) and hence can be an important probe for the initial vacuum as well. Secondly, the shape of the auto correlation of tensor modes can shed some light on the source of PGW. Thirdly, the mixed correlator of scalar and tensor modes can probe additional properties of PGW which will be discussed in the next sections. To name one, correlators of tensor-scalar-scalar type can serve as a probe of spatial diffeomorphism breaking during inflation [32]. From observational point of view, this mixed correlator also reflects on the quadrupole moment and might be of interest for future CMB missions. Last but not the least, these non-Gaussian properties serve as additional probe for PGW along with the 2-point function r. Thus, detection of any of the correlators would give us a hint on PGW and initial state. Some preliminary studies on the prospects of tensor non-Gaussianities have been reported by the present authors in [33, 34] and also by some other authors [19, 29, 35,36,37]. However, almost all of them consider BD vacuum. Here we would like to extend the analysis for NBD states and explore the prospects of both auto and mixed correlators.

As of now, the observational bounds on tensor non-Gaussianities are not too tight. The current constraints on the amplitude of tensor bispectrum in equilateral limit is given by Planck 2018 as: \(f_{NL}^{T} = 800 \pm 1100\) [38]. However, for the reasons mentioned above, the hunt for any possible non-Gaussian behavior of PGW in upcoming CMB missions will be more relevant than ever. These constraints will be further improved in next generation CMB missions. For example, LiteBIRD [14, 15] targets to improve the constraint of the amplitude of tensor bispectra by three orders of magnitude [14, 15]. The constraint on tensor-tensor-scalar mixed correlator will be improved by CMB-S4 [13]. Others have their own specific target. Keeping this in mind, in this article, we would like to explore all possible correlators, namely, the tensor-tensor-tensor (auto) correlator and tensor-tensor-scalar and tensor-scalar-scalar (both mixed) correlators and study the possible enhancement in signal strength in the light of TCC. The theoretical analysis is done using the model independent framework of Effective Field Theory (EFT) of inflation [39] to calculate the tensor-tensor-tensor and scalar-tensor-tensor correlators. To calculate the tensor-scalar-scalar correlator we have used the EFT of inflation with broken space-time diffeomorphism [32] as this type of correlator can reflect a unique feature of broken spatial diffeomorphism. Once we have the correlators in our hand, we would move on to proposing templates for the corresponding nonlinearity parameters \(f_{NL}\) for different shapes of interest and would also investigate if any of them could be the point of interest for future CMB missions by finding out the possible upper limits for each one allowed by the parameters of the theory under consideration. We would like to reiterate that because of the background EFT of inflation, our calculations and results are more or less generic and model-independent.

2 Swampland, TCC and Non Bunch Davies states

As already mentioned, it is the non Bunch Davies states that can give rise to a viable inflationary scenario respecting the SC and TCC. Let us begin our discussion with a brief review on the role of NBD states and how that can help bypass the SC and relax the bound on r coming from TCC in the same vein of [4, 20, 21]. This will also help us develop the rest of the article from a consistent theoretical setup. However it should be noted that in our analysis we would be primarily focusing on TCC to study the primordial correlators. To this end, we will first discuss the scenario with the minimal model, i.e., single field inflation with canonical kinetic term, and will subsequently move on to discussing the non-canonical inflationary models.

2.1 Canonical models of inflation

For a canonical inflation scenario the power spectra of scalar and tensor modes for NBD states are given by

$$\begin{aligned} P_{\zeta }(k)= \frac{H^2}{8 \epsilon M_{pl}^2}|\alpha ^{s}_k+\beta ^{s}_k|^2 \end{aligned}$$
(2.1)

and,

$$\begin{aligned} P_{\gamma }(k)= \frac{2 H^2}{M_{pl}^2}|\alpha ^{t}_k+\beta ^{t}_k|^2 \end{aligned}$$
(2.2)

where \(\zeta \) and \(\gamma \) represent scalar and tensor modes respectively; \(\alpha \) and \(\beta \)’s are Bogolyubov coefficients and the indices s and t signify scalar and tensor respectively as we have considered different vacua for scalar and tensor modes. Setting \(\alpha ^{s/t}_k=1\) and \(\beta ^{s/t}_k=0\) one readily gets back the BD states.

We also, introduce two quantities,

$$\begin{aligned} \Gamma _{s}= & {} \vert \alpha _k^{s} + \beta _k^{s}\vert ^2 \end{aligned}$$
(2.3)
$$\begin{aligned} \Gamma _{t}= & {} \vert \alpha _k^{t} + \beta _k^{t}\vert ^2 \end{aligned}$$
(2.4)

The tensor-to-scalar ratio with NBD states can be written as,

$$\begin{aligned} r=\frac{P_{\gamma }(k)}{P_{\zeta }(k)}=16 \epsilon \Gamma \end{aligned}$$
(2.5)

where \(\epsilon \) is the first slow roll parameter and

$$\begin{aligned} \Gamma =\frac{|\alpha ^{t}_k+\beta ^{t}_k|^2}{|\alpha ^{s}_k+\beta ^{s}_k|^2} \end{aligned}$$
(2.6)

The first theoretical constraint on the Bogolyubov coefficients come via the Wronskian condition

$$\begin{aligned} |\alpha ^{s/t}_k|^2-|\beta ^{s/t}_k|^2=1 \end{aligned}$$
(2.7)

using which the Bogolyubov coefficients can further be parameterized as

$$\begin{aligned} \alpha ^{s/t}_k= & {} \sqrt{1+N_k^{(s/t)}} e^{i \theta _{\alpha }^{(s/t)}(k)} \end{aligned}$$
(2.8)
$$\begin{aligned} \beta ^{s/t}_k= & {} \sqrt{N_k^{(s/t)}}e^{i\theta _{\beta }^{(s/t)}(k)} \end{aligned}$$
(2.9)

Here, \(N_k^{(s/t)}\) represents the number of NBD particles in BD state and \(\theta _{\alpha }^{(s/t)}(k)\) and \(\theta _{\beta }^{(s/t)}(k)\) are the phase factors. Consequently, one can define the relative phase as

$$\begin{aligned} \theta ^{(s/t)}(k)=\theta _{\alpha }^{(s/t)}(k)-\theta _{\beta }^{(s/t)}(k) \end{aligned}$$
(2.10)

This parametrisation would help us to reduce the number of parameters since the individual phase factors are degenerate. Also in our analysis we consider \(\theta ^{(s/t)}(k)\) to be constant.

Further, there is a theoretical constraint on the parameters \(\beta ^{(s/t)}_k\) coming from backreaction condition [23, 40]. For this one can model them as following [23]

$$\begin{aligned} \beta ^{s/t}_k \sim \beta ^{(s/t)}_0 e^{-\frac{k^2}{(M_{(s/t)}a(\eta _0))^2}} \end{aligned}$$
(2.11)

where \(\eta _0\) describes the time when modes are below cut-off scale \(M_{(s/t)}\). One can readily check that for \(k > M_{(s/t)}\), \(\beta ^{s/t}\rightarrow 0\). Now, in order a theory of inflation to be valid within the regime of EFT, it has to satisfy \( M_{(s/t)}>H\). With the requirement that excited initial state does not spoil the single field slow roll inflationary conditions one can write the backreaction condition as [23]:

$$\begin{aligned} \beta _0^{(s/t)}\le \sqrt{\epsilon \eta '} \frac{H M_{pl}}{M_{(s/t)}^2} \end{aligned}$$
(2.12)

From now we will represent the second slow roll parameter with \(\eta '\) to avoid confusion with conformal time.

As mentioned earlier, the SC forces the first slow roll parameter \(\epsilon \sim M^2_{pl}/2\left\{ V'(\phi )/V(\phi )\right\} ^2\sim c^2/2\) with \(c \sim \mathcal {O}(1)\) and as a result the single field consistency relation now violates the observational bound on r. From (2.5) and (2.6) one can see that for \(\Gamma <1\) the observational constraint on r can still be satisfied even with a large \(\epsilon \) coming from SC. Now there are two ways to make \(\Gamma <1\). The first one is to have NBD states for scalar fluctuations and BD state for tensor fluctuation. One can choose a model where \(\Gamma _s\left( =|\alpha ^{s}_k+\beta ^{s}_k|^2\right) \gg 1\) and suppress the value of r, without breaking the backreaction condition (2.12) as shown in [23]. But as explained in [4] this choice of \(\Gamma _s\) can ruin the constraint on scalar three point function. On the other hand, if one starts with tensor modes in NBD state and scalar modes in BD state one can find a region in the parameter space that satisfy the PGW bispectrum constraints and allow \(c\sim 0.8\); larger value of \(c\sim 0.9\) can also be achievable in this region of parameter space [20] thus satisfying the SC.

Secondly, TCC puts a very tight constraint on \(r<10^{-30}\) and hence from single field consistency relation for BD vacuum, the first slow roll parameter \(\epsilon < 10^{-31}\). This bound on the tensor to scalar ratio basically states that in future if any PGW gets detected that can not be due to inflation but can be produced from other sources during inflation [34,35,36,37]. So, apparently, PGW loses its ‘Holy Grail’ status in the light of TCC [41]. However, this theoretical bound on r placed by TCC can be relaxed significantly if one uses NBD states for both tensor and scalar modes [21]. Consequently, the consistency relation now modifies to (2.5),

$$\begin{aligned} r=16 \epsilon \frac{\Gamma _t}{\Gamma _s} \end{aligned}$$
(2.13)

where the \(\Gamma \) in (2.5) factor is re-written in terms of \(\Gamma _{s/t}\) defined earlier in this section. In this scenario TCC places the bound not on r alone but on the combined parameter \(\epsilon /\Gamma _s<10^{-31}\). So if one can enhance the \(\Gamma _t\) then the bound on r can be relaxed significantly. To do so we take a look at the backreaction condition (2.12). If one uses (2.1) to properly replace the \(M_{pl}\) factor of (2.12) one arrives at

$$\begin{aligned} \beta _0^{(t)}\le \frac{\sqrt{\eta '}}{8 \pi ^2 P_{\zeta }} \left( \frac{H}{M_{(t)}}\right) ^2 \sqrt{\Gamma _s} \end{aligned}$$
(2.14)

So with \(\beta _0^{(s)}\gg 1\) we can have a large \(\beta _0^{(t)}\). In this limit of \(\beta _0^{(s)}\), \(\sqrt{\Gamma _s}\sim \beta _0^{(s)}\) and with \(P_{\zeta }\sim 10^{-9}\), \(\eta '\sim -0.01755\) [3] if one considers, \(\Gamma _s\sim 10^{23}\) with \(M_{(t)}=10 H\) we can have \(r \le 0.001\) which is still within the detectable range of next generation CMB missions. Here one important thing to note is that \(\beta _0^{(s)}\gg 1\) does not spoil the scalar non-Gaussianity bound as TCC requires a very small value of \(\epsilon \) that guarantees that the bispectrum amplitude remains within the observational bound as it is evident from [21, 42, 43].

$$\begin{aligned} f_{NL}^{loc}\sim \frac{k_s}{k_l} \epsilon \end{aligned}$$
(2.15)

where \(f_{NL}^{loc}\) is the amplitude of local configuration of scalar bispectrum and \(k_s\) and \(k_l\) are respectively the shortest and longest wavelength probed by any CMB mission under consideration (e.g., Planck mission as of today).

2.2 Non-canonical models of inflation

Until now we have only discussed the scenario with canonical kinetic term. However, EFT of inflation can take into account inflationary models with non-canonical terms as well. This will modify the consistency relation [44] within the single field framework as well as the backreaction condition [27]. Effectively, the modifications come via the scalar and tensor sound speeds \(c_{s/t}\), including which (2.1) and (2.2) now look

$$\begin{aligned} P_{\zeta }(k)= & {} \frac{H^2}{8 \epsilon M_{pl}^2 c_s}\Gamma _s \end{aligned}$$
(2.16)
$$\begin{aligned} P_{\gamma }(k)= & {} \frac{2 H^2}{M_{pl}^2 c_t}\Gamma _t \end{aligned}$$
(2.17)

Consequently,, the consistency relation now takes the form

$$\begin{aligned} r=16 \epsilon \frac{\Gamma _t}{\Gamma _s}\frac{c_s}{c_t} \end{aligned}$$
(2.18)

and the backreaction condition modifies to

$$\begin{aligned} \beta _0^{(s/t)}\le \sqrt{\epsilon \eta '} \frac{H M_{pl}}{M_{(s/t)}^2}\frac{1}{\sqrt{c_{s/t}}} \end{aligned}$$
(2.19)

It is straightforward to check that for \(c_{s/t} =1\) one gets back the canonical scenario. From (2.18) we can see in the context of SC, apart from the \(\Gamma _t/\Gamma _s\) term, there is another factor \(c_s/c_t\) which can also act as a suppression factor for a small value for \(c_s\). However, \(c_s\) can not be arbitrarily small as there is another constraint on it coming from the bounds on scalar non-Gaussianities. In the equilateral limit, the amplitude of scalar bispectrum reads [45, 46],

$$\begin{aligned} f_{NL}^{eq}=\frac{35}{108}\left( -1+\frac{1}{c_s^2}\right) \end{aligned}$$
(2.20)

Hence, together with the constraint from scalar non-Gaussianity \(f_{NL}^{eq}=-4\pm 40\) [50], the value of factor c coming from SC becomes \(c\sim 0.37\) with \(c_s>0.067\).

Clearly, the above value of c is not compatible with SC, as discussed earlier. So, in order to bypass the SC, one need take shelter of the NBD factor \(\frac{\Gamma _t}{\Gamma _s}\) [20]. However, for TCC this non-trivial sound speed can help in relaxing the bound on r. From (2.19) one can write

$$\begin{aligned} \beta _0^{(t)}\le \frac{\sqrt{\eta '}}{8 \pi ^2 P_{\zeta }} \left( \frac{H}{M_{(t)}}\right) ^2 \sqrt{\frac{\Gamma _s}{c_s c_t}} \end{aligned}$$
(2.21)

Together with (2.18) this equation tells us that in order to relax the bound on r, one needs to have a small value for the sound speed of tensor fluctuation such that the factor \(\frac{c_s}{c_t}\) acts as an enhancing factor.

Fig. 1
figure 1

Allowed region of \(N_0^{(t)}\) and \(c_t\) using Planck constraint on the amplitude of two point function

Full size image

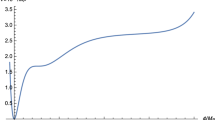
Combining all the above constraints on the parameters, we have \(\epsilon c_s/\Gamma _{(s)}<10^{-31}\) and \(r<0.064\). Figure 1 shows the region between \(c_t\) and \(N_0^{(t)}\) that is allowed considering both the theoretical (TCC bound) and latest observational constraints (Planck 2018). The figure show that for particular combinations of \(c_t\) and \(N_0^{(t)}\) one can have a bound on r which can match the upper bound set by Planck 2018, thereby bringing back its relevance as the smoking gun for inflationary cosmology.

3 The second order action from EFT

In this section we briefly summaries the major equations staring from the EFT of inflation [39], a model independent framework developed to analyze primordial fluctuations, that will help us calculate the 3-point function for PGW with NBD states. As pointed out earlier, the prospects of EFT of inflation in exploring tensor non-Gaussianities have been investigated to some extent by the present authors in couple of articles [33, 34]. In this article, our analysis takes under consideration NBD states as well as is consistent with theoretical constraint of TCC.

A consistent EFT of inflation can be given starting from the fact that time diffeomorphism is broken spontaneously after inflation and as a result Goldstone Boson is produced. In unitary gauge the Lagrangian can be written as,

$$\begin{aligned} \mathcal {S}= & {} \int d^4x \sqrt{-g}\left[ \frac{1}{2}M_{pl}^2R-\Lambda (t)-c(t)g^{00}\right. \nonumber \\&\left. +\frac{1}{2}M_2(t)^4(g^{00}+1)^2\right. \nonumber \\&\left. -\frac{\bar{M}_1(t)^3}{2}(g^{00}+1)\delta K_{\mu }^{\mu } -\frac{\bar{M}_2(t)^2}{2}\delta K_{\mu }^{\mu 2} \right. \nonumber \\&\left. -\frac{\bar{M}_3(t)^2}{2}\delta K_{\mu }^{\nu } K_{\nu }^{\mu }\right. \left. + \frac{M_3(t)^4}{3!}(g^{00}+1)^3\right. \nonumber \\&\left. -\frac{\bar{M}_4(t)^3}{3!}(g^{00}+1)^2\delta K_{\mu }^{\mu } -\frac{\bar{M}_5(t)^2}{3!}(g^{00}+1)\delta K_{\mu }^{\mu 2}\right. \nonumber \\&\left. -\frac{\bar{M}_6(t)^2}{3!}(g^{00}+1) \delta K_{\mu }^{\nu } \delta K_{\nu }^{\mu } \right. \nonumber \\&\left. -\frac{\bar{M}_7(t)}{3!}\delta K_{\mu }^{\mu 3} -\frac{\bar{M}_8(t)}{3!}\delta K_{\mu }^{\mu } \delta K_{\nu }^{\rho } \delta K_{\rho }^{\nu }\right. \nonumber \\&\left. - \frac{\bar{M}_9(t)}{3!}\delta K_{\mu }^{\nu } \delta K_{\nu }^{\rho } \delta K_{\rho }^{\mu }+\ldots .\right] \end{aligned}$$
(3.1)

Here \(\delta K\) is the fluctuation in extrinsic curvature. \(M_{i}\) and \(\bar{M}_i\) denotes parameters that measures the strength of higher order fluctuations. Different combination of \(M_{i}\) and \(\bar{M}_i\) produce results for different kind of theory. Note that the scalar fluctuation is now represented by the Goldstone Boson \(\pi \) produced by broken time diffeomorphism and it is related to curvature perturbation \(\zeta \) as \(\zeta =-H \pi \).

Another aspect to note here is that the sound speed of scalar and tensor fluctuations get modified due to the presence of higher order fluctuation term. From (3.1) the second order Lagrangian for scalar fluctuation can be written as,

$$\begin{aligned} \mathcal {S}^{s}_{2} =\int dt~d^3x~ a^3\left( \frac{\frac{\bar{M_{1}}^3}{2}H-M_{p}^2\dot{H}}{c^2_s}\right) \left[ \dot{\pi }^2-c^2_s\frac{(\partial _i \pi )^2}{a^2}\right] \end{aligned}$$
(3.2)

where scalar sound speed is given by

$$\begin{aligned} c_s^2=\frac{\frac{\bar{M_{1}}^3}{2}H-M_{p}^2\dot{H}}{2M_2^4-M_{p}^2\dot{H}} \end{aligned}$$
(3.3)

Further, from (3.1) the second order tensor fluctuation can be written as,

$$\begin{aligned} S^{T}_2=\int d^4x \sqrt{-g}\left[ \frac{M_{pl}^2}{8}\left( \dot{\gamma }_{ij}^2- \frac{(\partial _k \gamma _{ij})^2}{a^2}\right) -\frac{\bar{M}_{3}^{2}}{8}\dot{\gamma }_{ij}^2 \right] \end{aligned}$$
(3.4)

and the corresponding sound speed of tensor perturbation is given by

$$\begin{aligned} c_{t}^2= \frac{M_{pl}^2}{M_{pl}^2-\bar{M}_3^2} \end{aligned}$$
(3.5)

As we have seen in the last section, these modified sound speeds of perturbations can significantly influence the backreaction condition and hence the parameter space to relax TCC bound. In the rest of the article, we will make use of the above actions as well as the non-trivial sound speeds for scalar and tensor perturbations to analyse the 3-point statistics for tensor modes using NBD initial state.

4 The tensor-tensor-tensor (\(\gamma \gamma \gamma \)) correlator

Let us begin with calculating the auto-correlation of tensor modes that gives rise to the auto-bispectrum, i, e the tensor-tensor-tensor correlator. To calculate the bispectrum we have to look at the third order Lagrangian of tensor fluctuation and the most general Lagrangian can be written as [33, 51],

$$\begin{aligned} S_{3}^{T}= & {} \int d^4x \sqrt{-g}\left( -\frac{M_{pl}^2}{8}\left( 2 \gamma _{ik} \gamma _{jl}-\gamma _{ij}\gamma _{kl} \right) \right. \nonumber \\&\left. \times \frac{\partial _k \partial _l \gamma _{ij}}{a^2}-\frac{\bar{M}_9}{3!} \dot{\gamma }_{ij} \dot{\gamma }_{jk} \dot{\gamma }_{ki}\right) \end{aligned}$$
(4.1)

In the above action, the term proportional to \(M_{pl}\) is the sole contribution of the so-called Einstein or R part and the term proportional to \(\bar{M_9}\) is the contribution of higher order gravitational fluctuations. As it will be revealed below, together they play a crucial role in determining the strength of tensor bispectra.

In order to calculate the 3-point correlation function of tensor fluctuations, we make use of the IN-IN formalism. With the NBD states the \(\langle \gamma \gamma \gamma \rangle \) 3-point function for any general interaction Hamiltonian \(H_I(t)\) can be written as,

$$\begin{aligned} \langle \gamma ^{s_1}_{k_1} \gamma ^{s_2}_{k_2} \gamma ^{s_3}_{k_3}\rangle =-i\int _{\eta _0}^{0} dt' \left\langle 0\left| \left[ \gamma ^{s_1}_{k_1} \gamma ^{s_2}_{k_2} \gamma ^{s_3}_{k_3}, H_I(t')\right] \right| 0 \right\rangle \end{aligned}$$
(4.2)

where \(s_i =\{+, \times \}\) are the polarization indices. An essential point to note here is that the lower limit of the integration is different from the BD case which can give rise to a non-trivial oscillatory term proportional to \(e^{i K \eta _0}\), where K can be any possible combination of \((k_1\pm k_2\pm k_3)\). We will work with sub-horizon modes where \(\vert k_i \eta _0 \vert \gg 1\).

So, with NBD states the contribution of the R part to the \(\langle \gamma \gamma \gamma \rangle \) correlator is given by

$$\begin{aligned}&\langle \gamma ^{s_1}_{k_1} \gamma ^{s_2}_{k_2} \gamma ^{s_3}_{k_3}\rangle |_R= \frac{H^4}{32 M_{pl}^4 c_{t}^3}\frac{1}{k_1^3 k_2^3 k_3^3}(s_1 k_1+s_2 k_2+s_3 k_3)^2 F(s_1 k_1,s_2 k_2,s_3 k_3) (\alpha ^t_1+\beta ^t_1)(\alpha ^t_2+\beta ^t_2)(\alpha ^t_3+\beta ^t_3) \nonumber \\&\times \left[ \left( -c_t (k_1+k_2+k_3)+c_{t}\frac{k_1^2(k_2+k_3)+k_2 k_3(k_2+k_3)+k1(k_2^2+4k_2 k_3+k_3^2)}{(k_1+k_2+k_3)^2}\right) \left( \alpha _1^{t*}\alpha _2^{t*}\alpha _3^{t*}-\beta _1^{t*}\beta _2^{t*}\alpha _3^{t*}\right) \right. \nonumber \\&\left. + \left( -c_t (-k_1+k_2+k_3)+c_t\frac{k_1^2(k_2+k_3)+k_2 k_3(k_2+k_3)-k_1(k_2^2+4k_2 k_3+k_3^2)}{(-k_1+k_2+k_3)^2}\right) \left( \alpha _2^{t*}\alpha _3^{t*}\beta _1^{t*}-\beta _1^{t*}\beta _2^{t*}\alpha _3^{t*}\right) \right. \nonumber \\&\left. -\left( -c_t (k_1-k_2+k_3)+c_t\frac{k_1^2(k_2-k_3)+k_2 k_3(-k_2+k_3)-k_1(k_2^2-4k_2 k_3+k_3^2)}{(k_1-k_2+k_3)^2}\right) \left( \alpha _1^{t*}\alpha _3^{t*}\beta _2^{t*}-\beta _1^{t*}\beta _3^{t*}\alpha _2^{t*}\right) \right. \nonumber \\&\left. +\left( -c_t (k_1+k_2-k_3)+c_t\frac{k_1^2(k_2-k_3)+k_2 k_3(-k_2+k_3)-k_1(k_2^2-4k_2 k_3+k_3^2)}{(k_1+k_2-k_3)^2}\right) \left( \alpha _1^{t*}\alpha _2^{t*}\beta _3^{t*}-\beta _1^{t*}\beta _2^{t*}\alpha _3^{t*}\right) \right] \nonumber \\&+c.c. + g_{osc,R} (k_1,k_2,k_3) \end{aligned}$$
(4.3)

with the following notations: \(\alpha _i= \alpha _{k_i}\), \(\beta _i=\beta _{k_i}\) and so on, and the momentum conserving delta function is dropped here. Here on the right hand side the \(s_i\) indices will determine the sign before the momentum hands \(k_i\) (whenever the \(s_i\) indices appear before \(k_i\)) which follows from the fact that the polarization tensors satisfy \(\epsilon ^s_{ij}(k)=\epsilon ^{\bar{s}}_{ij}(-k)\) where if s is ‘\(+\)’ then \(\bar{s}\) is ‘\(\times \)’ and vice versa [47]. The \(g_{osc,R}\) is the oscillatory part of the bispectrum which is explicitly written in 1. Also, a ‘\(*\)’ stands for the complex conjugate of \(\alpha _i\) and \(\beta _i\), as the case may be.

The term F(x, y, z) appears due to the contraction of polarization tensors. Written explicitly, it reads,

$$\begin{aligned} F(x,y,z)=\frac{(x+y+z)^3(x+y-z)(x-y+z)(-x+y+z)}{x^2y^2z^2} \nonumber \\ \end{aligned}$$
(4.4)

with x, y, z are, in this particular scenario, given by the combination of \(s_i\) and \(k_i\) as given in (4.3). For rapid oscillations i,e if \(K \eta _0\gg 1\), the contribution of \(g_{osc,R}\) can be neglected as in this limit the average of the exponential will be zero. But in some configurations where the oscillation is not rapid for relevant modes, \(g_{osc,R}\) can induce oscillatory features on the bispectrum [48, 49]. From (A.1) one can check that for flattened limit configuration where, \(k_2+k_3=k_1\) or similar configurations, \(K=k_2+k_3-k_1\) vanishes and the three-point function can get an enhancement by appropriate powers of \(\eta _0\) as seen for scalar fluctuations [23], but the presence of the function F(x, y, z) in (4.3) and (A.1) ensures that the tensor bispectrum due to Einstein term always vanishes in flattened limit as one can see from (4.4) that F(x, y, z) contains the term \((k_i+k_j-k_l)\) for which F(x, y, z) vanishes in flattened limit. In other momentum configurations the \(g_{osc,R}\) will induce an oscillatory feature and can have an enhancement proportional to \(\vert k \eta _0 \vert \), but projecting this oscillatory part onto different observational templates of bispectrum one power of \(\vert k \eta _0 \vert \) gets reduced [48] and observationally there is no enhancement in the signal due to this factor. Also these oscillatory features induced by \(g_{osc,R}\) are hard to detect observationally, so for any kind of enhancement in the signal we focus solely on the non-oscillatory part.

To calculate the amplitude of bispectrum we will use the parameterisation (2.8) and (2.9). \(N_k^{(s/t)}\) can be modeled as \(N_k^{(s/t)}\sim N_0^{(s/t)} e^{-k^2/(M_{(s/t)}\eta _0)^2}\). Further, if \(M_{(s)}\) lies within the observable mode, i.e if the exponential factor is non-negligible, then the amplitude of bispectrum also gets suppressed. So, we consider \(N_k^{(s/t)}\sim N_0^{(s/t)}\).

Following [19, 38]. let us define the amplitude of tensor non-Gaussianity, i.e., the tensor nonlinearity parameter \(f_{NL}\) as,

$$\begin{aligned} f_{NL}^{s_1 s_2 s_3}=\frac{5}{6} \frac{\langle \gamma ^{s_1}_{k_1} \gamma ^{s_2}_{k_2} \gamma ^{s_3}_{k_3}\rangle }{P_{\zeta }(k_1) P_{\zeta }(k_2)+P_{\zeta }(k_2)P_{\zeta }(k_3)+P_{\zeta }(k_3)P_{\zeta }(k_1)} \end{aligned}$$
(4.5)

In the limit \(N_0^{(s/t)}\gg 1\), one finds that \(\Gamma _{(s/t)}\sim N_0^{(s/t)}\). It can also be shown that in the limit \(N_0^{(s/t)}\gg 1\), Eq. (4.3) can be estimated as,

$$\begin{aligned} \langle \gamma ^{s_1}_{k_1} \gamma ^{s_2}_{k_2} \gamma ^{s_3}_{k_3}\rangle |_R\propto \frac{H^4}{32 M_{pl}^4 c_{t}^2} (N_0^{(t)})^2 \times f(k_i) \end{aligned}$$
(4.6)

where \(f(k_i)\) encodes all the momentum dependence. The \((N_0^{(t)})^2\) comes from different combinations of \(\alpha _i^t\) and \(\beta _i^t\) in Eq (4.3).

Consequently, from (4.5) and (2.16) the nonlinearity parameter for \(\langle \gamma \gamma \gamma \rangle \) correlation can be estimated as,

$$\begin{aligned} f_{NL}\vert _{\gamma \gamma \gamma (R)}\propto \left( \frac{\epsilon c_s}{c_t}\frac{\Gamma _{(t)}}{\Gamma _{(s)}}\right) ^2\sim r^2 \end{aligned}$$
(4.7)

Because of the above definition of \(f_{NL}\), it will always be proportional to \(r^2\), hence, even if we manage to produce a large value for \(N_0^{(t)}\) we can not generate a large bispectrum from the R part of the Einstein term alone.

However, we have in our hand contribution from another operator, namely, the \(\bar{M}_9\) operator, that arises from the higher order gravitational fluctuations in EFT. Let us now discuss the contribution of \(\bar{M}_9\) operator to the 3-point tensor correlator. With this term playing the central role, the 3-point function for the EFT term can be written as,

$$\begin{aligned} \langle \gamma ^{s_1}_{k_1} \gamma ^{s_2}_{k_2}\gamma ^{s_3}_{k_3}\rangle |_{EFT}= & {} \frac{\bar{M_9}H^5}{M_{pl}^6}(\alpha ^t_1+\beta ^t_1)(\alpha ^t_2+\beta ^t_2)\nonumber \\&\times (\alpha ^t_3+\beta ^t_3) F(x,y,z)\nonumber \\&\times \left[ \frac{\left( \alpha _1^{t*}\alpha _2^{t*}\alpha _3^{t*}-\beta _1^{t*}\beta _2^{t*}\beta _3^{t*}\right) }{(k_1+k_2+k_3)^3}\right. \nonumber \\&\left. -\frac{\left( \alpha _2^{t*}\alpha _3^{t*}\beta _1^{t*}-\beta _2^{t*}\beta _3^{t*}\alpha _1^{t*}\right) }{(k_1-k_2-k_3)^3}\right. \nonumber \\&\left. +\frac{\left( \alpha _1^{t*}\alpha _3^{t*}\beta _2^{t*}-\beta _1^{t*}\beta _3^{t*}\alpha _2^{t*}\right) }{(k_1-k_2+k_3)^3}\right. \nonumber \\&\left. +\frac{\left( \alpha _1^{t*}\alpha _2^{t*}\beta _3^{t*}-\beta _1^{t*}\beta _2^{t*}\alpha _3^{t*}\right) }{k_1+k_2-k_3}\right] \nonumber \\&+c.c. + g_{osc,EFT}(k_1,k_2,k_3) \end{aligned}$$
(4.8)

where, \(g_{osc,EFT}\) is the oscillatory part.

The TCC constraint \(\epsilon <10^{-31}\) gives the maximum value for H as \(H\sim 3^{3/2}\times 10^{-20}M_{pl}\); Consequently, with the current observational constraints mentioned earlier, the estimates for different limits of \(f_{NL}\) for the operator \(\bar{M_9}\) from the non-oscillatory part of the bispectrum are as: for equilateral limit \(f_{NL}^{eq}\sim 10^{-23}\) whereas for squeezed limit: \(f_{NL}^{sq}\sim 10^{-21}\). These estimations are done under the assumption that \(\bar{M_9}\sim M_{pl}\) and \(c_t=1\) to estimate the maximum contribution of this operator. The details of \(f_{NL}\) parameter is given in 1. It is also important to note that after projecting onto different templates \(g_{osc,EFT}\) can have an effective enhancement by a factor of \(\vert k \eta _0 \vert \) (as one can see from (A.4)) but as the signal strength is extremely small this enhancement will be rather irrelevant from the observational perspective. This indicates that the contribution of this operator is highly suppressed for TCC as compared to the result reported in [33]. From this above discussion we can see that even with NBD states the signal strength for \(\langle \gamma \gamma \gamma \rangle \) correlator arising from the combination of Einstein R and the EFT term is too feeble to be detected, at least in next generation CMB missions.

5 The tensor-tensor-scalar (\(\gamma \gamma \zeta \)) correlator

As the auto bispectrum, the mixed correlation between scalar and tensor modes can also help us to estimate the parameters of PGW. In [52] it is shown that \(\bar{M}_3 \delta K_{\nu }^{\mu }\delta K_{\mu }^{\nu }\) operator can contribute to \(\langle \gamma \gamma \zeta \rangle \) correlation in decoupling limit and it is very sensitive to the sound speed of tensor fluctuation. This is because (3.5) reveals that the tensor sound speed is modified due to the presence of \(\bar{M}_3\). So it is evident that a non zero \(\bar{M}_3\) i, e \(c_t \ne 1\) will lead to non zero amplitude of \(\langle \gamma \gamma \zeta \rangle \) correlator.

In decoupling limit, the part of the action that is contributing to the above mixed correlator arises from \(\bar{M}_3 \delta K_{\nu }^{\mu }\delta K_{\mu }^{\nu }\) and can be written as,

$$\begin{aligned} \mathcal {S}_{\gamma \gamma \zeta }=\frac{\bar{M}_3}{4} \int d^4 x \sqrt{-g} \dot{\gamma }_{ij} \frac{\partial _k \gamma _{ij}\partial _k \pi }{a^2} \end{aligned}$$
(5.1)

From the above action (5.1), we can calculate the \(\langle \gamma \gamma \zeta \rangle \) correlator that reads

$$\begin{aligned} \langle \zeta _{k_1} \gamma _{k_2}^{s_2}\gamma _{k_3}^{s_3} \rangle= & {} -\frac{\bar{M_3}H^4}{16 M_{pl}^6 c_s \epsilon }(\alpha ^s_1+\beta ^s_1)(\alpha ^t_2+\beta ^t_2)(\alpha ^t_3+\beta ^t_3)\epsilon _{ij}^{s_2}(k_2)\epsilon _{ij}^{s_3}(k_3)\frac{(\vec {k_1}.\vec {k_2})}{k_1^3k_2^3k_3}\nonumber \\&\times \left[ -\frac{2c_s^2 k_1^2+3 c_s c_t k_1(2 k_2+k_3)+c_t^2(k_2+k_3)(2k_2+k_3)}{(c_s k_1+ c_t(k_2+k_3))^3}\left( \alpha _1^{s*}\alpha _2^{t*}\alpha _3^{t*}-\beta _1^{s*}\beta _2^{t*}\alpha _3^{t*}\right) + \right. \nonumber \\&\times \left. \frac{2c_s^2 k_1^2-3 c_s c_t k_1(2 k_2+k_3)+c_t^2(k_2+k_3)(2k_2+k_3)}{(c_s k_1-c_t(k_2+k_3))^3} \left( \alpha _2^{t*}\alpha _3^{t*}\beta _1^{s*}-\beta _2^{t*}\beta _3^{t*}\alpha _1^{s*}\right) -\right. \nonumber \\&\times \left. \frac{2c_s^2 k_1^2-3 c_s c_t k_1(2 k_2+k_3)+c_t^2(-k_2+k_3)(-2k_2+k_3)}{(c_s k_1+c_t(-k_2+k_3))^3} \left( \alpha _1^{s*}\alpha _3^{t*}\beta _2^{t*}-\beta _1^{s*}\beta _3^{t*}\alpha _2^{t*}\right) -\right. \nonumber \\&\times \left. \frac{2c_s^2 k_1^2-3 c_s c_t k_1(2 k_2-k_3)+c_t^2(k_2-k_3)(2k_2-k_3)}{(c_s k_1+c_t(k_2-k_3))^3} \left( \alpha _1^{s*}\alpha _2^{t*}\beta _3^{t*}-\beta _1^{s*}\beta _2^{t*}\alpha _3^{t*}\right) \right] \nonumber \\&+k_2 \leftrightarrow k_3+c.c. + g_{osc,\gamma \gamma \zeta } \end{aligned}$$
(5.2)

Here, as before, the \(s_i\) are the polarization indices and \(\alpha _i\) and \(\beta _i\) follow the definition as given earlier. The \(\epsilon _{ij}^s(k)\)’s are the polarization tensors (not to be confused with the first slow roll parameter \(\epsilon \) used in the analysis). Note that these tensors did not appear in the earlier correlators as they were completely contracted. Eq. (5.2) is calculated considering nontrivial sound speeds of scalar and tensor fluctuations.

However, current observations do not put any constraint on this correlator. So, in what follows we will mostly be interested to find out how much this signal can be enhanced with the theoretical constraints from TCC, and whether or not that can be of interest for upcoming CMB missions.

First let us analyze the contribution of the non-oscillatory part. From Eq. (5.2) it transpires that both \(\beta _k^{(s)}\) and \(\beta _k^{(t)}\) contribute to the mixed correlator. As a consequence, both \(N_0^{(s/t)}\) and \(\theta ^{(s/t)}\) would eventually contribute to the signal strength of the corresponding mixed bispectrum. As we have argued earlier that to avoid TCC we need to have \(N_0^{(t)}\gg 1\) and as large \(N_0^{(s)}\) to large \(N_0^{(t)}\) we will work in a regime where \(N_0^{(s)}\gg 1\). For the estimation of the signal strength we set \(\theta ^{(s)}=\pi \). Further, we can also write the term \(\epsilon _{ij}^{s_2}(k_2)\epsilon _{ij}^{s_3}(k_3)\) as,

$$\begin{aligned} \epsilon _{ij}^{s_2}(k_2)\epsilon _{ij}^{s_3}(k_3)= & {} \frac{1}{2} (1-\cos \phi ) ~~~\text {for } s_2=s_3 \end{aligned}$$
(5.3)
$$\begin{aligned} \epsilon _{ij}^{s_2}(k_2)\epsilon _{ij}^{s_3}(k_3)= & {} \frac{1}{2} (1+\cos \phi ) ~~~\text {for } s_2=-s_3 \end{aligned}$$
(5.4)

Also (3.5) gives \(\bar{M}_3=(1-c_t^{-2})M_{pl}\) and using (2.16) one can estimate the correlator as,

$$\begin{aligned} \langle \zeta _{k_1} \gamma _{k_2}^{s_2}\gamma _{k_3}^{s_3} \rangle \propto (c_t^{-2}-1) \frac{c_s \epsilon }{\Gamma _s^2} P_{\zeta }^2 (N_0^{(t)})^2 \end{aligned}$$
(5.5)

Therefore, using the same definition of \(f_{NL}\) from (4.5) one can write,

$$\begin{aligned} f_{NL}\vert _{\gamma \gamma \zeta } \propto (c_t^{-2}-1) \frac{c_s \epsilon }{\Gamma _s^2} (N_0{(t)})^2 \sim r c_t (c_t^{-2}-1) \frac{\Gamma _t}{\Gamma _s} \end{aligned}$$
(5.6)

Here we make use of the fact that a large \(N_0^{(s)}\) can lead to large \(N_0^{(t)}\) and in some region of parameter space \(N_0^{(t)}>N_0^{(s)}\), this is why there is no \(N_0^{(s)}\) in the numerator of the first relation of (5.6). In this region of parameter space where \(N_0^{(t)}>N_0^{(s)}\) and as a consequence \(\Gamma _t > \Gamma _s\), (5.6) suggests that for NBD state it is possible to have \(\left( r\, \Gamma _t/\Gamma _s>1\right) \) and the mixed correlator gets an enhancement in the signal.

The signal strength of the above nonlinearity parameter for the \(\langle \gamma \gamma \zeta \rangle \) mixed correlator is enhanced due to the presence of the parameters of EFT and NBD states. However, before that, let us explore another nontrivial aspect of the correlator under consideration. We can see from (5.2) that the shape of the signal is changed with respect to the BD case and now it gets peaked at either of the following configurations: \(c_t(k_2+k_3)=c_s k_1\), \(c_s k_1+c_t k_3=c_t k_2\), \(c_s k_1+c_t k_2=c_t k_3\). These configurations are not strictly the flattened limit where, \(k_i+k_j=k_l\) but is nontrivially modified by the sound speed of perturbations. However, with \(c_{s/t} =1\), they get back to the flattened limit. It is important to note here is that in these configurations the \(g_{osc,\gamma \gamma \zeta }\) affects the signal non-trivially. As one can see from (A.5) the dominant contribution of \(g_{osc,\gamma \gamma \zeta }\) in \(c_t(k_2+k_3)=c_s k_1\) configuration can be written as,

$$\begin{aligned}&\langle \zeta _{k_1} \gamma _{k_2}^{s_2}\gamma _{k_3}^{s_3} \rangle \propto -\frac{\bar{M_3}H^4}{16 M_{pl}^6 c_s \epsilon }(\alpha ^s_1+\beta ^s_1)(\alpha ^t_2+\beta ^t_2)\nonumber \\&\quad \times (\alpha ^t_3+\beta ^t_3)\epsilon _{ij}^{s_2}(k_2)\epsilon _{ij}^{s_3}(k_3) \frac{(\vec {k_1}.\vec {k_2})}{k_1^3k_2^3k_3}\nonumber \\&\quad \left( \frac{c_s k_1 c_t k_2 \eta _0^2}{-c_s k_1+c_t(k_2+k_3)}\right) \left( \alpha _2^{t*}\alpha _3^{t*}\beta _1^{t*}-\beta _1^{t*}\beta _2^{t*}\alpha _3^{t*}\right) \nonumber \\ \end{aligned}$$
(5.7)

Replacing \(c_s k_1\) with \(c_t(k_2+k_3)\) one can see that there is an enhancement of \(\vert c_t k \eta _0\vert ^2\) which after angular averaging one power of \(\eta _0\) will drop [23] and it will enhance the signal by \(\vert c_{t}k \eta _0 \vert \). So in these configurations the amplitude of the correlator will get an additional enhancement factor of \(\vert c_t k \eta _0 \vert \) on top of \(\Gamma _t/\Gamma _s\).

It is however important to note that in [52] the authors used a different route to show that the mixed correlator for \(c_t\ne 1\) can be larger than mixed correlator generated due to shift and lapse function for \(c_t=1\). For BD case one can show that

$$\begin{aligned} \frac{\langle \gamma _{k_2}^{s_2}\gamma _{k_3}^{s_3} \zeta \rangle \vert _{c_t\ne 1}}{\langle \gamma _{k_2}^{s_2}\gamma _{k_3}^{s_3} \zeta \rangle \vert _{c_t=1}}\sim \frac{1}{\epsilon } \end{aligned}$$
(5.8)

In the light of TCC we can see that, the mixed correlator for \(c_t \ne 1\) is now significantly larger than the \(c_t=1\) case even with BD state. So, in principle, the chance of detection of this correlator should be much higher if \(c_t\ne 1\). As a result, the signal strength is significantly enhanced for a nontrivial tensor sound speed that arises from the higher curvature terms in EFT of inflation. However, as mentioned earlier, absence of any observational constraint on this correlator from present observation forbids us to do a numerical estimate of the corresponding signal strength. Even in absence of that, one can claim from the above analysis that these enhanced signals might of interest for future CMB missions and the estimates might be more relevant once the constraints come in.

6 The tensor-scalar-scalar (\(\gamma \zeta \zeta \)) correlator

Till now we have analyzed the correlators with NBD states using EFT of inflation where only consideration was that the time diffeomorphism gets broken after the end of inflation. In order to calculate the tensor-scalar-scalar mixed correlator, we consider a scenario where spatial diffeomorphism is also broken along with the usual time diffeomorphism breaking. This formalism is more rich in structure and has enormous potential to give rise to novel features, e.g., the blue tilt of tensor power spectrum. Corresponding EFT for the scenario considering the breaking of space-time diffeomorphism can be written as follows [32]. The expectation value of the symmetry breaking fields look

$$\begin{aligned} \bar{\phi }^0(t)=t ~~ ; ~~ \bar{\phi }^{x^i}=\alpha x^i \end{aligned}$$
(6.1)

The fields \(\bar{\phi }^0(t)\) and \(\bar{\phi }^{x^i}\) are identified as clock and ruler respectively, during inflation [32] and the parameter \(\alpha \) measures the breaking of spatial diffeomorphism. In this framework, the general Lagrangian can be written as,

$$\begin{aligned} \mathcal {S}=\int d^4 x \sqrt{-g} \left[ \frac{M_{pl}^2}{2} R+ F(X,Y,Z)\right] \end{aligned}$$
(6.2)

where the parameters X, Y, Z defining F(X, Y, Z), which can be any function of the above quantities respecting the symmetry, are given by

$$\begin{aligned} X^{00}= & {} g^{\mu \nu } \partial _{\mu } \phi ^0 \partial _{\nu } \phi ^0 \end{aligned}$$
(6.3)
$$\begin{aligned} Y^{0i}= & {} g^{\mu \nu } \partial _{\mu } \phi ^0 \partial _{\nu } \phi ^i \end{aligned}$$
(6.4)
$$\begin{aligned} Z^{ij}= & {} g^{\mu \nu } \partial _{\mu } \phi ^i \partial _{\nu } \phi ^j \end{aligned}$$
(6.5)

First notice that due to the presence of \(\alpha \) in the action (6.2), the expression for power spectrum of scalar fluctuations is non trivially modified in this scenario. Written explicitly,

$$\begin{aligned} P_{\zeta }=\frac{H^4}{8 \pi c_s (-{\bar{F}}_X-\alpha ^2 {\bar{F}}_Y^2/2a^2)} \Gamma _{s} \end{aligned}$$
(6.6)

Here, the bar on the quantities represents their values as evaluated in the background and the subscripts represents derivative with respect to X, Y or Z. Note that the quantity \({\bar{F}}_y^2/2a^2\) is slowly varying and can be treated as more or less a constant for our evaluation of observable parameters. The parameter \(\alpha \) is also responsible for a tensor mass \(m^2_{\gamma }=\alpha ^2 ({\bar{F}}_z+\alpha ^2 {\bar{F}}_{zz})/a^2\); but in the limit \(\alpha \ll 1\) this can be ignored and the power spectrum for tensor modes closely resembles (2.17) so far as its numerical values are concerned.

The second nontrivial effect of the action (6.2) appears in the \(\langle \gamma \zeta \zeta \rangle \) correlator via the interaction term \(F_Y/(2 a^2) (\gamma _{ij}\partial _i\pi \partial _j \pi /(2 a^2))\). The \(\langle \gamma \zeta \zeta \rangle \) correlator describes how much local quadruple will affect the power spectrum of scalar perturbations when a long wavelength tensor mode correlates with small wavelength scalar mode. The importance of this term in the action is that the behaviour of \(\langle \gamma \zeta \zeta \rangle \) generated from this term does not satisfy the consistency relation of \(\langle \gamma \zeta \zeta \rangle \) correlator and can be a distinct signature of spatial diffeomorphism breaking during inflation. With NBD state the correlator can be written as,

$$\begin{aligned}&\langle \gamma ^{s}_{k_1} \zeta _{k_2} \zeta _{k_3} \rangle \nonumber \\&\quad = \frac{H^6}{M_{pl}^2 c_{s}^2}\frac{\alpha ^2}{8 \pi c_s (-{\bar{F}}_X-\alpha ^2 {\bar{F}}_Y^2/2a^2)} \frac{F_Y}{2 a^2} \frac{1}{k_1^3 k_2^3 k_3^3} \epsilon _{ij}^2(k_1)k_2^{i}k_3^j (\alpha ^t_1+\beta ^t_1)(\alpha ^s_2+\beta ^s_2)(\alpha ^s_3+\beta ^s_3)\nonumber \\&\qquad \times \left[ \left( -(k_1+c_s k_2+c_s k_3)+\frac{c_s k_1^2(k_2+k_3)+c_s^3 k_2 k_3(k2+k3)+c_s^2 k1(k_2^2+4k_2 k_3+k_3^2)}{(k_1+c_s k_2+c_s k_3)^2}\right) \left( \alpha _1^{t*}\alpha _2^{s*}\alpha _3^{s*}-\beta _1^{t*}\beta _2^{s*}\alpha _3^{s*}\right) \right. \nonumber \\&\qquad \left. + \left( (-k_1+c_s k_2+c_s k_3)+\frac{c_sk_1^2(k_2+k_3)+c_s^3 k_2 k_3(k_2+k_3)-c_s^2 k_1(k_2^2+4k_2 k_3+k_3^2)}{(-k_1+c_s k_2+c_s k_3)^2}\right) \left( \alpha _2^{s*}\alpha _3^{s*}\beta _1^{t*}-\beta _1^{t*}\beta _2^{s*}\alpha _3^{s*}\right) \right. \nonumber \\&\qquad \left. -\left( -(k_1-c_s k_2+c_s k_3)+\frac{c_s k_1^2(k_2-k_3)+c_s^3 k_2 k_3(-k_2+k_3)-c_s^2 k_1(k_2^2-4k_2 k_3+k_3^2)}{(k_1-c_s k_2+c_s k_3)^2}\right) \left( \alpha _1^{t*}\alpha _3^{s*}\beta _2^{s*}-\beta _1^{t*}\beta _3^{s*}\alpha _2^{s*}\right) \right. \nonumber \\&\qquad \left. +\left( -(k_1+c_s k_2-c_s k_3)+\frac{c_s k_1^2(k_2-k_3)+c_s^3 k_2 k_3(-k_2+k_3)-c_s^2 k_1(k_2^2-4k_2 k_3+k_3^2)}{(k_1+c_s k_2-c_s k_3)^2}\right) \left( \alpha _1^{t*}\alpha _2^{s*}\beta _3^{s*}-\beta _1^{t*}\beta _2^{s*}\alpha _3^{s*}\right) \right] \nonumber \\&\qquad +k_2\rightarrow k_3 +c.c. + g_{osc,\gamma \zeta \zeta } \end{aligned}$$
(6.7)

The momentum dependence of the oscillatory term \(g_{osc,\gamma \zeta \zeta }\) is exactly same as \(g_{osc,R}\) and as we are only interested about the squeezed limit configuration of this correlator we will only focus on the non-oscillatory term to study the enhancement in the signal. In squeezed limit \(k_1\ll k_2,k_3\) if one chooses \(\theta ^{(s)}=\pi \) and

\(\theta ^{(t)}=0\) one finds that,

$$\begin{aligned} \langle \gamma ^{s}_{k_1} \zeta _{k_2} \zeta _{k_3} \rangle \sim \frac{1}{k_1^3 k_2^3}\frac{k_2}{k_1} N^{(s)}_0+ \frac{1}{k_1^3 k_2^3} N^{(t)}_0 \end{aligned}$$
(6.8)

The interesting point to note here is that the second term in (6.8) can be produced with a BD state, but the first term is a unique contribution of NBD state which gets an enhancement in squeezed limit of \(\mathcal {O}(\frac{k_2}{k_1})\). Also it is important to note that for \(\theta ^{(s)}=\pi \) choice the \((N_0^{(s)})^2\) and \(N_0^{(s)}N_0^{(t)}\) terms in the correlator vanish. For the first term of (6.8) the expression for the mixed correlator in squeezed limit can be rewritten using the expressions for scalar and tensor power spectra in NBD state, as follows

$$\begin{aligned} \langle \gamma ^{s}_{k_1} \zeta _{k_2} \zeta _{k_3} \rangle \sim P_{\zeta } P_{\gamma } \frac{1}{\Gamma _t} \frac{k_2}{k_1} \end{aligned}$$
(6.9)

It appears from the above expression that in order to obtain an enhancement of signal for \(f_{NL}\) for this correlator, the following condition has to be satisfied: \(1/\Gamma _t\, (k_2/k_1)>1\). However, as we have mentioned before, TCC requires a large \(\Gamma _t\sim 10^{29}\) in order to have a detectable signal of PGW and thus suppressing this effect. On the other hand if we are not strict about the theoretical effect on \(\theta ^{(s)}\) and set it any value other than \(\pi \) we can have,

$$\begin{aligned} \langle \gamma ^{s}_{k_1} \zeta _{k_2} \zeta _{k_3} \rangle \sim P_{\zeta } P_{\gamma } \frac{\Gamma _s}{\Gamma _t} \frac{k_2}{k_1} \end{aligned}$$
(6.10)

From (6.10) it is evident that in order to have a large signal for this mixed bispectrum, the parameters need to satisfy the following condition: \(\Gamma _s/\Gamma _t (k_2/k_1)>1\) which is possible in some region of parameter space even for large \(\Gamma _s\) and \(\Gamma _t\). Thus, a considerably strong signal for this correlator is achievable with NBD initial state for both scalar and tensor modes along with non-trivial sound speeds, satisfying TCC. The non-linearity parameter can be defined for this correlator as,

$$\begin{aligned} f_{NL}\vert _{\gamma \zeta \zeta }= \frac{\langle \gamma ^{s} \zeta \zeta \rangle }{P_{\zeta } P_{\gamma }} \end{aligned}$$
(6.11)

It is easy to see from (6.9) and (6.10) that \(f_{NL}\vert _{\gamma \zeta \zeta }\propto 1/\Gamma _t\, (k_2/k_1)\) for \(\theta ^{(s)}= \pi \) and \(f_{NL}\vert _{\gamma \zeta \zeta }\propto \Gamma _s/\Gamma _t\, (k_2/k_1)\) for \(\theta ^{(s)}\ne \pi \). It is worth mentioning that this enhancement in the mixed correlator is reflected on the quadrupole moment and might be of interest for future CMB missions. This makes the present investigation for this correlator relevant from the point of view of observations.

7 Summary and outlook

Recently proposed TCC put stringent theoretical constraints on the amplitude of 2-point correlation function of PGW the so-called tensor-to-scalar ratio r. TCC bound reveals that with the usual BD vacuum, a detectable PGW signal can not be produced from vacuum fluctuation during inflation. However, subsequently, it was found that if the initial states are NBD both for scalar and tensor modes, one can relax the bound on r sufficiently bringing it back to the observational limit of next generation CMB missions with the help of the NBD parameters \(\Gamma _s\) and \(\Gamma _t\) (functions of scalar and tensor Bogolyubov coefficients, respectively). In this article we have explored the 3-point statistics of tensor modes respecting the constraints coming from TCC, thereby considering NBD states for both scalar and tensor modes to study any possible enhancement in the signal strength. Using a model-independent framework of EFT of inflation that helps us keep the analysis and results more or less generic, we have calculated all possible correlators (auto and mixed) related to tensor non-Gaussianities, followed by proposing the possible templates for the non-linearity parameters \(f_{NL}\) for different relevant shapes. We have also tried to explore if at all any of the bispectra could be observationally relevant for future CMB missions by simply calculating the possible upper bounds for each by tuning the parameters under consideration.

Our analysis reveals that the auto correlator \(\langle \gamma \gamma \gamma \rangle \) generated from Einstein term R does not get significantly enhanced even with a choice of large Bogolyubov coefficient \(\beta ^{s/t}\), since the definition of the amplitude of bispectrum always keeps it proportional to \(r^2\). The amplitude of the auto correlator due to the higher derivative EFT operator too is highly suppressed when one considers TCC. Thus, the prospects of detecting the tensor auto corrector are almost nil, at least in next generation CMB missions. We have also analyzed the mixed \(\langle \gamma \gamma \zeta \rangle \) correlator which is a good probe of sound speed of PGW. We have found that the shape of the correlator is modified due to the NBD state and gets peaked at flattened limit modified by the sound speed of perturbation. Also the amplitude of this correlator from the non-oscillatory part can be estimated as \(r\, \Gamma _t/\Gamma _s\) which can be large in the large \(\Gamma _s\) limit and in the flattened limit modified by sound speed the signal strength gets an additional enhancement from \(\eta _0\). Thus, this correlator can be relevant for future CMB missions. The behaviour of the other mixed correlator, namely, the \(\langle \gamma \zeta \zeta \rangle \) generated due to space-time diffeomorphism breaking is also explored. We have used the approach of EFT of space-time diffeomorphism breaking for this scenario. This type of correlator can be a probe of spatial diffeomorphism breaking during inflation. We have found that using NBD state there will be an extra contribution on top of the BD contribution. In squeezed limit this contribution is proportional to \(k_s/k_l\), where \(k_s\) and \(k_l\) are respectively the short and the long wavelength that can be probed by any CMB mission under consideration. The amplitude of this signal is highly dependent on the phase factor given by the \(\theta ^{(s)}\) parameter. For any choice of \(\theta ^{(s)}\ne \pi \), the amplitude of this correlator can be significantly enhanced, thereby making it relevant to future CMB missions.

In a nutshell, if one begins with the theoretical constraints in the light of TCC for slow roll, single field inflation, the nonlinearity parameter \(f_{NL}\) for tensor auto correlation would still be undetectable whereas the corresponding parameters for mixed correlations might be a point of interest for future CMB missions. Our results are more or less generic as we investigated for he parameters from a model-independent framework of EFT.

We must, however, admit that our analysis in this article is mostly theoretical and in order to find out the prospects of tensor non-Gaussianities in CMB, we made use of the simplistic numerical calculations based on current bounds given by Planck 2018 as well as the future goals of next generation missions like CMB-S4, LiteBIRD and COrE. A detailed forecast with particular mission is required to analyze the finer details of the results as well as to estimate the parameters with error in an observation-first approach. Such an analysis is beyond the scope of the present paper. We hope to be back with that in near future.