1 Introduction

The Einstein-aether theory is an intriguing vector-tensor theory invented by Jacobson and Mattingly two decades ago [1]. It breaks Lorentz invariance by coupling a unit timelike vector field to the metric. The vector field defines a congruence of timelike curves filling the full spacetime like an omnipresent fluid [2]. For this reason, the field is called the aether field, and the theory is dubbed the Einstein-aether theory. The Einstein-aether theory has been investigated from various aspects in the past two decades, and even more intensively in the past decade. For very recent studies on this theory, see [3,4,5,6,7,8,9,10,11,12,13] as a partial list and references therein.

Ever since its invention, various solutions to the Einstein-aether theory have been worked out in the literature. In \(3+1\) dimensions, there are a wormholelike static aether solution [14, 15], some numerical black hole solutions [16, 17], as well as analytical solutions of spherical neutral black holes [18, 19], spherical charged black holes [20] and slowly rotating black holes [21]. In \(2+1\) dimensions, a family of rotating black hole solutions were discovered in Ref. [22], while their charged counterparts were reported in Ref. [23]. In \(1+1\) dimensions, all solutions to the Einstein-aether theory have been presented in Ref. [24].

When deriving the above solutions, it is customary to choose the Schwarzschild type coordinates [14, 23], the Eddington–Finkelstein type coordinates [16, 18,19,20], or their rotating analogs [21, 22]. In all of these choices, the metric has an angular component of the same form, that is \(g_{22}=\rho ^2\). In other words, these references have chosen the same radial coordinate \(\rho \), often named as the areal radius [15]. One exception is Ref. [15], in which the isotropic coordinates are utilized to study spherically symmetric solutions of the Einstein-aether theory in \(3+1\) dimensions. Interestingly, for the wormholelike static aether solution, all components of the metric are explicit functions of the isotropic radial coordinate r [15]. In contrast, for the same solution [25], the radial and temporal components of the metric are implicit functions of the areal radius [14]. It indicates that the isotropic coordinates have an advantage over the Schwarzschild coordinates in the Einstein-aetehr theory. This impression motivates us to extend the work in isotropic coordinates [15] to lower dimensions.

Another motivation of this paper is similar to Ref. [24]. Both classical and quantum gravity become more tractable in lower dimensions [26], so the Einstein-aether theory in lower dimensions might provide a manageable setting for studying the possible role of a preferred frame in quantum gravity. We have to work in \(2+1\) dimensions, because the \(1+1\)-dimensional solutions have been derived exhaustively in Ref. [24], and the isotropic coordinates are meaningless in \(1+1\) dimensions.

In \(2+1\) dimensions, a circularly symmetric nonrotating solution can be written in isotropic coordinates as

$$\begin{aligned} ds^2=-e^{2\mu (t,r)}dt^2+e^{2\nu (t,r)}\left( dr^2+r^2d\theta ^2\right) \end{aligned}$$
(1)

with a unit timelike aether field

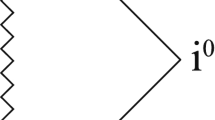
$$\begin{aligned} u^a\partial _a=e^{-\mu (t,r)}\cosh \alpha (r,t)\partial _t+e^{-\nu (t,r)}\sinh \alpha (r,t)\partial _r. \end{aligned}$$
(2)

It is easy to check \(\epsilon ^{abc}u_a\nabla _bu_c=0\), that is to say, the aether field is hypersurface orthogonal [16, 22, 27]. It is challenging to find all solutions of this form, which will be left for an ongoing exhaustive study. In this paper, as a pathfinding work, we will focus on solutions with \(\alpha (r,t)=0\) and satisfying a necessary condition of locally maximally symmetric spacetime [22],

$$\begin{aligned} R_{ab}-\frac{R}{3}g_{ab}=0 \end{aligned}$$
(3)

where \(a,b=0,1,2\) are spacetime indices.

The remainder of this paper is organized as follows. Starting with the \(2+1\)-dimensional action of Einstein-aether theory and then focusing on the line element (1) and the aether field (2) with \(\alpha (r,t)=0\), we will write down the Einstein equations, the aether equations and the maximal symmetry condition (3) in Sect. 2, all followed by some necessary comments. General solutions to these equations will be derived and classified in Sect. 3, where Eqs. (21), (22) will be ingored deliberately. Taking the two equations into consideration, we will put the solutions into their final forms in Sect. 4. As a result, there will be five types or fourteen subtypes of solutions, presented orderly in Sects. 4.1.2, 4.1.4, 4.2.1, 4.2.2, 4.2.3, 4.3.1, 4.3.2, 4.3.3, 4.4.1, 4.4.2, 4.4.3, 4.5.1, 4.5.2, 4.5.3. All of them are maximally symmetric as will be demonstrated in Sect. 5.1, where the Ricci scalar, the Kretschmann scalar and the aether stress-energy tensor will be calculated. In Sect. 5.2, restricted to constant time slices, solutions of the same type yield the same form of spatial line element, which will be employed for illustrations in Fig. 1 and for analyzing conical singularities. After interpreting the physical significance of all solutions in Sect. 6, we will summarize our main results in Sect. 7.

Throughout this paper, we will denote the derivatives with respect to t and r by dots and primes respectively. As we have done in Eqs. (2), (3), the lowercase Latin letters \(a,b,\ldots \) run over spacetime indices 0, 1, 2 or \(t,r,\theta \). In the Einstein-aether theory, there are four coupling constants, notated by \(c_1,c_2,c_3,c_4\) conventionally. When integrating differential equations, we will introduce two types of integration constants. Some are independent of both t and r, and we will denote them as \(b_i\) (\(i=1,2,3,\ldots \)). Others are dependent on t but independent of r, so they will be represented by \(a_i(t)\) (\(i=1,2,3,\ldots \)), where the argument t shows the time-dependence. However, in the case that \(a_i(t)\) is set to a time-independent constant, we will suppress its argument t. From now on, the arguments of \(\mu (t,r)\), \(\nu (t,r)\), \(\alpha (t,r)\), \(\beta (t,r)\) will be omitted for succinctness.

2 Action and equations

Incorporating a cosmological constant \(\Lambda \), the action for Einstein-aether theory in \(2+1\) dimensions can be written as [23]

$$\begin{aligned} S= & {} \frac{1}{16\pi G}\int dx^3\sqrt{-g}\left[ R-2\Lambda -K^{ab}_{~~~cd}\nabla _au^c\nabla _bu^d\right. \nonumber \\&\quad \left. +\lambda \left( g_{ab}u^au^b+1\right) \right] , \end{aligned}$$
(4)

in which \(\nabla \) denotes the covariant derivative, indices \(a,b,c,d=0,1,2\), and the tensor

$$\begin{aligned} K^{ab}_{~~~cd}=c_1g^{ab}g_{cd}+c_2\delta ^a_c\delta ^b_d+c_3\delta ^a_d\delta ^b_c-c_4u^au^bg_{cd}. \end{aligned}$$
(5)

Here \(c_1,c_2,c_3,c_4\) are dimensionless coupling constants.Footnote 1 In Eq. (4), \(\lambda \) is the Lagrangian multiplier to ensure that the aether field \(u^a\) is a unit timelike vector. Note that \(1/(16\pi G)\) is an overall factor in this action, thus the Einstein equations are

$$\begin{aligned} R_{ab}-\frac{1}{2}Rg_{ab}+\Lambda g_{ab}=T^{\ae }_{ab} \end{aligned}$$
(6)

in our conventions of notation [23], where \(T^{\ae }_{ab}\) is the stress-energy tensor of the aether field.

Substituting Eqs. (1) and (2) into the Einstein-aether equations in \(2+1\) dimensions [23], we find

$$\begin{aligned} \Gamma r\dot{\nu }^2e^{2\nu }= & {} e^{2\mu }\left[ c_{14}\left( \mu '+r\mu ''+\frac{r}{2}\mu '^2\right) +\nu '+r\left( \Lambda e^{2\nu }+\nu ''\right) \right] ,\nonumber \\ \end{aligned}$$
(7)
$$\begin{aligned} \mu '\dot{\nu }-\dot{\nu }'= & {} c_{14}\dot{\mu }', \end{aligned}$$
(8)
$$\begin{aligned} \Gamma \beta e^{2\nu }= & {} e^{2\mu }\left[ -\frac{1}{2}c_{14}\mu '^2-\Lambda e^{2\nu }-\mu '\left( \nu '+\frac{1}{r}\right) \right] , \end{aligned}$$
(9)
$$\begin{aligned} \Gamma \beta e^{2\nu }= & {} e^{2\mu }\left( \frac{1}{2}c_{14}\mu '^2-\Lambda e^{2\nu }-\mu ''+\mu '\nu '-\mu '^2\right) \end{aligned}$$
(10)

and

$$\begin{aligned} \left( \Gamma -1\right) \left( \dot{\nu }'-\mu '\dot{\nu }\right) =c_{14}\dot{\mu }'. \end{aligned}$$
(11)

For brevity, we have used the notations

$$\begin{aligned} c_{14}= & {} c_1+c_4,\nonumber \\ \Gamma= & {} 1+c_1+2c_2+c_3,\nonumber \\ \beta= & {} \dot{\mu }\dot{\nu }-\dot{\nu }^2-\ddot{\nu }. \end{aligned}$$
(12)

We can eliminate \(\Lambda \) by combing Eqs. (7) and (9),

$$\begin{aligned} \Gamma \left( \dot{\mu }\dot{\nu }-\ddot{\nu }\right) e^{2\nu }=e^{2\mu }\left[ c_{14} \left( \frac{\mu '}{r}+\mu ''\right) +\frac{\nu '-\mu '}{r}+\nu ''-\mu '\nu '\right] \end{aligned}$$
(13)

or combing Eqs. (9) and (10),

$$\begin{aligned} \left( c_{14}-1\right) \mu '^2-\mu ''+2\mu '\nu '+\frac{\mu '}{r}=0. \end{aligned}$$
(14)

Note that Eq. (14) can be integrated to obtain

$$\begin{aligned} \mu '=a_1(t)re^{2\nu +\left( c_{14}-1\right) \mu }. \end{aligned}$$
(15)

In \(2+1\) dimensions, a maximally symmetric spacetime obeys the condition (3). Corresponding to metric (1), this condition takes the form

$$\begin{aligned} 2\left( \dot{\mu }\dot{\nu }-\ddot{\nu }\right) e^{2\nu }= & {} e^{2\mu }\left( 2\nu ''+\frac{2\nu '-\mu '}{r}-\mu '^2-\mu ''\right) , \end{aligned}$$
(16)
$$\begin{aligned} \mu ' \dot{\nu }-\dot{\nu }'= & {} 0, \end{aligned}$$
(17)
$$\begin{aligned} \left( \dot{\mu }\dot{\nu }-\ddot{\nu }\right) e^{2\nu }= & {} e^{2\mu }\left( \nu ''+\frac{\nu '-2\mu '}{r}-3\mu '\nu '+\mu '^2+\mu ''\right) ,\nonumber \\ \end{aligned}$$
(18)
$$\begin{aligned} \left( \dot{\mu }\dot{\nu }-\ddot{\nu }\right) e^{2\nu }= & {} e^{2\mu }\left( \nu ''+\frac{\nu '+\mu '}{r}+3\mu '\nu '-2\mu '^2-2\mu ''\right) .\nonumber \\ \end{aligned}$$
(19)

The four equations are not independent, because the sum of (18) and (19) reproduces Eq. (16) exactly. Subtracting (19) from (18), we get a simple equality

$$\begin{aligned} 2r\mu '\nu '-r\mu '^2-r\mu ''+\mu '=0 \end{aligned}$$
(20)

which can be converted to

$$\begin{aligned} \mu '=a_1(t)re^{2\nu -\mu }. \end{aligned}$$
(21)

Meanwhile, integration of Eq. (17) gives

$$\begin{aligned} \dot{\nu }=a_2(t)e^{\mu }. \end{aligned}$$
(22)

Subtracting (13) from (16),

$$\begin{aligned}&\left( 1-\Gamma \right) \left( \dot{\mu }\dot{\nu }-\ddot{\nu }\right) e^{2\nu } \nonumber \\&\quad =e^{2\mu }\left[ -c_{14}\left( \frac{\mu '}{r}+\mu ''\right) +\frac{\mu '}{2r} +\mu '\nu '-\frac{\mu '^2}{2}-\frac{\mu ''}{2}\right] \nonumber \\ \end{aligned}$$
(23)

and then inserting Eq. (20), we obtain

$$\begin{aligned} \left( 1-\Gamma \right) \left( \dot{\mu } \dot{\nu }-\ddot{\nu }\right) e^{2\nu }=-c_{14}e^{2\mu }\left( \frac{\mu '}{r}+\mu ''\right) . \end{aligned}$$
(24)

Comparing (8) with (17) and (14) with (20) respectively, one can see that \(c_{14}\dot{\mu }'=0\) and \(c_{14}\mu '^2=0\), which means

$$\begin{aligned} c_{14}\mu '=0. \end{aligned}$$
(25)

Consequently, Eq. (11) is satisfied in virtue of Eq. (17), and the right hand side of Eq. (24) vanishes, resulting in

$$\begin{aligned} \left( 1-\Gamma \right) \left( \dot{\mu }\dot{\nu }-\ddot{\nu }\right) e^{2\nu }=0. \end{aligned}$$
(26)

In principle, finding maximally symmetric solutions of the form (1) requires us to solve the Einstein equations (7), (8), (9), (10), the aether equation (11) and the maximal symmetry condition (16), (17), (18), (19). Based on the above discussions, the task is simplified to looking for solutions of Eqs. (7), (16), (17), (20), (25), (26). In the next section, we will show that Eq. (26) can be derived from Eqs. (7), (16), (17), (25).

It is noteworthy that Eq. (17) is equivalent to (22), while Eq. (20) is equivalent to (21).As a result, Eqs. (25) and (26) can be replaced respectively by

$$\begin{aligned} c_{14}a_1(t)re^{2\nu -\mu }= & {} 0, \end{aligned}$$
(27)
$$\begin{aligned} \left( \Gamma -1\right) \dot{a}_2(t)e^{2\nu +\mu }= & {} 0. \end{aligned}$$
(28)

3 Classification and general solutions

3.1 Five classes of general solutions

Equations (7), (16) are clumsier than the other equations. In this subsection, we will attack them with Eqs. (17), (20), (21), (22) and (25). As an outcome, we will write down the general solutions of \(\mu \) and \(\nu \).

Equation (25) enables us to briefly rewrite Eq. (7) as

$$\begin{aligned} \Gamma r\dot{\nu }^2e^{2\nu }=e^{2\mu }\left[ \nu '+r\left( \Lambda e^{2\nu }+\nu ''\right) \right] . \end{aligned}$$
(29)

Combining it with Eqs. (16), (20), we can obtain

$$\begin{aligned} \left( \Gamma \dot{\nu }^2-\dot{\mu }\dot{\nu }+\ddot{\nu }\right) re^{2\nu }=e^{2\mu }\left( \Lambda re^{2\nu }+r\mu '\nu '+\mu '\right) \end{aligned}$$
(30)

in which both \(\mu ''\) and \(\nu ''\) have been carefully cancelled. Substituting Eqs. (21), (22) into (30) and then multiplying it with \(e^{-\mu -2\nu }/r\), we arrive at

$$\begin{aligned} a_1(t)\frac{\partial \left( \nu +\ln \frac{r}{b_1}\right) }{\partial \ln \frac{r}{b_1}}=\left[ \Gamma a_2(t)^2-\Lambda \right] e^{\mu }+\dot{a}_2(t) \end{aligned}$$
(31)

with \(b_1\) being a time-independent positive constant. Substituting (22) into Eq. (29) and then multiplying it with \(re^{-2\mu }\), we find

$$\begin{aligned} \frac{\partial ^2\left( \nu +\ln \frac{r}{b_1}\right) }{\partial (\ln \frac{r}{b_1})^2}=b_1^2\left[ \Gamma a_2(t)^2-\Lambda \right] e^{2\left( \nu +\ln \frac{r}{b_1}\right) }. \end{aligned}$$
(32)

Because each step of our derivation here is reversible, one can reverse it to reproduce (7), (16) from Eqs. (31), (32). From now on, we will pay attention to Eqs. (31), (32) which are similar to each other and more tractable. In fact, they can be integrated in closed forms to give the general solutions of \(\mu \) and \(\nu \). We will present their solutions exhaustively in the rest of this subsection.

In the simplest case, we consider

  1. (A)

    \(\Gamma a_2(t)^2-\Lambda =0\), for which the solution of Eq. (32) is

    $$\begin{aligned} \nu =a_3(t)\ln \frac{r}{b_1}+a_4(t). \end{aligned}$$
    (33)

    Inserting it into Eq. (31), we get a constraint

    $$\begin{aligned} a_1(t)\left[ a_3(t)+1\right] =\dot{a}_2(t). \end{aligned}$$
    (34)

Otherwise, we have \(\partial \left( \nu +\ln \frac{r}{b_1}\right) /\partial \ln \frac{r}{b_1}\ne 0\). Multiplying Eq. (32) with \(\partial \left( \nu +\ln \frac{r}{b_1}\right) /\partial \ln \frac{r}{b_1}\), one can put it into the form

$$\begin{aligned} \frac{\partial }{\partial \ln \frac{r}{b_1}}\left[ \frac{\partial \left( \nu +\ln \frac{r}{b_1}\right) }{\partial \ln \frac{r}{b_1}}\right] ^2=b_1^2\left[ \Gamma a_2(t)^2-\Lambda \right] \frac{\partial }{\partial \ln \frac{r}{b_1}}e^{2\left( \nu +\ln \frac{r}{b_1}\right) }, \end{aligned}$$
(35)

which can be integrated as

$$\begin{aligned} \frac{\partial }{\partial \ln \frac{r}{b_1}}e^{-\left( \nu +\ln \frac{r}{b_1}\right) }=\pm \left\{ b_1^2\left[ \Gamma a_2(t)^2-\Lambda \right] +\sigma a_5(t)^2e^{-2\left( \nu +\ln \frac{r}{b_1}\right) }\right\} ^{1/2}\nonumber \\ \end{aligned}$$
(36)

with \(\sigma \) being \(\pm 1\) or 0, while \(a_5(t)\) is an undetermined function of t. Keep in mind that \(b_1\) is a positive constant. The analytical solution of this equation takes different forms depending on the signs of \(\Gamma a_2(t)^2-\Lambda \) and \(\sigma a_5(t)^2\). There are four cases to be considered. Let us present them one by one.

  1. (B)

    If \(\Gamma a_2(t)^2-\Lambda <0\), then \(\sigma a_5(t)^2\) should be positive on the right hand side of Eq. (36), and the solution of Eq. (36) is of the form

    $$\begin{aligned} e^{-\left( \nu +\ln \frac{r}{b_1}\right) }=\frac{b_1\sqrt{\Lambda -\Gamma a_2(t)^2}}{\left| a_5(t)\right| }\cosh \left[ a_5(t)\ln \frac{r}{b_1}+a_6(t)\right] . \end{aligned}$$
    (37)

    Substituting this solution into Eq. (31), it is easy to obtain the expression

    $$\begin{aligned} e^{\mu }=\frac{1}{\Lambda -\Gamma a_2(t)^2}\left\{ \dot{a}_2(t)+a_1(t)a_5(t)\tanh \left[ a_5(t)\ln \frac{r}{b_1}+a_6(t)\right] \right\} . \end{aligned}$$
    (38)
  2. (C)

    If \(\Gamma a_2(t)^2-\Lambda >0\), \(\sigma a_5(t)^2>0\), we find a similar form of solution of Eq. (36),

    $$\begin{aligned} e^{-\left( \nu +\ln \frac{r}{b_1}\right) }=\pm \frac{b_1\sqrt{\Gamma a_2(t)^2-\Lambda }}{a_5(t)}\sinh \left[ a_5(t)\ln \frac{r}{b_1}+a_6(t)\right] \end{aligned}$$
    (39)

    and that of Eq. (31),

    $$\begin{aligned} e^{\mu }=\frac{1}{\Lambda -\Gamma a_2(t)^2}\left\{ \dot{a}_2(t)+a_1(t)a_5(t)\coth \left[ a_5(t)\ln \frac{r}{b_1}+a_6(t)\right] \right\} . \end{aligned}$$
    (40)
  3. (D)

    When \(\Gamma a_2(t)^2-\Lambda >0\), \(\sigma a_5(t)^2<0\), the solution of Eq. (36) turns out to be

    $$\begin{aligned} e^{-\left( \nu +\ln \frac{r}{b_1}\right) }=\pm \frac{b_1\sqrt{\Gamma a_2(t)^2-\Lambda }}{a_5(t)}\sin \left[ a_5(t)\ln \frac{r}{b_1}+a_6(t)\right] . \end{aligned}$$
    (41)

    Inserting it into Eq. (31), we get the expression

    $$\begin{aligned} e^{\mu }=\frac{1}{\Lambda -\Gamma a_2(t)^2}\left\{ \dot{a}_2(t)+a_1(t)a_5(t)\cot \left[ a_5(t)\ln \frac{r}{b_1}+a_6(t)\right] \right\} . \end{aligned}$$
    (42)
  4. (E)

    The remaining possibility is \(\Gamma a_2(t)^2-\Lambda >0\), \(\sigma a_5(t)^2=0\), for which we find

    $$\begin{aligned} e^{-\left( \nu +\ln \frac{r}{b_1}\right) }=\pm b_1\sqrt{\Gamma a_2(t)^2-\Lambda }\left[ \ln \frac{r}{b_1}+a_6(t)\right] . \end{aligned}$$
    (43)

    In this case, the general solution of Eq. (31) is

    $$\begin{aligned} e^{\mu }=\frac{1}{\Lambda -\Gamma a_2(t)^2}\left[ \dot{a}_2(t)+\frac{a_1(t)}{\ln \frac{r}{b_1}+a_6(t)}\right] . \end{aligned}$$
    (44)

3.2 Equation (26) is not independent

In passing we mention that Eq. (26) is not an independent equation, because it can be derived from Eqs. (16), (17), (29) as follows. After multiplying Eq. (29) with \(e^{-2\mu -2\nu }/r\), we differentiate it with respect to r. Eliminating \(\dot{\nu }'\) and \(\dot{\nu }''\) in the resulted equation with Eq. (17), we find either \(\dot{\nu }=0\) or

$$\begin{aligned} 2\Gamma \left( \dot{\mu }\dot{\nu }-\ddot{\nu }\right) e^{2\nu } =e^{2\mu }\left( 2\nu ''+\frac{2\nu '-\mu '}{r}-\mu '^2-\mu ''\right) . \end{aligned}$$
(45)

In both situations, one can directly verify Eq. (26) with the help of Eq. (16).

3.3 Further classification

In Sect. 3.1, we have obtained general solutions of \(\mu \) and \(\nu \) from Eqs. (7) and (16). In the next section, we will insert these solutions into Eqs. (21), (22) to determine the value of integration constants such as \(a_i(t)\). This will be done case by case in accordance to the classification in Sect. 3.1. In view of Eqs. (27) and (28), we will divide each case into four subcases:

  1. (1)

    \(a_1(t)=0\), \(\dot{a}_2(t)\ne 0\). In this subcase, Eq. (27) is satisfied for an arbitrary value of \(c_{14}\), while Eq. (28) can be satisfied if \(\Gamma =1\).

  2. (2)

    \(a_1(t)\ne 0\), \(\dot{a}_2(t)=0\). In this subcase, Eq. (27) can be satisfied if \(c_{14}=0\), while Eq. (28) is satisfied for an arbitrary value of \(\Gamma \).

  3. (3)

    \(a_1(t)\ne 0\), \(\dot{a}_2(t)\ne 0\). In this subcase, Eqs. (27) and (28) demand \(c_{14}=0\) and \(\Gamma =1\).

  4. (4)

    \(a_1(t)=0\), \(\dot{a}_2(t)=0\). In this subcase, Eqs. (27) and (28) are both satisfied for arbitrary values of \(c_{14}\) and \(\Gamma \).

In case A, according to the constraint (34), \(a_2(t)\) should be a constant if \(a_1(t)=0\), so we can safely exclude the subcase A1. In cases B, C, D and E, \(a_1(t)\) and \(\dot{a}_2(t)\) cannot vanish simultaneously, otherwise the expressions of \(e^{\mu }\) will reduce to zero and the metric (1) will fail to describe a \(2+1\)-dimensional spacetime. Therefore, we need not consider subcases B4, C4, D4 and E4.

4 Final solutions

4.1 Type A: \(\Gamma a_2(t)^2-\Lambda =0\)

4.1.1 Subtype A1: \(a_1(t)=0\), \(\dot{a}_2(t)\ne 0\)

In this subcase, the conditions \(a_1(t)=0\) and \(\dot{a}_2(t)\ne 0\) are in contradiction with Eq. (34).

4.1.2 Subtype A2: \(a_1(t)\ne 0\), \(\dot{a}_2(t)=0\)

For convenience, we combine Eqs. (21), (22) into the form

$$\begin{aligned} \dot{\nu }'=a_1(t)a_2(t)re^{2\nu }. \end{aligned}$$
(46)

Inserting Eq. (33) into it, we get

$$\begin{aligned} \dot{a}_3(t)=a_1(t)a_2(t)r^2\left( \frac{r}{b_1}\right) ^{2a_3(t)}e^{2a_4(t)}. \end{aligned}$$
(47)

In the present subcase, this equality dictates \(a_3(t)=-1\) and \(a_2(t)=0\), which further implies \(\Lambda =0\). Consequently, inserting Eq. (33) into Eqs. (21), (22), we obtain

$$\begin{aligned} \dot{a}_4(t)=0,~~~~\frac{\partial }{\partial r}e^{\mu }=a_1(t)\frac{b_1^2}{r}e^{2a_4}. \end{aligned}$$
(48)

Up to a transformation of time coordinate and a redefinition of \(b_1\), the metric and the aether field can be written as

$$\begin{aligned} ds^2= & {} -\left[ \ln \frac{r}{b_1}+a_7(t)\right] ^2dt^2+\left( \frac{b_1}{r}\right) ^2\left( dr^2+r^2d\theta ^2\right) ,\nonumber \\ u^a= & {} \left[ \ln \frac{r}{b_1}+a_7(t)\right] ^{-1}\delta ^a_t. \end{aligned}$$
(49)

4.1.3 Subtype A3: \(a_1(t)\ne 0\), \(\dot{a}_2(t)\ne 0\)

There is no suitable value for \(a_3(t)\) to meet Eqs. (34) and (47) in this subcase.

4.1.4 Subtype A4: \(a_1(t)=0\), \(\dot{a}_2(t)=0\)

In this subcase, Eq. (34) is well satisfied. Inserting Eq. (33) into Eqs. (21), (22), we obtain

$$\begin{aligned} \mu =\mu (t),~~~~\dot{a}_3(t)=0,~~~~\dot{a}_4=a_2(t)e^{\mu }, \end{aligned}$$
(50)

in which \(a_2(t)=\pm \sqrt{\Lambda /\Gamma }\). Up to a coordinate transformation, the metric and the aether field can be written as

$$\begin{aligned} ds^2= & {} -dt^2+\left( \frac{r}{b_1}\right) ^{2a_3}e^{\pm 2t\sqrt{\Lambda /\Gamma }}\left( dr^2+r^2d\theta ^2\right) ,\nonumber \\ u^a= & {} \delta ^a_t. \end{aligned}$$
(51)

4.2 Type B: \(\Gamma a_2(t)^2-\Lambda <0\), \(\sigma a_5(t)^2>0\)

4.2.1 Subtype B1: \(a_1(t)=0\), \(\dot{a}_2(t)\ne 0\)

Inserting Eqs. (37), (38) into Eq. (22), we find in this subcase

$$\begin{aligned} \Gamma =1,~~~~\dot{a}_5(t)=\dot{a}_6(t)=0. \end{aligned}$$
(52)

Then from \(\Gamma a_2(t)^2-\Lambda <0\) we can infer that \(\Lambda >0\). Up to a coordinate transformation and a redefinition of \(b_1\), the metric and the aether field can be written as

$$\begin{aligned} ds^2= & {} -dt^2+\frac{4a_5^2}{\Lambda r^2}\cosh ^2\left( \sqrt{\Lambda }t\right) \nonumber \\&\quad \left[ \left( \frac{r}{b_1}\right) ^{a_5}+\left( \frac{b_1}{r}\right) ^{a_5}\right] ^{-2} \left( dr^2+r^2d\theta ^2\right) ,\nonumber \\ u^a= & {} \delta ^a_t. \end{aligned}$$
(53)

4.2.2 Subtype B2: \(a_1(t)\ne 0\), \(\dot{a}_2(t)=0\)

Inserting Eqs. (37), (38) into Eqs. (21), (22), we find

$$\begin{aligned} \dot{a}_5(t)=\dot{a}_6(t)+\frac{a_1(t)a_2(t)a_5(t)}{\Lambda -\Gamma a_2(t)^2}=0. \end{aligned}$$
(54)

Up to a transformation of time coordinate, the metric and the aether field are of the form

$$\begin{aligned} ds^2= & {} -\tanh ^2\left( a_5\ln \frac{r}{b_1}+a_2t\right) dt^2+\frac{a_5^2}{\left( \Lambda -\Gamma a_2^2\right) r^2}\cosh ^{-2}\nonumber \\&\times \left( a_5\ln \frac{r}{b_1}+a_2t\right) \left( dr^2+r^2d\theta ^2\right) ,\nonumber \\ u^a= & {} \coth \left( a_5\ln \frac{r}{b_1}+a_2t\right) \delta ^a_t. \end{aligned}$$
(55)

In particular, when \(a_2(t)=0\), the metric and the aether field are

$$\begin{aligned} ds^2= & {} -\tanh ^2\left( a_5\ln \frac{r}{b_1}\right) dt^2+\frac{4a_5^2}{\Lambda r^2}\left[ \left( \frac{r}{b_1}\right) ^{a_5}\right. \nonumber \\&\left. +\left( \frac{b_1}{r}\right) ^{a_5}\right] ^{-2}\left( dr^2+r^2d\theta ^2\right) ,\nonumber \\ u^a= & {} \coth \left( a_5\ln \frac{r}{b_1}\right) \delta ^a_t \end{aligned}$$
(56)

with \(\Lambda >0\).

4.2.3 Subtype B3: \(a_1(t)\ne 0\), \(\dot{a}_2(t)\ne 0\)

Inserting Eqs. (37), (38) into Eqs. (21), (22), we find

$$\begin{aligned} \Gamma =1,~~~~\dot{a}_5(t)=\dot{a}_6(t)+\frac{a_1(t)a_2(t)a_5(t)}{\Lambda -\Gamma a_2(t)^2}=0. \end{aligned}$$
(57)

After transforming the time coordinate, we can write the metric and the aether field as

$$\begin{aligned} ds^2= & {} -\left\{ 1-\frac{\dot{a}_6(t)}{\sqrt{\Lambda }}\coth \left( \sqrt{\Lambda }t\right) \tanh \left[ a_5\ln \frac{r}{b_1}+a_6(t)\right] \right\} ^2dt^2\nonumber \\&\quad +\frac{a_5^2}{\Lambda r^2}\cosh ^2\left( \sqrt{\Lambda }t\right) \cosh ^{-2}\left[ a_5\ln \frac{r}{b_1}+a_6(t)\right] \left( dr^2+r^2d\theta ^2\right) ,\nonumber \\ u^a= & {} \left\{ 1-\frac{\dot{a}_6(t)}{\sqrt{\Lambda }}\coth \left( \sqrt{\Lambda }t\right) \tanh \left[ a_5\ln \frac{r}{b_1}+a_6(t)\right] \right\} ^{-1}\delta ^a_t. \end{aligned}$$
(58)

4.3 Type C: \(\Gamma a_2(t)^2-\Lambda >0\), \(\sigma a_5(t)^2>0\)

4.3.1 Subtype C1: \(a_1(t)=0\), \(\dot{a}_2(t)\ne 0\)

Inserting Eqs. (39), (40) into Eq. (22), we find in this subcase

$$\begin{aligned} \Gamma =1,~~~~\dot{a}_5(t)=\dot{a}_6(t)=0. \end{aligned}$$
(59)

Up to a coordinate transformation and a redefinition of \(b_1\), the metric and the aether field can be written in the form

$$\begin{aligned} ds^2= & {} -dt^2+\frac{4a_5^2}{\Lambda r^2}\sinh ^2 \left( \sqrt{\Lambda }t\right) \left[ \left( \frac{r}{b_1}\right) ^{a_5}\right. \nonumber \\&\left. -\left( \frac{b_1}{r}\right) ^{a_5}\right] ^{-2}\left( dr^2+r^2d\theta ^2\right) ,\nonumber \\ u^a= & {} \delta ^a_t \end{aligned}$$
(60)

for \(\Lambda \ge 0\), and a similar form with \(\sinh ^2\left( \sqrt{\Lambda }t\right) \) replaced by \(-\cos ^2\left( \sqrt{-\Lambda }t\right) \) for \(\Lambda <0\).

4.3.2 Subtype C2: \(a_1(t)\ne 0\), \(\dot{a}_2(t)=0\)

Inserting Eqs. (39), (40) into Eqs. (21), (22), we find

$$\begin{aligned} \dot{a}_5(t)=\dot{a}_6(t)+\frac{a_1(t)a_2(t)a_5(t)}{\Lambda -\Gamma a_2(t)^2}=0. \end{aligned}$$
(61)

Up to a transformation of time coordinate, the metric and the aether field are of the form

$$\begin{aligned} ds^2= & {} -\coth ^2\left( a_5\ln \frac{r}{b_1}+a_2t\right) dt^2 \nonumber \\&+\frac{a_5^2}{\left( \Gamma a_2^2-\Lambda \right) r^2}\sinh ^{-2}\left( a_5\ln \frac{r}{b_1}+a_2t\right) \left( dr^2+r^2d\theta ^2\right) ,\nonumber \\ u^a= & {} \tanh \left( a_5\ln \frac{r}{b_1}+a_2t\right) \delta ^a_t. \end{aligned}$$
(62)

Especially, if \(a_2(t)=0\), the metric and the aether field can be written as

$$\begin{aligned} ds^2= & {} -\coth ^2\left( a_5\ln \frac{r}{b_1}\right) dt^2-\frac{4a_5^2}{\Lambda r^2} \left[ \left( \frac{r}{b_1}\right) ^{a_5}\right. \nonumber \\&\quad \left. -\left( \frac{b_1}{r}\right) ^{a_5}\right] ^{-2}\left( dr^2+r^2d\theta ^2\right) ,\nonumber \\ u^a= & {} \tanh \left( a_5\ln \frac{r}{b_1}\right) \delta ^a_t \end{aligned}$$
(63)

with \(\Lambda <0\).

4.3.3 Subtype C3: \(a_1(t)\ne 0\), \(\dot{a}_2(t)\ne 0\)

Inserting Eqs. (39), (40) into Eqs. (21), (22), we find

$$\begin{aligned} \Gamma =1,~~~~\dot{a}_5(t)=\dot{a}_6(t)+\frac{a_1(t)a_2(t)a_5(t)}{\Lambda -\Gamma a_2(t)^2}=0. \end{aligned}$$
(64)

Up to a transformation of time coordinate, the metric and the aether field are of the form

$$\begin{aligned} ds^2= & {} -\left\{ 1-\frac{\dot{a}_6(t)}{\sqrt{\Lambda }}\tanh \left( \sqrt{\Lambda }t\right) \coth \left[ a_5\ln \frac{r}{b_1}+a_6(t)\right] \right\} ^2dt^2\nonumber \\&+\frac{a_5^2}{\Lambda r^2}\sinh ^2\left( \sqrt{\Lambda }t\right) \sinh ^{-2}\left[ a_5\ln \frac{r}{b_1}+a_6(t)\right] \left( dr^2+r^2d\theta ^2\right) ,\nonumber \\ u^a= & {} \left\{ 1-\frac{\dot{a}_6(t)}{\sqrt{\Lambda }}\tanh \left( \sqrt{\Lambda }t\right) \coth \left[ a_5\ln \frac{r}{b_1}+a_6(t)\right] \right\} ^{-1}\delta ^a_t \end{aligned}$$
(65)

for \(\Lambda \ge 0\), and a similar form with \(-\tanh \left( \sqrt{\Lambda }t\right) /\sqrt{\Lambda }\), \(\sinh ^2\left( \sqrt{\Lambda }t\right) \) replaced by \(\cot \left( \sqrt{-\Lambda }t\right) /\sqrt{-\Lambda }\), \(-\cos ^2\left( \sqrt{-\Lambda }t\right) \) respectively for \(\Lambda <0\).

4.4 Type D: \(\Gamma a_2(t)^2-\Lambda >0\), \(\sigma a_5(t)^2<0\)

4.4.1 Subtype D1: \(a_1(t)=0\), \(\dot{a}_2(t)\ne 0\)

Inserting Eqs. (41), (42) into Eq. (22), we find in this subcase

$$\begin{aligned} \Gamma =1,~~~~\dot{a}_5(t)=\dot{a}_6(t)=0. \end{aligned}$$
(66)

Up to a coordinate transformation and a redefinition of \(b_1\), the metric and the aether field are of the form

$$\begin{aligned} ds^2= & {} -dt^2+\frac{a_5^2}{\Lambda r^2}\sinh ^2\left( \sqrt{\Lambda }t\right) \sin ^{-2}\left( a_5\ln \frac{r}{b_1}\right) \left( dr^2+r^2d\theta ^2\right) ,\nonumber \\ u^a= & {} \delta ^a_t \end{aligned}$$
(67)

for \(\Lambda \ge 0\), and a similar form with \(\sinh ^2\left( \sqrt{\Lambda }t\right) \) replaced by \(-\cos ^2\left( \sqrt{-\Lambda }t\right) \) for \(\Lambda <0\).

4.4.2 Subtype D2: \(a_1(t)\ne 0\), \(\dot{a}_2(t)=0\)

Inserting Eqs. (41), (42) into Eqs. (21), (22), we find

$$\begin{aligned} \dot{a}_5(t)=\dot{a}_6(t)+\frac{a_1(t)a_2(t)a_5(t)}{\Lambda -\Gamma a_2(t)^2}=0. \end{aligned}$$
(68)

The metric and the aether field are of the form

$$\begin{aligned} ds^2= & {} -\cot ^2\left( a_5\ln \frac{r}{b_1}+a_2t\right) dt^2+\frac{a_5^2}{\left( \Gamma a_2^2-\Lambda \right) r^2}\sin ^{-2}\nonumber \\&\qquad \left( a_5\ln \frac{r}{b_1}+a_2t\right) \left( dr^2+r^2d\theta ^2\right) ,\nonumber \\ u^a= & {} \tan \left( a_5\ln \frac{r}{b_1}+a_2t\right) \delta ^a_t \end{aligned}$$
(69)

up to a transformation of time coordinate.

In the special limit \(a_2(t)=0\), the metric and the aether field can be written as

$$\begin{aligned} ds^2= & {} -\cot ^2\left( a_5\ln \frac{r}{b_1}\right) dt^2\nonumber \\&-\frac{a_5^2}{\Lambda r^2}\sin ^{-2}\left( a_5\ln \frac{r}{b_1}\right) \left( dr^2+r^2d\theta ^2\right) ,\nonumber \\ u^a= & {} \tan \left( a_5\ln \frac{r}{b_1}\right) \delta ^a_t \end{aligned}$$
(70)

with \(\Lambda <0\).

4.4.3 Subtype D3: \(a_1(t)\ne 0\), \(\dot{a}_2(t)\ne 0\)

Inserting Eqs. (41), (42) into Eqs. (21), (22), we find

$$\begin{aligned} \Gamma =1,~~~~\dot{a}_5(t)=\dot{a}_6(t)+\frac{a_1(t)a_2(t)a_5(t)}{\Lambda -\Gamma a_2(t)^2}=0. \end{aligned}$$
(71)

After a coordinate transformation, we can write the metric and the aether field as

$$\begin{aligned} ds^2= & {} -\left\{ 1-\frac{\dot{a}_6(t)}{\sqrt{\Lambda }}\tanh \left( \sqrt{\Lambda }t\right) \cot \left[ a_5\ln \frac{r}{b_1}+a_6(t)\right] \right\} ^2dt^2\nonumber \\&+\frac{a_5^2}{\Lambda r^2}\sinh ^2\left( \sqrt{\Lambda }t\right) \sin ^{-2} \left[ a_5\ln \frac{r}{b_1}+a_6(t)\right] \left( dr^2+r^2d\theta ^2\right) ,\nonumber \\ u^a= & {} \left\{ 1-\frac{\dot{a}_6(t)}{\sqrt{\Lambda }}\tanh \left( \sqrt{\Lambda }t\right) \cot \left[ a_5\ln \frac{r}{b_1}+a_6(t)\right] \right\} ^{-1}\delta ^a_t \end{aligned}$$
(72)

for \(\Lambda \ge 0\), and a similar form with \(-\tanh \left( \sqrt{\Lambda }t\right) /\sqrt{\Lambda }\), \(\sinh ^2\left( \sqrt{\Lambda }t\right) \) replaced by \(\cot \left( \sqrt{-\Lambda }t\right) /\sqrt{-\Lambda }\), \(-\cos ^2\left( \sqrt{-\Lambda }t\right) \) respectively for \(\Lambda <0\).

4.5 Type E: \(\Gamma a_2(t)^2-\Lambda >0\), \(\sigma a_5(t)^2=0\)

4.5.1 Subtype E1: \(a_1(t)=0\), \(\dot{a}_2(t)\ne 0\)

Inserting Eqs. (43), (44) into Eq. (22), we find in this subcase

$$\begin{aligned} \Gamma =1,~~~~\dot{a}_6(t)=0. \end{aligned}$$
(73)

Up to a coordinate transformation and a redefinition of \(b_1\), the metric and the aether field can be written as

$$\begin{aligned} ds^2= & {} -dt^2+\frac{1}{\Lambda r^2}\sinh ^2\left( \sqrt{\Lambda }t\right) \left( \ln \frac{r}{b_1}\right) ^{-2}\left( dr^2+r^2d\theta ^2\right) ,\nonumber \\ u^a= & {} \delta ^a_t \end{aligned}$$
(74)

for \(\Lambda \ge 0\), and a similar form with \(\sinh ^2\left( \sqrt{\Lambda }t\right) \) replaced by \(-\cos ^2\left( \sqrt{-\Lambda }t\right) \) for \(\Lambda <0\).

4.5.2 Subtype E2: \(a_1(t)\ne 0\), \(\dot{a}_2(t)=0\)

Inserting Eqs. (43), (44) into Eqs. (21), (22), we find

$$\begin{aligned} \dot{a}_6(t)+\frac{a_1(t)a_2(t)}{\Lambda -\Gamma a_2(t)^2}=0. \end{aligned}$$
(75)

In an appropriate time coordinate, the metric and the aether field can be written as

$$\begin{aligned} ds^2= & {} -\left( \ln \frac{r}{b_1}+a_2t\right) ^{-2}dt^2+\frac{1}{\left( \Gamma a_2^2-\Lambda \right) r^2}\nonumber \\&\qquad \left( \ln \frac{r}{b_1}+a_2t\right) ^{-2}\left( dr^2+r^2d\theta ^2\right) ,\nonumber \\ u^a= & {} \left( \ln \frac{r}{b_1}+a_2t\right) \delta ^a_t. \end{aligned}$$
(76)

In the limit \(a_2(t)=0\), the metric and the aether field are

$$\begin{aligned} ds^2= & {} -\left( \ln \frac{r}{b_1}\right) ^{-2}dt^2\nonumber \\&-\frac{1}{\Lambda r^2}\left( \ln \frac{r}{b_1}\right) ^{-2}\left( dr^2+r^2d\theta ^2\right) ,\nonumber \\ u^a= & {} \left( \ln \frac{r}{b_1}\right) \delta ^a_t. \end{aligned}$$
(77)

4.5.3 Subtype E3: \(a_1(t)\ne 0\), \(\dot{a}_2(t)\ne 0\)

Inserting Eqs. (43), (44) into Eqs. (21), (22), we find

$$\begin{aligned} \Gamma =1,~~~~\dot{a}_6(t)+\frac{a_1(t)a_2(t)}{\Lambda -\Gamma a_2(t)^2}=0. \end{aligned}$$
(78)

Up to a transformation of time coordinate, the metric and the aether field are of the form

$$\begin{aligned} ds^2= & {} -\left[ 1-\frac{\dot{a}_6(t)}{\sqrt{\Lambda }} \tanh \left( \sqrt{\Lambda }t\right) \frac{1}{\ln \frac{r}{b_1}+a_6(t)}\right] ^2dt^2\nonumber \\&+\frac{1}{\Lambda r^2}\sinh ^2\left( \sqrt{\Lambda }t\right) \left[ \ln \frac{r}{b_1}+a_6(t)\right] ^{-2}\left( dr^2+r^2d\theta ^2\right) ,\nonumber \\ u^a= & {} \left[ 1-\frac{\dot{a}_6(t)}{\sqrt{\Lambda }}\tanh \left( \sqrt{\Lambda }t\right) \frac{1}{\ln \frac{r}{b_1}+a_6(t)}\right] ^{-1}\delta ^a_t \end{aligned}$$
(79)

for \(\Lambda \ge 0\), and a similar form with \(-\tanh \left( \sqrt{\Lambda }t\right) /\sqrt{\Lambda }\), \(\sinh ^2\left( \sqrt{\Lambda }t\right) \) replaced by \(\cot \left( \sqrt{-\Lambda }t\right) /\sqrt{-\Lambda }\), \(-\cos ^2\left( \sqrt{-\Lambda }t\right) \) respectively for \(\Lambda <0\).

5 Some properties

5.1 Maximal symmetry and curvature singularities

Maximally symmetric solutions, such as the Friedmann–Lemaître–Robertson–Walker (FLRW) metric and the Bañados–Teitelboim–Zanelli (BTZ) black hole [29], are of great interest in physics. For the BTZ black hole, the spacetime is maximally symmetric. In the FLRW metric, only the space is maximally symmetric. As we have mentioned, Eq. (3) is a necessary condition for maximal symmetry, thus it is still uncertain whether the obtained solutions are maximally symmetric at last. In this subsection, we will confirm that all of the solutions presented in Sect. 4 are maximally symmetric.

By definition, maximally symmetric spacetimes are those with the maximal number of independent Killing vectors. In \(2+1\) dimensions, this number is three. However, given the metric of a spacetime, it is often difficult to find all of the Killing vectors. Here we turn to a convenient criterion in [30]. As argued in [30], if the Riemann tensor satisfies

$$\begin{aligned} R_{abcd}=\frac{1}{6}R(g_{ac}g_{bd}-g_{ad}g_{bc}) \end{aligned}$$
(80)

with the Ricci scalar R a constant, the metric will be maximally symmetric. In Eq. (80) we have fixed the dimension of spacetime to \(2+1\). After some tedious but straightforward computations, one can check Eq. (80) and

$$\begin{aligned} R=6\Lambda -6a_2^2(\Gamma -1) \end{aligned}$$
(81)

for each solution in Sect. 4, so we conclude that they are all maximally symmetric solutions.

Some remarks are in order here. First, Eqs. (3) and (80) are actually equivalent. It is easy to derive Eq. (3) from Eq. (80). Reversely, one can derive Eq. (80) from Eq. (3) by remembering that in \(2+1\) dimensions, the Riemann tensor is entirely determined by the Ricci tensor,

$$\begin{aligned} R_{abcd}= & {} \left( g_{ac}R_{bd}-g_{ad}R_{bc}-g_{bc}R_{ad}+g_{bd}R_{ac}\right) \nonumber \\&+\frac{1}{2}R\left( g_{ac}g_{bd}-g_{ad}g_{bc}\right) . \end{aligned}$$
(82)

Second, in the special case \(T^{\ae }_{ab}=0\), Eqs. (3) and (80) are trivial results of the Einstein equations. Generally, they put a constraint on the stress–energy tensor,

$$\begin{aligned} T^{\ae }_{ab}=\left( \Lambda -\frac{1}{6}R\right) g_{ab}. \end{aligned}$$
(83)

Inserting Eq. (81), we find

$$\begin{aligned} T^{\ae }_{ab}=a_2^2(\Gamma -1)g_{ab}, \end{aligned}$$
(84)

which can be checked with solutions in Sect. 4 straightforwardly.

From Eq. (80), one can directly prove a relation between the Ricci and Kretschmann scalars

$$\begin{aligned} R_{abcd}R^{abcd}=\frac{1}{3}R^2. \end{aligned}$$
(85)

Together with Eq. (81), it suggests that the solutions we have obtained are free of curvature singularities. As we will illustrate in the coming subsection, they are not free of conical singularities unless appropriate values are set to parameters \(a_3\) and \(a_5\).

5.2 Spatial slices and conical singularities

Restricted to a constant time slice \(t=t_0\), the line element (1) reduces to

$$\begin{aligned} dl^2= & {} e^{2\nu (t_0,r)}\left( dr^2+r^2d\theta ^2\right) \nonumber \\= & {} \left[ \pm \left( \frac{dz}{d\varrho }\right) ^2+1\right] d\varrho ^2+\varrho ^2d\theta ^2, \end{aligned}$$
(86)

which describes a spatial surface as long as \(e^{2\nu (t,r)}>0\). To illustrate this surface, we will embed it in a 3-dimensional Euclidean or Minkowski space \(ds^2=\pm dz^2+d\varrho ^2+\varrho ^2d\theta ^2\), contingent on the value of terms in the square bracket in Eq. (86). Taking \(e^{\nu (t,r)}>0\) without loss of generality, the parametric equations for the surface are determined by

$$\begin{aligned} \varrho= & {} re^{\nu (t_0,r)},\nonumber \\ z'^2= & {} \pm \left[ e^{2\nu (t_0,r)}-\left( re^{\nu (t_0,r)}\right) '^2\right] . \end{aligned}$$
(87)

Here the upper and the lower signs are in accordance with Eq. (86). The signs should be appropriately chosen to guarantee that \(z'^2\ge 0\). For example, if \(e^{2\nu (t_0,r)}-\left( re^{\nu (t_0,r)}\right) '^2>0\), then one have to choose the plus sign, and \((\varrho ,\theta ,z)\) are exactly cylindrical coordinates in a 3-dimensional Euclidean space. Once the parametric equations are gained from Eq. (87), we can depict the surface straightforwardly by plotting the parametric equations in 3D spaces.

Indeed, we find \(e^{2\nu (t,r)}>0\) for all of the solutions in Sect. 4, hence the constant time slices of these solutions are all spatial. In previous sections, we have classified the solutions into five types, tagged as A to E, and we have divided each type into several subtypes. Fortunately, for solutions of the same type but different subtypes, the function \(e^{2\nu (t,r)}\) depends on r in the same form. Therefore, the same type of solutions have the same form of spatial slice. Applying the above procedure to these solutions, we have successfully drawn the 3D pictures of their spatial slices in Fig. 1. In the figure, surfaces embedded in the Euclidean space are drawn in color without meshes. In contrast, meshed surfaces in black and white are embedded in the Minkowski space. Note that even for the same solution, the sign of \(e^{2\nu (t_0,r)}-\left( re^{\nu (t_0,r)}\right) '^2\) depends not only on the value of \(a_3\) or \(a_5\), but also on the value of r. Therefore, as clear in the figure, different parts of one surface are probably embedded in different spaces. In Fig. 1, we have not depicted the spatial slice for type A solutions in the cases \(\left| 1+a_3\right| =1\), which is a 2-dimensional flat plane.

Fig. 1
figure 1

Illustrations of constant time slices of the solutions in Sect. 4 assuming \(0\le \theta <2\pi \). Colored surfaces (or colored patches) without meshes are embedded in the Euclidean space, whereas uncolored surfaces (or uncolored patches) with meshes are embedded in the Minkowski space. The first row plots solutions of type A with \(\left| 1+a_3\right| =0,0.5,2\) from left to right, the second row is for type B solutions with \(\left| a_5\right| =0.5,1,2\) from left to right, the third row corresponds to solutions of type C with \(\left| a_5\right| =0.5,1,2\) from left to right, and subfigures in the fourth row depict type D (left) and type E (right) solutions. The constant time slices for type A solutions with \(\left| 1+a_3\right| =1\) is an Euclidean plane (not shown in this figure). In the subfigure for type E solutions, the spike extends to infinity

Full size image

There is an alternative method to draw the figure. For all solutions in Sect. 4, one can rewrite the spatial line elements in terms of \(\varrho \) as

$$\begin{aligned} dl_A^2\propto & {} \left( \frac{r}{b_1}\right) ^{2a_3}\left( dr^2+r^2d\theta ^2\right) \nonumber \\&={\left\{ \begin{array}{ll} (1+a_3)^{-2}d\varrho ^2+\varrho ^2d\theta ^2,&{}\quad \mathrm {for~}a_3\ne -1;\\ dz^2+b_1^2d\theta ^2,&{}\quad \mathrm {for~}a_3=-1, \end{array}\right. }\nonumber \\ dl_B^2\propto & {} \frac{b_1^2}{r^2}\left[ \left( \frac{r}{b_1}\right) ^{a_5}+\left( \frac{b_1}{r}\right) ^{a_5}\right] ^{-2}\left( dr^2+r^2d\theta ^2\right) \nonumber \\&\quad =\frac{b_1^2}{a_5^2(b_1^2-4\varrho ^2)}d\varrho ^2+\varrho ^2d\theta ^2,\quad \varrho <\frac{b_1}{2},\nonumber \\ dl_C^2\propto & {} \frac{b_1^2}{r^2}\left[ \left( \frac{r}{b_1}\right) ^{a_5}-\left( \frac{b_1}{r}\right) ^{a_5} \right] ^{-2}\left( dr^2+r^2d\theta ^2\right) \nonumber \\&\quad =\frac{b_1^2}{a_5^2(b_1^2+4\varrho ^2)}d\varrho ^2+\varrho ^2d\theta ^2,\nonumber \\ dl_D^2\propto & {} \frac{b_1^2}{r^2}\sin ^{-2}\left( a_5\ln \frac{r}{b_1}\right) \left( dr^2+r^2d\theta ^2\right) \nonumber \\&\quad =\frac{b_1^2}{a_5^2(\varrho ^2-b_1^2)}d\varrho ^2+\varrho ^2d\theta ^2,\quad \varrho >b_1,\nonumber \\ dl_E^2\propto & {} \frac{b_1^2}{r^2}\left( \ln \frac{r}{b_1}\right) ^{-2}\left( dr^2+r^2d\theta ^2\right) \nonumber \\&\quad =\frac{b_1^2}{\varrho ^2}d\varrho ^2+\varrho ^2d\theta ^2. \end{aligned}$$
(88)

Comparing each line element with Eq. (86), it is not hard to derive \(dz/d\varrho \) and therefore the surface equation, which can be plotted to produce Fig. 1.

The line elements in Eq. (88) are helpful for explaining many features in Fig. 1. Here we make use of them to analyze conical singularities in this figure. In the figure, it is apparent that there are usually conical singularities at \(\varrho =0\) in solutions of types A, B and C. To better understand such singularities, let us take the limit \(\varrho \rightarrow 0\) of \(dl_A^2\), \(dl_B^2\) and \(dl_C^2\). Assuming \(\theta \) ranges from 0 to \(2\pi \), we find in this limit the cone angle is \(2\pi \left| 1+a_3\right| \) (for type A solutions) or \(2\pi \left| a_5\right| \) (for solutions of type B or C). This elucidates the absence of conical singularities in subfigures with \(\left| 1+a_3\right| =1\) or \(\left| a_5\right| =1\). When \(\left| 1+a_3\right| <1\) or \(\left| a_5\right| <1\), the cone angle is less than \(2\pi \), so there is a conical singularity at the point \(\varrho =0\), near which the surface is embedded in the Euclidean space. Otherwise, if \(\left| 1+a_3\right| >1\) or \(\left| a_5\right| >1\), then the cone angle is greater than \(2\pi \), and there is a conical singularity at the point \(\varrho =0\) embedded in the Minkowski space. To get rid of conical singularities in solutions of types A, B and C, we can set \(a_3=0\) or \(-2\), \(a_5=\pm 1\) or change the range of \(\theta \) equivalently. From the expression of \(dl_E^2\), it is clear that the point \(\varrho =0\) is not a conical singularity but a spike extending to infinity.

6 Physical interpretation

From Eqs. (6) and (84), we observe that all line elements obtained in this paper are solutions of the equations

$$\begin{aligned} R_{ab}-\frac{1}{2}Rg_{ab}+\left( \Lambda -\Gamma a_2^2+a_2^2\right) g_{ab}=0, \end{aligned}$$
(89)

which can be regarded as vacuum Einstein equations with an effective cosmological constant \(\Lambda _{eff}=\Lambda -\Gamma a_2^2+a_2^2\). This value of \(\Lambda _{eff}\) was unknown before we obtained the solutions, but rewriting Eq. (6) in such a form helps to understand the physical significance of the solutions.

Enlightened by the above observation, we transform the coordinates t, r into \(\tau \), \(\rho \), and put solutions of subtypes B2, C2, D2, E2 in a unified form

$$\begin{aligned} ds^2= & {} -\left[ \sigma a_5^2-\left( \Lambda -\Gamma a_2^2+a_2^2\right) \rho ^2\right] d\tau ^2\nonumber \\&\quad +\left[ \sigma a_5^2-\left( \Lambda -\Gamma a_2^2+a_2^2\right) \rho ^2\right] ^{-1}d\rho ^2+\rho ^2d\theta ^2,\nonumber \\ \end{aligned}$$
(90)
$$\begin{aligned} u^a= & {} \left[ \sigma a_5^2-\left( \Lambda -\Gamma a_2^2+a_2^2\right) \rho ^2\right] ^{-1}\nonumber \\&\times \sqrt{\sigma a_5^2 -\left( \Lambda -\Gamma a_2^2\right) \rho ^2}\delta ^a_\tau -a_2\rho \delta ^a_\rho . \end{aligned}$$
(91)

In the parameter region \(\Lambda _{eff}<0\), which is permissible in subcases C2, D2, E2, this line element has been discussed in Ref. [29]. In subcase C2, \(\sigma a_5^2>0\), the line element describes an anti-de Sitter spacetime if \(a_5^2=1\), or a similar spacetime with a conical singularity otherwise. In subcase D2, \(\sigma a_5^2<0\), the line element (90) represents a static BTZ black hole of mass \(a_5^2/(8G)\), whose vacuum state [29] is described by the subtype E2 solution (\(\sigma a_5^2=0\)). In the parameter region \(\Lambda _{eff}>0\), which is possible in subcases B2, C2, D2, E2, the above line element can be interpreted as the 3-dimensional Schwarzschild-de Sitter solution with a mass \(\left( 1-\sigma a_5^2\right) /(8G)\) [31, 32], akin to the solutions in flat spacetime [33, 34]. We should remind that the expression (91) for \(u^a\) is well-defined only if \(\sigma a_5^2-\left( \Lambda -\Gamma a_2^2\right) \rho ^2\ge 0\). This inequality can be satisfied by any value of \(\rho \) in subcases C2 and E2, but only by \(\rho ^2\ge \sigma a_5^2/\left( \Lambda -\Gamma a_2^2\right) \) in subcases B2 and D2. Therefore, in subcases B2 and D2, the solution covers only a patch of the spacetime mentioned here.

Likewise, the subtype A4 solution can be put in the form

$$\begin{aligned} ds^2= & {} -\left[ \left( 1+a_3\right) ^2-\frac{\Lambda \rho ^2}{\Gamma }\right] d\tau ^2 \nonumber \\&+\left[ \left( 1+a_3\right) ^2-\frac{\Lambda \rho ^2}{\Gamma }\right] ^{-1}d\rho ^2+\rho ^2d\theta ^2,\nonumber \\ u^a= & {} \left[ \left( 1+a_3\right) ^2-\frac{\Lambda \rho ^2}{\Gamma }\right] ^{-1}\left( 1+a_3\right) \delta ^a_\tau \pm \sqrt{\frac{\Lambda }{\Gamma }}\rho \delta ^a_\rho . \end{aligned}$$
(92)

Clearly it corresponds to a 3-dimensional Schwarzschild-de Sitter spacetime with the mass \(\left[ 1-\left( 1+a_3\right) ^2\right] /(8G)\) and the effective cosmological constant \(\Lambda _{eff}=\Lambda /\Gamma >0\).

In the subtype A2 solution, the effective cosmological constant \(\Lambda _{eff}\) is zero. The physical significance of this solution can be better understood by transforming into

$$\begin{aligned} ds^2= & {} -\left[ \kappa (\tau )x+1\right] ^2d\tau ^2+dx^2+dy^2,\nonumber \\ u^a= & {} \left[ \kappa (\tau )x+1\right] ^{-1}\delta ^a_\tau . \end{aligned}$$
(93)

In the special case that \(\kappa (\tau )\) is a constant, the solution describes a \(2+1\)-dimensional Rindler spacetime. Generally, it describes a spacetime with a uniform surface gravity \(\kappa (\tau )\) [35].

We find \(\Gamma =1\) and thus \(\Lambda _{eff}=\Lambda \) for all of the remaining solutions, i.e., solutions of subtypes B1, B3, C1, C3, D1, D3, E1, E3. After some tedious algebras, we are able to rewrite the line elements of these solutions in the form

$$\begin{aligned} ds^2=-\left[ \sigma a_5^2-\Lambda \rho ^2\right] d\tau ^2+\left[ \sigma a_5^2-\Lambda \rho ^2\right] ^{-1}d\rho ^2+\rho ^2d\theta ^2, \end{aligned}$$
(94)

whose physical significance is similar to metric (90). However, the aether field cannot be expressed explicitly in the Schwarzschild type coordinates \(\tau \) and \(\rho \) in all solutions. For instance, in subcase B3, the metric is related to Eq. (94) by the coordinate transformation

$$\begin{aligned} \rho= & {} \frac{a_5}{\sqrt{\Lambda }}\cosh \left( \sqrt{\Lambda }t\right) \cosh ^{-1}\left[ a_5\ln \frac{r}{b_1}+a_6(t)\right] ,\nonumber \\ a_5d\tau= & {} \frac{1}{\sqrt{\Lambda }}d\ln \frac{\sinh \left[ a_5 \ln \frac{r}{b_1}+a_6(t)+\sqrt{\Lambda }t\right] }{\sqrt{\cosh ^2\left[ a_5\ln \frac{r}{b_1}+a_6(t)\right] -\cosh ^2\left( \sqrt{\Lambda }t\right) }}\nonumber \\&-\frac{1}{\sqrt{\Lambda }}\coth \left( \sqrt{\Lambda }t\right) \dot{a}_6(t)dt. \end{aligned}$$
(95)

Unless \(a_6(t)\) takes very special forms, the coordinate \(\tau \) is not an explicit function of t and r, and thus the aether field (58) cannot be expressed in \(\tau \) and \(\rho \) in a closed form. This situation is similar to the wormholelike static aether solution, which can be written in a closed form in the isotropic coordinates but not in the Schwarzschild coordinates.

Although there is a timelike Killing field \(\partial _\tau \) in most solutions, we emphasize that the aether field \(u^a\partial _a\) is seldom parallel to the Killing field.

We should warn that the above interpretation of our solutions are not unique, because the interpretation of a gravitational solution is observer-dependent. A well-known example is the de Sitter solution, which can be interpreted either as a static spacetime by a static observer or as an expanding spacetime by an comoving observer. Solutions of subtypes B1, C1, D1, E1 can be rewritten in a form generalizing the \(2+1\)-dimensional FLRW metric

$$\begin{aligned} ds^2= & {} -dt^2+\tilde{a}(t)^2\left( \frac{d\tilde{r}^2}{\sigma a_5^2+k\tilde{r}^2}+\tilde{r}^2d\theta ^2\right) , \end{aligned}$$
(96)
$$\begin{aligned} u^a= & {} \delta ^a_t, \end{aligned}$$
(97)

where \(k=\mathrm {sign}\left[ \Gamma a_2(t)^2-\Lambda \right] \). Here again \(\left( 1-\sigma a_5^2\right) /(8G)\) can be interpreted as the mass located at the origin, inducing a conical singularity. In subcase B1, the scale factor \(\tilde{a}(t)=\frac{1}{\sqrt{\Lambda }}\cosh \left( \sqrt{\Lambda }t\right) \). In subcases C1, D1 and E1, \(\tilde{a}(t)^2=\frac{1}{\Lambda }\sinh ^2\left( \sqrt{\Lambda }t\right) \) for \(\Lambda >0\), while \(\tilde{a}(t)^2=-\frac{1}{\Lambda }\cos ^2\left( \sqrt{-\Lambda }t\right) \) if \(\Lambda <0\).

7 Summary

In this paper, we have found all maximally symmetric solutions of the form (1) for Einstein-aether theory, with \(\alpha (r,t)=0\) in the aether field (2). The solutions are classified into fourteen subtypes and presented orderly in Sects. 4.1.2, 4.1.4, 4.2.1, 4.2.2, 4.2.3, 4.3.1, 4.3.2, 4.3.3, 4.4.1, 4.4.2, 4.4.3, 4.5.1, 4.5.2, 4.5.3. All of the solutions are maximally symmetric and nonrotating. No evidence for curvature singularity appears in the Ricci and Kretschmann scalars, while conical singularities can be avoided by setting \(\left| 1+a_3\right| =1\), \(\left| a_5\right| =1\).

There are several issues to investigate in the future. First, one can study the perturbations of these solutions. Although \(2+1\) Einstein gravity does not have local degrees of freedom, the aether field should introduce extra degrees of freedom. Second, making use of these solutions, it will be interesting to study possible roles of the aether field in quantum gravity. Third, the authors are seeking for more general solutions of the form (1) without the maximal symmetric condition and the ansatz \(\alpha (r,t)=0\).