1 Introduction

It is widely accepted that the effects of higher-order curvature terms are significant as we are exploring the strong gravity regime via detections of gravitational waves and black hole shadows. In theoretical framework, the inclusion of such terms usually involves the well-known ghost problem [1]. A counterexample which can be ghost-free is including the Gauss–Bonnet (GB) correction, however, it becomes a topological term in four-dimensional spacetime and has no dynamics when minimally coupled with Einstein–Hilbert action. One way to make this term contribute to the dynamic in four-dimensional spacetime is to introduce a coupling between the GB term and scalar field [2]. The theory which includes this kind of coupling is dubbed Einstein-scalar–Gauss–Bonnet (EsGB) gravity, which has attracted plenty of attention as it admits hairy black holes. Various black hole solutions and compact objects in four-dimensional EsGB theories were studied in the literatures [3,4,5,6,7,8,9,10,11,12] and therein. More recently, the spontaneous scalarization of scalar-free black hole with particular coupling functions in EsGB theory was proposed. It was addressed that below a certain mass the Schwarzschild black hole background may become unstable in regions of strong curvature, and then a scalarized hairy black hole emerges when the scalar field backreacts to the geometry. The process evades the well-known no-hair theorems [13,14,15]. This proposal on spontaneous scalarization has inspired wide generalizations in the literatures [16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39]. For various reasons, physicists have great interest in de Sitter (dS) spacetime. On one hand, the theoretical model of our expansion universe consists on assuming positive cosmological constant, implying that the physical universe is asymptotically dS. Besides, dS spacetime plays an important role in primordial inflation theory, which is now part of the standard cosmological model [40, 41]. On the other hand, the holographic duality between quantum gravity in dS spacetime and a conformal field theory on it boundary sheds remarkable application on the asymptotically dS spacetime [42, 43].

Due to the above consideration, the spontaneous scalarization in EsGB theory has been soon extensively studied in dS spacetime [44, 45]. It was found that the positive cosmological constant does not change the local conditions for a tachyonic instability of the background black hole, Schwarzschild dS (SdS) in this case, to emerge. In details, in [44], the authors claimed that a regular black hole horizon with a non-trivial hair may be always formed after an analysis in the near-horizon asymptotic regime. But the complete hairy solution was absent, the deep reason of which is not clear. Later in [45], it was addressed if the scalar field is confined between the black hole and cosmological horizons, then it is not likely to form scalarised black hole solution; while a new hairy black hole was numerically constructed if the scalar field is permitted to extend beyond the cosmological horizon. Thus, it is obvious that the existence of cosmological horizon introduces particular situation in the black hole scalarization in dS spacetime, which deserves further study.

It is noted that though the analysis of (in)stability on the background black hole under the massless scalar field perturbation was present in [44, 45], however, the quasi-normal mode (QNM) frequencies and the dynamical evolution of the scalar field in the SdS background is still missing. This paper intends to fill this gap. We shall consider a massive scalar field as a probe field on the SdS black hole and admit the scalar field can extend beyond the cosmological horizon. By computing its fundamental QNM frequencies and the linear time domain dynamical evolution, we fix the unstable/stable parameter regions in \((\Lambda ,\alpha )\)-plane and \((m,\alpha )\)-plane, respectively for various angular momentum modes. Then we analyze the possible existence of scalar cloud by solving the static perturbation equation. We show that the bifurcation points from the lowest state of scalar field with node \(k=0\) match well with the border of unstable/stable region obtained in the fundamental frequency for various modes massless/massive scalar perturbation. Finally, we analyze the possible constraint on the models that can have scalarised solutions and address that it could emerge from the scalar could with node \(k\ge 1\). Considering the backreaction, we construct the scalarized hairy black hole solution for different scalar masses from the complete non-linear differential equations, and we also see how the scalar cloud evolves into the hairy solution by comparing their profiles.

The remaining of this paper is organized as follows. In Sect. 2, we briefly present the EsGB model with a positive cosmological constant, and the equations of motion. In Sect. 3, we analyze the (in)stability of the SdS black hole under the perturbation of massive scalar field via investigating its fundamental QNM frequencies and the time evolution. We investigate the bifurcation points at which the SdS black hole supports spherical scalar clouds with different modes, and then construct the scalarized hairy black hole solutions for different scalar masses in Sect. 4. The last section contributes to our conclusion and discussion. We shall work with the units \(\hbar =G=c=1\).

2 Model

The action of EsGB gravity in dS spacetime with the scalar field coupled with the GB invariant is given by

$$\begin{aligned} S= & {} \frac{1}{16 \pi }\int d^4x\sqrt{-g}[R-2 \Lambda -2\nabla _{\mu }\phi \nabla ^{\mu }\phi \nonumber \\&-\,m^2 \phi ^2-f( \phi ) {\mathscr {L}}_{\text {GB}}], \end{aligned}$$
(1)

where R is the Ricci scalar, \(\Lambda \) is a positive cosmological constant, \(\phi \) is scalar field with mass m, \(f( \phi )\) is the coupling function, and

$$\begin{aligned} {\mathscr {L}}_{\text {GB}}=R^2-4 R_{\mu \nu } R^{\mu \nu }+R_{\mu \nu \rho \sigma } R^{\mu \nu \rho \sigma }. \end{aligned}$$
(2)

Noted that different forms of \(f(\phi )\) shall give different properties of the EsGB theory. As mentioned in [15], to admit Schwarzschild black hole as background solution, \(f(\phi )\) could satisfy the conditions \(\frac{df(\phi )}{d\phi }\mid _{\phi =0}=0\) and \(\frac{d^2f(\phi )}{d\phi ^2}\mid _{\phi =0}={\mathfrak {b}}^2>0\), where \({\mathfrak {b}}\) is a constant. Moreover, one usually assumes that the scalar field vanishes at infinity and normalizes the constant \({\mathfrak {b}}\) to be unity. Thus, to fulfill the requirement, we shall follow [45] and choose the simplest form of the coupling function as

$$\begin{aligned} f(\phi )=a_{0}-\alpha \phi ^2, \end{aligned}$$
(3)

where \(\alpha _0\) can be an arbitrary value, and \(\alpha \) is the coupling parameter with dimension \([length]^2\) such that we will use the dimensionless parameter \( \alpha /M^2 \rightarrow \alpha .\) (Here M is kind of black hole mass with length dimension as we will see soon.)

Then the equations of motion for the scalar field and the gravity field are

$$\begin{aligned}&\nabla _{\mu }\nabla ^{\mu }\phi =\frac{1}{2}m^2\phi -\frac{\alpha \phi {\mathscr {L}}_{\text {GB}}}{2}, \end{aligned}$$
(4)
$$\begin{aligned}&R_{\mu \nu }-\frac{1}{2}Rg_{\mu \nu }+\Lambda g_{\mu \nu }=2(T_{\mu \nu }^{\phi }+T_{\mu \nu }^{GB}) \end{aligned}$$
(5)

where

$$\begin{aligned} T_{\mu \nu }^{\phi }= & {} \partial _{\mu }\phi \partial _{\nu }\phi -\frac{1}{4}g_{\mu \nu }m^2\phi ^2 -\frac{1}{2}g_{\mu \nu }\partial _{\rho }\phi \partial ^{\rho }\phi , \end{aligned}$$
(6)
$$\begin{aligned} T_{\mu \nu }^{GB}= & {} -2\alpha \left( -\frac{1}{4}\varepsilon _{\mu \sigma \gamma \tau }R^{\gamma \tau \epsilon \delta }\varepsilon _{\nu \rho \epsilon \delta }\right) \nabla ^{\rho }\nabla ^{\sigma }f(\phi ) .\end{aligned}$$
(7)

In the above sector, we shall firstly treat the scalar field as perturbation and study the (in)stability of the sector, and then we involve the backreaction of the scalar field to the geometry and construct the scalarized hairy black hole solution.

3 Analysis on the (in)stability from massive scalar field perturbation

With \(\phi =0\), the above equations admit the Schwarzschild de-Sitter (SdS) black hole solution

$$\begin{aligned}&ds^2= -g(r) d t^2+ \frac{ d r^2}{g(r)}+r^2 \left( \text {sin}^2\theta d\theta ^2 +d \phi ^2\right) \end{aligned}$$
(8)
$$\begin{aligned}&\text {with}\ g(r)= 1-\frac{2 M}{r}-\frac{\Lambda r^2}{3} \end{aligned}$$
(9)

where the constant M is the black hole mass. In this background, the GB term is evaluated as

$$\begin{aligned} {\mathscr {L}}_{\text {GB}}=\frac{48 M^2}{r^6}+\frac{8 \Lambda ^2}{3}. \end{aligned}$$
(10)

Depending on the model parameters, \(g(r)=0\) could have two positive real roots, \((r_e,r_c)\), and one negative real root, \(r_o\). The positive roots, \(r_e\) and \(r_c\), represent the black hole event horizon and cosmological horizon, respectively, of the SdS black hole. Note that these two horizons only hold when \(3M\sqrt{\Lambda }<1\), known as the Nariai limit, within which their analytic formulas are

$$\begin{aligned} r_e= & {} \frac{2}{\sqrt{\Lambda }}\cos \left( \frac{1}{3} \cos ^{-1}\left( 3M\sqrt{\Lambda }\right) +\frac{\pi }{3}\right) ,\nonumber \\ r_c= & {} \frac{2}{\sqrt{\Lambda }}\cos \left( \frac{1}{3} \cos ^{-1}\left( 3M\sqrt{\Lambda }\right) -\frac{\pi }{3}\right) . \end{aligned}$$
(11)

Approaching the Nariai limit, the event horizon and the cosmological horizon tend to merge into one horizon; and beyond the limit, no black hole horizon exists.

Considering \(r_c>r_e>r_o\), the metric function g(r) can be further expressed as,

$$\begin{aligned} g(r)=\frac{\Lambda }{3 r}(r-r_e)(r_c-r)(r-r_o). \end{aligned}$$
(12)

Introducing the surface gravity \(\kappa _i =\frac{1}{2}\mid g'(r) \mid _{r=r_i}\) associated with each root \(r=r_i~(i=e,c,o)\), one could calculate the tortoise coordinate \(r_{*}= \int g^{-1}(r) \, dr\) in an analytic form

$$\begin{aligned} r_{*}(r)= & {} \frac{1}{2\kappa _e} \ln \left( \frac{r}{r_e}-1\right) -\frac{1}{2\kappa _c} \ln \left( 1-\frac{r}{r_c}\right) \nonumber \\&+\,\frac{1}{2\kappa _o} \ln \left( \frac{r}{r_o}-1\right) \end{aligned}$$
(13)

which will play an important role in our later numerical study.

Then we consider a small scalar field perturbation on the background of SdS black hole in the linear regime, which is governed by the covariant equation

$$\begin{aligned} \square \phi =\frac{\partial f(\phi )}{\partial \phi } \frac{{\mathscr {L}}_{\text {GB}}}{4}+\frac{m^2}{2}\phi \equiv \mu _{\text {eff}}^2 \, \phi . \end{aligned}$$
(14)

Here the box denotes the d’Alembertian operator and the effective mass is

$$\begin{aligned} \mu _{\text {eff}}^2= \frac{m^2}{2}-\frac{ \alpha }{2} \left( \frac{8 \Lambda ^2}{3}+\frac{48 M^2}{r^6}\right) . \end{aligned}$$
(15)

The tachyonic instability may occur only when \(\mu _{\text {eff}}^2<0\), which requires \(\alpha >0\). As addressed in [45], this instability may trigger the emergence of a hairy solution on the SdS background via the spontaneous scalarization process, though the authors only considered the massless \(r-\)dependent scalar field. The possible parameter regions which give unstable situation and how the scalar field grows up were not present. Here we shall answer those questions by studying the dynamical perturbation of scalar field with various modes in both frequency domain and time domain.

3.1 Preliminary preparation

3.1.1 Frequency domain analysis

To analyze the (in)stability in frequency domain, one usually decompose the scalar field as

$$\begin{aligned} \phi (t,r,\theta ,\psi )=\sum _{\ell {\mathfrak {m}}}\frac{R_{\ell {\mathfrak {m}}} (r)}{r} Y_{\ell {\mathfrak {m}}} (\theta ,\psi )e^{-i\omega t} \end{aligned}$$
(16)

where \(Y_{\ell {\mathfrak {m}}} (\theta ,\psi )\) is the spherical harmonic function with angular momentum l and azimuthal number \({\mathfrak {m}}\). Working under the tortoise coordinate \(r_{*}\), we obtain that each wave function R satisfies

$$\begin{aligned} \frac{\partial ^2 R(r)}{\partial r_{*}^2}+\left( \omega ^2-V_{eff}(r)\right) R(r)=0, \end{aligned}$$
(17)

where the effective potential is

$$\begin{aligned} V_{eff}(r)=g(r)\left[ \frac{\ell (\ell +1)}{r^2}+\frac{g^{'}(r)}{r}+\mu _{\text {eff}}^2 \right] , \end{aligned}$$
(18)

and it is not dependent of the azimuthal number \({\mathfrak {m}}\) because of the spherical symmetry. This potential could present a negative well between \(r_e\) and \(r_c\), which plays an important role in the instability of the SdS black hole under this perturbation as we will see soon. The asymptotic behavior of the perturbation near the horizons are

$$\begin{aligned} R(r\rightarrow r_e)\sim e^{-i\omega r_{*} }\quad \text {and}\quad R(r\rightarrow r_c)\sim e^{i\omega r_{*} } \end{aligned}$$
(19)

which correspond to ingoing and outgoing boundary condition near the event horizon and cosmological horizon, respectively. It is known that only discrete eigenfrequencies \(\omega =\omega _R+i \omega _I\) (QNM frequency), where \(\omega _R\) and \(\omega _I\) respectively denote the real part and imaginary part of the QNM frequency, satisfy the perturbation equation and the boundary conditions. Once \(\omega _I>0\), the amplitude of the perturbation will grow up, implying that the black hole is unstable under this perturbation. There are many methods developed to compute the QNM frequencies, for instance, WKB method, shooting method, Horowitz–Hubeny method, AIM method, spectral method, etc., and readers could refer to [46, 47] and therein for nice reviews. In this work, we will employ the spectral method, which has been well described in [48]. Moreover, we shall also testify our results with the time domain evolution.

3.1.2 Time domain analysis

To study the dynamical evolution of the perturbed scalar field, we decompose the scalar field as

$$\begin{aligned} \phi (t,r,\theta ,\psi )=\sum _{\ell {\mathfrak {m}}}\frac{R_{\ell {\mathfrak {m}}} (t,r)}{r} Y_{\ell {\mathfrak {m}}} (\theta ,\psi ). \end{aligned}$$
(20)

In the tortoise coordinate, the perturbation equation reduces to

$$\begin{aligned} \left( -\frac{\partial ^2}{\partial t^2}+\frac{\partial ^2}{\partial r_{*}^2}-V_{eff}(r)\right) R(t,r)=0 \end{aligned}$$
(21)

where \(V_{eff}(r)\) has been defined in (18).

We have to solve the wave equation numerically since there is no analytic form of this time-dependent wave equation. We adopt the discretization method proposed in [49], and discretize the wave equation (21) by defining \(R(r_*,t)=R(j\Delta r_*,i\Delta t)=R_{j,i}\), \(V\left( r(r_*)\right) =V(j\Delta r_*)=V_j\). Then it can be deformed as

$$\begin{aligned}&-\frac{(R_{j,i+1}-2R_{j,i}+R_{j,i-1})}{\Delta t^2}\nonumber \\&\quad +\frac{(R_{j+1,i}-2R_{j,i}+R_{j-1,i})}{\Delta r_*}\nonumber \\&\quad -V_j R_{j,i}+O(\Delta t^2)+O(\Delta r^2_*)=0. \end{aligned}$$
(22)

With the initial Gaussian distribution \(R(r_*,t=0)=\exp [-\frac{(r_*-a)^2}{2b^2}]\) and \(R(r_*,t<0)=0\), we can derive the evolution of R by

$$\begin{aligned} R_{j,i+1}= & {} -R_{j,i-1}+\frac{\Delta t^2}{\Delta r^2_*} R_{j+1,i}\nonumber \\&+R_{j-1,i}+\left( 2-2\frac{\Delta t^2}{\Delta r^2_*}-\Delta t^2 V_j\right) R_{j,i}. \end{aligned}$$
(23)

For the sake of the numerical precision, we shall fix \(\frac{\Delta t^2}{\Delta r^2_*}=0.5\) to fit the von Neumann stability conditions, and set \(a=10,b=3\) in the profile of Gaussian wave.

3.2 The QNM frequencies and instability

We will study how the coupling parameter and the mass of scalar field affect the (in)stability of SdS black hole. We will also consider different cosmological constants and angular momentums of the perturbation modes. To this end, we fix \(M=1\) without loss of generality.

3.2.1 \(\ell \)-dependence

In this subsection, we compute the fundamental (with overtone \(n=1\)) QNM frequency of different \(\ell \)-modes perturbation around the SdS black hole. We focus on the effect of \(\ell \) on the GB coupling dependent QNM frequencies by fixing \(m=0\) and \(\Lambda =0.1\).

The results are shown in Fig. 1. For the \(\ell = 0\) mode, both \(\omega _R\) and \(\omega _I\) are zero in minimal coupling case implying that the mode is prone to instability. As the coupling parameter, \(\alpha \), increases, the black lines shows that \(\omega _I\) becomes positive while \(\omega _R\) is still zero. This phenomena means that the \(\ell = 0\) mode is always unstable. For the \(\ell \ne 0\) modes, the left plot shows that as \(\alpha \) increases, \(\omega _I\) first decreases and then increases. There exists a critical value, \(\alpha _c\), at which \(\omega _I=0\) for each mode. When \(\alpha >\alpha _c\), \(\omega _I\) becomes positive implying that the corresponding perturbation could grow up to destabilize the background SdS black hole. \(\alpha _c\) is larger for modes with larger \(\ell \) and the samples are listed in Table 1, which implies that under larger \(\ell \) mode perturbation, stronger GB coupling is called for to trigger the instability.

Moreover, comparing the two plots in Fig. 1, we see that the cases with decreasing \(\omega _I\) have non-vanishing \(\omega _R\), while the cases with increasing \(\omega _I\) possess purely imaginary QNM frequency. As addressed in [50], the former cases are dubbed photon sphere modes while the latter are dS modes. In our study, since the critical \(\alpha \) from photon sphere mode to dS mode is always smaller than \(\alpha _c\), so the unstable perturbation modes are all dS modes, which is an interesting phenomena deserving further study.

Fig. 1
figure 1

The fundamental QNM frequency as a function of the GB coupling for different \(\ell \) modes

Full size image
Table 1 The critical coupling for different momentum angular
Full size table
Fig. 2
figure 2

The time evolution of the perturbation modes with \(\ell =1\), \(\ell =2\) and \(\ell =3\) from left to right

Full size image
Fig. 3
figure 3

The profile of the effective potential between the event horizon and cosmological horizon for \(\ell =0,1,2\) from left to right

Full size image
Fig. 4
figure 4

The fundamental QNM frequency as a function of GB coupling for different cosmological constant. The modes from left to right are \(\ell =1,2\) and 3, respectively

Full size image

We also directly calculate the time evolution of the perturbation field and further reveal the instability of SdS in EsGB gravity. The pedagogy on evolutionary analysis has been shown in Sect. 3.1.2. The evolutions of the perturbation with different \(\ell \) in semi-log plot are shown in Fig. 2. For \(\ell =0\) mode, non-vanishing GB coupling makes the perturbation grow as time, meaning that the system is unstable. For \(\ell \ne 0\), when \(\alpha <\alpha _c\), the perturbation will decay as the time evolves, but it grows up when \(\alpha >\alpha _c\). The phenomenon indicates that the system will become unstable under the perturbed modes once the GB coupling is larger than the corresponding \(\alpha _c\). These findings in time domain are consistent with those in frequency domain analysis. The effect of the GB coupling on the dynamical evolution is different from that of the non-minimally coupled to curvature studied in [51] which always makes the evolution decay in SdS black hole.

The effect of the GB coupling on the (in)stability of the scalar perturbation could be explained by analyzing the effective potential (18). It is straightforward to obtain that the effective potential with a fixed radius near the event horizon could be suppressed by larger \(\alpha \) but enhanced by larger \(\ell \). Then in Fig. 3, we explicitly show the profile of the potential between the event horizon and cosmological horizon. It is obvious that in each case, when \(\alpha \) is smaller than a certain value, the effective potential is always positive. As \(\alpha \) increases, a negative potential well would form, and becomes more deeper as \(\alpha \) is further enlarged. It is noted that comparing \(\alpha _c\) in the frequency as well as time domain analysis, the critical value of \(\alpha \) for the emergence of negative potential well in Fig. 3 is smaller in all cases. This is because the negative potential well is not a sufficient condition for the instability. Only deep enough potential well could help the scalar to collect near the event horizon and finally trigger the instability of system.

3.2.2 \(\Lambda \)-dependence

We then study the effect of the cosmological constant \(\Lambda \) on the fundamental QNM frequency. The results are shown in Fig. 4, which shows that the effect of \(\Lambda \) on various \(\ell \)-modes is similar. Specifically, for small \(\alpha \), \(\omega _I\) is negative and larger for larger \(\Lambda \). It means that the perturbation in the spacetime with larger \(\Lambda \) can live longer and then decays, since the lifetime is connected with the QNM frequency via \(\tau \sim 1/|\omega _I|\). As \(\alpha \) increases, \(\omega _I\) increases and there exists an intersection for different \(\Lambda \). As \(\Lambda \) increases, the critical value \(\alpha _c\) at which \(\omega _I\) transits from negative to positive increases. Then for large enough \(\alpha \), \(\omega _I\) become positive and is smaller for larger \(\Lambda \). This indicates that in SdS black hole with larger \(\Lambda \), the perturbation has longer relax time and then grows up. The above picture can also explicitly reflected in the time domain analysis, see Fig. 5 for the \(\ell =2\) mode with \(\alpha =10\) as an example.

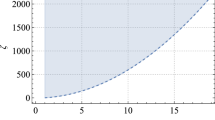
It is worthwhile to point out that for \(\alpha =0\), i.e., in Einstein gravity, our QNM frequencies with different \(\ell \) and \(\Lambda \) calculated via spectral method match well with the results computed by WKB method and Prony method in [52, 53]. Then in EsGB theory with \(\alpha \ne 0\), by scanning the cosmological constant inside the Nariai limit, we extract \(\alpha _c\) and figure out the unstable/stable region in \(\Lambda -\alpha \) plane under massless scalar perturbation. The results for samples of \(\ell \) are shown in Fig. 6. Under the perturbation mode with each \(\ell \), the instability can be triggered in the region above each line (the shading region), below which the system is stable. It is obvious that for the modes with larger \(\ell \), the system could be stable in a wider parameters region in \(\Lambda -\alpha \) plane.

Fig. 5
figure 5

The time evolution of perturbation mode with \(\ell =2\). Here the GB coupling parameters is fixed as \(\alpha =10\)

Full size image
Fig. 6
figure 6

The unstable/stable region of SdS black hole under massless scalar perturbation with \(\ell =0,1,2\) and 3 from fundamental QNM frequency

Full size image

3.2.3 m-dependence

In this subsection, with fixed \(\Lambda =0.1\), we shall turn on the mass of the scalar field and study its effect. The fundamental QNM frequencies for \(\ell =1\) mode with different m is shown in Fig. 7. It shows that the rule is similar to that for massless case, namely, as the GB coupling increases, \(\omega _I\) first decreases and then increases. And for larger m, the turning value of \(\alpha \) from decreasing to increasing is larger, so is \(\alpha _c\) at which \(\omega _I\) crosses the horizontal axis. This indicates that for the scalar field with larger mass, stronger GB coupling is required to destabilize the SdS black hole.

Fig. 7
figure 7

The fundamental QNM frequency for \(\ell =1\) mode as a function of GB coupling for different mass of scalar perturbation

Full size image
Fig. 8
figure 8

The dynamical evolution of massive scalar field in log plot. The upper-left, upper-right, lower-left and lower-right plots correspond to \(m=0.2,0.3,0.4\) and 0.5 respectively

Full size image

This conclusion is also testified by the dynamical evolution of the massive scalar field in Fig. 8. Each plot shows that when \(\alpha \) is smaller than a certain \(\alpha _c\), the scalar field would decay as the time evolves; while the scalar field will grow up when \(\alpha \) is larger than \(\alpha _c\). The growth of scalar field could finally destabilize the SdS black hole and trigger spontaneous scalarization. Comparing the value of \(\alpha _c\) in each plot, it is obvious larger m corresponds to larger \(\alpha _c\) which matches the findings in Fig. 7. More explicit effect of m on the dynamical evolution with fixed \(\alpha \) is shown in Fig. 9. This mass dependence is reasonable because even in Einstein gravity, increasing m would enhance \(\omega _I\) which is always negative and decrease the scalar field damping rate, such that the corresponding modes live longer [54].

For other modes, similar phenomena could be seen as for \(\ell =1\) mode. So instead of repeating the analysis, we collect \(\alpha _c\) with different m for \(\ell =0,1,2\) and 3 modes, and then draw the unstable/stable region in \(m-\alpha \) plane in Fig. 10. For each mode, the SdS black hole could be unstable when the parameters are in the regime above each line.

4 Scalarized hairy black hole solution

In this section, we shall fix the existence of scalar clouds and the scalarized black hole, whose profile functions between the black hole horizon and cosmological horizon will be explicitly constructed.

4.1 Bifurcation points and scalar clouds

The tachyonic instability provides the possibility of the scalar field to be non-trivial between the black hole and the cosmological horizon. Then we shall go on to seek the bound states (scalar clouds) of the test scalar around the SdS black hole. To obtain the scalar clouds with various modes, we only need to solve the perturbation equation (17) in static case with appropriate boundary conditions. With the two horizons \(r_e\) and \(r_c\), the equation is rewritten as

$$\begin{aligned}&\phi ''(r)+\frac{r_c \left( r_e-2 r\right) (r_c+ r_e)-2 r r_e^2+4 r^3}{r \left( r-r_c\right) \left( r-r_e\right) \left( r_c+r_e+r\right) }\phi '(r)\nonumber \\&\quad + \frac{\left( r_c r_e+r_c^2+r_e^2\right) \left( \ell ^2+\ell +r^2\mu _{eff}\right) }{r \left( r-r_c\right) \left( r-r_e\right) \left( r_c+r_e+r\right) }\phi '(r)=0 \end{aligned}$$
(24)

where we recover \(\phi (r)=R(r)/r\) and the effective mass is

$$\begin{aligned} \mu _{eff}=\frac{m^2}{2}-\frac{6 \alpha \left( r_c^2 r_e^2 \left( r_c+r_e\right) {}^2+2 r^6\right) }{r^6 \left( r_c r_e+r_c^2+r_e^2\right) {}^2}. \end{aligned}$$
(25)

The regularity near the black hole horizons give us

$$\begin{aligned} \phi (r\rightarrow r_e)= & {} \phi _{h}+{\tilde{\phi }}_{h}(r-r_e)+{\mathscr {O}}(r-r_e), \end{aligned}$$
(26)
$$\begin{aligned} \phi (r\rightarrow r_c)= & {} \phi _{c}+{\tilde{\phi }}_{c}(r-r_c)+{\mathscr {O}}(r-r_c) \end{aligned}$$
(27)

where \({\tilde{\phi }}_{h} ({\tilde{\phi }}_{c1})\) can be solved to be dependent on \(\phi _{h} (\phi _{c})\) .

Fig. 9
figure 9

The time evolution of the \(\ell =1\) mode with fixed \(\alpha =5.49\)

Full size image
Fig. 10
figure 10

The unstable/stable region of SdS black hole under massive scalar perturbation with \(\ell =0, 1,2\) and 3 from fundamental QNM frequency

Full size image
Fig. 11
figure 11

The scalar field profile of the lowest state for \(\alpha = bifurcation~point~\alpha _c\) (black), \(a=\alpha _c+0.5\) (red) and \(a=\alpha _c-0.5\) (blue) with \(m=0\) , \(\Lambda =0.1\). The left panel is for \(\ell =0\) with \(\alpha _c=0\) while the right panel is for \(\ell =1\) with \(\alpha _c=4.63\). Here we have set \(M=1\) and \(\phi (r_e)=1\)

Full size image
Fig. 12
figure 12

The coupling parameter against the cosmological constant for the critical SdS black hole that admits a spherical massless scalar could with the lowest state with \(k=0\) for various modes, and the insets exhibit the corresponding values of scalar field at \(r_c\). Here we have set \(M=1\) and \(\phi (r_e)=1\)

Full size image

It is known that in the construction of scalar cloud, solving (24) is in essence an eigenvalue problem [14, 55]. For given \(\ell \), m and \(\Lambda \), by imposing smoothness for the scalar filed at the horizons, one can select a discrete set of \(\alpha /M^2\), which give a discrete set scalar field profile characterized by different nodes k in between the two horizons. Those selected \(\alpha /M^2\) could be known as bifurcation points at which SdS black hole supports a spherical scalar could. In order to give an explicit picture, in Fig. 11 we show typical profiles of scalar field with the selected \(\alpha /M^2\) for the lowest state with \(k=0\) and two other \(\alpha /M^2\) with \(m=0\), \(\Lambda =0.1\) and \(\ell =0,1\). It is obvious that only the selected \(\alpha /M^2\) corresponds to a smooth scalar profile between the event horizon and cosmological horizon, giving the scalar clouds which satisfy the perturbed equation and the imposed boundary condition.

Fig. 13
figure 13

The coupling parameter against the mass of scalar field for the critical SdS black hole that admits a spherical massive scalar could with the lowest state with \(k=0\) for various modes, and the insets exhibit the corresponding values of scalar field at \(r_c\). Here we have set \(M=1\) and \(\phi (r_e)=1\)

Full size image

To study the bifurcation points for various modes and masses of scalar field, we focus on the lowest state with \(k=0\) for all cases. We show the results for \(\ell =0,1,2,3\) modes in Fig. 12. In each panel, the green dashed curve denotes the border of unstable/stable region we obtained in the analysis from fundamental frequencies (see the corresponding curves in Fig. 6). In Fig. 13, we exhibit the effect of scalar mass on the bifurcation point and the scalar field value at the cosmological horizon for scalar clouds, and again the green dashed curve in each plot denotes the border of unstable/stable region obtained from fundamental frequencies (see the corresponding curves in Fig. 10). As we expect, the bifurcation points for various mode scalar clouds match well with the critical value \(\alpha _c\) for the unstable/stable region obtained from the fundamental frequency and time domain.

Fig. 14
figure 14

The bifurcation points against \(\Lambda \) (left panel) and scalar mass (middle panel) at which it could emerge a scalarized black hole from zero mode with \(k=1\). The right panel shows a typical profile of such scalar cloud. We have set \(M=1\)

Full size image

4.2 Construction of scalarized hairy black hole

The existence of instability and smooth configurations cannot really guarantee the existence of the scalarized hairy solutions, but the authors of [45] gave possible constraints on this model in the case with massless zero mode scalar field. As aforementioned, the requirement of effective mass \(\mu ^2_{\text {eff}}<0\) should be fulfilled for tachyonic instability. Moreover, following [45], we integrate (14) along a hypersurface V bounded by \(r_e\) and \(r_c\), then considering no contribution from the boundary terms for smooth configurations could lead to the identity

$$\begin{aligned} \int _V d^4x\sqrt{-g}\mu ^2_{\text {eff}}\phi =0 \end{aligned}$$
(28)

which implies that \(\phi \) must change sign in the integration interval \(r_e<r<r_c\) for possible non-trivial scalar fields. Thus, the node k of the scalar field have to be \(k\ge 1\), such that for dS case, the lowest state of the scalar field from which a scalarized black hole may emerge is the first excited state with node \(k=1\), independent of the mass of scalar field and the modes with different \(\ell \).

Then here we shall focus on \(\ell =0\) mode for convenience and mainly study the effect of the scalar mass on the scalarized black hole.

We firstly reproduce the results of [45] on the bifurcation point \(\alpha \) against \(\Lambda \) for \(\ell =0\) massless scalar clouds with node \(k=1\), see the left panel of Fig. 14. In the middle panel, we show the bifurcation point for different scalar mass with fixed \(\Lambda =0.1\), which shows that for large m, the ratio \(\alpha /M^2\) could increase for the bifurcation. Again the green dashed lines are the unstable/stable border from the analysis of QNM frequency with overtone \(n=2\), which is consistent with the bifurcation points as expected. A typical profile of such scalar cloud is shown in right panel.

We proceed to construct the scalarized black hole solution and we will fix the profiles between the black hole horizon and cosmological horizon. So we consider the scalar field as \(\phi =\phi (r)\)Footnote 1 and take the ansatz of metric as

$$\begin{aligned} ds^2= & {} -e^{-2\delta (r)}N(r)dt^2+N^{-1}(r)dr^2\nonumber \\&+r^2(d\theta ^2+\sin ^2\theta d\varphi ^2), \end{aligned}$$
(29)

where N(r) can be parameterized as

$$\begin{aligned} N(r)=1-\frac{2{\mathscr {M}}(r)}{r}-\frac{\Lambda r^2}{3}. \end{aligned}$$
(30)

Then, recalling the equations of motion (4) and (5), we have the tt and rr components of Einstein equation as

$$\begin{aligned}&m^2 r^2 \varphi ^2-16 \alpha N^2 \left( \varphi \varphi ''+\varphi '^2\right) \nonumber \\&\quad +8 \alpha \varphi N' \varphi '+2 r N'+2 \Lambda r^2-2\nonumber \\&\quad +2 N \left( \varphi \left( 8 \alpha \varphi ''-12 \alpha N' \varphi '\right) +\left( 8 \alpha +r^2\right) \varphi '^2+1\right) =0, \end{aligned}$$
(31)
$$\begin{aligned}&m^2 r^2 \varphi ^2+48 \alpha N^2 \varphi \varphi ' \delta '+8 \alpha \varphi N' \varphi '+2 r N'+2 \Lambda r^2-2 \nonumber \\&\quad -2 N \left( 12 \alpha \varphi N' \varphi '+r^2 \varphi '^2+2 \delta ' \left( 4 \alpha \varphi \varphi '+r\right) -1\right) =0, \end{aligned}$$
(32)

and the scalar equation

$$\begin{aligned} \varphi ''+\frac{ \left( rN'+N \left( 2-r \delta '\right) \right) }{Nr}\varphi ' +\frac{r^2 \left( -2m^2\phi \right) +8\alpha \phi \left( (N-1) \left( N''+2 N \left( \delta '^2-\delta ''\right) \right) +(3-5 N) N' \delta '+N'^2\right) }{4 N r^2}=0. \end{aligned}$$
(33)
Fig. 15
figure 15

Profile functions for typical scalarized solutions with different scalar masses. Here we have set \(\Lambda =0.1\) and \(\phi (r_e)=0.02\). In the right plot, the solid curves denote the profile for the scalar field after scalarization while the dashed curves denote the corresponding scalar clouds

Full size image

To simplify the equations in numeric, we follow the skills in [45] and combine the above equations into two first order equations for the metric functions and a second order equation for scalar field as

$$\begin{aligned} \delta '= & {} F_1(N,\phi ,\phi '), \end{aligned}$$
(34)
$$\begin{aligned} N'= & {} F_2(N,\phi ,\phi '), \end{aligned}$$
(35)
$$\begin{aligned} \phi ''= & {} F_3(N,\phi ,\phi ') \end{aligned}$$
(36)

where the formulas of \(F_i\) are complex and we will not present here. Then we will numerically integrate the equation groups (35)–(36) between the event horizon and cosmological horizon. To do so, we should analyze the approximate form of the solutions at the boundary of our domain of integration. We first solve (35) and (36) by requiring that N(r) vanishes both at \(r_e\) and \(r_c\), and imposing that the scalar field smoothly goes between \(r_e\) and \(r_c\). Then we substitute the solutions of N(r) and \(\phi (r)\) into (34) by imposing \(\delta \) vanishing at cosmological horizon. With this process, we can numerically construct a branch of scalarized black holes at the bifurcation points from the zero modes. The typical solutions for different scalar masses are shown in Fig. 15. We see that the scalar mass has slight effect on the profile of N(r) but the effect on the profile of scalar field is significant. Moreover, from the right panel, we can see the difference between the profile for the scalar field for the scalarized solution (solid curves) and the corresponding scalar clouds (dashed curves).

In the numeric, similar to \(\Lambda =0\) case [13,14,15] and dS case with massless scalar field [45], there exists critical configurations that \(\phi '(r_e)\) becomes imaginary such that the numerical iterations fail to converge, which is reflected in the existence of critical value of \(\phi (r_e)\). Then with fixed \(\Lambda =0.1\) we show the ‘mass’ \({\mathscr {M}}_c={\mathscr {M}}(r_c)\) for the scalarized black hole as a function of the \(\phi (r_e)\) in Fig. 16 where the effect of the scalar mass is explicit. Here \(\phi (r_e)\rightarrow 0\) corresponds to the SdS limit while the rightmost dot represents the aforementioned critical configuration where the branches stop to exist.

Fig. 16
figure 16

The ‘mass’ \({\mathscr {M}}_c={\mathscr {M}}(r_c)\) for the scalarized black hole as a function of \(\phi (r_e)\) for different scalar masses

Full size image

5 Conclusion and discussion

In this paper, we firstly studied the dynamics of the massive scalar field perturbation on Schwarzschild de-Sitter black hole in a special EsGB theory. In both frequency and time domains, we analyzed the (in)stability of scalar-free dS black hole from the fundamental QNM frequency. To make sure the precision, we first repeat the results in Einstein theory without the GB coupling. In frequency domain, for various \(\ell \) perturbation modes, there exists a critical GB coupling \((\alpha _c)\) at which the imaginal part of QNM frequency, \(\omega _I\), is zero. When \(\alpha <\alpha _c\), \(\omega _I\) is negative indicating that the system is stable; while when \(\alpha >\alpha _c\), \(\omega _I\) turns to be positive implying that the system would undergo a tachyonic instability. Our calculation showed that larger angular momentum, cosmological constant and the mass of scalar field correspond to larger \(\alpha _c\), which means that in those cases, the SdS black hole is more difficult to be destabilized. The physical reason is that larger \(\alpha \) always give more deeper negative potential well which triggers the tachyonic instability and finally destroies the SdS black hole, while larger \(\ell \), \(\Lambda \) and m provide positive values into the effective potential and enhance the negative potential well. In time domain, for the case with \(\alpha <\alpha _c\), the scalar field perturbation would finally decay as time evolves while it would grow up for the case with \(\alpha >\alpha _c\). The growth of the perturbation could trigger the scalar-free black hole unstable and a scalarized hairy solution may emerge. By scanning the model parameters, we figured out the unstable/stable region in the \((\Lambda ,\alpha )\)-plane and also in the \((m,\alpha )\)-plane for various perturbation modes. It is noted that though the scalarization of SdS black hole with backreaction has been investigated in [44, 45], there are still many open issues as their authors addressed. Here we analyzed the (in)stability in probe limit, but our findings could be helpful to further understand the black hole scalarization in dS spacetime. For example, it is only possible to construct the scalarized hairy solution for the parameters in the shading region in Figs. 6 and 10.

Then we investigated the bifurcation points at which the SdS black hole supports spherical scalar clouds. We found that the bifurcation points from the lowest sate of scalar field with node \(k=0\) match well with the border of unstable/stable region obtained in the fundamental frequency for \(\ell =0,1,2,3\) modes massless/massive scalar perturbation. And for \(\ell =0\), the bifurcation points from the scalar field with node \(k=1\) match well with the border of unstable/stable region obtained in the frequency with overtone \(n=2\) massless/massive scalar perturbation. Finally, by including the backreaction, we constructed the scalarized hairy black hole solutions for different scalar masses. We also showed how the scalar cloud evolves into the hairy solution through the backreaction by comparing its scalar field with the corresponding scalar clouds. It is worthwhile to mention that allthrough this work, we fix our study in the region between the black hole horizon and cosmological horizon, two boundaries for dS black hole which are mostly concerned.

As a simple way to constrain the model parameters of possible spontaneous scalarization, it is interesting to extend our dynamical analysis into many cases. A straightforward case is the Schwarzschild or AdS black holes in EsGB theory as well as other modified gravities mentioned in the introduction. The second case is the dynamic of massive scalar filed perturbed on Kerr black hole in EsGB. Though this direction has been investigated in [56], but there the authors only considered the \(\ell =1\) mode of massless scalar field. Since besides the tachyonic instability, the superradiant instability may occur in rotating black hole, so considering the mass of the scalar field and different modes will introduce more physics on the fate of scalar-free background. The next but not the last case is to consider the dynamic of charged black hole before it was scalarized. The scalarization of charged black hole has been firstly proposed in [57] and soon been generalized in [58,59,60,61,62,63,64], and a complete dynamical analysis on the scalar-free charged black hole still deserves to be present.