Abstract
We investigate the potential of the channel mono-Higgs + missing transverse energy (MET) in yielding signals of dark matter at the high-luminosity Large Hadron Collider (LHC). As illustration, a Higgs-portal scenario has been chosen, where an extension of the Standard Model with a real scalar gauge-singlet which serves as a dark matter candidate. The phenomenological viability of this scenario has been ensured by postulating the existence of dimension-6 operators that enable cancellation in certain amplitudes for elastic scattering of dark matter in direct search experiments. These operators are found to have non-negligible contribution to the mono-Higgs signal. Thereafter, we carry out a detailed analysis of this signal, with the accompanying MET providing a useful handle in suppressing backgrounds. Signals for the Higgs decaying into both the diphoton and \(b{\bar{b}}\) channels have been studied. A cut-based simulation is presented first, optimizing over various event selection criteria. This is followed by a demonstration of how the statistical significance can be improved through analyses based on boosted decision trees and artificial neural networks.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Standard Model(SM) of particle physics has proven to be an extremely successful theory so far. Experimental studies have confirmed most of its predictions to impressive levels of accuracy [1,2,3,4,5]. It still remains an intense quest to look for physics beyond the standard model. Perhaps the most concrete and persistent reason for this is the existence of dark matter (DM) which constitutes to up to 23% of the energy density of the universe, and the belief that DM owes its origin to some hitherto unseen elementary particle(s). In such a situation, one would like to know if the DM particle interacts with those in the SM, and if so, what the signatures of such interactions will be. The literature is replete with ideas as to the nature of DM, a frequently studied possibility being one or more weakly interacting massive particle(s) (WIMP), with the DM particle(s) interacting with those in SM particles coupling strength of the order of the weak interaction strength.
The collider signal of a WIMP DM is commonly expected to consist in MET. In addition, signals of the mono-X type(where X = jet, \(\gamma \) Z, h etc) are advocated as generic probes of WIMP dark matter [6,7,8,9,10,11,12]. It may be asked whether one can similarly have mono-Higgs DM signals [13, 14], accompanied by hard MET caused by DM pairs (assuming that a \(Z_2\) symmetry makes the DM stable). Such analyses in the context of various supersymmetric [15, 16] and non-supersymmetric [17,18,19,20] models have been performed in the past. However, the existing studies in this context leave enough scope for refinement, including (a) thorough analyses of the proposed signals as well as their SM backgrounds at the Large Hadron Collider (LHC), and (b) the viability of Higgs + DM-pair production, consistently with already available direct search constraints. Such constraints already disfavour so-called ‘Higgs-portal’ scenarios in their simplest versions [21,22,23,24,25]. However, there exist theoretical proposals [26,27,28] involving new physics, where the Higgs-mediated contribution to spin-independent cross-section in direct search experiments undergo cancellations from additional contributing agents. Keeping this in mind, as also the fact that LHC is not far from its high-luminosity phase, it is desirable to sharpen search strategies for mono-Higgs + MET signals anyway, especially because it relates to the appealing idea that the Higgs sector is the gateway to new physics. However, such signals are understandably background-prone, and refinement of the predictions in a realistic LHC environment is a necessity. Furthermore, it needs to be ascertained how the additional terms in the low-energy theory cancelling the Higgs contributions in direct search experiments affect searches at the LHC. We address both issues in the current study.
As for the additional terms cancelling the contributions of the 125-GeV scalar to spin-independent inelastic scattering, scenarios with an extended Higgs sector have been studied earlier [27]. There is also a rich literature on Higgs-portal models with fermionic dark matter, where different contributions to the direct detection cross sections lead to cancellations (so-called blind-spots) [29,30,31,32]. Here, however, we take a model-independent approach, and postulate the new physics effects to come from dimension-6 and-8 operators which are suppressed by the scale of new physics. These lead to the rather interesting possibility of partial cancellation between the coefficients of dimension-4 and higher dimension operators. Thus at the same time, one obeys direct detection constraints, has not-so-small coupling between the Higgs and the DM, and matches the observed relic density.
We consider for illustration the \(\gamma \gamma \) and \(b {\bar{b}}\) decay modes of the mono-Higgs, along with substantial MET. We have started with rectangular cut-based analyses for both final states. The di-photon events not only have the usual SM backgrounds but also can be faked to a substantial degree by \(e\gamma \)-enriched di-jet events. Following up on a cut-based analysis, we switch on to machine learning (ML) techniques to improve the signal significance, going all the way to using artificial neural networks (ANN) and boosted decision tree (BDT) for both \(\gamma \gamma \) and \(b \bar{b}\) final states.
We present the salient features of our present work in the following:
-
We have thoroughly studied the possibility of probing mono-Higgs signature at the high-luminosity (HL)-LHC, and at the same time asserted the viability of such scenarios from the dark matter direct detection and relic density constraints. We have found out that simple Higgs-portal dark matter can satisfy all the relevant constraints in the presence of high scale physics and it can be probed at HL-LHC in the mono-Higgs final state. In this context, our study contributes significantly beyond the analysis of [13].
-
We have gone beyond specific models [8, 15, 16, 20] and employed model-independent effective theory approach to parametrize the high-scale physics.
-
We have examined the cleanest final state (
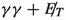 ) as well as the final state with maximum yield (
) as well as the final state with maximum yield (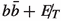 ) and thus presented an exhaustive and comparative study.
) and thus presented an exhaustive and comparative study. -
In the context of LHC, we have performed a thorough background analysis following the experimental studies in this direction, which was not done in such detail in earlier theoretical studies.
-
Lastly, we have predicted significant improvements compared to the cut-based analysis by using advanced machine-learning techniques.
The plan of our paper is as follows. In Sect. 2 we discuss the outline of the model-independent scenario that we have considered and we take into account all the relevant constraints on this scenario and find out viable and interesting parameter space which can give rise to substantial mono-Higgs signature at the high luminosity LHC. In Sect. 3 we discuss in detail our signals and all the major background processes. In Sect. 4 we present our results of a rectangular cut-based analysis. In Sect. 5 we employ machine-learning tools to gain improved signal significance over our cut-based analysis. In Sect. 7 we summarize our results and conclude the discussion.
2 Outline of the scenario and its constraints
2.1 The theoretical scenario
We illustrate our main results in the context of a scenario of a scalar DM particle. Where scalar sector is augmented by the gauge-singlet \(\chi \), the potential can be generally written by

Here \(\Phi \) is the SM Higgs doublet and \({\lambda }_{\Phi \chi }\) and \(\lambda _{\chi }\) are the relevant quartic couplings. A \(Z_2\) symmetry is imposed, under which \(\chi \) is odd. This legitimizes the potential role of \(\chi \) as DM candidate, and also prevents the mixing between \(\phi \) and \(\chi \), which would otherwise bring in additional constraints on the scenario.
It is clear from above that the simplest operator involving the Higgs boson and a scalar DM \(\chi \) is the dimension-4 renormalizable operator \(\Phi ^{\dagger } \Phi \chi ^2\). This operator gives rise to the dominant contribution to the mono-Higgs +  final state when Higgs is produced via gluon fusion, as can be seen from Fig. 1. We have illustrated with reference to the gluon-fusion channel because (a) it is the dominant Higgs production mode, and (b) other widely studied modes involved some additional associated particles, while our focus here specifically on the mono-Higgs final state. Of course similar final states can arise from the same operators, in quark-initiated processes as well, but their contribution will be negligible compared to the gluon-initiated ones. This operator also takes part in the DM-nucleon elastic scattering through t-channel Higgs exchange (see Fig. 2 (left)) and DM annihilation diagram with s-channel Higgs mediation (Fig. 2 (right)). The stand-alone presence of this operator makes it difficult to satisfy both direct detection constraints and relic density requirements simultaneously, as will be discussed in the next section. However, one can go beyond dimension-4 terms and construct higher-dimensional operators involving (anti-)quarks, Higgs and a pair of DM particles, which contribute to the mono-Higgs +
final state when Higgs is produced via gluon fusion, as can be seen from Fig. 1. We have illustrated with reference to the gluon-fusion channel because (a) it is the dominant Higgs production mode, and (b) other widely studied modes involved some additional associated particles, while our focus here specifically on the mono-Higgs final state. Of course similar final states can arise from the same operators, in quark-initiated processes as well, but their contribution will be negligible compared to the gluon-initiated ones. This operator also takes part in the DM-nucleon elastic scattering through t-channel Higgs exchange (see Fig. 2 (left)) and DM annihilation diagram with s-channel Higgs mediation (Fig. 2 (right)). The stand-alone presence of this operator makes it difficult to satisfy both direct detection constraints and relic density requirements simultaneously, as will be discussed in the next section. However, one can go beyond dimension-4 terms and construct higher-dimensional operators involving (anti-)quarks, Higgs and a pair of DM particles, which contribute to the mono-Higgs +  signal. At the same time such operators add credence to such a Higgs-portal scenario by cancelling the contribution to spin-independent cross-sections in direct search experiments.
signal. At the same time such operators add credence to such a Higgs-portal scenario by cancelling the contribution to spin-independent cross-sections in direct search experiments.
One can write two SU(2)\(_L \times \) U(1)\(_Y\) gauge-invariant and Lorentz invariant operators in this context, namely \({\mathscr {O}}_1\) and \({\mathscr {O}}_2\), which are of dimension-6 and-8 respectively, as follows:


 is a dimension-6 operator involving a quark–antiquark pair, the Higgs boson and a pair of DM particles. On the other hand,
is a dimension-6 operator involving a quark–antiquark pair, the Higgs boson and a pair of DM particles. On the other hand,  is of dimension-8, involving derivatives of \(\Phi \) as well as \(\chi \). Both of these operators are multiplied by appropriate Wilson coefficients \(f_i(i = 1,2\)).
is of dimension-8, involving derivatives of \(\Phi \) as well as \(\chi \). Both of these operators are multiplied by appropriate Wilson coefficients \(f_i(i = 1,2\)).
Our main purpose in this paper is to bring out the potential of mono-Higgs signals for dark matter. With this in view, we have chosen a smallest set of operators guided by the requirement to satisfy the dark matter constraints and yet have a respectable collider signature. This is achieved by choosing a pair of operators that interfere destructively with the Higgs-mediated amplitude in direct search experiment and choosing a collider channel that does not suffer this interference. For appropriate values of the Wilson coefficient a sizable collider signature can be obtained without violating the constraints.
Once the higher dimensional operators are introduced, they contribute to both spin-independent cross-section in direct searches and annihilation of \(\chi \) before freeze-out. The appropriate Feynman diagrams are shown in Fig. 3. One should note that contributions in Fig. 3 arises when \(\Phi \) acquires a VEV. Such contributions will interfere with those coming from the diagrams shown in Fig. 2.
Let us also mention the operators  and
and  contribute only to the spin-independent cross-section in direct search due to the absence of \(\gamma _5\) in them. And finally, the presence of higher dimensional operators also opens up additional production channels leading to the mono-Higgs signals via quark induced diagrams, whose generic representation can be found in Fig. 4.
contribute only to the spin-independent cross-section in direct search due to the absence of \(\gamma _5\) in them. And finally, the presence of higher dimensional operators also opens up additional production channels leading to the mono-Higgs signals via quark induced diagrams, whose generic representation can be found in Fig. 4.
2.2 Constraints from the dark matter sector and allowed parameter space
As the scenario under consideration treats \(\chi \) as a weakly interacting thermal dark matter candidate, it should satisfy the following constraints:
-
The thermal relic density of \(\chi \) should be consistent with the latest Planck limits at the 95% confidence level [33].
-
The \(\chi \)-nucleon cross-section should be below the upper bound given by XENON1T experiment [34] and any other data as and when they come up.
-
Indirect detection constraints coming from both isotropic gamma-ray data and the gamma ray observations from dwarf spheroidal galaxies [35] should be satisfied at the 95% confidence level. This in turn puts an upper limit on the velocity-averaged \(\chi \)-annihilation cross-section [36].
-
The invisible decay of the 125-GeV scalar Higgs h has to be \(\le \) 19% [41].
It has been already mentioned that the simplest models using the SM Higgs as the dark matter portal is subject to severe constraints. The constraints are two-fold: from the direct search results, especially those from Xenon-1T [34], and from the estimates of relic density, the most recent one coming from Planck [33]. While the simultaneous satisfaction of both constraints restricts SM Higgs-portal scenarios rather strongly, the same restrictions apply to additional terms in the Lagrangian as well. In our case, the coefficient of \(\Phi ^\dagger \Phi \chi ^2\), restricted to be ultra-small from direct search data, cannot ensure the requisite annihilation rate in the dominant modes such as \(f \bar{f}\) and \(W^+W^-\) (see Eq. (4) where the s-channel annihilation cross-sections are given in the centre of mass frame [42]).
where \(\beta _A = \sqrt{1-4m_A^2/s}\). It is thus imperative to have additional terms that might bring out cancellation of the Higgs contribution in direct search and thus make the quartic term less constrained. The signs of the tri-linear coupling \(\lambda _{h\chi \chi }\) (which is basically \(\lambda _{\Phi \chi }v)\) and the Wilson coefficients \(f_i\)s have to be appropriately positive or negative to ensure destructive interference. It will become clearer if we look at the analytical expression for spin-independent DM-nucleon scattering cross-section [43], in the presence of Higgs-portal as well as dimension-6 operator \({\mathscr {O}}_1\), given below.Footnote 1
Here \(m_N\) is the mass of the nucleon and \(f_N\) is the effective Higgs-nucleon coupling. A cancellation at the amplitude level will certainly produce small DM-nucleon scattering cross-section. While such cancellation may apparently be inexplicable, it is important to phenomenologically examine its implication, in a model-independent approach if possible. A similar approach has been taken in a number of recent works [26,27,28]. The higher-dimensional operators listed in the previous subsection are introduced in this spirit.
Parameter space (yellow points) allowed by the relic density observation. The black line is the upper limit on the spin-independent \(\chi -N\) scattering cross-section from XENON1T experiment. Region below the black line is allowed by direct detection bound from the XENON1T experiment. For this plot, we varied \(\lambda _{\Phi \chi }\) in the full range \(-4\pi \) to \(4\pi \), 5GeV \(<m_{\chi }<1\) TeV, \(4\text { TeV}< \Lambda < 50\) TeV, \(f_1, f_2 \approx 1\)
Region allowed by the relic density and direct detection observation in the parameter space spanned by the coefficients of dimension-4 and dimension-6 operators for scalar DM. The mass of the DM has been scanned in the range 5 GeV \(< m_{\chi }<\) 1 TeV for this plot. The mass of the dark matter is shown as the color-axis
In Fig. 5, we show regions of the parameter space consistent with the observed relic density (yellow points) as a function of dark matter mass \(m_{\chi }\). The black line in the figure represents the upper limit from Xenon-1T on the spin-independent DM-nucleon elastic scattering cross-section as a function of the mass of the DM particle. The region below this curve is our allowed parameter space. It is clearly seen from the figure that larger DM mass regions satisfy the direct detection bound easily, primarily because of the fact that the DM-nucleon scattering cross-section decreases with increasing DM mass (see Eq. (5)) and also the experimental limit becomes weaker for larger DM mass.
In Fig. 6, we show the region of parameter space in the \(\frac{1}{v}\lambda _{h\chi \chi } - \frac{\Lambda }{\sqrt{|f_1|}}\) plane, which is consistent with both relic density and direct detection upper bound. One can see that only a narrow region is allowed, where the aforementioned cancellation in the DM-nucleon scattering amplitude takes place. As the trilinear coupling decreases, the high scale gets pushed to a higher value, as expected. The broadness of the red curve owes itself to the \(2 \sigma \) band of the relic density as well as the the direct detection limit and most importantly, to the specified range of dark matter mass as described in Fig. 6. As discussed earlier, we can see from Eq. (5), the spin-independent scattering cross-section decreases with increasing DM mass \(m_{\chi }\). Also, from Fig. 5, it is clear that the upper limit on DM-nucleon scattering cross-section becomes weaker as one goes higher in DM mass. Therefore, it follows that if one varies DM mass to larger values, the direct detection limit will be less stringent and larger band will be allowed. One can see that looking at the color-axis in Fig. 6. All the relevant quantities in Figs. 5 and 6, such as relic density(\(\Omega h^2\)), spin-independent DM-neucleon scattering cross-section (\(\sigma _{\chi N}\)) have been calculated using MicrOMEGAs-5.0.8 [44], where we have implemented our model via Feynrules-2.3 [45].
We use MicrOMEGA-5.0.8 to also estimate the indirect detection cross-section for the benchmark points chosen in the upcoming sections. We find \(\langle \sigma v\rangle \) to be in the vicinity of \(10^{-29}\) cm\(^3\) for all six benchmark points we have chosen. These indirect detection cross-sections are way below the bound report from Fermi-LAT [35,36,37] (\(\langle \sigma v\rangle \gtrsim 10^{-26}\) cm\(^3\)) and AMS [38] (\(\langle \sigma v\rangle \gtrsim 10^{-28}\) cm\(^3\)).
We present in the next section, the collider analysis for a few benchmark points which satisfy all the aforementioned dark matter constraints. We mention here that our choice of benchmarks will be strongly guided by the phenomenological aspiration to probe the maximally achievable collider sensitivity. However, we have checked that all our benchmarks satisfy tree-level unitarity and vacuum stability using SARAH [39] and our own modification of 2HDME [40].
Production cross-section of \(p p \rightarrow h \chi \chi \) at 13 TeV as a function of dark matter mass, \(\lambda _{\Phi \chi } \approx 4\pi \) (perturbative upper limit) and \(\Lambda \approx 5\) TeV (the corresponding approximate lower limit derived from Fig. 6). The cross-sections are calculated at parton level using Madgraph@MCNLO [46]
3 Signals and backgrounds
Having identified the regions of allowed parameter space we proceed towards developing strategies to probe such scenarios at the high luminosity LHC. Our study is based on a scalar DM \(\chi \) as mentioned earlier. One should note that a corresponding fermionic DM will not allow the production channels in Fig. 1 purely driven by dimension-4 operator. Therefore one will have to depend on higher-dimensional operators with the production rate considerably suppressed. As has been discussed earlier, we are looking for the mono-Higgs +  final state. Since the process will lead to substantial number of events with missing energy, the decay products of the Higgs constitute the visible system recoiling against the missing transverse momenta. The main contribution to production comes from the top two diagrams in Fig. 1.
final state. Since the process will lead to substantial number of events with missing energy, the decay products of the Higgs constitute the visible system recoiling against the missing transverse momenta. The main contribution to production comes from the top two diagrams in Fig. 1.
In Fig. 7, we show the dependence of \(\sigma (p p \rightarrow h \chi \chi )\) on \(m_{\chi }\) for \(\lambda _{\Phi \chi } \approx 4\pi \) and \(\frac{\Lambda }{\sqrt{|f_{1,2}|}} \approx 5\) TeV. It is clear from this figure that a resonance takes place in the vicinity of \(\frac{m_h}{2}\), a behavior which can be intuitively understood from Fig. 1, where we have seen that, the first two diagrams make dominant contribution to the final state. It is worth mentioning that the effective operator \({\mathscr {O}}_1\) contributes close to 10% as much as the gluon fusion channel in \(h \chi \chi \) production, the contribution of \({\mathscr {O}}_2\) is about half of that of \({\mathscr {O}}_1\). Here also the assumption \(f_1 \approx f_2\) is made. While the choice of parameters in Fig. 7, as justified in the caption is on the optimistic side form the view-point of signals, they qualitatively capture the features of this scenario.
The next important task is to identify suitable visible final states which will recoil against the invisible \(\chi \chi \) system. The largest branching ratio of the 125 GeV scalar is seen in the \(b \bar{b}\) channel. However, while this assures one of a copious event rate, one is also deterred by the very large QCD backgrounds, whose tail poses a threat to the signal significance. While we keep the \(b \bar{b}\) channel within the purview of this study, we start with a relatively cleaner final state, namely a di-photon pair. Its branching ratio (2.27\(\times 10^{-3}\)) considerably exceeds that of the four-lepton channel (7.2\(\times 10^{-5}\)) which too is otherwise clean. As compared to the \(b \bar{b}\) channel, di-photon offers not only better four-momentum reconstruction but also a cleaner MET identification. We suggest in the discussion below, some strategies to overcome this disadvantage largely making use of one feature of the signal, namely a substantial missing  generated by the \(\chi \chi \) system.
generated by the \(\chi \chi \) system.
3.1
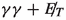 channel
channel
The di-photon channel is apparently one of the cleanest of Higgs signals. The absence of hadronic products is perceived as the main source of its cleanliness, together with the fact that there is a branching ratio suppression (though rather strong) at a single level only as opposed to the four-lepton final state. This channel has been under scrutiny from the earliest days of Higgs-related studies at the LHC. In the present context we are focussing on events with at least two energetic photons and substantial  . Searches for such events have been carried out by both CMS [47,48,49,50,51] and ATLAS [52,53,54].
. Searches for such events have been carried out by both CMS [47,48,49,50,51] and ATLAS [52,53,54].
As can be seen in Fig. 7, this channel is usable for \(m_{\chi } \lesssim 100\) GeV, and particularly in the resonant region. Moreover, the upper limit on the invisible decay of the Higgs prompts us to those benchmarks where \(m_{\chi } > m_h/2\). A set of such benchmark points, satisfying also all constraints related to dark matter, are listed in Table 1.
BP2 corresponds to the best possible scenario in terms of signal cross-section, with mass of the dark matter close to \(\frac{m_h}{2}\) and \(\lambda _{\Phi \chi }\) coupling satisfying the perturbativity limit. We move up in \(m_{\chi }\) in BP1, to illustrate the reach of  signal for higher DM masses. BP3, on the other hand, has been chosen to explore the reach of the signal in terms of the quartic coupling \(\lambda _{\Phi \chi }\).
signal for higher DM masses. BP3, on the other hand, has been chosen to explore the reach of the signal in terms of the quartic coupling \(\lambda _{\Phi \chi }\).
The apparent cleanliness of the signal, however, can be misleading. Various backgrounds as well as possibilities of misidentification or mismeasurement tend to vitiate the signal. In order to meet such challenges, the first step is to understand the backgrounds.
 final state. We have chosen \(f_1 = f_2 = 1\) for all the benchmarks
final state. We have chosen \(f_1 = f_2 = 1\) for all the benchmarksBackgrounds Contamination to the di-photon final state comes mainly from prompt photons that originate from the hard scattering process of the partonic system (e.g. \(q\bar{q} \rightarrow \gamma \gamma \) through Born process or \(gg \rightarrow \gamma \gamma \) through a one-loop process represented by “box diagram”) or non-prompt photons, that originate within a hadronic jet, either from hadrons that decay to photons or are created in the process of fragmentation, governed through the quark to photon and gluon to photon fragmentation function \(D^q_{\gamma }\) and \(D^g_{\gamma }\) [55,56,57,58,59]. Such non-prompt photons are always present in a jet, and can be misidentified as a prompt photon when most of the jet energy is carried by one or more of these photons. We shall refer to this effect as “jet faking photons”. Electrons with energy deposit in the electromagnetic calorimeter (ECAL), can be misidentified as a photon if the track reconstruction process fails to reconstruct the trajectory of the electron in the inner tracking volume, since both electron and photon deposit energy in the ECAL by producing an electromagnetic shower, with very similar energy deposit patterns (shower shapes). Therefore processes with energetic electrons in the final state can also contribute to the background. We shall refer to this type of misidentification as “electron faking photon”. It may be noted that the “jet faking photons ” also has a contribution from non-prompt electrons produced inside the jet, that fake a photon due to track misreconstruction. In the following we discuss the various SM processes that give rise to prompt and non-prompt backgrounds ordered according to their severity.
- QCD multijet::
-
Although the jet faking photon probability is small in the high \(p_T\) region of interest of this analysis(\(\sim 10^{-5}\) as estimated from our Monte-Carlo Analysis), the sheer enormity of the cross-section (\(\sim millibarns\) above our \(p_T\) thresholds) makes this the largest background to the di-photon final state.
To estimate this background as accurately as possible, we have first generated an \(e\gamma \)-enriched di-jet sample, which essentially means jets that contain photon-like(EM) objects within themselves. We mention here that, to achieve better statistics, we apply a generation level cut \(p_T > 30\) GeV and \(|\eta | < 2.5\) on both jets. The most common source of jet faking a photon is through \(\pi ^0\) inside the jet, which decays into two photons. Other meson decays, electron faking photon and fragmentation photons contribute a lesser but non-negligible amount. We have considered all QCD multijet final states which contain any one of the following objects: photon, electron, \(\pi ^0\) or \(\eta \) mesons (namely the EM-objects). Then we have categorized only those objects which have \(p_T > 5\) GeV and are within the rapidity-range \(|\eta | < 2.7\), as ‘seeds’. Then energies and \(p_T\) of all the EM-objects within \(\Delta R < 0.09 \) around the seed are added with the energy and \(p_T\) of the seed. Thus, out of all those EM-objects within a jet, photon candidates are created. If in a QCD multijet event, there are at least two photon candidates with \(p_T \gtrsim \) 30 GeV, those events can in principle fake as a photon with high probability. However, one should also demand a strong isolation around those photon candidates following the isolation criteria described earlier to differentiate between these jet faking photons and actual isolated hard photons.
- \(\gamma +\) jets::
-
This background already has an isolated photon candidate. However, here too, the jets in the final state can fake as photon with a rather small probability(\(\sim 0.003\) as estimated from our Monte-Carlo Analysis). But again the large cross-section (\(\approx 10^5\) pb) of this process makes suppression of the background challenging. For correct estimation of this background, we adopt the same method that has been applied for the multijet background discussed earlier. Like QCD multi-jet, this background is also generated with \(p_T > 30\) GeV and \(|\eta | < 2.5\) on the photon and the jet for gaining better statistics.
- \(t \bar{t} + \gamma \)::
-
Another major background comes from \(t \bar{t} + \gamma \) production, when one or more of the leptons or jets from top decay are mistagged as photon. Although the cross-section is significantly lower compared to \(\gamma \) + jets background, a real source of large
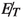 in this case makes it difficult to reduce this background. However, the isolation criterion as discussed above as well as an invariant mass cut help us suppress this background.
in this case makes it difficult to reduce this background. However, the isolation criterion as discussed above as well as an invariant mass cut help us suppress this background. - di-photon::
-
As mentioned above, this background includes production of two photons in the final state through gluon-initiated box diagram, and also via quark-initiated Born diagrams. Although this background gives rise to two isolated hard photons, it does not contribute much due to relatively low cross-section. Demanding a hard
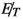 and using the fact that the invariant mass of the di-photon pair should peak around the Higgs mass, one can get rid of this background.
and using the fact that the invariant mass of the di-photon pair should peak around the Higgs mass, one can get rid of this background. - \(V+\gamma \)::
-
A minor background arises from \(W/Z + \gamma \) channel, when one or more leptons or jets from W or Z decay are mistagged as photons. However, the
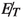 associated with this process is not significant and one of the photons is not isolated. Therefore, this process contributes only a small amount to the total background.
associated with this process is not significant and one of the photons is not isolated. Therefore, this process contributes only a small amount to the total background. - \(Z(\rightarrow \nu \bar{\nu }) h(\rightarrow \gamma \gamma )\)::
-
This is an irreducible background for our signal process. This gives rise to sizeable
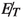 , with the invariant mass of the di-photon pair peaking around \(m_h\). However, this process has small enough cross-section compared to other backgrounds and proves to be inconsequential in the context of signal significance.
, with the invariant mass of the di-photon pair peaking around \(m_h\). However, this process has small enough cross-section compared to other backgrounds and proves to be inconsequential in the context of signal significance.
A few comments are in order before we delve deeper into our analysis. Some studies in the recent past have considered, Higgs production through higher dimensional operators, based on the di-photon signal [13]. However, the role of backgrounds from QCD multijets has not been fully studied there. Our analysis in this respect is more complete. Also, \(p p \rightarrow W^+ W^-\), too, in principle lead to substantial  + two ECAL hits with electrons from both the Ws being missed in the tracker. We can neglect, such fakes because (a) the event rate is double-suppressed by electronic branching ratios, (b) demand on the invariant mass helps to reduce the number of events and (c) two simultaneous fakes by energetic electrons is relatively improbable.
+ two ECAL hits with electrons from both the Ws being missed in the tracker. We can neglect, such fakes because (a) the event rate is double-suppressed by electronic branching ratios, (b) demand on the invariant mass helps to reduce the number of events and (c) two simultaneous fakes by energetic electrons is relatively improbable.
Events for the signals and most of the corresponding backgrounds (excepting QCD multijet and \(\gamma \)+jet) and have been generated using Madgraph@MCNLO [46] and their cross-sections have been calculated at the next-to-leading order (NLO). We have used the nn23lo1 parton distribution function. The QCD multijet and \(\gamma +\) jet backgrounds are generated directly using PYTHIA8 [60]. MLM matching with xqcut = 30 GeV is performed for backgrounds with multiple jets in the final state. PYTHIA8 has been used for the showering and hadronization and the detector simulation has been taken care of by Delphes-3.4.1 [61]. Jets are formed by the built-in Fastjet [62] of Delphes.
3.2
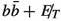 channel
channel
Signal The  channel resulting in hadronic final states, poses a seemingly tougher challenge, as compared to the di-photon final state. However, the substantial rate in this channel creates an opportunity to probe the mono-Higgs+MET signal, if backgrounds can be effectively handled. Searches in this channel have been carried out by both CMS [49, 63, 64] and ATLAS [65,66,67] experiments. We demand at least two energetic b-tagged jets, along with considerable
channel resulting in hadronic final states, poses a seemingly tougher challenge, as compared to the di-photon final state. However, the substantial rate in this channel creates an opportunity to probe the mono-Higgs+MET signal, if backgrounds can be effectively handled. Searches in this channel have been carried out by both CMS [49, 63, 64] and ATLAS [65,66,67] experiments. We demand at least two energetic b-tagged jets, along with considerable  .
.
It is clear from Fig. 7 that here too the resonance region (\(m_\chi \gtrsim \frac{m_h}{2}\)) offers the best signal prospect, as in the \(\gamma \gamma \) case. The enhancement in the resonant region enables one to probe \(\lambda _{\phi \chi } \lesssim 6\) in a cut-based analysis. We shall discuss later the possible improvements using machine learning techniques. This makes the \(b\bar{b}\) channel more attractive prima facie, as compared to the diphoton channel. the rates are large enough for probing up to \(\Lambda \approx \) 8 TeV, or, alternatively, DM masses up to 8 TeV. Although higher \(m_\chi \) implies lower yield (see Fig. 7), judicious demands on the \({\not {E}}_{T}\) lend discernibility to the final state. One thus starts by expecting to probe larger regions in the parameter space for the Higgs decaying into b-pairs. The benchmark points listed in Table 2 are selected, satisfying all the aforementioned constraints, by keeping this in mind. The prospect of detectability at the LHC is of course the other guiding principle here. BP5 offers the best prospect, with the dark matter mass in the resonant region and the quartic coupling \(\lambda _{\phi \chi }\) close to its perturbativity limit. One should note that BP5 here has similar potential as BP2 in the case of the diphoton channel. BP4 is more favorable for relatively heavy dark matter particles for the same quartic coupling. On the other hand, BP4 can be explored for smaller \(\lambda _{\phi \chi }\) compared to BP4 and BP5, so long as \(m_\chi \) continues to remain in the resonant region.
 final state. We have chosen \(f_1 = f_2 = 1\) for all the benchmarks
final state. We have chosen \(f_1 = f_2 = 1\) for all the benchmarksHaving chosen benchmark points for signal we proceed to analyse the corresponding backgrounds. Here too, for the backgrounds involving multiple jets in the final state, the MLM matching procedure has been used with xqcut = 30 GeV.
Background We list the dominant backgrounds for this channel in the following.
- \(t \bar{t} +\) single top::
-
The major background for the \( b \bar{b}\) channel comes from \(t \bar{t}\) production at the LHC when one of the resulting W’s decays leptonically. It is commonly known as semi-leptonic decay of \(t \bar{t}\) pair. This process has considerable production rate and it is also source of substantial
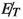 . A minor contribution comes from the leptonic decay of both W’s from \(t \bar{t}\). We call this leptonic decay of \(t \bar{t}\). It also has
. A minor contribution comes from the leptonic decay of both W’s from \(t \bar{t}\). We call this leptonic decay of \(t \bar{t}\). It also has 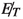 in the final state from two neutrinos coming from leptonic W decay. However, a veto on \(p_T\) of leptons \(> 10\) GeV reduces this background at the selection level itself, whereas the semileptonic \(t \bar{t}\) background is less affected by such veto. The hadronic background where both W’s from \(t \bar{t}\) decay hadronically, has the largest cross-section among all \(t \bar{t}\) backgrounds. However, in this case the source of
in the final state from two neutrinos coming from leptonic W decay. However, a veto on \(p_T\) of leptons \(> 10\) GeV reduces this background at the selection level itself, whereas the semileptonic \(t \bar{t}\) background is less affected by such veto. The hadronic background where both W’s from \(t \bar{t}\) decay hadronically, has the largest cross-section among all \(t \bar{t}\) backgrounds. However, in this case the source of 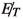 is essentially mismeasurement of jet energy. A full simulation shows that the hadronic \(t \bar{t}\) background plays a sub-dominant role. The single top background is also taken into account, but its contribution is rather small compared to the semileptonic and leptonic \(t \bar{t}\) because of its much smaller cross-section.
is essentially mismeasurement of jet energy. A full simulation shows that the hadronic \(t \bar{t}\) background plays a sub-dominant role. The single top background is also taken into account, but its contribution is rather small compared to the semileptonic and leptonic \(t \bar{t}\) because of its much smaller cross-section. - \(V+\) jets::
-
The next largest contribution to the background, in our signal region comes from \(V+\) jets (\(V = W, Z)\) production. These processes have large cross-sections (\(\approx 10^4\) pb) and also have significant sources of
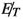 through the semileptonic decays of the weak gauge bosons. However, this background depends on the simultaneous mistagging of two light jets as b-jets. The double-mistag probability is rather small for these backgrounds (\(\approx 0.04\%\) as estimated from our Monte-Carlo simulation). It is worth mentioning here, that the contribution of \(W+\)jets is found to be sub-dominant compared to \(Z+\)jets. The main reason behind this is the presence of larger
through the semileptonic decays of the weak gauge bosons. However, this background depends on the simultaneous mistagging of two light jets as b-jets. The double-mistag probability is rather small for these backgrounds (\(\approx 0.04\%\) as estimated from our Monte-Carlo simulation). It is worth mentioning here, that the contribution of \(W+\)jets is found to be sub-dominant compared to \(Z+\)jets. The main reason behind this is the presence of larger 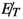 in the latter case and also the suppression of the former by the lepton veto.
in the latter case and also the suppression of the former by the lepton veto. - QCD \(b \bar{b}\)::
-
One major drawback of the \(b \bar{b}\) channel is the presence of QCD \(b \bar{b}\) production of events which has large cross-section (\(\approx 10^5\) pb). The nuisance value of this background, however,depends largely on
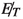 coming from jet-energy mismeasurement. On applying a suitable strategy which we will discuss in the next section (see Table 5), we find that this background becomes sub-dominant to those from \(t \bar{t}\) and \(Z+\)jets processes. To gain enough statistics, we have applied a generation level cut on the b-jets, i.e. \(p_T > 20\) GeV and \(|\eta | < 4.7\) on the QCD \(b \bar{b}\) events.
coming from jet-energy mismeasurement. On applying a suitable strategy which we will discuss in the next section (see Table 5), we find that this background becomes sub-dominant to those from \(t \bar{t}\) and \(Z+\)jets processes. To gain enough statistics, we have applied a generation level cut on the b-jets, i.e. \(p_T > 20\) GeV and \(|\eta | < 4.7\) on the QCD \(b \bar{b}\) events. - Diboson(WZ/ZZ)::
-
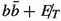 final state can also come from diboson production in the SM. However, the production cross-section in this case (\(\approx 1.3\) pb) is much smaller compared to the aforementioned backgrounds. Moreover, a hard lepton veto will significantly reduce WZ events and finally, a strong
final state can also come from diboson production in the SM. However, the production cross-section in this case (\(\approx 1.3\) pb) is much smaller compared to the aforementioned backgrounds. Moreover, a hard lepton veto will significantly reduce WZ events and finally, a strong 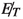 cut will help us control the ZZ as well as WZ background.
cut will help us control the ZZ as well as WZ background. - \(Z(\rightarrow \nu \bar{\nu })h(\rightarrow b \bar{b})\)::
-
Similar to the \(\gamma \gamma \) case, this background too is irreducible. The
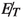 and invariant mass of the \(b \bar{b}\) system are also similar to the signal processes. However the smallness of its cross-section (\(\approx 100\) fb) makes this background least significant among all the background processes discussed here.
and invariant mass of the \(b \bar{b}\) system are also similar to the signal processes. However the smallness of its cross-section (\(\approx 100\) fb) makes this background least significant among all the background processes discussed here.
The signal and background events (except QCD \(b \bar{b}\)) are generated using Madgraph@MCNLO [46] and showered through PYTHIA8 [60]. The QCD \(b \bar{b}\) background is generated directly using PYTHIA8. The detector simulation is performed by Delphes-3.4.1 [61], the jet formation is taken care of by the built-in Fastjet [62] of Delphes.
We have used the CMS card in Delphes for the b-tagging procedure, which yields an average tagging-efficiency of 70% per b-jet approximately, in the \(p_T\) range of our interest (50–150 GeV). We have checked that this efficiency differs by not more than 5% on using the ATLAS specifications.s
4 Collider analysis: cut-based
4.1
 channel
channel
The discussion in the foregoing section convinces us that it is worthwhile to look at the  channel because of the ‘clean’ di-photon final state. Our analysis strategy goes beyond the existing ones [13, 14] even at the level of rectangular cut-based studies, for example, we make the background analysis more exhaustive, detector information particularly that pertaining to the inner tracker is also studied in greater detail and of course we have subsequently upgraded our analysis using the methods based on gradient boosting as well as neural network. This will be described in detail in later sections.
channel because of the ‘clean’ di-photon final state. Our analysis strategy goes beyond the existing ones [13, 14] even at the level of rectangular cut-based studies, for example, we make the background analysis more exhaustive, detector information particularly that pertaining to the inner tracker is also studied in greater detail and of course we have subsequently upgraded our analysis using the methods based on gradient boosting as well as neural network. This will be described in detail in later sections.
We will discuss the results of our cut-based analysis for a few benchmarks presented in Table 1 which are allowed by all the constraints mentioned earlier. We will first identify variables which give us desired separation between the signal and backgrounds. We present in Fig. 8 the distribution of the transverse momenta of the leading and sub-leading photon for the signal and all the background processes. The signal photons are recoiling against the dark matter and therefore are boosted. On the other hand, in case of di-jet events the photons are part of a jet, and it is unlikely that those photons will carry significant energy and \(p_T\) themselves. In case of \(\gamma \) + jet background at least one photon is isolated and it can carry considerable \(p_T\). Therefore the \(p_T\) distribution of the leading photon is comparable with the signal in this case, while for the sub-leading photon, which is expected to come from a jet, it falls off faster as expected.
 final state after applying various cuts at 13 TeV. The cross-sections are calculated at NLO
final state after applying various cuts at 13 TeV. The cross-sections are calculated at NLOIn Fig. 9 (left), we plot the  distribution for signal and background processes.
distribution for signal and background processes.  distributions for di-jet, \(\gamma \)+jet and di-photon show that these background events will have much less
distributions for di-jet, \(\gamma \)+jet and di-photon show that these background events will have much less  compared to the signal and Zh background. In the background events involving jets the source of missing energy is via the mismeasurement of jet energy or from the decay of some hadron inside the jet. \(\gamma \gamma \) background naturally shows lowest
compared to the signal and Zh background. In the background events involving jets the source of missing energy is via the mismeasurement of jet energy or from the decay of some hadron inside the jet. \(\gamma \gamma \) background naturally shows lowest  contribution owing to the absence of real
contribution owing to the absence of real  or jets in the final state. On the other hand, the signal and Zh background have real source of
or jets in the final state. On the other hand, the signal and Zh background have real source of  . It is evident that
. It is evident that  observable will play a significant role in signal-background discrimination. In Fig. 9 (right), we have shown the invariant mass of the di-photon pair. In case of signal and Zh background the \(m_{\gamma \gamma }\) distribution peaks at Higgs mass and for all other backgrounds no such peak is observed. This distribution is also extremely important for background rejection.
observable will play a significant role in signal-background discrimination. In Fig. 9 (right), we have shown the invariant mass of the di-photon pair. In case of signal and Zh background the \(m_{\gamma \gamma }\) distribution peaks at Higgs mass and for all other backgrounds no such peak is observed. This distribution is also extremely important for background rejection.
In Fig. 10 (left) we plot the distribution of \(\Delta R\) between the two photons for signal and background. We can see from the figure that in case of di-jet and \(\gamma + \)jet background there is a peak at \(\Delta R \approx 0\), resulting from the cases where the two photons have come from a single jet. However the di-jet and \(\gamma + \)jet events have a second peak too because of the events where each photon is part of a single jet and therefore the two photons are back to back. However, we do not really observe any peak in the \(\Delta R\) distribution of the signal or Zh background because in these cases the di-photon system is exactly opposite to the dark matter pair. Next we plot the jet multiplicity distribution for signal and background in Fig. 10 (right).
In Fig. 11 (left) and (right), we have plotted the \(\Delta \phi \) distribution between the  and the leading and sub-leading photon respectively. We know that in case of signal and the Zh background the di-photon system is exactly opposite to the dark matter system. Therefore the photons from the Higgs boson decay tend to be mostly opposite to the
and the leading and sub-leading photon respectively. We know that in case of signal and the Zh background the di-photon system is exactly opposite to the dark matter system. Therefore the photons from the Higgs boson decay tend to be mostly opposite to the  . On the other hand in case of di-jet or \(\gamma +\)jet events, the the
. On the other hand in case of di-jet or \(\gamma +\)jet events, the the  is aligned with either of the jets for aforementioned reasons. This behaviour is visible from the Fig. 11.
is aligned with either of the jets for aforementioned reasons. This behaviour is visible from the Fig. 11.
We would like to remind the reader that no special strategy has been devised for the irreducible Zh background. This is because of its low rates compared to both the signal and the other background channels.
Results Having discussed the distributions of the relevant kinematical variables, we go ahead to analyse the signal and background events. Our basic event selection criteria here is, at least two photons with \(p_T > 10\) GeV and \(|\eta | < 2.5\). We also impose veto on leptons (\(e, \mu )\) with \(p_T > 10\) GeV. For our analysis, we further apply the following cuts in succession for the desired signal-background separation.
- Cut 1::
-
\(p_T\) of the leading(sub-leading) photon \(> 50(30)\) GeV
- Cut 2::
-
\(\Delta R\) between two photons \(> 0.3\)
- Cut 3::
-
\(\Delta \phi \) between leading(sub-leading) photon and
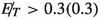
- Cut 4::
-
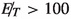 GeV
GeV - Cut 5::
-
\(\Delta \phi \) between leading(sub-leading) jet and
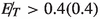
- Cut 6::
-
115 GeV \(< m_{\gamma \gamma } < 135\) GeV
A clarification is in order on the way in which we apply the isolation requirement on each photon. We have imposed the requirement that the total scalar sum of transverse momenta of all the charged and neutral particles within \(\Delta R < 0.5\) of the candidate photon can not be greater than 12% of the \(p_T\) of the candidate photon i.e \(\frac{\sum _{i} p_T^i(\Delta R< 0.5)}{p_T^{\gamma }} < 0.12\). Thereafter we have estimated the isolation probability of a photon, defined by this criterion, as a function of \(p_T\). We have then multiplied this \(p_T\)-weighted isolation probability with all the events surviving after applying the previously mentioned cuts (up to Cut6). We call this criterion Cut7 which goes somewhat beyond the rectangular cut-based strategy.
Table 3, indicates the cut-efficiencies of various kinematic observables. We can see from this table that  , \(m_{\gamma \gamma }\) and the isolation criterion turn out to be most important in the separation of the signal from the background. Having optimized cut values, we calculate the projected significance (\({\mathscr {S}})\) for each benchmark point for the 13 TeV LHC with 3000 fb\(^{-1}\) in Table 4. The significance \({\mathscr {S}}\) is defined as
, \(m_{\gamma \gamma }\) and the isolation criterion turn out to be most important in the separation of the signal from the background. Having optimized cut values, we calculate the projected significance (\({\mathscr {S}})\) for each benchmark point for the 13 TeV LHC with 3000 fb\(^{-1}\) in Table 4. The significance \({\mathscr {S}}\) is defined as
Where S and B are the number of signal and background events surviving the succession of cuts. This formula holds under the assumption that the signal as well as the background follow Poisson distribution, and the right-hand side reduces to the familiar form \(\frac{S}{\sqrt{B}}\) in the limit \((S + B) \gg 1\) and \(S \ll B\) (see Equation 97 of [68]).
 channel, after using the cuts listed in Table 3
channel, after using the cuts listed in Table 3From Table 4, one can see that our cuts have improved the S/B ratio from \(10^{-12}\) to of the order 0.05. And with our cut-based analysis it is possible to achieve \(\gtrsim 4 \sigma \) significance for BP2 which has the largest production cross-section. The other benchmarks with heavier dark matter mass or small quartic coupling do not perform very well. One should note that although we have identified the strongest classifier observables through our cut-based analysis and used them, it is possible to make use of the weaker classifiers too if we go beyond cut-based set-up, which will precisely be our goal with machine learning in the next section. We hope to achieve some improvement over the results quoted in Table 4.
4.2
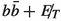 channel
channel
We proceed to discuss the kinematic variables which yield significant signal-background separation. In Fig. 12, we plot the \(p_T\) distribution of the leading and sub-leading b-jets for the signal and all the background processes. We can see from the figures that for the signal, the \(p_T\) distribution of the b jets peak at a higher value compared to the QCD \(b \bar{b}\) and \(V+\)jets background. This behaviour is expected since the \(b \bar{b}\) system is recoiling against a massive DM particle in case of signal. The distribution of \(p_T\) of leading and sub-leading b-jets from \(t \bar{t}\) backgrounds however peak at a similar region as the signal. The b-jets in those cases come from the decay of top quarks and are therefore boosted. Guided by the distributions we put appropriate cut on the transverse momenta of the leading and sub-leading b-jets in our cut-based analysis.
In Fig. 13 (left) we plot the  distribution for signal and background processes. We can see that the QCD background produces the softest
distribution for signal and background processes. We can see that the QCD background produces the softest  spectrum. The reason behind this is that there is no real source of
spectrum. The reason behind this is that there is no real source of  for this final state. It is mainly the mismeasurement of the visible momenta of the jets, which leads to
for this final state. It is mainly the mismeasurement of the visible momenta of the jets, which leads to  . Though large
. Though large  arising from such mismeasurement contributes mostly to the tail of the distribution, the sheer magnitude of the cross-section can still constitute a menace. However, a strong
arising from such mismeasurement contributes mostly to the tail of the distribution, the sheer magnitude of the cross-section can still constitute a menace. However, a strong  cut helps us reduce the \(b \bar{b}\) background to a large extent, as will be clear from the cut-flow analysis in the next subsection. The
cut helps us reduce the \(b \bar{b}\) background to a large extent, as will be clear from the cut-flow analysis in the next subsection. The  peaks at much lower values in case of V+jets as well. However, \(t \bar{t}\) and Zh background also produce large enough
peaks at much lower values in case of V+jets as well. However, \(t \bar{t}\) and Zh background also produce large enough  , although less than our signal. Therefore a hard
, although less than our signal. Therefore a hard  cut enhances the signal background separation. In Fig. 13 (right), we plot the invariant mass distribution of two b-jets. In case of signal and Zh background it peaks at Higgs mass, whereas for all other backgrounds it falls off rapidly. It is evident that a suitable cut on the invariant mass of the b-jet pair will also be effective in reducing the background.
cut enhances the signal background separation. In Fig. 13 (right), we plot the invariant mass distribution of two b-jets. In case of signal and Zh background it peaks at Higgs mass, whereas for all other backgrounds it falls off rapidly. It is evident that a suitable cut on the invariant mass of the b-jet pair will also be effective in reducing the background.
In Fig. 14 (left) we show the jet multiplicity distribution of the signal and background processes. Jet multiplicity distribution here indicates the number of light jets in the process. We know that in \(t \bar{t}\) semileptonic case, which is one of the primary backgrounds, the number of light jets is expected to be more than the signal and other backgrounds, because it has two hard light jets coming from the W decay. This feature can be used to distinguish this background from signal. We also present the distribution of the invariant mass distribution of the leading and sub-leading light jet pair in Fig. 14 (right). In case of \(t \bar{t}\) semileptonic background, the two leading light jets come from W decay and therefore this \(m_{jj}\) distribution peaks at W mass. An exclusion of the \(m_{jj} \approx m_W\) region in the cut-based analysis as well as a suitable cut on the number of light jets help us control the severe \(t \bar{t}\) background.
In Fig. 15 (left) and (right), we plot the \(\Delta \phi \) distribution between the  and the leading and sub-leading b-jets respectively. In case of signal and the Zh background the \(b \bar{b}\) system is exactly opposite to the dark matter system. Therefore the b-jets from the Higgs boson decay tend to be mostly opposite to the
and the leading and sub-leading b-jets respectively. In case of signal and the Zh background the \(b \bar{b}\) system is exactly opposite to the dark matter system. Therefore the b-jets from the Higgs boson decay tend to be mostly opposite to the  . On the other hand in case of QCD \(b \bar{b}\) events, the the
. On the other hand in case of QCD \(b \bar{b}\) events, the the  is aligned with either of the b-jets because the
is aligned with either of the b-jets because the  arises mainly due to the mismeasurement of the b-jet energy in this case. This behaviour is visible from the Fig. 15 (left) and (right).
arises mainly due to the mismeasurement of the b-jet energy in this case. This behaviour is visible from the Fig. 15 (left) and (right).
Results From the discussion on various kinematical observables, it is clear that we can choose suitable kinematical cuts on them to enhance the signal-background separation. However, our basic event selection criteria in this case are, at least two b-tagged jets with \(p_T > 20\) GeV and \(|\eta | < 4.7\). We also impose a veto on leptons (\(e, \mu )\) with \(p_T > 10\) GeV. In addition, the following cuts are applied for our analysis.
- Cut 1::
-
\(p_T\) of leading b-jet \(> 50\) GeV and \(p_T\) of sub-leading b-jet \(> 30\) GeV
- Cut 2::
-
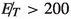 GeV
GeV - Cut 3::
-
80 GeV \(< M_{b_1 b_2} < 140\) GeV
- Cut 4::
-
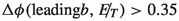 and
and 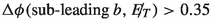
- Cut 5::
-
Number of light jets (not b-tagged) \( < 3\)
- Cut 6::
-
Invariant mass of two leading light jet pair \(<70\) GeV or \(>90\) GeV
- Cut 7::
-
\(\Delta R\) between the leading b-jet and the leading light jet \(> 1.5\)
We have applied these cuts on signal and background processes in succession. The cut efficiencies of various cuts for signal and backgrounds are given in Table 5.
 final state after applying various cuts at 13 TeV. The cross-sections are calculated at NLO
final state after applying various cuts at 13 TeV. The cross-sections are calculated at NLOFrom the cut-flow efficiencies quoted in Table 5 we can see that Cut2 i.e. the  cut is most essential in eliminating the major backgrounds such as \(t \bar{t}\) semileptonic and QCD \(b \bar{b}\). The other severe background \(V+\)jets is under control after applying the b-veto at the selection level. Having optimized cut values, we calculate the projected significance (\({\mathscr {S}})\) for each benchmark point for the 13 TeV LHC with 3000 fb\(^{-1}\) in Table 6. The formula used for calculating signal significance is given in Eq. (6).
cut is most essential in eliminating the major backgrounds such as \(t \bar{t}\) semileptonic and QCD \(b \bar{b}\). The other severe background \(V+\)jets is under control after applying the b-veto at the selection level. Having optimized cut values, we calculate the projected significance (\({\mathscr {S}})\) for each benchmark point for the 13 TeV LHC with 3000 fb\(^{-1}\) in Table 6. The formula used for calculating signal significance is given in Eq. (6).
From Table 6 one can see that our cuts have improved S/B ratio from \(10^{-7}\)–\(10^{-8}\) to the order 0.01. And with our cut-based analysis it is possible to achieve \(\sim 6\sigma \) signal significance for BP5 with the  final state. As we have chosen BP5 to be exactly same as BP2 of the di-photon case, one can compare the reach of the two channels with this benchmark. At this level of analysis, we can see that
final state. As we have chosen BP5 to be exactly same as BP2 of the di-photon case, one can compare the reach of the two channels with this benchmark. At this level of analysis, we can see that  clearly performs better than
clearly performs better than  channel in this regard. BP4 for which dark matter mass is 120 GeV, performs fairly well even within the cut-based framework. We have used mainly the strong classifiers in our cut based analysis. However, it is well known in the machine learning literature that a large number of weak classifiers can also lead to a good classification scheme. To that end, we include a range of kinematical variables (weak classifiers) along with our strong classifiers to help us improve our reach in couplings and masses of the dark matter.
channel in this regard. BP4 for which dark matter mass is 120 GeV, performs fairly well even within the cut-based framework. We have used mainly the strong classifiers in our cut based analysis. However, it is well known in the machine learning literature that a large number of weak classifiers can also lead to a good classification scheme. To that end, we include a range of kinematical variables (weak classifiers) along with our strong classifiers to help us improve our reach in couplings and masses of the dark matter.
5 Improved analysis through machine learning
Having performed the rectangular cut-based analysis in the \(\gamma \gamma \) +  and
and  channel, we found that it is possible to achieve considerable signal significance at the HL-LHC for certain regions of the parameter space. Those regions are highly likely to be detected in the future runs. However, there are some benchmarks, namely the ones with small quartic coupling \(\lambda _{\Phi \chi }\) which predict rather poor signal significance in a cut-based analysis. We will explore the possibility of probing those regions of parameter space with higher significance with machine learning. As we discussed in the previous section, we go beyond the rectangular cut-based approach here and use more observables, even the weaker classifiers, and take into account the correlation between the observables.
channel, we found that it is possible to achieve considerable signal significance at the HL-LHC for certain regions of the parameter space. Those regions are highly likely to be detected in the future runs. However, there are some benchmarks, namely the ones with small quartic coupling \(\lambda _{\Phi \chi }\) which predict rather poor signal significance in a cut-based analysis. We will explore the possibility of probing those regions of parameter space with higher significance with machine learning. As we discussed in the previous section, we go beyond the rectangular cut-based approach here and use more observables, even the weaker classifiers, and take into account the correlation between the observables.
In cut-based analysis we apply rectangular cuts on the chosen observables. Therefore, the shape of the selected signal region is a n-dimensional rectangular hypervolume. However, the actual shape of the signal region might be more complicated. In order to capture the relevant signal region, we have to adopt a more intricate scheme of selecting regions of the phase space. One such way is Boosted Decision Tree [69], which iteratively partitions the rectangular volume to select the relevant signal region. Alternatively, the Artificial Neural Network [70] attempts to encompass the relevant signal region with a set of hyperplanes, to as good accuracy as possible.
 channel, after using the cuts listed in Table 5
channel, after using the cuts listed in Table 5We have performed the analysis with BDT as well as ANN in order to make a comparison between the two as well as with the cut-based analysis. The usefulness of BDT and ANN has been widely demonstrated in [71,72,73,74,75] including studies in the Higgs sector [27, 76,77,78,79,80,81]. For ANN, we have used the toolkit Keras [82] with Tensorflow as backend [83]. For BDT, we have used the package TMVA [84]. Like the cut-based analysis here too, we present a comparison between the performances of  and
and  channels using ML.
channels using ML.
5.1
 channel
channel
For our analysis in the  channel, we have used 16 observables as feature variables. Those observables are listed in Table 7. For our BDT analysis, we have used 100 trees. A condition of minimum 2% events of the training sample has been set for leaf formation. Maximum depth of decision tree allowed is 2. An ANN has been constructed feeding these 16 variables in the input layer followed by 4 hidden layers with nodes 200, 150, 100 and 50 in them respectively. We have used rectified linear unit (RELU) as the activation function acting on the output of each layer. A regularization has been applied using 20% dropout. Finally there is a fully connected output layer with binary mode owing to softmax activation function. Categorical cross-entropy was chosen as the loss function with adam as the optimizer [85] for network training with a batch-size 1000 for each epoch, and 100 such epochs. For training we use 80% of the data, while rest 20% was kept aside for test or validation of the algorithm.
channel, we have used 16 observables as feature variables. Those observables are listed in Table 7. For our BDT analysis, we have used 100 trees. A condition of minimum 2% events of the training sample has been set for leaf formation. Maximum depth of decision tree allowed is 2. An ANN has been constructed feeding these 16 variables in the input layer followed by 4 hidden layers with nodes 200, 150, 100 and 50 in them respectively. We have used rectified linear unit (RELU) as the activation function acting on the output of each layer. A regularization has been applied using 20% dropout. Finally there is a fully connected output layer with binary mode owing to softmax activation function. Categorical cross-entropy was chosen as the loss function with adam as the optimizer [85] for network training with a batch-size 1000 for each epoch, and 100 such epochs. For training we use 80% of the data, while rest 20% was kept aside for test or validation of the algorithm.
 channel. The observables which were used in the cut-based analysis have been separated from the new ones by a horizontal line
channel. The observables which were used in the cut-based analysis have been separated from the new ones by a horizontal lineWe introduce a few new observables compared to the cut-based analysis, namely \(M_R\), \(M^T_R\), R [86] among others. These variables are collectively called the Razor variables. The definitions are as follows.



The \(M_R\) variable gives an estimate of the mass scale, which in the limit of massless decay products equals the mass of the parent particle. This variable contains both longitudinal and transverse information. \(M^T_R\) on the other hand, is derived only from the transverse momenta of the visible final states and  . The ratio R between \(M_R\) and \(M^T_R\) captures the flow of energy along the plane perpendicular to the beam and separating the visible and missing momenta. We show the distribution of R for signal and background processes in Fig. 16, which indicates the variable R and correspondingly all the razor variables possess substantial discriminating power.
. The ratio R between \(M_R\) and \(M^T_R\) captures the flow of energy along the plane perpendicular to the beam and separating the visible and missing momenta. We show the distribution of R for signal and background processes in Fig. 16, which indicates the variable R and correspondingly all the razor variables possess substantial discriminating power.
From the BDT analysis, we found out that the  and \(m_{\gamma \gamma }\) play the most important role in distinguishing between signal and background, which was already expected from our cut-based analysis. \(\Delta R_{\gamma \gamma }\), \(p_T\) of the leading and sub-leading photons and the Razor variables are also good discriminating variables in this regard. However, there can be significant correlation between various important observables, which should be taken into account. We have calculated such correlations directly in BDT and used only those variables which have \(< 25 \%\) correlation between them, in our final BDT analysis. We have used the observable with highest ranking among the correlated (\(\gtrsim 75\%\)) ones. For example, we found that the razor variables (particularly \(M^T_R\)) are correlated with
and \(m_{\gamma \gamma }\) play the most important role in distinguishing between signal and background, which was already expected from our cut-based analysis. \(\Delta R_{\gamma \gamma }\), \(p_T\) of the leading and sub-leading photons and the Razor variables are also good discriminating variables in this regard. However, there can be significant correlation between various important observables, which should be taken into account. We have calculated such correlations directly in BDT and used only those variables which have \(< 25 \%\) correlation between them, in our final BDT analysis. We have used the observable with highest ranking among the correlated (\(\gtrsim 75\%\)) ones. For example, we found that the razor variables (particularly \(M^T_R\)) are correlated with  . One should also note that the significant background rejection (di-jet, \(\gamma +\) jet) happens while two isolated photons are demanded as has been discussed in the cut-based analysis.
. One should also note that the significant background rejection (di-jet, \(\gamma +\) jet) happens while two isolated photons are demanded as has been discussed in the cut-based analysis.
 final state, using ML. A comparison between BDT, ANN and cut-and-count(CC) results are presented in last three columns, in terms of the ratio of respective signal significance
final state, using ML. A comparison between BDT, ANN and cut-and-count(CC) results are presented in last three columns, in terms of the ratio of respective signal significance channel. The observables which were used in the cut-based analysis have been separated from the new ones by a horizontal line
channel. The observables which were used in the cut-based analysis have been separated from the new ones by a horizontal lineWe apply the following cuts, after demanding at least two photons and lepton-veto, and introduce the resulting training sample for the BDT as well as ANN analysis:
-
\(p_T\) of the leading photon > 30 GeV,
-
\(p_T\) of the sub-leading photon > 20 GeV,
-
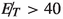 GeV,
GeV, -
\(50~\text {GeV}< m_{\gamma \gamma } < 200\) GeV,
-
\(\Delta R_{\gamma \gamma } > 0.1\),
-
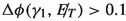 and
and -
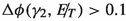 .
.
We emphasize that the cuts given above are weaker than those used in the cut-based analysis. This allows our algorithms to look at the larger phase-space, learn about the the background features better and then use them to come up with a better decision boundary that helps us cut down the background even more strongly.
In Fig. 17, we show the Receiver Operating Characteristic (ROC) curves for two mass points \(m_{\chi } = 64\) GeV and \(m_{\chi } = 70\) GeV from the ANN(left) and BDT(right) analyses. We can see from Fig. 17, that with increase in the dark matter mass, the discriminating power increases, the ROC curve for \(m_{\chi } = 70\) GeV performs better than \(m_{\chi } = 64\) GeV. The area under the ROC curve is 0.994(0.993) for \(m_{\chi } = 70\) GeV and 0.992(0.991) for \(m_{\chi } = 64\) GeV using ANN(BDT). In Table 8, we present the S/B ratio, the signal significance for BP1, BP2 and BP3 using both ANN and BDT. We have scanned along the ROC curves and presented results for selected true positive (\(\sim 0.55\)) and false negative rates (\(\sim 0.001\)) that will yield the best signal significance for respective benchmark points. The signal significance is calculated using the formula (6).
 final state, using ML. A comparison between BDT, ANN and cut-and-count(CC) results are presented in last three columns, in terms of the ratio of respective signal significance
final state, using ML. A comparison between BDT, ANN and cut-and-count(CC) results are presented in last three columns, in terms of the ratio of respective signal significanceFrom Table 8, it is clear that machine learning improves the results of our cut-based analysis to a large extent. We notice that the S/B ratio has improved 4 to 8 fold depending upon the benchmark point and the machine learning methods that lead to improved significance. We also notice that ANN performs better than BDT in this case. With machine learning techniques at our disposal, regions with weaker dark matter couplings can be probed at the HL-LHC in the  final state, which was unattainable through an exclusive rectangular cut-based method.
final state, which was unattainable through an exclusive rectangular cut-based method.
5.2
 channel
channel
We proceed towards the analysis in  channel with ML in this subsection. Here we have used 22 observables as feature variables which are listed in Table 9. Like the
channel with ML in this subsection. Here we have used 22 observables as feature variables which are listed in Table 9. Like the  case, here too, we have used 100 trees, minimum 2% events of the training sample for leaf formation and maximum allowed depth of decision tree 2, for BDT analysis. An ANN was constructed with these 22 variables fed into the input layer and then a similar structure of the network has been used as described in the \(\gamma \gamma \) analysis. The input layer is followed by 4 hidden layers with nodes 200, 150, 100 and 50 respectively using rectified linear unit (RELU) as the activation function acted on the outputs of each layer. The final layer is a fully connected binary output layer with softmax as the activation function. A 20% dropout has been applied for regularization. For the loss function categorical cross-entropy was chosen with adam as the optimizer [85] and the network was trained with a batch-size 1000 for each epoch, and 100 such epochs. For training, 90% of the data was used, while rest 10% was used for test or validation of the algorithm.
case, here too, we have used 100 trees, minimum 2% events of the training sample for leaf formation and maximum allowed depth of decision tree 2, for BDT analysis. An ANN was constructed with these 22 variables fed into the input layer and then a similar structure of the network has been used as described in the \(\gamma \gamma \) analysis. The input layer is followed by 4 hidden layers with nodes 200, 150, 100 and 50 respectively using rectified linear unit (RELU) as the activation function acted on the outputs of each layer. The final layer is a fully connected binary output layer with softmax as the activation function. A 20% dropout has been applied for regularization. For the loss function categorical cross-entropy was chosen with adam as the optimizer [85] and the network was trained with a batch-size 1000 for each epoch, and 100 such epochs. For training, 90% of the data was used, while rest 10% was used for test or validation of the algorithm.
We can see from Table 9, that a number of new observables have been introduced for the ML analysis, compared to the cut-based approach. One such important addition is the  significance which has been widely used in experimental analyses for the mono-Higgs + DM search in the
significance which has been widely used in experimental analyses for the mono-Higgs + DM search in the  final state [66]. The
final state [66]. The  significance is defined as the ratio of
significance is defined as the ratio of  and the square-root of scalar sum of \(p_T\) of all the visible final states (\(\sqrt{H_T}\)). This observable (albeit correlated with
and the square-root of scalar sum of \(p_T\) of all the visible final states (\(\sqrt{H_T}\)). This observable (albeit correlated with  ) is particularly useful in reducing the \(b \bar{b}\) background as pointed out in [87]. We can see the distribution of
) is particularly useful in reducing the \(b \bar{b}\) background as pointed out in [87]. We can see the distribution of  significance for signal and background from Fig. 18 (left). We show the distribution of \(H_T\) for signal and backgrounds in Fig. 18 (right).
significance for signal and background from Fig. 18 (left). We show the distribution of \(H_T\) for signal and backgrounds in Fig. 18 (right).
BDT analysis ranks  , \(m_{bb}\), \(H_T\), \(N_{jets}\) observables highest in terms of signal and background separation, reinforcing our understanding from the cut-based analysis. Here too, the correlated observables are identified in BDT and only the most important ones among the correlated were retained for an effective BDT performance.
, \(m_{bb}\), \(H_T\), \(N_{jets}\) observables highest in terms of signal and background separation, reinforcing our understanding from the cut-based analysis. Here too, the correlated observables are identified in BDT and only the most important ones among the correlated were retained for an effective BDT performance.
We apply the following cuts after demanding two b-jets and lepton-veto, and introduce the resulting training sample for the BDT as well as ANN analysis:
-
\(p_T\) of the leading b-jet > 30 GeV,
-
\(p_T\) of the sub-leading b-jet > 20 GeV,
-
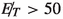 GeV,
GeV, -
\(60~\text {GeV}< m_{bb} < 170\) GeV and
-
\(m_{jj} < 70\) GeV or \(m_{jj} > 90\) GeV.
Like in the case of  channel, here too we use cuts weaker than those used in the cut-based analysis to better estimate the decision boundary in the phase-space. In Fig. 19, we present the ROC curve for two mass points for the dark matter particle \(\chi \), \(m_{\chi } = 64\) GeV and \(m_{\chi } = 120\) GeV using ANN(left) as well as BDT(right). We can see that as the mass of the dark matter increases, the discriminating power between signal and background increases. This can certainly be attributed to the larger
channel, here too we use cuts weaker than those used in the cut-based analysis to better estimate the decision boundary in the phase-space. In Fig. 19, we present the ROC curve for two mass points for the dark matter particle \(\chi \), \(m_{\chi } = 64\) GeV and \(m_{\chi } = 120\) GeV using ANN(left) as well as BDT(right). We can see that as the mass of the dark matter increases, the discriminating power between signal and background increases. This can certainly be attributed to the larger  in case of heavier dark matter mass which is clear from Fig. 13 (left). The area under the ROC curve is 0.95(0.93) in case of \(m_{\chi } = 120\) GeV and 0.93(0.91) for \(m_{\chi } = 64\) GeV using ANN(BDT). We have scanned along the ROC curves and presented results for selected true positive (\(\sim 0.20\)) and false negative rates (\(\sim 0.001\)) that will yield the best signal significance. In Table 10, we present the S/B ratio, the signal significance for the benchmark points given in Table 2, calculated using Eq. 6. We note that both BDT and ANN models give us about a factor 10 improvement in the S/B ratio and about 3 to 6 times improvement in the signal significance.
in case of heavier dark matter mass which is clear from Fig. 13 (left). The area under the ROC curve is 0.95(0.93) in case of \(m_{\chi } = 120\) GeV and 0.93(0.91) for \(m_{\chi } = 64\) GeV using ANN(BDT). We have scanned along the ROC curves and presented results for selected true positive (\(\sim 0.20\)) and false negative rates (\(\sim 0.001\)) that will yield the best signal significance. In Table 10, we present the S/B ratio, the signal significance for the benchmark points given in Table 2, calculated using Eq. 6. We note that both BDT and ANN models give us about a factor 10 improvement in the S/B ratio and about 3 to 6 times improvement in the signal significance.
Table 10 shows that machine learning significantly improves the prospect of the  channel, compared to the cut-and-count analysis. Here too, ANN performs consistently better than BDT. There are certain regions of the parameter space in which the predictions for the
channel, compared to the cut-and-count analysis. Here too, ANN performs consistently better than BDT. There are certain regions of the parameter space in which the predictions for the  signal are more optimistic owing to the large cross-sections and several percent levels S/B ratio. All three benchmark points, BP4, BP5 and BP6 can be probed at significances much larger than \(5\sigma \). This indicates that we can probe larger masses and/or smaller couplings than the ones we have chosen for the benchmark points. But we must take note that the large significance reported in Table 10 are caused by a small statistical error of order 0.5% which is significantly smaller than the best estimates for systematic errors. Thus it becomes essential to repeat the analysis in the presence of systematic errors, which is done in the next section.
signal are more optimistic owing to the large cross-sections and several percent levels S/B ratio. All three benchmark points, BP4, BP5 and BP6 can be probed at significances much larger than \(5\sigma \). This indicates that we can probe larger masses and/or smaller couplings than the ones we have chosen for the benchmark points. But we must take note that the large significance reported in Table 10 are caused by a small statistical error of order 0.5% which is significantly smaller than the best estimates for systematic errors. Thus it becomes essential to repeat the analysis in the presence of systematic errors, which is done in the next section.
6 Analysis with systematic uncertainty
It is well-known that the proposed future HL-LHC will be extremely prone to large amount of systematic uncertainty coming from various sources. Therefore, it is imperative that we study the effect of systematics on our analysis. In order to check the effect of systematic uncertainty on our results, we have repeated the analysis, using BDT as well as ANN, in the presence of suitable chosen sets of values for systematic uncertainty in Tables 11, 12, 13 and 14. The signal significance in the presence of systematic uncertainty is given in Eq. (10) [68, 88] below:
 final state, using ANN with 1%, 2.5% and 5% systematic uncertainty
final state, using ANN with 1%, 2.5% and 5% systematic uncertainty final state, using BDT with 1%, 2.5% and 5% systematic uncertainty
final state, using BDT with 1%, 2.5% and 5% systematic uncertainty final state, using ANN with 2.5%, 5%, 10% and 15% systematic uncertainty
final state, using ANN with 2.5%, 5%, 10% and 15% systematic uncertainty final state, using BDT with 2.5%, 5%, 10% and 15% systematic uncertainty
final state, using BDT with 2.5%, 5%, 10% and 15% systematic uncertaintyHere x is the fractional systematic error. We note that the expression for the significance given in Eq. 6 and Eq. 10 depend upon three fractions: the signal to background ratio S/B, the fractional statistical uncertainty \(1/\sqrt{B}\) and the fractional systematic error x. To obtain a large significance, we need to have S/B much larger than combined statistical and systematic error.
For the  channel, one expects to have a systematic uncertainty of up to 2.5% on integrated luminosity [90]. For this channel, we choose to repeat the analysis with \(x=1\%, \ 2.5\%\) and \(5\%\). For these choices of systematic uncertainty, we scan the ROC curve again looking for the best operating point and found that the earlier point still gives the best signal significance. These are presented in Tables 11 and 12. We see that BP1 and BP2 still remain above \(5\sigma \) for the ANN case with \(2.5\%\) systematic errors while in the case of BDT they remain above \(4\sigma \).
channel, one expects to have a systematic uncertainty of up to 2.5% on integrated luminosity [90]. For this channel, we choose to repeat the analysis with \(x=1\%, \ 2.5\%\) and \(5\%\). For these choices of systematic uncertainty, we scan the ROC curve again looking for the best operating point and found that the earlier point still gives the best signal significance. These are presented in Tables 11 and 12. We see that BP1 and BP2 still remain above \(5\sigma \) for the ANN case with \(2.5\%\) systematic errors while in the case of BDT they remain above \(4\sigma \).
For the case of  channel, one has additional uncertainty of about 15% coming from double b-tagging [89]. We choose to repeat the analysis with \(x=2.5\%, \ 5\%, \ 10\%\) and \(15\%\) and present the results in Tables 13 and 14. All the chosen values of systematic errors are about 5 to 30 times larger than the corresponding fractional statistical error and also comparable to or a few times larger than the S/B ratio. To improve the sensitivity with these choices of systematic errors we scan the ROC curve and find that with a false negative rate \(\sim 0.0001\) and true positive rate \(\sim 0.05\) we get maximum signal significance. We note that with the new operating point the S/B has almost doubled, reaching \(\sim 0.3\) for BP5. This leads to signal significance for BP5 to \(\sim 2\sigma \) for both ANN and BDT models with 15% systematics. We also note that one can improve the significance if one can reduce the large systematic uncertainty coming from double b-tagging along with the enhancement of S/B ratio by possibly choosing another operating point on the ROC curve. The former will requires a better understanding of the b-tagging while the latter requires a larger sample of the background events.
channel, one has additional uncertainty of about 15% coming from double b-tagging [89]. We choose to repeat the analysis with \(x=2.5\%, \ 5\%, \ 10\%\) and \(15\%\) and present the results in Tables 13 and 14. All the chosen values of systematic errors are about 5 to 30 times larger than the corresponding fractional statistical error and also comparable to or a few times larger than the S/B ratio. To improve the sensitivity with these choices of systematic errors we scan the ROC curve and find that with a false negative rate \(\sim 0.0001\) and true positive rate \(\sim 0.05\) we get maximum signal significance. We note that with the new operating point the S/B has almost doubled, reaching \(\sim 0.3\) for BP5. This leads to signal significance for BP5 to \(\sim 2\sigma \) for both ANN and BDT models with 15% systematics. We also note that one can improve the significance if one can reduce the large systematic uncertainty coming from double b-tagging along with the enhancement of S/B ratio by possibly choosing another operating point on the ROC curve. The former will requires a better understanding of the b-tagging while the latter requires a larger sample of the background events.
7 Summary and conclusion
In this work, we concentrate on the collider search for dark matter in the mono-Higgs +  final state. This channel along with mono-jet, mono-photon, and mono-V final states has garnered substantial interest among experimentalists and theorists alike for dark matter hunting. We have chosen the dark matter to be a WIMP-like scalar that interacts with the SM particles via Higgs mediation. Using a Higgs portal description and at the same time higher dimensional operators, we alleviate the tension between the constraints from direct searches and relic density. One is thus guided to optimal coupling strengths suitable to yield partial cancellation in the direct detection experiments and still reproduce the observed relic density. In addition, the presence of higher-dimensional operators may enhance the production cross-section for the \(h+\chi \chi \) state.
final state. This channel along with mono-jet, mono-photon, and mono-V final states has garnered substantial interest among experimentalists and theorists alike for dark matter hunting. We have chosen the dark matter to be a WIMP-like scalar that interacts with the SM particles via Higgs mediation. Using a Higgs portal description and at the same time higher dimensional operators, we alleviate the tension between the constraints from direct searches and relic density. One is thus guided to optimal coupling strengths suitable to yield partial cancellation in the direct detection experiments and still reproduce the observed relic density. In addition, the presence of higher-dimensional operators may enhance the production cross-section for the \(h+\chi \chi \) state.
Accounting for all the constraints we identify benchmark points that yield large production cross-sections for \(h+\chi \chi \) state at the LHC. We would like to point out that the resonant Higgs mass region (\(m_\chi \sim m_h/2\)) is the best possible region to probe in the mono-Higgs final state because of the large production cross-section. We choose the  and
and  final states.
final states.
For the di-photon channel, we go beyond the SM backgrounds with prompt photons usually considered in the literature and estimate the fake/non-prompt photons coming from QCD di-jet and \(\gamma +\) jets events. We find that the tail of these backgrounds with large production cross-sections can be detrimental for signal background separation in the di-photon channel however strong isolation of photons along with suitable cuts on kinematical observables enable us to get considerable signal significance at the high luminosity (3000 fb\(^{-1}\)) LHC. For the \(b\bar{b}\) channel we simulate full backgrounds coming from QCD multi-jets, \(V+\)jets, and \(t\bar{t}\) final states. We find that the \(b\bar{b}\) channel fares better than the di-photon channel when the systematic uncertainties are ignored.
We consider (almost) an exhaustive list of kinematical variables to perform BDT- and ANN-based analysis of the signal significance. We find that both these method leads to a significant improvement in the signal significance for all three benchmark points in the di-photon channel with ANN performing better than BDT. For the \(b\bar{b}\) channel the improvement is even more exciting if we consider only the statistical error.
Noting that the systematic uncertainties can be large [89, 90], we have also estimated their impact on our analysis. The experimental analysis on  [89] demonstrates that uncertainty in the double-b tagging has the highest impact(\(\approx 15\%\)) on the signal strength. For our analysis, we have considered a similar impact on our signal strengths to estimate its effect on the quoted significance and found out that for the most optimistic benchmark choice (BP5) in our
[89] demonstrates that uncertainty in the double-b tagging has the highest impact(\(\approx 15\%\)) on the signal strength. For our analysis, we have considered a similar impact on our signal strengths to estimate its effect on the quoted significance and found out that for the most optimistic benchmark choice (BP5) in our  analysis, considering the systematic uncertainty of 15% in the double-b tagging can reduce our signal significance by up to 18 times. For
analysis, considering the systematic uncertainty of 15% in the double-b tagging can reduce our signal significance by up to 18 times. For  analysis, a systematic uncertainly of 2.5% on integrated luminosity [90] impacts our signal significance by \(\lesssim 25\%\).
analysis, a systematic uncertainly of 2.5% on integrated luminosity [90] impacts our signal significance by \(\lesssim 25\%\).
One can in principle extend this analysis to other Higgs decay modes such as WW, ZZ and \(\tau \tau \). However, such channels are either prima facie beset with low rates for the viable final states, or have challenges in the reconstruction of the Higgs peak. It may be useful to try the \(\tau \tau \) mode in particular as a confirmatory channel. It remains a challenge to see how much improvement occurs via neural network techniques. We plan to take this up in a follow-up study.
Data Availability
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: The data set simulated for this paper is too large in size and requires a compute intensive pipeline to be useful to anyone else. Thus we choose not to share it.]
Notes
The spin-independent cross-section in direct search, however receives considerably lower contributions from \({\mathscr {O}}_2\), because of velocity suppression for a non-relativistic DM candidate. We have included both the contributions from \({\mathscr {O}}_1\) and \({\mathscr {O}}_2\) in mono-Higgs production at the LHC. However the estimates pertain to \(f_1 = f_2\) which may not be valid in some theoretical scenarios.
References
CDF Collaboration, F. Abe et al., Observation of top quark production in \(\bar{p}p\) collisions. Phys. Rev. Lett. 74, 2626–2631 (1995). arXiv:hep-ex/9503002
D0 Collaboration, S. Abachi et al., Observation of the top quark. Phys. Rev. Lett. 74, 2632–2637 (1995). arXiv:hep-ex/9503003
J. Drees, Review of final LEP results, or, a tribute to LEP. Int. J. Mod. Phys. A 17, 3259–3283 (2002). arXiv:hep-ex/0110077
ALEPH, DELPHI, L3, OPAL, SLD, LEP Electroweak Working Group, SLD Electroweak Group, SLD Heavy Flavour Group collaboration, S. Schael et al., Precision electroweak measurements on the \(Z\) resonance. Phys. Rep. 427, 257–454 (2006). arXiv:hep-ex/0509008
ATLAS, CMS Collaboration, G. Aad et al., Measurements of the Higgs boson production and decay rates and constraints on its couplings from a combined ATLAS and CMS analysis of the LHC pp collision data at \( \sqrt{s}=7 \) and 8 TeV. JHEP 08, 045 (2016). arXiv:1606.02266
CMS Collaboration, V. Khachatryan et al., Search for dark matter, extra dimensions, and unparticles in monojet events in proton–proton collisions at \(\sqrt{s} = 8\) TeV. Eur. Phys. J. C 75, 235 (2015). arXiv:1408.3583
ATLAS Collaboration, E. Diehl, The search for dark matter using monojets and monophotons with the ATLAS detector. AIP Conf. Proc. 1604, 324–330 (2015)
J.M. No, Looking through the pseudoscalar portal into dark matter: novel mono-Higgs and mono-Z signatures at the LHC. Phys. Rev. D 93, 031701 (2016). arXiv:1509.01110
ATLAS Collaboration, S. Schramm, ATLAS sensitivity to WIMP dark matter in the monojet topology at \(\sqrt{s}=\) 14 TeV. Nucl. Part. Phys. Proc. 273–275, 2397–2399 (2016)
ATLAS Collaboration, M. Aaboud et al., Search for new phenomena in events with a photon and missing transverse momentum in \(pp\) collisions at \(\sqrt{s}=13\) TeV with the ATLAS detector. JHEP 06, 059 (2016). arXiv:1604.01306
ATLAS Collaboration, T. A. Collaboration, Prospects for dark matter searches in mono-photon and VBF+\(E_T^{miss}\) final states in ATLAS, ATL-PHYS-PUB-2018-038
CMS Collaboration, C. Collaboration, Projection of the mono-Z search for dark matter to the HL-LHC, CMS-PAS-FTR-18-007
L. Carpenter, A. DiFranzo, M. Mulhearn, C. Shimmin, S. Tulin, D. Whiteson, Mono-Higgs-boson: a new collider probe of dark matter. Phys. Rev. D 89, 075017 (2014). arXiv:1312.2592
A.A. Petrov, W. Shepherd, Searching for dark matter at LHC with Mono-Higgs production. Phys. Lett. B 730, 178–183 (2014). arXiv:1311.1511
W. Abdallah, A. Hammad, S. Khalil, S. Moretti, Search for Mono-Higgs signals at the LHC in the B-L supersymmetric standard model. Phys. Rev. D 95, 055019 (2017). arXiv:1608.07500
S. Baum, K. Freese, N.R. Shah, B. Shakya, NMSSM Higgs boson search strategies at the LHC and the mono-Higgs signature in particular. Phys. Rev. D 95, 115036 (2017). arXiv:1703.07800
A. Berlin, T. Lin, L.-T. Wang, Mono-Higgs detection of dark matter at the LHC. JHEP 06, 078 (2014). arXiv:1402.7074
L. Basso, Resonant mono Higgs at the LHC. JHEP 04, 087 (2016). arXiv:1512.06381
K. Ghorbani, L. Khalkhali, Mono-Higgs signature in a fermionic dark matter model. J. Phys. G44, 105004 (2017). arXiv:1608.04559
A. Ahriche, A. Arhrib, A. Jueid, S. Nasri, A. de La Puente, Mono-Higgs signature in the scotogenic model with Majorana dark matter. Phys. Rev. D 101, 035038 (2020). arXiv:1811.00490
A. Djouadi, A. Falkowski, Y. Mambrini, J. Quevillon, Direct detection of Higgs-portal dark matter at the LHC. Eur. Phys. J. C 73, 2455 (2013). arXiv:1205.3169
A. Greljo, J. Julio, J.F. Kamenik, C. Smith, J. Zupan, Constraining Higgs mediated dark matter interactions. JHEP 11, 190 (2013). arXiv:1309.3561
H. Han, J.M. Yang, Y. Zhang, S. Zheng, Collider signatures of Higgs-portal scalar dark matter. Phys. Lett. B 756, 109–112 (2016). arXiv:1601.06232
ATLAS Collaboration, M. Aaboud et al., Constraints on mediator-based dark matter and scalar dark energy models using \(\sqrt{s} = 13\) TeV \(pp\) collision data collected by the ATLAS detector. JHEP 05, 142 (2019). arXiv:1903.01400
G. Arcadi, A. Djouadi, M. Raidal, Dark matter through the Higgs portal. Phys. Rep. 842, 1–180 (2020). arXiv:1903.03616
C. Gross, O. Lebedev, T. Toma, Cancellation mechanism for dark-matter–nucleon interaction. Phys. Rev. Lett. 119, 191801 (2017). arXiv:1708.02253
A. Dey, J. Lahiri, B. Mukhopadhyaya, LHC signals of a heavy doublet Higgs as dark matter portal: cut-based approach and improvement with gradient boosting and neural networks. JHEP 09, 004 (2019). arXiv:1905.02242
N. Okada, D. Raut, Q. Shafi, Pseudo-goldstone dark matter in gauged \(B-L\) extended standard model. arXiv:2001.05910
S. Baum, M. Carena, N.R. Shah, C.E.M. Wagner, Higgs portals for thermal dark matter. EFT perspectives and the NMSSM. JHEP 04, 069 (2018). arXiv:1712.09873
T. Han, H. Liu, S. Mukhopadhyay, X. Wang, Dark matter blind spots at one-loop. JHEP 03, 080 (2019). arXiv:1810.04679
M.E. Cabrera, J.A. Casas, A. Delgado, S. Robles, Generalized blind spots for dark matter direct detection in the 2HDM. JHEP 02, 166 (2020). arXiv:1912.01758
M.E. Cabrera, J.A. Casas, A. Delgado, S. Robles, 2HDM singlet portal to dark matter. JHEP 01, 123 (2021). arXiv:2011.09101
Planck Collaboration, P.A.R. Ade et al., Planck 2013 results. XVI. Cosmological parameters. Astron. Astrophys. 571, A16 (2014). arXiv:1303.5076
XENON Collaboration, E. Aprile et al., Dark matter search results from a one ton-year exposure of XENON1T. Phys. Rev. Lett. 121, 111302 (2018). arXiv:1805.12562
Fermi-LAT Collaboration, M. Ackermann et al., Searching for dark matter annihilation from Milky Way dwarf spheroidal galaxies with six years of fermi large area telescope data. Phys. Rev. Lett. 115, 231301 (2015). arXiv:1503.02641
MAGIC, Fermi-LAT Collaboration, M.L. Ahnen et al., Limits to dark matter annihilation cross-section from a combined analysis of MAGIC and fermi-LAT observations of dwarf satellite galaxies. JCAP 1602, 039 (2016). arXiv:1601.06590
Fermi-LAT, DES Collaboration, A. Albert et al., Searching for dark matter annihilation in recently discovered Milky Way satellites with fermi-LAT. Astrophys. J. 834, 110 (2017). arXiv:1611.03184
AMS Collaboration, M. Aguilar et al., Towards understanding the origin of cosmic-ray positrons. Phys. Rev. Lett. 122, 041102 (2019). arXiv:2107.10261
F. Staub, SARAH 4: a tool for (not only SUSY) model builders. Comput. Phys. Commun. 185, 1773–1790 (2014). arXiv:1309.7223
J. Oredsson, 2HDME: two-Higgs-doublet model evolver. Comput. Phys. Commun. 244, 409–426 (2019). arXiv:1811.08215
CMS Collaboration, A.M. Sirunyan et al., Search for invisible decays of a Higgs boson produced through vector boson fusion in proton–proton collisions at \(\sqrt{s} =\) 13 TeV. Phys. Lett. B 793, 520–551 (2019). arXiv:1809.05937
M. Duerr, P. Fileviez Pérez, J. Smirnov, Scalar dark matter: direct vs. indirect detection. JHEP 06, 152 (2016). arXiv:1509.04282
GAMBIT Collaboration, P. Athron et al., Status of the scalar singlet dark matter model. Eur. Phys. J. C 77, 568 (2017). arXiv:1705.07931
G. Belanger, A. Mjallal, A. Pukhov, Recasting direct detection limits within micrOMEGAs and implication for non-standard Dark Matter scenarios. Eur. Phys. J. C 81, 239 (2021). arXiv:2003.08621
A. Alloul, N.D. Christensen, C. Degrande, C. Duhr, B. Fuks, FeynRules 2.0—a complete toolbox for tree-level phenomenology. Comput. Phys. Commun. 185, 2250–2300 (2014). arXiv:1310.1921
J. Alwall, R. Frederix, S. Frixione, V. Hirschi, F. Maltoni, O. Mattelaer et al., The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations. JHEP 07, 079 (2014). arXiv:1405.0301
CMS Collaboration, Search for dark matter produced in association with a Higgs boson decaying to two photons, CMS-PAS-EXO-16-011
CMS Collaboration, Search for dark matter produced in association with a Higgs boson decaying to two photons, Tech. Rep. CMS-PAS-EXO-16-054. CERN, Geneva (2017)
CMS Collaboration, A.M. Sirunyan et al., Search for associated production of dark matter with a Higgs boson decaying to \( b\overline{b} \) or \(\gamma \gamma \) at \( \sqrt{s}=13\) TeV. JHEP 10, 180 (2017). arXiv:1703.05236
CMS Collaboration, A.M. Sirunyan et al., Search for dark matter produced in association with a Higgs boson decaying to \(\gamma \gamma \) or \(\tau ^+\tau ^-\) at \(\sqrt{s} =\) 13 TeV. JHEP 09, 046 (2018). arXiv:1806.04771
CMS Collaboration, A.M. Sirunyan et al., Search for dark matter particles produced in association with a Higgs boson in proton-proton collisions at \( \sqrt{s} \) = 13 TeV. JHEP 03, 025 (2020). arXiv:1908.01713
ATLAS Collaboration, G. Aad et al., Search for dark matter in events with missing transverse momentum and a Higgs boson decaying to two photons in \(pp\) collisions at \(\sqrt{s}=8\) TeV with the ATLAS detector. Phys. Rev. Lett. 115, 131801 (2015). arXiv:1506.01081
ATLAS Collaboration, Search for new phenomena in events with missing transverse momentum and a Higgs boson decaying into two photons at \(\sqrt{s}\) = 13 TeV with the ATLAS detector, Tech. Rep. ATLAS-CONF-2017-024. CERN, Geneva (2017)
ATLAS Collaboration, G. Aad et al., Search for dark matter in events with missing transverse momentum and a Higgs boson decaying into two photons in \(pp\) collisions at \(\sqrt{s} = 13\) TeV with the ATLAS detector. arXiv:2104.13240
L. Bourhis, M. Fontannaz, J.P. Guillet, Quarks and gluon fragmentation functions into photons. Eur. Phys. J. C 2, 529–537 (1998). arXiv:hep-ph/9704447
L. Bourhis, M. Fontannaz, J.P. Guillet, M. Werlen, Next-to-leading order determination of fragmentation functions. Eur. Phys. J. C 19, 89–98 (2001). arXiv:hep-ph/0009101
B.A. Kniehl, G. Kramer, B. Potter, Fragmentation functions for pions, kaons, and protons at next-to-leading order. Nucl. Phys. B 582, 514–536 (2000). arXiv:hep-ph/0010289
J. Binnewies, B.A. Kniehl, G. Kramer, Neutral kaon production in \(e^{+} e^{-}\), \(e p\) and \(p \bar{p}\) collisions at next-to-leading order. Phys. Rev. D 53, 3573–3581 (1996). arXiv:hep-ph/9506437
S. Kretzer, Fragmentation functions from flavor inclusive and flavor tagged e+ e- annihilations. Phys. Rev. D 62, 054001 (2000). arXiv:hep-ph/0003177
T. Sjostrand, S. Mrenna, P.Z. Skands, PYTHIA 6.4 physics and manual. JHEP 05, 026 (2006). arXiv:hep-ph/0603175
DELPHES 3 Collaboration, J. de Favereau, C. Delaere, P. Demin, A. Giammanco, V. Lemaître, A. Mertens et al., DELPHES 3, A modular framework for fast simulation of a generic collider experiment. JHEP 02, 057 (2014). arXiv:1307.6346
M. Cacciari, FastJet: a code for fast \(k_t\) clustering, and more, in Deep inelastic scattering. In: Proceedings, 14th International Workshop, DIS 2006, Tsukuba, Japan, April 20–24, 2006, pp. 487–490 (2006). arXiv:hep-ph/0607071
CMS Collaboration, Search for associated production of dark matter with a Higgs boson that decays to a pair of bottom quarks, Tech. Rep. CMS-PAS-EXO-16-050. CERN, Geneva (2018)
CMS Collaboration, A.M. Sirunyan et al., Search for dark matter produced in association with a Higgs boson decaying to a pair of bottom quarks in proton–proton collisions at \(\sqrt{s}=13\,\text{Te}\text{ V } \). Eur. Phys. J. C 79, 280 (2019). arXiv:1811.06562
Search for dark matter in association with a Higgs boson decaying to \(b\)-quarks in \(pp\) collisions at \(\sqrt{s} = 13\) TeV with the ATLAS detector, Tech. Rep. ATLAS-CONF-2016-019. CERN, Geneva (2016)
ATLAS Collaboration, M. Aaboud et al., Search for dark matter produced in association with a Higgs boson decaying to \(b\bar{b}\) using 36 fb\(^{-1}\) of \(pp\) collisions at \(\sqrt{s}=13\) TeV with the ATLAS detector. Phys. Rev. Lett. 119, 181804 (2017). arXiv:1707.01302
ATLAS Collaboration, T. A. Collaboration, Search for dark matter produced in association with a Higgs boson decaying to \(b\bar{b}\) at \(\sqrt{s}= 13\) TeV with the ATLAS detector using 79.8 fb\(^{-1}\) of proton–proton collision data
G. Cowan, K. Cranmer, E. Gross, O. Vitells, Asymptotic formulae for likelihood-based tests of new physics. Eur. Phys. J. C 71, 1554 (2011). arXiv:1007.1727
B.P. Roe, H.-J. Yang, J. Zhu, Y. Liu, I. Stancu, G. McGregor, Boosted decision trees, an alternative to artificial neural networks. Nucl. Instrum. Meth. A 543, 577–584 (2005). arXiv:physics/0408124
L. Teodorescu, Artificial neural networks in high-energy physics. In: Computing. Proceedings, Inverted CERN School of Computing, ICSC2005 and ICSC2006, Geneva, Switzerland, February 23–25, 2005, and March 6–8, 2006, pp. 13–22 (2008). http://doc.cern.ch/yellowrep/2008/2008-002/p13.pdf
P. Baldi, P. Sadowski, D. Whiteson, Searching for exotic particles in high-energy physics with deep learning. Nat. Commun. 5, 4308 (2014). arXiv:1402.4735
S. Ghosh, A. Harilal, A. Sahasransu, R. Singh, S. Bhattacharya, A simulation study to distinguish prompt photon from \(\pi ^0\) and beam halo in a granular calorimeter using deep networks. JINST 14, P01011 (2019). arXiv:1808.03987
MicroBooNE Collaboration, K. Woodruff, Automated proton track identification in MicroBooNE using gradient boosted decision trees. In: Proceedings, Meeting of the APS Division of Particles and Fields (DPF 2017): Fermilab, Batavia, Illinois, USA, July 31–August 4, 2017 (2018). arXiv:1710.00898. http://lss.fnal.gov/archive/2017/conf/fermilab-conf-17-440-e.pdf
K.Y. Oyulmaz, A. Senol, H. Denizli, O. Cakir, Top quark anomalous FCNC production via \(tqg\) couplings at FCC-hh. Phys. Rev. D 99, 115023 (2019). arXiv:1902.03037
B. Bhattacherjee, S. Mukherjee, R. Sengupta, Study of energy deposition patterns in hadron calorimeter for prompt and displaced jets using convolutional neural network. JHEP 11, 156 (2019). arXiv:1904.04811
K. Hultqvist, R. Jacobsson, K.E. Johansson, Using a neural network in the search for the Higgs boson, DELPHI-95-61 PHYS 496
R.D. Field, Y. Kanev, M. Tayebnejad, P.A. Griffin, Using neural networks to enhance the Higgs boson signal at hadron colliders. Phys. Rev. D 53, 2296–2308 (1996)
N. Bakhet, M.Yu. Khlopov, T. Hussein, Neural networks search for charged Higgs boson of two doublet Higgs model at the hadrons colliders. arXiv:1507.06547
A. Dey, J. Lahiri, B. Mukhopadhyaya, LHC signals of triplet scalars as dark matter portal: cut-based approach and improvement with gradient boosting and neural networks. JHEP 06, 126 (2020). arXiv:2001.09349
A. Adhikary, N. Chakrabarty, I. Chakraborty, J. Lahiri, Probing the \(H^\pm W^{\mp } Z\) interaction at the high energy upgrade of the LHC. Eur. Phys. J. C 81, 554 (2021). arXiv:2010.14547
K. Lasocha, E. Richter-Was, M. Sadowski, Z. Was, Deep Neural Network application: Higgs boson CP state mixing angle in H to tau tau decay and at LHC. arXiv:2001.00455
J.R. Hermans, Distributed Keras: distributed deep learning with Apache spark and Keras, CERN IT-DB. https://joerihermans.com/work/distributed-keras/
TensorFlow. https://www.tensorflow.org/
A. Hocker et al., TMVA—Toolkit for Multivariate Data Analysis. arXiv:physics/0703039
D.P. Kingma, J. Ba, Adam: a method for stochastic optimization. arXiv:1412.6980
CMS Collaboration, S. Chatrchyan et al., Search for supersymmetry with razor variables in pp collisions at \(\sqrt{s}\)=7 TeV. Phys. Rev. D 90, 112001 (2014). arXiv:1405.3961
V. Fabiani, The flavour of dark matter. A search for dark matter in association with a Higgs boson decaying to bottom quarks with the ATLAS detector, 2066/219235, urn:nbn:nl:ui:22-2066/219235, Ph.D. thesis, Nijmegen University (2020)
B. Coleppa, B. Fuks, P. Poulose, S. Sahoo, Seeking heavy Higgs bosons through cascade decays. Phys. Rev. D 97, 075007 (2018). arXiv:1712.06593
CMS Collaboration, A.M. Sirunyan et al., Search for dark matter produced in association with a Higgs boson decaying to a pair of bottom quarks in proton–proton collisions at \(\sqrt{s}=13\,\text{ Te }\text{ V } \). Eur. Phys. J. C 79, 280 (2019). arXiv:1811.06562
CMS Collaboration, A.M. Sirunyan et al., Search for dark matter produced in association with a Higgs boson decaying to \(\gamma \gamma \) or \(\tau ^+\tau ^-\) at \(\sqrt{s} =\) 13 TeV. JHEP 09, 046 (2018). arXiv:1806.04771
Acknowledgements
We would like to thank Shamik Ghosh for useful discussions and help with the ANN codes. The work of JL and BM is partially supported by funding available from the Department of Atomic Energy, Government of India, for the Regional Centre for Accelerator-based Particle Physics (RECAPP), Harish-Chandra Research Institute. The work of RKS is partially supported by SERB, DST, Government of India through the project EMR/2017/002778. JL would like to thank Saha Institute of Nuclear Physics, HBNI and Indian Institute of Science Education and Research, Kolkata for their hospitality where substantial part of this work was done. SB and DB would like to thank RECAPP, HRI for their hospitality, where initial part of the work was done.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3. SCOAP3 supports the goals of the International Year of Basic Sciences for Sustainable Development.
About this article
Cite this article
Bhowmik, D., Lahiri, J., Bhattacharya, S. et al. The mono-Higgs + MET signal at the Large Hadron Collider: a study on the \(\gamma \gamma \) and \(b\bar{b}\) final states. Eur. Phys. J. C 82, 914 (2022). https://doi.org/10.1140/epjc/s10052-022-10828-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-022-10828-6




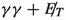 ) as well as the final state with maximum yield (
) as well as the final state with maximum yield (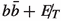 ) and thus presented an exhaustive and comparative study.
) and thus presented an exhaustive and comparative study.
 final state from dimension -4 operators
final state from dimension -4 operators


 signal with contributions from dimension-6 and -8 operators
signal with contributions from dimension-6 and -8 operators


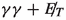 channel
channel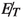 in this case makes it difficult to reduce this background. However, the isolation criterion as discussed above as well as an invariant mass cut help us suppress this background.
in this case makes it difficult to reduce this background. However, the isolation criterion as discussed above as well as an invariant mass cut help us suppress this background.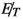 and using the fact that the invariant mass of the di-photon pair should peak around the Higgs mass, one can get rid of this background.
and using the fact that the invariant mass of the di-photon pair should peak around the Higgs mass, one can get rid of this background.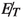 associated with this process is not significant and one of the photons is not isolated. Therefore, this process contributes only a small amount to the total background.
associated with this process is not significant and one of the photons is not isolated. Therefore, this process contributes only a small amount to the total background.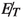 , with the invariant mass of the di-photon pair peaking around
, with the invariant mass of the di-photon pair peaking around 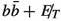 channel
channel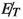 . A minor contribution comes from the leptonic decay of both W’s from
. A minor contribution comes from the leptonic decay of both W’s from 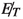 in the final state from two neutrinos coming from leptonic W decay. However, a veto on
in the final state from two neutrinos coming from leptonic W decay. However, a veto on 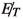 is essentially mismeasurement of jet energy. A full simulation shows that the hadronic
is essentially mismeasurement of jet energy. A full simulation shows that the hadronic 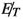 through the semileptonic decays of the weak gauge bosons. However, this background depends on the simultaneous mistagging of two light jets as b-jets. The double-mistag probability is rather small for these backgrounds (
through the semileptonic decays of the weak gauge bosons. However, this background depends on the simultaneous mistagging of two light jets as b-jets. The double-mistag probability is rather small for these backgrounds (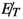 in the latter case and also the suppression of the former by the lepton veto.
in the latter case and also the suppression of the former by the lepton veto.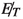 coming from jet-energy mismeasurement. On applying a suitable strategy which we will discuss in the next section (see Table
coming from jet-energy mismeasurement. On applying a suitable strategy which we will discuss in the next section (see Table 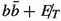 final state can also come from diboson production in the SM. However, the production cross-section in this case (
final state can also come from diboson production in the SM. However, the production cross-section in this case (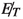 cut will help us control the ZZ as well as WZ background.
cut will help us control the ZZ as well as WZ background.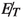 and invariant mass of the
and invariant mass of the 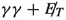 channel
channel

 (left) and invariant mass of leading and sub-leading (right) photons
(left) and invariant mass of leading and sub-leading (right) photons

 and leading (left) and sub-leading (right) photons
and leading (left) and sub-leading (right) photons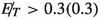
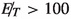 GeV
GeV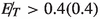


 (left) and invariant mass of leading and sub-leading (right) b jets
(left) and invariant mass of leading and sub-leading (right) b jets

 and leading (left) and sub-leading (right) b-jets
and leading (left) and sub-leading (right) b-jets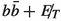 channel
channel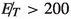 GeV
GeV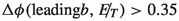 and
and 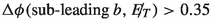
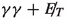 channel
channel

 final state with ANN(left) and BDT(right)
final state with ANN(left) and BDT(right)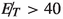 GeV,
GeV,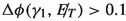 and
and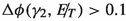 .
.
 significance (left) and
significance (left) and 
 final state with ANN (left) and BDT(right)
final state with ANN (left) and BDT(right)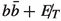 channel
channel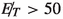 GeV,
GeV,