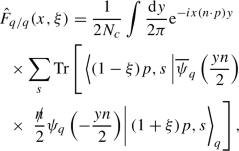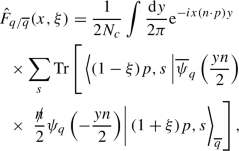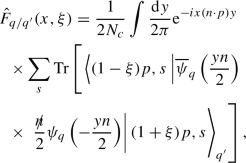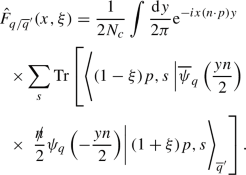Revisiting evolution equations for generalised parton distributions

Abstract

We revisit the evolution of generalised parton distributions (GPDs) in momentum space. We formulate the evolution kernels at one loop in perturbative quantum chromodynamics (pQCD) in a form that is suitable for numerical implementation and that allows for an accurate study of their properties. This leads to the first open-source implementation of GPD evolution equations able to cover the entire kinematic region and allowing for heavy-quark-threshold crossings. The numerical implementation of the GPD evolution equations is publicly accessible through the APFEL++ evolution library and is available within the PARTONS framework. Our formulation makes use of the operator definition of GPDs in light-cone gauge renormalised in the $\overline{\text{ MS }}$ scheme. For the sake of clarity, we recompute the evolution kernels at one loop in pQCD, confirming previous calculations. We obtain general conditions on the evolution kernels derived from the GPD sum rules and show that our formulation obeys these conditions. We analytically show that our calculation reproduces the DGLAP and the ERBL equations in the appropriate limits and that it guarantees the continuity of GPDs. We numerically check that the evolved GPDs fulfil DGLAP and ERBL limits, continuity, and polynomiality. We benchmark our numerical implementation against analytical evolution in conformal space. Finally, we perform a numerical comparison to an existing implementation of GPD evolution, finding general good agreement on the kinematic region accessible to the latter. This work provides a pedagogical description of GPD evolution equations which benefits from a renewed interest as future colliders, such as the electron-ion colliders in the United States and in China, are being designed. It also paves the way for the extension of GPD evolution codes to higher accuracies in pQCD desirable for precision phenomenology at these facilities.

1 Introduction

Generalised parton distributions (GPDs) were introduced in the 1990s [1,2,3,4,5] and have been thoroughly studied ever since (see e.g. the review papers in Refs. [6,7,8]). There are many reasons for their interest. GPDs can be interpreted in terms of partonic probability densities in longitudinal momentum and transverse position [9, 10]. Therefore, an understanding of GPDs would allow us to obtain a spatial picture of hadrons (hadron tomography) that is not achievable otherwise. Moreover, GPDs are closely related to the form factors of the energy-momentum tensor, allowing for a gauge-invariant spin decomposition of the hadron [3] and for a formal analogy with pressure and shear force distributions [11]. GPDs emerge from the factorisation of exclusive hard processes such as deeply virtual Compton scattering [2, 12]. This ultimately gives us the possibility to achieve an experimentally driven tomography of hadrons. In fact, this has been one of the main motivations for investing in current experimental programmes, such as the Jefferson Laboratory upgrade to 12 GeV, and in future facilities like the electron-ion colliders in the United States (EIC) [13, 14] and in China (EicC) [15].

Already in the early days of GPDs, and guided by the work done on both parton distribution functions (PDFs) and distribution amplitudes (DAs), several groups derived evolution equations for GPDs, generalising both the Dokshitzer–Gribov–Lipatov–Altarelli–Parisi (DGLAP) and Efremov–Radyushkin–Brodsky–Lepage (ERBL) evolution equations. Leading-order (LO) results were readily obtained [1, 2, 5, 16,17,18,19], followed shortly thereafter by the calculation of the next-to-leading order (NLO) corrections [20,21,22,23,24], which were recently confirmed by an independent study [25] and even extended to three loops (NNLO) in the non-singlet case [26].

On the phenomenological side, early efforts were devoted to developing GPD evolution codes. Vinnikov [27] developed the first open-source code in momentum space able to evolve GPDs at LO accuracy. However, the code webpage no longer exists and, as far as we can tell, the only public version of this code is its implementation in the PARTONS framework [28]. A few years earlier, Freund and McDermott [29] developed a code able to evolve GPDs at NLO tailored to the computation of deeply virtual Compton scattering. However, to the best of our knowledge, this code was never made fully open-source, and as of today it is difficult to find a clean copy. In parallel, a strong effort was put into obtaining an evolution procedure at NLO in conformal space (see e.g. Ref. [30]), yielding the only public NLO evolution code available today [31, 32]. We point out that all the codes mentioned above are rigidly associated with specific GPD models or families of parameterisations, and can hardly be used out of the box to evolve different input GPDs. Moreover, to the best of our knowledge, none of them allows for the treatment of heavy flavours, while a significant amount of current experimental data lies above the charm threshold. In the last decade, these codes have not taken the front stage mainly because the latest and most precise experimental data related to GPDs were obtained in relatively small ranges and at relatively small values of the hard scale $Q^2$. The necessity of using evolution equations for a consistent theoretical analysis of experimental data was jeopardised by the poor accuracy of LO perturbative QCD at low scales. This has made evolution of GPDs less critical for phenomenological purposes. However, with the forthcoming EIC and EicC, the situation is expected to change drastically, as exclusive processes will be measured in a larger kinematic range, making the need for evolution pressing.

In this paper, we revisit the LO evolution equations of GPDs in momentum space computing the one-loop unpolarised anomalous dimensions renormalised in the $\overline{\text{ MS }}$ scheme in the light-cone gauge. In order to make the paper self-contained, we provide a pedagogical description of the computation targeting newcomers unfamiliar with the most technical aspects of the field, a community which is expected to grow in view of the timeline of the EIC and EicC projects. We formalise our results in a way that allows us to study their properties and that facilitates the numerical implementation. The solution of the evolution equations is implemented in the open-source code APFEL++ [33, 34] that is interfaced to the PARTONS framework.

In Sect. 2, we derive the GPD evolution equations and present our calculation of the kernels. These equations are presented in a form that resembles the DGLAP equations, thus allowing us to exploit the capabilities of existing evolution codes such as APFEL++ for their solution. In Sect. 3, we present a thorough study of the analytical properties of the ensuing evolution kernels. In Sect. 4, we discuss the numerical implementation and provide quantitative evidence that the evolution fulfils fundamental requirements such as correct DGLAP and ERBL limits, continuity, polynomiality, and equivalence with the conformal-space approach. To the best of our knowledge, these numerical consistency checks have not been discussed in a detailed manner in the existing literature concerning GPD evolution codes. Finally, in Sect. 5 we summarise and give some concluding remarks. Appendices are devoted to some technical aspects. Appendix A discusses the general method used to compute the evolution kernels by the introduction of the parton-in-parton GPDs, Appendix B gives some details concerning the explicit calculation of the one-loop evolution kernel ${\mathcal {P}}_{q/q}^{[0]}$, and Appendix C presents the explicit calculation of its conformal moments.

2 Operator definition of GPDs and evolution equations

GPDs enjoy an operator definition that results from the collinear factorisation of processes like deeply virtual Compton scattering and deeply virtual meson production [12, 35]. This operator definition is affected by UV divergences related to the integration over the transverse momenta $k_T$ of the constituent partons and that need to be renormalised. As is customary, the renormalisation procedure introduces an unphysical scale, $\mu$, that roughly speaking corresponds to a cut-off on the integral in $k_T$. The fact that unrenormalised (bare) GPDs do not depend on $\mu$ allows one to derive a set of renormalisation-group equations (RGEs) that governs the dependence of the renormalised GPDs on $\mu$: the evolution equations. The anomalous dimensions (sometimes referred to as evolution kernels or splitting functions) of these evolution equations can be computed in perturbation theory by isolating the coefficient of the UV divergences of the bare GPDs order by order in the expansion in powers of the strong coupling $\alpha _s$. GPDs cannot be computed in perturbation theory, but for the purpose of extracting the UV poles, one can replace the hadronic states that enter their operator definition with partonic states, thus enabling an explicit computation. This follows from the fact that GPDs emerge from factorisation theorems that apply to any target. As a consequence, the extraction of the anomalous dimensions related to UV poles (as well as of the partonic cross sections) is conveniently accomplished using partonic on-shell targets [36]. Although GPDs are not physical observables, they are gauge-invariant quantities. In a covariant formulation, gauge invariance is guaranteed by the presence of the so-called Wilson line that connects the bi-local GPD operator along the light-cone direction.

When using the operator definition of GPDs in perturbative calculations, the presence of the Wilson line introduces substantial complications [37]. This is because a Wilson line can be pictured as the radiation of an arbitrary number of collinear gluons with scalar polarisation (i.e. with polarisation proportional to the gluon momentum and thus to the collinear direction) that massively increase the number of diagrams to be considered at any given perturbative order. This problem can be overcome by adopting an axial gauge, $n\cdot A = 0$, in which the gauge vector n is on the light cone, $n^2=0$: this is usually called light-cone gauge. By definition, scalar gluons are absent in the light-cone gauge, thus enormously reducing the number of diagrams to be considered. In addition, in light-cone gauge there are no ghosts [38], which further reduces the complexity of the calculation. These simplifications however come at the price of a complication of the gluon propagator that in the light-cone gauge takes the form:

$$\begin{aligned} {\mathcal {D}}_{\mu \nu }(k) = \frac{1}{k^2+i\varepsilon }\left( -g_{\mu \nu }+\frac{k_\mu n_\nu +k_\nu n_\mu }{k\cdot n}\right) . \end{aligned}$$

(1)

A particularly unpleasant feature of this propagator is that it develops a spurious pole at $k\cdot n=0$. However, it has been argued that poles deriving from the gluon propagator in the light-cone gauge must cancel in gauge-invariant quantities [39]. Therefore, when computing GPD anomalous dimensions, it is enough to regularise these poles on a diagram-by-diagram basis using a suitable prescription, bearing in mind that they eventually cancel when summing up all diagrams.¹

Finally, the operator defining the bare quark and gluon unpolarised GPDs of a generic hadron species H in the light-cone gauge with gauge vector n reads

(2)

where $\psi _q$ is the quark field for the flavour q in the fundamental colour representation, and $F_{a}^ {\mu \nu }$ is the gluon field strength for the colour configuration a in the adjoint representation. The integrals are understood to run between $-\infty$ and $+\infty$. The variable x is the longitudinal fraction of the average momentum P carried by the parton, while $\xi$, often referred to as skewness, is the longitudinal fraction of the momentum transfer $\Delta$. In addition, an average over the initial-state spin/helicity physical states is understood. The index j in the gluon distribution runs over the longitudinal components ($j=1,2$) and is summed over as well as the colour index a. Note the absence of the Wilson line as a consequence of the light-cone gauge. A further simplification induced by this gauge is that the contraction of the gauge vector with the gluon field strength reduces to $n_\mu F_a^{\mu j}(x)=\left( n\cdot \partial \right) A_a^j(x)$. The tensorial decomposition of the correlators in Eq. (2) leads to the actual definition of the bare GPDs ${\hat{H}}_{i/H}$ and ${\hat{E}}_{i/H}$ [6]:

(3)

with $i=q,g$ and where u is spinor of the external state H and M is its mass. Note that the definitions in Eq. (2) are such that GPDs in the forward limit $\Delta \rightarrow 0$ exactly reproduce the standard collinear parton distribution functions (PDFs):

$$\begin{aligned} \begin{array}{l} \lim _{\Delta \rightarrow 0}{\hat{F}}_{q/H}(x,\xi , \Delta ^2) = {\hat{f}}_{q/H}(x),\\ \lim _{\Delta \rightarrow 0}{\hat{F}}_{g/H}(x,\xi , \Delta ^2) = {\hat{f}}_{g/H}(x). \end{array} \end{aligned}$$

(4)

In order to fulfil Eq. (4) for the gluon, we adopt the off-forward generalisation of the definition of gluon PDF given in Ref. [45]. This differs by a factor $2/(n\cdot P)$ w.r.t. Ref. [2] and by factor 1/x w.r.t. Ref. [6]. From now on, we will drop the dependence on the total momentum transfer $\Delta ^2$ because it does not participate in the evolution of GPDs.

Fig. 1

Graphical representation of the parton-in-hadron GPDs defined in Eq. (2)

A graphical representation of the GPDs defined in Eq. (2) is displayed in Fig. 1. In these graphs, the crosses represent the operator insertion and the integration over y, that is,

for quarks and

for gluons.

Assuming dimensional regularisation in $4-2\varepsilon$ dimension, with $\varepsilon >0$, the bare GPD correlator in Eq. (2) can be renormalised in the $\overline{\text{ MS }}$ scheme as follows:

$$\begin{aligned} F_{i/H}(x,\xi ,\mu )= & {} \sum _{j=q,g}\int _{-1}^1\frac{{\mathrm{d}}y}{|y|}Z_{ij}\left( \frac{x}{y},\frac{\xi }{x},\alpha _s(\mu ),\varepsilon \right) \nonumber \\&\times {\hat{F}}_{j/H}(y,\xi ,\varepsilon ),\quad i = q,g, \end{aligned}$$

(5)

where the sum runs over all active quark flavours at the scale $\mu$. Due to longitudinal boost invariance, the $\overline{\text{ MS }}$ renormalisation constants $Z_{ij}$ can only be functions of ratios of momentum fractions, of the coupling $\alpha _s$, and of the regulator $\varepsilon$, and can be expanded as [36]:²

$$\begin{aligned} Z_{ij}\left( \frac{x}{y},\frac{\xi }{x},\alpha _s,\varepsilon \right)= & {} \sum _{n=0}^{\infty }a_s^n Z_{ij}^{[n]}\left( \frac{x}{y},\frac{\xi }{x},\varepsilon \right) \nonumber \\= & {} \delta _{ij}\delta \left( 1-\frac{x}{y}\right) \nonumber \\&+\sum _{n=1}^{\infty }a_s^n \sum _{p=1}^{n}\frac{1}{\varepsilon ^p}Z_{ij}^{[n,p]}\left( \frac{x}{y},\frac{\xi }{x}\right) , \end{aligned}$$

(7)

where we have defined $a_s=g^2/16\pi ^2=\alpha _s/4\pi$. Exploiting the fact that ${\hat{F}}$ does not depend on the renormalisation scale $\mu$, the logarithmic derivative w.r.t. $\mu$ of Eq. (5) gives

$$\begin{aligned} \frac{{\mathrm{d}}F_{i/H}(x,\xi ,\mu )}{{\mathrm{d}}\ln \mu ^2}= & {} \sum _{k=q,g}\int _{-1}^1\frac{{\mathrm{d}}z}{|z|}{\mathcal {P}}_{i/k} \left( \frac{x}{z},\frac{\xi }{x},\alpha _s(\mu )\right) \nonumber \\&\times F_{k/H}(z,\xi ,\mu ), \end{aligned}$$

(8)

with

$$\begin{aligned} {\mathcal {P}}_{i/k}\left( \frac{x}{z},\frac{\xi }{x},\alpha _s\right)= & {} \lim _{\varepsilon \rightarrow 0}\sum _{j=q,g}\int _{-1}^1\frac{{\mathrm{d}}y}{|y|}\frac{{\mathrm{d}}Z_{ij} \left( \frac{x}{y},\frac{\xi }{x},\alpha _s(\mu ),\varepsilon \right) }{{\mathrm{d}}\ln \mu ^2}\nonumber \\&\times Z_{jk}^{-1}\left( \frac{y}{z},\frac{\xi }{y},\alpha _s,\varepsilon \right) , \end{aligned}$$

(9)

where $Z_{kj}^{-1}$ is defined by means of the following equality:

$$\begin{aligned}&\sum _{j=q,g}\int _{-1}^1\frac{{\mathrm{d}}x}{|x|}Z_{kj}^{-1} \left( \frac{z}{x},\frac{\xi }{z},\alpha _s,\varepsilon \right) Z_{ji}\left( \frac{x}{y},\frac{\xi }{x},\alpha _s,\varepsilon \right) \nonumber \\&\quad =\delta _{ki}\delta \left( 1-\frac{z}{y}\right) . \end{aligned}$$

(10)

Note that the definition of ${\mathcal {P}}_{i/k}$ allows one to take the limit $\varepsilon \rightarrow 0$ because these quantities are finite order by order in perturbation theory and therefore permit the perturbative expansion:

$$\begin{aligned} {\mathcal {P}}_{i/k}\left( \frac{x}{z},\frac{\xi }{x},\alpha _s\right) = \sum _{n=0}^{\infty }a_s^{n+1} {\mathcal {P}}_{i/k}^{[n]}\left( \frac{x}{z},\frac{\xi }{x}\right) . \end{aligned}$$

(11)

From Eq. (9), ${\mathcal {P}}_{i/k}$ can be seen as an x-dependent generalisation of the anomalous dimension introduced in the renormalisation of local operators. Exploiting the fact that $Z_{ij}$ depend on the scale $\mu$ only through the strong coupling $\alpha _s$, one can further manipulate the derivative in Eq. (9) as follows:

$$\begin{aligned} \frac{{\mathrm{d}}Z_{ij}\left( \frac{x}{y},\frac{\xi }{x},\alpha _s(\mu ),\varepsilon \right) }{{\mathrm{d}}\ln \mu ^2}= & {} \left( -\varepsilon a_s+\beta (a_s)\right) \frac{{\mathrm{d}}Z_{ij}\left( \frac{x}{y},\frac{\xi }{x},\alpha _s,\varepsilon \right) }{{\mathrm{d}}a_s}\nonumber \\= & {} \left( -\varepsilon a_s+\beta (a_s)\right) \sum _{n=1}^{\infty }na_s^{n-1}\nonumber \\&\times \sum _{p=0}^{n} \frac{1}{\varepsilon ^p}Z_{ij}^{[n,p]}\left( \frac{x}{y},\frac{\xi }{x}\right) \end{aligned}$$

(12)

where we have used the $(4-2\varepsilon )$-dimensional RGE for the strong coupling:

$$\begin{aligned} \frac{{\mathrm{d}}a_s}{{\mathrm{d}}\ln \mu ^2}=-\varepsilon a_s+\beta (a_s). \end{aligned}$$

(13)

Since in this paper we are mainly concerned with the leading-order contribution to perturbative expansion of the anomalous dimensions in Eq. (11), considering that $\beta (a_s)={\mathcal {O}}(\alpha _s^2)$, we find

$$\begin{aligned} {\mathcal {P}}_{i/k}^{[0]}\left( \frac{x}{z}, \frac{\xi }{x}\right) =-Z_{ik}^{[1,1]}\left( \frac{x}{z},\frac{\xi }{x}\right) . \end{aligned}$$

(14)

Therefore, the calculation of the one-loop anomalous dimension of the GPD evolution boils down to computing the coefficient of the divergence of the one-loop renormalisation constant of the bare GPDs themselves. However, the procedure is totally general and can be extended to any fixed order in perturbation theory.

The calculation of the renormalisation constants can be accomplished by using the parton-in-parton GPDs defined in Appendix A. As mentioned above, owing to the universality of the UV structure of the partonic correlator, one can replace the hadronic states in Eq. (2) with partonic states, thus enabling a perturbative calculation. Therefore, both the bare and renormalised parton-in-parton GPDs enjoy the perturbative expansions:

$$\begin{aligned}&{\hat{F}}_{i/j}(x,\xi ,\varepsilon ) = \sum _{n=0}^{\infty }a_s^n {\hat{F}}_{i/j}^{[n]}(x,\xi ,\varepsilon ),\nonumber \\&F_{i/j}(x,\xi , \mu ) = \sum _{n=0}^{\infty }a_s^n F_{i/j}^{[n]}(x,\xi ,\mu ), \end{aligned}$$

(15)

which plugged into Eq. (5), along with the expansion in Eq. (7), allow us to relate bare and renormalised parton-in-parton GPDs order by order in $\alpha _s$:

$$\begin{aligned} F_{i/k}^{[n]}(x,\xi ,\mu )= & {} \sum _{j=q,g}\sum _{p=0}^{n}\int _{-1}^1\frac{{\mathrm{d}}y}{|y|} Z_{ij}^{[p]}\left( \frac{x}{y},\frac{\xi }{x},\varepsilon \right) \nonumber \\&\times {\hat{F}}_{j/k}^{[{n-p}]}(y,\xi ,\varepsilon ). \end{aligned}$$

(16)

The first two orders explicitly read:

$$\begin{aligned} F_{i/k}^{[0]}(x,\xi ,\mu )= & {} {\hat{F}}_{i/k}^{[0]}(x,\xi ,\varepsilon )\equiv D_i(\xi )\delta _{ik}\delta (1-x),\nonumber \\ F_{i/k}^{[1]}(x,\xi ,\mu )= & {} {\hat{F}}_{i/k}^{[1]}(x,\xi ,\varepsilon ) +Z_{ik}^{[1]}\left( x,\frac{\xi }{x},\varepsilon \right) D_k(\xi ),\nonumber \\ \end{aligned}$$

(17)

where the first equality is the result of a tree-level computation using the definitions in Eq. (2) (see Appendix A, where the factors $D_i$ are also derived). The second equality instead allows us to extract $Z_{ik}^{[1,1]}$ in Eq. (14) by requiring that $F_{i/k}^{[1]}(x,\xi ,\mu )$ be finite in the $\varepsilon \rightarrow 0$ limit, finally obtaining:

$$\begin{aligned} {\mathcal {P}}_{i/k}^{[0]}\left( x,\frac{\xi }{x}\right) = {\mathrm{P.P.}}\left[ {\hat{F}}_{i/k}^{[1]}(x,\xi ,\varepsilon )\right] D_k^{-1}(\xi ), \end{aligned}$$

(18)

where P.P. stands for “$\overline{\text{ MS }}$ UV pole part”. ${\hat{F}}_{i/k}^{[1]}$ can be obtained through the calculation of the appropriate one-loop diagrams. Using the definitions given in Appendix A, we have computed the one-loop corrections to all (non-vanishing) parton-in-parton GPDs and extracted the pole part. Finally, using Eq. (18), we found that the one-loop anomalous dimensions have the following structure:³

$$\begin{aligned} {\mathcal {P}}_{i/k}^{[0]}\left( x,\frac{\xi }{x}\right)= & {} \theta (1-x) \left[ \theta \left( x+\xi \right) p_{ik}\left( x,\frac{\xi }{x}\right) \right. \nonumber \\&\left. +\theta \left( x-\xi \right) p_{ik}\left( x,-\frac{\xi }{x}\right) \right] \nonumber \\&+ \delta _{ik}\delta (1-x) 2C_i\left[ K_i-2\int _0^1 \frac{{\mathrm{d}}z}{1-z}\right. \nonumber \\&\left. -\ln \left( \left| 1-\frac{\xi ^2}{x^2}\right| \right) \right] , \end{aligned}$$

(19)

where

$$\begin{aligned} p_{qq}(y,\kappa )= & {} C_F \frac{(1+\kappa ) (1-y+2\kappa y)}{\kappa (1+\kappa y)(1-y)},\nonumber \\ p_{qg}(y,\kappa )= & {} T_R\frac{(1+\kappa ) (1-2y+\kappa y)}{\kappa (1+\kappa y) (1-\kappa ^2 y^2)} ,\nonumber \\ p_{gq}(y,\kappa )= & {} C_F\frac{(1+\kappa ) (2-y+\kappa y)}{\kappa y (1+\kappa y)},\nonumber \\ p_{gg}(y,\kappa )= & {} -C_A\frac{1-\kappa ^2}{\kappa (1-\kappa ^2 y^2)}\nonumber \\&\times \left[ 1-\frac{2\kappa y}{1-y}-\frac{2(1+y^2)}{y (1-\kappa ) (1+\kappa y)}\right] , \end{aligned}$$

(20)

and

$$\begin{aligned} K_q = \frac{3}{2},\quad K_g = \frac{11C_A-4n_fT_R}{6C_A}, \end{aligned}$$

(21)

with $C_g=C_A=N_c=3$, $C_q=C_F=(N_c^2-1)/2N_c=4/3$, $T_R=1/2$, and $n_f$ the number of active quark flavours. For the sake of illustration, the explicit calculation of ${\hat{F}}_{q/q}^{[1]}$, which allowed us to extract ${\mathcal {P}}_{q/q}^{[0]}$, is presented in Appendix B. The remaining one-loop parton-in-parton GPDs and the corresponding anomalous dimensions can be computed in a similar fashion.

In the following, we will formulate the GPD evolution equations in a form that resembles the DGLAP equations for PDFs. On the one hand, this facilitates the implementation in existing computer codes able to compute the DGLAP evolution. Indeed, relying on solid and well-established numerical techniques, several DGLAP evolution codes have nowadays reached a numerical accuracy well below the per-mil level [33, 34, 46,47,48]. On the other hand, this formulation allows us to highlight some interesting properties of the anomalous dimensions. To do so, we restrict ourselves the longitudinal momentum fraction x to be non-negative. This can be done first by observing that, using the definition in Eq. (2), the gluon GPD is an odd function of x, so that ${F}_{g/H}(-x,\xi , \Delta ^2)=-{F}_{g/H}(x,\xi , \Delta ^2)$, and second by defining the anti-quark GPDs as ${F}_{{\overline{q}}/H}(x,\xi , \Delta ^2)=-{F}_{q/H}(-x,\xi , \Delta ^2)$. In addition, from Eq. (19) it is apparent that evolution kernels and thus GPDs are symmetric under the transformation $\xi \rightarrow -\xi$. Therefore, without loss of generality we can restrict to considering non-negative values of $\xi$. We can then write leading-order evolution equations for quark, antiquark, and gluon GPDs separately as

$$\begin{aligned}&\frac{{\mathrm{d}}F_{q/H}( x,\xi ,\mu )}{{\mathrm{d}}\ln \mu ^2}\nonumber \\&\quad = \frac{\alpha _s(\mu )}{4\pi }\Bigg \{\int _{0}^1\frac{{\mathrm{d}}z}{z} {\mathcal {P}}^{[0]}_{q/q}\left( \frac{x}{z},\frac{\xi }{x}\right) F_{q/H}(z,\xi ,\mu )\nonumber \\&\qquad - \int _{0}^1\frac{{\mathrm{d}}z}{z}{\mathcal {P}}^{[0]}_{q/q} \left( -\frac{x}{z},\frac{\xi }{x}\right) F_{{\overline{q}}/H}(z,\xi ,\mu )\nonumber \\&\qquad + \int _{0}^1\frac{{\mathrm{d}}z}{z}\left[ {\mathcal {P}}^{[0]}_{q/g}\left( \frac{ x}{z},\frac{\xi }{x}\right) -{\mathcal {P}}^{[0]}_{q/g}\left( -\frac{ x}{z},\frac{\xi }{x}\right) \right] \nonumber \\&\qquad \times F_{g/H}(z,\xi ,\mu )\Bigg \}, \end{aligned}$$

(22)

$$\begin{aligned}&\frac{{\mathrm{d}}F_{{\overline{q}}/H}(x,\xi ,\mu )}{{\mathrm{d}}\ln \mu ^2}\nonumber \\&\quad = \frac{\alpha _s(\mu )}{4\pi }\Bigg \{ -\int _{0}^1\frac{{\mathrm{d}}z}{z}{\mathcal {P}}^{[0]}_{q/q}\left( -\frac{x}{z},\frac{\xi }{x}\right) F_{q/H}(z,\xi ,\mu )\nonumber \\&\qquad + \int _{0}^1\frac{{\mathrm{d}}z}{z}{\mathcal {P}}^{[0]}_{q/q} \left( \frac{x}{z},\frac{\xi }{x}\right) F_{{\overline{q}}/H}(z,\xi ,\mu )\nonumber \\&\qquad +\int _{0}^1\frac{{\mathrm{d}}z}{z}\left[ {\mathcal {P}}^{[0]}_{q/g}\left( \frac{ x}{z},\frac{\xi }{x}\right) \right. \nonumber \\&\qquad \left. -{\mathcal {P}}^{[0]}_{q/g}\left( -\frac{ x}{z},\frac{\xi }{x}\right) \right] F_{g/H}(z,\xi ,\mu ) \Bigg \}, \end{aligned}$$

(23)

$$\begin{aligned}&\frac{{\mathrm{d}}F_{g/H}( x,\xi ,\mu )}{{\mathrm{d}}\ln \mu ^2}\nonumber \\&\quad =\frac{\alpha _s(\mu )}{4\pi }\Bigg \{\int _{0}^1\frac{{\mathrm{d}}z}{z}{\mathcal {P}}^{[0]}_{g/q} \left( \frac{x}{z},\frac{\xi }{x}\right) F_{q/H}(z,\xi ,\mu )\nonumber \\&\qquad - \int _{0}^1\frac{{\mathrm{d}}z}{z}{\mathcal {P}}^{[0]}_{g/q} \left( -\frac{x}{z},\frac{\xi }{x}\right) F_{{\overline{q}}/H}(z,\xi ,\mu )\nonumber \\&\qquad +\int _{0}^1\frac{{\mathrm{d}}z}{z}\left[ {\mathcal {P}}^{[0]}_{g/g} \left( \frac{x}{z},\frac{\xi }{x}\right) -{\mathcal {P}}^{[0]}_{g/g}\right. \nonumber \\&\qquad \times \left. \left( -\frac{x}{z},\frac{\xi }{x}\right) \right] F_{g/H}(z,\xi ,\mu ) \Bigg \}, \end{aligned}$$

(24)

where we have used the following equality:

$$\begin{aligned} {\mathcal {P}}_{i/k}^{[0]}\left( x,-\frac{\xi }{x}\right) = {\mathcal {P}}_{i/k}^{[0]}\left( x,\frac{\xi }{x}\right) , \end{aligned}$$

(25)

which is a consequence of a general symmetry of GPDs and follows immediately from Eq. (19). It is now possible to define parton-in-hadron GPD combinations that maximally diagonalise the matrix of one-loop anomalous dimensions ${\mathcal {P}}_{i/k}^{[0]}$. More precisely, one defines the total-valence non-singlet GPD as

$$\begin{aligned} F^- = \sum _{q=1}^{n_f}F_{q/H}-F_{{\overline{q}}/H}, \end{aligned}$$

(26)

and a bidimensional vector of GPDs made of the total-singlet and the gluon GPDs, often collectively referred to as singlet

$$\begin{aligned} F^+= \begin{pmatrix} \sum _{q=1}^{n_f}F_{q/H}+F_{{\overline{q}}/H}\\ F_{g/H} \end{pmatrix}. \end{aligned}$$

(27)

These combinations obey the following evolution equations:⁴

$$\begin{aligned} \frac{{\mathrm{d}}F^{\pm }(x,\xi ,\mu )}{{\mathrm{d}}\ln \mu ^2} =\frac{\alpha _s(\mu )}{4\pi } \int _x^\infty \frac{{\mathrm{d}}y}{y}{\mathcal {P}}^{\pm ,[0]} \left( y,\kappa \right) F^{\pm }\left( \frac{x}{y},\xi ,\mu \right) , \nonumber \\ \end{aligned}$$

(28)

with $\kappa =\xi /x$. The evolution kernel of the non-singlet GPD is given by

$$\begin{aligned} {\mathcal {P}}^{-,[0]}\left( y,\kappa \right) ={\mathcal {P}}_{q/q}^{[0]}\left( y,\kappa \right) + {\mathcal {P}}_{q/q}^{[0]}\left( -y,\kappa \right) , \end{aligned}$$

(29)

while that of the singlet is given by

$$\begin{aligned}&{\mathcal {P}}^{+,[0]}\left( y,\kappa \right) \nonumber \\&\quad = \begin{pmatrix} {\mathcal {P}}_{q/q}^{[0]}\left( y,\kappa \right) -{\mathcal {P}}_{q/q}^{[0]} \left( -y,\kappa \right) &{} 2n_f\left( {\mathcal {P}}_{q/g}^{[0]}\left( y,\kappa \right) -{\mathcal {P}}_{q/g}^{[0]}\left( -y,\kappa \right) \right) \\ {\mathcal {P}}_{g/q}^{[0]}\left( y,\kappa \right) -{\mathcal {P}}_{g/q}^{[0]}\left( -y,\kappa \right) &{}{\mathcal {P}}_{g/g}^{[0]}\left( y,\kappa \right) -{\mathcal {P}}_{g/g}^{[0]}\left( -y,\kappa \right) \end{pmatrix}.\nonumber \\ \end{aligned}$$

(30)

Using Eq. (19), it is easy to see that for $x>0$ and $\xi \ge 0$

$$\begin{aligned} {\mathcal {P}}_{i/k}^{[0]}\left( -y,\kappa \right) =\theta \left( \kappa -1\right) p_{ik}\left( -y,-\kappa \right) , \end{aligned}$$

(31)

so that the splitting kernels can be recast as

$$\begin{aligned} {\mathcal {P}}^{\pm ,[0]}\left( y,\kappa \right)= & {} \theta (1-y) {\mathcal {P}}_1^{\pm ,[0]}\left( y,\kappa \right) \nonumber \\&+\theta (\kappa -1) {\mathcal {P}}_2^{\pm ,[0]}\left( y,\kappa \right) . \end{aligned}$$

(32)

For the non-singlet evolution kernel one finds:⁵

$$\begin{aligned}&{\mathcal {P}}_1^{-,[0]}\left( y,\kappa \right) = p_{qq}\left( y,\kappa \right) +p_{qq}\left( y,-\kappa \right) \nonumber \\&\quad + \delta (1-y) 2C_q\left[ K_q-2\int _0^1 \frac{{\mathrm{d}}z}{1-z}-\ln \left( \left| 1-\kappa ^2\right| \right) \right] ,\nonumber \\&{\mathcal {P}}_2^{-,[0]}\left( y,\kappa \right) = -p_{qq}\left( y,-\kappa \right) +p_{qq}\left( -y,-\kappa \right) , \end{aligned}$$

(33)

while for the single components of the matrix associated with the singlet evolution

$$\begin{aligned}&{\mathcal {P}}_{1,ik}^{+,[0]}\left( y,\kappa \right) = p_{ik}\left( y,\kappa \right) +p_{ik}\left( y,-\kappa \right) \nonumber \\&\quad + \delta _{ik}\delta (1-y) 2C_i\left[ K_i-2\int _0^1 \frac{{\mathrm{d}}z}{1-z} -\ln \left( \left| 1-\kappa \right| \right) \right] ,\nonumber \\&{\mathcal {P}}_{2,ik}^{+,[0]}\left( y,\kappa \right) = -p_{ik}\left( y,-\kappa \right) -p_{ik}\left( -y,-\kappa \right) . \end{aligned}$$

(34)

The decomposition in Eq. (32) is particularly convenient. The ${\mathcal {P}}_1$ terms, being proportional to $\theta (1-y)$, reduce Eq. (28) to the exact same form of a DGLAP evolution equation. As a matter of fact, we will show below that in the limit $\xi \rightarrow 0$, the one-loop ${\mathcal {P}}_1$ kernels exactly reduce to the one-loop DGLAP splitting functions. The ${\mathcal {P}}_2$ terms instead come into play for $\kappa >1$ ($x<\xi$) and thus represent the contribution to the evolution due to the ERBL region. Of course, for $\xi \rightarrow 0$ these terms do not contribute, leaving only the DGLAP kernels. A graphical representation of the integration domain covered by ${\mathcal {P}}_1$ and ${\mathcal {P}}_2$ is displayed in Fig. 2.

Fig. 2

Integration domain covered by the convolution integral in the r.h.s. of the evolution equations in Eq. (28). The coverage of the single functions ${\mathcal {P}}_1$ and ${\mathcal {P}}_2$ according to the decomposition in Eq. (32) is shown in red and blue, respectively. The dot-dashed line corresponding to $y = x/\xi$ is relevant in that, along this line, both ${\mathcal {P}}_1$ and ${\mathcal {P}}_2$ separately diverge (see Sect. 3.3)

Using the $p_{ik}$ functions given in Eq. (20), we can obtain the explicit expressions for the ${\mathcal {P}}_{1,2}$ kernels. For the non-singlet sector they read

$$\begin{aligned} \left\{ \begin{array}{l} {\mathcal {P}}_{1}^{-,[0]}(y,\kappa ) \\ \quad = 2C_F\left\{ \left( \frac{2}{1-y}\right) _+-\frac{1 +y}{1-\kappa ^2y^2}+\delta (1-y)\left[ \frac{3}{2}- \ln \left( |1-\kappa ^2|\right) \right] \right\} ,\\ {\mathcal {P}}_{2}^{-,[0]}(y,\kappa ) = 2C_F\left[ \frac{1+(1+\kappa )y+(1+\kappa -\kappa ^2)y^2}{(1+y)(1-\kappa ^2y^2)}-\left( \frac{1}{1-y}\right) _{++}\right] , \end{array}\right. \nonumber \\ \end{aligned}$$

(35)

while for the singlet sector we find

$$\begin{aligned}&\left\{ \begin{array}{l} {\mathcal {P}}_{1, qq}^{+,[0]}(y,\kappa )={\mathcal {P}}_{1}^{-,[0]}(y,\kappa ),\\ {\mathcal {P}}_{2, qq}^{+,[0]}(y,\kappa )= 2C_F\left[ \frac{1+y+\kappa y+\kappa ^3y^2}{\kappa (1+y)(1-\kappa ^2y^2)}-\left( \frac{1}{1-y}\right) _{++}\right] , \end{array}\right. \end{aligned}$$

(36)

$$\begin{aligned}&\left\{ \begin{array}{l} {\mathcal {P}}_{1, qg}^{+,[0]}(y,\kappa ) = 4n_f T_R\left[ \frac{y^2+(1-y)^2 -\kappa ^2y^2}{(1-\kappa ^2y^2)^2}\right] , \\ {\mathcal {P}}_{2, qg}^{+,[0]}(y,\kappa ) = 4n_f T_R(1-\kappa )\left[ \frac{1-\kappa (\kappa +2)y^2}{\kappa (1-\kappa ^2y^2)^2}\right] , \end{array}\right. \end{aligned}$$

(37)

$$\begin{aligned}&\left\{ \begin{array}{l} {\mathcal {P}}_{1, gq}^{+,[0]}(y,\kappa ) = 2C_F\left[ \frac{1+(1-y)^2-\kappa ^2y^2}{y(1-\kappa ^2y^2)}\right] , \\ {\mathcal {P}}_{2, gq}^{+,[0]}(y,\kappa ) = -2C_F\frac{(1-\kappa )^2}{\kappa (1-\kappa ^2 y^2)}, \end{array}\right. \end{aligned}$$

(38)

$$\begin{aligned}&\left\{ \begin{array}{l} {\mathcal {P}}_{1, gg}^{+,[0]}(y,\kappa ) = 4C_A\left[ \left( \frac{1}{1-y}\right) _+-\frac{1+\kappa ^2y}{1-\kappa ^2y^2}\right. \\ \quad \left. +\frac{1}{(1-\kappa ^2y^2)^2}\left( \frac{1-y}{y}+y(1-y)\right) \right] \\ \quad +\delta (1-y)\left[ \left( \frac{11C_A-4 n_f T_R}{3}\right) -2C_A\ln (|1-\kappa ^2|)\right] ,\\ {\mathcal {P}}_{2, gg}^{+,[0]}(y,\kappa ) = 2C_A\Bigg [\frac{2(1-\kappa )(1+y^2)}{(1-\kappa ^2y^2)^2}\\ \quad +\frac{\kappa ^2(1+y)}{1-\kappa ^2y^2}+\frac{1-\kappa ^2}{1-\kappa ^2y^2}\left( 2-\frac{1}{\kappa }-\frac{1}{1+y}\right) -\left( \frac{1}{1-y}\right) _{++}\Bigg ] . \end{array}\right. \nonumber \\ \end{aligned}$$

(39)

In the expressions above, two kinds of distributions are present. The first is the familiar $+$-distribution (with round brackets) that only appears in the ${\mathcal {P}}_1$ terms (and thus in the DGLAP region) and is defined upon integration with a test non-singular function f as

$$\begin{aligned}&\int _x^1{\mathrm{d}}y\left( \frac{1}{1-y}\right) _+f(y) \nonumber \\&\quad = \int _x^1{\mathrm{d}}y\frac{f(y)-f(1)}{1-y} + f(1)\ln (1-x). \end{aligned}$$

(40)

The $+$-prescription is a consequence of the cancellation of soft divergences between real and virtual diagrams and emerges thanks to the divergent integral in Eq. (19) [39]. The second distribution is the $++$-distribution that only appears in the ${\mathcal {P}}_2$ terms. This distribution is meant to provide a numerically amenable implementation of the Cauchy principal-value distribution for integrals of the following kind:

$$\begin{aligned} I=\int _x^\infty {\mathrm{d}}y\,\frac{f(y)}{1-y}. \end{aligned}$$

(41)

If one subtracts and adds back the divergence at $y=1$, i.e.

$$\begin{aligned} f(1)\int _0^1\frac{{\mathrm{d}}y}{1-y}, \end{aligned}$$

(42)

one can rearrange the integral I as follows:

$$\begin{aligned} I= & {} \int _x^\infty \frac{{\mathrm{d}}y}{1-y}\left[ f(y)-f(1) \left( 1+\theta (y-1)\frac{1-y}{y}\right) \right] \nonumber \\&+f(1)\ln (1-x)\equiv \int _x^\infty {\mathrm{d}}y\left( \frac{1}{1-y}\right) _{++}f(y), \end{aligned}$$

(43)

which effectively defines the $++$-distribution. The advantage of this rearrangement is that the integrand is free of the divergence at $y=1$, making the numerical computation easier. Interestingly, the $++$-distribution reduces to the standard $+$-distribution when the upper integration bound is 1 rather than infinity. In this sense, the $++$-distribution generalises the $+$-distribution to integrals in the ERBL region.

3 Properties of the evolution kernels

In the previous section we provided a thorough derivation of the leading-order evolution equations for unpolarised GPDs, providing explicit expressions for the evolution kernels. In this section, we analyse these kernels in detail, highlighting some prominent properties.

3.1 The DGLAP limit

One of the most important requirements for the GPD evolution equations is that they reduce to the DGLAP evolution equations [49,50,51] in the forward limit $\xi \rightarrow 0$. As already mentioned, the decomposition in Eq. (32) nicely isolates the DGLAP contribution to the evolution kernels into the ${\mathcal {P}}_1$ functions, causing the ERBL contribution embedded in ${\mathcal {P}}_2$ to automatically drop out for $\xi \rightarrow 0$. Therefore, to ensure that our GPD evolution tends to the DGLAP, it is enough to show that the forward limit of the ${\mathcal {P}}_1$ functions coincides with the one-loop DGLAP splitting functions. This is easily done by taking the limit for $\kappa \rightarrow 0$ of the expressions given in Eqs. (35)–(39):

$$\begin{aligned} \lim _{\kappa \rightarrow 0}{\mathcal {P}}_{1}^{-,[0]}(y,\kappa )= & {} 2C_F\left[ \frac{y^2+1}{(1-y)_+}+\frac{3}{2}\delta (1-y)\right] ,\nonumber \\ \lim _{\kappa \rightarrow 0}{\mathcal {P}}_{1, qq}^{+,[0]}(y,\kappa )= & {} \lim _{\kappa \rightarrow 0}{\mathcal {P}}_{1}^{-,[0]}(y,\kappa ),\nonumber \\ \lim _{\kappa \rightarrow 0}{\mathcal {P}}_{1, qg}^{+,[0]}(y,\kappa )= & {} 4n_f T_R\left[ y^2+(1-y)^2\right] , \nonumber \\ \lim _{\kappa \rightarrow 0} {\mathcal {P}}_{1, gq}^{+,[0]}(y,\kappa )= & {} 2C_F\left[ \frac{1+(1-y)^2}{y}\right] , \nonumber \\ \lim _{\kappa \rightarrow 0} {\mathcal {P}}_{1, gg}^{+,[0]}(y,\kappa )= & {} 4C_A\left[ \frac{y}{(1-y)_+}+\frac{1-y}{y}+y(1-y)\right] \nonumber \\&+ \delta (1-y)\left[ \left( \frac{11C_A-4 n_f T_R}{3}\right) \right] , \nonumber \\ \end{aligned}$$

(44)

that indeed are equal to the one-loop DGLAP splitting functions (see e.g. Ref. [52]).

3.2 The ERBL limit

Sound GPD evolution equations also need to reproduce the ERBL evolution equations [38, 53] that govern the evolution of DAs in the $\xi \rightarrow 1$ limit. To prove that this is the case, it is useful to rearrange Eq. (28) as follows:

$$\begin{aligned}&\frac{{\mathrm{d}}}{{\mathrm{d}}\ln \mu ^2} F^{\pm }(x,\xi ,\mu )\nonumber \\&\quad = \frac{\alpha _s(\mu )}{4\pi }\int _{-1}^1\frac{{\mathrm{d}}y}{|\xi |} {\mathbb {V}}^{\pm ,[0]}\left( \frac{x}{\xi },\frac{y}{\xi }\right) F^{\pm }(y,\xi ,\mu ), \end{aligned}$$

(45)

with

$$\begin{aligned}&\frac{1}{|\xi |}{\mathbb {V}}_{ik}^{+,[0]}\left( \frac{x}{\xi }, \frac{y}{\xi }\right) = \frac{1}{y}\bigg \{\left[ \theta (x-\xi ) \theta (y-x)\right. \nonumber \\&\quad \left. -\theta (-x-\xi ) \theta (x-y)\right] \left[ p_{ik}\left( \frac{x}{y}, \frac{\xi }{x}\right) +p_{ik}\left( \frac{x}{y}, -\frac{\xi }{x}\right) \right] \nonumber \\&\quad + \theta (\xi -x)\theta (x+\xi ) \left[ \theta (y-x) p_{ik}\left( \frac{x}{y}, \frac{\xi }{x}\right) \right. \nonumber \\&\quad \left. -\theta (x-y) p_{ik}\left( \frac{x}{y}, -\frac{\xi }{x}\right) \right] \nonumber \\&\quad + \delta \left( 1-\frac{x}{y}\right) \delta _{ik}2C_i\left[ K_i+\int _\xi ^{x}\frac{{\mathrm{d}}z}{z-x}\right. \nonumber \\&\quad \left. +\int _{-\xi }^{x}\frac{{\mathrm{d}}z}{z-x}\right] \bigg \},\nonumber \\&\frac{1}{|\xi |}{\mathbb {V}}^{-,[0]}\left( \frac{x}{\xi }, \frac{y}{\xi }\right) = \frac{1}{|\xi |} {\mathbb {V}}_{qq}^{+,[0]}\left( \frac{x}{\xi }, \frac{y}{\xi }\right) . \end{aligned}$$

(46)

For the moment, we are again allowing x to be negative. However, the combinations $F^{\pm }$ have a definite behaviour upon sign change of x, that is, $F^{\pm }(-x,\xi ,\mu )=\mp F^{\pm }(x,\xi ,\mu )$ , and therefore the negative branch in x is determined in terms of the positive one. Before taking the limit, it is convenient to introduce the variables t and u defined as

$$\begin{aligned} t = \frac{1}{2}(x+1),\quad \text{ and }\quad u=\frac{1}{2}(y+1), \end{aligned}$$

(47)

spanning the range [0, 1], and to write the ERBL evolution equation in a more conventional form as

$$\begin{aligned} \frac{{\mathrm{d}}}{{\mathrm{d}}\ln \mu ^2} \Phi ^{\pm }(t,\mu )= \frac{\alpha _s(\mu )}{4\pi }\int _{0}^1{\mathrm{d}}u V^{\pm ,[0]}(t,u) \Phi ^{\pm }(u,\mu ),\nonumber \\ \end{aligned}$$

(48)

such that

$$\begin{aligned} \Phi ^{\pm }(t,\mu ) = \lim _{\xi \rightarrow 1}F^{\pm }(2t-1,\xi ,\mu ), \end{aligned}$$

(49)

and

$$\begin{aligned} V^{\pm ,[0]}(t,u) = \lim _{\xi \rightarrow 1}\frac{1}{|\xi |}{\mathbb {V}}^{\pm ,[0]}\left( \frac{2t-1}{\xi }, \frac{2u-1}{\xi }\right) . \end{aligned}$$

(50)

For the non-singlet anomalous dimension, we find

$$\begin{aligned} V^{-,[0]}(t,u)= & {} C_F\left\{ \left[ \frac{\theta (u-t)}{u-t}\right] _+ \right. \nonumber \\&\left. +\theta (u-t)\frac{t-1}{u}-\left[ \frac{\theta (t-u)}{u-t}\right] _+\right. \nonumber \\&\left. -\theta (t-u)\frac{t}{1-u} + \frac{3}{2}\delta \left( u-t\right) \right\} , \end{aligned}$$

(51)

which reproduces the results of Refs. [19, 38], where the $+$-prescription (with square brackets) here has to be interpreted as

$$\begin{aligned}{}[f(t,u)]_+=f(t,u) - \delta (u-t)\int _0^1{\mathrm{d}}t\, f(t,u), \end{aligned}$$

(52)

which generalises the definition in Eq. (40) to a two-variable function with support $t,u\in [0,1]$ with a single pole at $t=u$. One can also check that the integral of $V^{-,[0]}$ over t vanishes:

$$\begin{aligned} \int _0^1{\mathrm{d}}t\,V^{-,[0]}(t,u) = 0, \end{aligned}$$

(53)

which allows us to write it in a fully $+$-prescribed form as:

$$\begin{aligned} V^{-,[0]}(t,u)= & {} C_F\left[ \theta (u-t)\left( \frac{t-1}{u}+\frac{1}{u-t}\right) \right. \nonumber \\&\left. -\theta (t-u)\left( \frac{t}{1-u}+\frac{1}{u-t}\right) \right] _+. \end{aligned}$$

(54)

This property was also explicitly derived in Ref. [54], and it was argued that it must hold for symmetry reasons. For the singlet sector instead we find

$$\begin{aligned} V_{qq}^{+,[0]}(t,u)= & {} V^{-,[0]}(t,u),\nonumber \\ V_{qg}^{+,[0]}(t,u)= & {} T_R\frac{2u-1}{2u(u-1)}\left[ \theta (u-t)\frac{t(u-2t+1)}{u}\right. \nonumber \\&\left. +\theta (t-u)\frac{(t-1)(u-2t)}{u-1}\right] ,\nonumber \\ V_{gq}^{+,[0]}(t,u)= & {} \frac{2C_F}{2t-1}\left[ \theta (u-t)\frac{t(2u-t)}{u}\right. \nonumber \\&\left. +\theta (t-u)\frac{(t-1)(2t-t-1)}{u-1}\right] ,\nonumber \\ V_{gg}^{+,[0]}(t,u)= & {} C_A\frac{t(t-1)(2u-1)}{u(u-1)(2t-1)}\Bigg [\frac{1}{u-t}-\theta (u-t)\nonumber \\&\times \left( 1-\frac{2t^2+2u^2-2t-2u+1}{2u(t-1)(2t-1)^2}\right) \nonumber \\&+\theta (t-u)\left( 1-\frac{2t^2+2u^2-2t-2u+1}{2t(u-1)(2t-1)^2}\right) \Bigg ].\nonumber \\ \end{aligned}$$

(55)

We could not find any reference reporting the explicit ERBL singlet kernels to compare our results with.

3.3 Spurious divergences and continuity of GPDs at $x=\xi$

All the expressions for the GPD evolution kernels given in Eqs. (35)–(39) are affected by a non-integrable singularity at $y=\kappa ^{-1}$ denoted by the dot-dashed line in Fig. 2. These singularities may potentially spoil the convergence of the integral in the r.h.s. of Eq. (28), but fortunately they cancel between the ${\mathcal {P}}_1$ and ${\mathcal {P}}_2$ contributions to the evolution kernels. As a matter of fact, they appear in the region $\kappa >1$ in which both ${\mathcal {P}}_1$ and ${\mathcal {P}}_2$ contribute. In addition, for each single kernel, the coefficient of the divergence of ${\mathcal {P}}_1$ is equal in absolute value but opposite in sign w.r.t. that of ${\mathcal {P}}_2$, so that they finally cancel out, yielding a convergent integral. The value of the coefficient of the divergences can be explicitly computed by taking the appropriate limits. For the non-singlet kernels, ${\mathcal {P}}_1^{-,[0]}$ and ${\mathcal {P}}_2^{-,[0]}$, we find

$$\begin{aligned}&\lim _{y\rightarrow \kappa ^{-1}} (1-\kappa ^2y^2) {\mathcal {P}}_1^{-,[0]}(y,\kappa ) \nonumber \\&\quad = - \lim _{y\rightarrow \kappa ^{-1}} (1-\kappa ^2y^2) {\mathcal {P}}_2^{-,[0]}(y,\kappa ) = -2 C_F \frac{1+\kappa }{\kappa },\nonumber \\ \end{aligned}$$

(56)

while for the singlet kernels we find:

$$\begin{aligned}&\lim _{y\rightarrow \kappa ^{-1}} (1-\kappa ^2y^2) {\mathcal {P}}_{1, qq}^{+,[0]}(y,\kappa ) \nonumber \\&\quad = - \lim _{y\rightarrow \kappa ^{-1}} (1-\kappa ^2y^2) {\mathcal {P}}_{2, qq}^{+,[0]}(y,\kappa ) = -2C_F\frac{1+\kappa }{\kappa },\nonumber \\&\lim _{y\rightarrow \kappa ^{-1}} (1-\kappa ^2y^2)^2 {\mathcal {P}}_{1, qg}^{+,[0]}(y,\kappa )\nonumber \\&\quad = - \lim _{y\rightarrow \kappa ^{-1}} (1-\kappa ^2y^2)^2 {\mathcal {P}}_{2, qg}^{+,[0]}(y,\kappa ) = \frac{8 n_f T_R(1-\kappa )}{\kappa },\nonumber \\&\lim _{y\rightarrow \kappa ^{-1}} (1-\kappa ^2y^2) {\mathcal {P}}_{1, gq}^{+,[0]}(y,\kappa ) \nonumber \\&\quad = - \lim _{y\rightarrow \kappa ^{-1}} (1-\kappa ^2y^2) {\mathcal {P}}_{2, gq}^{+,[0]}(y,\kappa ) = 2C_F\frac{(1-\kappa )^2}{\kappa },\nonumber \\&\lim _{y\rightarrow \kappa ^{-1}} (1-\kappa ^2y^2)^2 {\mathcal {P}}_{1, gg}^{+,[0]}(y,\kappa ) \nonumber \\&\quad = - \lim _{y\rightarrow \kappa ^{-1}} (1-\kappa ^2y^2)^2 {\mathcal {P}}_{2, gg}^{+,[0]}(y,\kappa )\nonumber \\&\quad = 4C_A\frac{(\kappa -1)(\kappa ^2+1)}{\kappa ^2}. \end{aligned}$$

(57)

Importantly, all the coefficients above are finite at $\kappa =1$, i.e. at the crossover point $x=\xi$ between the DGLAP and ERBL regions. This is a requisite to ensure that GPDs remain finite at the crossover point upon evolution. The continuity of GPDs at the crossing point is finally ensured by the following additional property:⁶

$$\begin{aligned} {\mathcal {P}}_2^{\pm ,[0]}(y,k)\propto (1-\kappa ). \end{aligned}$$

(58)

Since the ${\mathcal {P}}_2$ functions multiply $\theta (\kappa -1)$, Eq. (58) guarantees a continuous transition from the DGLAP region ($\kappa <1$) into the ERBL region ($\kappa >1$). However, this property does not guarantee that GPDs remain smooth at the crossover point upon evolution. In fact, the very presence of the term proportional to $\theta (\kappa -1)$ in Eq. (32) makes the derivative w.r.t. to x of the kernels discontinuous at $x = \xi$. Therefore, the evolution is expected to generate a cusp at $x=\xi$.

3.4 Sum rules

A very important aspect of GPDs is that their first two Mellin moments can be connected to physical quantities. In order to exemplify the discussion, let us first consider the forward limit of GPDs, i.e. PDFs. It is well known that PDFs must obey the so-called valence (or counting) and momentum sum rules. The valence sum rule ensures the conservation of the flavour quantum numbers and reads

$$\begin{aligned}&\int _0^1{\mathrm{d}}x \left[ f_{q/H}(x,\mu )-f_{{\overline{q}}/H}(x,\mu )\right] \nonumber \\&\quad =\int _0^1{\mathrm{d}}x f^-(x,\mu ) = c_q, \end{aligned}$$

(59)

where the $c_q$s are constants depending on the valence structure of the hadron H (for example for the proton $c_u=2$, $c_d=1$, and $c_q=0$ for all other flavours). The momentum sum rule guarantees that the total momentum carried by all partons equals the momentum of the parent hadron and reads

$$\begin{aligned}&\int _0^1{\mathrm{d}}x\,x\left[ \sum _{q}(f_{q/H}(x,\mu ) +f_{{\overline{q}}/H}(x,\mu ))+f_{g/H}(x,\mu )\right] \nonumber \\&\quad = \int _0^1{\mathrm{d}}x\,x\left[ f^{+}(x,\mu )+f_{g/H}(x,\mu )\right] = 1. \end{aligned}$$

(60)

The fact that both Eqs. (59) and (60) are independent of the factorisation scale $\mu$ implies a set of constraints on the DGLAP splitting functions. Specifically, denoting with $P^{\pm ,[n]}$ the $(n+1)$-loop contribution to the singlet and non-singlet splitting functions, the valence sum rule implies

$$\begin{aligned} \int _0^1{\mathrm{d}}x P^{-,[n]}(x) = 0, \end{aligned}$$

(61)

while the momentum sum rule implies

$$\begin{aligned}&\int _0^1{\mathrm{d}}x \,x\left[ P_{qq}^{+,[n]}(x)+P_{gq}^{+,[n]}(x)\right] = 0,\nonumber \\&\int _0^1{\mathrm{d}}x \,x\left[ P_{qg}^{+,[n]}(x)+P_{gg}^{+,[n]}(x)\right] = 0, \end{aligned}$$

(62)

that must hold for any n.

It turns out that the GPD evolution kernels must also fulfil similar relations that generalise those for the DGLAP splitting functions. The generalisation of the valence sum rule follows from the fact that the integral of a non-singlet GPD is

$$\begin{aligned} \int _0^1{\mathrm{d}}x F^-(x,\xi ,\mu ) = G, \end{aligned}$$

(63)

where G is an observable (Dirac or Pauli) elastic form factor that cannot depend on $\mu$.⁷ Therefore, one can follow the same reasoning applied to the DGLAP splitting function to obtain the following order-by-order constraint on the non-singlet GPD evolution kernels:

$$\begin{aligned} \int _0^1{\mathrm{d}}z\,{\mathcal {P}}_1^{-,[n]}\left( z,\frac{\xi }{yz}\right) + \int _0^{\xi /y} {\mathrm{d}}z\, {\mathcal {P}}_2^{-,[n]}\left( z,\frac{\xi }{yz}\right) =0. \nonumber \\ \end{aligned}$$

(64)

Note that for $\xi \rightarrow 0$, the equality above reduces to Eq. (61). It is interesting to verify Eq. (64) plugging in the explicit one-loop expressions for ${\mathcal {P}}_1^{-,[0]}$ and ${\mathcal {P}}_2^{-,[0]}$ given in Eq. (35). One finds that

$$\begin{aligned}&\int _0^1{\mathrm{d}}z\,{\mathcal {P}}_1^{-,[0]}\left( z,\frac{\xi }{yz}\right) \nonumber \\&\quad =-2C_F\left[ \frac{3}{2}\frac{\xi ^2}{\xi ^2-y^2}+ \ln \left( \left| 1-\frac{\xi ^2}{y^2}\right| \right) \right] , \end{aligned}$$

(65)

which correctly tends to zero as $\xi \rightarrow 0$, and

$$\begin{aligned}&\int _0^{\xi /y} {\mathrm{d}}z\, {\mathcal {P}}_2^{-,[0]}\left( z,\frac{\xi }{yz}\right) \nonumber \\&\quad =2C_F\left[ \frac{3}{2}\frac{\xi ^2}{\xi ^2-y^2}+ \ln \left( \left| 1-\frac{\xi ^2}{y^2}\right| \right) \right] , \end{aligned}$$

(66)

such that Eq. (64) is indeed fulfilled.

Now we move to considering the generalisation of the momentum sum rule. To do so, we use the property of polynomiality of GPDs, given in Eq. (99) below, to write⁸

$$\begin{aligned} \int _0^1{\mathrm{d}}x\,xF_{q(g)}^+(x,\xi ,\mu ) = A_{q(g)}^{F}(\mu )+\xi ^2 D_{q(g)}^{F} (\mu ). \end{aligned}$$

(67)

However, it is well known that unpolarised helicity-conserving (H) and helicity-flip (E) GPDs have the same D-term but with opposite sign [6], i.e. $D_{q(g)}^{H} (\mu )= -D_{q(g)}^{E}$. Therefore, if we assume for the moment that $F=H+E$, the $\xi$-dependent term cancels out. In addition, Ji’s sum rule [3] ensures that the sum $A_{q}^{F}+A_{g}^{F}$ has to be independent of the factorisation scale because it is related to the physically observable total angular momentum of the hadron. Therefore, one finally has

$$\begin{aligned} \int _0^1{\mathrm{d}}x\,x\left[ F_{q}^+(x,\xi ,\mu )+F_{g}^+(x,\xi ,\mu )\right] = \text{ constant }. \end{aligned}$$

(68)

Since H and E obey the same evolution equations, so does their sum. This allows us to take the derivative with respect to $\ln \mu ^2$ of both sides of the equation above and use the evolution equations to obtain the following order-by-order constraints on the GPD evolution kernels:

$$\begin{aligned}&\int _0^1{\mathrm{d}}z\,z\left[ {\mathcal {P}}_{1, qq}^{+,[n]}\left( z,\frac{\xi }{yz}\right) +{\mathcal {P}}_{1, gq}^{+,[n]}\left( z,\frac{\xi }{yz}\right) \right] \nonumber \\&\quad +\int _0^{\xi /y} {\mathrm{d}}z\, z\left[ {\mathcal {P}}_{2, qq}^{+,[n]}\left( z,\frac{\xi }{yz}\right) +{\mathcal {P}}_{2, gq}^{+,[n]}\left( z,\frac{\xi }{yz}\right) \right] =0,\nonumber \\&\int _0^1{\mathrm{d}}z\,z\left[ {\mathcal {P}}_{1, qg}^{+,[n]}\left( z,\frac{\xi }{yz}\right) +{\mathcal {P}}_{1, gg}^{+,[n]}\left( z,\frac{\xi }{yz}\right) \right] \nonumber \\&\quad + \int _0^{\xi /y} {\mathrm{d}}z\, z\left[ {\mathcal {P}}_{2, qg}^{+,[n]}\left( z,\frac{\xi }{yz}\right) +{\mathcal {P}}_{2, gg}^{+,[n]}\left( z,\frac{\xi }{yz}\right) \right] =0. \nonumber \\ \end{aligned}$$

(69)

As in the case of the valence sum rule, these relations reduce to Eq. (62) in the forward limit $\xi \rightarrow 0$. We now verify that the one-loop splitting functions in Eqs. (36)–(39) do fulfil the equalities in Eq. (69). The explicit computation of the integrals gives

$$\begin{aligned}&\int _0^1{\mathrm{d}}z\,z\left[ {\mathcal {P}}^{+,[0]}_{1, qq}\left( z,\frac{\xi }{yz}\right) +{\mathcal {P}}^{+,[0]}_{1, gq}\left( z,\frac{\xi }{yz}\right) \right] \nonumber \\&\quad =-2C_F\left[ \frac{1}{2}\frac{\xi ^2}{y^2-\xi ^2}+ \ln \left( \left| 1-\frac{\xi ^2}{y^2}\right| \right) \right] ,\nonumber \\&\int _0^{\xi /y} {\mathrm{d}}z\, z\left[ {\mathcal {P}}^{+,[0]}_{2, qq}\left( z,\frac{\xi }{yz}\right) +{\mathcal {P}}^{+,[0]}_{2, gq}\left( z,\frac{\xi }{yz}\right) \right] \nonumber \\&\quad =2C_F\left[ \frac{1}{2}\frac{\xi ^2}{y^2-\xi ^2}+ \ln \left( \left| 1-\frac{\xi ^2}{y^2}\right| \right) \right] , \end{aligned}$$

(70)

and

(71)

which evidently cancel pairwise so that the equalities in Eq. (69) are satisfied. In addition, they all tend to zero, as $\xi \rightarrow 0$ as required by Eq. (62).

We finally point out that the constraints in Eqs. (64) and (69) can be used to simplify the perturbative calculation of the evolution kernels in that they allow one to determine the contribution due to virtual diagrams by knowing the real ones. To be more specific, virtual diagrams give rise to contributions proportional to $\delta (1-y)$ that are naturally associated to ${\mathcal {P}}_1$ such that, order by order in $\alpha _s$, it can be decomposed as

$$\begin{aligned} {\mathcal {P}}_1^{\pm ,[n]}(y,\kappa )= & {} {\mathcal {P}}_1^{\mathrm{real},\pm ,[n]}(y,\kappa )\nonumber \\&-\delta (1-y) {\mathcal {P}}_1^{\mathrm{virtual},\pm ,[n]}(\kappa ). \end{aligned}$$

(72)

Conversely, ${\mathcal {P}}_2$ only contains real-diagram contributions:

$$\begin{aligned} {\mathcal {P}}_2^{\pm ,[n]}(y,\kappa )={\mathcal {P}}_2^{\mathrm{real},\pm ,[n]}(y,\kappa ). \end{aligned}$$

(73)

Taking as an example Eq. (64), the consequence of this decomposition is that

(74)

making it unnecessary to explicitly compute the virtual-diagram contributions. Of course, the two equalities in Eq. (69) also have to be simultaneously fulfilled. Since by construction only ${\mathcal {P}}^-$ and the diagonal terms of ${\mathcal {P}}^+$, i.e. ${\mathcal {P}}_{qq}^+$ and ${\mathcal {P}}_{gg}^+$, can get virtual corrections with the additional constraint ${\mathcal {P}}^{\mathrm{virtual},-,[n]}={\mathcal {P}}_{qq}^{\mathrm{virtual},+,[n]}$, at each order in perturbation theory there are two virtual contributions to be determined. On the other hand, Eqs. (64) and (69) provide us with a set of three constraints. Consequently, these equalities not only give us access to the virtual corrections, but also provide a strong check of the calculation of the real contributions. However, we point out that we have explicitly computed the one-loop virtual diagrams, verifying that the resulting contribution agrees with the calculation obtained by means of the sum rules. In Appendix B, we present this check for the case of ${{\mathcal {P}}_{q/q}^{[0]}}$.

3.5 Conformal moments

In this section, we consider the so-called conformal moments of GPDs which in the non-singlet case are defined as [6]

$$\begin{aligned} {\mathcal {C}}_n^-(\xi ,\mu ) = \xi ^{n}\int _{-1}^{1}{\mathrm{d}}x\,C_n^{(3/2)}\left( \frac{x}{\xi }\right) F^{-}(x,\xi ,\mu ), \end{aligned}$$

(75)

where $C_n^{(3/2)}$ are Gegenbauer polynomials of rank 3/2 and degree n (with n even). The choice of these specific moments (and thus the underlying local conformal operators) comes from the fact that they do not mix under renormalisation at one loop [55]. First we highlight the consequences of this property and then sketch a way to prove it.

Multiplying Eq. (45) by $\xi ^{n}C_n^{(3/2)}\left( x/\xi \right)$ and integrating over x between $-1$ and 1 yields

$$\begin{aligned} \frac{{\mathrm{d}} {\mathcal {C}}_n^-(\xi , \mu )}{{\mathrm{d}}\ln \mu ^2}= & {} \frac{\alpha _s(\mu )}{4\pi }\xi ^{n}\int _{-1}^1 {\mathrm{d}}y F^{-}(y,\xi ,\mu )\nonumber \\&\times \int _{-1}^{1}\frac{{\mathrm{d}}x}{|\xi |}\,C_n^{(3/2)}\left( \frac{x}{\xi }\right) {\mathbb {V}}^{-,[0]}\left( \frac{x}{\xi },\frac{y}{\xi }\right) . \end{aligned}$$

(76)

In the absence of mixing, the conformal moments of the non-singlet GPD obey the following equality:

$$\begin{aligned}&\int _{-1}^1\frac{{\mathrm{d}}x}{\xi }\,C_n^{(3/2)}\left( \frac{x}{\xi }\right) {\mathbb {V}}^{-,[0]}\left( \frac{x}{\xi },\frac{y}{\xi }\right) \nonumber \\&\quad ={\mathcal {V}}_{n}^{-,[0]}(\xi )C_n^{(3/2)}\left( \frac{y}{\xi }\right) , \end{aligned}$$

(77)

where the anomalous dimension of the associated local conformal operator is labelled by ${\mathcal {V}}_{n}^{-,[0]}$. Looking at Eq. (77), one may think that ${\mathcal {V}}_{n}^{-,[0]}$ generally depends on $\xi$. However, in the $\overline{\text{ MS }}$ scheme, anomalous dimensions of local operators are fixed independently of incoming or outgoing states. Thus, as we will see, one should expect ${\mathcal {V}}_{n}^{-,[0]}$ to be $\xi$-independent. If Eq. (77) held true, Eq. (76) would then become

$$\begin{aligned} \frac{{\mathrm{d}} {\mathcal {C}}_n^-(\xi ,\mu )}{{\mathrm{d}}\ln \mu ^2} =\frac{\alpha _s(\mu )}{4\pi }{\mathcal {V}}_{n}^{-,[0]}(\xi ){\mathcal {C}}_n^-(\xi ,\mu ), \end{aligned}$$

(78)

making explicit the fact that GPD conformal moments evolve multiplicatively. An interesting indication that this is true and also that the anomalous dimension ${\mathcal {V}}_{n}^{-,[0]}$ does not depend on $\xi$ comes from considering the DGLAP ($\xi \rightarrow 0$) and the ERBL ($\xi \rightarrow 1$) limits of Eq. (78).

Let us start with the DGLAP limit. For $\xi \rightarrow 0$, conformal moments coincide with Mellin moments up to a multiplicative numerical factor. This can be seen by observing that Gegenbauer polynomials are such that

$$\begin{aligned} \lim _{\xi \rightarrow 0} \xi ^{n}C_n^{(3/2)}\left( \frac{x}{\xi }\right) = \frac{(2n+1)!}{2^n(n!)^2}x^{n}. \end{aligned}$$

(79)

Therefore, the conformal moments of the non-singlet distribution in the forward limit become

$$\begin{aligned} \lim _{\xi \rightarrow 0}{\mathcal {C}}_n^-(\xi ,\mu ) = \frac{(2n+1)!}{2^n(n!)^2}[1+(-1)^n]f_{n+1}^{-}(\mu ), \end{aligned}$$

(80)

where Mellin moments of the forward distribution (PDF) are defined as

$$\begin{aligned} f_n^{-}(\mu ) = \lim _{\xi \rightarrow 0} \int _0^1{\mathrm{d}}x\,x^{n-1}F^{-}(x,\xi ,\mu ), \end{aligned}$$

(81)

and are known to diagonalise the DGLAP equation to all orders. Using Eq. (79) and the fact that

$$\begin{aligned}&\lim _{\xi \rightarrow 0} \frac{1}{|\xi |}{\mathbb {V}}^{-,[0]}\left( \frac{x}{\xi }, \frac{y}{\xi }\right) \nonumber \\&\quad = \left[ \theta (x)\theta (y-x)-\theta (-x)\theta (x-y)\right] \nonumber \\&\qquad \times \frac{1}{|y|} P^{-,[0]}\left( \frac{x}{y}\right) , \end{aligned}$$

(82)

which derives from Eq. (46), one finally finds that [52]

$$\begin{aligned}&\lim _{\xi \rightarrow 0} {\mathcal {V}}_{n}^{-,[0]}(\xi ) = P_{n+1}^{-,[0]}\nonumber \\&\quad = 2C_F\left[ \frac{3}{2}+\frac{1}{(n+1)(n+2)}-2\sum _{k=1}^{n+1}\frac{1}{k}\right] . \end{aligned}$$

(83)

In the ERBL limit, the conformal moments yield this time [38]:

$$\begin{aligned}&\int _{-1}^{1}{\mathrm{d}}x\,C_n^{(3/2)}\left( x\right) V_\mathrm{NS}^{-,[0]}\left( x,y\right) \nonumber \\&\quad =2C_F\left[ \frac{3}{2}+\frac{1}{(n+1)(n+2)}-2\sum _{k=1}^{n+1}\frac{1}{k}\right] C_n^{(3/2)}\left( y\right) . \nonumber \\ \end{aligned}$$

(84)

Comparing Eq. (84) with Eq. (83), one immediately sees that conformal moments do not mix either in DGLAP or in ERBL limits and that ${\mathcal {V}}_{n}$ is the same in both cases. In order to explicitly prove the general case, we need to compute Eq. (77) for a generic value of $\xi$ and for all n. To do so, we use the decomposition in Eq. (46) with the explicit form of the $p_{qq}$ function given in Eq. (20), which yields

$$\begin{aligned}&\int _{-1}^1\frac{{\mathrm{d}}x}{|\xi |}\,C_n^{(3/2)}\left( \frac{x}{\xi }\right) {\mathbb {V}}^{-,[0]}\left( \frac{x}{\xi },\frac{y}{\xi }\right) \nonumber \\&\quad = 2C_F \left\{ \frac{3}{2}C_n^{(3/2)}\left( \frac{y}{\xi }\right) \right. \nonumber \\&\qquad -\frac{1}{2}\int _{\xi }^{y}{\mathrm{d}}x\left[ \frac{x+\xi }{\xi (y-\xi )} C_n^{(3/2)}\left( \frac{x}{\xi }\right) \right. \nonumber \\&\qquad \left. -2\frac{C_n^{(3/2)}\left( x/\xi \right) -C_n^{(3/2)}\left( y/\xi \right) }{y-x}\right] \nonumber \\&\qquad +\frac{1}{2}\int _{-\xi }^{y}{\mathrm{d}}x\left[ \frac{x-\xi }{\xi (y+\xi )} C_n^{(3/2)}\left( \frac{x}{\xi }\right) \right. \nonumber \\&\qquad \left. \left. +2\frac{C_n^{(3/2)} \left( x/\xi \right) -C_n^{(3/2)}\left( y/\xi \right) }{y-x}\right] \right\} . \end{aligned}$$

(85)

The explicit calculation is presented in Appendix C and indeed confirms that

$$\begin{aligned}&\int _{-1}^1\frac{{\mathrm{d}}x}{|\xi |}\,C_n^{(3/2)}\left( \frac{x}{\xi }\right) {\mathbb {V}}^{-,[0]}\left( \frac{x}{\xi },\frac{y}{\xi }\right) \nonumber \\&\quad =2C_F\left[ \frac{3}{2}+\frac{1}{(n+1)(n+2)}-2\sum _{k=1}^{n+1}\frac{1}{k}\right] C_n^{(3/2)}\left( \frac{y}{\xi }\right) . \nonumber \\ \end{aligned}$$

(86)

A similar calculation for the singlet sector can be achieved in a similar fashion.

3.6 Comparison with other calculations

In this section, we compare our calculation with previous results for the one-loop GPD unpolarised evolution kernels. We will show that our calculation agrees with those already present in the literature. For definiteness, we will concentrate on the non-singlet evolution kernel ${\mathcal {P}}^{^-,[0]}$, but we have checked that agreement is also found for the other one-loop evolution kernels.

We start with the computation by Ji presented in Ref. [2]. In that paper, the GPD evolution equations are written in the DGLAP and in the ERBL regions separately. To find the correspondence, we use the evolution equation in the form given in Eq. (45). In the DGLAP region ($x>\xi$), the evolution kernel reduces to

$$\begin{aligned}&\frac{1}{|\xi |}{\mathbb {V}}^{-,[0]}\left( \frac{x}{\xi }, \frac{1}{\xi }\right) \nonumber \\&\quad = \theta (1-x) \left[ p_{qq}\left( x, \frac{\xi }{x}\right) +p_{qq}\left( x, -\frac{\xi }{x}\right) \right] \nonumber \\&\qquad + \delta \left( 1-x\right) 2C_F\left[ \frac{3}{2}+\int _\xi ^{x}\frac{{\mathrm{d}}z}{z-x}+\int _{-\xi }^{x} \frac{{\mathrm{d}}z}{z-x}\right] \nonumber \\&\quad = \theta (1-x)2C_F \frac{1+x^2-2\xi ^2}{(1-x)(1-\xi ^2)}\nonumber \\&\qquad + \delta (1-x) 2C_F \left[ \frac{3}{2}+ \int _{\xi }^x\frac{{\mathrm{d}}z}{z-x}+\int _{-\xi }^x\frac{{\mathrm{d}}z}{z-x}\right] . \end{aligned}$$

(87)

Considering the shift $\xi \rightarrow \xi /2$ due to a different definition of the external momenta and an overall factor of 2 to the fact that we are using $\alpha _s/(4\pi )$ rather than $\alpha _s/(2\pi )$ as an expansion parameter, we exactly reproduce the results given in Eqs. (15)–(17) of Ref. [2]. In the ERBL region ($x<\xi$) the evolution kernel reads

$$\begin{aligned}&\frac{1}{|\xi |}{\mathbb {V}}^{-,[0]}\left( \frac{x}{\xi }, \frac{1}{\xi }\right) = \left[ \theta (1-x) p_{qq}\left( x, \frac{\xi }{x}\right) \right. \nonumber \\&\qquad \left. -\theta (x-1) p_{qq}\left( x, -\frac{\xi }{x}\right) \right] \nonumber \\&\qquad + \delta \left( 1-x\right) 2C_F\left[ \frac{3}{2}+\int _\xi ^{x}\frac{{\mathrm{d}}z}{z-x}+ \int _{-\xi }^{x}\frac{{\mathrm{d}}z}{z-x}\right] \nonumber \\&\quad = C_F \left[ \theta (1-x) \frac{x+\xi }{\xi (1+\xi )}\left( 1+\frac{2\xi }{1-x}\right) \right. \nonumber \\&\qquad \left. -\theta (x-1) \frac{x-\xi }{\xi (1-\xi )}\left( 1-\frac{2\xi }{1-x}\right) \right] \nonumber \\&\qquad + \delta \left( 1-x\right) 2C_F\left[ \frac{3}{2}+\int _\xi ^{x}\frac{{\mathrm{d}}z}{z-x}+\int _{-\xi }^{x} \frac{{\mathrm{d}}z}{z-x}\right] , \end{aligned}$$

(88)

which agrees with Eqs. (18)–(19) of Ref. [2].

We now compare our calculation with that of Ref. [56], which is also reported in Eq. (101) of Ref.  [6]. We again use the form of the evolution given in Eq. (45) and, setting $\xi =1$ but allowing |x| and |y| to be larger than 1, the evolution kernel becomes

$$\begin{aligned}&{\mathbb {V}}^{-,[0]}\left( x,y\right) = \rho (x,y)C_F \frac{1+x}{1+y}\left( 1+\frac{2}{y-x}\right) +\left( \begin{array}{c} x\rightarrow -x \\ y\rightarrow -y \end{array}\right) \nonumber \\&\quad + \delta \left( y-x\right) C_F\left[ 3+2\int _1^{x}\frac{{\mathrm{d}}z}{z-x}+2\int _{-1}^{x}\frac{{\mathrm{d}}z}{z-x}\right] , \end{aligned}$$

(89)

with

$$\begin{aligned} \rho (x,y)= & {} \theta (x+1)\theta (y-x)-\theta (-x-1)\theta (x-y) \nonumber \\= & {} \theta \left( \frac{y-x}{1+y}\right) \theta \left( \frac{1+x}{1+y}\right) \text{ sign }(1+y). \end{aligned}$$

(90)

It is easy to verify that

$$\begin{aligned} \int _{-\infty }^{\infty }{\mathrm{d}}x\,{\mathbb {V}}^{-,[0]}\left( x,y\right) = 0. \end{aligned}$$

(91)

Therefore, one can rewrite

$$\begin{aligned}&{\mathbb {V}}^{-,[0]}\left( x,y\right) \nonumber \\&\quad = \left\{ \rho (x,y)C_F \frac{1+x}{1+y}\left( 1+\frac{2}{y-x}\right) +\left( \begin{array}{c} x\rightarrow -x \\ y\rightarrow -y \end{array}\right) \right\} _+, \end{aligned}$$

(92)

where the $+$-prescription (with curly brackets) here is defined in a yet different manner and generalises that in Eq. (52) to a two-dimensional function with support $x,y\in {\mathbb {R}}$ and a single pole at $x = y$:

$$\begin{aligned} \{f(x,y)\}_+=f(x,y) - \delta (x-y)\int _{-\infty }^{\infty }{\mathrm{d}}x\, f(x,y). \end{aligned}$$

(93)

This finally allows us to recover the results of Refs. [6, 56].

Finally, we compare our result with that of Ref. [7]. Adopting the notation of that reference, one can show that

$$\begin{aligned} \vartheta _{11}^0(x_1,x_1-y_1)= & {} \frac{2}{\xi +y}\rho \left( \frac{x}{\xi }, \frac{y}{\xi }\right) \quad \text{ and }\quad \nonumber \\ \vartheta _{11}^0(x_2,x_2-y_2)= & {} \frac{2}{\xi -y}\rho \left( -\frac{x}{\xi }, -\frac{y}{\xi }\right) , \end{aligned}$$

(94)

and

$$\begin{aligned}&\vartheta _{111}^0(x_1,-x_2,x_1-y_1) = -\frac{\xi +x}{\xi (\xi +y)}\rho \left( \frac{x}{\xi }, \frac{y}{\xi }\right) \nonumber \\&\quad -\frac{\xi -x}{\xi (\xi -y)}\rho \left( -\frac{x}{\xi }, -\frac{y}{\xi }\right) , \end{aligned}$$

(95)

with $\rho$ given in Eq. (90). This allows us to recast the evolution kernel $K_{(0)}^{qq;V}(x_1,x_2|y_1,y_2)$ given in Eq. (4.42) of Ref. [7] into the following form:

$$\begin{aligned}&K_{(0)}^{qq;V}(x_1,x_2|y_1,y_2) = -\left\{ \rho \left( \frac{x}{\xi }, \frac{y}{\xi }\right) C_F\frac{\xi +x}{\xi +y}\right. \nonumber \\&\quad \times \left. \left( \frac{1}{\xi }+\frac{2}{y-x}\right) +\left( \begin{array}{c} x\rightarrow -x \\ y\rightarrow -y \end{array}\right) \right\} _+. \end{aligned}$$

(96)

Considering that a factor of 2 due to the different expansion parameter ($\alpha _s/(2\pi )$ vs. $\alpha _s/(4\pi )$) is compensated by an opposite factor that comes from the fact that in Ref. [7] the evolution equations are differential w.r.t. to $\ln \mu$ rather than $\ln \mu ^2$, and accounting for a minus sign in the definition of the evolution kernels, this result coincides with Eq. (92), which we have already proven to agree with our result.⁹

4 Numerical results

In Sect. 2, we recast the GPD evolution kernel in a form suitable for a straightforward implementation in the numerical code APFEL++ [33, 34], allowing for robust evaluations and handling of heavy-flavour thresholds. In Sect. 3, we detailed the theoretical properties of this particular form. In this section, we present a series of numerical checks aimed at establishing the validity of our implementation to high numerical accuracy. To the best of our knowledge, this provides the most extensive set of tests of an implementation of GPD evolution equations ever presented in the literature, at least with respect to publicly released codes. Although here we are not concerned with performance and computing speed, our implementation guarantees a fast evaluation of GPD evolution suitable for phenomenological extractions.

4.1 DGLAP limit and skewness dependence

As discussed in Sect. 3.1, in the forward limit, $\xi \rightarrow 0$, our derivation of the GPD evolution equations reproduces the one-loop DGLAP evolution. In the following, we provide numerical evidence for this statement. To do so, we need to evolve a set of distributions defined at some initial scale $\mu _0$ up to a different scale $\mu$ using the solution of Eq. (28). To this end, we use the leading-order PDF set MMHT2014lo68cl [57] through the LHAPDF interface [58] with $\mu _0=1$ GeV. The running of the strong coupling is computed at one loop using $\alpha _s(M_Z)=0.135$, consistently with MMHT2014lo68cl. In addition, the evolution is performed using the variable-flavour-number scheme; i.e. we allow for heavy-quark-threshold crossings during the evolution, with charm and bottom thresholds set to $m_c=1.4$ GeV and $m_b=4.75$ GeV, respectively.

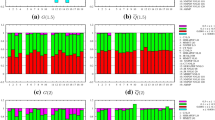
Figure 3 shows the effect of evolving the MMHT2014lo68cl PDF set to $\mu =10$ GeV for different values of $\xi$, including the DGLAP limit $\xi \rightarrow 0$, using the numerical solution of Eq. (28) as implemented in APFEL++. Evolution is probed for x ranging between $10^{-3}$ and 1, relevant for the fixed target (Jefferson Lab, COMPASS) and collider (EIC, EIcC) experiments, while the evolution range spans two orders of magnitude in the hard scale $\mu ^2$, from 1 to 100 $\hbox {GeV}^2$. The top-left plot displays the up-quark non-singlet distribution $F_u^-=F_u-F_{{\overline{u}}}$, the top-right one displays the singlet distribution $F_u^+=F_u+F_{{\overline{u}}}$, and the bottom plot displays the gluon distribution $F_g$. The upper insets show the absolute distributions while the lower ones show the ratio to the DGLAP evolution as delivered by the LHAPDF grid [58]. The first observation is that, as is clear from the bottom insets, our GPD evolution in the $\xi \rightarrow 0$ limit reproduces the DGLAP evolution very accurately. It is also interesting to observe how GPD evolution modifies the shape of the distributions w.r.t. the DGLAP when changing the skewness $\xi$. Differences are sizeable particularly in the ERBL region, $x<\xi$, where the GPD evolution tends to suppress the distributions w.r.t. the DGLAP one. Particularly striking is the singlet sector in which steeply rising low-x distributions are turned into decreasing distributions. In addition, as anticipated in Sect. 3.3, distributions are continuous at the crossing point $x=\xi$ but develop a cusp, although the initial scale distributions are smooth.

Fig. 3

Non-singlet up-quark (upper left) and singlet up-quark (upper right), and gluon (bottom) distributions evolved from $\mu _0=1$ GeV to $\mu =10$ GeV using the GPD evolution equations in Eq. (28) with different values of the skewness $\xi$. Initial-scale distributions are taken from the MMHT2014lo68cl PDF set. To tame the fast rise of gluons at low-x, we weight the distribution with an additional power of x. The lower inset displays the ratio to the DGLAP evolution as delivered by the LHAPDF grid

4.2 ERBL limit

Having ascertained that with the use of our GPD evolution equations the DGLAP limit is recovered, we now turn to check the opposite limit, i.e. the ERBL limit $\xi \rightarrow 1$. To do so, we exploit the fact that functions of this kind

$$\begin{aligned} F_{2n}(x,\mu _0) = (1-x^2)C_{2n}^{(3/2)}(x), \end{aligned}$$

(97)

diagonalise the (non-singlet) leading-order ERBL evolution equation such that they evolve multiplicatively as

$$\begin{aligned} F_{2n}(x,\mu ) =\exp \left[ \frac{P_{2n+1}^{-,[0]}}{4\pi } \int _{\mu _0}^{\mu }{\mathrm{d}}\ln \mu '^2\alpha _s(\mu ')\right] F_{2n}(x,\mu _0), \nonumber \\ \end{aligned}$$

(98)

with anomalous dimensions $P_{n+1}^{-,[0]}$ given in Eq. (83). Figure 4 shows the non-singlet evolution of Eq. (97) with $n=2$ from $\mu _0^2=1$ $\hbox {GeV}^2$ to a number of higher scales $\mu ^2$, up to $\mu ^2=10^{4}$ $\hbox {GeV}^2$, using the numerical solution of Eq. (28) with $\xi =1$. The upper panel displays the absolute distributions including the initial-scale one, while the lower panel displays the ratio to the analytical evolution given in Eq. (98). As is clear from the bottom panel, the agreement between numerical and analytical solutions is excellent,¹⁰ confirming that our implementation of the GPD evolution also gives sound results in the ERBL limit. We could not find other numerical tests of the recovery of the ERBL limit for other public GPD evolution codes in the existing literature.

Fig. 4

Non-singlet leading-order ERBL evolution from $\mu _0=1$ GeV to different values of the final scale $\mu$ of the distribution in Eq. (97) with $n=2$. The upper inset displays the distributions obtained by numerically solving Eq. (28) with $\xi =1$, while the bottom inset shows the ratio to Eq. (98). Note that the curves in the bottom inset overlap almost completely, making them hardly distinguishable

4.3 Polynomiality

GPDs enjoy the so-called polynomiality property that for quarks can be written as

$$\begin{aligned}&\int _0^1 {\mathrm{d}}x\,x^{2n} F_q^{-}(x,\xi ,\mu ) = \sum _{k=0}^{n}A_k(\mu )\xi ^{2k},\quad \text{ and }\quad \nonumber \\&\int _0^1 {\mathrm{d}}x\,x^{2n+1} F_q^{+}(x,\xi ,\mu ) = \sum _{k=0}^{n+1}B_k(\mu )\xi ^{2k}, \end{aligned}$$

(99)

with $F_q^\pm =F_q\pm F_{{\overline{q}}}$. It is important to note that these relations must be valid at any scale $\mu$, implying that GPD evolution must preserve polynomiality. In this section we quantitatively show that this is the case when using the solution of Eq. (28).

Fig. 5

Non-singlet (left) and singlet (right) up-quark Mellin moments for GPDs evolved from $\mu _0=1$ GeV to $\mu =10$ GeV using the GPD evolution equations in Eq. (28) as functions of skewness $\xi$. Initial-scale distributions are taken from the MMHT2014lo68cl PDF set. Each set of points is fitted with the power law predicted by polynomiality

We consider the set-up of Sect. 4.1 in which a set of $\xi$-independent PDFs, which thus trivially obey polynomiality, is evolved from $\mu _0=1$ GeV to $\mu =10$ GeV. In order to check that polynomiality is conserved, we evaluate the integrals in Eq. (99) for the first three moments ($n=0,1,2$) and for different values of $\xi$. We then fit the points thus obtained using the expected power laws in $\xi ^2$. We point out that higher moments can be computed analogously. However, a solid check of polynomiality requires that the number of points in $\xi$ used for the fit be much larger than the degree of the expected polynomial in $\xi ^2$. For this reason we limit the check to the first three moments using ten points in $\xi$: this should be enough to guarantee that the power-law behaviours are accurately reproduced. The result is shown in Fig. 5. The l.h.s. plot displays the first two moments of the up-quark non-singlet distribution $F_u^-$ as functions of $\xi$, while the r.h.s. one shows the same for the up-quark singlet distribution $F_u^+$. The computed values (plain dots) are superimposed on the fitted curves, proving that the expected behaviour is obtained to very good accuracy over the entire range in $\xi \in [0,1]$. Some additional comments are in order. First, the first moment ($n=0$) of the non-singlet distribution $F_u^-$ is not only constant, as expected, but also equal to 2, which reflects the valence sum rule for the up-quark in the proton. Secondly, the first moment ($n=0$) of the singlet distribution $F_u^+$, despite being allowed to depend on $\xi$ through a quadratic term, is also constant. This is because the term proportional to $\xi ^{2n+2}$ in the second equation of Eq. (99) gives rise to the so-called D-term [59] that evolves independently. Since the initial scale distributions do not include any D-term, none is generated by evolution, and thus only the constant term contributes to the first moment of $F_u^+$.

Fig. 6

Leading-order evolution of the second ($n=4$) conformal moment of the non-singlet distribution of the Radyushkin double-distribution ansatz (RDDA) described in the text. The evolution starts from $\mu _0=1$ GeV up to different values of the final scale $\mu$. The upper inset displays the moment as a function of the skewness $\xi$ obtained by numerically solving Eq. (28) and by computing the conformal moment of the final-scale distribution by means of Eq. (75), while the bottom inset shows the ratio to the solution of Eq. (78). As in Fig. 4, the curves in the bottom inset are hardly distinguishable because they all lie on top of each other

4.4 Conformal-space evolution

In Sect. 3.5 we explicitly proved that the one-loop non-singlet evolution kernel computed in this paper is such that the evolution of the GPD conformal moments is diagonal; i.e. each moment evolves multiplicatively with its own kernel. In the following, we show that our implementation of the solution of the evolution equations numerically fulfils this property. To do so, we consider as an initial-scale non-singlet GPD at $\mu _0=1$ GeV the quark GPD $H^q$ given by the Radyushkin double-distribution ansatz (RDDA) [60]:

$$\begin{aligned} H^q(x,\xi ) = \int _\Omega {\text {d}}\beta {\text {d}}\alpha \delta \left( x - \beta - \xi \alpha \right) q(|\beta |) \pi (\beta , \alpha ), \end{aligned}$$

(100)

where $\Omega$ is such that $|\alpha |+|\beta |\le 1$ and

$$\begin{aligned} q(x)&= \frac{35}{32} x^{-1/2} (1-x)^3, \end{aligned}$$

(101)

$$\begin{aligned} \pi (\beta ,\alpha )&= \frac{3}{4} \frac{((1-|\beta |)^2-\alpha ^2)}{(1-|\beta |)^3}. \end{aligned}$$

(102)

This simple ansatz allows us to benchmark our x-space evolution code using a realistic behaviour of the non-singlet GPDs with respect to conformal evolution.

In Fig. 6, we compare the second $(n=4)$ conformal moment, computed by means of Eq. (75), of the RDDA-based model evolved to $\mu =2,5,10,100$ GeV obtained by numerically solving Eq. (28) to the solution of Eq. (78) with the evolution kernel given in Eq. (86). The upper panel of the plot displays the evolved conformal moment as a function of $\xi$ for the different values of $\mu$ computed by solving Eq. (28), while the lower panel shows the ratio to the solution of Eq. (78). It is clear that the agreement between the two evolution methods is excellent over the entire range in $\xi$ considered, validating our implementation in the light of Sect. 3.5.

Before proceeding to comparing our evolution code with another implementation, we emphasise that all the numerical tests performed in Sects. 4.1–4.4 turned out to be very successful. Namely, we found that all the fundamental properties of GPD evolution, including DGLAP and ERBL limits, polynomiality conservation, and equivalence with the conformal-moment approach, are fulfilled to the sub-per-mil level or better. We regard this as a very strong consistency check of our code.

4.5 Comparison with Vinnikov’s code

In this section, we compare the evolution obtained with APFEL++ to that presented in Ref. [27], which in the following will be referred to as “Vinnikov’s code” after its author. Specifically, we use an implementation of Vinnikov’s code available in the PARTONS framework [28]. A limitation of Vinnikov’s code is that it does not implement the variable-flavour-number scheme; i.e. it does not allow one to cross heavy-quark thresholds along the evolution. Therefore, for the comparison, we have used the $n_f=3$ fixed-flavour-number scheme in which three quark flavours (up, down, and strange) are active at all scales. Like APFEL++, Vinnikov’s code can perform GPD evolution only at LO. As initial-scale distributions we have used the model presented in Refs. [61,62,63] which also depends on the momentum transfer t that we set to $t=-0.1$ $\hbox {GeV}^2$. In Fig. 7 we present the comparison for the evolution between $\mu _0=2$ GeV and $\mu =10$ GeV for the GPDs $H_u^-$, $H_u^+$, and $H_g$. The upper panels display the absolute distributions for four different values of the skewness parameter $\xi =10^{-4}, 0.05,0.5,1$ with the solid lines showing the results obtained with Vinnikov’s code and the dashed lines those obtained with APFEL++. The lower panels show the same curves normalised to APFEL++. We observe general very good agreement between the two codes for almost all values of $\xi$ and across the full range in x considered. The only exception is $\xi =1$, for which a disagreement at the percent level for $H_u^-$ (non-singlet sector) and as large as 20% for $H_u^+$ and $H_g$ (singlet sector) is observed. We could not identify the origin of this disagreement, but in view of the reported numerical instabilities of Vinnikov’s code in the large-$\xi$ region [64], we suspect that the results of this code at $\xi =1$ might be affected by numerical inaccuracies. Indeed, we point out that Vinnikov’s code does not allow one to set either $\xi =1$ or $\xi =0$, and the smallest stable value of $\xi$ we could find is $\xi =10^{-4}$. Regarding the large $\xi$ region, in the plots in Fig. 7 we have actually used $\xi =1-\epsilon$ with $\epsilon =10^{-6}$ for both codes. Finally, we found severe numerical instabilities for $0.6\lesssim \xi \lesssim 0.95$. Therefore, we were not able to perform a comparison in this region. This also justifies the need for a new open and maintained evolution code. Moreover, the modular architecture of APFEL++ and PARTONS will facilitate the integration of higher-order corrections to the evolution, while this task would probably require an almost complete rewriting of Vinnikov’s code.

Fig. 7

Comparison between Vinnikov’s code [27] and APFEL++. The evolution is performed at LO in the $n_f=3$ scheme (no threshold crossing) between the scales $\mu _0=2$ GeV and $\mu = 10$ GeV. As initial-scale distributions we have used the model of Refs. [61,62,63] (GK model) setting $t=-0.1$ $\hbox {GeV}^2$ as momentum transfer squared

5 Conclusions

The main purpose of this paper is to provide a solid and public implementation of GPD evolution that can be used for phenomenological studies. To this end, we have revisited GPD evolution in view of an efficient numerical implementation spelling out the computational details. We rederived the evolution equations and recomputed the evolution kernels at one-loop accuracy in perturbative QCD. For the calculation, we adopted a Feynman-diagram approach using the operator definition of GPDs in the light-cone gauge, which reduces the number of diagrams to be considered, renormalised in the $\overline{\text{ MS }}$ scheme. Our formulation of the evolution equations allowed us to easily study some relevant properties of the evolution kernels. Specifically, we have shown that our calculation correctly reproduces both the DGLAP and the ERBL limits and that it guarantees continuity of GPDs at the crossover point $x=\xi$. In addition, we have worked out the consequences of the GPD sum rules on the evolution kernels, deriving equalities that need to be obeyed order by order in perturbation theory, finally showing that our one-loop calculation fulfils these equalities. Moreover, we have computed the conformal moments of our non-singlet evolution kernels showing that, as expected, they diagonalise upon Gegenbauer transform and that their eigenvalues coincide with the well-know DGLAP and ERBL one-loop anomalous dimensions. Finally, we have also explicitly shown that our computation reproduces previous results present in the literature.

Our calculation has been implemented in the public code APFEL++ that in turn has been interfaced to PARTONS. This allowed us to perform detailed numerical studies. We have checked that DGLAP and ERBL evolutions are reproduced to very high accuracy in the $\xi \rightarrow 0$ and $\xi \rightarrow 1$ limits, respectively. Moreover, we have checked that the evolution preserves GPD polynomiality. In addition, we have verified that our implementation of GPD evolution agrees with the evolution computed in conformal space. As a last check, we have compared our GPD evolution against another existing implementation, Vinnikov’s code, finding general good agreement.

In this paper, we limited ourselves to the one-loop (LO) evolution of unpolarised GPDs. The next natural short-term step is the extension to longitudinally and transversely polarised evolutions. In the longer run, we plan to implement the two-loop (NLO) corrections to the evolution. Facing a new era for GPD experiments at colliders, we believe that the public release of a documented and carefully checked implementation of GPD evolution equations meets the need of the hadron-physics community. The code is flexible and can run with any GPD model expressed in x space. It also provides for the first time an implementation of the variable-flavour-number scheme in a public solver of GPD-evolution equations.

We conclude by stressing once again that the implementation of GPD evolution presented here is publicly available in the APFEL++ code:

https://github.com/vbertone/apfelxx

that is in turn interfaced to the PARTONS framework:

https://partons.cea.fr/partons/doc/html/index.html

that gives access to a large variety of GPD models, some of which are used in this paper. The user can find ready-to-use example codes to evolve any of the GPD models available in PARTONS.

Appendices

Appendix A: Parton-in-parton GPDs

In this appendix, we introduce the unpolarised parton-in-parton GPDs and give explicit definitions that can be used to compute them in perturbation theory. As shown in Sect. 2, this allows one to determine the anomalous dimensions that govern the evolution of GPDs. We explicitly compute the tree-level contribution to these GPDs showing that, to this order, they coincide with the corresponding PDFs times a $\xi$-dependent factor, thereby setting their normalisation. In Appendix B, we will use these definitions to compute the one-loop quark-in-quark anomalous dimension.

The parton-in-parton GPDs can be easily obtained by replacing the hadronic states in the parton-in-hadron GPDs defined in Eq. (2) with the appropriate partonic states. Specifically, we consider on-shell massless partons moving along the direction defined by the gauge vector n with incoming momentum $(1+\xi )p$ and outgoing momentum $(1-\xi )p$. In addition, we also have to include an average over the colour states of the external partons. To do so, we need to invoke for a moment the Wilson line. Since we are working in the light-cone gauge, the Wilson line does not contribute in the sense that it reduces to the unitary operator in the fundamental representation of the colour group for the quark operator and in the adjoint representation for the gluon operator. Therefore, when averaging over the colour states of the external partons, since the probe is assumed to be a colour singlet, we effectively need to take the trace over the colour indices and divide by the dimension of the colour representation. This amounts to

$$\begin{aligned} \frac{1}{N_c}\text{ Tr}_c[\dots ], \end{aligned}$$

(103)

for external quark states and to:

$$\begin{aligned} \frac{1}{N_c^2-1}\text{ Tr}_c[\dots ], \end{aligned}$$

(104)

for external gluon states, where “$\hbox {Tr}_c$” indicates the trace over the colour indices and $N_c=3$ is the number of colours. Finally, we also need to include an average over the physical spin/helicity states and a trace over the Dirac indices

$$\begin{aligned} \frac{1}{2}\sum _s \text{ Tr}_D[\dots ], \end{aligned}$$

(105)

with s running over the spin index for quark states and the helicity index for gluon states. In the following, we will denote with “Tr” the trace over both colour and Dirac indices.

In the presence of more than one massless quark flavour, one can define seven different combinations between external partonic states and GPD operators. We list them all below by also including the appropriate averaging discussed above. Let us start with the gluon operator. In this case, we can have the gluon-in-gluon GPD in which the gluon operator acts on gluon external states

$$\begin{aligned}&{\hat{F}}_{g/g}(x,\xi ) =\frac{n_\mu n_\nu }{2(N_c^2-1) x(n\cdot p)}\int \frac{{\mathrm{d}}y}{2\pi }{\mathrm{e}}^{-ix(n\cdot p)y}\nonumber \\&\quad \times \sum _s\mathrm{Tr}\left[ \left\langle (1-\xi )p,s\left| F_{a}^ {\mu j}\left( \frac{yn}{2}\right) \right. \right. \right. \nonumber \\&\quad \times \left. \left. \left. F_{a}^{\nu j}\left( -\frac{yn}{2}\right) \right| (1+\xi )p,s\right\rangle _g\right] , \end{aligned}$$

(106)

where we have made the helicity index s explicit in the states and indicated with the subscript g that the states refer to external gluons. A second possibility is to bracket the gluon operator between quark states, which defines the gluon-in-quark GPD:

$$\begin{aligned}&{\hat{F}}_{g/q}(x,\xi ) = \frac{n_\mu n_\nu }{2N_c x(n\cdot p)}\int \frac{{\mathrm{d}}y}{2\pi }{\mathrm{e}}^{-ix(n\cdot p)y}\nonumber \\&\quad \times \sum _s\mathrm{Tr}\left[ \left\langle (1-\xi )p,s\left| F_{a}^{\mu j}\left( \frac{yn}{2}\right) \right. \right. \right. \nonumber \\&\quad \times \left. \left. \left. F_{a}^{\nu j}\left( -\frac{yn}{2}\right) \right| (1+\xi )p,s\right\rangle _q\right] , \end{aligned}$$

(107)

with the subscript q denoting external quark states and the index s this time referring to the quark spin state.

Now we move to considering the quark operator. This can be bracketed between gluon states giving the quark-in-gluon GPD:

(108)

The quark operator for a specific flavour (or antiflavour) q can finally be bracketed between four different quark states:

• states of exactly the same flavour q and charge-conjugation quantum number:

  

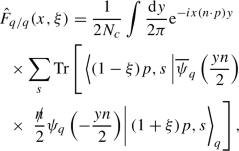  (109)

• states of the same flavour q but opposite charge-conjugation quantum number:

  

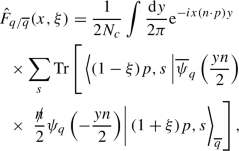  (110)

• states of different flavour $q'$ but same charge-conjugation quantum number:

  

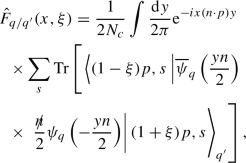  (111)

• states of different flavour $q'$ and opposite charge-conjugation quantum number:

  

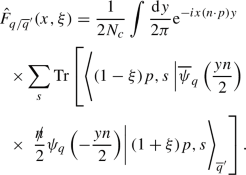  (112)

A graphical representation of the seven parton-in-parton GDPs listed above is given in Fig. 8.

Fig. 8

Graphical representation of the parton-in-parton GPDs defined in Eqs. (106)–(112)

It should be stressed that in general, the quark and gluon fields in Eqs. (106)–(112) are interacting fields in the sense that they can radiate and absorb partons, possibly changing species, before interacting with the external asymptotic states. In this way, these definitions can be used to compute perturbative corrections in $\alpha _s$ to the anomalous dimensions by considering diagrams with additional radiation. For any given GPD, non-vanishing diagrams are those that have the appropriate external free fields to annihilate the asymptotic states according to

$$\begin{aligned}&\psi _q^{(0)}(x) |k,s\rangle _q = {\mathrm{e}}^{-ik\cdot x} u_{q,s}(k) |0\rangle \quad \text{ and }\quad \nonumber \\&\psi _q^{(0)}(x) |k,s\rangle _{{\overline{q}}} = {\mathrm{e}}^{ik\cdot x} v_{q,s}(k) |0\rangle , \end{aligned}$$

(113)

for quarks and

$$\begin{aligned} A_a^{(0),j}(x) |k,s\rangle _g = {\mathrm{e}}^{-ik\cdot x}e_{a,s}^{j}(k)|0\rangle , \end{aligned}$$

(114)

for gluons. Here, $u_{q,s}(k)$ $(v_{q,s}(k))$ is the quark (antiquark) spinor for the flavour q of momentum k and spin s, and $e_{a,s}^{\alpha }(k)$ is the gluon polarisation vector of momentum k, colour index a, and helicity s. $\psi _q^{(0)}$ and $A_a^{(0),\alpha }$ are respectively the quark and gluon free fields that can be regarded as the asymptote of the original interacting fields after radiation.

A detail worth discussing is the fact that the gluon field $A_a^{j}$ always appears through $n_\mu F_a^{\mu j}$. As discussed in Sect. 2, the light-cone gauge greatly simplifies the form of this combination, which reduces to $n_\mu F_a^{\mu j}(x)=\left( n\cdot \partial \right) A_a^j(x)$. When this operator is acting on a partonic state with plus momentum $(1\pm \xi )p^+$, since it appears in a Fourier transform, the derivative can be traded for a factor $(1\pm \xi )p^+-k^+=i(x\pm \xi )p^+$. This finally allows us to write the gluon-in-gluon and gluon-in-quark GPDs in terms of the gluon field rather than in terms of the field strength, as follows:

$$\begin{aligned}&{\hat{F}}_{g/g}(x,\xi ) = \frac{(n\cdot p)(x^2-\xi ^2)}{2(N_c^2-1)x}\nonumber \\&\quad \times \int \frac{{\mathrm{d}}y}{2\pi }{\mathrm{e}}^{-ix(n\cdot p)y}\sum _s\mathrm{Tr}\left[ \left\langle (1-\xi )p,s\left| A_{a}^ { j}\left( \frac{yn}{2}\right) \right. \right. \right. \nonumber \\&\quad \times \left. \left. \left. A_{a}^{j}\left( -\frac{yn}{2}\right) \right| (1+\xi )p,s \right\rangle _g\right] , \end{aligned}$$

(115)

and

$$\begin{aligned}&{\hat{F}}_{g/q}(x,\xi ) = \frac{(n\cdot p) (x^2-\xi ^2)}{2N_cx}\nonumber \\&\quad \times \int \frac{{\mathrm{d}}y}{2\pi }{\mathrm{e}}^{-ix(n\cdot p)y}\sum _s\mathrm{Tr}\left[ \left\langle (1-\xi )p,s\left| A_{a}^{ j}\left( \frac{yn}{2}\right) \right. \right. \right. \nonumber \\&\quad \times \left. \left. \left. A_{a}^{j}\left( -\frac{yn}{2}\right) \right| (1+\xi )p,s\right\rangle _q\right] . \end{aligned}$$

(116)

Using Eqs. (113)–(114) and the orthogonality relations for quark spinors

(117)

and gluon polarisation vectors

$$\begin{aligned} \sum _s e_{a,s}^j((1-\xi )p) e_{a,s}^{ j}((1+\xi )p) = -2, \end{aligned}$$

(118)

the computation of parton-in-parton GPDs reduces to integrals of this form:

(119)

for quark (minus sign) and antiquark external states (plus sign) and to

Fig. 9

Tree-level graphs contributing to the gluon-in-gluon GPD ${\hat{F}}_{g/g}$, Eq. (106), (left) and to the fully diagonal quark-in-quark GPD ${\hat{F}}_{q/q}$, Eq. (109) (right)

$$\begin{aligned} -2\int \frac{{\mathrm{d}}y}{2\pi }{\mathrm{e}}^{i (1-x) y p\cdot n} \mathrm{Tr}_c\left[ \dots {\mathbb {I}}_c\dots \right] , \end{aligned}$$

(120)

for gluon external states. Therefore, given a specific diagram, one just needs to replace the ellipses using standard QCD Feynman rules in light-cone gauge. This allows parton-in-parton GPDs to have the following perturbative expansion:

$$\begin{aligned} {\hat{F}}_{i/j}(x,\xi ) = \sum _{n=0}^{\infty }\left( \frac{\alpha _s}{4\pi }\right) ^n {\hat{F}}_{i/j}^{[n]}(x,\xi ). \end{aligned}$$

(121)

At ${\mathcal {O}}(\alpha _s^0)$, where no additional radiation is allowed, only the gluon-in-gluon GPD ${\hat{F}}_{g/g}$, Eq. (115), and the fully diagonal quark-in-quark GPD ${\hat{F}}_{q/q}$, Eq. (109), are different from zero. The corresponding Feynman diagrams are shown in Fig. 9. The explicit computation can be done using Eqs. (119) and (120) by simply removing the ellipses and inserting in the quark case the operator . This yields

$$\begin{aligned}&{\hat{F}}_{q/q}^{[0]}(x,\xi )=\sqrt{1-\xi ^2}\,\delta (1-x),\nonumber \\&{\hat{F}}_{g/g}^{[0]}(x,\xi )=(1-\xi ^2)\delta (1-x), \end{aligned}$$

(122)

which compared with Eq. (17) allows us to find that $D_q(\xi )=\sqrt{1-\xi ^2}$ and $D_g(\xi )=1-\xi ^2$. It should be noted that this result, which derives from the calculation of the disconnected diagrams in Fig. 9, relies on imposing the conservation of the momentum injected into the operator-insertion vertices (see Fig. 1). In other words, the momentum that flows into the vertices equals the external momentum.¹¹

At ${\mathcal {O}}(\alpha _s)$, the interacting fields radiate one additional parton before interacting with the external states. This also allows ${\hat{F}}_{g/q}$, Eq. (107), and ${\hat{F}}_{q/g}$, Eq. (108), to be different from zero, while the remaining quark-in-quark GPDs (110)–(112) get their first contribution at higher orders. Contrary to the tree-level calculations, loop corrections to the parton-in-parton GPDs are divergent. It is the renormalisation of these divergences that defines the anomalous dimensions responsible for the evolution of GPDs. The seven anomalous dimensions obtained from Eqs. (106)–(112) are usually arranged in seven specific combinations that are convenient for the implementation of the evolution equations. Using the same indexing as for GPDs, there are three non-singlet anomalous dimensions, defined as

$$\begin{aligned}&{\mathcal {P}}_{\pm }^{-}=\left( {\mathcal {P}}_{q/q}-{\mathcal {P}}_{q/q'}\right) \pm \left( {\mathcal {P}}_{q/{\overline{q}}}-{\mathcal {P}}_{q/{\overline{q}}'}\right) ,\nonumber \\&{\mathcal {P}}_V^{-}={\mathcal {P}}_{-}^-+n_f({\mathcal {P}}_{q/q'}- {\mathcal {P}}_{q/{\overline{q}}'}), \end{aligned}$$

(123)

and four singlet anomalous dimensions

$$\begin{aligned}&{\mathcal {P}}_{qq}^+={\mathcal {P}}_{+}^-+n_f({\mathcal {P}}_{q/q'}+ {\mathcal {P}}_{q/{\overline{q}}'}),\nonumber \\&{\mathcal {P}}_{qg}^+=2n_f{\mathcal {P}}_{q/g},\nonumber \\&{\mathcal {P}}_{gq}^+={\mathcal {P}}_{g/q},\nonumber \\&{\mathcal {P}}_{gg}^+={\mathcal {P}}_{g/g}. \end{aligned}$$

(124)

As mentioned above, at one loop one finds ${\mathcal {P}}_{q/{\overline{q}}}={\mathcal {P}}_{q/q'}={\mathcal {P}}_{q/{\overline{q}}'}=0$ which in turn implies ${\mathcal {P}}_{+}^-={\mathcal {P}}_{-}^-={\mathcal {P}}_V^-={\mathcal {P}}_{qq}^+={\mathcal {P}}_{q/q}$.

Appendix B: One-loop quark-in-quark anomalous dimension

In this appendix, we present the details of the calculation of the one-loop anomalous dimensions in the $\overline{\text{ MS }}$ renormalisation scheme using the light-cone gauge. As discussed in Sect. 2, the anomalous dimensions can be determined by extracting the pole part of appropriately defined parton-in-parton GPDs that can be computed in perturbation theory. In Appendix A we introduced the parton-in-parton GPDs and carried out the tree-level computation. For illustrative purposes, here we consider the one-loop correction to the quark-in-quark GPD ${\hat{F}}_{q/q}^{[1]}$, and using Eq. (18) we immediately obtain the one-loop quark-in-quark anomalous dimension ${\mathcal {P}}_{q/q}^{[0]}$. The remaining one-loop anomalous dimensions can be extracted in an analogous way by simply considering the appropriate parton-in-parton GPDs.

Fig. 10

Real graph contributing to the quark-in-quark GPD at one loop

The advantage of using the light-cone gauge is a reduction of the number of diagrams to be considered. Specifically, ${\hat{F}}_{q/q}^{[1]}$ results from the computation of a single diagram displayed in Fig. 10. For the calculation, we will use a gauge vector that in light-cone coordinates¹² reads $n^\mu =(0,1,{\mathbf {0}}_T)$, such that the scalar product of any vector v with n gives $n\cdot v=v^+$. Using the definition in Eq. (109) and the manipulation in Eq. (119), we obtain:

(125)

with

(126)

and where ${\mathcal {D}}_{\mu \nu }$ is defined in Eq. (1), and $t_\alpha$ are the SU(3) generators. Expressing the integration measure in light-cone coordinates

$$\begin{aligned} {\mathrm{d}}^{4-2\epsilon }k = {\mathrm{d}}k^+{\mathrm{d}}k^-{\mathrm{d}}^{2-2\epsilon }{\mathbf {k}}_T, \end{aligned}$$

(127)

the integral reduces to

(128)

The gluon propagator ${\mathcal {D}}_{\mu \nu }$ has two components (see Eq. (1)): one proportional to the metric tensor $g_{\mu \nu }$ and one to the gauge vector $n_\mu$. It is thus convenient to split the integral into two components that we respectively denote with the superscripts (g) and (n):

$$\begin{aligned} {\hat{F}}_{q/q}^{[1]}(x,\xi ) = {\hat{F}}_{q/q}^{[1],(g)}(x,\xi ) + {\hat{F}}_{q/q}^{[1],(n)}(x,\xi ). \end{aligned}$$

(129)

Integrating over $k^+$, using the identity $\text{ Tr}_c[t_\alpha t_\alpha ]=N_cC_F$, plus some additional manipulations, we obtain

$$\begin{aligned} {\hat{F}}_{q/q}^{[1],(g)}(x,\xi )= & {} \frac{iC_F \sqrt{1-\xi ^2}}{(p^+)^2(1-x)(x^2-\xi ^2)}\mu ^{2\epsilon }\nonumber \\&\times \int \frac{{\mathrm{d}}^{2-2\epsilon }{\mathbf {k}}_T}{(2\pi )^{2-2\epsilon }} {\mathbf {k}}_T^2\,I({\mathbf {k}}_T^2),\nonumber \\ {\hat{F}}_{q/q}^{[1],(n)}(x,\xi )= & {} \frac{2x}{1-x} {\hat{F}}_{q/q}^{[1],(g)}(x,\xi ) + \frac{4i C_F \sqrt{1-\xi ^2}}{p^+ (1-x)^2}\mu ^{2\epsilon }\nonumber \\&\times \int \frac{{\mathrm{d}}^{2-2\epsilon }{\mathbf {k}}_T}{(2\pi )^{2-2\epsilon }}\,J({\mathbf {k}}_T^2), \end{aligned}$$

(130)

where

$$\begin{aligned} I({\mathbf {k}}_T^2)= & {} \int _{-\infty }^{+\infty }\frac{{\mathrm{d}}k^-}{(k^-- k_1^-) (k^--k_2^-)(k^--k_3^-)},\nonumber \\ J({\mathbf {k}}_T^2)= & {} \int _{-\infty }^{+\infty }\frac{k^-{\mathrm{d}}k^-}{(k^-- k_1^-) (k^--k_2^-)(k^--k_3^-)}, \end{aligned}$$

(131)

with

$$\begin{aligned} k_1^-= & {} \frac{{\mathbf {k}}_T^2}{2 (1-x)p^+ }-i(1-x)\varepsilon ,\nonumber \\ k_2^-= & {} - \frac{{\mathbf {k}}_T^2}{2(x +\xi ) p^+}+i (x+\xi )\varepsilon ,\nonumber \\ k_3^-= & {} - \frac{{\mathbf {k}}_T^2}{2(x -\xi ) p^+}+i(x-\xi )\varepsilon . \end{aligned}$$

(132)

In defining $k_2^-$ and $k_3^-$, we have multiplied the term $i\varepsilon$ coming from the quark propagators (see e.g. Eq. (128)) by $(x\pm \xi )$ to account for the correct sign of these terms. This derives from the fact that, precisely like the finite term ${\mathbf {k}}_T^2$, the infinitesimal contribution $i\varepsilon$ also gets a factor $1/[2(x\pm \xi )p^+]$. Since we are only interested in the position of the pole w.r.t. the integration path, i.e. the real axis, we only need to know the sign of the factor $1/[2(x\pm \xi )p^+]$. Considering that $p^+$ is positive, in the limit $\epsilon \rightarrow 0^+$, this is equivalent to multiplying $i\varepsilon$ by $(x\pm \xi )$, hence the definitions in Eq. (132). This is crucial for determining the pole configuration of the integrand in $k^-$ as a function of the relative position of x and $\xi$. In addition, for the same reason, we have multiplied the $i\varepsilon$ term of $k_1^-$ by $(1-x)$.

In order to compute these integrals, we need to consider different configurations depending on the position of the poles relative to the real axis. We close the integration path upwards in such a way that it runs anticlockwise, and all the residues get a factor $+2\pi i$. We start by assuming $-\xi<x<1$. In this configuration the relevant cases are as follows:

• $x>\xi$: In this case the position of the poles is shown in the left plot of Fig. 11. The contour picks up the poles in $k_2^-$ and $k_3^-$, producing

  $$\begin{aligned}&I ({\mathbf {k}}_T^2) \mathop {=}^{x>\xi } \frac{2\pi i}{k_2^--k_3^-}\times \left[ \frac{1}{k_2^--k_1^-}-\frac{1}{k_3^--k_1^-}\right] ,\nonumber \\&J ({\mathbf {k}}_T^2) \mathop {=}^{x>\xi } \frac{2\pi i}{k_2^--k_3^-}\times \left[ \frac{k_2^-}{k_2^--k_1^-}-\frac{k_3^-}{k_3^--k_1^-}\right] . \nonumber \\ \end{aligned}$$

  (133)

• $x<\xi$: The poles are placed as shown in the right plot of Fig. 11. The poles in $k_1^-$ and $k_3^-$ are now external, and only the pole in $k_2^-$ contributes, giving

  $$\begin{aligned}&I ({\mathbf {k}}_T^2) \mathop {=}^{x<\xi } \frac{2\pi i}{k_2^--k_3^-}\times \frac{1}{k_2^--k_1^-},\nonumber \\&J ({\mathbf {k}}_T^2) \mathop {=}^{x<\xi } \frac{2\pi i}{k_2^--k_3^-}\times \frac{k_2^-}{k_2^--k_1^-}. \end{aligned}$$

  (134)

Fig. 11

Position of the poles in the complex plane defined by $k^-$ in the integrals in Eq. (131). The red arrows indicate the integration path

The net result is that the integrals I and J can generally be written as

$$\begin{aligned} I ({\mathbf {k}}_T^2)= & {} \frac{2\pi i}{k_2^--k_3^-}\left[ \frac{1}{k_2^--k_1^-}-\theta (x-\xi )\frac{1}{k_3^--k_1^-}\right] \nonumber \\= & {} -\frac{4\pi i (p^+)^2(1-x)(x^2-\xi ^2)}{\xi {\mathbf {k}}_T^4}\nonumber \\&\times \left[ \frac{x+\xi }{1+\xi }-\theta (x-\xi ) \frac{x-\xi }{1-\xi }\right] ,\nonumber \\ J ({\mathbf {k}}_T^2)= & {} \frac{2\pi i}{k_2^--k_3^-}\left[ \frac{ k_2^- }{k_2^--k_1^-}-\theta (x-\xi ) \frac{k_3^-}{k_3^--k_1^-}\right] \nonumber \\= & {} \frac{2\pi i p^+(1-x)(x^2-\xi ^2)}{\xi {\mathbf {k}}_T^2}\left[ \frac{1}{1+\xi }-\theta (x-\xi ) \frac{1}{1-\xi }\right] . \nonumber \\ \end{aligned}$$

(135)

These results were obtained under the assumption $-\xi<x<1$. If $x>1$, the pole in $k_1^-$ moves into the upper half of the complex plane in $k^-$. In this configuration, the case $x>\xi$ in the l.h.s. of Fig. 11 produces a vanishing result because all poles lie above the integration path, which can then be closed downwards where there are no poles. In addition (assuming $\xi <1$), the conditions $x>1$ and $x<\xi$ cannot be simultaneously fulfilled. Therefore, the r.h.s. configuration of Fig. 11 is ruled out. In conclusion, the results in Eq. (135) effectively multiply $\theta (1-x)$. If $x<-\xi$, the pole in $k_2^-$ moves into the lower half of the complex plane. In this way, for $x<\xi$, all poles are below the integration path, thus again yielding a vanishing result, while the configuration $x>\xi$ is ruled out. Therefore, the results above also multiply a factor $\theta (x+\xi )$. This allows us to recast Eq. (135) as follows:

$$\begin{aligned} I ({\mathbf {k}}_T^2)= & {} -\frac{4\pi i (p^+)^2(1-x)(x^2-\xi ^2)}{\xi {\mathbf {k}}_T^4}\theta (1-x)\nonumber \\&\times \left[ \theta (x+\xi )\frac{x+\xi }{1+\xi }-\theta (x-\xi ) \frac{x-\xi }{1-\xi }\right] ,\nonumber \\ J ({\mathbf {k}}_T^2)= & {} \frac{2\pi i p^+(1-x)(x^2-\xi ^2)}{\xi {\mathbf {k}}_T^2}\theta (1-x)\nonumber \\&\times \left[ \theta (x+\xi )\frac{1}{1+\xi }-\theta (x-\xi ) \frac{1}{1-\xi }\right] . \end{aligned}$$

(136)

We can finally put everything together using Eqs. (129) and (130) to obtain the one-loop real correction to the bare quark-in-quark GPD:

$$\begin{aligned} {\hat{F}}_{q/q}^{[1]}(x,\xi )= & {} {\hat{F}}_{q/q}^{[1], (g)}(x,\xi )+{\hat{F}}_{q/q}^{[1], (n)}(x,\xi )\nonumber \\= & {} \frac{C_F \sqrt{1-\xi ^2}\theta (1-x)}{\xi (1-x)}\nonumber \\&\times \left[ \theta (x+\xi )\frac{(x+\xi ) (1-x+2\xi )}{1+\xi }-\theta (x-\xi ) \right. \nonumber \\&\times \left. \frac{(x-\xi ) (1-x-2\xi )}{1-\xi }\right] \mu ^{2\epsilon }S_{\epsilon }\int \frac{{\mathrm{d}}k_T^2}{k_T^{2+2\epsilon }}, \nonumber \\ \end{aligned}$$

(137)

where for the $(2-2\epsilon )$-dimensional integral in ${\mathbf {k}}_T$ we have used the identity

$$\begin{aligned} \int \frac{{\mathrm{d}}^{2-2\epsilon }{\mathbf {k}}_T}{(2\pi )^{2-2\epsilon }}\frac{1}{{\mathbf {k}}_T^2} =\frac{S_\epsilon }{4\pi }\int _0^\infty \frac{{\mathrm{d}}k_T^2}{k_T^{2+2\epsilon }}, \end{aligned}$$

(138)

with $S_\epsilon$ given in Eq. (6). It turns out that the integral over $k_T$ in Eq. (137) vanishes [65]. This result can be regarded as the consequence of the cancellation of two divergences due to the use of dimensional regularisation to regularise both the UV divergence when $k_T\rightarrow \infty$ and the IR divergence when $k_T\rightarrow 0$. Therefore, this integral can be interpreted as

$$\begin{aligned} \int _0^\infty \frac{{\mathrm{d}}k_T^2}{k_T^{2+2\epsilon }}\sim \frac{1}{\epsilon _\mathrm{UV}}-\frac{1}{\epsilon _{\mathrm{IR}}}. \end{aligned}$$

(139)

This structure could be more clearly highlighted by regularising UV and IR divergences differently, as for example done in Refs. [66, 67]. For infrared-safe observables, the IR divergence cancels against an opposite divergence produced in the calculation of the partonic cross section. Therefore, what we are concerned with is the UV divergence that needs to be cancelled by a renormalisation constant. for this purpose, we discard the IR divergence and write the result of the calculation above as

$$\begin{aligned}&{\hat{F}}_{q/q}^{[1]}(x,\xi ) = \frac{C_F \sqrt{1-\xi ^2} \theta (1-x)}{\xi (1-x)}\nonumber \\&\quad \times \left[ \theta (x+\xi )\frac{(x+\xi ) (1-x+2\xi )}{1+\xi }-\theta (x-\xi ) \right. \nonumber \\&\quad \times \left. \frac{(x-\xi ) (1-x-2\xi )}{1-\xi }\right] \frac{\mu ^{2\epsilon } S_{\epsilon }}{\epsilon _{\mathrm{UV}}}. \end{aligned}$$

(140)

The calculation of the one-loop quark-in-quark GPD is still incomplete because, so far, we have only considered the “real” contribution in Fig. 10. We still need to include the “virtual” contribution. As discussed in Sect. 3.4, an explicit calculation is unnecessary, as this contribution can be obtained from the knowledge of the real one. As a matter of fact, writing

$$\begin{aligned} {\hat{F}}_{q/q}^{[1]}(x,\xi ) \rightarrow {\hat{F}}_{q/q}^{[1]}(x,\xi ) + A(\xi )\delta (1-x), \end{aligned}$$

(141)

and imposing the valence sum rule gives¹³

$$\begin{aligned} A(\xi )=2C_F \sqrt{1-\xi ^2}\left[ \frac{3}{2}-2\int _0^1\frac{{\mathrm{d}}z}{1-z}-\ln (|1-\xi ^2|)\right] \frac{\mu ^{2\epsilon } S_{\epsilon }}{\epsilon _{\mathrm{UV}}}. \nonumber \\ \end{aligned}$$

(142)

Once the full one-loop quark-in-quark GPD has been computed, we can use Eq. (18), with $D_q(\xi )=\sqrt{1-\xi ^2}$, to extract the anomalous dimension, finally obtaining ${\mathcal {P}}_{q/q}^{[0]}$ as in Eq. (19).

It is however instructive to perform the calculation of the virtual contribution to ${\mathcal {P}}_{q/q}^{[0]}$ to explicitly verify that, at least at one-loop accuracy, the constraints discussed in Sect. 3.4 are actually fulfilled. Figure 12 displays the relevant diagrams.

Fig. 12

Virtual graphs contributing to the quark-in-quark GPD at one loop

These diagrams correspond to self-energy corrections to the external legs. As a consequence, they can be included by means of the Lehmann–Symanzik–Zimmermann (LSZ) reduction formula [68]. Specifically, virtual corrections to the one-loop quark-in-quark GPD are included by computing

$$\begin{aligned} \frac{Z_F(1+\xi )+Z_F(1-\xi )}{2}{\hat{F}}_{q/q}(x,\xi ), \end{aligned}$$

(143)

where ${\hat{F}}_{q/q}(x,\xi )$ is computed with amputated external legs and $Z_F$ is the residue of the quark propagator. We have included a correction for each external leg along with a factor of 1/2 as a consequence of the LSZ reduction formula. As we will show below, the explicit dependence of $Z_F$ on the longitudinal momentum fractions $1\pm \xi$ emerges from the regularisation of the 1/(nk) divergence caused by the light-cone gluon propagator.

In order to identify the residue $Z_F$, we follow Ref. [39]. The quark propagator in momentum space in the vicinity of the pole behaves as follows:¹⁴

(144)

which effectively defines the residue $Z_F$ and where the finite corrections are related to the quark spectral function in the continuum region [69]. As is well known, the 1PI contribution to the self-energy, $\Sigma$, can be resummed to all orders, producing

(145)

We now show how $\Sigma$ is related to the residue $Z_F$. First of all, we observe that in light-cone gauge, $\Sigma$ must have this structure:

(146)

where A and B are scalar coefficients. Plugging this equation into Eq. (145), one finds

(147)

By comparison with Eq. (144), one immediately sees that

$$\begin{aligned} Z_F = \frac{1}{1-A-B}. \end{aligned}$$

(148)

Since $\Sigma$ starts at ${\mathcal {O}}(\alpha _s)$:

$$\begin{aligned} \Sigma (q) = \sum _{n=1}^{\infty }a_s^n \Sigma ^{[n]}(q), \end{aligned}$$

(149)

so do A and B:

$$\begin{aligned} A = \sum _{n=1}^{\infty }a_s^n A^{[n]},\quad \text{ and }\quad B = \sum _{n=1}^{\infty }a_s^n B^{[n]}. \end{aligned}$$

(150)

This implies that the perturbative expansion of the residue reads

$$\begin{aligned} Z_F = 1+a_s(A^{[1]}+B^{[1]})+{\mathcal {O}}(\alpha _s^2). \end{aligned}$$

(151)

Using this equality in Eq. (143), one finds that the contribution to the one-loop correction of the quark-in-quark GPD due to the virtual diagrams in Fig. 12 amounts to

$$\begin{aligned}&{\hat{F}}_{q/q}^{\mathrm{virt}}(x,\xi ) \nonumber \\&\quad = \frac{[A^{[1]}(1+\xi )+B^{[1]}(1+\xi )]+[A^{[1]}(1-\xi )+B^{[1]}(1-\xi )]}{2}\nonumber \\&\qquad \sqrt{1-\xi ^2}\delta (1-x), \end{aligned}$$

(152)

where we have used Eq. (122) for ${\hat{F}}_{q/q}^{[0]}$. The values of $A^{[1]}$ and $B^{[1]}$ can be extracted by computing the diagram in Fig. 13.

Using light-cone-gauge Feynman rules, this diagram evaluates to

(153)

where we have defined

(154)

and

(155)

The numerator of the integrand of $\Sigma _A$ can be rearranged as follows:

(156)

The term proportional to $(q-k)^2$ can be discarded because it cancels one of the poles in the denominator. This leaves a single pole in $k^-$ (or $k^+$) that produces a vanishing result because the integration path can be closed in a way that it contains no poles. Finally, we have

Fig. 13

One-loop quark self energy

(157)

In view of the use of the Feynman-parameter method to solve the integrals in Eqs. (154) and (157), we have omitted the $i\epsilon$ terms from the propagators. Denoting

$$\begin{aligned}&J_F = \int \frac{{\mathrm{d}}^{4-2\epsilon }k}{k^2(q-k)^2}, \quad J_F^\mu = \int \frac{{\mathrm{d}}^{4-2\epsilon }k\,k^\mu }{k^2(q-k)^2},\nonumber \\&J_A = \int \frac{{\mathrm{d}}^{4-2\epsilon }k}{(nk)k^2(q-k)^2},\quad J_A^\mu = \int \frac{{\mathrm{d}}^{4-2\epsilon }k\,k^\mu }{(nk)k^2(q-k)^2},\nonumber \\ \end{aligned}$$

(158)

and using the Feynman-parameter identity

$$\begin{aligned} \frac{1}{QR} = \int _0^1\frac{{\mathrm{d}}x}{[xQ+(1-x)R]^2}, \end{aligned}$$

(159)

with $Q=k^2$ and $R=(q-k)^2$, allows us to recast these integrals as follows:

$$\begin{aligned} J_{F,A}^{(\mu )} = \int _0^1{\mathrm{d}}x I_{F,A}^{(\mu )}(x), \end{aligned}$$

(160)

with

$$\begin{aligned} I_F(x)= & {} \int \frac{{\mathrm{d}}^{4-2\epsilon }k}{[k^2-2(1-x)(p k)+(1-x) q^2]^2},\nonumber \\ I_F^\mu (x)= & {} \int \frac{{\mathrm{d}}^{4-2\epsilon }k\,k^\mu }{[k^2-2(1-x)(p k)+(1-x) q^2]^2},\nonumber \\ I_A(x)= & {} \int \frac{{\mathrm{d}}^{4-2\epsilon }k}{(nk) [k^2-2(1-x)(p k)+(1-x) q^2]^2},\nonumber \\ I_A^\mu (x)= & {} \int \frac{{\mathrm{d}}^{4-2\epsilon }k\,k^\mu }{(nk) [k^2-2(1-x)(p k)+(1-x) q^2]^2}. \end{aligned}$$

(161)

These integrals can finally be computed using, for example, Eqs. (A.1), (A.2), (A.6) and (A.7) of Ref. [70]. The result is

$$\begin{aligned} I_F(x)= & {} i\pi ^{2-\epsilon }{\mathrm{e}}^{\epsilon i\pi } \frac{\Gamma (\epsilon )}{[x(1-x) q^2]^\epsilon },\nonumber \\ I_F^\mu (x)= & {} i\pi ^{2-\epsilon }{\mathrm{e}}^{\epsilon i\pi } \frac{\Gamma (\epsilon )}{[x(1-x) q^2]^\epsilon }(1-x) q^\mu ,\nonumber \\ I_A(x)= & {} i\pi ^{2-\epsilon }{\mathrm{e}}^{\epsilon i\pi } \frac{\Gamma (\epsilon )}{[x(1-x) q^2]^\epsilon (nq)}\frac{1}{1-x},\nonumber \\ I_A^\mu (x)= & {} i\pi ^{2-\epsilon }{\mathrm{e}}^{\epsilon i\pi }\frac{\Gamma (\epsilon )}{[x(1-x) q^2]^\epsilon (nq)}\nonumber \\&\quad \times \left[ q^\mu +\frac{x}{1-x}\frac{q^2}{2(nq)}n^\mu \right] . \end{aligned}$$

(162)

Gathering all pieces, we obtain

(163)

and

(164)

so that

(165)

The integral in x is clearly divergent because of the singularity at $x=1$ caused by the 1/(nk) term in the gluon propagator. Therefore, before identifying the coefficients A and B using Eq. (146), it is first necessary to make this integral convergent. To do so, we first note that any regularisation needs somehow to rely on the light-cone projection of the incoming/outgoing parton, i.e. (np), that defines the direction along which the so-called rapidity divergences take place [36]. Therefore, we introduce a generic regularisation that we denote by the subscript “Reg(np)”:

(166)

With this at hand, we can extract from the regularisation sign anything that is not affected by the regularisation itself. In addition, we take $(nq)=y(np)$, with $y=1\pm \xi$, as required by Eq. (143). This leads to

(167)

It is important to note that the factor 1/y that comes from 1/(nq) must remain inside the regularisation sign. We are therefore forced to multiply and divide by y outside the regularisation sign to reconstruct 1/(nq), leaving a leftover factor of y. This finally allows us to identify the one-loop coefficients $A^{[1]}$ and $B^{[1]}$ by inspection of Eq. (146), whose sum relevant to Eq. (152) is

$$\begin{aligned}&A^{[1]}(y)+B^{[1]}(y) = 2C_F \frac{\mu ^{2\epsilon } S_\epsilon }{\epsilon _{\mathrm{UV}}} \nonumber \\&\quad \times \left[ \frac{3}{2}-2 \int _0^1{\mathrm{d}}x\,y \left[ \frac{1}{y(1-x)}\right] _{\mathrm{Reg}(np)}\right] . \end{aligned}$$

(168)

We now focus on the integral in x in Eq. (168) and manipulate it as follows:

$$\begin{aligned}&\int _0^1 {\mathrm{d}}x\, y\left[ \frac{1}{y(1-x)}\right] _{\mathrm{Reg}(np)} = \int _0^{y} {\mathrm{d}}t \left( \frac{1}{t}\right) _{\mathrm{Reg}(np)}\nonumber \\&\quad =\int _0^{1}\frac{{\mathrm{d}}z}{1-z}+\ln y. \end{aligned}$$

(169)

In the first equality we have made the change of variable $y(1-x) = t$. In the second equality we have extended the integral in t to the interval [0, 1] and subtracted the residual that can now be integrated, giving $\ln y$. We have then made another change of variable, $t=1-z$, and removed the regularisation sign to match the notation in Eq. (142). This finally gives

$$\begin{aligned}&A^{[1]}(y)+B^{[1]}(y) =2C_F \frac{\mu ^{2\epsilon } S_\epsilon }{\epsilon _{\mathrm{UV}}} \nonumber \\&\quad \times \left[ \frac{3}{2}-2 \int _0^{1}\frac{{\mathrm{d}}z}{1-z}-2\ln y\right] . \end{aligned}$$

(170)

Plugging this identity into Eq. (152) finally yields

$$\begin{aligned}&{\hat{F}}_{q/q}^{\mathrm{virt}}(x,\xi ) = 2C_F\sqrt{1-\xi ^2} \left[ \frac{3}{2}-2\int _0^{1}\frac{{\mathrm{d}}z}{1-z}\right. \nonumber \\&\quad \left. -\ln (1-\xi ^2)\right] \frac{\mu ^{2\epsilon } S_\epsilon }{\epsilon _{\mathrm{UV}}}\delta (1-x), \end{aligned}$$

(171)

which agrees with Eq. (142).

Appendix C: Diagonalisation of the conformal moments

In this appendix we provide a general proof of Eq. (86). To do so, we define $z=y/\xi$ and, using the change of variable $v=x/\xi$ in the integrals, rewrite the r.h.s. of Eq. (85) without the factor $2C_F$ as follows:

$$\begin{aligned} I= & {} \frac{3}{2}C_n^{(3/2)}\left( z\right) - \frac{1}{2}\int _{1}^{z}{\mathrm{d}}v\left[ \frac{v+1}{z-1}C_n^{(3/2)}\left( v\right) \right. \nonumber \\&\left. -2\frac{C_n^{(3/2)}\left( v\right) -C_n^{(3/2)}\left( z\right) }{z-v}\right] \nonumber \\&+ \frac{1}{2}\int _{-1}^{z}{\mathrm{d}}v\left[ \frac{v-1}{z+1}C_n^{(3/2)}\left( v\right) \right. \nonumber \\&\left. +2\frac{C_n^{(3/2)}\left( v\right) -C_n^{(3/2)}\left( z\right) }{z-v}\right] . \end{aligned}$$

(172)

Now, we use the fact that $C_n^{(3/2)}$ is indeed a polynomial of degree n whose expansion reads

$$\begin{aligned} C_n^{(3/2)}(x)= & {} \sum _{k=0}^{\lfloor n/2 \rfloor } a_k^{(n)}x^{\ell }\,\quad \text{ with }\quad \nonumber \\ a_k^{(n)}= & {} (-1)^k2^{\ell }\frac{\Gamma (\ell +k+3/2)}{\Gamma (3/2)k!\ell !}, \end{aligned}$$

(173)

with $\ell = n-2k$. This allows us to write

$$\begin{aligned} I= & {} \frac{3}{2}C_n^{(3/2)}\left( z\right) \nonumber \\&- \frac{1}{2}\sum _{k=0}^{\lfloor n/2 \rfloor } a_k^{(n)}\left[ \int _{1}^{z}{\mathrm{d}}v\frac{v^{\ell +1}+v^{\ell }}{z-1}\right. \nonumber \\&\left. -\int _{-1}^{z}{\mathrm{d}}v\frac{v^{\ell +1}-v^{\ell }}{z+1} +2 \int _{1}^{z}{\mathrm{d}}v\frac{z^{\ell }-v^{\ell }}{z-v}\right. \nonumber \\&\left. +2 \int _{-1}^{z}{\mathrm{d}}v\frac{z^{\ell }-v^{\ell }}{z-v}\right] . \end{aligned}$$

(174)

Let us now solve all the integrals in the r.h.s. of this equation. The first gives

$$\begin{aligned}&\int _{1}^{z}{\mathrm{d}}v\frac{v^{\ell +1}+v^{\ell }}{z-1} = \frac{1}{\ell +2}\frac{1-z^{\ell +2}}{1-z}+\frac{1}{\ell +1}\frac{1-z^{\ell +1}}{1-z}\nonumber \\&\quad =\frac{1}{\ell +2}\sum _{j=0}^{\ell +1}z^{j}+\frac{1}{\ell +1}\sum _{j=0}^{\ell }z^{j}, \end{aligned}$$

(175)

and similarly, the second:

$$\begin{aligned}&\int _{-1}^{z}{\mathrm{d}}v\frac{v^{\ell +1}-v^{\ell }}{z+1} =-\frac{(-1)^{\ell +2}}{\ell +2}\sum _{j=0}^{\ell +1}(-z)^{j}\nonumber \\&\quad +\frac{(-1)^{\ell +1}}{\ell +1}\sum _{j=0}^{\ell }(-z)^{j}, \end{aligned}$$

(176)

where we have used the geometric series

$$\begin{aligned} \sum _{j=0}^{n} v^{j}=\frac{1-v^{n+1}}{1-v}. \end{aligned}$$

(177)

Their combination evaluates to

$$\begin{aligned}&\int _{1}^{z}{\mathrm{d}}v\frac{v^{\ell +1}+v^{\ell }}{z-1}- \int _{-1}^{z}{\mathrm{d}}v\frac{v^{\ell +1}-v^{\ell }}{z+1}\nonumber \\&\quad = \left[ \frac{1}{\ell +2}+\frac{1}{\ell +1}\right] \sum _{j=0}^{\ell }\left[ 1+(-1)^{\ell -j}\right] z^{j}. \end{aligned}$$

(178)

Note that the $z^{\ell +1}$ term vanishes because the projector is null for $j=\ell +1$. Now we turn to the third and fourth integrals in Eq. (172):

$$\begin{aligned} \int _{1}^{z}{\mathrm{d}}v\frac{z^{\ell }-v^{\ell }}{z-v}= & {} z^{\ell -1}\int _{1}^{z}{\mathrm{d}}v\frac{1-(v/z)^{\ell }}{1-v/z}\nonumber \\= & {} \sum _{j=0}^{\ell -1}z^{\ell -j-1}\int _{1}^{z}{\mathrm{d}}v\,v^j = \sum _{j=0}^{\ell -1}\frac{z^{\ell }-z^{\ell -j-1}}{j+1} \nonumber \\= & {} -\sum _{j=0}^{\ell -1}\frac{z^{j}}{\ell -j}+z^{\ell }\sum _{j=1}^{\ell }\frac{1}{j}, \end{aligned}$$

(179)

and

$$\begin{aligned} \int _{-1}^{z}{\mathrm{d}}v\frac{z^{\ell }-v^{\ell }}{z-v} =-\sum _{j=0}^{\ell -1}\frac{(-1)^{\ell -j}z^{j}}{\ell -j}+z^{\ell }\sum _{j=1}^{\ell }\frac{1}{j}, \end{aligned}$$

(180)

so that their combination gives

$$\begin{aligned}&2\int _{1}^{z}{\mathrm{d}}v\frac{z^{\ell }-v^{\ell }}{z-v}+ 2\int _{-1}^{z}{\mathrm{d}}v\frac{z^{\ell }-v^{\ell }}{z-v}\nonumber \\&\quad =-2\sum _{j=0}^{\ell -1}\frac{1+(-1)^{\ell -j}}{\ell -j} z^{j}+z^{\ell }\sum _{j=1}^{\ell }\frac{4}{j}. \end{aligned}$$

(181)

Gathering all pieces, one finds

$$\begin{aligned} I= & {} \frac{3}{2}C_n^{(3/2)}\left( z\right) \nonumber \\&- \sum _{k=0}^{\lfloor n/2 \rfloor } a_k^{(n)}\left[ \sum _{j=0}^{\ell -1}\left( \frac{1}{\ell +2}+\frac{1}{\ell +1} -\frac{2}{\ell -j}\right) \right. \nonumber \\&\times \left. \frac{1+(-1)^{\ell -j}}{2}z^{j} +\left( \frac{1}{\ell +2}+\frac{1}{\ell +1} +\sum _{j=0}^{\ell -1}\frac{2}{j+1}\right) z^{\ell }\right] .\nonumber \\ \end{aligned}$$

(182)

Now we exchange the sums over k and the first sum over j in the second line of the equation above by using the following equality:

$$\begin{aligned} \sum _{k=0}^{\lfloor n/2 \rfloor } \sum _{j=0}^{\ell -1}\dots =\sum _{k=0}^{\lfloor n/2 \rfloor } \sum _{j=0}^{n-2k-1}\dots = \sum _{j=0}^{n-1}\sum _{k=0}^{\lfloor \frac{n-j-1}{2} \rfloor }\dots , \end{aligned}$$

(183)

finding

$$\begin{aligned} I= & {} \frac{3}{2}C_n^{(3/2)}\left( z\right) \nonumber \\&- \sum _{j=0}^{n-1}z^{j} \frac{1+(-1)^{n-j}}{2}\sum _{k=0}^{\lfloor \frac{n-j-1}{2} \rfloor } a_k^{(n)}\nonumber \\&\times \left( \frac{1}{n-2k+2}+\frac{1}{n-2k+1} -\frac{2}{n-2k-j}\right) \nonumber \\&- \sum _{k=0}^{\lfloor n/2 \rfloor } z^{\ell } a_k^{(n)}\left( \frac{1}{\ell +2}+\frac{1}{\ell +1} +\sum _{j=0}^{\ell -1}\frac{2}{j+1}\right) . \end{aligned}$$

(184)

where in the first line we have made explicit $\ell =n-2k$ and used the equality

$$\begin{aligned} \frac{1+(-1)^{\ell -j}}{2} = \frac{1+(-1)^{n-2k-j}}{2}=\frac{1+(-1)^{n-j}}{2}. \end{aligned}$$

(185)

This projector nullifies all the terms in the first series over j for which $n-j$ is odd, selecting only the even ones. Therefore, we can identify the combination $n-j$ with an even index, i.e. $n-j=2h$, and remove the projector. Replacing the summation index k with h and also making explicit the index $\ell$ in the second line gives

$$\begin{aligned} I= & {} \frac{3}{2}C_n^{(3/2)}\left( z\right) \nonumber \\&- \sum _{h=0}^{\lfloor n/2 \rfloor }a_h^{(n)}z^{n-2h} \Bigg [\frac{1}{n-2h+2}+\frac{1}{n-2h+1}\nonumber \\&\quad + 2\sum _{j=1}^{n-2h}\frac{1}{j} + \sum _{j=1}^{h} \frac{a_{h-j}^{(n)}}{a_h^{(n)}}\left( \frac{1}{n-2h+2j+2}\right. \nonumber \\&\quad \left. +\frac{1}{n-2h+2j+1}-\frac{1}{j}\right) \Bigg ]. \end{aligned}$$

(186)

It turns out that the term in the square brackets is independent of the summation index h (this statement can be easily verified numerically). Therefore, without loss of generality, we can set $h=0$ inside the square brackets and pull it out from the summation symbol, obtaining

$$\begin{aligned} I= & {} \left[ \frac{3}{2}-\frac{1}{n+2}-\frac{1}{n+1}- 2\sum _{j=1}^{n}\frac{1}{j}\right] C_n^{(3/2)}\left( z\right) \nonumber \\= & {} \left[ \frac{3}{2}+\frac{1}{(n+1)(n+2)}- 2\sum _{j=1}^{n+1}\frac{1}{j}\right] C_n^{(3/2)}\left( z\right) , \end{aligned}$$

(187)

which finally proves the identity in Eq. (86).