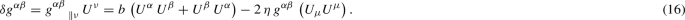Abstract
Using the Gödel metric, we obtain some relevant solutions compatible with spatiotemporal jumps for the geodesic equations, by using an extension of General Relativity with nonzero boundary terms, which are described on an extended manifold generated by the connections \(\delta \Gamma ^{\mu }_{\alpha \beta } = b\,U^{\mu }\,g_{\alpha \beta }\). These terms are given by a flow of velocities with components \(U^{\nu }\): \(3\,b^2\,\nabla _{\nu }U^{\nu }=g^{\alpha \beta }\, \delta R_{\alpha \beta } = \lambda \left[ s\left( x^{\alpha }\right) \right] \,g^{\alpha \beta }\, \delta g_{\alpha \beta }\) in the varied Einstein–Hilbert action. The solutions are valid for an arbitrary equation of state with ordinary matter: \(\Omega =P/(c^2\,\rho ) = \frac{\left( \frac{\omega }{c}\right) ^2-\lambda (s)}{\left( \frac{\omega }{c}\right) ^{2}+\lambda (s)}\).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and motivation
A few years ago, was introduced an extension of General Relativity in which we use a geometrical displacement from a semi-Riemann manifold to an extended one, in order for describe physical systems in which boundary conditions are physically relevant. In such formalism, back-reaction effects [1,2,3,4,5,6] are described as nonperturbative geometric fluctuations with respect to the background semi-Riemann manifold [7,8,9], in the framework of an extended General Realtivity with boundary terms included. Other approaches on extended manifolds have been considered in the framework of the Weyl connections [10,11,12,13,14].
In 1949, Gödel discovered unexpected solutions to the Einstein equations corresponding to universes in which no universal temporal ordering is possible [15]. An hypothetical habitant of such a universe could, in principle, travel to his own past. The geodesic solutions obtained from the Gödel proposal has many unusual properties, such that the existence of closed timelike curves that would allow time travel in a universe. Its definition is somewhat artificial in that the value of the cosmological constant must be carefully chosen to match the density of the dust grains, but this spacetime is an important pedagogical example.In his work it is considered that the pressure \(P=0\), so that the universe is dust dominated. However, it is very interesting the fact that the energy density \(\rho \) is positive, so that, in principle some type of exotic matter would not be necessary to travel to the past. The Gödel universe is a system with angular velocity \(\omega \), that rotates along the z-axis.
In this work we introduce a new extended manifold to describe the dynamics of a Gödel system which interacts with an external system with a dynamics described by \(\lambda \left[ s\left( x^{\alpha }\right) \right] \), in a such manner that the system is no longer dominated by dust and can take an equation of state with ordinary matter. The extended manifold is generated by the components of the relativistic velocity that are related with a flow through the 3d-closed hypersurface that alters the dynamics of the Gödel’s universe. This is relevant for the geodesic equations, because self-interactions of relativistic observers modifies the own trajectories. We shall explore how can evolve this system when we take into account the boundary conditions when we variate the Einstein–Hilbert action [16]. The manuscript is organized as follows: In Sect. 2 se revisit of the Einstein–Hilbert action with boundary terms included in the Einstein’s equations. In Sect. 3 we introduce the varied curvature and the flux equation on the extended manifold, using varied connections which depends on the relativistic velocities. In Sect. 4 we obtain the geodesic equations for an external flow and we study the field equations of the stress tensor for a perfect fluid. In Sect. 5 we study the Gödel system introduced in 1949 with the taking into account the boundary terms in the dynamics for the geodesic equations. Some spatiotemporal closed solutions compatible with spatiotemporal jumps are obtained. Finally, in Sect. 6 we add some concluding remarks.
2 Extension of General Relativity with an extended manifold
We consider the Einstein–Hilbert action \(\mathcal{I}\), which describes gravitation and matter
where \(\kappa = 8 \pi G/c^4\), G is the cosmological constant, \({\mathcal{L}_m}\) is the Lagrangian density that describes the background physical dynamics and R is the background scalar curvature, and g is the determinant of the background metric tensor \(g_{\alpha \beta }\), such that the line element is defined by \(ds^2= g_{\alpha \beta }\,dx^{\alpha } dx^{\beta }\).Footnote 1 We consider the variation of the Einstein–Hilbert action (1), with boundary terms included:
The last terms in (2) are very important and cannot be neglected in the dynamics of the system. These terms \( {g}^{\alpha \beta } \delta R_{\alpha \beta }= \delta \Phi \), describes the flux of the 4-vector \(\delta W^{\alpha }=\delta \Gamma ^{\epsilon }_{\beta \epsilon } {g}^{\beta \alpha }-\delta \Gamma ^{\alpha }_{\beta \gamma } {g}^{\beta \gamma }\), through the 3D closed hypersurface \(\partial M\). An important case results when the varied Ricci tensor: \(\delta R_{\alpha \beta }\), is related to the variation of the metric tensor [17]
Here, \(\lambda \left[ s\left( x^{\alpha }\right) \right] \) is a function of all the coordinates \(x^{\alpha }\). The covariant derivative of \(g_{\alpha \beta }\) on the extended manifold is nonzero: \(\nabla _{\nu }g_{\alpha \beta }=0\). Therefore, using the propose (3) and the fact that \(\delta \left[ g_{\alpha \beta }\, g^{\alpha \beta }\right] =0\), we obtain that the varied action \(\delta \mathcal{I}\) in (2), is
where \({\bar{T}}_{\alpha \beta }\) is the background stress tensor: \({\bar{T}}_{\alpha \beta } = 2 \frac{\delta {\mathcal{L}_m}}{\delta g^{\alpha \beta }} - g_{\alpha \beta } {\mathcal{L}_m}\). Therefore, the dynamics of the system with boundary conditions included will be given by the Einstein equations with the boundary terms assimilated, that now takes the form
The boundary terms with \(\lambda \left[ s\left( x^{\alpha }\right) \right] \) in (5) can be assimilated to the Einstein tensor, or the stress tensor. In the first case the boundary additional terms in the Einstein equations should be considered as geometrical sources, but in the second one, they are of physical nature and the redefined stress tensor is given by
and the dynamics for the physical fields is given by the equation
where the geometric dynamics is given by the equation \(\nabla _{\beta }\,G^{\alpha \beta }=0\). This means that the flux due to the boundary terms in the minimized action will be the source for the dynamics of the physical fields. In a cosmological context, \(\lambda \left[ s\left( x^{\alpha }\right) \right] \) can be assimilated with a cosmological parameter, which in models which comply with a vacuum equation of state \(\Omega =P/(c^2\,\rho ) = -1\),Footnote 2\(\lambda \left[ s\left( x^{\alpha }\right) \right] \) has the same effect as an intrinsic energy density of the vacuum such that \(c^2\rho =-P = \frac{\lambda _0}{\kappa }\). Using the values known in 2018 and Planck units for a cosmological constant \(H_0= 67.66\,\,\pm \,\,0.42\,\mathrm{\left( \frac{km}{seg}\right) \frac{1}{Mpc}} = \left( 2.1927664 \pm 0.0136\right) \times 10^{-18} \,\mathrm{seg^{-1}}\), it is obtained the value of \(\lambda \left[ s\left( x^{\alpha }\right) \right] \) at the moment when radiation decoupled from matter [18]:
which is a very small value. In general, it is believed that \(\lambda \left[ s\left( x^{\alpha }\right) \right] \) has varied along the history of the universe. In this case the right hand of (7) must be taken into account in order to make a good relativistic description of the physical system [19, 20]. However, as we shall see later in this work, the conceptual meaning of \(\lambda \left[ s\left( x^{\alpha }\right) \right] \) is very much broader than the cosmological meaning.
3 Curvature on the extended manifold
With the aim to describe the curvature in the extended manifold, we shall consider the varied Ricci tensor as an extension of the Palatini expression [21]
Because we are interested to study the dynamics of relativistic velocities in a Gödel metric using EGR, in this note we shall propose the novel extension of the semi-Riemann manifold which can be generated by the connections
where \(U^{\alpha } = \frac{dx^{\alpha }}{ds}\) are the components of the relativistic velocity. The connections (9) takes into account the perturbed geometry of spacetime with respect to the semi-Riemann background manifold, which is described by the Levi–Civita connections \(\left\{ \begin{array}{cc} \alpha \, \\ \beta \, \nu \end{array} \right\} \):
The perturbations will be considered finite, but they can be large, because our formalism is non-perturbative. The closed 3d-hypersurface is finite and can be defined on any region of the background manifold. We shall consider cases where the metric is hyperbolic, so that
Here, \(\epsilon \) is a constant that can take the values \(\epsilon =0,\pm 1\). The case \(\epsilon =0\) corresponds to massless particles, and \(\epsilon =\pm 1\) correspond respectively to particles with nonzero mass with metrics with signature \((\pm ,\mp ,\mp ,\mp )\). Therefore, we can define the variation of the metric tensor on the extended manifold, asFootnote 3
Notice the additional last term in (14), which takes into account the effect of the massive test-particles on the varied metric tensor: \(\delta g_{\alpha \beta }\). The origin of this term in the last one in (12), that describes the interaction of the derived tensor (in this case \(g_{\alpha \beta }\)), with the field of the varied connection: \(U_{\mu }\). Another interesting fact is that \(\delta g= g^{\alpha \beta } \delta g_{\alpha \beta }=2\left( 4\eta - b\right) \,\epsilon \), so that one obtains a null flow \(\delta \Phi = \lambda \left[ s\left( x^{\alpha }\right) \right] \,\delta g=0\) for relativistic massless test particles with \(\epsilon =0\), or for the particular gauge: \(b=4\eta \). In such cases the Einstein equations (5) are not altered by the boundary terms:
In order for calculate the dynamics of the energy density we must use the varied action (2) with an external flow that affects the background dynamics: \( \delta g^{\alpha \beta }\left( G_{\alpha \beta } + \kappa {\bar{T}}_{\alpha \beta }\right) + g^{\alpha \beta } \delta R_{\alpha \beta } =0\). This expression takes the formFootnote 4
One interesting case is \(\eta = - 2b\). If we take into account the equation for the flow (17), we obtain
Notice that the right hand of (18) is the source of \(U^{\mu }\), which also depends on \(U^{\mu }=\frac{dx^{\mu }}{ds}\). This is because the self-interaction of the back-reaction effects. When the flux is null \(\delta \Phi =0\), we recover the background dynamics for \(U^{\mu }\) for the Eqs. (7) and (18): \(\nabla _{\nu } \,U^{\nu } = 0\), and \(\nabla _{\beta }\,{\bar{T}}^{\alpha \beta } = 0\). Therefore, the differential equation (18), takes the form
A singular case is that in which \(\lambda \left[ s\left( x^{\alpha }\right) \right] \) is a constant: \(\lambda \left[ s\left( x^{\alpha }\right) \right] \equiv \lambda _0\). In this case the boundary terms can be nonzero for \(\epsilon \ne 0\), but the field equations (7) are unmodified: \(\nabla _{\beta }{\bar{T}}^{\alpha \beta }=0\). Furthermore, the background equations: \(\nabla _{\nu } \,U^{\nu }=0\), must be modified by introducing the right side term in (19) for massive particles, but not for massless particles.
4 Geodesic equations in Extended General Relativity
The dynamics of the relativistic velocities in extended General Relativity are given by the expression \(\delta U^{\alpha }=0\), which, written in terms of the covariant derivatives on the extended manifold, takes the form \(U^{\beta } \,U^{\alpha }_{\Vert \beta } =0\). This expression can be expanded in terms of the semi-Riemann covariant derivative, and using the fact that \(\frac{d}{ds}= U^{\beta }\,\frac{\partial }{\partial x^{\beta }}\), we obtain
which, for \(\eta = -2b\), holds
The Eq. (21) give us the geodesic equations for a open relativistic system with boundary terms included, that takes into account self-interactions. These terms alter its own background dynamics, which is reflected in the source term on the right side of (21), as well as in the right side of (7). The reader can see that the background Einstein equations (5), are also altered by the second term of the left side: \( - \lambda \left[ s\left( x^{\alpha }\right) \right] \,{g}_{\alpha \beta }\). From the general relativistic point of view, this term takes into account how the space-time curvature produced by the massive test-particle alters his own background trajectory.
To make a complete description of a relativistic system we must specify the background stress tensor, which we shall assume that is a perfect fluid
where both, P and \(\rho \) are the pressure and energy density with boundary terms included. Hence, from (22) and (7), we obtain the geodesic equation for a perfect fluid with arbitrary pressure P and energy density \(\rho \), when the flux the crosses the 3d-hypersurface of the varied action (2) is considered. Using the Eq. (19) and the fact that \(\delta U^{\alpha }=0\), we obtain after multiplying by \(U_{\alpha }\), that
where we have used the fact that \(\frac{d}{ds}= U^{\beta }\,\frac{\partial }{\partial x^{\beta }}\) and \(P+c^2\rho =c^2\rho \left( 1+\Omega \right) \).
5 Gödel proposal with Extended General Relativity
We consider the coordinates \((\tau ,x,y,z)\), such that \(\tau =c\,t\), where c is the light velocity and t is the time. The line element \(ds^2=g_{\alpha \beta }\,dx^{\alpha } dx^{\beta }\) for the Gödel metric can be written
where \(\omega >0\) is a constant related with the vorticity of matter. The geodesic equations (21) for the Gödel metric (24), are
where the dot denotes the total derivative with respect to the line element s: \(U^{\alpha }={\dot{x}}^{\alpha }\equiv \frac{d x^{\alpha }}{ds}\). The contravariant components of the metric tensor are
The covariant components of the Einstein tensor are
where \(G_{\alpha \beta }\) is related with the stress tensor by the expression (5). Using the Einstein equations (5), we obtain that
where we have used the fact that \(g_{i\beta }\,g^{i\beta }=3\), \(g_{0\beta }\,g^{0\beta }=1\), \(g_{0\beta }\,U^0\,U^{\beta }=\,\epsilon \) and \(g_{i\beta }\,U^i\,U^{\beta }=0\). Here, P is the averaged pressure over the main three spatial exes of inertia, by using the expression:
In the following we shall study an application of Extended Relativity in the metric proposed by Gödel in 1949 [15], in order for study some particular solutions compatible with spatiotemporal jumps, when boundary conditions are taken into account in the varied Einstein–Hilbert action.
5.1 Particular solution for the Gödel proposal: spatiotemporal jumps
We consider the case for a massive test particle such that \(U^{\alpha }\,U_{\alpha } = 1\). In this case \(\epsilon =1\) and for an arbitrary flux with \(\lambda (s)\) the system will be described by an equation of state
Notice that the particular case considered by Gödel, in which the pressure is \(P=0\) and the physical system is in absence of any external flow in our case will be described by the choice \(\lambda =\left( \frac{\omega }{c}\right) ^2\) and \(b=0\). However, more interesting are the cases with \(\lambda \ne \left( \frac{\omega }{c}\right) ^2\) and \(b\ne 0\), because can be testable by experiments.
A particular solution of the system (25)–(28), is:
The solutions (35)–(38) are valid for an arbitrary equation of state (34), for
and therefore the varied connections (9), take the form
where the components for the relativistic velocity \(U^{\alpha }={dx^{\alpha }\over ds}\), are:
In order for the solutions to be consistent with relativistic causality, we must require that
From (42) we obtain that
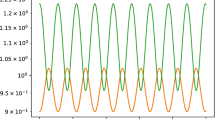
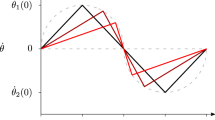
and from (43), it is required that \(x^2_0=\tau ^2_0\). In the Figs. 1 and 2 we have plotted the evolution of the geodesic curves \(\tau (s)\), x(s) and y(s), for \(\tau _0=x_0=0.5\,\sqrt{2} \,G^{1/2}\), \(y_0=0.5\,G^{1/2}\), \(\omega =\frac{1}{\tau _0\,\left[ 1+2\sqrt{2}\right] ^{1/2}}\,G^{-1/2}\) and \(c=1\). Notice that all the variables jump at \(s=(\frac{1}{2}+n)\pi \,\left( \frac{c}{\omega }\right) \), (with n-integer). In particular, \(\tau (s)\) jumps towards the past of the relativistic observer and later continues evolving from its past until the following cycle describing a closed orbit.
6 Final comments
In this work we have studied the Gödel’s original system by using an extension of General Relativity where nonzero boundary terms are included in the global dynamics of the system. In this framework, the geodesic equations are altered as son as the field equations for the stress tensor \(T_{\mu \nu }\), which was considered as a ideal fluid. Some similar results were obtained for geodesic equations in a cosmological framework from a five dimensional vacuum in General Relativity [22], for a massive and confined test particle in a four dimensional spacetime where the effective equation of state is vacuum dominated: \(\Omega =-1\). However in such case the extra force in the geodesic equation being induced by the extra dimension on the four dimensional spacetime. In the approach here studied the relevant fact is that the extra term can be experimentally manipulated through \(\lambda \left[ s(x^{\alpha })\right] \). In particular, we have obtained new relevant geodesic solutions of the geodesic equations which are compatible with spatiotemporal jumps for standard matter which is compatible with an equation of state that depends on \(\lambda \left[ s(x^{\alpha })\right] \), which is a function that characterizes the flux [see Eq. (34)] and could be assimilated with a potential function. The interesting of the results here obtained is that the energy density is positive and the geodesic trajectories obtained are compatible with a massive test mass, so that they could be testable in a laboratory with the manipulation of \(\lambda (s)\). The main difference with the Gödel solutions [15] is that, meanwhile in both cases timelike trajectories are closed curves (see Fig. 1), in our case the trajectories are not derivable at the points \(s=(\frac{1}{2}+n)\pi \,\left( \frac{c}{\omega }\right) \), (with n-integer). For this reason we identify those points as those where a spacetime jump occurs. The jumps are spatiotemporal because the discontinuities also occur on the x(s) and y(s) trajectories [see the solutions (35)–(38)], which also are closed and continues (see Fig. 2). The components of the relativistic velocities are summarized in (41) and the varied connections that generate the extended manifold take the form given in (40). The importance of these solutions is that they are valid only for massive test particles, because when particles are massless we recover in (21) the geodesic differential equations obtained by Gödel in his original manuscript [15]. This particular case corresponds to a null flow \(\delta \Phi =0\), due to the fact \(\delta g=g^{\alpha \beta }\,\delta g_{\alpha \beta }=0\) for \(\epsilon =0\). To finalize, a remarkable point of the approach here introduced is that the original system proposed by Gödel is dust dominated [i.e. for \(P=0\)], but the system here proposed is described by an equation of state with ordinary matter: \(\Omega =P/(c^2\,\rho ) = \frac{\left( \frac{\omega }{c}\right) ^2-\lambda (s)}{\left( \frac{\omega }{c}\right) ^2+\lambda (s)}\), such that the Gödel particular system is recovered when \(\lambda (s)\) is a constant that takes the value \(\lambda _0=\left( \frac{\omega }{c}\right) ^2\) and the test particles are massless with \(\epsilon =0\).
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: The work is purely mathematical and all the techniques are standard. Thus there is no data required to be deposited.]
Notes
Along the note, we shall consider that Arabic letters run from 1 to 3 (to describe spatial coordinates), and that Greek letters run from 0 to 4.
Here, c is the light velocity and \(\rho \), P are respectively the energy density and the pressure.
We shall denote as \(\delta g_{\alpha \beta }\) the variations of \(g_{\alpha \beta }\) on the extended manifold, and the variations on the semi-Riemannian manifold is \(\Delta g_{\alpha \beta }=0\). In general, this notation will be used for any tensor along the work. The covariant derivative of the metric tensor on the extended manifold, with self-interactions included can be defined as

so that \(\delta g_{\alpha \beta }\) is given by

We use the expression
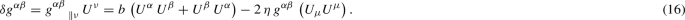
References
N.C. Tsamis, R.P. Woodard, Ann. Phys. 253, 1 (1997)
H.J. De Vega, Norma G. Sánchez, Phys. Rev. D 50, 7202 (1994)
M. Bellini, Nuovo Cim. B 119, 191 (2004)
R.H. Brandenberger, J. Martin, Phys. Rev. D 71, 023504 (2005)
Wu. Puxun, Hong Wei Yu, JCAP 0605, 008 (2006)
A. Tronconi, G. Venturi, Phys. Rev. D 84, 063517 (2011)
M.R.A. Arcodía, M. Bellini, Eur. Phys. J. C 76, 326 (2016)
M. Bellini, Phys. Dark Univ. 31, 100773 (2021)
M. Bellini, L.S. Ridao, Phys. Lett. B 835, 136901 (2022)
H. Weyl, Gravitation and electricity. Sitzungsber. Preuss. Akad. Wiss. Berlin (Math. Phys.) 1918, 465 (1918)
H. Weyl, Space, Time, Matter (Dover Publications, New York, 1952)
Markus J. Pflaum, Lett. Math. Phys. 45, 277 (1998)
Kuo-Wei. Huang, Nucl. Phys. B 879, 370 (2014)
I.P. Lobo, A.B. Barreto, C. Romero, Eur. Phys. J. C 75, 448 (2015)
K. Gödel, Rev. Mod. Phys. 21, 447–450 (1949)
M. Bellini, L.S. Ridao, Phys. Lett. B 825, 136901 (2022)
A. Morales, M. Bellini, Phys. Dark Univ. 34, 100895 (2021)
N. Aghanim et al., (Planck) A & A 641, A8 (2020)
M. Bellini, Phys. Scr. 96, 065301 (2021)
M. Bellini, P.A. Sánchez, Eur. Phys. J. C 81, 1137 (2021)
A. Palatini. Deduzione invariantiva delle equazioni gravitazionali dal principio di Hamilton. Rend. Circ. Mat. Palermo 43, 203–212 (1919) [English translation by R.Hojman and C. Mukku in P.G. Bergmann and V. De Sabbata (eds.) Cosmology and Gravitation, Plenum Press, New York (1980)]
J.E. Madriz Aguilar, M. Bellini, Phys. Lett. B 679, 306 (2009)
Acknowledgements
M. B. acknowledges CONICET, Argentina (PIP 11220200100110CO), and UNMdP (EXA955/20) for financial support.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3. SCOAP3 supports the goals of the International Year of Basic Sciences for Sustainable Development.
About this article
Cite this article
Bellini, M. Spatiotemporal jumps as particular solutions in geodesic trajectories with the Gödel metric on an extended manifold. Eur. Phys. J. C 82, 817 (2022). https://doi.org/10.1140/epjc/s10052-022-10786-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-022-10786-z