1 Introduction

The pioneering direct detection of gravitational waves by the LIGO-Virgo collaboration [1, 2] and the first ever observed image of a supermassive BH at the center of the elliptic galaxy M87 by the Event Horizon Telescope (EHT) collaboration using very long baseline interferometry (VLBI) [3,4,5,6,7,8] have made grate impact on development of both theoretical and experimental/observational investigations in relativistic astrophysics. Meanwhile these two discoveries open window to research related to development of new tests of the gravity theories in the strong field regime. General relativity proposed by Albert Einstein has been successfully tested in weak field regime using, e.g. solar system tests [9]. Although the gravitational wave detection [10] and black hole shadow [3] observation justify the general relativity the current resolution of these observations leave open the window for the modified and alternative theories of gravity [11]. Accordingly, the numerous authors have started to develop the theoretical research devoted to study the effects of main parameters coming from the alternative theories of gravity on shadow and optical properties of black holes.

The original idea on possible observation of the shadow of the black hole has been first suggested by Synge in [12] and later the size of BH shadow has been deeply studied by Luminet [13] and by Bardeen [14]. After that, the shape and size of BH shadow in various theories of gravity have been extensively studied by numerous authors, see e.g. in [13, 15,16,17,18,19, 19,20,21,22,23, 23,24,25, 25,26,28, 28,29,49]. Since the formation of BH shadow is strongly related to effect of gravitational lensing in general relativity it is worth noting that there exists extensive current literature devoted to study the gravitational lensing effect in strong field regime, see e.g. in [50,51,52,53,54,55,56,57,58].

The presence of plasma around compact objects is very interesting and important evidence in the Nature. The plasma (of both inhomogeneous and homogeneous plasma density) effect on observational shape of BH shadow has been studied in various spacetimes in the recent literature (see, e.g. [38, 41, 59,60,61,62,63,64,65]). On the other hand the effects of plasma of different configurations on gravitational lensing and consequently on deflection angle of light rays in various BH spacetimes have been investigated, see e.g. in [63, 66,67,68,69,70,71,72,73,74,75,76].

Recently, in [77] a rotating regular black hole with asymptotically Minkowski core has been developed. It has been shown that the suggested Kerr-like geometry possesses the full “Killing tower” of nontrivial Killing, Killing-Yano, and principal tensors [77]. Earlier detailed study of the spherical symmetric regular black hole was performed by the same authors in [78]. Later, photon sphere, innermost stable circular orbits around regular black holes with asymptotically Minkowski cores have been studied in [79] and efect of plasma on gravitational weak lensing is also considered in Schwarzschild-like black hole in [80]. Now our main goal in this study is to develop earlier works on Kerr-like spacetime and investigate the optical properties of Kerr-like BHs. We also plan to study the effects of metric parameters and plasma on the shape and size of BH shadow.

The paper is organized as follows: In Sect. 2 we have studied the horizon structure and the equation of motion in Kerr-like spacetime metric. Observable BH shadow is considered in Sect. 3. Then, effect of plasma medium on BH shadow and photon motion are investigated in Kerr-like spacetime in Sect. 4. Finally, the detailed discussion of the obtained results is presented in Sect. 5. Whole of the work, we used geometric units system that fix the speed of light and the gravitational constant via \(G = c = 1\).

2 Kerr-like black hole

The gravitational field of a Kerr-like compact object in Boyer-Lindquist coordinates can be expressed through the following line element [77]

$$\begin{aligned} ds^2= & {} -\frac{\Delta _{eos}}{\rho ^2}(dt-a\sin ^2\theta d\phi )^2+\frac{\rho ^2}{\Delta _{eos}}dr^2+\rho ^2d\theta ^2 \nonumber \\&+\frac{\sin ^2\theta }{\rho ^2}\left( a dt-(r^2+a^2)d\phi \right) ^2. \end{aligned}$$
(1)

For the spacetime metric (1), the metric functions defined as

$$\begin{aligned} \rho ^2= & {} r^2+a^2\cos ^2\theta , \end{aligned}$$
(2)
$$\begin{aligned} \Delta _{eos}= & {} r^2+a^2-2 M r e^{-l/r}, \end{aligned}$$
(3)

where M is the BH mass, a is the spin parameter of the BH and l is deviation parameter which was introduced by Simpson and Visser in [77, 78]. The above space-time metrics refer to the case of the standard Kerr BH (\(l \rightarrow 0\)) and Schwarzschild BH (\(l \rightarrow 0\), and \(a \rightarrow 0\)) in general relativity in the limiting cases. In order to interpret the physical meaning of the parameter l introduced one has to first mention that in Ref. [77, 78] the exponential term into the spacetime metric has been included as general extension of rotating Kerr BH solution. Accordingly, one may treat that nonzero l parameter is parameterized extension of rotating BH solutions which covers Kerr one as special case when \(l=0\). On the other hand nonzero deviation parameter l bypass the physical singularity located at the origin of the BH solutions existing e.g. in the standard Kerr spacetime. Meanwhile, the Bardeen’s regular BH solution can be also characterized by this parameterized extension [77, 78].

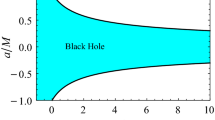
Now we analyze properties of horizon structure for Kerr-like BH with nonzero parameter l. Using eq. (3), one may study horizon in detail. Figure 1 shows the variation of the outer horizon with the change of parameter l. One may see that with the increase of parameter l the radius of outer horizon is decreased. In addition, we may get the extreme point for the parameter l and spin parameter a of the BH as shown in Fig. 2. We have found that there are BH and naked singularity regions and got the dependence of the boundary between them from the BH parameters a and l. The separatrix line indicates the decrease of the maximum value of the extremal BH spin with the increase of the parameter l. One can see that under the effect of the parameter l less value for BH spin is requested in order for an extremal black hole to be transformed into the naked singularity. In Fig. 3 we have shown the dependence of \(\Delta _{eos}\) from the radial coordinate. From the obtained dependence one may easily explain the extreme point for various values of BH parameters l and a. Radius of event horizon is decreased with the increase in BH parameters a, l. Accordingly, the Kerr-like BH has smaller event horizon radii than the Kerr BH with l parameter.

Fig. 1
figure 1

Variation of horizon radius with increase of BH spin parameter a for the selected values of parameter l

Full size image
Fig. 2
figure 2

The separatrix line indicates the border corresponding to extremal black holes which separates black holes from no black holes

Full size image
Fig. 3
figure 3

The dependence of delta function from the radial coordinate for selected values of the BH spin parameter a and parameter l: \(a=0.5\) (top, left panel); \(a=0.7\) (top, right panel); \(l=0.2\) (bottom, left) and \(l=0.4\) (bottom, right panel) with \(M=1\)

Full size image
Fig. 4
figure 4

Plots showing the radial dependence of the effective potential for chosen values of BH parameters a and l: \(a=0.5\) (top panel) and \(l=0.2\) (bottom panel)

Full size image

2.1 Null geodesics

In this subsection we investigate massless particle motion around BH described by the Kerr-like spacetime metric (1). The equations of motion properly describe the light rays trajectory around a compact object. The equations of motion of photon can be found using the Hamilton-Jacobi equation [81] as

$$\begin{aligned} \frac{\partial S}{\partial \lambda }=-\frac{1}{2}g^{\mu \nu }\frac{\partial S}{\partial x^{\mu }}\frac{\partial S}{\partial x^{\nu }}, \end{aligned}$$
(4)

where \(\lambda \) is an affine parameter and \(g^{\mu \nu }\) is the metric tensor. Using method of separation of variables, one can write action S for the photon as

$$\begin{aligned} S=-Et+L\phi +S_{r}(r)+S_{\theta }(\theta ), \end{aligned}$$
(5)

where \(E=-g_{t\mu }\dot{x}^{\mu }\) and \(L=g_{\phi \mu }\dot{x}^{\mu }\) are constants of motion (conserved quantities) and refer to the conserved energy and momentum of the particles, respectively. \(S_r(r)\), \(S_{\theta }(\theta )\) in (5) are the function of r and \(\theta \), respectively. Using the Eq. (5) and the Eq. (4) one may obtain the geodesic equations in the following form

$$\begin{aligned} \rho ^{2}\frac{dt}{d\lambda }= & {} a(L-aE\sin ^{2}\theta ) \nonumber \\&+\frac{r^{2}+a^{2}}{\Delta _{eos}}\Big (E(r^{2}+a^{2})-aL\Big ), \end{aligned}$$
(6)
$$\begin{aligned} \rho ^{2}\frac{dr}{d\lambda }= & {} \pm \sqrt{{\mathcal {R}}}, \end{aligned}$$
(7)
$$\begin{aligned} \rho ^{2}\frac{d\theta }{d\lambda }= & {} \pm \sqrt{\Theta }, \end{aligned}$$
(8)
$$\begin{aligned} \rho ^{2}\frac{d\phi }{d\lambda }= & {} (L\csc ^{2}\theta -aE)+\frac{a}{\Delta _{eos}}\Big (E(r^{2}+a^{2})-aL\Big ), \end{aligned}$$
(9)

where \(\mathcal {R}\) and \(\Theta \) have the following forms

$$\begin{aligned} \mathcal {R}= & {} \Big [(r^2+a^2)E-aL\Big ]^2-\Delta _{eos}\Big [\mathcal {K}+(L-aE)^2\Big ], \end{aligned}$$
(10)
$$\begin{aligned} \Theta= & {} \mathcal {K}+\cos ^2\theta \left( a^2 E^2-L^2\sin ^{-2}\theta \right) , \end{aligned}$$
(11)

where \(\mathcal {K}\) is the Carter constant. Using the expression for \({dr}/{d\lambda }\) one may rewrite connection between radial equation of motion and effective potential in the form

$$\begin{aligned} \left( \rho ^{2}\frac{dr}{d\lambda }\right) ^2+V_{eff}=0. \end{aligned}$$
(12)

The effective potential of radial motion in the equatorial plane (where \(\theta =\pi /2\)) has the following form

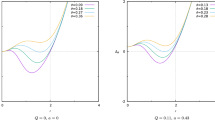
$$\begin{aligned} V_{eff}= & {} \frac{\Delta _{eos} ({{\mathcal {K}}} + (L - a E)^2)-((a^2 + r^2) E - a L)^2}{2r^4}.\nonumber \\ \end{aligned}$$
(13)

Using the expression (13) one may plot the graphs of the dependence of the effective potential from the radial coordinate. Figure 4 shows the radial dependence of the effective potential of radial motion of photons for the selected values of a an l. It is the general property of effective potential with respect to circular orbits (or photon orbits) for different values of spacetime metric. One can see that a peak of the effective potential corresponding to photon orbit is increased and shifted towards the left direction with the increase of the value of spin parameter a, and parameter l. It can be seen from the plots of the effective potential that the photon orbits come more closer towards the central object with an increase in the rotation parameter a and parameter l in Kerr-like spacetime metric.

3 Black hole shadow

In order to study the shadow of a BH one may introduce the following impact parameters \(\xi = L/E\) and \(\eta = \mathcal {K} /E^2\) and obtain the following equation for R(r) as

$$\begin{aligned} \mathcal {R}= & {} \Big [(r^2+a^2)-a\xi \Big ]^2-\Delta _{eos}\Big [\eta +(\xi -a)^2\Big ]. \end{aligned}$$
(14)

The following conditions should be satisfied in order to have unstable circular orbits of photons

$$\begin{aligned} \mathcal {R}=0,\quad \frac{\partial \mathcal {R}}{\partial r}=0, \quad \frac{\partial ^2 \mathcal {R}}{\partial r^2}<0, \end{aligned}$$
(15)

where the parameters \(\xi \) and \(\eta \) describe the borders of the BH shadow. Using Eqs. (14) and (15) one can get \(\xi \) and \(\eta \) as

$$\begin{aligned} \xi= & {} \frac{\left( a^2+r^2\right) \Delta _{eos}'-4 \Delta _{eos} r}{a \Delta _{eos}'}, \end{aligned}$$
(16)
$$\begin{aligned} \eta= & {} \frac{r^2 \left( 16 \Delta _{eos} \left( a^2-\Delta _{eos}\right) -r^2 \Delta _{eos}'^2+8 \Delta _{eos} r \Delta _{eos}'\right) }{a^2 \Delta _{eos}'^2},\nonumber \\ \end{aligned}$$
(17)
$$\begin{aligned}&r+2\frac{\Delta _{eos}}{\Delta _{eos}'^2}(\Delta _{eos}'-r\Delta _{eos}'')>0, \end{aligned}$$
(18)
Fig. 5
figure 5

Shadow of the Kerr-like black hole for selected values of parameter l at fixed values for BH spin a (left panel \(a=0.5\), right panel \(a=0.7\)) and for selected values of a at fixed l (left panel \(l=0.1\), right panel \(l=0.2\)) with \(M=1\)

Full size image
Fig. 6
figure 6

Shadow of the Kerr-like black hole for selected values of parameter l at fixed values for BH spin a and for selected values of a at fixed l for the different inclination angles with \(M=1\)

Full size image
Fig. 7
figure 7

The dependence of BH shadow area A from the parameters of Kerr-like black hole. Top panel is for dependence from deviation l for selected values of BH spin a. Bottom panel is for dependence from BH spin a for selected values of deviation l

Full size image
Fig. 8
figure 8

The dependence of the oblateness D from the parameters of Kerr-like black hole. Top panel is for dependence from deviation l for selected values of BH spin a. Bottom panel is for dependence from BH spin a for selected values of deviation l

Full size image
Fig. 9
figure 9

Contour plots of the observables \(A/M^2\) and D in the parameter space (a/M, l/M) of rotating Kerr-like black hole. Dashed red curves correspond to constant contours of \(A/M^2\) while the blue solid curves correspond to 15 equispaced constant contours of D ranging from 0.914 to 0.998

Full size image

The shadow of a rotating BH is described by the null geodesics represented in celestial coordinates \( \alpha \) and \( \beta \) [18, 21]

$$\begin{aligned} \alpha= & {} \lim _{r\rightarrow \infty } \bigg (-r^{2}\sin \theta \frac{d\phi }{dr} \bigg |_{\theta \rightarrow \theta _{0}}\bigg ) =-\xi \csc \theta _{0}, \end{aligned}$$
(19)
$$\begin{aligned} \beta= & {} \lim _{r\rightarrow \infty } \bigg (r^{2}\frac{d\theta }{dr}\bigg |_{\theta \rightarrow \theta _{0}}\bigg ) \nonumber \\= & {} \pm \sqrt{\eta +a^{2}\cos ^{2}\theta _{0}-\xi ^{2}\cot ^{2}\theta _{0}}. \end{aligned}$$
(20)

We analyze BH shadow in an equatorial plane (\(\theta _0 = \pi /2\)) where Eqs. (19) and (20) can be rewritten in the form

$$\begin{aligned} \alpha= & {} -\xi \end{aligned}$$
(21)
$$\begin{aligned} \beta= & {} \pm \sqrt{\eta }. \end{aligned}$$
(22)

In order to obtain the silhouette of the BH shadow one may plot the line described by the \(\xi \) vs \(\eta \) in the celestial coordinates. Figure 5 shows the shadows of the BH for selected values of the BH spin parameter a and parameter l of Kerr-like spacetime. It can be seen from the results (see Fig. 5) that the size of the BH shadow is decreased with increasing parameter l of the Kerr-like BH. Under influence of BH spin parameter a, pure circle for the border of BH shadow is violated. Additionally, in Fig. 6 the silhouette of the BH shadow for the different values of inclination angle of observer’s site has been explored.

It is well known that any spherically symmetric black hole will form shadow in perfectly circle form. For axial symmetric black hole, the shadow is distorted and Hioki and Maedia [18] have first introduced two parameters as radius for the size of BH shadow and deflection to fully describe them. There were other approaches and among them is the coordinate independent formalism developed in [36] to study distortion of borderline of shadow. Accordingly, one may introduce the area of BH shadow A and oblateness D (compared to the circle) being associated with the deformation of the black hole shadow in the following form

$$\begin{aligned} A= & {} 2\int _{r_-}^{r_+} \left( \beta (r) \frac{d\alpha (r)}{dr}\right) dr, \end{aligned}$$
(23)
$$\begin{aligned} D= & {} \frac{\Delta \alpha }{\Delta \beta },\ . \end{aligned}$$
(24)

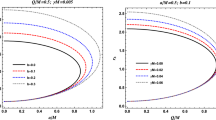
The area A with respect to parameters a and l can be calculated based on the results of Fig. 5. Figure 7 illustrates the dependence of the area of the BH from the metric parameters a and l. From Fig. 7 one can conclude that the increase of the parameters l and a leads to the decrease of the size of the BH shadow. Similar behaviour has been observed for the dependence of oblateness parameter shown in Fig. 8, as the parameters a and l are increased, the oblateness is decreased. We have also presented the contour plots to analyse BH parameters in Fig. 9 which may provide a tool to get information about parameters being responsible for the Kerr-like spacetime. The dependence of the radius of the BH shadow from different values of BH parameters is shown in the Table 1. One can see that the increase of spin and/or deviation parameters leads to the decrease of the size of the BH shadow radius and oblateness parameter.

4 Black hole shadow in the presence of plasma

In this section we will analyze the shadow of Kerr-like BH in the plasma environment for the different distribution of plasma.

4.1 Photon motion in a plasma

First, we plan to discuss photon motion around Kerr-like BH in the presence of plasma for its further application to analyze the dependence of observable radius of BH shadow from the plasma properties. One may use the the Hamiltonian for light rays propagating around a black hole surrounded by plasma to obtain the equation of motion in the form [12, 62]:

$$\begin{aligned} \mathcal {H}=\frac{1}{2}\Big [g^{\mu \nu }p_{\mu }p_{\nu }+\omega _{\text {p}}(x)^2\Big ]\ , \end{aligned}$$
(25)

where \(\omega _p\) is the electron plasma frequency defined as [66]

$$\begin{aligned} \omega _p(x)^2=\frac{4\pi e^2}{m_e}N_e(x)\ , \end{aligned}$$
(26)

with e and \(m_e\) are the charge and mass of electron, respectively, \(N_e\) is the number density of electrons. EHT collaboration has presented the image of M87* SMBH in polarised light estimating a signature of magnetic fields, in close vicinity to the edge of a black hole [82]. The observations of polarization by EHT suggest that the magnetic fields at the black hole’s edge are strong enough and in agreement with theoretical predictions. According to the EHT observations, the gas that slips through the magnetic field spirals inwards to the event horizon of M87* SMBH [82]. It is usually assumed that the plasma density along the photon trajectory in the vicinity of the gravitational compact objects is of the order of \(10^5\) cm\(^{-3}\). The effect depends on the temperature of the plasma in a nonexplicit way which means that temperature can be arbitrary. However, with the increase in the temperature plasma becomes more uniform. On the other hand, the radiative temperature of the plasma in the accretion disk around SMBH is in the ultraviolet wavelength. These facts give us the opportunity to use the plasma density as shown in Eq. (26) as toy model to describe the photon-plasma interaction near the black holes.

The Hamilton-Jacobi equation for the photon can be expressed as

$$\begin{aligned} \mathcal {H}\Big (x,\frac{\partial S}{\partial x}\Big )=0\ . \end{aligned}$$
(27)

One may use the method of separation of variables and introduce the action in the separable form

$$\begin{aligned} S=-\omega _0 t+p_{\phi }\phi +S_{r}(r)+S_{\theta }(\theta )\ , \end{aligned}$$
(28)

where \(p_{\phi }\), \(\omega _0\) are conserved quantities which are angular momentum and energy of the test particle, respectively. The plasma frequency model is chosen in the following form:

$$\begin{aligned} \omega _p(x)^2=\frac{f(r)+g(\theta )}{\rho ^2}\ , \end{aligned}$$
(29)

where f(r) and \(g(\theta )\) are the functions related to the radial and angular parts [83], respectively. Substituting (28) and (29) into Eq. (27), one may get the following expression

$$\begin{aligned}&\frac{a^2\Delta _{eos} \sin ^2\theta -(r^2+a^2)^2}{\Delta _{eos}}\omega _0^2 + \frac{4aMre^{-l/r}}{\Delta _{eos}}\omega _0p_\phi \nonumber \\&\quad +\Delta _{eos} (S'_r)^2 +(S'_\theta )^2+ \frac{\Delta _{eos}-a^2\sin ^2\theta }{\Delta _{eos} \sin ^2\theta }p^2_\phi \nonumber \\&\quad + f(r)+g(\theta )=0 \ , \end{aligned}$$
(30)

in the Kerr-like spacetime in presence of plasma medium. Then, using the Carter constant \({{\mathcal {K}}}\) one may separate the equation into two parts as

$$\begin{aligned} (S'_\theta )^2+\big (a\omega _0\sin \theta -\frac{p_\phi }{\sin \theta }\big )^2+g(\theta )=\mathcal {K}, \end{aligned}$$
(31)
$$\begin{aligned} \frac{1}{\Delta _{eos}} -\Delta _{eos} (S'_r)^2 ((r^2+a^2)\omega _0-ap_\phi )^2-f(r)=\mathcal {K}\ .\nonumber \\ \end{aligned}$$
(32)

Using the Eq. (30) one can get equation of motion around BH in the presence of plasma as

$$\begin{aligned} \rho ^{2}\frac{dt}{d\tau }= & {} a(p_\phi -a\omega _0\sin ^{2}\theta ) +\frac{r^{2}+a^{2}}{\Delta _{eos}} P(r), \end{aligned}$$
(33)
$$\begin{aligned} \rho ^{2}\frac{dr}{d\tau }= & {} \pm \sqrt{\mathcal {R}}, \end{aligned}$$
(34)
$$\begin{aligned} \rho ^{2}\frac{d\theta }{d\tau }= & {} \pm \sqrt{\Theta }, \end{aligned}$$
(35)
$$\begin{aligned} \rho ^{2}\frac{d\phi }{d\tau }= & {} \frac{p_\phi }{\sin ^{2}\theta }-a\omega _0+\frac{a}{\Delta _{eos}}P(r)\ , \end{aligned}$$
(36)

where P(r) is introduced for simplicity and has the form

$$\begin{aligned} P(r)=(r^2+a^2)\omega _0-ap_\phi \ , \end{aligned}$$
(37)

\(\mathcal {R}\) and \(\Theta \) are the functions related to the radial and angular equations of motion, respectively, and have the following form:

$$\begin{aligned} \mathcal {R}= & {} P(r)^2-\Delta _{eos}\Big [\mathcal {Q}+(p_\phi -a\omega _0)^2+f(r)\Big ], \end{aligned}$$
(38)
$$\begin{aligned} \Theta= & {} \mathcal {Q}+\cos ^2\theta \left( a^2\omega ^2-p_\phi ^2\sin ^{-2}\theta \right) -g(\theta ), \end{aligned}$$
(39)

where \(\mathcal {Q}=\mathcal {K}-(p_\phi -a\omega _0)^2\).

Table 1 Estimated values of BH parameters a/M and l/M from shadow observables \(A/M^2\) and D
Full size table
Fig. 10
figure 10

Shadow of a Kerr-like black hole with spin \(a=0.5\) surrounded by a Shapiro type plasma distribution with \(f(r)=\omega _c^2\sqrt{M^3r}\), as viewed by an equatorial observer

Full size image
Fig. 11
figure 11

The area (A) and the oblateness (D) of the shadow of a Kerr-like black hole with spin \(a/M = 0.5\) in a Shapiro-type plasma distribution with \(f(r)=\omega _c^2\sqrt{M^3r}\), as viewed by an equatorial observer

Full size image

4.2 Shadow of black hole in plasma

In order to find the shadow of a black hole one needs to evaluate the boundary of light rays. Accordingly, one may use the conditions \(\mathcal {R}=0\) and \(\mathcal {R}'=0\). From these conditions one can derive the constants of motion \(\mathcal {Q}\) and \(p_\phi \) in terms of the radius r of the circular photon orbits as

$$\begin{aligned} \mathcal {Q}= & {} \frac{\left( a p_\phi - \omega _0 \left( a^2+r^2\right) \right) ^2}{\Delta _{eos}}-(p_\phi -a \omega _0)^2-f(r), \end{aligned}$$
(40)
$$\begin{aligned} p_\phi= & {} \frac{\omega _0}{a}\left[ r^2+a^2- \frac{\Delta _{eos}}{a \Delta _{eos} '} \left( \sqrt{4 r^2-\frac{f'(r) \Delta _{eos} '(r)}{\omega _0}}+2 r \right) \right] .\nonumber \\ \end{aligned}$$
(41)

One may now use the celestial coordinates to represent the silhouette of BH shadow and in presence of plasma it can be expressed in the form [83]

$$\begin{aligned} \alpha= & {} -\frac{p_\phi }{\omega _0\sin {\theta _0}}, \end{aligned}$$
(42)
$$\begin{aligned} \beta= & {} \pm \frac{1}{\omega _0}\sqrt{\mathcal {Q}+\cos ^2{\theta _0}\Big (a^2\omega _0^2-\frac{p_\phi ^2}{\sin ^2{\theta _0}}\Big )-g(\theta _0)}. \end{aligned}$$
(43)

Here we choose plasma frequency as [83]

$$\begin{aligned} f(r)= & {} \omega _c^2\sqrt{M^3r}, \end{aligned}$$
(44)
$$\begin{aligned} g(\theta )= & {} 0, \end{aligned}$$
(45)

with

$$\begin{aligned} \omega _p^2= & {} \omega _c^2\frac{\sqrt{M^3r}}{r^2+a^2\cos ^2\theta }\ , \end{aligned}$$
(46)

where \(\omega _c\) is a constant and M is the mass of the black hole.

Combining Eqs. (42), (43), (44), and (45) in equatorial plane one may easily get BH shadow plots. Figure 10 shows the shadow of the BH for the different values of metric and plasma parameters. It can be seen from this graph that with an increase in the plasma parameter surrounding the BH, the size of the BH shadow decreases, as well as the same effect observed on the parameters l, a.

Now to get more detailed information on observable quantities of BH shadow we may consider again area A and oblateness parameter D. Above we have already used Eqs. (23) and (24) and here using these equations we may also study BH shadow in the presence of plasma medium. The dependence of area and oblateness parameter from metric and plasma parameters has been represented in Fig. 11. It can be seen that as the parameters l, a, \(\omega _c^2/\omega _0^2\) increase, the area of the BH shadow decreases. The contour plot generated to estimate the parameters in the presence of plasma has been shown in Fig. 12. From this graph we may get constrains for Kerr-like parameters. The numerical results for the dependence of radius of the BH shadow from metric and plasma parameters are shown in Table 2. One can see that with the increase of plasma frequency the size of the BH shadow radius and oblatness parameter decrease.

Fig. 12
figure 12

Contour plots of the observables \(A/M^2\) and D in the rotating Kerr-like black hole parameter space (\(\omega _c^2/\omega _0^2\), l/M) wit the presence of plasma for \(a/M=0.5\). Dashing red curves and solid blue curves correspond to constant contours of \(A/M^2\) and D respectively

Full size image

5 Conclusions and discussions

In this work we have studied in detail the shadow of the Kerr-like BH described by line element  (1). The obtained results can be summarized based on the following statements:

  • The structure of the rotating BH horizon in the presence of the additional Kerr-like parameter l is studied. Radius of horizon of the BH is decreased under effect of the parameter l which is presented in Fig. 1.

  • The orbits of photons in Kerr-like spacetime have been analyzed using the effective potential. It has been shown that with the increase the spin parameter a of the BH and the parameter l in Kerr-like space-time the circular orbits of photon around a BH shift toward the central object.

  • The equation of motion of the photon around BH in Kerr-like spacetime metric is obtained analytically using the Hamilton-Jacobi equation and the separability method. The shadow of BH in celestial coordinates is obtained from the geodesic equations  (see Fig. 5).

  • We have analyzed two observable parameters of shadow of BH, namely, area of BH shadow and oblateness parameter in Kerr-like spacetime. With the increase of the parameters l and a of the Kerr-like BH the size of radius BH shadow decrease, so does the oblateness of BH shadow.

  • In addition, we have also studied the effect of plasma on the observable parameters which are the radius of the BH shadow and the oblateness parameter. From our numerical results, it can be seen that the radius of the BH shadow decreases and the properties for the oblateness parameter are the same in the presence of a plasma medium.

Table 2 Estimated values of BH parameter l/M and plasma parameter from shadow observables \(A/M^2\) and D for \(a/M=0.5\)
Full size table