1 Introduction

Knot theory in 3d is currently among the most important topics in theoretical physics. It is closely related to the well studied conformal Wess–Zumino–Witten model in 2d, which is fully controlled by group theory. On the other hand, this is the theory where observables are the true Wilson lines, like in 4d gauge theories, which we understand much worse. Still, the theory is topological, and the averages do not depend on the shape of integration contours, only on the way they are knotted and linked. This puts knot theory at the border between group theory and quantum field theory, and it is usually at such borders that the new knowledge is generated intensively and fast. From the point of view of field theory the most important is the possibility to go beyond perturbation theory and study the implication of symmetries for non-perturbative correlators. As already known from conformal field theory in 2d the symmetries are naturally deformed, and the underground machinery is that of quantum groups and \({{\mathcal {R}}}\)-matrices.

Wilson line averages for \(\mathfrak {sl}_N\) in knot theory are named HOMFLY-PT polynomials and they are described by matrix elements of \({{\mathcal {R}}}\)-matrix products along various braids. Somewhat surprisingly they are indeed polynomials in non-perturbative variables \(q=\exp \left( \frac{2\pi i}{g+N}\right) \) and \(A=q^N\) (these are the standard notations for \(\mathfrak {sl}_N\), the situation for other series of simple Lie algebras is similar). Generic representation theory constrains the dependence of HOMFLY-PT polynomials on representation R, which is used to define the Wilson line

$$\begin{aligned} H_R^{{\mathcal {K}}} = \left\langle {\textrm{Tr}}\,\!_R \, \textrm{Pexp}\left( \oint _{{\mathcal {K}}} {{\mathcal {A}}}\right) \right\rangle \end{aligned}$$
(1)

and these restrictions can be formulated in terms of the differential (cyclotomic) expansion [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36]. Despite the simplicity of definitions, this expansion is rather difficult to get and study even in particular examples, and we are still at the stage when new examples provide new insights. For recent developments in another direction – perturbative expansion of HOMFLY-PT polynomials, see [37, 38].

For every particular knot the differential expansion appears enhanced over requirements of the pure representation theory, and the level of enhancement is characterized by the defect. For zero defect the structure is almost two times stronger than anticipated, the enhancement decreases for larger defects, but it is always present. The puzzling story of defects is not yet broadly known, and there is a lot to study and understand.

The task of this paper is to to formulate a new hypothesis: that defect is invariant under the antiparallel evolution and linearly changes along the parallel one. We test this hypothesis on various examples. Dedicated technique for proving this kind of properties remains to be developed.

In Sect. 2 we remind the original definition of the differential expansion (DE) from [3, 4]. Section 3 is devoted to the concept of defect of DE, introduced in [13], and surveys various hypothesis about it, old and new. Section 4 provides the two basic examples, of antiparallel triple pretzel (which include twist and double braids) and 2-strand torus knots. The second case illustrates the subtleties in the formulation of our conjecture for parallel evolution. Another kind of subtleties are introduced in Sect. 5, they concern the ”simplified” description of defect, which is often, but not always, related to degree of the fundamental Alexander polynomial. Calculations with this definition are tremendously easier, but additional care is needed in interpreting the results. In the Appendix at the end of the paper we remind the basics of arborescent calculus and its generalization to a wider class of knots – this is what we need to consider more complicated examples in Sect. 6. Section 7 provides a short summary. In this paper we consider defects only for symmetric representations, generalizations to rectangular and non-rectangular cases require more details [8, 9, 15, 20] and will be considered elsewhere.

2 Differential expansion for symmetric representations [r]

(Reduced) HOMPLY-PT polynomialsFootnote 1 are analytically continued matrix elements or weighted traces of various products of \({{\mathcal {R}}}\)-matrices in particular representation R and its conjugate \({\bar{R}}\) of \(\mathfrak {sl}_N\). Accordingly they inherit the basic properties of the representation theory. Translation language includes several rules:

  • HOMFLY-PT is a clever analytical continuation in N. Reduction to particular N, i.e to the quantum \(\mathfrak {sl}_N\) invariants appears at \(A=q^N\).

  • For a given N representation theory of \(\mathfrak {sl}_N\) is applicable only for Young diagrams R with no more than N rows \(l_R\leqslant N\). We do not discuss the ”non-physical” region \(l_R \geqslant N\), that appears to be rather interesting due to the presence of tug-the-hook symmetry and stability property [13, 39, 40].

  • Transposition of the Young diagram \(R\longrightarrow R^{T}\) is equivalent to the substitution \(q\longrightarrow q^{-1}\):

    (2)

  • Conjugation \(R\longrightarrow {\overline{R}}\) is a symmetry of HOMFLY-PT. The symmetry depends on the rank N, we provide an example diagram for \(N=5\):

    (3)

Using these group-theoretical properties we drastically restrict the form of HOMFLY-PT for the symmetric representations [r]. In what follows we use the standard abbreviationsFootnote 2\(\{x\} := x-x^{-1}\) and \([k]_q:=\frac{\{q^k\}}{\{q\}}\).

For \(N=1\) representation theory is trivial, this means that \(H^{\mathcal {K}}_R(A=q,q)=1\), i.e.

$$\begin{aligned} H^{\mathcal {K}}_R(A,q) - 1 \ \vdots \ \{A/q\} \end{aligned}$$
(4)

but only for \(l_R\leqslant 1\), i.e. for symmetric representations \(R=[r]\). Also we have for \(l_{R^{T}}\leqslant 1\), i.e. for anti-symmetric representations \(R = [1^{r}]\):

$$\begin{aligned} H^{\mathcal {K}}_{R^{T}}(A,q) - 1 \ \vdots \ \{A/q\} \Longrightarrow H^{\mathcal {K}}_R(A,q)-1 \ \vdots \ \{Aq\} \end{aligned}$$
(5)

Both restrictions hold for the fundamental representation \(R=[1]\) and therefore we have:

$$\begin{aligned} H^{\mathcal {K}}_{[1]}-1 \ \vdots \ \{Aq\}\{A/q\} \end{aligned}$$
(6)

or alternatively

$$\begin{aligned} H_{[1]}^{{\mathcal {K}}}(A,q) = 1 + {\textbf {F}}_{[1]}^{{\mathcal {K}}}(A,q)\cdot \{Aq\}\{A/q\} \end{aligned}$$
(7)

with some function \({\textbf {F}}_{[1]}^{{\mathcal {K}}}(A,q)\). This is the simplest example of differential expansion [1, 4,5,6,7,8,9,10,11,12,13,14,15] (it is also known as cyclotomic expansion [18,19,20,21,22,23, 25,26,27]).

Further we discuss first symmetric representation [2] in detail while generic symmetric representation [r] could be obtain with the same logic. For \(N = 2\) the first anti-symmetric representation \(R = [1,1]\) is trivial:

$$\begin{aligned} H^{\mathcal {K}}_{[1,1]}(A,q) - 1 \ \vdots \ \{A / q^2\} \Longrightarrow H^{\mathcal {K}}_{[2]}(A,q)-1 \ \vdots \ \{Aq^2\} \end{aligned}$$
(8)

Combining this result with (4) we get

$$\begin{aligned}{} & {} H^{\mathcal {K}}_{[2]}(A,q) - 1 \ \vdots \ \{A q^2\} \{A/q\}\nonumber \\ {}{} & {} \quad \Longrightarrow H^{\mathcal {K}}_{[2]}(A,q) = 1 + \{A q^2\} \{A/q\} \cdot T^{\mathcal {K}}_{[2]}(A,q) \end{aligned}$$
(9)

with some auxiliary function \(T_{[2]}^{\mathcal {K}}\). Next, we use relation from \(N=3\) representation theory \([1,1] \approx [1]\):

$$\begin{aligned}{} & {} H^{\mathcal {K}}_{[1,1]}(A,q) - H^{\mathcal {K}}_{[1]}(A,q) \ \vdots \ \{A /q^3\}\nonumber \\ {}{} & {} \quad \Longrightarrow H^{\mathcal {K}}_{[2]}(A,q) - H^{\mathcal {K}}_{[1]}(A,q) \ \vdots \ \{A q^3\} \end{aligned}$$
(10)

Resolving (9) and (10) with the help of identity \( [2]_q \{ A q^2 \} = \{ A q \} + \{ A q^3 \}\) we obtain:

$$\begin{aligned} T_{[2]}^{\mathcal {K}}(A,q) - [2]_q \cdot {\textbf {F}}_{[1]}^{\mathcal {K}}(A,q) \ \vdots \ \{A q^3\} \end{aligned}$$
(11)

or in alternative form

$$\begin{aligned} H^{\mathcal {K}}_{[2]}(A,q)= & {} 1 + [2]_q \cdot {\textbf {F}}_{[1]}^{\mathcal {K}}(A,q) \cdot \{A q^2\} \{A/q\} \nonumber \\{} & {} + {\textbf {F}}_{[2]}^{\mathcal {K}}(A,q) \cdot \{A q^3 \}\{A q^2\} \{A/q\} \end{aligned}$$
(12)

for some knot-dependent function \({\textbf {F}}_{[2]}^{\mathcal {K}}(A,q)\). For bigger symmetric representations we follow the same method as for [2] and use the fact from the representation theory for anti-symmetric representations \([1^r]\approx [1^{N-r}]\). By induction one can prove the differential expansion (DE) formula for generic symmetric representation [r] [1]

(13)

For non-symmetric R the story gets more involved, see [6,7,8,9,10, 14, 15, 20]. DE formula (13) shows that the topological information is carried only by DE coefficients \({\textbf {F}}_{[s]}^{\mathcal {K}}(A,q)\), while the other constituents of the HOMFLY-PT do not help in distinguishing knots.

Interestingly, for every symmetric representations [r] there are exactly r DE coefficients, most of them \({\textbf {F}}_{[s]}^{\mathcal {K}}(A,q) s = 1,\ldots ,r-1\) came from smaller representations and only one \({\textbf {F}}_{[r]}^{\mathcal {K}}(A,q)\) is new.

3 Defect of the differential expansion

3.1 The basic idea and the ladder structure

For generic knots \({{\mathcal {K}}}\) expansion (13) is the best one can achieve from the naive group-theoretical reasoning. However, sometime, e.g. for figure-eight knot \(4_1\) or a trefoil \(3_1\), it can be significantly enhanced:

$$\begin{aligned} H^{{{\mathcal {K}}}_0}_{[r]}(A,q)= & {} 1 + \sum _{s=1}^r \frac{[r]_q!}{[s]_q! [r-s]_q!} \nonumber \\{} & {} \cdot {{\mathcal {F}}}_{[s]}^{{{\mathcal {K}}}_0}(A,q)\cdot \prod _{i=0}^{s-1} \{Aq^{r+i}\}\{Aq^{i-1}\} \end{aligned}$$
(14)

in other words

$$\begin{aligned} \textbf{F}^{{{\mathcal {K}}}_0}_{[s]} = {{\mathcal {F}}}^{{{\mathcal {K}}}_0}_{[s]}\cdot \prod _{i=1}^{s-1} \{Aq^{i-1}\} \end{aligned}$$
(15)

the DE coefficients are further factorized for particular knots. The knots \({{\mathcal {K}}}_0\) with this property are said to have defect zero [13], \(\delta ^{{\mathcal {K}}}=0\). For a generic knot the factorization of \(\textbf{F}^{{\mathcal {K}}}\) is only partial,

$$\begin{aligned} \textbf{F}_{[s]}^{{{\mathcal {K}}}_\delta }(A,q) = {{\mathcal {F}}}_{[s]}^{{{\mathcal {K}}}_\delta }(A,q)\cdot \prod _{i=1}^{\nu _s^\delta }\{Aq^{i-1}\} \end{aligned}$$
(16)

and defect \(\delta \) can take any non-negative integer value [13], with

$$\begin{aligned} \nu _s^{\delta } = {\textrm{entier}}\left( \frac{s-1}{\delta +1}\right) \end{aligned}$$
(17)

These formulas illustrate a conjecture, that for a knot \({{\mathcal {K}}}\) one can identify one non-negative number \(\delta ^{{{\mathcal {K}}}}\) measuring factorization of the DE coefficients. While this conjecture appears to be true in numerous examples, we observe certain anomalies for knots with unit Alexander polynomial and discuss it in Sect. 3.3.

The number of additional brackets (17) can be represented as a peculiar ladder diagrams:

(18)
(19)
(20)
(21)

Each box in these diagram correspond to the particular brackets as in (18). We provide values of defect for several simple knot families. For antiparallelFootnote 3 pretzel knots \((\overline{N_1},\ldots , \overline{N_k})\) for odd \(N_i\) and odd k, where \(N_i\) are the numbers of crossings in each 2-strand braid :

$$\begin{aligned} \delta ^{(\overline{N_1},\ldots , \overline{N_k})} = \frac{k-3}{2} \end{aligned}$$
(22)

This pretzel family contains all twist \((\overline{N_1},1,1)\) and double braid \((\overline{N_1}, \overline{N_2}, 1)\) knots for which defect vanishes. Another family of torus knots T[M, N] for \(M,N >0\) have the following defects:

$$\begin{aligned} \delta ^{T[M,N]} = \frac{M N - M - N - 1}{2} \end{aligned}$$
(23)

More complicated examples are discussed in Sect. 6.

Every particular knot \({{\mathcal {K}}}\) has a certain defect, and this means that its DE is enhanced as compared to (13). By enhancement we mean factorization of DE coefficients. For example, for figure eight \(4_1\) knot the DE coefficients are fully factorized \(\textbf{F}^{4_1}_{[s]} = \prod _{i=1}^{s-1} \{Aq^{i-1}\}\). However, there are knots with arbitrarily large defects and additional factorization of \(\textbf{F}^{{\mathcal {K}}}_{[s]} \) occurs only for large values of s starting from \(s_{\text {min}}=\delta + 2\).

For the unknot, defect is not well defined: all the coefficients \(\textbf{F}^{{\textrm{unknot}}} = 0\), i.e. one can prescribe any degree of factorization to them. Since (17) has an apparent singularity at \(\delta =-1\), it looks natural to put

$$\begin{aligned} \delta ^{{\textrm{unknot}}}\ {\mathop {=}\limits ^{?}}\ -1 \end{aligned}$$
(24)

Indeed, this is often the implication of evolution formulas for families, which involve unknots at particular values of evolution parameter.

3.2 Evolution of defect

Analysis of various examples, which will be partly described in the text below, leads us to the following hypothesis that we call defect evolution hypothesis:

  • Defect does not change when any vertex is substituted by an odd antiparallel braid of any length.

  • When the length of any parallel braid is increased by two, defect changes by one.

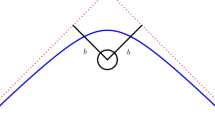
In other words, we can pick up any vertex in the knot graph and substitute it by a triple – in two possible directions. The conjecture is then equivalent to the following picture:

(25)

Two additional comments make the statement more accurate:

  • Note that the length is a modulus of the evolution parameter, thus there is a non-analyticity of defect when parameter changes sign. We explain this fact on a particular examples in Sects. 4.2 and 6.

  • In the case of anti-parallel evolution this non-analyticity is reflected in a possible drop of the defect by unity for one particular length of the anti-parallel braid, Sect. 6.

Changing of one vertex for two rather than three converts a knot into a link and is not considered in this paper (we remind that we deal with reduced HOMFLY-PT, which are defined differently for knots and links).

3.3 Defect and Alexander polynomial

As conjectured in the original paper [13], defect \(\delta _{{\mathcal {K}}}\) is related to the degree of the fundamental Alexander polynomial in \(q^{\pm 1}\):

$$\begin{aligned} {\textrm{Al}}^{{\mathcal {K}}}_{[1]} = 1 + \{q\}^2 \cdot {\textrm{Pol}}^{{{\mathcal {K}}}_\delta } (q^2,q^{-2}) \end{aligned}$$
(26)

where \({\textrm{Pol}}^{{{\mathcal {K}}}_\delta }\) is a Laurent polynomial in \(q^2\) of degree \(\delta ^{{\mathcal {K}}}\), symmetric under the change \(q^2\leftrightarrow q^{-2}\). This observation could be used as an ”alternative definition” of defect. In particular, for \(\delta ^{{\mathcal {K}}}=0\) the coefficient of \(\{q\}^2\) in the fundamental Alexander reduces to a constant.

The quantity \({\textrm{Pol}}^{{{\mathcal {K}}}_\delta }\) depends on the knot, and sometimes it can vanish, so that \({\textrm{Al}}_{[1]} = 1\). In [13] it was suggested to treat this situation as defect \(\delta =-1\), but this turns out to be a wrong idea. We suggest to substitute it by a more viable alternative – that defect is a property of an evolution family, and some coefficients \(\textbf{F}_{[s]}\) can ”accidently” factorize further at some particular values of the evolution parameters. Notably, in all the examples additional factorization (38) does not break the ladder structures (18)–(20), just extends the list of allowed ladders over the one in Sect. 3.1. As to \(\delta =-1\), we now reserve this value to the unknot only, in accordance with (24).

Since (26) involves only the fundamental representation, in this case we can apply HOMFLY-PT skein relation

(27)

to (25) at the particular point \(A = 1\) reducing HOMFLY-PT to the Alexander polynomial. Then we can substitute the evolution hypothesis for a relation between Alexander polynomials for a knot and a pair of associated links:

(28)
(29)

The Alexander skein relations appear to be useful in testing the defect evolution hypothesis. For the anti-parallel evolution, the hypothesis is true if the second term has a smaller or equal degree than the first term on the r.h.s. Similarly, for the parallel evolution, the second term should have greater degree than the first term on the r.h.s.

3.4 Stability of unphysical \(H_{[r]}(A=q^{-m})\) for a given defect

As a corollary of differential expansion, HOMFLY-PT at \(A=q^{-m}\) possesses a remarkable stability property [13]: its coefficients do not change with the increase of the representation [r] if r is big enough as compared to \(m\cdot \delta ^{{\mathcal {K}}}\). In particular, as an illustration of the stability property one can write the following formula:

$$\begin{aligned}&H^{T[2,5]}_{[r]}(A=q^{-1},q) \nonumber \\&\quad = -q^{-6 r-2}+2 q^{-4 r-2}-q^{-2 r-4}-2 q^{-2 r-2}+q^{-8 r}\nonumber \\&\qquad -q^{-6 r}+q^{-4 r}-q^{-2 r}-q^{2 r-6}-2 q^{2 r-4}\nonumber \\&\qquad -q^{2 r-2}+2 q^{4 r-6}+q^{4 r-4}-q^{6 r-8}-q^{6 r-6}+q^{8 r-8}\nonumber \\&\qquad +\frac{2}{q^4}+\frac{2}{q^2}+1 \end{aligned}$$
(30)

Due to the relation \(H_{[r]}(A=q^{-m}) = H_{[1^r]}(A = q^{m})\) this is deep in unphysical domain, where the rank of the group exceeds the number of lines in the Young diagram (\(r>m\)), still reduced HOMFLY-PT remain well defined.

This stability is fully governed by the defect. For example, the above knot T[2, 5] has defect \(\delta = 1\), then DE coefficients have factor \(\{ A q \}\) for \(s \ge 5\) (19). As a consequence the corresponding HOMFLY at the point \(A = q^{-1}\) have only finite number of items for arbitrary large representations [r]. We do not deal with this stabilization in the present paper, thus do not formulate it in details, just mention it in the list of defect properties in the conclusion.

4 Basic examples

4.1 Triple anti-parallel pretzels have defect 0

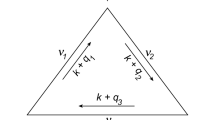
In this section we analyze the family of triple antiparallel pretzels \(({\overline{N}},{\overline{M}},{\overline{L}})\). To get a knot (rather then link) all the three parameters N, M, L should be odd. The family contains the previously studied twist and double braid knots as particular cases \(({\overline{N}},1,1)\) and \(({\overline{N}},{\overline{M}},1)\). The whole family can be considered as a triple antiparallel evolution of the trefoil: each of the three \({{\mathcal {R}}}\)-matrices are substituted by an antiparallel 2-strand braid.

According to [41] colored HOMFLY-PT for antiparallel pretzels in symmetric representations \(R=[r]\) could be calculated by the following arborescent formula:

$$\begin{aligned} H_R^{({\overline{N}},{\overline{M}},{\overline{L}})}= & {} \ d_R^2\!\! \sum _{X \in R\otimes R}\!\! \frac{\left( {\bar{S}}{\bar{T}}^{N}S\right) _{1 X} \left( {\bar{S}}{\bar{T}}^{M}S\right) _{1 X}\left( {\bar{S}}{\bar{T}}^{L}S\right) _{1 X}}{\sqrt{d_X}}\nonumber \\= & {} \ d_R^2\!\! \sum _{X\in R\otimes {\bar{R}}}\!\! \frac{{{\mathcal {A}}}^{{\textrm{ea}}}_{1X}({\overline{N}}){{\mathcal {A}}}^{{\textrm{ea}}}_{1X}({\overline{M}}) {{\mathcal {A}}}^{{\textrm{ea}}}_{1X}({\overline{L}})}{\sqrt{d_X}} \end{aligned}$$
(31)

where \(d_X\) are quantum dimensions of representations X. In the last expression we used the generic notation for pretzel fingers from Sect. 1.

All these knots have defect zero, thus the differential expansion is

$$\begin{aligned} H_{[1]}^{({\overline{N}},{\overline{M}},{\overline{L}})}&= 1 + {{\mathcal {F}}}_{[1]}^{({\overline{N}},{\overline{M}},{\overline{L}})}(A)\cdot \{Aq\}\{A/q\} \nonumber \\ H_{[2]}^{({\overline{N}},{\overline{M}},{\overline{L}})}&= 1 + [2] \cdot {{\mathcal {F}}}_{[1]}^{({\overline{N}},{\overline{M}},{\overline{L}})}(A)\cdot \{Aq^2\}\{A/q\} \nonumber \\&\quad + {{\mathcal {F}}}_{[2]}^{({\overline{N}},{\overline{M}},{\overline{L}})}(A,q)\cdot \{Aq^3\}\{Aq^2\}\{A\}\{A/q\}\nonumber \\&\ldots \nonumber \\ H_{[r]}^{({\overline{N}},{\overline{M}},{\overline{L}})}&= 1+ \sum _{s=1}^r \frac{[r]!}{[s]![r-s]!} \cdot {{\mathcal {F}}}_{[s]}^{({\overline{N}},{\overline{M}},{\overline{L}})} \nonumber \\&\quad \cdot \prod _{j=0}^{s-1} \{Aq^{r+j}\}\{Aq^{j-1}\} \end{aligned}$$
(32)

This is the simplest illustration – and, actually, the origin – of our hypothesis that defect does not change with the antiparallel evolution.

It is instructive to comment on the relation with ”alternative definition” of defect in the Sect. 3.3 – to better illustrate and understand its limitation. We will do this in Sect. 5.

4.2 Antiparallel pretzels as descendants of 2-strand torus knots

HOMFLY-PT for the 2-strand torus knots are just traces of \({{\mathcal {R}}}\)-matrices for the parallel 2-strand braid,

$$\begin{aligned} H^{T[2n-1,2]}_{[r]} = d_{[r]} \cdot \left( S T^{2n-1} S^{\dagger } \right) _{11} \end{aligned}$$
(33)

and can be calculated by a variety of methods [42]. It is easy to check that they have defects

$$\begin{aligned} \delta ^{T[2n-1,2]}= & {} \left\{ \begin{array}{lll} n-2 &{} {\textrm{for}} &{} n\ge 2 \\ -n-1 &{}{\textrm{for}} &{} n\le -1 \end{array} \right. = \left| n-\frac{1}{2}\right| -\frac{3}{2}\nonumber \\= & {} \frac{|2n-1|-3}{2} \end{aligned}$$
(34)

(\(n=0,1\) correspond to the unknot, when defect is not well defined), in particular the trefoil, which we get at \(n=- 1,2\) has defect zero. In the previous subsection we considered trefoil as a starting point for triple antiparallel evolution, now it is an origin of a single parallel one.

The formula (34) is precise formulation of the parallel part of our conjecture: parallel evolution increases defect by one per pair of added vertices. It also reflects the main subtlety of this formulation: the break of analyticity of the defect as function of n through occurrence of absolute value and the presence of a ”blind zone” at \(n=0,1\). The structure of these blind zones will get more sophisticated in more general examples.

A somewhat similar break of analyticity takes place [43,44,45] in evolution of Khovanov and super-polynomials – it would be interesting to establish a more clear relation between the two.

This example (34) also nicely explains the defects of odd antiparallel pretzels (22): they are obtained by the antiparallel evolution from 2-strand torus knots. In other words, the family of antiparallel k-pretzels have the same defect as torus knot \(T[2n-1,2]\) provided \(k = |2n-1|\). For illustrative purposes we provide a picture of evolution from T[2, 5] to \(\left( {\overline{N}}_1,{\overline{N}}_2,{\overline{N}}_3,{\overline{N}}_4,{\overline{N}}_5 \right) \):

(35)

5 Comments on the fundamental Alexander

Calculations of the defect could be drastically simplified, if one used the ”alternative definition” of defect in the Sect. 3.3 – only Alexander polynomial in the very first fundamental representation would be needed. This is indeed very helpful in majority of cases, but unfortunately this method is not truly reliable. Sometime defect, ”measured” by this method, is actually smaller than the true one, i.e Alexander polynomial is unit. As suggested in Sect. 4.1, we illustrate this with the example of triple pretzels. More sophisticated examples will be provided in Sect. 6.

For Alexander description the only relevant one is the fundamental representation, where

$$\begin{aligned}{} & {} {{\mathcal {F}}}_{[1]}^{(2n-1,2m-1,2l-1) }(A)\nonumber \\{} & {} \quad = -\frac{A^{2(n+m+l-1)}\!+\!A^{2(n+m+l-2)} \!-\! A^{2(n+m-1)}\!-\!A^{2(n+l-1)}\!-\!A^{2(m+l-1)} \!+\!1}{\{A\}^2}\nonumber \\ \end{aligned}$$
(36)

so that

$$\begin{aligned}{} & {} {\textrm{Al}}_{[1]}^{(2n-1,2m-1,2l-1)} \nonumber \\{} & {} \quad = 1 + (nm+nl+ml-m-n-l+1)\cdot \{q\}^2 \end{aligned}$$
(37)

Clearly, one can adjust (n, m, l) so that the second term vanishes. For example, it does so for \((N,M,L)=(-3,5,7)\), i.e. \(\textbf{F}_{[1]}^{(-3,5,7)}\sim \{A\}\). However, no extra factorization occurs for other \(\textbf{F}_{[s]}^{(-3,5,7)}\) with \(s>1\), and the rest of the pattern follows the standard one for defect zero:

(38)

In this sense the extra box at \(s=1\) is just accidental. However, such accidents make the very convenient ”definition” of defect a la Sect. 3.3 somewhat limited – one can not fully trust it, more thorough analysis, involving higher representations can be needed. At the same time we see that a natural way to fight against the ambiguities with such definition of defect for particular knots is to consider entire families.

Table 1 The table provides data for knots with quadratic Alexander polynomials
Full size table

Coming bact to \((-3,5,7)\), note that some additional simplifications occur for this knot in higher representations:

$$\begin{aligned} {{\mathcal {F}}}_{[s]}^{(-3,5,7)}(A=1)\sim \{q\} \quad {\textrm{for}} \ \ s\ge 2 \end{aligned}$$
(39)

However, this is not interesting – it is a direct corollary of factorization property of the special polynomial at \(q=1\) [42]:

$$\begin{aligned} H_R(q=1,A) = \Big (1 + {{\mathcal {F}}}_{[1]}(q=1,A)\cdot \{A\}^2\Big )^{|R|} \end{aligned}$$
(40)

– then vanishing of \({{\mathcal {F}}}_{[1]}(A=1,q)\) implies that all \(\textbf{F}_{[s]}(A=1,q) \sim \{q\}\).

In fact, \((-3,5,7)\) is not a unique ”accident” in the triple-pretzel family. There are many other solutions to the constraint \(l=-\frac{(m-1)(n-1)}{m+n-1} \in {\mathbb {Z}}\). e.g. \((-5,9,11), \ (-5,7,17), (-7,9,31), \ \ldots \) However, extra degenerations of \({{\mathcal {F}}}_{[s]}\) with \(s\ge 2\) never occur in this series of accidental zeroes of \({{\mathcal {F}}}_{[1]}(A=1)\) – the pattern of DE is always like (38).Footnote 4 In fact, this is not a big surprise, because, say, the degeneration condition \({{\mathcal {F}}}_{[1]}(A=q^{-1})\) is a non-trivial Laurent polynomial in q, and all of its coefficients do not vanish simultaneously for any triple of variables n, m, l.

Still, for some other series of knots such improbable multiple degenerations can happen, as we will see in the next section.

In search for anomalies we checked the defects for all knots up to 11 intersections with quadratic Alexander polynomials. The knot data was taken from wonderful source [46] and collected in Table 1.

6 More complicated examples

6.1 \(\left( N,M,{\overline{K}}\right) \) pretzel knots

The one-parametric series \((3,3,{\overline{2k}})\) with two parallel and one antiparallel fingers is described by

$$\begin{aligned} H_R^{(3,3,{\overline{2k}})} = d_R^2\sum _{X\in R\otimes {\bar{R}}} \frac{{{\mathcal {A}}}^{{\textrm{par}}}_{1X}(3)\,{{\mathcal {A}}}^{{\textrm{par}}}_{1X}(3) \, {{\mathcal {A}}}^{{\textrm{ea}}}_{1X}({\overline{2k}})}{\sqrt{d_X}} \end{aligned}$$
(41)

has defect \(\delta ^{(3,3,{\overline{2k}})}=2\) for all values of k, except \(k=0\). This illustrates the antiparallel invariance of defect.

For particular value of \(k=0\) this series contains a composite of two trefoils. Defect of a composites differs significantly from that of the constituents. Explicit expression is easily obtained from the Alexander property of the defect. Since the reduced HOMFLY-PT is a product of two constituent HOMFLY-PT, the same is true for Alexander polynomials, and

$$\begin{aligned}{} & {} {\textrm{Al}}^{{{\mathcal {K}}}_1\cup {{\mathcal {K}}}_2} = {\textrm{Al}}^{{{\mathcal {K}}}_1} \cdot {\textrm{Al}}^{{{\mathcal {K}}}_2} \nonumber \\{} & {} \quad {\mathop {=}\limits ^{(26)}} \ \left( 1 + \{q\}^2 \cdot {\textrm{Pol}}^{{{\mathcal {K}}}_{\delta _1} } \right) \left( 1 + \{q\}^2 \cdot {\textrm{Pol}}^{{{\mathcal {K}}}_{\delta _2} } \right) \nonumber \\{} & {} \quad = 1 + \{q\}^2 \cdot \left( {\textrm{Pol}}^{{{\mathcal {K}}}_{\delta _1}} + {\textrm{Pol}}^{{{\mathcal {K}}}_{\delta _2} } + \{q\}^2 \cdot {\textrm{Pol}}^{{{\mathcal {K}}}_{\delta _1} } \cdot {\textrm{Pol}}^{{{\mathcal {K}}}_{\delta _2} } \right) \nonumber \\ \end{aligned}$$
(42)

implies that

$$\begin{aligned} \delta ^{{{\mathcal {K}}}_1\cup {{\mathcal {K}}}_2} =\delta ^{{{\mathcal {K}}}_1}+ \delta ^{{{\mathcal {K}}}_2}+ 1 \end{aligned}$$
(43)

For our particular example of (3, 3, 0) this means that \(\delta ^{(3,3,0)}=1\), i.e. the defect accidentally drops down from 2 to 1 in a particular member \(k=0\) of the family.

Table 2 The left table lists the defects \(\delta ^{(2n-1,2m-1,{\overline{2k}})}\). The right table shows the critical values of k where the defect decreases by one. The empty box means that the defect does not drop for these values of n and m. The item \(\emptyset \) means unknot
Full size table

For the full family \((2n-1,2m-1,{\overline{2k}})\)

$$\begin{aligned}{} & {} H_R^{(2n-1,2m-1,{\overline{2k}})} \nonumber \\{} & {} \quad = d_R^2 \sum _{X\in R\otimes {\bar{R}}} \frac{ {{\mathcal {A}}}^{{\textrm{par}}}_{1X}(2n-1) \, {{\mathcal {A}}}^{{\textrm{par}}}_{1X}(2m-1) \, {{\mathcal {A}}}^{{\textrm{ea}}}_{1X}({\overline{2k}}) }{\sqrt{d_X}} \end{aligned}$$
(44)

the defect is

$$\begin{aligned} \delta ^{(2n-1,2m-1,{\overline{2k}})} = n+m-2 \ \ \ {\textrm{for}} \ \ n,m\ge 1 \end{aligned}$$
(45)

i.e. does not depend on the antiparallel evolution and depends linearly on the parallel ones. This is in full accordance with our general suggestion.

Again, at \(k=0\) we get a composite of the 2-strand torus knots \((2n-1,1)\) and \((2m-1,1)\) and from (43) and (34) the defect is \(n+m-3\) (for \(n,m\ge 1\)), i.e. at \(k=0\) there is an accidental decrease of the defect by one. In the particular case \((1,1,{\overline{2k}})\) at \(k=0\) the composite of two unknots is an unknot, and our formula is consistent with \(\delta ^{{\textrm{unknot}}}=-1\), suggested in (24).

If n or m are not positive, the formula (45) gets slightly more involved:

$$\begin{aligned} \delta ^{(2n-1,2m-1,{\overline{2k}})}= & {} \left| n-\frac{1}{2}\right| + \left| m-\frac{1}{2}\right| \nonumber \\{} & {} + \frac{{\textrm{sign}}\left( n-\frac{1}{2}\right) \cdot {\textrm{sign}}\left( m-\frac{1}{2}\right) }{2} -\frac{3}{2} \end{aligned}$$
(46)

It is apparently symmetric under the permutation of n and m and under the simultaneous sign change of \(2n-1\) and \(2m-1\). This expression is obtained from both criteria (16) and (26) and demonstrates the relatively sophisticated structure of the switching region between positive and negative parameters of the parallel evolution.

The drop of defect by one takes place at \(k=0\) when \(2n-1\) and \(2m-1\) have the same sign. Otherwise this happens at \(2k= 2\) when \(2n-1>0\) and \(2m-1=- 1\) or \(2n-1=-1\) and \(2m-1>0\) and at \(2k=-2\) when \(2n-1<0\) and \(2m-1=1\) or \(2n-1=1\) and \(2m-1<0\). In the regions of different signes of \(2n-1\) and \(2m-1\) no drop of the defect is observed. Also there are unknots when \(2n-1=-(2m-1)=\pm 1\).

The left Table 2 is symmetric with respect to the main diagonal, since on the topological level pretzel knots \((2n-1,2m-1,{\overline{2k}})\) and \((2m-1,2n-1,{\overline{2k}})\) are identical. Moreover, this table is symmetric with respect to the secondary diagonal. This fact follows from the relation:

$$\begin{aligned} \delta ^{ (2n-1,2m-1,{\overline{2k}})} = \delta ^{(-2n+1,-2m+1,-{\overline{2k}})} \end{aligned}$$
(47)

That is a simple corollary of two facts:

  1. 1.

    Mirror image of a knot \(\bar{\mathcal {K}}\) has HOMFLY polynomial \(H^{\bar{\mathcal {K}}}_{R}(A,q) = H^{\mathcal {K}}_{R}(A^{-1},q^{-1})\), while the reflection \(A \rightarrow A^{-1}, q \rightarrow q^{-1}\) changes differentials \(\{ A q^{k} \}\) only by sign. Therefore mirror image of a knot has the same defect.

  2. 2.

    \(\delta ^{(-2n+1,-2m+1,-{\overline{2k}})} = \delta ^{(-2n+1,-2m+1,{\overline{2k}})}\) due to the hypothesis of the anti-parallel evolution

6.2 KTC mutant and its relatives

KTC mutants \( 11n34 \ \& \ 11n42\) are \( (3, -2|{\bar{2}}| -3, 2)\ \& (3, -2|{\bar{2}}|2, -3)\) have unit Alexander and provide the most anomalous examples of DE structure. In the fundamental representation

$$\begin{aligned}{} & {} H_{[1]}^{[11n34]} = H_{[1]}^{[11n42]}:= 1 - \frac{[6][4]}{[2]^2[3]A} \{Aq\}\underline{\{A\}}\{A/q\}\nonumber \\{} & {} \quad \Longrightarrow {\textrm{Al}}_{[1]}^{[11n34]} = 1 \end{aligned}$$
(48)

there is one extra factor, \(\{A\}\), in \(F_{[1]}^{[11n34]}\).

The difference between the two mutants shows up already for the first non-rectangular representation \(H_{[21]}\), but it remains absent for arbitrary large symmetric and even rectangular ones. In this paper we are not so much interested in mutant property [47,48,49,50], our emphasize here is rather on the trivial Alexander (we just use the well know fact that it is unity for the KTC pair). Therefore we concentrate on symmetric representations. Due to the property [42] \({\textrm{Al}}_{[r]}(q) = {\textrm{Al}}_{[1]}(q^r)\) (actually true for all one-hook representations) Alexander will be remain unity for all of them.Footnote 5

KTC mutants are arborescent knots of type \((p,q | {\overline{2k}} | s,r)\), but not pretzels, they contain a ”propagator” between two double-finger vertices and are described by (57) of [41]:

(49)

Therefore, the reduced HOMFLY polynomial for the diagram (49) is

$$\begin{aligned} H_{R}^{(p,q|{\overline{2k}}|s,r)}= d_R^2 \sum _{Z\in R\otimes {\bar{R}}} \frac{ {{\mathcal {A}}}^{ppS}_Z(p,q)\, {{\mathcal {A}}}^{{\textrm{ea}}}_{1Z}({\overline{2k}})\, {{\mathcal {A}}}^{ppS}_Z(r,s) }{\sqrt{d_Z}}\nonumber \\ \end{aligned}$$
(50)

where

$$\begin{aligned} {{\mathcal {A}}}^{ppS}_Z(N,M) = d_{R} \sum _{X\in R\otimes {\bar{R}}} \frac{ {{\mathcal {A}}}^{{\textrm{par}}}_{1X}(N) \, {\bar{S}}_{XZ} \, {{\mathcal {A}}}^{{\textrm{par}}}_{1X}(M)}{\sqrt{d_X}} \end{aligned}$$
(51)

and expressions \({{\mathcal {A}}}\) for particular fingers are provided in Sect. 1. The four external fingers involve parallel braids, while that of the even length 2k in the propagator is antiparallel. The evolution along this obvious antiparallel braid from the KTC mutant generates a family \((3,-2|{\overline{2k}}|-3,2)\) with the following structure of the DE coefficients:

(52)

Again, the extra boxes at are just accidental, still now it is an ”accident” which appears simultaneously at many places and for the whole one-parametric family \((3,-2|{\overline{2k}}|-3,2)\). If one performs antiparallel evolution at any crossing except antiparallel braid \({\overline{2k}}\), all the extra boxes vanish and the defect becomes \(\delta ^{{{\mathcal {K}}}} = 1\). Therefore we treat black boxes as ”accident”, appearing in a highly symmetric point in the space of knots - KTC mutant.

6.3 The family \((2a-1,2b\,\big |\,{\overline{2k}}\,\big |\,2c-1,2d)\)

Entire two-parametric families

$$\begin{aligned}{} & {} (2n+1,-2n\,\big |\,{\overline{2k}}\,\big |\,-2n-1,2n) \ \ {\textrm{and}} \nonumber \\{} & {} (2n-1,-2n\,\big |\,{\overline{2k}}\,\big |\,2n,-2n+1) \end{aligned}$$
(53)

have unit fundamental Alexander, and k-independent defects. However, these defects increase with |n| and the structure of additional degenerations remain obscure.

Instead one can study the ”plateaux” in parallel evolution in the full 5-parametric family \((2a-1,2b\,\big |\,{\overline{2k}}\,\big |\,2c-1,2d)\).

The family \((2a-1,2b\,\big |\,{\overline{2k}}\,\big |\,2c-1,2d)\) is symmetric under the permutations of fingers

$$\begin{aligned}{} & {} (2a-1,2b\,\big |\,{\overline{2k}}\,\big |\,2c-1,2d) \nonumber \\{} & {} \quad = (2b,2a-1\,\big |\,{\overline{2k}}\,\big |\,2c-1,2d)\nonumber \\{} & {} \quad =(2c-1,2d\,\big |\,{\overline{2k}}\,\big |\,2a-1,2b) \end{aligned}$$
(54)

but one is not allowed to break the pairs:

$$\begin{aligned}{} & {} (2a-1,2b\,\big |\,{\overline{2k}}\,\big |\,2c-1,2d)\nonumber \\{} & {} \quad \ne (2a-1,2d\,\big |\,{\overline{2k}}\,\big |\,2c-1,2b) \ \ {\textrm{if}} \ \ a\ne c \ \ {\textrm{and}} \ \ b\ne d\nonumber \\ \end{aligned}$$
(55)

These symmetries are respected by explicit formula for the defect:

$$\begin{aligned}{} & {} \delta ^{(2a-1,2b\,\big |\,{\overline{2k}}\,\big |\,2c-1,2d)} = \left| a -\frac{1}{2}\right| + \left| c -\frac{1}{2}\right| + |b|+|d|-2\, \nonumber \\{} & {} \quad +\!\!\left\{ \!\begin{array}{lll} a,c\le 0 &{}\ \ \ {} &{} + \theta (-a)\theta (-c)\cdot \Big \{-2\cdot {\textrm{min}}(b,d)\cdot \theta (b-1)\theta (d-1) + \big (2\cdot {\textrm{min}}(b,d)\!+\!2\cdot {\textrm{max}}(a,c)\!-\!1\big )\cdot \theta \big ({\textrm{min}}(b,d)+{\textrm{max}}(a,c)\!-\!1\big )\Big \} \\ a\le 0,\ c\ge 1 &{}&{} + \theta (-a)\theta (c-1)\Big \{-2\cdot {\textrm{min}}\big (b,|d|\big )\cdot \theta (b-1)\theta (-d) + \ldots \Big \} \\ a\ge 1,\ c\le 0 &{}&{} + \theta (a-1)\theta (-c)\cdot \Big \{-2\cdot {\textrm{min}}\big (|b|,d\big )\cdot \theta (-b)\theta (d-1) + \ldots \Big \} \\ a,c\ge 1 &{}&{} + \theta (a-1)\theta (c-1)\Big \{ \underbrace{2\cdot {\textrm{max}}(b,d)}_{-2\cdot {\textrm{min}}\big (|b|,|d|\big )}\cdot \theta (-b)\theta (-d) - \big (2\cdot {\textrm{max}}(b,d)+2\cdot {\textrm{min}}(a,c)-1 \big ) \cdot \theta \big (-{\textrm{max}}(b,d)-{\textrm{min}}(a,c)\big )\Big \} \end{array}\right. \nonumber \\ \end{aligned}$$
(56)

Correction terms in the second line do not grow when absolute value of any of the four variables becomes much bigger that the others – the linear growth is provided by the main terms in the first line.

6.4 (Anti)parallel evolution for any arborescent knots

Turns out, that the (anti)parallel evolution does not lead us out of the family of arborescent knots. For example, we provide picture of antiparallel evolution of a crossing in a parallel braid:

(57)

For \(m = 0\) the left picture is a part of the parallel braid, while for the other values of m the horizontal antiparallel braid considered as the pretzel finger in the right picture. This is a contraction of three blocks, where the middle one is exactly the odd antiparallel pretzel finger from Sect. 1. Schematically, it is

$$\begin{aligned} d_{R}^2\sum _{Z\in R\otimes R} \frac{\Big (\bar{T} \bar{S} \bar{T} S\Big )_{YZ} \, {{\mathcal {A}}}^{{\textrm{oa}}}\left( \overline{2m+1}\right) _{1Z} \, \Big (S^\dagger \bar{T}^{-1} \bar{S} \bar{T}^{-1} \Big )_{ZX} }{\sqrt{d_Z}}.\nonumber \\ \end{aligned}$$
(58)

Using this method we can check the defect evolution hypothesis for any arborescent knots. Similarly, one can write an answer for insertion of a parallel braid into a antiparallel one.

6.5 1-loop family as an example of non-arborescent knots

To check the defect evolution hypothesis out of the arborescent family we used the technique developed in [41, 51]. The method allows to insert any arborescent propagator instead of any \({{\mathcal {R}}}\)-matrix in a braid. This class of knots is called 1-loop family and it is richer than the arborescent knots. The simplest non-arborescent examples are provided by the 3-strand braid. For example, we provide simplest non-arborescent knot \(8_{19}\) which is included in 8-parametric antiparallel family \((\overline{n_0},\overline{n_1},\overline{n_2},\overline{n_3},\overline{n_4},\overline{n_5},\overline{n_6},\overline{n_7},) = (1,-1,1,-1,1,-1,1,-1)\) of defect \(\delta = 2\).

(59)

7 Conclusion

This paper studies the evolution of the defect [13] of the differential (cyclotomic) expansion [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36]. Evolution arises when one vertex of the knot diagram is substituted by a 2-strand braid and describes the dependence of the answer (knot polynomial) on this exponent. In the case of ”locally build” polynomials, like HOMFLY-PT, this means that one of the \({{\mathcal {R}}}\)-matrices is raised to some power and evolution describes the dependence of the answer (knot polynomials) on this exponent. The power of a rank-four tensor can be defined in two different ways, which are nicknamed parallel and antiparallel evolution:

$$\begin{aligned} {{\mathcal {R}}}^{ia}_{kb}{{\mathcal {R}}}^{bj}_{al} \ {\mathop {\longleftarrow }\limits ^{{\textrm{apar}}}} \ {{\mathcal {R}}}^{ij}_{kl} \ {\mathop {\longrightarrow }\limits ^{{\textrm{par}}}} \ {{\mathcal {R}}}^{ij}_{ab}{{\mathcal {R}}}^{ab}_{kl} \end{aligned}$$

At the first glance this evolution has nothing to do with defect. It is a local feature, while defect is a global characteristic. It is easy to treat evolution as a property of Lagrangian (input in the QFT formalism), while defect is the one of the correlators (output). Still these turn out to be intimately related. This paper provides a lot of evidence for a very general conjecture: invariance of defect under the antiparallel braid evolution. Then, answering a naturally arising question about parallel evolution, we find out that it changes the defect by one/step. Altogether this looks like a strange and powerful statement, which can attract more attention to the notion of know defects. It adds to the mysteries of knot theory and is a new manifestation of the still unrevealed symmetry (conspiracy) of the non-perturbative calculations – which can be significant far beyond the 3d topological theories.

To summarize, what we now know about the defect are the four claims from [13]:

  1. 1.

    For any given knot \({{\mathcal {K}}}\) the DE coefficients \(\textbf{F}_Q^{{\mathcal {K}}}\) factorize for big enough representations Q, the integer-valued defect \(\delta ^{{\mathcal {K}}}\) measures when and how this happens.

  2. 2.

    Factorization follows one of the ladder patterns, described in Sect. 3.1.

  3. 3.

    Defect is related to the power of the fundamental Alexander in \(q^{\pm 2}\).

  4. 4.

    Defect governs the stabilization property, mentioned in Sect. 3.4.

In this paper we added three more facts:

  1. 5.

    Defect does not change under antiparallel evolution. It can drop for particular lengths of the braid.

  2. 6.

    Defect changes linearly under parallel evolution. There is a non-trivial pattern of switching between negative and positive evolution parameters.

  3. 7.

    When fundamental Alexander is unit (and probably in some other circumstances) the patterns can be somewhat richer than in 2, with added steps and certain irregularities.

The subtle details mentioned in 5–7 do not contradict 2, but emphasize that for particular knots (and even entire families) there can be additional degeneracites in the coefficients of DE, which are not captured by the defect itself. The fully detailed structure of degeneracies is probably controlled by a more sophisticated quantity, which is not just a single number.