1 Introduction

Quantizing gravity is one of the most intensively pursued areas of physics [1, 2]. The superstring theory is a promising candidate for theorizing quantum gravity (e.g., [3]). However, the lack of empirical evidence for quantum aspects of gravity has led to controversy. This debate includes a significant community who subscribes to the breakdown of quantum mechanics itself at scales macroscopic enough to produce prominent gravitational effects [4,5,6,7,8], so that gravity doesn’t need to be a quantized field in the usual sense. Indeed it is quite possible to treat gravity as a classical agent at the cost of including additional stochastic noise [9,10,11,12]. Moreover, oft-cited necessities for quantum gravity (e.g., the big bang singularity) can be averted by modifying the Einstein action such that gravity becomes weaker at short distances and small time scales [13]. Thus it is crucial to test whether fundamentally gravity is quantum entity.

Recently, some advances in quantum sciences have opened the possibility of testing the quantum features of gravity [14,15,16]. Quantum entanglement, which is considered the most characteristic feature that separates quantum systems from the classical world, can serve as a means to measure the quantum features of the gravity. A notable experiment [17, 18] proposed to test the quantum nature of gravity, has mainly considered two massive particles interacting only gravitationally. This scheme is based on the theorem that local operation and classical communication (LOCC) [19] cannot produce quantum entanglement in quantum information theory. Due to gravity based on a local theory, if the gravitational interaction produces entanglement between two massive particles, then quantum nature of gravity can be verified. In this experiment called the BMV experiment, micron-sized diamond ( microdiamonds with an embedded nitrogen-vacancy center spin) has been designed as the superposition of two massive particles at a certain distance parallel to their separation direction. The gravitational interaction between the particles could cause quantum entanglement. For the feasible detection of an entanglement, one requires the superposition of a mesoscopic particle. In Ref. [20], an experimental setup for realizing such a superposition is presented. Further, the origin of generating the quantum entanglement is discussed in [21]. These studies have in turn stimulated several studies on testing the quantum properties of gravity [22,23,24,25,26,27,28,29]. Among them, Nguyen and Bernards have proposed a setup similar to that of the BMV experiment [29], in which they assume the superposition of two separated massive particles in the direction perpendicular to their separation direction. Due to the symmetry of the configuration, the gravitational interaction between two massive particle can be simplified and the model is easy to achieve.

In view of the current experimental verification and theoretical research on the quantum nature of gravity, some efforts have been recently devoted to investigating the role played by gravity on the dynamics control of the massive particles [23, 24, 28,29,30,31]. For instance, by studying the entanglement dynamics between two particles due to gravity, the authors showed that the system entangles as long as the coupling between the particles is strong [29]. Then the dynamics of a gravity-induced entanglement for N massive particles can be analyzed [30] by extending the model proposed by Nguyen and Bernards [29] to include N massive particles. The above studies focus on the influence of the presence of gravity on entanglement and decoherence dynamics. However, how to protect the quantum properties of the system such as quantum entanglement and quantum coherence under the action of gravity has not been studied yet. Understanding how to protect the quantum properties of a system under gravity is crucial for detecting the quantum properties of gravity. Currently, several studies have shown non-Markovian effects [32,33,34,35,36,37] not only suppress the decay of the coherence or the entanglement of quantum systems [38,39,40], but also accelerate the quantum evolution speed of the systems [41,42,43,44,45,46]. A non-Markovian speedup evolution of an open system would be preferable to deal with the robustness of quantum simulators and computers against decoherence [47, 48]. That is to say, the non-Markovian accelerated evolution of the system can resist the decoherence of the quantum system in the environment, thus protecting the quantum properties of the system, which in turn has a positive effect on the detection of the quantum nature of gravity. Therefore, in the background of the gravity, how to control the dynamics of a massive particle as a quantum system due to gravity, in particular, to manipulate non-Markovian effects and to improve the quantum dynamical speed, becomes extremely significant for detecting the quantum properties of gravity.

To do so, we will investigate two linear configurations (one-side model and two-side model) in which a system massive particle interacts with the environment composed of multiple massive particles. All particles are separated by a same distance from their immediate neighbors. For these two models, we demonstrate how the non-Markovian speedup dynamics control of a massive particle can be achieved by manipulating the parameters of the adjustable environmental particles due to gravity. To quantify the non-Markovian speedup dynamics of the system massive particle, here we apply the quantum speed limit time (QSLT) to define the border between no-speedup and speedup quantum evolution of the massive system [41, 49,50,51,52,53,54,55,56]. And a general measure for non-Markovianity defined by Breuer et al. [32] is used to distinguish the Markovian dynamics and the non-Markovian dynamics. By investigating the influences of the separation distance of each massive particle and the mass of the environmental particles on the non-Markovianity and QSLT, two dynamical crossover behaviors of the system, from Markovian dynamics to non-Markovian dynamics and from no-speedup evolution to speedup evolution, can be realized via the gravitational interactions between the system particle and each environmental particle. Additionally, we also have quantitatively analyzed the regions of the environment parameters for the occurrence of the non-Markovian speedup of the system particle.

The structure of this paper is as follows. In Sect. 2, we introduce one-side model and two-side model and also calculate the reduced density matrix of the system respectively. In Sect. 3, we analyze the non-Markovian accelerated evolution of massive particles under the influence of gravity. In Sect. 4, the conclusion is put forward.

Fig. 1
figure 1

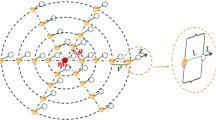
Schematic representation. The direction of the separation between each particle is orthogonal to the direction of the separation of the particle with its superposed position. a One-side model: The j-th particle from the left (\(0\le j\le n\)) has mass \(m_j\). The particles interact with one another through gravity. b Two-side model: the subscripts “l” or “r” to distinguish the environmental particles to the left or right of the system particle \(m_0\). The jth (\(1\le j\le \frac{n}{2}\)) particle to the left of \(m_0\) has a mass of \(m_{jl}\). The jth (\(1\le j\le \frac{n}{2}\)) particle to the right of \(m_0\) has mass \(m_{jr}\)

Full size image

2 Model and dynamics

Because gravity is a long-range force, it is interesting to study quantum dynamics of a massive particle influenced by gravitational interactions among the massive particles. In this section, we would consider two linear configurations in which a system massive particle (the mass \(m_{0}\)) interacts with the environment composed of n massive particles (\(m_{j}s\)). All particles are separated by a distance d from their immediate neighbors. The jth particle has the mass \(m_{j}\). And each particle is initially formed by the superposition of two spatially localized states separated by a distance L in the same direction. We align the massive particles so that the superposition is along the vertical direction.

An illustration of these two linear configurations (the system massive particle plus the environmental massive particles) is shown in Fig. 1. Two cases: one is the one-side model (i.e., Fig. 1a), in which the system massive particle \(m_{0}\) is at the leftmost end of the linear structure, and couples with the other particles \(m_{j}s\) with gravitational interaction. The other is the two-side model (i.e., Fig. 1b), which consists of the system massive particle \(m_0\) in the middle and symmetrical environmental particles on both sides. These linear configurations are the extension of the model in Ref. [29], which mainly has considered two massive particles.

The states of the jth particle at the left and right paths are represented by the notations \({\left| \uparrow \right\rangle _j}\) and \({\left| \downarrow \right\rangle _j}\), respectively. For the one-side model, the initial state of the total system is chosen as

$$\begin{aligned} \left| \varPsi (0)\right\rangle&={\left| \psi (0)\right\rangle }_0\otimes {\left| \psi (0)\right\rangle }_1\otimes \cdots \otimes {\left| \psi (0)\right\rangle }_n, \end{aligned}$$
(1)

And the initial state of the total system for the two-side model can be written by transforming Eq. (1)

$$\begin{aligned} \left| \varPsi (0)\right\rangle&={\left| \psi (0)\right\rangle }_{\frac{n}{2}l}\otimes \cdots \otimes {\left| \psi (0)\right\rangle }_{1l}\otimes {\left| \psi (0)\right\rangle }_0\nonumber \\&\quad \otimes {\left| \psi (0)\right\rangle }_{1r}\otimes \cdots \otimes {\left| \psi (0)\right\rangle }_{\frac{n}{2}r}, \end{aligned}$$
(2)

where \(\left| \psi (0)\right\rangle _j =\frac{1}{\sqrt{2}}(\left| \uparrow \right\rangle _j+\left| \downarrow \right\rangle _j)\) is the initial state of the massive particle \(m_{j}\). And the subscripts “l” and “r” distinguish the environmental particles to the left and right of the system particle \(m_0\).

In this work, we mainly consider that all massive particles are in a zero-gravity environment, and the wave packet of each particle does not spread. So the kinetic term is neglected. The initial state evolves under the gravitational interactions, then in the one-side model, the corresponding Hamiltonian is

$$\begin{aligned} H&=\sum _{j=1}^{n}H_{0,j}+\sum _{j<k}^{n}H_{j,k}, \end{aligned}$$
(3)
$$\begin{aligned} \quad H_{0,j}&=-\frac{\varDelta _{0,j}}{2}\sigma _{z}^{(0)}\otimes \cdots \otimes \sigma _{z}^{(j)}\otimes \cdots \otimes I_{n}, \end{aligned}$$
(4)
$$\begin{aligned} \quad H_{j,k}&=-\frac{\varDelta _{j,k}}{2}I_{0}\otimes \cdots \otimes \sigma _{z}^{(j)}\otimes \cdots \otimes \sigma _{z}^{(k)}\otimes \cdots \otimes I_{n}, \end{aligned}$$
(5)

here \(H_{0,j}\) represents the gravitational interaction between the system particle \(m_0\) and the environmental particle \(m_{j}\) (\(j\in [1,n]\)), and \(H_{j,k}\) describes the Newtonian potential energy between the jth environmental particle and the kth environmental particle (\(j,k\in [1,n]\)). \(j<k\) is set to avoid double-counting when calculating the Newtonian potential energy between two particles. Therefore, \(\varDelta _{j,k}\) can be uniformly expressed as

$$\begin{aligned} \varDelta _{j,k}&=Gm_jm_k (\frac{1}{{d(k-j)}}-\frac{1}{\sqrt{{{d^2(k-j)^2}}+L^2}}), \end{aligned}$$
(6)

with \(d(k-j)\) is the distance between particle \(m_k\) and particle \(m_j\) in the same state (\({\left| \uparrow _k\uparrow _j\right\rangle }\) or \({\left| \downarrow _k\downarrow _j\right\rangle }\)), \(\sqrt{{{d^2(k-j)^2}}+L^2}\) is the distance between these two environmental particles in different states (\({\left| \uparrow _k\downarrow _j\right\rangle }\) or \({\left| \downarrow _k\uparrow _j\right\rangle }\)).

And then for the two-side model, the corresponding Hamiltonian can be shown as

$$\begin{aligned} H&=\sum _{j=1}^{\frac{n}{2}}(H_{0,jl}+H_{0,jr})+\sum _{j=1<k}^{\frac{n}{2}}(H_{jl,kl}+H_{jr,kr})\nonumber \\&\quad +\sum _{k=1,j=1}^{\frac{n}{2}}H_{jl,kr}, \end{aligned}$$
(7)

with

$$\begin{aligned} \quad H_{0,jl}&=-\frac{\varDelta _{0,jl}}{2}I_{\frac{n}{2}l}\otimes \cdots \otimes \sigma _{z}^{(jl)}\otimes \cdots \otimes \sigma _{z}^{(0)}{\otimes }I_{1r}\nonumber \\&\quad \otimes \cdots \otimes I_{\frac{n}{2}r}, \end{aligned}$$
(8)
$$\begin{aligned} \quad H_{0,jr}&=-\frac{\varDelta _{0,jr}}{2}I_{\frac{n}{2}l}\otimes \cdots {\otimes }I_{1l}\otimes \sigma _{z}^{(0)}\otimes \cdots \otimes \sigma _{z}^{(jr)}\nonumber \\&\quad \otimes \cdots \otimes I_{\frac{n}{2}r}, \end{aligned}$$
(9)
$$\begin{aligned} \quad H_{jl,kl}&=-\frac{\varDelta _{jl,kl}}{2}I_{\frac{n}{2}l}\otimes \cdots \otimes \sigma _{z}^{(jl)}\otimes \cdots \otimes \sigma _{z}^{(kl)}\otimes \nonumber \\&\quad \cdots \otimes I_{0}{\otimes }I_{1r}\otimes \cdots \otimes I_{\frac{n}{2}r} \end{aligned}$$
(10)
$$\begin{aligned} \quad H_{jr,kr}&=-\frac{\varDelta _{jr,kr}}{2}I_{\frac{n}{2}l}\otimes \cdots {\otimes }I_{1l}\otimes I_{0}\otimes \cdots \otimes \sigma _{z}^{(jr)}\otimes \nonumber \\&\cdots \otimes \sigma _{z}^{(kr)}\nonumber \\&\quad \otimes \cdots \otimes I_{\frac{n}{2}r} \end{aligned}$$
(11)
$$\begin{aligned} \quad H_{jl,kr}&=-\frac{\varDelta _{jl,kr}}{2}I_{\frac{n}{2}l}\otimes \cdots \otimes \sigma _{z}^{(jl)}\otimes \cdots {\otimes }I_{1l}\otimes I_{0}{\otimes }I_{1r}\nonumber \\&\quad \otimes \cdots \otimes \sigma _{z}^{(kr)}\otimes \cdots \otimes I_{\frac{n}{2}r} \end{aligned}$$
(12)

where \(H_{0,jl}\) and \(H_{0,jr}\) represent the gravitational interaction between the system particle and the environmental particle to its left and right, respectively. \(H_{jl,kl}\) and \(H_{jr,kr}\) respectively describe the gravitational interaction between two environmental particles to the left and right of \(m_0\). Similarly, \(H_{jl,kr}\) means the gravitational interaction between two environmental particles on the both sides of \(m_0\). By considering the mass of environmental particles satisfy the condition \(m_{jl}=m_{jr}=m_{j}\), then \(\varDelta _{0,jl}\) and \(\varDelta _{0,jr}\) can be expressed as

$$\begin{aligned} \varDelta _{0,jl}=\varDelta _{0,jr}=\varDelta _{0,j}&=Gm_{0}m_{j} \left( \frac{1}{{dj}}-\frac{1}{\sqrt{{{d^2j^2}}+L^2}}\right) . \end{aligned}$$
(13)

By considering the environmental particles are on the same side of the system particle \(m_0\) (\(\frac{n}{2}{\ge }k>j\ge 1\))

$$\begin{aligned} \varDelta _{jl,kl}&=\varDelta _{jr,kr} \nonumber \\&=Gm_{j}m_{k} \left( \frac{1}{{d(k-j)}}-\frac{1}{\sqrt{{{d^2(k-j)^2}}+L^2}}\right) . \end{aligned}$$
(14)

However, for the case the environmental particles are on opposite sides (\(\frac{n}{2}{\ge }k\ge 1,\frac{n}{2}{\ge }j\ge 1\))

$$\begin{aligned} \varDelta _{jl,kr}=Gm_{j}m_{k}(\frac{1}{{d(k+j)}}-\frac{1}{\sqrt{{{d^2(k+j)^2}}+L^2}}). \end{aligned}$$
(15)

For the initial states in Eqs. (1) and (2), the evolution density matrix of the total system at time t can be obtained by \(\rho (t)=e^{-iHt/\hbar }\left| \varPsi (0)\right\rangle \left\langle \varPsi (0)\right| e^{iHt/\hbar }\). In order to explore the dynamical behavior of the system massive particle, we should calculate the evolution-reduced density matrix of the particle \(m_{0}\) from the density matrix of the total system by tracing over the environmental particles. Therefore, in the basis of the system particle \(\{{\left| \uparrow \right\rangle _0},{\left| \downarrow \right\rangle _0}\}\), the evolution-reduced density matrix of the system particle \(m_0\) in the one-side model is

$$\begin{aligned} \rho _{m_0}(t)&=\text {Tr}_{1,2,3\cdots ,n}[\rho (t)]\nonumber \\&=\frac{1}{2}{ \left( \begin{array}{cccc} 1&{}\prod \limits _{j=1}^n\cos (\frac{\varDelta _{0,j}t}{\hbar })\\ \prod \limits _{j=1}^n\cos (\frac{\varDelta _{0,j}t}{\hbar })&{}1\\ \end{array} \right) }. \end{aligned}$$
(16)

Similarly, the evolution-reduced density matrix of the quantum system in the two-side model can be obtained

$$\begin{aligned} \rho _{m_0}(t)&=\text {Tr}_{\frac{n}{2}l,\cdots ,1l,1r\cdots ,\frac{n}{2}r}[\rho (t)]\nonumber \\&=\frac{1}{2} { \left( \begin{array}{cccc} 1&{}\prod \limits _{j=1}^{\frac{n}{2}}\cos ^{2}(\frac{\varDelta _{0,{j}}t}{\hbar })\\ \prod \limits _{j=1}^{\frac{n}{2}}\cos ^{2}(\frac{\varDelta _{0,{j}}t}{\hbar })&{}1\\ \end{array} \right) }. \end{aligned}$$
(17)

From the Eqs. (16) and (17), we want to stress that the dynamical behavior of the system particle can only be influenced by the gravitational interactions between the quantum system \(m_0\) and the environmental particles. The gravitational interactions between environmental particles have no effect on the dynamics of the system particle. In the next section, we would monitor the system particle dynamical behavior (such as the non-Markovianity and the QSLT) by manipulating the various parameters of the environmental particles.

3 Dynamical crossover behaviors

The QSLT effectually defines the bound of minimal evolution time for an actual dynamics process from the initial state \(\rho _{s}(0)\) to the target final state \(\rho _{s}(\tau )\). And it is helpful to analyze the maximal evolutional speed of the dynamics process [41, 43, 46]. To describe the dynamics speedup of the system particle \(m_0\) by manipulating the environmental particles, a proper QSLT could be effectually defined by the bound of minimal evolution time for an arbitrary initial state \(\rho _{s}(0)\) to the corresponding target final state \(\rho _{s}(\tau )\) , which can facilitate to analyze the maximal evolution speed of the quantum system. In Campaioli et al. [58], the author have redefined a new bound from a geometric perspective by using the method of states of geometric distance in a generalized Bloch sphere. The QSLT is as follows

$$\begin{aligned} \tau _{QSL}&=\frac{{\Vert \rho _{s}(0)-\rho _{s}(\tau )\Vert }_{hs}}{\overline{\Vert {\dot{\rho _{s}(t)}}\Vert }}, \end{aligned}$$
(18)

with \({\overline{\Vert {\dot{\rho _{s}(t)}}\Vert }}={\frac{1}{\tau }}\int _0^\tau dt{\Vert {\dot{\rho _{s}(t)}}\Vert } \) and \( {\Vert {A}\Vert }_{hs}=\sqrt{\sum _iM_i^2} \). Here \(M_i\) are the singular values of A, and \(\tau \) is set as the actual evolution time of the dynamics process. The advantage of this definition is tighter and easier to calculate for almost all quantum evolution processes. The physical interpretation of \(\tau _{QSL}\) is as follows: If \(\tau _{QSL}/\tau \) is equal to 1, the dynamics evolution of the quantum state would not be speedup. That is to say, the evolutional speed is already maximum. While for \(\tau _{QSL}/\tau <1\), the dynamics evolution of the quantum state may be speedup. Moreover, the smaller this \(\tau _{QSL}/\tau \) is, the greater the quantum speedup could be.

As noted in [41, 43, 44], the non-Markovian behavior in the dynamics process from \(\rho (0)\) to \(\rho (\tau )\) can be attributed to quantum speedup evolution of a quantum system. That is, the associated information back-flow from the environment to the system, can lead to faster quantum evolution, and hence, to a smaller \(\tau _{QSL}/\tau \). To further analyze the connection between the non-Markovian behavior and quantum speedup process, in the following, we would try to explore the dynamics control from Markovianity to non-Markovianity of the system particle \(m_0\) by adjusting the environment particles, i.e., by tuning the particle’ separation distance L or changing the mass of the particles \(m_{j}\), and the environmental particles’ number n.

It is well known that quantum non-Markovianity is a multifaceted phenomenon and different methods for quantifying memory effects do not agree with each other in general [59,60,61]. However, for a simple single quantum system such as the considered single massive particle in our work, a measure of non-Markovianity \({\mathcal {N}}({\varPhi })\) (Breuer–Laine–Piilo method [32]) can be introduced. For a quantum process \(\varPhi (t)\), \(\rho _s(t)=\varPhi (t)\rho _s(0)\), with \(\rho _s(0)\) and \(\rho _s(t)\) denoting the density operators at time \(t=0\) and at any time \(t>0\), then the non-Markovianity \({\mathcal {N}}({\varPhi })\) is quantified by

$$\begin{aligned} {\mathcal {N}}({\varPhi })&=\max \limits _{\rho _s^{1,2}(0)}\int _{\sigma >0}\quad {dt\sigma [t,\rho _s^{1,2}(0)]}, \end{aligned}$$
(19)

here \(\sigma [t,\rho _s^{1,2}(0)]\) is the rate of change of the trace distance, \(\sigma [t,\rho _s^{1,2}(0)]=\frac{d}{dt}{{\mathcal {D}}(\rho _s^1(t),\rho _s^2(t))}\) representing the information flow. The trace distance \({\mathcal {D}}\) describing the distinguishability between the two states is defined as \({{\mathcal {D}}(\rho _s^1(t),\rho _s^2(t))}=\frac{1}{2}{\Vert \rho _s^1-\rho _s^2\Vert }\), \(\Vert {M}\Vert =\sqrt{M^\dag M}\)and \(0<{\mathcal {D}}<1.\) And \(\sigma [t,\rho _s^{1,2}(0)]\le 0\) corresponds to all dynamical semigroups and all time-dependent Markovian processes. A non-Markovian evolution is defined as a process in which, for certain time intervals \(\sigma [t,\rho _s^{1,2}(0)]>0\), the information flows back into the system temporarily, originating from the appearance of quantum memory effects. we needs to take the maximum over all initial states for calculating the non-Markovianity. In Refs. [32, 57], by drawing a sufficiently large sample of random pairs of initial states, it was proven that the optimal state pair of the initial states can be selected as \(\rho _{s}^1(0)=\frac{1}{\sqrt{2}}(\left| \uparrow \right\rangle _s+\left| \downarrow \right\rangle _s)\) and \(\rho _{s}^2(0)=\frac{1}{\sqrt{2}}(\left| \uparrow \right\rangle _s-\left| \downarrow \right\rangle _s)\).

Therefore, by considering each environment massive particle prepared to be in a spatially localized superposition state (\(\rho _{j}^1(0)=\frac{1}{\sqrt{2}}(\left| \uparrow \right\rangle _j+\left| \downarrow \right\rangle _j\)), and choosing the optimal state pair of the initial states of the system particle as \(\rho _{m_{0}}^1(0)=\frac{1}{\sqrt{2}}(\left| \uparrow \right\rangle _{m_{0}}+\left| \downarrow \right\rangle _{m_{0}})\) and \(\rho _{m_{0}}^2(0)=\frac{1}{\sqrt{2}}(\left| \uparrow \right\rangle _{m_{0}}-\left| \downarrow \right\rangle _{m_{0}})\), the trace distances \({{\mathcal {D}}(\rho _s^1(t),\rho _s^2(t))}\) in the one-side model and two-side model can be respectively obtained

$$\begin{aligned} {{\mathcal {D}}(\rho _{m_0}^1(t),\rho _{m_0}^2(t))}&=\left| \prod \limits _{j=1}^n\cos (\frac{\varDelta _{0j}t}{\hbar })\right| , \end{aligned}$$
(20)

and

$$\begin{aligned} {{\mathcal {D}}(\rho _{m_0}^1(t),\rho _{m_0}^2(t))}&=\left| \prod \limits _{j=1}^{\frac{n}{2}}\cos (\frac{\varDelta _{0j}t}{\hbar })^2\right| . \end{aligned}$$
(21)

The rate of change of the trace distance \(\sigma [t,\rho _s^{1,2}(0)]\) can be acquired from Eqs. (20) and (21). Then one can readily verify the non-Markovianity \({\mathcal {N}}({\varPhi })\) of the dynamics process of the system particle. The above is an illustration of the basic calculation of the non-Markovianity and the QSLT. In the following, by controlling the parameters (such as the mass of environmental particles, the number of environmental particles and the separation distance of each massive particle), the dynamical crossover behaviors from Markovian to non-Markovian and from no-speedup to speedup can be achieved in the one-dimensional linear one-side model and two-side model. In order to be more discriminative, we use the symbol \(n_1\) to represent the number of environmental particles in the one-side model and \(n_2\) to represent the number of environmental particles in the two-side model, and consider that all environmental particles have the same mass m.

3.1 One-side model

Fig. 2
figure 2

For the one-side model, the actual evolution time \(\tau =0.4\) s, d = 250 \(\upmu \)m and \(m_0=10^{-13}\) kg. a, c Non-Markovianity \(N({\varphi })\) of the dynamics process of the system particle \(m_0\) as a function of L/d and \(m/m_0\). b, d The QSLT for the dynamics process of the system particle \(m_0\) from the initial state \(\rho _{s}(0)=\frac{1}{\sqrt{2}}(\left| \uparrow \right\rangle _s+\left| \downarrow \right\rangle _s)\) to the target final state \(\rho _{s}(\tau )\) as a function of L/d and \(m/m_0\)

Full size image

For the one-side model, we mainly explore the dynamical crossover behaviors of the system particle \(m_{0}\) which is at the leftmost end of the linear structure and couples with the other environmental particles with gravitational interactions. In Fig. 2, the non-Markovianity \(N({\varphi })\) and the QSLT \(\tau _{QSL}\) of the system particle dynamics process from \(\rho _{m_0}(0)\) to \(\rho _{m_0}(\tau )\) as a function of the separation distance L and the mass m for different \(n_{1}\) of environmental particles, with the actual evolution time \(\tau = 0.4\) s, \(d= 250\,\upmu \)m and \(m_0 =10^{13}\) kg. For the condition \(m=m_{0}\), it is worth noting that a remarkable dynamical behavior crossover from Markovian dynamics to non-Markovian dynamics (\(\rho _{m_0}(0)\rightarrow \rho _{m_0}(\tau )\)) can occur at a certain critical separation distance \(L_{c}=0.64d\) of each environmental particle. When \(L<L_{c}\), the dynamics process abides by Markovian behavior, and then the non-Markovianity would occur in the case \(L>L_{c}\), as shown in Fig. 2a. And another dynamical crossover behavior from no-speedup to speedup of the dynamics process from \(\rho _{m_0}(0)\) to \(\rho _{m_0}(\tau )\) can also emerge at a different critical separation distance \(L_{c'}=1.1d\). In the case \(L<L_{c'}\), \(\tau _{QSL}/\tau =1\) as shown in Fig. 2b), the quantum evolution process of the system particle cannot be accelerated. And when \(L>L_{c'}\), \(\tau _{QSL}/\tau <1\) can be acquired, the quantum dynamics process can be speedup. So the dynamical crossover behaviors from Markovian to non-Markovian and from no-speedup to speedup can be achieved by controlling the separation distance L of each particle.

Fig. 3
figure 3

For the one-side model: a phase diagram of the non-Markovianity \(N({\varphi })\) in the \(L-m\) plane for the crossover behavior between Markovian and non-Markovian. b Phase diagram of QSLT \(\tau _{QSL}\) in the \(L-m\) plane for the crossover between no-speedup dynamics and speedup dynamics. Here the actual evolution time \(\tau =0.4\) s, \(d=250\,\upmu \)m and \(m_0=10^{-13}\) kg

Full size image

Furthermore, we also find that the dynamics process of the system particle would abides by the Markovian no-speedup behavior in the condition of the shorter separation distance L, such as \(L=0.5d\). In order to achieve the non-Markovian speedup dynamics process of the system particle in \(L=0.5d\), the role of the environmental particles’ mass m on the dynamics behavior has been cleared in Fig. 2c, d. By adjusting the mass of environmental particles satisfying \(m> 1.48 m_0\), the evolution of the system particle can transfer from Markovian behavior to the non-Markovian behavior. And when \(m>3 m_0\), the dynamics of the system can also achieve dynamic crossover behavior from no-speedup to speedup.

As expressed by the above description of two dynamical crossover behaviors, non-Markovianity of the studied dynamics process exists, whereas the evolution speed of this dynamics process will not be accelerated, as indicated by Fig. 2. Although the non-Markovianity may play an active role in the QSLT, the quantum speedup of the dynamics process is not only affected by the non-Markovianity in the considered one-side model. The geometric distance \({\Vert \rho _{m_{0}}(0)-\rho _{m_{0}}(\tau )\Vert }_{hs}\) between the initial state \(\rho _{m_{0}}(0)\) and final target state \(\rho _{m_{0}}(\tau )\) may also be an important factor affecting the QSLT. So the non-Markovianity is not decisive for the speedup dynamics process.

Except for the separation distance L and the environmental particles’ mass m, the environmental particles’ number \(n_{1}\) can also be related to the dynamics behavior of the system particle. The transition critical point causing the non-Markovian behavior (Fig. 2a, c) and the transition critical point at which the dynamics process of the system particle starts to accelerate (Fig. 2b, d) are both independent of the environmental particles’ number \(n_{1}\). And \(n_{1}\) plays an important role in controlling non-Markovian behavior or speedup behavior of the system. Through verification, it is found that the smaller \(n_{1}\), the greater the non-Markovianity and the smaller QSLT appear. And then when the number of particles \(n_{1}\) reaches a certain value, the non-Markovianity and the QSLT will not be affected by \(n_{1}\).

In addition, in order to clearly give the region of parameters for the dynamical crossover behaviors from Markovian to non-Markovian and from no-speedup to speedup, by fixed number of the environmental particles \(n_{1}=2\), Fig. 3 depicts the phase diagrams for the non-Markovianity \(N({\varphi })\) and QSLT \(\tau _{QSL}\) of the system particle dynamics process from \(\rho _{m_0}(0)\) to \(\rho _{m_0}(\tau )\) in the \(L-m\) plane with \(\tau =0.4\) s, \(d=250\,\upmu \)m, \(m_0\)=\(10^{-13}\) kg. If the environment contains a fixed number massive particles (here, setting \(n_{1}=2\)), the dynamical crossover behaviors from Markovian to non-Markovian and from no-speedup to speedup can be controlled by the parameters L and m. The whole region in the \(L-m\) plane is divided into two parts by the borderline, Markovianity area and non-Markovianity area (Fig. 3a), no-speedup area and speedup area (Fig. 3b). Moreover, numerical calculation also shows that the critical separation distance is mainly determined by the environmental particles’ mass m. The larger the value of m is, the smaller the value of the critical separation distance should be requested. Take the cases in Fig. 3a as examples; when \(m=3.5m_{0}\), we find the value of the critical separation distance is \(L_{c}=0.31d\), while in the cases \(m=2m_{0}\) and \(m=m_{0}\), we can acquire \(L_{c}=0.42d\) and \(L_{c}=0.64d\), respectively.

Fig. 4
figure 4

For the two-side model, the actual evolution time \(\tau =0.4\) s, \(d=250\,\upmu \)m and \(m_0=10^{-13}\) kg. a, c Non-Markovianity \(N({\varphi })\) of the dynamics process of the system particle \(m_0\) as a function of L/d and \(m/m_0\). b, d The QSLT for the dynamics process of the system particle \(m_0\) from the initial state \(\rho _{s}(0)=\frac{1}{\sqrt{2}}(\left| \uparrow \right\rangle _s+\left| \downarrow \right\rangle _s)\) to the target final state \(\rho _{s}(\tau )\) a function of L/d and \(m/m_0\)

Full size image

3.2 Two-side model

In this section, we would explore the dynamical crossover behaviors of the system particle under the two-side model, which consists of the system particle \(m_0\) in the middle and symmetrical environmental particles on both sides. By setting the mass of the system particle \(m_0\) equals to that of the environmental particles, that is, \(m=m_0\), the results can be easily obtained that, when \(L<0.64d\), the system dynamics process (\(\rho _{m_0}(0)\) to \(\rho _{m_0}(\tau ) \)) shows the Markovian behavior. By increasing L and making \(L>0.64d\), the system evolution would display the non-Markovian behavior. Therefore, \(L_{c} =0.64d\) is the transition point from Markovian behavior to non-Markovian behavior (as shown Fig. 4a). Moreover, when \(L=0.5d\), \(m=m_0\) satisfies, the evolution of the system is always Markovian behavior. Figure 4c describes the dynamics crossover behavior from Markovian to non-Markovian by adjusting the mass m of environmental particles, the transition point of this dynamics behavior of the system is \(m_{c}=1.48 m_0\). Compared to the results in the one-side model, the transition point for the dynamics crossover behavior from Markovian to non-Markovian is the same in both models.

While for the transition point for the dynamical crossover behavior from no-speedup to speedup of the dynamics process of the system particle as shown in Fig. 4b, d, the critical separation distance and the environmental particles’ mass satisfy \(L_{c} =0.64d\) and \(m_{c}=1.48m_{0}\). Obviously, in this two-side model, two dynamics crossover behaviors would be converted at the same transition point. As noted in Refs. [41,42,43], the non-Markovianity in the dynamics process (\(\rho _{m_0}(0)\) to \(\rho _{m_0}(\tau ) \)), and the associated information backflow from the environment, can lead to faster quantum evolution and hence to smaller QSLT. Also, in our two-side model, the dynamical crossover behavior from no-speedup to speedup is strictly related to the dynamics crossover behavior from Markovian to non-Markovian. This conclusion is obviously different from the result in one-side model.

Fig. 5
figure 5

For the two-side model: a phase diagram of the non-Markovianity \(N({\varphi })\) in the \(L-m\) plane for the crossover behavior between Markovian and non-Markovian. b Phase diagram of QSLT \(\tau _{QSL}\) in the \(L-m\) plane for the crossover between no-speedup dynamics and speedup dynamics. Here the actual evolution time \(\tau =0.4\) s, \(d=250\,\upmu \)m and \(m_0\)=\(10^{-13}\) kg

Full size image

This regularity is also shown in Fig. 5. If there is a smaller gravitational interactions between the system particle and each one environmental particle (that is corresponding to the smaller mass m), the separation distance L of each environmental particle should be increased to drive the non-Markovian speedup evolution of the system particle. Additionally, the boundary from the Markovianity to the non-Markovianiny is basically consistent with the dynamical crossover from no-speedup to speedup, which further illustrates our traditional relationship between non-Markovianity and the acceleration dynamics process. By comparing the boundary conditions of the transition of the two regions in Figs. 3b and 5b (for example, when \(m=3.5m_0\), \(L_{c}=0.46d\) needs to be fulfilled in one-side model, while \(L_{c}=0.31d\) should be satisfied in two-side model), so it is obviously find that, it is easier to realize the speedup evolution of the system particle in two-side model than in one-side model under the other same conditions.

So far, according to two linear configurations (one-side model and two-side model), we have observed that the dynamical crossover behaviors for a massive particle can be manipulated by the appropriate parameters of the controllable environment. Generally in the realizable experiments, the parameters such as the environmental particles’ number \(n_{1}\) or \(n_{2}\), the mass m of the environmental particles and the separation distance L for each particle can be monitored. Then we need to emphasize that the change of particles’ number will not affect the value of transition point, but will affect the value of the non-Markovianity and the QSLT. In addition, the non-Markovianity tends to be gentle with the increase of separation distance. Finally, the greater the environmental particles’ mass m satisfies, the greater the non-Markovianity is achieve, and the greater degree of dynamic acceleration will also occur. The physical reason for the conclusion can be explained as: for the models in our work, the greater the gravitational interaction between the system particle and the environmental particles, can lead to the stronger the information back-flow from the environmental particles to the system particle. And the larger non-Markovianity of dynamics process leads to the greater acceleration of the system particle’ quantum state evolution. It is worth emphasizing that, the remarkable conclusion declares that our mechanism to control the non-Markovianity of a massive particle can also be used to accelerate the evolution speed of this massive particle.

4 Conclusions

In summary, we have demonstrated that the non-Markovian dynamics speedup control of a massive particle can be achieved by manipulating the parameters of the environment particles due to gravity. By considering two linear configurations (one-side model and two-side model) consisting of a massive particle gravitationally interacting with multiple massive particles as a environment, two dynamical crossover behaviors of the system particle, from Markovian dynamics to non-Markovian dynamics and from no-speedup evolution to speedup evolution, have been realized by adjusting the separation distance of each massive particle and the mass of the environment particles.

At the same time, some remarkable physical conclusions are also revealed. In this work we mainly consider the parameters (such as the environmental particles’ number n, the environmental particles’ mass m, the system particle’ mass \(m_{0}\), the separation distance L and the distance d between two adjacent particles) in the total system to manipulate the dynamical crossover behaviors of the system particle. When other parameters are fixed, only one of these variables is regulated. We can acquire the results as following: the increasing separation distance L of each massive particle can lead to the increase of information back-flow capacity and the acceleration of quantum evolution. With the increasing of the mass of the environmental particles, the greater the gravitational interaction between the system particle and each environmental particle is, and the larger non-Markovianity of dynamics process and the faster the quantum evolution process appear. In addition, the environment particles’ number is also one of the factors that can affect the non-Markovian speedup dynamic evolution process, but the limitation of its influence is obvious.

In addition, we can clearly find that in the case of the two-side model, the dynamical crossover behavior from no-speedup to speedup is strictly related to the dynamics crossover behavior from Markovian to non-Markovian. They are one-to-one correspondence, and quantum acceleration is caused by the non-Markovianity. However, in the one-side case, the quantum speedup of the dynamics process is not only affected by the non-Markovianity. The geometric distance \({\Vert \rho _{s}(0)-\rho _{s}(\tau )\Vert }_{hs}\) between \(\rho _{s}(0)\) and \(\rho _{s}(\tau )\) may also be an important factor affecting the QSLT. So the non-Markovianity is not decisive for the speedup dynamics process.

Finally, we will make three additional explanations on our proposed scheme for the control of a massive particle evolution due to gravity. (a) Our model is considered as a closed system composed of the system massive particle \(m_{0}\) and its environmental particles, the influence of the external gravity on this whole closed system has been removed as much as possible, so an ideal experimental environment needs to be established. When both the particles and the experimental setup, including the magnetic field gradient, are in perfect free fall, the equivalence principle prevents any observable effect of the other external gravitational fields [22]. Therefore, our proposed scheme should be ideally performed in a zero-gravity environment. Of course, when the zero-gravity environment does not satisfy, the external quantized gravitational field [62, 63] would affect the dynamic behavior of the system particle.

(b) As mentioned in [17], the micro-size diamonds with an embedded nitrogen-vacancy center spin could be candidates for the massive system particle and environmental particles in this work. In order to exclude the interference of the Casimir-Polder interaction on the gravitational interaction, the physically relevant quantities in our model have been set: the mass of the system particle \(m_{0}\sim 10^{-13}\) kg, the distance from two immediate neighbors \(d\sim 250\,\upmu \)m, and the distance L and the mass of the environmental particles m satisfies \(L/d<10\) and \(m/m_{0}<10\). According to the above results in our manuscript, the increase of the number of environmental particles to a certain extent would no longer affect the non-Markovianity and the QSLT. If the experiment needs to be controlled within three massive particles, the total size of the experiment needs to be controlled within \(500\,\upmu \)m. So our proposed control scheme for a massive particle evolution is experimentally feasible.

(c) Similar to the scheme [17] which fully demonstrates the necessity of Newton’s gravitational field to test the development of entanglement between masses and proves that gravity is a quantum coherent medium by testing spin correlation, this method of choosing Newtonian potential is more for the simplicity and suitability of the analysis of a massive particle evolution due to gravity in our work. However, beyond the Newtonian approximation, the relativistic nature of gravity plays a crucial role. Generally, in the relativistic domain the existence of time dilation entails more drastic effects on quantum coherence [63,64,65,66]. Due to the non-Markovianity and QSLT are closely related to the dynamical behavior of quantum coherence. When the conditions for the establishment of Newtonian potential are not met, the relativistic effects should be taken into account, the dynamics behavior of a massive particle would definitely be different. The effects of general relativity on the quantum dynamics of a massive particle due to gravity would be a broader idea for our further research.