1 Introduction

While being the most abundant massive particles in the universe, neutrinos still retain many of their mysteries. The last decades changed the way we look at neutrinos, especially with the experimental discovery of the neutrino’s mass, and their place in the Standard Model of Particle Physics [1,2,3,4,5]. But, there are still many undiscovered facts about these mysterious particles. In order to uncover their unknown properties, the experimental techniques and technologies are constantly evolving.

Among these new technologies, one can find Water-based Liquid Scintillator (WbLS), Gadolinium-doped medium, and fast-timing photo-detectors such as Large area Picosecond Photo-Detectors (LAPPDs).

  • Water-based Liquid Scintillator: A novel detection medium that consists of a mixture of a small volume of Liquid Scintillator (LS) with a large volume of water. The high percentage of water provides both a low manufacturing cost and an easier experimental handling of the detector medium. Beyond that, this liquid emits both Cherenkov light from water and scintillation light from the LS, in a ratio set by the LS concentration. Cherenkov light provides information about the direction of charged particles in the medium with a cone-like topology. Scintillation light gives a high light yield and allows the detection of low energy charged particles below the Cherenkov threshold [6,7,8,9,10,11,12]. While the WbLS concept is not new [13], recent developments in the chemistry and properties of WbLS [6] made it more deployable for use in the field as an active medium.

  • Gadolinium doped medium: When it comes to detecting neutrons in hydrogenated media, Gd and its high thermal neutron capture cross-section (\(\sim \)49,000 barns), compared to Hydrogen (0.3 barns), is an element often chosen by physicists. Gd can be found at a moderate price and is easy to incorporate in aqueous solutions thanks to its highly soluble nature in water [14,15,16,17].

  • Large Area Picosecond Photo-Detectors (LAPPDs): A new photodetector technology, based on the principle of micro-channel plates, capable of reaching time resolutions of a few tenths of pico-seconds and high spatial resolutions down to the mm scale. LAPDDs are significantly promising when trying to separate prompt Cherenkov light from delayed scintillation light [18,19,20,21,22].

Neutrinos come from different natural and man-made sources such as cosmic rays, supernovae, atmospheric muon decays, the Sun, accelerators and nuclear reactors. The first experimental evidence of neutrinos came from a nuclear reactor in 1956 [23] and since then, reactor neutrinos have been studied extensively. As they are intensely generated in only one flavor, \(\bar{\nu _{e}}\), reactor neutrinos have been particularly helpful for neutrino oscillation studies where the flavor change is observed through a disappearance of the initial anti-neutrino flux.

The emission of electron anti-neutrinosFootnote 1 in a reactor core is directly correlated with the fission rate and the thermal power of the core and the emission rate, \(N_\nu \), can be expressed as:

$$\begin{aligned} N_\nu =\gamma (1+k)P_{th} \end{aligned}$$
(1)

where \(\gamma \) refers to a constant number containing all invariable terms, \(P_{\text {th}}\) indicates the reactor thermal power and k represents a time-dependent factor representing the variation of fuel composition over time. For the remainder of this study, this k factor will be assumed equal to zero (\(k=0\)) and time-dependent fuel composition will be considered constant [24]. Assuming the reactor thermal power is constant over time, a safe assumption for commercial reactors focusing on power generation, the rate of anti-neutrinos emission is considered constant over time as well.

About 200 MeV of energy are emitted per fission and most of this energy is shared between multiple fission products. These neutron-rich nuclei then undergo a series of beta decays leading to the total average emission of 6 \(\bar{\nu _{e}}\) per fission. The total amount of neutrinos emitted as a function of the reactor thermal power is approximately \(2 \times 10^{20}\) \(\bar{\nu _{e}}\) GW\(_{th}^{-1}\).s\(^{-1}\). The energy of those neutrinos, mostly below \(\sim \)1.8 MeV, is driven by the isotopes at the origin of the fission, \(^{235}U\), \(^{238}U\), \(^{239}Pu\), or \(^{241}Pu\) [25, 26].

The Akkuyu Nuclear Power Plant (ANPP), Turkey’s first nuclear power plant, is planned to start operating in 2023 in Mersin. It is the product of a cooperation agreement signed between the governments of Russia and Turkey in 2010 and its construction has started in 2018. The power plant will be equipped with four AES-2006 Generation III+ VVER units, a new generation pressurized water reactor constructed by the Rosatom company, fueled with uranium dioxide enriched to 5% \(^{235}U\). The nominal electrical power of each reactor will be approximately 1200 MW\(_{\text {e}}\), for a thermal power of 3200 MW\(_{\text {th}}\). Upon the successful operation of the first reactor, Akkuyu-1, the 2nd, 3rd, and 4th units will be put into operation in 2024, 2025, and 2026, respectively [27, 28].

The rate of anti-neutrino interactions expected in a detector from such a reactor can be expressed as:

$$\begin{aligned} S_\nu =\frac{N_{f}N_{p}}{4{\pi }L^2}<\sigma > \end{aligned}$$
(2)

where, \(N_p\) is the number of protons in the detector and L indicates the distance from the reactor core to the neutrino detector. The \(<{\sigma }>=5.8 \times 10^{-43}\) barn is the average inverse beta decay cross section at reactor neutrino energies and \(N_f\) represents the average fission rate, which is obtained from the following equation [29]:

$$\begin{aligned} N_{f}=6.24 \times 10^{18} \bigg (\frac{P_{th}}{MW^{-1}}\bigg )\bigg (\frac{MeV}{W_{e}}\bigg )s^{-1} \end{aligned}$$
(3)

where the mean energy delivered per fission is given by \(W_{e} = 203.78~\text {MeV}\). If we calculate the neutrino interaction rate for the Akkuyu NPP, we obtain:

$$\begin{aligned} S_\nu =9.86 \times 10^{5}\bigg (\frac{V}{m^3}\bigg )\bigg (\frac{m}{L}\bigg )^2 \quad \text {events/day}. \end{aligned}$$
(4)

The anti-neutrino interaction rate, expressed in events per day, at different reactor-detector distances of 25 m, 50 m and 100 m for the proposed detector (\(\sim \)2.65 m\(^3\)) was calculated to be 4180, 1050 and 261, respectively [30]. For the detailed information regarding the detector geometry and size can be found in Sect. 3.

Electron neutrinos, produced in the beta decays of fission products in nuclear reactors, are detected via Inverse Beta Decay, or IBD (\({\bar{\nu }} + p \rightarrow e^+ + n \)). This reaction leads to the creation of two distinct signals, one from the positron, the other from the neutron, both separated in time and with different signatures. The first signal comes from the energy deposition of the positron followed by its annihilation on an electron in the detection medium, leading to the emission of two 511 keV gamma rays. This process is referred to as a prompt signal, \(E_{prompt}\).

The second signal, generated by the capture of the neutron on an atom in the medium, occurs several microseconds (\(\sim \) 10–100 \(\mu \)s depending on the detection medium) after the prompt signal.

Fig. 1
figure 1

Inverse beta decay (IBD) process and signal reconstruction in the Gd-doped water-based liquid scintillator (WbLS) detector

Full size image

Most IBD detectors utilize hydrogenated materials (water, liquid scintillator) loaded with isotopes having a high neutron capture cross section in order to efficiently and quickly thermalize and capture neutrons. For most of the aforementioned detectors and for the rest of this study, Gadolinium is the isotope being used. Radiative neutron capture on hydrogen releases \(\sim \)2.2 MeV of energy in the form of a single gamma ray, while neutron capture on Gd releases a gamma cascade with a total energy of about 8 MeV. These captures lead to a delayed signal, \(E_{delayed}\), with a visible energy higher than most backgrounds due to natural radioactivity. A sketch of the IBD detection in a detector is shown in Fig. 1.

2 Low energy neutrino studies in Turkey

In recent years, several design and simulation studies have been performed with the goal of detecting neutrinos from the Akkuyu NPP. The first study conducted by Ozturk et al. is a Geant-4 based simulation of a small, 1-ton Gadolinium-doped water Cherenkov detector in very close vicinity of one of the reactor cores [31]. Another study, by Ozturk, focused on using a segmented detector, made of Gadolinium-loaded plastic scintillators. In this study, he showed the benefits of using a multi-variable analysis technique to suppress cosmic backgrounds [32]. On the other hand, Kandemir and Cakir proposed a small segmented hexagonal detector composed of plastic scintillators attached to photomultiplier tubes (PMTs) [33]. The common purpose of these studies is to monitor the reactor anti-neutrinos flux for nuclear non-proliferation purposes. But in a broader perspective, we propose to develop a program for low-energy neutrino studies in Turkey, which includes both a small size detector at a short-distance to the reactor, as mentioned here, and a medium size detector located 1–2 km from the reactor core. Previously, our co-authors V. Fischer and E. Tiras proposed a 30-ton detector, which consists of cylindrical tank filled with 0.1% Gadolinium-doped WbLS placed a few km away from the reactor cores [34]. The Reactor Neutrino Experiments of Turkey (RNET) program will consist of a 2–3 ton near detector placed very close to the reactor core (\(\sim \) 50 m) and a 30-ton far detector about 1–2 km from the power plant for nuclear non-proliferation studies using new techniques and pioneering technologies. In terms of oscillation measurements, the RNET program will not be competitive with existing k-ton neutrino experiments around the globe but will still be sensitive to short-baseline neutrino oscillations.

Both detectors will be complementary and they will have versatile designs to be able to test new detectors, sub-detectors and detection media in-situ. They will be instrumented with the same type of High Quantum Efficiency (HQE) PMTs, which have \(\sim \)35% QE at 390 nm. The medium concentration of the detectors will be similar in order to help cancel systematic effects related to the detector response. The RNET program will be a great opportunity for neutrino studies in Turkey with the aims of; (1) monitoring the Akkuyu NPP for nuclear non-proliferation purposes [35,36,37,38], (2) being a testbed for new detector technologies and new detection media as an integration with neutrino physics collaborations around the globe, (3) researching and developing more sensitive detectors and (4) training the next generation of neutrino physics researchers.

3 Experimental setup

The experimental setup, designed to be compact and easily accessible, includes a cylindrical tank, two layers of cosmic veto paddles on the sides of the tank, an electronics rack, and a DAQ system.

The tank, a stainless steel cylinder 1.5-m tall and 1.5-m in diameter, will be filled with a water-based liquid scintillator solution with a 0.1% Gd concentration and a 3% liquid scintillator concentration. The detector will be instrumented with 24 8-in. HQE PMTs facing the inside the detector and placed homogeneously around the detector barrel and on the top and bottom of the detector. Such a PMT placement corresponds to a photo-coverage of 28%. Figure 2 shows the RAT-PAC generated visualization of the detector, including the locations of all its PMTs in the inner volume. Several 2-in. PMTs could also be placed in the gaps between 8-inch PMTs to increase photo-coverage and provide additional granularity for light pattern reconstruction. Figure 3 shows the location and direction of all types of PMTs in the detector. For the remainder of this study, only the 8-inch PMTs will be taken into account.

Fig. 2
figure 2

Visualization of the detector and its inner PMTs using the RAT-PAC simulation framework

Full size image

The cosmic ray veto will consist of layers of plastic scintillator paddles attached to light guides (\(\sim 20\)-cm long) and coupled with 2-in. PMTs. Each layer, made of several scintillator paddles, is expected to have dimensions of at least 1.7 m (width) \(\times \) 1.7 m (length) in order to efficiently cover all sides of the detector for cosmic ray tagging purposes. Plastic scintillator was chosen as the main detection material for this veto as it has a high light yield and a fast scintillation decay time, thus making it a effective and inexpensive choice for efficiently rejecting cosmic backgrounds.

Fig. 3
figure 3

Sketch of the orientation of each PMTs in the detector. Each arrow indicates a PMT location in the detector and the direction of the arrow indicates the direction of the face (photocathode) of the PMTs. Orange arrows corresponds to 8-in. PMTs while green arrows correspond to possible additional 2-in. PMTs

Full size image

Inside the tank, a PMT holding structure, machined out of stainless steel, attached to the tank lid will be holding all PMTs. This design allows for an easy removal of each photosensors in case of repairs or upgrades. Once the PMTs are mounted on the structure, the inner structure will be wrapped with a thin, Gd-compatible black plastic liner (1–2 mm). This barrier will isolate the fiducial volume from the light generated by neutron captures occurring in the outer volume of the tank.

The lid and tank cylinder will be equipped with handles in order to easily lift and move the detector using a simple winch mechanism. With the added benefits of allowing quick and easy maintenance operations on the detector, this will also make the detector more portable and deployable at various locations. The detector is going to be portable in the sense that the inner PMTs and the cosmic paddles can be replaced easily in-situ. The ability to transport the detector on a truck or in a crate for field data taking is being investigated, but, ultimately, the decision will be made after discussions with the reactor operator and government agencies.

4 Electronics and data acquisition system

The whole detector system will be based on three major components: a Gd-doped WbLS tank, a cosmic muon veto, and a trigger and Data Acquisition System (DAQ) system.

The trigger system will rely on the coincidence-based detection of light depositions in the tank. Signals from the water PMTs will be received by VME-based 500 Mhz analog to digital converters (ADC) used for waveform digitization. The signals from the PMTs part of the cosmic veto system will be read out through a NIM system and fed into VME: Time-to-Digital Converters (TDC) that will only record the hit times of each paddle and allow a simple reconstruction of the muon track in the detector.

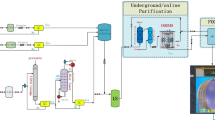
The whole system will be powered by a high voltage power supply, capable of providing positive (tank PMTs) and negative (veto PMTs) polarities. Figure 4 shows the schematic view of the detector components, electronics and Data Acquisition (DAQ) system.

Fig. 4
figure 4

Schematic view of the detector components, electronics and DAQ system

Full size image

5 Simulation studies

5.1 Signal simulation

In order to simulate particles transport in an accurate model of the Gd-doped WbLS detector, we used RAT-PAC (Reactor Analysis Tool-Plus Additional Code), a simulation framework that utilizes Geant4 and GLG4Sim libraries.

A series of simulations have been performed to understand the detector response to IBD interactions. For that purpose, a build-in RAT-PAC algorithm generating realistic IBD positron-neutron pairs was used. The kinematics (energy and momentum) of each IBD pair are obtained from the inverse beta decay differential cross section assuming a realistic ratio of fission products (\(^{235}U\), \(^{238}U\), \(^{239}Pu\), \(^{241}Pu\)) in the reactor core. For this study, this ratio of fission products is considered uniform in time.

In order to make statistical effects negligible, a total of 500,000 IBD events was simulated uniformly throughout the detector. Electrons with a fixed energy, ranging from 1 to 10 MeV, were also simulated uniformly in the detector to determine the conversion factor between the number of photon hits, expressed after correction for the quantum efficiency as a total number of photo-electrons, and the visible energy in MeV. This conversion factor, that varies for different media, was used to display all energy distributions in terms of visible energy and better compare different detector designs.

Several IBD events simulations were carried out with different WbLS concentrations (1%, 3%, and 5% LS) and with different mass fractions of Gd (0.1%, 0.3%, and 0.5% by weight). Figure 5 shows the photo-electrons distributions using different WbLS concentrations. As expected, the number of photo-electrons is directly correlated with the concentration of liquid scintillator in the medium, thus allowing a better efficiency at detecting low energy particles. This is a crucial feature when observing reactor anti-neutrinos where positron spectrum after IBD reaction peaks around 2–3 MeV. Figure 6 shows the reconstructed delayed energy distributions for different mass fractions of Gd in a 3% WbLS medium. Increasing the gadolinium concentration results in an enhanced efficiency to detect an n-Gd capture at a fixed threshold of 4 MeV.

Fig. 5
figure 5

Photo-electron distributions of \(E_{prompt}\) for several WbLS cocktails (1%, 3%, and 5% LS)

Full size image
Fig. 6
figure 6

Reconstructed delayed energy, \(E_{delayed}\), distributions for several WbLS cocktails with different mass fractions of Gd (0.1%, 0.3%, and 0.5%)

Full size image

While many different WbLS solutions have already been synthesized on a small scale, the WbLS cocktail with 3% LS and 0.1% Gd is one of the most studied and is expected to be manufactured on a bigger scale (\(\ge \) 100 tons) [39]. This WbLS mixture is thus the one we decided to focus on for the rest of this study. Similar simulations were also performed with a 5% LS solution as a cross-check since it has been manufactured and thoroughly studied as well. In the following, we discuss the energy and vertex resolutions for a 3% LS and 0.1% Gd WbLS solution in our detector model.

A widely accepted approximation is that pure LAB-based liquid scintillators have a light yield of about 10,000 photons per MeV. Following this approximation as well as linearly scaling the light yield with the LS concentration, an approximation valid at first order, the aforementioned medium with 3% LS yields about 300 photons per MeV. Figure 7 shows the photo-electron distribution as a function of energy from simulated electrons at the center of the detector.

To obtain the energy resolution, electrons with a fixed energy of 1 MeV were simulated uniformly in the fiducial volume of the detector. The photo-electron distribution of these simulated electrons along with its best Gaussian+Landau fit is shown in Fig. 8. Here, we detect about 15 photo-electrons per 1 MeV electron, and the fit yields an energy resolution of 32% at 1 MeV.

On the other hand, when we simulate electrons at the center of the detector, we detect an average of 16 photo-electrons per 1 MeV electron and the Gaussian fit yields an energy resolution of 24% at 1 MeV.

Since the energy resolution directly depends on the photon statistics, the energy resolution can be extrapolated at different energies by using of \(32\%/ \sqrt{\text {E (MeV)}}\).

Fig. 7
figure 7

Photo-electron distribution as a function of energy ranging from 1 to 10 MeV with 1MeV step obtained using simulated electrons generated at the center of the detector

Full size image
Fig. 8
figure 8

Photo-electron distribution of 1 MeV electrons simulated uniformly in the inner fiducial volume of the detector and fitted with a convolution of Gaussian and Landau function using RooFit

Full size image

Accurately reconstructing the positions of events in a detector is essential when trying to select IBD pairs amidst backgrounds as prompt and delayed events are correlated in time and space. In the RAT-PAC simulation framework, BONSAI [40] can be used as a position reconstruction algorithm to obtain the best reconstructed position and direction of a particle in the detector. Since BONSAI was mostly designed to study low energy events, 1 MeV electrons were simulated to verify the position reconstruction capabilities of the detector. The spatial separation between simulated and reconstructed vertices, shown as the distribution of \(\varDelta R\), is displayed in Fig. 9. Figure 10 shows the cumulative distribution of \(\varDelta R\) and indicates that 68% of the interaction vertices are reconstructed within 41 cm of their true position. Similarly to the energy resolution, the vertex resolution is dependent of the photon statistics at first order and can thus be expressed as a function of energy through the following formula: 41 cm/\(\sqrt{\text {E (MeV)}}\). Given the relatively small size of the detector, such a position resolution does not yield a significant advantage for background discrimination. However, several studies are ongoing to improve reconstruction algorithms in WbLS and extract information from both the Cherenkov and scintillation components of the emitted light.

Fig. 9
figure 9

Reconstructed \(\varDelta R\) distribution from simulated 1 MeV electrons using the BONSAI position reconstruction algorithm

Full size image
Fig. 10
figure 10

Cumulative \(\varDelta R\) distribution obtained from the reconstructed \(\varDelta R\) distribution displayed in Fig. 9

Full size image

At this point, the behavior of ionizing particles in our detector model is understood enough to efficiently simulate and interpret events from IBD pairs generated by reactor neutrinos.

While positrons and neutrons are generated at the same time in the simulation, the separation between prompt and delayed events is performed in the analysis in a fashion similar to what a simple DAQ would do. All hits (photo-electrons) on the detector’s PMTs within the [0–200] ns time range are considered part of the prompt event, caused by the interaction of the positron in the medium. Similarly, all hits recorded in the [1–200] \(\mu \)s time range are considered to be part of the delayed event, caused by the neutron capture on gadolinium or hydrogen.

The sum of those hits per event for both time ranges makes up the prompt and delayed energy distributions shown in Figs. 11 and 12. Both distributions have been scaled using the conversion factor obtained previously, from the gaussian fit in Fig. 8, and expressed in term of visible energy. On Fig. 12, the ratio between the amplitudes of both peaks, at 2.2 MeV from neutron capture on hydrogen and at \(\sim \)8 MeV peak neutron captures on gadolinium, is directly dependent on the gadolinium concentration. Higher gadolinium concentrations yield a higher number of captures in the latter peak and an increased detection efficiency above a fixed threshold. As mentioned in Sect. 1, the time difference between the reconstructed prompt and delayed events is expected to behave like an exponential function after the thermalization of neutrons with a constant, or rate, of \(\sim \)30 \(\upmu \)s. This behavior is confirmed in the simulation, as shown in Fig. 13.

Fig. 11
figure 11

Reconstructed prompt events energy distribution from the simulated IBD events

Full size image
Fig. 12
figure 12

Reconstructed delayed events energy distribution from the simulated IBD events

Full size image
Fig. 13
figure 13

Time difference between prompt and delayed events for IBD events

Full size image

5.2 Signal selection

Background rejection is of the utmost importance when detecting neutrinos, and in particular low energy reactor neutrinos at shallow depths. In order to purify our signal, we consider a cut on \(\varDelta \)T, the time difference between the prompt and delayed events, as well as the visible prompt and delayed energies, \(E_{prompt}\) and \(E_{delayed}\). The \(\varDelta \)T selection cut is based on the fact IBD events are correlated in time, due to the exponential nature of the capture time of the neutron. With an average capture time of \(\sim \)30 \(\upmu \)s in Gd-loaded WbLS, applying a selection such that both IBD events are detected within 100 \(\upmu \)s of each other yields a signal purity of 97%. The efficiency of this selection cut to discard accidental backgrounds, caused by two events uncorrelated in time, will be confirmed after deployment. While most reactor neutrino detectors also apply a cut on \(\varDelta \)R, the spatial difference between the prompt and delayed events, the small size of this detector and the low spatial resolution presented in the section above limit our ability to use such a selection cut.

Applying selection cuts on the prompt and delayed energies helps to discard background events that could mimic a positron energy deposition or a neutron capture. Since the visible energy distribution for reactor neutrinos has no threshold, unlike the actual IBD interaction on a free proton, better detection efficiencies can be reached by lowering the selection cut threshold for prompt events. However, care must be taken to limit the impact of electronics and PMT-originated backgrounds (dark noise, PMT flashes). For that purpose, a threshold of 10 photo-electrons, corresponding to about 0.58 MeV, has been implemented. Such a selection cut yields a signal purity of 99% while ensuring electronics and PMT-based backgrounds will be kept to a minimum. This threshold will be adjusted after deployment once backgrounds are assessed in-situ.

The use of gadolinium as a neutron capture enhancement element allows a better discrimination of accidental backgrounds from IBD events in terms of reconstructed time difference, as discussed above, as well as in terms of reconstructed delayed energy. With a total energy of 8 MeV, a gamma cascade following a neutron capture of Gd can be distinguished from other backgrounds such as natural radioactivity, mostly contained below 3 MeV. After applying a selection threshold at 4 MeV, or about 68 photo-electrons, on the reconstructed delayed energy distribution, a signal purity of 79% can be reached.

When selecting only interactions occurring in the fiducial volume, the total signal efficiency due to these selection cuts is reduced to \(\sim \)52% for prompt events, \(\sim \)40% for delayed events and \(\sim \)50% for \(\varDelta \)T. All the selection cuts presented and applied above after the fiducial volume cut, are independent from one another at first order, as applying a threshold to one will not bias the others. After applying the selection cuts of fiducial, prompt, delayed and DeltaT all together, a total signal efficiency of 29.2% is achieved for our detector design. Note that this affirmation isn’t valid when applying the spatial separation cut on \(\varDelta \)R as the neutron travel time and distance before capture are correlated with each other.

The fluctuation on delayed events is about 4–5% when applying the energy cut with an increment of 0.2 MeV on the 4 MeV cut and the fluctuation on prompt events is roughly 2–2.5% within one photo-electron.

In order to limit the effect of external backgrounds such as gamma rays and neutrons, the inner detector, encompassed within the volume delimited by the PMTs, optically separated from the rest of the detector. This active area consists of a cylinder, \(\sim \)1 m in height and \(\sim \)1 m in diameter, excluding the volume occupied by the PMT themselves. When considering only this active area as well as applying the 29.2% signal efficiency, the daily rates of anti-neutrinos at different distances from the reactor cores are calculated as 76, 306 and 1220 events at 100, 50 and 25 m, respectively. The statistical uncertainty on the event rate was calculated as 11.5% at 100 m, 5.7% at 50 m, and 2.9% at 25 m from the reactor core.

6 Discussion

The detector design proposed and modeled in this study will be addressing the following motivations:

  • Being the first neutrino detector built and operated in Turkey. In addition, it will act as an educational platform for neutrino researchers, provide hands-on experience for the development of new detector technologies, and train the next generation of scientists in Turkey.

  • Aiming to become a testbed for experiments around the globe interested in testing and deploying new detector technologies.

  • Act as a near detector to the 30-ton detector mentioned in [34]. Operating both detectors would provide additional measurements of reactor-based neutrino oscillations at medium (>1 km) and short (\(\le \)100 m) baselines.

The simulation results obtained from this study show that a detector with a 3% LS and 0.1% Gd WbLS solution can adequately and efficiently detect neutrinos from the Akkuyu NPP. As mentioned previously, this particular medium was considered mainly because it has already been manufactured and could be ready to be deployed on a short timescale. Since R &D studies on WbLS are advancing quickly, thanks to a global effort and an interest from the particle and nuclear physics communities, one can imagine that more WbLS solutions with different liquid scintillator content will be manufactured on a large scale in the near future. In anticipation of this possibility, simulation studies similar to the ones presented above were carried out with different WbLS mixtures. Since the scintillation light yield increases with the WbLS liquid scintillator concentration, studies using a realistic 5% LS mixture yield a better energy and vertex resolution. Table 1 shows the energy and vertex resolutions of the electrons simulated at the center of the detector for different WbLS mixtures.

Table 1 The energy and vertex resolutions for different WbLS concentrations (1%, 3%, and 5%) with a 0.1% Gd
Full size table

This detector is intended to be used and operated as a testbed for experiments, such as THEIA [39] and WATCHMAN [41], that expressed interest in using WbLS in addition to new photosensors in their detectors. One of the main features that makes this combination of WbLS and new photosensors attractive for such experiments is the ability to separate Cherenkov and scintillation lights in the same event, thus providing a precise kinematic and calorimetric reconstruction of a detected particle. While this separation was not explored in details in these simulation studies, it is the focus of several research groups both in terms of hardware and software. While the effort on the software side focuses on machine learning based methods to select the fast Cherenkov component from the slow scintillation one, new hardware is being designed and developed to perform this task in-situ in the detector. Dichroic filters are one way to separate these two light components at the hardware level. With their ability to sort incoming light as a function of wavelengths, dichroic filters are an efficient, cheap and yet reliable way of separating the Cherenkov and scintillation components of the light emitted by a particle interacting in WbLS [42, 43]. Such filters could be easily installed in the detector presented in his study, thanks to its design allowing for an easy access to its PMTs and inner structure. Another method to separate the fast and the slow component of light is to use fast photosensors, able to separate all photon hits on a picosecond time scale, such as LAPPDs [44]. Such photodetectors can also be easily deployed in the detector, with only minimal changes to the inner structure.

While this study focused on the detector’s design and its response to reactor neutrinos, one should note that deploying a detector in the vicinity of a nuclear reactor is a major challenge in terms of background mitigation. If located more than 25 m from a reactor core, direct backgrounds from fission and fission products (gammas and neutrons) may not be a concern with a sufficient shielding. Similarly, accidental backgrounds from radioactive decays within the detector can be mitigated by carefully screening and choosing materials with a high level of radio-purity as well as utilizing the fact that, unlike IBD pairs, such events are not correlated in time. As observed by the authors of [45], the main background we anticipate for such a detector is correlated background caused by cosmic muon interactions in, or in the vicinity of, the detector. Such interactions are likely to cause spallation reactions that, in turn, are likely to emit neutrons with energies in the MeV range, or fast neutrons. With enough kinetic energy to generate a signal equivalent to a few MeV of visible energy followed by a capture on gadolinium, those neutrons can easily mimic an IBD pair. Even assuming an efficient tagging of the muons entering the detector and its surroundings, this correlated background can not be fully excluded, especially with a detector placed at shallow depth such as the one modeled in this study. Prior to deployment, a dedicated and thorough background measurement campaign must be carried out to understand and quantify this background. The cosmic muon and neutron background fluxes measured during this campaign will be simulated and compared to expected reactor neutrino rates in the detector. The results of this study will drive the design of the detector’s passive shielding and active vetos.

To reduce the external backgrounds from natural radioactivity and atmospheric muon spallation on the surrounding materials, the detector could be placed in a cavity, surrounded by a passive 50-cm thick water shield as well as instrumented cosmic paddles. The \(\sim \) 50 cm passive water medium will provide a low-Z shield for fast neutrons as well as a sufficient barrier for 90% of the 2.2 MeV gamma rays generated upon their captures on hydrogen nuclei. The thickness of \(\sim \) 50 cm would be sufficient since it corresponds to more than 2 attenuation lengths for 2.2 MeV gammas. Depending on the results of the aforementioned in-situ muon and neutron flux measurements, the thickness of this passive water shield will be subject to optimization. Other background discrimination techniques such as Cherenkov-scintillation separation or pulse-shape discrimination studies for WbLS media [46] would also enhance the background rejection capabilities of the detector.

7 Conclusion

Here, we present and discuss the simulation results of a 2–3 ton compact Gd-doped Water-based Liquid Scintillator detector, near the Akkuyu Nuclear Power Plant (ANPP), as Turkey’s first low-energy neutrino detector. The simulation studies in this paper are carried out using the RAT-PAC simulation package based on Geant4. The goal of this study was to study the response of a ton-scale detector to reactor neutrinos while investigating the feasibility of a deployment using existing mixtures of WbLS, with varying concentrations of liquid scintillator and gadolinium. With an experimental setup consisting of a 1.5 m high and 1.5 wide cylindrical stainless steel tank instrumented by 24 PMTs, surrounded by scintillation paddles acting as an active cosmic veto and operated through basic high voltage and DAQ systems, this detector aims at being compact and easily deployed. This \(\sim \)2.5 ton detector filled with a 3% LS and 0.1% Gd WbLS solution would observe approximately 230 neutrino candidates per day, after selection cuts, if placed 50 m away from the reactor cores. Further studies will be carried out, in collaboration with the power plant operators, to estimate the ideal location for this detector and assess the impact of correlated backgrounds at this location. This project is still in the proposal stage and, upon the approval of its funding, it will be built at the Detector R &D Lab at Erciyes University for calibration and commissioning before being moved in the vicinity of the ANPP. This detector is intended to serve as a standalone detector able to monitor the thermal power of the ANPP in real-time, for nuclear non-proliferation R &D purposes, but also as a near detector for a planned program of short-baseline low energy neutrino studies in Turkey. It will also be an opportunity to test new equipment and techniques for the growing field of neutrino physics, as well as train the next generation of neutrino and detector physicists under the Reactor Neutrino Experiments of Turkey (RNET) program.