Fermion masses and mixings and $g-2$ muon anomaly in a 3-3-1 model with $D_4$ family symmetry

Abstract

We propose a predictive model based on the $SU(3)_C\times SU(3)_L\times U(1)_X$ gauge symmetry, which is supplemented by the $D_4$ family symmetry and several auxiliary cyclic symmetries whose spontaneous breaking produces the observed SM fermion mass and mixing pattern. The masses of the light active neutrinos are produced by an inverse seesaw mechanism mediated by three right handed Majorana neutrinos. To the best of our knowledge the model corresponds to the first implementation of the $D_4$ family symmetry in a $SU(3)_C\times SU(3)_L\times U(1)_X$ theory with three right handed Majorana neutrinos and inverse seesaw mechanism. Our proposed model successfully accommodates the experimental values of the SM fermion mass and mixing parameters, the muon anomalous magnetic moment as well as the Higgs diphoton decay rate and meson oscillations constraints. The consistency of our model with the muon anomalous magnetic moment requires charged exotic vector like leptons at the TeV scale.

1 Introduction

Despite its great success and consistency with the experimental data, Standard Model (SM) have several unexplained issues such as the number of SM fermion families, the electric charge quantization, the huge SM fermion mass hierarchy, the small quark mixing angles and the sizeable leptonic mixing ones. Whereas the quark mixing angles are small, two of the leptonic mixing angles are large and one is of the order of the Cabibbo angle. In addition, the SM charged fermion mass pattern spread over a range of 13 orders of magnitude from the light active neutrino mass scale up to the top quark mass. This is the so called flavour puzzle of the SM which motivates the construction of several extensions of the SM with augmented particle spectrum and extra symmetries, which be continuous and (or) discrete, introduced to provide a successful explanation of the observed SM fermion mass and mixing hierarchy. Discrete flavor symmetries have been shown to be successful in describing the SM fermion mass and mixing pattern. Some reviews of discrete flavor groups are provided in [1,2,3,4]. In particular, the $D_4$ discrete flavor group, which has a small amount of doublets and singlets in their irreducible representations has been employed in extensions of the SM [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20], since it allows to get viable predictions for the SM fermion mass and mixing hierarchy, with a moderate amount of particle content. Furthermore, several theories with enlarged particle spectrum and symmetries have been constructed to explain the experimental value of the muon anomalous magnetic moment, anomaly recently confirmed by the muon $g-2$ experiment at FERMILAB. See [21] for a very recent review.

To address the aforementioned issues of the SM, in this paper, we construct a theory based on the $SU(3)_C\times SU(3)_L\times U(1)_X$ gauge symmetry (3-3-1 model) with extended particle spectrum and discrete symmetries which allows to get predictive SM fermion mass matrices consistent with the low energy SM fermion flavor data. In our proposed theory, we considered the $SU(3)_C\times SU(3)_L\times U(1)_X$ gauge symmetry, since models having this symmetry naturally explain the number of SM fermion families as well as the electric charge quantization, see for instance [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43] . Apart from successfully addressing these features, our proposed model also successfully explains and accommodates the SM fermion mass and mixing hierarchy the muon anomalous magnetic moment as well as the Higgs diphoton decay rate constraints. Our theory is based in the $D_4$ discrete symmetry, which is supplemented by several cyclic symmetries. In our proposed theory, the SM fermion mass and mixing pattern is produced by the spontaneous breaking of the discrete symmetries, whereas the tiny masses of the light active neutrinos are produced by an inverse seesaw mechanism mediated by three right handed Majorana neutrinos. To the best of our knowledge our work corresponds to the first implementation of the $D_4$ family symmetry in a $SU(3)_C\times SU(3)_L\times U(1)_X$ theory with three right handed Majorana neutrinos and inverse seesaw mechanism. The layout of the reminder of the paper is as follows. In Sect. 2 we describe the proposed model. The consequences of the model in quark masses and mixings are analyzed in Sect. 3. Lepton masses and mixings are described in Sect. 4. The low energy scalar of the model is discussed in Sect. 5. In Sect. 6 we discuss the implications of the model in the Higgs diphoton decay rate. The implications of the model in the muon anomalous magnetic and meson oscillations are discussed in Sects. 7 and 8. We conclude in Sect. 9.

2 The model

The model under consideration is based on the $SU(3)_{C}\times SU(3)_{L}\times U(1)_{X}$ gauge symmetry, which is supplemented by the $D_{4}\times Z_{4}\times Z_{3}^{\left( 1\right) }\times Z_{3}^{\left( 2\right) }\times Z_{16}$ discrete group, whose spontaneous breaking generates viable and predictive fermion mass matrices consistent with the observed pattern of SM fermion masses and mixings. We choose the $D_{4}$ symmetry since it is the smallest non-Abelian discrete symmetry group having five irreducible representations (irreps), explicitly, four singlets and one doublet irreps. The auxiliary cyclic symmetries $Z_{4}$, $Z_{3}^{\left( 1\right) }$ and $Z_{3}^{\left( 2\right) }$ select the allowed entries of the SM fermion mass matrices that yield a predictive and viable pattern of SM fermion masses and mixings. These cyclic symmetries also allows a successful implementation of the inverse seesaw mechanism. These symmetries together with the $Z_{16}$ symmetry shape the hierarchical structure of the SM charged fermion mass matrices crucial to yield the observed pattern of SM charged fermion masses and mixing angles. Furthermore, the $Z_{16}$ discrete symmetry is also crucial to get sufficiently suppressed non renormalizable mass terms involving gauge singlet right handed Majorana neutrinos, required for the implementation of the inverse seesaw mechanism that produces small masses for the light active neutrinos. The model fermionic sector contains $SU(3)_{L}$ fermionic triplets and antitriplets, transforming under the $SU(3)_{C}\times SU(3)_{L}\times U(1)_{X}$ gauge symmetry as follows:

$$\begin{aligned} Q_{1L}= & {} \begin{pmatrix} u_{1} \\ d_{1} \\ J_{1} \\ \end{pmatrix} _{L}\sim \left( \mathbf {3},\mathbf {3},\frac{1}{3}\right) ,\nonumber \\ Q_{nL}= & {} \begin{pmatrix} d_{n} \\ -u_{n} \\ J_{n} \\ \end{pmatrix} _{L}\sim \left( \mathbf {3},\varvec{\bar{3}},0\right) ,\nonumber \\ u_{iR}\sim & {} \left( \mathbf {3},\mathbf {1},\frac{2}{3}\right) , d_{iR}\sim \left( \mathbf {3},\mathbf {1},-\frac{1}{3}\right) , \nonumber \\ J_{1R}\sim & {} \left( \mathbf {3},\mathbf {1},\frac{2}{3}\right) , J_{nR}\sim \left( \mathbf {3},\mathbf {1},-\frac{1}{3}\right) , \nonumber \\ L_{iL}= & {} \begin{pmatrix} \nu _{i} \\ l_{i} \\ \nu _{i}^{c} \\ \end{pmatrix} _{L} \sim \left( \mathbf {1},\mathbf {3},-\frac{1}{3}\right) , l_{iR}\sim \left( \mathbf {1},\mathbf {1},-1\right) ,\nonumber \\ N_{iR}\sim & {} \left( \mathbf {1},\mathbf {1},0\right) ,n=2,3;i=1,2,3. \end{aligned}$$

(1)

All $SU(3)_{L}$ singlets $\left\{ \xi ,\Xi ,\sigma , \phi _{1,2},\Phi ,\phi ,\zeta ,\eta ,\varphi _{1,2}\right\}$ transform as $(\mathbf {1},\mathbf {1},0)$ under the $SU(3)_{C}\times SU(3)_{L}\times U(1)_{X}$ gauge symmetry.Furthermore, in the model fermionic sector, three right handed Majorana neutrinos are included as well, in order to allow a successful implementation of the inverse seesaw mechanism that produces the tiny active neutrino masses. Notice that the fermions in our model do not feature exotic electric charges, from which it follows that the electric charge is given by:

$$\begin{aligned} Q=T_{3}+\beta T_{8}+X=T_{3}-\frac{1}{\sqrt{3}}T_{8}+X. \end{aligned}$$

(2)

On the other hand, the model scalar sector is composed of two $SU(3)_{L}$ triplet scalars $\chi$ and $\rho$ and several gauge singlet scalar fields to be specified below. The $SU(3)_{L}$ scalar $\chi$ and $\rho$ can be expanded around the minimum as follows:

$$\begin{aligned}&\chi = \begin{pmatrix} \chi _{1}^{0} \\ \chi _{2}^{-} \\ \frac{1}{\sqrt{2}}(v_{\chi }+\xi _{\chi }\pm i\zeta _{\chi }) \end{pmatrix}, \quad \nonumber \\&\rho =\begin{pmatrix} \rho _{1}^{+} \\ \frac{1}{\sqrt{2}}(v_{\rho }+\xi _{\rho }\pm i\zeta _{\rho }) \\ \rho _{3}^{+} \end{pmatrix}. \end{aligned}$$

(3)

This implies that the $SU(3)_L$ scalar triplets acquire the following VEV pattern:

$$\begin{aligned}&\langle \chi \rangle ^T = \left( 0\,,\quad 0 \,, \quad v_{\chi }/\sqrt{2}\right) ,\nonumber \\&\langle \rho \rangle ^T=\left( 0\,, \quad v_{\rho }/\sqrt{2 }\, ,\quad 0 \right) \, . \end{aligned}$$

(4)

The scalar and fermionic spectrum and their assignments under the $SU(3)_{C} \times SU(3)_{L} \times U(1)_{X} \times D_{4}\times Z_{4}\times Z_{3}^{(1) } \times Z_{3}^{(2)} \times Z_{16}$ group are shown in Tables 1 and 2, respectively.

Table 1 Scalar transformations under the $SU(3)_{C} \times SU(3)_{L} \times U(1)_{X} \times D_{4}\times Z_{4}\times Z_{3}^{(1) } \times Z_{3}^{(2)} \times Z_{16}$ group

Table 2 Fermion transformations under the $SU(3)_{C} \times SU(3)_{L} \times U(1)_{X} \times D_{4}\times Z_{4}\times Z_{3}^{(1) } \times Z_{3}^{(2)} \times Z_{16}$ group

With the fermion and scalar contents in Tables 1 and 2, the following quark and lepton Yukawa terms arise:

$$\begin{aligned} -\mathcal {L}_{Y}^{\left( q\right) }= & {} y_{1}^{\left( J\right) }\overline{Q} _{1L}\chi J_{1R}+\sum _{n=2}^{3}y_{n}^{\left( J\right) }\overline{Q}_{nL}\chi ^{*}J_{nR}\nonumber \\&+y_{33}^{\left( u\right) }\overline{Q}_{3L}\rho ^{*}u_{3R}+y_{22}^{\left( u\right) }\overline{Q}_{2L}\rho ^{*}u_{2R}\frac{ \sigma ^{4}}{\Lambda ^{4}}\nonumber \\&+y_{11}^{\left( u\right) }\varepsilon _{abc}\overline{Q}_{1L}^{a}\left( \rho ^{*}\right) ^{b}\left( \chi ^{*}\right) ^{c}u_{1R} {\frac{\sigma ^{7}}{\Lambda ^{7}} }\nonumber \\&+y_{11}^{\left( d\right) }\overline{Q}_{1L}\rho d_{1R}\frac{\sigma ^{4}\left( \xi \xi \right) _{\mathbf {1}_{-+}}\left( \xi \xi \right) _{ \mathbf {1}_{+-}}}{\Lambda ^{8}}\nonumber \\&+y_{12}^{\left( d\right) }\overline{Q} _{1L}\rho \left( \xi D_{R}\right) _{\mathbf {1}_{ {+-}}}\frac{\phi _{1}\sigma ^{4}}{\Lambda ^{6}}\nonumber \\&+ {\,y_{13}^{\left( d\right) }\overline{Q}_{1L}\rho \left( \xi D_{R}\right) _{\mathbf {1}_{-+}}\frac{\phi _{2}\sigma ^{4}}{ \Lambda ^{6}}} \nonumber \\&+y_{22}^{\left( d\right) }\varepsilon _{abc}\overline{Q}_{2L}^{a}\rho ^{b}\chi ^{c}\left( \xi D_{R}\right) _{\mathbf {1}_{+-}} {\frac{\sigma ^{3}}{\Lambda ^{5}}}\nonumber \\&+ {y_{33}^{\left( d\right) }\varepsilon _{abc}\overline{Q} _{3L}^{a}\rho ^{b}\chi ^{c}\left( \Xi D_{R}\right) _{\mathbf {1}_{++}}\frac{\sigma }{\Lambda ^3}}\,+\,H.c, \end{aligned}$$

(5)

$$\begin{aligned} -\mathcal {L}_{Y}^{\left( l\right) }= & {} y_{1}^{\left( l\right) }\left( \overline{L}_{L}\rho E_R\right) _{\mathbf {1}_{++}}+z_{1}^{\left( l\right) }\left( \overline{E}_{L}\Phi \right) _{\mathbf {1}_{+-}}l_{1R}\frac{\sigma ^4}{\Lambda ^4}\nonumber \\&+z_{2}^{\left( l\right) }\left( \overline{E}_{L}\Phi \right) _{\mathbf {1}_{-}{-}}l_{2R}+m_E\left( \overline{E}_{L}E_R\right) _{\mathbf {1}_{++}}\nonumber \\&+y_{3}^{\left( l\right) }\overline{L}_{3L}\rho l_{3R}\frac{\sigma ^3}{\Lambda ^{3}} \nonumber \\&+ {y_{1\chi }^{\left( L\right) }\left( \overline{L}_{L}\chi \right) _{\mathbf {2}}N_{R}+y_{2\chi }^{\left( L\right) }\overline{L}_{3L}\chi N_{3R}}\nonumber \\&+x_{\rho }^{\left( 1\right) }\varepsilon _{abc} {\left[ \left( \overline{L^C_{L}}\right) ^{a}\left( L_{L}\right) ^{b}\right] _{\mathbf {1}_{-}{-}}\left( \rho \right) ^{c}\frac{\zeta ^*}{\Lambda }} \nonumber \\&+x_{\rho }^{\left( 2\right) }\varepsilon _{abc} {\left[ \left( \overline{L^C_{L}}\right) ^{a}\left( L_{3L}\right) ^{b} \left( \rho \right) ^{c}\right] _{\mathbf {2}}\frac{\eta ^*}{\Lambda }}\nonumber \\&+x_{\rho }^{\left( 3\right) }\varepsilon _{abc}{\left[ \left( \overline{L^C_{3L}}\right) ^{a}\left( L_{L}\right) ^{b} \left( \rho \right) ^{c}\right] _{\mathbf {2}}\frac{\eta ^*}{\Lambda }} \nonumber \\&+y_{N_{1}}\left( {\overline{N_{R}^{C}}N_{R}}\right) _{\mathbf {1} _{+-}}\varphi _{1}\frac{\sigma ^{8}}{\Lambda ^{8}}\nonumber \\&+y_{N_{2}}\left( {\overline{N_{R}^{C}}N_{R}}\right) _{\mathbf {1}_{++}}\varphi _{2}\frac{\sigma ^{8}}{ \Lambda ^{8}}\nonumber \\&+y_{N_{3}} {\overline{N_{3R}^{C}}N_{3R}}\varphi _{2}\frac{\sigma ^{8}}{\Lambda ^{8}}+H.c. \end{aligned}$$

(6)

The large amount of parametric freedom of the scalar potential allows to consider the following vacuum expectation value (VEV) configuration for the $D_4$ doublets SM gauge singlet scalars:

$$\begin{aligned} \langle \xi \rangle= & {} \left( v_{\xi _1},v_{\xi _2}\right) =v_{\xi }\left( 1,r\right) , \langle \Xi \rangle =v_{\Xi }\left( 1,0\right) ,\nonumber \\ \left\langle \eta \right\rangle= & {} \left( v_{{\eta _1}}, v_{{\eta _2}}\right) ,\quad \langle \Phi \rangle =(v_1, v_2), \end{aligned}$$

(7)

whereas for the VEVs of the gauge singlet scalars one has:

$$\begin{aligned} \langle \sigma \rangle= & {} v_\sigma ,\langle \phi _{1}\rangle =v_{\phi _{1}}, \langle \phi _{2}\rangle = v_{\phi _{2}}, \nonumber \\ \langle \phi \rangle= & {} v_\phi , \langle \zeta \rangle =v_\zeta , \langle \varphi _{1}\rangle =v_{\varphi _{1}}, \langle \varphi _{2}\rangle =v_{\varphi _{2}}. \end{aligned}$$

(8)

The above given VEV pattern allows to get a predictive and viable pattern of SM fermion masses and mixings as it will be shown in the next sections.

3 Quark masses and mixings

From the quark Yukawa terms given in Eq. (5), it follows that the SM mass matrices for quarks are:

$$\begin{aligned} M_{U}= & {} \left( \begin{array}{ccc} a_{1}^{(U)} \lambda ^{ {8}} &{} 0 &{} 0 \\ 0 &{} a_{2}^{(U)} \lambda ^{4} &{} 0 \\ 0 &{} 0 &{} a_{3}^{(U)} \end{array} \right) ,\nonumber \\ M_{D}= & {} \left( \begin{array}{ccc} a_{ {1}}^{(D)} \lambda ^{ {8}} &{} {\left( a_{4}^{(D)}+a_{5}^{(D)}\right) \lambda ^{6}} &{} {\left( a_{4}^{(D)}-a_{5}^{(D)}\right) r \lambda ^{6}} \\ 0 &{} a_{ {2}}^{(D)} \lambda ^{ {5}} &{} {a_{23}^{(D)} \lambda ^{5}} \\ 0 &{} 0 &{} a_{ {3}}^{(D)} \lambda ^{ {3}} \end{array} \right) \nonumber \\= & {} \left( \begin{array}{ccc} a_{ {1}}^{(D)}\lambda ^{ {8}} &{} {a_{12}^{(D)}\lambda ^{6}} &{} {a_{13}^{(D)} \lambda ^{6}} \\ 0 &{} a_{ {2}}^{(D)}\lambda ^{ {5}} &{} {a_{23}^{(D)}\lambda ^{5}} \\ 0 &{} 0 &{} a_{ {3}}^{(D)}\lambda ^{ {3}} \end{array} \right) , \end{aligned}$$

(9)

where $a_{1}^{(U)}, a_{ {1}}^{(D)},\ldots$ are $\mathcal {O}(1)$ dimensionless parameters which are given by:

$$\begin{aligned} a_1^{(U)}= & {} \frac{y_{11}^{(u)}}{2}v_\rho , {a_2^{(U)}=\frac{y_{22}^{(u)}}{\sqrt{2}} v_\rho , a_3^{(U)}=\frac{y_{33}^{(u)}}{\sqrt{2}} v_\rho },\nonumber \\ a_1^{(D)}= & {} \frac{y_{11}^{(d)}}{\sqrt{2}} v_\rho , a_{2}^{(D)}=\frac{y_{22}^{(d)}}{2} v_\rho , a_{3}^{(D)}=\frac{y_{33}^{(d)}}{2} v_\rho , \nonumber \\ a_{4}^{(D)}= & {} \frac{y_{12}^{(d)}}{\sqrt{2}} v_\rho , a_{5}^{(D)}=\frac{y_{13}^{(d)}}{\sqrt{2}} v_\rho , \nonumber \\ {\frac{v_\Xi }{\Lambda }}\sim & {} \frac{v_\xi }{\Lambda }\sim \frac{v_\chi }{\Lambda }\sim \frac{v_{\phi _1}}{\Lambda }\sim \frac{v_{\phi _2}}{\Lambda }\sim \frac{v_\sigma }{\Lambda }=\lambda . \end{aligned}$$

(10)

Here $v=246$ GeV is the scale of electroweak symmetry breaking and the Wolfenstein parameter $\lambda =0.225$ is used for characterization of the hierarchy between the parameters defining quark mass matrix elements in Eq. (9). We find that the experimental values for the physical quark mass spectrum [44, 45], mixing angles and CP violating phase [44, 45] can be well reproduced for the following benchmark point:

$$\begin{aligned} a_{1}^{\left( U\right) }\simeq & {} 1.085,\quad a_{2}^{\left( U\right) }\simeq 1.413,\quad a_{3}^{\left( U\right) }\simeq 0.994,\nonumber \\ a_{1}^{\left( D\right) }\simeq & {} 2.329, \quad a_{2}^{\left( D\right) } \simeq 0.554, \quad \nonumber \\ a_{3}^{\left( D\right) }\simeq & {} 1.439,\quad a_{12}^{\left( D\right) }\simeq 0.570,\nonumber \\ a_{13}^{\left( D\right) }\simeq & {} -(0.123 + 0.438i),\quad a_{23}^{\left( D\right) }\simeq 1.152. \end{aligned}$$

(11)

Table 3 Model and experimental values of the quark masses and CKM parameters

In addition, Fig. 1 shows the correlation plot between the quark mixing parameter $\sin \theta _{13}$ and the Jarlskog invariant. As indicated by Fig. 1, $\sin \theta _{13}$ is predicted to be in range $0.0033 \lesssim \sin \theta _{13} \lesssim 0.0040$ in the allowed parameter space. Furthermore, the quark mixing parameter $\sin \theta _{13}$ increases when the Jarlskog invariant takes larger values.

Fig. 1

Correlation plot between the quark mixing parameter $\sin \theta _{13}$ and the Jarlskog invariant

4 Lepton masses and mixings

From the charged-lepton Yukawa interactions in Eq. (6 ) and the VEV alignments in Eq. (8), we find the following charged -lepton mass terms:

$$\begin{aligned} -\mathcal {L}^{l}_{Y}= & {} (\bar{l}_{1L} \bar{l}_{2L} \bar{l}_{3L} \bar{E}_{1L} \bar{E}_{2L}) M_l \left( \begin{array}{c} l_{1R} \\ l_{2R} \\ l_{3R} \\ E_{1R} \\ E_{2R} \\ \end{array} \right) + \mathrm {H.c,} \end{aligned}$$

(12)

where the charged-lepton mass matrix is given by

$$\begin{aligned} M_{E}&=\left( \begin{array}{cc} C_{E} &{} A_{E} \\ B_{E} &{} X_{E} \end{array} \right) ,\quad C_{E}=\left( \begin{array}{ccc} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} y_{3}^{\left( l\right) } \end{array} \right) \frac{v_{\sigma }^{3}v_{\rho }}{\Lambda ^{3}\sqrt{2}}\nonumber \\&=\left( \begin{array}{ccc} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} c \end{array} \right) \frac{v_{\rho }}{\sqrt{2}},\end{aligned}$$

(13)

$$\begin{aligned} A_{E}&=y_{1}^{\left( l\right) }\left( \begin{array}{cc} 0 &{} 1 \\ 1 &{} 0 \\ 0 &{} 0 \end{array} \right) \frac{v_{\rho }}{\sqrt{2}},\nonumber \\ B_{E}&=\left( \begin{array}{ccc} z_{1}^{\left( l\right) }\frac{v_{\sigma }^{2}}{\Lambda ^{2}}v_{1} &{} z_{2}^{\left( l\right) }v_{2} &{} 0 \\ z_{1}^{\left( l\right) }\frac{v_{\sigma }^{2}}{\Lambda ^{2}}v_{2} &{} -z_{2}^{\left( l\right) }v_{1} &{} 0 \end{array} \right) \nonumber \\&=\left( \begin{array}{ccc} av_{1} &{} bv_{2} &{} 0 \\ av_{2} &{} -bv_{1} &{} 0 \end{array} \right) , \end{aligned}$$

(14)

$$\begin{aligned} X_{E}&=\left( \begin{array}{cc} 0 &{} 1 \\ 1 &{} 0 \end{array} \right) m_{E},\nonumber \\&a=z_{1}^{\left( l\right) }\frac{ v_{\sigma }^{2}}{\Lambda ^{2}},\quad b=z_{2}^{\left( l\right) },\quad c=y_{3}^{\left( l\right) }\frac{ v_{\sigma }^{3}}{\Lambda ^{3}}. \end{aligned}$$

(15)

Then, the SM charged lepton mass matrix takes the form:

$$\begin{aligned} M_{l}= & {} C_{E}+A_{E}X_{E}^{-1}B_{E}=\left( \begin{array}{ccc} \alpha v_{1} &{} \beta v_{2} &{} 0 \\ \alpha v_{2} &{} -\beta v_{1} &{} 0 \\ 0 &{} 0 &{} c\frac{v_{\rho }}{\sqrt{2}} \end{array} \right) \nonumber \\\equiv & {} \left( \begin{array}{ccc} m_{11} &{} -m_{12} &{} 0 \\ m_{21} &{} m_{22} &{} 0 \\ 0 &{} 0 &{} m_{33} \\ &{} &{} \end{array} \right) \end{aligned}$$

(16)

Let us define a Hermitian matrix $M_l$ as follows

$$\begin{aligned} m^2_l= & {} M_{l} M^+_{l} = \left( \begin{array}{ccc} |m_{11}|^2 +|m_{12}|^2 &{} m_{11} m^2_{21} -m_{12} m^*_{22} &{} 0 \\ (m_{11} m^*_{21} -m_{12} m^*_{22})^* &{} |m_{21}|^2+ |m_{22}|^2 &{} 0 \\ 0 &{} &{} |m_{33}|^2 \\ &{} &{} \end{array} \right) , \nonumber \\ \end{aligned}$$

(17)

which can be diagonalized by $U_{L, R}$ satisfying $U^+_{L} m^2_l \,U_R= \mathrm {diag} (m^2_e, m^2_\mu , m^2_\tau )$, where

$$\begin{aligned}&U_L =U_R=\left( \begin{array}{ccc} \mathrm {cos} \theta &{} -\mathrm {sin} \theta . e^{-i \alpha } &{} 0 \\ \mathrm {sin} \theta . e^{i \alpha } &{} \mathrm {cos} \theta &{} \,\,\,\,\,\, \\ 0 &{} &{} 1 \\ &{} &{} \end{array} \right) , \end{aligned}$$

(18)

$$\begin{aligned}&m^2_{e, \mu }= \lambda _1 \mp \lambda _2, m^2_\tau =|m_{33}|^2, \end{aligned}$$

(19)

with

$$\begin{aligned} 2\lambda _2= & {} \left\{ |m_{11}|^4 + (|m_{21}|^2 - |m_{12}|^2)^2 + 2 (|m_{21}|^2 + |m_{12}|^2) |m_{22}|^2 \nonumber \right. \\&\left. + 2 |m_{11}|^2 (|m_{21}|^2 + |m_{12}|^2 - |m_{22}|^2) \right. \nonumber \\&+\left. |m_{22}|^4 -8 |m_{11}| |m_{21}| |m_{12}| |m_{22}| \cos (\delta _{12}-\beta _{12})\right\} ^{\frac{1}{2}}, \nonumber \\ \delta _{12}= & {} \alpha _1-\alpha _2, \beta _{12}=\beta _1-\beta _2, \end{aligned}$$

(20)

$$\begin{aligned} 2\lambda _1= & {} |m_{11}|^2 + |m_{21}|^2 + |m_{12}|^2 + |m_{22}|^2, \alpha _i \nonumber \\= & {} \arg (a_i), \beta _i = \arg (b_i) (i=1,2), \end{aligned}$$

(21)

$$\begin{aligned} \alpha= & {} \frac{i}{2}\log \left( \frac{m_{11} m^*_{21} - m_{12} m^*_{22}}{ m^*_{11} m_{21} - m^*_{12} m_{22}}\right) , \nonumber \\ \theta= & {} \arctan \left( \frac{(m^*_{11}m_{21} - m^*_{12} m_{22}) e^{-i \alpha }}{ |m_{11}|^2 + |m_{12}|^2 - m^2_\mu }\right) . \end{aligned}$$

(22)

By comparing the obtained result in Eq. (19) with the experimental values of the charged-lepton masses taken from Ref. [45], $m_e=0.51099 \,\mathrm {MeV}, m_\mu = 105.65837\,\mathrm {MeV}, m_\tau = 1776.86 \,\mathrm {MeV}$, we obtain:

$$\begin{aligned} |m_{33}|= & {} 1.77686 \times 10^{9}\, \mathrm {eV}, \lambda _1=5.58198 \times 10^{15}\, \mathrm {eV}^2,\, \nonumber \\ \lambda _2= & {} 5.58172 \times 10^{15} \, \mathrm {eV}^2. \end{aligned}$$

(23)

In the case $v_1=v.e^{i\vartheta _1}, \, v_2=v.e^{i\vartheta _2}$, we get:

$$\begin{aligned} |m_{11}|= & {} |m_{21}|=3.61324\times 10^5 \, \mathrm {eV},\nonumber \\ |m_{12}|= & {} |m_{22}|=7.47117\times 10^7 \, \mathrm {eV}. \end{aligned}$$

(24)

Fig. 2

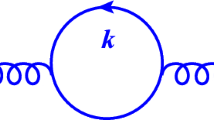
Feynman diagram contributing to the 22 block of the full neutrino mass matrix. Here, $i,j,r,s=1,2,3$ and the cross mark $\otimes$ in the internal lines corresponds to the Majorana mass terms induced by the dimension twelve Majorana neutrino Yukawa interactions of Eq. (6)

As we will see below, since the charged lepton mixing matrix $U_L$ is non trivial, it can contribute to the leptonic mixing matrix, defined by $U=U^+_{L} U_{\nu }$ where $U_{\nu }$ being neutrino mixing matrix.

Regarding the neutrino sector, from the lepton Yukawa terms in Eq. (6 ) and the VEV alignments in Eq. (8), we find the following neutrino mass terms:

$$\begin{aligned} -\mathcal {L}_{mass}^{\nu }=\frac{1}{2}\left( \begin{array}{ccc} \overline{\nu _{L}^{C}}&\overline{\nu _{R}^{ {C}}}&\overline{N_{R}^{ {C}}} \end{array} \right) M_{\nu }\left( \begin{array}{c} \nu _{L} \\ \nu _{R} \\ N_{R}\\ \end{array} \right) +H.c, \end{aligned}$$

(25)

where the neutrino mass matrix reads:

$$\begin{aligned} M_{\nu }= \begin{pmatrix} 0_{3\times 3} &{} M_{\nu _{D}} &{} 0_{3\times 3} \\ M_{\nu _{D}}^{T} &{} 0_{3\times 3} &{} M_{\chi } \\ 0_{3\times 3} &{} M_{\chi }^{T} &{} M_{R} \end{pmatrix} , \end{aligned}$$

(26)

and the submatrices are given by:

$$\begin{aligned} M_{\nu _{D}}= & {} \left( \begin{array}{ccc} 0 &{} -a &{} - b_1 \\ a &{} 0 &{} - b_2 \\ b_1 &{} b_2 &{} 0 \end{array} \right) \frac{1}{\Lambda }\frac{v_{\rho }}{\sqrt{2}}, M_{\chi } {\,=\,} {m_{N}}\left( \begin{array}{ccc} {1} &{} {0} &{} 0 \\ {0} &{} {1} &{} 0 \\ 0 &{} 0 &{} x \end{array} \right) , \nonumber \\ M_{R}= & {} \left( \begin{array}{ccc} \kappa _{1} &{} \kappa _{2} &{} 0 \\ \kappa _{2} &{} \kappa _{1} &{} 0 \\ 0 &{} 0 &{} \kappa _{3} \end{array} \right) \mu , \end{aligned}$$

(27)

with

$$\begin{aligned} {a}= & {} {x^{(1)}_\rho v_\zeta , \quad b_{1,2}=x^{(2)}_\rho v_{\eta _{2,1}}=-x^{(3)}_\rho v_{\eta _{2,1}},} \nonumber \\ x= & {} \frac{y_{2\chi }^{\left( L\right) }}{y_{1\chi }^{\left( L\right) }}, m_{N}=y_{1\chi }^{\left( L\right) }\frac{v_{\chi }}{\sqrt{2}} , \kappa _{1} =y_{1N}, \kappa _{2}=y_{2N}\frac{ v_{\varphi _{2}}}{v_{\varphi _{1}}},\nonumber \\ \kappa _{3}= & {} y_{3N}\frac{ v_{\varphi _{2}}}{v_{\varphi _{1}}}, \mu =\frac{v_{\varphi _{1}}v_{\sigma }^{8}}{\Lambda ^{8}}. \end{aligned}$$

(28)

It is worth mentioning that the 22 block of the full neutrino mass matrix can be generated from the Feynman diagram of Fig. 2, which involves the virtual exchange of $\xi _{\chi }$, $\zeta _{\chi }$, $Z^{\prime }$ as well as the Majorana mass terms in the internal lines of the loop. These Majorana mass terms arise from the non renormalizable Majorana neutrino Yukawa interactions of Eq. (6). Given that the non renormalizable Majorana neutrino Yukawa terms are of dimension 12 as shown in Eq. (6), we have that the entries of the the 22 block of the full neutrino mass matrix are much smaller than the entries of the $M_R$ submatrix and thus they give very subleading corrections to the physical neutrino mass matrices.

The light active masses arise from an inverse seesaw mechanism and the physical neutrino mass matrices are:

$$\begin{aligned} M_{\nu }^{\left( 1\right) }= & {} M_{\nu _{D}}\left( M_{\chi }^{T}\right) ^{-1}M_{R}M_{\chi }^{-1}M_{\nu _{D}}^{T}, \end{aligned}$$

(29)

$$\begin{aligned} M_{\nu }^{\left( 2\right) }= & {} -\frac{1}{2}\left( M_{\chi }+M_{\chi }^{T}\right) +\frac{1}{2}M_{R}, M_{\nu }^{\left( 3\right) }\nonumber \\= & {} \frac{1}{2}\left( M_{\chi }+M_{\chi }^{T}\right) +\frac{1}{2}M_{R}, \end{aligned}$$

(30)

where $M_{\nu }^{\left( 1\right) }$ is the light active neutrino mass matrix whereas $M_{\nu }^{\left( 2\right) }$ and $M_{\nu }^{\left( 3\right) }$ are the exotic Dirac neutrino mass matrices. It is worth mentioning that physical neutrino spectrum consists of three light active neutrinos and six exotic neutrinos. The exotic neutrinos are pseudo-Dirac, with masses $\sim \pm v_{\chi }\sim \mathcal {O}(10)$ TeV and a small splitting $\sim \mu$.

The mass matrix for light active neutrinos takes the form:

$$\begin{aligned} M_{\nu }^{\left( 1\right) }=\left( \begin{array}{ccc} a^2 \kappa _1 + \frac{b_1^2 \kappa _3}{x^2} &{} - a^2 \kappa _2 + \frac{b_1 b_2 \kappa _3}{x^2} &{} -a (b_2 \kappa _1 + b_1 \kappa _2) \\ - a^2 \kappa _2 + \frac{b_1 b_2 \kappa _3}{x^2} &{} a^2 \kappa _1 + \frac{ b_2^2 \kappa _3}{x^2} &{} a (b_1 \kappa _1 + b_2 \kappa _2) \\ -a (b_2 \kappa _1 + b_1 \kappa _2) &{} a (b_1 \kappa _1 + b_2 \kappa _2) &{} (b_1^2 + b_2^2) \kappa _1 + 2 b_1 b_2 \kappa _2 \\ \end{array} \right) m_{\nu },\nonumber \\ \end{aligned}$$

(31)

where:

$$\begin{aligned} m_{\nu }=\frac{v_{\rho }^{2}}{2\Lambda ^{2}}m_{N}^{2}\mu . \end{aligned}$$

(32)

The mass matrix $M_{\nu }^{( 1) }$ has three exact eigenvalues as follows:

$$\begin{aligned} m_1= & {} 0, m_{2,3}=\Bbbk _1 \mp \Bbbk _2, \end{aligned}$$

(33)

where

$$\begin{aligned} \Bbbk _1= & {} \frac{m_\nu }{2}\left[ 2 a^2 \kappa _1 + (b_1^2 + b_2^2) \kappa _1 + 2 b_1 b_2 \kappa _2 + \frac{(b_1^2 + b_2^2) \kappa _3}{x^2}\right] , \nonumber \\ \Bbbk _2= & {} \frac{m_\nu }{2}\frac{\sqrt{\Bbbk }}{x^2}, \nonumber \\ \Bbbk= & {} (b_1^2 + b_2^2)^2 \kappa _3^2 - 2 \left[ (b_1^2 + b_2^2)^2 \kappa _1 \nonumber \right. \\&\left. +2 b_1 b_2 (2 a^2 + b_1^2 + b_2^2) \kappa _2\right] \kappa _3 x^2 \end{aligned}$$

(34)

$$\begin{aligned}&+ \left[ (b_1^2 + b_2^2)^2 \kappa _1^2 + 4 b_1 b_2 (2 a^2 + b_1^2 + b_2^2) \kappa _1 \kappa _2 \nonumber \right. \\&\left. +4 (a^2 + b_1^2) (a^2 + b_2^2) \kappa _2^2\right] x^4, \end{aligned}$$

(35)

and the corresponding mixing matrix is:

$$\begin{aligned} R=\left( \begin{array}{ccc} \frac{K_1}{\sqrt{K_1^2+N_1^2+1}} &{} \frac{K_2}{\sqrt{K_2^2+N_2^2+1}} &{} \frac{ K_3}{\sqrt{K_3^2+N_3^2+1}} \\ \frac{N_1}{\sqrt{K_1^2+N_1^2+1}} &{} \frac{N_2}{\sqrt{K_2^2+N_2^2+1}} &{} \frac{ N_3}{\sqrt{K_3^2+N_3^2+1}} \\ \frac{1}{\sqrt{K_1^2+N_1^2+1}} &{} \frac{1}{\sqrt{K_2^2+N_2^2+1}} &{} \frac{1}{ \sqrt{K_3^2+N_3^2+1}} \end{array} \right) P, \end{aligned}$$

(36)

where $P=\mathrm {diag}(1,\,1,\,i)$ and $K_{1,2,3},\, N_{1,2,3}$ are defined as

$$\begin{aligned} K_1= & {} \frac{b_2}{a}, N_1=-\frac{b_{2}}{a}, K_{2}=\kappa _{21} +\kappa _{22},\nonumber \\ K_{3}= & {} \kappa _{31}-\kappa _{22}, N_{2} =\epsilon _{21} + \epsilon _{22}, N_{3} =\epsilon _{31} - \epsilon _{22}, \end{aligned}$$

(37)

where

$$\begin{aligned} \kappa _{21}= & {} \left[ 2 (a^2 + b_1^2) b_2 \kappa _2 x^2 + b_1^3 (\kappa _1x^2-\kappa _3)\right] \kappa _0, \nonumber \\ \kappa _{22}= & {} b_1 \left[ b_2^2 (\kappa _1 x^2-\kappa _3) + \sqrt{\Bbbk }\right] \kappa _0, \nonumber \\ \kappa _{31}= & {} \kappa _{21}+\left[ b_1 b_2^2 (\kappa _1 x^2-\kappa _3)\right] \kappa _0, \epsilon _{21}\nonumber \\= & {} \left[ 2 b_1 (a^2 + b_2^2) \kappa _2 x^2 + b_2(b_1^2+ b_2^3)(\kappa _1 x^2-\kappa _3)\right] \kappa _0, \nonumber \\ \epsilon _{22}= & {} b_2 \sqrt{\Bbbk }\kappa _0, \epsilon _{31} =\left\{ \left[ b_2 (b_1^2 + b_2^2)\nonumber \right. \right. \\&\left. \left. \kappa _1 + 2 b_1 (a^2 + b_2^2) \kappa _2 \right] x^2-b_2 (b_1^2 + b_2^2) \kappa _3\right\} \kappa _0, \nonumber \\ \kappa _0= & {} \left[ 2 a (b_1^2 - b_2^2)\kappa _2 x^2\right] ^{-1}. \end{aligned}$$

(38)

It is easy to check that $K_{i}, N_{i}\, (i=1,2,3)$ satisfy the following relations

$$\begin{aligned}&1 + K_1 K_2 + N_1 N_2=0,\nonumber \\&1 + K_1 K_3 + N_1 N_3=0,\,\, 1 + K_2 K_3 + N_2 N_3=0. \end{aligned}$$

(39)

The matrix $M_{\nu }^{\left( 1\right) }$ is diagonalized as

$$\begin{aligned}&U_{\nu }^\mathrm {\dagger } M_{\nu }^{\left( 1\right) } U_{\nu }\nonumber \\&=\left\{ \begin{array}{l} \left( \begin{array}{ccc} 0 &{} 0 &{} 0 \\ 0 &{} m_{2} &{} 0 \\ 0 &{} 0 &{} m_{3} \end{array} \right) , U_{\nu }=\left( \begin{array}{ccc} \frac{K_1}{\sqrt{K_1^2+N_1^2+1}} &{} \frac{K_2}{\sqrt{K_2^2+N_2^2+1}} &{} \frac{ iK_3}{\sqrt{K_3^2+N_3^2+1}} \\ \frac{N_1}{\sqrt{K_1^2+N_1^2+1}} &{} \frac{N_2}{\sqrt{K_2^2+N_2^2+1}} &{} \frac{ iN_3}{\sqrt{K_3^2+N_3^2+1}} \\ \frac{1}{\sqrt{K_1^2+N_1^2+1}} &{} \frac{1}{\sqrt{K_2^2+N_2^2+1}} &{} \frac{i}{ \sqrt{K_3^2+N_3^2+1}} \end{array} \right) \hbox {for NH,}\ \ \\ \left( \begin{array}{ccc} m_{3} &{} 0 &{} 0 \\ 0 &{} m_{2} &{} 0 \\ 0 &{} 0 &{} 0 \end{array} \right) , U_{\nu }=\left( \begin{array}{ccc} \frac{K_3}{\sqrt{K_3^2+N_3^2+1}} &{} \frac{K_2}{\sqrt{K_2^2+N_2^2+1}} &{} \frac{ iK_1}{\sqrt{K_1^2+N_1^2+1}} \\ \frac{N_3}{\sqrt{K_3^2+N_3^2+1}} &{} \frac{N_2}{\sqrt{K_2^2+N_2^2+1}} &{} \frac{ iN_1}{\sqrt{K_1^2+N_1^2+1}} \\ \frac{1}{\sqrt{K_3^2+N_3^2+1}} &{} \frac{1}{\sqrt{K_2^2+N_2^2+1}} &{} \frac{i}{ \sqrt{K_1^2+N_1^2+1}} \end{array} \right) \hbox {for IH,} \end{array} \right. \nonumber \\ \end{aligned}$$

(40)

where $m_{2,3}$ and $K_{1,2,3}, N_{1,2,3}$ are respectively given in Eqs. (33) and (37).

The final leptonic mixing matrices then read:

$$\begin{aligned} U= & {} U^+_{L} U_{\nu }\nonumber \\= & {} \left\{ \begin{array}{l} \left( \begin{array}{ccc} \frac{K_1 \cos \theta + N_1 \sin \theta .e^{-i\alpha }}{\sqrt{K_1^2+N^2_1+1}} &{} \frac{K_2 \cos \theta + N_2 \sin \theta . e^{-i\alpha }}{\sqrt{K_2^2+N^2_2+1}} &{} \frac{K_3 \cos \theta + N_3 \sin \theta .e^{-i \alpha }}{\sqrt{K_3^2+N^2_3+1}}\\ \frac{N_1 \cos \theta - K_1 \sin \theta .e^{i\alpha }}{\sqrt{K_1^2+N^2_1+1}} &{} \frac{N_2\cos \theta -K_2\sin \theta .e^{i \alpha }}{\sqrt{K^2_2+N^2_2+1}} &{} \frac{N_3 \cos \theta - K_3 \sin \theta .e^{i\alpha }}{\sqrt{K^2_3+N^2_3+1}} \\ \frac{1}{\sqrt{K_1^2+N^2_1+1}} &{} \frac{1}{\sqrt{K_2^2+N^2_2+1}} &{} \frac{1}{ \sqrt{K_3^2+N^2_3+1}} \\ \end{array} \right) .P \,\,\,\,\hbox {for \, NH}, \\ \left( \begin{array}{ccc} \frac{K_3 \cos \theta + N_3 \sin \theta .e^{-i\alpha }}{\sqrt{K_3^2+N^3_2+1}} &{} \frac{K_2 \cos \theta + N_2 \sin \theta .e^{-i\alpha }}{\sqrt{K_2^2+N^2_2+1}} &{} \frac{K_1 \cos \theta + N_1 \sin \theta .e^{-i\alpha }}{\sqrt{K_1^2+N^2_1+1}} \\ \frac{N_3\cos \theta -K_3 \sin \theta .e^{i \alpha }}{\sqrt{K^2_3+N^2_3+1}} &{} \frac{N_3 \cos \theta - K_2 \sin \theta .e^{i\alpha }}{\sqrt{K^2_2+N^2_2+1}} &{} \frac{N_1 \cos \theta - K_1 \sin \theta .e^{i\alpha }}{\sqrt{K_1^2+N^2_1+1}} \\ \frac{1}{\sqrt{K_3^2+N^3_2+1}} &{} \frac{1}{\sqrt{K_2^2+N^2_2+1}} &{} \frac{1}{ \sqrt{K_1^2+N^2_1+1}} \\ \end{array} \right) .P \hbox {for \ IH}. \end{array} \right. \nonumber \\ \end{aligned}$$

(41)

In the three neutrino oscillation picture [45], the leptonic mixing angles $\theta _{12}, \theta _{23}, \theta _{13}$ can be defined via the elements of the leptonic mixing matrix as¹:

$$\begin{aligned} s^2_{13}= & {} |U_{13}|^2\nonumber \\= & {} \left\{ \begin{array}{l} \frac{K_3^2 \cos ^2\theta + K_3 N_3 \cos (2\theta )\cos \alpha + N_3^2 \sin ^2\theta }{1 + K^2_3 + N^2_3} \hbox {for \, NH}, \\ \frac{K_1^2\cos ^2\theta + K_1 N_1 \sin (2\theta )\cos \alpha + N_1^2 \sin ^2\theta }{1 + K_1^2 + N_1^2} \hbox {for \ IH}, \end{array} \right. \nonumber \\ t^2_{12}= & {} \left| \frac{U_{12}}{U_{11}}\right| ^2\nonumber \\= & {} \left\{ \begin{array}{l} \frac{(1 + K_1^2 + N_1^2) (K_2^2 \cos ^2\theta + K_2 N_2 \sin (2\theta )\sin \alpha + N_2^2 \sin ^2\theta )}{(1 + K_2^2 + N_2^2) (K_1^2 \cos ^2\theta + K_1 N_1 \sin (2\theta )\sin \alpha + N_1^2 \sin ^2\theta )} \,\,\,\,\hbox {for \, NH}, \\ \frac{(1 + K_3^2 + N_3^2) (K_2^2 \cos ^2\theta + K_2 N_2 \sin (2\theta )\cos \alpha + N_2^2 \sin ^2\theta )}{(1 + K_2^2 + N_2^2) (K_3^2 \cos ^2\theta + K_3 N_3 \sin (2\theta )\cos \alpha + N_3^2 \sin ^2\theta )} \,\, \hbox {for \, IH}, \end{array} \right. \nonumber \\ t^2_{23}= & {} \left| \frac{U_{23}}{U_{33}}\right| ^2\nonumber \\= & {} \left\{ \begin{array}{l} N_3^2 \cos ^2\theta -K_3 N_3 \sin (2\theta ) \cos \alpha + K_3^2 \sin ^2\theta \hbox {for \, NH}, \\ N_1^2 \cos ^2\theta -K_1 N_1 \sin (2\theta ) \cos \alpha + K_1^2 \sin ^2\theta \,\, \hbox {for \, IH}. \end{array} \right. \nonumber \\ \end{aligned}$$

(42)

In fact, the neutrino mass spectrum is currently unknown and it can have a normal or inverted ordering depending on the sign of $\Delta m^2_{31}$ (or $\Delta m^2_{32}$) [45]. As will see below, the lepton mixing matrices in Eq. (54) and neutrino masses in Eq. (33) can fit the observed neutrino mass and mixing pattern taken from Ref. [46] for both Normal and Inverted hierarchies.

The Jarlskog invariant $J_{CP}$ associated with the Dirac phase $\delta _{CP}$, which controls the magnitude of CP violation effects in neutrino oscillations [45], is given by:

$$\begin{aligned} J_{CP}= & {} \mathrm {Im} (U_{23} U^*_{13} U_{12} U^*_{22})\nonumber \\= & {} \left\{ \begin{array}{l} \frac{(K_2 N_3-K_3 N_2)(K_2 K_3+ N_2 N_3)}{(1 + K_2^2 + N_2^2) (1 + K_3^2 + N_3^2)}\sin \theta \cos \theta \sin \alpha \hbox {for \, NH}, \\ \frac{(K_2 N_1-K_1 N_2)(K_1 K_2+ N_1 N_2)}{(1 + K_1^2 + N_1^2) (1 + K_2^2 + N_2^2)}\sin \theta \cos \theta \sin \alpha \hbox {for \, IH}. \end{array} \right. \nonumber \\ \end{aligned}$$

(43)

where Eqs. (39) and (41) were taken into account.

By comparing Eq. (43) with its corresponding expression taken from Ref. [45], $J_{CP}=s_{13} c_{13}^2 s_{12} c_{12} s_{23} c_{23} \sin \delta$, we get:

$$\begin{aligned} \sin \delta= & {} \left\{ \begin{array}{l} \frac{(K_2 N_3-K_3 N_2)(K_2 K_3+ N_2 N_3)}{(1 + K_2^2 + N_2^2) (1 + K_3^2 + N_3^2)}\frac{\sin \theta \cos \theta \sin \alpha }{s_{13} c_{13}^2 s_{12} c_{12} s_{23} c_{23}} \hbox {for \, NH}, \\ \frac{(K_2 N_1-K_1 N_2)(K_1 K_2+ N_1 N_2)}{(1 + K_1^2 + N_1^2) (1 + K_2^2 + N_2^2)}\frac{\sin \theta \cos \theta \sin \alpha }{s_{13} c_{13}^2 s_{12} c_{12} s_{23} c_{23}} \hbox {for \, IH}. \end{array} \right. \nonumber \\ \end{aligned}$$

(44)

Combining Eqs. (39), (41) and (42), we found that $N_i, K_i \, (i=1,2,3)$ and all the elements of leptonic mixing matrix U depend on five parameters $\theta _{12}, \theta _{13}, \theta _{23}$, $\theta$ and $\alpha$. By using the best-fit values of leptonic mixing angles taken from Ref. [46],

$$\begin{aligned}&\sin ^2 \theta _{12}=0.304, \sin ^2 \theta _{23}=\left\{ \begin{array}{l} 0.573 \hbox {for \, NH}, \\ 0.575 \hbox {for \, IH}, \end{array} \right. \nonumber \\&\sin ^2 \theta _{13}=\left\{ \begin{array}{l} 0.02219 \hbox {for \, NH}, \\ 0.02238 \hbox {for \, IH}, \end{array} \right. \end{aligned}$$

(45)

we find out the regions of $\theta$ and $\alpha$ which can reproduce the recent experimental data. Indeed, in the case where $\sin \theta =0.25\, (\theta =14.5^\circ )$, $N_i$ and $K_i$ depend on $\alpha$ with $\sin \alpha \in (0.40, 0.50)$ for NH and $\sin \alpha \in (0.65, 0.75)$ for IH which is plotted in Fig. 3.

Fig. 3

$K_{i},\, N_{i}$ versus $\sin \alpha$ with $\sin \alpha \in (0.40,\, 0.50)$ for NH (left figure) and $\sin \alpha \in (0.65,\, 0.75)$ for IH (right figure)

Fig. 4

$\langle m_{ee}\rangle$ and $m_{\beta }$ versus $\sin \alpha$ with $\sin \alpha \in (0.40,\, 0.50)$ for NH (left figure) and $\sin \alpha \in (0.65,\, 0.75)$ for IH (right figure)

Next, taking the best-fit values of the solar and atmospheric neutrino squared-mass differences taken form Ref. [46],

$$\begin{aligned} \Delta m^2_{21}= & {} 7.42 \times 10^{-5}\,\mathrm {eV}^2, \nonumber \\&\times \left\{ \begin{array}{l} \Delta m^2_{31}=2.517 \times 10^{-3}\, \mathrm {eV}^2 \hbox {for NH}, \\ \Delta m^2_{32}=-2.498 \times 10^{-3}\, \mathrm {eV}^2 \hbox {for IH}, \end{array} \right. \end{aligned}$$

(46)

we get a solution

$$\begin{aligned} \Bbbk _1= & {} \left\{ \begin{array}{l} 2.94\times 10^{-2}\, \mathrm {eV} \hbox {for NH}, \\ 4.96 \times 10^{-2}\, \mathrm {eV} \hbox {for IH}, \end{array} \right. \nonumber \\ \Bbbk _2= & {} \left\{ \begin{array}{l} 2.08\times 10^{-2}\, \mathrm {eV} \hbox {for NH}, \\ -3.74 \times 10^{-4}\, \mathrm {eV} \hbox {for IH}, \end{array} \right. \end{aligned}$$

(47)

and three neutrino masses are explicitly given as

$$\begin{aligned} m_1= & {} 0 \, \mathrm {eV},\, \, m_2= 8.61\times 10^{-3} \, \mathrm {eV}, \, \, \nonumber \\ m_3= & {} 5.02\times 10^{-2}\, \mathrm {eV} \mathrm {for NH}, \end{aligned}$$

(48)

$$\begin{aligned} m_1= & {} 4.92 \times 10^{-2}\, \mathrm {eV},\, \, m_2= 5.0 \times 10^{-2}\, \mathrm {eV}, \, \, \nonumber \\ m_3= & {} 0 \, \mathrm {eV} \mathrm {for IH}. \end{aligned}$$

(49)

The sum of three neutrino masses is thus found to be

$$\begin{aligned} \sum _{i=1}^3 m_i=\left\{ \begin{array}{l} 5.88\times 10^{-2} \,\mathrm {eV} \hbox {for NH}, \\ 9.92\times 10^{-2} \,\mathrm {eV} \hbox {for IH}, \end{array} \right. \end{aligned}$$

(50)

which are well consistent with the updated bounds from cosmology [47].

Furthermore, in the NH, $m_1\approx m_2<m_3$, so $m_{1}=0$ is the lightest neutrino mass while $m_{3}=0$ is the lightest neutrino mass for IH. The effective neutrino mass parameters governing the beta decay and neutrinoless double beta decay, $m_{\beta }= \sqrt{\sum ^3_{i=1} \left| U_{1i}\right| ^2 m_i^2}$ and $\langle m_{ee}\rangle =\left| \sum ^3_{i=1} U_{1i}^2 m_i \right|$ depend only on $\sin \alpha$ with $\sin \alpha \in (0.40,\, 0.50)$ for NH and $\sin \alpha \in (0.65,\, 0.75)$ for IH which is depicted in Fig. 4.

In the case where $\sin \alpha =0.445\, (\alpha =26.4^\circ )$ for NH and $\sin \alpha =0.75\, (\alpha =48.6^\circ )$ for IH, $m_{\beta }$ and $\langle m_{ee}\rangle$ are found to be:

$$\begin{aligned} \langle m_{ee}\rangle= & {} \left\{ \begin{array}{l} 2.61 \times 10^{-3} \,\mathrm {eV} \mathrm {for} \mathrm {NH}, \\ 4.69\times 10^{-2} \,\mathrm {eV} \mathrm {for} \mathrm {IH}, \end{array} \right. \end{aligned}$$

(51)

and

$$\begin{aligned} m_{\beta } =\left\{ \begin{array}{l} 8.83 \times 10^{-3} \,\mathrm {eV} \mathrm {for} \mathrm {NH}, \\ 4.89\times 10^{-2} \,\mathrm {eV} \mathrm {for} \mathrm {IH}. \end{array} \right. \end{aligned}$$

(52)

The Jarlskog invariant $J_{CP}$, determined from Eq. (43 ), possessed the following values:

$$\begin{aligned} J_{CP}=\left\{ \begin{array}{l} -0.0199 \mathrm {for} \mathrm {NH}, \\ -0.0323 \mathrm {for} \mathrm {IH}. \end{array} \right. \end{aligned}$$

(53)

The lepton mixing matrices for both normal and inverted hierarchies take the explicit forms

$$\begin{aligned} U=\left\{ \begin{array}{l} \left( \begin{array}{ccc} -0.823+0.0511i &{} 0.543+0.0508i &{} 0.0847+0.123 i \\ -0.279+0.0828 i &{} -0.591-0.0741i &{} -0.0051+0.749 i \\ 0.481 &{} 0.589 &{} 0.646i \end{array} \right) \hbox {for \, NH}, \\ \left( \begin{array}{ccc} -0.82+0.0863i &{} 0.538+0.086i &{} 0.143+0.0455i \\ -0.319+0.144 i &{} -0.549-0.119i &{} -0.0155+0.75i \\ 0.444 &{} 0.622 &{} 0.645i \end{array} \right) \hbox {for \, IH}, \end{array} \right. \nonumber \\ \end{aligned}$$

(54)

which are unitary and consistent with the constraint on the absolute values of the entries of the lepton mixing matrix given in Ref. [46]. The other model parameters are obtained as in Table 4.

Table 4 The model parameters in the case $\sin \theta =0.25$, and $\sin \alpha =0.445$ for NH  and $\sin \theta =0.25$ and $\sin \alpha =0.75$ for IH

5 Scalar potential with two $SU\left( 3\right) _{L}$ triplets

To simplify our analysis, we neglect the mixing terms between the $SU\left( 3\right) _{L}$ scalar triplets and the gauge singlet scalars. Then, the scalar potential for the two $SU\left( 3\right) _{L}$ scalar triplets is given by:

$$\begin{aligned} V= & {} -\mu _{\chi }^{2}(\chi ^{\dagger }\chi ) -\mu _{\rho }^{2}(\rho ^{\dagger }\rho ) + \lambda _{1}(\chi ^{\dagger }\chi )(\chi ^{\dagger }\chi ) \nonumber \\&+ \lambda _{2}(\rho ^{\dagger }\rho )(\rho ^{\dagger }\rho ) \nonumber \\&+ \lambda _{3}(\chi ^{\dagger }\chi )(\rho ^{\dagger }\rho ) + \lambda _{4}(\chi ^{\dagger }\rho )(\rho ^{\dagger }\chi ) + H.c., \end{aligned}$$

with $\chi$ and $\rho$, the $SU(3)_{L}$ scalar triplets. Furthermore, the global minimum conditions of the scalar potential give the relations:

$$\begin{aligned} \mu _{\chi }^{2}= & {} \dfrac{1}{2} \left( 2v_{\chi }^{2} \lambda _{1} + v_{\rho }^{2} \lambda _{3} \right) , \end{aligned}$$

(55)

$$\begin{aligned} \mu _{\rho }^{2}= & {} \dfrac{1}{2} \left( 2v_{\rho }^{2} \lambda _{2} + v_{\chi }^{2} \lambda _{3} \right) . \end{aligned}$$

(56)

After spontaneous symmetry breaking we get the squared mass matrices for the scalar fields:

$$\begin{aligned} M_{CPeven}^{2}= & {} \left( \begin{array}{ccc} 0 &{} 0 &{} 0 \\ 0 &{} v_{\rho }^{2} \lambda _{2} &{} \dfrac{1}{2} v_{\rho } v_{\chi } \lambda _{3} \\ 0 &{} \dfrac{1}{2} v_{\rho } v_{\chi } \lambda _{3} &{} v_{\chi }^{2} \lambda _{1} \end{array} \right) , \nonumber \\ M_{CPodd}^{2}= & {} \left( \begin{array}{ccc} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \end{array} \right) , \nonumber \\ M_{charged}^{2}= & {} \left( \begin{array}{ccc} 0 &{} 0 &{} 0 \\ 0 &{} \dfrac{1}{2} v_{\rho }^{2} \lambda _{4} &{} \dfrac{1}{2} v_{\rho } v_{\chi } \lambda _{4} \\ 0 &{} \dfrac{1}{2} v_{\rho } v_{\chi } \lambda _{4} &{} \dfrac{1}{2} v_{\chi }^{2} \lambda _{4} \end{array} \right) . \end{aligned}$$

(57)

This shows that the resulting physical scalar spectrum arising from the $SU(3)_L$ scalar triplets $\chi$ and $\rho$ is composed of the 126 GeV SM like Higgs boson, a heavy neutral CP even scalar $H^0$ associated with the spontaneous breaking of the $SU(3)_L\times U(1)_X$ symmetry and the electrically charged scalars $H^{\pm }$. The massless degrees of freedom in the scalar spectrum correspond to the Goldstone boson associated with the longitudinal components of the $W^{\pm }$, Z, $W^{\prime \pm }$, $Z^{\prime }$ , $K^{0}$ and $\bar{K}^{0}$ massive gauge bosons.

6 Higgs diphoton decay rate constraints

The decay rate for the $h\rightarrow \gamma \gamma$ process takes the form [48,49,50,51,52,53,54]:

$$\begin{aligned}&\Gamma (h \rightarrow \gamma \gamma ) =\dfrac{\alpha _{em}^2 m_h^3}{256 \pi ^3 v^2}\nonumber \\&\quad \left| \sum _f a_{hff} N_C Q_f^2 F_{1/2}(\rho _f)+a_{hWW} F_{1}(\rho _W)+\frac{C_{hH^{\pm }H^{\mp }}}{2m^{2}_{H^{\pm }}} vF_{0}(\rho _{H^{\pm }})\right| ^2,\nonumber \\ \end{aligned}$$

(58)

where $\rho _i$ are the mass ratios $\rho _i= \frac{m_h^2}{4 M_i^2}$ with $M_i=m_f, M_W$; $\alpha _{em}$ is the fine structure constant; $N_C$ is the color factor ($N_C=1$ for leptons and $N_C=3$ for quarks) and $Q_f$ is the electric charge of the fermion in the loop. From the fermion-loop contributions we only consider the dominant top quark term. Furthermore, $C_{hH^{\pm }H^{\mp }}$ is the trilinear coupling between the SM-like Higgs and a pair of charged Higgs bosons, whereas $a_{htt}$ and $a_{hWW}$ are the deviation factors from the SM Higgs top quark coupling and the SM Higgs-W gauge boson coupling, respectively (in the SM these factors are unity). Such deviation factors are very close to unity in our model, which is a consequence of the numerical analysis of its scalar, Yukawa and gauge sectors. Besides, $F_{1/2}(z)$ and $F_{1}(z)$ are the dimensionless loop factors for spin-1/2 and spin-1 particles running in the internal lines of the loops. They are given by:

$$\begin{aligned} F_{1/2}(z)&= 2(z + (z -1)f(z))z^{-2}, \end{aligned}$$

(59)

$$\begin{aligned} F_{1}(z)&= -2(2z^2 + 3z + 3(2z-1)f(z))z^{-2}, \end{aligned}$$

(60)

$$\begin{aligned} F_{0}(z)&= -(z - f(z))z^{-2}, \end{aligned}$$

(61)

with

$$\begin{aligned} f(z) = \left\{ \begin{array}{lll} \left( \arcsin \sqrt{2}\right) ^2 &{} \text {for} &{} z \le 1, \\ -\frac{1}{4}\left( \ln \left( \frac{1+\sqrt{1-z^{-1}}}{1-\sqrt{1-z^{-1}}-i\pi } \right) ^2 \right) &{} \text {for} &{} z > 1. \end{array} \right. \end{aligned}$$

(62)

In order to study the implications of our model in the decay of the 126 GeV Higgs boson into a photon pair, one introduces the Higgs diphoton signal strength $R_{\gamma \gamma }$, which is defined as:

$$\begin{aligned} R_{\gamma \gamma }&= \frac{\sigma (pp \rightarrow h)\Gamma (h \rightarrow \gamma \gamma )}{ \sigma (pp \rightarrow h)_{SM}\Gamma (h \rightarrow \gamma \gamma )_{SM}} \nonumber \\&\simeq a^{2}_{htt} \frac{\Gamma (h \rightarrow \gamma \gamma )}{\Gamma (h \rightarrow \gamma \gamma )_{SM}}. \end{aligned}$$

(63)

That Higgs diphoton signal strength, normalizes the $\gamma \gamma$ signal predicted by our model in relation to the one given by the SM. Here we have used the fact that in our model, single Higgs production is also dominated by gluon fusion as in the Standard Model.

The ratio $R_{\gamma \gamma }$ has been measured by CMS and ATLAS collaborations with the best fit signals [55, 56]:

$$\begin{aligned} R^{CMS}_{\gamma \gamma } = 1.18^{+0.17}_{-0.14} \quad \text {and} \quad R^{ATLAS}_{\gamma \gamma } = 0.96 \pm 0.14. \end{aligned}$$

(64)

The Higgs diphoton signal strength as a function of the electrically charged scalar mass is shown in Fig. 5. This shows that our model successfully accommodates the current Higgs diphoton decay rate constraints.

Fig. 5

Higgs diphoton signal strength as a function of the charged scalar mass $m_{H^{\pm }}$, with $600\,[GeV]< m_{H^{\pm }} < 7000\,[GeV]$

7 Muon anomalous magnetic moment

In this section we discuss the implications of our model in the muon anomalous magnetic moment. It is worth mentioning that the dominant contribution to the muon anomalous magnetic moment arises from the one-loop diagram involving the exchange of the electrically neutral scalars h and H and the charged exotic vector like leptons $E_1$ and $E_2$. It is worth mentioning that there other contributions to the muon anomalous magnetic moments like the ones arising from the virtual exchange of heavy neutral and electrically charged gauge bosons together with charged and neutral leptons, respectively as well as contributions due to electrically charged scalars and neutrinos. However those extra contributions are subleading. Regarding the contribution arising from the virtual exchange electrically charged scalars and light active neutrinos, we have numerically checked that it can reproduce the magnitude of the $g-2$ muon anomaly for electrically charged scalars lower than 400 GeV. However such contribution turn out to be negative and thus not allow to reproduce the correct sign of the $g-2$ muon anomaly. Consequently, in our analysis of the muon anomalous magnetic moment, we only consider the leading contribution arising from the virtual exchange of electrically neutral scalars h and H and the charged exotic vector like leptons $E_1$ and $E_2$. Furthermore, in order to simplify our numerical analysis, we restrict to the region of parameter space where the electrically charged scalars are heavier than about 400 GeV, thus implying that the contribution to the $g-2$ muon anomaly arising from the virtual exchange electrically charged scalars and light active neutrinos is suppressed and therefore subleading. The Feynman diagrams corresponding the Beyond Standard Model contributions to the muon anomalous magnetic moment in the 3-3-1 model under consideration are shown in Fig. 6.

Fig. 6

Feynman diagrams corresponding to Beyond Standard Model contributions to the muon anomalous magnetic moment in the 3-3-1 model under consideration. Notice that the second diagram involving the virtual exchange of charged exotic leptons $E_{1,2}$ and neutral scalars $\Phi ^0=h,H$ is the one that provides the leading contribution to the muon anomalous magnetic moment

In view of the previous discussion, the dominant contribution to the muon anomalous magnetic moment in our model has the form:

$$\begin{aligned} \Delta a_{\mu }\simeq \frac{y_{1}^{\left( l\right) }z_{2}^{\left( l\right) }m_{\mu }^{2}}{8\pi ^{2}}\left[ J\left( m_{E_{2}},m_{h}\right) - J\left( m_{E_{2}},m_{H}\right) \right] \sin \theta \cos \theta ,\nonumber \\ \end{aligned}$$

(65)

where, $y_{1}^{\left( l\right) }$ and $z_{2}^{\left( l\right) }$ are the leptonic Yukawa couplings appearing in the first line of Eq. (6). Here, in order to simplify our analysis we have restricted to the case $v_1 \ll v_2$, which implies that only $\phi _1$ (the first component of the $D_4$ scalar doublet $\Phi$) mixes with the CP even neutral part of the $SU(3)_L$ scalar triplet $\rho$. Then, the neutral scalars h and H are defined as: $H\simeq \cos \theta \,{\hbox {Re}}\,\phi _{1}+\sin \theta \xi _{\rho }$ , $h\simeq -\sin \theta \,{{\hbox {Re}}}\,\phi _{1}+\cos \theta \xi _{\rho }$, and $m_{E_{2}}$ is the mass of the VLL $E_{2}$. Furthermore, the loop $J\left( m_{E},m_{S}\right)$ function has the following form [57,58,59,60]:

$$\begin{aligned} J\left( m_{E},m_{S}\right) =\int _{0}^{1}dx\frac{x^{2}\left( 1-x+\frac{m_{E}}{ m_{\mu }}\right) }{m_{\mu }^{2}x^{2}+\left( m_{E}^{2}-m_{\mu }^{2}\right) x+m_{S}^{2}\left( 1-x\right) }.\nonumber \\ \end{aligned}$$

(66)

The above given expression for the muon anomalous magnetic moment can be approximately rewritten as follows:

$$\begin{aligned} \Delta a_{\mu }\simeq & {} \frac{y_{1}^{\left( l\right) }z_{2}^{\left( l\right) } }{8\pi ^{2}}\left[ \frac{m_{\mu }m_{E_{2}}}{m_{h}^{2}}G_{1}\left( \frac{ m_{E_{2}}^{2}}{m_{h}^{2}}\right) \nonumber \right. \\&\left. -\frac{m_{\mu }m_{E_{2}}}{m_{H}^{2}} G\left( \frac{m_{E_{2}}^{2}}{m_{H}^{2}}\right) \right] \sin \theta \cos \theta , \end{aligned}$$

(67)

where the corresponding loop function as the form [61]:

$$\begin{aligned} G\left( z\right) =\frac{3-4z+z^{2}+2\ln z}{2\left( z-1\right) ^{3}}. \end{aligned}$$

(68)

Considering that the muon anomalous magnetic moment is constrained to be in the range [62,63,64,65,66,67,68,69]

$$\begin{aligned} \left( \Delta a_{\mu }\right) _{\exp }={a_{\mu }^{\mathrm {exp}}-a_{\mu }^{\mathrm {SM}}}=\left( 2.51\pm 0.59\right) \times 10^{-9}. \end{aligned}$$

(69)

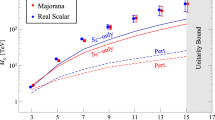
We display in Fig. 7 the muon anomalous magnetic moment as a function of the charged exotic vector like mass. As shown in Fig. 7, we have that our model successfully accommodates the experimental value of $\Delta a_{\mu }$ for charged exotic lepton masses at the TeV scale.

Fig. 7

Muon anomalous magnetic moment as a function of the charged exotic lepton mass $m_E$

8 Meson oscillations

The non universal $U(1)_X$ charge assignments for the left handed quark fields yield tree level $Z^{\prime }$ mediated flavour changing neutral processes (FCNC) which will yield $K^0- \bar{K}^0$, $B^0_d-\bar{B}^0_d$ and $B^0_s-\bar{B}^0_s$ meson oscillations. These meson mixings are described by the following effective Hamiltonian interactions [70]:

$$\begin{aligned} \mathcal {H}_{eff}^{\left( K^{0}-\bar{K}^{0}\right) }= & {} \frac{4\sqrt{ 2 }G_{F}c_{W}^{4}m_{Z}^{2}}{\left( 3-4s_{W}^{2}\right) m_{Z^{\prime }}^{2}} \left| \left( V_{DL}^{*}\right) _{32}\left( V_{DL}\right) _{31}\right| ^{2}\nonumber \\&O^{\left( K^{0}-\bar{K}^{0}\right) }, \end{aligned}$$

(70)

$$\begin{aligned} \mathcal {H}_{eff}^{\left( B_{d}^{0}-\bar{B}_{d}^{0}\right) }= & {} \frac{ 4\sqrt{2}G_{F}c_{W}^{4}m_{Z}^{2}}{\left( 3-4s_{W}^{2}\right) m_{Z^{\prime }}^{2}}\left| \left( V_{DL}^{*}\right) _{31}\left( V_{DL}\right) _{33}\right| ^{2}\nonumber \\&O^{\left( B_{d}^{0}-\bar{B}_{d}^{0}\right) }, \end{aligned}$$

(71)

$$\begin{aligned} \mathcal {H}_{eff}^{\left( B_{s}^{0}-\bar{B}_{s}^{0}\right) }= & {} \frac{ 4\sqrt{2}G_{F}c_{W}^{4}m_{Z}^{2}}{\left( 3-4s_{W}^{2}\right) m_{Z^{\prime }}^{2}}\left| \left( V_{DL}^{*}\right) _{32}\left( V_{DL}\right) _{33}\right| ^{2}\nonumber \\&O^{\left( B_{s}^{0}-\bar{B}_{s}^{0}\right) }. \end{aligned}$$

(72)

where the corresponding operators are given by:

$$\begin{aligned} O^{\left( K^{0}-\bar{K}^{0}\right) }= & {} \left( \overline{s}\gamma _{\mu }P_{L}d\right) \left( \overline{s}\gamma ^{\mu }P_{L}d\right) ,\nonumber \\ O^{\left( B_{d}^{0}-\bar{B}_{d}^{0}\right) }= & {} \left( \overline{ d }\gamma _{\mu }P_{L}b\right) \left( \overline{d}\gamma ^{\mu }P_{L}b\right) , \end{aligned}$$

(73)

$$\begin{aligned} O^{\left( B_{s}^{0}-\bar{B}_{s}^{0}\right) }= & {} \left( \overline{s}\gamma _{\mu }P_{L}b\right) \left( \overline{s}\gamma ^{\mu }P_{L}b\right) . \end{aligned}$$

(74)

Furthermore, the following relations have been taken into account:

$$\begin{aligned} \widetilde{M}_{f}= & {} \left( M_{f}\right) _{diag}=V_{fL}^{\dagger }M_{f}V_{fR},\nonumber \\ f_{\left( L,R\right) }= & {} V_{f\left( L,R\right) }\widetilde{f}_{\left( L,R\right) }, \nonumber \\ \overline{f}_{iL}\left( M_{f}\right) _{ij}f_{jR}= & {} \overline{\widetilde{f}} _{kL}\left( V_{fL}^{\dagger }\right) _{ki}\left( M_{f}\right) _{ij}\left( V_{fR}\right) _{jl}\nonumber \\ \widetilde{f}_{lR}= & {} \overline{\widetilde{f}}_{kL}\left( V_{fL}^{\dagger }M_{f}V_{fR}\right) _{kl}\widetilde{f}_{lR}\nonumber \\= & {} \overline{ \widetilde{f}}_{kL}\left( \widetilde{M}_{f}\right) _{kl}\widetilde{f} _{lR}\nonumber \\= & {} m_{fk}\overline{\widetilde{f}}_{kL}\widetilde{f}_{kR}, k =1,2,3\,. \end{aligned}$$

(75)

Here, $\widetilde{f}_{k\left( L,R\right) }$ and $f_{k\left( L,R\right) }$ ($k=1,2,3$) are the SM fermionic fields in the mass and interaction bases, respectively.

On the other hand, the $K-\bar{K}$, $B_{d}^{0}-\bar{B}_{d}^{0}$ and $B_{s}^{0}-\bar{B}_{s}^{0}$ mass splittings are given by:

$$\begin{aligned} \Delta m_{K}= & {} \left( \Delta m_{K}\right) _{SM}+\Delta m_{K}^{\left( NP\right) },\nonumber \\ \Delta m_{B_{d}}= & {} \left( \Delta m_{B_{d}}\right) _{SM}+\Delta m_{B_{d}}^{\left( NP\right) },\nonumber \\ \Delta m_{B_{s}}= & {} \left( \Delta m_{B_{s}}\right) _{SM}+\Delta m_{B_{s}}^{\left( NP\right) }, \end{aligned}$$

(76)

where $\left( \Delta m_{K}\right) _{SM}$, $\left( \Delta m_{B_{d}}\right) _{SM}$ and $\left( \Delta m_{B_{s}}\right) _{SM}$ are the SM contributions, whereas $\Delta m_{K}^{\left( NP\right) }$ , $\Delta m_{B_{d}}^{\left( NP\right) }$ and $\left( \Delta m_{B_{s}}\right) _{SM}$ are new physics contributions.

The new physics contributions to meson mass differences are [70]:

$$\begin{aligned} \Delta m_{K}^{\left( NP\right) }= & {} \frac{4\sqrt{2}G_{F}c_{W}^{4}m_{Z}^{2}}{ \left( 3-4s_{W}^{2}\right) m_{Z^{\prime }}^{2}}\left| \left( V_{DL}^{*}\right) _{32}\left( V_{DL}\right) _{31}\right| ^{2}\nonumber \\&f_{K}^{2}B_{K}\eta _{K}m_{K}, \end{aligned}$$

(77)

$$\begin{aligned} \Delta m_{B_{d}}^{\left( NP\right) }= & {} \frac{4\sqrt{2}G_{F}c_{W}^{4}m_{Z}^{2}}{ \left( 3-4s_{W}^{2}\right) m_{Z^{\prime }}^{2}}\left| \left( V_{DL}^{*}\right) _{31}\left( V_{DL}\right) _{33}\right| ^{2}\nonumber \\&f_{B_{d}}^{2}B_{B_{d}}\eta _{B_{d}}m_{B_{d}}, \end{aligned}$$

(78)

$$\begin{aligned} \Delta m_{B_{s}}^{\left( NP\right) }= & {} \frac{4\sqrt{2}G_{F}c_{W}^{4}m_{Z}^{2}}{ \left( 3-4s_{W}^{2}\right) m_{Z^{\prime }}^{2}}\left| \left( V_{DL}^{*}\right) _{32}\left( V_{DL}\right) _{33}\right| ^{2}\nonumber \\&f_{B_{s}}^{2}B_{B_{s}}\eta _{B_{s}}m_{B_{s}}. \end{aligned}$$

(79)

Using the following parameters [70,71,72,73,74,75,76]:

$$\begin{aligned} \Delta m_{K}= & {} \left( 3.484\pm 0.006\right) \times 10^{-12}\,MeV,\\ \left( \Delta m_{K}\right) _{SM}= & {} 3.483\times 10^{-12}\,MeV \\ f_{K}= & {} 160\,MeV,\quad B_{K}=0.85,\nonumber \\ \eta _{K}= & {} 0.57, \quad m_{K}=497.614\,MeV.\\ \left( \Delta m_{B_{d}}\right) _{\exp }= & {} \left( 3.337\pm 0.033\right) \times 10^{-10}\,MeV,\\ \left( \Delta m_{B_{d}}\right) _{SM}= & {} 3.582\times 10^{-10}\,MeV, \\ f_{B_{d}}= & {} 188\,MeV,\quad B_{B_{d}}=1.26,\quad \eta _{B_{d}}=0.55,\\ m_{B_{d}}= & {} 5279.5\,MeV.\\ \left( \Delta m_{B_{s}}\right) _{\exp }= & {} \left( 104.19\pm 0.8\right) \times 10^{-10}\,MeV,\\ \left( \Delta m_{B_{s}}\right) _{SM}= & {} 121.103\times 10^{-10}\,MeV, \\ f_{B_{s}}= & {} 225\,MeV,\quad B_{B_{s}}=1.26,\quad \eta _{B_{s}}=0.55,\\ m_{B_{s}}= & {} 5366.3\,MeV. \end{aligned}$$

Fig. 8

The $B_{d}^{0}-\bar{B}_{d}^{0}$ mass splitting as a function of the $Z^{\prime }$ mass

We plot in Fig. 8 the $B_{d}^{0}-\bar{B}_{d}^{0}$ mass splitting as as function of the $Z^{\prime }$ mass. As seen from Fig. 8, the obtained values for the $B_{s}^{0}-\bar{B}_{s}^{0}$ mass difference are consistent with the experimental data where the $Z^{\prime }$ mass is larger than about 4.6 TeV and lower than about 4.9 TeV. Regarding the $K^{0}-\bar{K}^{0}$, $B_{d}^{0}-\bar{B}_{d}^{0}$ mass splittings, we have numerically checked that the obtained values are in accordance with the meson oscillation experimental data in the above described region of parameter space.

9 Conclusions

We have constructed a theory based on the $SU(3)_C\times SU(3)_L\times U(1)_X$ gauge symmetry, where the scalar sector is composed of two $SU(3)_L$ scalar triplets and several gauge singlet scalar fields. The theory incorporates the $D_4$ family symmetry, which is supplemented by several auxiliary cyclic symmetries, whose spontaneous breaking yield viable and predictive fermion mass matrix textures with hierarchical entries thus allowing a natural explanation of the current hierarchy of SM fermion masses and mixings. The tiny masses of the light active neutrinos are produced by an inverse seesaw mechanism mediated by three right handed Majorana neutrinos. The smallness of the $\mu$ parameter of the inverse seesaw, generated after the spontaneous breaking of the discrete symmetries of the model, is attributed to a right-handed neutrino nonrenormalizable Yukawa terms. Our proposed model is consistent with Higgs diphoton decay rate constraints,with the muon anomalous magnetic moment and the meson oscillation experimental data. The consistency of our model with the muon anomalous magnetic moment requires charged exotic vector like leptons at the TeV scale.

Appendix A: The product rules for \(D_{4}\)

The $D_4$ group has four singlets and one doublet, $\mathbf {1} _{++}$, $\mathbf {1}_{+-}$, $\mathbf {1}_{-+}$, $\mathbf {1}_{-}{-}$, and $\mathbf {2}$, respectively. The multiplication of the singlets is simply given by

$$\begin{aligned} \mathbf {1}_{x_1 y_1} \times \mathbf {1}_{x_2 y_2} = \mathbf {1}_{x_3 y_3} \end{aligned}$$

(A1)

where $x_3 = x_1 x_2$ and $y_3 = y_1 y_2$. While the tensor product for two doublets, $\mathbf {a} = (a_1,a_2)^T$ and $\mathbf {b} = (b_1 ,b_2)^T$, is

$$\begin{aligned} \mathbf {a} \times \mathbf {b}&= (a_1 b_2 + a_2 b_1)_{\mathbf {1}_{++}} + (a_1 b_2 - a_2 b_1)_{\mathbf {1}_{-}{-}}\nonumber \\&\quad + (a_1 b_1 + a_2 b_2)_{\mathbf {1}_{+-}} + (a_1 b_1 - a_2 b_2)_{\mathbf {1}_{-+}}. \end{aligned}$$

(A2)