Particle dynamics and gravitational weak lensing around black hole in the Kalb-Ramond gravity

Abstract

In this paper, we have studied the particle dynamics, gravitational lensing and energy processes around the black hole (BH) in Kalb–Ramond (KR) gravity. The motion of particles is considered with parameters in KR BH and investigated for massive and massless particles. From this work, we have got the horizon structure, photon orbit of photon and ISCO (inner stable circular orbit) of a mass particle with parameters in KR gravity. The effective potential is also studied for the massless and mass particles. Additionally, we tested energy extracted from BH using the BSW (Banados–Silk–West) method and derived the expression of center mass-energy in KR gravity. The impact of the model parameters $\gamma$ and $\lambda$ is checked to study the size of the BH shadow in the KR gravity. Gravitational weak lensing has been explored using the general method and the derived deflection angle of light rays around the BH for the plasma of various concentration distributions. The magnification of brightness is obtained using the angle of deflection of the light rays.

1 Introduction

The metric theory of gravity, first proposed by Albert Einstein in 1915, considers the gravitational interaction as a consequence of the (4-dimensional) spacetime curvature due to the presence of a massive object. Being a mathematically well-defined theory, the general relativity has been successfully tested in both weak [1] and strong field [2,3,4] regimes. On the other hand, the current resolution of experiments and observations used to test the general relativity [5, 6] allow us to consider modifications and alternative theories to develop gravitational field theory further. In this regard, Sohan and Anisur [7] considered the bumblebee gravity model with a Lorentz-violating scenario and sketched the shadow for Kerr-Sen like BH solution. Maluf and Juliano [8] calculated the shadow angular radius for black hole solutions with a cosmological constant in bumblebee gravity. Ali and his coauthors [9] calculated the gravitational lensing under the effect of Weyl and bumblebee gravities in the background of Gauss-Bonnet theorem. In another study, they [10] explored the new wormhole models in bumblebee gravity. The greybody factor with a Lorentz violation model was discussed by Chikun and Xiongwen [11] for slowly rotating Einstein-bumblebee black hole solution. Some other interesting aspects like, shadow with plasma [12], quasinormal modes [13], greybody radiation [14], gravitational deflection angle [15], and Hawking radiation [16], also discussed in the background of bumblebee gravity.

One of the modifications of the Einstein action is due to the presence of the KR field [17] which can be expressed as a self-interacting second-rank antisymmetric tensor. The KR modification can be related to the heterotic string theory [18] and can be interpreted as the closed string excitation. Due to the presence of nonminimal coupling of the tensor field with Ricci scalar, one may observe the violation of the Lorentz symmetry [19]. One may distinguish several features of the KR field; particularly, one may derive the third-rank antisymmetric tensor, which can be interpreted as a source of spacetime torsion [20]. Other interpretations of that third-rank asymmetric tensor related to topological defects can be led to the intrinsic angular momentum of the structures in galaxies [21]. In Ref. [22] authors studied the effect of the KR field on the observed anisotropy in the cosmic microwave background. For the review of the gravitational nature of the KR field as well as its effects on particle physics, we refer the readers to Refs. [23,24,25,26]. The solar system test of the gravity, including the KR field, has been explored in [27]. In Ref. [26], authors have also studied shadow and gravitational lensing of rotating BH in KR gravity. However, In Ref. [26] authors have considered the case of strong lensing. Here we have considered the cases of weak lensing and in the presence of plasma. Additionally, we have also studied the energy extraction, ISCO and other types of orbits.

Particularly, in order to construct the action for the KR field, one may consider the analogy between electromagnetic field where the vector potential can be replaced by tensor $B^{\alpha \beta }$ which is a second-rank antisymmetric tensor field associated with $H_{\alpha \beta \gamma }=\partial _{\alpha [}B_{\beta \gamma ]}$. Here, $H_{\alpha \beta \gamma }$ represents the third-rank antisymmetric tensor and can be interpreted as an analog of the electromagnetic field tensor. The action for the Einstein-Hilbert coupled with the KR field can be expressed as [28]

$$\begin{aligned} S= & {} \int \sqrt{-g}d^4x\Bigg [\frac{R}{16\pi G}-\frac{1}{12}H_{\alpha \mu \nu }H^{\alpha \mu \nu }\nonumber \\&-V(B_{\mu \nu }B^{\mu \nu }\,{\mu \nu }b^{\mu \nu })\nonumber \\&+\frac{1}{16\pi G}(\xi _2B^{\mu \nu }B^{\nu }_{\lambda }R_{\mu \nu }+\xi _3B_{\mu \nu }B^{\mu \nu }R)\Bigg ]\ , \end{aligned}$$

(1)

where R is Ricci scalar, $\xi _{2,3}$ are the nonminimal coupling constants and V is the constant associated with the nonzero vacuum expectation value of the tensor $<B_{\mu \nu }>=b_{\mu \nu }$.

The analysis of the electromagnetic wave propagation in the space within metric theories of gravity leads to the light bending effect. The deflection of the light in the curved spacetime near the Sun had been used to test the general relativity in 1919 during the solar eclipse observed in Africa by A. Eddington [29]. Later photon motion and the so-called gravitational lensing have been extensively studied in Refs. [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48]. The effect of plasma on photon motion and, consequently, gravitational lensing has been discussed in Refs. [49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64].

On the other hand, the study of electromagnetic wave propagation in the curved spacetime may also lead to the concept of the shadow of the BH [65, 66]. For review the detailed study of the shadow we refer the Readers to Refs. [67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87].

Test particle motion can also be considered as a useful tool to test the metric theories of gravity since spacetime structure strongly changes the behaviour of the geodesic lines. The effects of the spacetime curvature and gravitational field parameters on particle dynamics have been extensively studied in Refs. [88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105]. The analysis of the dynamics of test particles with nonzero electric (or/and magnetic) charge may directly lead to understand the nature of the gravitational and electromagnetic field around compact gravitating object.

The work is arranged as follows: in Sect. 2 we start with the consideration of properties of KR gravity around compact objects together with an analysis of particle motion around BH in KR gravity. We analyze the energy extraction from the KR BH in Sect. 3. In Sect. 4, we explore observable BH shadow in KR gravity. In Sect. 5 we analyze the gravitational weak lensing for various plasma distributions around KR BH. The magnification of the image source in the presence of uniform and non-uniform plasma is considered in Sect. 6. Finally, in Sect. 7 we provide the analysis of the main results of the paper. Throughout, we use a system of units in which $G=c=1$. Latin (Greek) indices run from 1 (0) to 3.

2 Particle motion around KR BH

The static spherically symmetric solution of the modified Einstein equations leads to the hairy BH solution [106] with the line element

$$\begin{aligned} ds^2= & {} -\left( 1-\frac{2M}{r}+\frac{\gamma }{r^{2/\lambda }}\right) dt^2 +\frac{1}{\left( 1-\frac{2M}{r}+\frac{\gamma }{r^{2/\lambda }}\right) }dr^2\nonumber \\&+r^2d\theta ^2+r^2\sin ^2\theta d\phi ^2, \end{aligned}$$

(2)

where M is the BH mass, $\gamma$ and $\lambda$ are the spontaneous Lorentz violating parameters related to the vacuum expectation value of the KR field defined in (1) and the nonminimal coupling parameters, viz., $s=|b^2|\xi _2$ with $b^2=b_{\mu \nu }b^{\mu \nu }$. It is worth to note that $\gamma$ has dimensions of $[L]^{2/\lambda }$. The power-law hairy BH (2) encompasses the Schwarzschild solution when $\lambda =0$, Schwarzschild de-Sitter for $\lambda =-1$, and when $\lambda =1$ it resembles the Reissner−Nordström BH.

Now we start to explore the horizon structure of the BH in KR gravity, the motion of massive and massless particles around a BH. Each case is considered separately with details in the subsections below.

2.1 Horizon structure

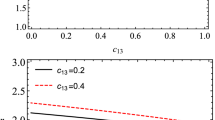
First, we start with the analysis of the horizon structure of the BH in KR gravity with its parameters $\gamma$ and $\lambda$. According to the condition $g_{00}=0$ (or $V_{eff}=0$), we get the expression of horizon orbits (see Fig. 1). It is interesting to mention that the radius of the horizon depends upon the parameters $\gamma$ and $\lambda$ in KR spacetime. Figure 1 shows the horizon orbit comes to the central compact object with the presence of parameters $\lambda$ and $\gamma$ in this gravity field.

Fig. 1

Dependence of the event horizon radius $r_h$ on parameters $\gamma$ and $\lambda$ for BH in KR gravity and we use $M=1$

2.2 Massive particle motion

This subsection studies the motion of test (massive) particle around BH in the KR gravity. To describe particle motion, one can use the Hamilton–Jacobi equation in the following form

$$\begin{aligned} g^{\mu \nu }\frac{\partial S}{\partial x^\mu } \frac{\partial S}{\partial x^\nu }= & {} -m^2, \end{aligned}$$

(3)

where $g^{\mu \nu }$ is the metric tensor of the spacetime (2), m is the mass of a particle and S is action. Using the separation of variable method and symmetry of the spacetime (2), one can express the action S as

$$\begin{aligned} S=\frac{1}{2}m^2\delta -Et+L\varphi +S_r(r)+S_{\theta }(\theta ), \end{aligned}$$

(4)

where E and L are energy and angular momentum of massive particle, respectively. Using Eqs. (3) and (4) one may rewrite the Hamilton–Jacobi equation in the equatorial plane ($\theta =\frac{\pi }{2},\ S_{\theta }( \theta )=const$) in the following form

$$\begin{aligned}&-\left( 1-\frac{2M}{r}+\frac{\gamma }{r^{2/\lambda }}\right) ^{-1}E^2+\frac{L^2}{r^2}\nonumber \\&\quad +\left( 1-\frac{2M}{r}+\frac{\gamma }{r^{2/s}}\right) \left( \frac{\partial {S_r}}{\partial {r}}\right) ^2=-m^2. \end{aligned}$$

(5)

From Eq. (5), one can find $S_r(r)$

$$\begin{aligned} S_r(r)=\displaystyle \int \frac{\sqrt{E^2-\left( \frac{L^2}{r^2}+m^2\right) \left( 1-\frac{2M}{r} +\frac{\gamma }{r^{2/\lambda }}\right) }}{1-\frac{2M}{r}+\frac{\gamma }{r^{2/\lambda }}}dr. \end{aligned}$$

(6)

The equation of motion can be obtained by using the expression ${\partial {S}}/{\partial {L}}=\mathrm{const}.$ and one can write $dr/d\varphi$ in the form as

$$\begin{aligned} \frac{L}{r^2}\frac{dr}{d\varphi }=\sqrt{E^2-\left( \frac{L^2}{r^2}+m^2\right) \left( 1-\frac{2M}{r} +\frac{\gamma }{r^{2/\lambda }}\right) }. \end{aligned}$$

(7)

At the turning point near the the gravitational field the value of ${dr}/{d\varphi }$ becomes zero and $E = V_{eff}(r)$. $V_{eff}(r)$ is the effective potential of radial motion of the particle and can be written as

$$\begin{aligned} V_{eff}(r)={\left( m^2+\frac{L^2}{r^2}\right) \left( 1-\frac{2M}{r} +\frac{\gamma }{r^{2/\lambda }}\right) }. \end{aligned}$$

(8)

Fig. 2

The dependence of effective potential $V_{eff}$ on radial coordinates for different values of $\lambda$ and $\gamma$ for the massive particle

Fig. 3

Radial dependence of L for the different values of parameters $\gamma$ and $\lambda$. Where $M=m=1$

Fig. 4

Radial dependence of E for the different values of parameters $\gamma$ and $\lambda$. Where $M=m=1$

Fig. 5

Relation of $r_{_\mathrm{ISCO}}$ on parameters $\gamma$ and $\lambda$ in KR gravity

Fig. 6

The dependence of effective potential $V_{eff}$ on radial coordinates for different values of $\lambda$ and $\gamma$ for the photon ($m=0$)

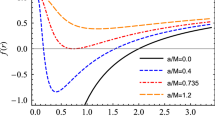
The radial dependence of $V_{eff}(r)$ for various values of the $\lambda$ and $\gamma$ parameters for a massive particle is plotted in Fig. 2. It can be seen from Fig. 2 that with the increase in the value of the parameter $\gamma$, the circular orbits shift toward the central object. A similar effect can be observed with the increasing of the $\lambda$ parameter.

In order to extract more information about the circular orbits, one can study an innermost stable circular orbit (ISCO) using the following conditions

$$\begin{aligned} \frac{dr}{d\phi }=0, \quad V'_{eff}(r)=V''_{eff}(r)=0. \end{aligned}$$

(9)

From the conditions (9), one can find expressions for angular momentum L and energy E of the test particle at circular orbits as

$$\begin{aligned} \frac{L^2}{m^2}= & {} \frac{r^2(M\lambda -\gamma r^{1-2/\lambda })}{\gamma r^{1-2/\lambda }-3M\lambda +r\lambda +\gamma \lambda r^{1-2/\lambda }}, \end{aligned}$$

(10)

$$\begin{aligned} \frac{E^2}{m^2}= & {} \frac{\lambda (-2Mr^{2/\lambda }+r^{1+2/\lambda }+r \gamma )^2}{r^{2/\lambda }(-3Mr^{2/\lambda -1}\lambda +r^{2/\lambda }\lambda +\gamma (1+\lambda ))}. \end{aligned}$$

(11)

The radial dependence of angular momentum and energy for different values of parameters $\gamma$ and $\lambda$ in KR gravity are presented in Figs. 3 and 4. The vertical asymptotes of these graphs correspond to marginally stable circular orbits or photon orbits. From these plots, one can easily see that conservative quantities depend on radial coordinates in different values of KR parameters.

Now one can obtain the dependence of ISCO on the parameters of KR fields using the Eqs. (9)–(11). The graphical representations of numerical results are shown in Fig. 5. From Fig. 5 one may conclude that ISCO comes to central object with increase of $\gamma$ and $\lambda$ for the various values of $\lambda$(bottom panel) and $\gamma$(up panel).

Fig. 7

Dependence of radius of photon $r_{ph}$ on parameters $\gamma$ and $\lambda$ in the KR spacetime

2.3 Massless particle (photon) motion

Now, we consider photon motion around a BH in KR gravity exploring the effective potential $V_{eff}$. For photons ($m=0$) the Eqs. (7) and (8) can be rewritten in the following form

$$\begin{aligned} \frac{L}{r^2}\frac{dr}{d\varphi }= & {} \sqrt{E^2-\frac{L^2}{r^2}\left( 1-\frac{2M}{r}+\frac{\gamma }{r^{2/\lambda }}\right) }, \end{aligned}$$

(12)

$$\begin{aligned} V_{eff}(r)= & {} \frac{L^2}{r^2}\left( 1-\frac{2M}{r}+\frac{\gamma }{r^{2/\lambda }}\right) . \end{aligned}$$

(13)

The radial dependence of effective potential $V_{eff}$ of photon radial motion, the different values of $\gamma$ and $\lambda$ are shown in Fig. 6. From Fig. 6 one may easily see that the pick values of the graph are shifted with the effect of parameters $\gamma$ and $\lambda$, even though we may easily get information about the circular orbits of particles around BH.

The study of circular orbits reflects special interest while considering the photon motion. Photon circular orbits are defined using the conditions

$$\begin{aligned} \frac{dr}{d\phi }=0, \quad V'_{eff}=0. \end{aligned}$$

Using these conditions, one may obtain the equation defining the radius of circular photon orbits in the following form

$$\begin{aligned} 1-\frac{3M}{r}+\left( \frac{1}{\lambda }+1\right) \frac{\gamma }{r^{2/\lambda }}=0. \end{aligned}$$

(14)

The dependence of photon orbit $r_{p}$ on parameters $\gamma$ and $\lambda$ are shown in Fig. 7. One can see from the graph shown in Fig. 7 that with the increase of the $\gamma$ parameter, the photon orbit shifts toward the central compact object. One may observe a similar effect with the trend of the $\lambda$ parameter increase.

The solution of the differential equation (12) defines the photon trajectory and has the form

$$\begin{aligned} \varphi =\int \frac{dr}{r^2\sqrt{\frac{1}{b^2}-\frac{1}{r^2}\left( 1-\frac{2M}{r} +\frac{\gamma }{r^{2/\lambda }}\right) }}, \end{aligned}$$

(15)

where $b={E}/{L}$ is the impact parameter for the photon. In the weak-field approximation, one may take the power series of the expression in ${2M}/{r}-{\gamma }/{r^{2/\lambda }}$ on the right-hand side of Eq. (15). Keeping leading order terms of the expansion may obtain the following expression

$$\begin{aligned} \varphi= & {} \int \frac{bdr}{r\sqrt{r^2-b^2}}-\int \frac{Mb^3dr}{r^2(r^2-b^2)^{3/2}}+\nonumber \\&+\frac{1}{2}\int \frac{\gamma b^3dr}{r^{2/\lambda +1}(r^2-b^2)^{3/2}}=\alpha _1+\alpha _2+\alpha _3. \end{aligned}$$

(16)

The deflection angle can be found using the expression $\Delta \varphi =2\underset{r\rightarrow \infty }{lim}\varphi =\Delta \varphi _1+\Delta \varphi _2+\Delta \varphi _3$. In Eq. (16) $\alpha _1$ corresponds to the motion of a photon along a straight line in flat spacetime and gives the result $\Delta \varphi _1=\pi$. The second term $\alpha _2$ is the deflection angle of the photon in the Schwarzschild spacetime and gives the contribution $|\Delta \varphi _2|=4M/b$. $\alpha _3$ comes due to KR modification and can be expressed as

$$\begin{aligned} \alpha _3= & {} \frac{i\gamma \lambda }{4r^{2/\lambda }}\ _2F_1\left[ \frac{3}{2},-\frac{1}{\lambda },1-\frac{1}{\lambda },\frac{r^2}{b^2}\right] . \end{aligned}$$

(17)

where i is imaginary unit and $_2F_1$ is Hypergeometric function (see Appendix). Particularly, $\Delta \varphi _3={3\gamma \pi }/{4b^2}$ when $\lambda =1$ and $\Delta \varphi _3={8\gamma }/{3b^3}$ when $\lambda ={2}/{3}$.

3 Extracted energy by collisions

Here we explore the particle acceleration process of two charged particles colliding near the horizon of the BH in KR gravity. We study two particles that have rest masses $m_1$ and $m_2$ at a distance far away from BH and we may write equations of motion as

$$\begin{aligned} p^{\mu }= & {} mu^{\mu }\ , \end{aligned}$$

(18)

$$\begin{aligned} u^t= & {} \frac{E}{F(r)}\ , \end{aligned}$$

(19)

where F(r) represents the metric function.

$$\begin{aligned} u^{\phi }= & {} \frac{L}{r^2}\ , \end{aligned}$$

(20)

$$\begin{aligned} u^r= & {} \sqrt{E^2-F(r)\left( 1+\frac{L^2}{r^2}\right) }\ . \end{aligned}$$

(21)

The extracted energy $E_{C.M.}$ by collision between two particles is defined by [88]

$$\begin{aligned} \frac{E_{C.M.}}{2 m_{1} m_{2}}= & {} \dfrac{m^2_1+m^2_2}{2 m_1 m_2}-g_{\mu \nu }u^{\mu }_1 u^{\nu }_2\ , \end{aligned}$$

(22)

with $F(r)=1-\frac{2M}{r}+\frac{\gamma }{r^{2/\lambda }}$, is the lapse function. By using Eqs. (19), (20) and (21), we can rewrite Eq. (22) for the energy extracted as

$$\begin{aligned} \frac{E_{C.M.}}{2 m_1 m_2}= & {} 1+\dfrac{(m_1-m_2)^2}{2 m_1 m_2}+\frac{E_1E_2}{F(r)}-\frac{L_1L_2}{r^2}-\nonumber \\&-\frac{1}{F^2(r)}\sqrt{E^2_1-F(r)\left( 1+\frac{L^2_1}{r^2}\right) }\sqrt{E^2_2-F(r)\left( 1+\frac{L^2_2}{r^2}\right) }\ \nonumber \\ \end{aligned}$$

(23)

In Fig. 8, it can be seen the radial dependence $E_{C.M.}$ energy of BH. From Fig. 8 the minimum energy shows that two particles have opposite angular momentum.

Fig. 8

Center-mass energy for $L_1$, $L_2$ and $\lambda$ different values

4 BH shadow

In this section, we study the shadow of the BH in KR theory. For the angular radius of the BH shadow [72, 107], we have the following relation

$$\begin{aligned} \sin ^2 \alpha _{sh}=\frac{Y(r_{p})^2}{Y(r_{obs})^2}, \end{aligned}$$

(24)

with

$$\begin{aligned} Y(r)^2=\frac{g_{22}}{g_{00}}=\frac{r^2}{F(r)}, \end{aligned}$$

(25)

$\alpha _{sh}$ is the angular radius of the BH shadow and $r_{obs}$ is observe distance and the quantity $r_{p}$ is the radius of the photon sphere as it was mentioned previously.

Now we combine Eqs. (24) and  (25), and for an observer the Eq. (24) takes the following form

$$\begin{aligned} \sin ^2 \alpha _{sh}=\frac{r_{p}^2}{F(r_{p})}\frac{F(r_{obs})}{r^2_{obs}}. \end{aligned}$$

(26)

One can find the radius of the BH shadow for an observer at a large distance [107] by using Eq. (26) as

$$\begin{aligned} R_{sh}\simeq & {} r_{obs} \sin \alpha _{sh} \simeq \frac{r_{p}}{\sqrt{F(r_{p})}}. \end{aligned}$$

(27)

Finally, Eq. (27) can explain the shadow of BH for the non-rotating case. In Fig. 9, we have shown the graphical representation of the shadow radius of BH in KR gravity for different values of involved KR parameters. It is worth noticing that the shadow decreases with the increase in value of both $\lambda$ and $\gamma$. It is evident that the shadows of the BH are smaller as compared to the Schwarzschild BH shadow as depicted by the black solid curves in Fig. 9.

Fig. 9

The radius of KR BH shadow depends on KR parameters $\gamma$ (up panel) and $\lambda$ (down panel). Where $M=1$

5 Deflection angle

This section explores the deflection angle of photons around BH in the weak gravitational field regime. In the weak-field regime, one can express the spacetime metric in the following form

$$\begin{aligned} ds^2= & {} ds{^2_0}+\left( \frac{2M}{r}-\frac{\gamma }{r^{2/\lambda }}\right) (dt^2+dr^2). \end{aligned}$$

(28)

where $ds{^2_0}=-dt^2+dr^2+r^2d\theta ^2+r^2\sin ^2\theta d\phi ^2$ is the Minkowski metric for the flat spacetime. The components of $h_{\alpha \beta }$ can be expressed in the following form

$$\begin{aligned} h_{00}= & {} \frac{2M}{r}-\frac{\gamma }{r^{2/\lambda }},\nonumber \\ h_{ik}= & {} \left( \frac{2M}{r}-\frac{\gamma }{r^{2/\lambda }}\right) {s_i}{s_k},\nonumber \\ h_{33}= & {} \left( \frac{2M}{r}-\frac{\gamma }{r^{2/\lambda }}\right) \cos ^2{\theta }, \end{aligned}$$

(29)

where $s_{i}$ is a unit vector in the direction of the radius-vector $r_{i} =(x_1,x_2,x_3)$, the components of which are equal to directional cosines, the angle $\theta$ is the polar angle between the 3-vector ${r^i}={r_i}$ and the z-axis, and ${s_3}={\cos \theta }=z/r=z/\sqrt{b^2+z^2}$ [49]. Now the expression for deflection angle of light rays around BH can be expressed as [49, 54]

$$\begin{aligned} \alpha _{b}= & {} \frac{1}{2}{\underset{-\infty }{\overset{+\infty }{\int }}}\frac{b}{r}\left[ \frac{\partial {h_{33}}}{\partial {r}} +\left( 1-\frac{\omega _{e}^{2}}{\omega ^{2}}\right) ^{-1}\frac{\partial {h_{00}}}{\partial {r}}\right. \nonumber \\&\left. -\frac{K_{e}}{\omega ^{2}-\omega ^{2}_{e}}\frac{\partial {N}}{\partial {r}}\right] dz, \end{aligned}$$

(30)

where $\omega$ and $\omega _{e}$ are the photon and plasma frequencies, respectively, N is the plasma concentration around the BH.

By using Eqs. (29) and (30) one can get the final expression for the deflection angle around BH as

$$\begin{aligned} \alpha _{b}= & {} \frac{2M}{b}-\frac{\gamma }{2b^{2/\lambda }}\frac{\sqrt{\pi }\Gamma (\frac{1}{2} +\frac{1}{\lambda })}{\Gamma (1+\frac{1}{\lambda })}-\frac{1}{2}{\underset{-\infty }{\overset{+\infty }{\int }}} \left( 1-\frac{\omega _{e}^{2}}{\omega ^{2}}\right) ^{-1}\nonumber \\&\left( -\frac{2Mb}{r^{3}} +\frac{2{\gamma }b}{{\lambda }r^{\frac{2}{\lambda }+2}}\right) dz+\frac{1}{2}{\underset{-\infty }{\overset{+\infty }{\int }}}\frac{b}{r}\frac{K_{e}}{\omega ^{2}-\omega ^{2}_{e}}\frac{\partial {N}}{\partial {r}}dz.\nonumber \\ \end{aligned}$$

(31)

Here $\Gamma (x)$ represents the Gamma function (see Appendix). Now, we test the effect of plasma on the deflection angle of photons around a BH for various plasma density distributions: vacuum, uniform, and non-uniform cases.

Fig. 10

$\alpha _b$ for different value $\lambda$ and $\gamma$ in the vacuum

Fig. 11

The dependence of the deflection angle on the impact parameter b for the different values of parameters $\beta$ and $\lambda$ in KR gravity

5.1 Vacuum case

In this subsection, we investigate deflection angle for a vacuum ($\omega _{e}=0$) case and using Eq. (31) one can rewrite it as

$$\begin{aligned} \alpha _{b}= & {} \frac{4M}{b}-\frac{\gamma \sqrt{\pi }}{b^{2/\lambda }}\left( 1+\frac{\lambda }{2}\right) \frac{\Gamma (\frac{1}{2}+\frac{1}{\lambda })}{\Gamma (\frac{1}{\lambda })}. \end{aligned}$$

(32)

From expression (32) one can consider some special cases. For example, when $\Gamma (1)=1$ and $\gamma =\beta (2M)^2$ (where $\beta$ is small parameter) we get

$$\begin{aligned} \alpha _{b}= & {} \frac{4M}{b}-\left( \frac{2M}{b}\right) ^2\frac{3\beta \pi }{4}, \end{aligned}$$

(33)

and for the values $\lambda =2/3$ and $\gamma =\beta (2M)^3$ one gets

$$\begin{aligned} \alpha _{b}= & {} \frac{4M}{b}-\left( \frac{2M}{b}\right) ^3\frac{8\beta }{3}. \end{aligned}$$

(34)

For imagination, we plot the dependence of the deflection angle on the parameters $\gamma$, $\lambda$ and the impact parameter b in Figs. 10 and 11 according to the Eq. (32). From these graphs, we may get that the deflection angle of light rays decreases with an increase in KR parameters. The above discussion confirms that the photon orbits come closer to the central object.

5.2 Uniform plasma with $\omega _e^2(r)= \text {const}$

Now, we consider the uniform plasma effect on deflection angle and using Eq. (31), it can be found in the following form

$$\begin{aligned} \alpha _{b}=\frac{2M}{b}\frac{2-\frac{\omega ^2_e}{\omega ^2}}{1-\frac{\omega ^2_e}{\omega ^2}} -\frac{\gamma \sqrt{\pi }}{b^{2/\lambda }}\frac{\Gamma (\frac{1}{2} +\frac{1}{\lambda })}{\Gamma (\frac{1}{\lambda })} \frac{1+\frac{\lambda }{2}-\frac{\omega ^2_e}{\omega ^2}}{1-\frac{\omega ^2_e}{\omega ^2}}. \end{aligned}$$

(35)

Fig. 12

$\alpha _b$ for different value $\omega ^2_e/\omega ^2$, $\beta$ and $\lambda$ in the uniform plasma

Fig. 13

$\alpha _b$ for different value $\omega ^2_e/\omega ^2, \beta$ and b in the uniform plasma, $\lambda =1$ case

Now, we test special case when $\lambda =1$ and $\gamma =\beta (2M)^2$ (where $\beta$ is small parameter). In this case Eq. (35) takes the form

$$\begin{aligned} \alpha _{b}=\frac{2M}{b}\frac{2-{\omega ^2_e}/{\omega ^2}}{1-{\omega ^2_e}/{\omega ^2}} -\frac{\beta \pi }{4}\left( \frac{2M}{b}\right) ^2\frac{3-{\omega ^2_e}/{\omega ^2}}{1-{\omega ^2_e}/{\omega ^2}}. \end{aligned}$$

(36)

For the case when $\lambda =2/3$ and $\gamma =\beta (2M)^3$ (with $\beta$ being a small parameter), Eq. (35) takes the form

$$\begin{aligned} \alpha _{b}=\frac{2M}{b}\frac{2-{\omega ^2_e}/{\omega ^2}}{1-{\omega ^2_e}/{\omega ^2}} -{2\beta }\left( \frac{2M}{b}\right) ^3\frac{{4}/{3} -{\omega ^2_e}/{\omega ^2}}{1-{\omega ^2_e}/{\omega ^2}}. \end{aligned}$$

(37)

Fig. 14

$\alpha _b$ for different value $\omega ^2_e/\omega ^2, \beta$ and b in the uniform plasma, $\lambda =2/3$ case

Using Eq. (35) we have generated the Figs. 12, 13 and 14 representing the dependence of deflection angle of light rays around a compact object on the parameters $\lambda$, $\gamma$, b in KR gravity and uniform plasma. In Figs. 12, 13 and 14 we performed the analysis for the different values of parameters of KR spacetime. Moreover, we have considered the effect of uniform plasma for the various values of parameters $\lambda$ and $\gamma$. It can be seen from Figs. 12, 13 and 14 that the effect of plasma on the deflection angle increases. The formation of these graphs can be explained by an increase in the parameters of the KR, and the angle of deflection of the light rays decreases.

5.3 Singular isothermal sphere

We explore a non-uniform plasma medium on deflection angle using a singular isothermal sphere (SIS) [49] model for plasma. SIS model is often used in the lens models of galaxies and clusters of galaxies [34]. The density distribution is written as [34, 49]

$$\begin{aligned} \rho (r)=\frac{\sigma ^2_\nu }{2{\pi }m_pr^2}\ , \end{aligned}$$

(38)

where $\sigma ^2_\nu$ is a one-dimensional velocity dispersion (for galaxies in clusters of galaxies). One can now easily get the dependence of plasma frequency and photon frequency as

$$\begin{aligned} \frac{\omega ^2_e}{\omega ^2}=\frac{K_eN(r)}{\omega ^2}=\frac{a^2}{r^2},\,a^2=\frac{2e^2\sigma ^2_\nu }{\omega ^2k^2m_pm_e}. \end{aligned}$$

(39)

From the Eq. (39) one can find expression of deflection angle of photon around BH using Eq. (31) in the following form

$$\begin{aligned} \alpha _{b}= & {} \frac{2M}{b}\left( 1+\frac{\arcsin {\eta }}{\eta \sqrt{1-\eta ^2}}\right) -\frac{\gamma \sqrt{\pi }}{2b^{2/\lambda }}\frac{\Gamma (\frac{1}{2} +\frac{1}{\lambda })}{\Gamma (1+\frac{1}{\lambda })}\nonumber \\&-\frac{\gamma }{\lambda b^{\frac{2}{\lambda }}} \frac{\sqrt{\pi }\Gamma (-\frac{1}{2}+\frac{1}{\lambda })_2F_1(\frac{1}{2},1,\frac{3}{2} -\frac{1}{\lambda },\frac{1}{1-\eta ^2})}{(1-\eta ^2)\Gamma (\frac{1}{\lambda })}\nonumber \\&-\frac{\gamma }{\lambda b^{\frac{2}{\lambda }}} \left( -\frac{1}{\eta ^2}\right) ^{\frac{1}{\lambda }} \frac{\pi }{\sqrt{1-\eta ^2}\cos {\frac{2\pi }{\lambda }}}\nonumber \\&-\frac{\pi \eta ^2}{1-\eta ^2-\sqrt{1-\eta ^2}}\ . \end{aligned}$$

(40)

Here $\eta =a/b$. The presence of the expression $\left( -{1}/{\eta ^2}\right) ^{{1}/{\lambda }}$ in Eq. (40) requires that certain conditions to be imposed on $\lambda$. Therefore, it does not make sense to look at the case $\lambda =2/3$. This may be caused due to approximation used in calculations or the absence of such a field in the form we are looking at. For the $\lambda =1$ and $\gamma =\beta (2M)^2$ (where $\beta$ is small parameter) we get

$$\begin{aligned} \alpha _{b}= & {} \frac{2M}{b}\left( 1+\frac{\arcsin {\eta }}{\eta \sqrt{1-\eta ^2}}\right) \nonumber \\&-\left( \frac{2M}{b}\right) ^2\frac{\beta \pi }{4}\left( 1-\frac{4}{\eta ^2}+\frac{4}{\eta ^2\sqrt{1-\eta ^2}}\right) \nonumber \\&-\frac{\pi \eta ^2}{1-\eta ^2-\sqrt{1-\eta ^2}}. \end{aligned}$$

(41)

Fig. 15

$\alpha _b$ for different value a, b and $\beta$ in the singular isothermal sphere, $\lambda =1$ case

Using Eq. (41) in the weak lensing approximation, one can get plots of dependence of deflection angle on impact parameter and KR parameters for different values of non-uniform plasma can be seen in Fig. 15. The influence of a non-uniform plasma on the deflection angle is shown, which increases with an increase in the plasma deflection angle and vice versa for the KR parameters.

5.4 Non-singular isothermal sphere

Consider a gravitational lens model of a non-singular isothermal sphere (NSIS) model for non-uniform plasma medium [49], which is defined as

$$\begin{aligned} \rho (r)=\frac{\sigma ^2_\nu }{2\pi r^2_c}\frac{1}{1+\frac{r^2}{r^2_c}},\,\frac{\omega ^2_e}{\omega ^2} =\frac{K_eN(r)}{\omega ^2}=\frac{\frac{a^2}{r^2_c}}{1+\frac{r^2}{r^2_c}}, \end{aligned}$$

(42)

where $r_c$ is the core radius, a is constant in the distance scale of the form

$$\begin{aligned} a^2=\frac{2e^2\sigma ^2_\nu }{\omega ^2k^2m_pm_e}\ . \end{aligned}$$

(43)

Form Eqs. (31) and (42) one may get expression of deflection angle in NSIS medium as

$$\begin{aligned} \alpha _{b}= & {} \frac{2M}{b}\left( 1+\frac{\arcsin {\sqrt{A}}}{C\sqrt{A}\sqrt{1-A}}+1-\frac{1}{C}\right) \nonumber \\&-\frac{\gamma \sqrt{\pi }}{2b^{\frac{2}{\lambda }}}\frac{\Gamma (\frac{1}{2} +\frac{1}{\lambda })}{\Gamma (1+\frac{1}{\lambda })}+I_1\nonumber \\&-\frac{\pi }{\sqrt{1-A}}+\frac{\pi }{\sqrt{1-A+\frac{A}{C}}}, \end{aligned}$$

(44)

where $A={a^2}/{b^2}-{r_c^2}/{b^2}$ and $C=1-{r_c^2}/{a^2}$, $I_1$ is in the appendix. When $\lambda =1$ and $\gamma =\beta (2M)^2$ (where $\beta$ is small parameter) we get

$$\begin{aligned} \alpha _{b}= & {} \frac{2M}{b}\Big [2-\frac{1}{C}+\frac{\arcsin {\sqrt{A}}}{C\sqrt{A}\sqrt{1-A}}\Big ]\nonumber \\&-\left( \frac{2M}{b}\right) ^2\frac{\beta \pi }{4}\Big [1-\frac{1}{AC}+\frac{1}{AC\sqrt{1-A}}-\frac{2C}{1-C}\Big ]\nonumber \\&-\frac{\pi }{\sqrt{1-A}}+\frac{\pi }{\sqrt{1-A+\frac{A}{C}}}\nonumber \\ \end{aligned}$$

(45)

Fig. 16

$\alpha _b$ for different value $a,b, r_c$ and $\beta$ in the non-singular isothermal sphere uniform plasma, $\lambda =1$ case

Using the expression for the deflection angle, we construct the dependence of the deflection angle of light rays around a BH in non-uniform plasma on the impact parameter b and the parameters $\lambda$, $\gamma$ in the KR gravity. This dependence is shown in Fig. 16. It can be seen that different values of parameters of KR gravity affect the deflection angle in the presence of non-uniform plasma.

5.5 Non uniform plasma

In this subsection, we consider another special case of plasma distribution defined as

$$\begin{aligned} \omega ^2_e=\frac{Z_0}{r},\quad \frac{\omega ^2_e}{\omega ^2}=\frac{Z_0}{\omega ^2r}=\frac{d}{r}\ . \end{aligned}$$

(46)

Using the condition $\frac{\omega ^2_e}{\omega ^2}<<1$ one may generate the following approximate expression

$$\begin{aligned} \left( 1-\frac{\omega ^2_e}{\omega ^2}\right) ^{-1}\approx {1+\frac{\omega ^2_e}{\omega ^2}}=1+\frac{d}{r}. \end{aligned}$$

(47)

For the deflection angle we get the following expression

$$\begin{aligned} \alpha _{b}= & {} \frac{4M}{b}-\frac{\gamma \sqrt{\pi }(\lambda +2)}{2b^{\frac{2}{\lambda }}} \frac{\Gamma (\frac{1}{2}+\frac{1}{\lambda })}{\Gamma (\frac{1}{\lambda })}\nonumber \\&+\frac{\gamma d \sqrt{\pi }}{\lambda b^{\frac{2}{\lambda }+1}}\frac{\Gamma (1+\frac{1}{\lambda })}{\Gamma (\frac{3}{2} +\frac{1}{\lambda })}+\frac{dM\pi }{2b^2}-\frac{d}{2b}-\frac{\pi }{4}\left( \dfrac{d}{b}\right) ^2.\quad \end{aligned}$$

(48)

When $\lambda =1$ and $\gamma =\beta (2M)^2$ (where $\beta$ is small parameter) one may get

$$\begin{aligned} \alpha _{b}= & {} \frac{4M}{b}-\left( \frac{2M}{b}\right) ^2\left( \frac{3\beta \pi }{4}-\frac{4d\beta }{3b}\right) \nonumber \\&+\frac{dM\pi }{2b^2}-\frac{d}{2b}-\frac{\pi }{4}\left( \dfrac{d}{b}\right) ^2. \end{aligned}$$

(49)

When $\lambda =2/3$ and $\gamma =\beta (2M)^3$ (where $\beta$ is small parameter) we get

$$\begin{aligned} \alpha _{b}= & {} \frac{4M}{b}-\left( \frac{2M}{b}\right) ^3\left( \frac{8\beta }{3}-\frac{9d\pi \beta }{16b}\right) \nonumber \\&+\frac{dM\pi }{2b^2}-\frac{d}{2b}-\frac{\pi }{4}\left( \dfrac{d}{b}\right) ^2. \end{aligned}$$

(50)

The dependence of deflection angle on parameters of KR spacetime with non-uniform plasma is presented in Figs. 17, 18, and 19. From this dependence, we may get that deflection angle increases in the presence of a non-uniform plasma medium and vice versa for the parameters in KR theory.

Fig. 17

$\alpha _b$ for different value d in the non uniform plasma ($M=1, b=4$)

Fig. 18

$\alpha _b$ for different value b, d and $\beta$ in the non uniform plasma, $\lambda =1$ case

6 Magnification

Here we study the brightness of the image in the presence of plasma through the deflection angle of light rays around BH in KR theory. Using the lens equation, we can write combination of light angles around BH in KR gravity (${\hat{\alpha }}$, $\theta$ and $\sigma$) [51, 54] as

$$\begin{aligned} \theta D_\mathrm {s}=\sigma D_\mathrm {s}+{\hat{\alpha }}D_\mathrm {ds}, \end{aligned}$$

(51)

where $D_\mathrm {s}$, $D_\mathrm {d}$ and $D_\mathrm {ds}$ are the distances from the source to the observer, from the lens to the observer, and from the source to the lens, respectively, and $\theta$ and $\sigma$ refer to the angular position of the image and the source. Now, from the above equation, we can rewrite the equation for $\beta$ as following

$$\begin{aligned} \sigma =\theta -\frac{D_\mathrm {ds}}{D_\mathrm {s}}\frac{\xi (\theta )}{D_\mathrm {d}}\frac{1}{\theta }, \end{aligned}$$

(52)

where $\xi (\theta )=|{\hat{\alpha }}_b|b$ and $b=D_\mathrm {d}\theta$ have been used in [54]. If the shape of the image looks like a ring, it is defined as Einstein’s ring and the radius of Einstein’s ring is $R_s=D_\mathrm {d}\theta _E$. The angular $\theta _E$ due to spacetime geometry between the images of the source in a vacuum [34] can be written as

$$\begin{aligned} \theta _E=\sqrt{2R_s\frac{D_{ds}}{D_dD_s}}\ . \end{aligned}$$

(53)

Now, we explore expression of the magnification of brightness [34]

$$\begin{aligned} \mu _{\Sigma }=\frac{I_\mathrm {tot}}{I_*}=\underset{k}{\sum }\bigg |\bigg (\frac{\theta _k}{\sigma }\bigg ) \bigg (\frac{d\theta _k}{d\sigma }\bigg )\bigg |, \quad k=1,2, \ldots , j\ , \end{aligned}$$

(54)

where $I_*$ and $I_\mathrm {tot}$ are the unlensed brightness of the source and the total brightness of all images, respectively. The expressions of the magnification of the source are written in the following form [34]

$$\begin{aligned} \mu _+^{pl}=\frac{1}{4}\left( \frac{x}{\sqrt{x^2+4}}+\frac{\sqrt{x^2+4}}{x}+2\right) , \end{aligned}$$

(55)

$$\begin{aligned} \mu _-^{pl}=\frac{1}{4}\left( \frac{x}{\sqrt{x^2+4}}+\frac{\sqrt{x^2+4}}{x}-2\right) , \end{aligned}$$

(56)

where $x={\sigma }/{\theta ^{\mathrm {pl}}}$ is a dimensionless quantity [54] and $\mu _{+}^{\mathrm {pl}}$ and $\mu _{-}^{\mathrm {pl}}$ are the images. Using Eqs. (55) and (56) one can get formula for the total magnification in the following form

$$\begin{aligned} \mu ^\mathrm {pl}_\mathrm {tot}=\mu ^\mathrm {pl}_{+}+\mu ^\mathrm {pl}_{-}=\frac{x^2+2}{x\sqrt{x^2+4}}. \end{aligned}$$

(57)

Fig. 19

$\alpha _b$ for different value b, d and $\beta$ in the non uniform plasma, $\lambda =2/3$ case

Using Eqs. (35) and $x={\xi }/{\theta ^{\mathrm {pl}}}$ one can find expression

$$\begin{aligned} \frac{x_o}{x}=\frac{\theta _{uni}^{pl}}{\theta _0}=\sqrt{\frac{1}{2} \left( \frac{1-\frac{4f}{\lambda +2}}{1-f} +\frac{1-\frac{2f\lambda }{\lambda +2}}{1-f}\frac{1}{1-\frac{\omega ^2_e}{\omega ^2}}\right) }, \end{aligned}$$

(58)

where $x_0={\sigma }/{\theta _{0}}$ and

$$\begin{aligned} f=\frac{\gamma \lambda \sqrt{\pi }}{8Mb^{2/\lambda -1}}\left( \frac{2}{\lambda }+1\right) \frac{\Gamma (\frac{1}{2}+\frac{1}{\lambda })}{\Gamma (\frac{1}{\lambda })}. \end{aligned}$$

(59)

For the special case when $\lambda =1$ we get

$$\begin{aligned} \frac{\theta _{uni}^{pl}}{\theta _0}=\sqrt{\frac{1}{2}\left( \frac{1-\frac{4\delta _1}{3}}{1-\delta _1} +\frac{1-\frac{2\delta _1}{3}}{1-\delta _1}\frac{1}{1-\frac{\omega ^2_e}{\omega ^2}}\right) }, \end{aligned}$$

(60)

where $\delta _1=f|_{\lambda =1}=\frac{3\pi \gamma }{16Mb}$.

When $\lambda =2/3$ we get

$$\begin{aligned} \frac{\theta _{uni}^{pl}}{\theta _0}=\sqrt{\frac{1}{2}\left( \frac{1-\frac{3\delta _2}{2}}{1-\delta _2} +\frac{1-\frac{\delta _2}{2}}{1-\delta _2}\frac{1}{1-\frac{\omega ^2_e}{\omega ^2}}\right) }, \end{aligned}$$

(61)

where $\delta _2=f|_{\lambda =2/3}=\frac{2\gamma }{3Mb^2}$

Fig. 20

Magnification for $\lambda =1$ and $\lambda =2/3$ in uniform plazma

The dependence of total magnification on plasma parameter is shown in Fig. 20. From Fig. 20 one may see that with the increase of plasma parameter, the magnification is decreasing. Fig. 20 also shows the dependence of total magnification on $x_{0}$ in the presence of plasma for the fixed values of the parameters $\lambda$ and $\gamma$.

7 Conclusions

In this paper, we have studied the optical and energy processes around the BH RK for mass and massless particles, and from this work, we can indicate the following conclusions:

• We have studied the structure of the horizon of BH in the KR theory. It can be seen from the obtained results that with the increase of the parameters $\gamma$ and $\lambda$ radius of the event horizon is decreased, as represented in Fig. 1.

• For particle (mass and massless) motion around BH, we have analysed the dependence of effective potential $V_{eff}$ on radial coordinates for different values of the parameters $\gamma$ and $\lambda$ in KR gravity.

• ISCO is considered for the massive particles around BH in KR theory with its parameters $\gamma$ and $\lambda$. It is analysed that the increase of both parameters, $\gamma$ and $\lambda$ radius of ISCO is decreased as shown in Fig. 5.

• Radius of photon sphere is demonstrated around BH in KR spacetime metric. Orbits of photons are calculated using the general method based on the study of the effective potential and represented with more details in Fig. 7.

• Additional, we have studied the mass-energy around BH with nonvanishing KR parameters $\gamma$ and $\lambda$. We analysed it for different values of the angular momentum and KR parameters of two particles and made plot the dependence of the energy of the centre of mass on the radial coordinate. Further, we have studied the shadow cast by the BH in KR gravity and have noticed the role of the model parameters $\gamma$ and $\lambda$ on the shadow of the BH. It can be observed that with the increasing values of parameters $\gamma$ and $\lambda$ the radius of the shadow of the BH decreases and it can be confirmed from Fig. 9.

• Optical properties around the BH in KR gravity through light rays or photon motion that is weak gravitational lensing. We study the deflection angle of light rays around BH in KR gravity in the presence of plasma (different distributions: uniform and non-uniform cases). In this part of our work, we have analysed and obtained the effect of the uniform and several types of non-uniform plasma on the deflection angle for different parameters of BH in KR gravity.

• Magnification of image is considered using deflection angle of light rays around BH and it is shown with more details in Fig. 20.

Current resolutions of the observational data on the shadow of supermassive black holes at the center of our Galaxy SgrA* and elliptic galaxy M87 [3, 4] do not allow us to use them to get proper constraints on the parameters of modified gravity theories including the KR model. However, we hope that future improvements of the EHT collaboration including more radio telescopes around the globe will allow us to get more precise constraints and develop new tests of the gravity theories. On the other hand, the inclusion of more parameters into the spacetime metric may cause the degeneracy problem of the effects due to those parameters. Consequently, one parameter may mimic the effect of another parameter. However, developing independent tests of the spacetime metric using photon motion, lensing, the shadow of BH, particle motion, energetic processes and etc. One may exclude the degeneracy issues.

Appendix

The Gamma function is as follows

$$\begin{aligned} \Gamma (x)= & {} {\underset{0}{\overset{+\infty }{\int }}}t^{x-1}e^{-t}dt \end{aligned}$$

(62)

$_2F_1$-is $Hypergeometric_2F_1$ function, it is equal to case series

$$\begin{aligned} \displaystyle _{2}F_{1}(a,b;c;z)= & {} \sum _{n=0}^{\infty }{\frac{(a)_{n}(b)_{n}}{(c)_{n}}}{\frac{z^{n}}{n!}}\nonumber \\= & {} 1+{\frac{ab}{c}}{\frac{z}{1!}}+{\frac{a(a+1)b(b+1)}{c(c+1)}}{\frac{z^{2}}{2!}}+\cdots . \nonumber \\ \end{aligned}$$

(63)

and it solution is following differential equation

$$\begin{aligned} z(1-z)\frac{d^{2}u}{dz^2}+[c-(a+b+1)z]\frac{du}{dz}-abu=0. \end{aligned}$$

(64)

Where a, b, c- is complex constants.

$$\begin{aligned} I_1= & {} -\frac{\gamma }{\lambda b^{2/\lambda }}\frac{\sqrt{\pi }}{2A}\Bigg [\frac{\Gamma (-\frac{1}{2} +\frac{1}{\lambda })}{(1-A)\Gamma (\frac{1}{\lambda })}\nonumber \\&\times \Big (2(1-A)(\lambda -1)_2F_1\Big (-\frac{1}{2},1,\frac{3}{2}-\frac{1}{\lambda },\frac{1}{1-A}\Big )\nonumber \\&+2AC(\lambda -2)_2F_1\Big (\frac{1}{2},1,\frac{1}{2}-\frac{1}{\lambda },\frac{1}{1-A}\Big )\nonumber \\&+(2-A)(\lambda -2)_2F_1\Big (\frac{1}{2},1,\frac{3}{2}-\frac{1}{\lambda },\frac{1}{1-A}\Big )\Big )\nonumber \\&-\frac{r_c^2}{b^2}\frac{2\sqrt{\pi }}{\sqrt{1-A}A^{\frac{1}{\lambda }} \cos {\frac{\pi }{\lambda }}}\Bigg ] \end{aligned}$$

(65)