1 Introduction

Black hole physics has received a remarkable interest from many years. This physics has become primordial to understand quantum gravity models. The associated contributions have been supported by the gravitational wave detections and the black hole imaging provided by Event Horizon Telescope international collaborations [1,2,3]. Concretely, many works have been elaborated dealing with the thermodynamic and the optical aspects of such fascinating objets. Interpreting the pressure as a cosmological constant in Anti-de Sitter (AdS) geometries, the black hole thermodynamic has taken a central place in gravity model investigations. This provides new developments in such a physics by unveiling data on certain transitions shearing similarities with Van der Waals fluids. Precisely, the Hawking-Page transition has been examined for four and higher dimensional gravity theories [4,5,6]. Precisely, it has been revealed that such a transition generates certain universalities [7, 8]. Moreover, the optical aspect has been approached by investigating the deflection angle of the light rays and the shadow behaviors [9,10,11,12,13,14,15,16,17,18,19,20,21]. In four dimensions, the black hole shadows of various black holes have been engineered using one dimensional real curves [22,23,24,25]. In particular, the visualization of the shadow casts are obtained from the null geodesic equations. This finding has been supported by the study of geometrical observables showing information about the involved size and the shape of such closed real curves. For non-rotating black holes, it has been revealed that the black hole shadows exhibit circular geometric configurations. It has been remarked that the associated size can be controlled by internal and external moduli spaces including the dark field sector [10]. The circular geometric manifestation can be distorted by introducing the rotating parameter which generates non-trivial geometries involving either D or cardioid shapes [22, 23, 25,26,27,28]. The latter has been appeared in the study of AdS black holes obtained from type superstrings and M-theory scenarios using brane physics [27, 29]. Certain distorted geometrical behaviors have been observed for rotating stringy solutions exhibiting cardioid shapes by varying the brane number.

Most recently, the pulsar SGR J174-2900 near supermassive black holes SgrA* has been investigated providing physical aspects of the involved horizon and the horizonless of events [30, 31]. The relation between the thermodynamical volume aspect and the black hole entropy, including the associated area, has been investigated by the help of the Reverse Isoperimetric Inequality [32]. Concretely, the black holes in the (AdS) spacetime provide interesting results. For generic values of the cosmological constant \(\Lambda \), the domain of outer communication is bounded by a cosmological horizon. This has been considered as a relevant relation which has been exploited to link the optical proprieties of the black hole with the associated spacetime. A special interest has been devoted to four dimensional superentropic black holes being a fascinate solution with non compact horizon topologies with exceeding maximum bound entropies [32,33,34].

Up to certain limits, the superentropic black holes have been investigated by using an ultra-spinning limit of the Kerr–Newman–AdS solutions [35,36,37]. The associated optical and thermodynamic aspects have been studied. Precisely, the thermodynamic behaviors of such black holes have been examined by exploiting ultra-spinning approximation limits [38, 39]. Concerning the optical aspect, the four dimensional shadows have been studied using the Hamilton–Jacobi formalism [22]. Among others, it has been found many geometrical configurations including ellipse shaped and naked singularity behaviors.

Motivated by various activities including the optical properties in higher dimensional supergravity models [9, 33], the AdS space could open many interesting roads since it opens windows associated with the gauge-gravity duality in string theory and related topics. Among others, it has been remarked that the involved size parameter \(\ell \) has been liked to the mass parameter of the superentropic black hole and its charge Q. In this way, the mass behaves differently. This could bring different optical behaviors compared to the trivial black hole solutions. Moreover, the intrinsic symmetries of the associated metric gives a complete integrability of the geodesic motion including the separation of the Hamilton–Jacobi equations. Constrains on such black holes could make contact with current or future observations given by EHT collaborations. The aim of this work is to investigate the shadows of the superentropic black holes in arbitrary dimensions. We obtain the corresponding null geodesic equations of motion using the Hamilton–Jacobi scenarios. Exploiting a spheric stereographic projection, we approach the shadows in terms of one-dimensional real curves. Fixing the mass parameter, we find certain shadow shapes being remarkably different than four dimensional geometric configurations. We then examine theirs behaviors by varying the black hole mass parameter. Concretely, we reveal that the shadows undergo transitions depending on the spacetime dimension. Varying the mass with respect to a critical value \(m_c\), we show that the four dimensional shadows exhibit three configurations being the D-shape, the cardioid and the naked singularity associated with \(m>m_c\), \(m=m_c\) and \(m<m_c\), respectively. Precisely, we observe that the D-shape passes to the naked singularity via the cardioid critical curve. In higher dimensions, however, we reveal that such behaviors are removed.

This paper is organized as follows. In Sect. 2, we present a concise review on superentropic black holes in higher dimensions. In Sect. 3, we investigate the shadow behaviors in arbitrary dimensions. In Sect. 4, we reconsider the study of four dimensions by showing a possible geometric transitions in shadow behaviors. In Sect. 5, we provide a study for dimensions more than four. The last section is devoted to concluding discussions.

2 Superentropic black holes in higher dimensions

We start by exposing a concise review on higher dimensional superentropic neutral black hole solutions. Certain physical aspects of these solutions have been dealt with in arbitrary dimensions [36]. They could be considered as new solutions to the Einstein–Maxwell equations being supported by supergravity models relying on extra dimensions. In particular, we consider single rotating black hole solutions. Following [36, 38], the associated metric line element corresponding to a d dimensional spacetime reads as

$$\begin{aligned} ds^{2}= & {} -\frac{\Delta }{\rho ^2} \left( dt - {\ell } \sin ^2\theta d\phi \right) ^2 +\rho ^2 \left( \frac{dr^2}{\Delta } +\frac{d\theta ^2}{\sin ^2\theta } \right) \nonumber \\&+ \frac{ \sin ^4\theta }{\rho ^2} \left( \ell dt -{(r^2+\ell ^2)}d\phi \right) ^2+ r^2\cos ^2\theta d\Omega ^2_{d-4},\nonumber \\ \end{aligned}$$
(2.1)

where \(\ell \) is a length parameter linked to the cosmological constant. \(\Delta \) and \(\rho ^2\) are relevant functions taking the following form

$$\begin{aligned} \rho ^2=r^2+\ell ^2\cos ^2\theta ,\quad \Delta =\left( \ell +\frac{r^2}{\ell }\right) ^2-2mr^{5-d}, \end{aligned}$$
(2.2)

where m is the mass parameter. \(d\Omega ^2_{d-4}\) denotes the line element of the \((d-4)\)-dimensional unit sphere. To obtain a compact black hole object, one should introduce a new chemical potential K in order to consider a periodic direction \(\phi \) as follows \(\phi \sim \phi + \alpha \), where \(\alpha \) is a dimensionless parameter [35, 36, 38]. A close inspection shows that the existence of the black hole horizon depends on the spacetime dimension d as well as on the involved moduli space. In \(d=4\), for instance, the horizon existence generates a constraint between the black hole parameters including m and \(\ell \). It is given by

$$\begin{aligned} m\geqslant \frac{8}{3\sqrt{3}}\ell , \end{aligned}$$
(2.3)

where the critical mass parameter

$$\begin{aligned} m_c= \frac{8}{3\sqrt{3}}\ell , \end{aligned}$$
(2.4)

will be involved in the discussion of the shadow behaviors of such black holes. For \(d\geqslant 5\), however, the above constraint reduces to a simple one provided by \(m>0\). Having elaborated the essential backgrounds, we move to investigate the superentropic neutral black hole shadow behaviors in higher dimensions. Varying the mass parameter, we will show that the shadow geometries undergo certain geometric transitions. This could be interpreted as possible transitions in the optical aspect going beyond to the ones observed in thermodynamics. This feature could be illustrated in terms of one dimensional real curves embedded in a two-dimensional plane supported by the above metric form.

3 Shadows in arbitrary dimensions

Motivated by string theory and related supergravity models, we would like to study the shadow behaviors of superentropic neutral black holes in arbitrary dimensions. Before elaborating shadow geometries in arbitrary dimensions, we establish first the null geodesic equations of motion. Employing the Hamilton–Jacobi formalism, we write down the equations of the photons near the superentropic black hole horizons. Following [40], certain relations are needed. Indeed, one has

$$\begin{aligned} 0= & {} \frac{\partial S}{\partial \tau }+\frac{1}{2}g^{\mu \nu }\frac{\partial S}{\partial x^\mu }\frac{\partial S}{\partial x^\nu } \end{aligned}$$
(3.1)

where \(\tau \) is an affine parameter along the geodesics. The action S is proposed to take the following form

$$\begin{aligned} S= & {} -Et+L_\phi \phi +S_r(r)+S_{\theta }(\theta )+\sum _{i=1}^{d-4}S_{\psi _i}(\psi _{i}) \end{aligned}$$
(3.2)

where one has used \(E=-p_t\) and \(L=p_\phi \) being the total energy and the angular momentum of the photons, respectively. In this regards, \(S_r(r)\), \(S_{\theta }(\theta )\) and \(S_{\psi _{i}}(\psi _{i})\) represent functions depending on r, \(\theta \) and \(\psi _{i}\) variables, respectively. It is worth noting that the variables \(\psi _{i}\) and the functions \(S_{\psi _{i}}(\psi _{i})\) are associated with the extra dimensions. Sending these extra dimensional functions to zero, we recover the expressions of the four dimensional action reported in [22]. Using the separation method and the Carter constant, we can get the complete null geodesic equations. Precisely, they are given by

$$\begin{aligned} \rho ^2 \frac{d \, t}{d \tau }&= E \left[ \frac{\lambda \left( r^2 +\ell ^2 \right) }{\Delta } + \frac{ \ell \left( \xi - \ell \sin ^2 \theta \right) }{ \sin ^2\theta } \right] , \end{aligned}$$
(3.3)
$$\begin{aligned} \rho ^2 \frac{d \, r}{d \tau }&=\sqrt{{\mathcal {R}}(r}), \end{aligned}$$
(3.4)
$$\begin{aligned} \rho ^2\frac{d \, \theta }{d \tau }&=\sqrt{\Theta (\theta )} \end{aligned}$$
(3.5)
$$\begin{aligned} \rho ^2 \frac{d \, \phi }{d \tau }&= E \left[ \frac{\lambda \;\ell }{\Delta } + \frac{ \xi -\ell \sin ^2 \theta }{\sin ^4 \theta } \right] , \end{aligned}$$
(3.6)
$$\begin{aligned} \rho ^2\frac{d \, \psi _i}{d \tau }&=\sqrt{\Psi _i(\psi _i)}, \qquad i=1,\ldots ,d-4 \end{aligned}$$
(3.7)

where one has used \(\lambda = \left( r^2 +\ell ^2 \right) - \ell \xi \). The quantities \(\xi =\frac{L_{\phi }}{E}\) and \(\eta =\frac{{\mathcal {K}}}{E^2}\), representing the impact parameters, have been introduced in such equations. \({\mathcal {K}}\) is a separable constant [10, 40]. The computation shows that \({\mathcal {R}}(r)\), \(\Theta (\theta )\), and the extra dimension functions \(\Psi _i(\psi _i)\) take the following forms

$$\begin{aligned} {\mathcal {R}}(r)= & {} E^2\left[ \lambda ^2- \Delta \left( {(\ell -\xi )^2}+\eta \right) \right] , \end{aligned}$$
(3.8)
$$\begin{aligned} \Theta (\theta )= & {} E^2 \left[ \eta \sin ^2\theta - \xi ^2\cos ^2\theta \left( \cot ^2\theta -2\left( \frac{\ell }{\xi }-1\right) \right) \right] , \nonumber \\ \end{aligned}$$
(3.9)
$$\begin{aligned} \Psi _i(\psi _{i})= & {} E^2\left[ 2\eta \rho ^2\sum _{k=1}^i r^2\cos ^2\theta \prod _{j=1}^{k-1}\sin ^2\psi _j \right] . \end{aligned}$$
(3.10)

At this level, it is interesting to comment these equations. Taking \(\psi _{i}=0\), we recover the four dimensional geodesic equations reported in [22]. The functions \(\Psi _i(\psi _{i})\) and \(\Delta \) share data on the shadow behaviors in higher dimensions. The radial and the polar contributions in \(\Psi _i\) could be understood in terms of the fibration properties used in the compactification scenarios of higher dimensional supergravity models including superstrings, M-theory, and related topics. This means that four dimensional models could be considered as a base space where the (\(d-4\))-dimensional real sphere moves on it. Roughly, the unstable circular of the photons around the black hole horizon can be obtained by solving the following equations

$$\begin{aligned} {\mathcal {R}}(r)\Big |_{r=r_s}=\frac{d\, {\mathcal {R}}(r)}{d r}\Big |_{r=r_s}=0, \end{aligned}$$
(3.11)

where \(r_s\) is the circular orbit radius of the photon [10, 24,25,26]. The computations provide

$$\begin{aligned}&\eta =\frac{r^2 \left( 16 \ell ^2 \Delta -\csc ^2\theta \left( 4 \Delta -r \Delta ^{\prime }\right) ^2\right) }{\ell ^2{ \Delta ^{\prime }}^2}\bigg \vert _{r=r_s}, \end{aligned}$$
(3.12)
$$\begin{aligned}&\xi =\frac{\left( r^2+ \ell ^2\right) \Delta ^\prime -4r \Delta }{\ell \Delta ^\prime } \bigg \vert _{r=r_s}. \end{aligned}$$
(3.13)

Fixing the observer distance \(r_{ob}\), we can find the shadow behaviors in the domain of outer communications \((\Delta >0)\) [23,24,25]. In this way, the corresponding vectors of the observer are needed to get the associated null geodesic equations of motion. The extra dimensions push one to introduce new vectors from four dimensional point of views. These vectors are given by

$$\begin{aligned} e_0= & {} \frac{ (r^2+\ell ^2)\partial _t+\ell \partial _\phi }{\sqrt{\Delta \rho ^2}} \bigg \vert _{(r_{ob}\,,\theta _{ob})}, \end{aligned}$$
(3.14)
$$\begin{aligned} e_1= & {} \frac{\sin \theta }{\sqrt{\rho ^2}} \partial _{\theta }\bigg \vert _{(r_{ob}\,,\theta _{ob})}, \end{aligned}$$
(3.15)
$$\begin{aligned} e_2= & {} -\frac{ \ell \sin ^2{\theta }\partial _t+\partial _\phi }{\sqrt{\rho ^2}\sin ^2{\theta }} \bigg \vert _{(r_{ob}\,,\theta _{ob})}, \end{aligned}$$
(3.16)
$$\begin{aligned} e_3= & {} -\frac{\sqrt{\Delta }}{\sqrt{\rho ^2}} \partial _r\bigg \vert _{(r_{ob}\,,\theta _{ob})} , \end{aligned}$$
(3.17)
$$\begin{aligned} e_{i+3}= & {} \frac{1}{\sqrt{\sum \limits _{k=1}^{i-3} r^2\cos ^2\theta \prod \limits _{j=1}^{k-1}\sin ^2\psi _j}} \partial _{\theta _i} \bigg \vert _{(r_{ob}\,,\theta _{ob})} \end{aligned}$$
(3.18)

where one has used \(i=1,\ldots ,d-4\). The timelike vector \(e_0\) indicates the four-velocity of the observer and \(e_3\) represents the third vector along the spatial direction pointing toward the center of the black hole. Here, \(e_0\pm e_3\) are considered as tangent directions to the one of principal null congruences where \(r_{ob}\) and \(\theta _{ob}\) are the distance and the angle of the observer, respectively. The vectors \(e_{i+3}\) are associated with the higher extra dimensions. Taking \(d=4\) and evincing such vectors, we recover the four dimensional ones proposed in [22]. In generic configurations, the light equation being tangent to the observer position can be defined via the relation

Fig. 1
figure 1

Shadows of superentropic black holes. Left panel: Five dimensional shadows by varying \(\ell \) and fixing m. Right panel: Shadows for different values of d by fixing m and \(\ell \). The observer is positioned at \(r_{ob}=50\) and \(\theta _{ob}=\frac{\pi }{2}\)

Full size image
$$\begin{aligned} \dot{\lambda }=\dot{r}\partial _r+\dot{\theta }\partial _\theta +\dot{\phi }\partial _ \phi +\dot{t}\partial _t+\sum _{i=1}^{d-4}\dot{\psi _i}\partial _{\psi _i} \end{aligned}$$
(3.19)

where the \((d-1)\) vectors of the spacelike can be represented in a basis corresponding to the spherical coordinates. This can be exploited to establish the tangent equation in terms of the orthonormal vectors \(\{e_0,\ldots ,e_{d-1}\}\) and the celestial coordinates \((\gamma ,\delta , \sigma _i)\). Using the spherical coordinates in higher dimensions, we obtain

$$\begin{aligned} \dot{\lambda }= & {} \beta \Bigg (-e_0+\cos \delta e_3+\sin \delta \cos \gamma e_1\nonumber \\&+\sin \delta \sin \gamma \cos \sigma _1 e_2\nonumber \\&+\sin \delta \sin \gamma \left[ \sum _{i=1}^{d-5}\left( \prod _{j=1}^{i-1}\sin \sigma _{j}\right) \cos \sigma _{i+1}e_{i+3}\right. \nonumber \\&\left. +\prod _{i=1}^{d-4}\sin \sigma _ie_{d-1}\right] \Bigg ) \end{aligned}$$
(3.20)

where \(\beta \) is a scalar factor. Combining the equations of the light rays and Eq. (3.20), we get

$$\begin{aligned} \beta =g(\dot{\lambda },e_0)=\frac{E}{\sqrt{\Delta _r\rho ^2}}\Big (\ell \xi -(r^2+\ell ^2)\Big ) \bigg \vert _{(r_{ob}\,,\theta _{ob})}. \end{aligned}$$
(3.21)

An examination reveals that the celestial coordinates are functions only of the impact parameters \(\xi \) and \(\eta \) needed to illustrate one-dimensional real curves describing the associated shadow behaviors. Exploiting the null geodesic equations and comparing the coefficients of Eq. (3.19) with Eq. (3.20), we can express the celestial coordinates in terms of \(\xi \) and \(\eta \). Indeed, it follows that the spheric coordinates should verify

$$\begin{aligned} \sin {\delta }= & {} \frac{\pm \sqrt{\Delta \eta }}{((r^2+\ell ^2)-\ell \xi )}\bigg \vert _{(r_{ob}\,,\theta _{ob})},\end{aligned}$$
(3.22)
$$\begin{aligned} \sin {\gamma }= & {} \frac{\sqrt{\Delta }}{\sin \delta }\left( \frac{(\ell -\csc ^2{\theta }\xi )}{\ell \xi -(r^2+\ell ^2)}\right) \bigg \vert _{(r_{ob}\,,\theta _{ob})},\end{aligned}$$
(3.23)
$$\begin{aligned} \sin \sigma _i= & {} \frac{r^2\cos ^2\theta \sqrt{2\eta \Delta }}{\sin \delta \sin \gamma \prod \limits _{j=1}^{i-1}\sin \sigma _j}\left( \frac{\sum \limits _{k=1}^{i}\prod \limits _{j=1}^{k-1}\sin ^2\psi _j}{\ell \xi -(r^2+\ell ^2)}\right) \bigg \vert _{(r_{ob}\,, \theta _{ob})}.\nonumber \\ \end{aligned}$$
(3.24)

Applying the \({\mathbb {S}}^{d-2}\) sphere stereographic projections, we can get the local cartesian coordinates of the coordinate system (\(x,y, z_1, \ldots , z_{d-4}\)). These coordinates could be exploited to represent the shadow geometries in an appropriate spheric projection. The computations give

$$\begin{aligned} x= & {} -2 \tan {\left( \frac{\delta }{2}\right) }\cos {\gamma },\nonumber \\ y= & {} -2 \tan {\left( \frac{\delta }{2}\right) }\sin {\gamma }\cos {\sigma _1},\nonumber \\ z_{j}= & {} -2 \tan {\left( \frac{\delta }{2}\right) }\sin {\gamma }\left( \prod _{k=1}^{d-5}\sin \sigma _{k}\right) \cos \sigma _{j+1}\nonumber \\ z_{d-4}= & {} -2 \tan {\left( \frac{\delta }{2}\right) }\sin {\gamma }\left( \prod _{k=1}^{d-5}\sin {\sigma _k}\right) \sin {\sigma _{d-4}} \end{aligned}$$
(3.25)

where one has used \( j=1,\ldots ,d-5\). In extra dimensions, it has been remarked that the equations needed to get such geometries describing the optical aspects of the neutral superentropic black holes involve a factor given by \(\cos ^2\theta \). Placing the observer in the equatorial plane, we get

$$\begin{aligned} \sin \sigma _{i}=0 i=1,\ldots ,d-4. \end{aligned}$$
(3.26)

Up to the periodicity conditions, it is obvious that these constraints are solved by

$$\begin{aligned} \sigma _{i}=0. \end{aligned}$$
(3.27)

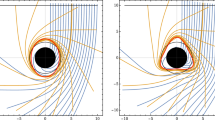
These conditions automatically impose \(z_{i}=0, \; i=1,\ldots ,d-4\). It is interesting to note that the remaining information on the extra dimensions are now hidden only in \(\Delta \). This allows one to consider only the cartesian coordinates (x, y) to visualize the shadow behaviors in arbitrary dimensions by exploiting one-dimensional real curves. This situation of the observer matches perfectly with the stereographic projection procedure \( {\mathbb {S}}^{d-2} \longmapsto \mathbb {R}^2\). In this way, the relevant parameter in the shadow discussion is the dimension d. In what follows, we inspect such optical behaviors by varying two essential parameters m and d. First, we consider the variations of the dimension d. After that, the mass variation will be discussed. In Fig. 1, we illustrate the shadow behaviors for different values of d by fixing m and varying \(\ell \).

Fig. 2
figure 2

Shadow geometries of four dimensional superentropic AdS black holes for different values of m and \(\ell \) in four dimensions. The observer is positioned at \(r_{ob}=50\) and \(\theta _{ob}=\frac{\pi }{2}\)

Full size image

The left panel presents the shadow behaviors of the special case \(d=5\) for different values of \(\ell \). It has been remarked that the shadow size increases by decreasing \(\ell \). The right panel shows the effect of the spacetime dimension d on the shadow aspect. It has been observed that the shadow size decreases by increasing d. An examination reveals that the geometric configurations of the higher dimensional black hole solutions are different than the ones obtained in \(d=4\) [22]. In particular, the elliptic geometry has been modified. It should be interesting to make contact with the shadow observation of the supermassive black hole associated with \(M87^*\) data, obtained by the EHT international collaboration. Indeed, the observational data can put certain constraints on the relevant black hole parameters. Motivated by such activities, we could compare the shadow of the superentropic black hole with such observational data by taking \(M = 1\) in units of the \(M87^*\) black hole mass given by \(M_{BH} = 6.5\times 109\,M\odot \) and \(r_0 = 91.2\,\text {kpc}\). According to [1, 2, 41], it has been remarked that the experimental shadow size is around 5.19. However, the shadow size of the superentropic black hole is around 2 for generic regions of the moduli space. The shadow size given by EHT is bigger compared with the present studied black holes. We believe that such a difference is due to the involved geometry. Indeed, the shadow shape given by EHT is almost D-shape circle. However, the shadow shape of the superentropic black holes involve an elliptic geometrical form. This could be supported by the relation between the mass parameter m and \(\ell \) of the superentropic black holes. For higher dimensional theories, we could speculate on a possible link with primordial black holes having certain relations with extra dimension models. This could be supported by the fact that such black holes, involving a small mass parameter, exhibit also a small length scale. We could expect that such black holes could find a place in future observational data associated with EHT collaborations including the recent one.

4 Shadow transitions in four dimensions

A close inspection on the study of the black hole shadows shows that the involved geometries exhibit several configurations including circular and D-shapes. In AdS backgrounds, a non expected geometry called cardioid have been found [25, 27, 28]. We will show that this geometry is relevant to unveil a nice phenomena in shadow behaviors which could be understood as a transition in the optical aspect of the neutral superentropic black holes in certain dimensions. Moreover, the elliptic geometry arises naturally in the domain of the horizon existence [22,23,24,25]. Due to the horizonless, however, the naked singularity for certain black hole solutions has been observed [22, 25, 42]. It is worth noting that it appears when \(\Delta \) involves complex roots. Motivated by non-trivial horizon geometries of the superentropic black holes, we study the associated shadow behaviors by varying the mass parameter being fixed in the previous investigations. Various dimensions can be dealt with. In this way, the roots of the equation

$$\begin{aligned} \left( \ell +\frac{r^2}{\ell }\right) ^2-2mr^{5-d}=0 \end{aligned}$$
(4.1)

will be needed in the elaboration of the shadow behaviors. The geometry and the mass constraints of such black holes push one to unveil new data on the associated shadow aspects. To show that, we first reconsider the study of four dimensions. Precisely, we investigate the shadow geometrical configurations for the superentropic black holes by varying the mass parameter m with respect to the critical value \(m_c\) in certain ranges of the AdS radius \(\ell \). Three situations \(m>m_c\), \(m=m_c\), and \(m<m_c\) will be examined. In Fig. 2, we present the associated behaviors.

It follows form this figure that the shadows of these black holes exhibit an interesting phenomena according to the value of the critical mass parameter. It has been remarked that for \(m<m_c\), we obtain the naked singularity. For \(m>m_c\), however, the horizon of the black hole exists and the corresponding shadow involves either the elliptic or the D-shape elliptic geometry for the mass values bigger or a litter bigger to \(m_c\), respectively, for different values of \(\ell \). Considering a generic value of \(\ell \) and identifying m with \(m_c\), an unusual cardioid shadow geometry appears. The latter could be supported by limaçon approximations in which such a geometry can be considered as a special case. It is noted that this approximation provides similar configurations using other methods [25, 28]. Varying the mass, these three different geometric configurations can be obtained by passing from one shape to another one. We refer to them as a transition in the optical aspect. To check this phenomena, we consider higher dimensional black holes.

5 Shadow behaviors of higher dimensional solutions

It seems possible to extend the previous analysis to higher dimensions. The extension of the four dimensional transition picture to higher dimensions is based on Eq. (4.1). A rapid examination shows that one should consider two situations associated with \(d=5\) and \(d>5\), respectively.

5.1 Five dimensional behaviors

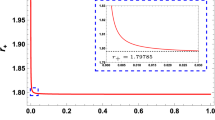
We first engineer the shadow shapes for five-dimensional solutions by using the above mentioned stereographic projection. Considering the constraint \(m>0\) and taking different values of m and \(\ell \), we can approach the shadow behaviors. Solving \(\Delta =0\) in five dimensions, we find that one has only two geometric configurations based on the following constraints

$$\begin{aligned} \left\{ \begin{array}{ll} \ell >\sqrt{2m} &{} \text {elliptic shape} \\ &{}\\ \ell <\sqrt{2m}&{} \text {naked singularity} . \end{array} \right. \end{aligned}$$
(5.1)

The associated shadows are presented in Fig. 3. It has been remarked that the cardioid geometry disappears. In this way, the shadow geometry passes directly from a naked singularity to an elliptic geometry. An examination shows that these behaviors are different than the four dimensional ones. Fixing \(\ell \), indeed, the naked singularity arises for small mass values contrary to four dimensions in which large values are needed. Similar aspects are observed in elliptic geometries.

Fig. 3
figure 3

Shadow geometries of the superentropic AdS black holes for different values of m and \(\ell \) in four dimensions. The observer is positioned at \(r_{ob}=50\) and \(\theta _{ob}=\frac{\pi }{2}\)

Full size image

5.2 Behaviors in more than five dimensions

Here, we study the shadow behaviors for \(d>5\). Concretely, we show that the naked singularity should be evinced. To reveal that, we need to solve the equation of \(\Delta =0\) in higher dimensions. It has been remarked that it is complicated to provide analytical solutions. However, we can reveal that this equation involves at least a real root which removes the naked singularity behaviors. For generic values of r, it is obvious that \(\Delta \) is a continuous radial function. Taking into account the limits \(\lim _{r \rightarrow 0^+}\Delta =-\infty \) and \( \lim _{r \rightarrow +\infty }\Delta =+\infty \), we can safely say that \(\Delta =0\) has a real solution. Based on this argument, the naked singularity has been removed for \(d>5\) due to the existence of the real roots. To inspect the associated behaviors, we illustrate the six dimensional shadow geometries in terms of m and \(\ell \). In particular, we fix one parameter and vary the remaining one. Figure 4 provides the performed computations.

Fig. 4
figure 4

Shadow geometries of superentropic AdS black holes in \(d=6\) for different values of m and \(\ell \) in four dimensions. The observer is positioned at \(r_{ob}=50\) and \(\theta _{ob}=\frac{\pi }{2}\)

Full size image

The left panel illustrates the mass variations, while the right one gives \(\ell \) variations. For a fixed value of \(\ell \), we remark that the shadow size increases with m contrary to \(\ell \). Fixing m, the shadow size decreases by increasing \(\ell \) being an expected behavior.

6 Discussion and concluding remarks

The study of the optical properties of the black holes in higher dimensions could bring global pictures associated with non-trivial gravity models including superstrings and M-theory. Motivated by such supergravity extended models, we have investigated the shadow behaviors of the superentropic black holes in arbitrary dimensions. Applying the Hamilton–Jacobi method, we have first obtained the null geodesic equations of motion in terms of the space-time dimension d where a discussion on the extra direction contributions has been elaborated. Considering a mass constraint in arbitrary dimensions, we have generalized the shadow equations by exploiting the higher dimensional spheric coordinates. Applying a spheric stereographic projection, we have studied shadow behaviors in terms of one-dimensional real curves. The present results recover the previous findings obtained in four dimensions [22]. Fixing the mass parameter, we have investigated the shadow shapes in arbitrary dimensions. We have shown that the shadow size decreases by increasing d. For a fixed value of d, the size increases by decreasing \(\ell \). In addition, we have remarked that d and \(\ell \) involve the same effect. Varying the mass parameter, we have found nice optical properties. In four dimensions, for instance, we have shown that the optical behaviors exhibit transitions from the D-shaped elliptic geometry to the naked singularity via the cardioid curve associated with a critical mass value. It has been remarked that the metric of the elliptic geometry depends on certain parameters. According to theirs values, we have discussed event horizon and horizonless behaviors [43]. A close inspection shows that a similar critical geometry has been obtained being called critical curve [44]. Concerning five dimensions, this intermediate critical geometry has been evinced, due to the absence of the mass parameter in terms of the involved remaining ones. In dimensions more than five, however, we have revealed that the naked singularity has been disappeared. For higher dimensions, the four dimensional transition behaviors have been removed. The present work could be compared with certain results associated with non-rotating and rotating black hole solutions. First, for small values of the \(\ell \), the shadow of the superentropic black hole could involve certain similarities with non-rotating black holes in non-trivial backgrounds. A close examination shows that the obtained shadows could be compared with the ones of the black holes in the presence of strong magnetic fields [45, 46]. Motivated by these activities, this could open new windows to provide a comparative discussion with Kerr and Kerr-like black holes. It has been observed certain distinctions associated with the shadow size. Such distinctions could be understood from the involved solutions where the mass parameter is constrained with other involved ones. In this way, it has been not considered as a free parameter. These constraints many provide certain differences compared to known black hole properties including thermodynamic and optical aspects. Coming back to the transition of the superentropic black holes in four dimensions, the cardioid geometry has appeared as a relevant shadow configuration linked to the critical value of the mass parameter. This mass is considered as a primordial parameter controling the thermodynamic aspect. Indeed, many works show that the thermodynamic behaviors of the superentropic black holes are different than the trivial solutions [32, 35,36,37,38,39]. This difference has appeared also in the optical behaviors. Precisely, we have remarked a distinction in the shadow geometries compared with ordinary black hole solutions [47, 48]. In this way, the optical transition in four dimensional could be considered as a relevant difference. In addition, this optical transition of the superentropic black holes could be exploited to unveil the optical behaviors of certain black holes in non-trivial solutions. We hope to link such a transition with future EHT dada to support the present results.

This work comes up with certain open questions. A possible issue concerns the observational data supporting the four dimensional shadow geometric transitions. It should be interesting to examine the present behaviors by considering external field contributions including dark energy and dark matter. It should be interesting to make contact with the associated interesting findings. Moreover, the shadows of higher dimensional multi-center black objects, obtained from supergravity theories, have been explored in [49]. It would therefore be of interest to try to make contact with such a work. We hope to address such open questions in future works.