Search for invisible dark photon in $\gamma e$ scattering at future lepton colliders

Abstract

For the first time, the production of a massive dark photon (DP) in the $\gamma e^-$ scattering at the future lepton colliders ILC, CLIC, and CEPC is examined. The invisible decay mode of the DP is addressed. We have studied both the unpolarized scattering and the collision of the Compton backscattered photons with the polarized electron. The missing energy distributions are shown. We have considered the wide range 1–1000 GeV of the DP mass $m_{A'}$. The excluded regions at the 95% CL in the plane $(\varepsilon , m_{A'})$, where $\varepsilon$ is the kinetic mixing parameter, are obtained. In particular, in the low mass region, 1–10 GeV our bounds for the 90 GeV CEPC are several times stronger than experimental limits obtained by the BaBar collaboration. For the polarized scattering, the excluded bounds for all three colliders are approximately 20% stronger as compared with the unpolarized case.

1 Introduction

One of the main goals of the present and proposed collider experiments is to search for dark matter (DM) particles. The DM makes up approximately 85% of the total mass in the Universe. Its existence is firmly confirmed by gravitational experiments [1, 2], but composition and nature are still an open question. We consider a DM scenario in which no DM fields are charged under the SM gauge group, and the lightest stable DM particles, $\chi$, can only interact with SM through the exchange of a vector mediator, dark photon (DP) (also known as hidden or heavy photon) [3,4,5,6,7,8,9,10,11,12]. It is usually denoted as $A'$. In its turn, the DP kinetically mixes with the SM $U(1)_Y$ hypercharge gauge field at the renormalizable level (kinematic-mixing portal) [7]. Such mixing can be generated by loops of massive particles charged under both $U(1)_Y$ and secluded $U(1)'$ symmetries. That kinetic-mixing portal model may be extended to 5D by adding one flat ED [13]. The existence of a new light dark sector can be also connected to a generation of neutrino masses [14]. An electroweak gauge extension of the SM by adding an extra $U(1)'$, with mixing with the standard $U(1)_Y$ can also result in a new boson [15,16,17]. For recent reviews on the DP, see, for instance, [18,19,20,21,22,23,24,25]. In particular, astrophysical constraints on the DP parameters can be found in [26,27,28,29,30,31,32,33,34], while bounds from $(g-2)_{\mu ,e}$ are presented in [35, 36].

The main mechanisms of the DP production are meson decays ($\pi ^0, \eta \rightarrow A' \gamma$) [37], bremsstrahlung ($eZ \rightarrow eZA'$ and $pZ \rightarrow pZA'$) [38, 39], Drell-Yan ($q {\bar{q}} \rightarrow A'$), and annihilation ($e^+e^- \rightarrow A' \gamma$). The process of pair annihilation into a dark and an ordinary photon provided a striking benchmark (mono-photon plus missing energy) for the DP search at the LEP [40,41,42,43]. A probing new physics in final states containing a photon and missing transverse momentum in proton-proton collisions was presented by the ATLAS and CMS Collaborations [44,45,46,47]. For the most recent results on the DPs from the LHC, see [48,49,50,51]. The ATLAS and CMS search sensitivities for DPs at the high luminosity LHC can be found in [52, 53]. A DP phenomenology at the LHC and HL-LHC was studied in [54,55,56,57], and searches of the DPs at the LHeC and FCC-he colliders were discussed in [58].

A probing new light gauge boson similar to the photon in $e^+e^-$ collisions is of particular interest [59,60,61,62,63,64,65,66,67,68,69,70,71,72]. The searches for the DP at $e^+e^-$ colliders [73,74,75,76,77,78] (see also review papers [18,19,20,21,22,23,24,25]) have looked for its decays to the $e^+e^-, \mu ^+\mu ^-$ and $\pi ^+\pi ^-$ final states, as well as for invisible decays of $A'$. The DP production in the Compton-like $\gamma e \rightarrow A' e$ process is studied in [79, 80]. The inverse process, $A' e \rightarrow \gamma e$, is recently considered in [81]. The gamma factory’s discovery potential through the low energy dark Compton scattering is analyzed in [82]. In [83] the $\gamma \gamma \rightarrow \gamma A'$ process for MeV scale collider is considered.

In the present paper we examine a novel DP production based on a high energy $\gamma e^-$ scattering at the lepton colliders ILC [84, 85], CLIC [86, 87], and CEPC [88, 89], the $\gamma e^- \rightarrow A' e^-$ process. Both unpolarized and polarized collisions are considered in the wide DP mass region 1–1000 GeV. We expect the DP to decay predominantly into invisible dark-sector particles. Let us underline that up to now the DP production at high energy lepton colliders was studied only for the $e^+e^-$ mode of these colliders [68,69,70,71].

2 Massive dark photon

As it was already mentioned above, the DP does not directly couple to SM fields. But there could be a small coupling to the electromagnetic current $J_\mu$ due to kinetic mixing between the SM hypercharge and the field strength tensor of the DP field. Consider the case when the dark sector is represented by just a single extra $U(1)'$ gauge group. Let $B_\mu$, ${\bar{A}}'_\mu$ be the mediator fields of the SM $U(1)_Y$ symmetry and dark $U(1)'$ gauge group. The gauge Lagrangian can be taken in the following form

$$\begin{aligned} {\mathcal {L}}_{\mathrm {gauge}} = - \frac{1}{4} B_{\mu \nu }B^{\mu \nu } - \frac{1}{4} {\bar{F}}'_{\mu \nu }{\bar{F}}'^{\mu \nu } - \frac{\varepsilon }{2 c_W} {\bar{F}}'_{\mu \nu }B^{\mu \nu } \;, \end{aligned}$$

(1)

where $B_{\mu \nu } = \partial _\mu B_\nu - \partial _\nu B_\mu$ and ${\bar{F}}'_{\mu \nu } = \partial _\mu {\bar{A}}'_\nu - \partial _\nu {\bar{A}}'_\mu$ are the field strength tensors of $U(1)_Y$ and $U(1)'$, respectively, $c_W$ is the cosine of the Weinberg angle $\theta _W$, and $\varepsilon \ll 1$ is the kinetic mixing parameter. The kinetic mixing can be generated at the one-loop level by massive particles charged under both $U(1)_Y$ and $U(1)'$ symmetries. After diagonalization of the gauge fields $W^3_\mu$, $B_\mu$, and DP field ${\bar{A}}'_\mu$ [23],

$$\begin{aligned} \left( \begin{array}{c} W^3_\mu \\ B_\mu \\ {\bar{A}}'_\mu \\ \end{array} \right) = \left( \begin{array}{ccc} c_W &{} s_W &{} -s_W \varepsilon \\ -s_W &{} c_W &{} -c_W \varepsilon \\ t_W \varepsilon &{} 0 &{} 1 \\ \end{array} \right) \left( \begin{array}{c} Z_\mu \\ A_\mu \\ A'_\mu \\ \end{array} \right) , \end{aligned}$$

(2)

where $s_W$ and $t_W$ are the sine and tangent of $\theta _W$, we obtain the interaction Lagrangian up to $\mathrm {O}(\varepsilon ^2)$

$$\begin{aligned} {\mathcal {L}}_{\mathrm {int}}= & {} e J_\mu A^\mu - \varepsilon e J_\mu A'^\mu + \varepsilon e' t_W J'_\mu Z_\mu + e' J'_\mu A'^\mu \nonumber \\&\quad + {\mathcal {L}}_{A'\chi } \;. \end{aligned}$$

(3)

Here $A_\mu$, $Z_\mu$ are the physical gauge fields, and $A'^\mu$ is the physical field of the DP. $J'_\mu$ and $e'$ are the DM matter current and DP coupling to the dark-sector matter, respectively. In (3) we have added the last term which describes a $A'\chi \chi$ interaction, where $\chi$ is a dark matter particle. The form of this interaction is left unspecified. As one can see in (3), the coupling of the massive DP the SM fermions is $-\varepsilon e$. The Z gauge boson acquires the coupling strength $\varepsilon e' t_W$ to the dark sector current.

Thus, there are three unknown parameters: the DP mass, $m_{A'}$, the mixing parameter, $\varepsilon$, and the $A'\rightarrow \chi {\bar{\chi }}$ branching. The latter is taken to be unity, if we assume that $m_{A'} > 2m_\chi$. The dimensionless mixing parameter $\varepsilon$ is a priori unknown and presumably lies in the $10^{-12} - 10^{-2}$ region, depending on the DP mass [33, 39, 90,91,92,93,94,95] (see also Fig. 8.16 in [96], where sensitivities for the DP in the plane mixing parameter $\varepsilon$ versus $m_{A'}$ are collected). The DP mass $m_{A'}$ can also vary in a wide range, but most of experimental searches for the invisible DP were aimed at the $m_{A'}$ in the region $1 \mathrm {\ MeV} - 10 \mathrm {\ GeV}$ [18,19,20,21,22,23,24,25], see Fig. 1. We will examine the wider DP mass region 1–1000 GeV.

Fig. 1

The existing limits for the massive dark photon going to invisible final states. The constraints from $a_e = (g-2)_e$ and $a_\mu = (g-2)_\mu$ are also shown. The figure is taken from [24]

3 Invisible dark photon production in Compton-like scattering

The production of the DP in the center-of-mass system of the $\gamma e^-$ scattering,

$$\begin{aligned} \gamma + e^- \rightarrow A' + e^- , \end{aligned}$$

(4)

is depicted in Fig. 2. As is known, linear $e^+e^-$ colliders can operate in $\gamma e$ and $\gamma \gamma$ modes [97,98,99]. The $\gamma \gamma$ facilities at the future circular colliders are examined in [100,101,102,103,104]. In particular, a number of processes in $\gamma e$ and $\gamma \gamma$ collisions at the CEPC have been studied in [105]. At the lepton collider hard real photons may be generated by the laser Compton backscattering, when soft laser photons collide with electron beams. As a result, a large flux of photons is produced which carry a great amount of the parent electron energy. A $\gamma e$ ($\gamma \gamma$) collider has a number of advantages over $e^+e^-$ collider. Among they are (i) Higgs can be s-channel produced; (ii) higher cross sections for charged particles; (iii) higher mass reach in some channels; (iv) pure QED interaction (in $e^+e^-$ a Z boson exchange is present); (v) higher polarization of initial states. The $\gamma e$ and $\gamma \gamma$ modes were considered for a number of processes at the future lepton colliders [106,107,108,109,110,111,112,113,114,115,116,117], but the DP production in $\gamma e$ or $\gamma \gamma$ collisions have not yet been studied at the ILC, CLIC, or CEPC.

Fig. 2

The production of the dark photon $A'$ in the $\gamma e^-$ collision

Fig. 3

The diagrams for the production of the dark photon in the $\gamma e^-$ collision, with its subsequent invisible decay into dark matter particles

Fig. 4

The s-channel diagrams for the SM process $\gamma e^- \rightarrow e^- + E{\!\!\!\!/}$

Let $E_0$ be the energy of the initial laser photon beam, $E_e$ be the energy of the initial electron beam, while $E_\gamma$ be the energy of the Compton backscattered (CB) photon. The differential cross section for the unpolarized DP production accompanied by electron at the lepton collider operating in the $\gamma e$ mode is defined as

$$\begin{aligned} \frac{d\sigma }{d\cos \theta } = \int _{x_{\min }}^{x_{\max }} dx f_{\gamma /e}(x) \,\frac{d{\hat{\sigma }}}{d\cos \theta } \;. \end{aligned}$$

(5)

Here $f_{\gamma /e}(x)$ is the distribution of the CB photon in the variable $x = E_\gamma /E_e$,

$$\begin{aligned} x_{\min } = \frac{p_\bot ^2}{E_e^2} \;, \quad x_{\max } = \frac{\zeta }{1 + \zeta } \;, \quad \zeta = \frac{4E_0 E_e}{m^2} \;, \end{aligned}$$

(6)

$p_\bot$ is the transverse momentum of the outgoing particles, m is the electron mass, and $\theta$ represents the scattering angle of the outgoing DP (see Fig. 2). The laser beam energy $E_0$ is chosen to maximize $E_\gamma$. It is achieved, if $\zeta = 4.8$, and we get $x_{\max } = 0.83$, see Eq. (6).

Fig. 5

The u-channel diagrams for the SM process $\gamma e^- \rightarrow e^- + E{\!\!\!\!/}$

Fig. 6

The differential cross sections for the unpolarized $\gamma e^- \rightarrow e^- + E{\!\!\!\!/}$ scattering at the collider CEPC. The mixing parameter is fixed to be $\varepsilon = 0.1$

Fig. 7

The same as in Fig. 6, but for the collider ILC

Fig. 8

The same as in Fig. 6, but for the collider CLIC

The spectrum of the CB photons in formula (5) is defined as follows [97]

$$\begin{aligned} f_{\gamma /e}(x)= & {} \frac{1}{g(\zeta )}\left[ 1-x+\frac{1}{1-x} - \frac{4x}{\zeta (1-x)} \right. \nonumber \\&\left. + \frac{4x^{2}}{\zeta ^{2}(1-x)^{2}}\right] , \end{aligned}$$

(7)

where

$$\begin{aligned} g(\zeta ) = \left( 1-\frac{4}{\zeta }-\frac{8}{\zeta ^2}\right) \ln {(\zeta +1)} + \frac{1}{2} + \frac{8}{\zeta }-\frac{1}{2(\zeta +1)^2} \;.\nonumber \\ \end{aligned}$$

(8)

The differential cross section for the process $\gamma e^- \rightarrow A' e^-$ in the center-of-mass system of the colliding particles is defined as

$$\begin{aligned} \frac{d{\hat{\sigma }}}{d\cos \theta }= & {} \frac{1}{32\pi {\hat{s}}}\frac{\sqrt{({\hat{s}} + m_{A'}^2 - m^2)^2 - 4{\hat{s}} m_{A'}^2}}{{\hat{s}} - m^2}\nonumber \\&\times \,|F({\hat{s}}, \cos \theta )|^2 \;, \end{aligned}$$

(9)

where $\sqrt{{\hat{s}}} = \sqrt{sx}$ is the center-of-mass energy of the backscattered photon and electron, ${\hat{s}} \geqslant (m_{A'} + m)^2$. A matrix element of the process (4) is a sum of two diagrams in Fig. 3, in which the $A'e^-e^+$ coupling constant is equal to $-\varepsilon e$. An explicit expression for the square matrix element $|F|^2$ is given in Appendix A.

Fig. 9

The excluded bounds at the 95% CL on the dark photon mass $m_{A'}$ and kinetic mixing parameter $\varepsilon$ for the invisible dark photon production in the unpolarized $\gamma e^- \rightarrow A' e^-$ collision

Fig. 10

The excluded bounds at the 95% CL on the dark photon mass $m_{A'}$ and kinetic mixing parameter $\varepsilon$ for the invisible dark photon production in the collision of the unpolarized real photon with the electron whose polarization is equal to 80%

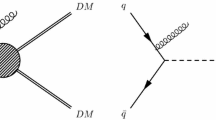
The main background comes from the SM process

$$\begin{aligned} \gamma e^- \rightarrow e^- \nu {\bar{\nu }} \;, \end{aligned}$$

(10)

see the diagrams in Figs. 4 and 5. In detector it looks like an event with an isolated electron and missing transverse energy. We apply the cut on the transverse momenta of the final electron, $p_\perp > 10$ GeV, and its rapidity, $|\eta | < 2.5$. In order to reduce the SM background, we also impose the cut on an invisible invariant mass, $|m_{A'} - m_{\mathrm {invis}}| < 5$ GeV. In numerical calculations, especially in background calculations, CalcHEP program was also used [118]. We have used the following statistical significance (SS) formula [119],

$$\begin{aligned} SS = \sqrt{2[(S+B) \,\ln (1 + S/B) - S]}, \end{aligned}$$

(11)

where S and B are the numbers of the signal and background events, respectively. Note that $SS \simeq S/\sqrt{B}$ for $S \ll B$.

In Figs. 6, 7 and 8 we present differential cross sections of the $\gamma e^- \rightarrow e^- + E{\!\!\!\!/}$ scattering as functions of the missing energy for a fixed value of the mixing parameter $\varepsilon$. The results for the colliders CEPC, ILC, and CLIC are given, for the DP masses $m_{A'} = 50$ GeV, 100 GeV, and 200 GeV, respectively. In all figures, red (black) curves correspond to the cross sections with (without) account of the dark photon contributions. It turns out that DP is the dominant effect for high missing energy values. We have also made calculations for different values of $m_{A'}$. Our calculations show that deviations of the cross sections from the SM predictions become smaller as the DP mass $m_{A'}$ grows.

The excluded bounds for the massive DP going to invisible final states are presented in Figs. 9 and 10 in the plane the kinetic mixing parameter $\varepsilon$ versus DP mass $m_{A'}$. In Fig. 9 the results for the unpolarized $\gamma e^- \rightarrow A' e^-$ collision are given for the CEPC (left panel), ILC (middle panel), and CLIC (right panel). The strongest bound on $\varepsilon$ is achieved for the 90 GeV CEPC. In the region $m_{A'} = 1$–10 GeV it is 2–4 orders of magnitude stronger than the experimental bounds obtained by the BaBar collaboration shown in Fig. 1. The constraints for the ILC collider with the energy of 160 GeV and 240 GeV are comparable with the BaBar constraints in this mass region. The sensitivity decreases as $m_{A'}$ grows.

The results for the polarized case are shown in Fig. 10. The polarized electron sources of the future linear colliders have been discussed in the current ILC [85], CLIC [86], and CEPC [88] designs. We consider the unpolarized CB photons and $\mathrm {P}(e^-) = 80\%$ polarization of the initial electron beam for all three colliders. By analogy with the ILC project, we assume that for the polarized $\gamma e^-$ collision, the CEPC integrated luminosity is 50% less than the integrated luminosity for the unpolarized $\gamma e^-$ scattering. One can see that the obtained excluded bounds are on average 20% better compared to the unpolarized bounds (Fig. 9). For the CLIC, a 10% improvement takes place only for the energy $\sqrt{s} = 380$ GeV. As for the electron beam polarization of $\mathrm {P}(e^-) = -80\%$, our calculations show that it does not offer any advantage over the unpolarized case. The reason is that the SM background gets larger for $\mathrm {P}(e^-) = -80\%$ with respect to the unpolarized collision, while the signal remains almost the same.

4 Conclusions

In the present paper, we have studied the production of the massive dark photon (DP) in the $\gamma e^-$ scattering at the future lepton colliders ILC, CLIC, and CEPC, when the DP decays predominantly into invisible dark matter particles. The real photons are generated by the laser Compton backscattering when the soft laser photons collide with the electron beams. Both the unpolarized and polarized collisions are studied. For the polarized $\gamma e^- \rightarrow A' e^-$ process we have assumed that the incoming CB photon is unpolarized, while the polarization of the electron beam is taken to be 80% for all three colliders. The wide region 1–1000 GeV of the DP mass $m_{A'}$ is considered. The missing energy distributions for signal and background are presented. We have derived the excluded regions at the 95% CL in the plane $(\varepsilon , m_{A'})$, where $\varepsilon$ is the kinetic mixing parameter. Our excluded bounds for the polarized collisions at the ILC and CEPC are approximately 20% stronger compared to the unpolarized excluded bounds. In particular, in the low mass region 1–10 GeV our excluded bounds for the 90 GeV CEPC are in average 2–4 orders of magnitude stronger that the experimental bounds obtained by the BaBar collaboration. The CEPC constraints with energies of 160 GeV and 240 GeV are comparable with the BaBar bounds in this mass range, and the ILC excluded bounds are close to them.

Note that up to now the production of the DP at future lepton colliders (both for the visible and invisible DP decays) was studied only for the $e^+e^-$ mode of these colliders.

As was already mentioned in Introduction, the DP production in the Compton-like $\gamma e \rightarrow A' e$ process was studied in the fixed target experiments [79, 80, 82]. However, these low energy experiments were dealing with low mass DPs ($m_{A'} < 100$ MeV), while we examine heavy DPs ($m_{A'} > 1$ GeV).

Our method can be also applied to dark axionlike pseudoscalars (scalars). Consider the coupling of a pseudoscalar ALP a to a electron field $\psi$. It is given by the Lagrangian (see, for instance, [120])

$$\begin{aligned} {\mathcal {L}} = g_{a{\bar{\psi }}\psi } \partial _\mu a {\bar{\psi }}\gamma ^\mu \gamma ^5\psi \;. \end{aligned}$$

(12)

Then the amplitude of the process $\gamma e^- \rightarrow a e^-$ will be proportional to the electron mass $m_e$. So, we expect that the pseudoscalar cross section will be suppressed with respect to the dark photon cross section. Nevertheless, we consider studying axionlike (pseudo)scalars as a future direction.

Appendix A

The matrix element of the process (4) is given by the sum of s- and u-channel diagrams presented in Fig. 3. Correspondingly, we get

$$\begin{aligned}&|F(s, \cos \theta )|^2\nonumber \\&\quad = (\varepsilon e^2)^2 \,\big [ |F_s|^2 + |F_u|^2 + (F_s F_u^* + F_s^* F_u) \big ] \;, \end{aligned}$$

(A.1)

where

$$\begin{aligned} |F_s|^2&= \frac{2}{(s - m^2)^2} \left[ -su + m^2(3s + u + 2m_{A'}^2) + m^4 \right] , \nonumber \\ |F_u|^2&= \frac{2}{(u - m^2)^2} \left[ -su + m^2(3u + s + 2m_{A'}^2) + m^4 \right] \;, \nonumber \\ F_s F_u^*&= F_s^* F_u = \frac{2}{(s - m^2)(u - m^2)} \nonumber \\&\quad \times \left[ m_{A'}^2(s + u) - m_{A'}^4 + m^2(s + u - 2m_{A'}^2) + 2m^4 \right] . \end{aligned}$$

(A.2)

The Mandelstam variable u is equal to

$$\begin{aligned} u&= m_{A'}^2 + m^2 - \frac{1}{2s}\Big [ (s + m^2)(s + m_{A'}^2 - m^2) \nonumber \\&\quad + (s - m^2)\sqrt{(s + m_{A'}^2 - m^2)^2 - 4s \,m_{A'}^2}\cos \theta \Big ] , \end{aligned}$$

(A.3)

where $\theta$ is a scattering angle of the DP in the center-of-mass frame of the colliding particles (see Fig. 2). For $m_{A'}=0$, $\varepsilon = 1$, the above formulas coincide with well-known formulas for the Compton scattering [121].