Abstract
Recent observations of the orbits of star clusters around Sgr \(A^\star \), imaging of black holes and gravitational waveforms of merging compact objects require a detailed understanding of the general relativistic geodesic motion. We came up with a method to provide all the possible geodesics in an axially symmetric space-time. The Kerr metric is explicitly worked out, recovering the Schwarzschild geodesics in the static limit. We also found the most general Killing tensor and its associated constant of motion for an axisymmetric space-time. The relevance of these results is crucial to understanding the different scenarios and the fundamental nature of the compact object at the galactic center.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
From the orbits of stars [1,2,3], and the imaging around supermassive black holes [4, 5] through gravitational lensing [6], geodesic motions of particles and photons have a venerable history bringing results of General Relativity to observational grounds. Other important scenarios like frame dragging [7], radiation transport effects from accretion flows in the vicinity of relativistic stars [8], and gravitational waveform of merging compact objects [9], also require a detailed understanding of the geodesic motion in a general relativistic background.
Rotation is a crucial feature for celestial bodies from the an astrophysical viewpoint, and the Kerr solution of Einstein equations describes the gravitational field outside spinning compact objects and black holes [10]. Thus, geodesics across a Kerr gravitational background are very important and have a long history, since Carter’s study of the existence of a new conserved quantity associated with each geodesic [11, 12]. The astrophysical relevance of tracking particles & photons in Kerr space-times motivates a significant effort to obtain analytical and numerical trajectories in this gravitation background (see [13, 14] and references therein).
We have recently implemented a tetrad formalism by an orthogonal splitting of the Riemann tensor, introducing a complete set of equations equivalent to the Einstein system and applying it to the spherical case [15,16,17]. This formalism provides coordinate-free results expressed in terms of structure scalars related to the kinematical and physical properties of the fluid.
We devise an exhaustive classification for all geodesic motion for any axisymmetric source establishing the equations which describe each alternative. Based on the tetrad scheme, we provide a method to integrate all possible orbits for any stationary axially symmetric solutions, illustrating each case with the Kerr metric.
We present the most general Killing tensor corresponding to any axisymmetric space-time and its associated constant of motion, which has not previously been obtained. This Killing tensor and its conserved quantity allow us to obtain the orbits by solving a system of algebraic equations. We recovered the famous Carter constant along the geodesic as a particular case.
2 The tetrad and kinematical variables
We shall consider stationary and axially symmetric sources with the line element written as
with \(A = A( r, \theta )\), \(B = B( r, \theta )\), \(R = R( r, \theta )\), and \(\omega _3~=~\omega _3( r, \theta )\).
In this case the tetrad is:
where \(\Delta _2=A^2R^2+\omega _3^2\).
2.1 The scalars and the tetrad covariant derivative
The covariant derivative of \(V_{\alpha }\) in the 1+3 formalism can be written as \(V_{\alpha ;\beta }=-a_\alpha V_\beta +\Omega _{\alpha \beta }\), where the kinematical variables (\(a_\alpha \) the acceleration and \(\Omega _{\alpha \beta }\) the vorticity) can be written, in terms of the tetrad, as
Follows the covariant derivative of K, i.e.
Now, the covariant derivative of L, can be written as
Finally the covariant derivative of S is
2.2 Scalars for a general axisymetric metric
Assuming \(\omega _3=A^2 \psi \), the scalars for the axisymmetric metric (1) are:
3 All geodesic
To obtain all possible geodesics in any axially symmetric space-time, we define the tangent vector to the geodesic \(Z^{\alpha }\) as
and, its norm, \( \epsilon = Z_\alpha Z^\alpha = -z_0^2 +z_1^2 +z_2^2 +z_3^2\), represents photon (\(\epsilon = 0\)) and particle (\(\epsilon = -1\)) trajectories.
In what follows we shall make use of the geodesic equations \(Z_{\alpha ;\beta }Z^\beta =0\), written in the tetrad formalism as
and
Because the norm of the tangent vector \(Z^\alpha \) is constant: \(Z_\alpha Z^\alpha =\epsilon \Rightarrow \quad Z_{\alpha ;\beta } Z^\alpha =0\), and we get
where we have the derivatives \(z^\dag \equiv \frac{1}{B}z_{,r} \) and \(z^\theta \equiv \frac{1}{C}z_{,\theta }\).
3.1 First order geodesic equations
Substracting (10) from (8) and (11) from (9) we have
This system describes all possible geodesic equations for any axially symmetric space-time, having Kerr and Schwarzschild metrics as particular cases.
3.2 Solutions for all geodesic cases
The four cases which solve the system (12)–(13):
-
1.
\(z_2=0\) and \(z_1=0\), are circular orbits for \(\theta = const\).
-
2.
\(z_2=0\) and \(z_1^\theta =j_1 z_1\), are orbits for \(\theta = const\).
-
3.
\(z_1=0\) and \(z_2^\dag =-j_2z_2\), are spherical orbits.
-
4.
\(z_2^\dag -z_1^\theta +j_1z_1+j_2 z_2=0\) is the most general case.
This is an exhaustive classification containing all possible cases for geodesic motions. Following subsections present the equations for each alternative and an application to the Kerr space-time.
3.3 Circular orbit on a plane
In the first case the system (12)–(13) is solved by \(z_2=0\) and \(z_1=0\), i.e the radial and the angular coordinate, \(\theta \), are constant. Thus, we obtain bounded orbits confined to a plane and the set of equations becomes,
3.4 General orbital motion on a constant plane
The second solution for Eqs. (12)–(13), emerges from the conditions \(z_2=0\) and \(z^{\theta }_1 = j_1 z_1\). Then, the geodesic equations reduce to
3.5 General orbits on the two-sphere
The third set of solutions we shall consider are general orbits circumscribed on a 2-sphere (\(\theta -\phi \)), recently reported in reference [13]. This occurs having \(z_1=0\) and \(z_2^\dag =-j_2z_2\), and the corresponding geodesic equations are
3.6 The general case
The last case emerges from \(z_2^\dag -z_1^\theta +j_1z_1 +j_2 z_2=0\). This is the most general case, and the system of geodesic equations becomes
The solution of the equation is
with \(f=f(r,\theta )\) an arbitrary function of its arguments. Consequently, \(z_1^\theta =j_1z_1\) and \(z_2^\dag =-j_2z_2\), which in turn allows us to transform (8) and (9) into
and
4 Symmetry and geodesic equations
In this section we shall discuss the consequences on imposing symmetries, i.e. Killing vectors and tensors, on the source generating the geodesic equations.
4.1 Killing vectors
From the Killing equation
we can identify temporal and axial Killing vectors as
These Killing vectors provide the energy \(E~=~\tau ^\alpha Z_\alpha \) and angular momentum \(l~=~\xi ^\alpha Z_\alpha \).
Thus, \(z_{0;\alpha } = -z_0 a_1 K_\alpha -a_2 z_0 L_\alpha \quad \Rightarrow z_0=-\frac{E}{A} \, ,\) and
with \(z_3=\frac{A^2 l +E \omega _3}{A\sqrt{\Delta _2}} \, .\)
Now the set of equations for the parallel transport of the vector \(Z^\alpha \), can be written as
The above equations lead to the following characteristic expressions:
4.2 Killing tensor
Killing tensors are useful because they also provide conserved quantities for geodesic motion. The most famous is obtained for the Kerr space-time where the Killing tensor leads to the Carter constant [12].
For the stationary axially symmetric space-time, the Killing tensor \(\xi _{\alpha \beta }\) satisfies \(\xi _{\alpha \beta ;\mu }+\xi _{\mu \alpha ;\beta }+\xi _{\beta \mu ;\alpha }=0\), which can be written as
Integrating the Killing tensor equation we obtain
We have \(\Phi =(r^2-2mr+a^2)\sin \theta \) and \(\xi (r)\) an r-function.
Thus, the general conserved quantity Q for \(\xi _{\alpha \beta }\) is
Since Z has a constant modulus we found
obtaining that the scalars \(z_1\) and \(z_2\) are
with
and
The new conserved quantity Q recovers the Carter constant \(Q_c\) for the Kerr metric [11, 12]
The following sections implement all the previous cases to the particular example of the Kerr space-times.
5 The Kerr metric
To illustrate the different cases mentioned above, we consider \(\Lambda = r^2+a^2\cos ^2\theta \) in the Kerr metric, i.e.
5.1 Kerr killing tensor and geodesic motions
It is easy to verify that, assuming the metric (44), the general solution of the system (12)–(13), for \(z_1~\ne ~0\) and \(z_2~\ne ~0\) is
Thus, the separation constant method devised by Carter is equivalent to solve the geodesic equations (27) and (28), for the Kerr metric where Eqs. (42) and (43) become \(g_1(r,\theta )~=~g_1(r)\) and \(g_2(r,\theta )~=~g_2(\theta )\), i.e.
and \(g_2(\theta )=-Q_c-\frac{l^2}{\sin ^2\theta } +a^2(\epsilon +E^2)\cos ^2\theta \), where \(Q_c\) is the Carter constant.
5.2 Kerr circular orbit on a plane
Considering the set of Eqs. (14)–(16) for the metric (44) with \(\theta =\frac{\pi }{2}\), \(Q_c=l^2\) we get:
and
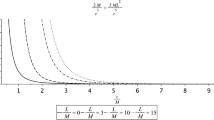
Equations (46) and (47) determine the radius of the circumference and related the physical constants. For instance, when we have the specific case \(\epsilon =a=0\) we obtain that \(r=3m\) and \(l=\sqrt{27}Em\).
5.3 Kerr general orbital motion on a constant plane
Equations (17)–(19) with \(\theta =\frac{\pi }{2}\), and \(Q=l^2\) lead to
For a null geodesics and \(a=-\frac{l}{E}\) we integrate (34) as
where \(\phi _0\) is a constant of integration.
Now for a time-like geodesic we have
with
where \(\beta _k\) (\(k=1,2,3,4,5,6\)) are functions of the physical parameters.
5.4 Kerr general orbits on the two-sphere
In this case, from Eq. (22) we get
and
where we have redefined \({\tilde{a}}=a^2(\epsilon +E^2)\).
Next, substituting (54) into (34) we obtain
with \({\tilde{E}}=2marlE+a^2l\) and \(F^2=r^2-2mr+a^2\).
5.5 The Kerr general case
The module of Z for the Kerr metric can be written as
Substituting (26) into (56) we find
which is an equation for the function f with a solution \(f=f_1(r)+f_2(\theta )\) where
Next, substituting (25) into (34) and considering \(z_1^\theta =j_1z_1\) and \(z_2^\dag =-j_2z_2\), we obtain
where \(F^2=r^2+a^2-2mr\).
Now, combining Eq. (59) we get
and by introducing
we get
Next, substituting \(r=x+b\) into (61) we get
with
Consequently first integrals in r and \(\theta \) of the Eq. (60) can be obtained as
where \( \Gamma (x)=\sqrt{\frac{b_2+x}{b_3+x}}\), where \(\gamma _i\) and \(\alpha _j\), with \(i=1,2,3\) and \(j=0,1,2,3\).
Now, implementing the procedure described above for the polynomial (63) we get
and find \(b=0\), \(b_3=0\), \(a_0=\epsilon +E^2\), \(b_1^2+\frac{2m\epsilon }{\sqrt{\epsilon +E^2}}b_1+a^2(\epsilon +E^2)-l^2 = 0\) and \(b_2- \frac{2m(aE+l)^2}{b_1^2}=0\).
Next, integrating the Eq. (60) we get
and
with \(\Xi =\sqrt{\frac{r}{b_2+r}}\), where \(G=G(C_1,C_2)\) becomes its general solution.
6 Conclusions
This work presents a method to classify and solve all geodesic motion analytically around any stationary axially symmetric source. The method summarises all these possible geodesic trajectories into two simple Eqs. (12) and (13), with ease in obtaining solutions. These distinct solutions allow us to classify the different trajectories for particles and photons. All the possible geodesics have been implemented for the Kerr metric, representing the gravitational field produced by a rotating compact object. In particular, those orbiting on a two-sphere surface could be especially relevant for describing observational data ( see [3, 18, 19] and references therein). Now, it will be possible to build templates from exact General Relativistic analytical solutions, i.e. without any approximations for the orbits of stars [1,2,3], and the imaging of black holes [4, 5, 20]. The method shown here allows us to find solutions of the form \(f_1(r,\theta ) = C_1\) and \(f_2(r,\theta ) = C_2\) (equations (70) and (71)) which complement the standard elliptic integrals procedure handling in writing down the geodesics trajectories ( see for example references [21,22,23] ). It is clear that in the equations mentioned above (i.e.(70) and (71)), the elliptic integrals can be avoided only for very particular choices of \(\alpha _i\).
We found the most general for this Killing tensor corresponding to any axisymmetric space-time and its linked constant of motion. The existence this general constant of motion –along the geodesic– is clear from a simple system of algebraic equations (39) and (40). Again, the general expression for the constant along the geodesic could help to obtain solutions for the geodesic in a more general context where the Kerr metric may not adequately describe the gravitational field (see [24] and references therein). This new conserved quantity recovers the Carter constant for the Kerr metric ( [11, 12]).
Although we have considered Kerr space-time a helpful example, the equations for each case in our classification are general and valid for any axisymmetric metric. Analytic solutions for geodesic with more complex Kerr-like sources describing richer rotational compact objects could fit better the trajectories of the stars or represent more accurate black hole imaging or open the possibility of new information from gravitational wave astronomy.
Data Availability
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: This is a theoretical paper with no data or code to be shared.]
Change history
22 July 2022
An Erratum to this paper has been published: https://doi.org/10.1140/epjc/s10052-022-10607-3
References
A.M. Ghez, S. Salim, N.N. Weinberg et al., Measuring distance and properties of the milky way’s central supermassive black hole with stellar orbits. Astrophys. J. 689(2), 1044 (2008)
R. Genzel, F. Eisenhauer, S. Gillessen, The galactic center massive black hole and nuclear star cluster. Rev. Mod. Phys. 82(4), 3121 (2010)
R. Abuter, A. Amorim, M Bauböck, et al., and Gravity Collaboration. Detection of orbital motions near the last stable circular orbit of the massive black hole sgra. Astron. Astrophys. 618, L10 (2018)
K. Akiyama, A. Alberdi, R. Azulay, et al., and EHT Collaboration. First m87 event horizon telescope results. i. the shadow of the supermassive black hole. Astrophys. J. Lett. 875(1), L4 (2019)
D. Psaltis, L. Medeiros, P. Christian et al., Gravitational test beyond the first post-newtonian order with the shadow of the m87 black hole. Phys. Rev. Lett. 125(14), 141104 (2020)
G. He, W. Lin. Kerr-newman black hole lensing of relativistic massive particles in the weak field limit. arXiv preprint arXiv:2112.08142, (2021)
L.F. Costa, J. Natário, Frame-dragging: meaning, myths, and misconceptions. Universe 7(10), 388 (2021)
F. Yuan, R. Narayan, Hot accretion flows around black holes. Ann. Rev. Astron. Astrophys. 52, 529–588 (2014)
B.P. Abbott, R. Abbott, T.D. Abbott, et al., and LIGO-Virgo Collaboration. Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 116(6), 061102 (2016)
R.P. Kerr, Gravitational field of a spinning mass as an example of algebraically special metrics. Phys. Rev. Lett. 11(5), 237 (1963)
B. Carter, Global structure of the kerr family of gravitational fields. Phys. Rev. 174(5), 1559 (1968)
B. Carter, Hamilton-Jacobi and Schrodinger separable solutions of Einstein’s equations. Commun. Math. Phys. 10, 280 (1968)
E. Teo, Spherical orbits around a kerr black hole. Gen. Relativ. Gravit. 53(1), 1–32 (2021)
C. Chan, L. Medeiros, F. Özel, D. Psaltis, Gray2: A general purpose geodesic integrator for kerr spacetimes. Astrophys. J. 867(1), 59 (2018)
J. Ospino, J. L. Hernández-Pastora, L. A. Nú nez. An equivalent system of einstein equations. J. Phys. Conf. Ser. 831, 012011 (2017)
J. Ospino, J.L. Hernández-Pastora, H. Hernández, L.A. Nú nez. Are there any models with homogeneous energy density? General Relativ. Gravit. 50(11), 146 (2018)
J. Ospino, L. A. Nú nez. Karmarkar scalar condition. Eur. Phys. J. C 166 (2020)
R. Abuter, A. Amorim, N. Anugu, et al., and Gravity Collaboration. Detection of the gravitational redshift in the orbit of the star S2 near the Galactic centre massive black hole. Astron. Astrophys. 615, L15 (2018)
R. Abuter, A. Amorim, et al., and Gravity Collaboration. Detection of the Schwarzschild precession in the orbit of the star S2 near the Galactic centre massive black hole. Astron. Astrophys. 636, L5 (2020)
J.M. Velásquez-Cadavid, J.A. Arrieta-Villamizar, F.D. Lora-Clavijo, O.M. Pimentel, J.E. Osorio-Vargas, Osiris: a new code for ray tracing around compact objects. Eur. Phys. J. C 82(2), 1–12 (2022)
R. Fujita, W. Hikida, Analytical solutions of bound timelike geodesic orbits in kerr spacetime. Class. Quantum Gravity 26(13), 135002 (2009)
E. Hackmann, C. Lämmerzahl, V. Kagramanova, J. Kunz, Analytical solution of the geodesic equation in kerr-(anti-) de sitter space-times. Phys. Rev. D 81(4), 044020 (2010)
E. Lämmerzahl, C. Hackmann. Analytical solutions for geodesic equation in black hole spacetimes. in: Nicolini p., kaminski m., mureika j., bleicher m. (eds) 1st karl schwarzschild meeting on gravitational physics. Springer Proceedings in Physics, (2016)
K. Destounis, K.D. Kokkotas, Gravitational-wave glitches: Resonant islands and frequency jumps in nonintegrable extreme-mass-ratio inspirals. Phys. Rev. D 104(6), 064023 (2021)
Acknowledgements
LAN gratefully acknowledges the support of the Vicerrectoría de Investigación y Extensión from Universidad Industrial de Santander under the exchange scholar program. This work was partially supported by Ministerio de Ciencia, Innovacion y Universidades. Grant number: PGC2018 096038 B I00, and Junta de Castilla y Leon. Grant number: SA096P20.
Author information
Authors and Affiliations
Corresponding author
Additional information
The original online version of this article was revised. In this article the acknowledgment was incorrectly given as: LAN gratefully acknowledges the support of the Vicerrectoría de Investigación y Extensión from Universidad Industrial de Santander under project VIE2814.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Ospino, J., Hernández-Pastora, J.L. & Núñez, L.A. All analytic solutions for geodesic motion in axially symmetric space-times. Eur. Phys. J. C 82, 591 (2022). https://doi.org/10.1140/epjc/s10052-022-10544-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-022-10544-1