1 Introduction

Black holes (BHs) are considered as the natural laboratories to test our understanding of nature. Although BHs were first theoretically devised but recent developments in the field are continuously making them better observed scientific facts rather than fiction. As BHs provide us the natural framework to test and enhance the currently available scientific picture of gravity, hence the study of their physical properties becomes one of the most important initial steps in this direction. It has been more than a century when BHs appeared as the theoretical solution of Einstein’s field equations (EFE). First such solution, known as Schwarzschild BH (SBH) [1] had just one parameter i.e. BH mass. But the involved parameters kept on increasing [2,3,4,5] with more generalised description of the background gravitational field.

In this article we study the tidal forces and their effect in the background of SBH surrounded with quintessence and string cloud. Recent studies of null and timelike geodesics around this BH spacetime have shown how the presence of cloud of strings along with quintessence modifies the corresponding geodesic structure [6,7,8]. As the presence of cloud of strings originates from string theory and quintessence is considered as one of the potential candidate for dark energy in the Universe, their combined incorporation as the solution of EFE gives some unique properties to the background spacetime geometry. In order to trace these unique features we opted to study the tidal forces and evolution of geodesic deviation vectors around this BH metric. We have formulated generalised geodesic deviation equations and solved them to analyse the behaviour of geodesic deviation vectors in order to look for the possible effects of the various parameters involved therein.

The article is arranged as follows, in Sect. 2 SBH surrounded with clouds of strings and quintessence metric and its horizon structure is reviewed. In Sect. 3 the generalised set up of first integrals of geodesic equations and effective potential is discussed in brief. In Sect. 4, the newtonian acceleration for radially infalling neutral test particle is discussed in detail along with the tidal forces. Generalised geodesic deviation equations and their generalised and specific solutions are discussed in Sect. 5. Conclusions and future directions are presented in Sect. 6.

2 SBH spacetime in cloud of strings and quintessence

Spacetime metric for the spherically symmetric and static BH in the background of cloud of strings and quintessence [9, 10] has the following form,

$$\begin{aligned} d s^{2}= f(r) d t^{2} -\frac{1}{f(r)} d r^{2} -r^{2}\left( d \theta ^{2}+\sin ^{2} \theta d \phi ^{2}\right) , \end{aligned}$$
(1)

where

$$\begin{aligned} f(r)=\left( 1-a-\frac{2 M}{r}-\frac{q}{r^{3 \omega _{q}+1}}\right) , \end{aligned}$$
(2)

M represents the mass of the BH, \(\omega _{q}\) is the equation of state parameter (EoS) for quintessence field, a is the string cloud parameter and q is the quintessence parameter respectively. The EoS parameter for the quintessence field ranges as, \(-1<\omega _{q}<-\frac{1}{3}\). In the absence of a and q the above spacetime reduces to the SBH spacetime. Lapse function of above metric given in Eq. (2) has two roots given by,

$$\begin{aligned} r_{q}= & {} \frac{1-a+\sqrt{a^{2}-2 a-8 M q+1}}{2 q} \nonumber \\ r_{e}= & {} \frac{1-a-\sqrt{a^{2}-2 a-8 M q+1}}{2 q}. \end{aligned}$$
(3)

The mathematical condition on the involved parameters for both of the above roots to be real is, \(0<q<\frac{a^{2}-2 a+1}{8 M}\) and \(0<a<1\). \(r_{e}\) is known as the event horizon for given BH metric while \(r_{q}\) is generally termed as the cosmological horizon, which arises due to the quintessence term. The event horizon acquires the respective value for SBH in the prescribed limit.

Lapse function for above BH spacetime given in Eq. (2) is presented graphically in Fig. 1. Left diagram shows the effect of increasing the value of quintessence parameter q on the horizon radius, for fixed values of M, a and \(w_q\), if one increases the value of q within the allowed range, the event horizon shrinks. Similar is the effect of the increment of \(w_q\), for all other parameters having fixed values. One can easily observe the possibility of the presence of two horizons when cloud of strings and quintessence both are present from Fig. 1. The detailed discussion of the horizon structure for this BH metric can be found in [8].

Fig. 1
figure 1

Variation of lapse-function of unit mass SBH surrounded with cloud of strings string and quintessence with radial distance form the centre; left figure: \(a=0.1\), \({w_q}=-0.95\) and different values of q as mentioned in the diagram. Right figure: \(a=0.1\), \(q=0.1\) and different values of \(w_q\) as mentioned in the diagram solid line curve represents the function for SBH

Full size image

3 First integrals of geodesic equations

The geodesic equations [11, 12] and its constraint equations are given by,

$$\begin{aligned}&{\ddot{x}}^{\mu }+{{\Gamma }^{\mu }_{\nu \lambda }}{\dot{x}}^{\nu }{\dot{x}}^{\lambda }=0, \end{aligned}$$
(4)
$$\begin{aligned}&g_{\mu \nu }{\dot{x}}^{\mu }{\dot{x}}^{\nu }=e. \end{aligned}$$
(5)

Here dot denotes the differentiation with respect to the affine parameter \(\tau \) and \(x^{\mu }\) are the spacetime coordinates. Null and timelike geodesics correspond to \(e = 0\) and 1 respectively. The geodesic equations for given BH metric take the following forms,

$$\begin{aligned}&\ddot{t} + \frac{ f'(r)}{f(r)}\, \dot{r} \, \dot{t} = 0, \end{aligned}$$
(6)
$$\begin{aligned}&\ddot{r} + \left( \frac{ f'(r) \, \dot{t}^2 + {f'(r)}^{-1} \,\dot{r}^2 - 2 r \, {{\dot{\theta }}}^2 -2 r \, \sin ^2 \theta \, {{\dot{\phi }}}^2}{2 \, f^{-1} (r)} \right) = 0, \end{aligned}$$
(7)
$$\begin{aligned}&\ddot{\theta }+ \frac{2}{r}\, \dot{r} \, {{\dot{\theta }}} - \cos \theta \, \sin \theta \, {{\dot{\phi }}}^2 = 0, \end{aligned}$$
(8)
$$\begin{aligned}&\ddot{\phi }+ \frac{2}{r} \, \dot{r} \, {{\dot{\phi }}} + 2 \, \cot \theta \, {{\dot{\theta }}} \, {{\dot{\phi }}} =0, \end{aligned}$$
(9)

where the prime and dot denote the differentiation with respect to r and t respectively. The time-like constraint on the trajectories is given by

$$\begin{aligned}&\left( 1-a-\frac{2 M}{r}-\frac{q}{r^{3 \omega _{q}+1}}\right) \dot{t}^2- \left( 1-a-\frac{2 M}{r}-\frac{q}{r^{3 \omega _{q}+1}}\right) ^{-1}\dot{r}^2 \nonumber \\&\quad -r^2({{\dot{\theta }}}^2 + {\sin }^2 \theta {{\dot{\phi }}}^2) = 1. \end{aligned}$$
(10)

Equations (6)–(10) forms the complete set for the study of timelike geodesics in given background geometry.

3.1 Effective potential

For the constrained motion of test particles on equatorial plane one can set \(\theta = \pi /2\) and with this one can integrate Eqs. (6) and (9) which leads to:

$$\begin{aligned} \dot{t}= & {} \frac{C_1}{f(r)}, \end{aligned}$$
(11)
$$\begin{aligned} {\dot{\phi }}= & {} \frac{C_2}{r^2}, \end{aligned}$$
(12)

where the integrating constants \(C_1 \) and \(C_2\) correspond to the conserved total energy E and the conserved angular momentum L of the test particle respectively. Substituting the above Eqs. (11) and (12) along with \(\theta =\pi /2\) in the constraint Eq. (10), the energy conservation equation for the time-like geodesics reads as,

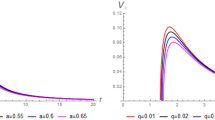
$$\begin{aligned} \frac{{\dot{r}}^2}{2}=\frac{{E^2}-{V_{eff}}}{2}, \end{aligned}$$
(13)

where \({V_{eff}}\) is defined as an effective potential and can be expressed as,

$$\begin{aligned} {V_{eff}} (r)= & {} f(r)\left( \frac{L^2}{r^2}+1\right) \nonumber \\= & {} \left( 1-\frac{2M}{r}\right) +\frac{L^2}{r^2} -\frac{2ML^2}{r^3}-\left( a+\frac{q}{r^{3{w_q}+1}}\right) \nonumber \\&\times \left( 1+\frac{L^2}{r^2}\right) . \end{aligned}$$
(14)

Here the first three terms come out to be exactly same as that of the standard SBH case [12] (first term represents the Newtonian gravitational potential, second term represents a repulsive centrifugal potential and third term as a relativistic correction of general relativity, i.e. proportional to \(1/r^3\)). The extra term \( \left( a+\frac{q}{r^{3{w_q}+1}}\right) \left( 1+\frac{L^2}{r^2}\right) \) in Eq. (14) is due to the presence of cloud of strings and quintessence scalar field around the SBH.

Fig. 2
figure 2

Variation of radial tidal force of a unit mass SBH surrounded with cloud of strings and quintessence with radial distance from centre, left figure: \({w_q}=-0.95\) and different values of q as mentioned in the diagram. Right figure: \(q=0.05\) and different values of \({w_q}\) as mentioned in the diagram

Full size image
Fig. 3
figure 3

Variation of angular tidal force of a unit mass SBH surrounded with cloud of strings and quintessence with radial distance from centre, left figure: \({w_q}=-0.95\) and different values of q as mentioned in the diagram. Right figure: \(q=0.05\) and different values of \({w_q}\) as mentioned in the diagram

Full size image
Fig. 4
figure 4

Variation of geodesic vectors for \(M=1\), \(q=0.05\), \(a=0.3\) and different mentioned values of \(w_q\); left figure: radial geodesic vector with ICI, right figure: angular geodesic vector with ICI; solid line curve represents the corresponding variation for SBH

Full size image
Fig. 5
figure 5

Variation of geodesic vectors for \(M=1\), \(q=0.05\), \(a=0.3\) and different mentioned values of \(w_q\); left figure: radial geodesic vector with ICII, right figure: angular geodesic vector with ICII; solid line curve represents the corresponding variation for SBH

Full size image
Fig. 6
figure 6

Variation of geodesic vectors for \(M=1\), \({w_q}=-0.95\), \(a=0.1\) and different mentioned values of q; left figure: radial geodesic vector with ICI, right figure: angular geodesic vector with ICI; solid line curve represents the corresponding variation for SBH

Full size image
Fig. 7
figure 7

Variation of geodesic vectors for \(M=1\), \({w_q}=-0.95\), \(a=0.1\) and different mentioned values of q; left figure: radial geodesic vector with ICII, right figure: angular geodesic vector with ICII; solid line curve represents the corresponding variation for SBH

Full size image

4 Newtonian acceleration for radial geodesics

For radial geodesics the equation of motion reduces to the following form:

$$\begin{aligned} {\dot{r}}^2={E^2}-f(r). \end{aligned}$$
(15)

Now for a particle falling freely from rest at some fixed position b, one will have its initial energy \(E=\sqrt{f(r=b)}\) [13]. Newtonian radial acceleration [14] is defined as:

$$\begin{aligned} A^{\left( R\right) }\equiv \ddot{r}, \end{aligned}$$
(16)

Using Eq. (15), it can be written as:

$$\begin{aligned} A^{\left( R\right) }=-\frac{M}{r^{3}}-\left( \frac{3{w_q}+1}{2}\right) \frac{q}{r^{3{w_q}+1}}. \end{aligned}$$
(17)

Equation (17) gives the mathematical formulae for the “Newtonian radial acceleration” exerted by SBH surrounded with cloud of strings and quintessence on any neutral test particle entering in its gravitational field. The effect of extra term to that of SBH metric i.e. \(-\left( \frac{3{w_q}+1}{2}\right) \frac{q}{r^{3{w_q}+1}}\) will be examined more precisely in the next section with the analysis of geodesic deviation. Although for Reissner Nordström BH metric such additional terms have established a long standing discussions on their relativistic effects [15,16,17].

Now one can look for the distance in the given background geometry, from where a neutral test particle bounces back. For this one has to calculate the root of \({E^2}(r=b)-f(r)=0\) [18]. For given spacetime this condition gives,

$$\begin{aligned} r^{\left( 3{w_q}+1\right) }\left( q+2Mb^{3{w_q}}\right) -\left( 2Mr^{3{w_q}}+q\right) b^{\left( 3{w_q}+1\right) }=0, \end{aligned}$$
(18)

As the equation of state parameter \(w_q\) can have values ranging as \(-1<w_q<-\frac{1}{3}\), the above Eq. (18) is solved analytically for different allowed values of parameter \(w_q\). Interestingly it has been found that this stopping radius does not depend on the parameters a as well as \(w_q\). The radius depends only on the quintessence parameter q as below:

$$\begin{aligned} R^{stop}=\frac{2M}{q}. \end{aligned}$$
(19)

4.1 Tidal forces acting in the SBH spacetime in the background of clouds of strings and quintessence

Another interesting way to observe the effect of the presence of cloud of strings and quintessence field is to study the geodesic deviation. It depicts the relative acceleration of test particles falling freely in the gravitational field of any BH. The study of geodesic deviation not only enables to understand the physical effects of the gravitational field but one can also get a clear idea about the effect of surrounding cloud of strings and quintessence field on the geometry of the spacetime. We have followed the method given in [18,19,20,21] in order to derive the geodesic deviation equation (Jacobi field equation),

$$\begin{aligned} {\frac{{{D^2}{{\eta }^a}}}{D{{\tau }^2}}}-{{R^a}_{bcd}}{v^b}{v^c}{\eta ^d}=0, \end{aligned}$$
(20)

where \(v^a\) represents a tangent vector to the geodesics and \(\eta ^a\) represents a connection vector between two neighbouring geodesics. The tetrad basis for radial free-fall reference frames have the following form:

$$\begin{aligned} {e^a_0}= & {} \left( \frac{E}{f},\sqrt{{E^2}-f},0,1\right) ;\quad {e^a_1}=\left( -\frac{{{E^2}-f}}{f},-E,0,1\right) ; \nonumber \\ {e^a_2}= & {} \left( 0,0,\frac{1}{r},0\right) ;\quad {e^a_3}=\left( 0,0,0,{\frac{1}{r\sin \theta }}\right) . \end{aligned}$$
(21)

where \(e^{\mu }_{\alpha }\) satisfy the normalisation condition \({e^{\mu }_{\alpha }}{e^{\mu }_{\beta }}{g_{\mu \nu }}=\eta _{\alpha \beta }\), here \(\eta _{\alpha \beta }\) is Minkowski metric. Further, the geodesic deviation vector can also be represented as:

$$\begin{aligned} {\tilde{\eta }}={e^{\mu }_{\nu }} {\eta }^{\nu }. \end{aligned}$$
(22)

Substituting Eq. (22) into Eq. (20), equations for tidal forces in free-fall frame can be written as:

$$\begin{aligned} {\ddot{\eta }}^{{\hat{1}}}= & {} \left[ \frac{2M}{r^3} - \frac{q(3{w_q}+1)(3{w_q}+2)}{r^{3{w_q}+3}}\right] {{\eta }^{{\hat{1}}}}, \end{aligned}$$
(23)
$$\begin{aligned} {\ddot{\eta }}^{{\hat{i}}}= & {} \left[ -\frac{M}{r^3} + \frac{q(3{w_q}+1)}{r^{3{w_q}+3}}\right] {{\eta }^{{\hat{i}}}}, \end{aligned}$$
(24)

where \(i=2,3\), correspond to \(\theta \) and \(\phi \) directions respectively. Geodesic deviation equation corresponding to time coordinate i.e. \( {\ddot{\eta }}^{{\hat{t}}}=0 \) is insignificant. Equation (23) represents the tidal force in radial direction while the Eq. (24) manifests the pressure or compression effects in the angular directions. Radial as well as angular tidal forces due to this BH spacetime depend on BH mass M, quintessence parameter q and EOS parameter \(w_q\) while is independent of string cloud parameter a. Figure 2 shows that radial tidal force in SBH is always positive. As quintessence field is turned on, although the qualitative nature of tidal force remains similar but the curves shift downwards continuously with increasing values of q as well as \(w_q\). As one approaches towards central singularity, the force diverges which represents the infinite radial stretching [12, 18]. Figure 3 shows the non-zero angular tidal forces for different values of the parameters involved therein. Angular force diverges to negative infinity as one approaches to singularity, representing the infinite angular compressing present there [12, 18].

For more precise knowledge of relative acceleration of infalling particles around such BH spacetime, one needs to solve the geodesic deviation equations to find out the deviation vectors in each direction.

Radial tidal force given in Eq. (23) vanishes at,

$$\begin{aligned} {{{\mathcal {R}}_0}^{rtf}}=\left( \frac{q}{4M} (3{w_q}+1)(3{w_q}+2)\right) ^{1/3{w_q}}. \end{aligned}$$
(25)

If radial tidal force takes maximum value at \({{{\mathcal {R}}_{max}}^{rtf}}\). One can infer from Eq. (23) that this distance is given by,

$$\begin{aligned} {{{\mathcal {R}}_{max}}^{rtf}}=\left( \frac{q}{6M} (3{w_q}+1)(3{w_q}+2)(3{w_q}+3)\right) ^{1/3{w_q}}. \end{aligned}$$
(26)

Substituting Eq. (26) in Eq. (23) one can obtain the maximum radial tidal force as,

$$\begin{aligned} {\ddot{\eta }}^{{\hat{1}}}\mid _{max}= M\left( \frac{2{w_q}+1}{{w_q}+1}\right) \left[ \frac{6M}{q (3{w_q}+1)(3{w_q}+2)(3{w_q}+3)}\right] ^{1/{w_q}}{{\eta }^{{\hat{1}}}}. \nonumber \\ \end{aligned}$$
(27)

Angular tidal force given in Eq. (24) vanishes at,

$$\begin{aligned} {{{\mathcal {R}}_0}^{atf}} = \left( \frac{q}{2M} (3{w_q}+1)\right) ^{1/3{w_q}}. \end{aligned}$$
(28)

Again if angular tidal force takes maximum value at \({{{\mathcal {R}}_{max}}^{atf}}\). One can infer from Eq. (24) that this distance is given by,

$$\begin{aligned} {{{\mathcal {R}}_{max}}^{atf}}=\left( \frac{q}{6M} (3{w_q}+1)(3{w_q}+3)\right) ^{1/3{w_q}}. \end{aligned}$$
(29)

Substituting Eq. (29) in Eq. (24) one can obtain the maximum angular tidal force as,

$$\begin{aligned} {\ddot{\eta }}^{{\hat{i}}}\mid _{max}= -M\left( \frac{{w_q}}{{w_q}+1}\right) \left[ \frac{6M}{q (3{w_q}+1)(3{w_q}+3)}\right] ^{1/{w_q}}{{\eta }^{{\hat{i}}}}. \nonumber \\ \end{aligned}$$
(30)

5 Solutions of geodesic deviation equations

For radially freely infalling freely particles, the relation between radial coordinate r and the affine parameter \(\tau \) can be obtained easily as,

$$\begin{aligned} \frac{dr}{d\tau }=-\sqrt{{E^2}-f(r)}. \end{aligned}$$
(31)

With Eq. (31), one can rewrite the system of geodesics deviation Eqs. (23)–(24), in term of radial coordinate derivative as:

$$\begin{aligned}&\sqrt{{E^2}-f(r)}\frac{{{d^2}{{{\hat{\eta }}}^1}}}{d{{r}^2}}-\frac{1}{2}\left( \frac{2M}{r^2}+\frac{q(3{w_q}+1)}{r^{3{w_q}+2}}\right) {\frac{{d}{{{\hat{\eta }}}^1}}{d{r}}}\nonumber \\&\quad =\left( \frac{4M}{r^3}+\frac{q(3{w_q}+1)(3{w_q}+3)}{r^{3{w_q}+3}}\right) {{{\hat{\eta }}}^1}, \end{aligned}$$
(32)
$$\begin{aligned}&\sqrt{{E^2}-f(r)}\frac{{{d^2}{{{\hat{\eta }}}^i}}}{d{{r}^2}}-\frac{1}{2}\left( \frac{2M}{r^2}+\frac{q(3{w_q}+1)}{r^{3{w_q}+2}}\right) {\frac{{d}{{{\hat{\eta }}}^i}}{d{r}}}\nonumber \\&\qquad +\frac{1}{2r}\left( \frac{2M}{r^2}+\frac{q(3{w_q}+1)}{r^{3{w_q}+2}}\right) {{{\hat{\eta }}}^i}=0, \end{aligned}$$
(33)

where Eqs. (32) and (33) represent the radial and angular components of geodesic deviation equation respectively. The analytic solutions [18] of Eqs. (32) and (33) can be obtained as,

$$\begin{aligned}&{{{\hat{\eta }}}^1}=\left[ {A_1}+{B_1}\int \frac{dr}{{(E^2-1+a+\frac{2M}{r}+\frac{q}{r^{3{w_q}}+1})^{3/2}}}\right] \nonumber \\&\quad \times \sqrt{E^2-1+a+\frac{2M}{r}+\frac{q}{r^{3{w_q}}+1}} , \end{aligned}$$
(34)
$$\begin{aligned}&{{{\hat{\eta }}}^i}=\left[ {A_i}+{B_i}\int \frac{dr}{{r^2}\sqrt{E^2-1+a+\frac{2M}{r}+\frac{q}{r^{3{w_q}}+1}}}\right] r. \end{aligned}$$
(35)

where \(A_1\), \(B_1\), \(A_i\) and \(B_i\) are constants of integration. Both of the above solutions are given in form of elliptical integrals.

Two types of initial conditions [19, 20] are considered for the numerical solutions of the geodesic deviation equations. Both of these conditions represent particles starting at the region outside the event horizon \(r=b>{r_H}\).

First initial condition ICI is,

$$\begin{aligned} {\eta }^{{\hat{\alpha }}}(b)=1, {\dot{\eta }}^{{\hat{\alpha }}}(b)=0, \end{aligned}$$
(36)

which correspond to test particle released from rest \(r=b>{r_H}\) (Figs. 4, 6). It implies that the 4-velocity component of the test particle \(\dot{r}=0\) and thus the energy of the particles is fixed i.e., \(E=f(b)\). Second kind of initial condition ICII is,

$$\begin{aligned} {\eta }^{{\hat{\alpha }}}(b)=0, {\dot{\eta }}^{{\hat{\alpha }}}(b)=1. \end{aligned}$$
(37)

which now corresponds to the particles ‘exploding’ at \(r=b>{r_H}\) (Figs. 5, 7). Under this initial condition,

$$\begin{aligned} {{\eta }^{{\hat{\mu }}\prime }}(b)=\frac{1}{\sqrt{\frac{E^2}{f(b)}-1}}, \end{aligned}$$
(38)

where energy of the infalling test particle is not a fixed parameter. Thus energy of the particles also affects the kinematical evolution of the geodesic deviation vectors. It can be observed from Figs. 6 and 7 that initially diverging radial geodesics kept on diverging under both ICs although the relative separation between neighbouring geodesics become smaller as \(w_q\) decreases within its allowed range.

Angular deviation vector decreases under ICI for SBH while the neighbouring geodesics start diverging further as \(w_q\) increases further negatively. Under ICII, the variation is qualitatively similar to corresponding variation for radial geodesic vectors , although the magnitude of separation is further weaker.

6 Conclusions

In this article, we have investigated the effect of tidal forces and geodesic deviation vectors in SBH surrounded by cloud of strings and quintessence field. Some of the important results are summarised below:

  1. (i)

    Two horizons are present around SBH surrounded with cloud of strings and quintessence. BH event horizon radius shrinks if parameters q, a and \(w_q\) are increased while other parameters are fixed.

  2. (ii)

    Tidal forces in radial as well as angular directions are independent of a. Qualitative nature of tidal forces is similar to that of SBH.

  3. (iii)

    Radial infinite stretching and angular infinite compressing is present for any body approaching singularity.

  4. (iv)

    Geodesic deviation around SBH surrounded with cloud of strings and quintessence are devised and solved analytically in radial as well as transverse directions.

  5. (v)

    Geodesic deviation equations are also solved numerically under two different initial conditions. It is observed that radially diverging geodesics keep on diverging under both of the applied ICs, although the magnitude of separation reduces as \(w_q\) becomes more negative or quintessence parameter q increases.

  6. (vi)

    Presence of cloud of strings along with quintessence assists divergence in angular direction, as the initially converging geodesics for SBH become diverging under ICI while the behaviour of diverging geodesics is qualitatively similar to corresponding radial geodesics, although the magnitude of vectors become smaller. This study would be helpful in understanding the gravitational field of SBH surrounded with cloud of strings and quintessence. For more generalised discussions and results we hope to report the related study of the rotating counterpart in near future.