Towards a full general relativistic approach to galaxies

Abstract

We analyse the dynamics of a single disk galaxy from a general relativistic viewpoint. We investigate dark matter (DM) effects in terms of a known family of stationary axially-symmetric solutions of Einstein equations coupled to a rotating dust. These effects are generated by the non-Newtonian features of such solutions and are ascribed to the essential role of frame dragging. Indeed, in such models, the off-diagonal elements of the metric are, in general, of the same order of magnitude of the diagonal ones. We generalize the results of Balasin and Grumiller (BG) to the physical case of differentially rotating dust. In particular, we find that for differential rotation the amount of energy density required to account for the flat rotation curves of disk galaxies is reduced with respect to the BG rigid rotation case. This stresses the discrepancy between Newtonian gravity and general relativity (GR), even at low velocities and low energy densities.

1 Introduction

The description of galactic dynamics using ordinary Newtonian theory leads to several disagreements with the observational data. One of the main problems unexplained by Newtonian theory resides in the justification of the non-Keplerian velocity profiles observed in galaxies: e.g., far from their centre, spiral galaxies display an almost flat rotation curve. In recent years there have been several attempts to reconcile these facts with theory. Some approaches attempt to take this discrepancies into account by modifying gravitational theory itself. Examples are MOND theory [1] as well as large classes of theories complementing the Einstein–Hilbert action with new invariants [2]. For interesting critiques to the MOND models see [3, 4]. As regards modifications of Einstein equations by adding suitable higher order scalars to the action it is worth noting that, were these to be viable, at the very least they do not appear to play any role in clean astrophysical systems such as e.g. the Double Pulsar [5, 6]. Another approach is that of introducing new hypothetical types of particles (dark matter) integrating the Newtonian picture, which interact only gravitationally with the usual baryonic matter; see [7] for a review. Since the speeds of stars in galaxies are much smaller than the speed of light and gravity is assumed to be “weak” far from the central region, the general consensus is that the Newtonian limit of the Einstein equations is applicable in this setting. Therefore, full GR is not usually considered to be a viable solution. However, the matter is far more delicate than what it might seem at first glance.

Indeed, though in the presence of low velocities and weak gravitational fields the Newtonian approximation is certainly valid everywhere locally, it turns out not to be valid anymore globally in spatially extended rotating systems, such as galaxies. The reason for this lies in the dynamical nature of the gravitational field, which in such systems manifests itself primarily through the dragging effect due to the off-diagonal elements of the metric, which, in general, are of the same order of magnitude of the diagonal ones. This was first noted in the pioneering works [8, 9] and, subsequently, in [10]. Later on, Balasin and Grumiller introduced a new model [11] (BG), eliminating the unphysical behaviour affecting some previous solutions and showing explicitly that for extended rotating sources the weak-field approximation is indeed not-Newtonian globally. See also [12]. This model gained relevance recently because of Ref. [13], in which the authors claimed that BG is a good modelization of the average velocity profile of the Milky Way stars obtained from the Gaia DR2 catalogue, thus favoring the conclusion that the galaxy’s flat rotational curves are a purely GR effect, and hence do not require the existence of dark matter! However, the results in [13] must be taken with a grain of salt, as their use of the Gaia DR2 data is limited to an 11 kpc range from the galactic centre and BG themselves claim that theis rigid model might explain only about 30% of the DM effect.

In this paper we extend the results of BG by relaxing the condition of rigid rotation (the BG corotation condition, see Appendix B), thus modeling a disk galaxy by the most general stationary axisymmetric solution of Einstein’s equations with a dust energy-momentum tensor [14]. The dust condition is equivalent to assuming the approximation that the star velocities can be described locally by their average velocity field v(r, z). In other words, we neglect the contribution of velocity dispersion, which is expected to be a reasonable approximation outside the central bulge, where the density of stars is low.

In Sect. 2 we introduce and discuss the dust model expressed in standard cylindrical coordinates [15,16,17,18,19,20]. The model depends on a largely arbitrary spacetime field $\eta$ and on a likewise arbitrary negative function $H=H(\eta )$. We derive the expressions for the matter density $\rho$ and for the angular velocity $\Omega =\frac{d\phi }{dt}$ of the dust, as functions of $\eta$ and H. It turns out that $\rho$ depends on H through its logarithmic derivative $l(\eta ):=\frac{\partial _{\eta }H}{H}$. The case of rigid rotation corresponds to a constant $\Omega \equiv \Omega _0$, or equivalently to a constant $H(\eta )\equiv -1$, and $l\equiv 0$. Interestingly, for a given field $\eta$, the case of rigid rotation corresponds to the highest distribution of total matter density and hence to the highest concentration of dark matter. We refer the relevant quantities to the so called ZAMO frames (Zero Angular Momentum Observers), namely to the locally non-rotating observers, which have no angular momentum with respect to flat infinity. These are the natural frames relative to which to measure the velocity distribution v(r, z). With respect to the ZAMO, v has a simple expression in terms of $\eta$:

$$\begin{aligned} v(r, z)=\frac{\eta (r, z)}{r}. \end{aligned}$$

(1.1)

Note that even though ZAMO play a privileged role in the definition of physical quantities, their velocity field v is not necessarily the empirical velocity that we measure for the other galaxies. Comparisons with such empirical data will be shown in a future work. As regards the matter distribution $\rho$, note that it depends in an essential way on both $\eta$ and H, which shows that different matter densities may give rise to the same velocity field.

In Sect. 3 we discuss the functional and differential equation (VFE) satisfied by the velocity field v(r, z) relative to ZAMO observers. Like the density $\rho$, the VFE depends on H through the function $l(\eta )$. In the general case of arbitrary differential rotation, this equation is unduly complicated and can only be treated numerically. However, it is not difficult to see that it allows for circular orbits out of the galactic plane, an interesting result which is a consequence of inertial dragging and which has no counterpart in the Newtonian case.

In the rigidly rotating case the VFE simplifies considerably, becoming equivalent to the Laplace equation in flat space. However, by taking a constant $l(\eta )$ proportional to a small dimensional parameter $\frac{v_c}{R_G}$ (where $v_c$ is a typical orbital velocity of a star element, of the order of tens or hundreds kilometers per second, and $R_G$ is the radius of the galaxy, of the order of $10^{18}$ kilometers), equation VFE can also be handled to first order in $\frac{v_c}{R_G}$. We do this in Sect. 4. We then show that, with such an approximation and disregarding higher order terms in v, for values of r larger than the galactic radius equation VFE simplifies to one which is satisfied by $v\equiv av_c$, independently of r. In other words, at least for galaxies which are liable to be reasonably modeled by an $(\eta , H)$ metric with l very small, the model explains the flat rotation curves without resorting to dark matter. The result of Ref. [13] based on the Gaia data would indicate that the Milky Way falls in this category. For a given velocity field and for small l, we also derive in this section the ratio between the matter densities of the non-rigid and the rigid case. It turns out that this ratio goes to zero for values of r larger than the galactic radius, an expected result since the dark matter halo is supposed to be distributed mostly in the exterior regions.

Section 5 is dedicated to the discussion of future perspectives.

2 Stationary axisymmetric rotating dust

We model a disk galaxy by a stationary, axisymmetric metric expressed in standard cylindrical coordinates and coupled to an energy-momentum dust tensor

$$\begin{aligned} T_{\mu \nu }= \rho (r, z)u_{\mu }u_{\nu }. \end{aligned}$$

(2.1)

Such a metric can be written as (we take units such that $c=1$)

$$\begin{aligned} ds^2= & {} g_{tt}(r, z)dt^2 + g_{t\phi }(r, z)dtd\phi \nonumber \\&+ g_{\phi \phi }(r, z) d\phi ^2+ e^{\mu (r,z)}\left( dr^2+dz^2\right) . \end{aligned}$$

(2.2)

The coupling condition was solved in [14]. Here,

$$\begin{aligned}&u^{\mu }=(-H)^{-1/2}(\partial _t+\Omega \partial _{\phi }), \end{aligned}$$

(2.3)

$$\begin{aligned}&{\left\{ \begin{array}{ll} g_{tt}=\frac{(H-\eta \Omega )^2-r^2\Omega ^2}{H} \\ g_{t\phi }=\frac{\eta ^2-r^2}{-H}\Omega +\eta \\ g_{\phi \phi }=\frac{r^2-\eta ^2}{-H} \end{array}\right. }, \end{aligned}$$

(2.4)

$$\begin{aligned}&\mu _r = \frac{1}{2r} \Big [ (g_{tt})_r (g_{\phi \phi })_r-(g_{tt})_z (g_{\phi \phi })_z \nonumber \\&\qquad - ((g_{t\phi })_r )^2+((g_{t\phi })_z )^2 \Big ],\nonumber \\&\mu _z = \frac{1}{2r} \Big [ (g_{tt})_z (g_{\phi \phi })_r + (g_{tt})_r (g_{\phi \phi })_z \nonumber \\&\qquad \qquad \qquad - 2 (g_{t\phi })_r (g_{t\phi })_z \Big ] , \end{aligned}$$

(2.5)

$$\begin{aligned}&8\pi G\rho =\frac{\eta ^2 r^{-2}(2-\eta l)^2-r^2l^2}{4g_{rr}}\frac{\eta _r^2+\eta _z^2}{\eta ^2}. \end{aligned}$$

(2.6)

The parameters $\eta$ and H are not gauge choices, as shown in Appendices A and B. $\eta$ is a function of r and z, H is an arbitrary negative function of $\eta$ and

$$\begin{aligned} \Omega :=\frac{1}{2}\int H'\frac{d\eta }{\eta }, \end{aligned}$$

(2.7)

$$\begin{aligned} l(\eta ):=\frac{1}{H}\frac{dH}{d\eta }. \end{aligned}$$

(2.8)

The arbitrariness of $\eta (r, z)$ can be expressed by an axially symmetric function $\mathcal {F}(r,z)$ which satisfies the harmonicity-like condition

$$\begin{aligned} \mathcal {F}_{rr}-\frac{1}{r}\mathcal {F}_r+\mathcal {F}_{zz}=0. \end{aligned}$$

(2.9)

The parameter $\eta (r, z)$ can then be implicitly found using

$$\begin{aligned} \mathcal {F}=2\eta +r^2\int \frac{H'}{H}\frac{d\eta }{\eta }-\int \frac{H'}{H}\eta d\eta . \end{aligned}$$

(2.10)

The $\Omega (r,z)$ parameter describes the angular velocity of the dust referred to the coordinates $\phi , t$: $\Omega =\frac{d\phi }{dt}$. The particular case of rigid rotation corresponds to a constant $\Omega \equiv \Omega _0$ or, equivalently, to a constant $H(\eta )\equiv -1$, e.g. to $l(\eta )\equiv 0$. Such a rigidly rotating dust was studied in [11], where the energy density $\rho _{Rig}$ is given by Eq. (2.6) with $l=0$. From the expression of (2.6) it is clear that for a generic non-rigid rotation, i.e. $l\ne 0$, the required density $\rho$ is less than the $\rho _{Rig}$ case. One could think of the difference as an “effective matter” term $\rho _{eff}\approx \frac{r^2l^2}{32\pi G}\frac{\eta _r^2+\eta _z^2}{\eta ^2}$ subtracted from that of the rigid model.

2.1 The ZAMO observer

The natural observers employed to measure the velocity in the galaxy are the Zero Angular Momentum Observers (ZAMO) [21]. These are defined by the tetrad

$$\begin{aligned} e^0&= \frac{r}{\sqrt{g_{\phi \phi }}} dt, \qquad e^1=\sqrt{g_{\phi \phi }}(d\phi -\chi dt),\nonumber \\ e^2&= e^{\mu /2}\, dr,\qquad e^3= e^{\mu /2}\, dz, \end{aligned}$$

(2.11)

where

$$\begin{aligned} \chi \equiv - \frac{g_{t\phi }}{g_{\phi \phi }}= \frac{H \eta }{(r^2-\eta ^2)}+\Omega . \end{aligned}$$

(2.12)

The function $\chi$ gives the angular velocity of such observers as measured from an inertial observer at infinity. Indeed, the relevant elements of the dual basis are

$$\begin{aligned} e^0 \rightarrow X\propto \left( \partial _t+ \chi \partial _\phi \right) , \nonumber \\ e^1 \rightarrow Y \propto \partial _\phi . \end{aligned}$$

(2.13)

Define v(r, z) as the velocity measured by the reference frame formed by the locally non rotating observers, i.e. the ZAMO, as

$$\begin{aligned} - (e^0)_{\mu } u^{\mu }:= \frac{1}{\sqrt{1-v^2}}, \end{aligned}$$

(2.14)

where u is the four velocity of the dust (2.3). We get

$$\begin{aligned} v(r,z)= \frac{\eta (r,z)}{r} , \end{aligned}$$

(2.15)

where $v\ll 1$. However, recall that the v measured by ZAMO is not necessarily the velocity one measures for the galaxies other than the Milky Way. From an observational perspective it is interesting to note that it is not possible to distinguish between a rigidly rotating or a differentially rotating galaxy if we only have information about the velocity profile v with respect to the ZAMO. Indeed, different choices of H can yield the same velocity profile.

3 Velocity field equation

We replace $\eta =rv$ inside all formulas of Sect. 2, making their dependence on the physical velocity $v:=v_{ZAMO}$ explicit. Then, from (2.9) we get

$$\begin{aligned} 0&= l'\left( \frac{1}{v}-v\right) [r^2v_z^2+(rv_r+v)^2]\nonumber \\&\quad +l \left[ \left( \frac{1}{v}-v\right) (rv_{zz}+rv_{rr}+3v_r) \right. \nonumber \\&\quad \left. -\left( \frac{1}{v}+v\right) \frac{r}{v}(v_z^2+v_r^2)+\frac{2}{r}\right] \nonumber \\&\quad +2\left( v_{zz}+v_{rr}+\frac{v_r}{r}-\frac{v}{r^2}\right) , \end{aligned}$$

(3.1)

See Appendix C for the derivation. Equation (3.1) is the Velocity Field Equation (VFE). It is an extremely complicated functional equation for l (or for H) involving the velocity profile v (and its partial derivatives). Vice versa, for any given choice of $l(\eta )$, one could in principle solve it for v(r, z). We can require $v(r, z)=v(r, -z)$, since disk galaxies are approximately symmetric w.r.t. the galactic plane. Therefore, the speed profile v(r, z) is fully determined by the choices of $l(\eta )$ and of v(r, 0). These are the two degrees of freedom of the relativistic model. In the rigid case $l\equiv 0$, only the third line of Eq. (3.1) survives, so that the equation boils down to the Laplace equation; cfr. [11]. In the Newtonian theory, the VFE would correspond to the constraint $v_z=0$. Indeed, it is well known that in Newtonian gravity an axisymmetric and non singular distribution of matter with no velocity dispersion can only be stationary when full cylindrical symmetry prevents its collapse onto the galactic plane. This can be seen as a consequence of the fact that the Newtonian model has only one degree of freedom $v(r, 0)\equiv v(r, z)$. A Newtonian galaxy can hence have a finite thickness only in the presence of velocity dispersion. Such qualitative difference between the relativistic and the Newtonian model persists even at low speeds $v\ll 1$ and weak fields $g_{\mu \nu }\approx \eta _{\mu \nu }$. Within GR, the matter distribution can be non singular and not cylindrically symmetric, even without velocity dispersion, thanks to the more complicated condition (3.1). In particular, this model allows for circular orbits with radius r and speed $v(r, z)\ne 0$ even at $z\ne 0$, namely out of the galactic plane [22]! This is an astonishing result for a Newtonian intuition, in which gravity is simply a force of attraction. On the other hand, in a general relativistic framework this feature can be understandable e.g. as the effect of a gravitomagnetic field [23, 24].

4 Behaviour far from the centre

We now analyze the expression for the energy density (2.6), with $\eta =v r$ and setting $\kappa = 8\pi G$. We study a model of galaxy far from the bulge, in the external part, where the observed velocities are almost constant and the dark matter effects would seem more conspicuous. The full solution of Eq. (3.1) is extremely hard to achieve and should be approached numerically. Nevertheless, we can gain some important insights from the following general considerations. As already stressed, the third line in the right-hand side of Eq. (3.1) describes the galaxy in the rigidly rotating approximation. Thus, to relax this condition, we consider as a first step an approximately constant l, which we take to be of the order of a characteristic ratio velocity/length of the system. In other words, compatibly with $\rho >0$, we choose

$$\begin{aligned} l= \frac{a v_{c}}{R_G}, \end{aligned}$$

(4.1)

where $v_c$ is of order $10^{-4}$ and $R_G$ is comparable to the radius of the galaxy, or even larger if we wish to describe farther regions. As to the choice of reasonable value of the number a, see Eq. (4.5) and the discussion thereafter. In such approximation one has

$$\begin{aligned} 4 g_{rr} \kappa \rho\approx & {} \frac{1}{v^2 r^2} \left[ v^2 \left( 4-a^2 \left( \frac{r}{R_G}\right) ^2 \right. \right. \nonumber \\&\times \left. \left. \left( \frac{v_c}{v}\right) ^2 \right) ((\eta _r)^2+(\eta _z)^2)\right] , \end{aligned}$$

(4.2)

where we have neglected higher order terms in $v^2$. Note that $a=0$ corresponds to the rigid case. With constant l, the first non-zero order term in v in (3.1) is

$$\begin{aligned}&\left( 2+a \frac{r}{R_G} \frac{v_c}{v}\right) (v_{zz}+v_{rr})+ \left( \frac{3a}{R_G} \frac{v_c}{v}+\frac{2}{r} \right) v_{r}\nonumber \\&- a \frac{v_c}{v^2} \frac{r}{R_G}((v_z)^2+(v_r)^2) + \frac{2a}{R_G r} v_c -\frac{2}{r^2} v=0. \end{aligned}$$

(4.3)

In the limit $r \ll R_G$, namely in the inner part of the galaxy, we get

$$\begin{aligned} v_{zz}+v_{rr}+ \frac{v_r}{r}- \frac{v}{r^2}\approx 0, \end{aligned}$$

(4.4)

as in the BG case. Therefore, the discrepancy with the rigid case arises as we approach the “edges” of the galaxy. Indeed, for $r \approx R_G$, we get

$$\begin{aligned}&\left( 2+a \frac{v_c}{v} \right) (v_{zz}+v_{rr})+\left( 3a \frac{v_c}{v} +2\right) \frac{v_r}{r} \nonumber \\&-a\frac{v_c}{v^2}((v_z)^2+(v_r)^2)+ 2\left( a \frac{v_c}{v}-1\right) \frac{v}{r^2}\approx 0. \end{aligned}$$

(4.5)

Among its solutions this equation allows the constant case $v=av_c$, which indeed corresponds to the observed flat rotation curves. However, recall that here v is the one measured by ZAMO. On the basis of the observed velocity of the halo stars, we see that a is the order of magnitude of 10. Then, with our assumptions of slight deviation from rigidity and with the choice of v constant, we find the approximate expression of the metric. Explicitly

$$\begin{aligned} H=&- e^{lvr} \approx -(1+lvr), \nonumber \\ H'=&\frac{dH}{d\eta }= - l e^{lvr}\approx -l, \qquad H''=0. \end{aligned}$$

(4.6)

From (2.7) we get

$$\begin{aligned} \Omega =- \frac{l}{2} \int \frac{e^{v l r}}{r} \approx - \frac{l}{2} \log \left( \frac{r}{r_0}\right) , \end{aligned}$$

(4.7)

where we are neglecting squared velocities, and $r_0$ is an integration constant. The, from Eqs. (2.4), we find the components of the metric to order v:

$$\begin{aligned} g_{tt}&\approx -1, \nonumber \\ g_{t\phi }&\approx \frac{l}{2} \log (r/r_0) r^2 + v r, \nonumber \\ g_{\phi \phi }&\approx r^2. \end{aligned}$$

(4.8)

As regards $\mu$, we have

$$\begin{aligned} \mu _r \approx - \frac{1}{2r} \left[ \frac{a}{2} v_c \frac{r}{R_G} \left( 1+ 2 \log \left( \frac{r}{r_0}\right) \right) +v \right] ^2=O(v^2), \nonumber \\ \end{aligned}$$

(4.9)

which gives an approximately constant $\mu$. Therefore, up to order v, the metric and the four-velocity of the dust read

$$\begin{aligned} ds^2&=- \left( dt- \chi d\phi \right) ^2 + r^2 d\phi ^2+ e^{\mu }\left( dr^2 +dz^2 \right) , \end{aligned}$$

(4.10)

$$\begin{aligned} \chi&=\frac{a}{2} v_c \log (r/r_0) \frac{r^2}{R_G} + v r, \end{aligned}$$

(4.11)

$$\begin{aligned} u^{\mu }&= \left( \partial _t - \frac{a}{2} \frac{v_c}{R_G} \log \left( \frac{r}{r_0}\right) \partial _\phi \right) . \end{aligned}$$

(4.12)

Then, the mass density expression reduces to

$$\begin{aligned} \kappa \rho \approx e^{-\mu }\frac{4-a^2 (r/R_G)^2 (v_c/v)^2}{4} \frac{(\eta _r)^2+(\eta _z)^2}{r^2}. \end{aligned}$$

(4.13)

Comparing the densities in the rigid ($l=0$) and the non rigid cases, and assuming the same velocity profiles, we have

$$\begin{aligned}&\kappa \rho _{Rig}\approx e^{-\mu }\frac{(\eta _r)^2+(\eta _z)^2}{r^2} \Rightarrow \nonumber \\&\frac{\rho _{nRig}}{\rho _{Rig}}\approx \frac{4-a^2 (r/R_G)^2 (v_c/v)^2}{4}=1-\frac{a^2}{4} \left( \frac{r}{R_G}\right) ^2 \left( \frac{v_c}{v}\right) ^2. \end{aligned}$$

(4.14)

This last formula makes the reduction effect on the required matter even more evident. For comparison, we also recall the Newtonian density on the galactic plane [11]

$$\begin{aligned} \rho _{Rig}<\rho _N(r, 0)\propto \frac{v^2+2rvv_r}{r^2}. \end{aligned}$$

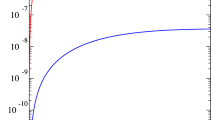
Note that the ratio (4.14) is inhomogeneously distributed, becoming relevant for r bigger than the radius of the visible galaxy – namely, in those regions where the dark matter halo is usually supposed to be located. For more distant regions, this relativistic effect would become even more relevant, as v is expected to tend to zero. $\rho$ would eventually reach zero for some finite value $R_M$, which could be considered as a “scale radius” of the galaxy. In [13] it was shown how the rigid model of the Milky Way already fits the Gaia’s data without any need for dark matter (at the present precision level). Wheras for our galaxy the approximation of small constant l appears to be viable, for other galaxies the differential rotation might be more important though, leading to a further reduction of the needed mass density, thus exhibiting an apparently greater amount of dark matter.

5 The relativistic paradigm and future perspectives

When, in the XIX century, the anomalous precession of the perihelion of the planet Mercury, amounting to $43''$ per century, was accurately measured, Urbain Le Verrier, the discoverer of Neptune, believed that the discrepancy could be solved by attributing the anomaly to the gravitational influence on Mercury of an additional hypothetical planet, dubbed Vulcan, orbiting the Sun somewhere in between Mercury and the Sun itself. Or, alternatively, to an unknown asteroid belt near the Sun. Careful search failed to discover these objects. Another suggestion was that the anomaly might be attributed to the dust particles present in the orbital planes of the solar system and responsible for the faint zodiacal light. However, it was soon realized that this zodiacal dust did not have enough mass to explain the anomaly. The problem was not solved until 1915, when the anomalous precession was neatly explained by Einstein’s general relativity theory. Hence, no need of extra matter to explain the phenomenon; it was simply Newton’s theory which had failed. Instead, it was general relativity which fixed things, by means of its post-Newtonian corrections.

It was a breakthrough then, hence why shouldn’t it be a breakthrough again now, with the problem of dark matter? Compare [13] about this analogy. The general-relativistic models of disk galaxies put forth in the present work lead to a significant reduction in the mass required to generate their rotation curves compared to the requirements of the Newtonian approximation, and to those of other simpler GR models. This suggests a new interpretation of astrophysical observations which reweight the dark matter amount required in galaxies. Indeed, it was shown in [11] how the rigid model already reduces the required DM by 30%. We expect an even bigger reduction by the non rigid model. For example, if the total reweight provided by the latter would lead to a DM reduction of about 90%, the remaining amount of DM would be explainable by isolated non luminous objects in the galactic halo (MaCHOs): rogue planets, brown dwarfs, neutron stars, isolated black holes... See [25, 26] for the evaluation of the contribution of these objects.

Of course, dark matter effects do not manifest themselves in galaxies alone; they appear everywhere in the universe: in the relative motions of galaxies in galaxy clusters [27, 28], in the motion of clusters in superclusters, in Bullet clusters [29,30,31], in gravitational lensing effects [32], in the temperature of hot gases in galaxies [28], in the peaks of the CMB [33, 34], in the evaluation of cosmological parameters according to SNIa redshift [35, 36], and so on. However, the results obtained so far encourage us to believe that it should be possible to reweight these effects with analogous general-relativistic non negligible, and maybe dominant, corrections. It is usually assumed that the low energy limit of GR would always reduce to the Newtonian theory, but this is true only under suitable hypotheses (compare the hypotheses required in [37]). There exist many examples of this: the gravitational field shielding, proven by Carlotto and Shoen [38, 39]; the stationary vacuum solutions, called geons, which are localized gravitational waves held together by their own field energy [40]; and even the propagating gravitational waves, whose existence has been confirmed in recent years [41]. All these are all non-Newtonian phenomena allowed by GR, in spite of low energy density and low particle speeds. The studies of stationary, axisymmetric metrics such as (2.2) are another example of these phenomena, since the off-diagonal component plays the role of an additional degree of freedom, which is in general not negligible at the first order. This term has no Newtonian interpretation, and it gives rise to the well known gravitomagnetic field [23, 24]. Gravitomagnetism covers a large class of phenomena for which the discrepancy between GR and Newtonian theory can be clearly appreciated.

All these non-Newtonian phenomena can be theoretically understood as the relativistic gravitational field has more degrees of freedom than the Newtonian one, being a dynamical field, which carries its own energy and momentum. These additional dynamical degrees of freedom are not necessarily frozen in the low energy limit. Therefore, we propose the following “relativistic paradigm”, to the purpose of studying all kinds of DM effects: for any such effect, develop an appropriate general GR model, then perform the low energy limit and compare its matter content with the usual models found in the literature. Whenever the additional dynamical degrees of freedom of GR are involved, we can expect non negligible differences. To our knowledge, most attempts made so far in order to explain “dark matter” related phenomena require that some extra variables be added to the Newtonian model. The simplest addition is that of an unknown kind of matter. MOND theories add parameters to the very laws of gravity. Here we stress the fact that suitable additional degrees of freedom can be found within general relativity itself, which is arguably a more natural and conservative choice. The existence of some kind of particle or interaction beyond our present knowledge is plausible, but even then a fully general-relativistic model would be necessary as a serious theoretical framework for the interpretation of the observational data.

For example, it should be possible to apply such an approach to the motion of galaxies in galaxy clusters. In other words, it may be that the dark matter effects which keep clusters together, in spite of the rapid orbital motions of their individual galaxy components, could once more be reweighted by the combined effect of the gravitational dragging originating from the angular momenta of the individual galaxies and the angular momentum of the whole cluster itself. This could be expressed using a relativistic generalization of Virial’s Theorem, taking the energy-momentum of the gravitational field into account. These relativistic corrections to the Virial of a system of bodies could also be applied to the dynamics of the Bullet clusters, to the temperature of hot gases, and to other DM effects of the same kind. Several examples are known of background galaxies which are lensed by massive elliptical and lenticular-shaped foreground galaxies. The light from the background galaxy is distorted and warped by the lenses. Even some examples of perfect alignments are known, which give rise to Einstein’s rings, complete circular images of the lensed galaxies. The nature, structure and shape of the lensed images are normally employed as probes of the dark matter distribution around the galactic lenses. Our program is to tackle the problem of showing that these images can be explained, at least to some extent, by the general relativistic dynamics of the gravitational field of the lenses. We suggest to compare the observed lensing with the geodesic deformation in a dragging metric, instead of a Schwartzshild one, as it is usually done. We expect that the relevant off-diagonal components produce some corrections to the apparent mass of the galaxy. Similar reweighting should could done for any other DM effect which involves the spacetime metric curvature, as the CMB’s peaks and the SNIa redshifts.

We conclude by mentioning some future perspectives about the studies on disk galaxies. There exists a rich variety of phenomenology of disk galaxies, about their dark matter content, speed of rotation, and total mass amount. The arbitrariness of the parameter l should make our model sufficiently flexible to justify such differences. For example, what about the recent discovery of so-called ultra-diffuse galaxies, namely of fluffy galaxies whose star density is very low and which are spread over vast distances [42, 43]? These galaxies seem to have very little dark matter, or no dark matter at all. We would like to justify theoretically this characteristic as following from $(\eta , H)$-metrics for which the dust density is very low. If we look at the phenomenology of disk galaxies other than our own, we have no possibility to reconstruct for them their respective fields $\eta$ with any accuracy, as we are able to do with the Milky Way using the Gaia data. Instead, we have to rely on the observational data that we are able to gather about their luminosities, densities, spectra, gas content, structure of the central bulge, etc. We expect these data to give some reasonable indications about the values of theirs model parameters $\eta$ and H (and, consequently, l). In particular, what are the dark matter effects that we can expect from galaxies, if any, for which the parameter l is large? At any rate, the dark matter effects expected for large values of l could be achieved by tackling Eqs. (2.10) and (3.1) numerically.

Since the Milky Way appears to be very old [44,45,46] and well described by an $(\eta , H)$-metric with l very small, it may be interesting to investigate whether the value of the parameter l may somehow be linked to the age of the galaxy. In other words, if it may perhaps turn out that l decreases as the age of the galaxy increases. This seems reasonable, given the fact that the Milky Way is an old and big galaxy, hence its matter and gravitational field have had enough time to exchange angular momentum. A detailed description of such mechanism would include a breaking of stationarity and would deserve further study, a problem we intend to tackle in a following work. If true, this would also suggest a higher chance to find more dark matter in younger galaxies. Therefore, we plan to apply GR to the time dependent problem of the formation of a galaxy, in particular of a disk galaxy. Most models of galaxy formation envisage smaller or larger clouds of gas, dust, stars and dark matter swirling through space, careening by gravity into other analogous clouds and aggregating into denser spinning material. What we believe is that the role of spinning dark matter in this process is actually ascribable, at least for some fraction, to the frame dragging effect of the dynamical angular momentum of the gravitational field, therefore reweighting the extra matter for its explanation. In particular, we expect the incoming data from JWST on the dynamical formation of early galaxies to be very useful in this respect. From this point of view, great expectations rely on the COSMOS (Cosmic Evolution Survey)-Webb program, the large General Observer program selected for JWST’s first year.

Appendices

Appendix A: The precession of gyroscopes

The study of the effects of GR on the global behavior of disk galaxies has so far only been limited to the rigid rotation case ($\Omega$ constant), see e.g. [11, 13]. Since in the present paper we have generalized the treatment of these effects to the differentially rotating case ($\Omega =\Omega (r,z)$), it may be interesting to investigate, at least in principle, what distinguishes physically the two situations. Therefore, we propose a hypothetical observation capable to distinguish between the two cases. Let the ZAMO observers carry gyroscopes along with them. Then we could compare the gyroscope precessions in the rigid and non-rigid case. To this end, consider the connection 1-forms

$$\begin{aligned} \omega ^0_{\,1}&= \frac{1}{2} \frac{1}{\sqrt{g_{rr}}\,r} \left( \partial _r \chi \, e^2+\partial _z \chi \,e^3 \right) , \nonumber \\ \omega ^0_{\,j}&= - \left( \partial _j \log \frac{r}{\sqrt{g_{\phi \phi }}} \right) \frac{e^0}{\sqrt{g_{rr}}}+ \frac{1}{2} \frac{\partial _j \chi }{\sqrt{g_{rr}}\,r} e^1, \nonumber \\ \omega ^j_{\,1}&= \left( \partial _j \log \frac{1}{\sqrt{g_{\phi \phi }}} \right) \frac{e^1}{\sqrt{g_{rr}}}- \frac{1}{2} \frac{\partial _j \chi }{\sqrt{g_{rr}}\,r} e^0, \nonumber \\ \omega ^2_{\,3}&= \left( -\left( \partial _z \log \sqrt{g_{rr}} \right) e^2+ \left( \partial _r \log \sqrt{g_{rr}} \right) e^3 \right) , \end{aligned}$$

(A1)

where $j=(2,3)$. We see from (A1) that the ZAMO frame is non inertial, since the three-acceleration $a_j$ which an observer with four-velocity $e_0$ experiences is

$$\begin{aligned} a_j \propto \partial _j \log \left( \frac{r}{\sqrt{g_{\phi \phi }}}\right) , \qquad j=r,z, \end{aligned}$$

(A2)

this being the force required by its thrusters to keep the observer in its orbit. The corresponding gyroscopes precess relatively to the orthonormal frame with angular velocities

$$\begin{aligned} \omega _j \propto \partial _j \chi , \qquad j=r,z. \end{aligned}$$

(A3)

The difference in the velocities measured by the ZAMO in the non rigid ${\omega }_{nRig}$ and the rigid ${\omega }_{Rig}$ cases is measured by the difference

$$\begin{aligned} \Delta \omega _j= & {} {\omega }_{nRig}\,{}_j-{\omega }_{Rig}\,{}_j \propto \frac{\eta }{r^2-\eta ^2} \partial _a H \nonumber \\&+ \partial _j \Omega + \Delta H \, \partial _j \left( \frac{\eta }{r^2-\eta ^2}\right) , \end{aligned}$$

(A4)

where $\Delta H:= H_{nRig}- H_{Rig}=H_{nRig}+1$. The precession observation can thus distinguish between the two situations.

Appendix B: Deformation tensor

Rigid bodies do not exists in GR, as a consequence of the Locality Principle. However, one can still give a definition of “rigidity” in a relativistic framework through the deformation tensor $\mathbf {P}$

$$\begin{aligned}&\mathbf {P}(u) := \mathcal {L}_u(g)= (u_{\mu ;\nu } + u_{\nu ;\mu }) dx^\mu \otimes dx^\nu , \end{aligned}$$

(B1)

where $\mathcal {L}$ is the Lie derivative. Then, the system is defined to be “rigid”when $\mathbf {P}(u)$ vanishes. Here we show that this happens for our metric when $H\equiv -1$, which justifies our use of the term “rigid” in this case. In order to see this, we proceed with the construction of a scalar that characterizes the physical non-rigidity of the system. Its explicit dependence on H shows again (compare Appendix A) that the differential rotation is a physically relevant parameter and not a gauge freedom.

To simplify the calculations, we use the approximation of small differential rotation

$$\begin{aligned} H(\eta )= - \left( 1+p^2 \eta ^2 \right) +o(p^2), \end{aligned}$$

(B2)

were p is a small parameter. In this case this, from (2.10) one finds

$$\begin{aligned} \eta (r,z) = \frac{1}{p} \tan \left( \frac{p \,\mathcal {F}(r,z)}{2(1+p^2 r^2)}\right) \end{aligned}$$

(B3)

and

$$\begin{aligned} u=\left( 1-\frac{p^2}{2} \mathcal {F}^2 \right) \left( \partial _t - p^2 \mathcal {F} \partial _{\phi }\right) +o(p^2). \end{aligned}$$

(B4)

Then, up to order $p^2$, the deformation tensor is

$$\begin{aligned} \mathbf {P}(u)=&-p^2r^2 \left( \mathcal {F}_r\, dr\odot d\phi +\mathcal {F}_z \,dz\odot d\phi \right) = \nonumber \\ =&-p^2 r^2 d\mathcal {F} \odot d\phi . \end{aligned}$$

(B5)

This formula proves our statement. Note that the deformation is only “spatial” in the proper reference frame of the dust. Hence, there exists no gauge transformation that maps a non constant $H(\eta )$ into $H\equiv -1$.

Appendix C: Deriving the velocity field equation

In this section we deduce the VFE. In [14] it is shown that the equations of motion of the co-moving element, of axisymmetric stationary dust solution, can be rewritten in the form

$$\begin{aligned} 1/r \left[ (r^2 \beta )_a + 2 \eta _a - \frac{\eta }{H} H_a \right] =\epsilon ^{ab}\gamma _b, \end{aligned}$$

(C 1)

$$\begin{aligned} \gamma _{rr}+ \gamma _{zz}+ \frac{\gamma _r}{r}=0, \end{aligned}$$

(C 2)

where we have employed the notations $f_a\equiv f_{,a}$ for the derivative of f with respect to $x_a$, for $f=H, \eta , \gamma , \beta$, $a=1,2$, $x_1=r$, $x_2=z$ and $\beta$ is defined by

$$\begin{aligned} \beta _a=\frac{H_a}{\eta H}. \end{aligned}$$

(C 3)

In terms of the function $\mathcal {F}$ of (2.10), Eq. (C 1) takes the form

$$\begin{aligned} \mathcal {F}_{,a}=r \epsilon ^{ab}\gamma _b. \end{aligned}$$

(C 4)

Then we can write

$$\begin{aligned}&\sum _a \partial _a \left[ 1/r \left[ (r^2 \beta )_a + 2 \eta _a -\frac{\eta }{H} H_a \right] \right] \nonumber \\&\qquad =\partial _a(\epsilon ^{ab}\gamma _b)=\gamma _{rz}-\gamma _{zr}=0, \end{aligned}$$

(C 5)

which is equivalent to Eq. (2.9). Written explicitly it gives

$$\begin{aligned} 0&= \partial _z\left[ \frac{1}{r}\left[ (r^2\beta )_z+2\eta _z-\frac{\eta }{H}H_z\right] \right] \\&\quad +\partial _r\left[ \frac{1}{r}\left[ (r^2\beta )_r+2\eta _r-\frac{\eta }{H}H_r\right] \right] \frac{1}{r}\partial _z\left[ r^2\beta _z+2\eta _z-\frac{\eta }{H}H_z\right] \\&\quad +\frac{1}{r}\partial _r\left[ 2r\beta +r^2\beta _r+2\eta _r-\frac{\eta }{H}H_r\right] \\&\quad -\frac{1}{r^2}\left[ 2r\beta +r^2\beta _r+2\eta _r-\frac{\eta }{H}H_r\right] \\&=\frac{1}{H}\left( \frac{\eta }{r}-\frac{r}{\eta }\right) \left[ \frac{H_z^2+H_r^2}{H}-(H_{zz}+H_{rr})\right] \\&\quad -\left( \frac{\eta }{r}+\frac{r}{\eta }\right) \frac{H_z\eta _z+H_r\eta _r}{H\eta }+\\&\quad +\left( \frac{\eta }{r}+3\frac{r}{\eta }\right) \frac{H_r}{rH}+\frac{2}{r^2}\left[ r(\eta _{zz}+\eta _{rr})-\eta _r\right] . \end{aligned}$$

Recalling that $H(r,z)=H(\eta (r,z))$, we get

$$\begin{aligned} 0&=\frac{1}{H}\left( \frac{\eta }{r}-\frac{r}{\eta }\right) \\&\quad \times \left[ \frac{(H'\eta _z)^2+(H'\eta _r)^2}{H}-(H''\eta _z^2+H'\eta _{zz}) \right. \\&\quad \left. (H''\eta _r^2+H'\eta _{rr})\right] \\&\quad -\left( \frac{\eta }{r}+\frac{r}{\eta }\right) \frac{H'\eta _z\eta _z+H'\eta _r\eta _r}{H\eta }\\&\quad +\left( \frac{\eta }{r}+3\frac{r}{\eta }\right) \frac{H'\eta _r}{rH}+\frac{2}{r^2}\left[ r(\eta _{zz}+\eta _{rr})-\eta _r\right] \\&=(\ln |H|)''\left( \frac{r}{\eta }-\frac{\eta }{r}\right) (\eta _z^2+\eta _r^2)\\&\quad +(\ln |H|)'\left[ \left( \frac{r}{\eta }-\frac{\eta }{r}\right) (\eta _{zz}+\eta _{rr}) \right. \\&\quad -\left. \left( \frac{r}{\eta }+\frac{\eta }{r}\right) \frac{\eta _z^2+\eta _r^2}{\eta }+\left( 3\frac{r}{\eta }+\frac{\eta }{r}\right) \frac{\eta _r}{r}\right] \\&\quad +\frac{2}{r^2}\left[ r(\eta _{zz}+\eta _{rr})-\eta _r\right] . \end{aligned}$$

Finally, relative to the ZAMO, for which $\eta (r, z)=rv(r, z)$, we get

$$\begin{aligned} 0&=(\ln |H|)''(\frac{1}{v}-v)[ (v+r v_r)^2 +r^2 v_z^2]\\&\quad +(\ln |H|)'\left[ \frac{r}{v}\left( v_{rr}+v_{zz}-\frac{v_r^2+v_z^2}{v}\right) -rv(v_{zz}+v_{rr})\right. \\&\quad \left. - r(v_z^2+v_r^2)+3\frac{v_r}{v}-3v_rv+\frac{2}{r}\right] \\&\quad +\frac{2}{r}[2v_r+r(v_{zz}+v_{rr})]-\frac{2}{r^2}(v+rv_r), \end{aligned}$$

which by (2.8) becomes (3.1).