Classical solutions of $\lambda$-deformed coset models

Abstract

We obtain classical solutions of $\lambda$-deformed $\sigma$-models based on $SL(2,{\mathbb {R}})/U(1)$ and SU(2)/U(1) coset manifolds. Using two different sets of coordinates, we derive two distinct classes of solutions. The first class is expressed in terms of hyperbolic and trigonometric functions, whereas the second one in terms of elliptic functions. We analyze their properties along with the boundary conditions and discuss string systems that they describe. It turns out that there is an apparent similarity between the solutions of the second class and the motion of a pendulum.

1 Introduction

Classical solutions are one of the main subjects in Quantum Field Theory and play an important role in studying its dynamics. A large class of such configurations are the so-called solitons, for instance see [1, 2]. In general, solitons are solutions which retain their shape, as they propagate at constant velocity. Usually such lumps are topological in nature and saturate a BPS bound. The most studied example, the kinks, interpolates between different classical vacua of the theory. It goes without saying that the existence of kink solutions requires a non-trivial vacuum structure. In general, these configurations are excitations of the theory, which even though they are not elementary, they exhibit a particle-like behaviour. Kinks can be made to scatter and even create bound states, which are called breathers. An appealing fact about these objects is that the equations describing them are obtained using topological arguments or exploiting integrability and not by attacking the equations of motion straight-forwardly. The reason is the high non-linearity of the equations of motion, which makes the derivation of their solution practically impossible. Having classical solutions one can utilise them in studying several aspects of QFT. These include semi-classical quantization, the vacuum structure of the theory and the effective theory around a non-trivial background solution.

In this work, focusing on two-dimensional field theories, we obtain classical solutions of an integrable class of deformations of WZW-models, namely the $\lambda$-deformations introduced in [3]. The generalization of these models for symmetric spaces is given in [4], while the asymmetric gauging is constructed in [5], building on the setup of [6]. Recently, a lot of attention has been paid in various aspects of these theories. The reason is that they also possess non-perturbative duality symmetries, enabling the exact calculations of various quantities among which $\beta$-functions, C-functions and anomalous dimensions for a large class of single and composite operators (see [7,8,9,10] and references therein).

It would be interesting though, to move one step further and obtain explicit expressions for classical solutions in order to enlarge the knowledge about the dynamics of such theories. Solving directly the equations of motion is a very hard task due to the high non-linearity. To overcome this, we study $\lambda$-deformations on the coset manifolds $SL(2,{\mathbb {R}})/U(1)$ and SU(2)/U(1). Even though the non-linearity is still present and the equations of motion are not drastically simplified, there is a way to proceed. In the case of non-linear sigma models having two-dimensional target space, solving the equations corresponding to the conservation of the Energy–Momentum tensor is essentially equivalent to solving the equations of motion. There is a small caveat in this equivalence but it does not affect our results. In any case, exploiting this remark, along with the fact that these equations are first order and much simpler than the equations of motion, we obtain two different classes of solutions of the models under consideration. It is not clear how they fit in the spectrum of the theory, since our results are not based on topological arguments.

The structure of the paper is as follows: in Sect. 2 we present the specific models under study emphasizing the relations between them via analytic continuations. These relations are useful when deriving solutions of the same class. In Sect. 3 we present the method for deriving the solutions of this work. By solving the Energy–Momentum tensor conservation equations we obtain two classes of solutions for vectorially and axially gauged $SL(2,{\mathbb {R}})/U(1)$ coset model, as well as for the SU(2)/U(1) model. In Sect. 4 we analyze the solutions and also present the admissible boundary conditions and possible brane configurations associated to them. In addition, we discuss the effects of the non-perturbative dualities on the solutions. Section 5 contains conclusions and future directions. Finally, let us mention that in Appendix B we briefly review some aspects of Jacobi elliptic functions. The properties of these functions are required in order to understand properties of the second class of solutions. Our main results are gathered in Tables 1, 2, 3, 4, 5 and 6.

2 $\lambda$-deformations on coset manifolds

In this section we introduce the models that will occupy our interest, namely the $SL(2,{\mathbb {R}})/U(1)$ and SU(2)/U(1) $\lambda$-deformed models. The vectorially gauged SU(2)/U(1) $\lambda$-deformed model has been worked out in [3]. In [11] its relation to the non-compact variant, i.e. the $SL(2,{\mathbb {R}})/U(1)$ $\lambda$-deformed model, was presented. The axial gauging of these models was constructed in [5]. Some additional technical details on the parametrization of the models are given in Appendix A.

2.1 SU(2)/U(1) vector gauging

As a first example we present the SU(2)/U(1) $\lambda$-deformed WZW model in the case of vector gauging.¹ The action reads

$$\begin{aligned} S= & {} \frac{k}{\pi }\int \,d^2\sigma \,e^{2\varPhi }\nonumber \\&\times \left[ \frac{1+\lambda }{1-\lambda }\,\partial _+y_1\,\partial _-y_1+\frac{1-\lambda }{1+\lambda }\,\partial _+y_2\,\partial _-y_2\right] , \end{aligned}$$

(1)

where the conformal factor reads

$$\begin{aligned} e^{-2\varPhi }=1-y_1^2-y_2^2. \end{aligned}$$

(2)

Coordinates $y_1$ and $y_2$ are related to the usual $(\theta ,\phi )$ coordinates by

$$\begin{aligned} y_1=\cos \theta \cos \phi ,\quad y_2=\cos \theta \sin \phi . \end{aligned}$$

(3)

It is evident that the coordinates $y_1$ and $y_2$ satisfy the inequality $y_1^2+y_2^2\le 1$. For completeness, we also write down the equations of motion, which read

$$\begin{aligned} \partial _+\partial _-y_1= & {} \frac{y_1\left( \partial _+y_1\partial _-y_1-\left( \frac{1-\lambda }{1+\lambda }\right) ^2\partial _+y_2\partial _-y_2\right) }{y_1^2+y_2^2-1}\nonumber \\&+\frac{y_2\left( \partial _-y_1\partial _+y_2+\partial _+y_1\partial _-y_2\right) }{y_1^2+y_2^2-1}, \end{aligned}$$

(4)

and

$$\begin{aligned} \partial _+\partial _-y_2= & {} \frac{y_2\left( \partial _+y_2\partial _-y_2-\left( \frac{1+\lambda }{1-\lambda }\right) ^2\partial _+y_1\partial _-y_1\right) }{y_1^2+y_2^2-1}\nonumber \\&+\frac{y_1\left( \partial _-y_2\partial _+y_1+\partial _+y_2\partial _-y_1\right) }{y_1^2+y_2^2-1}. \end{aligned}$$

(5)

Note that the action (1), including the $SL(2,{\mathbb {R}})/U(1)$ models presented below, respects the duality symmetries

$$\begin{aligned} \lambda \rightarrow 1/\lambda ,\quad k\rightarrow -k \end{aligned}$$

(6)

and also

$$\begin{aligned} \lambda \rightarrow -\lambda ,\quad y_1\leftrightarrow y_2 . \end{aligned}$$

(7)

These symmetries, if enforced on the solutions, imply that the parameters of the configurations transform in a specific way. We will come back to this later on.

The action (1) is also written in a new conformally flat form as

$$\begin{aligned} S=\frac{k}{\pi }\int \,d^2\sigma \,e^{2{\tilde{\varPhi }}}\left[ \partial _+\chi \partial _-\chi +\partial _+\psi \partial _-\psi \right] , \end{aligned}$$

(8)

where the conformal factor reads

$$\begin{aligned} e^{-2{\tilde{\varPhi }}}=e^{-2\chi }-\left( \frac{1+\lambda }{1-\lambda }-\frac{4\lambda }{1-\lambda ^2}\cos ^2\psi \right) \end{aligned}$$

(9)

and the coordinates $\chi$ and $\psi$ are defined in term of $\theta$ and $\phi$ by Eqs. (135) and (121). These coordinates are valued in an appropriate domain, so that the dilaton is real and the conformal factor $e^{-2{\tilde{\varPhi }}}$ positive.

2.2 $SL(2,{\mathbb {R}})/U(1)$ vector gauging

Starting with the SU(2)/U(1) model and applying the following transformations

$$\begin{aligned} k\rightarrow -k,\quad \kappa \rightarrow i\kappa ,\quad \theta \rightarrow i\rho . \end{aligned}$$

(10)

we obtain the $SL(2,{\mathbb {R}})/U(1)_V$ $\lambda$-deformed model.² Also, the level k ceases being quantized, but this does not concern our analysis. The transformation of $\kappa$ is required in order to leave the coupling $\lambda$ invariant. In addition, the transformation of $\theta$ amounts to exchanging the cosines to hyperbolic cosines. Notice that, the overall sign of the action, which is due to the transformation of k, is absorbed by the dilaton, so that the later remains manifestly positive in the new coordinates. In this case, the action reads

$$\begin{aligned} S= & {} \frac{k}{\pi }\int \,d^2\sigma \,e^{2\varPhi }\nonumber \\&\times \left[ \frac{1+\lambda }{1-\lambda }\,\partial _+y_1\,\partial _-y_1+\frac{1-\lambda }{1+\lambda }\,\partial _+y_2\,\partial _-y_2\right] , \end{aligned}$$

(11)

where the conformal factor reads

$$\begin{aligned} e^{-2\varPhi }=y_1^2+y_2^2-1 \end{aligned}$$

(12)

and the coordinates $y_1$ and $y_2$ are related to the coordinates $\rho$ and $\phi$ as

$$\begin{aligned} y_1=\cosh \rho \cos \phi ,\quad y_2=\cosh \rho \sin \phi . \end{aligned}$$

(13)

The equations of motion coincide with (4) and (5), since the actions (1) and (11) as functionals of $y_1$ and $y_2$, differ only by an overall sign. Nevertheless, in this case the coordinates $y_1$ and $y_2$ are defined in the complimentary region satisfying $y_1^2+y_2^2\ge 1$. Following the steps of the previous section, the action (11) can be rewritten as

$$\begin{aligned} S=\frac{k}{\pi }\int \,d^2\sigma \,e^{2{\tilde{\varPhi }}}\left[ \partial _+\chi \partial _-\chi +\partial _+\psi \partial _-\psi \right] , \end{aligned}$$

(14)

where the conformal factor reads

$$\begin{aligned} e^{-2{\tilde{\varPhi }}}=\frac{1+\lambda }{1-\lambda }-\frac{4\lambda }{1-\lambda ^2}\cos ^2\psi -e^{-2\chi } \end{aligned}$$

(15)

and the coordinates $\chi$ and $\psi$ are defined in terms of $\rho$ and $\phi$ by (120) and (121).

2.3 $SL(2,{\mathbb {R}})/U(1)$ axial gauging

Implementing the transformations $\rho \rightarrow \rho +i \pi /2$, which is equivalent to

$$\begin{aligned} y_I\rightarrow i y_I, \quad \, I=1,2, \end{aligned}$$

(16)

on $SL(2,{\mathbb {R}})/U(1)_V$ model we obtain the $SL(2,{\mathbb {R}})/U(1)_A$ $\lambda$-deformed model. Interestingly enough, the transformation, relating the axial and vector gauged WZW models at full quantum level [12], also relates the $\lambda$-deformed theories (at least semi-classically). The corresponding action reads

$$\begin{aligned} S= & {} \frac{k}{\pi }\int \,d^2\sigma \,e^{2\varPhi } \nonumber \\&\times \left[ \frac{1+\lambda }{1-\lambda }\,\partial _+y_1\,\partial _-y_1+\frac{1-\lambda }{1+\lambda }\,\partial _+y_2\,\partial _-y_2\right] , \end{aligned}$$

(17)

where the conformal factor reads

$$\begin{aligned} e^{-2\varPhi }=y_1^2+y_2^2+1 \end{aligned}$$

(18)

and the coordinates $y_1$ and $y_2$ are related to the coordinates $\rho$ and $\phi$ as

$$\begin{aligned} y_1=\sinh \rho \cos \phi ,\quad y_2=\sinh \rho \sin \phi . \end{aligned}$$

(19)

The equations of motion are obtained by applying the transformation (16) to the equations of motion (4) and (5). It amounts to setting $-\,1$ to $+\,1$ on the denominators of the right-hand-sides. The action (17) can be rewritten as

$$\begin{aligned} S=\frac{k}{\pi }\int \,d^2\sigma \,e^{2{\tilde{\varPhi }}}\left[ \partial _+\chi \partial _-\chi +\partial _+\psi \partial _-\psi \right] , \end{aligned}$$

(20)

where the conformal factor reads

$$\begin{aligned} e^{-2{\tilde{\varPhi }}}=\frac{1+\lambda }{1-\lambda }-\frac{4\lambda }{1-\lambda ^2}\cos ^2\psi +e^{-2\chi } \end{aligned}$$

(21)

the coordinates $\chi$ and $\psi$ are defined in terms of $\rho$ and $\phi$ by Eqs. (131) and (121). Finally, notice that the action (20) is obtain by (14) by sending $\chi \rightarrow \chi +i\pi /2$.

3 Classical solutions

In this section we derive two different classes of solutions for each model. The first class of solutions is derived using the actions in terms of the coordinates $y_1$ and $y_2$. For the second class of solutions we use the actions in terms of the coordinates $\chi$ and $\psi$. Even though we could have used a different ansatz to solve the equations of motion of the same action, i.e. the one in terms of $y_1$ and $y_2$, we employ the action in terms of $\chi$ and $\psi$, which motivates the ansatz more naturally.

The first class of solutions, corresponding to the actions (1), (11) and (17), is expressed using hyperbolic-trigonometric functions, whereas the second one, corresponding to the actions (8), (14) and (20), in terms of Jacobi elliptic functions. As expected, the relations of the models via analytic continuation, are also reflected to the classical solutions of the same type as well. Recall that (16) relates the axially and vectorially gauged $SL(2,{\mathbb {R}})/U(1)$ models, while the SU(2)/U(1) and the vectorially gauged $SL(2,{\mathbb {R}})/U(1)$ model merely differ by the fact that the coordinates are valued in complementary regions. Therefore, solving one model is enough for solving all of them and the differences of the solutions are highlighted wherever it is necessary.

3.1 A remark on the solution of the equations of motion

It is evident that solving directly the equations of motion (4) and (5) is quite difficult. To untie our hands, a trick is needed which will allows us to sidestep this obstacle. Let us consider a non-linear sigma model (we do not include $B_{\mu \nu }$ field since it is absent in our models)

$$\begin{aligned} S=\frac{1}{2\pi }\int d^2\sigma \,G_{\mu \nu }(X)\partial _+X^{\mu }\partial _-X^{\nu }. \end{aligned}$$

(22)

The non-vanishing components of the Energy–Momentum tensor are given by

$$\begin{aligned} T_{\pm \pm }=G_{\mu \nu }\partial _{\pm }X^{\mu }\partial _{\pm }X^{\nu } \end{aligned}$$

(23)

satisfying $\partial _{\mp }T_{\pm \pm }=0$ on-shell. Due to the previous equations, it follows that $T_{\pm \pm }$ satisfy

$$\begin{aligned} G_{\mu \nu }\partial _{\pm }X^{\mu }\partial _{\pm }X^{\nu }=f_{\pm }(\sigma _{\pm }). \end{aligned}$$

(24)

These are essentially, first integrals of the equations of motion and, as known, solutions of the equations of motion also solve (24). In addition, $f_{\pm }(\sigma _{\pm })$ are functions, which can be set to constants, denoted as $C_\pm$. Without loss of generality, we may additionally select $C_\pm =C$. Performing a Lorentz boost on the world-sheet we may always restore unequal values of $C_+$ and $C_-$. The models under study have a positive definite metric, thus these constants are necessarily positive. Notice that in order to embed this model in string theory, one has to consider the tensor product of this theory with another one, so that the overall Energy–Momentum vanishes, implying that the Virasoro constraints are satisfied. Slightly abusing the terminology and having the previous remark in mind, we will refer to (24) as the Virasoro constraints.

As mentioned, the Energy–Momentum tensor is conserved on-shell. Nevertheless, the converse is not generally true, unless the target space is two-dimensional. In this case it follows that

$$\begin{aligned} \begin{pmatrix} \partial _-T_{++}\\ \partial _+T_{--} \end{pmatrix}=\begin{pmatrix} \partial _+ X^1 &{} \partial _+ X^2\\ \partial _- X^1 &{} \partial _- X^2 \end{pmatrix} \begin{pmatrix} \frac{\delta {\mathcal {L}}}{\delta X^1}\\ \frac{\delta {\mathcal {L}}}{\delta X^2} \end{pmatrix} , \end{aligned}$$

(25)

where ${\mathcal {L}}$ is the Lagrangian density and $\delta {\mathcal {L}}/ \delta X^{\mu }$ is the variation of the action with respect to the $X^{\mu }$ field. Thus, if the matrix on the right-hand-side is invertible, the solutions of the Virasoro constraints are also solutions of the equations of motion.³ This approach resembles the Pohlmeyer reduction, where one gauge fixes the world-sheet diffeomorphisms [13].

3.2 First class of solutions

Having clarified our methodology, we derive the solutions of the models presented in the previous section.

3.2.1 $SL(2,{\mathbb {R}})/U(1)_V$ model

As a first example we derive classical solutions of the model described by the action (11). The Virasoro constraints (24) constitute the pair of differential equations

$$\begin{aligned} \frac{1+\lambda }{1-\lambda }(\partial _{\pm }y_1)^2 +\frac{1-\lambda }{1+\lambda }(\partial _{\pm }y_2)^2=\frac{m^2}{4}(y_1^2+y^2_2-1), \end{aligned}$$

(26)

where we have set $C=m^2/4$ so that the right-hand-side is manifestly positive, as the left-hand-side. The factor of 1/4 is introduced for future convenience. In order to obtain non-trivial solutions, it is required that $m\ne 0$. We can decouple the equations as follows

$$\begin{aligned}&\frac{1+\lambda }{1-\lambda }\,(\partial _{\pm }y_1)^2=\frac{m^2}{4}\left( y_1^2+c_{\pm }-\frac{1}{2}\right) , \end{aligned}$$

(27)

$$\begin{aligned}&\frac{1-\lambda }{1+\lambda }\,(\partial _{\pm }y_2)^2=\frac{m^2}{4}\left( y_2^2-c_{\pm }-\frac{1}{2}\right) . \end{aligned}$$

(28)

Table 1 First class of solution for the $SL(2,{\mathbb {R}})/U(1)_V$ $\lambda$-deformed model

The equations above have similar form, their only difference is the sign in front of $c_{\pm }$. Thus, solving one equation suffices to obtain solutions for both equations. Considering Eq. (27), we immediately obtain that

$$\begin{aligned} \frac{\partial _{\pm }y_1}{\sqrt{y_1^2+c_{\pm }-\frac{1}{2}}}=s_{\pm }\,\frac{m}{2}\sqrt{\frac{1-\lambda }{1+\lambda }}, \end{aligned}$$

(29)

where $s_{\pm }$ are constants that take independently the value 1 or $-\,1$. From now on, we also set $c_{\pm }=c$.⁴ Since is it straightforward to solve Eq. (29), we just present the solutions and make some comments.

First, the functional form of the solution of (29) depends on the value of the constant c. It turns out that the parametric space is divided in three regions, namely $c>1/2$, $1/2>c>-1/2$ and $-1/2>c$, along with the limiting values $c=\pm 1/2$. Secondly, a quick glimpse on (28) suffices in order to realize that the solutions for $y_2$ are obtained from the $y_1$ solutions by sending $c\rightarrow -c$ and $\lambda \rightarrow -\lambda$, while adapting the allowed values for c. Finally, one should combine the solutions for $y_1$ and $y_2$, taking into account the requirement that their derivatives are linearly independent as noted in (25). Essentially, this condition implies that the solutions for $y_1$ and $y_2$ should not be functions of the same variable. In following we choose $y_1=y_1(\tau )$ and also discard the various signs $s_\pm$. These can be recovered by parity transformations of the world-sheet coordinates, combined with the discrete symmetries of the action, such as $y_1\rightarrow -y_1$. We gather the solutions appropriately matched in Table 1. One can verify that these indeed satisfy the equations of motion (4) and (5).⁵ Notice that $\tau _0$ and $\sigma _0$ are integration constants, which may be regarded as collective coordinates of the solutions.

3.2.2 $SL(2,{\mathbb {R}})/U(1)_A$ model

In the axial gauging case, writing down the Virasoro constraints corresponding to the action (17), one realizes that the solutions are obtained by setting

$$\begin{aligned} c\rightarrow -c,\quad 1/2\rightarrow -1/2 \end{aligned}$$

(30)

on the coefficients of various functions in Table 1, while neglecting the overall minus sign to compensate the i factor of the transformation (16). Note that the range of c should be adjusted appropriately. The solutions are gathered in Table 2.

Table 2 First class of solution for the $SL(2,{\mathbb {R}})/U(1)_A$ $\lambda$-deformed model

3.2.3 SU(2)/U(1) model

The solutions of the SU(2)/U(1) model are obtain by the ones of $SL(2,{\mathbb {R}})/U(1)_V$ case, for $m^2\rightarrow -m^2$. As this coset is compact, the admissible values of the parameter c, are bounded. In particular, it turns out that c satisfies the inequality $1/2\ge c\ge -1/2$. The solution are gathered in Table 3. Notice that all solutions in Tables 1 and 2 (except the exponential ones) can be cast in the form given above.

Table 3 First class of solution for the SU(2)/U(1) $\lambda$-deformed model

3.3 Second class of solutions

The second class of solutions is expressed in terms of Jacobi elliptic functions. A short review is given in Appendix B where all the necessary definitions are provided, along with several properties of these functions. A careful study will help the unfamiliar reader for the better understanding of the material that follows.

3.3.1 $SL(2,{\mathbb {R}})/U(1)_V$ model

Let us now derive solutions for the action (14). We implement the same strategy that we used for the first class of solutions by solving the Virasoro constraints and combining the solutions appropriately to satisfy the equations of motion. Again, the form of the metric implies that the constants appearing at the right-hand-sides of the Virasoro constraints have to be positive definite. Thus, in the following we obtain solutions of the equations

$$\begin{aligned}&(\partial _{\pm }\chi )^2+(\partial _{\pm }\psi )^2 \nonumber \\&\quad =\frac{m^2}{4}\left( \frac{1+\lambda }{1-\lambda }-\frac{4\lambda }{1-\lambda ^2}\cos ^2\psi -e^{-2\chi }\right) . \end{aligned}$$

(31)

these equations can be decoupled as

$$\begin{aligned}&(\partial _{\pm }\chi )^2+\frac{m^2}{4}e^{-2\chi }=\frac{m^2}{4}c^2_{\pm }, \end{aligned}$$

(32)

$$\begin{aligned}&(\partial _{\pm }\psi )^2-\frac{m^2}{4}\left( \frac{1+\lambda }{1-\lambda }-\frac{4\lambda }{1-\lambda ^2}\cos ^2\psi \right) =-\frac{m^2}{4}c^2_{\pm }. \end{aligned}$$

(33)

Positivity of the constants on the right-hand-side of (32) is required, due to the manifest positivity of the left-hand-side. Immediately, it follows that $\chi$ is given by

$$\begin{aligned} e^{\chi }=\frac{1}{c}\cosh \left[ m\,c\left( \frac{\sigma ^+\pm \sigma ^-}{2}+\alpha \right) \right] , \end{aligned}$$

(34)

where $\alpha$ is an integration constant. Notice that the Eq. (32) are incompatible, unless $c_+=c_-=c>0$. Moving to the second pair of equations we can factorise it as

$$\begin{aligned}&(\partial _{\pm }\psi )^2=\frac{m^2}{4}\ell ^2\left( 1-\kappa ^2\cos ^2\psi \right) , \quad \lambda >0, \end{aligned}$$

(35)

$$\begin{aligned}&(\partial _{\pm }\psi )^2=\frac{m^2}{4}\ell ^2\left( 1-\kappa ^2\sin ^2\psi \right) , \quad \lambda <0, \end{aligned}$$

(36)

where $\kappa ^2$ is the elliptic modulus, which is given by

$$\begin{aligned} \kappa ^2=\frac{4\vert \lambda \vert }{1-\lambda ^2}\,\frac{1}{\ell ^2} \end{aligned}$$

(37)

and $\ell$ is defined by the equation

$$\begin{aligned} \ell ^2=\frac{1+\vert \lambda \vert }{1-\vert \lambda \vert }-c^2. \end{aligned}$$

(38)

As these equations are of the form of (140), it follows that their solution is

$$\begin{aligned} \psi =\mathrm {am}\left[ m\,\ell \left( \frac{\sigma ^+\mp \sigma ^-}{2}+\beta \right) \Big \vert \kappa ^2\right] +\frac{\pi }{2}\frac{\lambda +\vert \lambda \vert }{2\vert \lambda \vert }, \end{aligned}$$

(39)

where $\mathrm {am}(x\vert m)$ is the Jacobi amplitude.⁶ The reality of the solutions requires $\ell ^2\ge 0$, which implies that c is subject to the constraint

$$\begin{aligned} \sqrt{\frac{1+\vert \lambda \vert }{1-\vert \lambda \vert }}\ge c\ge 0. \end{aligned}$$

(40)

Choosing $\chi =\chi (\tau )$ (and necessarily $\psi =\psi (\sigma )$) we obtain the solution

$$\begin{aligned} e^{\chi (\tau )}&=\frac{1}{c}\cosh \left[ m\,c\left( \tau -\tau _0\right) \right] , \end{aligned}$$

(41)

$$\begin{aligned} \psi (\sigma )&=\mathrm {am}\left[ m\,\ell \left( \sigma -\sigma _0\right) \Big \vert \kappa ^2\right] +\frac{\pi }{2}\frac{\lambda +\vert \lambda \vert }{2\vert \lambda \vert }. \end{aligned}$$

(42)

Of course, the class of solutions $\chi =\chi (\sigma )$ and $\psi =\psi (\tau )$ is also admissible.

3.3.2 $SL(2,{\mathbb {R}})/U(1)_A$ model

For the axial gauging we have to solve the Virasoro constraints

$$\begin{aligned}&(\partial _{\pm }\chi )^2+(\partial _{\pm }\psi )^2=\frac{m^2}{4}\left[ \frac{1+\lambda }{1-\lambda }\right. \nonumber \\&\quad \left. -\frac{4\lambda }{1-\lambda ^2}\cos ^2\psi +e^{-2\chi }\right] . \end{aligned}$$

(43)

Notice that both contributions of the right-hand-side are manifestly positive. This fact has interesting consequences at the set of solutions. Decoupling the equations as in the case of vector gauging, there are two distinct pairs of equations

$$\begin{aligned}&(\partial _{\pm }{\chi })^2-\frac{m^2}{4}e^{-2{\chi }}=\pm \frac{m^2}{4}c^2_{\pm }, \end{aligned}$$

(44)

$$\begin{aligned}&(\partial _{\pm }\psi )^2-\frac{m^2}{4}\left( \frac{1+\lambda }{1-\lambda }-\frac{4\lambda }{1-\lambda ^2}\cos ^2\psi \right) =\mp \frac{m^2}{4}c^2_{\pm }, \end{aligned}$$

(45)

since the left-hand-side of (44) is not manifestly positive. Again, the equations are incompatible unless $c_+=c_-=c$. Choosing first, the plus sign in (44) we obtain the solution

$$\begin{aligned} e^{{\chi }}=\frac{1}{c}\sinh \left[ m\,c\left( \frac{\sigma ^+\pm \sigma ^-}{2}+\alpha \right) \right] . \end{aligned}$$

(46)

The solution for $\psi$ is provided by (39), where c is subjected to Eq. (40). Of course, c may be taken purely imaginary to provide a solution for the minus sign in (44). In such a case the solution is automatically real and the parameter c is unconstrained. Putting everything together, we obtain the following class of solutions

$$\begin{aligned} e^{{\chi }_1(\tau )}&=\frac{1}{c}\sinh \left[ m\,c\left( \tau -\tau _0\right) \right] , \end{aligned}$$

(47)

$$\begin{aligned} \psi _1(\sigma )&=\mathrm {am}\left[ m\,\ell \left( \sigma -\sigma _0\right) \Big \vert \kappa ^2\right] +\frac{\pi }{2}\frac{\lambda +\vert \lambda \vert }{2\vert \lambda \vert }, \end{aligned}$$

(48)

where the elliptic modulus $\kappa ^2$ and $\ell$ are defined in (37) and (38), respectively, as well as,

$$\begin{aligned} e^{\chi _2(\tau )}&=\frac{1}{c}\sin \left[ m\,c\left( \tau -\tau _0\right) \right] , \end{aligned}$$

(49)

$$\begin{aligned} \psi _2(\sigma )&=\mathrm {am}\left[ m\,\tilde{\ell }\left( \sigma -\sigma _0\right) \Big \vert \tilde{\kappa }^2\right] +\frac{\pi }{2}\frac{\lambda +\vert \lambda \vert }{2\vert \lambda \vert }, \end{aligned}$$

(50)

where the elliptic modulus $\tilde{\kappa }^2$ and $\tilde{\ell }$ are defined as

$$\begin{aligned} \tilde{\kappa }^2=\kappa ^2\vert _{\ell ^2\rightarrow {\tilde{\ell }}^2} , \quad \tilde{\ell }^2=\ell ^2\vert _{c^2\rightarrow -c^2} . \end{aligned}$$

(51)

Notice that this solution is valid for any c. Of course, one can interchange $\sigma$ and $\tau$ to obtain the rest of the solutions of this model.

3.3.3 SU(2)/U(1) model

Finally we proceed with the solutions on the SU(2)/U(1). Proceeding in the usual manner, by solving the Virasoro constraints, the decoupled equations read

$$\begin{aligned}&(\partial _{\pm }\chi )^2-\frac{m^2}{4}e^{-2\chi }=-\frac{m^2}{4}c^2_{\pm }, \end{aligned}$$

(52)

$$\begin{aligned}&(\partial _{\pm }\psi )^2+\frac{m^2}{4}\left( \frac{1+\lambda }{1-\lambda }-\frac{4\lambda }{1-\lambda ^2}\cos ^2\psi \right) =\frac{m^2}{4}c^2_{\pm }, \end{aligned}$$

(53)

where the right-hand-side of (53) is manifestly positive in view of (123). The solution of the first equation is

$$\begin{aligned} e^{\chi }=\frac{1}{c}\sin \left[ m\,c\left( \frac{\sigma ^+\pm \sigma ^-}{2}+a\right) \right] , \end{aligned}$$

(54)

while the pair of Eq. (53) can be written as

$$\begin{aligned}&(\partial _{\pm }\psi )^2=\frac{m^2}{4}\bar{\ell }^2\left( 1-\bar{\kappa }^2\sin ^2\psi \right) , \quad \lambda >0, \end{aligned}$$

(55)

$$\begin{aligned}&(\partial _{\pm }\psi )^2=\frac{m^2}{4}\bar{\ell }^2\left( 1-\bar{\kappa }^2\cos ^2\psi \right) , \quad \lambda <0, \end{aligned}$$

(56)

where the elliptic modulus $\bar{\kappa }^2$ is defined as

$$\begin{aligned} \bar{\kappa }^2=\frac{4\vert \lambda \vert }{1-\lambda ^2}\,\frac{1}{{\bar{\ell }}^2} \end{aligned}$$

(57)

and $\bar{\ell }$ is defined via the equation

$$\begin{aligned} \bar{\ell }^2=c^2-\frac{1-\vert \lambda \vert }{1+\vert \lambda \vert }. \end{aligned}$$

(58)

The reality of the solutions implies that c is subject to the constraint

$$\begin{aligned} c^2\ge \frac{1-\vert \lambda \vert }{1+\vert \lambda \vert }. \end{aligned}$$

(59)

Considering $\chi =\chi (\tau )$ and $\psi =\psi (\sigma )$, the solution reads

$$\begin{aligned} e^{\chi (\tau )}&=\frac{1}{c}\sin \left[ m\,c\left( \tau -\tau _0\right) \right] , \end{aligned}$$

(60)

$$\begin{aligned} \psi (\sigma )&=\mathrm {am}\left[ m\,\bar{\ell }\left( \sigma -\sigma _0\right) \Big \vert \bar{\kappa }^2\right] +\frac{\pi }{2}\frac{\vert \lambda \vert -\lambda }{2\vert \lambda \vert } . \end{aligned}$$

(61)

4 Properties of the solutions

In this section we study the properties of the solutions we derived in the previous one. First of all, we summarize the second class of solutions and present their basic features. Then, we specify their boundary conditions. This is required in order to eliminate the surface terms, rising when varying the action. In addition, since $\sigma$-models describe string theories, we also mention possible brane configurations, related to the aforementioned boundary conditions.⁷ Having specified all admissible cases, we plot the solutions and discuss them. Finally, the effect of the non-perturbative dualities (6) and (7) is described.

Table 4 This table summarizes the expressions for the coordinates $\chi$ and $\psi$, and the elliptic modulus for each of the models of the first column. Notice that there are two kinds of solutions for the $SL(2,{\mathbb {R}})/U(1)$ axially gauged model. There is no constraint on c for the second kind of solutions

Table 5 All solutions of the second class are classified by their characteristics. Solutions are characterized either as static (ST) if $\psi =\psi (\sigma )$ or as translationally invariant (TI) if $\psi =\psi (\tau )$. Similarly, they are characterized as oscillating if the value of the elliptic modulus is greater than 1 and as rotating if it is between zero and one. The expressions for the coordinates $\chi$ and $\psi$, and the elliptic modulus for each of the models of the first column are in Table 4

4.1 Overview of the 2nd class of solutions

In this section we summarize the second class of solutions and discuss some of their common features. Before doing so, we present the coordinates $y_1$ and $y_2$ for this class of solutions. Taking into account the definitions of $y_1$ and $y_2$ for each model, namely Eqs. (3), (13) and (19), along with (128), which is common for all models, as well as the Eqs. (125), (132) and (137), it follows that $y_1$ and $y_2$ are given in terms of $\chi$ and $\psi$ by

$$\begin{aligned} y_1=\sqrt{\frac{1-\lambda }{1+\lambda }}e^{\chi }\cos \psi ,\quad y_2=\sqrt{\frac{1+\lambda }{1-\lambda }}e^{\chi }\sin \psi , \end{aligned}$$

(62)

for all models. This expressions are free of the subtleties regarding the positivity of $e^\chi$, which appear in Eqs. (47), (49) and (60). It is evident that this class of solutions parametrize an ellipsis. The eccentricity of this ellipsis depends on $\lambda$.⁸ In the case $\chi =\chi (\tau )$ the overall scale of the ellipsis is time dependent, whereas in the case $\chi =\chi (\sigma )$, the solution is a rod, whose endpoint(s) lies on ellipses. In both cases, it is straightforward to show that these solutions satisfy

$$\begin{aligned} G_{y_1 y_1}\partial _{\sigma }y_1\partial _{\tau }y_1+G_{y_2 y_2}\partial _{\sigma }y_2\partial _{\tau }y_2=0,\quad \forall \sigma ,\tau . \end{aligned}$$

(63)

This implies that when considering open strings, they are always perpendicular to the surfaces traced by their endpoints. This equation is a direct consequence of the Virasoro constraints. The Virasoro constraints also imply

$$\begin{aligned}&G_{y_1 y_1}\left[ \left( \partial _{\tau }y_1\right) ^2+\left( \partial _{\sigma }y_1\right) ^2\right] \nonumber \\&\quad +G_{y_2 y_2}\left[ \left( \partial _{\tau }y_2\right) ^2+\left( \partial _{\sigma }y_2\right) ^2\right] =m^2,\quad \forall \sigma ,\tau , \end{aligned}$$

(64)

the physical time being $t=m\tau$. Thus, there is no momentum flow on strings endpoints. The exact behaviour of the solution depends on the values of the parameters and the boundary conditions. In Table 4 we gather all equations, which define the second class of solutions for each model. Table  5 presents the classification of all solutions of the second class according to their features. These include the cases $\psi =\psi (\sigma )$ and $\psi =\psi (\tau )$, as well as whether the value of the elliptic modulus is greater or smaller that one. This classification is analogous to the one performed in [14] regarding elliptic string solutions in ${\mathbb {R}}\times \text {S}^2$.

Regarding the solutions of $SL(2,{\mathbb {R}})/U(1)_V$ model and one of the two solutions of the $SL(2,{\mathbb {R}})/U(1)_A$ model, the elliptic modulus $\kappa ^2$, defined in (37), satisfies $0\le \kappa ^2\le 1$ when

$$\begin{aligned} \frac{1-\vert \lambda \vert }{1+\vert \lambda \vert } \le c^2\le \frac{1+\vert \lambda \vert }{1-\vert \lambda \vert } \end{aligned}$$

(65)

and is associated to rotating solutions. Similarly, when

$$\begin{aligned} 0 \le c^2\le \frac{1-\vert \lambda \vert }{1+\vert \lambda \vert } \end{aligned}$$

(66)

it satisfies $1\le \kappa ^2$ and it is related to oscillating solutions. For these solutions we define

$$\begin{aligned} \delta \sigma =\frac{\omega _1}{m\ell } . \end{aligned}$$

(67)

The half-period $\omega _1$ is defined in terms of the elliptic modulus via (149).

Table 6 The kink limit of the static solutions of the second class for $\lambda >0$. Translationally invariant ones are obtained via $\sigma \leftrightarrow \tau$, while the $\lambda <0$, are obtained using the duality (7)

Considering the other solution of the $SL(2,{\mathbb {R}})/U(1)_A$ model, the elliptic modulus $\tilde{\kappa }^2$, defined in (51), always satisfies $0\le \tilde{\kappa }^2\le 1$ for any value of c. In this case we define

$$\begin{aligned} \delta \tilde{\sigma }=\frac{\omega _1}{m{\tilde{\ell }}} . \end{aligned}$$

(68)

Finally, for the solutions of the SU(2)/U(1) model, the elliptic modulus $\bar{\kappa }^2$, defined in (57), satisfies $0\le \bar{\kappa }^2\le 1$ when

$$\begin{aligned} \frac{1+\vert \lambda \vert }{1-\vert \lambda \vert }\le c^2 \end{aligned}$$

(69)

related to rotating solutions. Similarly, it satisfies $1\le \bar{\kappa }^2$ when

$$\begin{aligned} \frac{1-\vert \lambda \vert }{1+\vert \lambda \vert } \le c^2\le \frac{1+\vert \lambda \vert }{1-\vert \lambda \vert } \end{aligned}$$

(70)

and is associated to oscillating solutions. Finally, in this case we define

$$\begin{aligned} \delta \bar{\sigma }=\frac{\omega _1}{m{\bar{\ell }}} . \end{aligned}$$

(71)

The lengths $\delta \sigma$, $\delta \tilde{\sigma }$ and $\delta \bar{\sigma }$ will be used when studying the boundary conditions and the periodicity properties.

4.1.1 Special limits

Solutions of the second class have two interesting limits. The first one is the limit of the vanishing elliptic modulus. This limit is obtained for $\lambda =0$. In this case the Jacobi amplitude becomes just the linear function x, see Eq. (141). The elliptic function degenerate to trigonometric ones. In general, elliptic functions are defined on a torus, since they are doubly periodic. In this limit the imaginary period diverges and the torus becomes singular. Starting from the undeformed solution, from a mathematical point of view, the $\lambda$-deformation resolves this singularity and the corresponding degenerate torus becomes non-degenerate.

A far more interesting limit is the one of the diverging real period. This is the case when the elliptic modulus equals to unity. The Jacobi amplitude is given by (143). The elliptic functions degenerate to hyperbolic ones. The form of the solutions in this limit is presented in Table 6. Notice that we present only the $\lambda >0$ solutions, while the rest of them are obtained using the duality (7) (m is invariant). Also, we present only the static solutions. The translationally invariant ones are obtained via the $\sigma \leftrightarrow \tau$ transformation.

4.2 Boundary conditions – analysis: 1st class

4.2.1 Generalities

Up to now we have not addressed the problem of surface terms of the actions. Besides the validity of the solution per se, considering the embedding of the sigma model in string theory, these boundary conditions may describe either open or closed strings and hint at the brane configurations, which are associated with the string solution. Note that our target space is two-dimensional restricting us in p2-branes as boundary configurations at most. The boundary terms, dropped, when varying the actions (1), (11) and (17), are

$$\begin{aligned} \delta y_i e^{2\varPhi }\partial _\sigma y_i\big \vert _{\sigma =\sigma _i}=\delta y_i e^{2\varPhi }\partial _\sigma y_i\big \vert _{\sigma =\sigma _f}, \end{aligned}$$

(72)

where $i=1,2$.

We first present the boundary conditions of the first class and then discuss the solutions of the second class. As the expressions for the first class are very simple, we can treat both vector and axial gauging simultaneously. Regarding the second class of solutions we use the classification introduced in Sect. 4.1. The reader may find Tables 4 and 5 particularly useful, since they provide an overview of the solutions, their classification and corresponding range of the parameters. As a last remark, for convenience we consider that for the second class of solutions the parameters $\sigma _0$ and $\tau _0$ vanish.

4.2.2 $SL(2,{\mathbb {R}})/U(1)$ models

The solutions we obtained, either in the case of vector gauging (Table 1) or in the case of axial gauging (Table 2), are hyperbolic and exponentials functions

$$\begin{aligned} y_{s,\tau }&=a\sinh \left( b\left( \tau -\tau _0\right) \right) , \end{aligned}$$

(73)

$$\begin{aligned} y_{c,\tau }&=a\cosh \left( b\left( \tau -\tau _0\right) \right) , \end{aligned}$$

(74)

$$\begin{aligned} y_{e,\tau }&=a\exp \left( b\left( \tau -\tau _0\right) \right) \end{aligned}$$

(75)

and

$$\begin{aligned} y_{s,\sigma }&=a^\prime \sinh \left( b^\prime \left( \sigma -\sigma _0\right) \right) , \end{aligned}$$

(76)

$$\begin{aligned} y_{c,\sigma }&=a^\prime \cosh \left( b^\prime \left( \sigma -\sigma _0\right) \right) , \end{aligned}$$

(77)

$$\begin{aligned} y_{e,\sigma }&=a^\prime \exp \left( b^\prime \left( \sigma -\sigma _0\right) \right) . \end{aligned}$$

(78)

satisfying $e^{2\varPhi }\partial _\sigma y_{i,\alpha }\big \vert _{\sigma =\pm \infty }=0$, where $i=c,s,e$ and $\alpha =\sigma ,\tau$.⁹ Thus, the variational problem is well defined for $\sigma \,\in \,(-\infty ,\infty )$ without imposing any further conditions and these solutions naturally represent long strings. The world-sheet of such solutions is the Minkowski plane.

One can impose boundary conditions in the following cases:

Neumann: Since

$$\begin{aligned} \partial _\sigma y_{c,\sigma }\big \vert _{\sigma =\sigma _0}=0, \end{aligned}$$

(79)

we can impose Neumann conditions both for $y_{c,\sigma }$ and $y_{I,\tau }$ at $\sigma =\sigma _0$.

Dirichlet: Since

$$\begin{aligned} \partial _\tau y_{I,\sigma }=0,\quad \partial _\sigma y_{I,\tau }=0, \end{aligned}$$

(80)

we can impose Dirichlet conditions for $y_{I,\sigma }$ and Neumann for $y_{I^\prime ,\tau }$ for any arbitrary $\sigma$.

Combining appropriately the above two cases, we can impose the following boundary conditions on the solutions:

• N for $y_{c,\sigma }$ and $y_{I,\tau }$ at $\sigma =\sigma _0$, corresponding to a space filling p2-brane.

• D for $y_{I,\sigma }$ and N for $y_{I^\prime ,\tau }$ at $\sigma =\sigma _D$, corresponding to semi-infinite sting ending on a single p1-brane.

• D-D for $y_{I,\sigma }$ and N-N $y_{I^\prime ,\tau }$ at $\sigma =\sigma _i$ and $\sigma =\sigma _f$, corresponding to a pair of p1-branes.

• D-N for $y_{c,\sigma }$ and N-N $y_{I,\tau }$ at $\sigma =\sigma _D$ and $\sigma =\sigma _0$, corresponding to a p1-brane and a space filling p2-brane.

All these solutions correspond to infinite, semi-infinite or finite moving line segments. Intestingly enough, the D-D and N-N boundary conditions are integrable [5].

4.2.3 SU(2)/U(1) model

Contrary to the $SL(2;{\mathbb {R}})/U(1)$ case, the conformal factor $e^{2\varPhi }$, defined in (1), does not vanish at $\sigma =\pm \infty$. This class of solutions is naturally periodic, corresponding to closed configurations. We discuss, the $y_1=y_1(\tau )$ and $y_2=y_2(\sigma )$ case, but similar conclusions hold for the other case too. In particular, the solutions (Table 3) are periodic under

$$\begin{aligned} \sigma \rightarrow \sigma +\delta \sigma ,\quad \delta \sigma =\frac{2\pi }{m}\sqrt{\frac{1-\lambda }{1+\lambda }}. \end{aligned}$$

(81)

These configurations are folded strings, which oscillate in the $y_1$ direction as time flows. The world-sheet of such solutions is a torus.

One can impose open string boundary conditions in the following cases:

Neumann: Since

$$\begin{aligned} \partial _\sigma y_2\big \vert _{\sigma =\sigma _N}=0,\quad \sigma _N=\sigma _0+n\sqrt{\frac{1-\lambda }{1+\lambda }}\frac{\pi }{m},\qquad n\in {\mathbb {N}} \end{aligned}$$

(82)

we can impose Neumann conditions both for $y_1$ and $y_2$ at $\sigma =\sigma _N$.

Dirichlet: Since

$$\begin{aligned} \partial _\tau y_2=0,\quad \partial _\sigma y_1=0, \end{aligned}$$

(83)

we can impose Dirichlet conditions for $y_2$ and Neumann for $y_1$ for any arbitrary $\sigma _D$.

Combining appropriately the above two cases, we can impose the following boundary conditions on the solutions:

• N-N for both $y_1$ and $y_2$ at $\sigma _i=\sigma _0$ and $\sigma _f=\sigma _0+\sqrt{\frac{1-\lambda }{1+\lambda }}\frac{\pi }{m}$, corresponding to a space-filling p2-brane.

• D-D for $y_2$ and N-N $y_1$ at $\sigma _i$ and $\sigma _f$, which correspond to a pair of p1-branes.

• D-N/N-D for $y_2$ and N-N $y_1$ at $\sigma =\sigma _D$ and $\sigma =\sigma _N$, corresponding to a p1-brane and a p2-brane.

These solutions correspond to finite moving line segments.

4.3 Boundary conditions – analysis: 2nd class

The second class of solutions reveals a much larger variety of results including static and translationally invariant configurations. It consists of fourteen distinct types of solutions. We keep the presentation as short as possible, presenting only basic facts for each of these types of solutions, but the overall presentation is lengthy.

4.3.1 $SL(2,{\mathbb {R}})/U(1)_{V}$ model

Static

These solutions are of the form

$$\begin{aligned} y_1&=\frac{1}{c}\sqrt{\frac{1-\lambda }{1+\lambda }}\cosh \left( m\,c\,\tau \right) \cos \psi (\sigma ), \end{aligned}$$

(84)

$$\begin{aligned} y_2&=\frac{1}{c}\sqrt{\frac{1+\lambda }{1-\lambda }}\cosh \left( m\,c\,\tau \right) \sin \psi (\sigma ), \end{aligned}$$

(85)

where $\psi$ is given by (42) and the corresponding elliptic modulus by (37). The world-sheet of such solutions is cylindrical.

Fig. 1

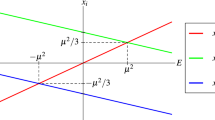
Indicative static solutions of the $SL(2,{\mathbb {R}})/U(1)_V$ model. The left panel corresponds to a rotating solution, while the right one to an oscillating solution, which is a folded string. Notice that as $\lambda >0$ the angle $\psi$ of the oscillating solution “oscillates” around $\pi /2$. The equation of the black ellipses is (87)

Closed strings In the case of rotating solutions, the angle $\psi$ is monotonous and satisfies

$$\begin{aligned} \psi (\sigma +4\delta \sigma )=\psi (\sigma )+2\pi , \end{aligned}$$

(86)

just like the angle of a rotating pendulum, depicted in the right panel of Fig. 8. Static rotating solutions correspond to closed strings. These solutions are ellipses, which, starting from infinity, approach the origin of the $y_1$-$y_2$ plane up to $\tau =0$, and reflect back to infinity. Their motion, is bounded in the exterior of the ellipsis

$$\begin{aligned} y_1=\frac{1}{c}\sqrt{\frac{1-\lambda }{1+\lambda }}\cos \omega ,\quad y_2=\frac{1}{c}\sqrt{\frac{1+\lambda }{1-\lambda }}\sin \omega ,\quad \omega \in [0,2\pi )\,. \end{aligned}$$

(87)

The background is a deformed version of the well-known trumpet geometry. Intuitively, it has the same features but its cross-section is of elliptic shape. As the cross-section of the trumpet grows towards the origin $\rho =0$, the string approaching the origin stretches. At some point there is no more kinetic energy to be absorbed for the string to keep stretching, thus, it reflects back.

In the case of oscillating solutions, the angle $\psi$ “oscillates” between two limiting values, see (148), and satisfies

$$\begin{aligned} \psi (\sigma +4\delta \sigma )=\psi (\sigma ), \end{aligned}$$

(88)

where $\delta \sigma$ is given by (67), just like the angle of an oscillating pendulum depicted on the left panel of Fig. 8. Intuitively, their motion is analogous to the rotating case, but the reason which prevents the string from collapsing to a points is not topological, but kinematic. The endpoints of the string move at the speed of light. Indeed, it is easy to show that

$$\begin{aligned} G_{y_1 y_1}\left( \partial _{t}y_1\right) ^2+G_{y_2 y_2}\left( \partial _{t}y_2\right) ^2\vert _{\sigma =(2n+1)\delta \sigma }=1,\quad \forall t, \end{aligned}$$

(89)

where the time t of the target space, defined as $t=m\tau$. Figure 1 depicts indicative examples of closed static oscillating and rotating strings.

Open strings As mentioned, in the case of rotating strings the angle $\psi$ is monotonous. Thus, in order to apply Dirichlet–Neumann (or Neumann–Dirichlet) boundary conditions, the only possibility is to set $\psi =n{\pi }/{2}$, where $n\in {\mathbb {N}}$. This is achieved for $\sigma =n\delta \sigma$. In this way we obtain strings, which are parts of the closed rotating strings ending on $y_1=0$ or $y_2=0$ axis. One can construct configurations, which extend along one, two or three quadrants and either end on different branes or on the same one.

For oscillating strings, the angle $\psi$ “oscillates” either around 0 or around $\pi /2$, depending on whether $\lambda >0$ or $\lambda <0$, see (42). The points of the string corresponding to $\sigma =n\delta \sigma$ either lie on an axis, or on the lines which are tangential to the motion of the folded string, like the dashed lines in the right panel of Fig. 1.

Translationally invariant

These solutions are of the form

$$\begin{aligned} y_1&=\frac{1}{c}\sqrt{\frac{1-\lambda }{1+\lambda }}\cosh \left( m\,c\,\sigma \right) \cos \psi (\tau ), \end{aligned}$$

(90)

$$\begin{aligned} y_2&=\frac{1}{c}\sqrt{\frac{1+\lambda }{1-\lambda }}\cosh \left( m\,c\,\sigma \right) \sin \psi (\tau ), \end{aligned}$$

(91)

where $\psi$ is given by (42) and the corresponding elliptic modulus by (37). The world-sheet of such solutions is cylindrical.

Fig. 2

Indicative translationally invariant solutions of the $SL(2,{\mathbb {R}})/U(1)_V$ model. The left panel corresponds to a rotating solution, while the right one to an oscillating solution. Notice that as $\lambda >0$ the angle $\psi$ of the oscillating solution “oscillates” around $\pi /2$. The equation of the dotted ellipses is (87)

These strings satisfy identically

$$\begin{aligned} G_{y_1 y_1}\left( \partial _{t}y_1\right) ^2+G_{y_2 y_2}\left( \partial _{t}y_2\right) ^2\vert _{\sigma =0}=1,\quad \forall t, \end{aligned}$$

(92)

where the time t of the target space is defined as $t=m\tau$.

One can consider these configurations either as folded strings, for $\sigma \in (-\infty ,\infty )$, in order to make the superficial terms vanish, or as open ones. As the $\sigma =0$ point moves at the speed of light, the string is prevented from collapsing. In the case of rotating strings, this point rotates on an elliptic trajectory, whereas in the case of oscillating strings, this point oscillates between two limiting points, see Fig. 2. In both cases the motion is periodic with period $T=4\delta \sigma$.

4.3.2 $SL(2,{\mathbb {R}})/U(1)_{A}$ model

Static 1

The static solutions of this class are of the form

$$\begin{aligned} y_1&=\frac{1}{c}\sqrt{\frac{1-\lambda }{1+\lambda }}\sinh \left( m\,c\,\tau \right) \cos \psi (\sigma ), \end{aligned}$$

(93)

$$\begin{aligned} y_2&=\frac{1}{c}\sqrt{\frac{1+\lambda }{1-\lambda }}\sinh \left( m\,c\,\tau \right) \sin \psi (\sigma ), \end{aligned}$$

(94)

where $\psi$ is given by (48) and the corresponding elliptic modulus by (37). The world-sheet of such solutions is cylindrical.

Fig. 3

Indicative static solutions of the $SL(2,{\mathbb {R}})/U(1)_A$ model. The left panel corresponds to a rotating solution, while the right one to an oscillating one, which is a folded string. Notice that as $\lambda >0$ the angle $\psi$ of the oscillating solution “oscillates” around $\pi /2$. The equation of the blue ellipses is (87)

Closed strings Angle $\psi$ satisfies (86) and (88) in the case of rotating and oscillating solutions, respectively. Similarly to the case of the vectorially gauged model, the rotating solutions are ellipses. The background is a deformed version of Witten’s cigar geometry [15]. Intuitively, it has the same characteristics but its cross-section is of elliptic shape. As the cross-section of the cigar shrinks towards the origin $\rho =0$, the string approaching the origin loosens. The incoming string becomes point-like at the tip of the cigar and then it is reflected back to infinity.

In the case of oscillating solutions, the motion of the strings is analogous to the rotating ones. Again the reason, which prevents the string from collapsing to a points is not the topological, but kinematic. The endpoints of the string move at the speed of light. Figure 3 depicts indicative examples of closed static oscillating and rotating strings.

Open strings As in the case of the vectorially gauged model, we can enforce Dirichlet–Neumann (or Neumann–Dirichlet) boundary conditions to the rotating solutions, for $\sigma =n\delta \sigma$. In this way we obtain strings, which are parts of the closed rotating strings and end at the axis $y_1=0$ or $y_2=0$. One can construct configurations, which extend along one, two or three quadrants and either end on different branes or on the same one.

A similar picture emerges in the the case of oscillating strings. The angle $\psi$ “oscillates” either around 0 or around $\pi /2$, depending on whether $\lambda >0$ or $\lambda <0$. The points of the string corresponding to $\sigma =n\delta \sigma$ either lie on an axis, or on the lines which are tangential to the motion of the folded string, the dashed lines in the right panel of Fig. 3.

Translationally invariant 1

These solutions are of the form

$$\begin{aligned} y_1&=\frac{1}{c}\sqrt{\frac{1-\lambda }{1+\lambda }}\sinh \left( m\,c\,\sigma \right) \cos \psi (\tau ),\ \end{aligned}$$

(95)

$$\begin{aligned} y_2&=\frac{1}{c}\sqrt{\frac{1+\lambda }{1-\lambda }}\sinh \left( m\,c\,\sigma \right) \sin \psi (\tau ), \end{aligned}$$

(96)

where $\psi$ is given by (48) and the corresponding elliptic modulus by (37). The world-sheet of such solutions is cylindrical.

Fig. 4

Indicative translationally invariant solutions of the $SL(2,{\mathbb {R}})/U(1)_A$ model. The left panel corresponds to a rotating solution, while the right one to an oscillating solution. Notice, again, that as $\lambda >0$ the angle $\psi$ of the oscillating solution “oscillates” around $\pi /2$. The equation of dotted ellipses is (87)

These strings satisfy identically

$$\begin{aligned} G_{y_1 y_1}\left( \partial _{t}y_1\right) ^2+G_{y_2 y_2}\left( \partial _{t}y_2\right) ^2\vert _{\sigma =0}=0,\quad \forall t, \end{aligned}$$

(97)

where the time t of the target space is defined as $t=m\tau$. One can consider these configurations either as infinite strings, for $\sigma \in (-\infty ,\infty )$, or semi-inifinite open ones, for $\sigma \in (0,\infty )$. In the second case, the string is considered to end on a D0 brane, which is located at the tip of the cigar. This way the string is prevent from collapsing to a point.

In the case of rotating strings the string rotates freely, whereas in the case of oscillating strings, the string oscillates between two limiting points. The configurations are like the vectorially gauged ones in Fig. 2, but either with the strings ending on the origin of the plot, or extending all the way to infinity. They are depicted in Fig. 4. In both cases the motion is periodic with period $T=4\delta \sigma$.

Static 2 These solutions are of the form

$$\begin{aligned} y_1&=\frac{1}{c}\sqrt{\frac{1-\lambda }{1+\lambda }}\sin \left( m\,c\,\tau \right) \cos \psi (\sigma ),\ \end{aligned}$$

(98)

$$\begin{aligned} y_2&=\frac{1}{c}\sqrt{\frac{1+\lambda }{1-\lambda }}\sin \left( m\,c\,\tau \right) \sin \psi (\sigma ), \end{aligned}$$

(99)

where $\psi$ is given by (50) and the corresponding elliptic modulus by (51). The angle $\psi$ of these solutions obeys equation (86), but in terms of $\delta \tilde{\sigma }$, defined in (68), instead of $\delta \sigma$. There are only rotating solutions of this form. The world-sheet of such solutions is toroidal.

Fig. 5

Indicative rotating solutions of the $SL(2,{\mathbb {R}})/U(1)_A$ model. The left panel corresponds to a static solution, while the right one to a translationally invariant one, which is a folded string. The equation of the cyan ellipsis on the left panel and the dotted one on the right is (87)

Closed strings Similar to the static solutions presented so far, these solutions are ellipses. Again, the background is a deformed version of the Witten’s cigar geometry [15]. Their motion is analogous to the static rotating solutions of the vectorially gauged model. Their motion is bounded by the same ellipsis, see equation (87), but these solutions move in the interior rather than the exterior. The string stretches until there is no more kinetic energy left and reflects back to the tip of the cigar. Such solutions are periodic both on the time-like and space-like world-sheet coordinates. The left panel of Fig. 5 depicts indicative examples of such closed static rotating strings.

Open strings As in the case of the vectorially gauged model, we can enforce Dirichlet–Neumann (or Neumann–Dirichlet) boundary conditions to the rotating solutions, for $\sigma =n\delta \tilde{\sigma }$. This way we obtain strings, which are parts of the closed rotating strings and end at axis $y_1=0$ or $y_2=0$. One can construct configurations, which extend along one, two or three quadrants and either end on different branes or on the same one.

Translationally invariant 2 The static solutions of this class are of the form

$$\begin{aligned} y_1&=\frac{1}{c}\sqrt{\frac{1-\lambda }{1+\lambda }}\sin \left( m\,c\,\sigma \right) \cos \psi (\tau ), \end{aligned}$$

(100)

$$\begin{aligned} y_2&=\frac{1}{c}\sqrt{\frac{1+\lambda }{1-\lambda }}\sin \left( m\,c\,\sigma \right) \sin \psi (\tau ), \end{aligned}$$

(101)

where $\psi$ is given by (50) and the corresponding elliptic modulus by (51). There are only rotating solutions of this form. The world-sheet of such solutions is toroidal.

These strings satisfy identically

$$\begin{aligned}&G_{y_1 y_1}\left( \partial _{t}y_1\right) ^2+G_{y_2 y_2}\left( \partial _{t}y_2\right) ^2\vert _{\sigma =0}=0,\quad \forall t, \end{aligned}$$

(102)

$$\begin{aligned}&G_{y_1 y_1}\left( \partial _{t}y_1\right) ^2+G_{y_2 y_2}\left( \partial _{t}y_2\right) ^2\vert _{\sigma =\pm \frac{1}{mc}\frac{\pi }{2}}=1,\quad \forall t, \end{aligned}$$

(103)

where the time t of the target space is defined as $t=m\tau$. These solutions correspond either to closed folded strings or to open ones, whose endpoint move at the speed of light. The motion of the endpoints prevents the string from shrinking to a point. One can also consider open strings which end on a D0-brane at the tip of the cigar. The right panel of Fig. 5 depicts an indicative example of such closed translationally invariant rotating strings.

4.3.3 SU(2)/U(1) model

Static These solutions are of the form

$$\begin{aligned} y_1&=\frac{1}{c}\sqrt{\frac{1-\lambda }{1+\lambda }}\sin \left( m\,c\,\tau \right) \cos \psi (\sigma ), \end{aligned}$$

(104)

$$\begin{aligned} y_2&=\frac{1}{c}\sqrt{\frac{1+\lambda }{1-\lambda }}\sin \left( m\,c\,\tau \right) \sin \psi (\sigma ), \end{aligned}$$

(105)

where $\psi$ is given by (61) and the corresponding elliptic modulus by (57). The world-sheet of such solutions is toroidal.

Fig. 6

Indicative static solutions of the SU(2)/U(1) model. The left panel corresponds to a rotating solution, while the right one to an oscillating one, which is a folded string. Notice that as $\lambda >0$ the angle $\psi$ of the oscillating solution “oscillates” around 0. The equation of the cyan ellipses is (87)

Closed strings The angle $\psi$ satisfies (86) and (88) in the case of rotating and oscillating solutions, respectively, but in terms of $\delta \bar{\sigma }$, defined in (71), instead of $\delta \sigma$.

Static rotating solutions correspond to closed strings. They are ellipses, whose scale oscillates. Their motion, is bounded by the ellipsis (87), which is expected as the manifold is compact. Considering the target space embedded in three dimensions, it has the shape of an spheroid. The string shrinks and stretches as it oscillates from a one pole to the other.

The oscillating solutions are folded strings. They are part of an ellipsis and their endpoints move at the speed of light. Their motion is analogous to the rotating ones, but in this case the reason, which prevents the string from collapsing to a points is not the topological, but kinematic. It is easy to show that

$$\begin{aligned} G_{y_1 y_1}\left( \partial _{t}y_1\right) ^2+G_{y_2 y_2}\left( \partial _{t}y_2\right) ^2\vert _{\sigma =(2n+1)\delta \sigma }=1,\quad \forall t, \end{aligned}$$

(106)

where the time t of the target space, defined as $t=m\tau$. Figure 6 depicts indicative examples of closed static oscillating and rotating strings.

Open strings In the case of rotating strings the angle $\psi$ is monotonous. Thus, in order to enforce Dirichlet–Neumann (or Neumann–Dirichlet) boundary conditions, the only possibility is to set $\psi =n{\pi }/{2}$, where $n\in {\mathbb {N}}$. This is achieved for $\sigma =n\delta \bar{\sigma }$. This way we obtain strings, which are parts of the closed rotating strings and end at the axis $y_1=0$ or $y_2=0$. One can construct configurations, which extend along one, two or three quadrants and either end on different branes or on the same one.

For oscillating strings, the angle $\psi$ “oscillates” either around 0 or around $\pi /2$, depending on whether $\lambda >0$ or $\lambda <0$. The points of the string corresponding to $\sigma =n\delta \bar{\sigma }$ either lie on an axis, or on the lines which are tangential to the motion of the folded string, like the dashed lines in the right panel of Fig. 6.

Translationally invariant These solutions are of the form

$$\begin{aligned} y_1&=\frac{1}{c}\sqrt{\frac{1-\lambda }{1+\lambda }}\sin \left( m\,c\,\sigma \right) \cos \psi (\tau ), \end{aligned}$$

(107)

$$\begin{aligned} y_2&=\frac{1}{c}\sqrt{\frac{1+\lambda }{1-\lambda }}\sin \left( m\,c\,\sigma \right) \sin \psi (\tau ), \end{aligned}$$

(108)

where $\psi$ is given by (61) and the corresponding elliptic modulus by (57). The world-sheet of such solutions is toroidal.

Fig. 7

Indicative translationally invariant solutions of the vectorially gauged SU(2)/U(1) model. The left panel corresponds to a rotating solution, while the right one to an oscillating solution. Notice that as $\lambda >0$ the angle $\psi$ of the oscillating solution “oscillates” around 0

These strings satisfy identically

$$\begin{aligned} G_{y_1 y_1}\left( \partial _{t}y_1\right) ^2+G_{y_2 y_2}\left( \partial _{t}y_2\right) ^2\vert _{\sigma =\pm \frac{1}{mc}\frac{\pi }{2}}=1,\quad \forall t, \end{aligned}$$

(109)

where the time t of the target space is defined as $t=m\tau$.

One can consider these configurations either as folded strings, or as open ones. As the endpoints moves at the speed of light, the string is prevent from collapsing. In the case of rotating strings, this point rotates on an elliptic trajectory, whereas in the case of oscillating strings, these points oscillate between two limiting ones, see Fig. 7. In both cases the motion is periodic with period $T=4\delta \bar{\sigma }$.

4.4 The effect of the non-perturbative symmetries

Regarding the first class of solutions, let us return for a moment in Eqs. (27) and (28) and impose invariance under the duality symmetry (6). In order to do so, we have to postulate that $m^2$ is a function of $\lambda$ transforming as

$$\begin{aligned} m^2\left( 1/\lambda \right) =-m^2(\lambda ). \end{aligned}$$

(110)

On the contrary, c is not affected, which implies that $c(1/\lambda )=c(\lambda )$.

As far as the duality (7) is concerned, one can easily see from (27) and (28), that invariance under this duality implies that

$$\begin{aligned} m^2(-\lambda )=m^2(\lambda )\quad c(-\lambda )= -c(\lambda ) \end{aligned}$$

(111)

We conclude that c, is even under (6) and odd under (7) symmetry. The inverse holds for $m^2$.¹⁰ One can easily verify that the sets of solutions in Tables 1, 2 and 3, are closed under symmetries (6) and (7) .

Let us turn to the second class of solutions. In the case of the $SL(2,{\mathbb {R}})/U(1)$ model, the duality symmetry (6) acts on the coordinates $\rho$ and $\phi$ as

$$\begin{aligned} \lambda \rightarrow 1/\lambda ,\quad \rho \rightarrow -\rho ,\quad \phi \rightarrow -\phi . \end{aligned}$$

(114)

Taking into account Eqs. (120), (121) and (122), we infer that $\chi$, $\psi$ and the dilaton ${\tilde{\varPhi }}$ transform as

$$\begin{aligned} \chi \rightarrow \chi +i\pi /2,\qquad \psi \rightarrow \psi , \qquad e^{2{\tilde{\varPhi }}}\rightarrow \,\,-e^{2{\tilde{\varPhi }}}. \end{aligned}$$

(115)

As a result, the action (14) is invariant under (6).

In order to retain the duality symmetry at the level of solutions, Eqs. (32) and (33) imply that $m^2$ and $c^2$ are functions of $\lambda$ satisfying

$$\begin{aligned} m^2\left( 1/\lambda \right) =-m^2(\lambda )\quad c^2\left( 1/\lambda \right) =-c^2(\lambda ). \end{aligned}$$

(112)

Equation (37) implies that $\kappa ^2$ is invariant, thus (42) implies that $\psi$ is indeed invariant. Finally, according to Eq. (41), $\chi$ transforms appropriately.

Last but not least, the symmetry (7), in terms of coordinates $(\theta ,\phi )$ is replaced by

$$\begin{aligned} \rho \rightarrow \rho ,\quad \phi \rightarrow \phi +\pi /2 \end{aligned}$$

(116)

and one can show that under (116)

$$\begin{aligned} \chi \rightarrow \chi ,\quad \psi \rightarrow \psi +\pi /2, \end{aligned}$$

(117)

while

$$\begin{aligned} m^2(-\lambda )=m^2(\lambda ),\qquad c^2(-\lambda )=c^2(\lambda ). \end{aligned}$$

(118)

Similar conclusions hold for the case of axial gauging too, as well as for the SU(2)/U(1) model.

5 Discussion

In this work we derived as a first example in the literature, two distinct classes of solutions of the $SL(2,{\mathbb {R}})/U(1)$ and SU(2)/U(1) $\lambda$-deformed models. We achieved this by exploiting a special property of the two-dimensional target spaces, namely the fact that the solutions of equations describing the conservation of Energy–Momentum tensor also solve the equations of motion.

The solutions of the first class are expressed in terms of trigonometric - hyperbolic functions. Overall we obtain eleven distinct solutions of this kind, which are gathered in Tables 1, 2 and 3. All these configurations are of the form $y_1=y_1(\tau )$ and $y_2=y_2(\sigma )$, but the $\sigma \leftrightarrow \tau$ transformed solutions are also valid. The solutions of the first class of the $SL(2,{\mathbb {R}})/U(1)$ $\lambda$-deformed models are infinite, semi-infinite or finite moving line segments, whereas the ones of the SU(2)/U(1) $\lambda$-deformed model are finite line segments, which oscillate.

The solutions of the second class are expressed in terms of Jacobi elliptic functions. Overall we obtain fourteen distinct solutions of this kind, which are gathered in Table 4. In addition, Table 5 present the classification of these solutions. These configurations are either of the form $y_1=f(\tau )\cos \psi (\sigma )$ and $y_2=f(\tau )\sin \psi (\sigma )$, which are referred to as static, or of the form $y_1=f(\sigma )\cos \psi (\tau )$ and $y_2=f(\sigma )\sin \psi (\tau )$, which are referred to as translationally invariant. It is important to point out, that in this case the $\sigma \leftrightarrow \tau$ transformation relates solutions, which are not related by any target space symmetry. The static solutions are of elliptical shape, whose scale is time-dependent, whereas the translationally invariant solutions are semi-infinite rotating line segments, whose endpoint lies on an ellipses. The second class of solutions has two special limits. The first one is obtained when the elliptic modulus vanishes and the elliptic functions degenerate to trigonometric functions. This is the case when $\lambda =0$. For this class of solutions, the $\lambda$-deformation turns the trigonometric functions to elliptic ones. The second one is obtained for some specific value of c, which depends on the model. In this limit the elliptic functions degenerate to hyperbolic ones and the corresponding configurations are presented in Table 6.

Both classes of configurations are not necessarily invariant under the non-perturbative duality symmetries, but this can be imposed as an extra demand. Solution profiles are time dependent and do not saturate a BPS bound. It remains obscure how these configurations are incorporated in the spectrum of the theory.

Several new directions emerge through this analysis. First of all, it would be interesting to study the Pohlmeyer reduced theory of the models [4]. Such a study may provide information relevant to the spectrum of the theory. For instance when the elliptic modulus of the second class of solutions equals to unity, are configurations are analogous to the Giant Magnon [16] and one expects that the Pohlmeyer avatar is a solitonic object.

On the same line, the derived solutions may be used in order to obtain new ones. This can be achieved via the application of the dressing method [17, 18]. The dressing method is a technique, which takes advantage of a known solution, usually refereed to as the seed solution, in order to obtain new ones. The advantage of this method is that in order to derive the solutions one has to solve a system of linear coupled first order PDEs, rather than the equations of motion, which constitute a system of coupled, non-linear, second order PDEs. This method has already been applied in the context of $\lambda$-deformations in [19]. In this work the seed solution is analogous to the BMN particle [20], a solution of the undeformed model, which also solves the deformed one. The solutions we derived are much more complicated and the application of the dressing method on such seed solutions may reveal interesting phenomena, such as the formation of spikes and memory effect regarding the propagation of the inserted kink on the non-trivial background [21].

It is worth noticing that the dressing method is also related with the stability analysis of the seed solutions [21]. Obviously, it also has the advantage that besides determining the fate of small perturbations, one also obtains the full non-linear solution as well. Of course, even a linear stability analysis is of interest. Its conclusions are expected to match the ones of the dressing method [22].

It would, also be interesting to derive kink configurations i.e time-independent lumps of finite energy, or time independent solutions in general. Unfortunately, for such configurations the approach based on the conservation of the Energy–Momentum tensor is inapplicable. This is also the case for models, whose target space is of higher dimension. Regarding models, generalizing the ones of this work, i.e. ones having the groups considered here as subgroups, one can obtain solutions via the dressing method. To do so, one needs to embed the solutions of this work in the higher-dimensional target space and apply the dressing method using this seed solution.

Besides further investigating the solutions themselves or the corresponding models, there are various studies, which are related to them. To begin with, it would be interesting to find classical solutions of other theories having a two-dimensional target space using the approach based on the conservation of the Energy–Momentum tensor. For instance, one may obtain solutions of various known integrable deformations, such as Yang Baxter [23]/$\eta$ [24, 25], bi Yang Baxter [26] and asymptotic $\lambda$-deformations [27]. Regarding the Yang Baxter and $\eta$ deformations, it is well known that they are related to $\lambda$-deformations via Poisson-Lie T-duality and appropriate analytic continuations [28].

Moreover, as we described a lot of open string configurations, another interesting direction, is to investigate the fitting of D-branes in this setup and derive classical solutions for such objects. One can also study whether the boundary conditions preserve the integrability of the theory or not [29].

Finally, the derived solutions enable various field theory calculations. In particular, one could study the effective theory related to a non-trivial classical solution and perform semi-classical quantization.

Appendices

Appendix A: The parametrization of the 2nd class of solutions

In this appendix we give some technical details on the second parametrization that we introduced in order to describe the models under study.

$SL(2,{\mathbb {R}})/U(1)_V$ model Let us first discuss the case of the vectorially gauged $SL(2,{\mathbb {R}})/U(1)$ model. Applying the change of variables (13), the action (11) is written as

$$\begin{aligned} S= & {} \frac{k}{\pi }\int \,d^2\sigma \,\Bigg \{\frac{1-\lambda }{1+\lambda }\left( \partial _+\rho \partial _-\rho +\coth ^2\rho \partial _+\phi \partial _-\phi \right) \nonumber \\&+\frac{4\lambda }{1-\lambda ^2}\left( \cos \phi \partial _+\rho -\sin \phi \coth \rho \partial _+\phi \right) \nonumber \\&\cdot \left( \cos \phi \partial _-\rho -\sin \phi \coth \rho \partial _-\phi \right) \Bigg \}. \end{aligned}$$

(119)

With some work one can show that defining the new coordinates $\chi$ and $\psi$ as

$$\begin{aligned} \chi (\rho ,\phi )&=\log \left[ \cosh \rho \sqrt{\frac{1-\lambda }{1+\lambda }+\frac{4\lambda }{1-\lambda ^2}\cos ^2\phi }\right] , \end{aligned}$$

(120)

$$\begin{aligned} \psi (\rho ,\phi )&=\arctan \left[ \frac{1-\lambda }{1+\lambda }\tan \phi \right] . \end{aligned}$$

(121)

the action can be written in a conformally flat form, see (14), where initially the dilaton is defined as

$$\begin{aligned} e^{2{\tilde{\varPhi }}}=\coth ^2 \rho \left( \frac{1-\lambda }{1+\lambda }+\frac{4\lambda }{1-\lambda ^2}\cos ^2\phi \right) . \end{aligned}$$

(122)

Note that the square root in the definition of the $\chi$ variable, Eq. (120), should not worry us, because it is well defined for $-1<\lambda <1$, since

$$\begin{aligned} \frac{1+\vert \lambda \vert }{1-\vert \lambda \vert }\ge \,\,\frac{1-\lambda }{1+\lambda }+\frac{4\lambda }{1-\lambda ^2}\cos ^2\phi \,\,\ge \frac{1-\vert \lambda \vert }{1+\vert \lambda \vert }. \end{aligned}$$

(123)

Of course, the dilaton field has to be expressed in terms of the new variables $(\chi ,\psi )$. To invert (120) and (121) we take advantage of the equation

$$\begin{aligned} \frac{1-\lambda }{1+\lambda }+\frac{4\lambda }{1-\lambda ^2}\cos ^2\phi =\left( \frac{1+\lambda }{1-\lambda }-\frac{4\lambda }{1-\lambda ^2}\cos ^2\psi \right) ^{-1}, \end{aligned}$$

(124)

which is a direct consequence of (121). Doing so, we obtain following expressions

$$\begin{aligned} \rho (\chi ,\psi )&=\text {arccosh}\left[ e^{\chi }\sqrt{\frac{1+\lambda }{1-\lambda }-\frac{4\lambda }{1-\lambda ^2}\cos ^2\psi }\right] , \end{aligned}$$

(125)

$$\begin{aligned} \phi (\psi )&=\arctan \left[ \frac{1+\lambda }{1-\lambda }\tan \psi \right] . \end{aligned}$$

(126)

It order to specify uniquely $\psi$ in terms of $\phi$ we choose

$$\begin{aligned} \begin{aligned} \cos \psi&=\frac{\cos \phi }{\sqrt{\left( \frac{1-\lambda }{1+\lambda }\right) ^2+\frac{4\lambda }{\left( 1+\lambda \right) ^2}\cos ^2\phi }}, \\ \sin \psi&=\frac{\frac{1-\lambda }{1+\lambda }\sin \phi }{\sqrt{\left( \frac{1-\lambda }{1+\lambda }\right) ^2+\frac{4\lambda }{\left( 1+\lambda \right) ^2}\cos ^2\phi }}. \end{aligned} \end{aligned}$$

(127)

Taking into account (124), the inverse transformation is

$$\begin{aligned} \begin{aligned} \cos \phi&=\frac{\cos \psi }{\sqrt{\left( \frac{1+\lambda }{1-\lambda }\right) ^2-\frac{4\lambda }{\left( 1-\lambda \right) ^2}\cos ^2\psi }}, \\ \sin \phi&=\frac{\frac{1+\lambda }{1-\lambda }\sin \psi }{\sqrt{\left( \frac{1+\lambda }{1-\lambda }\right) ^2-\frac{4\lambda }{\left( 1-\lambda \right) ^2}\cos ^2\psi }}. \end{aligned} \end{aligned}$$

(128)

These definitions are common for all three models.

In view of (123), the quantity under the square root in Eq. (125) is positive provided that $\psi$ is a real function. Nevertheless, the validity of this equation requires

$$\begin{aligned} e^{\chi }\sqrt{\frac{1+\lambda }{1-\lambda }-\frac{4\lambda }{1-\lambda ^2}\cos ^2\psi }\,\,\,\ge 1. \end{aligned}$$

(129)

This is a constraint that has to be imposed on the solutions. Implementing (125) and (126) on the dilaton profile (122), we can finally express it in terms of $\chi$ and $\psi$ as

$$\begin{aligned} e^{-2{\tilde{\varPhi }}}=\frac{1+\lambda }{1-\lambda }-\frac{4\lambda }{1-\lambda ^2}\cos ^2\psi -e^{-2\chi }. \end{aligned}$$

(130)

Provided the inequality (129) is satisfied, the dilaton ${\tilde{\varPhi }}$ is real valued as required.

$SL(2,{\mathbb {R}})/U(1)_A$ model

It is evident that the actions of the vectorially and axially gauged $SL(2,{\mathbb {R}})/U(1)$ models are essentially related by the interchange $\sinh \rho \leftrightarrow \cosh \rho$. This means that the action of the axially gauged model is provided by (119) upon the substitution $\coth \rho \rightarrow \tanh \rho$. Obviously the replacement discussed above, does not alter the definition of $\psi$, i.e. Eq. (121), but the definition of $\chi$ should be adjusted appropriately. Thus, $\chi$ is given by

$$\begin{aligned} \chi (\rho ,\phi )=\log \left[ \sinh \rho \sqrt{\frac{1-\lambda }{1+\lambda }+\frac{4\lambda }{1-\lambda ^2}\cos ^2\phi }\right] . \end{aligned}$$

(131)

Contrary to the case of vector gauging, the inverse transformation, namely

$$\begin{aligned} \rho (\chi ,\psi )=\text {arcsinh}\left[ e^{\chi }\sqrt{\frac{1+\lambda }{1-\lambda }-\frac{4\lambda }{1-\lambda ^2}\cos ^2\psi }\right] \end{aligned}$$

(132)

is valid automatically and does not impose any constraint on the parameters. The first new entry here is the expression relating the fields $\chi$ and $\psi$ with the new dilaton field. Following the step of the previous case, the conformal factor is given in terms of $\chi$ and $\psi$ by

$$\begin{aligned} e^{-2{\tilde{\varPhi }}}=\frac{1+\lambda }{1-\lambda }-\frac{4\lambda }{1-\lambda ^2}\cos ^2\psi +e^{-2\chi } . \end{aligned}$$

(133)

SU(2)/U(1) model

Using the analytic continuation (10), which relates the SU(2)/U(1) to the vectorially gauged $SL(2,{\mathbb {R}})/U(1)$ in (119), the action of the former reads

$$\begin{aligned} S= & {} \frac{k}{\pi }\int \,d^2\sigma \,\Bigg \{\frac{1-\lambda }{1+\lambda }\left( \partial _+\theta \partial _-\theta +\cot ^2\theta \partial _+\phi \partial _-\phi \right) \nonumber \\&+\frac{4\lambda }{1-\lambda ^2}\left( \cos \phi \partial _+\theta +\sin \phi \cot \theta \partial _+\phi \right) \nonumber \\&\cdot \left( \cos \phi \partial _-\theta +\sin \phi \cot \theta \partial _-\phi \right) \Bigg \}. \end{aligned}$$

(134)

The action can be written in the conformally flat form form (8) using

$$\begin{aligned} \chi (\theta ,\phi )=\frac{1}{2}\log \left[ \cos ^2 \theta \left( \frac{1-\lambda }{1+\lambda }+\frac{4\lambda }{1-\lambda ^2}\cos ^2\phi \right) \right] , \end{aligned}$$

(135)

and (121), while the new dilaton field is given by

$$\begin{aligned} e^{-2{\tilde{\varPhi }}}= e^{-2\chi } -\left( \frac{1+\lambda }{1-\lambda }-\frac{4\lambda }{1-\lambda ^2}\cos ^2\psi \right) . \end{aligned}$$

(136)

Implementing (124), one can show that $\theta$ is given by

$$\begin{aligned} \theta =\text {arccos}\left( e^{\chi }\sqrt{\frac{1+\lambda }{1-\lambda }-\frac{4\lambda }{1-\lambda ^2}\cos ^2\psi }\right) . \end{aligned}$$

(137)

Actually, this equation determines the absolute value of $\cos \theta$. One should define $\theta$, so that it is continuous and smooth. The validity of this equation requires

$$\begin{aligned} 1\ge e^{\chi }\sqrt{\frac{1+\lambda }{1-\lambda }-\frac{4\lambda }{1-\lambda ^2}\cos ^2\psi }\ge -1. \end{aligned}$$

(138)

This inequality guaranties that the dilaton is real valued.

Fig. 8

The Jacobi amplitude for $\kappa ^2=1.25$ (left panel), $\kappa ^2=1$ (middle panel) and $\kappa ^2=0.95$ (right panel). The dashed horizontal lines on the left panel mark the extremal values of the function. These values are obtained periodically. On the contrary, on the middle panel, the extremal values are obtained asymptotically. Finally, the dashed blue line of the right panel is the average value of the function over a large number of periods. The plots on the left and right panel clearly show the periodic and quasi-periodic behaviour of the function, respectively

Appendix B: The Jacobi elliptic functions

In this section we gather some properties of the Jacobi elliptic functions, which are relevant for this work. The fundamental object of Jacobi elliptic functions is the Jacobi amplitude $\mathrm {am}(x\vert m)$. Essentially, is generalizes the linear function $f(x)=x$. Using the Jacobi amplitude, one defines the elliptic sine and cosine as

$$\begin{aligned} \mathrm {sn}(x|m)=\sin \left( \mathrm {am}(x|m)\right) ,\quad \mathrm {cn}(x|m)=\cos \left( \mathrm {am}(x|m)\right) . \end{aligned}$$

(139)

The Jacobi amplitude satisfies the differential equation

$$\begin{aligned} \left( \frac{d}{dx} \mathrm {am}(x\vert m)\right) ^2=1-m \,\mathrm {sn}^2(x\vert m), \end{aligned}$$

(140)

where m is called the elliptic modulus. The second class of solutions is obtained using this equation.¹¹ Trivially, it follows that

$$\begin{aligned} \mathrm {am}(x\vert 0)=x. \end{aligned}$$

(141)

Additionally, the Jacobi amplitude obeys

$$\begin{aligned} \mathrm {am}(0\vert m)=0. \end{aligned}$$

(142)

In this work, the elliptic modulus is always positive, so we set $m=\kappa ^2$, where $\kappa \in {\mathbb {R}}$. Depending on whether $0<\kappa ^2<1$ or $1<\kappa ^2$ the Jacobi amplitude is either periodic or quasi-periodic function. In the special case $\kappa ^2=1$ it follows that

$$\begin{aligned} \mathrm {am}(x\vert 1)=2\arctan \left( e^x\right) -\frac{\pi }{2}. \end{aligned}$$

(143)

The function is neither periodic nor quasi-periodic and interpolates monotonically from $-\pi /2$ to $\pi /2$. This is the famous kink of the sine-Gordon equation. In this case the elliptic functions degenerate to hyperbolic ones, namely

$$\begin{aligned} \mathrm {sn}(x|1)=\tanh (x),\quad \mathrm {cn}(x|1)=\mathrm {sech}(x). \end{aligned}$$

(144)

In order to proceed, let us consider a simple pendulum. This physical system will reveal all features of the Jacobi amplitude. The energy conservation of the pendulum reads

$$\begin{aligned} \frac{1}{2}\left( \frac{d\phi }{dt}\right) ^2+\omega ^2\left( 1-\cos \phi \right) =E. \end{aligned}$$

(145)

The energy is normalized so that the (stable) equilibrium point $\phi =0$ corresponds to $E=0$. Trivially, this equation assumes the form

$$\begin{aligned} \frac{1}{2E}\left( \frac{d\phi }{dt}\right) ^2=1-\frac{2\omega ^2}{E}\sin ^2\frac{\phi }{2}, \end{aligned}$$

(146)

which is solved by

$$\begin{aligned} \phi (t)=2\text {am}\left( \sqrt{\frac{E}{2}}(t-t_0)\big \vert \frac{2\omega ^2}{E}\right) \end{aligned}$$

(147)

If $E<2\omega ^2$, the pendulum oscillates between the angles $-\phi _0$ and $\phi _0$, where $\phi _0=\arcsin \left( \sqrt{\frac{E}{2\omega ^2}}\right)$. This behaviour is general, if $\kappa ^2>1$, the Jacobi amplitude is bounded. In particular, it follows that

$$\begin{aligned} -\arcsin (1/\kappa )\le \text {am}\left( x\vert \kappa ^2\right) \le \arcsin (1/\kappa ),\, \kappa \ge 1. \end{aligned}$$

(148)

If $E>2\omega ^2$, the motion of the pendulum is no longer oscillatory. The pendulum rotates, but its motion is modulated by the gravitational force. On average the angle grows linearly with time. Of course, as the energy grows, the modulation becomes less significant. Finally, if $E=2\omega ^2$ the motion of the pendulum is aperiodic. Starting from the unstable equilibrium point $\phi =-\pi$, after an infinite amount of time, the pendulum reaches the unstable equilibrium point $\phi =\pi$. In the main text, solutions corresponding to $\kappa ^2>1$ are referred to as oscillating, whereas solutions corresponding $0<\kappa ^2<1$ as rotating.

Elliptic functions are doubly periodic on the complex plane. The elliptic functions appearing in the solutions derived in this work have one real and one imaginary period. These periods form a lattice on the complex plane. Denoting the real half-period as $\omega _1$, it turns out that

$$\begin{aligned} \omega _1={\left\{ \begin{array}{ll} K(\kappa ^2),\qquad 0\le \kappa ^2\le 1\\ \frac{K(\kappa ^{-2})}{\kappa },\qquad 1\le \kappa ^2 \end{array}\right. }, \end{aligned}$$

(149)

where K(m) is the complete elliptic integral of the first kind, defined as

$$\begin{aligned} K(m)=\int _0^{\pi /2}\frac{d\phi }{\sqrt{1-m\sin ^2\phi }}. \end{aligned}$$

(150)

If $\kappa ^2=1$ the real period diverges. The first case of (149) is the usual definition of the real period, whereas the second one follows from the properties of the complete elliptic integral and corresponds to a modular transformation on the complex plane. Using the above definition, the quasi-periodicity and periodicity of the Jacobi amplitude reads:

$$\begin{aligned} \mathrm {am}\left( x+2\omega _1\vert \kappa ^2\right)&=\mathrm {am}\left( x\vert \kappa ^2\right) +\pi ,\quad 0\le \kappa ^2\le 1, \end{aligned}$$

(151)

$$\begin{aligned} \mathrm {am}\left( x+4\omega _1\vert \kappa ^2\right)&=\mathrm {am}\left( x\vert \kappa ^2\right) ,\quad 1\le \kappa ^2. \end{aligned}$$

(152)

Figure 8 depicts examples of the different kinds of behaviour of the Jacobi amplitude.