1 Introduction

Einstein’s General theory of Relativity (GR) is one of the most successful theory of gravity in understanding the local universe. Inspite of its success there are several unresolved issues in GR at very high energy scale and in higher dimensions. In astrophysics, the information paradox problem [1], behaviour of spacetime in the vicinity of a Black Hole [2, 3], all the above issues led to an extensive search for an alternative to the General theory of Relativity. The gravitational theories with higher order curvature terms are of great interest for a modification, the modified theory is important to investigate compact objects embedded in higher dimensional spacetime. The origin of the concept of higher dimensions goes back to the early era from the seminal work done independently by Kaluza [4] and Klein [5], they independently unify gravity with the electromagnetic interaction introducing an extra dimension. Eddington [6] considered a higher dimensional spacetime to describe astrophysical objects known in the usual four dimensional spacetime that can be considered embedded in a flat higher dimensional spacetime. Mandelbrot [7] investigated the issue of dimensional variability where it was described precisely how a ball of thin thread varies when the scale of an observer changes. It is argued that an object which appears a point object from a far distance becomes a three-dimensional ball at a closer distance. Consequently as the viewer moves down the scales, the ball appears to change its form. The embedding dimensions of the ball have not changed, but the effective dimension of the contents changed. Thus it is relevant to study an object which is known in the usual four dimensions in the context of higher dimensional spacetime. The mass to radius ratio in higher dimensions for a uniform density star is generalized and new results are reported by Paul [8] to construct stellar models. Emparan and Real [9] obtained relativistic solution for a black ring in 5 dimensions, which indicates existence of other topologies in higher dimensions. Cassisi et al. [10] discussed the effects of higher dimensions on stellar evolution. Thereafter, a number of theories have been proposed in higher dimensions namely Brane world gravity [11] and Lovelock gravity [12, 13]. At present, higher dimensional studies become an active field of theoretical research with some outstanding physical outputs. Einstein–Gauss–Bonnet (henceforth, EGB) gravity theory is one such theory, which is a natural extension of GR to higher dimensions and it arises from the incorporation of an additional term to the standard Einstein–Hilbert action. The Gauss–Bonnet (GB) term arises as a low energy effective action of heterotic string theory [14, 15]. Interestingly, the GB term is a topological invariant in 4D space-time, and hence does not contribute to the gravitational dynamics. However, the Gauss–Bonnet terms provide a rich structure in the theory which are relevant both in higher dimensional astrophysics and in cosmology [16]. Nevertheless, to get a non-trivial contribution, one can generally associate the GB term with the scalar field or in higher dimensions [17, 18].

Historically black hole solutions in EGB theory have been intensively studied in \(D \ge 4\). In particular, Boulware and Deser [19] first obtained spherically symmetric static black hole solution within the frame of the EGB gravity. Later on, in higher dimension black hole solutions are generalised in higher dimensions by Wheeler [20], Torii and Maeda [21] and Myers and Simons [22]. The Vaidya radiating black-holes in EGB gravity reveals that the location of the horizons changes considerably compared to that in the standard 4-dimensional gravity [23]. In addition to this, Dadhich et al. [24] showed that the constant density Schwarzschild interior solution is universal in the sense that it is valid both in higher dimensional Einstein theory as well as in EGB gravity. EGB gravity also plays an important role in obtaining relativistic solutions for constructing realistic stellar models in higher dimensional space-time. Bhar et al. [52] used Krori–Barua ansatz to obtain relativistic solutions in EGB gravity and compared the physical properties of stellar models in EGB and that in GR only. Tangphati et al. [25] have also found out that an anisotropic quark star in the context of EGB gravity leads to considerable change both in the structure of the star and the mass-radius relation. Hansraj and Mkhize [26] recently obtained exact solutions in EGB gravity in a six dimensional fluid sphere and used it to construct stellar models, using barotropic fluid in a higher dimensional Krori–Barua metric. However, for a given equation of state (EoS) the metric solutions can be obtained from the gravitational field equations. Anisotropic stellar models have been constructed using interacting quark EoS in EGB gravity [27]. Banerjee et al. [28] obtained exact solutions in EGB gravity using the MIT bag model. In the literature, models of compact objects are obtained in the usual four and in higher dimensions in EGB gravity [29,30,31,32].

Finch–Skea (FS) metric was proposed to correct the Dourah and Ray [33] metric for ultra compact object which is not an acceptable description in GR. Subsequently, FS metric is further modified in 4-dimensions to accommodate an anisotropic compact star [34]. However it is shown recently that the original FS metric permits an anisotropic star in higher dimensions [35]. If the spacetime dimension is four then the original metric permits only isotropic stellar configuration. Thus FS metric is very useful for describing the compact stellar configuration in \(D \ge 4\) which will be considered here.

On the other hand, when testing alternative theories of gravity one may start from strong-field regime [36]. With this point in mind the formation and evolution of stars can be taken as a suitable test-beds for higher curvature gravity theories. Thus, compact objects such as Neutron stars are considered ideal for astrophysical environments in order to explore suitability of the gravity in the strong-field regime. However, the matter in the inner core of such astrophysical objects are compressed to nuclear density and can not be reproduced in the laboratory. In the absence of equation of state (EoS) of matter at such ultra high densities and high temperatures one can predict the EoS. For a given interior geometry it is known that the anisotropic pressure is likely to discuss a compact object having high density nuclear matter. The reason for incorporating anisotropy is due to the fact that in the high density regime, the radial pressure (\(P_r\)) and the transverse pressure (\(P_{\perp }\)) are not equal as pointed out by Canuto [37]. Bowers and Liang [38] investigated the anisotropic relativistic matter distributions in general relativity and obtained relativistic solutions for a static spherically symmetric configuration to probe the changes in the surface redshift and gravitational mass generalizing the hydrostatic equation. The theoretical investigations by Ruderman [39] indicated that at very high densities of order \(10^{15} \) \({ \mathrm{g}/\mathrm{cm}^{3}}\) i.e., nuclear matter density when the compact objects tend to become anisotropic in nature. Kippenhahn and Weigert [40] proposed that in relativistic stars anisotropy might originate due to the existence of a solid core or type 3A super fluid in the star. Weber [41] showed that a strong magnetic field in a compact star generate an anisotropic pressure. It is also pointed out that anisotropy originates for other reasons namely, viscosity, phase transition [42], pion condensation [43], etc in astrophysical objects. The shear of the fluid may be considered to be another source of the origin of anisotropy in a self gravitating object [44]. A class of exact solutions of Einstein field equation describing spherically symmetric static anisotropic star is obtained by Mak and Herko [45]. Petri [46] obtained an exact solution in the case of a self gravitating compact object with local anisotropic pressure. Ivanov [47] obtained a bound on the surface redshift for realistic anisotropic star. Recently a number of literature [48,49,50,51] appeared, where anisotropic stellar structure and the role of pressure anisotropy on such configurations are investigated. It is interesting to explore such compact objects in the framework of higher dimensional configuration.

The Einstein field equation can be used to obtain solution for a known matter configuration. In the absence of known matter configuration an alternative way to solve the Einstein equations was considered by assuming the geometry which is given by Finch–Skea. In an compact object the EoS is not yet known hence the motivation of the paper is to construct stellar models of compact objects so that the models predict the equation of state (EoS) of matter in the framework of EGB gravity making use of Finch–Skea geometry. Considering a known pulsar J0348+0432 we explore the physical features and stability of the pulsar making use of the realistic solutions. These solutions were subjected to rigorous physical tests and were shown to describe realistic stellar objects of particular interest where the modifications to the mass-radius relation and EoS which were different from their 4D and classical 5D counterparts in EGB gravity. A comparative study between EGB gravity models and their 4D counterparts was carried out by Bhar et al. [52] in which they showed that higher order effects leads to more compact stars. As the concept of higher dimensions is important for a consistent description of particle physics, it is legitimate to assume that the compact object is embedded in a higher dimensional space-time which will be considered in the paper. The effects of extra dimensions in understanding realistic stars in EGB gravity will be explored following the prescription as suggested by Delgaty and Lake [53].

The present paper is organized as follows: in Sect. 2 the EGB gravity is briefly presented. In Sect. 3 we write down the basic field equations in EGB gravity in D-dimensions for a spherically symmetric metric. In Sect. 4 we considered FS metric as input in EGB gravity considering Finch–Skea metric. In Sect. 5 we analysed the physical features such as density and pressure for a suitable set of model parameters and predicted the EoS. Section 6 consists of a comparative study of the model with some well-known stars. In Sect. 7 we presented a brief discussion.

2 Einstein–Gauss–Bonnet (EGB) gravity

The gravitational action for Einstein–Gauss–Bonnet (EGB) gravity is given by,

$$\begin{aligned} S = \int \sqrt{-g}\left[ \frac{1}{2}(R+\alpha L_{GB} )\right] d^{D}x + S_{m} \end{aligned}$$
(1)

where, R is the Ricci scalar, \(L_{GB}\) is the Gauss–Bonnet term, g is the determinant of the metric in higher dimension, \(S_m\) is the matter Lagrangian and \(\alpha \) is the Gauss–Bonnet coupling parameter. We have taken the gravitational unit \(8\pi G_D = c^2 = 1\). The coupling parameter \(\alpha \) is of dimension \([length]^2\) which appears in the string theory and may be considered with its signature different from the string theory for academic interest [16]. The Gauss–Bonnet Lagrangian (\(L_{GB}\)) is a specific combination of Ricci scalar, Ricci tensor and Reimann curvature, given by,

$$\begin{aligned} L_{GB} = R^{2}-4R_{ab}R^{ab}+R_{abcd}R^{abcd} \end{aligned}$$
(2)

where, the indices a, b, c and d run from 0 to (\(D-1\)).

Variation of the action (1) with respect to \(g_{ab}\) yields

$$\begin{aligned} G_{ab}+\alpha H_{ab} = T_{ab} \end{aligned}$$
(3)

where, \(G_{ab}\) denotes the Einstein tensor, \(T_{ab}\) is the total energy-momentum tensor and \(H_{ab}\) denotes the Lanczos tensor with the following expression,

$$\begin{aligned}&G_{ab} = R_{ab} - \frac{1}{2}Rg_{ab},\end{aligned}$$
(4)
$$\begin{aligned}&T_{ab} = - \frac{2}{\sqrt{-g}}\frac{\delta (\sqrt{-g}S_m)}{\delta g^{ab}} ,\end{aligned}$$
(5)
$$\begin{aligned}&H_{ab}= 2(R R_{ab}-2 R_{ac}R^{c}_{b}-2R^{cd}R_{abcd}\nonumber \\&\qquad \quad +R^{cde}_{a}R_{bcde})-\frac{1}{2}g_{ab}L_{ab} . \end{aligned}$$
(6)

3 Field equations

For a spherically symmetric space-time, the D-dimensional line element is given by,

$$\begin{aligned} ds^{2}= - e^{\nu (r)}dt^{2}+e^{\lambda (r)}dr^{2}+r^{2} d\Omega ^{2}_{D-2} \end{aligned}$$
(7)

where, \(d\Omega ^{2}_{D-2}\) is metric on a unit \((D-2)\)-dimensional sphere. \(\nu (r)\) and \(\lambda (r)\) are the metric potentials. For anisotropic matter distribution in D-dimensions, the energy momentum tensor of matter is given by,

$$\begin{aligned} T^{a}_{b}=diag (-\rho , P_{r}, P_{\perp },.......,P_{\perp }) , \end{aligned}$$
(8)

where, \(\rho \) is the energy density, \(P_{r}\) is the radial pressure and \(P_{\perp }\) is the tangential pressure for anisotropic fluid. Now, using the Eqs. (3), (7) and (8), the field equation can be written as,

$$\begin{aligned} \frac{2}{r}\frac{d\lambda }{dr}= & {} e^{2\lambda }\Bigg [\frac{2}{(D-2)}\rho - \frac{(1-e^{-2\lambda })}{r^2}\nonumber \\&\times \Bigg ((D-3) + \frac{\alpha (D-5)(1-e^{-2\lambda })}{r^2}\Bigg )\Bigg ]\nonumber \\&\times \Bigg [1 + \frac{2\alpha (1 - e^{-2\lambda })}{r^2}\Bigg ]^{-1} , \end{aligned}$$
(9)
$$\begin{aligned} \frac{2}{r}\frac{d\nu }{dr}= & {} e^{2\lambda }\Bigg [\frac{2}{(D-2)} P_{r} + \frac{(1-e^{-2\lambda })}{r^2}\nonumber \\&\times \Bigg ((D-3) + \frac{\alpha (D-5)(1-e^{-2\lambda })}{r^2}\Bigg )\Bigg ]\nonumber \\&\times \Bigg [1 + \frac{2\alpha (1 - e^{-2\lambda })}{r^2}\Bigg ]^{-1} , \end{aligned}$$
(10)
$$\begin{aligned} P_\perp= & {} \frac{1}{2 r^2 e^{2\lambda }} \Bigg [ 2r^2\frac{d^2\nu }{dr^2} - 2r\Bigg ( r\frac{d\nu }{dr} + (D-3) \Bigg )\nonumber \\&\times \Bigg (\frac{d\lambda }{dr} - \frac{d\nu }{dr} \Bigg ) - (D-3)(D-4)(e^{2\lambda } -1) \Bigg ]\nonumber \\&+ \frac{\alpha }{2 r^4 e^{4\lambda }} \Bigg [ 4r^2 (e^{2\lambda } -1)\frac{d^2\nu }{dr^2} + 8r^2\frac{d\nu }{dr} \frac{d\lambda }{dr} - 4r(e^{2\lambda } -1)\nonumber \\&\times \Bigg ( r\frac{d\nu }{dr} + (D-5) \Bigg ) \nonumber \\&\times \Bigg (\frac{d\lambda }{dr} - \frac{d\nu }{dr} \Bigg ) - (D-5)(D-6)(e^{2\lambda } -1)^2 \Bigg ]. \end{aligned}$$
(11)

Using the Eqs. (10) and (11), TOV equation in higher dimension is obtained which is given by,

$$\begin{aligned} \frac{dP_{r}}{dr} = -(\rho + P_{r})\frac{d\nu }{dr} + \frac{(D-2)}{r}(P_{\perp }-P_{r}) . \end{aligned}$$
(12)

The field Eqs. (9)–(11) are highly non-linear, therefore we can solve them by a numerical technique for Finch–Skea metric in order to construct stellar models. It is important to note that the GR limit is obtained when \(\alpha \) = 0.

4 EGB gravity with Finch–Skea geometry

The physical parameters are determined considering the metric potential given by the Finch–Skea (FS) metric, which is given by [35],

$$\begin{aligned} e^{2\lambda (r)} = 1 + C r^2 , \end{aligned}$$
(13)
$$\begin{aligned} e^{2\nu (r)}= & {} (B - A\sqrt{1 + Cr^2} ) \cos (\sqrt{1 + Cr^2}) \nonumber \\&+ (A + B * \sqrt{1 + C*r^2} ) \sin (\sqrt{1 + Cr^2}) . \end{aligned}$$
(14)

where A, B and C are constants, prescribing the specific geometry of the interior space-time of the star. The unknown parameters A, B and C can be obtained using the matching conditions of the metric with the exterior vacuum solution at the boundary. Therefore, using the metric given in Eqs. (13) and (14), the field equations yields,

$$\begin{aligned}&\rho = \frac{C (D-2)}{2 e^{6\lambda }} \Big [e^{2\lambda } \big (C r^2(D-3)+D-1\big )\nonumber \\&\qquad + \alpha C \big (C r^2(D-5)+D-1\big )\Big ] , \end{aligned}$$
(15)
$$\begin{aligned}&P_r = \frac{C (D-2)}{2 e^{4\lambda }}\nonumber \\&\qquad \times \Bigg [ \frac{(A U e^{\lambda } - B V) \cos (e^{\lambda }) - (A V + B U e^{\lambda }) \sin (e^{\lambda }) }{(B - A e^{\lambda }) \cos (e^{\lambda }) + (A + B e^{\lambda }) \sin (e^{\lambda }) } \Bigg ] .\nonumber \\ \end{aligned}$$
(16)

where, \(U = \big ((D-3) e^{2\lambda } + \alpha C (D-5) \big )\), \(V = \big ((D-4) e^{2\lambda } + \alpha C (D-7) \big )\). The anisotropy in pressure \((P_{\perp }-P_r)\) can be obtained using Eqs. (16) and (12). The transverse component of pressure \((P_{\perp })\) can be determined in different space-time dimensions from Eq. (11). As there are three equations and and five unknown parameters, we assume ad hoc relations to solve. Both the metric potentials \(\lambda (r)\) and \(\nu (r)\) are given by Finch–Skea geometry given above [35], the field equations will be employed to analyse the physical features namely, density, pressures and the anisotropy inside the star for a set of model parameters namely, \(A, B, C, \alpha \) and the dimensions of the geometry D of a star with known mass and radius. The equation of state (EoS) can be predicted from the parametric plot of \(\rho \) and \(P_r\) for a set of model parameters permitted by the constraints to be imposed in constructing the model. The interesting feature is that the anisotropic models of the compact objects can be constructed without prescribing any EoS a priori and at the same time satisfying all the criterion for a realistic stellar prescribed by [53], which will be discussed in the next section. For simplicity \(\alpha =0\) reduces to GR in higher dimension. We consider the following dimensions as a special case and express the density and the two pressures as given below:

4.1 Case I: D = 5

In the case of five-dimensions (5D), i.e. \(D=5\) in Eqs. (15) and (16), the density, the radial pressure and the transverse pressure become

$$\begin{aligned} \rho= & {} \frac{3 C (2 + C (3 r^2 + C r^4 + 2 \alpha ))}{e^{6\lambda }} ,\end{aligned}$$
(17)
$$\begin{aligned} P_r= & {} \frac{3C }{2 e^{4\lambda }} \Bigg [ \frac{(2A e^{3\lambda } + BX_{1}) \cos (e^{\lambda }) + (A X_{1} - 2B e^{3\lambda }) \sin (e^{\lambda })}{(B-A e^{\lambda }) \cos (e^{\lambda }) + (A+B e^{\lambda }) \sin (e^{\lambda }) } \Bigg ],\nonumber \\ \end{aligned}$$
(18)
$$\begin{aligned} P_\perp= & {} \frac{C }{8 e^{7\lambda }} \Bigg [ \frac{\xi _{1} \cos (2e^{\lambda }) + 2\xi _{2} \sin (2e^{\lambda }) - (A^2 + B^2)\xi _{3} e^{\lambda } }{(B-A e^{\lambda }) \cos (e^{\lambda }) + (A+B e^{\lambda }) \sin (e^{\lambda }) } \Bigg ] . \nonumber \\ \end{aligned}$$
(19)

where, we defined,

\(X_{1} = (2 \alpha C - C r^2 - 1)\) ,

\(\psi _{1} = 9 - 6\alpha C + C r^2 (12 + 3 C r^2 + 2 \alpha C) \) ,

\(\psi _{2} = 6 + 2C(6 + C r^2 + C^2 r^2) + C r^2 (23 + C r^2(22 + 5C r^2)) \) ,

\(\xi _{1} = 4AB\psi _{1} e^{2\lambda } - A^2 \psi _{2} e^{2\lambda } + B^2 \psi _{2} e^{2\lambda } \) ,

\(\xi _{2} = AB\psi _{2} e^{\lambda } + A^2 \psi _{1} e^{2\lambda } - B^2 \psi _{1} e^{2\lambda }\) ,

\(\xi _{3} = 18 + 6C\alpha (-2 + Cr^2 + C^2 r^2) + Cr^2 (37+ Cr^2(26+7Cr^2))\) .

Table 1 Different values of parameters A, B and C for PSR J0348+0432 for different values of \(\alpha \) in 5D and 6D
Full size table

4.2 Case II: D = 6

In the case of six-dimensions (6D), i.e. \(D=6\) in eqs. (15) and (16), the density, the radial pressure and the transverse pressure become

$$\begin{aligned} \rho= & {} \frac{2 C [5 + C \{5 \alpha +3 C r^4+r^2 (\alpha C + 8)\}]}{e^{6\lambda }} ,\end{aligned}$$
(20)
$$\begin{aligned} P_r= & {} \frac{2C }{e^{4\lambda }} \Bigg [ \frac{(A X_{2} e^{\lambda } - BY_{1}) \cos (e^{\lambda }) - (AY_{1} + B X_{2} e^{\lambda }) \sin (e^{\lambda }) }{(B-A e^{\lambda }) \cos (e^{\lambda }) + (A+B e^{\lambda }) \sin (e^{\lambda }) } \Bigg ] ,\nonumber \\ \end{aligned}$$
(21)
$$\begin{aligned} P_\perp= & {} \frac{C }{8 e^{7\lambda }} \Bigg [ \frac{\xi _{4} \cos (2e^{\lambda }) - 2\xi _{5} \sin (2e^{\lambda }) + (A^2+B^2)\xi _{6} e^{\lambda } }{(B-A e^{\lambda }) \cos (e^{\lambda }) + (A+B e^{\lambda }) \sin (e^{\lambda }) } \Bigg ] . \end{aligned}$$
(22)

where in this case we defined,

\(X_{2} = (3 e^{2\lambda } + \alpha C)\), \(Y_{1} = (2 e^{2\lambda } - \alpha C)\),

\(\psi _{3} = 8 + Cr^2 \{ 41 + Cr^2 (68 + 35Cr^2)\} + 2C\{ 8+Cr^2 (17 + 7Cr^2)\} \),

\(\psi _{4} = 10(3 e^{2\lambda } -1) \),

\(\xi _{4} = A^2 \psi _{3} e^{\lambda } - B^2 \psi _{3} e^{\lambda } - 4AB \psi _{4} e^{4\lambda } \),

\(\xi _{5} = AB \psi _{3} e^{\lambda } + A^2 \psi _{4} e^{4\lambda } - B^2 \psi _{4} e^{4\lambda }\),

\(\xi _{6} = 40 + Cr^2 \{ 123 + 6\alpha C + Cr^2 (116+33Cr^2+10\alpha C) \} \).

The two special cases in the EGB gravity will be taken up here for constructing stellar models for their physical analysis.

5 Criteria for physical acceptability

The following conditions are imposed for a realistic stellar model for compact object in EGB gravity :

(i) Hydrostatic equilibrium: The energy-density (\(\rho \)) must be positive throughout the compact object i.e., \(\rho \ge 0\). It’s value must be positive at the center and should be monotonically decreasing towards the boundary of the compact object. The radial pressure (\(P_r\)) and the transverse pressure (\(P_\perp \)) must be positive inside the fluid configuration i.e., \(P_r \ge 0\) and \(P_\perp \ge 0\). The radial pressure drops from its maximum value (at the center) to a vanishing value (\( P_r|_{(r=R)} = 0\)) at the boundary. The tangential pressure should be greater than the radial one except at the center i.e., at r = 0, \(P_r(0)= P_\perp (0)\). All the matter variables are expected to be maximum at the center of the compact object. The gradient of radial pressure, transverse pressure and energy-density should be negative inside the stellar configuration, \(\frac{dP_{r}}{dr} < 0 \), \(\frac{dP_{\perp }}{dr} < 0 \) and \( \frac{d\rho }{dr} < 0 \) .

(ii) Behaviour of anisotropy: At the center both radial and transverse pressure are equal which means the anisotropy vanishes at the center. Also it should be increasing towards the boundary.

(iii) Causality conditions: For a stable stellar configuration, \( 0 \le \frac{dP_r}{d\rho } \le 1\) and \( 0 \le \frac{dP_\perp }{d\rho } \le 1\) , so that the sound propagation is causal.

(iv) Stability condition: The adiabetic index i.e., ratio of two specific heats should be greater than \(\frac{4}{3}\).

(v) Boundary of the interior fluid: It is defined as the point where the radial pressure will be zero, i.e. the boundary of the star (R) is determined from \(P_r|_{(r=R)} = 0\).

(vi) Exterior metric and matching conditions: At the boundary of a star \((r = R)\), the interior space-time will be matched with a definite exterior solution that corresponds to vacuum EGB gravity. In the EGB gravity we consider the exterior solution given by Wiltshire [54] in D-dimensional space-time, which is :

$$\begin{aligned} ds^{2}= - f(r)dt^{2}+\frac{dr^{2}}{f(r)}+r^{2} d\Omega ^{2}_{D-2} \end{aligned}$$
(23)

where, f(r) is given by,

$$\begin{aligned} f(r)= 1+ \frac{r^2}{8 {\bar{\alpha }}} \Bigg [ 1 - \sqrt{1 + \frac{32 {\bar{\alpha }} M}{r^{D-1}}} \Bigg ] \end{aligned}$$
(24)

with \({\bar{\alpha }} = \alpha (D-3)(D-4)\) and M is the gravitational mass of the stellar model. Thus, the matching conditions at the boundary of the star can be obtained from Eqs. (7) and (23) which yields,

$$\begin{aligned}&e^{\nu (r)}|_{(r=R)} = f(R) , \end{aligned}$$
(25)
$$\begin{aligned}&e^{\lambda (r)}|_{(r=R)} = \frac{1}{f(R)}. \end{aligned}$$
(26)

In the theory we note that there are four unknowns and three equations in total for a given compact object. So, in order to solve the set of equations we need one adhoc relation. Thus to construct stellar models, the unknown metric parameters A, B and C for a given mass (M) and radius (R) of a star can be determined from the boundary conditions making use of permissible values of \(\alpha \) for a realistic stellar configuration in a given dimension D.

To begin with, we consider the compact object namely, PSR J0348+0432 with mass M= 2.01±0.04 \(M_{\odot }\) [55, 56] to construct the relativistic stellar model. The physical features analysed here are done taking different values of the metric parameters for different values of \(\alpha \) which are tabulated in Table 1.

Fig. 1
figure 1

Radial variation of matter density (\(\rho \)) in PSR J0348+0432 for different \(\alpha \) values in 5D with \(\alpha =0\) in 4D

Full size image
Fig. 2
figure 2

Radial variation of radial pressure (\(P_r\)) in PSR J0348+0432 for different \(\alpha \) values in 5D with \(\alpha =0\) in 4D

Full size image

5.1 Energy-density and pressure

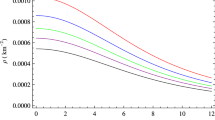
The variation of energy-density (\(\rho \)), radial pressure (\(P_{r}\)) and transverse pressure (\(P_{\perp }\)) of the star PSR J0348+0432 are shown in Fig. 1 for different values of the coupling parameter \(\alpha \). It is evident that the energy-density is maximum at the center, which decreases away from the center. As the coupling parameter \(\alpha \) increases, the energy-density at the center decreases, i.e., lower value of \(\alpha \) permits a star with larger mass than that of a star with a larger value of \(\alpha \) for the same radius as evident frim the inset in Fig. 1. It is found that stellar models also can be constructed with \(\alpha < 0\) in 5D, which is a new result. Thw stellar models with \(\alpha < 0\) are interesting theoretically as they predict more massive star in a given dimension.

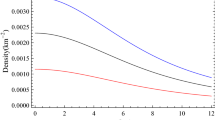
The variation of two pressures namely, the radial pressure (\(P_r\)) and tangential pressure (\(P_{\perp }\)) are plotted in In Figs. 2 and 3 respectively. The radial pressure (\(P_r\)) vanishes at the boundary, but the transverse pressure (\(P_{\perp }\)) is found to be non-zero at the boundary of the star. We note that both the pressure decreases with the increase in the coupling parameter \(\alpha \). At the center \(P_r\) and \(P_{\perp }\) are found same but away from the centre there is a branch of the pressure and it is found that \(P_{\perp } > P_r\) leading to anisotropy. The stellar model in discussion here also satisfies the inequalities \({\frac{d\rho }{dr} < 0}\), \({\frac{dP_r}{dr} < 0}\), \({\frac{dP_{\perp }}{dr} < 0}\), which are necessary for a realistic star configuration.

Fig. 3
figure 3

Radial variation of transverse pressure (\(P_{\perp }\)) in PSR J0348+0432 for different \(\alpha \) values in 5D

Full size image
Fig. 4
figure 4

Comparison of radial variation of energy-density (\(\rho \)) in PSR J0348+0432 for \(\alpha = 25\) in 4D, 5D and 6D

Full size image
Fig. 5
figure 5

Comparison of radial variation of radial pressure (\(P_r\)) in PSR J0348+0432 for \(\alpha = 25\) in 4D, 5D and 6D

Full size image

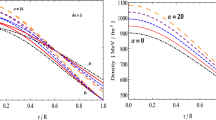
It is evident that as the space-time dimension is more than the usual 4 dimensions with \(\alpha =0\), both the energy density and pressure decreases as shown in Figs. 1 and 2. For a non-zero \(\alpha \) the variation of energy density and radial pressure are plotted in Figs. 4 and 5 with usual 4 dimensions as well as 5D and 6D for \(\alpha = 25\). It is found that as the dimension increases, the central density and the radial pressure of the star decreases for a star with given mass and radius.

5.2 Anisotropy factor

We define the anisotropy factor as,

$$\begin{aligned} \Delta = \frac{P_{\perp }-P_{r}}{P_{r}} . \end{aligned}$$
(27)

The above equation is defined as the measure of anisotropy. The TOV equation described in (12) is modified due to the anisotropy in the pressure and it yields an extra force gradient term. Consequently for \(P_\perp > P_r\), the force gradient that appears due to anisotropy signifies outward pressure, resulting an increase in repulsive force gradient and for \(P_{\perp } < P_{r}\), the anisotropy results a decrease in anisotropic force gradient implying an increase in attractive force [57].

Fig. 6
figure 6

Radial variation of anisotropy factor (\(\Delta \)) in PSR J0348+0432 for different \(\alpha \) values in 5D

Full size image

In the model the radial variation of anisotropy factor is plotted in Fig. 6 for different values of \(\alpha \) in 5D. It is clear from Fig. 6 that the positive anisotropy i.e., \(P_{\perp } > P_{r}\), corresponds to a repulsive nature of the anisotropic force gradient in the star that helps to counter balance the gravitational force gradient leading to an equilibrium and stability of the model [57]. It is noted that the anisotropic factor vanishes at the center (\(r=0\)) of the star and \(\Delta _{(r>0)} > 0\) as we move towards the boundary, r = R [38]. In Fig. 7 we compare the radial variation of anisotropy factor (\(\Delta \)) in 4D, 5D and 6D for \(\alpha = 25\) and found that the anisotropy decreases for a given radius as one increases the dimension. Thus in the EGB gravity as the dimension increases for a given \(\alpha \) the anisotropy increases very slowly and near the surface it increases sharply for higher dimensions.

Fig. 7
figure 7

Comparison of radial variation of anisotropy factor (\(\Delta \)) in PSR J0348+0432 for \(\alpha = 25\) in 4D, 5D and 6D

Full size image

5.3 Stability conditions

In this section, we discuss both (i) Herrera’s cracking criteria and (ii) Adiabatic index estimation to test the stability of the stellar models.

5.3.1 Herrera’s cracking criteria

For physically acceptability of a relativistic anisotropy stellar model, it should satisfy the causality condition, i.e., square of the radial sound velocity (\(v_{r}^{2}=\frac{dP_{r}}{d\rho }\)) and square of the transverse sound velocity (\(v_{\perp }^{2}=\frac{dP_{\perp }}{d\rho }\)) must lie in the ranges \(0< v_{r}^{2} \le 1\) and \(0< v_{\perp }^{2} \le 1\) [58]. The variation of \(v_{r}\) and \(v_{\perp }\) are drawn in Figs. 8 and 9. We note that as the coupling parameter \(\alpha \) increases the sound speed is found to decrease, for the set of values of the parameters that permits a realistic stellar models.

Fig. 8
figure 8

Radial variation of square of the radial sound velocity (\(v_{r}^{2}\)) for different \(\alpha \) in PSR J0348+0432 in 5D

Full size image
Fig. 9
figure 9

Radial variation of square of the transverse sound velocity (\(v_{\perp }^{2}\)) for different \(\alpha \) in PSR J0348+0432 in 5D

Full size image

The cracking concept suggests that a potentially stable region is the one for which the inequality \(-1 \le v_{\perp }^{2}-v_{r}^{2} \le 0\) holds good and the region where \(0 < v_{\perp }^{2}-v_{r}^{2} \le 1\) is unstable. We plot the radial variation of \(v_{\perp }^{2}-v_{r}^{2}\) in Fig. 10 for different values of \(\alpha \) and it is found that the inequality \(-1 \le v_{\perp }^{2}-v_{r}^{2} \le 0\) is satisfied, i.e., leading to a stable configuration.

Fig. 10
figure 10

Radial variation of \(v_{\perp }^{2}-v_{r}^{2}\) in PSR J0348+0432 for \(\alpha \) equals to 50, 25, 0, \(-25\), \(-50\) (in order of top to bottom) in 5D

Full size image

5.3.2 Adiabatic index

The stiffness of the EoS for given energy density is characterised by adiabatic index which has significant importance for understanding the matter present in a relativistic compact objects. For anisotropic fluid distribution the two different adiabatic indices are defined as,

$$\begin{aligned} \Gamma _{r}= & {} \frac{\rho + P_{r}}{P_{r}} \Bigg ( \frac{dP_{r}}{d\rho } \Bigg ) \nonumber \\ \Gamma _{\perp }= & {} \frac{\rho + P_{\perp }}{P_{\perp }} \Bigg ( \frac{dP_{\perp }}{d\rho } \Bigg ) \end{aligned}$$
(28)

In the EGB gravity, the expressions of \(\Gamma _{r}\) and \(\Gamma _{\perp }\) are highly non-linear for which it is not possible to explore in a closed form. Thus we will study the radial variance of \(\Gamma _{r}\) and \(\Gamma _{\perp }\) numerically for different values of \(\alpha \).

Fig. 11
figure 11

Radial variation of \(\Gamma _{r}\) in PSR J0348+0432 for different \(\alpha \) values in 5D

Full size image

The condition for the stability of a stellar configuration is obtained by Bondi, which satisfies \(\Gamma > \frac{4}{3}\) [59]. The radial variation of \(\Gamma _{r}\) and \(\Gamma _{\perp }\) for different \(\alpha \) plotted in Figs. 11 and 12 show that these are greater than \( \frac{4}{3}\) inside the star, indicating stable configuration of the star. We found the critical values for the central adiabatic index corresponding to the radial part as well as the transverse part which are 17.1819 and 14.3582 respectively (Note that we set \(r_0 = 10^{-5}\) to avoid discontinuities in the denominator).

Fig. 12
figure 12

Radial variation of \(\Gamma _{\perp }\) in PSR J0348+0432 for different \(\alpha \) values in 5D

Full size image

5.4 Energy conditions

The energy conditions are:

$$\begin{aligned}&WEC : \rho +P_{r} \ge 0, \rho +P_{\perp } \ge 0 \end{aligned}$$
(29)
$$\begin{aligned}&SEC : \rho -P_{r}-2 P_{\perp } \ge 0 \end{aligned}$$
(30)
$$\begin{aligned}&DEC : \rho - \mid P_{r} \mid \ge 0, \rho -\mid P_{\perp } \mid \ge 0 \end{aligned}$$
(31)

In Figs. 13, 14 and 15, we plot graphically the profiles of all the energy conditions and it is found that the energy conditions are satisfied in both the EGB and GTR models, for the parameters considered here.

Fig. 13
figure 13

WEC against radial distance r in PSR J0348+0432 for different \(\alpha \) values in 5D

Full size image
Fig. 14
figure 14

SEC against radial distance r in PSR J0348+0432 for different \(\alpha \) values in 5D

Full size image
Fig. 15
figure 15

DEC against radial distance r in PSR J0348+0432 for different \(\alpha \) values in 5D

Full size image
Fig. 16
figure 16

Nature of EoS in PSR J0348+0432 for \(\alpha \) equals to \(50,25,0,-25,-50\) (in order of left to right in fig.) in 5D

Full size image

5.5 Equation of state of matter inside the compact object

A parametric plot of EoS of the matter distribution plotted in Fig. 16 with different model parameters for 5D. Then the curves are fitted with both the linear and the non-linear polynomial functions. It is found that although both the linear and the quadratic relationship between density and pressure exists, best fitted EoS points a non-linear nature which are presented in Tables 2 and 3. Thus we construct models of compact objects without prescribing any EoS, however the geometry plays here an important role in the EGB gravity.

Table 2 Fitting parameters od EoS for PSR J0348+0432 for different values of \(\alpha \) in 5D
Full size table
Table 3 Fitting parameters of EoS in PSR J0348+0432 for different values of \(\alpha \) in 6D
Full size table

5.6 Hydrostatic equation

In astrophysics, the Tolman–Oppenheimer–Volkoff (TOV) equation constrains the structure of a spherically symmetric body of isotropic material which is in static gravitational equilibrium. In the present model there is an anisotropy force gradient in addition to other force gradients. Therefore, three different force gradients, namely gravitational force gradient, hydrostatic force gradient and anisotropy force gradient are in action here. The equilibrium conditions inside the star in the presence of all the three forces is ensured by the Hydrostatic equation which yields here as ,

$$\begin{aligned} -\nu '(\rho +P_{r}) -\frac{dP_{r}}{dr}+\frac{(D-2)}{r}(P_{\perp }-P_{r})=0. \end{aligned}$$
(32)

For \(D=5\), the above expression reduces to,

$$\begin{aligned} -\nu '(\rho +P_{r}) -\frac{dP_{r}}{dr}+\frac{3}{r}(P_{\perp }-P_{r})=0. \end{aligned}$$
(33)

Thus we can express the above equation as

$$\begin{aligned} f_{g} + f_{h} + f_{a} = 0 \end{aligned}$$
(34)

where, \(f_{g}\), \(f_{h}\) and \(f_{a}\) represents the gravitational force gradient, hydrostatic force gradient and anisotropy force gradient respectively, where we denoted

$$\begin{aligned} f_{g}= & {} -\nu '(\rho +P_{r})\end{aligned}$$
(35)
$$\begin{aligned} f_{h}= & {} -\frac{dP_{r}}{dr}\end{aligned}$$
(36)
$$\begin{aligned} f_{a}= & {} \frac{3}{r} (P_{\perp } - P_{r}) \end{aligned}$$
(37)

The profile of the three different force gradients inside the star are shown in Fig. 17 for different values of \(\alpha \). It can be seen that the hydrostatic (\(f_{h}\)) and anisotropy force gradients (\(f_{a}\)) are positive (i.e. repulsive in nature), whereas, the gravitational force gradient (\(f_{g}\)) is negative (i.e. attractive in nature) and dominating the other two. Thus \(f_{g}\) counterbalances the other two force gradients and keep the system in static equilibrium.

Fig. 17
figure 17

ToV relation in PSR J0348+0432 for different \(\alpha \) in 5D

Full size image

It is also noted that both the effect of pressure anisotropy and hydrostatic force gradient decreases with the increase in \(\alpha \), whereas, the gravitational force gradient is found to increase with the increase in \(\alpha \).

5.7 Mass–radius relation

The mass-radius relation and the maximum mass are of special significance in determining the viability of any prescribed model. To study the model we choose the surface density as \(\rho (r=R) = 4.68 \times 10^{14} \, {\text {g cm}}^{-3}\), and plot the mass-radius relationship in Fig. 18. For PSR J0348+0432 mass vs radius relation in Fig. 18 shows a curve which attains the observed mass and radius of the star for \(\alpha = -104\) in 5D EGB gravity. From the fitting it is noted that the maximum mass of a neutron star in the model is \(2.267 M_{\odot }\) with a maximum radius of 13.28 km permitted. This implied a star of compactification (mass to radius ratio) factor 0.1707. The compactification factor of the neutron star considered is 0.1665, thus the model can be used to predict more compact neutron star.

Fig. 18
figure 18

Mass–radius (M–R) relation in 5D

Full size image

6 Comparative study of the model

The admissibility of the stellar model for a star is tested considering a known pulsar using data from the LIGO/VIRGO collaboration. The different physical parameters obtained are shown in Table 4. It can be noted that for all the stars the central density (\(\rho _0\)) is higher than the density at the surface (\(\rho _b\)). We can also observe the central radial pressure for different compact objects, taking \(\alpha =25\) in 5D.

Table 4 Best fitted values of model parameters for different known compact objects for \(\alpha =25\) in 5D
Full size table

7 Discussion

In the paper stellar models for compact objects are constructed in EGB gravity with higher dimensional Finch–Skea metric. In this case we consider stars in hydrostatic equilibrium in \(D \ge 4\). We explore the stellar models taking the spacetime dimension upto \(D = 6\) and analyzed the physical features of compact objects for a given mass and radius. The stellar models satisfy all the criteria required for stability and physical viability as pointed our by Delgaty and Lake [53]. The methodology adopted here permits different stars of a given mass with different radii or for a given mass with different masses depending on the model parameters including the coupling parameters of the EGB gravity. The contribution from the Gauss–Bonnet term on the energy-density, pressure profiles and other physical features are also studied. As the field equations are highly non-linear and it is not possible to determine the exact solutions for compact objects in higher curvature gravity we adopt numerical technique. We note the followings:

(i) The pressure and energy density profiles are found positive for the given choices of model parameters which are obtained from the criteria for a realistic star. The radial pressure \(P_{r}\) vanishes at the boundary, while the transverse pressure \(P_{\perp }\) does not vanishes. From Figs. 2 and 3, it is evident that both \(P_{r}\) and \(P_\perp \) decreases at the center of the star as one increases the coupling parameter \(\alpha \) of the EGB gravity. However, for a given dimension the energy density increases as \(\alpha \) decreases which is evident from Fig. 1. The energy density is found to decrease away from the center of the star. The coupling constant \(\alpha \) in EGB gravity is found to play an important role in determining the physical quantities such as energy density and pressure of the star, which is different from that in GR. The role of negative \(\alpha \) in the stellar model is interesting as it increases the energy density and pressure inside the star for \(D=5\) compared to a positive \(\alpha \) which is known from the string theory. In the literature EGB gravity with \(\alpha < 0\) accommodates an interesting cosmological scenario [16] and it cannot be ruled out. Thus \(\alpha < 0\) permits a compact star which may be accommodated with some new features.

(ii) The density and radial pressure diminishes at the center as the spacetime dimension is increased for a given \(\alpha \) as evident from Figs. 4 and 5. In the usual four dimensional GR both the energy density and the radial pressure are more than in higher dimensional space-time which is also found in EGB gravity in higher dimensions when \(\alpha \ne 0\) .

(iii) The stellar modles in EGB gravity are found to satisfy the inequalities, \(\frac{dP_{r}}{dr} < 0 \), \(\frac{dP_{\perp }}{dr} < 0 \) and \( \frac{d\rho }{dr} < 0 \) for a set of model parameters considered here for a realistic stellar model.

(iv) The tangential pressure satisfy the inequality, \(P_{\perp } > P_{r}\), away from the center of the star, which indicates that the anisotropic force is repulsive in nature and balance the gravitational force. The anisotropy in the stellar model enhances the hydrostatic equilibrium leading to stability of the model. The anisotropy in the pressure which is zero at the center but it increases outward inside the star (Fig. 6).

(v) The stability of the stellar models in EGB gravity with FS metric is ensured from the evolution of the sound speed (Figs. 8, 9, 10) which is subliminal and hence causality is maintained inside the star.

(vi) The radial variation of the adiabatic indices \(\Gamma _{r}\) and \(\Gamma _{\perp }\) plotted for different values of \(\alpha \) in Figs. 11 and 12 and it emerged that both \(\Gamma _{r}\) and \(\Gamma _{\perp }\) are greater than \( \frac{4}{3}\) inside the star. The analysis once again is important for the acceptability of a stable stellar configuration. In Figs. 11 and 12, the variation of \(\Gamma _{r}\) and \(\Gamma _{\perp }\) is almost identical, overlapping on each other satisfying the limit indicating that the model is stable.

(vii) The radial variation of the weak, strong and dominant energy conditions are drawn in Figs. 13, 14 and 15 and found that these energy conditions are not violated.

(viii) The parameter plot of energy density and pressure (Fig. 16) can be fitted with a functional form and the best fit function is used to predict the equation of state (EoS) of matter in the star when \(D=5\) for different \(\alpha \). In Tables 2 and 3 we have shown the best fitted EoS for \(D=5\) and \(D=6\) respectively. We note that the quadratic fit is better than the linear fit, for a given compactification. It is also noted that the EoS is mostly non-linear if the space-time dimension is more than the usual four dimensions.

(ix) The profile of the radial variation of three different forces inside the star are shown in Fig. 17 for different values of \(\alpha \). It is evident that the gravitational force (\(f_{g}\)) is negative in nature and the rest two forces (\(f_{a}\) and \(f_{h}\)) are positive. Thus, \(f_{g}\) dominates over the other two forces and it counterbalance the other two forces leading to static equilibrium.

(x) Considering a known star namely, PSR J0348+0432 whose mass and radius are known, a radial variation of the mass of star studied in Fig. 18 for different values of the metric parameter (C) in the EGB gravity with \(\alpha = -104\) in \(D=5\) dimensions. It is observed that a star with maximum mass 2.267\(M_{\odot }\) and radius of 13.28 km having surface density \(\rho (r=R) = 4.68 \times 10^{14} \mathrm{g}\) \(\mathrm{cm}^{-3}\) in 5D EGB gravity can be accommodated. A star with mass same as PSR J0348+0432 but with greater radius than that star is also possible. But in the later case the compactification factor is less.

The method adopted here permits a class of new relativistic stellar models in EGB gravity employing FS metric. The new result in this case is that a dense star in EGB gravity can be obtained for \(\alpha < 0\) compared to GR. For \(\alpha > 0\) it permits less dense star compared to a star in GR. The precise measurement of the radius of a star in future will be useful to understand the role of modification incorporated in the gravitational action. Thus we conclude that compact objects indeed do exist in the EGB framework and that the GB higher curvature terms improve the likelihood of our models conforming a compact star with realistic distributions. Also we conclude that the non-linearity in the EoS develops as the spacetime dimensions are extended. Central density, pressure and anisotropy are found to decrease as the dimension increases. Implication of the results obtained, in the context of current observational data of relativistic compact stars, needs to be probed further and will be taken up elsewhere.