Abstract
In this paper, we have studied a new class dynamical model of spherically symmetric radiating collapsing stars. The solution of field equations has been discussed by using the boundary condition and obtained all the physical parameters in terms of mass M and surface radius \(R_0\) which will be significant in astrophysical applications. We have also studied the thermal behavior of the stars and discussed the horizon formation and its temperature. We have shown that horizon temperature increases with time under certain conditions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
General relativity theory (GTR) has an important roles in the studies of gravitational collapse of massive stars and their remnants like neutron stars or black-holes [1,2,3,4]. A star that losses its equilibrium, collapse under its own gravity and ultimately culminates in the state of space-time singularity. The state of space-time singularity may be naked(light rays emanating from it can reach any far-away observer) or, a black hole (implying that the light rays from it may be trapped within a surface called its event horizon). The studies of mathematical models of gravitationally collapsing systems are expected to play a key role in the understanding of the nature of collapsing stellar system and its singularities [5, 6]. Therefore, a comprehensive description of gravitational collapse and the modeling of the structure of compact objects under a variety of circumstances remain among the most interesting problems that general relativity theory has to deal with [7,8,9,10,11,12]. This fact elucidates the attraction that these problems exert on the community of the relativists. The collapsing gravitating system possesses different stages of evolutions involving physical quantities that determine the end state of relativistic fluid configuration [7, 13, 15,16,17,18].
The space-time in the exterior region of the radiating stars is known to be described by Vaidya metric [9, 10]. The formulation of the junction conditions smoothly joining the interior space-time metric of the collapsing matter across its boundary with the appropriate form of Vaidya metric, as first proposed by Santos [11] has given an impetuous for studies in this direction. The thermodynamical nature of black holes in general relativity was first noted by Hawking and his collaborators in their works that established what are known now as the laws of black hole thermodynamics [19, 20]. These thermodynamics laws study the area and surface gravity of the event horizon of a stationary black hole in general relativity to the entropy and temperature of a thermodynamic system at equilibrium. A lot of effort has been devoted in the studies of the connection between gravity and thermodynamics that the analogy can be extended to the theory, making it valid not only on the horizon-surface, and therefore showing possibly how gravity could be considered as a thermodynamic theory [21,22,23,24,25].
In the present work, we have considered spherically symmetric relativistic star, whose collapse is accompanied with dissipation in the form of radial heat flux. The geometry of the interior space-time of the collapsing system is chosen to be conformal to that of the space-time of FLRW metric so that the Weyl tensor is known to vanish (conformally flat). Conformally flat space-times, in the context of radiating star, were first studied by Som and Santos [26]. Later, the most general class of conformally flat solutions for a shear-free radiating star were obtained and examined by various researchers [5, 6, 27,28,29]. Herrera et al. [29] have critically examined models of shear-free collapsing fluids accompanied with dissipation of heat on the space-time background subject to the constraint that the associated Weyl tensor should vanish. This paper is organised as follows-after introduction, in Sect. 2, we have provided the field equations for the spherically symmetric conformally flat metric and energy momentum tensor for the interior space time is that of perfect fluid with heat flux. In Sect. 3, the junction conditions (boundary conditions) required for the smooth matching of the interior and exterior space times across a time-like hypersurface are presented and luminosity and red shift expression are obtained. The transport equations for the dissipative fluxes within the framework of non causal thermodynamics are also considered in here. The dynamical model of radiating collapsing star is discussed by using boundary condition for \(k =0\) and \(k \ne 0\) in Sect. 4. Last section contains the discussion and concluding remarks.
2 Interior space-time and field equation
Consider a class of spherically symmetric conformally flat space time which describes the interior of collapsing fluids undergoing dissipation in the form of heat flow,
The interior of the collapsing fluid considered to be here perfect fluid with heat flux, is represented by the energy momentum tensor,
where p is isotropic pressure and \(\rho \) is the energy density, \(v_i\) and \(q_i\) are four velocity of fluid and radial heat flux vector respectively, satisfying
where q is function of \(\left( t,r\right) \) represents heat flux of radiation.
The shearing tensor \(\sigma _{ij}\) is define as,
with the acceleration vector \(\left( a_i\right) \) and expansion scalar \(\left( \theta \right) \)
For line-element (1), one obtained the four acceleration vector
and the expansion scalar
For gravitational collapsing configuration,
The Einstein field equations \(G_{ij} = \alpha T_{ij}\) (where \(\alpha \)=\(\frac{8\pi G}{c^4}\)) for (1) and (2) yield the following equations,
where dot (.) and dash (’) represent the derivative with respect to t and r respectively.
The mass function which describes the mass of collapsing star at \(\left( t,r\right) \) is given by [30, 31]
3 The junction condition and the thermodynamics
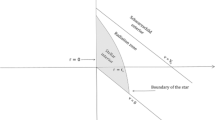
The spherically symmetric collapsing fluid which undergoing dissipation in the form of heat flow is bounded by a time-like spherical surface \(\sum \) and it described by the intrinsic metric
where \({\xi ^i}\)=\((\tau ,\theta ,\phi )\) is the intrinsic co-ordinate and \(R_0(\tau )\) intrinsic geometrical radius. The exterior space-time to a radiating star is represented by Vaidya metric which is given by [11, 32, 33]
with co-ordinate \(x_{+}^i\)=\((\nu ,\Omega ,\theta ,\phi )\) and \(M(\nu )\) is the mass of star is function of retarded time \(\nu \) i.e. Newtonian mass of gravitating star as measured by distant observer. The time-like spherical surface \(\sum \) separates the interior space time \(ds^2_{-}\) to exterior space time \(ds^2_{+}\). The metric (15) is the unique solution of the spherically symmetric field for the radiating star and the Einstein’s tensors for this,
The energy momentum tensor for radiation(exterior to star)
where \(\epsilon \) is energy density of radiation and \(w_i = (1,0,0,0)\) the four velocity vector. Thus from (16) and (17) the field equations produced,
which is energy density of radiation measured by an observer on \(\sum \). Since the star is radiating \((\epsilon >0)\) to the exterior space time, therefore it must have \(\frac{dM}{d \nu } \le 0\) that is, mass of the star diminishes during radiation [7, 11, 32, 33].
The junction condition require the continuity of the metric (1) and 15 at surface \(\sum \),
known as continuity of first fundamental form and
known as continuity of second fundamental form, where
and \(\eta ^{\pm }_k\) represent the extrinsic curvature and the normal vector to the surface \(\sum \) in \(x^i_{\pm }\) coordinate respectively. Using the junction condition (19) with the metric (1), (14) and (15), one obtain
The non-zero components of extrinsic curvature for the line-element (1) and (15) are,
and
Now using the Eqs. (26) and (28), the condition (20) gives
by taking use of Eqs. (21)–(24) with Eqs. (25) and (27), the condition (20) gives
The energy density of radiation \(\epsilon \) measured by an observed on surface \(\sum \)
The luminosity observed on the surface \(\sum \)
and boundary redshift
The luminosity observed for distant observer at infinity
3.1 Thermodynamics
The evolution of a system such as a massive star undergoing gravitational collapse, the temperature profile and luminosity are necessary parameters for discussion [7, 24, 25]. We consider the non casual thermodynamics to obtain the temperature of collapsing star. The first order Eckart formalism was used to study the temperature where heat flux is governed by the Fourier’s law,
where \({\mathbb {K}}\) is thermal conductivity, \(\mathbf {T}\) is the temperature, \(h^{ij}=(g^{ij}+v^iv^j)\) is the projection tensor and \(q^i\) = (0, q, 0, 0). Therefore we have,
The thermal conductivity
where a and b are positive constant.
The effective surface temperature observed by the external observer [34]
where for photon the constant \(\delta \) is given by
where \(k_1\) and \(\hbar \) denoting respectively Boltzmann’s and Plank’s constant.
4 Dynamics of the collapsing star
From Eqs. (10) and (11), one obtained
The Eq. (40) is usually describe the isotropy condition and is integrable in two different cases:
For \(\mathbf{k}=0 \),
For k\(\ne \)0,
where \(\lambda _1\), \(\lambda _2\), \(\mu _1\) and \(\mu _2\) are orbitrary function of ’t’. Further we shall consider the cases for \(k=0\) and \(k \ne 0\) separately.
4.1 Case I: k=0
The collapsing fluid configuration of this class are described by Eq. (41). To determine the orbitray constants \(\lambda _1\),\(\mu _1\), we use the boundary conditions given by Eqs. (22)–(29). Then we obtain,
Thus Eq. (41) now becomes
for collapsing configuration \(r<r_{\sum }\). Here \(R_0\) is the intrinsic geometrical radius of star, \(R^*_0=\frac{dR_0}{d\tau }\) and M is the mass(Newtonion) of the star at surface \(\sum \).
Taking use of Eq. (45) into Eqs. (9)–(12), one obtain
where
and
Using Eqs. (10), (13), (21), (24) and (45) into Eqs. (33) and (34) one obtained
and
From Eqs. (56) and (57) one can observe that the horizon formation \(\left( L_{\infty } \rightarrow 0, q \ne 0\right) \) occurs when (\(r_{\sum }-2MR_0) \rightarrow 0\)
In view of Eqs. (12) and (36), we have
by integrating above, gives
where \(A_1(t)\) is arbitrary constant.
In Eq. (59), choosing \(b=3\) which represents radiation interaction with matter through the diffusive approximation [7]. The orbitrary function \(A_1(t)\) is determined by using boundary conditions (38) and Eq. (57),
Therefore, the temperature inside the star becomes
One can observe from Eq. (61) that \(\mathbf {T}_{H}\)(the temperature of star at the horizon formation \(r=r_H\)) is,
where
From Eq. (45), the mass of collapsing star at horizon surface \(r=r_H\),
where \(R_{H}\) and \(M_{H}\) are geometrical radius and mass of collapsing star at horizon \(r=r_H\).
It can be seen from Eqs. (62) and (63) that the temperature \((\mathbf{T} _{H})\) of star is increases when \( \frac{\partial }{\partial t}\log \left( \int ^0_{r_H} \frac{\dot{R'}}{R^4}dr\right) > 0 \).
4.2 Case II: k \(\ne \) 0
In this case, we discussed the behaviour of collapsing fluids with equation (42), for \(k \ne 0\).
Using boundary condition (22)–(29) to obtain orbitrary constant \(\lambda _2\) and \(\mu _2\),
and the we have
using Eq. (68) into Eqs. (9)–(12), one obtained
where C, \(C_1\), \(C_2\), \(C_3\) are given by (51)–(55) and
The redshift (\(z_{\sum }\)) and luminosity (\(L_{\infty }\)) are obtained by using Eqs. (10), (13), (21), (24) and (68) into Eqs. (33) and (34)
and the luminosity
The horizon formation in this case is same as in previous case (i.e. independent of k).
Now in view of Eqs. (12) and (36),
using Eq. (37) and integrating gives (with b = 3)
where \(A_2(t)\) is arbitrary constant. The arbitrary constant \(A_2(t)\) is determined by using Eq. (38)
Therefore,
Thus the temperature of star at the horizon surface \(r=r_{H}\) becomes
and
where
where \(R_{H}\) and \(M_{H}\) are geometrical radius and mass of collapsing star at horizon surface \(r=r_H\).
It can be seen from Eq. (80) \(\frac{\dot{\mathbf {T}}_H}{\mathbf {T}_H}>0\) when \(\frac{\partial }{\partial t}\log \left( \int ^0_{r_H} (1-kr^2)\frac{\dot{R'}}{R^4}dr\right) > 0\)
5 Discussion and concluding remarks
In this paper, we have described the dynamical solution of relativistic conformally flat spherically symmetric collapsing radiating star and discussed its thermal behaviour.We consider interior metric as a class of conformally flat spherically symmetric consists of dissipative perfect fluid distribution and the exterior region of star is described by the Vaidya space time metric. By employing the Darmois-Israel junction conditions for the smooth matching of interior(\(\sum ^-\)) and exterior (\(\sum ^+\)) spacetime at the boundary \(\sum \), we have obtained the boundary conditions (29) and (30) over hypersurface\(\sum \). We have presented new class of solution of spherical collapsing fluid distribution using boundary conditions in two separate cases \(k=0\) and \(k \ne 0\). All the physical quantities namely p, \(\rho \) and q are obtained in terms of M(Newtonion mass) and intrinsic surface radius \(R_0\). The redshift \((z_{\sum })\) and luminosity (\(L_{\infty }\)) of radiating star to distant observer are also calculated in the terms of M and \(R_0\). We can see from Eq. (57) and (74) that \(L_{\infty } \rightarrow 0\) when \(r_{\sum }-2MR_0 \rightarrow 0\) (with \(q \ne 0\)) which is the horizon formation condition. This shows that the stars still emitting radiation after formation of horizon [35]. Further we discussed the noncausal thermodynamics with the heat transport equation which predicts temperatures of the star given by Eqs. (61) and (78) for \(k=0\) and \(k \ne 0\) respectively. Also we showed that the temperature of radiating star is increases under certain condition . The mass of the star at horizon surface are also obtained in both cases. Since blac-khole are highly thermal objects in the universe and their thermodynamics properties are well understood. The present study determined the event horizon and its temperature in non-static space time. Since in this work the solutions are described in terms of the mass and radius of the stars, therefore the presented model will be significant for the studies of the astrophysical phenomena such as blackhole and high energy compact objects.
Data availability
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
Data availability
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: ...].
References
G.C. McVittie, Gravitational motions of collapse or of expansion in general relativity. Annales de l’IHP Physique théorique 6(1) (1967)
A.H. Taub, Restricted motions of gravitating spheres. Annales de l’IHP Physique théorique 9(2) (1968)
M.C. Faulkes, Non-static fluid spheres in general relativity. Prog. Theor. Phys. 42(5), 1139–1142 (1969)
E.N. Glass, B.A.H.R.A.M. Mashhoon, On a spherical star system with a collapsed core. Astrophys. J. 205 , 570–577 (1976)
S.R. Maiti, Fluid with heat flux in a conformally flat space-time. Phys. Rev. D 25(10), 2518 (1982)
B. Modak, Cosmological solution with an energy flux. J. Astrophys. Astron. 5(3), 317–322 (1984)
A.K.G. De Oliveira, N.O. Santos, C.A. Kolassis, Collapse of a radiating star. Mon. Not. R. Astron. Soc. 216, 1001–1011 (1985)
O.J. Robert, H. Snyder, On continued gravitational contraction. Phys. Rev. 56(5), 455 (1939)
P.C. Vaidya, Nonstatic solutions of Einstein’s field equations for spheres of fluids radiating energy. Phys. Rev. 83(1), 10 (1951)
P.C. Vaidya, An analytical solution for gravitational collapse with radiation. Astrophys. J. 144, 943 (1966)
N.O. Santos, Non-adiabatic radiating collapse. Mon. Not. R. Astron. Soc. 216, 403–410 (1985)
R. Chan, L. Herrera, N.O. Santos, Dynamical instability for radiating anisotropic collapse. Mon. Not. R. Astron. Soc. 265(3), 533–544 (1993)
B.C. Tewari, K. Charan, Radiating star, shear-free gravitational collapse without horizon. Astrophys. Space Sci. 351(2), 613–617 (2014)
P. Chandra, A. Mitra, Eternally Collapsing Objects: A Review of 22 Years of Misconceptions (2020). Preprint in free for all electronic platform: arXiv:2001.0501
A. Mitra, N.K. Glendenning, Likely formation of general relativistic radiation pressure supported stars or ‘eternally collapsing objects. Mon. Not. R. Astron. Soc. Lett. 404(1), L50–L54 (2010)
A. Mitra, Radiation pressure supported stars in Einstein gravity: eternally collapsing objects. Mon. Not. R. Astron. Soc. 369(1), 492–496 (2006)
P.S. Joshi, T.P. Singh, Role of initial data in the gravitational collapse of inhomogeneous dust. Phys. Rev. D 51(12), 6778 (1995)
P.S. Joshi, I.H. Dwivedi, Initial data and the end state of spherically symmetric gravitational collapse. Class. Quantum Gravity 16(1), 41 (1999)
J.D. Bekenstein, Black holes and entropy. JACOB BEKENSTEIN: The Conservative Revolutionary, 307–320 (2020)
J.M. Bardeen, B. Carter, S.W. Hawking, The four laws of black hole mechanics. Commun. Math. Phys. 31(2), 161–170 (1973)
T. Padmanabhan, Gravity: the inside story. Int. J. Mod. Phys. D 17(13), 2585–2591 (2008)
W. Israel, J.M. Stewart, Transient relativistic thermodynamics and kinetic theory. Ann. Phys. 118(2), 341–372 (1979)
R. Maartens, Dissipative cosmology. Class. Quantum Gravity 12, 1455–1465 (1995)
J. Martinez, Transport processes in the gravitational collapse of an anisotropic fluid. Phys. Rev. D 53(12), 6921 (1996)
G. Megan, S.D. Maharaj, R. Maartens, A causal model of radiating stellar collapse. Class. Quantum Gravity 15(2), 323 (1998)
M.M. Som, N.O. Santos, Expanding viscous fluid with heat flow. Phys. Lett. A 87(3), 89–90 (1981)
A. Banerjee, S.B.D. Choudhury, B.K. Bhui, Conformally flat solution with heat flux. Phys. Rev. D 40(2), 670 (1989)
D. Schäfer, H.F. Goenner, The gravitational field of a radiating and contracting spherically-symmetric body with heat flow. Gen. Relativ. Gravit. 32(11), 2119–2130 (2000)
B.V. Ivanov, Collapsing shear-free perfect fluid spheres with heat flow. Gen. Relativ. Gravit. 44(7), 1835–1855 (2012)
M.E. Cahill, G.C. McVittie, Spherical symmetry and mass-energy in general relativity. I. General theory. J. Math. Phys. 11(4), 1382–1391 (1970)
C.W. Misner, D.H. Sharp, Relativistic equations for adiabatic, spherically symmetric gravitational collapse. Phys. Rev. B 136(2B), 571 (1964)
L. Herrera, J. Martinez, Gravitational collapse: a case for thermal relaxation. Gen. Relativ. Gravit. 30(3), 445–471 (1998)
V.P. Chunilal, The gravitational field of a radiating star. Proc. Indian Acad. Sci. Sect. A 33(5) (1951)
M. Schwarzschild, Structure and Evolution of Stars (Dover, New York, 1958)
Z. Zheng, D. Xianxin, Hawking radiation from a non-static black hole. Chin. Phys. Lett. 8(10), 548 (1991)
Funding
There is no fund available for the publication of this research article.
Author information
Authors and Affiliations
Contributions
GV did all the calculation parts of article and the draft of the manuscript was written by the RK. Both the authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors have no relevant financial or non-financial interests to disclose.
Ethical statements
The submitted work is original and has not been published elsewhere in any form or language (partially or in full).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Verma, G., Kumar, R. A dynamical model of radiating stars and their thermal behavior. Eur. Phys. J. C 82, 513 (2022). https://doi.org/10.1140/epjc/s10052-022-10473-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-022-10473-z