Two-particle Bose–Einstein correlations in ${ pp }$ collisions at $\mathbf {\sqrt{s} = 13}$ TeV measured with the ATLAS detector at the LHC

Abstract

This paper presents studies of Bose–Einstein correlations (BEC) in proton–proton collisions at a centre-of-mass energy of 13 TeV, using data from the ATLAS detector at the CERN Large Hadron Collider. Data were collected in a special low-luminosity configuration with a minimum-bias trigger and a high-multiplicity track trigger, accumulating integrated luminosities of 151 $\upmu$b$^{-1}$ and 8.4 nb$^{-1}$, respectively. The BEC are measured for pairs of like-sign charged particles, each with $|\eta | < 2.5$, for two kinematic ranges: the first with particle $p_{\mathrm {T}} > 100$ MeV and the second with particle $p_{\mathrm {T}} > 500$ MeV. The BEC parameters, characterizing the source radius and particle correlation strength, are investigated as functions of charged-particle multiplicity (up to 300) and average transverse momentum of the pair (up to 1.5 GeV). The double-differential dependence on charged-particle multiplicity and average transverse momentum of the pair is also studied. The BEC radius is found to be independent of the charged-particle multiplicity for high charged-particle multiplicity (above 100), confirming a previous observation at lower energy. This saturation occurs independent of the transverse momentum of the pair.

1 Introduction

Particle correlations play an important role in the understanding of multiparticle production in hadron–hadron, hadron–nucleus and nucleus–nucleus collisions. Correlations between two identical bosons, called Bose–Einstein correlations, (BEC), are a well known phenomenon in high-energy and nuclear physics (for reviews see Refs. [1,2,3,4,5,6,7,8]). The BEC are often considered to be the analogue of the Hanbury Brown and Twiss effect [9,10,11] in astronomy, describing the interference of incoherently emitted identical bosons [12,13,14,15]. The BEC constitute a sensitive probe of the space-time geometry of the hadronization region, and allow the determination of the size and shape of the source from which particles are emitted. High-multiplicity data in proton–proton interactions can serve as a reference for studies of nucleus–nucleus collisions [16]. The effect of BEC is reproduced in both the hydrodynamical/hydrokinetic [17,18,19] and the Pomeron-based [20, 21] approaches for modelling of high-multiplicity hadronic interactions. The BEC between a pair of particles depend on the particle multiplicity in the event and on the average transverse momentum of the pair. The dependence on these parameters is particularly sensitive to the space-time features of the hadronization region, as discussed by the authors of various models [22,23,24,25,26,27].

The BEC can be studied for two, three, or more identical bosons, assuming a hadronization region parametrized by one, two, or three size parameters. At the Large Hadron Collider (LHC), the BEC with one size parameter, the source radius, have been studied by the ATLAS Collaboration in pp collisions at the centre-of-mass energies $\sqrt{s} = 0.9$ and 7 TeV [28], and in p+Pb collisions at $\sqrt{s_\mathrm {NN}} = 5.02$ TeV per nucleon–nucleon pair [29]. The BEC source radius parameter, R, was observed by ATLAS to saturate, i.e. to reach a plateau level, at high charged-particle multiplicity, in $\sqrt{s} = 7$ TeV pp collisions [28]. The BEC in pp collisions have also been studied in the ALICE [30,31,32,33,34], CMS [35,36,37,38] and LHCb [39] experiments. The CMS results at 13 TeV also show a plateau in R at high multiplicity [38].

Pomeron-based models predict a plateauing of R at intermediate multiplicities as a consequence of the overlap of the colliding protons, followed by the return to a lower value of R at high multiplicities [20, 21]. The IP-Glasma model [40] predicts some tendency to R saturation at high multiplicities for pp interactions.

In a different approach, two-particle correlations have been analysed at $\sqrt{s} = 7$ TeV by ATLAS in the framework of a phenomenological model based on ordered hadron chains. This approach provides an alternative interpretation of the correlations commonly attributed to Bose–Einstein interference [41].

In this paper, studies of the BEC in pp collisions at $\sqrt{s} = 13$ TeV using the ATLAS detector [42] are presented. The same methodology is used in this analysis as was used in the previous ATLAS BEC studies [28], and the same minimum-bias (MB) trigger is used as was used in an earlier study of charged-particle distributions at 13 TeV [43, 44]. In addition, the study is extended to the region of high-multiplicity collisions by using the high-multiplicity track (HMT) trigger previously used for studies of long-range elliptic azimuthal anisotropies [45].

This paper is organized as follows. The analysis method is described in Sect. 2. The ATLAS detector is described in Sect. 3. The Monte Carlo (MC) and data samples are presented in Sect. 4. The track selection criteria and data correction procedure are presented in Sect. 5 and the reference sample is discussed in Sect. 6. The systematic uncertainties are presented in Sect. 7. The BEC source radius and correlation strength dependence on, separately, charged-particle multiplicity and average transverse momentum of the pair is shown in Sect. 8. This section also presents the double-differential dependence of the BEC parameters on multiplicity and average transverse momentum. A comparison with previous, lower-energy ATLAS results is presented, as well as a comparison with CMS results at 13 TeV. The summary and conclusions are given in Sect. 9.

2 Analysis method

The BEC are observed at small values of the square of the four-momentum difference, $Q^2$, between two identical bosons, where $Q^2 = - (p_1 - p_2)^2 = {M_{12}^2} - {4 m^2}$, $p_1$ and $p_2$ are the four-momenta of the particles, $M_{12}$ is the invariant mass of the particle pair and m is the particle mass. The BEC parameters are measured in terms of a two-particle correlation function,

$$\begin{aligned} C_{2} (Q) = {\rho (Q) }/{ \rho _0 (Q) }, \end{aligned}$$

(1)

where $\rho (Q)$ is the distribution of Q formed from all like-sign charged-particle pairs, assuming in this analysis that all charged particles are pions, and $\rho _0 (Q)$ is a reference distribution specially constructed to exclude the effect of BEC. In this analysis, $\rho _0 (Q)$ is constructed from unlike-sign charged-particle pairs, as discussed in Sect. 6. The distributions $\rho (Q)$ and $\rho _0 (Q)$ are normalized to unity, i.e. they are probability density functions.

To account for the effects of resonances (for example $\eta$, $\eta ^{\prime }$, $\omega$, $\rho$, $K^{*}$, $\phi$), the $C_2 (Q)$ correlation function is corrected by dividing by the corresponding quantity constructed from MC simulations that contain resonances but not the BEC:

$$\begin{aligned} R_{2}(Q) = \frac{ C_{2}^{\mathrm {data}}(Q) }{ C_{2}^{\mathrm {MC}}(Q) } = \frac{ \rho ^{\mathrm {data}}{ (Q) } }{\rho _0^{\mathrm {data}} (Q) } \Bigg / \frac{ \rho ^{\mathrm {MC}} { (Q) } }{ \rho _0^{\mathrm {MC}} (Q) }, \end{aligned}$$

(2)

where $C_{2}^{\mathrm {data}}(Q)$ and $C_{2}^{\mathrm {MC}}(Q)$ are the $C_{2} (Q)$ functions reconstructed from data and MC samples, respectively.

The BEC effect is usually described by a function, $\Omega$, with two parameters: the effective R parameter, and the strength parameter, $\lambda$, where the latter is also called the incoherence or chaoticity parameter [46]. If measurement can be made down to a very small value of Q ($\lesssim 10$ MeV), the parameter $\lambda$ may also be sensitive to a “halo” contribution due to long-lived resonances [5], but this is not possible in this analysis. A typical functional form is:

$$\begin{aligned} R_{2}(Q) = c_{0} [1 + \Omega (\lambda , Q R)] (1 + \varepsilon Q). \end{aligned}$$

(3)

In a simplified scheme for fully coherent emission of identical bosons, $\lambda =0$, while for incoherent (chaotic) emission, $\lambda =1$. Various parameterizations of the $\Omega (\lambda , Q R)$ function in Eq. (3) can be found in the literature (see for example Refs. [3, 47]), each assuming a different shape for the particle-emitting source. The parameter $c_{0}$ is a constant depending on the normalizations of $\rho (Q)$ distributions and is chosen such that $R_2 (Q)$ is unity at large Q.

A Lévy-type parameterization for $\Omega$ introduces a further free parameter, $\alpha$:

$$\begin{aligned} \Omega (\lambda , Q R, \alpha ) = \lambda \, {\mathrm {e}}^{{- (R Q)}^\alpha }, \end{aligned}$$

with $0 < \alpha \le 2$. The Lévy distribution is a simple exponential when $\alpha = 1$ and a Gaussian when $\alpha = 2$. Fits to $R_2 (Q)$ with $\alpha$ free usually return a value between 1 and 2, and the fit quality, in terms of $\chi ^2 / ndf$, is generally better than the fit using an exponential or Gaussian. However, the interpretation of the R parameter in terms of the distribution of space-time points is then less clear. Also, in studies for the 7 TeV analysis it was found that $\alpha$ varied when $R_2 (Q)$ was studied more differentially in terms of charged multiplicity or pair transverse momentum. So, in common with the other LHC experiments, this analysis constrains $\alpha$ to be 1 or 2. Investigation of the Gaussian parameterization is found to give a significantly poorer description of the data in the low-Q region. (See Sect. 8.1). So, in the study presented here, the BEC parameters are extracted using an exponential parameterization,

$$\begin{aligned} \Omega (\lambda , Q R) = \lambda \, {\mathrm {e}}^{- R Q}, \end{aligned}$$

(4)

of a static source assuming a radial Lorentzian distribution of the source. The fitted parameter $\varepsilon$ in Eq. (3) takes into account possible long-distance correlations that have not been removed fully by $\rho (Q)$.

3 The ATLAS detector

ATLAS is a multipurpose particle physics experiment operating at one of the beam interaction points at the LHC. The ATLAS detector¹ covers almost the whole solid angle around the collision point with layers of tracking detectors, calorimeters and muon chambers. It is designed to study a wide range of physics topics at LHC energies. For the measurements presented in this paper, the tracking devices and the trigger system are of particular importance.

The innermost part of the ATLAS detector is the inner tracking detector (ID), which has full coverage in $\phi$ and covers the pseudorapidity range $|\eta |<2.5$. The ID is immersed in the $\mathrm {2\, T}$ axial magnetic field of a superconducting solenoid and measures the trajectories of charged particles. It consists of a silicon pixel detector (Pixel), a silicon microstrip detector (SCT) and a straw-tube transition radiation tracker (TRT), each split into a barrel and two endcap components. The Pixel, SCT and TRT are located around the interaction point spanning radial distances of 33–150 mm, 299–560 mm and 563–1066 mm, respectively. The barrel (each endcap) consists of four (three) pixel layers, four (nine) double layers of silicon microstrips and 73 (160) layers of TRT straws. The Pixel, SCT and TRT have $(r, \phi )$-position resolutions of 10 $\upmu$m, 17 $\upmu$m, and 130 $\upmu$m, respectively.

For Run 2 a new innermost pixel layer, the insertable B-layer (IBL) [48], was installed around a new, narrower and thinner beam pipe. The IBL is composed of 14 lightweight staves arranged in a cylindrical geometry, each made of 12 silicon planar sensors in its central region and $2\times 4$ three-dimensional sensors at the ends. The IBL pixel dimensions are 50 $\upmu$m in the $\phi$-direction and 250 $\upmu$m in the z-direction (compared with 50 $\upmu$m by 400 $\upmu$m for the other pixel layers). The intrinsic spatial resolution of the IBL readout is 10 $\upmu$m in $(r, \phi )$-position and 75 $\upmu$m in z-position [49]. The smaller radius and the reduced pixel size result in improvements in both the transverse and longitudinal impact parameter resolutions [43, 44]. The services for the existing pixel detector were upgraded, significantly reducing the amount of material in the region $|\eta | > 1.5$, in particular at the boundaries of the active tracking volume.

A track from a charged particle traversing the barrel detector typically has 12 silicon measurement points (hits), of which 4 are Pixel and 8 are SCT, and more than 30 TRT straw hits. Requirements on an IBL hit and on impact parameters strongly suppress the number of tracks from secondary particles.

The ATLAS detector has a two-level trigger system: the first-level (L1) trigger and the high-level trigger (HLT) [50]. Events used in this analysis were required to satisfy L1 triggers using the minimum-bias trigger scintillators (MBTS). These are mounted at each end of the detector in front of the liquid-argon endcap-calorimeter cryostats at $z = \pm 3.56$ m, and are segmented into two rings in pseudorapidity ($2.07< |\eta | < 2.76$ and $2.76< |\eta | < 3.86$) with 8 azimuthal sectors in the inner ring and 4 in the outer. The MB events were selected on the basis of the MBTS alone, while the HMT events satisfied additional HLT criteria. Further details are given in Sect. 4.1.

An extensive software suite [51] is used in the reconstruction and analysis of real and simulated data, in detector operations and in the trigger and data acquisition systems of the experiment.

4 Monte Carlo and data samples

4.1 Data samples and event selection

This study uses the pp-collision datasets at $\sqrt{s} = 13$ TeV that were used in previous ATLAS studies of MB events [43, 44, 52] and HMT events [53]. The MB and HMT datasets were taken in a special configuration of the LHC in June 2015, with low beam currents and reduced beam focusing, producing a low mean number of interactions per bunch-crossing, $\langle \mu \rangle$: in the range 0.003–0.007 for MB events and 0.01–0.04 for HMT events. This configuration and the event selection used are documented in detail in the ATLAS $\sqrt{s} = 13$ TeV MB analysis [43, 44]. For the MB data sample, events were selected from colliding proton bunches using the MBTS trigger. This trigger selection required one counter above threshold from either side of the detector, and is referred to as a single-arm trigger. The HMT trigger is a combination of an L1 requirement on the number of hits in the MBTS and an HLT requirement on the multiplicity of HLT-reconstructed charged-particle tracks. This trigger required more than 900 SCT space-points and more than 60 reconstructed good-quality charged tracks with $p_{\mathrm {T}}> 400$ MeV associated with the reconstructed vertex with the highest multiplicity in the event. These selections correspond to integrated luminosities of 151 $\upmu$b$^{-1}$ and 8.4 nb$^{-1}$ for the MB and HMT triggers, respectively.

In the offline selection, track candidates are reconstructed in the Pixel and SCT detectors and extended to include measurements in the TRT [54]. The selected tracks satisfy the following criteria: $p_{\mathrm {T}} > 100$ MeV and $|\eta |< 2.5$; at least one Pixel hit and an IBL hit if expected²; at least two, four or six SCT hits for $p_{\mathrm {T}} < 300$ MeV, $p_{\mathrm {T}} < 400$ MeV or $p_{\mathrm {T}} > 400$ MeV, respectively, in order to account for the dependence of track length on $p_{\mathrm {T}}$. All events are required to have at least one vertex [55], formed from a minimum of two tracks. The vertex position is required to be consistent with the beam-spot position within the ATLAS detector [54]. If more than one vertex is reconstructed, the primary vertex (PV) is defined as the vertex with the largest number of associated reconstructed tracks, weighted by the square of their transverse momenta [54]. Selected tracks are then also required to satisfy $|d_0^{\mathrm {BL}}| < 1.5$ mm, where the transverse impact parameter $d_0^{\mathrm {BL}}$ is calculated with respect to the measured beam line (BL) [56]; and $|z_0^{\mathrm {BL}}\times \sin {\theta }| < 1.5$ mm, where $z_0^{\mathrm {BL}}$ is the difference between the longitudinal coordinate of the track along the beam line at the point where $d_0^{\mathrm {BL}}$ is measured and the longitudinal coordinate of the PV, and $\theta$ is the polar angle of the track. High-momentum tracks with mismeasured $p_{\mathrm {T}}$ are removed by requiring the track-fit $\chi ^2$ probability to be larger than 0.01 for tracks with $p_{\mathrm {T}} > 10$ GeV. A special configuration of the track reconstruction algorithms is used in this analysis to reconstruct low-momentum tracks [54]. The track reconstruction efficiency at $p_{\mathrm {T}}\approx 100$ MeV is about 28% and increases rapidly to almost 75% at $p_{\mathrm {T}}\approx 300$ MeV [44]. For the MB trigger, the low-$p_{\mathrm {T}}$ selected dataset consists of $9.3\times 10^{6}$ events with a total of $2.4 \times 10^{8}$ tracks with $p_{\mathrm {T}} > 100$ MeV. The high-$p_{\mathrm {T}}$ selection requires in addition at least two tracks with $p_{\mathrm {T}} > 500$ MeV. This yields $8.9 \times 10^{6}$ events with $1.1 \times 10^{8}$ tracks with $p_{\mathrm {T}} > 500$ MeV. For the HMT trigger, which requires at least 60 tracks with $p_{\mathrm {T}} > 400$ MeV at the trigger level, the low-$p_{\mathrm {T}}$ selection requires at least 60 tracks with $p_{\mathrm {T}} > 100$ MeV and results in $9.1 \times 10^{6}$ events with $9.8 \times 10^{8}$ tracks with $p_{\mathrm {T}} > 100$ MeV. For $p_{\mathrm {T}} > 500$ MeV the requirement is at least 40 tracks with $p_{\mathrm {T}} > 500$ MeV; the sample consists of $9.1 \times 10^{6}$ events with $5.3 \times 10^{8}$ tracks with $p_{\mathrm {T}} > 500$ MeV.

To reduce contamination from multiple proton–proton interactions (pile-up) in the colliding bunches, events with a second vertex containing four or more tracks are removed. Such events represent less than 0.3% of the sample. Secondary vertices can be reconstructed with high efficiency provided the distance, $\Delta z$, between the z-coordinates of the primary and pile-up vertices satisfies $|\Delta z|\ge 4$ mm. To estimate any possible residual influence of multiple pp interactions in MB- and HMT-triggered data, a dedicated study of the $\Delta z$ distribution was performed, using a sample with no pile-up rejection. This distribution was extrapolated to estimate the level of pile-up that will survive the maximum track-multiplicity limit on a second vertex. For the MB events, the fraction of events with pile-up vertices in the region $|\Delta z|\le 4$ mm around the PV is about 0.006%. For the HMT events, it is about 0.05%.³ The average track multiplicities per pile-up vertex for the MB and HMT samples are 9.4 and 23, respectively. For the primary vertices these multiplicities are 26 and 108. The fractions of surviving pile-up tracks in the MB and HMT samples are approximately 0.002% and 0.01% per event, respectively, and these levels have a negligible influence on the BEC studies.

The contributions from beam–gas collisions and from non-collision background (cosmic rays and detector noise) were investigated in Ref. [57] and found to be negligible.

4.2 Monte Carlo samples

The Pythia 8 MC generator [58] was used to calculate the $C_2^{\mathrm {MC}}(Q)$ correlation functions (Eq. (2)). The generator was used with parameter values set to the A2 tune [59] and with the MSTW2008lo PDF set [60]. Pythia 8 models the effects of colour coherence, which is important in dense parton environments and effectively reduces the number of particles produced in multiple parton–parton interactions. In Pythia 8, the simulation is split into non-diffractive and diffractive processes. The non-diffractive process is dominated by t-channel gluon exchange, comprising approximately 80% of the selected events. The diffractive processes, which are further split into single- and double-diffractive processes, are described by a Pomeron-based approach [61]. The contributions from non-diffractive, single-diffractive and double-diffractive processes were included in proportion to the cross sections predicted by Pythia 8 with the A2 tune. Large MC samples of MB and HMT events were generated and passed through the ATLAS simulation program [62], which is based on Geant4 [63], and the reconstruction chain, which is exactly that used for collision dataset. In addition, all selection criteria applied to the data were also applied as appropriate to the MC samples.

In order to estimate the systematic uncertainty due to the choice of MC model, large MC samples, comparable to the size of the collision dataset, were also generated with three other programs. These were the Pythia 8 Monash tune [64], the EPOS MC generator [65] and Herwig++ [66] using the UE-EE-5 tune [67]. The Monash underlying-event tune is based on the NNPDF2.3lo PDF [68] and incorporates updated fragmentation parameters. EPOS implements a parton-based Gribov–Regge [69] theory, which is an effective field theory describing both hard and soft scattering. The EPOS generator was used with the LHC tune [70]. The Herwig++ UE-EE-5 tune is based on the CTEQ6L1 PDF. All sets of generated events were passed through the ATLAS simulation program and reconstruction chain.

The purity of the analysis sample of particle pairs is defined as the fraction of identical particle pairs ($\pi ^\pm \pi ^\pm$, $K^\pm K^\pm$, pp and ${\bar{p}}{\bar{p}}$) in the sample relative to all like-charge particle (LCP) pairs. The purity of the analysis sample in terms of identical boson pairs is estimated from Pythia 8 with the A2 tune to be about 74% (where about 73% are $\pi ^\pm \pi ^\pm$ and about 1% are $K^\pm K^\pm$), using the selection criteria described above for MB $p_{\mathrm {T}}>100$ MeV. In studies for the 7 TeV analysis [28] it was found that the impurity reduces the value of $\lambda$ by a factor that is approximately equal to the impurity of the sample, where a 100% purity has no effect, but the parameter R is unaffected.

5 Data correction procedure

To correct for the inefficiencies in the trigger and in the reconstruction of tracks and vertices, event-by-event and track-by-track weighting procedures are applied as appropriate and as used in the previous ATLAS measurements [43, 44].

The efficiency of the MB trigger was studied with an independent control trigger [43, 44]. The control trigger selects events randomly at L1, which are then filtered in the HLT by requiring at least one reconstructed track with $p_{\mathrm {T}} > 200$ MeV. The MB trigger efficiency increases from 97% for events with low track multiplicity, $n_{\mathrm {sel}} =2$, to 100% for events with higher multiplicity, $n_{\mathrm {sel}} \ge 7$, where $n_{\mathrm {sel}}$ is the number of tracks reconstructed offline and satisfying the selection criteria given in Sect. 4.1. The efficiency of the HMT trigger is studied using MB-triggered events as the control sample. The efficiency is found to be 15% for events with $n_{\mathrm {sel}} \simeq 85$ and reaches a plateau at 100% for $n_{\mathrm {sel}} \geqslant 110$. The measured MB and HMT trigger inefficiencies as a function of $n_{\mathrm {sel}}$ are used to correct each event. These corrections are found to have a negligible impact on the extraction of the BEC parameters discussed in Sect. 8. The effect of the vertex-reconstruction efficiency on the BEC parameters is also negligible.

In addition, each track is assigned a weight that corrects for the track reconstruction efficiency, for the fraction of secondary particles, for the effect of detector resolution smearing primary particles⁴ into and out of the fiducial region ($p_{\mathrm {T}} > 100$ MeV, $|\eta | < 2.5$) and for the fraction of fake tracks formed by a random combination of hits [43, 44]. The effect of the loss of reconstructed pairs at small opening angles is negligible in comparison with the track reconstruction corrections.

The Q resolution is found to be similar for all MC generators. For the BEC region $Q < 0.2$ GeV, where the Q distribution rises steeply, the Q resolution is better than 5 MeV and much smaller than the bin size. For $Q > 0.2$ GeV, where the Q distribution is essentially flat, the resolution increases linearly with Q, rising to $\simeq 40$ MeV for $Q \simeq 2$ GeV. Overall, no unfolding of Q is required.

The track reconstruction inefficiency is such that $n_{\mathrm {sel}}$ differs significantly from the true charged-particle multiplicity, $n_{\mathrm {ch}}$. In order to present and study $R_2 (Q)$ (Eq. (2)) as a function of the true charged-particle multiplicity, $n_{\mathrm {ch}}$, the correlation functions $R_2 (Q, n_{\mathrm {sel}})$ must be unfolded. In the earlier ATLAS MB study at 13 TeV [43, 44] an unfolding matrix that reflects the probability of reconstructing $n_{\mathrm {sel}}$ charged tracks in an event with a generated charged-particle multiplicity $n_{\mathrm {ch}}$ was constructed, using MC simulation with the Pythia 8 ATLAS A2 tune. For the present analysis this unfolding matrix was applied to both the MB and HMT data. It is found that, on average, an event with $n_{\mathrm {sel}} = 100$ reconstructed tracks corresponds to $n_{\mathrm {ch}} = 127.6 \pm 0.1$ charged particles at particle level.

Table 1 Systematic uncertainties (in percent) in the correlation strength, $\lambda$, and source radius, R, for the exponential fit of the two-particle double-ratio correlation functions, $R_2 (Q)$, for $p_{\mathrm {T}} > 100$ MeV at $\sqrt{s}= 13$ TeV for the MB and HMT events. The choice of MC generator gives rise to asymmetric uncertainties, denoted by $\uparrow$ and $\downarrow$. This asymmetry propagates through to the cumulative uncertainty. The columns under ‘Uncertainty range’ show the range of systematic uncertainty from the fits in the various $n_{\mathrm {ch}}$ intervals

As a check of the entire analysis chain, the distribution of $C_2(Q)$ (Eq. (1)) using the generated particles, $C_2^\mathrm {MC, gen}(Q)$, was compared with the $C_2^\mathrm {MC, rec} (Q)$ distribution using the simulated detector response to reconstruct the tracks and vertices, which were then corrected for inefficiencies as described above, and unfolded to the particle level. This study was carried out for several $n_{\mathrm {ch}}$ and $k_{\mathrm {T}}$ intervals, where $k_{\mathrm {T}}$ is the average transverse momentum of the pair:

$$\begin{aligned} k_{\mathrm {T}} = |{{\mathbf {p}}}_{{\mathrm {T}}, 1} + {{\mathbf {p}}}_{{\mathrm {T}}, 2}|/2. \end{aligned}$$

In the small-Q region the difference between the unfolded and particle-level distributions varies, depending on $n_{\mathrm {ch}}$ and $k_{\mathrm {T}}$, but is a few percent on average. The effect is significant for the first two Q-bins used, $0.02 \le Q < 0.04$ GeV and $0.04 \le Q < 0.06$ GeV, and for these bins it is accounted for by adding it in quadrature to the statistical uncertainty in the $R_2 (Q)$ distribution. It is therefore not included in the systematic uncertainties discussed in Sect. 7 and listed in Table . A large part of the difference in the first Q-bin, $0.02 \le Q < 0.04$ GeV, is due to photon conversions in the detector material, which are included in the simulated detector response but are not part of the set of generated particles. Since $C_2$ is a ratio of like-sign pairs to unlike-sign pairs, the denominator in $C_2^\mathrm {MC,rec} (Q)$ contains the contribution of pairs from photon conversions, which show up at small Q, whereas $C_2^\mathrm {MC,gen} (Q)$ does not. For MB events the difference for the first bin is 4%, of which 3.5% is the contribution of photon conversions. For HMT events, the corresponding numbers are 3.25% and 2%. Conversion photons are less significant for the HMT events, because the number of track combinations increases quadratically with $n_{\mathrm {ch}}$ while the number of conversion photons increases only linearly. The effect of photon conversions in the region $Q > 0.04$ GeV is negligible.

The long-range Coulomb force causes a momentum shift between particles in the LCP and unlike-charge particle (UCP) pairs. The density distributions are corrected for this effect by applying the Gamow penetration factor per track pair with a weight 1/G(Q) such that $\rho _{\mathrm {corr}} (Q) = {\rho (Q) / G(Q)}$ [71,72,73] (for a review see Ref. [74]). The Gamow factor is given by

$$\begin{aligned} G(Q) = 2 \pi \zeta / [\exp {(2 \pi \zeta )} - 1], \end{aligned}$$

with the dimensionless parameter $\zeta$ defined as $\zeta = \pm \alpha m/ Q$, where $\alpha$ is the electromagnetic fine-structure constant and m is the pion mass. The corrected two-particle density function, $\rho _{\mathrm {corr}} (Q)$, is normalized to unity. The sign of $\zeta$ is positive for LCP pairs and negative for UCP pairs. The Gamow factor particularly affects pairs with $Q < 0.1$ GeV, and the correction is 24% for $0.02 \le Q < 0.04$ GeV, 14% for $0.04 \le Q < 0.06$ GeV and 10% for $0.04 \le Q < 0.06$ GeV. The Coulomb interaction is not included in the generated MC event samples, and so the correction is applied only to data events.

6 Reference sample

A good choice of reference sample is important in obtaining an unbiased estimate of the BEC signal. Ideally, $\rho _0 (Q)$ should include all momentum correlations present in the signal dataset except for those arising from BEC. Several different methods of constructing an appropriate reference sample have been investigated by various collaborations and authors.

The main methods are:

• take UCP pairs from the same event;

• take LCP pairs from the same event, but invert the momentum of one of the selected particles: ($p_{\mathrm {x}}, p_{\mathrm {y}}, p_{\mathrm {z}} \rightarrow -p_{\mathrm {x}}, -p_{\mathrm {y}}, -p_{\mathrm {z}}$). This is the opposite hemisphere (OHP) technique [7];

• take LCP pairs from the same event, but invert the transverse momentum of one of the selected particles: ($p_{\mathrm {x}}, p_{\mathrm {y}}, p_{\mathrm {z}} \rightarrow -p_{\mathrm {x}}, -p_{\mathrm {y}}, p_{\mathrm {z}}$). This is the z-rotation method [7];

• take LCP pairs from different events, randomly mixed; this is the ‘mixed event’ (MIX) technique [75].

In addition, most of the recently used methods compare the data with a reference sample having global event parameter values that are the same as, or similar to, those in data – such as the event multiplicity, the invariant mass of the pair, or the rapidity of the pair. For the previous ATLAS analysis [28] the UCP, OHP and MIX procedures were investigated in detail using dedicated MC studies, and it was observed that MIX and OHP behaved similarly. For this analysis, the UCP and OHP were studied.

As the MC models do not implement BEC, the single-ratio correlation functions $C_2^{\mathrm {MC}} (Q)$ are expected to be close to 1, and to be a rather flat function of Q, particularly in the low-Q, BEC-sensitive region. This is indeed the behaviour observed in the earlier analysis [28] over much of the parameter space in $n_{\mathrm {ch}}$ and $k_{\mathrm {T}}$ for the MIX or OHP technique, and for the OHP technique in this analysis. However, in high-multiplicity and high-$k_{\mathrm {T}}$ intervals, which are relevant for this analysis, $C_2^{\mathrm {MC}} (Q)$ constructed with the MIX or OHP technique exhibits an increase in the low-Q, BEC-sensitive region.

Fig. 1

Comparison of single-ratio two-particle correlation functions, $C_2^{\mathrm {data}}(Q)$ and $C_2^{\mathrm {MC}}(Q)$, with the two-particle double-ratio correlation function, $R_2(Q)$, for the high-multiplicity track (HMT) events using a the opposite hemisphere (OHP) like-charge particles pairs reference sample for $k_{\mathrm {T}}$-interval $1000 < k_{\mathrm {T}} \le 1500$ MeV and b the unlike-charge particle (UCP) pairs reference sample for $k_{\mathrm {T}}$-interval $1000 < k_{\mathrm {T}} \le 1500$ MeV

As an example, Fig. a shows the correlation functions using the OHP technique for the reference sample. The correlation functions shown are the single ratios $C_2^{\mathrm {data}}(Q)$ and $C_2^{\mathrm {MC}}(Q)$, and the double ratio $R_2(Q)$, all for HMT events, and for the average transverse momentum of the pair $1000 < k_{\mathrm {T}} \le 1500$ MeV. The $C_2^{\mathrm {MC}} (Q)$ exhibits a rise similar to that seen in $C_2^{\mathrm {data}} (Q)$ in the BEC-sensitive region, although no such effect should be present in $C_2^{\mathrm {MC}}(Q)$. Such a rise would have a marked effect on the BEC parameters extracted from $R_2(Q)$. Figure 1a also shows that $R_2 (Q)$ is less than 1 in the region $0.7<Q<1.2$ GeV.

The use of UCP pairs for the reference sample was also investigated in detail. As in the other techniques, $C_2^{\mathrm {MC}} (Q)$ behaves satisfactorily over much of the parameter space in $n_{\mathrm {ch}}$ and $k_{\mathrm {T}}$, although resonances distort the region $Q \approx 0.5$ GeV, particularly at low multiplicity or at high $k_{\mathrm {T}}$. An example is shown in Fig. 1b, using the UCP reference sample, and for the same $n_{\mathrm {ch}}$ and $k_{\mathrm {T}}$ intervals as in Fig. 1a. Although there is some distortion in the resonance region, where $C_2^{\mathrm {MC}} (Q)$ and $C_2^{\mathrm {data}} (Q)$ do not match perfectly, the resultant $R_2 (Q)$ matches well the BEC region of $C_2^{\mathrm {data}} (Q)$. Accordingly, the UCP method is used in this analysis, as it was for the previous ATLAS analysis [28], and the other methods are not suitable.

The UCP reference sample used in this analysis is taken from the same events used to form pairs of like-charge particles, i.e. $\rho _0 (Q) \equiv \rho (p_1^\pm , p_2^\mp )$. By construction, this UCP sample has the same topology and global parameters as the LCP sample $\rho (p_1^\pm , p_2^\pm )$, but is naturally free of any BEC effect. However, the UCP sample contains oppositely charged hadron pairs from the decay of resonances such as $\eta$, $\eta ^{\prime }$, $\omega$, $\rho$, $K^{*}$, and $\phi$, which are not present in the LCP combinations. Details concerning resonances are given in Appendix A. These resonances contribute to the low-Q region, and can give a spurious BEC signature with a large effective R [76,77,78,79,80,81,82]. The effect of the resonant states in the Q variable was checked in MC studies, and the most affected regions are excluded from the analysis of the BEC effect, as described in Sect. 8.1.

7 Systematic uncertainties

In this section the systematic uncertainties in values of the BEC parameters R and $\lambda$ are summarized. These parameter values are obtained from a fit to the exponential model (4). This fit is applied to the ‘inclusive’ distributions, corresponding to $2 \le n_{\mathrm {ch}} \le 250$ for MB and $100 < n_{\mathrm {ch}} \le 300$ for HMT, and all $k_{\mathrm {T}}$. The fit is also applied to selected ranges of $n_{\mathrm {ch}}$ or $k_{\mathrm {T}}$, and to the double-differential ($n_{\mathrm {ch}}$, $k_{\mathrm {T}}$)-distributions. The discussion in this section is mainly in terms of the ‘inclusive’ fits, but the systematic uncertainties have been evaluated for all selections applied to the data.

The systematic uncertainties resulting from the track reconstruction efficiency, which are parameterized as a function of $p_{\mathrm {T}}$ and $\eta$, were determined in earlier analyses [43, 44] and these are implemented as uncertainties in the track weights for particle pairs in the Q distributions that enter the correlation functions. The effects of track splitting and merging have been studied in detail. They are largest for Q values below 0.04 GeV, but even for the first used bin ($0.02 \le Q < 0.04$ GeV) the effect is only 0.4% and is negligible in comparison with other uncertainties.

The effects of uncertainties in the unfolding matrix on the BEC parameters $\lambda$ and R are found to be negligible for $n_{\mathrm {ch}} < 200$. For the highest-multiplicity MB ($201 \le n_{\mathrm {ch}} < 250$) and HMT ($231 \le n_{\mathrm {ch}} < 300$) events this systematic uncertainty is very small and not more than 0.01% for $\lambda$ and 0.03% for R.

Fig. 2

The Bose–Einstein correlation (BEC) parameters $\lambda$ and R as a function of $n_{\mathrm {ch}}$ and $k_{\mathrm {T}}$ using different MC generators in the calculation of $R_2 (Q)$. a R versus $n_{\mathrm {ch}}$ for MB events, b R versus $n_{\mathrm {ch}}$ for HMT events, c R versus $k_{\mathrm {T}}$ for MB events and d $\lambda$ versus $k_{\mathrm {T}}$ for MB events. The uncertainties shown are statistical. The lower panel of each plot shows the ratio of the BEC parameters obtained using EPOS LHC (red circles), Pythia 8 Monash (blue squares) and Herwig++ UE-EE-5 (green triangles) compared with the parameters obtained using Pythia 8 A2. The grey band in the lower panels is the MC systematic uncertainty, obtained as explained in the text

The leading source of uncertainty in $\lambda$ and R is the choice of MC generator used in the calculation of $R_2(Q)$. Figure  shows a selection of plots of the BEC parameters as a function of $n_{\mathrm {ch}}$ or $k_{\mathrm {T}}$, for different choices of MC generator. The values of the parameters $\lambda$ and R obtained using EPOS LHC, Pythia 8 Monash or Herwig++ UE-EE-5 are compared with the parameter values obtained using Pythia 8 A2 in terms of the ratios shown in the lower panel of each plot in Fig. 2.

As can be seen in this figure, there are some regions of $n_{\mathrm {ch}}$ and $k_{\mathrm {T}}$ where there are pronounced and significant differences between the results obtained using the different generators. In order to assign the systematic uncertainty due to the MC modelling, a conservative approach is adopted: for each generator the weighted deviation is evaluated with respect to Pythia 8 A2, where the weight is inversely proportional to the statistical uncertainty for that generator. The systematic uncertainty is taken as the largest (in magnitude) of these weighted deviations, treating positive and negative deviations separately, which leads to asymmetric uncertainties. This procedure is followed for MB and HMT events separately.

An important source of systematic uncertainty for the determination of the parameter $\lambda$ arises from the Coulomb correction. This uncertainty is estimated by varying the Gamow factor G(Q) by $\pm 0.15$, which is the magnitude of the effect on UCP or LCP pairs at $Q = 0.02$ GeV. This is the standard variation for a conservative estimate of the systematic uncertainty in the Coulomb correction [28, 35], and accounts also for effects that include the extended size of the emission source, as discussed in Ref. [83]. The resulting systematic uncertainties for the inclusive fit of the parameter $\lambda$ are the same for both triggers and are equal to 1.8%. For the parameter R the resulting systematic uncertainties are small compared to the cumulative systematic uncertainties, and equal to 0.1% and 0.3% for MB and HMT events, respectively.

The effect of the upper limit of the fit range in Q is estimated by changing it from the nominal 2 GeV by $\pm 0.1$ GeV, which corresponds to a total variation of about five times the nominal Q-resolution for $Q \approx 2$ GeV. This gives an estimate of the residual uncertainty due to long-range correlations accounted for by $\varepsilon$, the parameter in the linear term of Eq. (3). Other effects contributing to the systematic uncertainties are the lowest value of Q for the fit, the bin size, and the exclusion of Q regions where resonances are not modelled perfectly, as discussed in Sect. 8.1. These uncertainties are estimated by varying the lowest Q value in the fit by $\pm 0.01$ GeV, by changing the bin size by $\pm 0.01$ GeV, and by broadening the excluded intervals by 0.02 GeV on both sides.

The systematic uncertainties for the inclusive study are summarized in Table 1. The systematic uncertainties are combined by adding them in quadrature, and the resulting values are given in the bottom row of the table. The cumulative systematic uncertainties are $^{+ 3.9}_{- 5.9}$% and $^{+ 5.6}_{- 2.6}$% for the inclusive determination of $\lambda$, and $^{+ 5.0}_{- 5.8}$% and $^{+ 5.7}_{- 2.5}$% for R, for the MB and HMT events, respectively.

The same sources of uncertainty are considered for the single- and double-differential measurements in $n_{\mathrm {ch}}$ and $k_{\mathrm {T}}$. The results for the $n_{\mathrm {ch}}$ distribution are also shown in Table 1. The pattern of uncertainties is similar to the inclusive case, but shows a wider spread. Away from the BEC region, the MC description of $C_2^{data}$ improves as the multiplicity increases, and this is reflected in Table 1 by smaller systematic uncertainties for the HMT results. This is also true for the $k_{\mathrm {T}}$ distribution and the double-differential distribution.

8 Results

The BEC parameters, $\lambda$ and R, are extracted from a fit to the $R_2 (Q)$ distribution in intervals of $n_{\mathrm {ch}}$ and $k_{\mathrm {T}}$. In addition, there are two possible selections on the $p_{\mathrm {T}}$ threshold of the final-state particles. In order to give a reasonably complete picture of all of this information, the parameters describing the dependencies of $\lambda$ and R on variables of interest are themselves fitted to simple functions (usually exponentials), and the parameters of these fits are presented.

In Sect. 8.1 the procedure used to fit the $R_2 (Q)$ distribution is described. The dependence on multiplicity is presented in Sect. 8.2. The comparison with previous ATLAS results at 7 TeV is discussed in Sect. 8.3. The behaviour with $k_{\mathrm {T}}$ is presented in Sect. 8.4. The ‘double-differential’ dependence of the BEC parameters on multiplicity and $k_{\mathrm {T}}$ at 13 TeV is explored in Sect. 8.5, by looking at the dependence on one variable for different intervals of the other. Finally, a comparison with CMS results at 13 TeV is shown in Sect. 8.6.

8.1 Procedure for BEC parameter extraction from $R_2 (Q)$

Fig. 3

Top panel: The two-particle double-ratio correlation function, $R_2 (Q)$, for pp collisions for track $p_{\mathrm {T}} >100$ MeV at $\sqrt{s}=13$ TeV in the multiplicity intervals a $71 \le n_{\mathrm {ch}} < 80$ for the minimum-bias (MB) events, and b $231 \le n_{\mathrm {ch}} < 300$ for the high-multiplicity track (HMT) events. The blue dashed and red solid lines show the results of the exponential and Gaussian fits, respectively. The region excluded from the fits is shown. The statistical uncertainty and the systematic uncertainty for imperfections in the data reconstruction procedure are added in quadrature. Bottom panel: The difference between the experimental $R_2 (Q)$ function and the result of the exponential fit normalized to the experimental uncertainty, $\Delta R_2 (Q)/\sigma (Q)$, is presented

Figure  shows examples of the $R_2(Q)$ correlation functions measured at $\sqrt{s} = 13$ TeV for two different multiplicity intervals, and the fits to the Gaussian and exponential forms. In the lower panels of Fig. 3 the differences between the measured $R_2 (Q)$ and the fit to the exponential form, normalized to the experimental uncertainty $\sigma (Q)$, $\Delta R_2 (Q)/\sigma (Q)= [R_2^{\mathrm {data}} (Q) - R_2^{\mathrm {fit}} (Q)]/\sigma (Q)$, are shown for both multiplicity intervals. It is evident from Fig. 3 that the Gaussian function does not give a good description of the low-Q, BEC-sensitive region, $Q \le 0.1$ GeV, while the exponential function matches the data well in this region. Therefore, the quantity $\Delta R_2 (Q)/\sigma (Q)$ is not shown for the Gaussian case, and the Gaussian fit is not considered further.

Figure 3 shows structure in $R_2 (Q)$, compared with the smooth fitting functions, in the regions $Q\approx 0.25$ GeV and $0.4 \le Q \le 0.9$ GeV. If the MC modelling of resonance production, particularly the $\eta$, $\rho$ and $\omega$, does not agree very well with data, then this Q region will be affected, as appears to be the case. Accordingly, the regions $0.2 \le Q \le 0.3$ GeV and $0.4 \le Q \le 0.9$ GeV are excluded from the fits to the $R_2(Q)$ correlation functions for the MB and HMT events. For the MB events, similar arguments lead to the additional exclusion of the region $1.0 \le Q \le 1.16$ GeV, as it appears to be influenced by the reflection of the $f_0(980)$ and $f_2(1270)$ mesons in the case of $100 \le k_{\mathrm {T}} \le 200$ MeV and in the multiplicity region $n_{\mathrm {ch}} \le 40$. These excluded regions lie outside the BEC-sensitive region and the main effect of the exclusions is to markedly reduce the $\chi ^2$ without significantly changing the fitted BEC parameters.

The results for the BEC parameters obtained using the exponential fit with the UCP reference sample for the MB and HMT samples, summed over all multiplicities for $p_{\mathrm {T}} > 100$ MeV, are

$$\begin{aligned}&\lambda = 1.03^{+0.04}_{-0.06},\quad R = 3.32^{+0.17}_{-0.19}~{\mathrm {[fm]}}\\&\quad {\mathrm {for}} \ 2 \le n_{\mathrm {ch}}(p_{\mathrm {T}}>100~\text {MeV}) \le 250\ {\mathrm {(MB)}} \end{aligned}$$

and

$$\begin{aligned}&\lambda = 1.00^{+0.09}_{-0.07},\quad R = 3.76^{+0.22}_{-0.14}~{\mathrm {[fm]}}\\&\quad {\mathrm {for}} \ 100 <n_{\mathrm {ch}}(p_{\mathrm {T}}>100~\text {MeV}) \le 300 \ {\mathrm {(HMT)}} . \end{aligned}$$

The results for the BEC parameters for tracks with $p_{\mathrm {T}} > 500$ MeV are

$$\begin{aligned}&\lambda = 0.61^{+0.05}_{-0.06},\quad R = 2.38^{+0.20}_{-0.25}~{\mathrm {[fm]}}\\&\quad {\mathrm {for}} \ 2\le n_{\mathrm {ch}}(p_{\mathrm {T}}>500~\text {MeV}) \le 115 \ {\mathrm {(MB)}} \end{aligned}$$

and

$$\begin{aligned}&\lambda = 0.66^{+0.08}_{-0.08},\quad R = 2.82^{+0.39}_{-0.40}~{\mathrm {[fm]}}\\&\quad {\mathrm {for}}\ 46 < n_{\mathrm {ch}}(p_{\mathrm {T}}>500~\text {MeV}) \le 136 \ {\mathrm {(HMT)}} . \end{aligned}$$

In both cases the uncertainties are the statistical and systematic uncertainties summed in quadrature. The overall quality of the fits is not good, as the high number of events in the inclusive distributions exposes the imperfections in the models used. As noted in Sect. 2, the fits would be better using a Lévy distribution with an additional free parameter. For all fits throughout Sect. 8, the statistical uncertainty is multiplied by the factor $\sqrt{\chi ^2/ndf}$ if this factor is significantly greater than 1 [84]. This applies in relatively few cases, see e.g. 4 of the 8 entries in Table .

8.2 Multiplicity dependence

The dependence of R and $\lambda$ on $n_{\mathrm {ch}}$ is studied in multiplicity intervals that are chosen to be well populated, and comparable to those used by other LHC experiments [30, 31, 35, 36, 38].

To compare the BEC parameters from different $p_{\mathrm {T}}$-thresholds, a scaled charged-particle multiplicity is introduced as follows. At 13 TeV, the average charged-particle multiplicity per unit of pseudorapidity in the region $|\eta |< 0.2$, $\langle \left. \mathrm {d}n_{\mathrm {ch}} / \mathrm {d}\eta \right| _{|\eta |<0.2} \rangle$, is 6.5 for particles with $p_{\mathrm {T}} > 100$ MeV [44] and 3.24 for particles with $p_{\mathrm {T}} > 500$ MeV [43]. A scaled charged-particle multiplicity for $|\eta |<2.5$, i. e. 5 units of pseudorapidity is then defined as:

$$\begin{aligned} m_{\mathrm {ch}} \equiv n_{\mathrm {ch}}/ ( 5 \cdot \langle \left. \mathrm {d}n_{\mathrm {ch}} / \mathrm {d}\eta \right| _{|\eta |<0.2} \rangle ) . \end{aligned}$$

Fig. 4

a The dependence of the correlation strength, $\lambda (m_{\mathrm {ch}})$, on rescaled multiplicity, $m_{\mathrm {ch}}$, obtained from the exponential fit of the $R_2 (Q)$ correlation functions for tracks with $p_{\mathrm {T}} > 100$ MeV and $p_{\mathrm {T}} > 500$ MeV at $\sqrt{s} = 13$ TeV for the minimum-bias (MB) and high multiplicity track (HMT) data. b The dependence of the source radius, $R (m_{\mathrm {ch}})$, on $m_{\mathrm {ch}}$. c The dependence of the $R (m_{\mathrm {ch}})$ on $\root 3 \of {m_{\mathrm {ch}}}$. The uncertainties represent the sum in quadrature of the statistical and asymmetric systematic contributions. The black and blue solid curves in a represent the exponential fit of $\lambda (m_{\mathrm {ch}})$ for $p_{\mathrm {T}} >100$ MeV and $p_{\mathrm {T}} >500$ MeV, respectively. The black and blue solid curves in b represent the fit of $R (m_{\mathrm {ch}})$ for $\root 3 \of {m_{\mathrm {ch}}} < 1.2$ for $p_{\mathrm {T}} >100$ MeV and $p_{\mathrm {T}} >500$ MeV, respectively. The black and blue dotted curves are extensions of the black and blue solid curves beyond $\root 3 \of {m_{\mathrm {ch}}} > 1.2$, respectively. The black and brown dashed curves represent the saturation value of $R (m_{\mathrm {ch}})$ for $\root 3 \of {m_{\mathrm {ch}}} > 1.45$ with $p_{\mathrm {T}} >100$ MeV and for $\root 3 \of {m_{\mathrm {ch}}} > 1.6$ with $p_{\mathrm {T}} >500$ MeV, respectively

Using the exponential fit, the extracted BEC parameters $\lambda (m_{\mathrm {ch}})$ and $R (m_{\mathrm {ch}})$ at 13 TeV are shown as a function of scaled multiplicity in Fig.  for $p_{\mathrm {T}} > 100$ and 500 MeV. The MB and HMT data agree well where they overlap.

For $p_{\mathrm {T}} > 100$ MeV the $\lambda$ parameter decreases with increasing $m_{\mathrm {ch}}$, and the dependence is well described by the exponential function:

$$\begin{aligned} \lambda (m_{\mathrm {ch}}) = \gamma \, {{\mathrm {e}}}^{- \delta m_{\mathrm {ch}}}. \end{aligned}$$

(5)

The R parameter increases with multiplicity up to about $m_{\mathrm {ch}} \simeq 3.08$. For $m_{\mathrm {ch}} \le 1.9$, the $m_{\mathrm {ch}}$ dependence of R is well described by:

$$\begin{aligned} R (m_{\mathrm {ch}}) = \alpha \root 3 \of {m_{\mathrm {ch}} }, \end{aligned}$$

(6)

which is also the function used in heavy-ion studies [8, 31]. A linear increase of R with $\root 3 \of {m_{\mathrm {ch}}}$ follows naturally if the hadronization volume is proportional to the number of produced particles.

For higher multiplicities, the measured R parameter is observed to be independent of multiplicity. This saturation of the BEC R parameter at high multiplicity is similar to that observed by ATLAS at $\sqrt{s} = 7$ TeV [28] and by CMS at $\sqrt{s} = 13$ TeV [38]. The dependence of R for the region $m_{\mathrm {ch}} > 3.08$ is then fitted simply by a constant:

$$\begin{aligned} R (m_{\mathrm {ch}}) = \beta . \end{aligned}$$

(7)

For the combined MB and HMT data at $\sqrt{s} = 13$ TeV and $p_{\mathrm {T}} > 100$ MeV the parameters of the $m_{\mathrm {ch}}$ dependence of R and $\lambda$ are given in the upper part of Table , with statistical and asymmetric systematic uncertainties summed in quadrature.

Table 2 The results of the fits to the dependencies of the correlation strength, $\lambda$, and source radius, R, on the average rescaled charged-particle multiplicity, $m_{\mathrm {ch}}$, for $|\eta | < 2.5$ and both $p_{\mathrm {T}} > 100$ MeV and $p_{\mathrm {T}} > 500$ MeV at $\sqrt{s} = 13$ TeV for the minimum-bias (MB) and the high-multiplicity track (HMT) events. The parameters $\gamma$ and $\delta$ resulting from a joint fit to the MB and HMT data are presented. The total uncertainties are shown

For $p_{\mathrm {T}} > 500$ MeV the variation of the BEC parameters is fitted to the same functional forms as used for $p_{\mathrm {T}} > 100$ MeV (Eqs. (5)–(7)), and the results are shown in the lower part of Table 2.

From Fig. 4a it can be seen that $\lambda (m_{\mathrm {ch}})$ shows only a weak dependence on multiplicity for $p_{\mathrm {T}}>500$ MeV. It is constant within measurement uncertainties, indicating a relatively high level of incoherence. Figure 4b, c show similar behaviour of $R (m_{\mathrm {ch}})$ for both $p_{\mathrm {T}}$ thresholds. There is a linear rise with $\root 3 \of {m_{\mathrm {ch}}}$ up to 1.2, after which there is some tapering off towards a plateau for $\root 3 \of {m_{\mathrm {ch}}} > 1.6$:

$$\begin{aligned} R = 2.78^{+0.23}_{-0.09} (\mathrm {total})~{\mathrm {[fm]}} \end{aligned}$$

for $p_{\mathrm {T}}>500$ MeV, and for $\root 3 \of {m_{\mathrm {ch}}} > 1.45$:

$$\begin{aligned} R = 3.35^{+0.20}_{-0.09} (\mathrm {total})~{\mathrm {[fm]}} \end{aligned}$$

for $p_{\mathrm {T}}>100$ MeV.

8.3 Comparison of $C_2 (Q)$ functions at 13 and 7 TeV

Fig. 5

Comparison of single-ratio two-particle correlation functions, using the unlike-charge particle (UCP) pair reference sample, for minimum-bias (MB) events, showing $C_2^{\mathrm {data}} (Q)$ (top panel) at 13 TeV (black circles) and 7 TeV (open blue circles), and the ratio of $C_{\mathrm {2}}^{\mathrm {7~TeV}} (Q)$ to $C_{\mathrm {2}}^{\mathrm {13~TeV}} (Q)$ (bottom panel). Comparison of $C_2^{\mathrm {data}} (Q)$ a for representative multiplicity region $3.09 < m_{\mathrm {ch}} \le 3.86$ and b for representative $k_{\mathrm {T}}$ region $400 < k_{\mathrm {T}} \le 500$ MeV. The statistical and systematic uncertainties, combined in quadrature, are presented. The systematic uncertainties include track efficiency, Coulomb correction, non-closure and multiplicity-unfolding uncertainties

The BEC parameters $\lambda$ and R were measured previously by ATLAS at 0.9 and 7 TeV [28]. The data sample at 7 TeV was large enough to explore high-multiplicity events, and a clear plateau in R was observed for $n_{\mathrm {ch}} \ge 50$. This plateau at high multiplicity is confirmed by the present analysis at 13 TeV, as shown in Fig. 4b, c. However, a direct comparison of the BEC parameters obtained at the two centre-of-mass energies is complicated by small but significant differences between the Monte Carlo generators used to construct $C_2^{\mathrm {MC}} (Q)$, and hence $R_2 (Q)$, in the two analyses (see Eqs. (1) and (2)). The BEC parameters obtained at 7 TeV are systematically lower than those at 13 TeV by about 1.5 standard deviations of the estimated 7 TeV uncertainties. For the previous 7 TeV analysis only limited MC modelling was available. For this paper, several MC models and tunings are used to estimate the modelling uncertainty.

This finding is supported by a comparison between the quantities $C_2^{\mathrm {data}} (Q)$ at the two centre-of-mass energies. Figure a, b show $C_2^{\mathrm {data}} (Q)$ for MB events at 7 and 13 TeV. Figure 5a shows a representative plot for a scaled-multiplicity interval ($3.09 < m_{\mathrm {ch}} \le 3.86$) and Fig. 5b shows a representative plot for a $k_{\mathrm {T}}$ interval ($400 < k_{\mathrm {T}} \le 500$ MeV). In Fig. 5 the uncertainties shown are the statistical and systematic uncertainties combined in quadrature. The systematic uncertainties include the effects of the track efficiency, Coulomb correction, non-closure and multiplicity unfolding. The plots shown in Fig. 5a, b are representative of all multiplicity and $k_{\mathrm {T}}$ intervals. The data from the two centre-of-mass energies are in agreement everywhere within the uncertainties, and the ratio of 7 TeV to 13 TeV data is 1 to better than 1% except in the very first one or two Q bins.

8.4 Dependence on the pair average transverse momentum

Fig. 6

The $k_{\mathrm {T}}$ dependence of a the correlation strength, $\lambda (k_{\mathrm {T}})$, and b the source radius, $R (k_{\mathrm {T}})$, obtained from the exponential fit to the $R_2 (Q)$ correlation functions for events with multiplicity $n_{\mathrm {ch}} \ge 2$ and transfer momentum of tracks with $p_{\mathrm {T}} >100$ MeV and $p_{\mathrm {T}} >500$ MeV at $\sqrt{s}=13$ TeV for the minimum-bias (MB) and high-multiplicity track (HMT) events. The uncertainties represent the sum in quadrature of the statistical and systematic contributions. The curves represent the exponential fits to $\lambda (k_{\mathrm {T}})$ and $R(k_{\mathrm {T}})$

Table 3 The results of the fits to the dependencies of the correlation strength, $\lambda$, and source radius, R, on the pair average transverse momentum, $k_{\mathrm {T}}$, for various functional forms and for minimum-bias (MB) and high-multiplicity track (HMT) events for $p_{\mathrm {T}} > 100$ MeV and $p_{\mathrm {T}} > 500$ MeV at $\sqrt{s} = 13$ TeV. The total uncertainties are shown

The BEC are studied in $k_{\mathrm {T}}$ intervals from 0.1 to 1.5 GeV that are chosen so that they are populated roughly equally. The fitted dependences of $\lambda (k_{\mathrm {T}})$ and $R (k_{\mathrm {T}})$ for the two $p_{\mathrm {T}}$ thresholds are shown in Fig.  for $p_{\mathrm {T}} > 100$ and 500 MeV. In the small-Q, BEC-sensitive region, the minimum $k_{\mathrm {T}}$ is highly correlated with the $p_{\mathrm {T}}$ threshold, and so $k_{\mathrm {T}}$ thresholds of 100 and 500 MeV are applied for the $p_{\mathrm {T}}$ thresholds of 100 and 500 MeV, respectively. The values of $\lambda (k_{\mathrm {T}})$ and $R (k_{\mathrm {T}})$ decrease with increasing $k_{\mathrm {T}}$. The decrease of $\lambda (k_{\mathrm {T}})$ with $k_{\mathrm {T}}$ is described by the function:

$$\begin{aligned} \lambda (k_{\mathrm {T}}) = \mu \, {{\mathrm {e}}}^{- \nu k_{\mathrm {T}}}. \end{aligned}$$

(8)

The $R (k_{\mathrm {T}})$ parameter shows similar behaviour:

$$\begin{aligned} R (k_{\mathrm {T}}) = \xi \, {{\mathrm {e}}}^{- \kappa k_{\mathrm {T}}}. \end{aligned}$$

(9)

The fitted parameters in Eqs. (8) and (9) are given in Table 3.

Fig. 7

The two-dimensional dependence on $m_{\mathrm {ch}}$ and $k_{\mathrm {T}}$ for $p_{\mathrm {T}} > 100$ MeV for a the correlation strength, $\lambda$, and b the source radius, R, obtained from the exponential fit to the $R_2 (Q)$ correlation functions using the MB sample for $m_{\mathrm {ch}} \le 3.08$ and the HMT sample for $m_{\mathrm {ch}} > 3.08$

Fig. 8

The parameter $\lambda$ for $p_{\mathrm {T}} > 100$ MeV: a as a function of $k_{\mathrm {T}}$ in selected low $m_{\mathrm {ch}}$ intervals, b as a function of $k_{\mathrm {T}}$ in selected high $m_{\mathrm {ch}}$ intervals, c as a function of $m_{\mathrm {ch}}$ in $k_{\mathrm {T}}$ intervals between 0.1 and 0.5 GeV, and d as a function of $m_{\mathrm {ch}}$ in $k_{\mathrm {T}}$ intervals between 0.5 and 1.5 GeV. The error bars and boxes represent the statistical and systematic contributions, respectively

Fig. 9

The parameter R for $p_{\mathrm {T}} > 100$ MeV: a as a function of $k_{\mathrm {T}}$ in selected low $m_{\mathrm {ch}}$ intervals, b as a function of $k_{\mathrm {T}}$ in selected high $m_{\mathrm {ch}}$ intervals, c as a function of $m_{\mathrm {ch}}$ in $k_{\mathrm {T}}$ intervals between 0.1 and 0.5 GeV, and d as a function of $m_{\mathrm {ch}}$ in $k_{\mathrm {T}}$ intervals between 0.5 and 1.5 GeV. The error bars and boxes represent the statistical and systematic contributions, respectively

Fig. 10

The fit parameters a $\mu$ and b $\nu$ (Eq. (8)), describing the dependence of the correlation strength, $\lambda$, on charged-particle scaled multiplicity (Eq. (5)), for track $p_{\mathrm {T}}>100$ MeV and track $p_{\mathrm {T}}>500$ MeV in the minimum-bias (MB) and high-multiplicity track (HMT) samples at $\sqrt{s} = 13$ TeV. The error bars and boxes represent the statistical and systematic contributions, respectively. The black solid (blue dashed) curve represents the exponential fit of the dependence of parameter $\mu$ ($\nu$) on $m_{\mathrm {ch}}$ for tracks with $p_{\mathrm {T}} >100$ MeV ($p_{\mathrm {T}} >500$ MeV)

Fig. 11

The parameters a $\xi$ and b $\kappa$ (Eq. (9)), describing the dependence of the source radius, R, on charged-particle scaled multiplicity, $m_{\mathrm {ch}}$, for track $p_{\mathrm {T}}>100$ MeV and track $p_{\mathrm {T}}>500$ MeV in the minimum-bias (MB) and high-multiplicity track (HMT) samples at $\sqrt{s} = 13$ TeV. The error bars and boxes represent the statistical and systematic contributions, respectively. a The black solid and blue dashed curves represent the saturated value of the parameter $\xi$ for $m_{\mathrm {ch}} > 3.0$ for tracks with $p_{\mathrm {T}} >100$ MeV and for $m_{\mathrm {ch}} > 2.8$ for tracks with $p_{\mathrm {T}} >500$ MeV, respectively. b The black solid and blue dashed curves represent the exponential fit to the parameter $\kappa$ for tracks with $p_{\mathrm {T}} >100$ MeV and for tracks with $p_{\mathrm {T}} >500$ MeV, respectively

8.5 Double-differential dependence on $m_{\mathrm {ch}}$ and $k_{\mathrm {T}}$

There is sufficient data at 13 TeV to study the double-differential dependence: $\lambda (m_{\mathrm {ch}}, k_{\mathrm {T}})$ and $R (m_{\mathrm {ch}}, k_{\mathrm {T}})$.

Figure  shows the two-dimensional (2D) dependence of $\lambda$ and R on $m_{\mathrm {ch}}$ and $k_{\mathrm {T}}$, for $p_{\mathrm {T}} > 100$ MeV. In order to convey a clear picture of the 2D dependence, the values are presented without uncertainties, but they are generally less than 10%.

The following features can be seen in Fig. 7:

• The parameter $\lambda$ decreases monotonically with $k_{\mathrm {T}}$ in all $m_{\mathrm {ch}}$ intervals, similar to the behaviour seen in Fig. 6a.

• The variation of $\lambda$ with $m_{\mathrm {ch}}$ is rather flat for $k_{\mathrm {T}} \lesssim 500$ MeV, which may be compared with the clear decrease of $\lambda$ as a function of $m_{\mathrm {ch}}$ seen in Fig. 4a for $p_{\mathrm {T}} > 100$ MeV. This is discussed below.

• The variation of $\lambda$ with $m_{\mathrm {ch}}$ for $k_{\mathrm {T}} > 500$ MeV indicates a slight rise with $m_{\mathrm {ch}}$ similar to what is seen in Fig. 4a for $p_{\mathrm {T}} > 500$ MeV.

• The parameter R also decreases monotonically with $k_{\mathrm {T}}$ in all $m_{\mathrm {ch}}$ intervals, with the decrease being more pronounced in lower $m_{\mathrm {ch}}$ intervals. A similar decrease is seen in Fig. 6b.

• R increases with $m_{\mathrm {ch}}$ in all $k_{\mathrm {T}}$ intervals, starting from a lower value at larger $k_{\mathrm {T}}$.

• This increase of R flattens off to a plateau level in all $k_{\mathrm {T}}$ intervals. This is similar to the plateau seen in Fig. 4b, c. Within the precision of the present data, the onset of the plateau occurs at $m_{\mathrm {ch}} \sim 3$ in all $k_{\mathrm {T}}$ intervals.

These features can be seen more clearly in selected 1D projections in Figs.  and for $\lambda$ and R, respectively. MB and HMT data agree where they overlap.

Figure 8c, d show the essentially flat behaviour of $\lambda$ as a function of $m_{\mathrm {ch}}$ for low $k_{\mathrm {T}}$, and the slight rise at higher $k_{\mathrm {T}}$, which are described above. As also noted above, Fig. 4a shows a slight but clear decrease of $\lambda$ with $m_{\mathrm {ch}}$ for $p_{\mathrm {T}} >100$ MeV when integrated over all $k_{\mathrm {T}}$. This arises because particle $p_{\mathrm {T}}$ and hence $k_{\mathrm {T}}$ of the pair increase with $m_{\mathrm {ch}}$, but $\lambda$ decreases as $k_{\mathrm {T}}$ increases. This leads to the overall decrease with $m_{\mathrm {ch}}$ seen in Fig. 4a for $p_{\mathrm {T}} >100$ MeV.

The 2D behaviour can be parameterized according to Eqs. (8) and (9):

$$\begin{aligned} \lambda ( m_{\mathrm {ch}} , k_{\mathrm {T}} ) = \mu (m_{\mathrm {ch}})\, {{\mathrm {e}}}^{- \nu ( m_{\mathrm {ch}} ) k_{\mathrm {T}}}, \end{aligned}$$

(10)

and

$$\begin{aligned} R ( m_{\mathrm {ch}} , k_{\mathrm {T}}) = \xi ( m_{\mathrm {ch}})\, {{\mathrm {e}}}^{- \kappa ( m_{\mathrm {ch}} ) k_{\mathrm {T}}}. \end{aligned}$$

(11)

The parameters $\mu , \nu , \xi$ and $\kappa$ are shown in Figs.  and 11 for both the $p_{\mathrm {T}} >100$ MeV and $p_{\mathrm {T}} >500$ MeV selections.

The parameters $\mu , \nu , \xi$ and $\kappa$ can themselves be fitted as functions of $m_{\mathrm {ch}}$. For the $\lambda$ parameters and $p_{\mathrm {T}} >100$ MeV:

$$\begin{aligned}&\mu (m_{\mathrm {ch}}) = (1.35\pm 0.05 (\mathrm {stat.})~^{+ 0.14}_{-0.01} (\mathrm {syst.})) \\&\quad \cdot \exp { \{ (-0.047\pm 0.009 (\mathrm {stat.})~^{+ 0.013}_{-0.013} (\mathrm {syst.}))\, m_{\mathrm {ch}} \} }, \\&\nu (m_{\mathrm {ch}}) = (1.84\pm 0.12 (\mathrm {stat.})~^{+ 0.63}_{- 0.34} (\mathrm {syst.}))\, {\mathrm {[GeV^{-1}]}} \\&\quad \cdot \exp { \{ (-0.146\pm 0.020 (\mathrm {stat.})~^{+ 0.008}_{- 0.008} (\mathrm {syst.}))\, m_{\mathrm {ch}} \} }. \end{aligned}$$

And for the R parameters and $p_{\mathrm {T}} >100$ MeV:

$$\begin{aligned} \xi (m_{\mathrm {ch}})= & {} 3.64\pm 0.04 (\mathrm {stat.})~^{+0.22}_{-0.08} (\mathrm {syst.}) \, {\mathrm {[fm]}} , \\ \kappa (m_{\mathrm {ch}})= & {} (1.20\pm 0.12 (\mathrm {stat.})~^{+ 0.09}_{- 0.45} (\mathrm {syst.}))\, {\mathrm {[GeV^{-1}]}} \\&\cdot \exp { \{ (-0.31\pm 0.03 (\mathrm {stat.})~^{+ 0.16}_{- 0.03} (\mathrm {syst.}))\, m_{\mathrm {ch}} \} }, \end{aligned}$$

where the fit for $\xi$ applies for $m_{\mathrm {ch}} > 3.0$.

Fig. 12

The two-dimensional dependence on $m_{\mathrm {ch}}$ and $k_{\mathrm {T}}$ for $p_{\mathrm {T}} > 500$ MeV for a the correlation strength, $\lambda$, and b the source radius, R, obtained from the exponential fit to the $R_2(Q)$ correlation functions using the MB sample for $m_{\mathrm {ch}} \le 3.08$ and the HMT sample for $m_{\mathrm {ch}} > 3.08$

Fig. 13

The parameter $\lambda$ for $p_{\mathrm {T}} > 500$ MeV: a as a function of $k_{\mathrm {T}}$ in selected low $m_{\mathrm {ch}}$ intervals, b as a function of $k_{\mathrm {T}}$ in selected high $m_{\mathrm {ch}}$ intervals, and c as a function of $m_{\mathrm {ch}}$ in $k_{\mathrm {T}}$ intervals between 0.5 and 1.5 GeV. The error bars and boxes represent the statistical and systematic contributions, respectively

Fig. 14

The parameter R for $p_{\mathrm {T}} > 500$ MeV: a as a function of $k_{\mathrm {T}}$ in selected low $m_{\mathrm {ch}}$ intervals, b as a function of $k_{\mathrm {T}}$ in selected high $m_{\mathrm {ch}}$ intervals, and c as a function of $m_{\mathrm {ch}}$ in $k_{\mathrm {T}}$ intervals between 0.5 and 1.5 GeV. The error bars and boxes represent the statistical and systematic contributions, respectively

The 2D dependence has also been studied for the $p_{\mathrm {T}} > 500$ MeV selection and is shown in Fig. . As explained above, the $p_{\mathrm {T}}$ selection constrains the BEC parameters to the region $k_{\mathrm {T}} > 500$ MeV.

The main features are similar to those observed in Fig. 7. In particular, the value of R tends to a plateau at large $m_{\mathrm {ch}}$ in all $k_{\mathrm {T}}$ intervals, but the plateau level is systematically lower than for $p_{\mathrm {T}} > 100$ MeV, in line with what is observed in Fig. 4b, c. Selected 1D projections are shown in Figs.  and for $\lambda$ and R, respectively. As with the lower $p_{\mathrm {T}}$ selection, MB and HMT data agree where they overlap.

The 2D behaviour is parameterized according to Eqs. (10) and (11). The fit parameters $\mu , \nu , \xi$ and $\kappa$ for $p_{\mathrm {T}} > 500$ MeV are shown in Figs. 10 and . As before, the parameters $\mu , \nu , \xi$ and $\kappa$ are themselves fitted as functions of $m_{\mathrm {ch}}$. For the $\lambda$ parameters and $p_{\mathrm {T}} > 500$ MeV:

$$\begin{aligned} \mu (m_{\mathrm {ch}})= & {} (1.61\pm 0.32 (\mathrm {stat.})~^{+ 0.36}_{- 0.48} (\mathrm {syst.})) \\&\cdot \exp { \{ (-0.057\pm 0.051 (\mathrm {stat.})~^{+ 0.005}_{- 0.022} (\mathrm {syst.}))\, m_{\mathrm {ch}} \} }, \\ \nu (m_{\mathrm {ch}})= & {} (1.64\pm 0.34 (\mathrm {stat.})~^{+ 0.53}_{- 0.72} (\mathrm {syst.}))\, {\mathrm {[GeV^{-1}]}} \\&\cdot \exp { \{ (-0.110\pm 0.061 (\mathrm {stat.})~^{+ 0.009}_{- 0.039} (\mathrm {syst.}))\, m_{\mathrm {ch}} \} }. \end{aligned}$$

And for the R parameters and $p_{\mathrm {T}} > 500$ MeV:

$$\begin{aligned} \xi (m_{\mathrm {ch}})= & {} 2.65\pm 0.10 (\mathrm {stat.})~^{+0.51}_{-0.78} (\mathrm {syst.})\, {\mathrm {[fm]}} . \\ \kappa (m_{\mathrm {ch}})= & {} (1.78\pm 2.22 (\mathrm {stat.})~^{+1.11}_{-1.82} (\mathrm {syst.}))\, {\mathrm {[GeV^{-1}]}} \\&\cdot \exp { \{ (-3.37\pm 3.10 (\mathrm {stat.})~^{+3.20}_{-6.61} (\mathrm {syst.}))\, m_{\mathrm {ch}} \} } , \end{aligned}$$

where the fit for $\xi$ applies for $m_{\mathrm {ch}} > 2.8$.

8.6 Comparison with CMS

Fig. 15

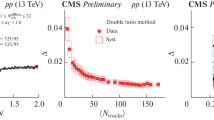
ATLAS and CMS results for the source radius R as a function of a $n_{\mathrm {ch}}$ and b $\root 3 \of {n_{\mathrm {ch}}}$ in pp interactions at 13 TeV. The CMS results (open circles) have been adjusted (by the CMS collaboration) to the ATLAS kinematic region: $p_{\mathrm {T}} > 100$ MeV and $|\eta |<2.5$. The ATLAS uncertainties are the sum in quadrature of the statistical and asymmetric systematic uncertainties. For CMS, only the systematic uncertainties are shown since the statistical uncertainties are smaller than the marker size. The dashed blue (ATLAS) and black (CMS) lines represent the fit to $\root 3 \of {n_{\mathrm {ch}}}$ at low multiplicity, continued as dotted lines beyond the fit range. The solid green (ATLAS) and broken black (CMS) lines indicate the plateau level at high multiplicity

As noted in the Introduction, BEC have been studied extensively at the LHC. In this section we compare our results on the BEC radius parameter with the only other published study at 13 TeV. The CMS Collaboration has studied BEC at 13 TeV in the kinematic region $p_{\mathrm {T}} > 200$ MeV, $|\eta |<2.4$ and $k_{\mathrm {T}} < 1$ GeV [38]. In the CMS publication comparison is made to the ATLAS 7 TeV results. To do so, CMS has adjusted its results for R to match the ATLAS kinematic region, $p_{\mathrm {T}} > 100$ MeV, $|\eta | < 2.5$, by extrapolating the $n_{\mathrm {ch}}$ values to the lower $p_{\mathrm {T}}$ threshold and excluding the same Q regions as ATLAS in the fit to $R_2 (Q)$. These adjusted CMS values are shown together with the ATLAS results in Fig. . The behaviour of R in the two experiments is qualitatively similar. However, there is a clear difference in the results, particularly at low $n_{\mathrm {ch}}$. Results from this analysis (Fig. 4b) and earlier studies for the lower-energy ATLAS analysis [28] indicate a direct dependence of R on the $p_{\mathrm {T}}$ threshold. So the effect of the difference in kinematic coverage as well as the differing approaches to constructing the reference sample requires further investigation.

9 Summary and conclusions

Results are presented of measurements of two-particle BEC of like-charge hadrons with track $p_{\mathrm {T}}$-thresholds of 100 and 500 MeV and $|\eta |< 2.5$ produced in pp collisions at $\sqrt{s}= 13$ TeV recorded by the ATLAS detector at the CERN LHC. The study is carried out using data collected with the MB and HMT triggers. The integrated luminosities are 151 $\upmu$b$^{-1}$ and 8.4 nb$^{-1}$ for the MB and HMT data samples, respectively.

The studies are performed using the $R_2 (Q)$ correlation function, which is the ratio of the $C_2^{\mathrm {data}} (Q)$ correlation function obtained from the data to the $C_2^{\mathrm {MC}} (Q)$ calculated using MC events with no BEC effect. The $C_2$ function is itself a ratio of like-charge particle pairs to a reference sample, and the reference sample is constructed using unlike-charge particle pairs. A clear indication of BEC is observed in the region of small four-momentum difference, $Q \lesssim 0.2$ GeV. The BEC parameters, R and $\lambda$, are studied as functions of a scaled charged-particle multiplicity $m_{\mathrm {ch}}$, the pair average transverse momentum $(k_{\mathrm {T}})$ and in $(m_{\mathrm {ch}}, k_{\mathrm {T}})$-intervals.

The parameter $R (m_{\mathrm {ch}})$ is found to increase as $\alpha \root 3 \of { m_{\mathrm {ch}} }$ for low multiplicity for both $p_{\mathrm {T}}$ thresholds. For $p_{\mathrm {T}} > 100$ MeV, $\alpha = 2.54^{+0.12}_{-0.22} (\mathrm {total})$ fm, for scaled multiplicity up to $m_{\mathrm {ch}} \approx 2$. For $m_{\mathrm {ch}} \ge 3$, the source radius R saturates at a value $R = 3.35^{+0.20}_{-0.09} (\mathrm {total})$ fm, confirming the previous observation of a high-multiplicity plateau by ATLAS at $\sqrt{s} = 7$ TeV. For $p_{\mathrm {T}} > 500$ MeV, the behaviour of R is similar, but systematically lower.

The parameter $\lambda (m_{\mathrm {ch}})$ decreases with multiplicity for the lower $p_{\mathrm {T}}$ threshold and is lower for the higher $p_{\mathrm {T}}$ threshold but increases slightly with multiplicity. The parameters $R (k_{\mathrm {T}})$ and $\lambda (k_{\mathrm {T}})$ both decrease with increasing pair average transverse momentum $k_{\mathrm {T}}$. Considering the combined $(m_{\mathrm {ch}}, k_{\mathrm {T}})$ dependence, $\lambda$ decreases with $k_{\mathrm {T}}$ in all $m_{\mathrm {ch}}$ intervals, for both $p_{\mathrm {T}}$ thresholds. The decrease is more pronounced at lower multiplicity. The radius parameter R also decreases with $k_{\mathrm {T}}$ for $p_{\mathrm {T}} >100$ MeV, decreasing more strongly in the lower $m_{\mathrm {ch}}$ intervals. For $p_{\mathrm {T}} > 500$ MeV the behaviour of R is rather flat with $k_{\mathrm {T}}$. As a function of $m_{\mathrm {ch}}$, R increases and reaches a plateau at large multiplicity in all $m_{\mathrm {ch}}$ intervals and for both $p_{\mathrm {T}}$ thresholds. Within the uncertainties of this analysis, the turn-on of the plateau occurs at the same value of $m_{\mathrm {ch}}$ in all $k_{\mathrm {T}}$ intervals and for both $p_{\mathrm {T}}$ thresholds. A comparison of the R parameter as a function of $n_{\mathrm {ch}}$ with CMS results at 13 TeV shows qualitatively similar behaviour and the differences at low $n_{\mathrm {ch}}$ require further investigation.

The measurements presented here complement the ATLAS measurements at $\sqrt{s} = 0.9$ and 7 TeV by extending the studies to higher multiplicities and pair average transverse momenta, and provide a more detailed study of the BEC parameters by exploring the double-differential $(m_{\mathrm {ch}}, k_{\mathrm {T}})$-dependence. The present results confirm the saturation of the source radius at higher multiplicities with $n_{\mathrm {ch}} \gtrsim 100$.

Appendix A: Effect of resonances on \(R_2(Q)\) correlation function

Fig. 16

The inclusive Q distribution of unlike-charge particle pairs for track pairs originating from the decays of various species of single resonances. The full range of multiplicities contribute to each distribution

The potential influence of resonances on the $R_2 (Q)$ is evident by studying the Q distributions of the UCP pairs ($h^\pm h^\mp$) where both particles come from the same species of resonance; this is shown in Fig. . The presented distributions are for track pairs with $p_{\mathrm {T}} > 100$ MeV. The reflections of the resonance peaks can be seen clearly, and arise mainly from contributions from the $\eta$, $\omega$, $\rho$ and $K^{*0}$ resonances, with much smaller contributions from the $\eta ^{\prime }$ and $\phi$ mesons. The contributions of $f_0 (980) \rightarrow \pi ^+ \pi ^-$ and $f_2 (1270) \rightarrow \pi ^+ \pi ^-$ are insignificant.