1 Introduction

T-duality of string theory has been studied for a long time. It presents a physical equivalence of moving strings in two compactified backgrounds with radii R and \(\alpha ^{\prime }/R\), where \(\alpha ^{\prime }\) denotes square of the string length. In low energy effective theory of closed strings, for certain configurations, background’s compactification is not necessary and T-duality can be replaced by a close duality, the scale-factor duality [1,2,3,4,5,6]. The scale-factor duality was first discovered in the equations of motion (EOM) of the closed string’s low energy effective action. It shows that the EOM in FLRW cosmological background are invariant under a transformation: \(a\left( t\right) \longleftrightarrow 1/a\left( t\right) \). Einstein’s gravity does not possess this property since a closed string dilaton \(\phi \) plays a central role in this duality. In addition, the scale-factor duality brings us a remarkable pre-big bang cosmology [7,8,9,10]. It implies that our universe was not created from an initial big bang singularity, but from a stage of evolution before the big bang. Pre- and post- big bang scenarios are disconnected due to the big bang singularity, which could be removed by higher loop corrections [10,11,12,13].

In 1997, Meissner found that when massless closed string fields only depended on time, zeroth and first order \(\alpha ^{\prime }\) corrections of the low energy effective action could be simplified and rewritten in \(O\left( d,d\right) \) invariant forms [14]. After that, Sen proved that all orders in \(\alpha ^{\prime }\) are O(d, d) invariant [4, 5]. By assuming that the standard \(O\left( d,d\right) \) form could be maintained, Hohm and Zwiebach [15,16,17] demonstrated that all order \(\alpha ^{\prime }\) corrections of the low energy effective action could be dramatically simplified in the FLRW cosmological background, namely the Hohm–Zwiebach action. Since the Hohm–Zwiebach action is a polynomial function of the standard \(O\left( d,d\right) \) matrix, the EOM only contain first two order derivative terms. This result made the whole theory stable (ghost free) and solvable. The higher-order derivative terms and \(O\left( d,d\right) \) breaking terms could be eliminated by a suitable field redefinition. Moreover, it turns out that non-perturbative dS vacua could be allowed in bosonic string theory. Based on these works, we and collaborators generalized the Hohm–Zwiebach action to a braneworld ansatz and provided a possibility of an existence of non-perturbative AdS vacua [18]. Then, we figured out non-singular string cosmological solutions of the Hohm–Zwiebach action, which showed that the big bang singularity could be smoothed out by \(\alpha ^{\prime }\) corrections [21]. The systematic method to construct the solutions of the Hohm–Zwiebach action were shown in our following work [22]. Moreover, since the EOM of the Hohm–Zwiebach action only contains the first two derivative terms of the metric, which meets the requirement of Lovelock gravity, we presented an equivalence between the Hohm–Zwiebach action and Lovelock gravity in cosmological background by appropriate field redefinitions [23]. On the other hand, there is still some work trying to introduce \(O\left( d,d\right) \) covariant matter sources into the Hohm–Zwiebach action [24] and double field theory [25, 26].

Since the Hohm–Zwiebach action has been generalized from the cosmological ansatz to the braneworld ansatz [18], it is possible to discuss the naked singularities in this model. Naturally, these new kinds of solutions will include non-perturbative effects of string theory, and then help us understand the weak cosmic censorship conjecture (WCCC) [19] from the viewpoint of string theory. In this paper, we start with the tree-level closed string’s low energy effective action. The braneworld solutions of this action possess the naked singularity. The previous discussions of naked singularities in bosonic string theory were presented in Ref. [20]. Based on our previous work [22], we provide two classes of non-singular and non-perturbative solutions, which match perturbative solutions to an arbitrary order in \(\alpha ^{\prime }\). It is worth noting that the term non-perturbative here means the solutions are valid everywhere in all regions of |y| and \(\alpha ^{\prime }\), in contrast to that the perturbative solutions only exist in \(|y|\rightarrow \infty \) (or equivalently \(\alpha ^{\prime }\rightarrow 0\)). Our results show that non-perturbative \(\alpha ^{\prime }\) corrections can smooth out the naked singularities of spacetime. In addition, we wish to stress that our work could be used to the braneworld scenarios in the near future, which was born from discussions and explorations of the theory of extra dimensions. The first step it to study how to define the junction functions, tensor perturbations and graviton localization in the Hohm–Zwiebach action. Good reviews for braneworld models can be found in refs. [27, 28].

The reminder of this paper is outlined as follows. In Sect. 2, we present naked singular solutions of the tree-level closed string’s low energy effective action. In Sect. 3, based on the Hohm–Zwiebach action, we provide two classes of non-singular solutions. Finally, we present some inspirations and conclusions in Sect. 4.

2 Naked singularities in tree-level effective action

We start with the low energy gravi-dilaton effective action of string theory. For simplicity, we only consider the gravi-dilaton system without any perfect fluid sources, and set anti-symmetric Kalb-Ramond field \(b_{ij}=0\). The action is given by

$$\begin{aligned} S=\frac{1}{2\kappa ^{2}}\int d^{d+1}x\sqrt{-g}e^{-2\phi }\left[ R+4\left( \partial _{\mu }\phi \right) ^{2}\right] , \end{aligned}$$
(1)

where \(D=d+1\) is the spacetime dimension, \(\phi \) is the closed string dilaton and \(g_{\mu \nu }\) is the string metric which relates to the Einstein metric through \(g_{\mu \nu }^{E}=\mathrm {exp}\left( -\frac{4}{D-2}\phi \right) g_{\mu \nu }\). By varying the action (1), the equations of motion (EOM) are obtained as

$$\begin{aligned} R_{\mu \nu }+2\nabla _{\mu }\nabla _{\nu }\phi= & {} 0,\nonumber \\ \nabla ^{2}\phi -2\left( \partial _{\mu }\phi \right) ^{2}= & {} 0. \end{aligned}$$
(2)

And then, we introduce the \(O\left( d,d\right) \) invariant dilaton field \(\Phi \) which is defined by the closed string dilaton \(\phi \) and string metric \(g_{\mu \nu }\):

$$\begin{aligned} \Phi =2\phi -\ln \sqrt{-g}. \end{aligned}$$
(3)

The braneworld ansatz is given by

$$\begin{aligned} ds^{2}=\bar{a}^{2}\left( y\right) \eta _{\mu \nu }dx^{\mu }dx^{\nu }+dy^{2}, \end{aligned}$$
(4)

where \(\bar{a}\left( y\right) \) denotes a wrap factor of braneworld theory and \(\eta _{\mu \nu }=\mathrm {diag}\left( -1,1,1,1,\ldots \right) \) is the metric of Minkowski spacetime. The EOM of (2) become

$$\begin{aligned} 2\Phi ^{\prime \prime }-\Phi ^{\prime 2}-d\bar{H}^{2}= & {} 0,\nonumber \\ -d\bar{H}^{2}+\Phi ^{\prime \prime }= & {} 0,\nonumber \\ \bar{H}^{\prime }-\Phi ^{\prime }\bar{H}= & {} 0, \end{aligned}$$
(5)

where we used a notation \(f^{\prime }\left( y\right) \equiv \partial _{y}f\left( y\right) \) for an arbitrary function \(f\left( y\right) \), and the definition of the Hubble-like parameter is given by \(\bar{H}\left( y\right) \equiv \frac{\bar{a}^{\prime }\left( y\right) }{\bar{a}\left( y\right) }\). It is noteworthy that \(\bar{H}\left( y\right) \) can be used to show the features of background curvature of (4). It is easy to check that the EOM (5) are invariant under the scale-factor duality:

$$\begin{aligned} \bar{a}\left( y\right)&\longleftrightarrow&\bar{a}\left( y\right) ^{-1},\quad \bar{H}\left( y\right) \longleftrightarrow -\bar{H}\left( y\right) ,\nonumber \\ \Phi \left( y\right)&\longleftrightarrow&\Phi \left( y\right) , \end{aligned}$$
(6)

and possess a \(Z_{2}\) symmetry: \(y\rightarrow -y\). The self-dual solutions are

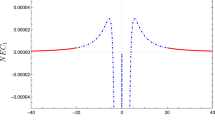
$$\begin{aligned} \bar{a}_{\pm }\left( y\right)= & {} \left| \frac{y}{y_{0}}\right| ^{{\pm 1}/\sqrt{d}},\quad \bar{H}_{\pm }\left( y\right) =\pm \frac{1}{\sqrt{d}y},\nonumber \\ \Phi \left( y\right)= & {} -\ln \left| \frac{y}{y_{0}}\right| , \end{aligned}$$
(7)

where \(y_{0}\) is an integral constant. This result also can be transformed to the solutions in the spherical coordinates [20]. The curvature properties of these solutions can be presented by Hubble-like parameters \(\bar{H}_{\pm }\left( y\right) \) in Fig. 1).

Fig. 1
figure 1

Hubble-like parameters \(\bar{H}\) vs. coordinate of dimension y of four solutions (we set \(d=4\) in this plot)

Full size image

Since the EOM (5) are invariant under the scale-factor duality (6), the action (1) can manifest this invariance. To present this invariance, let us define a new quantity

$$\begin{aligned} g_{\mu \nu }=\left( \begin{array}{ll} 1 &{} 0\\ 0 &{} \bar{G}_{\mu \nu }\left( y\right) \end{array}\right) , \end{aligned}$$
(8)

based on the following ansatz:

$$\begin{aligned} ds^{2}=\bar{G}_{\mu \nu }\left( y\right) dx^{\mu }dx^{\nu }+dy^{2}. \end{aligned}$$
(9)

Using this new notation, the action (1) can be rewritten as

$$\begin{aligned} \bar{I}_{0}=\int dxe^{-\Phi }\left[ \Phi ^{\prime 2}+\frac{1}{8}\mathrm {Tr}\left( \bar{\mathcal {S}}^{\prime 2}\right) \right] . \end{aligned}$$
(10)

where the \(O\left( d,d\right) \) standard metric \(\bar{\mathcal {S}}\) is defined by a symmetric \(2d\times 2d\) matrix \(\bar{M}\)

$$\begin{aligned} \bar{M}=\left( \begin{array}{ll} \bar{G}^{-1} &{} 0\\ 0 &{} \bar{G} \end{array}\right) , \end{aligned}$$

and

$$\begin{aligned} \bar{\mathcal {S}}=\eta \bar{M}=\left( \begin{array}{ll} 0 &{} \bar{G}\\ \bar{G}^{-1} &{} 0 \end{array}\right) , \end{aligned}$$
(11)

in which \(\eta \) is the invariant metric of the \(O\left( d,d\right) \) group

$$\begin{aligned} \eta =\left( \begin{array}{ll} 0 &{} I\\ I &{} 0 \end{array}\right) . \end{aligned}$$
(12)

Furthermore, the action (10) is invariant under the \(O\left( d,d\right) \) transformation:

$$\begin{aligned} \Phi \rightarrow \Phi ,\quad \bar{\mathcal {S}}\rightarrow \tilde{\bar{\mathcal {S}}}=\Omega ^{T}\bar{\mathcal {S}}\Omega , \end{aligned}$$
(13)

where \(\Omega \) is a constant matrix that satisfies

$$\begin{aligned} \Omega ^{T}\eta \Omega =\eta . \end{aligned}$$
(14)

It is worth noting that the \(O\left( d,d\right) \) invariant transformation

$$\begin{aligned} \bar{\mathcal {S}}=\left( \begin{array}{ll} 0 &{} \bar{G}\\ \bar{G}^{-1} &{} 0 \end{array}\right) \longleftrightarrow \tilde{\bar{\mathcal {S}}}=\left( \begin{array}{ll} 0 &{} \bar{G}^{-1}\\ { \bar{G}} &{} 0 \end{array}\right) , \end{aligned}$$
(15)

is the same as the scale-factor duality \(\bar{a}\left( y\right) \longleftrightarrow \bar{a}\left( y\right) ^{-1}\) in Eq. (6) when we utilize the braneworld ansatz (4), say \(\bar{G}_{\mu \nu }\left( y\right) =\bar{a}^{2}\left( y\right) \eta _{\mu \nu }\).

3 Non-singular solutions via \(\alpha ^{\prime }\) corrections

In this section, let us demonstrate how to obtain the regular solutions by introducing the \(\alpha ^{\prime }\) corrections to the gravi-dilaton system in the string frame (1). To include higher order \(\alpha ^{\prime }\) corrections, the action (1) can be rewritten as

$$\begin{aligned} S= & {} \int d^{d+1}x\sqrt{-g}e^{-2\phi }\left[ R+4\left( \partial _{\mu }\phi \right) ^{2}\right. \nonumber \\&\left. +\frac{\alpha ^{\prime }}{4}R_{\mu \nu \rho \sigma }R^{\mu \nu \rho \sigma }+\cdots \right] . \end{aligned}$$
(16)

In Ref. [29], Zwiebach showed that the first order \(\alpha ^{\prime }\) correction could be rewritten as a well-known Gauss–Bonnet term by a suitable field redefinition:

$$\begin{aligned} S= & {} \int d^{d+1}x\sqrt{-g}e^{-2\phi }\left[ R+4\left( \partial _{\mu }\phi \right) ^{2}\right. \nonumber \\&\left. +\frac{\alpha ^{\prime }}{4}\left( R_{\mu \nu \rho \sigma }R^{\mu \nu \rho \sigma }-4R_{\mu \nu }R^{\mu \nu }+R^{2}\right) +\cdots \right] . \end{aligned}$$
(17)

Using the \(O\left( d,d\right) \) invariant matrix (11) and applying a further field redefinition [14], this action can be simplified

$$\begin{aligned} \bar{I}= & {} -\int dxe^{-\Phi }\left[ -\Phi ^{\prime 2}-\frac{1}{8}\mathrm {Tr}\bar{\mathcal {S}}^{\prime 2}\right. \nonumber \\&\left. -\frac{\alpha ^{\prime }}{4}\left( \frac{1}{16}\mathrm {Tr}\bar{\mathcal {S}}^{\prime 4}-\frac{1}{32}\left( \mathrm {Tr}\bar{\mathcal {S}}^{\prime 2}\right) ^{2}\right) +\cdots \right] . \end{aligned}$$
(18)

Based on Sen’s proof [4, 5] and the action above, Hohm and Zwiebach conjectured that all orders in \(\alpha ^{\prime }\) corrections could be rewritten in terms of the \(O\left( d,d\right) \) invariant matrix \(\bar{\mathcal {S}}\) in Eq. (11). Considering all possible combinations of \(\bar{\mathcal {S}}\) and its trace and derivatives for higher-order terms, and using a set of field redefinitions, the action can be dramatically simplified as follows [17, 18]:

$$\begin{aligned} \bar{I}_{HZ}= & {} -\int dxe^{-\Phi }\left( -\Phi ^{\prime 2}+\sum _{k=1}^{\infty }\left( \alpha ^{\prime }\right) ^{k-1}\bar{c}_{k}\mathrm {Tr}\left( \bar{\mathcal {S}}^{\prime 2k}\right) \right. \nonumber \\&\left. +\text {multi-traces}\right) , \end{aligned}$$
(19)

in which we define a new set of coefficients \(\bar{c}_{k}\)’s. The new coefficients have a relationship with \(c_{k}\)’s in Hohm–Zweibach action as below:

$$\begin{aligned} \bar{c}_{1}=c_{1},\quad \bar{c}_{2k+1}=c_{2k+1},\quad \bar{c}_{2k}=-c_{2k},\quad k=1,2,\ldots ,\nonumber \\ \end{aligned}$$
(20)

where \(c_{1}=-\frac{1}{8}\), \(c_{2}=\frac{1}{64}\) for the bosonic string and \(c_{k\ge 3}\) are undetermined constants which could be fixed by string theory in future works. After substituting the braneworld ansatz (4) into the action (19), we have

$$\begin{aligned} \bar{I}_{HZ}{=}-\int dxe^{-\Phi }\left( -\Phi ^{\prime 2}{-}d\sum _{k=1}^{\infty }\left( -\alpha ^{\prime }\right) ^{k-1}2^{2k+1}\bar{c}_{k}\bar{H}^{2k}\right) .\nonumber \\ \end{aligned}$$
(21)

The complete derivation for the action (19) can be found in the appendix of Ref. [18]. The EOM of (21) can be obtained directly, which are

$$\begin{aligned} \Phi ^{\prime \prime }+\frac{1}{2}\bar{H}\bar{f}\left( \bar{H}\right)= & {} 0,\nonumber \\ \frac{d}{dy}\left( e^{-\Phi }\bar{f}\left( \bar{H}\right) \right)= & {} 0,\nonumber \\ \Phi ^{\prime 2}+\bar{g}\left( \bar{H}\right)= & {} 0, \end{aligned}$$
(22)

where

$$\begin{aligned} \bar{f}\left( \bar{H}\right)= & {} d\sum _{k=1}^{\infty }\left( -\alpha ^{\prime }\right) ^{k-1}2^{2\left( k+1\right) }k\bar{c}_{k}\bar{H}^{2k-1},\nonumber \\ \bar{g}\left( \bar{H}\right)= & {} d\sum _{k=1}^{\infty }\left( -\alpha ^{\prime }\right) ^{k-1}2^{2k+1}\left( 2k-1\right) \bar{c}_{k}\bar{H}^{2k}. \end{aligned}$$
(23)

Obviously, the EOM (22) reduce to (5) when \(\alpha ^{\prime }\) corrections disappear. Moreover, we have the following conditions:

$$\begin{aligned} \bar{g}^{\prime }\left( \bar{H}\right) {=}\bar{H}\bar{f}^{\prime }\left( \bar{H}\right) ,\,\,\,\mathrm{and}\,\,\,\bar{g}\left( \bar{H}\right) {=}\bar{H}\bar{f}\left( \bar{H}\right) {-}\int _{0}^{\bar{H}}\bar{f}\left( y\right) dy,\nonumber \\ \end{aligned}$$
(24)

It is straightforward to check that the EOM (22) are invariant under the \(O\left( d,d\right) \) transformations:

$$\begin{aligned} \bar{H}\left( y\right)\rightarrow & {} -\bar{H}\left( y\right) ,\quad \Phi \left( y\right) \rightarrow \Phi \left( y\right) ,\quad \bar{f}\left( y\right) \rightarrow -\bar{f}\left( y\right) ,\nonumber \\ \bar{g}\left( x\right)\rightarrow & {} \bar{g}\left( y\right) . \end{aligned}$$
(25)

Now, let us try to figure out non-singular and non-perturbative solutions of the EOM (22). Since the non-perturbative solutions must match the perturbative solutions to an arbitrary order in \(\alpha ^{\prime }\) as \(|y|\rightarrow \infty \) (or equivalently \(\alpha ^{\prime }\rightarrow 0\)), we will first calculate the perturbative solutions to an arbitrary order in the next subsection. Then, we will provide a systematic method to construct the non-singular and non-perturbative solutions which match the perturbative solutions.

3.1 Perturbative solution

We now discuss the perturbative solutions of the EOM (22) based on Ref. [17]. For convenient, we introduce a new variable \(\Omega \) as

$$\begin{aligned} \Omega \equiv e^{-\Phi }, \end{aligned}$$
(26)

where \(\Omega ^{\prime }=-\Phi ^{\prime }\Omega \) and \(\Omega ^{\prime \prime }=\left( -\Phi ^{\prime \prime }+\Phi ^{\prime 2}\right) \Omega \). And the EOM (22) become

$$\begin{aligned} \Omega ^{\prime \prime }-\bar{h}\left( \bar{H}\right) \Omega= & {} 0,\nonumber \\ \frac{d}{dy}\left( \Omega \bar{f}\left( \bar{H}\right) \right)= & {} 0,\nonumber \\ \Omega ^{\prime 2}+\bar{g}\left( \bar{H}\right) \Omega ^{2}= & {} 0, \end{aligned}$$
(27)

where we define a new function

$$\begin{aligned} \bar{h}\left( \bar{H}\right) \equiv \frac{1}{2}\bar{H}\bar{f}\left( \bar{H}\right) -\bar{g}\left( \bar{H}\right) =\alpha ^{\prime }2^{5}d\bar{c}_{2}H^{4}+\cdots , \end{aligned}$$
(28)

with

$$\begin{aligned} \bar{f}\left( \bar{H}\right)= & {} 2^{4}d\bar{c}_{1}\bar{H}-\alpha ^{\prime }4\cdot 2^{5}d\bar{c}_{2}\bar{H}^{3}+\cdots ,\nonumber \\ \bar{g}\left( \bar{H}\right)= & {} 2^{3}d\bar{c}_{1}\bar{H}^{2}-\alpha ^{\prime }3\cdot 2^{5}d\bar{c}_{2}\bar{H}^{4}+\cdots . \end{aligned}$$
(29)

It is easy to see that \(\bar{h}\left( \bar{H}\right) =0\) at zeroth order of \(\alpha ^{\prime }\). Now, we assume the perturbative solutions of the EOM (27) take forms:

$$\begin{aligned} \Omega \left( y\right)= & {} \Omega _{0}\left( y\right) +\alpha ^{\prime }\Omega _{1}\left( y\right) +\alpha ^{\prime 2}\Omega _{2}\left( y\right) +\cdots ,\nonumber \\ \bar{H}\left( y\right)= & {} \bar{H}_{0}\left( y\right) +\alpha ^{\prime }\bar{H}_{1}\left( y\right) +\alpha ^{\prime 2}\bar{H}_{2}\left( y\right) +\cdots . \end{aligned}$$
(30)

where we denote \(\Omega _{i}\) and \(\bar{H}_{i}\) as the i-th order of the perturbative solutions. Based on these perturbative solutions, functions \(\bar{h}\left( \bar{H}\right) \), \(\bar{f}\left( \bar{H}\right) \) and \(\bar{g}\left( \bar{H}\right) \) become

$$\begin{aligned} \bar{h}\left( \bar{H}\right)= & {} \alpha ^{\prime }2^{5}d\bar{c}_{2}H_{0}^{4}+\cdots ,\nonumber \\ \bar{f}\left( \bar{H}\right)= & {} 2^{4}d\bar{c}_{1}\bar{H}_{0}+\alpha ^{\prime }2^{4}d\left( \bar{c}_{1}\bar{H}_{1}-8\bar{c}_{2}\bar{H}_{0}^{3}\right) +\cdots ,\nonumber \\ \bar{g}\left( \bar{H}\right)= & {} 2^{3}d\bar{c}_{1}\bar{H}_{0}^{2}+\alpha ^{\prime }2^{4}d\left( \bar{c}_{1}\bar{H}_{0}\bar{H}_{1}-6\bar{c}_{2}\bar{H}_{0}^{4}\right) +\cdots .\nonumber \\ \end{aligned}$$
(31)

Then, we can substitute these perturbative forms back into the EOM (27), and solve the differential equations at each order of \(\alpha ^{\prime }\) to get \(\Omega _{i}\) and \(\bar{H}_{i}\). For example, the EOM (27) at zeroth order in \(\alpha ^{\prime }\) give:

$$\begin{aligned}&\Omega _{0}^{\prime \prime } = 0,\nonumber \\&\frac{d}{dy}\left( 2^{4}d\bar{c}_{1}\bar{H}_{0}\Omega _{0}\right) = 0,\nonumber \\&\Omega _{0}^{\prime 2}+2^{3}d\bar{c}_{1}\bar{H}_{0}^{2}\Omega _{0}^{2} = 0. \end{aligned}$$
(32)

Based on the first equation of (32), the solution is

$$\begin{aligned} \Omega _{0}\left( y\right) =\gamma \left( y-\sigma _{0}\right) , \end{aligned}$$
(33)

where \(\gamma \) and \(\sigma _{0}\) are integral constants. Then, considering the second and third equations of the EOM (32), the solution of \(\bar{H}_{0}\) is

$$\begin{aligned} \bar{H}_{0\pm }\left( y\right) =\mp \frac{\mathrm {sgn}\left( y\right) }{\sqrt{d}}\frac{1}{y-\sigma _{0}}. \end{aligned}$$
(34)

Next, the EOM (27) at first order of \(\alpha ^{\prime }\) give

$$\begin{aligned}&\alpha ^{\prime }\Omega _{1}^{\prime \prime }-\alpha ^{\prime }2^{5}d\bar{c}_{2}H_{0\pm }^{4}\Omega _{0} = 0,\nonumber \\&\frac{d}{dy}\left( \alpha ^{\prime }2^{4}d\bar{c}_{1}\bar{H}_{0\pm }\Omega _{1}+\alpha ^{\prime }2^{4}d\left( \bar{c}_{1}\bar{H}_{1\pm }-8\bar{c}_{2}\bar{H}_{0\pm }^{3}\right) \Omega _{0}\right) = 0,\nonumber \\&2\alpha ^{\prime }\Omega _{0}^{\prime }\Omega _{1}^{\prime }+\alpha ^{\prime }2^{4}d\bar{c}_{1}\bar{H}_{0\pm }^{2}\Omega _{0}\Omega _{1}{+}\alpha ^{\prime }2^{4}d\left( \bar{c}_{1}\bar{H}_{0\pm }\bar{H}_{1\pm }{-}6\bar{c}_{2}\bar{H}_{0\pm }^{4}\right) \Omega _{0}^{2} {=} 0.\nonumber \\ \end{aligned}$$
(35)

Based on the first equation of (35) and a zeroth-order solution (33), we will get

$$\begin{aligned} \Omega _{1}\left( y\right) =\frac{2^{4}\bar{c}_{2}\gamma }{d}\frac{1}{y-\sigma _{0}}. \end{aligned}$$
(36)

Combining the second and third equations of the EOM (35), and using solutions at zeroth-order (33) and (34), we have

$$\begin{aligned} \bar{H}_{1\pm }\left( y\right) =\mp \frac{80\mathrm {sgn}\left( y\right) c_{2}}{d^{3/2}}\frac{1}{\left( y-\sigma _{0}\right) ^{3}}. \end{aligned}$$
(37)

Therefore, we obtain the first two orders in perturbative solutions of the EOM (27)

$$\begin{aligned} \bar{H}_{\pm }\left( y\right)= & {} \mp \frac{\mathrm {sgn}\left( y\right) }{\sqrt{d}}\frac{1}{y{-}\sigma _{0}}\mp \alpha ^{\prime }\frac{80\mathrm {sgn}\left( y\right) c_{2}}{d^{3/2}}\frac{1}{\left( y{-}\sigma _{0}\right) ^{3}}{+}\cdots ,\nonumber \\ \Omega \left( y\right)= & {} \gamma \left( y-\sigma _{0}\right) +\alpha ^{\prime }\frac{2^{4}c_{2}\gamma }{d}\frac{1}{y-\sigma _{0}}+\cdots . \end{aligned}$$
(38)

Based on these methods, in the perturbative regime \(|y|\rightarrow \infty \) (or equivalently \(\alpha ^{\prime }\rightarrow 0\)), the EOM can be solved iteratively to arbitrary order in \(\frac{\sqrt{\alpha ^{\prime }}}{y}\) by using Eq. (23). For simpliciy, we set the integral constant \(\sigma _{0}=0\), and define \(y_{0}\equiv \frac{\sqrt{\alpha ^{\prime }}}{\sqrt{2d}}\), the solutions with positive sign become:

$$\begin{aligned} \bar{H}\left( y\right)= & {} \frac{\sqrt{2}}{\sqrt{\alpha ^{\prime }}}\left[ \frac{y_{0}}{y}-160\bar{c}_{2}\frac{y_{0}^{3}}{y^{3}}+\frac{256\left( 770\bar{c}_{2}^{2}+19\bar{c}_{3}\right) }{3}\frac{y_{0}^{5}}{y^{5}}\right. \nonumber \\&\left. -\frac{2048\left( 88232\bar{c}_{2}^{3}+4644\bar{c}_{3}\bar{c}_{2}+41\bar{c}_{4}\right) }{5}\frac{y_{0}^{7}}{y^{7}}+\mathcal {O}\left( \frac{y_{0}^{9}}{y^{9}}\right) \right] ,\nonumber \\ \Phi \left( y\right)= & {} -\frac{1}{2}\log \left( \beta ^{2}\frac{y^{2}}{y_{0}^{2}}\right) -32\bar{c}_{2}\frac{y_{0}^{2}}{y^{2}}+\frac{256\left( 44\bar{c}_{2}^{2}+\bar{c}_{3}\right) }{3}\frac{y_{0}^{4}}{y^{4}}\nonumber \\&-\frac{2048\left( 6976\bar{c}_{2}^{3}+352\bar{c}_{3}\bar{c}_{2}+3\bar{c}_{4}\right) }{15}\frac{y_{0}^{6}}{y^{6}}+\mathcal {O}\left( \frac{y_{0}^{8}}{y^{8}}\right) , \end{aligned}$$
(39)

where the second solution can be given by \(\Phi =-\log \Omega \) and

$$\begin{aligned} \bar{f}\left( \bar{H}\left( y\right) \right)= & {} -2d\bar{H}-128\bar{c}_{2}d\alpha ^{\prime }\bar{H}^{3}+768\bar{c}_{3}d\alpha ^{\prime 2}\bar{H}^{5}\nonumber \\&-4096\bar{c}_{4}d\alpha ^{\prime 3}\bar{H}^{7}+\mathcal {O}\left( \alpha ^{\prime 4}\bar{H}^{9}\right) ,\nonumber \\= & {} \frac{\sqrt{d}}{y_{0}}\left[ -\frac{2y_{0}}{y}+64\bar{c}_{2}\frac{y_{0}^{3}}{y^{3}}-\frac{512\left( 50\bar{c}_{2}^{2}+\bar{c}_{3}\right) }{3}\frac{y_{0}^{5}}{y^{5}}\right. \nonumber \\&\left. +\frac{4096\left( 2632\bar{c}_{2}^{3}+124\bar{c}_{3}\bar{c}_{2}+\bar{c}_{4}\right) }{5}\frac{y_{0}^{7}}{y^{7}}+\mathcal {O}\left( \frac{y_{0}^{9}}{y^{9}}\right) \right] ,\nonumber \\ \bar{g}\left( \bar{H}\left( y\right) \right)= & {} -dH^{2}-96\bar{c}_{2}d\alpha ^{\prime }\bar{H}^{4}+640\bar{c}_{3}d\alpha ^{\prime 2}\bar{H}^{6}\nonumber \\&-3584\bar{c}_{4}d\alpha ^{\prime 3}\bar{H}^{8}+\mathcal {O}\left( \alpha ^{\prime 4}\bar{H}^{10}\right) ,\nonumber \\= & {} \frac{1}{y_{0}^{2}}\left[ -\frac{y_{0}^{2}}{y^{2}}+128\bar{c}_{2}\frac{y_{0}^{4}}{y^{4}}-\frac{2048\left( 50\bar{c}_{2}^{2}+\bar{c}_{3}\right) }{3}\frac{y_{0}^{6}}{y^{6}}\right. \nonumber \\&\left. +\frac{8192\left( 24448\bar{c}_{2}^{3}+1136\bar{c}_{3}\bar{c}_{2}+9\bar{c}_{4}\right) }{15}\frac{y_{0}^{8}}{y^{8}}\right. \nonumber \\&\left. +\mathcal {O}\left( \frac{y_{0}^{10}}{y^{10}}\right) \right] , \end{aligned}$$
(40)

where \(\beta \) is an integration constant. Moreover, the dual solutions \(-\bar{H}\left( y\right) \), \(\Phi \left( y\right) ,\) \(-\bar{f}\left( y\right) \) and \(\bar{g}\left( y\right) \) are also included in Eq. (39). It is obvious that the leading term of solutions (39) covers the result of (7). And solutions possess the curvature singularity located at \(\left| y\right| \rightarrow 0\).

3.2 Non-perturbative solutions

Before starting the discussion on the non-perturbative solutions in this section, let us focus on a property of the EOM (22) at first. Based on the EOM (22), we find that all functions \(\bar{g}\left( y\right) \), \(\bar{f}\left( y\right) \) and \(\bar{H}\left( y\right) \) can be uniquely determined by \(\Phi \left( y\right) \):

$$\begin{aligned} \bar{g}\left( \bar{H}\left( y\right) \right)= & {} -\Phi ^{\prime 2},\nonumber \\ \bar{f}\left( \bar{H}\left( y\right) \right)= & {} \frac{2\sqrt{2}d}{\sqrt{\alpha ^{\prime }}}\beta e^{\Phi },\nonumber \\ \bar{H}\left( y\right)= & {} \frac{\sqrt{\alpha ^{\prime }/2}}{\beta d}\frac{\Phi ^{\prime \prime }}{e^{\Phi }}, \end{aligned}$$
(41)

where \(\beta \) is an integration constant. These Eq. (41) imply that we only need to choose a proper \(\Phi \left( y\right) \) to get the non-singular solutions. In other words, it suffices to find a regular function of \(\Phi \left( y\right) \) which can be expanded as (39) in the perturbative regime \(|y|\rightarrow \infty \) (or equivalently \(\alpha ^{\prime }\rightarrow 0\)). Then the solutions of \(\bar{g}\left( y\right) \), \(\bar{f}\left( y\right) \) and \(\bar{H}\left( y\right) \) will be automatically satisfied based on Eq. (41). In the following discussions, we will present two possible constructions for \(\Phi \left( y\right) \), and give their corresponding non-singular solutions \(\bar{g}\left( y\right) \), \(\bar{f}\left( y\right) \) and \(\bar{H}\left( y\right) \).

3.3 Solution A

The first solution is given by

$$\begin{aligned} \Phi \left( y\right) =\frac{1}{2}\log \left( \sum _{k=1}^{\infty }\frac{\lambda _{k}}{1+\gamma ^{2k}}\right) ,\quad \gamma \equiv \frac{y}{y_{0}}=\frac{\sqrt{2d}}{\sqrt{\alpha ^{\prime }}}y. \end{aligned}$$
(42)

From Eq. (41), we get

$$\begin{aligned}&\bar{H}\left( y\right) = \frac{-\left( \sum \nolimits _{k=1}^{\infty }\frac{2k\lambda _{k}\gamma ^{2k-1}}{\left( \gamma ^{2k}{+}1\right) ^{2}}\right) ^{2}{+}\left( \sum \nolimits _{k=1}^{\infty }\frac{\lambda _{k}}{\gamma ^{2k}{+}1}\right) \sum \nolimits _{k=1}^{\infty }\left( \frac{8k^{2}\lambda _{k}\gamma ^{4k-2}}{\left( \gamma ^{2k}{+}1\right) ^{3}}{-}\frac{2k(2k-1)\lambda _{k}\gamma ^{2k-2}}{\left( \gamma ^{2k}{+}1\right) ^{2}}\right) }{\sqrt{2}\sqrt{\alpha ^{\prime }}\beta \left( \sum \nolimits _{k=1}^{\infty }\frac{\lambda _{k}}{\gamma ^{2k}+1}\right) ^{5/2}},\nonumber \\&\bar{f}\left( \bar{H}\left( y\right) \right) = -\frac{2\sqrt{2}\beta d}{\sqrt{\alpha ^{\prime }}}\sqrt{\sum _{k=1}^{\infty }\frac{\lambda _{k}}{\gamma ^{2k}+1}},\nonumber \\&\bar{g}\left( \bar{H}\left( y\right) \right) = -\frac{2d\left( \sum \nolimits _{k=1}^{\infty }\frac{k\lambda _{k}\gamma ^{2k-1}}{\left( \gamma ^{2k}+1\right) ^{2}}\right) ^{2}}{\alpha ^{\prime }\left( \sum \nolimits _{k=1}^{\infty }\frac{\lambda _{k}}{\gamma ^{2k}+1}\right) ^{2}}. \end{aligned}$$
(43)

One of the big advantages of the ansatz (42) is that as long as \(\Phi \left( y\right) \) is non-singular, \(\bar{H}\left( y\right) \) is guaranteed to be non-singular. We therefore only need to care about the singularity of \(\Phi \left( y\right) \). Another advantage of the ansatz (42) is that every individual term inside the log is non-singular, in contrast to the perturbative solution where all terms are singular. Singularities appear if and only if

$$\begin{aligned} \sum _{k=1}^{\infty }\frac{\lambda _{k}}{1+\gamma ^{2k}}=0, \end{aligned}$$
(44)

has real roots. In the perturbative regime \(\left| y\right| \rightarrow \infty \) (\(\alpha ^{\prime }\rightarrow 0\)), the ansatz \(\Phi \left( x\right) \) is expanded as,

$$\begin{aligned}&\Phi (y/\sqrt{\alpha ^{\prime }}\rightarrow \infty ) = \frac{1}{2}\log \left( \frac{\lambda _{1}}{\gamma ^{2}}\right) \nonumber \\&\qquad +\frac{1}{2}\log \left( \sum _{k=1}^{\infty }\frac{1}{\gamma ^{2k-2}}\frac{\lambda _{k}/\lambda _{1}}{1+1/\gamma ^{2k}}\right) \nonumber \\&\quad = \frac{1}{2}\log \left( \frac{\lambda _{1}}{\gamma ^{2}}\right) +\frac{1}{2}\log \left( \frac{1}{1+1/\gamma ^{2}} \right. \nonumber \\&\qquad \left. +\sum _{k=2}^{\infty }\frac{1}{\gamma ^{2k-2}}\frac{\lambda _{k}/\lambda _{1}}{1+1/\gamma ^{2k}}\right) \nonumber \\&\quad = -\frac{1}{2}\log \left( \frac{\gamma ^{2}}{\lambda _{1}}\right) +\frac{\lambda _{2}-\lambda _{1}}{2\lambda _{1}}\frac{1}{\gamma ^{2}}\nonumber \\&\qquad +\frac{\lambda _{1}^{2}+2\left( \lambda _{2}+\lambda _{3}\right) \lambda _{1}-\lambda _{2}^{2}}{4\lambda _{1}^{2}}\frac{1}{\gamma ^{4}}\nonumber \\&\qquad -\frac{\lambda _{1}^{3}+3\left( \lambda _{2}-\lambda _{3}-\lambda _{4}\right) \lambda _{1}^{2}+3\lambda _{2}\left( \lambda _{2}+\lambda _{3}\right) \lambda _{1}-\lambda _{2}^{3}}{6\lambda _{1}^{3}}\frac{1}{\gamma ^{6}}+\cdots .\nonumber \\ \end{aligned}$$
(45)

To match the perturbative solution (39), the coefficients \(\lambda _{i}\) are fixed:

$$\begin{aligned} \lambda _{1}= & {} \frac{1}{\beta ^{2}},\quad \lambda _{2}=\frac{2}{\beta ^{2}},\quad \lambda _{3}=\frac{4+512\bar{c}_{3}}{3\beta ^{2}},\nonumber \\ \lambda _{4}= & {} \frac{8}{15\beta ^{2}}\left( 3136\bar{c}_{3}-1536\bar{c}_{4}+23\right) ,\nonumber \\ \lambda _{5}= & {} \frac{8\left( 1638400\bar{c}_{3}^{2}+66688\bar{c}_{3}-53248\bar{c}_{4}+20480\bar{c}_{5}+219\right) }{35\beta ^{2}},\nonumber \\&\cdots ,&\end{aligned}$$
(46)

where we used \(\bar{c}_{2}=-1/64\). In order to show the features of this solution more clearly, we require the solutions (42) and (43) to cover the first two terms of (39) in the perturbative regime, because the current string theory only gives the first two coefficients of \(\alpha ^{\prime }\) corrections, \(\bar{c}_{1}=c_{1}=-\frac{1}{8}\) and \(\bar{c}_{2}=-c_{2}=-\frac{1}{64}\). Although this example is special, it contains all the features of \(\alpha ^{\prime }\) corrections. To cover \(\bar{c}_{1}\) and \(\bar{c}_{2}\), we only need to keep two coefficients \(\lambda _{1}\) and \(\lambda _{2}\). Therefore, the solution (42) becomes

$$\begin{aligned} \Phi \left( y\right) =\frac{1}{2}\log \left( \frac{1}{4d}\frac{\alpha ^{\prime }}{\alpha ^{\prime }+2dy^{2}}+\frac{1}{2d}\frac{\alpha ^{\prime 2}}{\alpha ^{\prime 2}+4d^{2}y^{4}}\right) , \end{aligned}$$
(47)

where \(\beta ^{2}=4d\) to match the perturbative solutions. The \(O\left( d,d\right) \) invariant dilaton \(\Phi \left( y\right) \) and its associated Hubble-like parameters \(\bar{H}\left( y\right) \) are presented in Fig. 2.

Fig. 2
figure 2

The left panel shows the non-perturbative Hubble-like parameters \(\bar{H}\left( y\right) \) vs. coordinate of dimension y. The right panel presents the \(O\left( d,d\right) \) dilaton \(\Phi \left( y\right) \) along the dimension y. We set parameters \(d=4\) and \(\alpha ^{\prime }=1\)

Full size image

3.4 Solution B

Supposing the coefficients \(c_{k\le n}\) are known, another interesting ansatz is given by

$$\begin{aligned} \Phi \left( y\right) {=}-\frac{1}{2N}\log \left[ {\mathop {k}\limits ^{[}}{=}0]{N}{\sum }\rho _{k}\gamma ^{2k}\right] ,\,\,\,\gamma \equiv \frac{y}{y_{0}}{=}\frac{\sqrt{2d}}{\sqrt{\alpha ^{\prime }}}y,\nonumber \\ \end{aligned}$$
(48)

where \(N\ge n-1\) is some arbitrary integer and \(\rho _{0}>0\), \(\rho _{N}>0\). Also from Eq. (41), we have

$$\begin{aligned} \bar{H}\left( y\right)= & {} \frac{-\left( \sum \nolimits _{k=0}^{N}\rho _{k}\gamma ^{2k}\right) \sum \nolimits _{k=0}^{N}2k\left( 2k-1\right) \rho _{k}\gamma ^{2k-2}+\left( \sum \nolimits _{k=0}^{N}2k\rho _{k}\gamma ^{2k-1}\right) {}^{2}}{\sqrt{2}\sqrt{\alpha ^{\prime }}\beta N\left( \sum \nolimits _{k=0}^{N}\rho _{k}\gamma ^{2k}\right) {}^{2-\frac{1}{2N}}},\nonumber \\ \bar{f}\left( \bar{H}\left( y\right) \right)= & {} -\frac{2\sqrt{2}\beta d}{\sqrt{\alpha ^{\prime }}}\left( \sum _{k=0}^{N}\rho _{k}\gamma ^{2k}\right) ^{-\frac{1}{2N}},\nonumber \\ \bar{g}\left( \bar{H}\left( y\right) \right)= & {} -\frac{d\left( \sum \nolimits _{k=0}^{N}2k\rho _{k}\gamma ^{2k-1}\right) ^{2}}{2\alpha ^{\prime }N^{2}\left( \sum \nolimits _{k=0}^{N}\rho _{k}\gamma ^{2k}\right) ^{2}}. \end{aligned}$$
(49)

In the perturbative regime \(\left| y\right| \rightarrow \infty \) (\(\alpha ^{\prime }\rightarrow 0\)), the ansatz \(\Phi \left( y\right) \) in (48) can be expanded as

$$\begin{aligned} \Phi \left( y\right)= & {} -\frac{1}{2}\log \left( \gamma ^{2}\rho _{N}^{1/N}\right) -\frac{1}{2N}\Bigg \{\frac{\rho _{N-1}}{\rho _{N}}\frac{1}{\gamma ^{2}}\nonumber \\&+\frac{2\rho _{N}\rho _{N-2}-\rho _{N-1}^{2}}{2\rho _{N}^{2}}\frac{1}{\gamma ^{4}}+\frac{3\rho _{N}^{2}\rho _{N-3}-3\rho _{N}\rho _{N-1}\rho _{N-2}+\rho _{N-1}^{3}}{3\rho _{N}^{3}}\frac{1}{\gamma ^{6}}\nonumber \\&+\frac{4\rho _{N}^{3}\rho _{N-4}-2\rho _{N}^{2}\rho _{N-2}^{2}-4\rho _{N}^{2}\rho _{N-1}\rho _{N-3}+4\rho _{N}\rho _{N-1}^{2}\rho _{N-2}-\rho _{N-1}^{4}}{4\rho _{N}^{4}}\frac{1}{\gamma ^{8}}+\mathcal{O}\left( \frac{1}{\gamma ^{10}}\right) \Bigg \}. \end{aligned}$$
(50)

To match the perturbative solution (39), the coefficients \(\rho _{i}\) are fixed as:

$$\begin{aligned} \rho _{N}= & {} \beta ^{2N},\quad \rho _{N-1}=-N\beta ^{2N},\nonumber \\ \rho _{N-2}= & {} \frac{\beta ^{2N}}{12}N\left( 6N-2048\bar{c}_{3}-22\right) ,\cdots , \end{aligned}$$
(51)

where we use \(\bar{c}_{2}=-1/64\).

It is worth noting that these classes of solutions (48) and (49) are very special. They are not always non-singular, and the results depend on the specific values of \(\bar{c}_{k}\). For example, consider the simplest case that solutions (48) and (49) only cover the first two terms of Eq. (39) in the perturbative regime \(|y|\rightarrow \infty \) (or equivalently \(\alpha ^{\prime }\rightarrow 0\)). In other words, we only need to keep \(\rho _{0}\) and \(\rho _{1}\) in (48) and (49). The solution is

$$\begin{aligned} \Phi \left( y\right) =-\frac{1}{2}\log \left[ 4d\left( -1+\frac{2d}{\alpha ^{\prime }}y^{2}\right) \right] . \end{aligned}$$
(52)

It is not difficult to check that \(\Phi \left( y\right) \) has a singularity, and therefore the corresponding \(\bar{H}\left( y\right) \) is singular:

$$\begin{aligned} \bar{H}\left( y\right) =\frac{\sqrt{2}\left( 2dy^{2}+\alpha ^{\prime }\right) }{\left( 2dy^{2}-\alpha ^{\prime }\right) ^{3/2}}. \end{aligned}$$
(53)

To get a non-singular solution, the number of coefficients \(\rho _{i}\) must be more than two, namely we need to know \(\bar{c}_{3}\) and \(\rho _{3}\) . Considering the simplest case where \(N=2\), the Hubble parameter becomes

Fig. 3
figure 3

The left panel shows the non-perturbative Hubble-like parameters \(\bar{H}\left( y\right) \) vs. coordinate of dimension y. The right panel presents the \(O\left( d,d\right) \) dilaton \(\Phi \left( y\right) \) along the dimension y. We set parameters \(d=4\) and \(\alpha ^{\prime }=1\)

Full size image
Fig. 4
figure 4

The left panel shows the Kretschmann scalar of solution A vs. coordinate of dimension y. The right panel presents the Kretschmann scalar of solution B vs. coordinate of dimension y. We set parameters \(d=4\) and \(\alpha ^{\prime }=1\)

Full size image
Fig. 5
figure 5

Effective potential \(V\left( y\right) \) vs. coordinate of dimension y. We set \(d=4\) and \(\alpha ^{\prime }=1\) in this plot)

Full size image
$$\begin{aligned} \bar{H}\left( y\right) =\frac{\sqrt{2}3^{3/4}\left( 5\alpha ^{\prime 3}-1024\alpha ^{\prime 2}\bar{c}_{3}\left( 6dy^{2}-\alpha ^{\prime }\right) -24d^{3}y^{6}+12\alpha ^{\prime }d^{2}y^{4}-42\alpha ^{\prime 2}dy^{2}\right) }{\left( -5\alpha ^{\prime 2}-1024\alpha ^{\prime 2}\bar{c}_{3}+12d^{2}y^{4}-12\alpha ^{\prime }dy^{2}\right) {}^{7/4}}. \end{aligned}$$
(54)

To have a non-singular solution for all regions of y, there must be \(\bar{c}_{3}<-1/128\). Moreover, in the future, even if \(\bar{c}_{3}\) is determined by other theories and the condition is violated, we can still obtain solutions without singularity by taking \(\rho _{4}\) which may put a constraint on \(\bar{c}_{4}\), and so on. In the case of \(N=2\), the form of the relevant Ricci scalar is still very complicated. As an alternative, we give Fig. 3 to demonstrate the Hubble-like parameters \(\bar{H}\left( y\right) \).

3.5 Solutions in Einstein frame

To study the physical properties of the solutions, we may transform our regular solutions from the string frame to the Einstein frame. Let us recall the relation between string frame and Einstein frame:

$$\begin{aligned} g_{\mu \nu }^{E}=\exp \left( -\frac{4\phi }{d-1}\right) g_{\mu \nu }. \end{aligned}$$
(55)

Therefore, it is straightforward to get the solutions in the Einstein frame by:

$$\begin{aligned} \bar{H}_{\pm }^{E}\left( y\right) =\frac{\bar{a}_{E}^{\prime }\left( y\right) }{\bar{a}_{E}\left( y\right) }=-\frac{1}{d-1}\left( \Phi ^{\prime }\left( y\right) +\bar{H}_{\pm }\left( y\right) \right) . \end{aligned}$$
(56)

To verify the singularities of these solutions, we need to consider Kretschmann scalar, which can be given by

$$\begin{aligned} R_{\mu \nu \rho \sigma }R^{\mu \nu \rho \sigma }=4dH_{E}^{\prime 2}+8dH_{E}^{\prime }H_{E}^{2}+2\left( d+1\right) dH_{E}^{4}. \end{aligned}$$
(57)

The following pictures show the Kretschmann scalars of \(\bar{H}_{+}^{E}\) for solutions A and B (Fig. 4).

4 Concluding remarks

In this paper, we provided systematic methods to construct two classes of non-singular non-perturbative solutions, which matched the perturbative solutions to an arbitrary order in \(\alpha ^{\prime }\). The methods depended on the Hohm–Zwiebach action [15,16,17]. The results implied that the complete \(\alpha ^{\prime }\) corrections were able to remove naked singularities of spacetime, and then formed non-singular backgrounds.

In addition, if we consider all \(\alpha ^{\prime }\) corrections as an effective potential, say

$$\begin{aligned} S= & {} \int d^{d+1}x\sqrt{-g}e^{-2\phi }\left[ R+4\left( \partial _{\mu }\phi \right) ^{2}+\frac{\alpha ^{\prime }}{4}R_{\mu \nu \rho \sigma }R^{\mu \nu \rho \sigma }+\cdots \right] \nonumber \\= & {} \int d^{d+1}x\sqrt{-g}e^{-2\phi }\left[ R+4\left( \partial _{\mu }\phi \right) ^{2}-V\left( \phi \right) \right] , \end{aligned}$$
(58)

it is possible to figure out the effective potential \(V\left( \phi \right) \) by comparing actions (58) with (19). The result is

$$\begin{aligned} V\left( y\right) {=}\left( \bar{g}\left( \bar{H}\left( y\right) \right) {+}d\bar{H}\left( y\right) ^{2}\right) {-}\bar{H}\left( \bar{f}\left( \bar{H}\left( y\right) \right) {+}2d\bar{H}\left( y\right) \right) .\nonumber \\ \end{aligned}$$
(59)

For example, the effective potential for solution A (42) can be plotted in Fig. 5.

In the near future, it is worth discussing how to define the junction functions, tensor perturbations and graviton localization in the Hohm–Zwiebach action. Then, it is possible to study the non-perturbative stringy effects in the braneworlds.