nNNPDF3.0: evidence for a modified partonic structure in heavy nuclei

Abstract

We present an updated determination of nuclear parton distributions (nPDFs) from a global NLO QCD analysis of hard processes in fixed-target lepton-nucleus and proton-nucleus together with collider proton-nucleus experiments. In addition to neutral- and charged-current deep-inelastic and Drell–Yan measurements on nuclear targets, we consider the information provided by the production of electroweak gauge bosons, isolated photons, jet pairs, and charmed mesons in proton-lead collisions at the LHC across centre-of-mass energies of 5.02 TeV (Run I) and 8.16 TeV (Run II). For the first time in a global nPDF analysis, the constraints from these various processes are accounted for both in the nuclear PDFs and in the free-proton PDF baseline. The extensive dataset underlying the nNNPDF3.0 determination, combined with its model-independent parametrisation, reveals strong evidence for nuclear-induced modifications of the partonic structure of heavy nuclei, specifically for the small-x shadowing of gluons and sea quarks, as well as the large-x anti-shadowing of gluons. As a representative phenomenological application, we provide predictions for ultra-high-energy neutrino-nucleon cross-sections, relevant for data interpretation at neutrino observatories. Our results provide key input for ongoing and future experimental programs, from that of heavy-ion collisions in controlled collider environments to the study of high-energy astrophysical processes.

1 Introduction

The parton distribution functions (PDFs) of nuclei, known as nuclear PDFs (nPDFs) [1,2,3], are essential to a variety of experimental programs that collide nuclei (or nuclei with protons) at high energies [4]. At the Large Hadron Collider (LHC), nPDFs are required as a theoretical input to the heavy ion program that aims to disentangle cold from hot nuclear matter effects, making the detailed characterisation of the latter possible. Ongoing and upcoming heavy ion runs include high-luminosity proton–lead (pPb) and lead–lead (PbPb) collisions [5], dedicated proton–oxygen (pO) and oxygen–oxygen (OO) runs [6], and a fixed-target mode [7], where energetic proton beams collide with a nuclear gas target filling the detectors. A reliable determination of nPDFs is also critical in various astrophysical processes, for instance to make theoretical predictions of signal [8,9,10,11] and background [12,13,14] events in neutrino–nucleus scattering as measured at high-energy neutrino observatories such as IceCube [15] and KM3NeT [16]. In the longer term, nPDFs will be probed at the Electron Ion Collider (EIC) [17,18,19], by means of GeV-scale lepton scattering on light and heavy nuclei, and further tested at the proposed Forward Physics Facility (FPF) [20], by means of TeV-scale neutrino scattering on heavy nuclear targets.

In addition to their phenomenological role in the modelling of high-energy collisions involving nuclei, nPDFs are also a means towards an improved understanding of Quantum Chromodynamics (QCD) in the low-energy non-perturbative regime. Indeed, a global analysis of nPDFs provides a determination of the behaviour of nuclear modifications which are flavour, atomic mass number A, and x dependent. This information is critical to isolate the source of the different physical mechanisms that are responsible for the modification of nPDFs in comparison to their free-nucleon counterparts, such as (anti-)shadowing, the EMC effect, and Fermi motion. A detailed understanding of these effects is also necessary to provide a robust baseline in the search for more exotic forms of QCD matter, such as the gluon-dominated Color Glass Condensate [21], which is predicted to have an enhanced formation in heavy nuclei.

Knowledge of nPDFs also enters, albeit indirectly, the precise determination of free-proton PDFs. These are typically determined from global analyses that include, among others, measurements of neutrino–nucleus structure functions. These measurements uniquely constrain quark flavour separation at intermediate and large x. Uncertainties due to nPDFs may inflate the overall free-proton PDF uncertainty by up to a factor of two at large x when properly taken into account [22,23,24]. More precise nPDFs can therefore lead to more precise free-proton PDFs.

Taking into account these considerations, and building upon previous studies by some of us [25, 26], here we present an updated determination of nuclear PDFs from an extensive global dataset: nNNPDF3.0. This determination benefits from the inclusion of new data and improvements in the overall fitting methodology. Concerning experimental data, a broad range of measurements from pPb collisions at the LHC are considered. Notably, CMS dijet [27] and LHCb $D^0$-hadron [28] production data is included in both the proton baseline and the nPDF determination, revealing gluon PDF shadowing at small x. We also explicitly remove all deuterium data ($A= 2$) from the proton baseline fit and include it in the nPDF fit. Concerning the methodology, we follow the NNPDF3.1 approach [29] (but with an extended dataset) for the proton baseline fit, while we supplement the nNNPDF2.0 methodology [26] for the nuclear fit with a number of technical improvements in our machine learning framework, in particular with automated hyperparameter optimisation [30].

The combination of these various developments leads to substantially improved nPDFs for all partons in a wide range of x values. In particular, we obtain strong evidence of nuclear shadowing for both the gluon and quarks in the region of small-x and large-A values, as well as of gluon anti-shadowing at large x and large A. As customary, the nNNPDF3.0 parton sets are made publicly available for all phenomenologically relevant values of A via the LHAPDF [31] interface.

The outline of this paper is the following. In Sect. 2 we provide details of the experimental measurements and theoretical computations used as input for the nNNPDF3.0 determination. The updates in fitting methodology are described in Sect. 3. Section 4 presents the main results of this work, namely the nNNPDF3.0 parton sets, their comparison with other determinations (EPPS16 [32] and nCTEQ15WZSIH [33]), and an assessment of the dependence of the extracted nuclear modifications with respect to flavour, A, and x. The stability of the nNNPDF3.0 fit is studied in Sect. 5, where variants based on different kinematic cuts, proton PDF baseline sets, and theoretical settings are presented. As a representative phenomenological application of nNNPDF3.0, in Sect. 6 we provide predictions for the ultra-high-energy neutrino-nucleon cross-section for several A values as relevant for (next-generation) large-volume neutrino detectors. We indicate which nPDF sets are made available via LHAPDF, summarise our findings, provide usage prescriptions for the nNNPDF3.0 sets, and discuss some avenues for possible future investigations in Sect. 7.

Four appendices complete the paper. Appendix A summarises the notation used through the paper; Appendix B clarifies the kinematic transformation required to analyse pPb measurements in different reference frames; Appendix C collects several data/theory comparisons for measurements included and not included in nNNPDF3.0; and Appendix D presents a validation of the reweighting method used to assess the impact of LHCb D-meson measurements.

2 Experimental data and theoretical calculations

In this section we discuss the experimental data and theoretical calculations that form the basis of the nNNPDF3.0 analysis. We present an overview of the nNNPDF3.0 dataset and general theoretical settings, and then focus on the new measurements that are added in comparison to nNNPDF2.0. For each of these, we describe their implementation and the calculation of the corresponding theoretical predictions.

2.1 Dataset overview

The nNNPDF3.0 dataset includes all the measurements that were part of nNNPDF2.0. These are the neutral-current (NC) isoscalar nuclear fixed-target deep-inelastic scattering (DIS) structure function ratios measured, for a range of nuclei, by the NMC [34,35,36,37], EMC [38,39,40,41], SLAC [42], BCDMS [43, 44] and FNAL [45, 46] experiments; the charged-current (CC) neutrino-nucleus DIS cross-sections measured, respectively on Pb and Fe targets, by the CHORUS [47] and NuTeV [48] experiments; and cross-sections, differential in rapidity, for inclusive gauge boson production in pPb collisions measured by the ATLAS [49] and CMS [50,51,52] experiments at the LHC. These datasets are discussed in [26], to which we refer the reader for further details.

In addition, two different groups of new measurements are incorporated into the nNNPDF3.0 dataset. The first group consists of DIS and fixed-target Drell–Yan (DY) measurements that involve deuterium targets, specifically the NMC [53] deuteron to proton DIS structure functions; the SLAC [54] and BCDMS [55] deuteron structure functions; and the E866 [56] fixed-target DY deuteron to proton cross-section ratio. This group also includes the fixed-target DY measurement performed on Cu by the E605 experiment [57]. In nNNPDF2.0 these datasets entered the determination of the free proton PDF used as baseline in the nuclear PDF fit. As will be discussed in Sect. 3, in nNNPDF3.0 we no longer include them in the proton PDF baseline but rather choose to include them directly in the nuclear fit. This approach is conceptually more consistent, as it completely removes any residual nuclear effects from the proton baseline. Information loss on quark flavour separation for proton PDFs due to the removal of these datasets is partially compensated by the availability of additional measurements from proton–proton (pp) collisions [24], specifically concerning new weak gauge boson production data.

The second group of new measurements entering nNNPDF3.0 consists of LHC pPb data. Specifically, we consider forward and backward rapidity fiducial cross-sections for the production of $W^\pm$ bosons measured by ALICE [58] at $\sqrt{s}=5.02$ TeV in the centre-of-mass (CoM) frame; forward and backward rapidity fiducial cross-sections for the production of Z bosons measured by ALICE and LHCb at 5.02 TeV [58, 59] and 8.16 TeV [60]; the differential cross-section for the production of Z bosons measured by CMS at 8.16 TeV [61]; the ratio of pPb to pp differential cross-sections for dijet production measured by CMS at 5.02 TeV [27]; the ratio of pPb to pp differential cross-sections for prompt photon production measured by ATLAS at 8.16 TeV [62]; and the ratio of pPb to pp differential cross-sections for prompt $D^0$ production measured at forward rapidities by LHCb at 5.02 TeV [28]. The impact of the last measurement on nNNPDF3.0 is evaluated by means of Bayesian reweighting [63, 64], while that of all of the others by means of a fit, see Sect. 3. All these measurements are discussed in detail in Sect. 2.3 below.

Table 1 The new measurements included in nNNPDF3.0 with respect to nNNPDF2.0. For each dataset, we indicate the name used throughout the paper, the reference, the number of data points $n_{\mathrm{dat}}$ after/before kinematic cuts, the nuclear species involved, and the codes used to compute the corresponding theoretical predictions. The datasets in the upper (lower) part of the table correspond to the first (second) group described in the text

The main features of the new datasets entering nNNPDF3.0 (in comparison to nNNPDF2.0) are summarised in Table 1. For each process we indicate the name of the datasets used throughout the paper, the corresponding reference, the number of data points after/before kinematic cuts (described below), the nuclear species involved, and the code used to compute theoretical predictions. The upper (lower) part of the table lists the datasets in the first (second) group discussed above.

The kinematic coverage in the $(x,Q^2)$ plane of the complete nNNPDF3.0 dataset is displayed in Fig. 1. For hadronic data, kinematic variables are determined using leading order (LO) kinematics. Whenever an observable is integrated over rapidity, the centre of the rapidity range is used to compute the values of x. Data points are classified by process. Data points that are new in nNNPDF3.0 (in comparison to nNNPDF2.0) are marked with a grey edge.

As customary, kinematic cuts are applied to the DIS structure function measurements to remove data points that may be affected by large non-perturbative or higher-twist corrections, namely we require $Q^2\ge 3.5$ $\hbox {GeV}^2$ for the virtuality and $W^2\ge 12.5$ $\hbox {GeV}^2$ for the final-state invariant mass. Cuts are also applied to the FNAL E605 measurement to remove data points close to the production threshold that may be affected by large perturbative corrections. Namely we require $\tau \le 0.08$ and $|y/y_{\mathrm{max}}|\le 0.663$, where $\tau =m^2/s$ and $y_{\mathrm{max}}=-\frac{1}{2}\ln \tau$, with m and y the dilepton invariant mass and rapidity and $\sqrt{s}$ the CoM energy of the collision. These cuts were determined in [65] and are also adopted in NNPDF4.0 [24]. Data points excluded by kinematic cuts are displayed in grey in Fig. 1.

The total number of data points considered after applying these kinematic cuts is $n_{\mathrm{dat}}=2188$; in comparison, the nNNPDF2.0 analysis contained $n_{\mathrm{dat}}=1467$ points. Of the new data points, 210 correspond to LHC measurements and the remaining to fixed-target data. The kinematic coverage of the nNNPDF3.0 dataset is significantly expanded in comparison to nNNPDF2.0, in particular at small x, where the LHCb $D^0$-meson data covers values down to $x\simeq 10^{-5}$, and at high-Q, where the ATLAS photon and CMS dijet data reaches values close to $Q\simeq 500$ GeV.

Fig. 1

The kinematic coverage in the $(x,Q^2)$ plane of the nNNPDF3.0 dataset. The evaluation of x and $Q^2$ for the hadronic processes assumes LO kinematics. Data points are classified by process. Data points new in nNNPDF3.0 in comparison to nNNPDF2.0 are marked with a grey edge. Data points excluded by kinematic cuts are filled grey

2.2 General theory settings

The settings of the theoretical calculations adopted to describe the nNNPDF3.0 dataset follow those of the previous nNNPDF2.0 analysis [26].

Theoretical predictions are computed to next-to-leading order (NLO) accuracy in the strong coupling $\alpha _s(Q)$. The strong coupling and (nuclear) PDFs are defined in the $\bar{\mathrm{MS}}$scheme, whereas heavy-flavour quarks are defined in the on-shell scheme. The FONLL general-mass variable flavour number scheme [66] with $n_{f}^{\mathrm{max}} = 5$ (where $n_{f}^{\mathrm{max}}$ is the maximum number of active flavours) is used to evaluate DIS structure functions. Instead, for proton–nucleus collisions the zero-mass variable flavour number scheme is applied; the only exception being prompt D-meson production which is discussed in Sect. 2.3.4. The charm- and bottom-quark PDFs are evaluated perturbatively by applying massive quark matching conditions. In the fit, the following input values are used: $m_c=1.51$ GeV, $m_b=4.92$ GeV, and $\alpha _s(M_Z)=0.118$, respectively for the charm and bottom quark masses, and for the strong coupling at a scale equal to the Z-boson mass $M_Z$.

Predictions are made at LO in the electromagnetic coupling, with the following input values for the on-shell gauge boson masses (widths): $M_W=80.398$ GeV ($\Gamma _W=2.141$ GeV) and $M_Z=91.1876$ GeV ($\Gamma _Z=2.4952$ GeV). The $G_\mu$ scheme is used, with a value of the Fermi constant $G_F=1.1663787\ 10^{-5}$ $\hbox {GeV}^{-2}$.

The fitting procedure relies on the pre-computation of fast-interpolation grids for both lepton–nucleus and proton–nucleus collisions. The FK table format, provided by APFELgrid [67], is used for all fitted data. The format combines PDF and $\alpha _s$ evolution factors, computed with APFEL [68], with interpolated weight tables, whose generation is process specific. For each of the new LHC datasets included in nNNPDF3.0, this is detailed in the following. For the datasets already part of nNNPDF2.0, the set-up was detailed in [26].

2.3 New LHC measurements and corresponding theory settings

The new LHC measurements included in nNNPDF3.0 are discussed in the following: inclusive electroweak boson, prompt photon, dijet, and prompt $D^0$-meson production. For inclusive electroweak boson production we consider data for differential distributions obtained in pPb collisions. For all other processes, differential distributions measured in pPb collisions are always normalised to the corresponding distributions in pp collisions, measured at the same CoM energy. These ratios take the schematic form

$$\begin{aligned} \frac{\mathrm{d} R_{\mathrm{pPb}}}{\mathrm{d}X} = \frac{ \mathrm{d}\sigma ^{\mathrm{pPb}} }{\mathrm{d}X} \Bigg / \frac{ \mathrm{d}\sigma ^{\mathrm{pp}}}{\mathrm{d}X}, \end{aligned}$$

(2.1)

where X represents an arbitrary differential variable. The same form applies to more (e.g. double) differential quantities. The general rationale for applying this approach is that the LO predictions for prompt photon, dijet, and prompt D-meson production are ${\mathcal {O}}(\alpha _s)$. As a consequence, the theoretical predictions for the absolute rates of these processes (at NLO QCD accuracy) are subject to uncertainties due to missing higher order effects which are typically in excess of the uncertainty related to nPDFs. At the level of the ratio, uncertainties related to the overall normalisation of the distributions (e.g. the value of the coupling) cancel, while sensitivity to the nuclear modification of nPDFs is retained. In Sect. 4 it will be shown for prompt D-meson production (which has the largest relative theory uncertainties of the considered processes) that such observables ensure that nPDF uncertainties dominate over those due to scale uncertainties. Notably, a shortcoming of this approach is that it becomes necessary to exclude the reference pp data from the proton baseline which enters the nPDF fit. The extension of the perturbative accuracy of the fit to NNLO QCD and/or including theoretical uncertainties (as in [69, 70]) would allow one to consider absolute distributions instead of ratios for these selected processes. As a note, these ratios are constructed in the pp CoM frame. For collisions such as pPb, they do not coincide with ratios constructed in the laboratory frame. The role of this asymmetry for the interpretation of pPb observables is reviewed in Appendix B.

2.3.1 Inclusive electroweak boson production

The new datasets that we consider in this category are the following. First we include the ALICE measurements of the fiducial cross-section for W- and Z-boson production at $\sqrt{s}=5.02$ TeV in the muonic decay channel [58]. The data points cover the backward (Pb–going) and forward (p–going) rapidity regions. The integrated luminosity is 5.81 and 5.03 $\hbox {nb}^{-1}$ in each case. Then we also include the related LHCb [60] and ALICE [59] measurements of the fiducial cross-section for Z-boson production at $\sqrt{s}=5.02$ TeV and $\sqrt{s}=8.16$ TeV, respectively. Backward and forward rapidity measurements are considered in both cases. The integrated luminosities are, for ALICE, 8.40 and 12.7 $\hbox {nb}^{-1}$ in the Pb–going and in the p–going directions; and for LHCb, 1.6 $\hbox {nb}^{-1}$. Finally we include the CMS measurement of Z-boson production in the dimuon decay channel at $\sqrt{s}=8.16$ TeV [61]. In this latter case, differential cross-sections are presented with respect to the rapidity and the invariant mass of the dimuon system, after being corrected for acceptance effects. The integrated luminosity is 173 $\hbox {nb}^{-1}$.

As was already the case for nNNPDF2.0, theoretical predictions for electroweak gauge boson production are computed at NLO QCD accuracy with MCFM v6.8 [71,72,73]. The renormalisation and factorisation scales are set equal to the mass of the gauge boson, for total cross-sections, and to the central value of the corresponding invariant mass bin, in the case of the CMS differential cross-sections [61]. Note that the choice of the scale is partly restricted by the grid generation procedure – i.e. a fully dynamical event-by-event scale choice such as the invariant mass of the muon pair is not accessible. Experimental correlations are taken into account whenever available, namely for the measurements of [58, 59, 61], otherwise statistical and systematic uncertainties are added in quadrature.

2.3.2 Prompt photon production

In this category nNNPDF3.0 includes the ATLAS measurement at $\sqrt{s}=8.16$ TeV [62]. Cross-sections for isolated prompt photon production are presented in three pseudo-rapidity $\eta _{\gamma }$ bins and then differentially in the photon transverse energy $E_T^\gamma$. As discussed above, we only consider the ratio of the differential pPb cross-section normalised with respect to the reference pp results in the fit. Notably, for prompt photon production this means that uncertainties due to the treatment of photon fragmentation and the choice of the value of the electromagnetic coupling are not important. For completeness, in Sect. 4 we also indicate how the fit quality is deteriorated when the absolute cross-section is considered (without accounting for theory uncertainties). The ranges of the three photon pseudo-rapidity bins in the CoM frame are $-2.83<\eta _{\gamma }<-2.02$, $-1.84<\eta _{\gamma }<0.91$ and $1.09<\eta _{\gamma }<1.90$; the kinematic coverage in the photon transverse energy is, for each of these, $20<E_T^\gamma <550$ GeV. The integrated luminosity of this measurement is 165 $\hbox {nb}^{-1}$.

Theoretical predictions are computed at NLO QCD accuracy with MCFM (v6.8) following the calculational settings presented in [74]. The renormalisation and factorisation scales are set equal to the central value of the photon transverse energy $E_T^\gamma$ for each bin. Experimental correlations between transverse momentum and rapidity bins are taken into account following the prescription provided in [62].

2.3.3 Dijet production

In this category we consider the CMS measurement at $\sqrt{s}=5.02$ TeV [27]. The cross-section is presented double differentially in the dijet average transverse momentum $p_{T,\mathrm{dijet}}^{\mathrm{ave}}$, where $p_{T,\mathrm{dijet}}^{\mathrm{ave}} = \left( p_{T,1} + p_{T,2}\right) /2$, and the dijet pseudo-rapidity $\eta _{\mathrm{dijet}}$. As in the case of prompt photon production, we consider only data for the ratio of cross-sections obtained in pPb with respect to that from pp collisions. Again, for completeness, in Sect. 4 we also show how the fit quality deteriorates (without accounting for theory uncertainties) when the absolute cross-section is considered. The kinematic coverage in pseudo-rapidity and average transverse momentum is, in the CoM frame, $-2.456<\eta <2.535$ and $55~\mathrm{GeV}<p_{\mathrm{T,dijet}}^{\mathrm{avg}}<400$ GeV. The integrated luminosity is 35 (27) $\hbox {nb}^{-1}$ for the Pb–going (p–going) direction.

Theoretical predictions are computed at NLO QCD accuracy with NLOjet++ [75]. We have verified that the independent computation of [76] is reproduced. The renormalisation and factorisation scales are set equal to the dijet invariant mass $m_{jj}$, as in the dedicated pp study of [77]. Since experimental correlations for the pPb to pp cross-section ratio are not provided, statistical and systematic uncertainties are added in quadrature.

2.3.4 Prompt D-meson production

In this category we consider the LHCb measurements of prompt $D^0$-meson production in pPb collisions at $\sqrt{s}=5.02$ TeV [28]. The data is available both in the forward and backwards configurations, and is presented as absolute cross-sections differential in the transverse momentum $p^{D^0}_{\mathrm{T}}$ and rapidity $y^{D^0}$ of the $D^0$-mesons, namely

$$\begin{aligned} \frac{d^2\sigma ^{\mathrm{pPb}}}{dy^{D^0} dp^{D^0}_{\mathrm{T}}} \quad \mathrm{and} \quad \frac{d^2\sigma ^{\mathrm{Pbp}}}{dy^{D^0} dp^{D^0}_{\mathrm{T}}}. \end{aligned}$$

(2.2)

Following the discussion around Eq. (2.1), we only consider data for cross-section ratios (which are obtained with respect to reference pp data [78]). The double differential ratio for forward pPb measurements is

$$\begin{aligned} R_{\mathrm{pPb}}(y^{D^0}, p^{D^0}_{\mathrm{T}}) = \left. \frac{d\sigma ^{\mathrm{pPb}}(y^{D^0},p^{D^0}_{\mathrm{T}})}{dy^{D^0} dp^{D^0}_{\mathrm{T}}} \Bigg / \frac{d\sigma ^{\mathrm{pp}}(y^{D^0},p^{D^0}_{\mathrm{T}})}{dy^{D^0} dp^{D^0}_T}\right. , \end{aligned}$$

(2.3)

where both pPb and pp cross-sections are given in the pp CoM frame (and $y^{D^0}$ is the $D^0$-meson rapidity in that frame). The corresponding observable can be constructed for backwards Pbp collisions, which is denoted as $R_{\mathrm{Pbp}}$.

An additional ratio $R_{\mathrm{fb}}$ constructed from forward over backward cross-sections (defined in the pp CoM frame) can also be considered:

$$\begin{aligned}&R_{\mathrm{fb}}(y^{D^0}, p^{D^0}_{\mathrm{T}})\nonumber \\&= \frac{d^2\sigma ^{\mathrm{pPb}}(y^{D^0},p^{D^0}_{\mathrm{T}})}{dy^{D^0} dp^{D^0}_{\mathrm{T}}} \Bigg / \frac{d^2\sigma ^{\mathrm{Pbp}}(-|y^{D^0}|,p^{D^0}_{\mathrm{T}})}{dy^{D^0} dp^{D^0}_{\mathrm{T}}}. \end{aligned}$$

(2.4)

This ratio benefits from a cancellation of a number of experimental systematics, and, as motivated in [79], provides sensitivity to nuclear modifications while the theoretical uncertainty from all other sources is reduced to a sub-leading level.

The LHCb measurements cover the rapidity range of $2.0< y^{D^0} < 4.5$ for pp collisions, and the effective range of $1.5< y^{D^0} < 4.0$ in the forward pPb collisions. The data on the $R_{\mathrm{pPb}}$ ratio Eq. (2.3) is presented in four rapidity bins in the region $2.0< y^{D^0} < 4.0$, such that the coverage of the forward pPb and the baseline pp measurements overlap. For each of these bins in $y^{D^0}$, the coverage in the $D^0$-meson transverse momentum is $0< p^{D^0}_{\mathrm{T}} < 10$ GeV, adding up to a total of 37 data points. In contrast to pp measurements, for which different D meson species are detected, in the pPb case only $D^0$ mesons are reconstructed. Because bin-by-bin correlations for systematic uncertainties are not available for $R_{\mathrm{pPb}}$, we consider them as fully uncorrelated and add them in quadrature with the statistical uncertainties.

Theoretical predictions for D-meson production in hadron-hadron collisions are computed at NLO QCD accuracy in a fixed-flavour number scheme with POWHEG [80,81,82] matched to Pythia8 [83]. The Monash 2013 Tune [84] is used throughout. Our computational set-up has been compared with that used in the calculations of charm production in pp collisions from [85], finding good agreement. Furthermore, theoretical predictions for $R_{\mathrm{pPb}}$ and $R_{\mathrm{Pbp}}$ have been benchmarked against the corresponding calculations used in the EPPS analysis [86] (where the same set-up was considered). It is relevant to mention that a comparison of how different theoretical approaches to describing $D^0$-meson production in pPb collisions impacts the extraction of nPDFs has been considered in [86]. This study demonstrated that (see Fig. 15 of [86]), for suitably defined observables such as $R_{\mathrm{fb}}(y^{D^0}, p^{D^0}_{\mathrm{T}})$, consistent results are obtained between our chosen set-up (POWHEG+Pythia8) and those in a general-mass variable flavour number scheme [87].

The above discussion summarises how the various nuclear cross-section ratios for $D^0$-meson production are accounted for. However, it is also necessary to constrain the overall normalisation of the nPDFs, and not just the size of the nuclear correction – i.e. the normalisation of the free nucleon PDFs must also be known. To achieve this, we include the constraints from D-meson production in pp collisions at 7 TeV [88] and 13 TeV [89] into the proton PDF baseline which is used as a boundary condition for nNNPDF3.0. This is done following the analysis of [85], which considers LHCb D-meson data at the level of normalised differential cross-sections according to

$$\begin{aligned} N^{AA'}_X(y^D ,p^D_{\mathrm{T}}) \equiv \left. \frac{d\sigma ^{\mathrm{AA'}}\left( X\,\,\mathrm TeV\right) }{dy^D dp^D_{\mathrm{T}}} \Bigg / \frac{d\sigma ^{\mathrm{AA'}}\left( X\,\,\mathrm TeV\right) }{dy_{\mathrm{ref}}^D dp^D_T}\right. , \end{aligned}$$

(2.5)

in terms of a reference rapidity bin $y_{\mathrm{ref}}^D$. The main advantage of normalised observables such as Eq. (2.5) is that scale uncertainties cancel to good approximation (since these depend mildly on rapidity) while some sensitivity to the PDFs is retained (as the rate of the change of the PDFs in x is correlated with $y^D$). This has been motivated in [90] and subsequently in [12, 85]. As in [85] we consider pp measurements for the $\{D^0, D^+, D_s^+\}$ final states, adding up to a total of 79 and 126 data points for $N^{\mathrm{pp}}_7$ and $N^{\mathrm{pp}}_{13}$ respectively. To avoid double counting, the available data on $N^{\mathrm{pp}}_5$ is not included in the proton baseline, given that it will enter the nuclear PDF analysis through Eq. (2.3).

Finally, we note that in contrast to all other considered scattering processes in this work, there is currently no public interface for the computation of fast interpolation tables for prompt D-meson production in pp or pPb collisions. This complicates the inclusion of this data in the nNNPDF3.0 global analyses, which is realised by a multi-stage Bayesian reweighting procedure as detailed in Sect. 3.4 and summarised in Fig. 4.

3 Analysis methodology

In this section we describe the fitting methodology that is adopted in nNNPDF3.0. We start with an overview of the methodological aspects shared with nNNPDF2.0. We then discuss the improvements in the free-proton baseline PDF used as the $A=1$ boundary condition for the nuclear fit, and compare this baseline to the one used in nNNPDF2.0. We proceed by describing hyperoptimisation, the procedure adopted to automatically select the optimal set of model hyperparameters such as the neural network architecture and the minimiser learning rates. Finally we outline the strategy, based on Bayesian reweighting, used in order to include the LHCb measurements of D-meson production in a consistent manner both in the free-proton baseline PDFs and in the nPDFs.

3.1 Methodology overview

The fitting methodology adopted in nNNPDF3.0 closely follows the one used in nNNPDF2.0. Here we summarise the methodological aspects common to the two determinations. Additional methodological improvements will be discussed in Sects. 3.2 and 3.3.

3.1.1 Parametrisation

As in nNNPDF2.0, we parametrise six independent nPDF combinations in the evolution basis. These are:

$$\begin{aligned} x\Sigma ^{(p/A)}(x,Q_0)= & {} x^{\alpha _\Sigma } (1-x)^{\beta _\Sigma } \mathrm{NN}_\Sigma (x,A) , \nonumber \\ xT_3^{(p/A)}(x,Q_0)= & {} x^{\alpha _{T_3}} (1-x)^{\beta _{T_3}} \mathrm{NN}_{T_3}(x,A) , \nonumber \\ xT_8^{(p/A)}(x,Q_0)= & {} x^{\alpha _{T_8}} (1-x)^{\beta _{T_8}} \mathrm{NN}_{T_8}(x,A) , \nonumber \\ xV^{(p/A)}(x,Q_0)= & {} B_{V}x^{\alpha _V} (1-x)^{\beta _V} \mathrm{NN}_V(x,A) , \nonumber \\ xV_3^{(p/A)}(x,Q_0)= & {} B_{V_3}x^{\alpha _{V_3}} (1-x)^{\beta _{V_3}} \mathrm{NN}_{V_3}(x,A) \nonumber , \\ xg^{(p/A)}(x,Q_0)= & {} B_gx^{\alpha _g} (1-x)^{\beta _g} \mathrm{NN}_g(x,A) , \end{aligned}$$

(3.1)

where $f^{(p/A)}(x,Q_0)$, with $f=\Sigma ,T_3,T_8,V,V_3,g$, denotes the nPDF of a proton bound in a nucleus with atomic mass number A, see Appendix A for the conventions adopted. The parametrisation scale is $Q_0=1$ GeV, as in the free-proton baseline PDF set. The normalisation coefficients $B_V$, $B_{V_3}$ and $B_g$ enforce the momentum and valence sum rules, while the preprocessing exponents $\alpha _f$ and $\beta _f$ are required to control the small- and large-x behaviour of the nPDFs, see Sect. 3.1.2. In Eq. (3.1), $\mathrm{NN}_f(x,A)$ represents the value of the neuron in the output layer of the neural network associated to each independent nPDF. The input layer contains three neurons that take as input the values of the momentum fraction x, $\ln (1/x)$, and the atomic mass number A, respectively. The rest of the neural network architecture is determined through the hyperoptimisation procedure described in Sect 3.3. This is in contrast to nNNPDF2.0, where the optimal number of hidden layers and neurons were determined by trial and error. The corresponding distributions for bound neutrons are obtained from those of bound protons assuming isospin symmetry. Under the isospin transformation, all quark and gluon combinations in Eq. (3.1) are left invariant, except for:

$$\begin{aligned} xT_3^{(p/A)}(x,Q_0)= & {} -xT_3^{(n/A)}(x,Q_0) ,\quad \nonumber \\ xV_3^{(p/A)}(x,Q_0)= & {} -xV_3^{(n/A)}(x,Q_0) . \end{aligned}$$

(3.2)

While the nNNPDF3.0 fits presented in this work are carried out in the basis specified by Eq. (3.1), any other basis obtained as a linear combination of Eq. (3.1) could be used. In principle, the choice of any basis should lead to comparable nPDFs, within statistical fluctuations, as demonstrated explicitly in the proton case [24]. In the following, we will display the nNNPDF3.0 results in the flavour basis, given by

$$\begin{aligned} \left\{ xu^{(p/A)},\ xd^{(p/A)},\ x{\bar{u}}^{(p/A)},\ x{\bar{d}}^{(p/A)},\ xs^{+(p/A)},\ xg^{(p/A)}\right\} ,\nonumber \\ \end{aligned}$$

(3.3)

see Sect. 3.1 of [24] for the explicit relationship with the evolution basis of Eq. (3.1).

3.1.2 Sum rules and preprocessing

Momentum and valence sum rules are enforced by requiring that the normalisation coefficients $B_g$, $B_V$, and $B_{V_3}$ in Eq. (3.1) take the values:

$$\begin{aligned} B_g(A)&= \left( 1 - \int _0^1 dx\, x\Sigma ^{(p/A)}(x,Q_0)\right) \Big /\nonumber \\&\qquad \quad \left( \int _0^1 dx\, xg^{(p/A)}(x,Q_0)\right) ,\nonumber \\ B_V(A)&= 3\Big /\left( \int _0^1 dx\, V^{(p/A)}(x,Q_0)\right) ,\nonumber \\ B_{V_3}(A)&= 1\Big /\left( \int _0^1 dx\, V_3^{(p/A)}(x,Q_0)\right) . \end{aligned}$$

(3.4)

These coefficients must be determined for each value of A; perturbative evolution ensures that, once enforced at the initial parametrisation scale $Q_0$, momentum and valence sum rules are not violated for any $Q > Q_0$.

The preprocessing exponents $\alpha _f$ and $\beta _f$ in Eq. (3.1) facilitate the training process and are fitted simultaneously with the network parameters. The exponents $\alpha _V$ and $\alpha _{V_3}$ are restricted to lie in the range [0, 5] during the fit to ensure integrability of the valence distributions. The other $\alpha _f$ exponents are restricted to the range $[-1,5]$, consistently with the momentum sum rule requirements, while the exponents $\beta _f$ lie in the range [1, 10]. While we do not explicitly impose integrability of $xT_3$ and $xT_8$, consistently with the NNPDF3.1-like proton baseline, the fitted nPDFs turn out to satisfy these integrability constraints anyway. It is worth pointing out that a strategy to avoid preprocessing within the NNPDF methodology has been recently presented in [91]. This strategy, which leads to consistent results in the case of free-proton PDFs, may be applied to nPDFs in the future.

3.1.3 The figure of merit

The best-fit values of the parameters defining the nPDF parametrisation in Eq. (3.1) are determined by minimising a suitable figure of merit. As in nNNPDF2.0, this figure of merit is an extended version of the $\chi ^2$, defined as

$$\begin{aligned} \chi _{\mathrm{fit}}^2 = \chi _{\mathrm{t_0}}^2 + \kappa _{\mathrm{pos}}^2 + \kappa _{\mathrm{BC}}^2 . \end{aligned}$$

(3.5)

The first term, $\chi _{t_0}^2$, is the contribution from experimental data

$$\begin{aligned} \chi _{t_0}^2 = \sum _{ij}^{n_{\mathrm{dat}}} (T_i - D_i)\,\,(\text {cov}_{t_0})_{ij}^{-1}\,\,(T_j - D_j). \end{aligned}$$

(3.6)

This is derived by maximising the likelihood of observing the data $D_i$ given a set of theory predictions $T_i$. The covariance matrix is constructed according to the $t_0$ prescription [92], see Eq. (9) in [93].¹

The second term, $\kappa _{\mathrm{pos}}^2$, ensures the positivity of physical cross-sections and is defined as

$$\begin{aligned} \kappa _{\mathrm{pos}}^2 = \lambda _{\mathrm{pos}} \sum _{l=1}^{n_{\mathrm{pos}}}\sum _{j=1}^{n_A} \sum _{i_l=1}^{n_{\mathrm{dat}}^{(l)}} \mathrm{max}\left( 0, -{\mathcal {F}}_{i_l}^{(l)}(A_j) \right) , \end{aligned}$$

(3.7)

where l runs over the $n_{\mathrm{pos}}$ positivity observables ${\mathcal {F}}^{(l)}$ (defined in Table 3.1 of [26]) and each of the observables contain $n_{\mathrm{dat}}^{(l)}$ kinematic points that are computed over all $n_A$ nuclei for which there are experimental data in the fit. The Lagrange multiplier is fixed by trial and error to $\lambda _{\mathrm{pos}} = 1000$.

The third term, $\kappa _{\mathrm{BC}}^2$, ensures that, when taking the $A \rightarrow 1$ limit, the nNNPDF3.0 predictions reduce to those of a fixed free-proton baseline in terms of both central values and uncertainties. The choice of this baseline set differs from nNNPDF2.0 and is further discussed in Sect. 3.2. The $\kappa _{\mathrm{BC}}^2$ term is defined as

$$\begin{aligned} \kappa _{\mathrm{BC}}^2 = \lambda _{\mathrm{BC}} \sum _{f}\sum _{j=1}^{n_x} \left( f^{(p/A)}(x_j,Q_0,A=1) - f^{(p)}(x_j,Q_0) \right) ^2 ,\nonumber \\ \end{aligned}$$

(3.8)

where f runs over the six independent nPDFs in the evolution basis, and j runs over $n_x$ points in x as discussed in Sect. 3.2. The value of the Lagrange multiplier is fixed to $\lambda _{\mathrm{BC}}=100$. In Eq. (3.8), for each replica in the nNNPDF3.0 ensemble, we use a different random replica from the free-proton baseline set. This way the free-proton PDF uncertainty is propagated into the nPDF fit via the $A=1$ boundary condition.

In summary, in the present analysis the best-fit nPDFs are determined by maximising the agreement between the theory predictions and the corresponding Monte Carlo replica of the experimental data, subject to the physical constraints of cross-section positivity and the $A=1$ boundary condition, together with methodological requirements such as cross-validation to prevent overlearning.

3.2 The free-proton boundary condition

The neural network parametrisation of the nPDFs described by Eq. (3.1) is valid from $A=1$ (free proton) up to $A=208$ (lead). This implies that the nNNPDF3.0 determination also contains a determination of the free-proton PDFs (as $A\rightarrow 1$). However, as discussed above, the PDFs in this $A=1$ limit are fixed by means of the Lagrange multiplier defined in Eq. (3.8). The central values and uncertainties of nNNPDF3.0 for $A=1$ hence reproduce those of some external free-proton baseline PDFs, which effectively act as a boundary condition to the nPDFs. This is a unique feature of the nNNPDF methodology. We note that moderate deviations from this boundary condition may appear as a consequence of the positivity constraints enforced through Eq. (3.7). Distortions may also arise when nPDFs replicas are reweighted with new data, as we will discuss in Sect. 3.4.

In nNNPDF3.0, the free-proton baseline PDFs are chosen to be a variant of the NNPDF3.1 NLO parton set [29] where the charm-quark PDF is evaluated perturbatively by applying massive quark matching conditions. This baseline differs from that used in nNNPDF2.0 in the following respects.

• The free-proton baseline PDFs include all the datasets incorporated in the more recent NNPDF4.0 NLO analysis [24], except those involving nuclear targets (these are instead part of nNNPDF3.0), see in particular Tables 2.1–2.5 and Appendix B in [24]. The extended NNPDF4.0 dataset provides improved constraints on the free-proton baseline PDFs in a wide range of x for all quarks and the gluon. Note that, while our free-proton baseline PDFs are close to NNPDF4.0 insofar as the dataset is concerned, they are however based on the NNPDF3.1 fitting methodology. The reason being that the NNPDF4.0 methodology incorporates several modifications (see Sect. 3 in [24] for a discussion) that are not part of the nNNPDF3.0 methodology. Among these, a strict requirement of PDF positivity. Those modifications do not alter the compatibility between PDF determinations obtained with the NNPDF3.1 or NNPDF4.0 methodologies, however they lead to generally smaller uncertainties in the latter case, see Sect. 8 in [24]. One could therefore expect a reduction of nPDF uncertainties for low-A nuclei, and results consistent with those presented in the following, if the proton-only fit determined with the NNPDF4.0 methodology was used as a boundary condition.

• When implementing the free-proton boundary condition via Eq. (3.8), in nNNPDF3.0 we use a grid with $n_x=100$ points, half of which are distributed logarithmically between $x_{\mathrm{min}}=10^{-6}$ and $x_{\mathrm{mid}}=0.1$ and the remaining half are linearly distributed between $x_{\mathrm{mid}}=0.1$ and $x_{\mathrm{max}}=0.7$. This is different from nNNPDF2.0, where the grid had 60 points, 10 of which were logarithmically spaced between $x_{\mathrm{min}}=10^{-3}$ and $x_{\mathrm{mid}}=0.1$ and the remaining 50 were linearly spaced between $x_{\mathrm{mid}}=0.1$ and $x_{\mathrm{max}}=0.7$. This extension in the x range is necessary to account for the kinematic coverage of the LHCb D-meson production measurements in pp and pPb collisions, see also Fig. 1.

Furthermore, we produce two variants of these free-proton baseline PDFs, respectively with and without the LHCb D-meson production data in pp collisions at 7 and 13 TeV, see Sect. 2.3.4. The two variants are used consistently with variants of the nPDF fit in which LHCb $D^0$-meson production data in pPb collisions are included or not. These two variants are compared (and normalised) to the free-proton baseline PDFs used in nNNPDF2.0 in Fig. 2. We show the PDFs at $Q=10$ GeV in the same extended range of x for which the boundary condition Eq. (3.8) is enforced, that is between $x=10^{-6}$ and $x=0.7$.

Fig. 2

Comparison between the free-proton baseline PDFs used in nNNPDF2.0 and in nNNPDF3.0, without and with the LHCb D-meson data. These PDFs are used to enforce the $A=1$ boundary condition in the corresponding nPDF fits by means of Eq. (3.8). Results are normalised to the nNNPDF2.0 free-proton baseline PDFs and are shown at $Q=10$ GeV in the extended range of x for which the boundary condition is enforced

Differences between the three free–proton baseline PDFs displayed in Fig. 2 arise from differences in the fitted dataset: the nNNPDF3.0 baselines do not include nuclear data that were instead part of the nNNPDF2.0 baseline; and conversely the nNNPDF3.0 baselines benefit from the extended NNPDF4.0 dataset, which was not part of the nNNPDF2.0 baseline. The effect of these differences are: an increase of the up and down quark and anti-quark central values in the region ; a slight increase of the PDF uncertainties in the same region, in particular for the down quark and antiquark PDFs and for the total strangeness; and a suppression of the gluon central value for followed by an enhancement at larger values of x, accompanied by an uncertainty reduction in the same region.

The datasets responsible for each of the effects observed in the nNNPDF3.0 baseline PDFs have been identified in the NNPDF4.0 analysis [24] and in related studies [22, 23, 77, 94]. The enhancement of the central values of the up quark and antiquark PDFs in the region is a consequence of the new measurements of inclusive and associated DY production from ATLAS, CMS, and LHCb. The increase of uncertainties for the down quark and antiquark PDFs and for the total strangeness are due to the removal of the deuteron DIS and DY cross-sections. This piece of information is however not lost since it is subsequently included in the nuclear fit. The variation of the central value and the reduction of the uncertainty of the gluon PDF are a consequence of the new ATLAS and CMS dijet cross-sections at 7 TeV.

On the other hand, a comparison between the two nNNPDF3.0 free-proton baseline PDFs, with and without the pp 7 and 13 TeV LHCb D-meson production data, reveals that central values remain mostly unchanged. This fact indicates that the data is described reasonably well even if this is not included in the fit. Uncertainties are unaffected for , while they are reduced at smaller values of x, in particular for the sea quark and gluon PDFs.

It should be finally noted that several datasets and processes constrain both the free-proton baseline PDFs and the nPDFs to a similar degree of precision. There is therefore some interplay between the two. The free-proton baseline PDFs will directly constrain the low-A nPDFs, and indirectly the nPDFs corresponding to higher values of A.

Fig. 3

Graphical representation of a hyperparameter scan for representative hyperparameters produced with 1000 trial searches using the TPE algorithm. The values of the hyperparameter are represented on the x-axis while the hyperopt loss function is in the y-axis. In addition to the outcome of individual trials we display a reconstruction of the probability distribution by means of the KDE method. The red dots indicate the values of the hyperparameters used in the nNNPDF2.0 analysis

3.3 Hyperparameter optimisation

A common challenge in training neural-network based models is the choice of the hyperparameters of the model itself. These include, for instance, the architecture and activation functions of the neural network, the optimisation algorithm and learning rates. The choice of hyperparameters affect the performance of the model and of its training. Hyperparameters can be tuned by trial and error, however this is computationally inefficient and may leave unexplored relevant regions of the hyperparameter space. A heuristic approach designed to address this problem more effectively is hyperparameter scan, or hyperparameter optimisation (or hyperoptimisation in short). It consists in finding the best combination of hyperparameters through an iterative search of the hyperparameter space following a specific optimisation algorithm. In the context of NNPDF fits, this approach has been proposed in [30] and has been used in recent free-proton PDF fits [24].

Hyperoptimisation is realised as follows. First a figure of merit (also known as loss function) to minimise and a search domain in the hyperparameter space are defined. Here we define the loss function as the average of the training and validation $\chi ^2$,

$$\begin{aligned} L_{\mathrm{hyperopt}} = \frac{1}{2}\left( \chi ^2_{\mathrm{tr}} + \chi ^2_{\mathrm{val}}\right) , \end{aligned}$$

(3.9)

see [24] for alternative choices. We carry out the hyperparameter scan for various subsets of Monte Carlo data replicas and check that the results converge to a unique combination of hyperparameters. During the initialisation process, the loss function is evaluated for a few random sets of hyperparameters. Based on the results from these searches, the optimisation algorithm constructs models in which the hyperparameters that reduce the loss function are selected. The models are then updated during the trials based on historical observations and subsequently define new sets of hyperparameters to test. In this analysis, we implement the tree-structured Parzen Estimator (TPE), also known as Kernel Density Estimator (KDE) [95, 96], as optimisation algorithm for hyperparameter tuning. The TPE selects the most promising sets of hyperparameters to evaluate the loss function by constructing a probabilistic model based on previous trials, and has been proven to outperform significantly any random or grid searches.

Figure 3 is a graphical representation of a hyperparameter scan obtained with 1000 trial searches using the TPE algorithm. We show the results for the architecture, weight initialisation method, activation function, and learning rates of the optimiser. The values of the hyperparameters are represented on the x-axis while the loss function, Eq. (3.9), is reported on the y-axis. In addition to the outcome of individual trials, we also display a reconstruction of the probability distribution by means of the KDE method. The red dots indicate the values of the best hyperparameters used in nNNPDF2.0, which were determined by means of a trial and error selection procedure.

Parameters that exhibit denser tails in the KDE distributions of Fig. 3 are considered better choices as they yield more stable trainings. For instance, one observes that a network with one single hidden layer and 25 nodes significantly outperforms a network with two hidden layers. Indeed, not only the chosen architecture leads to the smallest value of the loss function but also to a more stable behaviour. Similar patterns are observed for the activation function and learning rate. On the other hand, no clear preference is seen for the initialisation of the weights. Despite the fact that the Glorot Uniform initialisation leads to the smallest value of the objective function, the Glorot Normal one appears to yield slightly better stability with more gray points concentrated at the tail and hence a fatter distribution.

Table 2 The neural-network hyperparameters used in nNNPDF3.0, determined by means of the automated hyperoptimisation algorithm, compared with its counterparts determined from trial and error selection in nNNPDF2.0

Following this hyperparameter optimisation process, we have determined the baseline hyperparameters to be used in the nNNPDF3.0 analysis. We list them in Table 2. For reference, we also show the hyperparameters that were chosen in nNNPDF2.0 by means of a trial and error selection procedure. Remarkably, the automatically-selected optimal hyperparameters in nNNPDF3.0 coincide in many case with those selected by trial and error in nNNPDF2.0, in particular for the neural network architecture, the initialisation of the weight, and the optimiser. In terms of the initialisation of the weights, the Glorot Normal and Glorot Uniform strategies exhibit similar training behaviours. The main differences between the hyperparameters of the nNNPDF2.0 and nNNPDF3.0 methodologies hence lie in the activation function and the learning rate, where for the latter it is found that faster convergence is achieved with a larger step size. We recall that situations where the model could converge to a suboptimal solution are avoided thanks to the Adaptive Momentum Stochastic Gradient Descent (Adam) optimiser that dynamically adjusts the learning rate.

All in all, the differences between the previous and new model hyperparameters listed in Table 2 are found to be rather moderate, confirming the general validity of the choices that were adopted in the nNNPDF2.0 analysis.

3.4 The LHCb D-meson data and PDF reweighting

As mentioned previously, the constraints on nNNPDF3.0 from the datasets described in Sect. 2 are accounted for by means of the experimental data contribution, $\chi ^2_{t_0}$, to the cost function in Eq. (3.5) used for the neural network training. The only exceptions are the LHCb measurements of D-meson production discussed in Sect. 2.3.4. The impact of these measurements is instead determined by means of Bayesian reweighting [63, 64]. The reason is that interpolation tables, that combine PDF and $\alpha _s$ evolution factors with weight tables for the hadronic matrix elements (see Sect. 2.2), need to be pre-computed to allow for a fast determination of theoretical predictions. The efficient computation of these theoretical predictions is critical for the fit, as they must be evaluated a large number of times, ${\mathcal {O}}(10^5)$, as part of the minimisation procedure. However, no interface is currently publicly available to generate interpolation tables in the format required to include LHCb D-meson data in the free-proton and nuclear nNNPDF3.0 fits. Bayesian reweighting then provides a suitable alternative to account for the impact of these measurements in the nPDF determination, since the corresponding theory predictions must be evaluated only once per each of the prior replicas.

Our strategy therefore combines fitting and reweighting procedures, as illustrated in the right branch of the flowchart in Fig. 4. We describe the various steps of this strategy in turn.

Fig. 4

Schematic representation of the fitting strategy used to construct the nNNPDF3.0 determination. The starting point is a dedicated proton global fit based on the NNPDF3.1 methodology but with the NNPDF4.0 proton-only dataset. This proton PDF fit is then reweighted with the LHCb D meson production data in pp collisions, which upon unweighting results into the proton PDF baseline to be used for nNNPDF3.0 (via the $A=1$ boundary condition). Then to assemble nNNPDF3.0 we start from the nNNPDF2.0 dataset, augment it with the NNPDF4.0 deuteron data and the new pPb LHC cross-sections, and produce a global nPDF fit with the hyperoptimised methodology. Finally this is reweighted by the LHCb $D^0$ meson production measurements in pPb collisions, and upon unweighting we obtain the final nNNPDF3.0 fits

• The first step concerns the free-proton PDF baseline. A variant of the NNPDF3.1 NLO fit is constructed as described in Sect. 3.2, which is then reweighted with the LHCb D-meson measurements of $N^{\mathrm{pp}}_7$ and $N^{\mathrm{pp}}_{13}$, see Eq. (2.5) and the discussion in Sect. 2.3.4. The NNPDF3.1 fit variant is composed of $N_{\mathrm{rep}}=500$ replicas; after reweighting one ends up with $N_{\mathrm{eff}}=250$ effective replicas. Table 3 collects the values of $\chi ^2/n_{\mathrm{dat}}$ for the LHCb D-meson measurements of $N^{\mathrm{pp}}_7$ and $N^{\mathrm{pp}}_{13}$ before and after reweighting. We observe that the dataset is relatively well described already before reweighting; the improvement after reweighting is therefore noticeable, although not dramatic. As shown in Fig. 2, the impact of the LHCb $N^{\mathrm{pp}}_7$ and $N^{\mathrm{pp}}_{13}$ data on the free-proton baseline PDFs consists of a reduction of uncertainties in the small-x region; central values are left mostly unaffected.

• The second step consists in producing the nNNPDF3.0 prior fit. This is based on the dataset described in Sect. 2 (except LHCb pPb $D^0$-meson data) and makes use of the free-proton PDF set determined at the end of the previous step. The nNNPDF3.0 prior fit is made of $N_{\mathrm{rep}}=4000$ replicas. Such a large number of replicas ensures sufficiently high statistics for the subsequent reweighting of this nNNPDF3.0 prior fit with the LHCb D-meson pPb data.

• The third step is the reweighting of the nNNPDF3.0 prior fit with the LHCb measurements of $D^0$-meson production in pPb collisions. As discussed in Sect. 2.3.4 we use the ratio of pPb to pp spectra, in the forward region, Eq. (2.3), by default. The stability of our results if instead the forward-to-backward ratio measurements Eq. (2.4) are used is quantified in Sect. 5. After reweighting, we end up with $N_{\mathrm{eff}}=200$ (500) effective replicas when reweighting with $R_{\mathrm{pPb}}$ ($R_{\mathrm{fb}}$). A satisfactory description of the LHCb $D^0$-meson data in pPb collisions is achieved, as will be discussed in Sect. 4.2. Our final nNNPDF3.0 set is constructed after unweighting [64] and contains $N_{\mathrm{rep}}=200$ replicas. This is released in the usual LHAPDF format for the relevant values of A, listed in Sect. 7.1.

In addition to this baseline nNNPDF3.0 fit, as indicated on the left branch of the flowchart in Fig. 4, we also produce and release a variant without any LHCb D-meson data, neither in the free-proton baseline nor in the nuclear fit. For completeness, we list here the specific procedure adopted to construct this variant.

• The first step concerns again the free-proton PDF baseline. This is the variant of the NNPDF3.1 NLO fit constructed as described in Sect. 3.2 and made of $N_{\mathrm{rep}}=1500$ replicas.

• The second step consists in producing the variant of the nNNPDF3.0 fit from the datasets described in Sect. 2, except the LHCb D-meson cross-sections. We produce two ensembles with $N_{\mathrm{rep}}=250$ and $N_{\mathrm{rep}}=1000$ replicas, which we also release in the usual LHAPDF format for the relevant values of A. In Sects. 4.1 and 4.2 we will compare the nNNPDF3.0 baseline fit and the variant without any LHCb D-meson data.

Table 3 Values of $\chi ^2/n_{\mathrm{dat}}$ for the LHCb D-meson measurements of $N^{\mathrm{pp}}_7$ and $N^{\mathrm{pp}}_{13}$ before and after reweighting

We have explicitly verified the validity of the reweighting procedure when applied to nPDFs (see Appendix D for more details), by comparing the outcome of a fit where a subset of the CMS dijet measurements from pPb collisions are included either by a fit or by reweighting. We have confirmed that the two methodologies lead to compatible results, in particular that nPDF central values are similarly shifted and uncertainties are similarly reduced. Nevertheless, we remark that the reweighting procedure has some inherent limitations as compared to a fit. First of all, reweighting is only expected to reproduce the outcome of a fit provided that statistics, i.e. the number of effective replicas, is sufficiently high. Second, the results obtained by means of reweighting may differ from those obtained after a fit in those cases where the figure of merit used to compute the weights is different from that used for fit minimisation. For instance, if the $\chi ^2$ function used for reweighting does not account for the cross-section positivity and the $A=1$ free-proton boundary condition constraints as in Eq. (3.5).

4 Results

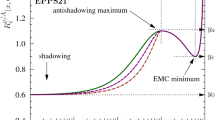
In this section we present the main results of this work, namely the nNNPDF3.0 global analysis of nuclear PDFs. First of all, we discuss the key features of the variant of nNNPDF3.0 without the LHCb D-meson data, and compare it with the nNNPDF2.0 reference. Second, we describe the outcome of the reweighting of a nNNPDF3.0 prior set with the LHCb D-meson data, which defines the nNNPDF3.0 default determination, and the resulting constraints on the nuclear modification factors. Third, we study the goodness-of-fit to the new datasets incorporated in the present analysis and carry out representative comparisons with experimental data. Fourth, we study the A-dependence of our results and assess the local statistical significance of nuclear modifications. Finally, we compare the nNNPDF3.0 determination with two other global analyses of nuclear PDFs, EPPS16 and nCTEQ15WZ+SIH.

The stability of nNNPDF3.0 with respect to methodological and dataset variations is then studied in Sect. 5, while its implications for the ultra high-energy neutrino-nucleus interaction cross-sections are quantified in Sect. 6. Furthermore, representative comparisons between the predictions from nNNPDF3.0 and experimental data from pPb collisions can be found in Appendix C.

4.1 The nNNPDF3.0 (no LHCb D) fit

We present first the main features of the nNNPDF3.0 variant that excludes the LHCb D meson data (from both pp and pPb collisions), following the strategy indicated in Sect. 3. In the following, this variant is denoted as nNNPDF3.0 (no LHCb D). This fit differs from nNNPDF2.0 due to three main factors: i) the significant number of new datasets involving D, Cu, and Pb targets, ii) the improved treatment of $A=1$ free-proton PDF boundary condition, and iii) the automated optimisation of the model hyperparameters.

The comparison between the nNNPDF2.0 and nNNPDF3.0 (no LHCb D) fits is presented in Fig. 5 at the level of lead PDFs and in Fig. 6 at the level of nuclear modification ratios, defined as

$$\begin{aligned} R_f^{(A)}(x,Q) \equiv \frac{ f^{(N/A)}(x,Q)}{\frac{Z}{A} f^{(p)}(x,Q) + \frac{(A-Z)}{A}f^{(n)}(x,Q)}, \end{aligned}$$

(4.1)

where $f^{(N/A)}$, $f^{(p)}$, and $f^{(n)}$ indicate the PDFs of the average nucleon N bound in a nucleus with Z protons and $A-Z$ neutrons, the free-proton, and the free-neutron PDFs respectively, see Appendix A for an overview of the conventions and notation used throughout this work.

In both cases, the results display the 68% CL uncertainties and are evaluated at $Q=10$ GeV.

Fig. 5

Comparison between the nNNPDF2.0 and nNNPDF3.0 (no LHCb D) fits for the lead PDFs at $Q=10$ GeV, normalised to the central value of the nNNPDF2.0 reference. The uncertainty bands indicate the 68% CL intervals

Fig. 6

Same as Fig. 5 now in terms of the nuclear modification ratios $R_f^{(A)}(x,Q^2)$

Fig. 7

Comparison between the LHCb data on $D^0$-meson production from pPb collisions in the forward region and the corresponding theoretical predictions based on the nNNPDF3.0 prior set described in Sect. 3.4. The ratio between $D^0$-meson spectra in pPb and pp collisions, $R_{\mathrm{pPb}}$ in Eq. (2.3), is presented in four bins in $D^0$-meson rapidity $y^{D^0}$ as a function of the transverse momentum $p_T^{D^0}$. We display separately the PDF and scale uncertainty bands, and the bottom panels show the ratios to the central value of the theory prediction based on the prior

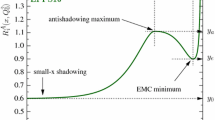
First of all, the two determinations are found to be consistent within uncertainties for all the nPDF flavours in the full range of x for which experimental data is available. The qualitative behaviour of the nuclear modification ratios defined in Eq. (4.1) is similar in the two determinations, with the strength of the small-x shadowing being reduced (increased) in the quark (gluon) nPDFs in nNNPDF3.0 (no LHCb D) as compared to the nNNPDF2.0 analysis. From Fig. 6, one also observes how the large-x behaviour of the nuclear modification factors for the quark PDFs is similar in the two fits, while for the gluon one finds an increase in the strength of anti-shadowing peaking at $x\simeq 0.2$. These differences in $R_g^{(A)}$ reported between nNNPDF3.0 (no LHCb D) and nNNPDF2.0 can be traced back to the constraints provided by the CMS dijet cross-sections in pPb, which will be further discussed in Sect. 5.3. One also finds that uncertainties in the small-x region, , where neither of the two fits includes direct constraints, are increased in nNNPDF3.0. This is a consequence of the improved implementation of the $A=1$ proton PDF boundary condition discussed in Sect. 3.2, as will be further studied in Sect. 5.1.

Furthermore, in the region where the bulk of experimental data on nuclear targets lies, , the uncertainties on the quark nPDFs of lead are also basically unchanged between the two analyses. The impact of the new LHC W and Z production measurements in nNNPDF3.0 is mostly visible for the up and down anti-quark PDFs, both in terms of a shift in the central values and of a moderate reduction of the nPDF uncertainties. The increase in the central value of the total strangeness is related to the inclusion of deuteron and copper cross-sections in nNNPDF3.0 together with the improved $A=1$ boundary condition, as will be demonstrated in Sect. 5.1.

4.2 The nNNPDF3.0 determination

The nNNPDF3.0 (no LHCb D) fit presented in the previous section is the starting point to quantify the constraints on the proton and nuclear PDFs provided by LHCb D-meson production data by means of Bayesian reweighting. As discussed in Sect. 3.4, the first step is to produce the nNNPDF3.0 prior fit, which coincides with nNNPDF3.0 (no LHCb D) with the only difference being that the proton PDF boundary condition now accounts for the constraints provided by the LHCb D-meson data in pp collisions at 7 and 13 TeV. The differences and similarities between the proton PDF boundary conditions used for the nNNPDF3.0 and nNNPDF3.0 (no LHCb D) fits and their nNNPDF2.0 counterpart were studied in Fig. 2. Subsequently, the LHCb data for $R_{\mathrm{pPb}}$ in the forward region is added to this prior nPDF set using reweighting.

Figure 7 displays the comparison between the LHCb data for $R_{\mathrm{pPb}}$, Eq. (2.3), for $D^0$-meson production in pPb collisions (relative to that in pp collisions) in the forward region, and the corresponding theoretical predictions based on this nNNPDF3.0 prior set. The LHCb measurements are presented in four bins in $D^0$-meson rapidity $y^{D^0}$ as a function of the transverse momentum $p_T^{D^0}$, and we display separately the PDF and scale uncertainty bands, and the bottom panels show the ratios to the central value of the theory prediction.

Fig. 8

Same as Fig. 7, now comparing the theory predictions based on the nNNPDF3.0 prior fit with the backward rapidity bins of the LHCb measurement of $D^0$-meson production in Pbp collisions. While the predictions are consistent with the LHCb data, uncertainties due to MHOs now are the dominant source of theory error (as opposed to the pPb forward data), hence this dataset is not amenable for inclusion in nNNPDF3.0

From Fig. 7 one can observe how PDF uncertainties of the prior (that does not yet contain $R_{\mathrm{pPb}}$ $D^0$-meson data) are very large, and completely dominate over the uncertainties due to missing higher order (MHOs), for the whole kinematic range for which the LHCb measurements are available. The uncertainties due to MHOs (or scale uncertainties) are evaluated here by independently varying the factorisation and renormalisation scales around the nominal scale $\mu = E_{T}^c$ with the constraint $1/2 \le \mu _F/\mu _R \le 2$, and correlating those scales choices between numerator and denominator of the ratio observable defined in Eq. (2.3). Furthermore, these PDF uncertainties are also much larger than the experimental errors, especially for the bins in the low $p_T^{D^0}$ region which dominate the sensitivity to the small-x nPDFs of lead. Within these large PDF uncertainties, the predictions based on the nNNPDF3.0 prior fit agree well with the LHCb measurements. This feature makes the LHCb forward $R_{\mathrm{pPb}}$ data amenable to inclusion in a nPDF analysis, as opposed to the situation with the corresponding measurements in the backward region, shown in Fig. 8, where uncertainties due to MHOs are larger than both PDF and experimental uncertainties. Because of this, the LHCb backward $R_{\mathrm{Pbp}}$ data are not further considered in the nNNPDF3.0 analysis. Considering the low $p_T^{D^0}$ region of the $R_{\mathrm{pPb}}$ measurements, one finds that the LHCb data prefer a smaller central value than the central prediction for the nNNPDF3.0 prior fit, indicating than a stronger shadowing at small-x is being favoured. Indeed, as we show next, once the LHCb D-meson constraints are included via reweighting, the significance of small-x shadowing in nNNPDF3.0 markedly increases.

The comparison between the nPDFs of lead nuclei at $Q=10$ GeV for the nNNPDF3.0 prior fit and the corresponding reweighted results, normalised to the central value of the former, is shown in Fig. 9. This comparison quantifies the impact of the LHCb D-meson production measurements when added to the nNNPDF3.0 prior fit. The reweighted nPDFs of lead nuclei are consistent with those of the prior, and display a clear uncertainty reduction for (for the gluon) and (for the sea quarks). For instance, in the case of the gluon the nPDF uncertainties are reduced by around a factor three for $x\simeq 10^{-4}$, highlighting the constraining power of these LHCb measurements. In terms of the central values, that of the gluon is mostly left unchanged as compared to the prior, while for the sea quarks one gets a suppression of up to a few percent. We note that the reweighting procedure also affects the proton baseline, given that weights are applied to each replica including the full A-dependence of the parametrisation.

Fig. 9

Comparison of the nPDFs of lead nuclei at $Q=10$ GeV between nNNPDF3.0 (no LHCb D) and nNNPDF3.0, normalised to the central value of the former

The same comparison as Fig. 9 is displayed now in terms of the nuclear modification ratios $R_f^{(A)}(x,Q)$ in Fig. 10. As discussed in Sect. 3.4, in the present analysis we consider in a coherent manner the constraints of the LHCb D-meson data both on the proton and nuclear PDFs while keeping track of their correlations, and hence the impact on the ratios $R_f^{(A)}$ is in general expected to be more marked as compared to that restricted to the lead PDFs. Indeed, considering first the nuclear modification ratio for the gluon, we find that the LHCb $D^0$-meson measurements in pPb collisions bring in an enhanced shadowing for together with an associated reduction of the PDF uncertainties in this region by up to a factor five. Hence the LHCb data constrain $R_g$ more than it does the absolute lead PDFs in Fig. 9, demonstrating the importance of accounting for the correlations between proton and lead PDFs. In the case of the sea quark PDFs, the enhanced shadowing for and the corresponding uncertainty reduction is qualitatively similar to that observed at the lead PDF level. The preference of the LHCb D-meson production measurements for a strong small-x shadowing of the quark and gluon PDFs of lead is in agreement with related studies of the same process in the literature [86, 97, 98].

Fig. 10

Same as Fig. 9 now presented in terms of the terms of the nuclear modification ratios $R_f^{(A)}(x,Q)$

Whenever the nuclear ratios deviate from unity, $R^{(A)}_f(x,Q)\ne 1$, the fit results favour non-zero nuclear modifications of the free-proton PDFs. However, such non-zero nuclear modifications will not be significant unless the associated nPDF uncertainties are small enough. In order to quantify the local statistical significance of the nuclear modifications, it is useful to evaluate the pull on $R^{(A)}_f(x,Q)$ defined as

$$\begin{aligned} P\left[ R_f^{(A)}\right] (x,Q) \equiv \frac{\left( R^{(A)}_f(x,Q)-1 \right) }{\delta R^{(A)}_f(x,Q)} , \end{aligned}$$

(4.2)

where $\delta R^{(A)}_f(x,Q)$ indicates the 68% CL uncertainties associated to the nuclear modification ratio for the f-th flavour. Values of these pulls such that indicate consistency with no nuclear modifications at the 68% CL, while corresponds to a local statistical significance of nuclear modifications at the $3\sigma$ level, the usually adopted threshold for evidence, in units of the nPDF uncertainty.

These pulls are displayed in Fig. 11 for both nNNPDF3.0 and the prior fit at $Q=10$ GeV, where dotted horizontal lines indicate the threshold for which nuclear modifications differ from zero at the $3\sigma$ ($5\sigma$) level. In the case of the quarks, the LHCb D-meson data enhances the pulls in the region $x\simeq 10^{-3}$, leading to a strong evidence for small-x shadowing in the quark sector. At larger values of x, the pull for anti-shadowing reaches between the $1\sigma$ the $2\sigma$ level for up and down quarks and the down antiquark, while for ${\bar{u}}$ it is absent. The significance of the EMC effect remains at the $1\sigma$ level of the up and down quarks. Considering next the pull on the gluon modification ratio, we observe how the LHCb D-meson measurements markedly increase both the significance and the extension of shadowing in the small-x region. Once the LHCb constraints are accounted for, one finds that nNNPDF3.0 favours a marked and statistically significant shadowing of the small-x gluon nPDF of lead in the region $x \le 10^{-2}$. To the best of our knowledge, this is the first time that such a strong significance for gluon shadowing in heavy nuclei has been reported.

Fig. 11

Same as Fig. 10 now presented in terms of the pulls defined in Eq. (4.2). The dotted horizontal lines indicate the threshold for which nuclear modifications differ from zero at the $3\sigma ~(5\sigma )$ level

4.3 Fit quality and comparison with data

We now turn to discuss the fit quality in the nNNPDF3.0 analysis, for both the variants with and without the LHCb D-meson data, and present representative comparisons between NLO QCD predictions and the corresponding experimental data. Table 4 reports the values of the $\chi ^2$ per data point for the DIS datasets that enter nNNPDF3.0. For each dataset we indicate its name, reference, the nuclear species involved, the number of data points, and the values of $\chi ^2/n_{\mathrm{dat}}$ obtained both with nNNPDF3.0 (no LHCb D) and with nNNPDF3.0. Datasets labelled with (*) are new in nNNPDF3.0 as compared to its predecessor nNNPDF2.0. Table 5 displays the same information as Table 4 now for the fixed-target and LHC DY production datasets, the CMS dijet cross-sections, and the ATLAS direct photon production measurements. The last row of the table indicates the values corresponding to the global dataset. Values indicated within brackets () correspond to datasets that are not part of the nNNPDF3.0 baseline, and whose $\chi ^2$ values are reported only for comparison purposes. Finally in Table 6 we report the details of the reweighting and unweighting procedures, including the number of effective replicas $N_{\text {eff}}$, the number of replicas in the unweighted set $N_{\mathrm{unweight}}$, the number of data points included and the values of the $\chi ^2$ before and after reweighting.

Table 4 The values of the $\chi ^2$ per data point for the DIS datasets that enter nNNPDF3.0. For each dataset we indicate its name, reference, the nuclear species involved, the number of data points, and the values of $\chi ^2/n_{\mathrm{dat}}$ obtained both with the nNNPDF3.0 prior fit (without the LHCb D-meson cross-sections) and with nNNPDF3.0. Datasets labelled with (*) are new in nNNPDF3.0 as compared to its predecessor nNNPDF2.0. The datasets are separated into neutral-current (upper) and charged-current (bottom part) structure functions

Table 5 Same as Table 4 now for the fixed-target and LHC DY production datasets, the CMS dijet cross-sections, and the ATLAS direct photon production measurements. The last row indicates the values corresponding to the global dataset. Values indicated within brackets () correspond to datasets that are not part of the nNNPDF3.0 baseline, and are reported only for comparison purposes. See Table 6 for the corresponding $\chi ^2$ values for the LHCb $D^0$-meson forward data

Table 6 The number of effective $N_{\text {eff}}$ and unweighted $N_{\text {unweight}}$ replicas associated to the inclusion of the LHCb $R_{\mathrm{pPb}}$ data on the nNNPDF3.0 prior fit via reweighting, together with the number of data points and the values of the $\chi ^2$ for this dataset before and after reweighting

Fig. 12

Comparison between the NLO QCD theory predictions based on the nNNPDF3.0 and nNNPDF3.0 (no LHCb D) fits with the corresponding experimental data for the first two $p_{T,\mathrm{dijet}}^{\mathrm{avg}}$ bins of the CMS $\sqrt{s}=5.02$ TeV dijet production measurement (upper) and for the two dimuon invariant mass bins from the CMS $\sqrt{s}=8.16$ Z production measurement (bottom panels)

Several interesting observations can be derived from the results presented in Tables 4 and 5. First of all, the global fit $\chi ^2/n_{\mathrm{dat}}$ values are satisfactory, with $\chi ^2/n_{\mathrm{dat}}\simeq 1.10$ for both nNNPDF3.0 variants. Actually, the values obtained for the nNNPDF3.0 fits with and without the constraints from the LHCb D-meson data are very similar in all cases. This observation is explained because, as discussed above, the LHCb D-meson data constraints are restricted to where there is little overlap with other datasets entering the nuclear fit, as also highlighted by the kinematic plot of Fig. 1. Given that one is combining $n_{\mathrm{dat}}=2151$ data points from 54 datasets corresponding to 7 different processes, such a satisfactory fit quality is a reassuring, non-trivial consistency test of the reliability of the QCD factorisation framework when applied to nuclear collisions. Likewise, a very good description of the nuclear DIS structure function data is achieved, with $\chi ^2/n_{\mathrm{dat}}\simeq 1.02$ (1.04) for 1784 data points for nNNPDF3.0 (its variant without LHCb D data). This fit quality is similar to that reported for nNNPDF2.0, see [25, 26] for a discussion of the somewhat higher $\chi ^2$ values obtained for a few of the DIS datasets.

Fig. 13

The dependence with the atomic mass number A of the pulls defined in Eq. (4.2) in nNNPDF3.0 for a range of nuclei from deuterium ($A=2$) up to lead ($A=208$). Recall from Eq. (4.2) that nuclear modifications associated to the different numbers of protons and neutrons have already been accounted for

Concerning the new LHC gauge boson production datasets from pPb collisions added to nNNPDF3.0, a satisfactory fit quality is obtained for all of them except for the ALICE $W^+$ at 5.02 TeV (2 points) and CMS Z at 8.16 TeV (36 points) measurements. From the data versus theory comparisons reported in Fig. 12 (see also Appendix C) for the case of the CMS Z dataset, in the low dimuon invariant mass bin with $15\le M_{\mu {{\bar{\mu }}}} \le 60$ GeV the NLO QCD theory predictions undershoot the data by around 10% to 20%. This shift should be reduced by the addition of the NNLO QCD corrections [123], which may be relatively large in this region. We have verified that the nNNPDF3.0 fit results are unaffected if this low invariant mass bin is removed. For the on-peak invariant mass bin, with $60\le M_{\mu {{\bar{\mu }}}} \le 120$ GeV and for which the NNLO QCD corrections are relatively small, a good description of the experimental data is obtained except for the left-most rapidity bin, where the cross-section is very small.

Concerning the CMS measurements of dijet production at 5.02 TeV and the ATLAS ones of isolated photon production at 8.16 TeV, in both cases presented as ratio between the pPb and pp spectra, one finds a fit quality of $\chi ^2/n_{\mathrm{dat}}\simeq 1.8$ and 1.0 respectively. In the case of the CMS dijets, inspection of the comparison between the fit results and data in the bottom panels of Fig. 12 (see Appendix C for the rest of the bins) reveals that in general one has a good agreement with the exception of one or two bins in the forward (proton-going) direction. In particular, the most forward bin systematically undershoots the NLO QCD theory prediction. We have verified that if the two most forward rapidity bins are removed in each $p_{T,\mathrm{dijet}}^{\mathrm{avg}}$ bin, the fit quality improves to $\chi ^2/n_{\mathrm{dat}}\simeq 1.3$ without any noticeable impact on the fit results. Hence, it is neither justified nor necessary to apply ad-hoc kinematic cuts in the dijet rapidity, and one can conclude that a satisfactory description of this dataset is obtained. In the case of the ATLAS isolated photon measurements, good agreement between data and theory is obtained for the whole range of $E_T^\gamma$ and $\eta ^\gamma$ covered by the data.

As indicated by Table 5, when the theory predictions based on nNNPDF3.0 are compared to the absolute pPb spectra for dijet production and isolated photon production, much worse $\chi ^2/n_{\mathrm{dat}}$ values are found, 13.6 and 3.3 for each dataset respectively. As discussed in Sect. 2.3, the prediction of the absolute cross-section rates at NLO QCD accuracy suffers from large uncertainties due to MHO effects. Dedicated studies of these two processes at NNLO QCD accuracy (such as those in [74, 77]) will be required to determine if this data can be reliably included in an nPDF fit.

4.4 A-dependence of nuclear modifications

The results discussed so far have focused on the nuclear modifications of lead, which is the nuclear species for which hard-scattering data from the LHC is available. Here we study how these nuclear modifications depend on the atomic mass number. Figure 13 displays the dependence with the atomic mass number A of the pulls defined in Eq. (4.2) for the nNNPDF3.0 global analysis. These pulls are displayed for $Q=10$ GeV as a function of x for a range of nuclei from deuterium ($A=2$) up to lead ($A=208$). Recall that nuclear modifications associated to different numbers of protons and neutrons have already been accounted for. We note that a small value of the pull in Fig. 13 does not necessarily imply that nuclear corrections for such value of A are small, it can also mean that nPDF uncertainties are relatively large (for example due to lack of direct experimental constraints) as compared to other nuclei.

In the case of the gluon nuclear modifications, one can observe how the pulls are small and similar for light nuclear, all the way up to $^{27}$Al. The pulls become somewhat larger as A is increased up to $^{131}$Xe, favoring shadowing and anti-shadowing at small and large-x respectively. However, it is only for the heavier nuclei, $^{197}$Au and $^{208}$Pb, for which the pulls reach the $3\sigma$ level, providing evidence for shadowing and anti-shadowing at small and large-x respectively. The large impact of the LHCb $D^0$-meson $R_{\mathrm{pPb}}$ data on $R_g$ for Pb is clearly visible, and indirectly also constrains the nuclear modifications of Au. The fact that the absolute pulls increase with A arises from the combination of two factors: nuclear effects are known to become more important for heavier nuclei, and that the heavier nuclei benefit from the nPDF uncertainty reduction provided by the LHC measurements from pPb collisions.

A similar picture is observed for the pulls associated to the quark and anti-quark nuclear modification ratios. One difference is that in this case one observes nuclear modifications with associated pulls at the $1\sigma$ level already for the light nuclei, from deuteron onwards, e.g. with anti-shadowing at $x\simeq 0.1$. As was also the case for the gluon, the significance of small-x shadowing in the quark sector increases with the atomic mass number A, and reaches the $3\sigma$ level for the heavier nuclei at $x\simeq 10^{-3}$. For smaller values of x, nPDF errors grow up and this significance is washed out except for the heavier nuclei considered. Interestingly, the strong dependence with A observed for small-x shadowing is less clear for larger-x phenomena such as anti-shadowing and the EMC effect in the quark sector. In the specific case of the down quark, the pulls in the anti-shadowing region reach the $2\sigma$ level for $x\simeq 0.1$ only when considering the heavier nuclei, but such trend is not observed in the case of its up quark counterpart.

Then in Fig. 14 we present the relative 68% CL uncertainties on the nuclear modification ratios, $\delta ( R_f^{(A)})$, evaluated at $Q=10$ GeV for the same nuclei as those presented in Fig. 13. For the lighter nuclei, these uncertainties are the smallest for the deuteron and then increase monotonically up to $^{27}$Al. The fact that nuclear modifications with low-A nuclei are well constrained follows not only from the free-proton boundary condition but also from the large amount of data taken on a deuteron target used in nNNPDF3.0. Even so, already for relatively light nuclei as $^{27}$Al the uncertainties have become quite large, demonstrating how the A-dependence of our parametrisation is not over-constraining.

Fig. 14

The relative 68% CL uncertainties on the nuclear modification ratios, $\delta ( R_f^{(A)})$, evaluated at $Q=10$ GeV for the same nuclei as those presented in Fig. 13

For heavier nuclei, the results for $\delta (R_f^{(A)})$ depend on the flavour. For the gluon, we see that uncertainties keep increasing with A until we get to $^{131}$Xe, but then $^{197}$Au and $^{208}$Pb are better constrained as compared to lighter nuclei. This is a direct consequence of the strong constraints imposed by the CMS dijet and LHCb D-meson data on the nuclear modifications of the gluon PDF. Remarkably, the PDF uncertainties for $A=208$ (lead) are smaller than those of light nuclei such as $A=12$ (carbon) for . A similar picture applies for the up and down quarks and anti-quarks, where for example the uncertainties in $^{208}$Pb (and $^{197}$Au) are clearly reduced as compared to $^{131}$Xe for the entire x region considered. In this case, the origin of this improvement can be traced back to the information provided by the LHC measurements of weak gauge boson production in pPb collisions. This trend is however absent for the PDF uncertainties in the case of the total strangeness, most likely since the fit does not contain direct constraints on the nuclear modifications of strangeness in heavy nuclei.

A complementary picture of the A-dependence of our results is provided by the nuclear modification factors $R_f^{(A)}(x,Q)$ for different values of A. Figure 15 compares $R_f^{(A)}$ for three representative values of A: $A=208$ (lead), $A=108$ (silver) and $A=31$ (the mean atomic mass number of nuclei typically encountered by ultra-high-energy neutrinos propagating through the Earth). While nuclear modifications are well constrained for lead, given the abundance of LHC data included in the fit for this nucleus, only a handful of points (corresponding specifically to DIS structure functions) are available for silver, and none for $A=31$. From this comparison one observes how the uncertainties on $R_f^{(A)}$ are largest for $A=108$, due to the scarcity of experimental data and to the fact that this value of A is far from both $A=1$, constrained by the proton boundary condition, and $A=208$, for which most of the heavier nuclear data is available. In particular, for $A=108$ the small-x gluon is consistent with no nuclear modifications within uncertainties. The predictions for $A=31$ are obtained from the outcome of the neural network parametrisation, Eq. (3.1) trained to other values of A, and for this nuclear species $R_f^{(A)}$ turns out to be consistent with unity at the 68% confidence level.

Fig. 15

The nuclear modification factors $R_f^{(A)}(x,Q)$ at $Q=10$ GeV for $A=208$ (lead), $A=108$ (silver) and $A=31$ (the mean atomic mass number of nuclei typically encountered by ultra-high-energy neutrinos propagating through the Earth)

Fig. 16

The nuclear modification ratios in nNNPDF3.0 for deuterium ($A=2$) compared to nNNPDF2.0

Fig. 17

The nNNPDF3.0 predictions for the nuclear modification ratios in lead at $Q=10$ GeV, compared to the corresponding results from the EPPS16 and nCTEQWZ+SIH global analyses. The PDF uncertainty bands correspond in all cases to 68% CL intervals

A particularly interesting case is that of the nuclear modification factors associated to the deuteron, $A=2$. The reason is that the treatment of deuteron data has been improved as compared to our previous analysis: in nNNPDF2.0, deuteron DIS and DY cross-sections were part of the proton baseline (where they were included assuming no nuclear effects), while now instead the free-proton baseline does not contain any deuteron data, which is instead considered entirely at the level of the nuclear fit. Hence, one expects the nuclear corrections associated to deuteron nuclei to be better constrained in nNNPDF3.0, since these are now being directly determined from the data rather than indirectly via the boundary condition. Figure 16 displays the nuclear modification ratios in nNNPDF3.0 for deuterium nuclei ($A\!=\!2$), compared to those of nNNPDF2.0. While in both cases the deuteron nuclear modification ratios agree with unity within uncertainties, the nNNPDF3.0 predictions are indeed rather more precise than those of its predecessor. From these results, deuteron corrections for the light quarks appear to be constrained to be at the level in the kinematic region where deuteron experimental data is available, with somewhat larger uncertainties in the case of large-x antiquarks.

4.5 Comparison with other global nPDF analyses

Several groups have presented determinations of nuclear PDFs [25, 32, 33, 97, 124,125,126,127,128,129,130,131,132], which differ in terms of the input dataset, fitting methodology, and/or theoretical settings. Here we compare the nNNPDF3.0 results with two other recent nuclear PDF analyses² based on global datasets, namely EPPS16 [32] and nCTEQ15WZ+SIH [33]. The EPPS16 study considers fixed-target DIS and DY cross-sections on nuclear targets complemented with LHC data on gauge boson and dijet production and with RHIC measurements. Follow up studies based on the EPPS16 framework have focused on the nPDF constraints provided by D-meson [86], dijet [133], and fixed-target large-x DIS [134] data. nCTEQ15WZ+SIH is the most recent nPDF analysis from the nCTEQ collaboration, building upon previous results first based on DIS, fixed-target DY, and RHIC data on nuclear targets [126], then extended to gauge boson production in pPb collisions [124, 125], and recently to single inclusive hadron (SIH) production from RHIC and the LHC [33]. Furthermore, a nCTEQ15 variant studying the nPDF constraints from low-$Q^2$ DIS structure functions at JLab has also been presented [135].

The nNNPDF3.0 predictions for the nuclear modification ratios $R^{(A)}_f(x,Q)$ are compared with its counterparts from the EPPS16 and nCTEQ analyses in Fig. 17. We display the results for the lead PDFs at $Q=10$ GeV, where the uncertainty bands correspond in all cases to the 68% CL intervals. We note that the EPPS16 and nCTEQ15WZ+SIH Hessian uncertainties are provided as 90% CL, hence we rescale them to obtain 68% CL bands. To ease the interpretation of this comparison, the relative 68% CL uncertainties associated to these nuclear modification ratios are plotted separately in Fig. 18.

Fig. 18

Same as Fig. 17, now comparing the relative nPDF uncertainties associated to $R^{(A)}_f(x,Q)$

In general one finds reasonable agreement between the results of the three global analyses, but also some differences both in terms of central values and uncertainties. Concerning the gluon nuclear modifications, nNNPDF3.0 favours both a stronger shadowing at small-x and a more intense anti-shadowing at large-x as compared to the other two groups. Except for the region around $x\simeq 0.2$, where the nNNPDF3.0 nuclear ratio is somewhat higher, the nNNPDF3.0 predictions agree within uncertainties in the full x range with EPPS16, while for the nCTEQ prediction for $R_g$ is instead higher and consistent with no gluon shadowing. In terms of the nPDF uncertainties on $R_g$, these turn out to be similar between the three groups in the region where the bulk of the data lies, , while at smaller x those of EPPS16 become larger than those of nNNPDF3.0, the latter result being explained by the strong constraints provided by the LHCb D-meson measurements in this kinematic region.

In the case of the nuclear modifications associated to the up and down quarks, good agreement is found both in terms of the central values and of the PDF uncertainties among the three groups for the whole range of x. The good agreement between the three fits is, as expected, also present for the up and down antiquarks for , where the valence contribution is negligible. On the other hand, for the predictions for $R_{{\bar{u}}}$ and $R_{{\bar{d}}}$ from nNNPDF3.0 are rather different as compared to the other two groups, and furthermore their uncertainties are also significantly larger in this region. We remark that the experimental constraints on the large-x nuclear antiquarks are limited, and hence the methodological assumptions play a bigger role.

The largest differences between the three groups are observed for the strange PDF: while nNNPDF3.0 and EPPS16 favour small-x shadowing along the lines of the up and down quark sea, nCTEQ displays a positive nuclear correction of up to 50% for followed by a strong suppression at larger x. It is unclear what the origin of this difference is, especially since EPPS16 and nCTEQ share the same free-proton PDF baseline.

It should be noted that, due to DGLAP evolution, the comparison of nuclear modification factors across various groups may be subject to a different interpretation if it were carried out at other values of Q. In general, DGLAP evolution effects tend to smoothen out differences present at medium- and small-x as Q is increased. To highlight this point, we display in Fig. 19 the same comparison as in Fig. 17 for both the lowest scale $Q=1.3$ GeV, common to all nPDF sets, and for a very high scale, $Q=1$ TeV. One sees that the PDF uncertainties in the low-x nuclear modification factors are large at $Q=1.3$ GeV, while they are markedly reduced at large energy scales $Q=1$ TeV. As expected, for the differences between groups are reduced as the scale Q is increased due to DGLAP evolution. Nevertheless, differences remain up to $Q=1$ TeV for the poorly known large-x antiquark and strange nuclear modification ratios. Interestingly, the evidence for small-x quark and gluon shadowing and for large-x gluon anti-shadowing found in nNNPDF3.0 at $Q=10$ GeV persists up to the high scale considered here.

Fig. 19

Same as Fig. 17 now displayed at $Q=1.3$ GeV (the lowest common scale among the three nPDF sets) and at $Q=1$ TeV in the upper and lower panels respectively

Fig. 20

Comparison of nNNPDF2.0 with the nNNPDF2.0r variant. Results are shown for the lead PDFs at $Q=10$ GeV normalised to the central value of nNNPDF2.0, and the uncertainty bands represent the 68% CL intervals

In summary, despite the several differences in input dataset, fitting methodology, and theory calculations adopted, a reasonably consistent picture emerges from the comparison between the three global analyses. Especially remarkable is the agreement for the up and down quark nuclear ratios, as well as for the corresponding antiquark ratios for . The main disagreements between the three groups are related to the gluon, in particular concerning the strength of small-x shadowing and large-x anti-shadowing, the strangeness nuclear modifications, and the behaviour of the nuclear antiquarks at large x. We note that for all these cases the choice of free-proton PDF baseline may play a role, e.g. the gluon and strange PDFs already exhibit discrepancies at the level of proton PDF fits.

5 Stability analysis

Here we present a number of studies assessing the stability of the nNNPDF3.0 results and studying the impact of specific datasets and methodological choices. First of all, we present the variant of nNNPDF2.0 used as starting point of the present analysis, differing from the published version in methodological improvements related to hyperparameter optimisation and to the implementation of the proton boundary condition. Second, we quantify the impact of those nuclear datasets that have been moved from the proton baseline to the nuclear PDF analysis as discussed in Sect. 2. Third, we study the constraints provided by the CMS dijet cross-sections from pPb collisions on the gluon nPDF. Finally, we demonstrate the stability of nNNPDF3.0 upon two variations in the treatment of the LHCb $D^0$-meson measurements: we apply different cuts on the $D^0$-meson transverse momentum (i.e. restricting that data set to larger transverse momentum values); and we replace the measurements for the forward pPb-to-pp cross-section ratio with those for the forward-to-backward ratio.

5.1 nNNPDF2.0 reloaded

We consider first a variant of the nNNPDF2.0 analysis denoted by nNNPDF2.0r (where ‘r’ stands for ‘reloaded’ set). This variant differs from the published nNNPDF2.0 set for the methodological improvements described in Sect. 3, that we also summarise as follows.

First, the range in x for which the proton boundary condition is imposed has been lowered from $x_{\mathrm{min}}=10^{-3}$ to $x_{\mathrm{min}}=10^{-6}$, motivated by the extension of the kinematic coverage that is provided by the nNNPDF3.0 dataset, in particular due to the LHCb $D^0$-meson production cross-section as shown in Fig. 1. Since these measurements are also included in the proton baseline, ensuring that the free-proton boundary condition is satisfied down to $x_{\mathrm{min}}=10^{-6}$ becomes necessary.

Second, the proton PDF baseline itself has been improved as compared to the one used in nNNPDF2.0. There, a variant of NNPDF3.1 with the heavy nuclear datasets (taken on iron and lead targets) removed was adopted. The new proton baseline in nNNPDF3.0 is also based on the NNPDF3.1 fitting methodology but it is now extended to include all the new datasets from pp collisions considered in NNPDF4.0 [24]. Specifically, this new proton baseline includes the datasets labelled with (*) in Tables 2.1–2.5 of [24] (with the exception of those included via reweighting), see also the discussion in App. B of [24] for more details. These datasets correspond, among others, to new measurements of inclusive and associated production of gauge bosons, single and top-quark pair production, and jet and photon production from ATLAS, CMS and LHCb. Furthermore, no deuteron or copper datasets are considered in this proton PDF baseline, since these enter the nuclear fit as discussed below. Crucially, the resulting proton PDF baseline contains the most updated measurements available from pp collisions for the same processes that are considered in the corresponding nuclear PDF analysis.

The third methodological improvement consists on the hyperparameter settings determined by means of the optimisation procedure described in Sect. 3.3. Interestingly, the optimal hyperparameters turn out to be very close to those found manually in the nNNPDF2.0 analysis, with the only moderate differences for the activation function, the weight initialization, and the learning rate of the SGD minimiser.

The aggregate impact of these various improvements is illustrated in Fig. 20, which compares the lead PDFs in nNNPDF2.0 and nNNPDF2.0r at $Q=10$ GeV normalised to the central value of the former. One observes how in all cases the two fits agree within the corresponding 68% CL uncertainties, except for the up antiquark at very large-x. We also find that the PDF uncertainties in the region in nNNPDF2.0r are increased as compared to the published variant. This result implies that the nPDF uncertainties in nNNPDF2.0 were somewhat underestimated there, due to imposing the $A=1$ limit in a restricted region of x. While differences are in general moderate in the data region, they can be marked in the extrapolation regions at small- and large-x where there are limited experimental constraints. Overall, good consistency between the two fits is found.

5.2 The impact of the deuteron and copper NNPDF3.1 datasets

As discussed in Sects. 2 and 3, the nNNPDF3.0 analysis contains a number of datasets taken on deuteron and copper targets that previously were accounted for by means of the proton PDF boundary condition. Specifically, these consist on the NMC [53] deuteron to proton DIS structure functions; the SLAC [54] and BCDMS [55] deuteron structure functions; and the E866 [56] fixed-target DY deuteron to proton cross-section ratio. Furthermore, this category also includes the fixed-target DY measurement performed on Cu by E605 [57]. Here we ascertain the impact of these deuteron and copper datasets by adding them on top of the nNNPDF2.0r fit.

Fig. 21

Comparison of nNNPDF2.0r with the same fit where the deuteron and copper datasets from NNPDF3.1 have been included, see text for more details. Results are shown for the deuterium PDFs ($A=2$) at $Q=10$ GeV normalised to the central value of nNNPDF2.0r, and the uncertainty bands represent the 68% CL intervals

Fig. 22

Same as Fig. 21 for the nPDFs corresponding to copper ($A=64$) nuclei

Figures 21 and 22 compare nNNPDF2.0r with the same fit where the deuteron and copper datasets from NNPDF3.1 have been included, showing the nPDFs of deuterium ($A=2$) and copper ($A=64$) nuclei respectively. Considering the results for $A=2$, one finds good stability, with the impact of the deuteron fixed-target data most visible for the large-x up and down antiquarks (which are identical for this isoscalar nucleus), an effect which is consistent with the smallness of nuclear effects in deuterium.

More marked effects are found at the level of copper nuclei, Fig. 22, where the proton-copper DY cross-sections from E605 lead to a reduction of the nPDF uncertainties, in particular in the region with where this data has kinematical coverage. The appreciable impact of these measurements on the nPDFs is consistent with the fact that direct constraints on the Cu nPDFs are limited to a few DIS structure function data points. Furthermore, while the central value of the up, down, and strange quarks is mostly unaffected (as is the case for the gluon), the large-x antiquarks are suppressed following the inclusion of the E605 data.

5.3 Impact of dijet production

Among the new datasets that enter the nNNPDF3.0 determination and discussed in Sect. 2, the CMS measurement of dijet production in pPb collisions at 5.02 TeV [27] is one of those carrying the most information on the nuclear PDFs. In our analysis we consider the ratio of pPb-to-pp dijet spectra, double-differential in the dijet average transverse momentum $p_{T,\mathrm{dijet}}^{\mathrm{ave}}$ and the dijet pseudo-rapidity $\eta _{\mathrm{dijet}}$. As indicated in Fig. 1, this measurement covers a range in x between $10^{-3}$ and 1 and in $Q^2$ between 400 $\hbox {GeV}^2$ and $10^5$ $\hbox {GeV}^2$. Since jet production in hadronic collisions is dominated in this kinematic region by quark-gluon scattering [136], the CMS measurement provides direct constraints on the nuclear modifications of the gluon PDF for . We also point out that the ATLAS and CMS measurements of dijet cross-sections in pp collisions at 7 TeV are already accounted for by means of the free-proton PDF boundary condition.

Here we present a variant of nNNPDF3.0 where the CMS dijet cross-section ratio is the only measurement added on top of the NNPDF2.0r baseline fit defined in Sect. 5.1. Figure 23 displays the impact of these CMS dijet measurements on the quark singlet and gluon nPDFs of lead when added to nNNPDF2.0r. Results are presented for the nuclear modification factor $R^{(A)}(x,Q)$ at $Q=10$ GeV as well as for the corresponding pulls defined in Eq. (4.2). For the quark singlet nPDF, the impact of the dijet data is moderate and restricted to the small-x region, where a stronger shadowing is favored. In the case of the gluon nPDF, it is found that the dijet measurements significantly reduce the uncertainties for . For smaller values of x, the nPDF uncertainty is unaffected but the central value of $R^{(A)}$ remains suppressed as compared to the nNNPDF2.0r reference, which in turn enhances the significance of small-x gluon shadowing. This comparison confirms that the CMS dijet cross-sections prefer a strong small-x shadowing of the lead gluon nPDF, a feature also reported in [133]. Furthermore, since the central value of the gluon around $x\simeq 0.2$ is unchanged but the uncertainties are almost halved, the CMS dijet data also enhances the fit preference for a strong gluon anti-shadowing in the large-x region.

Fig. 23

The impact of the CMS dijet pPb-to-pp ratio measurements at 5.02 TeV on the quark singlet (left) and gluon (right panel) nPDFs of lead. We display results for the nuclear modification factors $R^{(A)}(x,Q)$ at $Q=10$ GeV, comparing the nNNPDF2.0r fit with the variant including the CMS dijet data (upper) as well as for the corresponding pulls defined in Eq. (4.2) (bottom panels). The dotted horizontal lines indicate the $3\sigma$ thresholds

The impact of the CMS dijet measurements on the nPDF fit is also illustrated by the comparison of the pulls before and after its inclusion, displayed in the bottom panels of Fig. 23. For the quark singlet, the dijet data enhances the pull for , strengthening the evidence for quark sector shadowing in this region. For , outside the region covered by the CMS dijet data, uncertainties grow rapidly and the fit results are consistent with no nuclear modifications at the 68% CL. Considering the gluon nPDF, one finds that while the baseline fit is consistent with no small-x anti-shadowing within uncertainties, once the CMS dijets are accounted for this significance reaches the $3\sigma$ level, peaking at $x\simeq 10^{-2}$. The constraints provided by the CMS dijets are also visible for the large-x anti-shadowing, whose significance increases from the $2\sigma$ to the $3\sigma$ level. All in all, these comparisons illustrate how the CMS dijet measurements are instrumental in nNNPDF3.0 to pin down the modifications of the gluon PDF.

5.4 Impact of kinematic cuts on the $D^0$-meson transverse momentum

As mentioned in Sect. 2, no kinematic cuts are applied to the transverse momentum of the $D^0$ meson, $p_T^{D^0}$, in the analysis of the LHCb $D^0$-meson data entering our baseline fits. We assess the stability of our results upon this choice by repeating the reweighting of the prior fit displayed in Fig. 10 after applying a cut on $p_T^{D^0}$, for different values of the cut. We specifically consider the following cases: $p_T^{D^0}>2$ GeV, $p_T^{D^0}>3$ GeV, and $p_T^{D^0}>5$ GeV. For each of them, Table 7 collects the same statistical estimators reported in Table 6: the number of effective replicas $N_{\mathrm{eff}}$, the number of replicas in the unweighted set $N_{\mathrm{unweight}}$, the number of data points, and the values of the $\chi ^2$ per data point before and after reweighting. We note that, as the cut on $p_T^{D^0}$ is increased, the value of the prior $\chi ^2$ decreases, the number of effective replicas increases, and the value of the $\chi ^2$ after reweighting remains similar irrespective of the $p_T^{D^0}$ cut.

Table 7 Same as Table 6, now for varying cuts on the transverse momentum of the $D^0$ meson $p_T^{D^0}$

Figure 24 displays the resulting PDF nuclear modification factors for the nNNPDF3.0 variants carried out with kinematic cuts of $p_T^{D^0} \ge 3$ GeV and $p_T^{D^0} \ge 5$ GeV at $Q^2=10$ $\hbox {GeV}^2$. The effect of introducing a $p_T^{D^0}$ cut is moderate, though generally leads an increase in the resultant nPDF uncertainties. The more restrictive the cut, the larger the uncertainty increase. For instance, in the region $x\simeq 10^{-4}$, the nPDF errors on the gluon nuclear modification factor increase by around a factor of two for $p_T^{D^0} \ge 5$ GeV. However, even in the conservative case, where the restriction of $p_T^{D^0} \ge 5$ GeV is applied to the LHCb $D^0$-meson data, the reduction of nPDF uncertainties is substantial as compared to the no LHCb $D^0$-meson scenario (see for example the comparison in Fig. 10) This fact highlights how even only a subset of the LHCb data still imposes significant constraints on the small-x nPDFs. In addition, the consistency of the results obtained when restricting the data with a varying $p_T^{D^0}$ cut also indicate that the nNNPDF3.0 determination is robust upon introduction and variation of a cut on $p_T^{D^0}$.

Fig. 24

Same as Fig. 10, now at $Q^2=10$ $\hbox {GeV}^2$, comparing the baseline nNNPDF3.0 determination with the variants where kinematic cuts of $p_T^{D^0} \ge 3$ GeV and $p_T^{D^0} \ge 5$ GeV are applied to the LHCb $D^0$-meson cross-section data, see also Table 7

5.5 Constraints from the $D^0$-meson forward-to-backward ratio

In Sect. 4.2 we assessed the impact of the $D^0$-meson production measurements from LHCb in nNNPDF3.0 in terms of the ratio between pPb and pp spectra in the forward region defined in Eq. (2.3). An alternative observable to assess the impact of the LHCb $D^0$-meson data in the nPDF fit is provided by the ratio of forward-to-backward measurements defined in Eq. (2.4). Since in the nucleon-nucleon CoM frame LHCb measurements cover the range $1.5< y^{D^0} < 4.0$ and $2.5< y^{D^0} < 5.0$ for pPb (forward) and pPb (backwards) collisions respectively, the forward-to-backward ratio $R_{\mathrm{fb}}$ is provided in the three overlapping rapidity bins covering the region $2.5< y^{D^0} < 4.0$, adding up to a total of 27 data points.

First of all, in Fig. 25 we display theoretical predictions for $R_{\mathrm{fb}}$ in these three rapidity bins computed using nNNPDF3.0 as input (which includes the constraints provided by $R_{\mathrm{fb}}$). This comparison accounts for both uncertainties due to PDFs and MHOs, and demonstrates that predictions based on nNNPDF3.0 also provide a satisfactory description of the $R_{\mathrm{fb}}$ data, which were not included in the fit. Hence, the information on the nPDFs provided by the two LHCb observables is consistent.

Fig. 25

Comparison between the LHCb data on the ratio of forward-to-backward measurements $R_{\mathrm{fb}}$ and the corresponding theoretical predictions based on nNNPDF3.0 (which includes instead the data on $R_{\mathrm{pPb}}$). The $R_{\mathrm{fb}}$ ratio is available in the three rapidity bins for which the forward (pPb) and backward (Pbp) measurements overlap. We display separately the PDF and scale uncertainties

As an additional check of the stability of our results, we have studied the impact of the inclusion of the $R_{\mathrm{fb}}$ data on the nNNPDF3.0 prior described in Sect. 3.4. Figure 26 displays the theoretical predictions for the nNNPDF3.0 prior set (with the LHCb D-meson data accounted for only via the pp baseline) compared to the corresponding LHCb measurements of the forward-backward ratio $R_{\mathrm{fb}}$ as well as to the result of including this dataset in the fit by means of Bayesian reweighting. As in the case of Fig. 7, we display separately the uncertainties due to PDFs and MHOs for the prediction based on the prior fit. In the same manner as for the forward Pb-to-pp ratio Eq. (2.3), also in $R_{\mathrm{fb}}$ the PDF uncertainties dominate both over scale uncertainties (partially cancelling out in the ratio) and over the experimental errors. This assessment indicates that the LHCb measurements of $R_{\mathrm{fb}}$ are also suitable to be included in nNNPDF3.0 via reweighting. As was the case for the $R_{\mathrm{pPb}}$ data, the theoretical predictions for $R_{\mathrm{fb}}$ display a significantly reduced PDF uncertainty once this dataset has been added to the prior via reweighting. In Table 8 we report the details of the reweighting and unweighting procedures.

Fig. 26

Same as Fig. 7 now for the case in which the LHCb data on the forward-to-backward ratio $R_{\mathrm{fb}}$ defined in Eq. (2.4) is added to the prior set by reweighting

Figures 27 and 28 then compare the impact on the nNNPDF3.0 prior fit of the LHCb $D^0$-meson pPb data when accounted for using either the forward pPb-to-pp ratio $R_{\mathrm{pPb}}$, Eq. (2.3), or the forward-to-backward ratio $R_{\mathrm{fb}}$, Eq. (2.4), at the level of the lead PDFs and of the nuclear modification factors respectively. One finds that the outcome of including the LHCb $D^0$-meson data using either $R_{\mathrm{pPb}}$ or $R_{\mathrm{fb}}$ is fully compatible, with the former leading to a somewhat larger reduction of the PDF uncertainties and hence justifying our baseline choice in the nNNPDF3.0 dataset. The obtained central values are also similar for the two observables, especially in the case of the gluon nuclear modification factor. We note that, as already remarked in Sect. 4.2, the impact of the LHCb D-meson data is substantial in the nuclear ratio, which accounts for the correlations between the proton and lead PDF uncertainties. These results demonstrate that the impact of the LHCb D-meson data in the nNNPDF3.0 determination is robust upon variations of the experimental observable included in the fit.

6 (Ultra-)high-energy neutrino-nucleus interactions

As motivated in Sect. 1, precise and accurate knowledge of nPDFs is crucial for predicting the absolute rate of ultra-high-energy (UHE) neutrino–nucleon DIS interactions. This information is important for the interpretation of UHE neutrino events observed at large-volume based neutrino detectors such as IceCube [15] and KM3NeT [16], which can in turn provide vital information on the rates of atmospheric and cosmic neutrino production mechanisms. At yet higher energies (beyond the PeV), proposed large volume detectors such as GRAND [137] or POEMMA [138] may also contribute to our knowledge of the cosmic neutrino flux for energies up to $10^9$ GeV (see [139] for a feasibility study). In those cases, knowledge of nuclear corrections is either necessary for describing neutrino-matter interactions within the detector volume (e.g. water), or required to describe the attenuation rate of neutrinos as they travel through Earth towards the various detector [10]. The uncertainty related to the magnitude of these nuclear corrections is the dominant source of theoretical uncertainty in describing UHE neutrino-matter interactions (see Fig. 5 of [140] for a breakdown of the various uncertainties).

We are now in a position to present updated predictions for UHE neutrino-nucleus cross-sections based on nNNPDF3.0. Our calculational settings follow [9] for the neutrino-nucleon DIS cross-section and use APFEL [68] to evaluate the structure functions for both charged- and neutral-current interactions. These calculations are performed in the FONLL general-mass variable flavour number scheme (consistently with the nNNPDF3.0 fit), but differ from the calculation presented in [9] through the inclusion of two-quark mass contributions to the charged-current DIS structure function. The latter contributions are necessary to account for fixed-order corrections of the form $\alpha _s \ln [m_b] m_t^2$ when following the FONLL implementation [141], and become numerically relevant in the region of $E_{\nu } \ge 10^{6}~\hbox {GeV}$, where $E_\nu$ is the energy of the neutrino (see the discussion in App. B.3 of [10]). These additional corrections are evaluated with an independent code developed in [142].

In the following, we present results separately for inclusive cross-sections in charged- and neutral-current DIS as a function of $E_{\nu }$. Predictions are provided assuming an isoscalar nuclear target with nuclear mass numbers of $A\! \!=\!\! 1, 16$, and 31. These choices are representative of a free nucleon, and oxygen nucleon, and the average atomic mass number $\langle A \rangle$ encountered by a neutrino traversing Earth respectively. Those values of A are hence relevant for describing neutrino-matter interactions within a detector volume composed of $\mathrm{H}_{2}\mathrm{O}$ molecules (e.g. IceCube, KM3NeT), as well as neutrinos traveling through the Earth. Notably, here we focus only on the dominant neutrino-nucleon DIS contribution to the cross-section for which the presented nPDFs are relevant. There are additional (in)elastic resonant and coherent scattering contributions [140, 143,144,145,146] which must also be included to achieve percent-level accurate predictions (see [10] for a summary).

Table 8 Same as Table 6, now for the case of the inclusion of the LHCb data on $R_{\mathrm{fb}}$ to the prior fit by means of reweighting

Fig. 27

The impact of the $D^0$-meson production data from pPb collisions on the lead PDF at $Q=10$ GeV. We compare the nNNPDF3.0 prior set with the outcome of the reweighting with the LHCb $D^0$-meson pPb data using either the forward pPb-to-pp ratio $R_{\mathrm{pPb}}$, Eq. (2.3), or the forward-to-backward ratio $R_{\mathrm{fb}}$, Eq. (2.4). Results are presented normalised to the central value of the nNNPDF3.0 prior

Fig. 28

Same as Fig. 27 for the nuclear modification factors $R_f^{(A)}(x,Q^2)$

Fig. 29

Comparison of the inclusive CC (left) and NC (right) neutrino-nucleon cross-section as a function of incident neutrino energy. Predictions are shown for isoscalar nuclear target with $A = 1, 16, 31$, where the uncertainty bands represent the nPDF 68% CL intervals. The prediction are normalised with respect to the $A=1$ central value

In Fig. 29 the results for the charged- (left) and neutral-current (right) cross-sections are shown for predictions based on nNNPDF3.0 for $A = 1, 16, 31$. The central value and uncertainty band represent the median and 68% CL interval respectively, and in each case the cross-sections are shown normalised with respect to the $A=1$ central value. At low $E_{\nu }$ values, the nuclear corrections act to lower the inclusive cross-section by $1~(2)\%$ for $A=16~(31)$, which are corrections that are of the same magnitude as the $A=1$ PDF uncertainties (i.e. those in the absence of nuclear corrections). In the PeV ($10^{6}$ GeV) energy regime, a kinematic region currently accessible by neutrino telescopes, the nuclear corrections remain negative and amount to $\simeq 2~(3)\%$ for $A=16~(31)$. Even at the highest energies, the overall PDF uncertainties remain below $10\%$ and the nuclear-induced suppression of the central values is at most 4%. Note that unlike the previous determinations [9, 10, 140], the nuclear dependence of these cross-sections is computed directly without the need to factorise free-nucleon PDF and nPDF effects.

Fig. 30

Comparison of the inclusive CC neutrino-nucleon cross-section as a function of incident neutrino energy for different nPDF sets. Predictions are shown for an isoscalar nuclear target with $A = 16$ (left) and $A = 31$ (right), and the uncertainty bands represent the nPDF 68% CL intervals. Each prediction is shown normalised with respect to the nNNPDF3.0 central value

In Fig. 30 we display results for the absolute cross-sections in charged-current DIS predicted for $A=16$ (left) and $A=31$ (right). Predictions are obtained with nNNPDF3.0, nNNPDF3.0 (no LHCb D), nNNPDF2.0, and in each case the central value and uncertainties represent the median and 68% CL intervals. For comparison, these predictions have been normalised to the central value of the nNNPDF3.0 result. Overall, these predictions demonstrate the improvement with respect to the previous determination of nPDFs (nNNPDF2.0). This improvement is a result of the knowledge of the quark and gluon PDFs at small-x values, which is driven by the inclusion of both dijet and the LHCb D-meson data. In practice, the inclusion of LHCb D-meson data in nNNPDF3.0 is found to have only a moderate impact on these predictions. This is because the nuclear corrections for the PDFs of low mass nuclei (i.e. $A = 16, 31$) at small-x values are found to be small, combined with the fact that the boundary condition for the nPDF fit (i.e. the proton baseline) is similar whether the LHCb D-meson data is included or not (see Fig. 2).

Overall, the results presented here demonstrate the important role played by collider physics data in improving our understanding of scattering processes which are essential to the study of both atmospheric and astrophysical neutrinos.

7 Delivery, usage, summary and outlook

The nNNPDF3.0 analysis presented in this paper has led to the determination of two nPDF sets, obtained with and without the LHCb D-meson production data respectively. In comparison to the previous nNNPDF2.0 analysis, they both benefit from an extended dataset and from a more sophisticated fitting methodology. We list the nPDF grid files that are made available in the LHAPDF6 format in Sect. 7.1, provide prescriptions for their usage in Sect. 7.2, and present a summary of the main features of nNNPDF3.0 and of possible future developments in Sect. 7.3.

7.1 Delivery

The nNNPDF3.0 parton sets are made available as interpolation grids in the LHAPDF6 format [31] for all phenomenologically relevant nuclei from $A\!=\!1$ to $A\!=\!208$. Grid files are available both for the nPDFs of bound protons, $f^{(p/A)}(x,Q^2)$, and for bound average nucleons, $f^{(N/A)}(x,Q^2)$, see the conventions described in Appendix A. Each of these sets is composed by $N_{\mathrm{rep}}=200$ (250) correlated replicas for the fits with (without) the LHCb D-meson data. In addition, for the nNNPDF3.0 variant without the LHCb D-meson data, we also make available high-statistics grids with $N_{\mathrm{rep}}=1000$ replicas.

The nPDF sets that include the LHCb D-meson production measurements are named:

where each of these grid files contains $N_{\mathrm{rep}}=200$ replicas, fully correlated among the different values of A. The names indicated in blue correspond to nuclear species for which direct experimental constraints are not available, and which are made available (via the continuous A parameterisation of the nPDFs) because of their phenomenological relevance.

The nPDF sets that do not include the LHCb D-meson production measurements are named:

with $N_{\mathrm{rep}}=250$ replicas each. The corresponding sets with $N_{\mathrm{rep}}=1000$ replicas have the same names with an additional suffix _1000. The nPDF sets indicated in blue are as above.

The nPDF sets are also available on the NNPDF Collaboration website: http://nnpdf.mi.infn.it/for-users/nnnpdf3-0/.

7.2 Usage

As discussed in previous nNNPDF studies [25, 26], the recommended usage of the nNNPDF3.0 sets is given by the following prescription. Consider a general nPDF-depending quantity, indicated schematically by

$$\begin{aligned} {\mathcal {F}}\left[ f_{i_1}^{(p/A_1)}(x_1,Q_1),f_{i_2}^{(p/A_2)}(x_2,Q_2), \ldots \right] . \end{aligned}$$

(7.1)

This quantity could represent e.g. a nPDF, ${\mathcal {F}}= f_g^{(p/A)}(x,Q)$, a nuclear ratio, ${\mathcal {F}}= f_g^{(p/A)}(x,Q)/f_g^{(p)}(x,Q)$, a proton-lead LHC cross-section, or a UHE cross-section. To evaluate the most-likely value and uncertainty for ${\mathcal {F}}$ based on nNNPDF3.0, first one evaluates this quantity for the $N_{\mathrm{rep}}$ replicas composing this set:

$$\begin{aligned} {\mathcal {F}}^{(k=1)},{\mathcal {F}}^{(k=2)},{\mathcal {F}}^{(k=3)},\ldots ,{\mathcal {F}}^{(k=N_{\mathrm{rep}})} , \end{aligned}$$

(7.2)

recalling that within a given set, different values of A are fully correlated (including $A=1$, the free-proton baseline). Next, order the elements of Eq. (7.2) in ascending order and remove symmetrically $(100-X)\%$ of the replicas with the highest and lowest values. The resulting interval defines the $X\%$ confidence level for this quantity, given the nPDF set used in the calculation.

For instance, a 68% CL interval (corresponding to a 1-$\sigma$ interval for a Gaussian distribution) is obtained by keeping the central 68% replicas by removing the lowest 16% and highest 16% of the (ordered) replicas. The best-fit value for the quantity ${\mathcal {F}}$ is taken to be the median evaluated over all of the replicas.

The rationale for estimating the nPDF uncertainties as CL intervals, as opposed to the variance, is that nNNPDF3.0 probability distributions are not always well described by a Gaussian approximation. We also note that implementations of this procedure are available in most numerical libraries. For example in NumPy if F corresponds to the (unordered) array containing the $N_{\mathrm{rep}}$ replicas of ${\mathcal {F}}$, one can compute the lower and upper limits of the 68% CL interval with high = np.nanpercentile(F,84) and low = np.nanpercentile(F,16).

7.3 Summary and outlook

The nNNPDF3.0 analysis presented in this work is based on an extensive set of measurements using nuclear probes. These include in particular pPb LHC data for dijet, isolated photon and $D^0$-meson production. A key aspect of nNNPDF3.0 is the coherent treatment of the experimental input in both the proton, deuteron, and nuclear PDFs. This ensures its consistent theoretical and methodological treatment throughout the fitting procedure.

Overall we find an excellent compatibility between the constraints provided by the data already in nNNPDF2.0 and the new data in nNNPDF3.0. The new data significantly improves the precision with which nuclear modification factors are determined. In particular, we have established strong evidence of deviations from the free-proton baseline for small-x shadowing in lead nuclei both in the quark and in the gluon sector, as well as for gluon anti-shadowing at large-x also in the case of lead. Furthermore, we have studied the dependence of the nuclear modification factors on the atomic number A, assessed the robustness of nNNPDF3.0 with respect to variations in the input dataset and the fitting methodology, and outlined the impact on nPDFs of specific processes, in particular of dijet and D-meson production cross-sections.

As a representative phenomenological application of nNNPDF3.0, we have presented updated predictions for the ultra-high-energy neutrino-nucleus scattering cross-sections for different nuclear targets. We have considered $A=16$, relevant for neutrino scattering off water and ice targets, and $A=31$, required for the calculations of neutrino flux attenuation due to their interactions with matter within Earth before being detected. In both cases the significance of nuclear modification effects, in particular small-x shadowing, are enhanced in comparison to nNNPDF2.0, and exhibit substantially reduced theory uncertainties.

The results presented in this work could be expanded in several theoretical, experimental, and methodological aspects. Concerning theory, the accuracy of the nPDF determination could be improved by including NNLO QCD corrections in the solution of the DGLAP equations and in the hard-scattering cross-sections. One could also account for missing higher-order corrections as additional correlated uncertainties, e.g. by means of the method developed in [69, 70]. Even if the fit quality of nNNPDF3.0 is overall very good, the precision of forthcoming LHC measurements is expected to increase with the higher luminosity achieved in Run III. Higher-order corrections may therefore become essential to describe future data, especially for absolute spectra in processes such as dijet and isolated photon production for which the NLO calculations are currently unsatisfactory. The inclusion of higher-order corrections (and theory uncertainties) is likely relevant for the description of D-meson data, which has a large impact on nPDFs in the region of small-x. This was already indicated by the study [86], which showed that the treatment of ${\mathcal {O}}(\alpha _s^4)$ terms in D-meson production has a small but noticeable impact on the extracted value of the gluon PDF.

Concerning experimental data, additional analyses of LHC Run II pPb collision measurements are expected to become available, as are new analyses of LHC Run III. In particular, the upcoming pO and OO LHC runs [6] will constrain the nuclear modification factors for a much lower value of A than pPb collisions. One such example is dijet production [147]. In addition, nuclear structure function measurements in fixed-target DIS at JLab [134] may be used to improve the determination of nuclear modifications at very large values of x. In the longer term, nPDFs will be probed at the EIC [17,18,19], by means of GeV-scale lepton scattering on light and heavy nuclei, and at the FPF [20], by means of TeV-scale neutrino scattering on heavy nuclear targets.

Finally, concerning methodology, one may consider integrating more coherently the free-proton PDF boundary condition with the A-dependent nPDFs. Given that, in general, proton-nucleon collision constrain both proton and nuclear PDFs, and that both will be probed with similar precision, this separation appears to be artificial and undesirable. A more sophisticated approach should aim to determining proton, deuteron, and nuclear PDFs simultaneously within a single QCD analysis. Such an approach will bypass the need to carry out proton and nuclear fits separately, and to use one as input to the other. Such a program, which is being developed, e.g. for the simultaneous determination of (polarised) PDFs and fragmentation functions [148,149,150], represents a major milestone to fully exploit a much wider range of future measurements.

Appendices

Appendix A: Notation and conventions

Throughout this work we adopt the following conventions.

• The laboratory frame refers to the reference frame of the asymmetric pPb collisions as they take place at LHC, see also the discussion in Appendix B.

• The nucleon–nucleon (NN) or CoM frame refers to the reference frame where the two colliding nucleons (one from the proton beam and another from the lead nucleus) have a vanishing total three-momentum, $\mathbf {p}_{\mathrm{tot}} = \mathbf {p}_{\mathrm{p}} + \mathbf {p}_{\mathrm{N/Pb}} =0$, where $\mathbf {p}_{\mathrm{N/Pb}}$ indicates the average linear momentum carried by a nucleon N (proton or neutron) within the lead nucleus.

• pPb (Pbp) collisions indicate collisions where the proton beam circulates in the positive (negative) z-direction in the laboratory frame, corresponding to forward (backward) rapidity regions in this reference frame.

  Hence in pPb (Pbp) collisions the region $z >0$ ($z<0$) corresponds to the proton–going direction, and $z <0$ ($z>0$) to the lead–going direction instead.

• The nPDFs $f^{(A)}(x,Q)$ of a nucleus with atomic charge Z and atomic mass number A, following the convention used in nNNPDF2.0, are defined as:

  $$\begin{aligned}&f^{(A)}(x,Q) = A f^{(N/A)}(x,Q)\nonumber \\&\quad = \left( Z f^{(p/A)}(x,Q) + (A-Z)f^{(n/A)}(x,Q) \right) , \end{aligned}$$

  (A.1)

  such that the nPDF $f^{(N/A)}(x,Q)$ corresponding to the average bound nucleon N within the nucleus A is given by

  $$\begin{aligned}&f^{(N/A)}(x,Q) = \frac{ Z}{A} f^{(p/A)}(x,Q)\nonumber \\&\quad + \frac{(A-Z)}{A}f^{(n/A)}(x,Q) , \end{aligned}$$

  (A.2)

  where f is a quark or the gluon. For $(Z,A)=(1,1)$ one reproduces the free-proton PDFs.

  $f^{(p/A)}$ and $f^{(n/A)}(x,Q)$ denote the nPDFs of bound protons and neutrons, respectively, within a nucleus with atomic mass number A, and are related to each other via isospin symmetry e.g. $u^{(p/A)}=d^{(n/A)}$.

• Genuine nuclear effects on the nPDFs correspond to the case where these differ from their free-nucleon counterparts once isospin effects are accounted for, that is,

  $$\begin{aligned} R_f^{(A)}(x,Q) \equiv \frac{ f^{(N/A)}(x,Q)}{\frac{ Z}{A} f^{(p)}(x,Q) + \frac{(A-Z)}{A}f^{(n)}(x,Q)} \ne 1 ,\nonumber \\ \end{aligned}$$

  (A.3)

  where $f^{(p)}$ and $f^{(n)}$ are the free proton and neutron PDFs, again related to each other by isospin symmetry.

Appendix B: Reference frames in asymmetric pPb collisions

An important difference between pp and pPb collisions at the LHC is that the latter are asymmetric because the energy per nucleon of the lead projectile is smaller as compared to the proton one. This implies that the final state of the collision will be boosted along the proton–going direction, and hence that the laboratory frame does not coincide with the CoM frame in these collisions. In this appendix we review the treatment of asymmetric pPb collisions and the role played by the transformation between the laboratory and the center-of-mass frame in the global nPDF analysis.

Boost between laboratory and CoM frames When accelerated in opposite directions at the LHC, the proton and lead beams are required to have an equal magnetic rigidity³ [151]. This implies that the energy of lead in the laboratory frame, $E^{\mathrm{lab}}_{\mathrm{Pb}}$, must be related to that of the colliding protons $E^{\mathrm{lab}}_{\mathrm{p}}$ by $E^{\mathrm{lab}}_{\mathrm{Pb}} = Z E^{\mathrm{lab}}_{\mathrm{p}}$, where the atomic number for lead is $Z=82$. In the laboratory frame we can express the four-momenta of the proton $p_{\mathrm{p}}^{\mu }$ and of the average nucleon N in lead, denoted as $p_{\mathrm{N/Pb}}^{\mu }$, by

$$\begin{aligned} p_{\mathrm{p}}^{\mu }= & {} \left( E_p, 0, 0, E_p\right) , \nonumber \\ p_{\mathrm{N/Pb}}^{\mu }= & {} \left( \frac{Z}{A} E_p, 0, 0, -\frac{Z}{A} E_p\right) , \end{aligned}$$

(B.1)

where the atomic mass number for lead is $A=208$, we neglect nucleon mass effects, the beams collide along the z-direction, and the positive direction coincides with the proton direction of motion. The total four-momentum and CoM energy of the nucleon–nucleon collision is given by

$$\begin{aligned}&p_{\mathrm{tot}}^{\mu } = p_{\mathrm{p}}^{\mu } + p_{\mathrm{N/Pb}}^{\mu } = \left( E_p+\frac{Z}{A} E_p, 0, 0, E_p-\frac{Z}{A} E_p\right) , \nonumber \\\end{aligned}$$

(B.2)

$$\begin{aligned}&\sqrt{s_{\mathrm{NN}}} = \sqrt{ p_{\mathrm{tot}}^2} = 2\sqrt{\frac{Z}{A}}E_p \simeq 1.2558E_p . \end{aligned}$$

(B.3)

Since $\sqrt{s_{\mathrm{NN}}}$ is a Lorentz invariant, its value is the same in any reference frame and hence Eq. (B.3) holds both in the laboratory and in the (NN) CoM frame.

Equation (B.2), together with momentum conservation, implies that in the laboratory frame the final state of the pPb collision will move with a non-zero momentum $p_z>0$ along the proton direction. Therefore, the value of $p_z$ of the measured final state particles (and of their rapidity) will be different from that expected in the CoM frame, where $p_{\mathrm{z,tot}}=0$ vanishes by construction. Accounting for this asymmetry is necessary for the interpretation of hard-scattering cross-sections in pPb collisions. Indeed, the rapidity y of a particle with energy E and linear momentum in the beam direction $p_z$ is defined as

$$\begin{aligned} y = \frac{1}{2}\ln \left( {\frac{E+p_{z}}{E-p_{z}}}\right) , \end{aligned}$$

(B.4)

and depends on the specific reference frame (though rapidity differences do not). For a collision taking place in the CoM frame, one has that the final state is characterised by $p_z^{\mathrm{tot}}=0$ and hence $y=0$. However, in the laboratory frame instead, using the four-vector in Eq. (B.2) one finds that the rapidity of the collision final-state in the laboratory frame is

$$\begin{aligned} y^{\mathrm{lab}} = \frac{1}{2}\ln \frac{A}{Z} \simeq 0.46541 , \end{aligned}$$

(B.5)

reflecting how after the collision the system keeps moving in the proton–going direction. Hence, a rapidity boost arises, $\Delta y \equiv y^{\mathrm{lab}} -y = 0.46541$, between particle kinematics as measured in the laboratory frame and those predicted in the CoM frame that needs to be accounted for:

$$\begin{aligned} y^{\mathrm{lab}}= & {} y + \Delta y~(\mathrm{from~CoM~frame~to~lab~frame}) , \nonumber \\ y= & {} y^{\mathrm{lab}} - \Delta y~(\mathrm{from~lab~frame~to~CoM~frame}) . \end{aligned}$$

(B.6)

This rapidity shift $\Delta y$ between the two reference frames is invariant under longitudinal Lorentz boosts and therefore it is not affected by the partonic kinematics as discussed below.

Fig. 31

Comparison between the theoretical predictions based on both nNNPDF3.0 and the variant without the LHCb D-meson cross-sections and the ATLAS measurements of the ratio of isolated photon production spectra between pPb and pp collisions at $\sqrt{s}=8.16$ TeV. Results are presented differential in the photon transverse energy $E_T^\gamma$ for three photon pseudo-rapidity $\eta _{CM}$ bins in the CoM frame. The band in the theory prediction indicates the PDF uncertainty, and the bottom panels display the ratio to the central theory. No scale uncertainties are considered in this comparison. The value of the $\chi ^2$ to this dataset for both nNNPDF3.0 is also indicated in the legend

Partonic kinematics The general factorised expression for hard-scattering cross-sections in pPb collisions can be written as

$$\begin{aligned}&\frac{d\sigma _{\mathrm{pPb}}}{dQ^2dy} = \sum _{a,b} \int _{x_1}^1 d\xi _{1} \int _{x_2}^1 d\xi _{2}~~f_a^{(\mathrm {p})}(\xi _1,Q^2)f_b^{({\mathrm{Pb}})}(\xi _2,Q^2)\nonumber \\&\quad \times \frac{d{\hat{\sigma }}_{ab}}{dQ^2d{\hat{y}}}\left( \frac{x_1}{\xi _1},\frac{x_2}{\xi _2},Q^2\right) , \end{aligned}$$

(B.7)

where y (${\hat{y}}$) denotes the rapidity of the hadronic (partonic) final state, $Q^2$ is the hard scale that makes the process perturbative, $f_a^{(\mathrm {p})}$ and $f_b^{({\mathrm{Pb}})}$ indicate the PDFs of the proton and of the lead nucleus respectively (see Appendix A for the adopted conventions), and a, b are partonic indices. We have omitted the dependence on the factorisation and renormalisation scales for simplicity. Neglecting hadron and parton mass effects, and assuming the CoM reference frame, one can relate the incoming partonic ${\hat{p}}_i^{\mu }$ and hadronic $p_i^\mu$ four-momenta as

$$\begin{aligned} {\hat{p}}_i^{\mu } = x_ip_i^\mu = x_i E(1,0,0,\pm 1),\qquad i=\mathrm{p, N/Pb} , \end{aligned}$$

(B.8)

where $x_i$ is the momentum fraction carried by the colliding parton from nucleon i, $p_i^z = +x_iE$ ($-x_iE$) for $i=p$ ($i=\mathrm{N/Pb}$), and the nucleon energy E does not depend on i in this reference frame. One can then evaluate the hadronic and partonic collision energies in this reference frame as usual:

$$\begin{aligned} \sqrt{s}&= \sqrt{(p_1+p_2)^2} = 2E , \end{aligned}$$

(B.9)

$$\begin{aligned} \sqrt{{\hat{s}}}&= \sqrt{({\hat{p}}_1+{\hat{p}}_2)^2} = \sqrt{x_1x_2}\sqrt{s} . \end{aligned}$$

(B.10)

Even for collisions in this CoM frame, the final state particles will exhibit a non-trivial rapidity distribution related to the distribution in momentum fractions $x_1$ and $x_2$ dictated by the PDFs. Indeed, the rapidity of the produced final state assuming colliding partons carrying momentum fractions $x_1$ and $x_2$ is

$$\begin{aligned} y= & {} \frac{1}{2}\ln \left( {\frac{{\hat{E}}+{\hat{p}}_{z}}{{\hat{E}}-{\hat{p}}_{z}}}\right) \nonumber \\= & {} \frac{1}{2}\ln \left( {\frac{E(x_1+x_2)+E(x_1-x_2)}{E(x_1+x_2)-E(x_1-x_2)}}\right) \nonumber \\= & {} \frac{1}{2}\ln \left( {\frac{x_1}{x_2}}\right) . \end{aligned}$$

(B.11)

Note that the distribution in rapidity y hence follows closely the distribution in $x_1$ and $x_2$ dictated by the PDFs through Eq. (B.7). This distribution will be in general asymmetric due to the difference between the proton and nuclear PDFs. Even in the absence of genuine nuclear effects, nuclear PDFs are different from the proton ones due to isospin effects.

For a $2\rightarrow 1$ type process such as Drell–Yan, Eq. (B.11) can be re-arranged, assuming leading-order kinematics, to write the momentum fractions $x_1$ and $x_2$ in terms of the rapidity of the reconstructed gauge-boson as

$$\begin{aligned} x_{1(2)} = \sqrt{\frac{Q^2}{s}}e^{(-)y}, \end{aligned}$$

(B.12)

with $Q^2 = m_{V} = \sqrt{{\hat{s}}}$. For $2\rightarrow 2$ type processes a similar relation in terms of out-going particle kinematics may be written

$$\begin{aligned} x_{1(2)} = \frac{1}{\sqrt{s}} \left( E_{T,3} e^{(-)y_3} + E_{T,4} e^{(-)y_4} \right) , \end{aligned}$$

(B.13)

where the labels ‘3’ and ‘4’ refer to the outgoing particles. For the proton–nucleus scattering processes considered in this work, assuming leading-order kinematics, we have

$$\begin{aligned} E_{T,3} = E_{T,4} = {\left\{ \begin{array}{ll} p_{T}^{j} \quad &{} \text {Dijet production} \\ E_T^{\gamma }\quad &{} \text {Photon production} \\ \sqrt{(p_{T}^{c})^2 +m_c^2}\quad &{} c\text {-quark production} \end{array}\right. }\nonumber \\ \end{aligned}$$

(B.14)

This information, in combination with the approximation $y_3 \approx y_4$, is used to estimate the kinematic coverage of the available experiment data which are displayed in Fig. 1.

Fig. 32

Same as Fig. 31 for LHC datasets on gauge boson production in pPb collisions, specifically for the ATLAS and CMS Z production measurements at 5.02 TeV, and the charged lepton rapidity distributions for $W^+$ and $W^-$ collisions from CMS at 5.02 TeV and 8.16 TeV

Fig. 33

Same as Fig. 31 for other LHC datasets on gauge boson production in pPb collisions, in particular the ALICE and LHCb forward and backward measurements of W and Z production at 5.02 TeV and 8.16 TeV and the differential measurements of Z production at 8.16 TeV from CMS in two bins of the dimuon invariant mass $M_{\mu {{\bar{\mu }}}}$

Implications for pPb collisions. The relations in Eq. (B.6) make it possible to relate cross-sections measured in the laboratory frame with those predicted in the CoM frame and vice-versa by means of a rapidity shift

$$\begin{aligned} \frac{d\sigma (Q^2,y)}{dQ^2dy}\Bigg |_{\mathrm{lab}}= & {} \frac{d\sigma (Q^2,y-\Delta y)}{dQ^2dy}\Bigg |_{\mathrm{NN}}, \end{aligned}$$

(B.15)

$$\begin{aligned} \frac{d\sigma (Q^2,y)}{dQ^2dy}\Bigg |_{\mathrm{NN}}= & {} \frac{d\sigma (Q^2,y+\Delta y)}{dQ^2dy}\Bigg |_{\mathrm{lab}} . \end{aligned}$$

(B.16)

These relations are particularly useful when evaluating theoretical cross-sections for hard-probes in pPb collisions. The reason is that most available codes assume symmetric NN collisions, but the data is in many cases presented in the laboratory frame. As indicated by Eq. (B.15), it suffices to shift either the rapidity bins or equivalently the cross-section histograms by $\Delta y = 0.4651$ before or after the computation respectively. We also note that switching the (p) and (Pb) superscripts in Eq. (B.7) is equivalent to switching the minus and plus signs in Eq. (B.8), i.e. switching the proton and lead beams.

Fig. 34

Same as Fig. 31 for the CMS measurements of dijet production in proton-lead collisions at 5.02 TeV, presented in terms of the ratio between pPb and pp spectra

It is also worth mentioning that given pPb (Pbp) collisions, the data measured in the forward (backward) rapidity regions constrain the large-x region of the proton PDFs and the small-x region of the lead PDFs, see Eq. (B.13), and vice-versa in Pbp (pPb) collisions. The ATLAS and CMS detectors cover the central rapidity region and hence provide access to both forward and backward final states. The asymmetric configuration of the ALICE and LHCb detectors imply that final states are only detected in the forward rapidity region [152] and hence recording data from both pPb and Pbp collisions is instrumental to maximise the coverage in Bjorken-x for the lead PDF.

Appendix C: Comparison between nNNPDF3.0 and experimental data

In this appendix we present representative comparisons between the NLO QCD theoretical predictions obtained from nNNPDF3.0 and the corresponding experimental measurements. In particular, we focus on the LHC pPb datasets, with the exception of the LHCb $D^0$-meson measurements that have been already discussed in Sects. 4 and 5. We describe first of all the data versus theory comparisons for those datasets which are part of nNNPDF3.0, and then for completeness for those excluded from the nNNPDF3.0 baseline for the reasons discussed in Sect. 2.

Comparison with datasets included in nNNPDF3.0 To begin with, Fig. 31 displays a comparison between the theoretical predictions based on both nNNPDF3.0 and the variant without the LHCb D-meson cross-sections and the ATLAS measurements of the ratio of isolated photon production spectra between pPb and pp collisions at $\sqrt{s}=8.16$ TeV.

Results are presented differential in the photon transverse energy $E_T^\gamma$ for three photon pseudo-rapidity $\eta _{CM}$ bins in the CoM frame.

The band in the theory prediction indicates the PDF uncertainty, and the bottom panels display the ratio to the central theory.

No uncertainty due to MHOs is considered in this comparison.

The value of the $\chi ^2$ to this dataset for both nNNPDF3.0 is also indicated in the legend. We note that the same format will be used for the rest of the plots in this appendix.

This comparison confirms that a good description of this dataset is achieved by the NLO QCD calculation in the three rapidity bins available.

Then in Figs. 32 and 33 we display similar comparisons as those in Fig. 31 for LHC datasets on gauge boson production in pPb collisions. Specifically, we show in turn the ATLAS and CMS Z production measurements at 5.02 TeV; the charged lepton rapidity distributions for $W^+$ and $W^-$ collisions from CMS at 5.02 TeV and 8.16 TeV; the ALICE and LHCb forward and backward measurements of W and Z production at 5.02 TeV and 8.16 TeV; and the differential measurements of Z production at 8.16 from CMS in two bins of the dimuon invariant mass $M_{\mu {{\bar{\mu }}}}$.

From this comparison, one can observe that in general there is very good agreement between the NLO QCD predictions based on nNNPDF3.0 and the corresponding experimental measurements. As expected, given that their differences are localised at small-x, the predictions based on the variant without the LHCb D-meson data are very similar to those from the baseline fit. The only pPb gauge boson production dataset for which the quality of the data description is somewhat unsatisfactory are the CMS differential measurements of Z production at 8.16 TeV. From the bottom plots of Fig. 33, we see however that for the on-peak region, with $60\le M_{\mu {{\bar{\mu }}}}\le 120~\mathrm{GeV}$, there is excellent agreement between theory and data for all rapidity bins except for the most backward ones, where the data undershoots theory by about $3\sigma$. Concerning the off-peak invariant mass region, $15\le M_{\mu {{\bar{\mu }}}}\le 60~\mathrm{GeV}$, the theory undershoots the data by a factor which is more or less rapidity independent and that could be explained by the absence of NNLO QCD corrections, which are known to be non-negligible in this kinematic region.

Finally, Fig. 34 compares the NLO QCD calculations based on nNNPDF3.0 with the CMS measurements of dijet production at 5.02 TeV presented in terms of the ratio between pPb and pp spectra. These measurements are presented as a function of the dijet rapidity $\eta _{\mathrm{dijet}}$ in five bins of the dijet average transverse momentum $p_{T,\mathrm{dijet}}^{\mathrm{avg}}$. We find how in general there is good agreement between the CMS data and the theory calculations for most of the range in $\eta _{\mathrm{dijet}}$ and $p_{T,\mathrm{dijet}}^{\mathrm{avg}}$ covered. One difference with the LHC electroweak measurements is that for dijet production one can appreciate how the nNNPDF3.0 predictions exhibit reduced PDF uncertainties, especially for the forward and backward bins, as compared to the variant without the LHC D-meson cross-sections included. The only noticeable discrepancy arises for the two most forward bins in $\eta _{\mathrm{dijet}}$ for the first four $p_{T,\mathrm{dijet}}^{\mathrm{avg}}$ bins, where the CMS data markedly undershoots the theory predictions. We have verified that in a fit where these forward bins are removed, the fit quality to the CMS dijets is improved down to $\chi ^2/n_{\mathrm{dat}}$ without any appreciable change at the level of the nPDFs themselves.

Appendix D: Reweighting validation

In this appendix we assess the performance of the Bayesian reweighting method, by comparing it with the direct inclusion of the same dataset in the prior nPDF set. As discussed in Sect. 3.4, in general the results of including a new dataset on the prior nPDF fit will not be identical in both methods. One reason is that the figure of merit used in the reweighting procedure is $\chi _{\mathrm{t_0}}^2$ in Eq. (3.5), and hence it does not account for the theoretical constraints that enter the full $\chi _{\mathrm{fit}}^2$ in the fit, namely the $A=1$ free-proton PDF boundary condition and the positivity of cross-sections. Furthermore, Bayesian reweighting assumes some degree of compatibility between the prior fit and the new data, such that the $\chi ^2$ evaluated over the unweighted replicas for the new dataset follows (approximately) a $\chi ^2$-like distribution. This condition may not be satisfied in the case of e.g. internal inconsistencies of the added dataset. Within a direct fit this problem is avoided, since stopping is based on look-back cross-validation rather than in reaching target $\chi ^2$ values. Finally, finite-sample effects may also lead to small differences, since formally reweighting and refitting coincide only in the $N_{\mathrm{rep}},~N_{\mathrm{eff}}\rightarrow \infty$ limit.

Fig. 35

Comparison between the theoretical predictions based on nNNPDF2.0r and on two variants where the first bin ($55<p_{T,\mathrm{dijet}}^{\mathrm{avg}}<75~\mathrm{GeV}$) of the CMS dijet ratio data has been added either via direct inclusion in the fit or by means of Bayesian reweighting. The band in the theory prediction indicates the PDF uncertainty, while the bottom panels display the ratio to the central theory prediction. No estimate of uncertainties due to MHOs are considered in this comparison. We also indicate in the legend the corresponding values for the $\chi ^2/n_{\mathrm{dat}}$ in each case

For this validation exercise, we consider nNNPDF2.0r as the prior nuclear PDF set and the first bin of the CMS dijet pPb/pp ratio measurements ($55<p_{T,\mathrm{dijet}}^{\mathrm{avg}}<75~\mathrm{GeV}$) as the new dataset to be added either via direct inclusion in the fit or by means of Bayesian reweighting. Figure 35 displays the comparison between the theoretical predictions based on nNNPDF2.0r and in the two associated variants where this dataset has been added either via direct inclusion in the fit or by means of reweighting. The band in the theory prediction indicates the PDF uncertainty, while the bottom panels display the ratio to the central theory prediction. We also indicate in the legend the corresponding values for the $\chi ^2/n_{\mathrm{dat}}$ in each case.

Fig. 36

The nuclear modification ratios $R_f^{(A)}(x,Q^2)$ in nNNPDF2.0r, compared to the outcome of adding to nNNPDF2.0r the first $p_{T,\mathrm{dijet}}^{\mathrm{avg}}$ bin of the CMS dijet measurements either via direct inclusion in the fit of via Bayesian reweighting. We show the results for $^{208}$Pb (top) and $^{12}$C (bottom panels)

The nNNPDF2.0r prior describes this dataset (recall that only the first CMS dijet bin is considered here) rather poorly, with $\chi ^2/n_{\mathrm{dat}}=3.24$ for $n_{\mathrm{dat}}=18$. The fit quality is markedly improved once this dataset is included in the fit either by direct inclusion or via reweighting, with $\chi ^2/n_{\mathrm{dat}}=1.95$ and 1.23 respectively. In both cases, we observe how the theoretical predictions move closer to the data, favouring large-x anti-shadowing (central rapidities) and small-x shadowing (forward and backward rapidities) respectively for the gluon nPDF. The reweighted predictions agree within uncertainties with the direct fit results for all the $\eta _{\mathrm{dijet}}$ bins considered. For the most forward and backward rapidity bins the reweighted predictions prefer smaller values for the cross-section ratio (i.e. a stronger suppression of the nPDFs), providing a slightly better description of the data. This may be explained by the fact that the evaluation of the $\chi ^2$ in the reweighting procedure is not constrained by the free proton boundary condition constraint. Consequently, the proton boundary condition can be modified in the reweighting procedure, which provides extra flexibility when describing the ratio observable.

Figure 36 then displays the nuclear modification ratios $R_f^{(A)}\,(x,Q^2)$ in nNNPDF2.0r compared to those associated to the variant fits where the CMS dijet data is added to the prior either via direct inclusion in the fit of via Bayesian reweighting. From top to bottom, we show the results for lead ($^{208}$Pb) and then for carbon ($^{12}$C) nuclei. Recall that the reweighting procedure determines the weight of each replica taking into account the information contained in the new dataset, and hence it modifies the predictions for the nuclear modifications also for different values of A as compared to that for which the data is provided ($A=208$ in this case).

In the case of the nuclear modifications of lead, we observe that in the kinematic region for which the CMS data provides sensitivity () the reweighted results reproduce the qualitative behaviour of the direct fit predictions. In particular, for the gluon nuclear ratio the reweighting procedure correctly identifies the small-x suppression and the large-x enhancement as compared to the prior. As observed in Fig. 36, reweighting also tends to somewhat overestimate the impact of the new dataset as compared to direct inclusion in the fit, at least for this specific case. Hence this analysis confirms that reweighting captures the main features of the information provided by the new dataset on the nPDFs when the same value of A is considered. However, in the case of a low-A nuclei such as carbon ($A=12$), reweighting appears to induce a reduction of the nPDF uncertainty absent in the direct fit. As discussed above, this effect may be attributed to the absence of the $A=1$ boundary condition in the evaluation of the $\chi ^2$ value in the reweighting procedure.

We emphasise that the specific dataset considered in the exercise displayed in Figs. 35 and 36 represents an extreme case, in the sense that the CMS dijet measurement is one of the datasets carrying most information in the nNNPDF3.0 fit.