1 Introduction

It is now well established that the Universe at late times experienced the transition from the matter era to the accelerated expansion phase. Although the simplest explanation would be the consideration of the cosmological constant, the corresponding problem related to the quantum-field-theoretical calculation of its value, as well as the possibility of a dynamical nature, led to two main paths of constructing extended scenarios. The first is to maintain general relativity as the underlying theory of gravity, and consider new, exotic forms of matter that constitute the concept of dark energy [1,2,3]. The second is to construct extended or modified theories of gravity, that posses general relativity as a low-energy limit, but which in general provide the extra degrees of freedom that can drive the dynamical universe acceleration [4,5,6,7].

Nevertheless, one can acquire an alternative explanation of the dark energy origin, through the cosmological application [8,9,10] of the holographic principle [11,12,13]. The corresponding framework is based on the thermodynamics of black holes and the connection of the Ultraviolet cutoff of a quantum field theory (related to the vacuum energy), with the largest distance of the theory (which in turn is a requirement in order for the theory to be applicable at large distances) [14]. In particular, in a given system whose entropy is proportional to its volume, the total energy should not be larger than the mass of a black hole with the same size, whose entropy is proportional to its area, since in such a case the system would collapse to a black hole. If one considers the whole Universe as the system one extracts a vacuum energy of holographic origin, namely a form of holographic dark energy with dynamical nature [15, 16].

The cosmological implications of holographic dark energy proves to be very interesting [15,16,17,18,19,20,21,22,23,24,25,26] and it proves to be in agreement with observations [27,28,29,30,31,32]. In this scenario one is free of the naturalness problem of the cosmological constant [33], as well as from pathologies that may arise in various modified gravity constructions [7]. Additionally, it has been shown to be able to alleviate the \(H_0\) and growth tensions between \(\Lambda \)CDM scenario and some direct measurements [34]. That is why a large amount of research has been devoted to these investigations, and the basic models have been extended in various ways [35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71].

The basic expression in the construction of holographic dark energy is the one that connects the entropy of a system with geometrical quantities such as its radius. The standard one is the Bekenstein–Hawking entropy, which arises as the black-hole and cosmological application of the standard Boltzmann–Gibbs entropy. However, Kaniadakis has proposed a one-parameter generalization of the Boltzmann–Gibbs entropy, called Kaniadakis entropy [72, 73]. This results from a self-consistent and coherent relativistic statistical theory, in which the basic features of standard statistical theory are maintained. In such an extended statistical theory, the distribution functions are a one-parameter continuous deformation of the usual Maxwell–Boltzmann ones, and hence standard statistical theory is recovered in a particular limit.

In the present work we will use Kaniadakis entropy in order to formulate Kaniadakis holographic dark energy, and study its cosmological implications. Although in the literature there were some first attempts towards this direction [74,75,76] the resulting models were not correct. The reason for this failure was the fact that the authors used the Hubble horizon instead of the future event horizon in the basic holographic expression. Therefore, not only the resulting models could not recover usual holographic dark energy in the limit where Kaniadakis entropy becomes standard entropy, as it should, but in order to be able to describe the universe evolution one needs unacceptably large values of the Kaniadakis parameter, namely unacceptably large deviations from standard entropy. Hence, in this work we proceed to the consistent formulation of Kaniadakis holographic dark energy, which is indeed a well-defined extension of standard holographic dark energy, recovering it as a particular limit in the case where Kaniadakis entropy becomes standard Bekenstein-Hawking entropy.

The plan of the manuscript is the following: In Sect. 2 we formulate Kaniadakis holographic dark energy, we present the corresponding cosmological equations and we extract analytical relations for the dark energy density and equation-of-state parameters. Then in Sect. 3 we proceed to the study of the resulting cosmological behavior. Finally, in Sect. 4 we discuss our results and we summarize.

2 Kaniadakis holographic dark energy

In this section we proceed to the formulation of Kaniadakis holographic dark energy. The basic idea behind holographic dark energy is the inequality \(\rho _{DE} L^4\le S\), where L is the largest distance of the theory (the Infrared cutoff) and S the entropy relation applied in a black hole of radius L [15, 16]. In the case of standard Bekenstein-Hawking entropy \(S_{BH}\propto A/(4G)=\pi L^2/G\), with G the Newton’s constant, the saturation of the above inequality gives standard holographic dark energy, namely \(\rho _{DE}=3c^2 M_p^2 L^{-2}\), with \(M_p\) the Planck mass and c the model parameter. Hence, we can see that if instead of standard entropy we use a modified one, we will obtain a modified holographic dark energy.

As we mentioned in the Introduction, Kaniadakis entropy is a one-parameter generalization of the classical entropy. It is given by [72, 73]

$$\begin{aligned} S_{K}=- k_{_B} \sum _i n_i\, \ln _{_{\{{\scriptstyle K}\}}}\!n_i , \end{aligned}$$
(2.1)

with \(k_{_B}\) the Boltzmann constant, and where we have defined \(\ln _{_{\{{\scriptstyle K}\}}}\!x=(x^{K}-x^{-K})/2K\). Kaniadakis entropy is characterized by the single dimensionless parameter K, which quantifies the deviation from the case of standard statistical mechanics. Hence, standard entropy is recovered in the limit \(K\rightarrow 0\), while K can vary in the range \(-1<K<1\). Additionally, in such a generalized statistical theory the distribution function reads as \( n_i= \alpha \exp _{_{\{{\scriptstyle K}\}}}[-\beta (E_i-\mu )] , \) where \(\exp _{_{\{{\scriptstyle K}\}}}(x)= \left( \sqrt{1+K^2x^2}+K x\right) ^{1/K}\), \(\alpha =[(1-K)/(1+K)]^{1/2K}\), \(1/\beta =\sqrt{1-K^2}\,\,k_{_{B}}\!T\), and the chemical potential \(\mu \) can be fixed by normalization [72, 73]. Kaniadakis entropy can be expressed as [77,78,79,80,81,82]

$$\begin{aligned} S_{K} =-k_{_B}\sum ^{W}_{i=1}\frac{P^{1+K}_{i}-P^{1-K}_{i}}{2K}, \end{aligned}$$
(2.2)

where \(P_i\) is the probability the system to be in a specific microstate and W the total number of configurations.

Let us apply Kaniadakis entropy in the black-hole framework, which will then be needed for the holographic application. Assuming that \(P_i=1/W\), using the fact that Boltzmann-Gibbs entropy is \(S\propto \ln (W)\), while the Bekenstein-Hawking entropy is given by \(S_{BH}= A/(4G)\), we acquire \(W=\exp \left[ A/(4G)\right] \) [74], where from now on we impose units in which the Boltzmann constant, the light speed, and the reduced Planck constant are set to \(k_{_B}=c=\hbar =1\). Hence, inserting these into (2.2) we find

$$\begin{aligned} S_{K} = \frac{1}{K}\sinh {(K S_{BH})}. \end{aligned}$$
(2.3)

As expected in the limit \(K\rightarrow 0\) one recovers standard Bekenstein-Hawking entropy, i.e. \(S_{K\rightarrow 0}=S_{BH}\). Since in reality one expects the above modified entropy to be close to the standard Bekenstein-Hawking value, we expect that \(K\ll 1\) (we remind that \(-1<K<1\)). Thus, it is justified to expand the above Kaniadakis entropy for small K, obtaining

$$\begin{aligned} S_{K} = S_{BH}+ \frac{K^2}{6} S_{BH}^3+ \mathcal{{O}}(K^4). \end{aligned}$$
(2.4)

As one can see, the first term is the usual entropy, while the second term is the lowest-order Kaniadakis correction.

It is now easy to extract the relation of Kaniadakis holographic dark energy. In particular, inserting (2.4) into the inequality \(\rho _{DE} L^4\le S\), we obtain

$$\begin{aligned} \rho _{DE}= 3c^2 M_p^2 L^{-2}+ 3{\tilde{c}}^2K^2 M_p^6 L^2, \end{aligned}$$
(2.5)

with c and \({\tilde{c}}\) constants. As mentioned above, for \(K=0\) the above expression gives the usual holographic dark energy \(\rho _{DE}=3c^2 M_p^2 L^{-2}\). In the following we absorb the constant \({\tilde{c}}\) inside the parameter K, by setting \(3{\tilde{c}}^2K^2\equiv {\tilde{K}}^2\) and we drop the tildes for simplicity.

We proceed by considering a flat homogeneous and isotropic Friedmann–Robertson–Walker (FRW) geometry with metric

$$\begin{aligned} ds^{2}=-dt^{2}+a^{2}(t)\delta _{ij}dx^{i}dx^{j}, \end{aligned}$$
(2.6)

with a(t) the scale factor. As a next step, in any holographic dark energy scenario, one needs to determine the length L that appears in the corresponding relations. In the case of standard holographic dark energy models it is well known that L cannot be the Hubble horizon \(H^{-1}\) (where \(H\equiv {\dot{a}}/a\) is the Hubble function), since this choice leads to obvious inconsistencies [83], such as no acceleration. Thus, one must use the future event horizon [15]

$$\begin{aligned} R_h\equiv a\int _t^\infty \frac{dt}{a}= a\int _a^\infty \frac{da}{Ha^2}. \end{aligned}$$
(2.7)

As we mentioned in the Introduction, in some recent attempts to construct Kaniadakis holographic dark energy the authors used (2.3) but then they considered the Hubble horizon to be L [74,75,76]. Thus, the obtained models do not have standard holographic dark energy and standard thermodynamics as a sub-case, and this is a serious disadvantage. One can verify that in a clear way by observing that in order to have reasonable observational results the authors demand K values of the order of \(10^3\), namely a huge deviation from standard Bekenstein-Hawking entropy, which is not observed (not mentioning the fact that the initial K parameter of Kaniadakis entropy is bounded in \(-1<K<1\)).

In the present work we desire to formulate Kaniadakis holographic dark energy in a consistent way, and hence we use as L the future event horizon (2.7). In this way, as we will see, standard holographic dark energy is included as a sub-case, and can be obtained for \(K\rightarrow 0\). However, let us comment here that using the future event horizon does have the disadvantage that the dark-energy density at present depends on the future expansion of the Universe [16], in a similar way that the use of the Hubble horizon has the disadvantage that the dark-energy density, which is a local concept, depends on the global picture of the whole Universe, namely on the global expansion scale. Nevertheless, we mention that the use of both horizons, as well as other horizons, such as the Granda–Oliveros cutoff [84], is in principle justified exactly by the concept of holography and the dualities known from string theory, that relate the very small with the very large in space and time.

According to the above discussion, and using (2.5) with L the \(R_h\), the energy density of Kaniadakis holographic dark energy writes as

$$\begin{aligned} \rho _{DE}= 3c^2 M_p^2 R_h^{-2}+ K^2 M_p^6 R_h^2. \end{aligned}$$
(2.8)

The Friedmann equations in a universe containing the dark energy and matter perfect fluids are

$$\begin{aligned} 3M_p^2 H^2= & {} \ \rho _m + \rho _{DE} \end{aligned}$$
(2.9)
$$\begin{aligned} -2 M_p^2{\dot{H}}= & {} \rho _m +p_m+\rho _{DE}+p_{DE}, \end{aligned}$$
(2.10)

with \(p_{DE}\) the pressure of Kaniadakis holographic dark energy, and \(\rho _m\) and \(p_m\) respectively the energy density and pressure of the matter sector. The equations close by considering the matter conservation equation

$$\begin{aligned} {\dot{\rho }}_m+3H(\rho _m+p_m)=0. \end{aligned}$$
(2.11)

It proves convenient to introduce the dark energy and matter density parameters through

$$\begin{aligned} \Omega _m\equiv & {} \frac{1}{3M_p^2H^2}\rho _m \end{aligned}$$
(2.12)
$$\begin{aligned} \Omega _{DE}\equiv & {} \frac{1}{3M_p^2H^2}\rho _{DE}. \end{aligned}$$
(2.13)

Using these definitions, relations (2.7), (2.8), (2.13) lead to

$$\begin{aligned} \int _x^\infty \frac{dx}{Ha}=\frac{1}{a}\left( \frac{3H^2 \Omega _{DE}- \sqrt{9H^4 \Omega _{DE}^2 -12c^2 K^2M_p^4} }{2K^2M_p^4} \right) ^{\frac{1}{2}},\nonumber \\ \end{aligned}$$
(2.14)

where \(x\equiv \ln a\). Note that solving the fourth-degree algebraic equation (2.8) we have kept only the solutions that give positive \(R_h\) and moreover with the usual limiting result for \(K\rightarrow 0\). Indeed, as one can see, in the limit \(K\rightarrow 0\) the above relation gives the standard holographic dark energy result \( \int _x^\infty \frac{dx}{Ha}= \frac{c}{aH\sqrt{\Omega _{DE}}}\).

We focus on the physically interesting dust matter case, where the matter equation-of-state parameter is set to zero. Therefore, (2.11) leads to \(\rho _m=\rho _{m0}/a^3\), where \(\rho _{m0}\) is the matter energy density at the current scale factor \(a_0=1\) (we use the subscript “0” to denote the present value of a quantity). Hence, substituting into (2.12) leads to \(\Omega _m=\Omega _{m0} H_0^2/(a^3 H^2)\), and then, using the Friedmann equation \(\Omega _m+\Omega _{DE}=1\), we find

$$\begin{aligned} \frac{1}{Ha}=\frac{\sqrt{a(1-\Omega _{DE})}}{H_0\sqrt{\Omega _{m0}}}. \end{aligned}$$
(2.15)

Inserting (2.15) into (2.14) leads to

$$\begin{aligned}&\int ^{\infty }_{x}\frac{dx}{H_{0}\sqrt{\Omega _{m0}}}\sqrt{a(1-\Omega _{DE})}\nonumber \\&\quad =\frac{1}{a}\left( \frac{3H^2 \Omega _{DE}- \sqrt{9H^4 \Omega _{DE}^2 -12c^2 K^2M_p^4} }{2K^2M_p^4} \right) ^{\frac{1}{2}}.\nonumber \\ \end{aligned}$$
(2.16)

In the following we use \(x=\ln a\) as the independent variable, and therefore for a quantity f we acquire \({\dot{f}}=f' H\), with primes denoting derivatives with respect to x. Differentiating (2.16) in terms of x we obtain

$$\begin{aligned} \Omega _{DE}'= & {} \Omega _{DE}(1-\Omega _{DE})\left\{ 3-\frac{2({\mathcal {A}}-2K^{2}M_{p}^{4}{\mathcal {B}})}{{\mathcal {A}}}\right. \nonumber \\&\times \left. \left[ 1-\sqrt{3}\left( \frac{\Omega _{DE}}{{\mathcal {A}}{\mathcal {B}}}\right) ^{\frac{1}{2}}\right] \right\} , \end{aligned}$$
(2.17)

with

$$\begin{aligned} {\mathcal {A}}= & {} \frac{3\mathrm {e}^{-3x}H^{2}_{0}\Omega _{m0}\Omega _{DE}}{1-\Omega _{DE}}, \\ {\mathcal {B}}= & {} \frac{{\mathcal {A}}-\sqrt{{\mathcal {A}}^{2}-12c^{2}K^{2}M^{4}_{p}}}{ 2K^{2}M^{4}_{p}}. \end{aligned}$$

Differential equation (2.17) determines the evolution of Kaniadakis holographic dark energy as a function of \(x=\ln a\), in the case of flat spatial geometry and for dust matter. We mention that in the limit \(K\rightarrow 0\) we have \({\mathcal {B}}|_{K\rightarrow 0}=\frac{3c^{2}}{{\mathcal {A}}}\), and hence (2.17) recovers the corresponding differential equation of usual holographic dark energy [15], i.e. \(\Omega _{DE}'|_{K\rightarrow 0}= \Omega _{DE}(1-\Omega _{DE})\left( 1+2\sqrt{\frac{3M_p^2\Omega _{DE}}{3 c^2 M_p^2}} \right) \), which, since the x-dependence is absent, accepts an analytic solution in an implicit form [15].

We proceed by examining the behavior of the equation-of-state parameter \(w_{DE}\equiv p_{DE}/\rho _{DE}\) of Kaniadakis holographic dark energy. From the conservation of the matter sector (2.11), and using the two Friedmann equations (2.9), (2.10), we deduce that the dark energy sector is conserved too, i.e.

$$\begin{aligned} {\dot{\rho }}_{DE}+3H\rho _{DE}(1+w_{DE})=0. \end{aligned}$$
(2.18)

Differentiating (2.8) gives \({\dot{\rho }}_{DE}=2M^{2}_{p}\left( -3c^{2}R^{-4}_{h}+K^{2}M^{4}_{p}\right) R_{h}{\dot{R}}_{h}\). In this expression we have that \({\dot{R}}_h=H R_h-1\), as it is found from (2.7), where \(R_h\) can be further eliminated in terms of \(\rho _{DE}\) according to (2.8) as

$$\begin{aligned} R_h=\left( \frac{\rho _{DE}-\sqrt{\rho ^{2}_{DE}-12c^{2}K^{2}M^{8}_{p}}}{2K^{2}M^{6}_{p}} \right) ^{1/2}\equiv {\mathcal {C}}. \end{aligned}$$
(2.19)

Substituting all the above into (2.18) we acquire

$$\begin{aligned} 2M^{2}_{p}(H {\mathcal {C}}-1 )\left( \frac{{-}3c^{2}{+}K^{2}M^{4}_{p}{\mathcal {C}}^{4}}{{\mathcal {C}}^{3 }}\right) +3H\rho _{DE}(1+w_{DE})=0.\nonumber \\ \end{aligned}$$
(2.20)

Therefore, inserting H from (2.15), and using definition (2.13) after some algebra we find

$$\begin{aligned} w_{DE}= & {} -1-2\left( \frac{\Omega _{DE}}{3{\mathcal {A}}^{3}} \right) ^{\frac{1}{2}}\left( \frac{-3c^{2}+K^{2}M^{4}_{p}{\mathcal {B}}^{2}}{{\mathcal {B}}^{\frac{3}{2}}}\right) \nonumber \\&\times \left[ -1+\frac{\sqrt{3}}{3}\left( \frac{{\mathcal {A}}{\mathcal {B}}}{\Omega _{DE}} \right) ^{\frac{1}{2}}\right] . \end{aligned}$$
(2.21)

Hence, \(w_{DE}\) as a function of \(\ln a\) is known, as long as \(\Omega _{DE}\) is known from (2.17). Note that for \(K\rightarrow 0\) the above expression provides the standard holographic dark energy result, i.e. \(w_{DE}|_{K\rightarrow 0}=-\frac{1}{3}-\frac{2}{3}\frac{\sqrt{\Omega _{DE}}}{c}\) [16], as expected. Additionally, we mention that in general \(w_{DE}\) can be either quintessence-like or phantom-like, which is an advantage revealing the rich capabilities of the scenario at hand.

Lastly, for convenience we can introduce the deceleration parameter

$$\begin{aligned} q\equiv -1-\frac{{\dot{H}}}{H^2}=\frac{1}{2}+\frac{3}{2}\left( w_m\Omega _m+w_{DE} \Omega _{DE} \right) , \end{aligned}$$
(2.22)

which in the case of dust matter is straightforwardly known as long as \(\Omega _{DE}\) (and thus \(w_{DE}\) from (2.21)) is known.

We close this section by discussing the relation of Kaniadakis entropy with other extended entropies, and in particular with Tsallis one. As it is known, the non-extensive Tsallis entropy \(S^{T}_q\), with q the parameter which quantifies the deviation from Bekenstein–Hawking entropy [85, 86], is related to Kaniadakis one through [74, 79, 87]

$$\begin{aligned} S_{K} =\frac{S^{T}_{1+K}+S^{T}_{1-K}}{2}. \end{aligned}$$
(2.23)

Concerning the other recently proposed generalized entropy by Barrow, namely \(S^{B}_\Delta \), which arises from the intricate structure of the black-hole surface due to quantum-gravitational effects, with \(\Delta \) the parameter that quantifies the deviation from usual entropy [88], we mention that although mathematically one can extract the relation \( S_{K} =\frac{S^{B}_{\Delta }+S^{B}_{-\Delta }}{2}\), it cannot have a physical application since in Barrow entropy \(0\le \Delta \le 1\).

3 Cosmological evolution

In the previous section we formulated Kaniadakis holographic dark energy, and we provided the equations that determine the evolution of the corresponding dark energy density, equation-of-state and deceleration parameters. Hence, we can now proceed to a detailed investigation of the resulting cosmological behavior. Since Eq. (2.17) can be solved analytically only for \(K=0\), in the general case we should resort to numerical elaboration. As long as we have the solution for \(\Omega _{DE}(x)\) we can obtain its behavior in terms of the redshift z through the simple relation \(x\equiv \ln a=-\ln (1+z)\). Finally, we mention that Kaniadakis entropy is an even function, namely \(S_{K}=S_{-K}\), and that is why all the above expressions of Kaniadakis holographic dark energy depend only on \(K^2\). Thus, in the following we focus on the \(K\ge 0\) region.

Fig. 1
figure 1

Upper graph: the Kaniadakis holographic dark energy density parameter \(\Omega _{DE}\) (blue-solid) and the matter density parameter \(\Omega _{m}\) (red-dashed), as a function of the redshift z, for \(K=0.1\) and \(c=0.9\). Middle graph: the corresponding dark-energy equation-of-state parameter \(w_{DE}\). Lower graph: the corresponding deceleration parameter q. In all graphs we have set \(\Omega _{DE}(x=-\ln (1+z)=0)\equiv \Omega _{DE0}\approx 0.7\) in agreement with observations, and for convenience we have added a vertical dotted line marking the present time \(z=0\)

Full size image

We solve Eq. (2.17) numerically, imposing \(\Omega _{DE}(x=-\ln (1+z)=0)\equiv \Omega _{DE0}\approx 0.7\) and therefore \(\Omega _m(x=-\ln (1+z)=0)\equiv \Omega _{m0}\approx 0.3\) in agreement with observations [89]. In the upper graph of Fig. 1 we depict the evolution of the dark energy and matter density parameters in terms of the redshift. Additionally, in the middle graph we present the corresponding behavior of the dark-energy equation-of-state parameter as it arises from (2.21). Finally, in the lower graph we show the deceleration parameter as it is given from (2.22). We mention that for reader’s convenience we have extended the evolution up to the far future, namely for \(z\rightarrow -1\).

As we observe, the scenario at hand can provide the required thermal history of the universe, i.e. the sequence of matter and dark energy epochs, and the universe results asymptotically to a complete dark-energy dominated phase. Moreover, from the middle graph of Fig. 1 we can see that the value of \(w_{DE}\) at present is around \(-1\) in agreement with observational data. Note that in this specific example \(w_{DE}\) in the future enters slightly inside the phantom regime, which as mentioned above is allowed by (2.21) and shows the capabilities of the model. Finally, from the lower graph of Fig. 1 we deduce that the transition from deceleration to acceleration is realized at \(z\approx 0.6\), in agreement with observations.

Fig. 2
figure 2

The redshift-evolution of the equation-of-state parameter \(w_{DE}\) of Kaniadakis holographic dark energy, for fixed \(K=0.1\) and various values of c. We have imposed \(\Omega _{DE0}\approx 0.7\) and we have added a vertical dotted line marking the present time \(z=0\)

Full size image

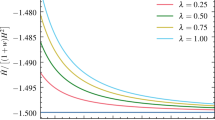
Let us now study the effect of the model parameters c and K on the dark-energy equation-of-state parameter \(w_{DE}\). In Fig. 2 we depict \(w_{DE}(z)\) for fixed \(K=0.1\) and various values of c. As we can see, with c decreasing \(w_{DE}(z)\), as well as its present value \(w_{DE}(z=0)\), acquire algebraically lower values, experiencing the phantom-divide crossing during the evolution. Note that for \(c<0.9\) the value of \(w_{DE}(z=0)\) lies in the phantom regime. Furthermore, in Fig. 3 we present \(w_{DE}(z)\) for fixed \(c=1\) and various values of K. Here we observe the interesting behavior that for increasing K, at earlier times \(w_{DE}\) slightly decreases, in future times in increases, however at times around the present ones it remains almost unaltered. Concerning the asymptotic value of \(w_{DE}\) in the far future, namely for \(z\rightarrow -1\), as can be deduced from the figures, as well as form (2.21), it depends on the combination of K and c. In summary, we can see that the scenario of Kaniadakis holographic dark energy can lead to very interesting cosmological phenomenology, in which \(w_{DE}\) can be quintessence-like, phantom-like, or cross the phantom divide before or after the present time. Note that these results are in agreement with other researches on Kaniadakis holographic dark energy, that appeared after the present work, especially with observational confrontation [90,91,92,93,94,95].

Fig. 3
figure 3

The redshift-evolution of the equation-of-state parameter \(w_{DE}\) of Kaniadakis holographic dark energy, for fixed \(c=1\) and various values of K. We have imposed \(\Omega _{DE0}\approx 0.7\) we have added a vertical dotted line marking the present time \(z=0\)

Full size image

4 Conclusions

In this work we formulated a holographic dark energy scenario based on Kaniadakis entropy. The latter is a generalization of Boltzmann-Gibbs entropy, arising form a coherent relativistic statistical theory and characterized by a single parameter K that quantifies the deviations from standard expressions. Hence, by applying the usual steps of holographic dark energy, imposing the future event horizon as the Infrared cutoff, and using Kaniadakis extended entropy, we obtained Kaniadakis holographic dark energy in a consistent way, namely a one-parameter extension of usual holographic dark energy, possessing it as a particular limit, namely for \(K\rightarrow 0\).

In order to investigate the cosmological application of Kaniadakis holographic dark energy we extracted the differential equation that determines the evolution of the effective dark energy density parameter \(\Omega _{DE}\). Moreover, we provided analytical expressions for the corresponding equation-of-state parameter \(w_{DE}\), as well as for the deceleration parameter.

The scenario of Kaniadakis holographic dark energy proves to lead to interesting cosmological behavior. In particular, the universe exhibits the standard thermal history, i.e. the sequence of matter and dark-energy eras, while the transition to acceleration takes place at \(z\approx 0.6\). Concerning the dark-energy equation-of-state parameter we saw that it can have a rich behavior, being quintessence-like, phantom-like, or experience the phantom-divide crossing in the past or in the future, depending on the values of the two model parameters c and K. In particular, for fixed K decreasing c leads to algebraically smaller \(w_{DE}\) values, while for fixed c by increasing K we acquire smaller \(w_{DE}\) values at higher redshifts, larger \(w_{DE}\) values in the future, and almost unaltered values at present. Finally, in the far future dark energy dominates completely, and the asymptotic \(w_{DE}\) value depends on c and K.

We comment here that, as we mentioned in the Introduction, it has been recently shown that holographic dark energy constructions may alleviate the \(H_0\) tension (see the corresponding sections in the recent review [34]), and the reason is that they may lead to \(w_{DE}<-1\) which seems to be a requirement if one desires to provide a solution based on late-time modifications [66, 96]. As we saw, the scenario at hand can fulfill this requirement and that is why it is a candidate to be able to alleviate the \(H_0\) tension too. Definitely the phantom regime may have potential disadvantages, however this is not in general the case in models which present phantom behavior in an effective way, among which is holographic dark energy [16].

In conclusion, Kaniadakis holographic dark energy exhibits richer and more interesting behavior in comparison to usual holographic dark energy. Additionally, due to the consistent formulation, it possesses the latter as a limiting sub-case. Definitely, before one considers it as a successful candidate for the description of dark energy, there are necessary investigations that should be performed. In particular, one should confront the scenario with observational data from Supernova type Ia (SNIa), baryon acoustic oscillation (BAO), cosmic microwave background (CMB), and Hubble parameter observations, and extract constraints on the model parameters. Additionally, one should analyze in detail the phase-space behavior, in order to examine the global dynamics and the asymptotic, late-time evolution of the scenario. These investigations will be performed in separate projects.