How to understand the X(2900)?

Abstract

In this work, the S- and P-wave $\bar{D}^*K^*$ interactions are studied in a coupled-channel formalism to understand the recently observed $X_0(2900)$ and $X_1(2900)$ at LHCb. The experimental event distributions can be well described, and two states with $I(J^P)=0(0^+)$ and $0(1^-)$ are yielded in a unified framework. The masses of the $0^+$ and $1^-$ states are consistent with the experimental data, but the width of the $0^+$ state is larger than that of the $1^-$ one. The $X_1(2900)$ can be interpreted as the P-wave excitation of the ground-state $X_0(2900)$ in the hadronic molecular picture. The S- and P-wave multiplets in the $\bar{D}^*K^*$ system have many members, so the present peak in the $D^-K^+$ invariant mass distributions might contain multi substructures.

1 Introduction

Recently, the LHCb Collaboration observed a clear peak in the $D^-K^+$ invariant mass spectrum of the $B^+\rightarrow D^+D^-K^+$ decay [1, 2], where the helicity angle distribution shows evident P-wave behavior. The peak is fitted with spin-0 and spin-1 states. Their resonance parameters are determined to be

$$\begin{aligned} X_0(2900): M= & {} 2866\pm 7\pm 2~\text {MeV},\\ \Gamma= & {} 57\pm 12\pm 4~\text {MeV};\\ X_1(2900): M= & {} 2904\pm 5\pm 1~\text {MeV},\\ \Gamma= & {} 110\pm 11\pm 4~\text {MeV}. \end{aligned}$$

The $D^-K^+$ decay channel implies their quark components should be $\bar{c}\bar{s}ud$, which means that they are the fully open flavor exotic hadrons.

Many theoretical interpretations have been proposed to understand the inner structures of X(2900), such as the molecular states from the $\bar{D}^*K^*$ and $\bar{D}_1K$ interactions [3,4,5,6,7], the compact tetraquarks $\bar{c}\bar{s}ud$ [3, 8,9,10,11,12], and kinematic effects from the triangle singularities [13, 14]. The production and decay properties were investigated in Refs. [15,16,17,18]. One can also consult Refs. [19,20,21,22,23,24,25,26,27,28,29,30,31] for other pertinent works.

In Ref. [8], the $X_0(2900)$ was interpreted as the S-wave compact tetraquark in a string-junction picture, while the subsequent calculations in Ref. [9] supported it to be the radial excited tetraquark with $J^P=0^+$. Meanwhile, the obtained masses with the refined quark model calculations in Refs. [12, 20, 22] are much lower than the measured mass of $X_0(2900)$. In other words, the isosinglet S-wave compact tetraquark $\bar{c}\bar{s}ud$ can not reconcile with the $X_0(2900)$. A typical feature of $X_0(2900)$ is its mass below the $\bar{D}^*K^*$ threshold about 30 MeV. The QCD sum rule calculations [3, 7] and the one-boson-exchange inspired models [4, 5] all supported the S-wave $\bar{D}^*K^*$ molecule for $X_0(2900)$. Besides, Refs. [15, 18] investigated the decays of $X_0(2900)$ and indicated large $\bar{D}^*K^*$ component in its wave function. Another hint comes from the width of $X_0(2900)$, which is close to the $K^*$ width, i.e., one may infer that the $X_0(2900)$ has an intrinsic $K^*$ width, and the residual part arises from its decays. Thus, it seems the $X_0(2900)$ is more likely to be the $\bar{D}^*K^*$ molecular state.

Most of the previous works cannot give a unified description for $X_0(2900)$ and $X_1(2900)$ if they are the genuine states. For example, Ref. [8] relegated the $X_1(2900)$ to the $\bar{D}^*K^*$ rescattering effect. Ref. [4] gave a virtual state explanation for $X_1(2900)$ that was generated from the $\bar{D}_1K$ interaction and the bound solution in the $\bar{D}_1K$ channel needs an unnaturally large cutoff. In Ref. [5], the $X_1(2900)$ cannot be interpreted as the P-wave $\bar{D}^*K^*$ molecule. If the $X_1(2900)$ is indeed the P-wave compact tetraquark as suggested in Refs. [3, 9], then where is the S-wave ground state? It definitely cannot be the $X_0(2900)$ as the results shown in Refs. [9, 12, 20, 22]. In addition, we also need to answer the different dynamics in b-decays for the formations of $X_0(2900)$ and $X_1(2900)$. In order to eschew the dilemmas as mentioned above, this work is devoted to describing these two states in a unified framework, and understanding their internal configurations in a more natural way.

With the discoveries of more and more near-threshold exotic states [32,33,34,35,36,37,38,39,40], we find the connections between hadronic physics and nuclear physics become closer and closer. The concepts of $\chi$EFT [41, 42], which have been successfully substantialized to describe the nuclear forces [43,44,45,46,47,48], can also be generalized to depict the interactions between heavy hadrons [40, 49,50,51,52,53,54,55,56,57,58,59,60]. This work dedicates to model the $\bar{D}^*K^*$ interactions with S- and P-waves in a coupled-channel formalism via mimicking the manipulations in $\chi$EFT. By fitting the $D^-K^+$ event distributions in experiments, we analyze the pole positions in the scattering T-matrix to see whether the $X_0(2900)$ and $X_1(2900)$ can be assigned as the S-wave and P-wave excited $\bar{D}^*K^*$ molecules. This can definitely resolve the problem we are facing now, and give a uniform description of the $X_0(2900)$ and $X_1(2900)$.

This paper is organized as follows. In Sect. 2, we establish the effective potentials of $\bar{D}^*K^*$ and iterate them into the coupled-channel Lippmann–Schwinger equations. In Sect. 3, we present our numerical results and discussions. In Sect. 4, we conclude this work with a short summary.

2 $\bar{D}^*K^*$ rescattering in coupled-channel formalism

In this work, we assume the $X_0(2900)$ and $X_1(2900)$ are the isosinglet S- and P-wave hadronic molecules which are generated from the $\bar{D}^*K^*$ interactions, respectively. Thus the flavor wave functions in $\bar{D}^*K^*$ and $\bar{D}K$ channels can be written as

$$\begin{aligned} |\bar{D}^*K^*,I=0\rangle= & {} \frac{1}{\sqrt{2}}[\bar{D}^{*0}K^{*0}-D^{*-}K^{*+}],\nonumber \\ |\bar{D} K,I=0\rangle= & {} \frac{1}{\sqrt{2}}[\bar{D}^{0}K^{0}-D^{-}K^{+}]. \end{aligned}$$

(1)

The mass of $K^*$ is close to the nucleon mass, thus $K^*$ can be regarded as a heavy matter field. We can generalize the approaches of $\chi$EFT as that in the NN system [43,44,45,46,47,48] to the $\bar{D}^*K^*$ case. The effective potentials in the $\bar{D}^*K^*$ system can be parameterized as follows,

$$\begin{aligned} \mathcal {V}=\sum _i V_i(\varvec{p}^\prime ,\varvec{p})\mathcal {O}_i(\varvec{p}^\prime ,\varvec{p},\varvec{\varepsilon },\varvec{\varepsilon }^\dagger ,\varvec{\varepsilon }^\prime ,\varvec{\varepsilon }^{\prime \dagger }), \end{aligned}$$

(2)

where $\varvec{p}$ and $\varvec{p}^\prime$ represent the three momenta of the initial and final states in the center of mass system (c.m.s) of $\bar{D}^*K^*$, respectively. $\varvec{\varepsilon }^{(\prime )}$ and $\varvec{\varepsilon }^{(\prime )^\dagger }$ denote the polarization vectors of initial and final $\bar{D}^*$ ($K^*$), respectively. $V_i$ are the scalar functions of $\varvec{p}$ and $\varvec{p}^\prime$. $\mathcal {O}_i$ are the pertinent operators that can be constructed from the scalar products among unit operator $\varvec{1}$, vectors $\varvec{p}^{(\prime )}$, $\varvec{\varepsilon }^{(\prime )}$ and $\varvec{\varepsilon }^{(\prime )^\dagger }$, which read

$$\begin{aligned} \mathcal {O}_1= & {} (\varvec{\varepsilon }^{\dagger }\cdot \varvec{\varepsilon }) (\varvec{\varepsilon }^{\prime \dagger }\cdot \varvec{\varepsilon }^{\prime }),\nonumber \\ \mathcal {O}_2= & {} (\varvec{\varepsilon }^{\prime \dagger }\cdot \varvec{\varepsilon })(\varvec{\varepsilon }^\dagger \cdot \varvec{\varepsilon }^\prime )-(\varvec{\varepsilon }^{\prime \dagger }\cdot \varvec{\varepsilon }^\dagger )(\varvec{\varepsilon }\cdot \varvec{\varepsilon }^\prime ),\nonumber \\ \mathcal {O}_3= & {} (\varvec{q}\cdot \varvec{\varepsilon }^{\prime \dagger })(\varvec{q}\cdot \varvec{\varepsilon })(\varvec{\varepsilon }^\dagger \cdot \varvec{\varepsilon }^\prime )+(\varvec{q}\cdot \varvec{\varepsilon }^\dagger )(\varvec{q}\cdot \varvec{\varepsilon }^\prime )(\varvec{\varepsilon }^{\prime \dagger }\cdot \varvec{\varepsilon }),\nonumber \\ \mathcal {O}_4= & {} (\varvec{q}\cdot \varvec{\varepsilon }^\dagger )(\varvec{q}\cdot \varvec{\varepsilon }^{\prime \dagger })(\varvec{\varepsilon }^\prime \cdot \varvec{\varepsilon })+(\varvec{q}\cdot \varvec{\varepsilon })(\varvec{q}\cdot \varvec{\varepsilon }^\prime )(\varvec{\varepsilon }^{\prime \dagger }\cdot \varvec{\varepsilon }^\dagger ),\nonumber \\ \mathcal {O}_5= & {} (\varvec{k}\cdot \varvec{\varepsilon }^{\prime \dagger })(\varvec{k}\cdot \varvec{\varepsilon })(\varvec{\varepsilon }^\dagger \cdot \varvec{\varepsilon }^\prime )+(\varvec{k}\cdot \varvec{\varepsilon }^\dagger )(\varvec{k}\cdot \varvec{\varepsilon }^\prime )(\varvec{\varepsilon }^{\prime \dagger }\cdot \varvec{\varepsilon }),\nonumber \\ \mathcal {O}_6= & {} (\varvec{k}\cdot \varvec{\varepsilon }^\dagger )(\varvec{k}\cdot \varvec{\varepsilon }^{\prime \dagger })(\varvec{\varepsilon }^\prime \cdot \varvec{\varepsilon })+(\varvec{k}\cdot \varvec{\varepsilon })(\varvec{k}\cdot \varvec{\varepsilon }^\prime )(\varvec{\varepsilon }^{\prime \dagger }\cdot \varvec{\varepsilon }^\dagger ),\nonumber \\ \mathcal {O}_7= & {} (\varvec{\varepsilon }^{\prime \dagger }\cdot \varvec{\varepsilon }^\prime )(\varvec{\varepsilon }^{\dagger }\times \varvec{\varepsilon })\cdot (\varvec{k}\times \varvec{q})\nonumber \\&+(\varvec{\varepsilon }^{\dagger }\cdot \varvec{\varepsilon })(\varvec{\varepsilon }^{\prime \dagger }\times \varvec{\varepsilon }^\prime )\cdot (\varvec{k}\times \varvec{q}),\dots , \end{aligned}$$

(3)

with $\varvec{q}=\varvec{p}-\varvec{p}^\prime$ the transferred momentum and $\varvec{k}=(\varvec{p}^\prime +\varvec{p})/2$ the average momentum. The ellipsis denotes the higher terms with more $\varvec{q}$ and $\varvec{k}$. The operators $\mathcal {O}_1$, $\mathcal {O}_2$, $\mathcal {O}_{3,\dots ,6}$ and $\mathcal {O}_7$ account for the central force, the spin-spin interaction, the tensor force, and the spin-orbital (SL) coupling, respectively.

In order to describe the transitions between $\bar{D}^*K^*$ and $\bar{D}K$, we define the corresponding transition operators,

$$\begin{aligned} \mathcal {O}_{1}^\prime= & {} \varvec{\varepsilon }\cdot \varvec{\varepsilon }^\prime \text {~or~}\varvec{\varepsilon }^\dagger \cdot \varvec{\varepsilon }^{\prime \dagger },\nonumber \\ \mathcal {O}_{2}^\prime= & {} (\varvec{q}\cdot \varvec{\varepsilon })(\varvec{q}\cdot \varvec{\varepsilon }^\prime )\text {~or~}(\varvec{q}\cdot \varvec{\varepsilon }^\dagger )(\varvec{q}\cdot \varvec{\varepsilon }^{\prime \dagger }),\nonumber \\ \mathcal {O}_{3}^\prime= & {} (\varvec{k}\cdot \varvec{\varepsilon })(\varvec{k}\cdot \varvec{\varepsilon }^\prime )\text {~or~}(\varvec{k}\cdot \varvec{\varepsilon }^\dagger )(\varvec{k}\cdot \varvec{\varepsilon }^{\prime \dagger }). \end{aligned}$$

(4)

For performing the partial wave decompositions in the following, the polarization vectors in above equations can be transformed into the spin transition operator $\varvec{S}_t$ with the approach given in the appendix C of Ref. [57].

The effective potentials of the elastic ($\bar{D}^*K^*\rightarrow \bar{D}^*K^*$) and the inelastic ($\bar{D}^*K^*\rightarrow \bar{D} K$, or in reverse) channels have both contributions from the contact and one-pion-exchange (OPE) interactions. The short-range contact terms for the elastic (el) and inelastic (in) scatterings are given as, respectively,

$$\begin{aligned} \mathcal {V}_{\text {ct}}^{\text {el}}= & {} \sum _{i=1}^{7}C_i\mathcal {O}_i+(C_{8}\varvec{q}^2+C_{9}\varvec{k}^2)\mathcal {O}_1\nonumber \\&+(C_{10}\varvec{q}^2+C_{11}\varvec{k}^2)\mathcal {O}_2, \end{aligned}$$

(5)

$$\begin{aligned} \mathcal {V}_{\text {ct}}^{\text {in}}= & {} C_2^\prime \mathcal {O}_2^\prime +C_3^\prime \mathcal {O}_3^\prime +(C_4^\prime \varvec{q}^2+C_5^\prime \varvec{k}^2)\mathcal {O}_1^\prime , \end{aligned}$$

(6)

where $C_i^{(\prime )}$ are the low energy constants (LECs).

The long-distance interaction for $\bar{D}^*K^*$ is depicted by the OPE contribution. The OPE effective potential can be easily obtained from the chiral Lagrangians, in which the anticharmed meson and pion coupling reads [61, 62]

$$\begin{aligned} \mathcal {L}_{\tilde{\mathcal {H}}\varphi }=g_{\varphi }\langle \bar{\tilde{\mathcal {H}}}\gamma ^\mu \gamma _5 u_\mu \tilde{\mathcal {H}}\rangle , \end{aligned}$$

(7)

where $g_{\varphi }\simeq 0.57$ is the axial coupling. $\tilde{\mathcal {H}}$ and $u_\mu$ are the superfield for anticharmed mesons and axial-vector current for pion, respectively, their expressions can be found in Refs. [56, 57]. In SU(2) case, if we treat the $\bar{s}$ quark as a relatively heavy quark, then the $K^*$ and pion coupling can be formulated as the same form as that in Eq. (7). Its axial coupling constant $g_\varphi \simeq 1.12$ is determined from the decay width of $K^*\rightarrow K\pi$ [63].

Fig. 1

The OPE diagrams in time-ordered perturbation theory. The black solid and dashed lines denote the $\bar{D}^{(*)}/K^{(*)}$ and pion, respectively. The red-dashed (horizontal) line indicates the time at which the intermediate state is evaluated. In diagram a, the particle B feels the effect of a pion that from the source particle A emitted at an earlier time, thus the A and B particles interact in this case through a retarded propagator. In diagram b, from the B’s point of view, the effect is felt before the source A emitted the pion, thus the pion propagator in this case is called an advanced propagator

The OPE effective potentials for elastic and inelastic scatterings read

$$\begin{aligned} \mathcal {V}_{\text {OPE}}^{\text {(a)}}= & {} -\frac{3g_\varphi ^2}{4f_\varphi ^2}\frac{\mathcal {O}^{\text {ch}}}{2E_\pi [E_\pi +E_{A^\prime }+E_B-E]}, \end{aligned}$$

(8)

$$\begin{aligned} \mathcal {V}_{\text {OPE}}^{\text {(b)}}= & {} -\frac{3g_\varphi ^2}{4f_\varphi ^2}\frac{\mathcal {O}^{\text {ch}}}{2E_\pi (E_\pi +E_{A}+E_{B^\prime }-E)}, \end{aligned}$$

(9)

where the $\mathcal {V}_{\text {OPE}}^{\text {(a)}}$ and $\mathcal {V}_{\text {OPE}}^{\text {(b)}}$ represent the contributions from Fig. 1a, b, respectively. The $\mathcal {O}^{\text {ch}}=-\varvec{q}^2\mathcal {O}_2+\mathcal {O}_3-\mathcal {O}_4$ for the elastic channel, and $\mathcal {O}^{\text {ch}}=\mathcal {O}_{2}^\prime$ for the inelastic channels, respectively. $g_\varphi =\sqrt{0.57\times 1.12}$ is the redefined coupling constant, $f_\varphi =92.4$ MeV is the pion decay constant, and $m_\pi \simeq 140$ MeV is the pion mass. Note that the non-static effect (the energy dependence) for the OPE potentials is considered with the time-ordered perturbation theory (see Refs. [51, 64,65,66]). The energies appearing in Eqs. (8) and (9) are given as

$$\begin{aligned} E_\pi= & {} \sqrt{\varvec{q}^2+m_\pi ^2}, \end{aligned}$$

(10)

$$\begin{aligned} E_{i^{(\prime )}}= & {} m_{i^{(\prime )}}+\frac{p^{(\prime )2}}{2m_{i^{(\prime )}}},\quad i=A,B, \end{aligned}$$

(11)

and E stands for the total energy of the system.

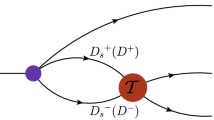
The $X_0(2900)$ and $X_1(2900)$ are observed in the b-decay process $B^+\rightarrow D^+D^-K^+$, so we need to simulate this production process. The corresponding Feynman diagrams are shown in Fig. 2. The reactions in Fig. 2 can be expressed with the coupled-channel Lippmann–Schwinger equations (LSEs),

$$\begin{aligned} \mathcal {U}_\alpha ^j(E,\varvec{p})= & {} \mathcal {M}_\alpha ^j+\sum _\beta \int \frac{d^3\varvec{q}}{(2\pi )^3}\nonumber \\&\times \mathcal {V}_{\alpha \beta }^j(E,\varvec{p},\varvec{q})\mathcal {G}_\beta (E,\varvec{q})\mathcal {U}_\beta ^j(E,\varvec{q}), \end{aligned}$$

(12)

where the subscript $\alpha (\beta )=1,2$ denotes the corresponding channels [the $\bar{D}K$ and $\bar{D}^*K^*$ channels are labeled as 1 and 2, respectively, e.g., see Fig. 2], while the superscript j represents the fixed total angular momentum. $\mathcal {M}$ is the direct production amplitude. E stands for the invariant mass of the $D^-K^+$ system. $\mathcal {G}$ is the Green’s function of the intermediate states, which read

$$\begin{aligned} \mathcal {G}_\beta (E,\varvec{q})=\frac{2\mu _\beta }{\varvec{p}_\beta ^2-\varvec{q}^2+i\epsilon }, |\varvec{p}_\beta |=\sqrt{2\mu _\beta (E-m_{\text {th}}^\beta )}, \end{aligned}$$

(13)

with $\mu _\beta$ and $m_{\text {th}}^\beta$ the reduced mass and the threshold of the $\beta$-th channel. The width of $K^*$ is 50.8 MeV [63], which is considered in $m_{\text {th}}^\beta$ by using a complex mass $m-i\Gamma /2$ for the $K^*$ [64].

Fig. 2

Diagrams a and b describe the direct production and rescattering contribution, respectively. The gray circle with cross represents the effective $B^+\rightarrow D^+\bar{D}K$ and $B^+\rightarrow D^+\bar{D}^{*}K^{*}$ coupling, while the gray box in diagram b signifies the rescattering T-matrix of the $\bar{D}^*K^*$ system. The dashed line denotes the spectator $D^+$, while the solid lines stand for the involved $\bar{D}K$ ($\bar{D}^{*}K^{*}$) in the rescattering

In order to solve the LSEs in Eq. (12), we need to make the partial wave decomposition. The effective potentials in Eq. (2) are given in the plane wave helicity basis, which can be transformed to the partial wave ($\ell sj$) basis via the approach in Ref. [67]. If the $X_0(2900)$ and $X_1(2900)$ are the S- and P-wave $\bar{D}^*K^*$ molecules with $J^P=0^+$ and $J^P=1^-$, respectively. Then the corresponding effective potentials in partial wave bases with the coupled-channels

$$\begin{aligned} j=0:|\bar{D}K\rangle _{^1S_0},|\bar{D}^*K^*\rangle _{^1S_0},|\bar{D}^*K^*\rangle _{^5D_0} \end{aligned}$$

(14)

and

$$\begin{aligned} j= & {} 1:|\bar{D}K\rangle _{^1P_1},|\bar{D}^*K^*\rangle _{^1P_1},|\bar{D}^*K^*\rangle _{^3P_1},|\bar{D}^*K^*\rangle _{^5P_1} \end{aligned}$$

(15)

can be written as the $3\times 3$ and $4\times 4$ matrices, respectively.

The contact interactions through the partial wave decompositions in S-wave with the coupled-channels read

$$\begin{aligned}{}[\mathcal {V}_{\text {ct}}]_{\ell ,\ell ^\prime }^S=\left[ \begin{array}{ccc} 0 &{}\quad \mathcal {C}_{12}(p^2+p^{\prime 2}) &{}\quad \mathcal {C}_{13}p^2\\ \mathcal {C}_{12}(p^2+p^{\prime 2}) &{}\quad \mathcal {C}_{22}+\mathcal {C}_{22}^\prime (p^2+p^{\prime 2}) &{}\quad \mathcal {C}_{23}p^2\\ \mathcal {C}_{13}p^{\prime 2}&{}\quad \mathcal {C}_{23}p^{\prime 2}&{}\quad 0 \end{array} \right] , \end{aligned}$$

(16)

where

$$\begin{aligned} \mathcal {C}_{12}= & {} -\frac{\pi }{\sqrt{3}}(4C_2^\prime +C_3^\prime +12C_4^\prime +3C_5^\prime ),\nonumber \\ \mathcal {C}_{13}= & {} \frac{\sqrt{2}}{\sqrt{3}}\pi (4C_2^\prime +C_3^\prime ),\nonumber \\ \mathcal {C}_{22}= & {} 4\pi (C_1-2C_2),\nonumber \\ \mathcal {C}_{22}^\prime= & {} \frac{\pi }{3}(8C_3+24C_4+2C_5+6C_6+12C_8+3C_{9}\nonumber \\&-24C_{10}-6C_{11}),\nonumber \\ \mathcal {C}_{23}= & {} -\frac{\sqrt{2}\pi }{3}(8 C_3 + 12 C_4 + 2 C_5 + 3 C_6), \end{aligned}$$

(17)

while the ones for the P-wave are given as

$$\begin{aligned}{}[\mathcal {V}_{\text {ct}}]_{\ell ,\ell ^\prime }^P=\left[ \begin{array}{cccc} 0 &{}\quad \mathbb {C}_{12}pp^\prime &{}\quad 0&{}\quad \mathbb {C}_{14}pp^\prime \\ \mathbb {C}_{12}pp^\prime &{}\quad \mathbb {C}_{22}pp^\prime &{} 0&{}\quad \mathbb {C}_{24}pp^\prime \\ 0&{}\quad 0&{}\quad \mathbb {C}_{33}pp^\prime &{}\quad 0\\ \mathbb {C}_{14}pp^\prime &{}\quad \mathbb {C}_{24}pp^\prime &{}\quad 0&{}\quad \mathbb {C}_{44}pp^\prime \end{array} \right] , \end{aligned}$$

(18)

where

$$\begin{aligned} \mathbb {C}_{12}= & {} \frac{2\pi }{3\sqrt{3}}(4C_2^\prime -C_3^\prime +12C_4^\prime -3C_5^\prime ),\nonumber \\ \mathbb {C}_{14}= & {} \frac{2\sqrt{5}\pi }{3\sqrt{3}}(4C_2^\prime -C_3^\prime ),\nonumber \\ \mathbb {C}_{22}= & {} \frac{2\pi }{9}(-8 C_3 - 24 C_4 + 2 C_5 + 6 C_6 - 12 C_8 + 3 C_9\nonumber \\&+24 C_{10} - 6 C_{11}),\nonumber \\ \mathbb {C}_{24}= & {} \frac{2\pi }{9\sqrt{5}}(-40 C_3 - 60 C_4 + 10 C_5 + 15 C_6 + 12 C_7),\nonumber \\ \mathbb {C}_{33}= & {} \frac{\pi }{3}(12 C_3 - 3 C_5 - 8 C_7 -8 C_8 + 2 C_9\nonumber \\&+8 C_{10} - 2 C_{11}), \nonumber \\ \mathbb {C}_{44}= & {} -\frac{\pi }{45}(220 C_3 - 55 C_5 + 144 C_7 + 120 C_8 \nonumber \\&- 30 C_9+120 C_{10} - 30 C_{11}). \end{aligned}$$

(19)

In above potentials, we switch off the $\bar{D}K$ interaction for reducing the free parameters, which may be described by the chiral perturbation theory [68]. However, the $\bar{D}K$ lies far below the $\bar{D}^*K^*$ threshold, thus their interactions should be irrelevant to the physics around the $\bar{D}^*K^*$ threshold.

The LSEs in Eq. (12) is regulated with a form factor, in which the $\mathcal {V}_{\ell ,\ell ^\prime }$ is multiplied by the Gaussian regulator,

$$\begin{aligned} \mathcal {V}_{\ell ,\ell ^\prime }\rightarrow \mathcal {V}_{\ell ,\ell ^\prime }\exp \left[ -\frac{p^2}{\Lambda ^2}-\frac{p^{\prime 2}}{\Lambda ^{\prime 2}}\right] . \end{aligned}$$

(20)

At the X(2900) energy, the center of mass momentum of the $\bar{D}K$ channel is 0.74 GeV, and hence we use a relatively hard cutoff $\Lambda =1.0$ GeV for this channel. For the elastic channel scattering, we vary the cutoff $\Lambda ^\prime$ [in this case, the $\Lambda$ and $\Lambda ^\prime$ in Eq. (20) have the equal value] over a wide range, i.e., from a soft scale 0.3 GeV to a hard scale 1.0 GeV.

Additionally, we also need to mimic the production vertex. We assume the $D^+D^-K^+$ and $D^+D^{*-}K^{*+}$ are produced from a point-like source. Then the S- and P-wave production amplitudes can be parametrized as [69]

$$\begin{aligned}&\mathcal {M}^S_{\{B^+\rightarrow D^+D^-K^+,B^+\rightarrow D^+D^{*-}K^{*+}\}_\alpha }\nonumber \\&~\quad =\{\tilde{g}_s,\tilde{g}_s^\prime \varvec{\varepsilon }^\dagger \cdot \varvec{\varepsilon }^{\prime \dagger }\}, \end{aligned}$$

(21)

$$\begin{aligned}&\mathcal {M}^P_{\{B^+\rightarrow D^+D^-K^+,B^+\rightarrow D^+D^{*-}K^{*+}\}_\alpha }\nonumber \\&~\quad =\{\tilde{g}_p\varvec{k}_1\cdot \varvec{k}_2,\tilde{g}_p^\prime (\varvec{k}_1\cdot \varvec{k}_2^\prime )(\varvec{\varepsilon }^\dagger \cdot \varvec{\varepsilon }^{\prime \dagger })\nonumber \\&~\qquad +\tilde{g}_p^{\prime \prime }(\varvec{k}_1\cdot \varvec{\varepsilon }^\dagger )(\varvec{k}_2^\prime \cdot \varvec{\varepsilon }^{\prime \dagger })+\tilde{g}_p^{\prime \prime \prime }(\varvec{k}_1\cdot \varvec{\varepsilon }^{\prime \dagger })(\varvec{k}_2^\prime \cdot \varvec{\varepsilon }^{\dagger })\},\quad \end{aligned}$$

(22)

where $\tilde{g}_{s(p)}^{(\prime )}$ represents the production strengths in corresponding channels. $\varvec{k}_1$ and $\varvec{k}_2^{(\prime )}$ denote the three momentum of $D^+$ and $D^{-}$ ($D^{*-}$) in the c.m.s of $D^-K^+$ ($D^{*-}K^{*+}$).

Projecting the production amplitudes to the bases in Eqs. (14) and (15), respectively, one easily obtains

$$\begin{aligned}&\mathcal {M}^{j=0}_{\{B^+\rightarrow D^+D^-K^+,B^+\rightarrow D^+D^{*-}K^{*+}\}_i}\nonumber \\&~\quad =\mathcal {N}_s\{1,\mathcal {R}_s,0\}, \end{aligned}$$

(23)

$$\begin{aligned}&\mathcal {M}^{j=1}_{\{B^+\rightarrow D^+D^-K^+,B^+\rightarrow D^+D^{*-}K^{*+}\}_i}\nonumber \\&~\quad =\mathcal {N}_p\{k_1 k_2,\mathcal {R}_p k_1 k_2^\prime ,\mathcal {R}_p^\prime k_1 k_2^\prime ,\mathcal {R}_p^{\prime \prime } k_1 k_2^\prime \}, \end{aligned}$$

(24)

where the irrelevant factors are absorbed into the $\mathcal {N}_{s(p)}$, while the $\mathcal {R}_{s(p)}$ describes the relative strengths between $|\bar{D}K\rangle _{^1S_0}$ and $|\bar{D}^*K^*\rangle _{^1S_0}$ ($|\bar{D}K\rangle _{^1P_1}$ and $|\bar{D}^*K^*\rangle _{^1P_1}$) channels, and similar meanings for the $\mathcal {R}_p^{\prime ,\prime \prime }$.

With the above preparations, the differential decay width for $B^+\rightarrow D^+D^-K^+$ reads

$$\begin{aligned} \frac{d\Gamma }{dE}=\mathcal {N}\frac{|\tilde{\varvec{k}}_1||\varvec{k}_2^*|}{4(2\pi )^3m_B^2}\left[ \mathcal {R}_{sp}\left| \mathcal {U}_1^{j=0}\right| ^2+\left| \mathcal {U}_1^{j=1}\right| ^2\right] , \end{aligned}$$

(25)

where an overall normalization factor $\mathcal {N}$ is used to match the event distributions in experiments. $\tilde{\varvec{k}}_1$ and $\varvec{k}_2^*$ are the three momentum of the spectator $D^+$ in the c.m.s of $B^+$ and the three momentum of $D^{-}$ in the c.m.s of $D^-K^+$, respectively. $\mathcal {R}_{sp}$ is introduced to designate the ratio $\mathcal {N}_s^2/\mathcal {N}_p^2$.

Fig. 3

Changes of the S- and P-wave LECs when the elastic channel’s cutoff is varied from 0.3 GeV to 1.0 GeV and the inelastic channel’s cutoff is fixed at 1.0 GeV

3 Numerical results and discussions

Unlike the $D_{s0}(2317)$ and $D_{s1}(2460)$ [63], there is no $\bar{c}\bar{s}$ bare core in the hadron spectrum, so the X(2900) provides us a relatively clean environment to study the coupled-channel effects between open-charm and open-strange mesons.

The values of partial wave LECs are constrained by fitting to the $D^-K^+$ event candidates that measured by the LHCb [2], which are given in Fig. 3 for the S- and P-waves. One can find that some LECs are sensitive to the variations of cutoff, such as $\mathcal {C}_{23}$, $\mathbb {C}_{22}$, $\mathbb {C}_{33}$, $\mathbb {C}_{44}$ and $\mathbb {C}_{24}$ [in effective field theory, the LECs are cutoff dependent, $C_i\equiv C_i(\Lambda )$, i.e., the cutoff dependence is absorbed by the LECs, which makes the observables cutoff independent]. The distribution behaviors of these LECs with the cutoff is similar to that of the spin singlet case of NN scattering [70], while the LECs of the spin triplet NN (the channel for deuteron) scattering show limit-cycle-like behavior (an unsmooth dependence on the cutoff). Meanwhile, the other LECs are not very sensitive to cutoffs, such as the $\mathcal {C}_{12}$, $\mathcal {C}_{13}$, $\mathbb {C}_{12}$ and $\mathbb {C}_{14}$. A more general analysis on the nonrelativistic two-body scattering of the single-channel case with renormalization-group invariance constraints was provided by Birse et al. [71].

The fitted line shape of the S- and P-wave components, as well as their total contributions are plotted in Fig. 4. We find the results are also insensitive to cutoffs, the $\chi ^2/{\text {d.o.f}}$ is around 1.3 when $\Lambda ^\prime \in [0.3,1.0]$ GeV. The fit with $\Lambda =1.0$ GeV, $\Lambda ^\prime =0.5$ GeV gives the least $\chi ^2$ ($\simeq 1.25$), so we adopt the results in this fit as our outputs. The corresponding values of LECs with the errors are given in Table. 1.

Table 1 The values of LECs $(\mathcal {C}_{22},\mathcal {C}_{22}^{\prime },\mathcal {C}_{23},\mathcal {C}_{12},\mathcal {C}_{13},\mathbb {C}_{22},\mathbb {C}_{33},\mathbb {C}_{44},\mathbb {C}_{24},\mathbb {C}_{12},\mathbb {C}_{14})/10^4$ with errors that fitted at $\Lambda =1.0$ GeV and $\Lambda ^\prime =0.5$ GeV

Two pronounced peaks around the $\bar{D}^*K^*$ threshold are obtained. One can notice that the signal of P-wave is much stronger than that of the S-wave, this can naturally explain why the angular distribution of $D^-K^+$ in experiments is overwhelmed by the P-wave structure [1, 2].

Fig. 4

The fitted $D^-K^+$ invariant mass distributions for $B^+\rightarrow D^+D^-K^+$ decay. The experimental data are extracted from Ref. [2], where the reflection contributions from the charmonia are subtracted. The dashed, dot-dashed and solid lines denote the S-, P- and $S+P$-wave contributions, respectively. The lineshapes are obtained with the cutoffs $\Lambda =1.0$ GeV, and $\Lambda ^\prime =0.5$ GeV

We then study the pole structures of the production $\mathcal {U}$-matrix in different Riemann sheets (the poles of the $\mathcal {U}$-matrix are the same as the T-matrix in this sense), which can be achieved through the analytical continuation of the Green’s functions in Eq. (13):

$$\begin{aligned} \mathcal {G}_1(E)\rightarrow & {} \mathcal {G}_1(E)+\zeta _1\frac{i\mu _1p_1}{4\pi ^2},\nonumber \\ \mathcal {G}_2(E)\rightarrow & {} \mathcal {G}_2(E)+\zeta _2\frac{i\mu _2p_2}{4\pi ^2}. \end{aligned}$$

(26)

Two channel coupling generally introduces four Riemann sheets [72], then the four Riemann sheets $(\zeta _1,\zeta _2)$ in the complex energy plane are defined as

$$\begin{aligned} \mathrm{Sheet ~I}:(\zeta _1,\zeta _2)= & {} (0,0),\nonumber \\ \mathrm{Sheet ~II}:(\zeta _1,\zeta _2)= & {} (1,0),\nonumber \\ \mathrm{Sheet ~III}:(\zeta _1,\zeta _2)= & {} (1,1),\nonumber \\ \mathrm{Sheet ~IV}:(\zeta _1,\zeta _2)= & {} (0,1), \end{aligned}$$

(27)

such as the physical sheet is denoted as (0, 0) in this definition. This is analogous to the commonly used notations in complex momentum plane [72]. Considering a lower channel-1 with particles A and B, and a higher channel-2 with particles C and D, a pole in Sheet II near $m_C+m_D$ corresponds to a bound state of CD (channel-2), such a pole is manifested as a resonance in channel-1 (AB) scattering process. For more general discussions on the pole distributions and classifications in different Riemann sheets, we refer to [72,73,74].

The S- and P-wave peaks correspond to two poles of the $\mathcal {U}$-matrix in the Sheet II. The masses and widths of the S-wave state with $I(J^P)=0(0^+)$ and P-wave state with $0(1^-)$ are extracted from the pole positions $E=m-i\Gamma /2$. Their values are insensitive to different cutoffs. We obtain

$$\begin{aligned}{}[m,\Gamma ]_{0^+}\simeq & {} [2873.6^{+11.3}_{-13.5},72.1^{+10.5}_{-9.8}] ~\mathrm {MeV},\nonumber \\ {[m,\Gamma ]_{1^-}}\simeq & {} [2892.7^{+6.8}_{-10.2},54.2^{+8.2}_{-1.5}] ~\mathrm {MeV}. \end{aligned}$$

(28)

Therefore, they correspond to the two bound states of $\bar{D}^*K^*$ in S- and P-waves, respectively. We find the masses of the $0^+$ and $1^-$ states are very consistent with the $X_0(2900)$ and $X_1(2900)$ [1, 2], respectively, while their widths deviate a lot. The analyses from the experimental work give $\Gamma _{X_1}>\Gamma _{X_0}$ [1, 2], whereas this relation is reversed in our results. The result in Ref. [15] agrees with ours.

Inspecting the S- and P-wave peaks in Fig. 4, one may intuitively infer that the width of P-wave state is larger than that of the S-wave. But as we mentioned above, we do have $\Gamma _{0^+}>\Gamma _{1^-}$ from the pole analyses. This is because the P-wave production vertex is momentum dependent, which broadens the line shape, but the pole position cannot be changed.

The experimental data may consist of multi substructures, similar to the stories of the $P_c$ states [the $P_c(4450)$ observed in 2015 by the LHCb [75] was proved to contain two distinct states $P_c(4440)$ and $P_c(4457)$ in 2019 [76]]. The S- and P-wave multiplets for the $\bar{D}^*K^*$ system are $[0^+,1^+,2^+]$ and $\{1^-,[0^-,1^-,2^-],[1^-,2^-,3^-]\}$, respectively. The present experimental data can be well reproduced with the inclusion of the $0^+$ and $1^-$ states, but the other states in the S- and P-wave multiplets might also exist. In 2010, Molina et al. predicted the existence of the S-wave multiplets in $\bar{D}^*K^*$ system [77], in which the $0^+$ state mass is roughly consistent with our result. The present resolution cannot distinguish the spin-spin and spin-orbital interactions, thus more experimental data are still needed. However, one should also note that these possibly existed substructures might be hard to be discerned in experiments given that their widths were similar to those of the $X_{0,1}(2900)$ states.

4 Summary

We have investigated the $D^-K^+$ invariant mass distributions for the decay process $B^+\rightarrow D^+D^-K^+$, where the $X_0(2900)$ and $X_1(2900)$ were observed by the LHCb Collaboration [1, 2]. We study the S- and P-wave $\bar{D}^*K^*$ interactions in a coupled-channel formalism via mimicking the $\chi$EFT. The short- and long-distance forces are both incorporated in our calculations.

The event distributions can be well described, and two sharp peaks that correspond to the $\bar{D}^*K^*$ molecular states with $0(0^+)$ and $0(1^-)$ are obtained. Their masses are in good agreement with the $X_0(2900)$ and $X_1(2900)$, respectively, but the width of $0^+$ state is larger than that of the $1^-$. We can simultaneously reproduce the $X_0(2900)$ and $X_1(2900)$ in an unified framework. Our calculations support the molecular interpretations for these two states. In other words, the $X_1(2900)$ may be the P-wave excitation of the ground state $X_0(2900)$. If this conclusion is verified in future, it shall be the first time that a ground-state hadronic molecule and its orbital excitation are synchronously observed in experiments.

However, the present experimental data cannot pin down the fine structures behind the $\bar{D}^*K^*$ interactions, i.e., we still cannot ascertain whether the other members in the S- and P-wave multiplets exist. The single whole peak now might contain multi substructures. In order to resolve the structures hidden in the peak, some refined measurements in this decay channel are still needed.