1 Introduction

Despite its enormous successes, General Relativity (GR) cannot be considered as the final theory of gravity, and needs to be modified [1]. Two of the most important motivations for modifying GR are the explanation of inflation, and the late-time cosmic acceleration [2]. Massive gravity theory is an approach to modify GR which includes a graviton of small mass [3]. In 1939, Fierz and Pauli (FP) [4] proposed massive gravity theory for the first time. By adding the fine-tuned mass term to the linearized Einstein–Hilbert action, they developed a theory that correctly leads to 5 degrees of freedom for the massive spin-2 particle [1, 5]. In 1970, van Dam and Veltman [6], and Zakharov (vDVZ) [7] discovered that, in the massless limit, the FP theory does not render GR [5]. In other words, the principle of conformity is violated leading to a deviation in the gravitational lensing prediction of theory about 25% compared to that of GR [8, 9]. This discontinuity is known as the vDVZ discontinuity [8].

Focusing on the nonlinear extensions of the FP theory, Vainshtein [10] found out a distance scale, called the Vainshtein radius \({{r}_{V}}={{(\frac{M}{M_{Pl}^{4}m_{g}^{4}})}^{\frac{1}{5}}}\), where \(M_{Pl}\) is the Planck mass, and \(m_g\) denotes the graviton mass) [10,11,12]. For \(r<{{r}_{V}}\), the nonlinear effects become highly important [10,11,12] meaning that the outcomes differ from those predicted by FP. As the graviton mass becomes less, the \({r}_{V}\) is boosted and at the massless limit, \({r}_{V}\) tends to infinity. Consequently, the results of the FP theory are no longer valid [10,11,12]. So, it seems possible to rectify the vDVZ discontinuity by considering the nonlinear effects [10,11,12], an approach called the Vainshtein mechanism [12].

According to the Vainshtein’s idea, Boulware and Deser (BD) [13] find that all nonlinear extensions of the FP theory have an additional degree of freedom (a ghost-like scalar mode), known as the BD ghost [14, 15]. The discovery of the late-time cosmic acceleration in 1998, and the unknown nature of cosmological constant led scientists to investigate modified gravity theories, such as massive gravity theory, more precisely. It is also realized that a non-renormalizable theory, such as the FP theory and even one with apparent instabilities, can be understood as an effective field theory, valid only at energies below an ultraviolet cutoff scale [16].

In 2003, Arkani-Hamed et al. [17] could return the gauge invariance to massive gravity theory by employing the St\(\ddot{\text {u}}\)ckelberg trick leading to develop an effective field theory for massive gravity. The St\(\ddot{\text {u}}\)ckelberg trick also helps us solve vDVZ discontinuity. In the massless limit, the effects of the strong decoupling neutralize the ghost-like scalar mode, and consequently the results of GR are reproduced. Moreover, in certain nonlinear extensions of FP, the cutoff scale \({\Lambda _{5}}={{( {{M}_{Pl}}m_{g}^{4})}^{{}^{1}/{}_{5}}}\) of FP can also be raised to \({{\text {}\!\!\Lambda \!\!\text { }}_{3}}={{( {{M}_{Pl}}m_{g}^{2})}^{{}^{1}/{}_{3}}}\). De Rham and Gabadadze [18] determine the coefficients of higher-order interaction terms in a way that the obtained action, as a generalization of FP, does not include the BD ghost in the decoupling limit. One year later, in 2011, De Rham et al. [19] could propose a covariant nonlinear theory of massive gravity that correctly describes the massive spin-2 field; the birth of dRGT theory. The dRGT theory is indeed ghost-free in the decoupling limit to all orders.

Although dRGT theory does not have flat, and closed FRW solutions, the open FRW solution yields an effective cosmological constant proportional to the graviton mass (\({{m}_{g}}\)) [20]. In the report of Ligo–Virgo Collaboration about the discovery of the first gravitational wave, the constraint \({{m}_{g}}<1.2\times {{10}^{-22}}\) eV is determined [21]. If \({{m}_{g}}\sim {{H}_{0}}\sim {{10}^{-33}}\) eV, then the effective cosmological constant can explain the late-time cosmic acceleration [22]. Since the graviton mass cannot be of the order of the Hubble constant during the inflation, dRGT theory is not capable to produce enough number of e-foldings [23].

Recently, a new type of Lagrangian, which may include pole and thus called pole Lagrangian, has attracted attempts to itself in order to model and describe the current and primary inflationary eras [24,25,26,27]. This kind of Lagrangian even supports evolving traversable wormholes satisfying energy conditions in the framework of GR [28]. Motivated by these attampets and also Ref. [23], here, we use the pole Lagrangian to build some models for the primary inflationary era in the framework of dRGT theory.

The action of the scalar field \(\sigma \) is written as

$$\begin{aligned} S_\sigma =\int {{d^4}x}\sqrt{-g}\left[ -\frac{1}{2}f(\sigma ){g^{\mu \nu }}{{\partial }_{\mu }}{{\sigma }^{{}}} {{\partial }_{\nu }}\sigma -V(\sigma )\right] , \end{aligned}$$
(1)

where \(V(\sigma )\) denotes the potential and \(f(\sigma )\) is a function of the scalar field \(\sigma \) [29]. The kinetic term can also be brought into canonical form

$$\begin{aligned} S_\varphi =\int {{d^4}x}\sqrt{-g}[-\frac{1}{2}{{g}^{\mu \nu }}{{\partial }_{\mu }}{{\varphi }^{{}}}{{\partial }_{\nu }}\varphi -V(\varphi )], \end{aligned}$$
(2)

using the transformation

$$\begin{aligned} d\varphi =\sqrt{f(\sigma )}d\sigma , \end{aligned}$$
(3)

leading to [30]

$$\begin{aligned} \varphi (\sigma )=\int _{\sigma _0}^{\sigma }{d{\sigma }} \sqrt{f({\sigma })}, \end{aligned}$$
(4)

in which \(\sigma _0\) denotes the desired point, which is considered as \({\sigma _0}=0\), here [30]. If \(f(\sigma )\) is singular at some points, i.e., then it possesses pole, it is impossible to integrate from \(f(\sigma )\) [30]. Assuming pole is located in \(\sigma =\sigma _p\), if \(\sigma _0 < \sigma _p\), then \(\sigma \) lies within the branch \((-\infty ,{\sigma _p})\). Also, when \(\sigma _0 > \sigma _p\), it lies within the branch \(({\sigma _p},\infty )\) [30]. To provide a general outlook on the possibility of describing inflation in the dRGT theory, we first derive the corresponding formulation for the general potential \(V(\sigma )\) and the general function \(f(\sigma )\). Then, we concentrate on the power and exponential potentials, as well as the particular function \(f(\sigma )={A}{{|\sigma |}^{-p}}\) which attended in Refs. [24,25,26,27,28, 30].

The paper is organized as follows. The dRGT theory and corresponding open FRW solutions are briefly reviewed in Sect. 2 and 3, respectively. In the continuation of the third section, the number of e-foldings \(N_e\), scalar spectral \(n_s\), and tensor-to-scalar ratio r are also derived. One of our main goals in Sect. 4 is to show the power of models in producing the appropriate number of e-foldings to solve the flatness problem, as well as the consistency of models with the Planck 2018 data and its combination with BK18 and BAO is investigated through employing \(r(n_s)\). Special solutions that lead to the invalidation of models are also discussed. A summary is finally presented in the last section. It is assumed that \({M_{Pl}}=1\).

2 The \(\mathbf{d} \)RGT theory

The dRGT theory is described by the physical metric \({{g}_{\mu \nu }}\), and the non-dynamical (or fiducial) metric \({{f}_{\mu \nu }}\) so that

$$\begin{aligned} {{g}_{\mu \nu }}={{f}_{\mu \nu }}+{{H}_{\mu \nu }}. \end{aligned}$$
(5)

Here, \({{H}_{\mu \nu }}\) denotes the covariantization of the metric perturbation (\({{h}_{\mu \nu }}\equiv {{g}_{\mu \nu }}-{{\eta }_{\mu \nu }}\)), and the fiducial metric is defined as

$$\begin{aligned} {{f}_{\mu \nu }}={{\tilde{f}}_{ab}}{{\partial }_{\mu }}{{\phi }^{a}}{{\partial }_{\nu }}{{\phi }^{b}}, \end{aligned}$$
(6)

where \({{\tilde{f}}_{\mu \nu }}\) is the reference metric, and \({{\phi }^{a}}(a=0,1,2,3)\) are the four fields introduced to restore general covariance. For a Minkowskian reference metric, \({{\phi }^{a}}\) form a 4-vector, implying that the dRGT theory carries the global Poincare symmetry [31].

The gravitational action consists of the Einstein–Hilbert term, and the mass term

$$\begin{aligned} \begin{aligned}&{{S}_{g}}={{S}_{EH}}+{{S}_{mass}}, \\&{{S}_{g}}=\int {{{d}^{4}}x}\sqrt{-g}\left[ \frac{R}{2}+m_{g}^{2} \mathcal {U}\left( {{g}_{\mu \nu }},{{H}_{\mu \nu }} \right) \right] , \\ \end{aligned} \end{aligned}$$
(7)

in which \(R=g_{{}}^{\mu \nu }R_{\mu \nu }^{{}}\) is the Ricci scalar, and \(\mathcal {U}\) is the potential without derivatives of terms originated from the interaction between \({{H}_{\mu \nu }}\) and \({{g}_{\mu \nu }}\) [22]. To prevent the appearance of the BD ghost, \(\mathcal {U}\) is constructed as

$$\begin{aligned} \mathcal {U}\left( {{g}_{\mu \nu }},{{H}_{\mu \nu }} \right) =\sum \limits _{n=0}^{4}{{{\alpha }_{n}}}{{\mathcal {L}}_{\text {n}}}. \end{aligned}$$
(8)

In this formula, \({{\alpha }_{n}}\) are the dimensionless parameters, and

$$\begin{aligned} \begin{aligned}&{{\mathcal {L}}_{0}}=1,~ \\&{{\mathcal {L}}_{1}}=\left[ \mathcal {K} \right] , \\&{{\mathcal {L}}_{2}}=\frac{1}{2}~\left( {{\left[ \mathcal {K} \right] }^{2}}-\left[ {{\mathcal {K}}^{2}} \right] \right) , \\&{{\mathcal {L}}_{3}}=~\frac{1}{6}\left( {{\left[ \mathcal {K} \right] }^{3}}-3\left[ \mathcal {K} \right] \left[ {{\mathcal {K}}^{2}}\left] +2 \right[{{\mathcal {K}}^{3}} \right] \right) , \\&{{\mathcal {L}}_{4}}=\frac{1}{24}~\left( \!{{\left[ \mathcal {K} \right] }^{4}}-6{{\left[ \mathcal {K} \right] }^{2}}\left[ {{\mathcal {K}}^{2}} \right] {+}3{{\left[ {{\mathcal {K}}^{2}} \right] }^{2}}{+}8\left[ \mathcal {K} \right] \left[ {{\mathcal {K}}^{3}}\left] -6 \right[{{\mathcal {K}}^{4}} \right] \!\right) , \\ \end{aligned} \end{aligned}$$
(9)

where \(\mathcal {K}_{~\nu }^{\mu }\) is defined as

$$\begin{aligned} \mathcal {K}_{~\nu }^{\mu }=\delta _{_{{}}\nu }^{\mu }-\sqrt{{{g}^{\mu \lambda }}{{f}_{\lambda \nu }}}, \end{aligned}$$
(10)

and the square brackets denote trace operation i.e.,

$$\begin{aligned} \begin{aligned}&\left[ \mathcal {K} \right] =\mathcal {K}_{~\mu }^{\mu },~~~~~~~~~~~~\left[ {{\mathcal {K}}^{2}} \right] =\mathcal {K}_{~\nu }^{\mu }\mathcal {K}_{~\mu }^{\nu },~~ \\&\left[ {{\mathcal {K}}^{3}} \right] =\mathcal {K}_{~\nu }^{\mu }\mathcal {K}_{~\lambda }^{\nu }\mathcal {K}_{~\mu }^{\lambda },\text { }\left[ {{\mathcal {K}}^{4}} \right] =\mathcal {K}_{~\nu }^{\mu }\mathcal {K}_{~\lambda }^{\nu }\mathcal {K}_{~\rho }^{\lambda }\mathcal {K}_{~\mu }^{\rho }.~ \\ \end{aligned} \end{aligned}$$
(11)

\({{g}_{\mu \nu }}\) raises, and lowers the indices, and moreover, \({\mathcal {L}}_{0}\) corresponds to a cosmological constant, \({\mathcal {L}}_{1}\) and \({\mathcal {L}}_{2}\) to a tadpole, and the mass term, respectively. \({\mathcal {L}}_{3,4}\) also include higher-order interaction terms [15]. Setting \({{\alpha }_{0}}={{\alpha }_{1}}=0\) Minkowskian spacetime becomes a vacuum solution [15], and in addition, if \({{\alpha }_{2}}=1\), then the FP theory, at a linearized level, is recovered [32]. \({{\alpha }_{3}}\), and \({{\alpha }_{4}}\) are the free parameters of the dRGT theory. Accordingly, the gravitational action (7) is finally rewritten as

$$\begin{aligned} \!{{S}_{g}}=\int {{{d}^{4}}x}\sqrt{-g}[\frac{R}{2}+m_{g}^{2}({{\mathcal {L}}_{2}}\text { }\!\!~\!\!\text { }+{{\text { }\!\!\alpha \!\!\text { }}_{3}}{{\mathcal {L}}_{3}}\text { }\!\!~\!\!\text { }+{{\text { }\!\!\alpha \!\!\text { }}_{4}}\text { }\!\!~\!\!\text { }{{\mathcal {L}}_{4}}\text { }\!\!~\!\!\text { })]. \end{aligned}$$
(12)

3 Background cosmology

The total action consists of three parts including (i) the gravitational action (12), (ii) the Lagrangian (1), and (iii) the matter action \(S_m\) so that

$$\begin{aligned} {{S}_{tot}}={{S}_{g}}+{{S}_{\sigma }}+{{S}_{m}}, \end{aligned}$$
(13)

where \(S_m\) corresponds to a perfect fluid, described by the energy-momentum tensor

$$\begin{aligned} T_{~\nu }^{\mu }=diag(-{{\rho }_{m}},{{p}_{m}},{{p}_{m}},{{p}_{m}}), \end{aligned}$$
(14)

in which \({{\rho }_{m}},\) and \({{p}_{m}}\) denote the energy density, and the pressure of matter, respectively.

Now, assuming the Universe is homogeneous and isotropic, the physical metric \({{g}_{\mu \nu }}\) is deemed as the Friedmann- Robertson–Walker (FRW) metric

$$\begin{aligned} {{g}_{\mu \nu }}d{{x}^{\mu }}d{{x}^{\nu }}=-N{{(t)}^{2}}{{(dt)}^{2}}+a{{(t)}^{2}}{{\Omega }_{ij}}d{{x}^{i}}d{{x}^{j}}. \end{aligned}$$
(15)

Here, N is the cosmological time, a is the scale factor, and \({{\Omega }_{ij}}\) denotes the metric of unit 3-sphere

$$\begin{aligned} {{\Omega }_{ij}}={{\delta }_{ij}}+\frac{k}{1-k{{r}^{2}}}{{x}^{i}}{{x}^{j}}, \end{aligned}$$
(16)

where k is the spatial curvature, and \({{r}^{2}}={{x}^{2}}+{{y}^{2}}+{{z}^{2}}\). In this paper, the Minkowskian form of the reference metric is chosen as

$$\begin{aligned} {{\tilde{f}}_{\mu \nu }}={{\eta }_{\mu \nu }}=diag(-1,1,1,1). \end{aligned}$$
(17)

As demonstrated in Ref [15], the flat FRW solution of the dRGT theory is equal to \(a=\)const, inconsistent with a dynamic Cosmos. Furthermore, the dRGT theory lacks closed FRW solutions, since the fiducial Minkowski metric cannot be foliated by closed slices [20]. Therefore, we only focus on open FRW of negative k very close to zero, in accordance with the Planck collaboration prescription [33, 34]. In order to carry the symmetries of an open FRW metric by the fiducial metric, the St\(\ddot{u }\)ckelberg fields should be chosen as

$$\begin{aligned} {{\phi }^{0}}=f(t)\sqrt{1-k{{r}^{2}}},\quad {{\phi }^{i}}=\sqrt{-k}f(t){{x}^{i}}, \end{aligned}$$
(18)

leading to

$$\begin{aligned} {{f}_{\mu \nu }}d{{x}^{\mu }}d{{x}^{\nu }}=-{{\dot{f}(t)}^{2}}{{(dt)}^{2}}-kf{{(t)}^{2}}{{\Omega }_{ij}}d{{x}^{i}}d{{x}^{j}}, \end{aligned}$$
(19)

where \(\dot{f}=\frac{df(t)}{dt}\). Without loss of generality, we also assume \(a>0,~N>0,~f\ge 0,~\dot{f}\ge 0\).

3.1 Equations of motion

Inserting the physical metric (15), and the fiducial metric (19) in Eq. (13), the total action is obtained as

$$\begin{aligned} S_{tot}&=\int d^{4}x\Bigg [3\Bigg [\!-\frac{a\dot{a}^{2}}{N}+kNa+m_{g}^{2}(NF(a,f) -\dot{f}G(a,f))\!\Bigg ]\nonumber \\&\quad +a^{3}\Bigg (\frac{1}{2N}f(\sigma )\dot{\sigma }^{2}-{N}V(\sigma )\Bigg )\Bigg ]+S_m, \end{aligned}$$
(20)

in which

$$\begin{aligned} \begin{aligned}&F(a,f)=a(a-\sqrt{-k}f)(2a-\sqrt{-k}f)~~~~\\&\quad + \frac{{{\alpha }_{3}}}{3}{{(a-\sqrt{-k}f)}^{2}}(4a-\sqrt{-k}f)+\frac{{{\alpha }_{4}}}{3}{{(a-\sqrt{-k}f)}^{3}},~~~~~~~~~ \\ \end{aligned} \end{aligned}$$
(21)

and

$$\begin{aligned} \begin{aligned} G(a,f)&={{a}^{2}}(a-\sqrt{-k}f)+\alpha _{3}^{{}}a{{(a-\sqrt{-k}f)}^{2}}\\&\quad +\frac{{{\alpha }_{4}}}{3}{{(a-\sqrt{-k}f)}^{3}}. \end{aligned} \end{aligned}$$
(22)

Now, variation of the total action (20) with respect to the field variables f,  N,  a, and\(~\sigma \) renders

$$\begin{aligned}&{{\delta }_{f}}{{S}_{tot}}{{|}_{N=1}}:\mathop {{}}_{{}}(\dot{a}-\sqrt{-k})\frac{\partial G(a,f)}{\partial a}=0, \end{aligned}$$
(23)
$$\begin{aligned}&{{\delta }_{N}}{{S}_{tot}}{{|}_{N=1}}:\mathop {{}}_{{}}3({{H}^{2}}+\frac{k}{{{a}^{2}}})={{\rho }_{MG}}+{{\rho }_{\sigma }}+{{\rho }_{m}}, \end{aligned}$$
(24)
$$\begin{aligned}&{{\delta }_{a}}{{S}_{tot}}{{|}_{N=1}}:\mathop {{}}_{{}}-(2\dot{H}+3{{H}^{2}}+\frac{k}{{{a}^{2}}})={{p}_{MG}}+{{p}_{\sigma }}+{{p}_{m}}, \end{aligned}$$
(25)
$$\begin{aligned}&{{\delta }_{\sigma }}{{S}_{tot}}{{|}_{N=1}}:\mathop {{}}_{{}}\frac{1}{2}{f}'(\sigma ){{\dot{\sigma }}^{2}}+f(\sigma )(\ddot{\sigma }+3H\dot{\sigma }) +{V}'(\sigma )=0, \end{aligned}$$
(26)

where \(H=\frac{{\dot{a}}}{a}\) is the Hubble parameter, and \({V}'(\sigma )=\frac{dV(\sigma )}{d\sigma }\).

In Eqs. (23)–(26), the effective energy density, and pressure of dRGT theory are given by

$$\begin{aligned} {{\rho }_{MG}}=-3m_{g}^{2}\frac{F(a,f)}{{{a}^{3}}}, \end{aligned}$$
(27)

and

$$\begin{aligned} {{p}_{MG}}=m{{_{g}^{2}}^{{}}}\Bigg [\frac{F(a,f)}{{{a}^{3}}}+(\dot{f}-\beta )\frac{\partial G(a,f)}{\partial a}\Bigg ]. \end{aligned}$$
(28)

respectively. Also, we have

$$\begin{aligned} {{\rho }_{\sigma }}=\frac{1}{2}f(\sigma ){{\dot{\sigma }}^{2}}+V(\sigma ), \end{aligned}$$
(29)
$$\begin{aligned} {{p}_{\sigma }}=\frac{1}{2}f(\sigma ){{\dot{\sigma }}^{2}}-V(\sigma ), \end{aligned}$$
(30)

for the energy density and pressure of \(\sigma \). For action (2), the equation of motion yields

$$\begin{aligned} {{\delta }_{\varphi }}{{S}_{tot}}{{|}_{N=1}}:\mathop {{}}_{{}}\ddot{\varphi }+3\,H\dot{\varphi }+\frac{dV(\varphi )}{d\varphi }=0. \end{aligned}$$
(31)

In this case, the energy density and pressure of \(\varphi \) are also given by

$$\begin{aligned} {{\rho }_{\varphi }}=\frac{1}{2}{{\dot{\varphi }}^{2}}+V(\varphi ), \end{aligned}$$
(32)

and

$$\begin{aligned} _{{}}^{{}}{{p}_{\varphi }}=\frac{1}{2}{{\dot{\varphi }}^{2}}-V(\varphi ), \end{aligned}$$
(33)

respectively.

Equation (23) has three solutions. For one of these solutions, one obtains \(\dot{a}=\sqrt{-k}\) which leads to \(a=\sqrt{-k}t+\text {const}\) that signals us to an open FRW universe as the physical metric \({{g}_{\mu \nu }}\). Similar to flat FRW solution, this solution is unacceptable. The other two solutions are obtained from \(\frac{\partial G(a,f)}{\partial a}=0\) which leads to

$$\begin{aligned} {{\beta }_{\pm }}=\frac{1+2{{\alpha }_{3}}+{{\alpha }_{4}}\pm \sqrt{^{{}}1+{{\alpha }_{3}}+\alpha _{3}^{2}-{{\alpha }_{4}}}}{{{\alpha }_{3}}+{{\alpha }_{4}}}, \end{aligned}$$
(34)

and

$$\begin{aligned} a=\frac{\sqrt{-k}f}{{{\beta }_{\pm }}}. \end{aligned}$$
(35)

Now, assuming a is positive, one finds that, according to Eq. (35), \({{\beta }_{\pm }}\) should also be positive. For the negative scale factor, Eq. (35) becomes \(a=-\frac{\sqrt{-k}f}{{{\beta }_{\pm }}}\). So, \({{\beta }_{\pm }}\) is always positive. If \(f(t)\propto a(t)\), then Eqs. (27)–(30) give us

$$\begin{aligned} \begin{aligned} {{\rho }_{MG}}&=-{{p}_{MG}}=\Lambda _{\pm }^{{}}\\&\quad = m_{g}^{2}({{\beta }_{\pm }}-1)[(3-{{\beta }_{\pm }})+{{\alpha }_{3}}(1-{{\beta }_{\pm }})], \end{aligned} \end{aligned}$$
(36)

where \(\Lambda _{\pm }\) denotes the effective cosmological constant of the theory. Although \({{\alpha }_{3}}\) and \({{\alpha }_{4}}\) are free parameters, Eq. (34) renders some constraints. Moreover, if \({{\alpha }_{3}}=-{{\alpha }_{4}}(\pm (1+{{\alpha }_{3}})>0)\), then the cosmological constant \(\Lambda _{\pm }^{{}}\) becomes infinite. On the other hand, \({{\alpha }_{4}}={{\frac{3+2{{\alpha }_{3}}+3\alpha _{3}^{2}}{4}}^{{}}}(\pm (1+{{\alpha }_{3}})>0)\) leads to \(\Lambda _{\pm }^{{}}=0\). Finally, the values of free parameters that lead to negative radicand in Eq. (34) are not acceptable (see Ref. [20]).

3.2 Inflation

This subsection examines inflation in the slow-roll regime for which the scale factor has an exponential behavior, (\(a\sim {{e}^{Ht}}(H\sim \text {const})\)), and grows rapidly. Therefore, after a few number of e-foldings, the term \(\frac{k}{{{a}^{2}}}\) becomes ignorable. Hence, Eq. (24) can be rewritten as

$$\begin{aligned} 3{{H}^{2}}=\frac{1}{2}{f(\sigma )}{{\dot{\sigma }}^{2}}+V(\sigma )+\Lambda _{\pm }^{{}}. \end{aligned}$$
(37)

Moreover, combining Eq. (24) with Eq. (25), one reaches at

$$\begin{aligned} \dot{H}=-\frac{1}{2}f(\sigma ){{\dot{\sigma }}^{2}}. \end{aligned}$$
(38)

The Hubble slow-roll parameters are also defined as

$$\begin{aligned} {\varepsilon }_H=-\frac{{\dot{H}}}{{{H}^{2}}}, \end{aligned}$$
(39)

and

$$\begin{aligned} {{\eta }_{H}}=-\frac{{\ddot{\varphi }}}{H\dot{\varphi }}. \end{aligned}$$
(40)

In this regard, as the slow-roll conditions, we have \({{\varepsilon }_{H}}, |{\eta }_{H}|<<1\), while the first condition leads to

$$\begin{aligned} f(\sigma ){{\dot{\sigma }}^{2}}<<V(\sigma )+\Lambda _{\pm }^{{}}, \end{aligned}$$
(41)

meaning that Eq. (37) can be recast as

$$\begin{aligned} 3{{H}^{2}}\approx V(\sigma )+\Lambda _{\pm }^{{}}. \end{aligned}$$
(42)

Additionally, for the relation between the first time- derivatives of \(\sigma \) and \(\varphi \), we have

$$\begin{aligned} \dot{\varphi }= \sqrt{f(\sigma )}{\dot{\sigma }}. \end{aligned}$$
(43)

On the other hand, the second time-derivatives of \(\sigma \) and \(\varphi \) address us to

$$\begin{aligned} \ddot{\varphi }=\sqrt{f(\sigma )}{\ddot{\sigma }}+\frac{1}{2}{{f(\sigma )}^{\frac{-1}{2}}}{f'(\sigma )}{{\dot{\sigma }}^{2}}, \end{aligned}$$
(44)

where \(f'(\sigma )=\frac{df}{d\sigma }\). Now, inserting \(\dot{\varphi }\) and \(\ddot{\varphi }\) in Eq. (40), \({{\eta }_{H}}\) is obtained as

$$\begin{aligned} \eta _{H}=-\frac{\ddot{\sigma }+\frac{1}{2}f(\sigma )^{-1}f'(\sigma ) \dot{\sigma }^2}{H \dot{\sigma }}. \end{aligned}$$
(45)

Using \(|{{\eta }_{H}}|<<1,\) Eq. (26) is approximately equal to

$$\begin{aligned} 3\,H\dot{\sigma }\approx -\frac{1}{f(\sigma )}{V}'(\sigma ). \end{aligned}$$
(46)

Combining Eqs. (38), (39), and (42) with each other, we get

$$\begin{aligned} {{\varepsilon }_H}=\frac{1}{2}{f(\sigma )}{{(\frac{{\dot{\sigma }}}{H})}^{2}}\approx \frac{1}{2f(\sigma )}{{\Bigg (\frac{{V}'(\sigma )}{V(\sigma )+\Lambda _{\pm }^{{}}}\Bigg )}^{2}}. \end{aligned}$$
(47)

and thus

$$\begin{aligned} 3\dot{H}\dot{\sigma }+3\,H\ddot{\sigma }\approx -\frac{1}{f(\sigma )} \Bigg [{V}''(\sigma )\dot{\sigma }-{\frac{{f}'(\sigma )}{f(\sigma )}}\dot{\sigma }{V}'(\sigma )\Bigg ], \end{aligned}$$
(48)

in which \({V}''(\sigma )=\frac{{{d}^{2}}V(\sigma )}{d{{\sigma }^{2}}}\). Finally, it is straightforward to achieve

$$\begin{aligned} {{\eta }_{H}}\approx \frac{1}{f(\sigma )}\Bigg (\frac{^{{}}{V}''(\sigma )-{\frac{{f}'(\sigma )}{2f(\sigma )}}{V}'{{(\sigma )}^{{}}}}{V(\sigma )+\Lambda _{\pm }^{{}}}\Bigg )+\frac{{\dot{H}}}{{{H}^{2}}}. \end{aligned}$$
(49)

The best method for investigating a specific potential is the calculation of parameters including \({{\varepsilon }_{V}}\), and \({{\eta }_{V}}\) combined with \({{\varepsilon }_{V}}\approx {{\varepsilon }_{H}}\), and \({{\eta }_{V}}\approx {{\eta }_{H}}+{{\varepsilon }_{H}}\) to reach [35]

$$\begin{aligned} {{\varepsilon }_{V}}=\frac{1}{2f(\sigma )} {{\Bigg (\frac{{V}'(\sigma )}{V(\sigma )+\Lambda _{\pm }^{{}}}\Bigg )}^{2}}, \end{aligned}$$
(50)

and

$$\begin{aligned} {{\eta }_{V}}=\frac{1}{f(\sigma )} \Bigg (\frac{^{{}}{V}''(\sigma )-{\frac{{f}'(\sigma )}{2f(\sigma )}}{V}'{{(\sigma )}^{{}}}}{V(\sigma ) +\Lambda _{\pm }^{{}}}\Bigg ). \end{aligned}$$
(51)

\({\varepsilon }_{V}, {|{\eta }_{V}|}<< 1\) are the neccessary conditions for the slow-roll inflation [35, 36]. The amount of inflation that occurs is measured by the number of e-foldings [37],

$$\begin{aligned} N_e= \int _{a}^{a_f}d\ln a=\int _{t}^{t_f} {H dt}, \end{aligned}$$
(52)

Thus, using \(H dt=\pm \frac{d\sigma }{\sqrt{2{\varepsilon _V}}}\), \(N_e\) is rewritten as

$$\begin{aligned} {N_e}(\sigma )=\left| \int _{\varphi }^{\varphi _f}d\varphi \frac{1}{\sqrt{2{\varepsilon _V}}}\right| =\left| \int _{\sigma }^{\sigma _f}{d\sigma } f(\sigma )\big (\frac{V(\sigma )+\Lambda _{\pm }}{{V}'(\sigma )}\big )\right| . \end{aligned}$$
(53)

In Eqs. (52) and (53), the subscript f point to the end of inflation [37]. The scalar spectral index \(n_s\), and tensor-to-scalar ratio r are thus calculated as

$$\begin{aligned} n_s=1-6{{\varepsilon }_{V}}+2{{\eta }_{V}}, \end{aligned}$$
(54)

and

$$\begin{aligned} r=16{{\varepsilon }_{V}}, \end{aligned}$$
(55)

respectively. Here, r is a significant observational quantity, and it is used to distinguish different inflationary models.

4 Numerical dynamics

This section focuses on the specific function \(f(\sigma )={A}{{|\sigma |}^{-p}} (p\not =0)\) which has pole at \(\sigma =0\) for \(p>0\) [24,25,26,27,28]. Because the field does not cross zero due to the pole, \(\sigma \) can be lie within one of the branches \(\sigma > 0\) or \(\sigma < 0\). The case \(p=2\), and \(V(\sigma )=0\) corresponds to minimal k-essence model [28].

Using Eq. (4), the relationships between \(\sigma \) and \(\varphi \) are easily achieved as

$$\begin{aligned} \varphi =\left\{ \begin{aligned}&\frac{2\sqrt{A}}{2-p}{{|\sigma |}^{\frac{2-p}{2}}}~~~\text {for}~~p\ne 2\underset{\underset{{}}{\mathop {}}\,}{\mathop {}}\, \\&\sqrt{A}\ln (|\sigma |) ~~~~~\text {for}~~p=2 \\ \end{aligned} \right. , \end{aligned}$$
(56)

and

$$\begin{aligned} \sigma =\left\{ \begin{aligned}&\pm \Bigg ({\frac{(2-p)\varphi }{2\sqrt{A}}}\Bigg )^{\frac{2}{2-p}}~~~\text {for}~~p\ne 2\underset{\underset{{}}{\mathop {}}\,}{\mathop {}}\, \\&\pm e^{\frac{\varphi }{\sqrt{A}}} ~~~~~\,\,\qquad \qquad \text {for}~~p=2 \\ \end{aligned} \right. , \end{aligned}$$
(57)

respectively, up to an integration constant.

4.1 The power potential

First, let us consider \(V(\sigma )={V_0}{{\sigma }^{n}}\), where \(V_0\) and n are non-zero constants. The general form of canonicalized potential is obtained using Eq. (57) as

$$\begin{aligned} V(\varphi ) =\left\{ \begin{aligned}&\pm {V_0} \Bigg ({\frac{(2-p)\varphi }{2\sqrt{A}}}\Bigg )^{\frac{2n}{2-p}}~~~\text {for}~~p\ne 2\underset{\underset{{}}{\mathop {}}\,}{\mathop {}}\, \\&\pm {V_0} e^{\frac{n\varphi }{\sqrt{A}}} ~~~~~\,\qquad \quad \, \quad \text {for}~~p=2 \\ \end{aligned} \right. . \end{aligned}$$
(58)

Inserting \({V_0}{{\sigma }^{n}}\) in Eq. (50), and using Eq. (51), \(\varepsilon _V\) and \(\eta _V\) are calculated as

$$\begin{aligned} \varepsilon _V=\frac{{|\sigma |}^{p}}{2A}{{\Bigg (\frac{n{{\sigma }^{n-1}}}{{{\sigma }^{n}}+c}\Bigg )}^{2}}, \end{aligned}$$
(59)

and

$$\begin{aligned} \eta _V=\frac{{|\sigma |}^{p}}{2A}\Bigg [\frac{^{{}}n(2n+p-2){{\sigma }^{n-2}}^{{}}}{{{\sigma }^{n}}+c}\Bigg ], \end{aligned}$$
(60)

respectively, where c is defined as \(c=\frac{{\Lambda }_{\pm }}{V_0}\). As inflation ends when \({\varepsilon _V}=|{\eta _V}|=1\) [38, 39], we have

$$\begin{aligned} {\tilde{\sigma }}_f={\Bigg (\frac{2n+p-2}{-3n-p+2}\Bigg )}^{\frac{1}{n}}, \end{aligned}$$
(61)

and

$$\begin{aligned} A=\frac{1}{2}{{\Bigg (c\frac{2n+p-2}{-3n-p+2}\Bigg )}^{\frac{p-2}{n}}}{{(2n+p-2)}^{2}}, \end{aligned}$$
(62)
Fig. 1
figure 1

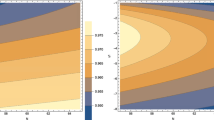
Plots of \(r(n_s)\) and \({N_e}(n_s)\) for \(V_0 \sigma \) (\(n=1\)) with \({V_0}>0\) (top plots) and \({V_0}<0\) (bottom plots). In left plots, green and blue regions are related to the Planck 2018 data [33] and its combination with BK18 and BAO [34], respectively. In addition, the 68% confidence regions are distinguished from the 95% confidence regions by highlighting the corresponding regions. Depending on the values of p, the curves of \(r(n_s)\) for \({V_0}>0\) lie within the 68 or 95% confidence regions of the Planck 2018 TT, TE, EE + lowE + lensing data, whereas the curves of \(r(n_s)\) for \({V_0}<0\) and \(2<p<200\) lie within the 68% confidence region of the Planck 2018 TT, TE, EE + lowE + lensing + BK18 + BAO data. More details on the text

Full size image

where \(\tilde{\sigma }\equiv {\sigma }{c^{\frac{-1}{n}}}\). Only \(n=1\) is acceptable for \(\sigma < 0\) because other values of n cause \(\sigma _f\) or \(V(\sigma )\) to become imaginary numbers, thus the branch \(\sigma > 0\) is considered here. In Table 1, three ranges of p for each n are obtained using condition \(\sigma _f > 0\), whereas \({V_0} > 0\) in case 1 and \({V_0} < 0\) in cases 2 and 3. It should be noted that \(p=-3n+2\) and \(p=-2n+2\) are unacceptable because they lead to \(A=0\) or \(A=\infty \), causing undifinable expressions for \(\varphi \) (56) and the canonicalized potential (58). Moreover, in this manner, the kinetic term in the Lagrangian (1) becomes zero or infinite. Consequently, we do not pay attention to these improper solutions. Case 3 leads to \( V(\sigma )+\Lambda _{\pm }^{{}} < 0\), indicating that the slow-roll condition (41) has been violated [40]. Hence, this case is not also studied in the following.

Table 1 Allowed ranges of p depending value of n whereas \({V_0} > 0\) in case 1 and \({V_0} < 0\) in cases 2 and 3
Full size table

Focusing on cases 1 (\({V_0}>0\)) and 2 (\({V_0}<0\)), two ranges of n (named i and j) for which the Lagrangian (1) may include pole gathered in Table 2. Indeed, while we have always \(p>0\) in the range i, both of the positive and negative values of p are allowed in range j.

Table 2 The ranges of n which lead to \(p > 0\) and thus pole
Full size table

Inserting \(V(\sigma )=V_0{{\sigma }^{n}}\) in Eq. (53), the number of e-foldings \(N_e\) is obtained as

$$\begin{aligned} {N_e}(\sigma )=\left| \frac{{A}'}{n}\int _{{\tilde{\sigma }}}^{{\tilde{\sigma }}_f} {d\tilde{\sigma }} ({{\tilde{\sigma }}^{-p+1}}+{{\tilde{\sigma }}^{-p-n+1}})\right| , \end{aligned}$$
(63)

in which

$$\begin{aligned} \int _{{\tilde{\sigma }}}^{{\tilde{\sigma }}_f} {d\tilde{\sigma }}{{\tilde{\sigma }}^{-p+1}}=\left\{ \begin{aligned}&\frac{1}{-p+2}({{\tilde{\sigma }}_f}^{-p+2}-{{\tilde{\sigma }}}^{-p+2})~~\,\text {for}~~p\ne 2 \\&\ln (\frac{{\tilde{\sigma }}_f}{{\tilde{\sigma }}}) ~~~~~~~~~~~~~~~~~~~~~~~~~\text {for}~~p=2 \\ \end{aligned} \right. , \end{aligned}$$
(64)
Fig. 2
figure 2

Plots of \(r(n_s)\) and \({N_e}(n_s)\) for the exponential potential \(V_0 e^{-\tilde{\sigma }}\), \(p>0\) and \(c=0\) (top plots) and \(c=0.5\) (bottom plots). In left plots, green and blue regions are related to the Planck 2018 data [33] and its combination with BK18 and BAO [34], respectively. In addition, the 68% confidence regions are highlighted compared to the 95% confidence regions. Depending on the values of p, the curves of \(r(n_s)\) for \(c=0\) lie within the 68 or 95% confidence regions of the Planck 2018 TT, TE, EE + lowE + lensing + BK18 + BAO data. In addition, all curves of \(r(n_s)\) for \(c=0.5\) lie within the 68% confidence region of the Planck 2018 TT, TE, EE + lowE + lensing + BK18 + BAO data. More details on the text

Full size image

and

$$\begin{aligned} \int _{\tilde{\sigma }}^{\tilde{\sigma }_f}{d\tilde{\sigma }}{{\tilde{\sigma }}^{-p-n+1}}= \end{aligned}$$
$$\begin{aligned} \left\{ \begin{aligned}&\frac{1}{-p-n+2}({{\tilde{\sigma }}_f}^{-p-n+2}-{{\tilde{\sigma }}}^{-p-n+2})~~~~\text {for}~~p\ne 2\underset{\underset{{}}{\mathop {}}\,}{\mathop {}}\, \\&\ln (\frac{{\tilde{\sigma }}_f}{\tilde{\sigma }}) ~~~~~~~~~~~~~~~~~~~~~~~~~~\qquad \qquad \,\,\text {for}~~p=2 \\ \end{aligned} \right. , \end{aligned}$$
(65)

where \(A'\equiv c^{\frac{2-p}{n}}{A}\). Now, equipped with Eqs. (54), (55), (59), and (60), the scalar spectral index \(n_s\), and tensor-to-scalar ratio r are obtained as

$$\begin{aligned} n_s=1+n\frac{{\tilde{\sigma }}^{p-2}}{{A}'}\Bigg [\frac{(-n+p-2)+(2n+p-2){{\tilde{\sigma }}^{-n}}}{{{(1+{{\tilde{\sigma }}^{-n}})}^{2}}}\Bigg ], \end{aligned}$$
(66)

and

$$\begin{aligned} r=8\frac{{\tilde{\sigma }}^{p-2}}{{A}'}\Bigg ({\frac{n}{1+{{\tilde{\sigma }}^{-n}}}}\Bigg )^{2}, \end{aligned}$$
(67)

respectively. From the given equations, two striking conclusions can be drawn. First, \(r(n_s)\) and \({N_e}(n_s)\) are independent of \(c\,(c\not =0)\) because \(\sigma _f\) and \(\sigma \) are proportional to \(c^{\frac{1}{n}}\) for each specific n and p. Secondly, the curves of \(r(n_s)\) and \({N_e}(n_s)\) are repeatable for any values of n, depending on the values of p. In this regard, three instances for each of cases 1 and 2 are given in Table 2. Note that for \(c=0\), \(p=-3n+2\), A becomes a free parameter, and therefore the second conclusion is rendered invalid.

Using Eq. (66), \(\sigma \) is obtained for \(0.942<n_s<0.988\). The values of \(r(n_s)\) and \({N_e}(n_s)\) are then calculated by substituting them into Eqs. (63) and (67). In Fig. 1, \(r(n_s)\) and \({N_e}(n_s)\) are shown for \(V(\sigma )=V_0 \sigma \), with top and bottom plots corresponding to cases 1 and 2, respectively. Depending on the values of p, the curves of \(r(n_s)\) for case 1 lie within the 68 or 95% confidence regions of the Planck 2018 TT, TE, EE + lowE + lensing data, whereas the curves of \(r(n_s)\) for case 2 and \(2<p<200\) lie within the 68 or 95% confidence regions of the Planck 2018 TT, TE, EE + lowE + lensing + BK18 + BAO data. For \(p>200\), the curves of \(r(n_s)\) increase very gradually, get away from the Planck 2018 TT, TE, EE + lowE + lensing + BK18 + BAO data, and fall into the 68% confidence region of the Planck 2018 TT, TE, EE + lowE + lensing data. Furthermore, \({N_e}(n_s)\) is highly similar to \(p=200\) for \(p>200\). As previously stated, only \(\sigma >0\) is admissible and correspondingly \(p<2\), leading to \(\sigma <0\) is ignored (Table 3).

Fig. 3
figure 3

Plots of \(r(n_s)\) and \({N_e}(n_s)\) for the exponential potential \(V_0 e^{-\tilde{\sigma }}\). Here, \(p<0\) and \(c=0\) (top plots) and \(c=10\) (bottom plots). In left plots, green and blue regions are related to the Planck 2018 data [33] and its combination with BK18 and BAO [34], respectively. In addition, the 68% confidence regions are highlighted compared to the 95% confidence regions. Depending on the values of p and c, the curves of \(r(n_s)\) lie within the 68 or 95% confidence regions of the Planck 2018 TT, TE, EE + lowE + lensing data, in such a way that \(c=0\) is obviously more consistent with observational data than \(c=10\). More details on the text

Full size image
Table 3 Different values of n and their corresponding intervals of p generating the same results as those of Fig. 1
Full size table

4.2 The exponential potential

In this subsection, we study the inflationary era generated by the exponential potential \(V(\sigma )=V_0 e^{-\gamma \sigma }\) where \(\gamma \) is a constant. Using Eq. (57), the general form of canonicalized potential is achieved as

$$\begin{aligned} V(\varphi ) =\left\{ \begin{aligned}&{V_0} e^{\pm \gamma {\Bigg (\frac{(2-p)\varphi }{2\sqrt{A}}\Bigg )}^{\frac{2}{2-p}}} ~~~\text {for}~~p\ne 2\underset{\underset{{}}{\mathop {}}\,}{\mathop {}}\, \\&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~.\\&{V_0} e^{\pm \gamma e^{\frac{\varphi }{\sqrt{A}}}} ~~~~~~~~~~~\,\,\,\,\text {for}~~p=2 \\ \end{aligned} \right. \end{aligned}$$
(68)

Inserting \(V_0 e^{-\gamma \sigma }\) in Eq. (50), and Eq. (51), the slow-roll parameters are obtained as

$$\begin{aligned} {\varepsilon }_{V}=\frac{|\sigma |^p}{2A}\Bigg (\frac{\gamma }{1+ce^{\gamma \sigma }}\Bigg )^2, \end{aligned}$$
(69)

and

$$\begin{aligned} {\eta }_{V}=\frac{|\sigma |^p}{A}\Bigg (\frac{\gamma (\gamma -\frac{p}{2}\sigma ^{-1})}{1+ce^{\gamma \sigma }}\Bigg ). \end{aligned}$$
(70)

At the point of \({\varepsilon }_{V}=|{\eta }_{V}|=1\), inflation is ended, a fact helps us find out

$$\begin{aligned} c(e^{{\tilde{\sigma }}_f})=\frac{-3{{\tilde{\sigma }}_f}+p}{2{{\tilde{\sigma }}_f}-p}, \end{aligned}$$
(71)

and

$$\begin{aligned} A=\gamma ^{2-p}\Bigg [\frac{1}{2}{{|{\tilde{\sigma }}_f|}^{p-2}}(2{{\tilde{\sigma }}_f}-p)^{2}\Bigg ], \end{aligned}$$
(72)

where \(\tilde{\sigma }\) is defined as \(\tilde{\sigma }=\gamma \sigma \). Inserting \(V_0 e^{-\tilde{\sigma }}\) in Eq. (53), the number of e-foldings \(N_e\) are obtained as

$$\begin{aligned} {N_e}(\sigma )=\left| A'\int _{\tilde{\sigma }}^{{\tilde{\sigma }}_f} d\tilde{\sigma }\big [{{|{\tilde{\sigma }}|}^{-p}}(1+ce^{\tilde{\sigma }})\big ]\right| , \end{aligned}$$
(73)

in which

$$\begin{aligned} \int _{{\tilde{\sigma }}}^{{\tilde{\sigma }}_f} {d\tilde{\sigma }}{|{\tilde{\sigma }|}^{-p}} \end{aligned}$$
$$\begin{aligned} = \left\{ \begin{aligned}&\frac{1}{-p+1}({|{{\tilde{\sigma }}_f}|}^{-p+1}-{|{\tilde{\sigma }}|}^{-p+1}) ~~\,~\text {for}~~p\ne 1 \\&\ln \Bigg (\left| \frac{\tilde{\sigma }_f}{\tilde{\sigma }}\right| \Bigg ) ~~~~~~~~~~~~~~~~~~~\qquad \,\,\quad \text {for}~~p=1 \\ \end{aligned} \right. , \end{aligned}$$
(74)

and

$$\begin{aligned}&\int _{\tilde{\sigma }}^{{\tilde{\sigma }}_f}d \tilde{\sigma }{{|{\tilde{\sigma }}|}^{-p}}e^{{\tilde{\sigma }}}=({|{{\tilde{\sigma }}_f}|}^{-p}e^{{\tilde{\sigma }}_f}-{|{\tilde{\sigma }}|}^{-p}e^{\tilde{\sigma }}) \nonumber \\&\quad + p\int _{\tilde{\sigma }}^{{\tilde{\sigma }}_f}d\tilde{\sigma } {{|{\tilde{\sigma }}|}^{-p-1}}e^{\tilde{\sigma }}, \end{aligned}$$
(75)

where \(A'\equiv \gamma ^{p-2}{A}\). Now, combining Eqs. (54), (55) with (69) and (70), the scalar spectral index \(n_s\), and tensor-to-scalar ratio r are calculated as

$$\begin{aligned} n_s=1+\frac{{|{\tilde{\sigma }}|}^{p}}{A'}\Bigg [\frac{-1-p{{\tilde{\sigma }}^{-1}}+c(2-p{{\tilde{\sigma }}^{-1}})e^{\tilde{\sigma }}}{(1+ce^{\tilde{\sigma }})^2}\Bigg ], \end{aligned}$$
(76)

and

$$\begin{aligned} r=8\frac{{|{\tilde{\sigma }}|}^{p}}{A'}\Bigg (\frac{1}{1+ce^{\tilde{\sigma }}}\Bigg )^2, \end{aligned}$$
(77)

respectively. According to our investigations, inflation occurs in the branches \(\tilde{\sigma }>0\) (\(\sigma \) and \(\gamma \) have same signs) and \(\tilde{\sigma }<0\) (\(\sigma \) and \(\gamma \) have opposite signs) for \(p>0\) and \(p<0\), respectively. Note that \(\sigma _f\) and \(\sigma \) are obtained inversely proportional to \(\gamma \), for any specific c and p, implying that \(r(n_s)\) and \({N_e}(n_s)\) are independent of \(\gamma \).

In Fig. 2, \(r(n_s)\) and \({N_e}(n_s)\) are shown for \(V_0 e^{-\tilde{\sigma }}\), \(p>0\), and two values of c. Depending on the values of p and c, the curves of \(r(n_s)\) lie within the 68 or 95% confidence regions of the Planck 2018 TT, TE, EE + lowE + lensing + BK18 + BAO data. When \(p>8\) and \(c=0\), \(r(n_s)\) increases, but \(c\not =0\) leads to \(\tilde{\sigma }_f=\frac{p}{2}\) and \({A}=0\), undifinable expressions for \(\varphi \) (56) and canonicalized potential (68), and zero for the kinetic term in the Lagrangian (1). Furthermore, \(r(n_s)\) approaches zero when p tends to zero. Similarly, \(r(n_s)\) and \({N_e}(n_s)\) have been plotted in Fig. 3 for \(V_0 e^{-\tilde{\sigma }}\), \(p<0\), and two values of c. The curves of \(r(n_s)\) lie within the 68% or 95% confidence regions of the Planck 2018 TT, TE, EE + lowE + lensing data, again depending on the values of p and c. When \(p<-80\), \(r(n_s)\) and \({N_e}(n_s)\) decrease gradually, and as p approaches zero, \(r(n_s)\) gets away from observations, and \({N_e}(n_s)\) grows rapidly. As shown in Figs. 2 and 3, for \(p>0\), \(r(n_s)\) decreases by increasing in c, and thus, the curves of \(r(n_s)\) are more consistent with the 68% confidence region of the Planck 2018 TT, TE, EE + lowE + lensing + BK18 + BAO data. For \(p<0\), \(r(n_s)\) increases as a function of c, and consequently, the consistency between \(r(n_s)\) and observations is reduced. It is worth noting that the evaluation \(r(n_s)\) versus c becomes more clear as the values of p increase.

5 Summary and discussions

dRGT theory cannot provide a unique source for both dark energy and inflation. Motivated by this shortcoming of dRGT theory, and also, the successes of Lagrangian (1) in describing the primary and current inflationary eras of the Universe [24,25,26,27,28,29,30], we addressed some inflationary scenarios in the framework of dRGT theory. Throughout our analysis, we only focused on the power and exponential potentials, both of which can satisfactorily produce 50–70 number of e-foldings, required to solve the flatness problem. Also, comparing the curves of \(r(n_s)\) with the Planck 2018 data [33] and its combination with BK18 and BAO [34], it has been obtained that the established models provide acceptable outcomes.