1 Introduction

Recently, the \(T_{cc}^+\) state was discovered by the LHCb Collaboration [1, 2]. As a very narrow resonance structure, the \(T_{cc}^+\) with the significance over \(10\sigma \) exists in the \(D^0D^0\pi ^+\) invariant mass spectrum, which shows that the \(T_{cc}^+\) has the minimal quark content \(cc\bar{u}\bar{d}\). The LHCb measurement indicates that the \(T_{cc}^+\) has mass difference and width

$$\begin{aligned} \delta= & {} m_{T_{cc}^+}-(m_{D^{0}}+m_{D^{*+}})=-273\pm 61\pm 5^{+11}_{-14}\,\,\mathrm{keV},\\ \Gamma= & {} 410\pm 165\pm 43^{+18}_{-38}\,\, \mathrm{keV}, \end{aligned}$$

respectively. The observation of the \(T_{cc}^+\) confirmed the existence of double charm tetraquark [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34], and inspired further discussions of its properties [35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52, 54,55,56,57,58,59,60]. The main reason why double charm tetraquark attracts the attention from both theorist and experimentalist is that double charm tetraquark is a manifestly exotic state, which can be distinguished from the conventional hadron. The zoo of exotic hadronic state becomes more abundant with adding the reported \(T_{cc}^+\).

When facing this novel phenomenon, different proposals to the inner structure of the the \(T_{cc}^+\) were proposed. At present, the molecular state [35,36,37,38,39,40,41,42,43,44,45,46] and compact tetraquark [47, 48] are two typical assignments to the \(T_{cc}^+\), which are competing with each other. The present experimental data cannot be applied to distinguish them. Under different assignment to the the \(T_{cc}^+\), the investigations of the mass spectrum [35,36,37,38,39,40,41,42,43,44,45,46,47,48], decay behavior [49,50,51,52], and production mechanism [53,54,55,56,57] can provide some important aspect of the spectroscopy behavior of the \(T_{cc}^+\). However, it is not the whole aspect of exploring hadronic spectroscopy.

In fact, the reaction of the \(T_{cc}^+\) with other hadrons can provide useful information to decode the property of the \(T_{cc}^+\). In this work, we find a novel quasi-fission phenomenon of the molecular \(T_{cc}^+\) induced by nucleon, which can be as a unique approach to test the molecular structure of the \(T_{cc}^+\). If the \(T_{cc}^+\) is the \(DD^*\) molecular state [17], the \(T_{cc}^+\) cannot decay into its hadronic components D and \(D^*\) which is kinematically forbidden. However, when a proton interacts with the molecular \(T_{cc}^+\), the quasi-fission phenomenon can be happened. In this work, we investigate the quasi-fission phenomenon of the molecular \(T_{cc}^+\) induced by a proton.

In realistic calculation, we select a simple but typical reaction \(p+T_{cc}^+\rightarrow p +D^+ +D^0\) to illustrate how this reaction occurs, by which future experimental exploration of such a reaction is suggested. Among the running and forthcoming experiments, High-Luminosity Large Hadron Collider, which will be upgraded to reach an instantaneous luminosity up to \(7\times 10^{34}\) cm\(^{-2}\)s\(^{-1}\), has a potential to find out the reaction of \(p+T_{cc}^+\rightarrow p +D^+ +D^0\). As peculiar phenomenon of the \(T_{cc}^+\) molecular state, its quasi-fission reaction behavior can be applied to test the molecular state assignment to the \(T_{cc}^+\).

Fig. 1
figure 1

The reaction of \(p+T^+_{cc}\rightarrow p+D^++D^0\). a The sketch map of the reaction. b The Feynman diagram of the reaction, the denotations of the momenta of particles are also given

Full size image

2 Reaction of the \(T_{cc}^+\) with a proton

Under the molecular state picture, the \(T^+_{cc}\) state can be expressed as

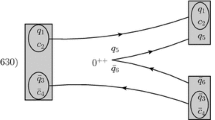
$$\begin{aligned} |T^+_{cc}\rangle&=\frac{1}{\sqrt{2}}\Big (|D^{*+}D^{0}\rangle -|D^{+}{D}^{*0}\rangle \Big ). \end{aligned}$$
(1)

Attacked by an incoming proton, the \(T^+_{cc}\) molecular state can be split into its constituents. The reaction mechanism for the precess \(p+T^+_{cc}\rightarrow p+D^++D^0\) is illustrated in Fig. 1. Here, only the first term of the \(T^+_{cc}\) molecular state in the above expression is presented, and the second term can be obtained analogously. The exchanged light mesons are assumed to attack on the vector meson \(D^{*+}\), which leads to a transition to a scalar \(D^+\) meson. The proton also possibly attacks on the \(D^0\) meson, which leads to another process with a final \(D^*\) meson. However, since no transition of the \(D^*\) meson to D meson happens, it is not a quasifssion process with extra energy release. Moreover, in the current work, only the process with D mesons, which are more stable, is considered. Hence, such process is not included in the current work.

In the current work, the most important physical quantity is the cross section of the discussed reaction process, which describes the possibility of the reaction of a proton and a \(T^+_{cc}\) molecular state. In the rest frame of the \(T^+_{cc}\), the cross section for the reaction \(p+T^+_{cc}\rightarrow p+D^++D^0\) reads as,

$$\begin{aligned} d\sigma =\frac{1}{4[(p_1\cdot p_2)^2-m_1^2m_2^2]^{1/2}}\frac{1}{6}\sum _{\lambda _p\lambda _{T_{cc}}\lambda '_p}|\mathcal{M}_{\lambda _p\lambda _{T_{cc}},\lambda '_p}|^2d\Phi _3,\nonumber \\ \end{aligned}$$
(2)

with the \(p_{1,2}\) and \(m_{1,2}\) being the momentum and mass of incoming proton or \(T^+_{cc}\). With the help of GENEV code in FAWL, the phase space \(d\Phi _3\) is produced as

$$R_3=(2\pi )^{5}d\Phi _3=\prod ^3_i\frac{d^3k_i}{2E_i}\delta ^4\left( \sum ^n_ik_i-P\right) ,$$

where the \(k_i\) and \(E_i\) are the momentum and energy of final particle i. The reaction of proton and the \(T^+_{cc}\) can be described by a split of the \(T^+_{cc}\) into two constituents and the scattering \(pD^{*+}\rightarrow pD^+\). For the first term of the wave function in Eq. (1), as shown in Fig. 1 the amplitude of total reaction can be written with an amplitude \(\mathcal{A}_{\lambda _{T_{cc}},\lambda _{{D}^{*+}}}\) for \(T^+_{cc}\rightarrow {D}^{*+}{D^0}\) and an amplitude \(\mathcal{A}'_{\lambda _p\lambda _{\bar{D}^{*+}},\lambda '_p}\) for \(p{D}^{*+}\rightarrow p{D}^+\) as

$$\begin{aligned} \mathcal{M}_{\lambda _p\lambda _{T_{cc}},\lambda '_p}=\sum _{\lambda _{{D}^{*+}}}\frac{\mathcal{A}_{\lambda _{T_{cc}},\lambda _{{D}^{*+}}}~\mathcal{A}'_{\lambda _p\lambda _{{D}^{*+}},\lambda '_p}}{p^2-m^2_{D^*}}, \end{aligned}$$
(3)

where the \(\lambda _p\), \(\lambda '_p\), \(\lambda _{T_{cc}}\), and \(\lambda _{{D}^{*+}}\) are helicities for incoming proton, final proton, initial \(T^+_{cc}\) state, and intermediate \({D}^{*+}\) meson. The p and \(m^2_{D^*}\) are the momentum and mass of intermediate \({D}^{*+}\) meson.

First, we need to deduce the amplitude \(\mathcal{A}_{\lambda _{T_{cc}},\lambda _{{D}^{*+}}}\) for the split of the \(T^+_{cc}\). The coupling of the molecular state to its constituents can be related to the binding energy [61]. Hence, the amplitude can be determined by the scattering length a as [62],

$$\begin{aligned} \mathcal{A}_{\lambda _{T_{cc}},\lambda _{{D}^{*+}}}= \sqrt{\frac{16\pi m_{T_{cc}}m_{D^*}m_D}{\mu ^2a}}\epsilon _{\lambda _{T_{cc}}}\cdot \epsilon ^*_{\lambda _{{D}^{*+}}}, \end{aligned}$$
(4)

where \(m_{T_{cc},D^*,D}\) is the mass of the \(T_{cc}^+\), and the constituent (\({D}^{*+}\) or \(D^0\)). The \(\epsilon _{\lambda _{T_{cc}}}\) and \(\epsilon _{\lambda _{{D}^{*+}}}\) are the polarized vectors for \(T^+_{cc}\) and \({D}^{*+}\), respectively. Scattering length \(a=1/\sqrt{2\mu E_B}\) with the reduced mass \(\mu =m_{D}m_{D^*}/(m_D+m_{D^*})\) and the \(E_B\) being the binding energy. As given in Ref. [63], the amplitudes for the \(T^+_{cc}\) splitting with the propagator of \(D^*\) meson can be expressed with wave function of the \(T_{cc}\), i.e., \(\psi ({\varvec{k}})=\sqrt{8\pi /a}/({\varvec{k}}^2+1/a^2)\) with normalization \(\int d^3k/(2\pi )^3|\psi (k)|^2=1\) [64], as

$$\begin{aligned} \frac{\mathcal{A}_{\lambda _{T_{cc}},\lambda _{{D}^{*+}}}}{p^2-m^2_{D^*}}&\simeq -\frac{\sqrt{8m_{T_{cc}}m_{D^*}m_D}}{m_{T_{cc}}-m_D+m_{D^*}}\psi ({\varvec{k}}_3)\epsilon _{\lambda _{T_{cc}}}\cdot \epsilon ^*_{\lambda _{{D}^{*+}}}. \end{aligned}$$
(5)

Besides the split of the \(T^+_{cc}\), we need describe the scattering \(pD^{*+}\rightarrow pD^+\) as shown in Fig. 1. To depict the scattering, the following Lagrangians under the heavy quark and chiral symmetries are adopted to construct the vertex of \(D^*\), D, and light meson [65],

$$\begin{aligned} \mathcal {L}_{\mathcal {P}^*\mathcal {P}\mathbb {P}}= & {} - \frac{2g}{f_\pi }(\mathcal {P}^{}_b\mathcal {P}^{*\dag }_{a\lambda }+\mathcal {P}^{*}_{b\lambda }\mathcal {P}^{\dag }_{a})\partial ^\lambda {}\mathbb {P}_{ba},\nonumber \\ \mathcal {L}_{\mathcal {P}^*\mathcal {P}\mathbb {V}}= & {} - 2\sqrt{2}\lambda {}g_V v^\lambda \varepsilon _{\lambda \alpha \beta \mu } (\mathcal {P}^{}_b\mathcal {P}^{*\mu \dag }_a + \mathcal {P}_b^{*\mu }\mathcal {P}^{\dag }_a) \partial ^\alpha {}\mathbb {V}^\beta _{ba},\nonumber \\ \end{aligned}$$
(6)

where \({\mathcal {P}}^{(*)T} =(D^{(*)+},D^{(*)0})\) is the fields for \(D^{(*)}\) meson. And \(\mathbb P\) and \(\mathbb V\) are two by two pseudoscalar and vector matrices

$$\begin{aligned} {\mathbb P}=\left( \begin{array}{ccc} \frac{\sqrt{3}\pi ^0+\eta }{\sqrt{6}}&{}\quad \pi ^+\\ \pi ^-&{}\quad \frac{-\sqrt{3}\pi ^0+\eta }{\sqrt{6}} \end{array}\right) ,\qquad \mathbb {V}=\left( \begin{array}{ccc} \frac{\rho ^{0}+\omega }{\sqrt{2}}&{}\quad \rho ^{+}\\ \rho ^{-}&{}\quad \frac{-\rho ^{0}+\omega }{\sqrt{2}} \end{array}\right) .\nonumber \end{aligned}$$
(7)

The parameters involved here were determined in the literature as \(g=0.59\), \(\beta =0.9\), \(\lambda =0.56\) GeV\(^{-1}\), \(g_V=5.9\), and \(f_\pi =132\) MeV [65, 66].

The Lagrangians for the vertex of nucleon and light meson are

$$\begin{aligned} \mathcal {L}_{{\mathbb P}NN}= & {} -\frac{g_{ {\mathbb P}NN}}{\sqrt{2}m_N} \bar{N}_b\gamma _5\gamma _\mu \partial _\mu {\mathbb P}_{ba} N_a,\\ \mathcal {L}_{\mathbb {V}NN}= & {} -\sqrt{2}g_{\mathbb {V} NN} \bar{N}_b\bigg (\gamma _\mu +\frac{\kappa }{2m_N}\sigma _{\mu \nu }\partial ^\nu \bigg ){\mathbb {V}} _{ba}^\mu N_a, \end{aligned}$$
(8)

where \(N^T=(p,n)\) is field for nucleon. The coupling constants \(g^2_{\pi NN}/(4\pi )=13.6\), \(g^2_{\rho NN}/(4\pi )=0.84\), \(g^2_{\omega NN}/(4\pi )=20\) with \(\kappa =6.1~(0)\) in Eq. (8) for \(\rho ~(\omega )\) meson, which are used in the Bonn nucleon–nucleon potential  [67] and meson productions in nucleon–nucelon collision [68,69,70]. The \(\eta \) exchange is neglected in the current work due to the weak coupling of \(\eta \) or \(\phi \) to nucleons as indicated in many previous works [67, 68].

Applying standard Feynman rules, the amplitude can be written as

$$\begin{aligned} \mathcal{M}_{\lambda _p\lambda _{T_{cc}},\lambda '_p}&= i\frac{\sqrt{8m_Tm_{D^*}m_D}}{m_T-m_D+m_{D^*}}\bar{u}_{\lambda '_p}\tilde{\mathcal{A}}_{\lambda _{T_{cc}}}u_{\lambda _p}, \end{aligned}$$
(9)

with

$$\begin{aligned} \tilde{\mathcal{A}}_{\lambda _{T_{cc}}}=&-\frac{1}{2}\left[ P_\rho (q^2)-P_\omega (q^2)\right] \psi ({\varvec{k}}_3)i\varepsilon _{\alpha \beta \rho \sigma }v_3^\alpha q^\beta \epsilon ^\rho _{\lambda _{T_{cc}}}\gamma ^\sigma (1-/q)\nonumber \\ {}&+\frac{1}{2}\left[ P_\rho (q^2)+P_\omega (q^2)\right] \psi ({\varvec{k}}_2)i\varepsilon _{\alpha \beta \rho \sigma }v_2^\alpha q^\beta \epsilon ^\rho _{\lambda _{T_{cc}}}\gamma ^\sigma (1-/q)\nonumber \\ {}&+\frac{1}{2} \left[ \psi ({\varvec{k}}_3)\tilde{\epsilon }_{\lambda _{T_{cc}}}^3\cdot q+\psi ({\varvec{k}}_2)\tilde{\epsilon }_{\lambda _{T_{cc}}}^2\cdot q\right] P_\pi (q^2)\gamma _5/q, \end{aligned}$$
(10)

with the abbreviations \(\tilde{\epsilon }_{\lambda _{T_{cc}}}^{3,2}=[\epsilon _{\lambda _{T_{cc}}}-(k_{2,3}-q)\cdot \epsilon _{\lambda _{T_{cc}}}~(k_{2,3}-q)/m_{D^*}^2]\) and \(v_{3,2}={k_{3,2}}/{\sqrt{m_Dm_{D^*}}}\). Here, the superscripts 2 and 3 are for the first and second parts of the wave function, respectively. \(P_i(q^2)\) is the product of the denominator of propagator of exchanged mesons \(1/(q^2-m_i^2)\), form factor \(f_i(q^2)=(m_i^2-\Lambda ^2)/(q^2-\Lambda ^2)\), and coupling constant as \(F_\pi ={\sqrt{2}gg_{ {\mathbb P}NN}\sqrt{m_Dm_{D^*}}}/{m_Nf_\pi }\) or \(F_\mathbb {V}=4g_{\mathbb {V} NN}\lambda g_V\sqrt{m_Dm_{D^*}} \).

With the preparation above, we can calculate the cross section of the \(p+T^+_{cc}\rightarrow p+D^++D^0\) reaction. The results with cutoffs \(\Lambda =0.5\), 1.5, and 3 GeV are presented in Fig. 2.

Fig. 2
figure 2

Cross section of the \(p+T^+_{cc}\rightarrow p+D^++D^0\) reaction as a function of momentum of incoming proton \(\mathrm{p}_p=|{\varvec{p}}_p|\). The results with cutoffs \(\Lambda =3\), 1.5, and 0.5 GeV are given as full (blue), dashed (black), and dotted (red) lines

Full size image

One can find that with small momentum of the coming proton, a very large cross section can be obtained. Such large cross section at small incoming momentum is a characteristic of the fission phenomenon. Of coarse, such small momentum of the proton is rare in real physical processes. Here, we provide the results at very small momenta for theoretical completeness. At a momentum of 1 eV, a cross section about \(10^7\) b can be reached. Such large cross section is from more reaction time with small speed of incoming proton. With the increase of the incoming momentum, the cross section will decrease very rapidly, and reach a cross section of an order of 10 mb at a momentum about 0.1 GeV. After that, the results becomes relatively stable. In the range of incoming momentum from 1 to 5 GeV, the cross sections with cutoffs \(\Lambda =0.5\), 1.5, and 3 GeV are of an order of magnitude of 1 to 10 mb.

In Fig. 3, we present the momentum distributions of final particles for the \(p+T^+_{cc}\rightarrow p+D^++D^0\) reaction at the momentum of incoming proton \(\mathrm{p}_p\)=0.1, 1, and 3 GeV. As expected, the distributions of the momenta become broader with the increase of the momentum of incoming proton. At a momentum of 0.1 GeV, the momenta of final particles are in a range smaller than 0.5 GeV while at a large momentum such as 3 GeV, the final particle can have a momentum about 3 GeV.

Fig. 3
figure 3

The momentum distributions of final particles for the \(p+T^+_{cc}\rightarrow p+D^++D^0\) reaction with cutoff \(\Lambda =1\) GeV. For each example choice of \(\mathrm p_p\), the figures represent the \(\mathrm{k}_p-\mathrm{k}_{D^+}\) (left) and \(\mathrm{k}_{D^0}-k_{D^+}\) (right) planes, showing the momentum \(\mathrm{k}_i=|{\varvec{k}}_i|\) of the final meson i. The colorbox means the ratio of event number in a bin of 0.01 GeV \(\times \) 0.01 GeV to the total number of events. The results are obtained with \(10^8\) simulation

Full size image

As show in the left panels in Fig. 3, the proton after reaction distributes in a large range of momentum. For example, at \(\mathrm{p}_p\)= 3 GeV, the final proton can carry momentum from about 1 to 3 GeV. More events can be observed at high momentum range, which means small energy loss. Due to the symmetry in the wave function, the distributions of final \(D^0\) and \(D^+\) is analogously. For the diagram in Fig. 1, which corresponds to the first term of wave function in Eq. (1), the final \(D^0\) meson is almost unaffected, which is shown in the \(\mathrm{k}_{D^0}-k_{D^+}\) plane as the vertical stripe with \(\mathrm{k}_{D^0}\sim 0\) GeV. The final \(D^+\) meson is from the \(D^{*+}\) meson struck by the proton, and has a broader distribution. The horizontal strip in the \(\mathrm{k}_{D^0}-k_{D^+}\) plane reflects the second term of the wave function where \(D^{*0}\) is struck and \(D^+\) is almost unaffected.

In Fig. 4, we also present the Dalitz plot against the invariant masses of the final particles. Here, three initial momenta of the proton are still chosen as 0.1, 1, and 3 GeV while the event distributes against momenta \(\mathrm{k}_p-\mathrm{k}_{D^+}\) and \(\mathrm{k}_{D^0}-k_{D^+}\) are replaced by invariant masses \(m_{D^+D^0}-m_{pD^0}\) and \(m_{pD^+}-m_{pD^0}\). The analogy distributions for \(m_{pD^+}\) and \(m_{pD^0}\) can be found which is also from the symmetry in the wave function. Obvious concentration of events is found especially with higher incoming momentum due to the \(D^*\) meson in the exotic state being almost static. For example, for the diagram in Fig. 1, with an incoming momentum \(\mathrm{p}_p=3\) GeV, the \(m_{pD^+}\) shown can be obtained as \(m_{pD^+}=\sqrt{(p_p+p)^2}=4.19\) GeV with an assumption of a static \(D^*\) meson in \(T^+_{cc}\). An obvious strip can be found at such \(m_{pD^+}\) in the plot.

Fig. 4
figure 4

The Dalitz plot for the \(p+T^+_{cc}\rightarrow p+D^++D^0\) reaction with cutoff \(\Lambda =1\) GeV. For each example choice of \(\mathrm p_p\), the figures represent the \(m_{D^+D^0}-m_{pD^0}\) (left) and \(m_{pD^+}-m_{pD^0}\) (right) planes, showing the invariant mass \(m_{ij}=\sqrt{(k_i+k_j)^2}\) of the final mesons i and j. The colorbox means the ratio of event number in a bin of 0.005 GeV \(\times \) 0.005 GeV to the total number of events. The results are obtained with \(10^8\) simulation

Full size image

3 Discussion and conclusion

As good candidate of exotic states, the newly observed \(T_{cc}^+\) [1, 2] not only confirms the former prediction of double charm tetraquark [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34], but also has aroused theorists’ interest in further revealing its property combing experimental data [35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60]. Since experimental precision is not enough to definitely conclude whether or not the \(T_{cc}^+\) is a \(DD^*\) molecular state, we should pay more effort to find peculiar phenomenon relevant to the \(T_{cc}^+\) molecular state. Although mass, decay, and production are important aspects to reflect the inner structure of the \(T_{cc}^+\), it is not the whole aspect of exploring the \(T_{cc}^+\) property. Just considering the situation of the study of the \(T_{cc}^+\), we propose that the reaction of the \(T_{cc}^+\) with a nucleon is an approach to reveal the nature of the \(T_{cc}^+\). Focusing on such a research issue, the concrete study is still not enough.

With the great interest of the reaction of the \(T_{cc}^+\), in this work, we study the reaction of a nucleon and a double charm \(T^+_{cc}\). Under the assumption of the \(T^+_{cc}\) as a molecular state of \(D^{*}D\), the reaction of the nucleon and \(T^+_{cc}\) is mediated by exchanges of \(\pi \), \(\eta \), \(\rho \), and \(\omega \) meson, which results in split of the \(T_{cc}^+\) state with two D mesons in final state. With the help of the effective Lagrangians, the cross section of \(p+T^+_{cc}\rightarrow p+D^++D^0\) process is calculated, and a very large cross section can be obtained with very small incoming momentum of proton. It decrease rapidly with the increase of the momentum to about 10 mb at momenta of order of GeV. Such large cross section suggests that the \(T^+_{cc}\) molecular state is very easy to decay and transit to two D mesons induced by a proton. We call this peculiar phenomenon as quasi-fission of double charm \(T_{cc}^+\) molecular state induced by nucleon, which can be applied to test the molecular state assignment to the \(T_{cc}^+\).

The \(T^+_{cc}\) was observed at LHCb in proton-proton collision. Naturally, it can be produced in the ion-ion collision. The X(3872) was observed at LHCb in Pb-Pb Collision [72]. The production of \(T^+_{cc}\) was also discussed in the literature [54]. In the nulceon-rich environment, the interaction of the nucleon and the produced exotic state will become important. The results in the current work can be a basis for further studies about such effects.

In summary, we predicted a quasi-fission phenomenon of double charm \(T_{cc}^+\) molecular state induced by nucleon, which can meet the physics aim of High-Luminosity Large Hadron Collider. Searching for the quasi-fission phenomenon of the \(T_{cc}^+\) induced by nucleon can shed light on the nature of the \(T_{cc}^+\), which is crucial step when constructing exotic hadron family.