1 Introduction

The gravity-thermodynamics conjecture is a cornerstone of modern Cosmology [1, 2]. In a nutshell, it states that Friedmann equations can be expressed as first law of thermodynamics by considering the Universe as a thermodynamical system bounded by an apparent horizon [3,4,5]. Equivalently, by following the reverse path, one can apply the first law of thermodynamics on the Universe horizon and extract Friedmann equations.

In the original formulation the above conjecture has been processed within the classical thermodynamics based on Boltzmann–Gibbs (BG) entropy. Recently, however, there have appeared several works in the literature that discuss generalizations of Friedmann equations arising from deformed entropies [6,7,8], all of which having the standard BG formula as a particular limit. Among these, special interest has been devoted to nonextensive Tsallis entropy [9, 10], whose cosmological implications have been studied in a variety of contexts [11,12,13,14,15,16].

The rationale behind these proposals has a twofold nature: (i) on one hand, the last two decades of observations have been revealing that the standard cosmological model is inadequate to explain the ‘dark side’ of the Universe and related effects; (ii) on the other hand, it is a fact that systems with divergent partition functions, such as large-scale gravitational systems, lie outside the validity of BG theory, requiring a suitable generalization of the usual BG entropy. For the sake of completeness, we mention that a conceptually different, but equally beaten track to construct alternative models of gravity relies on the modification of Einstein equations via the introduction of extra geometric terms [17,18,19,20] and/or new physical degrees of freedom [21,22,23] in the Einstein–Hilbert action.

Besides Tsallis’ prescription, an interesting one-parameter generalization of BG entropy arising from a coherent statistical theory which preserves relativity symmetries is the Kaniadakis entropy [24, 25]. This is given by

$$\begin{aligned} S_K\,=\,-\sum _{i}n_i \ln _Kn_i , \end{aligned}$$
(1)

where the deformed K-logarithm is defined as

$$\begin{aligned} \ln _Kx\,\equiv \, \frac{x^K-x^{-K}}{2K} , \quad -1<K<1 . \end{aligned}$$
(2)

Here we have set the Boltzmann constant \(k_B=1\).

In turn, the generalized distribution function for the i-th state of the system becomes

$$\begin{aligned} n_i\,=\,\alpha \exp _K\left[ -\beta \left( E_i-\mu \right) \right] , \end{aligned}$$
(3)

where the deformed K-exponential reads

$$\begin{aligned} \exp _K(x)\,\equiv \,\left( \sqrt{1+K^2\,x^2}\,+\,K\,x\right) ^{1/K} , \end{aligned}$$
(4)

with

$$\begin{aligned} \alpha =\left[ (1-K)/(1+K)\right] ^{1/2K} , \end{aligned}$$
(5)

and

$$\begin{aligned} 1/\beta =\sqrt{1-K^2}\,T . \end{aligned}$$
(6)

The chemical potential \(\mu \) can be fixed by requiring normalization. It is easy to check that the standard statistical mechanics is recovered in the \(K\rightarrow 0\) limit. Thus, the dimensionless K parameter quantifies the deviation of Kaniadakis statistics from the BG theory.

Using the microcanonical ensemble definition, it has been recently shown that Kaniadakis entropy for the case of black holes can be cast as [26, 27]

$$\begin{aligned} S_K\,=\,\frac{1}{K}\sinh \left( K\,S_{BH}\right) , \end{aligned}$$
(7)

where

$$\begin{aligned} S_{BH}\,=\,A/\left( 4G\right) \end{aligned}$$
(8)

is the standard Bekenstein–Hawking (BH) entropy based on BG statistics. Again, we can see that \(S_K\rightarrow S_{BH}\) as \(K\rightarrow 0\).

Equation (7) provides the basis for the study of cosmological applications in Kaniadakis theory. It should be emphasized that, since \(S_K=S_{-K}\), we can safely restrict to the \(K\ge 0\) domain. The connection between Tsallis and Kaniadakis entropies has been discussed in [26, 27] along with a further generalization introduced by Barrow [8], which appears to be particularly useful in the quantum gravitational framework.

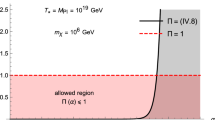
In general, the parameters appearing in the aforementioned deformed entropies are not fixed by the theory and should be estimated by observations and experiments. Therefore, it should not be entirely surprising to find different intervals for such parameters in meeting observational requirements, depending on the considered framework. While being largely conducted for Tsallis statistics [15, 28,29,30,31,32,33,34,35], this phenomenological investigation has only recently attracted interest for Kaniadakis entropy, with some attempts in holographic dark energy models [26, 27, 36,37,38] and Brans–Dicke cosmology [39]. Clearly, since \(S_{BH}\) assumes relatively large values for cosmological systems [40], from Eq. (7) we expect that \(K\ll 1\) in order to get reasonable predictions which do not deviate too much from standard BG ones. This will in fact be the domain of applicability of our next analysis.

Starting from the above premises, in this work we revisit Cosmology in Kaniadakis statistics. In particular, we apply the gravity-thermodynamics conjecture by using Eq. (7) as horizon entropy for the Friedmann–Robertson–Walker (FRW) Universe. We remark that this recipe finds its roots in the fact that physics of the early Universe is essentially relativistic. Thus, it is expected that relativistic corrections could also appear in the description of the effective horizon degrees of freedom of the Universe, thus motivating the usage of the relativistic Kaniadakis statistics instead of the classical BG one. Implications of the ensuing K-dependent Friedmann equations are analyzed in connection with the problems of baryogenesis and primordial \({}^7 Li\)-abundance. By demanding consistency between theoretical predictions and observational data, we estimate the Kaniadakis parameter. We also explore the possibility that a running (i.e. energy-dependent) K be allowed to trace the whole thermal history of the Universe within Kaniadakis framework.

The remainder of the manuscript is organized as follows: in the next Section we derive modified Friedmann equations through Kaniadakis entropy. Section 3 is devoted to the study of baryogenesis, while abundance of \({}^7 Li\) is addressed in Sect. 4. Discussion and Conclusions are finally summarized in Sect. 5. Throughout the manuscript we use natural units \(c=\hslash =1\), while keeping G explicit.

2 Modified Friedmann equations from Kaniadakis entropy

Let us start by reviewing the derivation of Friedmann equations in the case of standard Cosmology. Toward this end and in order to set the notation, we follow [27].

We describe the expanding Universe by a homogeneous and isotropic FRW geometry of metric

$$\begin{aligned} ds^2\,=\,-dt^2+a^2(t)\left( \frac{dr^2}{1-kr^2}+r^2d\varOmega ^2\right) , \end{aligned}$$
(9)

where a(t) denotes the time-dependent scale factor and the \(k=\) the spatial curvature, respectively. For our next purposes, we can safely set \(k=0\), corresponding to a flat geometry. Furthermore, we assume the Universe to be filled with a matter perfect fluid of mass density \(\rho _0\) and pressure \(p_0=w\rho _0\) at equilibrium, with \(-1\le w\le 1/3\) being the equation-of-state parameter. In the radiation dominated era of the Universe expansion, which is the phase of interest for our next analysis, we have \(w=1/3\).

According to the gravity-thermodynamics conjecture, we consider the Universe as a spherical volume physically bounded by an apparent horizon of radius

$$\begin{aligned} r_a\,=\,\frac{1}{H} , \end{aligned}$$
(10)

where \(H=\dot{a}(t)/a(t)\) is the Hubble parameter (the dot indicates time derivative). The Universe horizon is then endowed with an entropy and a temperature that arise from the corresponding thermodynamic relations for black holes [1,2,3,4,5].

The energy–momentum tensor of the matter content in the Universe obeys

$$\begin{aligned} T_{\mu \nu }\,=\,\left( \rho _0+p_0\right) u_\mu u_{\nu }+p_0\,g_{\mu \nu } , \end{aligned}$$
(11)

where \(u_{\mu }\) is the four-velocity of the matter fluid. The conservation equation \(\nabla _{\mu }T^{\mu \nu }=0\) for the FRW Universe then implies

$$\begin{aligned} {\dot{\rho }}_0\,=\,-3H(\rho _0+p_0) . \end{aligned}$$
(12)

In this picture, Friedmann equations in the bulk of the Universe follow from the first law of thermodynamics applied to its apparent horizon. Omitting standard textbook calculations, in the case of ordinary General Relativity based on the BH entropy (8), one gets

$$\begin{aligned} -4\pi \,G\left( \rho _0+p_0\right)= & {} {\dot{H}} , \end{aligned}$$
(13)
$$\begin{aligned} \frac{8\pi G}{3}\rho _0= & {} H^2 , \end{aligned}$$
(14)

where we have neglected the tiny observed cosmological constant \(\varLambda \).

The above procedure can be directly extended to modified theories of gravity by replacing the definition (8) of horizon entropy with that pertaining to the specific theory at hand. In particular, for the case of Kaniadakis entropy (7), we obtain [27]

$$\begin{aligned}&-4\pi \,G\left( \rho +p\right) =\cosh \left( K\,\frac{\pi }{G\,H^2}\right) {\dot{H}} , \end{aligned}$$
(15)
$$\begin{aligned}&\frac{8\pi G}{3}\rho =\cosh \left( K\,\frac{\pi }{G\,H^2}\right) H^2\nonumber \\&\quad -\frac{K\pi }{G}\,\mathrm {shi}\left( K\,\frac{\pi }{G\,H^2}\right) , \end{aligned}$$
(16)

where

$$\begin{aligned} \mathrm {shi}(x)\,\equiv \, \int _{0}^{x} \frac{\sinh (x')}{x'}\, dx' . \end{aligned}$$
(17)

These are the modified Friedmann equations ruling the evolution of the Universe in Kaniadakis statistics. As expected, for \(K\rightarrow 0\) they reduce to the standard relations (13) and (14), respectively.

In [27] the extra K-dependent terms appearing in Eqs. (15) and (16) are interpreted as effective dark energy density and pressure contributions. Here, we keep on a more general level and simply state that Kaniadakis entropy introduces energy density and pressure fluctuations respect to the BG-like equilibrium. We then rewrite the total energy density and pressure including these corrections as

$$\begin{aligned} \rho= & {} \rho _0+\delta \rho _K , \end{aligned}$$
(18)
$$\begin{aligned} p= & {} p_0+\delta p_K . \end{aligned}$$
(19)

In order to extract analytical solutions, we perform Taylor expansions of Eqs. (15) and (16) for \(K\ll 1\). This is a well-justified approximation, since Kaniadakis departure from BG entropy is expected to be relatively small. A similar assumption has been considered in [27, 36, 38].

By plugging Eqs. (18) and (19) into the modified Friedmann equations, we obtain to the leading order

$$\begin{aligned} \delta \rho _K= & {} -\frac{9}{128}\frac{K^2}{G^4\,\rho _0}, \end{aligned}$$
(20)
$$\begin{aligned} \delta p_K= & {} \frac{21}{128}\frac{K^2}{G^4\,\rho _0} , \end{aligned}$$
(21)

where we have included all the K-dependent terms in \(\delta \rho _K\) and \(\delta p_K\). Predictably, both these two quantities vanish for \(K\rightarrow 0\), which is consistent with the recovery of the standard cosmological scenario in this limit.

3 Implications of Kaniadakis Cosmology on baryogenesis

We now examine to what extent the mass density and pressure fluctuations (20) and (21) affect cosmic evolution and, in particular, the mechanism of baryogenesis.

Observational evidences indicate that matter prevails over antimatter in our Universe. This is in stark contrast with predictions from Quantum and Relativistic theories, as extensively discussed in [41]. The standard cosmological scenario envisages that baryogenesis is generated dynamically, while the Universe expands and cools. In particular, in [42] three necessary conditions have been set out for this mechanism to occur: (i) baryon number B violation, which is needed to generate an excess of baryons over anti-baryons; (ii) C-symmetry and CP-symmetry violation. The first ensures that the interactions producing more baryons than anti-baryons are not counterbalanced. Likewise, CP-violation is required in order not to generate equal numbers of left-handed baryons and right-handed anti-baryons (and vice-versa); (iii) out-of-thermal-equilibrium interactions, otherwise CPT symmetry would compensate between processes increasing and decreasing the baryon number.

Within our framework, the first two Sakharov conditions are satisfied by introducing the usual coupling between baryon current and spacetime. On the other hand, the last requirement is met by breaking thermal equilibrium through the modified Friedmann equations derived in the previous Section. In passing, we mention that a similar study has been conducted in [43] in the context of gravitational deformations of the Heisenberg Uncertainty Principle. In that case, the mechanism behind deviation from equilibrium is provided by minimal length effects arising from a phenomenologically motivated quantum description of gravity. Analysis along this direction also appear in [44] in f(T) gravitational baryogenesis.

As remarked in [43], in supergravity theories a mechanism for triggering baryon asymmetry by means of a dynamical breaking of CPT (and CP) during the expansion of the Universe has been considered [45]. While complying with the first two Sakharov conditions, such a mechanism preserves thermal equilibrium, thus violating Sakharov protocol. In this framework, the interaction responsible for CPT violation is described by a coupling between the derivative of the Ricci scalar R and the baryon current \(J^{\mu }\) in the form [46]

$$\begin{aligned} \frac{1}{M_*^2}\int d^4x\sqrt{-g}\,J^{\mu }\partial _{\mu }{\mathscr {R}} , \end{aligned}$$
(22)

where g is the determinant of the metric tensor and \(M_*\) the cutoff scale of the effective theory, which is taken to be of order of the reduced Planck mass \(M_*= (8\pi G)^{-1/2}\simeq 2.4\times 10^{18}\,\mathrm {GeV}\).

By further requiring some interaction that violates B in thermal equilibrium in compliance with the first Sakharov condition, a net matter/anti-matter asymmetry can be produced and get frozen-in below the decoupling temperature \(T_D\) at which B-violation goes out of equilibrium. Specifically, Eq. (22) leads to [46]

$$\begin{aligned} \frac{1}{M_*^2}J^{\mu }\partial _{\mu }{\mathscr {R}}\,=\,\frac{1}{M_*^2}\left( n_B-n_{\bar{B}}\right) \mathscr {\dot{R}} , \end{aligned}$$
(23)

where we have used the standard notation \(n_B\) (\(n_{\bar{B}}\)) for the baryon (anti-baryon) number density.

As discussed in [46], dynamical CPT-violation modifies thermal equilibrium in a similar fashion as a chemical potential. From Eq. (23), the expression of the effective potential for baryons and anti-baryons read \(\mu _B=-\mu _{{\bar{B}}}=-{\mathscr {\dot{R}}}/{M_*^2}\). The net baryon number density in the early Universe is then given by

$$\begin{aligned} n_B-n_{\bar{B}}\,=\,\bigg |\frac{g_b}{6}\mu _B T^2\bigg | , \end{aligned}$$
(24)

with \(g_b\sim {\mathscr {O}}(1)\) being the number of baryon degrees of freedom.

Baryon asymmetry is now quantified by introducing the parameter [47]

$$\begin{aligned} \frac{\eta }{7}\,\equiv \,\frac{n_B-n_{\bar{B}}}{s}\,=\, \left| \frac{15\,g_b}{4\pi ^2\,g_{*s}}\frac{\mathscr {\dot{R}}}{M_*^2\, T}\right| , \end{aligned}$$
(25)

where the r.h.s. must be evaluated for \(T=T_D\). Here, we have denoted by \(s=2\pi ^2g_{*s}T^3/45\) the entropy density in the radiation dominated era and \(g_{*s}\) is the number of degrees of freedom for particles contributing to the entropy of the Universe. As observed in [47], the approximation \(g_{*s}\approx g_*\) holds true for the present analysis, where \(g_*\simeq 106\) is the total number of degrees of freedom of relativistic Standard Model particles in the baryogenesis scenario.

From Eq. (25), it follows that \(\eta \ne 0\), provided that the Ricci scalar curvature varies over time. In the standard Cosmology based on BH entropy, \(\mathscr {\dot{R}}=0\) in the radiation dominated era, since thermal equilibrium is still satisfied. This entails that \(\eta =0\), with equal amounts of baryons and anti-baryons being produced. On the other hand, departure from equilibrium in Kaniadakis Cosmology is likely to be induced by the variations (18) and (19) in mass density and pressure, respectively.

Now, the Kaniadakis corrected derivative of the Ricci scalar \(\mathscr {\dot{R}}\) can be evaluated by observing that

$$\begin{aligned} {\mathscr {R}}\,=\,-8\pi G T_g , \end{aligned}$$
(26)

where \(T_g=\rho -3p\) is the trace of the energy–momentum tensor. By inserting Eqs. (18) and (19) into (26), we are led to

$$\begin{aligned} {\mathscr {R}}\,=\,{\mathscr {R}}_0\,+\,\frac{9\pi \left( 7+3w\right) }{16}\frac{K^2}{G^3\,\rho _0} , \end{aligned}$$
(27)

where we have defined the equilibrium Ricci scalar \({\mathscr {R}}_0\) as

$$\begin{aligned} {\mathscr {R}}_0\,=\,-8\pi G\left( 1-3w\right) \rho _0 . \end{aligned}$$
(28)

For the radiation dominated era (\(w=1/3\)), however, one simply has \({\mathscr {R}}_0=0\), giving

$$\begin{aligned} {\mathscr {R}}\,=\,\frac{9\pi }{2}\frac{K^2}{G^3\,\rho _0} . \end{aligned}$$
(29)

Now, the time derivative of the Ricci scalar takes the form

$$\begin{aligned} \dot{{\mathscr {R}}}\,=\,{12\sqrt{6\,\pi ^{3}}}\,\frac{K^2}{\sqrt{G^5\,\rho _0}}\ne 0 , \end{aligned}$$
(30)

where we have used the continuity equation (12) for the radiation dominated era.

From the above relation one can see that the usage of Kaniadakis entropy for the horizon degrees of freedom of the Universe provides a natural picture allowing to describe the departure from thermal equilibrium, thus satisfying the third and final Sakharov condition. Clearly, in the \(K\rightarrow 0\) limit, the standard cosmological scenario with \(\dot{{\mathscr {R}}}=0\) is restored.

We now plug Eq. \(\dot{{\mathscr {R}}}\) into the baryon asymmetry formula (25). A straightforward calculation gives

$$\begin{aligned} \eta \,=\,315\sqrt{\frac{6}{\pi }}\,\frac{g_b\,K^2}{g_{*s}\,M_*^2\,\sqrt{G^5\,\rho _0}\,T_D} . \end{aligned}$$
(31)

This can be further manipulated by expressing the equilibrium mass density \(\rho _0\) in terms of the temperature as

$$\begin{aligned} \rho _0(T)=\frac{\pi ^2\,g_{*s}}{30}\,T^4 . \end{aligned}$$
(32)

Substitution in Eq. (31) yields

$$\begin{aligned} \eta \,=\,15{,}120\,\sqrt{\frac{5}{\pi }}\frac{K^2}{\sqrt{\left( g_{*}\,G\right) ^3}\,T_D^3} , \end{aligned}$$
(33)

where we have used \(g_b\sim {\mathscr {O}}(1)\) and \(g_{*s}\approx g_{*}\), as discussed above. Following [43], we finally set \(T_D=M_I\), where \(M_I\simeq 3.3\times 10^{16}\,\mathrm {GeV}\) is the upper bound on the tensor mode fluctuation constraints in the inflationary scale [46]. By inserting numerical values, we get

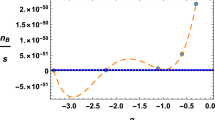
$$\begin{aligned} \eta \,\simeq \,8.4 \times 10^8\, K^2 . \end{aligned}$$
(34)

In order to constrain the dimensionless Kaniadakis parameter, let us consider observational bounds on baryon asymmetry. From [48,49,50,51,52], it is known that current measurements give

$$\begin{aligned} \eta \lesssim 9.9\times 10^{-11} , \end{aligned}$$
(35)

which constrains the K-parameter in units of \(k_B\) to be (for \(K\ge 0\), see Fig. 1).Footnote 1

$$\begin{aligned} {\widetilde{K}}\lesssim 0.34 . \end{aligned}$$
(36)

Here, we have introduced the rescaled Kaniadakis parameter \({\widetilde{K}}=K/10^{-9}\). This result substantiates the \(K\ll 1\) approximation we have employed throughout the above analysis. It is interesting to observe that a similar study has been developed in [36] by constraining Kaniadakis holographic dark energy with supernovae type Ia and Baryon Acoustic Oscillations (BAO) measurements.

Fig. 1
figure 1

Plot of baryon asymmetry parameter versus the (rescaled) Kaniadakis parameter

Full size image

4 Implications of Kaniadakis Cosmology on \({}^7 Li\)-abundance

We now explore the effects of Kaniadakis Cosmology on the primordial abundance of Lithium-7. In this regard, we emphasize that, while the standard Big Bang Nucleosynthesis (BBN) theory is able to fit the observed abundance of such elements as Hydrogen and Helium, glaring discrepancies arise for the case of Lithium [53]. This gives rise to the so-called Cosmological Lithium problem, which is one of the most debates issues in modern Cosmology.

For the purpose of this section, it is convenient to recast the modified Friedmann equation (16) to the leading order in the form

$$\begin{aligned} H(\rho )\,\equiv \,H(\rho _0)\, Z_K(\rho ) , \end{aligned}$$
(37)

where \(H(\rho _0)\) is the equilibrium Hubble parameter satisfying Eq. (14) and \(Z_K(\rho )\) is defined as

$$\begin{aligned} Z_K(\rho )\,\equiv \,1+\frac{9}{256}\,\frac{K^2}{G^4\rho ^2} . \end{aligned}$$
(38)

By use of Eqs. (18) and (20), \(Z_K(\rho )\) can be approximated to the leading order as

$$\begin{aligned} Z_K(\rho ) =1+\frac{2025}{64\,\pi ^4}\,\frac{K^2}{g_{*s}^2G^4T^8} , \end{aligned}$$
(39)

where in the second step we have used Eq. (32) for the mass density of relativistic particles filling up the Universe. \(g_{*s}\) is now the total number of relativistic degrees of freedom in the primordial scenario for \({}^7 Li\)-abundance production, i.e. \(g_{*s}\simeq 10\).

In the context of standard Cosmology based on General Relativity and BH entropy, one has \(Z=1\), which is indeed the result obtained from Eq. (39) for \(K\rightarrow 0\). In general, deviations from unity could be triggered by either alternative descriptions of gravitational interaction or the hypothesis of extra particle degrees of freedom, such as additional generations of neutrinos. In the latter case it has been shown that the modified Z-factor takes the form \(Z_\nu =\left[ 1+7/43\left( N_\nu -3\right) \right] ^{1/2}\) [54]. Nevertheless, since we are explicitly interested in corrections arising from the gravity sector, hereafter we assume three generations of neutrinos \(N_\nu =3\), thus excluding potential effects of exotic particles. Notice that such an analysis has been recently proposed in [35] by considering Tsallis statistics as a background framework and in [55] in connection with generalizations of Heisenberg relation.

Now, in order to explore the \({}^7 Li\)-abundance problem in Kaniadakis statistics and constrain the K-parameter, let us consider the processes involving the production/destruction of this isotope during BBN. It is known that soon after the Big Bang, our Universe was mostly made by hydrogen and helium, with smatterings of lithium and beryllium and very small abundances of all other heavier elements. Regarding the Lithium synthesis, BBN generated both \({}^7 Li\) and \({}^7 Be\) via the reactions

$$\begin{aligned} {}^3 _{1} H \,+\, {}^4 _{2} He\rightarrow & {} {}^7_{3} Li \,+\, \gamma , \end{aligned}$$
(40)
$$\begin{aligned} {}^3_{2} H \,+\, {}^4 _{2} He\rightarrow & {} {}^7_{4} Li \,+\, \gamma , \end{aligned}$$
(41)

with the \({}^7 Be\) dominating the production of mass 7 nuclides. On the other hand, they are destroyed by

$$\begin{aligned} {}^7_{3} Li \,+\, p\rightarrow & {} {}^4_{2} He \,+\, {}^4_{2} He, \end{aligned}$$
(42)
$$\begin{aligned} {}^7 _{4} Be \,+\, n\rightarrow & {} {}^7_{3} Li \,+\, p . \end{aligned}$$
(43)

The amount of lithium produced during BBN can be estimated as shown in [56]. In particular, the ratio of the expected value of \({}^7 Li\) abundance in the standard cosmological model with respect to the observed one lies in the range [54, 57]

$$\begin{aligned} \frac{Li|_{GR}}{Li_|{obs}}\,\in \,\left[ 2.4 - 4.3\right] , \end{aligned}$$
(44)

which indeed motivates corrections to General Relativity, as discussed above.

Fig. 2
figure 2

Plot of \(Z-1\) factor versus the (rescaled) Kaniadakis parameter

Full size image

Now, the numerical best fit expression for \({}^7 Li\) abundance is [58]

$$\begin{aligned} y_{Li}\,=\,4.82\left( 1\pm 0.1\right) \left[ \frac{\eta _{10}-3\left( Z-1\right) }{6}\right] ^2, \end{aligned}$$
(45)

where

$$\begin{aligned} \eta _{10}\,\equiv \, 10^{10}\eta _B\simeq 6 , \end{aligned}$$
(46)

is the baryon density parameter, \(\eta _B\) being the baryon to photon ratio. We can then constrain the Kaniadakis parameter by demanding consistency between this fit and the observational bound \(y_{Li}=1.6\pm 0.3\) [59]. Following [35, 59, 60], we have

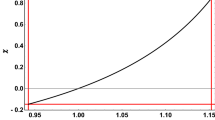
$$\begin{aligned} Z\lesssim 2.04 , \end{aligned}$$
(47)

where we have considered the maximal value allowed for Z taking into account uncertainty. By using Eq. (39) for the Z-factor, this implies (see Fig. 2)

$$\begin{aligned} {{\widetilde{K}}}\lesssim 8.08\times 10^{-75} , \end{aligned}$$
(48)

for \(T\simeq 10\,\mathrm {MeV}\). Therefore, though being relatively small, Kaniadakis effects on \({}^7 Li\) production might be non-vanishing, potentially opening a new window on the resolution of the Lithium puzzle in the context of relativistic Kaniadakis statistics. By comparison between Eqs. (36) and (48), it is worth noting that there is only partial overlap between the two ranges of K, the latter bound being more stringent than the former. A possible explanation for this apparent inconsistency is provided in the discussion below (see point 3).

Finally, we observe that the same considerations could in principle be extended to the study of \({}^4 He\) and D abundances. In that case, one has \(Z-1\sim {\mathscr {O}}(10^{-2})\), which entails a bound of one order lower than that in Eq. (48).

5 Discussion and conclusions

It is known that systems with divergent partition functions, such as large-scale gravitational systems, lie outside the domain of classical Boltzmann–Gibbs statistics. At the same time, physics of the early Universe is expected be fundamentally relativistic. Combined together, such conditions motivate the usage of a relativistic statistical theory for the effective horizon degrees of freedom of the early Universe. In this context, a coherent framework is provided by Kaniadakis theory, which is built upon a self-consistent relativistic generalization of Boltzmann–Gibbs entropy.

In this work, we have analyzed some implications of Kaniadakis statistics in Cosmology. Specifically, we have assumed Eq. (7) as horizon entropy for a homogeneous and isotropic FRW Universe and explored its effects on the problems of baryogenesis and primordial abundance of lithium. We stress that the values obtained for K are comparably smaller than those typically found in the literature for condensed matter and complex systems [61,62,63,64]. This is quite expected in cosmological scenarios, as discussed in the Introduction and also confirmed by the analysis of [27, 36].

We summarize the results of our analysis as following:

  1. 1.

    We have shown that corrections induced by Kaniadakis entropy on the mass density and pressure provide a natural mechanism allowing to drive the early Universe out of thermal equilibrium. This is in fulfillment of the third Sakharov condition. By assuming a coupling between space-time and the baryon current which satisfies the first two Sakharov conditions, all the necessary ingredients for baryogenesis are available in this scenario. Consistency between theoretical results and experimental bounds has led to the constraint (36) on the Kaniadakis parameter.

  2. 2.

    We have also argued that Kaniadakis Cosmology provides a viable solution for the \({}^7 Li\) problem, enabling us to explain the discrepancy between predictions of standard BBN theory and observational measurements. In this context, we have found that the Kaniadakis parameter is constrained by Eq. (48).

  3. 3.

    The two constraints do not overlap. Such an apparent shortcoming could be overcome by allowing the Kaniadakis parameter to vary over time. Although not contemplated in the original theory, the possibility of a running K in Kaniadakis Cosmology would be well-justified. Indeed, just as the matter fluid (i.e., the particle degrees of freedom) filling the Universe evolves from an almost pure relativistic gas to a system where most of constituents are semi- or non-relativistic as the temperature cools down, in the same way it is reasonable to expect that the holographic entropy (i.e. the horizon degrees of freedom) dynamically evolves from a relativistic (Kaniadakis-like) to a classical (BG-like) statistical description over time. Deviations from BG-statistics would then be quantified by a decreasing function of time, \(K\equiv K(t)\), or, equivalently, of the energy scale, \(K\equiv K(T).\)Footnote 2 The supposed behavior would explain why the constraint (48) (derived for \(T\simeq 10\,\mathrm {MeV}\)) is by far more stringent than the one in Eq. (36) (\(T\lesssim 10^{16}\,\mathrm {GeV}\)). Going backwards in time, in this picture it would be interesting to figure out when Kaniadakis corrections started to become appreciably relevant (\(K\gtrsim {\mathscr {O}}(10^{-1})\)) respect to the ordinary terms in the standard cosmological model. To substantiate the above conjecture, we remark that a similar analysis with a running parameter has been carried out in [16] within the framework of Tsallis statistics, motivated by renormalization considerations. In order to provide more solid mathematical basis to this paradigm, the present study should be addressed by considering ab initio a specific ansatz for K(t) and its time derivative in the modified Friedmann equations (15), (16). This will be reserved for future investigation.

As additional perspectives, we aim at further exploring the consequences of Kaniadakis statistics in Cosmology. Clearly, a first step forward is to develop an exact analysis. In fact, the Taylor expansion we have considered in Sect. 2 break down relativistic symmetries of Kaniadakis entropy, thus requiring to go beyond the linear approximation in K. This study requires much mathematical effort and is still in progress.

Furthermore, consistently with the discussion in point 3., a challenging research line is to look for imprints of inflationary tensor perturbations propagated during the would-be Kaniadakis cosmological era in current experiments on primordial gravitational waves. In this sense, promising hints could be provided by LIGO and VIRGO and, in the next future, by LISA measurements. Likewise, it is interesting to constrain Kaniadakis corrections by calculating the deviations of the freeze-out temperature \(\left| \frac{\delta T_f}{T_f}\right| \) in comparison to the \(\varLambda \)CDM paradigm.

In conclusions, the results here obtained can contribute to the debate of fixing the most realistic framework among models based on Kaniadakis Cosmology. Work in this direction is under active investigation and will be presented elsewhere.