1 Introduction

The profound connection between thermodynamics and gravitational field equations has received considerable attention since the discovery of the thermodynamic properties of black holes [1,2,3]. It has been confirmed that the field equations of general relativity are nothing but an equation of state for the spacetime [4]. In other words, when the spacetime is regarded as a thermodynamic system, the law of thermodynamics on the large scale can be interpreted as the law of gravity. The thermodynamics-gravity conjecture has now been well explored in the literature [5,6,7,8,9,10,11,12,13]. The investigation has been generalized to the cosmological background, where it has been shown that the Friedmann equations describing the evolution of the universe can be rewritten in the form of the first law of thermodynamics and vise versa [14,15,16,17,18,19,20,21]. Furthermore, one can apply this remarkable connection in the context of braneworld scenarios [22,23,24,25].

In the cosmological approach, it is possible to extract the Friedmann equations of the Friedmann–Lemaître–Robertson–Walker (FLRW) universe by applying the first law of thermodynamics \(\mathrm {d}E=T\mathrm {d}S+W\mathrm {d}V\) at the apparent horizon [20]. It was argued that, in any gravity theory, one can consider the entropy expression associated with the apparent horizon in the form of the black hole entropy in the same gravity theory. The only change needed is to replace the black hole horizon radius \(r_{+}\) in the entropy expression by the apparent horizon radius \({\tilde{r}}_\mathrm {A}\) in the entropy expression associated with the apparent horizon. While it is more convenient to apply the Bekenstein–Hawking area law relation defined as \(S_{BH}={A}/{(4G)}\) for the black hole entropy [3, 26] (with the black hole horizon area \(A=4 \pi r_{+}^2\)), it should be noted that there are several types of corrections to the area law entropy. Two possible corrections that occur due to quantum effects are known as logarithmic corrections arising from loop quantum gravity [27,28,29,30,31,32,33,34], and power-law corrections established in the entanglement between quantum fields inside and outside the horizon [35,36,37]. The other appropriate correction concerning the area law of entropy comes from the fact that the Boltzmann–Gibbs (BG) additive entropy should be generalized to non-additive entropy in divergent partition function systems such as gravitational systems [38,39,40,41,42,43,44]. Therefore, it has been argued that the entropy of these systems should be in the form of non-extensive Tsallis entropy \(S \sim A^{\beta }\), where \(\beta \) is the non-extensive or Tsallis parameter [45]. Studies on the non-additive Tsallis entropy and its applications in cosmology have been carried out in [46,47,48,49,50,51,52,53,54,55].

Moreover, it is worth turning our attention to Barrow correction to area law entropy due to quantum-gravitational effects [56]. Around 1 year ago, J. D. Barrow considered an intricate and fractal geometry for the black hole horizon, which leads to an increase in surface area. The modified entropy relation based on Barrow corrections takes the form [56]

$$\begin{aligned} S=\Bigg (\frac{A}{A_0}\Bigg )^{1+{\Delta }/2}, \end{aligned}$$
(1)

where A is the black hole horizon area, \(A_0\) is the Planck area, and the exponent \({\Delta }\), which quantifies the quantum-gravitational deformation, is in the range of \(0 \le {\Delta } \le 1\) [56,57,58]. The area law entropy expression is restored by choosing \({\Delta }=0\), which accordingly corresponds to the simplest horizon structure, while \({\Delta }=1\) expresses the most intricate surface structure. There are some investigations on Barrow entropy in the cosmological and gravitational setups [59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75].

In order to rewrite the modified field equations from Barrow entropy at the apparent horizon of the FLRW universe, one should replace the entropy in the Clausius relation \(\delta Q=T \delta S\) by the entropy expression (1) and consider A as the apparent horizon area given by \(A=4\pi {\tilde{r}}^2_\mathrm {A}\). Our approach in the present study is similar to that in [76], which considers the non-additive Tsallis entropy correction to the area law relation. However, it should be mentioned that the physical motivation and principles are completely different between the two investigations. In particular, the Tsallis non-additive entropy correction is motivated by generalizing standard thermodynamics to a non-extensive one, while the Barrow correction to entropy originates from the intricate, fractal structure on the horizon induced by quantum-gravitational effects.

It is worth noting that applying the Bekenstein–Hawking entropy in the Clausius relation leads to the Einstein field equations in the standard \(\mathrm {\Lambda }\)CDM model [7]. It is known that the standard model of cosmology is in excellent agreement with the majority of observational constraints; however, it suffers from some observational tensions which inspire investigations beyond the standard model. Specifically, low redshift measurements of the Hubble constant [77,78,79,80] and local determinations of the growth of structure [81] are inconsistent with the Planck cosmic microwave background (CMB) observations [82]. Accordingly, in this paper we study whether the discrepancies between local and global measurements can be resolved in Barrow cosmology. Throughout the paper we set \(k_\mathrm {B}=c=\hbar =1\) for simplicity.

This paper is structured as follows. In Sect. 2 we derive modified field equations describing the evolutions of the universe when the horizon entropy is given by Eq. (1). Numerical solutions based on Barrow entropy corrections to the field equations are presented in Sect. 3. Section 4 is dedicated to constraining Barrow cosmology with observational data. We summarize our conclusions in Sect. 5.

2 Modified gravitational field equations from Barrow corrections

In this part, we will derive the corresponding field equations in the cosmological setup when the entropy associated with the apparent horizon is in the form of Barrow entropy. In this respect, we consider a spatially flat FLRW universe with the background metric given by

$$\begin{aligned} \mathrm {d}s^2=a^2(\tau )\big (-\mathrm {d}\tau ^2+\mathrm {d}\pmb {x}^2\big ), \end{aligned}$$
(2)

where \(\tau \) is the conformal time. Also, the perturbed line element in linear perturbation theory in the conformal Newtonian gauge reads

$$\begin{aligned} \mathrm {d}s^2=a^2(\tau )\Big (-\big (1+2\mathrm {\Psi }\big )\mathrm {d}\tau ^2+\big (1-2\mathrm {\Phi }\big )\mathrm {d}\pmb {x}^2\Big ), \end{aligned}$$
(3)

with gravitational potentials \(\mathrm {\Psi }\) and \(\mathrm {\Phi }\). Similarly in the synchronous gauge we have

$$\begin{aligned} \mathrm {d}s^2=a^2(\tau )\Big (-\mathrm {d}\tau ^2+\big (\delta _{ij}+h_{ij}\big )\mathrm {d}x^i\mathrm {d}x^j\Big ), \end{aligned}$$
(4)

where \(h_{ij}=\mathrm {diag}(-2\eta ,-2\eta ,h+4\eta )\), with scalar perturbations h and \(\eta \).

Furthermore, we consider that the universe consists of radiation (R), matter (M) (dark matter [DM] and baryons [B]), and dark energy (DE), which are assumed to be perfect fluids, with the energy–momentum tensor defined as

$$\begin{aligned} T_{\mu \nu (i)}=\big (\rho _i+p_i\big )u_{\mu (i)}u_{\nu (i)}+g_{\mu \nu }p_i, \end{aligned}$$
(5)

where \(\rho _i={\bar{\rho }}_i+\delta \rho _i\) is the energy density, \(p_i={\bar{p}}_i+\delta p_i\) is the pressure and \(u_{\mu (i)}\) is the four-velocity of the \(i^{th}\) component in the universe (and a bar indicates the background level).

Employing the Clausius relation, \(\delta Q=T \delta S\), which is satisfied on a local causal horizon \({\mathscr {H}}\), we derive the gravitational field equations. Considering the universe as a thermodynamic system, we apply the Clausius relation on the apparent horizon of the universe with radius \({\tilde{r}}_\mathrm {A}\), defined as [83]

$$\begin{aligned} {\tilde{r}}_\mathrm {A}=\Big (H^2+\frac{K}{a^2}\Big )^{-1/2}, \end{aligned}$$
(6)

where H is the Hubble parameter and \(K=-1,0,1\) is the curvature constant corresponding to an open, flat and closed universe, respectively. Also, the associated temperature with the apparent horizon is given by

$$\begin{aligned} T=\frac{\kappa }{2\pi }, \end{aligned}$$
(7)

where \(\kappa \) is the surface gravity at the apparent horizon. As mentioned before, in the interest of deriving field equations in Barrow cosmology, we should apply the Borrow entropy defined in Eq. (1) in the Clausius relation. Thus, \(\delta S\) takes the form

$$\begin{aligned} \delta S=\Big (1+\frac{{\Delta }}{2}\Big ) A_0^{-1-{\Delta }/2} A^{{\Delta }/2} \delta A. \end{aligned}$$
(8)

According to Refs. [4, 7], \(\delta Q\) can be written as

$$\begin{aligned} \delta Q= -\kappa \int _{{\mathscr {H}}}^{} \lambda T_{\mu \nu } k^{\mu } k^{\nu } \mathrm {d}\lambda \mathrm {d}A, \end{aligned}$$
(9)

and \(\delta A\) is given by

$$\begin{aligned} \delta A=\int _{{\mathscr {H}}}^{} \theta \mathrm {d}\lambda \mathrm {d}A , \end{aligned}$$
(10)

with expansion \(\theta \) defined as

$$\begin{aligned} \theta =-\lambda R_{\mu \nu } k^{\mu } k^{\nu }. \end{aligned}$$
(11)

Thus, considering Eqs. (7), (8) and (9), the Clausius relation takes the form

$$\begin{aligned}&\kappa \int _{{\mathscr {H}}}^{} (-\lambda ) T_{\mu \nu } k^{\mu } k^{\nu } \mathrm {d}\lambda \mathrm {d}A \nonumber \\&\quad =\frac{\kappa }{2\pi } \Big (1+\frac{{\Delta }}{2}\Big ) A_0^{-1-{\Delta }/2} \int _{{\mathscr {H}}}^{} (-\lambda ) R_{\mu \nu } k^{\mu } k^{\nu } A^{{\Delta }/2} \mathrm {d}\lambda \mathrm {d}A , \end{aligned}$$
(12)
$$\begin{aligned}&\rightarrow \int _{{\mathscr {H}}}^{} (-\lambda ) \Bigg (-2\pi T_{\mu \nu }+\Big (1+\frac{{\Delta }}{2}\Big ) A_0^{-1-{\Delta }/2} R_{\mu \nu } A^{{\Delta }/2} \Bigg ) \nonumber \\&\quad \times k^{\mu } k^{\nu } \mathrm {d}\lambda \mathrm {d}A=0. \end{aligned}$$
(13)

Then, for all null vectors \(k^{\mu }\) we find

$$\begin{aligned} -2\pi T_{\mu \nu }+\Big (1+\frac{{\Delta }}{2}\Big ) A_0^{-1-{\Delta }/2} R_{\mu \nu } A^{{\Delta }/2}=f g_{\mu \nu }, \end{aligned}$$
(14)

where f is a scalar. Thus, according to energy–momentum conservation (\(\nabla ^{\mu } T_{\mu \nu }=0\)), we must have

$$\begin{aligned}&\nabla ^{\mu } \Bigg (\Big (1+\frac{{\Delta }}{2}\Big ) A_0^{-1-{\Delta }/2} R_{\mu \nu } A^{{\Delta }/2}-f g_{\mu \nu }\Bigg )=0, \end{aligned}$$
(15)
$$\begin{aligned}&\rightarrow \Big (1+\frac{{\Delta }}{2}\Big ) A_0^{-1-{\Delta }/2} \Bigg (\frac{1}{2}\big (\partial _{\nu } R\big ) A^{{\Delta }/2} + R_{\mu \nu } \partial ^{\mu } A^{{\Delta }/2}\Bigg )\nonumber \\&=\partial _{\nu } f. \end{aligned}$$
(16)

Considering Eq. (16), the left-hand side is not the gradient of a scalar, which means that this corresponds to non-equilibrium behaviour of thermodynamics, and the Clausius relation is not satisfied. Thus, the Clausius relation should be replaced by the entropy balance relation [7]

$$\begin{aligned} \delta S=\frac{\delta Q}{T}+\mathrm {d}_i S, \end{aligned}$$
(17)

where \(\mathrm {d}_i S\) is the entropy produced inside the system caused by irreversible transformations of the system [84]. Then, in order to resolve the contradiction with energy–momentum conservation, we assume \(\mathrm {d}_i S\) as the following form

$$\begin{aligned} \mathrm {d}_i S=\Big (1+\frac{{\Delta }}{2}\Big ) A_0^{-1-{\Delta }/2} \int _{{\mathscr {H}}}^{} (-\lambda ) \nabla _{\mu } \nabla _{\nu } A^{{\Delta }/2} k^{\mu } k^{\nu } \mathrm {d}\lambda \mathrm {d}A.\nonumber \\ \end{aligned}$$
(18)

Substituting \(\mathrm {d}_i S\) in relation (17) results in

$$\begin{aligned} \int _{{\mathscr {H}}}^{}&(-\lambda ) \Bigg (\Big (1+\frac{{\Delta }}{2}\Big ) A_0^{-1-{\Delta }/2} R_{\mu \nu } A^{{\Delta }/2}-2\pi T_{\mu \nu } \nonumber \\&-\Big (1+\frac{{\Delta }}{2}\Big ) A_0^{-1-{\Delta }/2} \nabla _{\mu } \nabla _{\nu } A^{{\Delta }/2}\Bigg ) k^{\mu } k^{\nu } \mathrm {d}\lambda \mathrm {d}A=0 . \end{aligned}$$
(19)

Again, for all null vectors \(k^{\mu }\) we should have

$$\begin{aligned}&\Big (1+\frac{{\Delta }}{2}\Big ) A_0^{-1-{\Delta }/2} R_{\mu \nu } A^{{\Delta }/2}-2\pi T_{\mu \nu } \nonumber \\&\quad -\Big (1+\frac{{\Delta }}{2}\Big ) A_0^{-1-{\Delta }/2} \nabla _{\mu } \nabla _{\nu } A^{{\Delta }/2}=f g_{\mu \nu } . \end{aligned}$$
(20)

Then, considering energy–momentum conservation, and after doing some calculations, we obtain

$$\begin{aligned} \Big (1+\frac{{\Delta }}{2}\Big ) A_0^{-1-{\Delta }/2} \Bigg (\frac{1}{2} \big (\partial _{\nu } R\big ) A^{{\Delta }/2}-\partial _{\nu } \Box A^{{\Delta }/2}\Bigg )=\partial _{\nu } f.\nonumber \\ \end{aligned}$$
(21)

Here, we can choose the scalar \({\mathscr {L}}\) as \({\mathscr {L}}=R A^{{\Delta }/2}\), which reads

$$\begin{aligned}&\frac{\partial {\mathscr {L}}}{\partial R}=A^{{\Delta }/2} , \nonumber \\&\partial _{\nu } R=\frac{\partial R}{\partial x^{\nu }}=\frac{\partial R}{\partial {\mathscr {L}}}\frac{\partial {\mathscr {L}}}{\partial x^{\nu }}=A^{-{\Delta }/2} \partial _{\nu }{\mathscr {L}}, \nonumber \\&\quad \rightarrow \big (\partial _{\nu } R\big ) A^{{\Delta }/2}=\partial _{\nu }{\mathscr {L}} . \end{aligned}$$
(22)

Therefore, the scalar f becomes

$$\begin{aligned} f&=\Big (1+\frac{{\Delta }}{2}\Big ) A_0^{-1-{\Delta }/2} \Big (\frac{1}{2} {\mathscr {L}}- \Box A^{{\Delta }/2}\Big ) \nonumber \\&=\Big (1+\frac{{\Delta }}{2}\Big ) A_0^{-1-{\Delta }/2} \Big (\frac{1}{2} R A^{{\Delta }/2} - \Box A^{{\Delta }/2}\Big ). \end{aligned}$$
(23)

Thus, the modified field equations in Barrow cosmology can be written as

$$\begin{aligned}&R_{\mu \nu } A^{{\Delta }/2}-\nabla _{\mu } \nabla _{\nu } A^{{\Delta }/2}-\frac{1}{2} R A^{{\Delta }/2} g_{\mu \nu }+\Box A^{{\Delta }/2} g_{\mu \nu } \nonumber \\&\quad =\frac{4\pi }{2+{\Delta }}A_0^{1+{\Delta }/2}T_{\mu \nu }, \end{aligned}$$
(24)

in which for a flat spacetime, we have

$$\begin{aligned} A^{{\Delta }/2}=(4\pi )^{{\Delta }/2} \Big (\frac{a'}{a^2}\Big )^{-{\Delta }}=(4\pi )^{{{\Delta }}/2} H^{-{{\Delta }}},\nonumber \\ \end{aligned}$$
(25)

where a prime indicates a deviation with respect to the conformal time. In this way, we derive the modified Einstein field equations based on Barrow corrections to area law entropy caused by quantum-gravitational effects on the apparent horizon of the FLRW universe. Considering \({\Delta }=0\), the standard field equations in Einstein gravity will be recovered. The (00) and (ii) components of gravitational field equations (24) at background level take the form

$$\begin{aligned} \Big (\frac{a'}{a^2}\Big )^{{-}{\Delta }}\Bigg \{\Big (\frac{a'}{a}\Big )^2{-} {\Delta }\bigg (\frac{a''}{a}{-}2\Big (\frac{a'}{a}\Big )^2\bigg )\Bigg \}{=}\frac{8\pi G}{3} a^2 \sum _{i}{\bar{\rho }}_i,\nonumber \\ \end{aligned}$$
(26)
$$\begin{aligned}&\Big (\frac{a'}{a^2}\Big )^{-{\Delta }}\Bigg \{-2\frac{a''}{a}+\Big (\frac{a'}{a}\Big )^2+{\Delta }\Bigg [-\frac{a''}{a}+\frac{a'''}{a'}-\Big (\frac{a''}{a'}\Big )^2 \nonumber \\&\quad -{\Delta }\bigg (\frac{a''}{a'}-2\frac{a'}{a}\bigg )^2\Bigg ]\Bigg \}=8\pi G a^2 \sum _{i}{\bar{p}}_i , \end{aligned}$$
(27)

where we have defined \(A_0\) as

$$\begin{aligned} A_0=\big (4\pi \big )^{({\Delta }-2)/(2+{\Delta })}\Big (\big (2+{\Delta }\big )8\pi G\Big )^{2/(2+{\Delta })}. \end{aligned}$$

Also, the background level equations in terms of the Hubble parameter are given by

$$\begin{aligned} H^{2-{\Delta }}-{\Delta } H^{-{\Delta }} H' \frac{1}{a}=\frac{8\pi G}{3} \sum _{i}{\bar{\rho }}_i, \end{aligned}$$
(28)
$$\begin{aligned}&H^{-{\Delta }}\Bigg \{\big ({\Delta }-2\big ) H' \frac{1}{a}-3H^2 \nonumber \\&\quad +{\Delta }\bigg (\frac{H''}{H}-\big (1+{\Delta }\big )\Big (\frac{H'}{H}\Big )^2\bigg )\frac{1}{a^2}\Bigg \}=8\pi G \sum _{i}{\bar{p}}_i . \end{aligned}$$
(29)

Then, from (28) and (29), the first modified Friedmann equation can be derived as

$$\begin{aligned} H^{2-{\Delta }}=\frac{1}{1+2{\Delta }}\frac{8\pi G}{3}\sum _{i}{\bar{\rho }}_i. \end{aligned}$$
(30)

It is also convenient to rewrite the Friedmann equation in terms of the total density parameter defined as \(\mathrm {\Omega }_\mathrm {tot}={\bar{\rho }}_\mathrm {tot}/\rho _\mathrm {cr}\), where \(\rho _\mathrm {cr}={3H^2}/{(8\pi G)}\) and \({\bar{\rho }}_\mathrm {tot}=\sum _{i}{\bar{\rho }}_i\). Hence, Eq. (30) can be written as

$$\begin{aligned} \mathrm {\Omega }_\mathrm {tot}=\big (1+2{\Delta }\big )H^{-{\Delta }}. \end{aligned}$$
(31)

It should be noted that in the limit \({\Delta } \rightarrow 0\), the Friedmann equation takes the standard form in general relativity.

Defining the total equation of state parameter \(w_\mathrm {tot}\) as \(w_\mathrm {tot}={\bar{p}}_\mathrm {tot}/{\bar{\rho }}_\mathrm {tot}\), the accelerated expansion of the universe in Barrow cosmology is satisfied when \(w_\mathrm {tot}<-(1+{\Delta })/3\). Taking into account the fact that \(0 \le {\Delta } \le 1\), Barrow corrections predict a more negative equation of state parameter in an accelerating universe (for example, for \({\Delta }=1\) we obtain \(w_\mathrm {tot}<-2/3\)), while in the limit \({\Delta } \rightarrow 0\), the accelerated expansion condition in standard cosmology will be restored.

Taking into account the modified field equations (24) to linear order of perturbations, in the conformal Newtonian gauge (con) we have

$$\begin{aligned}&\Big (\frac{a'}{a^2}\Big )^{-{\Delta }}\Bigg \{3\frac{a'}{a}\mathrm {\Phi }'+k^2\mathrm {\Phi }+3\Big (\frac{a'}{a}\Big )^2\mathrm {\Psi } \nonumber \\&\qquad -\frac{3}{2}{\Delta }\bigg (\frac{a''}{a'}-2\frac{a'}{a}\bigg )\bigg (\mathrm {\Phi }'+2\frac{a'}{a}\mathrm {\Psi }\bigg )\Bigg \}\nonumber \\ {}&\quad =-4\pi G a^2 \sum _{i}\delta \rho _{i(\mathrm {con})} , \end{aligned}$$
(32)
$$\begin{aligned}&\Big (\frac{a'}{a^2}\Big )^{-{\Delta }}\Bigg \{k^2\mathrm {\Phi }'+\frac{a'}{a}k^2\mathrm {\Psi }-\frac{1}{2}{\Delta }\bigg (\frac{a''}{a'}-2\frac{a'}{a}\bigg )k^2\mathrm {\Psi }\Bigg \} \nonumber \\&\quad =4\pi G a^2 \sum _{i}\big ({\bar{\rho }}_i+{\bar{p}}_i\big )\theta _{i(\mathrm {con})} , \end{aligned}$$
(33)
$$\begin{aligned} \mathrm {\Phi }=\mathrm {\Psi }, \end{aligned}$$
(34)
$$\begin{aligned}&\Big (\frac{a'}{a^2}\Big )^{-{\Delta }}\Bigg \{2\frac{a''}{a}\mathrm {\Psi }-\Big (\frac{a'}{a}\Big )^2\mathrm {\Psi }+\frac{a'}{a}\mathrm {\Psi }'+2\frac{a'}{a}\mathrm {\Phi }'+\mathrm {\Phi }'' \nonumber \\&\qquad +\frac{k^2}{3}\big (\mathrm {\Phi }-\mathrm {\Psi }\big )+{\Delta }\Bigg \{\mathrm {\Psi }\Bigg [{\Delta }\bigg (\frac{a''}{a'}-2\frac{a'}{a}\bigg )^2-\frac{a'''}{a'}+\frac{a''}{a} \nonumber \\&\qquad +\Big (\frac{a''}{a'}\Big )^2\Bigg ]+\mathrm {\Psi }'\bigg (\frac{a'}{a}-\frac{1}{2}\frac{a''}{a'}\bigg )+\mathrm {\Phi }'\bigg (2\frac{a'}{a}-\frac{a''}{a'}\bigg )\Bigg \}\Bigg \} \nonumber \\&\quad =4\pi G a^2 \sum _{i}\delta p_{i(\mathrm {con})} , \end{aligned}$$
(35)
Fig. 1
figure 1

The CMB power spectra (upper left) and their relative ratios with respect to \(\mathrm {\Lambda }\)CDM (upper right) for different values of \({\Delta }\). Lower panels show the analogous diagrams for the matter power spectrum

Full size image

while in the synchronous gauge (syn) we can write

$$\begin{aligned}&\Big (\frac{a'}{a^2}\Big )^{-{\Delta }}\Bigg \{\frac{a'}{a}h'-2k^2\eta -\frac{1}{2}{\Delta } h'\bigg (\frac{a''}{a'}-2\frac{a'}{a}\bigg )\Bigg \} \nonumber \\&\quad =8\pi G a^2 \sum _{i}\delta \rho _{i(\mathrm {syn})} , \end{aligned}$$
(36)
$$\begin{aligned} \Big (\frac{a'}{a^2}\Big )^{-{\Delta }}\, k^2\eta '=4\pi G a^2 \sum _{i}\big ({\bar{\rho }}_i+{\bar{p}}_i\big )\theta _{i(\mathrm {syn})}, \end{aligned}$$
(37)
$$\begin{aligned}&\Big (\frac{a'}{a^2}\Big )^{-{\Delta }}\Bigg \{\frac{1}{2}h''+3\eta ''+\frac{a'}{a}h'+6\frac{a'}{a}\eta '-k^2\eta \nonumber \\&\quad -\frac{1}{2}{\Delta }\bigg (\frac{a''}{a'}-2\frac{a'}{a}\bigg )\bigg (h'+6\eta '\bigg )\Bigg \}=0, \end{aligned}$$
(38)
$$\begin{aligned}&\Big (\frac{a'}{a^2}\Big )^{-{\Delta }}\Bigg \{-2\frac{a'}{a}h'-h''+2k^2\eta +{\Delta }\bigg (\frac{a''}{a'}-2\frac{a'}{a}\bigg )h'\Bigg \} \nonumber \\&\quad =24\pi G a^2 \sum _{i}\delta p_{i(\mathrm {syn})}. \end{aligned}$$
(39)

Choosing \({\Delta }=0\) would result in standard field equations at the perturbation level in Einstein gravity.

Furthermore, considering energy–momentum conservation, continuity and Euler equations would not be affected by Barrow corrections, and so conservation equations are identical to those in general relativity. In the rest of the paper, we explore Barrow cosmology in the synchronous gauge; hence, conservation equations for matter and dark energy components take the form

$$\begin{aligned} \delta '_\mathrm {M(syn)}=-\theta _\mathrm {M(syn)}-\frac{1}{2}h', \end{aligned}$$
(40)
$$\begin{aligned} \theta '_\mathrm {M(syn)}=-\frac{a'}{a}\theta _\mathrm {M(syn)}, \end{aligned}$$
(41)
$$\begin{aligned}&\delta '_\mathrm {DE(syn)}=-3\frac{a'}{a}\big (c^2_{s,\mathrm {DE}}-w_\mathrm {DE}\big )\delta _\mathrm {DE(syn)}-\frac{1}{2}h'\big (1+w_\mathrm {DE}\big ) \nonumber \\&\quad -\big (1+w_\mathrm {DE}\big )\bigg (1+9\Big (\frac{a'}{a}\Big )^2\big (c^2_{s,\mathrm {DE}}-c^2_{a,\mathrm {DE}}\big )\frac{1}{k^2}\bigg )\theta _\mathrm {DE(syn)}, \end{aligned}$$
(42)
$$\begin{aligned} \theta '_\mathrm {DE(syn)}=\frac{a'}{a}\big (3c^2_{s,\mathrm {DE}}-1\big )\theta _\mathrm {DE(syn)}+\frac{k^2c^2_{s,\mathrm {DE}}}{1+w_\mathrm {DE}}\delta _\mathrm {DE(syn)}. \end{aligned}$$
(43)

In the next section, we study Barrow cosmology using a modified version of the Boltzmann code CLASSFootnote 1 [85], in which we have included the Barrow parameter \({\Delta }\) that quantifies deviations from standard cosmology. Moreover, in order to constrain cosmological parameters from current observations, we employ the Markov chain Monte Carlo (MCMC) method by making use of the Monte Python code [86, 87].

3 Numerical analysis

In order to study the Barrow cosmology model numerically, we modify the CLASS code according to the Barrow cosmology field equations described in Sect. 2. In this direction, we consider Planck 2018 results [82] for the cosmological parameters, which read \(\mathrm {\Omega }_{\mathrm {B},0}h^2=0.02242\), \(\mathrm {\Omega }_{\mathrm {DM},0}h^2=0.11933\), \(H_0=67.66\) \(\mathrm {\frac{km}{s\,Mpc}}\), \(A_s=2.105 \times 10^{-9}\), and \(\tau _\mathrm {reio}=0.0561\), and also for the dark energy fluid we choose \(w_\mathrm {DE}=-0.98\) (to avoid divergences in dark energy perturbations) and \(c_{s,\mathrm {DE}}^2=1\).

Figure 1 displays the CMB temperature anisotropy and matter power spectra diagrams in Barrow cosmology compared to \(\mathrm {\Lambda }\)CDM (it should be noted that the case \({\Delta }=0\) corresponds to the wCDM model, where it consists of cold dark matter and a dark energy fluid with a constant equation of state).

Matter power spectra diagrams show an enhancement in structure growth in the Barrow cosmology model, which is inconsistent with low redshift measurements of galaxy clustering. The evolution of matter density contrast illustrated in Fig. 2 would also reflect the increase in the growth of structures in Barrow cosmology.

Fig. 2
figure 2

Matter density contrast diagrams in terms of conformal time in Barrow cosmology compared to \(\mathrm {\Lambda }\)CDM

Full size image

On the other hand, considering the Friedmann equation (30), it is possible to explore the expansion history of the universe in Barrow cosmology as demonstrated in Fig. 3. According to this figure, it can be understood that the current value of the Hubble parameter in Barrow cosmology is more compatible with its local determinations in comparison with the \(\mathrm {\Lambda }\)CDM model.

Fig. 3
figure 3

Hubble parameter in terms of conformal time in Barrow cosmology compared to \(\mathrm {\Lambda }\)CDM

Full size image

Moreover, in Fig. 4 we show the evolution of dark energy density, which illustrates an enhancement in \({\bar{\rho }}_\mathrm {DE}\) of Barrow cosmology in comparison with the \(\mathrm {\Lambda }\)CDM model, and consequently confirms the increase in the current value of the Hubble parameter in the Barrow model.

Fig. 4
figure 4

The evolution of dark energy density in terms of conformal time in Barrow cosmology compared to \(\mathrm {\Lambda }\)CDM

Full size image
Table 1 Best-fit values and 68% and 95% confidence level intervals for cosmological parameters of \(\mathrm {\Lambda }\)CDM, wCDM, and Barrow cosmology, considering dataset (I)
Full size table
Table 2 Best-fit values and 68% and 95% confidence level intervals for the cosmological parameters of \(\mathrm {\Lambda }\)CDM, wCDM, Barrow cosmology (with Barrow parameter \({\Delta }\)), and also the TMG model (with Tsallis parameter \(\beta \)) from Ref. [76], considering dataset (II)
Full size table
Fig. 5
figure 5

The one-dimensional posterior distribution and two-dimensional posterior contours with 68% and 95% confidence limits for the selected cosmological parameters of Barrow cosmology from dataset (I) (blue) and dataset (II) (orange) (left panel), and also for the TMG model from dataset (II) according to Ref. [76] (right panel)

Full size image

4 Comparison with observational data

In this section, we put constraints on the parameters of Barrow cosmology by applying an MCMC approach through the Monte Python code [86, 87]. The set of cosmological parameters used in MCMC analysis consists of {\(100\,\mathrm {\Omega }_{\mathrm {B},0} h^2\), \(\mathrm {\Omega }_{\mathrm {DM},0} h^2\), \(100\,\theta _s\), \(\ln (10^{10} A_s)\), \(n_s\), \(\tau _{\mathrm {reio}}\), \(w_\mathrm {DE}\), \({\Delta }\)}, where \(\mathrm {\Omega }_{\mathrm {B},0} h^2\) and \(\mathrm {\Omega }_{\mathrm {DM},0} h^2\) represent the baryon and cold dark matter densities relative to the critical density, respectively, \(\theta _s\) is the ratio of the sound horizon to the angular diameter distance at decoupling, \(A_s\) stands for the amplitude of the primordial scalar perturbation spectrum, \(n_s\) is the scalar spectral index, \(\tau _{\mathrm {reio}}\) is the optical depth to reionization, \(w_\mathrm {DE}\) is the dark energy equation of state parameter, and \({\Delta }\) indicates the Barrow parameter. Furthermore, we have four derived parameters including the reionization redshift (\(z_\mathrm {reio}\)), the matter density parameter (\(\mathrm {\Omega }_{\mathrm {M},0}\)), the Hubble constant (\(H_0\)), and the root-mean-square mass fluctuations on scales of 8 \(h^{-1}\) Mpc (\(\sigma _8\)). Considering preliminary numerical studies, we choose the prior range [0, 0.015] for the Barrow parameter, and additionally, we set no prior range on \(w_\mathrm {DE}\).

The following likelihoods are utilized in the MCMC method: the Planck likelihood with Planck 2018 data (containing high-l TT, TE, EE, low-l EE, low-l TT, and lensing) [82], the Planck-SZ likelihood for the Sunyaev–Zeldovich (SZ) effect measured by Planck [88, 89], the CFHTLenS likelihood with the weak lensing data [90, 91], the Pantheon likelihood with the supernovae data [92], the BAO likelihood with the baryon acoustic oscillations data [93, 94], and the BAORSD likelihood for BAO and redshift-space distortion (RSD) measurements [95, 96].

In order to constrain the cosmological model under consideration, we use two different dataset combinations: “Planck + Pantheon + BAO” [hereafter dataset (I)] and “Planck + Planck-SZ + CFHTLenS + Pantheon + BAO + BAORSD” [hereafter dataset (II)]. Tables 1 and 2 represent the observational constraints from two different datasets (I) and (II), respectively, where we have considered \(\mathrm {\Lambda }\)CDM and also wCDM as our base models.

Marginalized \(1\sigma \) and \(2\sigma \) confidence level contour plots from datasets (I) and (II) for selected cosmological parameters of Barrow cosmology are also depicted in Fig. 5. Furthermore, in order to compare Barrow cosmology with Tsallis modified gravity (TMG), the results based on the TMG model according to Ref. [76] are also displayed.

Considering dataset (I), we can see an enhancement in the Hubble constant in Barrow cosmology compared to the standard model, which indicates a slight amelioration in \(H_0\) tension. Moreover, dark energy has a phantom behaviour according to the best-fit and mean value of \(w_{\mathrm {DE}}\), which is influential in alleviating the \(H_0\) tension. However, a quintessential character of dark energy is also allowed within the \(1\sigma \) confidence level, where \(-1.048<w_{\mathrm {DE}}<-0.9735\). Also, to be more precise, we compare Barrow cosmology with the wCDM model, which also represents a phantom behaviour of dark energy. Then, there is a minor increase in the Hubble constant of the wCDM model in comparison with \(\mathrm {\Lambda }\)CDM, which confirms that Barrow cosmology is in acceptable agreement with wCDM. Furthermore, according to the obtained constraints on Barrow parameter \({\Delta }\) and dark energy equation of state, one can conclude that Barrow cosmology is in a reasonable consistency with the \(\mathrm {\Lambda }\)CDM model. For the last point, it should be emphasized that the best fit and mean value of \({\Delta }\) are compatible with \(\mathrm {\Lambda }\)CDM, and the minor increase in the Hubble constant caused by the phantom nature of dark energy would only slightly alleviate the \(H_0\) tension and not solve it completely.

On the other hand, dataset (II) results show a suppression in the growth of structure in Barrow cosmology with respect to the \(\mathrm {\Lambda }\)CDM model. Actually, one anticipates higher values of \(\sigma _8\) in Barrow cosmology according to numerical results described in Sect. 3. However, the quintessential behaviour of dark energy can reduce the structure growth and consequently provide more compatible results with local galaxy surveys. Likewise, the wCDM model has a quintessential character of a dark energy equation of state, which yields a lower \(\sigma _8\) growth rate than the standard cosmological model. Thus, MCMC analysis implies that Barrow cosmology is in good agreement with wCDM. Additionally, observational constraints on \(w_{\mathrm {DE}}\) and \({\Delta }\) confirm that the Barrow model is also compatible with \(\mathrm {\Lambda }\)CDM.

It should be noted that, considering datasets (I) and (II), simultaneous alleviation of existing discrepancies between local observations and CMB measurements is not possible in Barrow cosmology due to the correlation between \(\sigma _8\) and \(H_0\).

Moreover, it is worthwhile to compare Barrow cosmology with the TMG model based on the numerical results from dataset (II). Considering the fact that Barrow cosmology and the TMG model are established on absolutely different physical principles, the growth of structure is slightly reduced in both the Barrow and Tsallis scenarios, related to the quintessential behaviour of dark energy, which is also consistent with the wCDM model. The structure growth suppression is more important in the TMG model than in Barrow cosmology, according to the behaviour of \(\beta \) and \({\Delta }\). Specifically, the derived best fit and mean value of \({\Delta }\) correspond to higher values of \(\sigma _8\), in contrast to the quintessential character of dark energy which results in a decrease in the growth of structure.

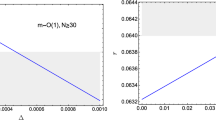
Also, the Akaike information criterion (AIC), defined as [97, 98]

$$\begin{aligned} \mathrm {AIC}=-2\ln {{\mathscr {L}}_{\mathrm {max}}}+2K, \end{aligned}$$
(44)

with \({\mathscr {L}}_{\mathrm {max}}\) the maximum likelihood function and K the number of free parameters, is helpful for evaluating which model is better supported by observational data. Considering \(\mathrm {\Lambda }\)CDM and wCDM as reference models, we obtain the following results

$$\begin{aligned} \mathrm {dataset (I):}&\; \mathrm {AIC_{(\Lambda CDM)}}=3817.12 ,\; \mathrm {AIC_{(wCDM)}}=3818.08 , \\&\; \mathrm {AIC_{(Barrow)}}=3820.20 , \\&\rightarrow \left\{ \begin{array}{l} \mathrm {AIC_{(Barrow)}}-\mathrm {AIC_{(\Lambda CDM)}}=3.08 , \\ \mathrm {AIC_{(Barrow)}}-\mathrm {AIC_{(wCDM)}}=2.12 , \end{array} \right. \end{aligned}$$
$$\begin{aligned} \mathrm {dataset (II):}&\; \mathrm {AIC_{(\Lambda CDM)}}=3847.12 \;,\; \mathrm {AIC_{(wCDM)}}=3849.38 , \\&\; \mathrm {AIC_{(Barrow)}}=3850.72 , \\&\rightarrow \left\{ \begin{array}{l} \mathrm {AIC_{(Barrow)}}-\mathrm {AIC_{(\Lambda CDM)}}=3.6 , \\ \mathrm {AIC_{(Barrow)}}-\mathrm {AIC_{(wCDM)}}=1.34 . \end{array} \right. \end{aligned}$$

Therefore, we can understand that the \(\mathrm {\Lambda }\)CDM model is better fitted to both datasets (I) and (II) compared to Barrow cosmology; however, one cannot rule out the Barrow cosmology model. On the other hand, according to dataset (I), wCDM is preferred to Barrow cosmology, while the Barrow model is still valid. Moreover, dataset (II) indicates that the Barrow model is supported by observational data as well as wCDM.

5 Conclusions

It is argued by Barrow [56] that a black hole horizon might have an intricate, fractal structure caused by quantum gravitational corrections to the area law of entropy. In this respect, the Barrow entropy relation (1) is associated with the black hole horizon, with the new exponent \({\Delta }\) that measures the deviation from standard cosmology. Furthermore, Einstein field equations can be derived from the first law of thermodynamics at the apparent horizon of the FLRW universe, and vice versa, inspired by the remarkable analogy between thermodynamics and gravity. In this direction, it is possible to associate an entropy to the apparent horizon as the same expression of black hole entropy, just by replacing the black hole horizon radius by the apparent horizon radius. Accordingly, we derived modified field equations in Barrow cosmology by applying Barrow entropy in a Clausius relation. Then, by performing MCMC analysis, we put constraints on the cosmological parameters, specifically the Barrow parameter \({\Delta }\) which quantifies deviations from \(\mathrm {\Lambda }\)CDM, based on two different combinations of datasets: “Planck + Pantheon + BAO” [dataset (I)] and “Planck + Planck-SZ + CFHTLenS + Pantheon + BAO + BAORSD” [dataset (II)].

Numerical results from dataset (I) indicate that the \(H_0\) tension can be slightly relieved in Barrow cosmology with a phantom behaviour of dark energy compared to the \(\mathrm {\Lambda }\)CDM model; however, the tension is not solved completely. Moreover, wCDM describes a phantom dark energy equation of state which is consistent with the Barrow cosmological model.

On the other hand, numerical results based on dataset (II) indicate that the quintessential nature of dark energy can slightly alleviate the \(\sigma _8\) tension in Barrow cosmology compared to the \(\mathrm {\Lambda }\)CDM model, while there is a satisfactory agreement between the Barrow model and wCDM.

In general, our MCMC investigation based on both datasets shows compatibility between Barrow cosmology and the reference models (\(\mathrm {\Lambda }\)CDM and wCDM). Further, the correlation between \(\sigma _8\) and \(H_0\) shows that a full reconciliation between local and global observations is not possible.

For the last point, it is interesting to compare the obtained constraints on Barrow cosmology with the results based on Tsallis cosmology reported in [76]. Considering both Barrow and Tsallis scenarios, there is a slight alleviation in \(\sigma _8\) tension with a quintessential behaviour of dark energy according to dataset (II), which is more significant in the TMG model. Also, the quintessential character of dark energy in Barrow and Tsallis cosmologies is in reasonable agreement with the wCDM model. However, considering physical principles and the motivation of correction, Barrow cosmology and the TMG model describe two different corrections to the area law of entropy.