1 Introduction

According to recent observations, the picture of the present Universe is that it is spatially flat and undergoing a period of accelerated expansion [1,2,3,4,5,6]. To dynamically address such a picture new ingredients must be necessarily introduced, the dark energy at and the dark matter. The former acts at cosmological scales and is related to the accelerated expansion of the Universe, the latter acts at galactic and extragalactic scales and is responsible for the clustering of structure. Many efforts and attempts have been done to explain the origin and nature of these two ingredients, without reaching an universal consensus. A possibility is related to the extended theories of gravity (ETG) [7] that allow to explain, on a pure gravitational setting and without the needed to invoke any exotic matter, the galactic rotation curves and the cosmic acceleration (see for example [8,9,10]). In the framework of ETG, hence the gravitational interaction acts differently at different scales, while the results of GR at solar system scales are preserved. Therefore, GR is a particular case of a more extended class of theories. From a conceptual viewpoint, there is no a priori reason to restrict the gravitational action to a linear function of the Ricci scalar minimally coupled to matter, as for the Hilbert–Einstein action [11].

It must be mentioned that modifications of GR are also motivated by the fact that Einstein’s theory of gravity breaks down in the UV [7, 12]. Such deviations from General Relativity occurs in several frameworks, such as Brans–Dicke and scalar–tensor (ST) theories [13,14,15], braneworld theories [16,17,18,19,20,21], higher order invariants such as f(R) and \(f(\phi ,\,R,\,R^2, R_{\mu \nu }R^{\mu \nu }, \Box R)\) (which correspond to Einstein’s gravity plus one or multiple conformally coupled scalar fields [22,23,24,25]) [26,27,28,29,30], noncommutative geometry [31], and compactified extra dimension/Kaluza–Klein models [32,33,34,35,36,37]. Moreover, they can also be generated from higher-order terms in the curvature invariants, nonminimal couplings to the background geometry in the Hilbert–Einstein Lagrangian [38,39,40,41]. Additional terms into the action of gravity may also come from string loop effects [42], dilaton fields in string cosmology [43], and nonlocally modified gravity induced by quantum loop corrections [44]. Moreover, ETG are not only curvature based but can involve also other formulations like affine connections independent of the metric, as in the case of metric-affine gravity [45] or purely affine gravity [46]. Metric-affine theories are also the Poincaré gauge gravity [47], the teleparallel gravity based on the Weitzenböck connection [48, 49], the symmetric teleparallel gravity [50]. The debate on the identification of variables describing the gravitational field is still open and it is a very active research area. In this paper, we are going to consider curvature based extended theories, confining ourselves to the case of metric theories. We analyze the weak field limit of Scalar–Tensor Four Order Gravity models and the effects of these corrections to the periastron advance of Planets. We consider several theories where higher-order curvature invariants and a scalar field are included. In particular, we study the Non-Commutative Spectral Gravity and the effect of the Quintessence field present around a Schwarzschild Black Hole. Then, we derive a lower bound on the adiabatic index of equation of state.

The Newtonian limit of some models of ETG have been studied in [51, 52], while the Minkowskian limit in [53,54,55,56,57,58,59]. Natural candidates for experimentally testing ETG are the galactic rotation curves, stellar systems and gravitational lensing [60,61,62,63,64,65] (see also [66,67,68]). In this perspective, corrections to GR were already considered by several authors [31, 55, 69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92]. Due to the large amount of possible models, an important issue is to select viable ones by experiments and observations. Therefore, the new born multimessenger astronomy is giving important constraints to admit or exclude gravitational theories (see e.g. [93, 94]). However, also fine experiments can be conceived and realized in order to fix possible deviations and extensions with respect to GR. They can involve space-based setups like satellites and precise electromagnetic measurements [95, 96].

We constrain the sizes of new gravitational forces (inferred in ETG or other scenarios) by making use the data coming from the precession of Planets. For this purpose, we follow the paper by Adkins and McDonnell [97] (see also [98, 99]), where it is calculated the precession of Keplerian orbits under the influence of arbitrary central-force perturbations. In the limit of nearly circular orbits, the perturbed orbit equation takes the form (\(u=1/r\))

$$\begin{aligned} \frac{d^2 u}{d \varphi ^2} + u = \frac{G M}{h^2} - \frac{g(u)}{h^2} \end{aligned}$$
(1)

where \(g(u) = r^2 \frac{F(r)}{m} \vert _{r=1/u}\) (\(\frac{F}{m}=-\nabla V\)) and \(h^2=G M a\). \(g(u)=0\) corresponds to the unperturbed solution. We refer to the corrections to the Planets precession induced by the Yukawa-like potential, \(V_Y(r)=\alpha \frac{e^{-\beta r}}{r}\), and power law (PL) potentials, \(V_{PL}(r) = \alpha _n r^n\). In GR, the first post-Newtonian correction is a perturbing potential given by \(V(r)\Big |_{\text {GR}} = - \frac{G M h^2}{c^2 r^3}\), which corresponds the precession \(\Delta \theta _p\Big |_{\text {GR}} = \frac{6 \pi G M}{c^2 a}\). This gives the well known 43 arcsec per century when applied to the orbit of Mercury. The correction to the Planet precessions induced by a generic perturbing force F(z) and perturbing potential V(z) is [97]

$$\begin{aligned} \Delta \theta _p= & {} -\frac{2 a^2}{G M \epsilon } \int _{-1}^1 \frac{dz \, z}{\sqrt{1-z^2}} \frac{F(z)}{(1+\epsilon z)^2} \end{aligned}$$
(2)
$$\begin{aligned}= & {} -\frac{2 a}{G M \epsilon ^2} \int _{-1}^1 \frac{dz \, z}{\sqrt{1-z^2}} \frac{d V(z)}{dz} , \end{aligned}$$
(3)

where, for the sake of convenience, the correction \(\Delta \theta _p\) is written in terms of the dimensionless integration variable z with a fixed range, while \(\epsilon \) is the eccentricity (\(\epsilon < 1\)). The perturbing force F(z) and V(z) are evaluated at radius \(r=a/(1+\epsilon z)\). In the following we refer to the Yukawa-like and power-law potentials following from different gravitational theories of gravity.

  • The Yukawa force – The Yukawa potential (as a correction to the Newtonian potential \(V_N=GM/r\)) is of the form [100, 101]

    $$\begin{aligned} V_Y(r) = \alpha \frac{e^{-r/\lambda }}{r}\equiv \alpha \frac{e^{-\beta r}}{r} \end{aligned}$$
    (4)

    where \(\alpha \) and \(\lambda \equiv 1/\beta \) are the strength and the range of the interaction, respectively. As we will see, such a potential occurs in several modified theories of gravity. The precession due to a Yukawa perturbation depends on two parameters: a range parameter \(\kappa =a/\lambda =\beta a\) and the eccentricity \(\epsilon \), i.e. \(\Delta \theta _p(\kappa ,\epsilon )\), where a is the semi-major axis. According to [97], the correction to the precession is of the integral form

    $$\begin{aligned} \Delta \theta _p(\kappa ,\epsilon ) = -\frac{2 \alpha }{G M \epsilon }\, I_{\epsilon , \beta } , \end{aligned}$$
    (5)

    where

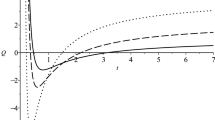
    $$\begin{aligned} I_{\epsilon , \beta }\equiv \int _{-1}^1 \frac{dz \, z}{\sqrt{1-z^2}} \left( 1+ \frac{\kappa }{1+\epsilon z} \right) e^{-{\frac{\kappa }{1+\epsilon z}}} \, . \end{aligned}$$
    (6)

    The behavior of the integral (6) is represented in Fig. 1 for several Planets.

  • Power Law potential – The power law potential is of the form

    $$\begin{aligned} V_{PL}(r) = \alpha _{q}\, r^{q} , \end{aligned}$$
    (7)

    where the parameter q assume arbitrary values. The precession (2) can be exactly integrated, and leads to [97]

    $$\begin{aligned} \Delta \theta _p(q) = \frac{-\pi \alpha _q}{G M } a^{q+1} \sqrt{1-\epsilon ^2} \chi _q(\epsilon ) , \end{aligned}$$
    (8)

    where \(\chi _q(\epsilon )\) is written in terms of the Hypergeometric function

    $$\begin{aligned} \chi _q(\epsilon ) = q (q+1) \, {_2F_1} \left( \frac{1}{2}-\frac{q}{2},1-\frac{q}{2}\, ;2\, ;\epsilon ^2 \right) \, . \end{aligned}$$
    (9)
Fig. 1
figure 1

a \(I_{\epsilon , \beta }\) vs \(\beta \) for Mercury. b \(I_{\epsilon , \beta }\) vs \(\beta \) for Mars. c \(I_{\epsilon , \beta }\) vs \(\beta \) for Jupiter. d \(I_{\epsilon , \beta }\) vs \(\beta \) for Saturn

Full size image

These potentials occur in ETG and in Non-Commutative Spectral Geometry (the Yukawa-like potential), and Quintessence field surrounding a massive gravitational source (the Power Law potential). We shall infer the corrections to periastron advance for Solar Planets, referring in particular to Mercury, Mars, Jupiter and Saturn, as well as to S2 star orbiting around Sagittarius \(A^*\).

The paper is organized as follows. In Sect. 3 we study the weak field limit of Scalar–Tensor Four Order Gravity models, and the effects of these corrections to the periastron advance of Planets. As a particular case, we consider the Non-Commutative Spectral Gravity. In Sect. 3 we study the effect of the Quintessence field present around a Schwarzschild Black Hole, and derive a lower bound on the adiabatic index of equation of state. Finally, conclusions are drawn in last section.

2 Scalar–tensor-fourth-order gravity

The action for ETG is given by (see for example [7])

$$\begin{aligned} {\mathcal {S}}= & {} \int d^{4}x\sqrt{-g} [f(R,R_{\mu \nu }R^{\mu \nu },\phi )+\omega (\phi )\phi _{;\alpha }\phi ^{;\alpha }\nonumber \\&+\mathcal {X}\mathcal {L}_m ], \end{aligned}$$
(10)

where f is a generic function of the invariant R (the Ricci scalar), the invariant \(R_{\mu \nu }R^{\mu \nu }\,=\,Y\) (\(R_{\mu \nu }\) is the Ricci tensor), the scalar field \(\phi \), g is the determinant of metric tensor \(g_{\mu \nu }\) and \(\mathcal {X}\,=\,8\pi G\). The Lagrangian density \(\mathcal {L}_m\) is the minimally coupled ordinary matter Lagrangian density, \(\omega (\phi )\) is a generic function of the scalar field.

The field equations obtained by varying the action (10) with respect to \(g_{\mu \nu }\) and \(\phi \), In the metric approach, are:Footnote 1

$$\begin{aligned}&f_RR_{\mu \nu }-\frac{f+\omega (\phi )\phi _{;\alpha }\phi ^{;\alpha }}{2}g_{\mu \nu }-f_{R;\mu \nu }+g_{\mu \nu }\Box f_R\nonumber \\&\quad +2f_Y{R_\mu }^\alpha R_{\alpha \nu } \end{aligned}$$
(11)
$$\begin{aligned}&\quad -2[f_Y{R^\alpha }_{(\mu }]_{;\nu )\alpha }+\Box [f_YR_{\mu \nu }]+[f_YR_{\alpha \beta }]^{;\alpha \beta }g_{\mu \nu }\nonumber \\&\quad +\omega (\phi )\phi _{;\mu }\phi _{;\nu }\,=\, \mathcal {X}\,T_{\mu \nu } ,\nonumber \\&2\omega (\phi )\Box \phi +\omega _\phi (\phi )\phi _{;\alpha }\phi ^{;\alpha }-f_\phi \,=\,0 . \end{aligned}$$
(12)

where:

$$\begin{aligned} f_R\,=\,\frac{\partial f}{\partial R}, \,\,\,\,\,\,f_Y\,=\,\frac{\partial f}{\partial Y}, \,\,\,\,\,\,\omega _\phi \,=\,\frac{d\omega }{d\phi } , \,\,\,\, f_\phi \,=\,\frac{d f}{d\phi } , \end{aligned}$$

and \(T_{\mu \nu }\,=\,-\frac{1}{\sqrt{-g}}\frac{\delta (\sqrt{-g}\mathcal {L}_m)}{\delta g^{\mu \nu }}\) is the the energy-momentum tensor of matter. We confine ourselves to the case in which the generic function f can be expanded as follows (notice that the all other possible contributions in f are negligible [51, 52, 76, 92])

$$\begin{aligned} f(R,R_{\alpha \beta }R^{\alpha \beta },\phi )= & {} f_R(0,0,\phi ^{(0)})\,R+\frac{f_{RR}(0,0,\phi ^{(0)})}{2}\,R^2\nonumber \\&+ \frac{f_{\phi \phi }(0,0,\phi ^{(0)})}{2}(\phi -\phi ^{(0)})^2\nonumber \\&+f_{R\phi }(0,0,\phi ^{(0)})R\,\phi \nonumber \\&+ f_Y(0,0,\phi ^{(0)})R_{\alpha \beta }R^{\alpha \beta } . \end{aligned}$$
(13)

To study the weak-field approximation, we perturb Eqs. (11) and (12) in a Minkowski background \(\eta _{\mu \nu }\) [51], i.e. we look for perturbed solutions of the form

$$\begin{aligned}&g_{\mu \nu }\,\simeq \, \begin{pmatrix} -1-2\Phi &{} 2\mathbf{A} \\ 2\mathbf{A} &{} (1-2\Psi )\delta _{ij}\end{pmatrix} . \end{aligned}$$
(14)

and

Table 1 We report different cases of Extended Theories of Gravity including a scalar field and higher-order curvature terms. The free parameters are given as effective masses with their asymptotic behavior. Here, we assume \(f_R(0,\,0,\,\phi ^{(0)})\,=\,1\), \(\omega (\phi ^{(0)})\,=\,1/2\)
Full size table
Fig. 2
figure 2

a \(F_+\) vs \(\{\xi , \eta \}\) for Mercury (\(|F_+| \lesssim 0.28\)), with \(m_R=\frac{1}{{{\mathcal {R}}}}\). b \(F_-\) vs \(\{\xi , \eta \}\) for Mercury (\(|F_-| \lesssim 0.28\)) with \(m_R=\frac{1}{{{\mathcal {R}}}}\)

Full size image
$$\begin{aligned}&\phi \,\sim \,\phi ^{(0)}+\phi ^{(2)}+\cdots \,=\,\phi ^{(0)}+\varphi . \end{aligned}$$

For matter described as a perfect fluid, hence \(T_{00}\,=\,\rho \) and \(T_{ij}\,=\,0\), one gets that, for a ball-like source with radius \({{\mathcal {R}}}\), the gravitational potentials \(\{\Phi , \Psi , A_i\}\) and the scalar field \(\varphi \) take the form (\(c=1\)) [76, 82,83,84,85, 92]

$$\begin{aligned} \Phi (\mathbf {x})= & {} -\frac{GM}{|\mathbf {x}|}\big [1+\zeta (|\mathbf {x}|)\big ] , \end{aligned}$$
(15)
$$\begin{aligned} \zeta (|\mathbf {x}|)\equiv & {} g(\xi ,\eta )\,F(m_+ {{\mathcal {R}}})\,e^{-m_+|\mathbf {x}|}\nonumber \\&+\Big [\frac{1}{3}-g(\xi ,\eta )\Big ]\,F(m_- {{\mathcal {R}}})\,e^{-m_-|\mathbf {x}|}\nonumber \\&- \frac{4\,F(m_Y {{\mathcal {R}}})}{3}\,e^{-m_Y|\mathbf {x}|} , \end{aligned}$$
(16)
$$\begin{aligned} \Psi (\mathbf {x})= & {} -\frac{GM}{|\mathbf {x}|}\big [1-\psi (|\mathbf {x}|)\big ] , \end{aligned}$$
(17)
$$\begin{aligned} \psi (|\mathbf {x}|)\equiv & {} g(\xi ,\eta )\,F(m_+ {{\mathcal {R}}})\,e^{-m_+|\mathbf {x}|}\nonumber \\&+\Big [\frac{1}{3}-g(\xi ,\eta )\Big ]\,F(m_- {{\mathcal {R}}})\,e^{-m_-|\mathbf {x}|}\nonumber \\&+ \frac{2\,F(m_Y {{\mathcal {R}}})}{3}\,e^{-m_Y|\mathbf {x}|} , \end{aligned}$$
(18)
$$\begin{aligned} \mathbf {A}(\mathbf {x})= & {} -\frac{2\,G\,\big [1-{{\mathcal {A}}}(|\mathbf {x}|)\big ]}{|\mathbf {x}|^2}\,\mathbf {x}\times \mathbf {J} , \end{aligned}$$
(19)
$$\begin{aligned} {{\mathcal {A}}}(|\mathbf {x}|)\equiv & {} (1+m_Y|\mathbf {x}|)\,e^{-m_Y|\mathbf {x}|} , \end{aligned}$$
(20)
$$\begin{aligned} \varphi (\mathbf{x} )= & {} \frac{GM}{|\mathbf{x} |} \sqrt{\frac{\xi }{3}}\,\frac{2}{\omega _+-\omega _-} \biggl [F(m_+ {{\mathcal {R}}})\,e^{-m_+\,|\mathbf{x} |}\,\nonumber \\&-F(m_- {{\mathcal {R}}})\,e^{-m_-\,|\mathbf{x} |}\biggr ] , \end{aligned}$$
(21)

where \(\mathbf {J}\,=\,2M\mathcal {R}^2\varvec{\Omega }_0/5\) is the angular momentum of the ball, \(f_R(0,0,\phi ^{(0)})\,=\,1\), \(\omega (\phi ^{(0)})\,=\,1/2\), and

$$\begin{aligned} g(\xi ,\eta )\,= & {} \,\frac{1-\eta ^2+\xi +\sqrt{\eta ^4+(\xi -1)^2-2\eta ^2(\xi +1)}}{6\sqrt{\eta ^4+(\xi -1)^2-2\eta ^2(\xi +1)}} , \end{aligned}$$
(22)
$$\begin{aligned} F(m\,\mathcal {R})\,= & {} \,3\frac{m\,\mathcal {R} \cosh m\,\mathcal {R}-\sinh m\,\mathcal {R}}{m^3\mathcal {R}^3} , \end{aligned}$$
(23)
$$\begin{aligned} \xi \,= & {} \,3{f_{R\phi }(0,0,\phi ^{(0)})}^2 , \quad \eta \,=\,\frac{m_\phi }{m_R} , \end{aligned}$$
(24)
$$\begin{aligned} m_\pm ^2= & {} m_R^2\,\omega _\pm , \end{aligned}$$
(25)
$$\begin{aligned} \omega _\pm \,= & {} \,\frac{1-\xi +\eta ^2\pm \sqrt{(1-\xi +\eta ^2)^2-4\eta ^2}}{2} , \end{aligned}$$
(26)
$$\begin{aligned} {m_R}^2\,\doteq & {} \,-\frac{f_R(0,0,\phi ^{(0)})}{3f_{RR}(0,0,\phi ^{(0)})+2f_Y(0,0,\phi ^{(0)})} , \end{aligned}$$
(27)
$$\begin{aligned} {m_Y}^2\,\doteq & {} \,\frac{f_R(0,0,\phi ^{(0)})}{f_Y(0,0,\phi ^{(0)})} , \quad {m_\phi }^2\,\doteq \,-\frac{f_{\phi \phi }(0,0,\phi ^{(0)})}{2\omega (\phi ^{(0)})} . \end{aligned}$$
(28)

Some ETG models studied in literature and reported in Table 1 (see [76] for further details).

2.1 Planet precession in fourth order gravity

In this section we study the periastron shift of the orbital period of objects, both astrophysical and Solar System, in four order gravity (FOG). As we have seen, the FOG field equations lead to a gravitational potential of the Yukawa-like form (\(r=|\mathbf{x}|\))

$$\begin{aligned} V(r)=\frac{GM}{r} \left( 1+\sum _{i=\pm , Y} F_i e^{-\beta _i r}\right) , \end{aligned}$$
(29)

where \(F_i\) and \(\beta \) are the strength and range of the interaction corresponding to each mode \(i=+, -, Y\). Comparing (29) with (4), it follows the correspondence (referring to (15) and (16))

$$\begin{aligned} \alpha \rightarrow GM F_i , \quad \beta \rightarrow \beta _i , \quad i=\pm , Y . \end{aligned}$$
(30)

with

$$\begin{aligned}&F_+ =g(\xi ,\eta )\,F(m_+ {{\mathcal {R}}}) , \quad F_- = \Big [\frac{1}{3}-g(\xi ,\eta )\Big ]\,F(m_- {{\mathcal {R}}}) , \quad \nonumber \\&F_Y=- \frac{4}{3}\,F(m_Y {{\mathcal {R}}}) , \end{aligned}$$
(31)
$$\begin{aligned}&\beta _\pm = m_R \sqrt{\omega _\pm } , \quad \beta _Y = m_Y . \end{aligned}$$
(32)

We impose that the periastron shift \(\Delta \theta _p(\kappa ,\epsilon ) = -\frac{2 \alpha }{G M \epsilon }\, I_{\epsilon , \beta }\) given by (5), where \(I_{\epsilon , \beta }\) is defined in (6), is lesser than the error \(\eta \). Fixing \(I_{\epsilon , \beta }\) to the maximum values, one gets the bounds on the parameters \(F_i\):

$$\begin{aligned} |\Delta \theta _p(\kappa ,\epsilon )|\lesssim \eta \rightarrow |F_i|\lesssim \frac{\eta \epsilon }{2I_{\epsilon , \beta _i}} , \quad i=\pm , Y . \end{aligned}$$
(33)

In Fig. 1 are plotted the function \(I_{\epsilon , \beta }\) for the Mercury, Mars, Jupiter and Saturn planets. In Table III are reported the corresponding bounds on \(F_i\). As an illustrative example, we plot \(|F_\pm (\xi , \eta )|\) in Fig. 2, for \(m_R={{\mathcal {R}}}^{-1}\). The available values of the parameters \(\{\xi , \eta \}\) allow to fix the masses, via Eqs. (22)–(24), (27), of extra modes arising in Scalar Tensor Fourth Order Gravity. The analysis of Yukawa gravitational potential for f(R) has been carried out in [102].

Table 2 Values of periastron advance for the first six planets of the Solar System. In the table we present the values of the eccentricity \(\epsilon \), semi-major axis a in meters, the orbital period P in years, the periastron advance predicted in General Relativity (GR)
Full size table
Table 3 Bounds on \(F_i\), \(i=\pm , Y\) obtained from (33) using the values of periastron advance for planets of the Solar System
Full size table

2.2 Non-commutative geometry

As a special case of scalar–tensor-fourth-order gravity theory that we want discuss is the Non-Commutative Spectral Geometry (NCSG) [103,104,105]. Among the various attempts to unify all interactions, including gravity, NCSG is one of the most interesting candidate [103, 105,106,107]. It proposes that the Standard Model (SM) fields and gravity are packaged into geometry and matter on a Kaluza–Klein noncommutative space. In NCSG, geometry is composed by a two-sheeted space, made from the product of a four-dimensional compact Riemannian manifold \({{\mathcal {M}}}\) (with a fixed spin structure), describing the geometry of space-time, and a discrete noncommutative space \({{\mathcal {F}}}\), describing the internal space of the particle physics model. The SM fields and gravity enter into matter and geometry on a noncommutative space which has the product form \({{\mathcal {M}}}\times {{\mathcal {F}}}\). Such a product space is physically interpreted in the way that left- and right-handed fermions are placed on two different sheets with the Higgs fields being the gauge fields in the discrete dimensions (the Higgs can be seen as the difference (thickness) between the two sheets). The choice of a two-sheet geometry has a deep physical meaning since such a structure accommodate the gauge symmetries of the SM, and incorporates the seeds of quantisation (see [108] for details, and references therein).

In the gravitational sector, to which we are interested in, the action includes the coupling between the Higgs field \(\phi \) and the Ricci curvature scalar R [105]

$$\begin{aligned} S_\mathrm{grav}= & {} \int \left( \frac{R}{2\kappa ^2} + \alpha _0 C_{\mu \nu \rho \sigma }C^{\mu \nu \rho \sigma } + \tau _0 R R^\star - \xi _0 R|\mathbf{H}|^2 \right) \nonumber \\&\sqrt{-g} \mathrm{d}^4 x , \end{aligned}$$
(34)

where \(\kappa ^2\equiv 8\pi G\), \(\mathbf{H}=(\sqrt{af_0}/\pi )\phi \) is the Higgs field, with a a parameter related to fermion and lepton masses and lepton mixing, while \(C^{\mu \nu \rho \sigma }\) is the Weyl tensor (the square of the Weyl tensor can be expressed in terms of \(R^2\) and \(R_{\mu \nu }R^{\mu \nu }\): \(C_{\mu \nu \rho \sigma }C^{\mu \nu \rho \sigma }\,=\,2R_{\mu \nu }R^{\mu \nu }-\frac{2}{3}R^2\)) and \(R {}^*R=\frac{1}{2}\epsilon ^{\alpha \beta \gamma \delta }R_{\alpha \beta \sigma \rho }R_{\gamma \delta }^{\quad \sigma \rho }\) (\(R^\star R^\star \) is the topological term related to the Euler characteristic). At unification scale (fixed by the cutoff \(\Lambda \)), \(\alpha _0=-3f_0/(10\pi ^2)\). The NCSG model offers a framework to study several topics [109,110,111,112,113,114,115,116]). It is worth to note that the quadratic curvature terms in the action functional does not give rise to the emergence of negative [117] energy massive graviton modesFootnote 2 [118].

The variation of the action (34) with respect to the metric tensor yields the NCSG equations of motion [109]

$$\begin{aligned} G^{\mu \nu }+\frac{1}{\beta _{\small NCSG}^2}[2\nabla _\lambda \nabla \kappa C^{\mu \nu \lambda \kappa }+C^{\mu \lambda \nu \kappa }R_{\lambda \kappa }] = \kappa ^2 T^{\mu \nu }_{(\mathrm{matter})},\nonumber \\ \end{aligned}$$
(35)

where \(\beta _{\small NCSG}^{2}=\displaystyle {5\pi ^2/(6\kappa ^2f_0)}\). In the weak field approximation, \(g_{\mu \nu }=\eta _{\mu \nu }+\gamma _{\mu \nu }\), one gets [116].

$$\begin{aligned} ds^2 = -(1+2\Phi )dt^2+ 2\mathbf{A}\cdot d\mathbf{x} dt+(1+2\Psi ) d\mathbf{x}^2 , \end{aligned}$$
(36)

with

$$\begin{aligned} \gamma _{00}= & {} -2\Phi =\frac{2GM}{r}\left( 1-\frac{4}{3}e^{-\beta _{\small {NCSG}} r}\right) , \end{aligned}$$
(37)
$$\begin{aligned} \gamma _{0i}= & {} \gamma _{i0}= A_i \end{aligned}$$
(38)
$$\begin{aligned}= & {} -\frac{4G}{r^3}\left[ 1-(1+\beta _{\small {NCSG}} r)e^{-\beta _{\small {NCSG}} r}\right] (\mathbf{r}\wedge \mathbf{J})_i , \nonumber \\ \gamma _{ij}= & {} 2\Psi \delta _{ij} = \frac{2GM}{r}\left( 1+\frac{5}{9}e^{-\beta _{\small {NCSG}} r}\right) \delta _{ij} , \end{aligned}$$
(39)

The modifications induced by the NCSG action to the Newtonian potentials \(\Phi \) (and \(\Psi \)), Eq. (37), are similar to those induced by a Yukawa-like potential (4) (fifth-force [119]), with

$$\begin{aligned} \alpha =\frac{4}{3}GM , \quad \beta _{\small NCSG}=\beta \end{aligned}$$
(40)
Fig. 3
figure 3

a \(I_{\epsilon , \beta }\) vs \(\beta \) for Mercury. b \(I_{\epsilon , \beta }\) vs \(\beta \) for Mars. c \(I_{\epsilon , \beta }\) vs \(\beta \) for Jupiter. d \(I_{\epsilon , \beta }\) vs \(\beta \) for Saturn

Full size image

Following the previous section, Eqs. (5) (33), the periastron advance in NCSG for planets is given by

$$\begin{aligned} |\Delta \theta _p(\beta ,\epsilon )|\lesssim \eta \rightarrow |I_{\epsilon , \beta }|\lesssim I_0 , \quad I_0\equiv \frac{3 \eta \epsilon }{8} , \end{aligned}$$
(41)

where \(I_{\epsilon , \beta }\) is defined in (6). From Eq, (41) one infers the bounds on \(\beta \), or equivalently an upper bound on \(\lambda \). Results are reported in Table 4 (see also Fig. 3). These results show that the bounds on \(\beta \) improve several order of magnitude as compared with ones obtained using recent observations of pulsar timing, \(\beta \ge 7.55\times 10^{-13} \, \mathrm{m}^{-1}\) [120, 121]. Bounds on the parameter \(\beta \) have been obtained in different frameworks. From Gravity Probe B experiment one gets \(\beta >10^{-6} \, \mathrm{m}^{-1}\) [116]. A more stringent constraint on \(\beta \) can be obtained from laboratory experiments designed to test the fifth force, that is, by constraining \(\lambda \) through torsion balance experiments which implies to obtain a stronger lower bound on \(\beta \) (or equivalently an upper bound to the momentum \(f_0\) in NCSG theory). The test masses have a typical size of \(\sim 10\) mm and their separation is smaller than their size. As we have already mentioned above, in NCSG one has \(|\alpha | \sim {{\mathcal {O}}}(1)\), so that the tightest constraint on \(\lambda =\beta ^{-1}\) provided by Eöt-Wash [122] and Irvine [123] experiments is [124] \(\lambda \lesssim 10^{-4}\text{ m }\), or equivalently \(\beta \gtrsim 10^4 \text{ m}^{-1}\).

Table 4 Lower bounds on \(\beta \) obtained from (41) using the values of periastron advance for planets of the Solar System
Full size table

3 Quintessence: dark energy

An interesting possibility we wish to discuss is related to quintessence field, invoked to explain the speed-up of the present Universe [125]. Quintessence may generate a negative pressure, and, since it is diffuse everywhere in the Universe, it can be the responsible of the observed accelerated phase, as well as it is present around a massive astrophysical object deforming the spacetime around it [126]. The studies of quintessential black holes are also motivated from M-theory/superstring inspired models [127,128,129] (see [125, 130,131,132,133,134,135,136,137,138,139,140] for applications). The solution of Einstein’s field equations for a static spherically symmetric quintessence surrounding a black hole in 4 dimension is given by [126, 130]

$$\begin{aligned} g_{\mu \nu }=\text {diag}(-f(r), f^{-1}(r), r^2, r^2 \sin ^2 \theta ) , \end{aligned}$$
(42)

with

$$\begin{aligned} f(r)=1-\frac{2M}{r}-\frac{c}{r^{3\omega _Q+1}} , \end{aligned}$$
(43)

where \(\omega _Q\) is the adiabtic index (the parameter of equation of state), \(-1\leqslant \omega _Q\leqslant -\frac{1}{3}\), and c the quintessence parameter. The cosmological constant (\(\Lambda \)CMD model) follows from (42) and (43) with \(\omega _Q =-1\) and \(c=\Lambda /3\),

$$\begin{aligned} f(r)=1-\frac{2M}{r}-\frac{\Lambda r^2}{3} . \end{aligned}$$
(44)

The Quintessential potential reads \(V_Q=-\frac{c}{r^{3\omega _Q+1}}\), so that comparing with (7) one gets

$$\begin{aligned} q\rightarrow -(3\omega _Q+1)\quad \alpha _q \rightarrow c . \end{aligned}$$

The precession (8) leads to

$$\begin{aligned} |\Delta \theta _p(\omega _Q, \epsilon )| = \frac{\pi c}{G M} a^{-3\omega _Q} \sqrt{1-\epsilon ^2} \chi _{\omega _Q}(\epsilon ) , \end{aligned}$$
(45)

with

$$\begin{aligned} \chi _{\omega _Q}(\epsilon ) = 3\omega _Q (1+3\omega _Q) \,\, {_2F_1} \left( \frac{2+3\omega _Q}{2},\frac{3+3\omega _Q}{2}\, ;2\, ;\epsilon ^2 \right) \, .\nonumber \\ \end{aligned}$$
(46)

By requiring \(|\Delta \theta _p(\omega _Q, \epsilon )| \lesssim \eta \) one gets the bounds on the parameters \(\{\omega _Q, c\}\). Results are reported in Table 5 and Fig. 4 for fixed values of c.

4 Test on S2 Star

Finally, we shortly conclude our analysis testing the modified gravity predictions for S2 Star orbiting around Sagittarius A*, the Supermassive Black Hole at the center of the Milky Way, which has got a mass equal to \(M=(4.5 \pm 0.6)\times 10^{6} M_{\odot }\) and a Schwarzschild radius \(R_S = 2GM = 1.27 \times 10^{10} \, m\). The S2 Star orbit has an eccentrity \(\epsilon =0.88\) and a semi-major axis \(a=1.52917 \times 10^{14}\)m. According to Ref. [141,142,143], the periastron advance is \((0.2\pm 0.57)\)deg, hence \(\eta =0.57\) (it is expected that the interferometer GRAVITY may improve such an accuracy level). We discuss the periastron advance for the gravitational models above discussed:

  • STFOG – Referring to Scalar–Tensor Fourth Order Gravity, from Eq. (33) one gets

    $$\begin{aligned} |\Delta \theta _p(\kappa ,\epsilon )|\lesssim \eta \rightarrow |F_i|\lesssim \frac{\eta \epsilon }{2I_{\epsilon , \beta _i}}\sim 0.36 , \quad i=\pm , Y .\nonumber \\ \end{aligned}$$
    (47)

    where in Fig. 5a is plotted the function \(I_{\epsilon , \beta }\) for the S2 star. We ave taken the maximum value of \(I_{\epsilon , \beta }\) corresponding to \(\beta \sim 2\times 10^{-14} m^{-1}\) (see Fig. 5a). The analysis of S2 star orbit around the Galactic Centre in \(f(\phi , R)\) and \(f(R, \Box R)\) has been investigated in [144].

  • NCSG – The S2 star values \(\{\epsilon , \eta , a\}\) imply that, from (41),

    $$\begin{aligned} |\Delta \theta _p(\beta ,\epsilon )|\lesssim \eta \rightarrow |I_{\epsilon , \beta }|\lesssim I_0 , \quad I_0\equiv \frac{3 \eta \epsilon }{8} \simeq 0.19 .\nonumber \\ \end{aligned}$$
    (48)

    Results are reported in Fig. 5b. We can see that the lower bound on \(\beta \) is \(\beta \gtrsim 1.1 \times 10^{-13}m^{-1}\). These bounds are compatible with the astrophysical bounds [120, 121].

  • Quintessence – In the case of Quintessence field deforming the Schwarzschild geometry, Eq. (45) implies

    $$\begin{aligned} |\Delta \theta _p(\omega _Q, \epsilon )|= & {} \frac{\pi c}{G M} a^{-3\omega _Q} \sqrt{1-\epsilon ^2} \chi _{\omega _Q}(\epsilon )\lesssim 0.57 , \end{aligned}$$
    (49)
    $$\begin{aligned} \chi _{\omega _Q}(\epsilon )= & {} 3\omega _Q (1+3\omega _Q) \,\, {_2F_1} \left( \frac{2+3\omega _Q}{2},\right. \nonumber \\&\left. \frac{3+3\omega _Q}{2}\, ;2\, ;\epsilon ^2 \right) . \end{aligned}$$
    (50)

    Results are reported in Fig. 5c, from which it follows that for Quintessence \(|\Delta \theta _p(\omega _Q, \epsilon )|\lesssim 0.57\) provided \(\omega _Q \gtrsim 0.9\). Therefore, the exact value \(\omega _Q=-1\) corresponding to the cosmological constant is excluded in this range of values.

Table 5 Values of the parameter \(\omega _Q\) obtained from (45) using the values of periastron advance for planets of the Solar System
Full size table
Fig. 4
figure 4

a \(|\Delta \theta (\omega _Q, \epsilon )|\) vs \(\omega _Q\) for Mercury. b \(|\Delta \theta (\omega _Q, \epsilon )|\) vs \(\omega _Q\) for Mars. c \(|\Delta \theta (\omega _Q, \epsilon )|\) vs \(\omega _Q\) for Jupiter. d \(|\Delta \theta (\omega _Q, \epsilon )|\) vs \(\omega _Q\) for Saturn

Full size image
Fig. 5
figure 5

a \(I_{\epsilon , \beta }\) vs \(\beta \) for S2 star in FOG theories. b \(I_{\epsilon , \beta }\) vs \(\beta \) for S2 star. c \(|\Delta \theta {\omega _Q, \epsilon }|\) vs \(\omega _Q\) for S2 star. (c is in \(m^{3\omega _Q+1}\) units)

Full size image

5 Conclusions

In this paper we have studied the periastron advance of Solar system Planets in the case in which the gravitational interactions between massive bodies is described by modified theories of gravity. In these models the corrections to the Newtonian gravitational interaction is of the Yukawa-like form, \(V(r)=V_N(1+\alpha e^{-\beta r})\), where \(V_N=GM/r\) is the Newtonian potential, or the power-law form, \(V(r)=V_N+\alpha _q r^q\). To compute the corrections to the periastron advance, we have used results of Ref. [97] in which the general formulas are provided in terms of the central body’s mass M, and the orbital parameters a and \(\epsilon \), the semi-major axis and eccentricity of the orbit, respectively. This two-body system constitutes a good model for many astrophysical scenarios, such as those at the scale of Solar System, constituted by the Sun and a planet, as well as binary system composed by a Super Massive Black Hole and an orbiting star, which are both the most suitable candidates to test a gravitational theory.

In the case of Scalar Tensor Fourth Order Gravity, we find that the parameters of the model are given by (see Eqs. (32, 31, 30) \(\alpha \sim F_i\), \(\beta \sim \beta _i\), with \(i=\pm , Y\), \(F_+ =g(\xi ,\eta )\,F(m_+ {{\mathcal {R}}})\), \(F_- = \Big [\frac{1}{3}-g(\xi ,\eta )\Big ]\,F(m_- {{\mathcal {R}}})\), \(F_Y=- \frac{4}{3}\,F(m_Y {{\mathcal {R}}})\), \(\beta _\pm = m_R \sqrt{\omega _\pm }\), \(\beta _Y = m_Y\). The greatest value of \(\beta _i\) is \(\beta _i \sim 5\times 10^{-11}\, m^{-1}\), which leads to the constraint on \(F_i\) is \(F_i< 10^{-4}\). This allows to get a bound on the massive modes \(m_i\), \(i=\pm , Y\), corresponding to the extra modes presents in ETG.

In the case of Non-Commutative Spectral Gravity, we have found that the perihelion’s shift of planets allows to constrain the parameter \(\beta \) at \(\beta > (10^{-11} - 10^{-10}) \, \mathrm{m}^{-1}\) (in this theory the parameter \(\alpha \) is given and is of the order \(\alpha \sim {{\mathcal {O}}}(1)\)). Such a constraint on the parameter \(\beta \) improves several order of magnitude ones derived by using pulsar timing \(\beta \ge 7.55\times 10^{-13} \, \mathrm{m}^{-1}\) [120, 121]. These constraints, however, are weaker compared to the ones obtained from terrestrial experimental data, Eöt-Wash [122] and Irvine [123] experiments is [124], which give \(\beta \gtrsim 10^4 {m}^{-1}\) (a bound on \(\beta \) has been derived from Gravity Probe B experiment, giving \(\beta > 10^{-6}m^{-1}\) [116]).

We have also studied the Quintessence field surrounding a massive gravitational source. In this case the parameter characterizing the gravitational field are the adiabatic index \(\omega _Q\) and the quintessence parameter c. The analysis shows that c assumes tiny values, as expected, being essentially related to the cosmological constant, while \(\omega _Q\gtrsim - \) (0.9–0.8), that is it never assumes the value \(-1\) corresponding to the pure cosmological constant.

The case of the S2 Star around Sagittarius A*, the Super Massive Black Hole at the center of the Milky Way, has been also studied. In such a case we have found that for STFOG and NCSG \(\beta > 10^{-13} \, \mathrm{m}^{-1}\), a bound compatible with astrophysical constraints, while for the quitessence field we have inferred \(\omega _Q \gtrsim -\, 0.9\).

As a final comment, we point out that there could exist screening mechanism effects operating on Earth and Solar System scale [145,146,147,148,149,150], but could not be effective on larger scales, such as the astrophysical scales. Further observations over larger distances could provide limits on both screening mechanisms and higher derivative corrections, in particular on the effective gravitational model here discussed.