1 Introduction

There are an expressive number of exact solutions that play a very important role in both theoretical and experimental development of General Relativity (GR). For example, one of the most important solutions is the Schwarzschild’s, which represents the exterior of a massive body with spherical symmetry. This solution is at the basis of the three classic tests of GR: the displacement of spectral lines due the presence of the gravitational field, the deflection of light passing close to a massive body (stars, galaxies, clusters) and the perihelion precession of planets. Furthermore, this solution gave rise to the concept of a black hole. Solutions representing the gravitational field of a body with axial symmetry play an important role in both Newtonian and GR theory of gravitation, once the natural form of an isolated self-gravitating fluid has axial symmetry. In particular, disk-like configurations are of great interest in astrophysics since they can be used to model galaxies, accretion disks and indeed simple axially symmetric stellar systems to understand the galactic dynamics and star formation. In Newtonian gravity, globular clusters and spherical galaxies were calculated by the seminal model of Plummer [1] and King [2], and still serve as basis of N-body simulations of stellar systems. Toomre [3] and Kuzmin [4], and, later, Miyamoto [5] and Nagai [6] developed a series of axially symmetric models, described by potential pairs, the associated density functions and also the motion equations of the particles in the system, e.g., the effective velocity and galaxy rotation curves [7,8,9]. More details on the subject can be found in Refs. [10, 11].

Instead of using the standard parameterised post- Newtonian (or PPN) approximation [12], we look for an alternative methodology, which takes into account the slow-motion condition, being the weak-field condition relaxed. In the realm of GR, we use the Weyl axisymmetric metric [13] in cylindric coordinates to obtain a Newtonian-like potential in order to study possible gravitational effects at astrophysical scales. This Newtonian analogue of Weyl metric potential has been extensively studied in literature and can be found, e.g., in gravitation textbooks such as Hartle [14], Griffiths and Podolski [15], and Stephani et al. [16]. The so-called Weyl metrics define a class of static and axisymmetric solutions of Einstein’s equations. The present idea of this paper was applied in a series of previous works to different themes such as apsidal precession of different astrophysical systems [17,18,19,20] and to the dark matter problem [21]. It relies on the fact that from the standard GR configuration, a nearly-Newtonian limit [12] can be obtained, which carries non-linear effects as an heritage from a relativistic system not under the a priori assumption of a weak gravitational field. This apparent discrepancy between motion and field principles was a real problem in the early days of GR. For instance, Einstein and Grommer [22] proposed that the movement of matter must be through geodesics. On the other hand, the movement of a mass-energy content in a gravitational field must violate the field equations. Thus, the self-interacting gravitational field affects its own dynamics, then the equations of motion should appear through geodesics and an independent postulate of motion should not be required representing a necessary condition for the existence of solutions of field equations.

The issue of “motion versus field” in GR was only enlightened decades later by Infeld and Plebanski [23] showing that the Einstein field equations also implicitly contained the motion equations. To our applications, we have been investigating the fact that different parameters may lead to different physical configurations constrained by the analysis of geodesic motion itself. For instance, near black holes generally indicate that the velocities of nearby stars are of the order of a few hundreds of kilometers per second, which should be described by a slow geodesic motion in the presence of strong gravitational fields with highest-energy cosmic ray jets and active galactic nuclei [24, 25]. In addition, the linear gravitational wave equation and the Schwarzschild weak fields with the parameter 1/r are not velocity-related and show that strong gravitational field are possible in the slow motion regime. On the other hand, even with all success of PPN approximation, to establish bounds on PPN parameters are not a trivial task. For example, PPN is not uniformly valid for large distances [26] and has limitations on the study of the dynamics of pulsars [27], which breaks down in the radiation zone where gravitational waves propagate. The beforementioned examples give us a window of opportunities to search models or methodologies under those circumstances blending the subtleties of motion and field of GR to comply with astrophysical system characteristics. To such intent, there are several approaches to astrophysical applications. such as Modified Newtonian Dynamics (MOND) [28, 29] and its relativistic version [30, 31], relativistic frameworks beyond GR as F(R) [32, 33], relativistic corrections [34, 35] and normalization groups [36] and other models on galactic modelling [37,38,39,40].

In this paper, we keep applying the geodesic slow motion concept in GR to the motion of stars and focus on the obtainment of effective gravitational potentials to study their orbits to obtain a stable model profile for galaxy dynamics in axisymmetric astrophysical configurations. We use galpy [41]Footnote 1 numerical code written in python to study and evaluate how such potentials may respond and reproduce astrophysical systems. As an orbit integrator, the galpy code is used to obtain the resulting orbits from combinations of gravitational potentials. In Sect. 2, we discuss the slow motion limit of GR, which means that we use only the geodesic equations alone, leaving the deviation equation intact [17, 18, 23] to obtain a nearly-Newtonian limit [12]. In Sect. 3, we present the application of the nearly-Newtonian potential resulting from Weyl’s metric to determine the character of orbits. In Sect. 4, to complement our investigations, according to star formation frameworks, almost \(90\%\) of stars are clustered [42]. Thus, we test our methodology proposing a toy model to N-body simulation of disrupt clusters using the Amuse [43,44,45,46,47]Footnote 2 code for N-body simulations with galpy code. In the conclusion section, we present the final remarks and prospects. We adopt the Landau-Lifshitz spacelike convention \((+++-)\) for the signature of the four dimensional metric and speed of light c\(=1\). Greek indices count from 1 to 4.

2 The slender disk condition

In the present model, we start with an idea using a free test particle (star) that orbits a galactic bulge regarded as a point-like source centered at the circular basis of a cylinder by means of Weyl’s line element [13]

$$\begin{aligned} ds^{2}=e^{2\left( \lambda -\sigma \right) }dr^{2}+r^{2}e^{-2\sigma }d\theta ^{2}+e^{2(\lambda -\sigma )}dz^{2}-e^{2\sigma }dt^{2},\nonumber \\ \end{aligned}$$
(1)

where \(\lambda =\lambda (r,z)\) and \(\sigma =\sigma (r,z)\) are the Weyl’s coefficients. Thus, firstly obtained by Rosen [48], the exterior gravitational field is given by Einstein’s vacuum equations

$$\begin{aligned}&- \lambda _{,r} + r\sigma _{,r}^{2} -r \sigma _{,z}^{2} =0, \end{aligned}$$
(2)
$$\begin{aligned}&\sigma _{,r}+r\sigma _{,rr}+r\sigma _{,zz}=0, \end{aligned}$$
(3)
$$\begin{aligned}&2r\sigma _{,r}\sigma _{,z} =\lambda _{,z}, \end{aligned}$$
(4)

where the terms (, r), (, z) and (, rr), (, zz) denote respectively the first and the second derivatives with respect to the variables r and z. It is important to point out that Weyl’s metric does not lose its asymptotes when reduced to Schwarzschild symmetry [13, 48, 49] and is also asymptotically flat [13, 16, 48,49,50]. These two features turn such metric an interesting case for application to astrophysical systems.

Under specific conditions, the resulting gravitational field will be different like that of the one produced by Schwarzschild’s geometry to avoid Cartan’s equivalenceFootnote 3 [16, 51, 52]. Hence, the diffeomorphism invariance of GR is broken down by the slender disk condition, i.e., the cylinder thickness \(h_{0}\) is much smaller than its radius \(R_{0}\), i.e., \(h_{0}<< R_{0}\). At first, with this procedure, we avoid to attribute any surface density of the cylinder, which eventually would lead to a singularity at z-coordinate like those works of Refs. [39, 53,54,55] . Since we are interested in the particle’s orbit itself, we need to solve the nonlinear system of Eqs. (2), (3) and (4). In the same fashion as worked in Ref. [17], in order to obtain related solutions, we expand the coefficients \(\lambda (r,z)\) and \(\sigma (r,z)\) into a Taylor’s series in such a way

$$\begin{aligned}&\sigma (r,z) \approx \sigma (r,0) \nonumber \\&\quad + {z^2}{\left. {{{{\partial ^2}\sigma (r,z)} \over {\partial {z^2}}}} \right| _{z = 0}} + \cdots , \end{aligned}$$
(5)
$$\begin{aligned}&\lambda (r,z) \approx \lambda (r,0) \nonumber \\&\quad + z{\left. {{{\partial \lambda (r,z)} \over {\partial z}}} \right| _{z = 0}} + {z^2}{\left. {{{{\partial ^2}\lambda (r,z)} \over {\partial {z^2}}}} \right| _{z = 0}} + \cdots . \end{aligned}$$
(6)

Truncating the approximation up to the second order to guarantee the non-linearity in the expansion, we write

$$\begin{aligned} \sigma (r,z) = A(r) + a(r)z + c(r){z^2}, \end{aligned}$$
(7)

where we denote \(A(r)=\sigma (r,0)\), \(a(r)= {\left. {{{\partial \sigma (r,z)} \over {\partial z}}} \right| _{z = 0}}\) and \(c(r)=\left. {{{{\partial ^2}\sigma (r,z)} \over {\partial {z^2}}}} \right| _{z = 0}\).

In addition, we use the same procedure as in Eq. (7) to the coefficient \(\lambda (r,z)\) and define

$$\begin{aligned} \lambda (r,z) = B(r) + b(r)z + d(r){z^2}, \end{aligned}$$
(8)

where we denote \(B(r)=\lambda (r,0)\), \(b(r)= {\left. {{{\partial \lambda (r,z)} \over {\partial z}}} \right| _{z = 0}}\) and \(d(r)=\left. {{{{\partial ^2}\lambda (r,z)} \over {\partial {z^2}}}} \right| _{z = 0}\).

As shown in Ref. [17], for superior orders, the terms in the coefficients \(\sigma (r,z)\) and \(\lambda (r,z)\) turn to be redundant. It was found that the initial functions a(r), c(r) in Eq. (7) can be reduced to constants \(a_0\) and \(c_0\), respectively, and \(k_0\) is a constant factor. Hence, in Eq. (8), the functions b(r) and d(r) can be written as

$$\begin{aligned} b(r)= & {} k_0 a_0 - 2 a_0c_0r^2, \end{aligned}$$
(9)
$$\begin{aligned} d(r)= & {} k_0 c_0 - 2 c_0^2 r^2,\;\;\;\; \end{aligned}$$
(10)

Thus, taking the beforementioned results of the Taylor coefficients and replacing it in Eqs. (7) and (8) in the system given by Eqs. (2), (3) and (4), one obtains the final form of the coefficient \({\sigma (r,z)}\) as given by

$$\begin{aligned} {\sigma (r,z) = {{{k_0}} \over 2}\ln (r) - {{{{c_0}{r^2}} \over 2}} + {a_0}z + {c_0}{z^2}+c_1}\;. \end{aligned}$$
(11)

As a matter of completeness, one obtains a closed form for the coefficient \(\lambda (r,z)\) given by

$$\begin{aligned} \lambda (r,z) = {{{k_0}^2} \over 4}\ln (r) - {k_0}{c_0}{{{r^2}} \over 2} + \frac{1}{4}c_0^2 r^4+ D(r,z),\;&\end{aligned}$$
(12)

where \(D(r,z)=- {\left( {{a_0} + 2{c_0}z} \right) ^2}{{{r^2}} \over 2} + {k_0}{a_0}z + {k_0}{c_0}{z^2}+d_1\), \(c_1\) and \(d_1\) are true integration constants.

In this paper, we focus on the obtainment of simpler solutions noting that we only need \(\sigma (r,z)\) coefficient of Eq. (11) to determine the gravitational potential. Even so, it is important to note that from the study of dynamical systems, it is known that nonlinear systems propagate qualitative effects due to the nonlinear nature of the solutions that initially the variables to be determined are all intertwined. As a result, the related gravitational potential also carries an indirect influence of the coefficient \(\lambda (r,z)\).

3 The effective potentials and numerical implementation

In the geodesic analysis of motion, a small deviation from Minkowski’s metric does not necessarily depend on the velocity of an arbitrary particle. On the other hand, if once establishes the slow motion \(v<<c\), Newtonian coordinates can be used with \(x^4 =t\), t being the Newtonian time. As shown in traditional textbooks [12], integrating small increments \(\delta h_{\mu \nu }\) of the metric \(g_{\mu \nu }\) along the geodesic path, one obtain the nearly-Newtonian potential \(\varPhi _{nN}\):

$$\begin{aligned} \varPhi _{nN}= -\frac{c^2}{2}\int _{0}^{h_{44}} d(\delta h_{44})= -\frac{c^2}{2}(1+g_{44})\;. \end{aligned}$$
(13)

It is important to note that the potential \(\varPhi _{nN}\) is not necessarily the Newtonian gravitational field because the gravitational field was not a priori assumed to be weak. Moreover, assuming there is not external force, the gravitational field from the source continuously pull the test particle building up by small increments of the metric. Except at the beginning of the free fall, the weakness of a Newtonian gravitational field was not a priori condition. As a result, the component \(g_{44}\) of the metric is obtained from an exact solution of Einstein’s equations, whose solutions count with the contribution of all metric components. The symmetry group of this equation is similar to the generalized Galilean group. In this case, the Newtonian potential is replaced by Eq. (13), which means that diffeomorphic transformations are not allowed and the metric coordinates must be consistent with the metric symmetry of the local gravitational field. It is interesting to note that not only the slow motion condition in static gravitational configurations appears to be applied, but also a particular reduction on the nonlinearity contained in the affine connections. In addition, it may be possible the development of astrophysical models where the metric tensor is not trivial and restricted eventually to be symmetric.

In reality, the motion of stars in spiral galaxies tell that we need a gravitational model capable of describing a slow motion also valid for gravitational fields of any strength. In order to test this nearly-Newtonian limit, using Eqs. (11) and (13), one can calculate in the galactic plane the related gravitational potential generated by a point-like mass at a distance r given by

$$\begin{aligned} \varPhi _{nN}(r,z) = -\frac{c^2}{2}\left( 1-a_1 r^{k_0} e^{-c_0 r^2+2(a_0z+c_0z^2)} \right) \;. \end{aligned}$$
(14)

For convenience, hereon we refer \(\varPhi _{nN}\) just as Weyl potential.

In a previous publication [17], it was argued that at Solar system scale the parameter \(c_0<< 1\), which means that the quadratic radial term at Eq. (11) evolves slowly as the radial distance increases. In order to investigate the character of motion in the meridional plane of an axially symmetric galaxy model, we need to construct a galaxy model. At galactic scale, it may be interesting to explore some gravitational effects like that of the rotation curve problem [7,8,9, 56], which invariably leads to the dark matter concept that is a fundamental issue in galactic dynamics, particle physics and cosmology. As a starting point, we use the same model structure as presented in Ref. [21] applied to the study of the dark matter problem by means of an effective radial velocity \(v_{eff}\). Since the slow motion geodesic equation is not invariant under diffeomorphisms we may consider some gravitational stages separately such as

$$\begin{aligned} v_{eff}^2= v_{N}^2 + v_{nN}^2, \end{aligned}$$
(15)

which the terms \(v_{N}\) and \(v_{nN}\) are the standard Newtonian velocity (or a velocity resulted from another Newtonian-like potential such as Miyamoto-Nagai potential) and the nearly-Newtonian velocities, respectively. Due to the slender disk condition, it is not possible to simulate the galaxy bulge per se using a nearly-Newtonian potential alone and the passage of a pointlike source to an extended particle distribution is a must. Interestingly, such condition meets the so-called slender galaxies, such as the disk galaxies as NGC 4395 [57] and NGC 3621 [58], which are considered bulgeless galaxies in the sense that they cannot harbour a supermassive black hole.

Differently from Ref. [21], which in the analysis was used real data by means of non-linear least-squares fitting with the Levenberg-Marquardt algorithm, we focus now on the consistency of the numerical implementation of the galpy code to evaluate the resulting idealised rotation curves, i.e., if it produces a flat rotation curve at large radii. Hence, it serves as a reference for constraining the free parameters in the same fashion as Ref. [59], which studies the classification of orbits with dark matter influence.

Once much of galactic systems are fairly non-spherical, we expect to reproduce approximated spherical bulges and flat disks. In order to test this hypothesis, we model a mass distribution to extended source in a linearized framework with a Newtonian mass M(r), and we resort to additional potentials to provide a Newtonian velocity \(v_{N}\). To our numerical study, we use the Miyamoto-Nagai potential and the Milky-Way-like potential, dubbed as MWpotential2014 as provided in Ref. [41]. The Miyamoto Naygai model [5, 6] is given by

$$\begin{aligned} \varPhi (r,z) = -\frac{GM}{r^2+(a^2+\sqrt{z^2+b^2})^2}, \end{aligned}$$
(16)

that gives a thickened disk as an extended form of a Kuzmin disk [4]. For detailed derivation of this potential, see Refs. [5, 6, 11] and a discussion on general potential theory, see Ref. [11]. When \(a\rightarrow 0\) the potential is reduced to a Plummer sphere [1] and \(b\rightarrow 0\) to a Kuzmin disk. To enhance our analysis, we also use a Milky-way’s gravitational potential MWpotential2014 with no consideration of the central supermassive black hole’s gravity. From Eq. (14) and using the standard Newtonian formula for calculating the circular equatorial velocity \(v(r)=\sqrt{r\frac{\partial \varPhi }{\partial r}\rfloor _{z=0}}\), the nearly-Newtonian velocity is written as

$$\begin{aligned} v_{nN}(r)=\sqrt{\frac{GM(r)}{2R_0}A(r)}, \end{aligned}$$
(17)

where \(R_0\) is the optical disk length scale. In our application, it is assumed that the Sun is located at \(R_0=8\)kpc from the Galactic center. M(r) is the mass model to be adopted. Moreover, A(r) denotes the term

$$\begin{aligned} A(r)=\left( k_0+2c_0(r+1)^2\right) a_1(r+1)^{k_0}e^{-c_0r^2}\;. \end{aligned}$$
(18)

Accordingly, Eq. (17) evinces some important requirement for the effective velocity that should vanish asymptotically. From the theoretical point of view, \(v_{nN}\) vanishes at an infinite radius for an asymptotically flat rotation curve. In practice, this means that at maximum finite radius according to observations, the influence of a gravitational pull of the galaxy ceases to be. In addition, we point out that Eq. (17) does not reach the Newtonian limit. Actually, this situation was expected to happen since the Newtonian limit should be reached at \(k_0=1, c_0=0\), but the radial distance dependence remains in the A(r) term. When one sets \(k_0,c_0=0\), Eq. (17) is zero since the Weyl potential \(\sigma (r,z)\) vanishes. This result is as a relic of the breakage of diffeomorphic transformations and imposes a constraint on the parameter \(k_0\ne 0\).

The galpy numerical implementation is straightforward once there is a detailed public material available at https://github.com/jobovy/galpy besides of the galpy publication [41].Our modification to the code was just adding to the vanilla code our Weyl potential creating a new python class and C implementations. Hence, we update the related python files as \(\texttt {\_init\_}\).py, the directly related to orbit integration as integrateFullOr-bit.py and integratePlanarOrbit.py. The C files are needed to be declared as well to perform orbit integration with combinations of potentials as in the files integrateFullOrbit.c, integratePlanarOrbit.c and modify declarations in \(\texttt {galpy\_potentials}\).h, accordingly.

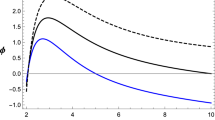
We present in Fig. 1 an idealised set of Milky-way rotation curves, in the sense they were not built with real data, thus galaxy rotation and inclination effects are not taken into account, but the curves must show a necessary asymptotically flat pattern in order to respond, as a first instance, to further analysis on rotation curve problem. References to colour, the reader is referred to check the electronic version of this article. We show the Milky-way rotation curves comparison between the effective velocity with the additional nearly-Newtonian contribution added to other potentials. The dashed, thick and dotted red lines are obtained with the values of \(k_0\) as \((-0.3,-0.07,-1.1)\), respectively. Accordingly, the other parameters \((a_0,a_1,c_0)\) are set up with the values \((-0.01,-0.01,0.0001)\).

The Miyamoto-Nagai potential and Milky-way potential MWpotential2014 are indicated by the thick green and dashed-thick blue lines. The curve of the Miyamoto-Nagai potential alone is obtained with the parameters \((a,b)=(0.9,0.09)\), while MWpotential2014 rotation curve is obtained by the default parameters internally defined by galpy code. The complete description of the parameters and properties of MWpotentia2014 can be found in Table 1 of Ref. [41]. In the same reference, one finds that galpy assumes by default internal natural units. To implement further calculations, we use the standard galpy units, which normalise the resulting velocities set up to value \(v=1\) at radius \(x=1\). To physical units, it corresponds to a circular velocity of \(V_c=220\) km/s at \(R_0=X=8\) kpc. Velocities and distances are scaled as \(v= V_c/[220\) km/s] and \(x = X/[8\) kpc], respectively. The capital letters V and X correspond to physical velocity and galactic distances.

Fig. 1
figure 1

Milky-way idealised rotation curves comparison between the effective velocity with the additional nearly-Newtonian contribution (referred to colour in electric version as the dashed, thick and dotted red lines in the curves). The Miyamoto-Nagai and MWpotential2014 potentials are indicated by the thick green and dashed-thick blue lines. The Newtonian curve is indicated by the dashed black line. We use galpy units normalised as the velocity \(v= 1\) at \(x= 1\)

Full size image

We compare the effective curves from the composition of Miyamoto-Nagai potential, Weyl potential to MWpotential2014. As shown in Fig. 1, the solid thick green line behaviour results from Miyamoto-Nagai potential alone. Meanwhile, having MWpotential2014 as a reference, it is possible to obtain curves by varying the parameters of composed potentials with higher (dashed red line) or lower (dotted red line) curves. A duly appropriate curve is shown by the solid thick red line that presents a substantial higher rotation curve in the asymptotic regions as compared with MWpotential2014 for a central Miyamoto-Nagai potential with \((a,b)=(1,0.004)\), which provides a more spherical bulge. This is fairly interesting since it reaches an approximate velocity in physical units as \(V\sim 150\) km s\(^{-1}\) at \(r\sim 100\) kpc. Those values match the constructed Milky-way rotation curve as in Ref. [60], which corresponds to \(v\sim 0.68\) and \(x\sim 12.5\) in galpy units. At first, we also notice that the effect of the inclusion of the Weyl potential improves the rotation curve of Miyamoto-Nagai potential with a higher bulge distribution and a far reaching disk dark component as a result from GR nonlinearity heritage in detriment of a dark matter component in accordance with Ref. [21]. On the other hand, as observed in real Milky-way rotation curve, its localised peaks and dips are not determined, and they are out of the scope of this work, which may be reconsidered in a future larger analysis with real data. For this particular numerical study, negative values of the parameters \((k_0, a_0, a_1)\) are preferred, while \(c_0\) is close to zero. For completeness purposes, we also add to Fig. 1, the Newtonian rotation curve in dashed black line.

Fig. 2
figure 2

Orbit collection of different types of orbits in axial symmetric galaxy model for different possible values of the parameters. The panels refer to the composition of Miyamoto-Nagai and Weyl potentials. The red dot signs the globular cluster Omega Centauri’s orbit

Full size image
Fig. 3
figure 3

Orbit collection of different types in axial symmetric galaxy model for different possible values of the parameters. The upper and middle panels refers to the composition of MWpotential2014 and Weyl potentials. The red dot signs the globular cluster Omega Centauri’s orbit

Full size image

4 Star orbits and cluster disruption

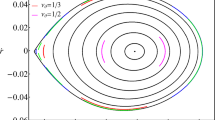
In order to get more understanding on the behaviour of model parameters, we numerically integrate several sets of orbits to understand the nature of motion produced by Weyl potential in combination with Newtonian-like potentials. This is an important issue for testing our methodology since the different types of orbit stars can tell us about the evolution of galaxies and clusters. In Figs. 2 and 3, we present the resulting orbits for possible parameter values as shown in Table 1.

For all cases in Fig. 2, we fix the values of parameters in Miyamoto-Nagai potential as \((a=0.9,b=0.09)\) combined with Weyl potential. Thus, we obtain the form of the orbits, which reveals related shapes for specific parameter values. In each case, if one varies the values as shown in Table 1, it provides small differences in overall shapes. For instance, high values in the (a, b) panels in Fig. 2 lead to box orbit with the increase of trajectories in the (x, y)-plane and will eventually fulfill its whole surface. In the (c, d) panels, it presents the higher possible values of parameters \(k_0\) and \(a_1\), in the same fashion of integrated orbits of the central test particle by means of Navarro–Frenk–White potential [61, 62] . As seen from the (x, y)-plane, it shows a rosette pattern which mimics the orbit of NGC 6544 [63], but in the (r, z)-plane, it might indicate a black hole in the center, which makes the stars speed-up and a possible chaotic pattern of orbit starts to grow rapidly. We also verified that for values of \(a_0>0\) compromise the stability of the plane (r, z) showing random spikes in the resulting orbit or even a crash in galpy orbit integration. For smoother orbits, we then define \(a_0\le 0\) for periodic orbits found to be stable. This is the case for the panels (e, f) and (g, h) in which \(a_1\) must be small for positive \(k_0\). If we reverse the signs of \((a_0,a_1)\), they will not change the overall shape of these curves.

Table 1 The defined values of parameters \((a_0,a_1,c_0,k_0)\) used in galpy code
Full size table

For the combination of MWpotential2014 with Weyl potential, we found that two possible cases happen. The first one happens when \(k_0<0\) for null values of \((a_0,c_0)\) and small \(a_1\) that provides a rosette orbit. The second case is for \(k_0>0\), and keeping the same previous values of the parameters, one obtains a tube-shaped orbit in the (x, y) plane while in the (r, z) plane, one reaches an edge-on orbit, which eventually might lead to chaotic orbit or mimics the same pattern as seen in the irregular orbit of galaxy M0175 trapped in a resonant region in the phase space [64]. As an overall result, we obtained basically box and loop orbits that appear to be compatible with disk-like and elliptical galaxies.

Fig. 4
figure 4

Numerical simulations of Weyl potential with Miyamoto-Nagai potential (top panels) and the conjunction of Weyl potential and MWpotential2014 in middle and bottom panels for different cluster masses and radii (cases (1) and (2), respectively.) in early stages of disruption

Full size image
Table 2 The adopted parameters in N-body simulation, where the cluster mass \(M_c\) is in sun mass units \(M_{\bigodot }\)
Full size table

In the following, we make a toy model of N-body simulation of clusters using a combination of Weyl potential with the Milky-way potential MWpotential2014 in order to evaluate the response of the inclusion of the Weyl potential to the cluster dynamics. In other to produce stable simulations, we use galpy code with Amuse [43,44,45,46,47] code for simulations. Then, we define the simplifying assumptions: the cluster is in dynamical equilibrium, Boltzmann’s molecular chaos is required (test stars and related fields are fairly independent). The total mass \(M_i\) of the cluster of set of i-stars is defined as \(M_i=\sum _{j=1}^{i}\) as a Plummer-sphere cluster and an additional external potential must be added to evaluate the evolution of the system with time. For our simulation, we set Weyl potential with the values of the parameters set as \((a_0,a_1,c_0,k_0)=(-0.01,-0.01,0.0001,-0.5)\). For the initial cluster parameters, we have that N accounts for the number of stars, \(M_c\) is the cluster mass in Sun mass units \(M_{\bigodot }\) and cluster radius \(R_c\) in parsec units, and stars initial velocity of 220 km/s and radius 10 kpc as default. In Table 2, we present the values of parameters \((N, M_c, R_c)\) considering Weyl potential with Miyamoto-Nagai potential and also in conjunction with MWpotential2014 in two cases: varying the cluster mass and the number of particles. For stability reasons, we adopted typical masses for globular cluster around \(10^4\) Sun masses \(M_{\odot }\) and are compatible with expected for solar neighbourhood (which is less than about \(10^4\) \(M_{\odot }\)). As a toy model, we check the Weyl potential in the top panels in Fig. 4. The evolution of the system indicates a fast disruption of a related cluster. When associated with MWpotential2014 in the case (1)(middle panel) the disruption occurs earlier for low-mass clusters in concordance with [65], and (2) (bottom panel) occurs later due to not only more massive stars but to a larger cluster radius. Thus, such later disruptions seem to be caused more by gravitational process than their baryonic content. A similar process occurs with the disruption of satellites galaxies clusters [65]. Our results suggest to be in accordance with Cold Dark Matter (\(\varLambda \)CDM) bottom-up hierarchy in which small objects collapse first to generate later massive structures [66,67,68]. We do not have much differences in evolution with the variation of star masses and the overall aspect of initial phase of disruption where the edge-on stars start falling apart but the cluster center remains unspoil.

5 Final remarks

In this paper, we have discussed the slow motion in GR. When considering the slow motion of stars near galaxies, also including near the bulge core, the slow motion condition breaks down the general covariance of GR but not Einstein’s equations, which are still valid in that scenario. In this terms, from using the geodesic equations alone, we are led to “in-between” gravitational potential close to but stronger than Newtonian gravity, the nearly-Newtonian potential dubbed by the traditional Misner, Thorne and Wheeler’s gravitation book. We have recovered such aspect of GR foundation in terms of a possible astrophysical implications. As it happens, we have proposed a toy model from an axisymmetric Weyl metric under a slender disk condition, which means that the height of the disk can be considered as such smaller than its radius. Thus, we have obtained a related gravitational potential in conjunction with Miyamoto-Nagai and Milky-way-like potentials adopted in galpy python code. Starting from the analysis on the idealised Milky-way rotation curves between the conjuncted potential as (Miyamoto+Weyl) and Milky-way-like potential, we have got an idealised steady rotation curve in the Milky-way outskirts, accordingly. It shows that the slender Weyl potential adds a considerable contribution to the far reaching dark sector of a galaxy due to nonlinearity propagations resulting from Einstein’s equations. Of course, Weyl metric is a symmetric and static metric, and some simplifications were adopted in our analysis since it is not possible to include neither rotation nor projection effects, which will be examined in a future work. The present analysis was important to obtain some restrictions on the free parameters of this model. As a result, we have obtained star orbits with periodic regular box and loops from (Miyamoto+Weyl) potential, which appear to be compatible with disk-like and elliptical galaxies. On the other hand, the apparent chaotic types in (Miyamoto+Weyl) and (Milky-way-like+Weyl) potential compositions may be caused by the model simplifications (rotation or projection effects, the lack of back-hole influence and/or stellar streams in the Milky-way halo [62]). It is important to note that in this work, we do not analyse the influence of the mass, scale length of the dark halo and the optical disk. In addition, the summarised possible values of the parameters that are shown in Table 1, and the extrapolation of those values may lead to nonphysical results. Eventually, the need of implementation of real data to the code may lead to a better constrains on the parameters and such regions may be studied properly. This result seems to be generalized somehow in terms of oblate/prolate orbit family should be investigated in a further study using Zipoy-Vorhees family metric. In cluster N-body simulation, we proposed a toy model using galpy in conjunction with Amuse code for N-body simulations to obtain a faster disruption cluster evolution adding the Weyl potential to Milky-way-like potential. Comparing two different mass clusters, the disruption occurs earlier in the lighter cluster mass and later in the most massive cluster. This later disruptions seemed to be caused more by gravitational process than their baryonic content once in the second proposed case, we have had a larger galactic radii. Since it seems to be in accordance with \(\varLambda \)CDM bottom-up hierarchy, it may serve merit of further investigations. Finally, a Milky-way-sized galaxies should be investigated in order to analyse if the profile obtained in this paper still remains in a complex model and in a high-resolution N-body simulation of cosmological volumes that is necessary to explore subtleties of satellite galaxy merging/disruption.