Thermodynamical and dynamical stability of a self-gravitating charged thin shell

Abstract

A study of the thermodynamical and dynamical stability of self-gravitating charged shells is presented. The matter on the shell is described by a barotropic equation of state, and the charge is assumed to be proportional to the mass. For a given form of the entropy of the matter on the shell, it is shown that strong restrictions on the states of the shell follow from the imposition of both types of stability plus the condition that the speed of sound is less than one, in some cases leading to the absence of stable states.

1 Introduction

Self-gravitating thin shells are solutions of a given gravitational theory describing two regions separated by an infinitesimally thin region where matter is confined. Such a system conjugates the notions of vacuum, typical of black holes, with that of the presence of matter, which may be described via statistical mechanics and thermodynamics. Thin shells have been frequently employed to probe mechanical and thermodynamical properties of black holes, see for instance [3, 18,19,20, 27]. Since they can be taken to their own gravitational radius, thin shells provide a toy model for the study of the Hawking radiation emitted during the collapse of a body until it settles as an ultra-compact object [9]. In addition, thin shells can model quasi-black holes [15] thus enabling the calculation of black hole properties (see for instance [16, 19, 20] for the extremal case).¹ It is worth mentioning that the thin shell formalism has been developed also for theories other than General Relativity, see for instance [5, 25] for metric f(R) theories, [22] for f(R) theories in the Palatini formalism, [2] for scalar-tensor theories, and [24] for hybrid $f(R,{{{\mathcal {R}}}})$ theories.

In view of their widespread application, it is important to determine the set of shell configurations that are dynamically and thermodynamically stable. The latter type of stability was studied in [21] in the case of a spherically symmetric thin shell in which the interior region is Minkowski’s spacetime and the exterior given by Schwarzschild’s geometry, while the linear dynamical stability of such systems under radial perturbations was analyzed in [3] for a linear EOS, and in [8] for a general EOS. Since these two types of stability yield inequivalent restrictions on the parameter space, we established in [23] the conditions needed for uncharged thin-shell configurations to be stable, both thermodynamically and dynamically, for different barotropic equations of state (EOS), and also for EOS of the type $P = P(\sigma , R)$, where R is the radius of the shell.

We shall generalize here the results obtained in [23] to the case of shells with nonzero charge. The study of such shells goes back at least to [4, 12], in relation to gravitational collapse. Among their many relevant applications, we could mention the study of very compact charged shells and the corresponding Buchdahl-like bound [1], and that of the entropy of extremal black holes through the entropy of charged thin shells [20].² The thermodynamical features of shells that separate a flat interior from the exterior geometry (described by the Reissner-Nordstrom solution), assuming that the mass and the charge of the shell are independent parameters, were studied in great detail in [18], while their dynamical stability was analyzed in [6].

The paper is organized as follows. In Sect. 2 a brief review of the relevant equations for the charged thin shell in equilibrium (mostly following [18]) will be presented. The equations obeyed by the perturbed shell for a barotropic EOS, as well as the condition for dynamical stability will be introduced in Sect. 3. The restrictions following from thermodynamical stability are exhibited in Sect. 4. The zero charge case (which was studied in [23] using a different parametrization) will be revisited in Sect. 5. The region of the parameter space of equilibrium configurations of the charged shells compatible with dynamical and thermodynamical equilibrium (assuming a linear relation between the charge density and the energy density) will be presented in Sect. 6, along with the imposition of the the dominant energy condition (DEC) and the upper limit on the velocity of sound. Our closing remarks are presented in Sect. 7.

2 Junction conditions of the shell

We consider a two-dimensional timelike massive electrically charged shell $\varSigma$ with radius R. The shell divides the spacetime in two parts: an inner region $r<R$, and an outer region $r>R$. The metric in both regions can be expressed as follows:

$$\begin{aligned} ds_{(\mathrm{I})}^2&=g_{\alpha \beta }^{(\mathrm{I})}dx^\alpha dx^\beta =-f^{(\mathrm{I})}{dt^{(\mathrm{I})}}^2+\frac{dr^2}{f^{(\mathrm{I})}} + r^2d\varOmega ^2. \end{aligned}$$

(1)

Here $\mathrm{I} =\mathrm {in}, \mathrm{out}$, refers to either the inner or outer region, and $t^{(\mathrm{in})}$ ($t^{(\mathrm{out})}$) is the inner (outer) time coordinate. The functions $f^{(\mathrm{in})}$ and $f^{(\mathrm{out})}$ are given by

$$\begin{aligned} f^{(\mathrm{in})}&=1,\quad f^{(\mathrm{out})}={1-\frac{2m}{r}+\frac{Q^2}{r^2}}, \end{aligned}$$

(2)

where m is the ADM mass and Q is the electric charge, with $G=c=1$.

The metric $h_{ab}$, defined on $\varSigma$, i.e. for $r=R$, is that of a 2-sphere with the addition of a time coordinate, and it can be written as

$$\begin{aligned} ds_{\varSigma }^2&=h_{ab}dy^a dy^b=-d\tau ^2 + R^2(\tau )d\varOmega ^2, \end{aligned}$$

(3)

where $\tau$ is the proper time for an observer located on the shell, and $y^a=(\tau ,\theta ,\phi )$. A solution of the Einstein–Maxwell equations on the shell can be obtained using the thin-shell formalism developed in [10]. Assuming a static shell, and considering that the matter that composes the shell is described by a perfect fluid, with surface energy density $\sigma$ and pressure p, the junction conditions yield the following form of the the components of the energy-momentum tensor of the matter on the shell (see [18] for details):

$$\begin{aligned} {{\mathcal {S}}^\tau }_\tau&= - \sigma =-\dfrac{\sqrt{1-\frac{2m}{R}+\frac{Q^2}{R^2}}-1}{4\pi R}, \end{aligned}$$

(4)

$$\begin{aligned} {{\mathcal {S}}^\theta }_\theta&= {{\mathcal {S}}^\phi }_\phi = p \nonumber \\&=\dfrac{\sqrt{1-\frac{2m}{R}+\frac{Q^2}{R^2}}-1}{8\pi R}+\dfrac{\frac{m}{R}-\frac{Q^2}{R^2}}{8\pi R \sqrt{1-\frac{2m}{R}+\frac{Q^2}{R^2}}}. \end{aligned}$$

(5)

The material mass M is defined by $M=4\pi \sigma \, R^2$. Hence, from Eq. (4) it follows that the ADM mass m is given by

$$\begin{aligned} m&=M-\frac{M^2}{2R}+\frac{Q^2}{2R}. \end{aligned}$$

(6)

Using this expression in Eq. (5), the pressure now is

$$\begin{aligned} p&=\frac{M^2-Q^2}{16\pi R^2(R-M)}. \end{aligned}$$

(7)

Taking into account that the total charge Q in terms of the charge density $\sigma _e$, is given by, $Q=4\pi R^2\sigma _e$, and the definition of M is in terms of $\sigma$, we get from Eq. (7)

$$\begin{aligned} R&={\frac{p}{\pi \, \left( 4\,p\sigma +{\sigma }^{2}-{\sigma _{{e}}}^{2} \right) }}. \end{aligned}$$

(8)

Proceeding in an analogous way,

$$\begin{aligned} M&={\frac{4{p}^{2}\sigma }{\pi \, \left( 4\,p\sigma +{\sigma }^{2}-\sigma _e^2 \right) ^{2}}}, \end{aligned}$$

(9)

$$\begin{aligned} m&=4\,{\frac{{p}^{2} \left( 2\,p{\sigma }^{2}+2\,{\sigma _{{e}}}^{2}p+{ \sigma }^{3}-\sigma \,{\sigma _{{e}}}^{2} \right) }{\pi \, \left( 4\,p \sigma +{\sigma }^{2}-{\sigma _{{e}}}^{2} \right) ^{3}}}. \end{aligned}$$

(10)

We shall follow [13] and parametrize a barotropic EOS using $p=x\sigma$. A linear relation between the charge density and the matter density will be assumed, namely $\sigma _e=\beta \sigma$. Hence, it follows that

$$\begin{aligned} M&={\frac{4{x}^{2}}{\pi \sigma \, \left( 1-\beta ^{2}+4\,x \right) ^{2}}}, \end{aligned}$$

(11)

$$\begin{aligned} R&={\frac{x}{\pi \sigma \, \left( 1-\beta ^{2}+4\,x \right) }}, \end{aligned}$$

(12)

$$\begin{aligned} m&=\frac{4{x}^{2}}{\pi \, \sigma \,} {\frac{(1-\beta ^{2})(1-2x) +4x }{ \left( 1-\beta ^{2}+4\,x \right) ^{3}}}. \end{aligned}$$

(13)

These equations will be useful to express the results in terms of the compactness defined as $C\equiv M/R$, and given by

$$\begin{aligned} C&=1-\left[ 1-\frac{2m}{R}+\frac{Q^2}{R^2} \right] ^\frac{1}{2} . \end{aligned}$$

(14)

Since $R\ge r_+$, where the gravitational radius $r_+=m+\sqrt{m^2-Q^2}$, the compactness satisfies $C\le 1$ (with $C=1$ corresponding to $R=r_+$). The relation between x and C can be obtained using Eqs. (11) and (12), and it is given by

$$\begin{aligned} x&=\frac{1-\beta ^2}{4}\,{\frac{ C}{1-{ C}}}. \end{aligned}$$

(15)

Hence, Eqs. (12) and (13) can be written as

$$\begin{aligned} R&={\frac{C}{4\pi \,\sigma (C,\beta )}}, \end{aligned}$$

(16)

$$\begin{aligned} m&=\frac{C^2}{8\pi \,\sigma (C,\beta )} [2-C(1-\beta ^2)] , \end{aligned}$$

(17)

with $M=CR$. The function $\sigma (C,\beta )$ follows the $p=x\sigma$, and Eq. (15), for a given EOS. This form of equations will be useful to display our results for both the dynamical stability (to be discussed in the next section) and the thermodynamical stability.

3 Dynamical stability

Let us outline the steps that lead to the condition for the linear dynamical stability of the shells introduced in the previous section. The equilibrium state of the shell is described by Eqs. (4) and (5) with $R=R_0$, while the corresponding expressions for a dynamical shell are (see for instance [7, 8])

$$\begin{aligned} \sigma&=\frac{1}{4\pi }\frac{\sqrt{f^{(\mathrm{out})}(R)+\dot{R}^2}-\sqrt{f^{(\mathrm{in})}(R)+\dot{R}^2}}{R}, \end{aligned}$$

(18)

$$\begin{aligned} p=&\frac{1}{8\pi }\left[ \frac{2{\ddot{R}}+f^{(\mathrm{out})\prime }(R)}{2\sqrt{f^{(\mathrm{out})}(R)+\dot{R}^2}}-\frac{2{\ddot{R}}+f^{(\mathrm{in})\prime }(R)}{2\sqrt{f^{(\mathrm{in})}(R)+\dot{R}^2}}\right. \nonumber \\&\left. +\frac{\sqrt{f^{(\mathrm{out})}(R)+\dot{R}^2}-\sqrt{f^{(\mathrm{in})}(R)+\dot{R}^2}}{R} \right] , \end{aligned}$$

(19)

where the overdot (prime) denotes the derivative with respect to $\tau$ (r), and $f^{(\mathrm{out})}(r)$ and $f^{(\mathrm{in})}(r)$ are given by Eq. (2). The conservation of ${\mathcal {S}}^{\mu }_{\;\nu }$ leads to

$$\begin{aligned} \frac{d\sigma }{d R} + \frac{2}{R}(p+\sigma )&=0. \end{aligned}$$

(20)

It follows from Eq. (18) that

$$\begin{aligned} {\dot{R}}^2 + V(R,\sigma (R))&=0, \end{aligned}$$

(21)

with

$$\begin{aligned} V (R)=&\frac{1}{2} \,({ f^{(\mathrm{in})}} \left( R \right) +{f^{(\mathrm{out})}} \left( R \right) ) \nonumber \\&-{ \frac{1}{64}}\,{\frac{ \left( {f^{(\mathrm{in})}} \left( R \right) -{f^{(\mathrm{out})}} \left( R \right) \right) ^{2}}{{\pi }^{2}{R}^{2} \sigma \left( R \right) ^{2}}}-4\,{\pi }^{2}{R}^{2} \sigma \left( R \right) ^{2}. \end{aligned}$$

(22)

It is important to point out that if Eq. (21) is strictly fulfilled, there can be no minimum of the potential at a configuration with zero velocity, since a slight increase of the potential around a static configuration would lead to a negative $\dot{R}^2$. This can be fixed by adding a small negative constant to the potential, which may be considered as an additional energy associated to the perturbation. With such an addition, the criterion of the derivative of V presented below is unchanged, as discussed in [26].

The linear stability of the shell can be studied by expanding the potential V in Eq. (21), around the equilibrium state up to second order in $\rho =R-R_0$, hence obtaining

$$\begin{aligned} \frac{d^2\rho }{d\tau ^2}+\omega _0^2 \rho&= 0. \end{aligned}$$

Stability implies that the frequency satisfies

$$\begin{aligned} \omega _0^2=\frac{1}{2}\left. \frac{d^2V}{dR^2}\right| _{R_0}>0. \end{aligned}$$

The calculation of $\omega _0^2$ involves $\dfrac{d\sigma }{dR}$ and $\dfrac{d^2\sigma }{dR^2}$, which are obtained from Eq. (20). For a general EOS of the type $p=p(R,\sigma )$, the latter includes the derivatives $\varOmega _1\equiv \dfrac{dp}{dR}$ and $\varOmega _2\equiv \dfrac{dp}{d\sigma }$, in terms of which [8]

$$\begin{aligned}&\omega _0^2 = -8\pi \,{\frac{H_0F_0 }{F_0-H_0}}\,{\varOmega _{10}}\nonumber \\&\quad + \,\frac{H_0(2F_0^2-f^{(\mathrm{in})\prime }_{0}R_0)-F_0(2H_0^2-f^{(\mathrm{out})\prime }_{0}R_0)}{(F_0-H_0)R_0^2}\varOmega _{20} \nonumber \\&\quad +\frac{\left[ 4F_{0}^4-2R_{0}F_{0}^2(f^{(\mathrm{in})\prime }_{0}+R_{0}f^{(\mathrm{in})}_{0}{''})+R_{0}^2(f^{(\mathrm{in})\prime }_{0})^2\right] H_{0}^3}{4(F_0-H_0)F_0^2H_0^2R_0^2}\nonumber \\&\quad -\frac{\left[ 4H_0^2-2R_0H_0^2(f^{(\mathrm{out})}_{0}{'}+R_0f^{(\mathrm{out})}_{0}{''})+R_0^2(f^{(\mathrm{out})\prime }_{0})^2 \right] F_0^3}{4(F_0-H_0)F_0^2H_0^2R_0^2}, \end{aligned}$$

(23)

where the sub-index “0” indicates that the quantity is evaluated at $R=R_0$, $F_0=\sqrt{f^{(\mathrm{in})}_{0}}$ and $H_0=\sqrt{f^{(\mathrm{out})}_{0}}$.

The line dividing stability from instability is obtained by setting $\omega _0^2=0$, which leads to the following expression for the critical values of $\varOmega _{20}$:

$$\begin{aligned} \varOmega _{20c} = \frac{A\;\varOmega _{10}+B}{D}, \end{aligned}$$

(24)

where

$$\begin{aligned} A&= 8\,\pi \,(f^{(\mathrm{out})}_{0})^3\,{{{R_0}}^{6} }, \\ B&={ R_0}^4(f^{(\mathrm{out})}_0)^3\left( f^{(\mathrm{out})}_0-1 \right) \\&\quad +{R_0}^2(f^{(\mathrm{out})}_0)^2\left( R_0\,m_0-2Q^2 \right) \\&\quad +Q^2\left( Q^2-2R_0 m_0\right) +{R_0}^2m_0^2, \end{aligned}$$

and

$$\begin{aligned} D&={2\,(f^{(\mathrm{out})}_0)^2\left( f^{(\mathrm{out})}_0{R_0}-2{Q}^{2}-{R_0}^2+3{R_0\,m_0} \right) }, \end{aligned}$$

with

$$\begin{aligned} f^{(\mathrm{out})}_0&= \sqrt{1-\frac{2m_0}{R_0}+\frac{Q^2}{{R_0}^2}}. \end{aligned}$$

For a barotropic EOS, $\varOmega _{10}=0$, and Eq. (24) reads

$$\begin{aligned} \varOmega _{20c}&={\frac{{ R_0}^4(f^{(\mathrm{out})}_0)^3\left( f^{(\mathrm{out})}_0-1 \right) +{R_0}^2(f^{(\mathrm{out})}_0)^2\left( R_0\,m_0-2Q^2 \right) +Q^2\left( Q^2-2R_0 m_0\right) +{R_0}^2m_0^2}{2{R_0}^2\,(f^{(\mathrm{out})}_0)^2\left( f^{(\mathrm{out})}_0{R_0}^2-2{Q}^{2}-{R_0}^2+3{R_0m_0} \right) }}. \end{aligned}$$

(25)

This equation defines the hypersurface $\varOmega _{20c}=$ $\varOmega _{20c}(m_0,R_0,Q)$. Any equilibrium configuration with $(m_0,R_0,Q)$ such that the corresponding $\varOmega _{20} =\left. \frac{dp}{d\sigma }\right| _{R_0}$ is greater than $\varOmega _{20c}$ will be dynamically stable.

In fact, when a specific EOS is chosen, there are other constraints that the system must satisfy. As will be shown below, an expression for $\varOmega _{20}=\varOmega _{20}(m_0,R_0,Q;\kappa )$, where $\kappa$ denotes the parameters of the EOS, can be obtained using the definition of $\sigma _0$ and $p_0$ along with the EOS. The EOS and the equilibrium equations also yield $m_0=m_0(R_0,Q;\kappa )$. Combining the latter with $\varOmega _{20}=\left. \frac{dp}{d\sigma }\right| _{R_0}$, we obtain $\varOmega _{20}=\varOmega _{20}(R^*_0,Q^*)$, where an asterisk denotes a quantity that has been rendered dimensionless using the parameters of the EOS. Using $m_0=m_0(R_0,Q;\kappa )$ in the equation for $\varOmega _{20c}$ we obtain $\varOmega _{20c}=\varOmega _{20c}(R^*_0,Q^*)$. The dinamically stable configurations for the given EOS will be those with $\varOmega _{20}(R^*_0,Q^*)> \varOmega _{20c}(R^*_0,Q^*)$. As will be shown in Sect. 5, such a condition for stability can be rephrased in terms of $\beta$ and C, using Eqs. (16) and (17). Let us present next the conditions for thermodynamical stability.

4 Thermodynamical stability

The formalism to study this type of stability for charged shells, along with some examples, was presented in [18] (see [19] for the extremal case), for shells in which the mass and the charge are independent state variables. By imposing that the shell be at a given local temperature and that the first law of thermodynamics holds on the shell, integrability conditions were derived for the temperature and for the thermodynamic electric potential. They lead to an expression for the entropy of the shell that is generically a function of the gravitational and Cauchy radii only. We shall present next a summary of the relevant results of [18].

Assuming that the shell is in static equilibrium with a well-defined temperature T(M, A, Q) and an entropy S(M, A, Q), both functions of the mass M, the area A, and the charge Q, the first law of thermodynamics is written as

$$\begin{aligned} TdS&=dM+pdA-\varPhi dQ, \end{aligned}$$

(26)

where $\varPhi$ is the electric potential on the shell. In this section it will be useful to adopt the notation used in [18], where M and Q were replaced by the gravitational radius $r_+$ and the Cauchy radius $r_-$, given by

$$\begin{aligned} r_+&=m+\sqrt{m^2-Q^2}, \end{aligned}$$

and

$$\begin{aligned} r_-&=m-\sqrt{m^2-Q^2}, \end{aligned}$$

respectively. To find the entropy $S(r_+,r_-,R)$, the equations of state $p=p(r_+,r_-,R)$, ${\alpha }=\alpha (r_+,r_-,R)$, where $\alpha \equiv 1/T$, and $\varPhi =\varPhi (r_+,r_-,R)$ are needed (see [18]). The relevant expressions are simpler in terms of the redshift function of the shell, given by

$$\begin{aligned} k&=\sqrt{1-\frac{2m}{R}-\frac{Q^2}{R^2}}, \end{aligned}$$

which is to be understood as $k=k(r_+,r_-,R)$. In particular, Eq. (7) can be rewritten as

$$\begin{aligned} p(r_+,r_-,R)&=\frac{R^2(1-k)^2-r_+\,r_-}{16\pi R^3k}. \end{aligned}$$

(27)

The temperature and the electric potential must satisfy integrability conditions in order to guarantee that the differential of the entropy is exact. Such conditions imply that $\alpha$ and $\varPhi$ can be written as [18]

$$\begin{aligned} \alpha (r_+,r_-,R)&=b(r_+,r_-)k, \end{aligned}$$

(28)

$$\begin{aligned} \varPhi (r_+,r_-,R)&=\frac{c(r_+,r_-)-\frac{1}{R}}{k}\sqrt{{r_+r_-}}, \end{aligned}$$

(29)

where $b(r_+,r_-)$ and $c(r_+,r_-)$ are arbitrary functions of $r_+$ and $r_-$. Using these equations, as well as $M=R(1-k)$ and $A=4\pi R^2$ in the first law given in Eq. (26), it follows that

$$\begin{aligned} dS&=b(r_+,r_-)\frac{1-c(r_+,r_-)\,r_-}{2}dr_+ \nonumber \\&\quad +b(r_+,r_-)\frac{1-c(r_+,r_-)\,r_+}{2}dr_-. \end{aligned}$$

(30)

For dS to be an exact differential, the following condition must be satisfied:

$$\begin{aligned} \frac{\partial b}{\partial r_-}(1-c\,r_- )-\frac{\partial b}{\partial r_+}(1-c\,r_+ )&=\frac{\partial c}{\partial r_-}b\,r_--\frac{\partial c}{\partial r_+}b\,r_+. \end{aligned}$$

(31)

This equation shows that either b or c should be specified to determine the entropy.³ We shall set

$$\begin{aligned} b&=\gamma \frac{{{ {r_+}}}^{a+1}}{{ {r_+}}-{ {r_-}}}, \end{aligned}$$

(32)

where $\gamma$ is an arbitrary constant. Such a choice leads to $c=1/r_+$, and

$$\begin{aligned} {S}=\gamma \frac{ { {r_+}}^{a+1}}{a+1}+S_0. \end{aligned}$$

(33)

This expression for the entropy of the shell coincides with the entropy of a Reissner-Nordstrom black hole when $a=1$ and the shell is taken to its gravitational radius (in which case the parameter $\gamma$ must take the value $\frac{4\pi }{\hbar }$) [18].

The regions of thermodynamical stability in the space of independent variables $\{M, A,Q\}$ (with $A=\pi R^2$) are determined by the conditions (see Appendix B of [18])

$$\begin{aligned}&\left( \frac{\partial ^2 S}{\partial M^2}\right) _{A,Q} \le 0, \end{aligned}$$

(34a)

$$\begin{aligned}&\left( \frac{\partial ^2 S}{\partial A^2}\right) _{M,Q} \le 0,\end{aligned}$$

(34b)

$$\begin{aligned}&\left( \frac{\partial ^2 S}{\partial Q^2}\right) _{M,A} \le 0,\end{aligned}$$

(34c)

$$\begin{aligned}&\left( \frac{\partial ^2 S}{\partial M^2}\right) \left( \frac{\partial ^2 S}{\partial A^2}\right) -\left( \frac{\partial ^2 S}{\partial M\partial A}\right) ^2 \ge 0,\end{aligned}$$

(34d)

$$\begin{aligned}&\left( \frac{\partial ^2 S}{\partial A^2}\right) \left( \frac{\partial ^2 S}{\partial Q^2}\right) -\left( \frac{\partial ^2 S}{\partial A\partial Q}\right) ^2 \ge 0,\end{aligned}$$

(34e)

$$\begin{aligned}&\left( \frac{\partial ^2 S}{\partial M^2}\right) \left( \frac{\partial ^2 S}{\partial Q^2}\right) -\left( \frac{\partial ^2 S}{\partial M\partial Q}\right) ^2 \ge 0,\end{aligned}$$

(34f)

$$\begin{aligned}&\left( \frac{\partial ^2 S}{\partial M^2}\right) \left( \frac{\partial ^2 S}{\partial Q\partial A}\right) - \left( \frac{\partial ^2 S}{\partial M\partial A}\right) \left( \frac{\partial ^2 S}{\partial M\partial Q}\right) \ge 0, \end{aligned}$$

(34g)

which ensure that the entropy does not increase due to inhomogeneities of the state variables.

Since we are assuming that the mass and the charge are related through $Q=\beta M$, the stability conditions are to be determined for S(M, A, Q(M)). The calculations can be carried out in parallel to what was done in [18], namely imposing that $d^2S\ge 0$ with $dS=0$, and adding the condition $Q=\beta M$, or by defining

$$\begin{aligned} h(M,A,Q)&=S(M,A,Q)-\lambda (Q-\beta M), \end{aligned}$$

(35)

where $\lambda$ is a Lagrange multiplier, and using the corresponding Hessian determinant. In either case, the ensuing conditions for thermodynamical stability are

$$\begin{aligned}&S_{MM}+2\beta S_{MQ}+\beta ^2 S_{QQ}\le 0, \end{aligned}$$

(36a)

$$\begin{aligned}&S_{AA}< 0, \end{aligned}$$

(36b)

$$\begin{aligned}&S_{AA}\left( S_{MM}+2\beta S_{MQ}+\beta ^2S_{QQ}\right) \nonumber \\&\quad -\left( S_{MA}+\beta S_{AQ}\right) ^2\ge 0 . \end{aligned}$$

(36c)

The conditions for dynamical and thermodynamical stability obtained above will be applied next to the zero charge case, which was presented in [23] using different variables.

5 Stability of the uncharged shell

Let us revisit the case of zero charge discussed in [23]. The relevant equations from Sect. 2 for $\beta =0$ are

$$\begin{aligned} M&={\frac{4{x}^{2}}{\pi \sigma \, \left( 4\,x+1 \right) ^{2}}},\end{aligned}$$

(37)

$$\begin{aligned} R&={\frac{x}{\pi \sigma \, \left( 4\,x+1 \right) }}, \end{aligned}$$

(38)

$$\begin{aligned} m&=4\,{\frac{{x}^{2} \left( 2\,x +1 \right) }{\pi \, \sigma \, \left( 4\,x+1 \right) ^{3}}}. \end{aligned}$$

(39)

It follows that the compactness parameter C is

$$\begin{aligned} C&=\frac{4x}{4x+1}. \end{aligned}$$

Notice that this expression is universal in the sense that it describes all the equilibrium states of the shell for any barotropic EOS, parameterized as $p=x\sigma$.

The condition for dynamical stability is $\varOmega _{20}\ge \varOmega _{20c}$, where

$$\begin{aligned} \varOmega _{20c}&=\frac{1}{2} \frac{x(8x^2+8x+3)}{(x+1)}, \end{aligned}$$

an equation which is also valid for any barotropic EOS.

Let us consider the barotropic EOS given by $P=\sigma ^n$ (using dimensionless quantities, the asterisks will be omitted to avoid clumsy notation). From the definition of $\varOmega _{20}$ and $\varOmega _{20}\ge \varOmega _{20c}$ it follows that

$$\begin{aligned} n&\ge \frac{8x^2+8x+3}{2(x+1)}, \end{aligned}$$

(40)

so, for a given n, this equality determines the critical value $x_c$ at which the stability changes. In terms of C,

$$\begin{aligned} n&\ge \frac{3C^2-8C+6}{(3C-4)(C-1)}. \end{aligned}$$

(41)

The matter on the shell satisfies the weak energy condition. We shall only consider in what follows configurations that also satisfy the dominant energy condition (DEC), namely $p\le \sigma$, or $x\le 1$. For the zero charge case, the DEC leads to the existence of a maximum value of C, given by $C=4/5$, and $3/2<n$ (from Eq. (40)).

Regarding the thermodynamical stability, the relevant conditions are $dS=0$ and $d^2S\le 0$. The first condition is satisfied for any isolated system, such as the shell under consideration. The second one leads to the following inequalities

$$\begin{aligned}&\left( \frac{\partial ^2 S}{\partial M^2}\right) _{A} \le 0,\end{aligned}$$

(42a)

$$\begin{aligned}&\left( \frac{\partial ^2 S}{\partial A^2}\right) _{M} \le 0,\end{aligned}$$

(42b)

$$\begin{aligned}&\left( \frac{\partial ^2 S}{\partial M^2}\right) \left( \frac{\partial ^2 S}{\partial A^2}\right) -\left( \frac{\partial ^2 S}{\partial M\partial A}\right) ^2 \ge 0, \end{aligned}$$

(42c)

Using the entropy given in Eq. (33), these inequalities yield restrictions on the (x, a) plane, which were found in [21] in terms of the redshift k and a. It turns out that Eq. (42c) sets the most stringent limits on the possible values of x and a, yielding

$$\begin{aligned} a&\le \frac{4x(2x+1)}{8x^2+8x+3}. \end{aligned}$$

(43)

In terms of C,

$$\begin{aligned} a&\le \frac{C(2-C)}{3C^2-8C+6}. \end{aligned}$$

(44)

The curve $a=a(C)$ obtained from the equality in the previous expression separates the thermodynamically stable states from the unstable ones. The equations determining the dynamical and thermodynamical stability, Eqs. (40) and (44) respectively, will be used in non-zero charge case to check the limit $\beta =0$, see next section.

6 Stability of the charged shell

The relevant equations from Sect. 2 are

$$\begin{aligned} M&={\frac{4{x}^{2}}{\pi \sigma \, \left( 1-\beta ^{2}+4\,x \right) ^{2}}},\end{aligned}$$

(45)

$$\begin{aligned} R&={\frac{x}{\pi \sigma \, \left( 1-\beta ^{2}+4\,x \right) }},\end{aligned}$$

(46)

$$\begin{aligned} m&=\frac{4{x}^{2}}{\pi \, \sigma \,} \frac{ (1-\beta ^2)(1-2x)+4\,x }{ \left( 1-\beta ^{2}+4\,x \right) ^{3}}. \end{aligned}$$

(47)

It follows that

$$\begin{aligned} C&=\frac{4x}{1-\beta ^2+4x}. \end{aligned}$$

(48)

The maximum value for x imposed by the DEC is $x=1$, which in turn, from Eq. (48), yields the maximum value of C as a function of $\beta$

$$\begin{aligned} C_\mathrm{m}(\beta )&=\frac{4}{5-\beta ^2}. \end{aligned}$$

(49)

For the marginal stability, Eq.  (25) in terms of x reads

$$\begin{aligned} \varOmega _{20c}&=\frac{x}{2}\, \frac{3(1-\beta ^2)+8x^2+8x}{(1-\beta ^2)(x+1)}. \end{aligned}$$

(50)

In terms of C,

$$\begin{aligned} \varOmega _{20c}&=\frac{C(1-\beta ^2)}{ 4}\, \frac{C^2(\beta ^2-3)+8C+6}{[C(\beta ^2+3)-4]\,(C-1)^2}. \end{aligned}$$

(51)

This equation defines a surface in terms of $\beta$ and C, such that the dynamically stable configurations are those that satisfy $\varOmega _{20}>\varOmega _{20c}$. Let us from now on restrict to the case of a barotropic EOS given by $P=\sigma ^n$. Combining $\varOmega _{20}=nx$ and Eq. (50), the curve that separates stability from instability is

$$\begin{aligned} \beta ^2&=\frac{2(x+1)(n-4x)-3}{2n(x+1)-3}. \end{aligned}$$

(52)

For each n, the stable configurations are those below the curve $\beta ^2=\beta ^2(x,n)$. The condition $\beta ^2\le 1$ is achieved if and only if $n>\frac{3}{2(x+1)}$, while the numerator of Eq. (52) is positive if and only if $n>\frac{3}{2(x+1)}+4x$. It follows that the potential divergences due to the denominator of Eq. (52) are excluded. Note that n must be larger than 3/2, since the latter is permitted only with $x=0$ (leading to $\beta ^2=0$). There is one more restriction to be imposed, namely, that the velocity of sound $c_s^2=\left. \frac{dp}{d\rho }\right| _0$ be less than one. In the case of a polytropic EOS, $c_s^2=nx$. Hence, for a given n, there is an upper limit for x, given by $x<\frac{1}{n}$, that actually supersedes the DEC condition, since $n>\frac{3}{2}$. Consequently, the maximum value of C allowed by the condition on $c_s^2$ is obtained from Eq. (48):

$$\begin{aligned} C_\mathrm{max}(n,\beta )&=\frac{4}{4+n(1-\beta ^2)}, \end{aligned}$$

(53)

and it is easily seen that it supersedes that given in Eq. (49). Hence, the states allowed by $c_s^2< 1$ are those that satisfy

$$\begin{aligned} \beta ^2&> 1+\frac{4(C-1)}{Cn}. \end{aligned}$$

The regions of dynamical stability in the $(\beta ,C)$ plane, determined using Eqs. (48), (52), and (53) are shown in Fig. 1 for different values of the polytropic index n. They grow with n (i.e. as matter gets “stiffer”), and for any given n, they shrink when the charge grows.⁴ The condition on $c_s$ restricts the region of dynamically stable states only for $n \gtrapprox 2.614795$. Notice also that highest value of C is reached for $\beta =0$ for any value of n (in fact, the results in this case are in agreement with those presented in [23]).

Fig. 1

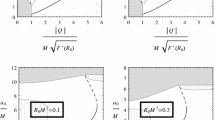
The figures show the regions of dynamical stability (in green) in the $(C,\beta )$ plane for different values of n, as well as the region excluded by $c_s\ge 1$ (the curve, Eq. (53), and the region below it)

Fig. 2

Points in the plane $\beta \times C$ satisfying inequalities (36a)–(36c) for $a=0.3$. The grey dots are those that satisfy inequalities (36a) (upper left), (36b) (upper right), and (36c) (lower left). The orange dots represent their intersection, which coincides with inequality (36c). The curve in the last panel follows from the condition $c_s=1$ (see Eq. (53)). Points $C_1$ and $C_2$ in the axis $\beta =0$ correspond to the values obtained from Eqs. (3.5) and (3.7) of [21]. $C_2$ is also obtained from Eq. (44)

Let us now analyze the restrictions imposed by thermodynamical stability, which follow from Eqs. (36a)–(36c), and the expression for the entropy, given in Eq. (33). They lead to inequalities involving a, $\beta$, and C, which we shall represent in the $(C,\beta )$ plane for different values of a. Fig. 2 shows that for $a=0.3$ the more restrictive condition is the one that follows from inequality (36c), as in the zero charge case [21]. This is actually the case for all the values of a explored here. It is also seen that the inequality linked to the area, Eq. (36b), leads to no restrictions. In fact, we have checked that Fig. 2 is representative of the behaviour of the area filled with thermodynamically stable states for any value of a, the only change being that for very low values of a, the border of the orange area moves to the left (practically all states are thermodinamicaly stable for very small a, as is the case for the zero charge shell), and for large a, the border moves to the right, keeping in both cases its shape.⁵ Points $C_1$ and $C_2$ in the plots correspond to the value of C for zero charge and a given a, which are given by Eqs. (3.5) and (3.7) of [21]. In particular, $C_2$ follows also from Eq. (44). Let us see now the restrictions imposed by the two kinds of stability together.⁶ Figures 1 and 2 show that the existence of nonzero charge states that are completely stable is determined by the condition $C(n)\ge C(a)$, where C(n) is the maximum C for dynamical stability, fixed n, and zero charge, and C(a), the minimum C for thermodynamical stability, fixed a and zero charge. The figures suggest that the curve that follows from the restriction $c_s< 1$ may exclude part of either the thermodynamically stable states, or the dynamically ones. This will be confirmed by the examples shown below.

The equation $C(n)=C(a)$, which follows from Eqs. (41) and (44) implicitly defines the curve $n=n(a)$ in such a way that those states with zero charge and satisfying

$$\begin{aligned} n&\ge n(a), \end{aligned}$$

(54)

are completely stable. The region defined by Eq. (54) is displayed in Fig. 3. The limits on the parameters are $\frac{3}{2}\le n$, and $0<a<\frac{12}{19}$. Notice that a point in the (a, n) diagram actually defines an interval of configurations with $C\in [C(a),C_\mathrm{max}(n)]$, given respectively by Eqs. (41) and (44). For instance, for $A=(0.1,3)$, $C\in [0.253,0.654]$. Taking into account the restriction coming from $c_s< 1$, see Eq. (53), the allowed values of C for the point A are in the interval [0.253, 0.571] (see the $\beta =0$ axis in Fig. 4).

Fig. 3

The coloured region corresponds to the configurations with $\beta =0$ that are completely stable. Its border is given by Eq. (54). Points $A=(0.1,3)$ and $B=(0.32,2)$ will be used as examples in Figs. 4 and 5 respectively

For any given configuration that is completely stable for zero charge, there are charged configurations that are also completely stable. Figure 4 shows the dynamically stable states (those in the green region) and the thermodynamically stable states (in the orange region), for point $A=(0.1,3)$ in Fig. 3. We see that the area of stable states is reduced on both the dynamical and the thermodynamical sides when $\beta$ grows, the reduction in the latter being more pronounced. Also shown is the curve corresponding to $c_s=1$ (the points below which are excluded). Figure 5 shows the relevant regions for point $B=(0.32,2)$ of Fig. 3, which is outside the region of complete stability in the case of zero charge. There are no completely stable states for nonzero charge, in agreement to what was presented above. Figure 6 corresponds to the values $n=4$, $a=0.285$, and shows a case in which most of the region of completely stable states is excluded by the restriction $c_s< 1$. In fact, for larger values of a, all the completely stable states are excluded by such condition (see Fig. 7).

Fig. 4

The figure shows the region of dynamically stable states (in green) and that of thermodynamically stable states (in orange) for the parameters n and a of the completely stable uncharged state $A=(0.1,3)$ in Fig. 3. The intersection of both regions (minus the set of states below the curve corresponding to $c_s = 1$) yields the completely stable states as a function of $\beta$

Fig. 5

The figure shows the region of dynamically stable states (in green) and that of thermodynamically stable states (in orange) for the parameters n and a of the the unstable point $B=(0.32,2)$ in Fig. 3. There is no region of complete stability

Fig. 6

The figure displays a case in which only a small part of the completely stable region is allowed by the condition $c_s < 1$

Fig. 7

The figure shows a case in which all the completely stable states are excluded by the condition $c_s < 1$

Fig. 8

The figures shows the $m\times C$ curves for $n=2$, $\beta =0$, 0.5, 0.85 and $a=0.15$, together with the regions of different stabilities as well as the region excluded by $c_s\ge 1$. The dot represents the maximum of the curve. The different regions on each curve were defined from the limiting compactness C obtained in Fig. 9 fixing the value of $\beta$

Fig. 9

The figure show the values of compactness C associated to the border of each region of stability and, below the curve, of the region with $c_s\ge 1$. The values of $\beta$ used in Fig. 8 are represented here by horizontal dashed lines

Figure 8 shows the $m\times C$ curves for $n=2$ and $\beta =0$, 0.5 and 0.85, with $a=0.15$, with the dimensionless m given by Eq. (47) where $\sigma$ has been rendered dimensionless using the parameters of the EOS. The figure also shows the regions of different stabilities of the equilibrium configurations, as well as the region excluded by the condition $c_s\ge 1$. The different regions of stability were obtained from the limiting values of compactness C taken from Fig. 9 for each value of $\beta$, represented by the horizontal dashed lines in the latter figure. The dot on each curve in Fig. 8 represents the maximum. The point that separates the dynamically stable states from the unstable ones coincides with the maximum of the curve only for $\beta =0$. It can be seen from Fig. 9 that, starting with $\beta =0$, when $\beta$ becomes higher the border of the region of dynamical stability moves to the left whereas the border of the region of thermodynamical stability moves to the right, thus reducing the region of complete stability, until it disappears altogether. This behavior is reflected in the $m\times C$ curves in Fig. 8. Due to the Coulomb repulsion present for $\beta \ne 0$ and acts against gravity, the maximum value of m grows with $\beta$. The same behavior of the $m\times C$ curves is obtained for other values of n and a.

7 Conclusions

We have presented a complete analysis of the dynamical and thermodynamical equilibrium of a charged thin shell in which the mass and the charge are related by $Q=\beta M$. For a barotropic EOS (parameterized by the index n) and a given form of the entropy (with parameter a), each kind of stability is determined by a given set of inequalities, which can be represented by regions in the $(C,\beta )$ plane, for any pair (n, a). The states that are completely stable belong to the intersection of such regions, taking into account the restriction that follows from $c_s< 1$. We have shown that the existence of the intersection actually follows from the zero charge case, and that the condition $c_s< 1$ is more restrictive than the imposition of the dominant energy condition. In fact, for some values of the parameters n and a, the former may even exclude all the states in the intersection. Our results show that for relatively low values of n and a, the region of completely stable states is rather large, and the condition $c_s< 1$ is not very restrictive, while already for moderate values of n and a, it is the condition on $c_s$ that limits the size of the region, leading ultimately to the non-existence of completely stable states.

To summarize, we have shown that the dynamical and thermodynamical stability, along with the condition $c_s<1$ can lead to strong restrictions on the equilibrium states of a charged shell, and even to the nonexistence of completely stable states. The application of the formalism presented here to the case of rotating shells (the thermodynamical stability of which was studied in [17]), and to shells in which Q and M are independent parameters is left for future work.