Impact of jet-production data on the next-to-next-to-leading-order determination of HERAPDF2.0 parton distributions

Abstract

The HERAPDF2.0 ensemble of parton distribution functions (PDFs) was introduced in 2015. The final stage is presented, a next-to-next-to-leading-order (NNLO) analysis of the HERA data on inclusive deep inelastic ep scattering together with jet data as published by the H1 and ZEUS collaborations. A perturbative QCD fit, simultaneously of $\alpha _s(M_Z^2)$ and the PDFs, was performed with the result $\alpha _s(M_Z^2)= 0.1156 \pm 0.0011~\mathrm{(exp)}~ ^{+0.0001}_{-0.0002}~ \mathrm{(model}$ $\mathrm{+ parameterisation)}~ \pm 0.0029~\mathrm{(scale)}$. The PDF sets of HERAPDF2.0Jets NNLO were determined with separate fits using two fixed values of $\alpha _s(M_Z^2)$, $\alpha _s(M_Z^2)=0.1155$ and 0.118, since the latter value was already chosen for the published HERAPDF2.0 NNLO analysis based on HERA inclusive DIS data only. The different sets of PDFs are presented, evaluated and compared. The consistency of the PDFs determined with and without the jet data demonstrates the consistency of HERA inclusive and jet-production cross-section data. The inclusion of the jet data reduced the uncertainty on the gluon PDF. Predictions based on the PDFs of HERAPDF2.0Jets NNLO give an excellent description of the jet-production data used as input.

1 Introduction

Data from deep inelastic scattering (DIS) of electrons¹ on protons, ep, at centre-of-mass energies of up to $\sqrt{s} \approx 320\,$GeV recorded at HERA, have been central to the exploration of proton structure and quark–gluon dynamics as described by perturbative Quantum Chromodynamics (pQCD) [1]. The combination of H1 and ZEUS data on inclusive ep scattering and the subsequent pQCD analysis, introducing the ensemble of parton density functions (PDFs) known as HERAPDF2.0, were milestones in the exploitation [2] of the HERA data. These analyses are based on pQCD fits to the HERA DIS data in the DGLAP [3,4,5,6,7] formalism using the $\overline{\mathrm{MS}}$ scheme [8].

The sets of PDFs presented in this work complete the HERAPDF2.0 ensemble [2] of PDFs. They were determined with a next-to-next-to-leading-order (NNLO) analysis of HERA inclusive DIS data [2] and selected jet-production data as published separately by the H1 and ZEUS collaborations [9,10,11,12,13,14]. An analysis of jet data at NNLO was not feasible at the time of the introduction of the HERAPDF2.0 ensemble but has become possible by the recent provision of jet cross-section predictions for ep scattering at NNLO [15,16,17,18,19,20,21,22,23].

The strategy chosen for the analysis presented here follows that of the previous HERAPDF2.0Jets NLO analysis [2]. First, the jet cross-section data were included in the pQCD analysis to constrain the gluon PDF. Since the gluon PDF is correlated with the value of the strong coupling constant, $\alpha _s(M_Z^2)$, a simultanous fit of the PDFs and $\alpha _s(M_Z^2)$ was performed. Subsequently, the resulting $\alpha _s(M_Z^2)$ was used to refit the PDFs with $\alpha _s(M_Z^2)$ fixed to this value. In this way, the uncertainties of the PDFs at this value of $\alpha _s(M_Z^2)$ were determined. The PDFs were also determined for the conventional fixed value of $\alpha _s(M_Z^2)=0.118$.

The calculation of jet cross sections at NNLO is based on jets constructed from massless partons. The inclusive data, on the other hand, are treated within the variable flavour number scheme (VFNS) RTOPT [24,25,26], which requires values of the parameters for the charm- and beauty-quark masses, $M_c$ and $M_b$, as input. These parameters were optimised via QCD fits using both the inclusive data and the cross sections for charm and beauty production that were published as combined data by the H1 and ZEUS collaborations [27]. However, the heavy-quark data were not explicitly included in the pQCD fits that included jet data.

The results presented here are based entirely on HERA data, i.e. inclusive DIS and jet-production data. The HERA inclusive data are a single, consistent data set, taking all systematic uncertainties into account. The jet and inclusive data have been found to be consistent in the framework of an NLO [2] and an NNLO [28] analysis. The analysis presented here also tests this consistency at NNLO. The HERAPDF2.0 ensemble of PDFs provides a benchmark to which PDFs including data from the LHC collider may be compared. Such comparison is sensitive to Beyond Standard Model effects or the need for an extension of the QCD analyses for some processes.

Table 1 The jet-production data sets from H1 and ZEUS used for the HERAPDF2.0Jets NNLO fits. The data were used as published by the collaborations. The term normalised indicates that these cross sections are normalised to the respective neutral current inclusive cross sections

Table 2 Central values of model input parameters and their one-sigma variations. It was not possible to implement the variations marked $^*$ because $\mu _{\mathrm{f0}} < M_c$ is required, see Sect. 3.3. In these cases, the uncertainty on the PDF obtained from the other variation was symmetrised

2 Data

Data taken by the H1 and ZEUS collaborations from 1993 to 2007 were combined to form a consistent set of inclusive HERA ep DIS cross sections [2] taking all systematic uncertainties into account. This set of data was already used as input to the determinations of all previous members of the HERAPDF2.0 ensemble. The HERAPDF2.0Jets analysis at NLO, in addition, used selected data [9,10,11,12,13] on inclusive jet and dijet production from H1 and ZEUS. These data were also used for the present analysis at NNLO. In addition, new data published by the H1 collaboration on jet production [14] were added as input to the present NNLO analysis. These data reach to lower $Q^2$, where $Q^2$ is the squared four-momentum-transfer in the DIS process, and also provide six new high-$Q^2$ points at low $p_{\mathrm{T}}$, where $p_{\mathrm{T}}$ is the transverse momentum of the jet. For all data sets used in the analysis, massless jets were identified with the $k_{\mathrm{T}}$ algorithm with the R parameter set to one. A summary of these data sets is provided in Table 1. All experimental correlations provided by H1 and ZEUS were carefully taken into account as in the previous analysis [2].

The predictions for inclusive jet and dijet production at NNLO were used for a slightly reduced phase space compared to HERAPDF2.0Jets NLO in order to limit the NNLO scale, $\mu$, uncertainties of the theoretical predictions to below 10 %. Jets from the inclusive-jet data with $\mu ^2 = ( p_{\mathrm{T}}^2 + Q^2) \le (10.0$ GeV$)^2$ and dijets with $\mu ^2 = (\langle p_{\mathrm{T}} \rangle _2^2 + Q^2) \le (10.0$ GeV$)^2$, where $\langle p_{\mathrm{T}} \rangle _2$ is the average of the transverse momenta of the two jets, were excluded. These requirements on $\mu$ also ensure that $\mu$ is larger than the b-quark mass, which is necessary because the jets are built from massless partons in the calculation of the NNLO predictions. In addition, for each $Q^2$ interval, the six data points with the lowest $\langle p_{\mathrm{T}}\rangle _2$, were excluded from the ZEUS dijet data set. Due to the kinematic cuts applied for the selection of dijet events, the Born-level dijet contribution vanishes in these bins. Consequently, the NNLO theory predictions for dijet production amount only to NLO accuracy here. The resulting reduction of data points is detailed in Table 1. Furthermore, the trijet data [13], which were used for HERAPDF2.0Jets NLO, were excluded as NNLO theory predictions for trijet production were not available. The theoretical predictions for the neutral current inclusive cross sections used for normalisation² were computed with the same code and theoretical settings used for the analysis of the inclusive data.

Since complete NNLO predictions were not available for heavy quarks, the inclusive charm data [29], which were included in the analysis at NLO [2], were not explicitly used in the PDF fits of the analysis presented here. Heavy-quark data [27] were used only to optimise the mass parameter values for charm, $M_c$, and beauty, $M_b$, which are required as input to the adopted RTOPT [26] NNLO approach to the fitting of the inclusive data.

3 QCD analysis

The present analysis was performed in the same way as all previous HERAPDF2.0 analyses [2]. Only cross sections for $Q^2 \ge Q^2_{\mathrm{min}}$, with $Q^2_{\mathrm{min}} = 3.5$ GeV$^2$, were used in the analysis. The $\chi ^2$ definition was taken from equation (32) of the previous paper [2]. The value of the starting scale for the DGLAP evolution was taken as $\mu _{\mathrm{f0}}^2 = 1.9$ GeV$^2$. The parameterisation of the PDFs and the choice of free parameters also followed the prescription for the HERAPDF2.0Jets NLO analysis, see Sect. 3.1.

All fits were performed using the program QCDNUM [30] within the xFitter (formerly HERAFitter) framework [31] and were cross-checked with an independent program, which was already used for cross-checks in the HERAPDF2.0 analysis. The results obtained using the two programs were in excellent agreement. All numbers presented here were obtained using xFitter. The light-quark coefficient functions were calculated in QCDNUM. The heavy-quark coefficient functions were calculated in the VFNS RTOPT [24], with recent modifications [25, 26], see Sect. 3.3.

The present analysis was made possible by the newly available calculation of jet-production cross sections at NNLO [15,16,17,18,19,20,21,22,23] using the zero-mass scheme. This is expected to be a reasonable approximation when the relevant QCD scales are significantly above the charm- and beauty-quark masses. The jet data were included in the fits at full NNLO using predictions for the jet cross sections calculated using NNLOJET [15,16,17], which was interfaced to the fast grid-interpolation codes, fastNLO [18,19,20] and APPLgrid [21, 22] using the APPLfast framework [23], in order to achieve the required speed for the convolutions needed in an iterative PDF fit. The NNLO jet predictions were provided in the massless scheme and were corrected for hadronisation and $Z^0$ exchange before they were used in the fits. A running electromagnetic $\alpha$ as implemented in the 2012 version of the programme EPRC [32] was used in the treatment of the jet cross sections. The predictions included estimates of the numerical precision, which were taken into account in all fits as 50% correlated and 50% uncorrelated between processes and bins. These uncertainties are very small, typically between 0.5 and 1.0%.

The choice of scales for the jet data had to be adjusted for the NNLO analysis. At NLO, the factorisation scale was chosen as for the inclusive data, i.e. $\mu _{\mathrm{f}}^2 = Q^2$, while the renormalisation scale was linked to the transverse momenta, $p_{\mathrm{T}}$, of the jets as $\mu _{\mathrm{r}}^2 = (Q^2 + p_{\mathrm{T}}^2)/2$. For the NNLO analysis, $\mu _{\mathrm{f}}^2 =\mu _{\mathrm{r}}^2= Q^2 + p_{\mathrm{T}}^2$ was used for inclusive jets and $\mu _{\mathrm{f}}^2 =\mu _{\mathrm{r}}^2= Q^2 + \langle p_{\mathrm{T}} \rangle _2^2$ for dijets. These changes resulted in improved $\chi ^2$ values for the fits, confirming previously published studies [33]. Scale variations were also considered and are discussed in Sects. 4.1 and 4.2. In general, scale variations are used to estimate the uncertainties due to missing higher-order contributions.

3.1 Choice of PDF parameterisation and model parameters

The choice of parameterisation follows the original concept of HERAPDF2.0, for which all details have been previously published [2]. The parameterisation is an effective way to store the information derived from many data points in a limited set of numbers. The parameterised PDFs, xf(x), are the gluon distribution xg, the valence-quark distributions $xu_v$, $xd_v$, and the u-type and d-type anti-quark distributions $x{\bar{U}}$, $x{\bar{D}}$, where $x{\bar{U}} = x{\bar{u}}$ and $x{\bar{D}} = x{\bar{d}} +x{\bar{s}}$ at the chosen starting scale. The generic form of the parameterisation for a PDF f(x) is

$$\begin{aligned} xf(x) = A x^{B} (1-x)^{C} (1 + D x + E x^2). \end{aligned}$$

(1)

For the gluon PDF, an additional term of the form $A_g'x^{B_g'}(1-x)^{C_g'}$ is subtracted.³

Not all the D and E parameters were required in the fit. The so-called $\chi ^2$ saturation method [2, 34] was used to reject redundant parameters. Initially, all D and E parameters as well as $A_g'$ were set to zero. Extra parameters were introduced one at a time until the $\chi ^2$ of the fit could not be further improved. This resulted in a final parameterisation

$$\begin{aligned} xg(x)= & {} A_g x^{B_g} (1-x)^{C_g} - A_g' x^{B_g'} (1-x)^{C_g'} , \end{aligned}$$

(2)

$$\begin{aligned} xu_v(x)= & {} A_{u_v} x^{B_{u_v}} (1-x)^{C_{u_v}}\left( 1+E_{u_v}x^2 \right) , \ \end{aligned}$$

(3)

$$\begin{aligned} xd_v(x)= & {} A_{d_v} x^{B_{d_v}} (1-x)^{C_{d_v}} , \end{aligned}$$

(4)

$$\begin{aligned} x{\bar{U}}(x)= & {} A_{{\bar{U}}} x^{B_{{\bar{U}}}} (1-x)^{C_{{\bar{U}}}}\left( 1+D_{{\bar{U}}}x\right) , \end{aligned}$$

(5)

$$\begin{aligned} x{\bar{D}}(x)= & {} A_{{\bar{D}}} x^{B_{{\bar{D}}}} (1-x)^{C_{{\bar{D}}}}. \end{aligned}$$

(6)

The normalisation parameters, $A_g, A_{u_v}, A_{d_v}$, were constrained by the quark-number and momentum sum rules. The B parameters, $B_{{\bar{U}}}$ and $B_{{\bar{D}}}$, were set equal, resulting in a single B parameter for the sea distributions.

The strange-quark distribution was expressed as an x-independent fraction, $f_s$, of the d-type sea, $x{\bar{s}}= f_s x{\bar{D}}$ at the starting scale $\mu _{\mathrm{f0}}$. The value $f_s=0.4$ was chosen to be a compromise between the suppressed strange sea seen in neutrino-induced di-muon production [35, 36] and the unsuppressed strange sea seen by the ATLAS collaboration [37]. The further constraint $A_{{\bar{U}}}=A_{{\bar{D}}} (1-f_s)$, together with the requirement $B_{{\bar{U}}}=B_{{\bar{D}}}$, ensured that $x{\bar{u}} \rightarrow x{\bar{d}}$ as $x \rightarrow 0$.

The final parameterisation together with the constraints became the basis of the 14-parameter fit which was used throughout the analysis. The parameterisation is identical to the parameterisation used previously for the analysis of the inclusive data [2].

3.2 Model and parameterisation uncertainties

Model and parameterisation uncertainties on the PDFs were evaluated by using fits with modified input assumptions. The central values of the model parameters and their variations are summarised in Table 2. The uncertainties on the PDFs obtained from variations of $M_c$, $M_b$, $f_s$ and $Q^2_{\mathrm{min}}$ were added in quadrature, separately for positive and negative uncertainties, and represent the model uncertainty.

The symmetrised uncertainty obtained from the downward variation of $\mu ^2_{\mathrm{f0}}$ from 1.9 to 1.6 GeV$^2$, see also Sect. 3.3, was taken as a parameterisation uncertainty. In addition, a variation of the number of terms in the polynomial $(1 + D x + E x^2)$ was considered for each of the parton distributions listed in Eqs. (2)–(6). For this, all 15-parameter fits which have one more non-zero free D or E parameter were considered as possible variants and the resulting PDFs compared to the PDF from the 14-parameter central fit. The only visible change in the shapes of the PDFs was observed for the addition of a $D_{u_v}$ parameter. The maximal deviation of the fit at each x value was considered an uncertainty, forming an envelope around the central fit.

3.3 Optimisation of $M_c$ and $M_b$

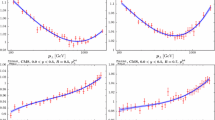
The RTOPT scheme used to calculate predictions for the inclusive data requires the charm- and beauty-mass parameters, $M_c$ and $M_b$, as input. As new combined HERA data on heavy-quark production [27] became available, the optimal values of these mass parameters were reevaluated. The previously established procedure [2, 34] was applied to these new heavy quark data together with the combined inclusive data [2]. The procedure comprises multiple pQCD fits with varying choices of the $M_c$ and $M_b$ parameters. The parameter values resulting in the lowest $\chi ^2$ values of the fit were chosen. This was done both at NNLO and NLO to provide consistent sets of $M_c$ and $M_b$ for future pQCD analyses. The uncertainties of the mass parameters were determined by fitting the $\chi ^2$ values with a quadratic function and finding the mass-parameter values corresponding to $\Delta \chi ^2 = 1$.

At NNLO (NLO), the fits for the optimisation were performed with fixed values of $\alpha _s=0.1155$⁴ ($\alpha _s=0.118$).⁵ As a first iteration at NNLO (NLO), the mass parameter values used for HERAPDF2.0 NNLO (NLO) were used as fixed points, so that $M_c$ was varied with fixed $M_b = 4.5$ GeV (4.5 GeV) and $M_b$ was varied with fixed $M_c = 1.43$ GeV (1.47 GeV). In every iteration to determine $M_b$ ($M_c$), the mass-parameter value for $M_c$ ($M_b$) as obtained from the previous iteration was used as a new fixed point. The iterations were terminated once values stable to within 0.1% for $M_c$ and $M_b$ were obtained. The final $\chi ^2$ scans at NNLO are shown in Fig. 1a, c and at NLO in Fig. 1b, d. The resulting values at NNLO are $M_c = 1.41 \pm 0.04$ GeV and $M_b=4.20 \pm 0.10$ GeV, compatible with the values determined for HERAPDF2.0 NNLO, with slightly reduced uncertainties. The values at NLO are $M_c = 1.46 \pm 0.04$ GeV and $M_b=4.30 \pm 0.10$ GeV. The minimum in $\chi ^2$ for the parameter $M_c$ at NNLO is observed close to the technical limit of the fitting procedure, $\mu _{\mathrm{f0}} < M_c$. The model uncertainty due to $M_b$ was obtained by varying $M_b$ by its one-standard-deviation uncertainty. The same procedure was not possible for $M_c$ because the downward variation created a conflict with $\mu _{\mathrm{f0}}$, which has to be less than $M_c$ in the RTOPT scheme, in order that charm can be generated perturbatively. Thus, only an upward variation of $M_c$ was considered and the resulting uncertainty on the PDFs was symmetrised. In addition, this requirement of $\mu _{\mathrm{f0}} < M_c$ created a conflict with the variation of $\mu _{\mathrm{f0}}^2$. The normal procedure would have included an upward variation of $\mu _{\mathrm{f0}}^2$ to 2.2 GeV$^2$ but $\mu _{\mathrm{f0}}$ would have become larger than the upper boundary of the uncertainty interval of $M_c$.⁶ Thus, $\mu _{\mathrm{f0}}^2$ was only varied downwards to 1.6 GeV$^2$, and, again, the resulting uncertainty on the PDFs was symmetrised. The continued suitability of the chosen central parameterisation was verified for the new settings for $M_c$ and $M_b$ using the $\chi ^2$ saturation method as described in Sect. 3.1.

3.4 Hadronisation uncertainties

For the jet-data analysis, it was also necessary to consider the effect of the uncertainties on hadronisation corrections. These, as determined for the original publications, were reviewed for this analysis. The H1 uncertainties were used as published; those for the ZEUS data were increased⁷ to the maximum value quoted in the publications, 2%. This change resulted in no significant difference to any of the results presented here.

Fig. 1

Difference between $\chi ^2$ and $\chi ^2_\mathrm{min}$ versus a $M_c$ for $M_b = 4.2$ GeV at NNLO with $\alpha _s(M_Z^2)=0.1155$, b $M_c$ for $M_b = 4.3$ GeV at NLO with $\alpha _s(M_Z^2)=0.118$, c $M_b$ with $M_c=1.41\,$GeV at NNLO with $\alpha _s(M_Z^2)=0.1155$, d $M_b$ with $M_c=1.46\,$GeV at NLO with $\alpha _s(M_Z^2)=0.118$

Fig. 2

Difference between $\chi ^2$ and $\chi ^2_\mathrm{min}$ versus $\alpha _s(M_Z^2)$ for HERAPDF2.0Jets NNLO fits with fixed $\alpha _s(M_Z^2)$. The result and all uncertainties determined for the HERAPDF2.0Jets NNLO fit with free $\alpha _s(M_Z^2)$ are also shown, added in quadrature

Fig. 3

Difference between $\chi ^2$ and $\chi ^2_\mathrm{min}$ versus $\alpha _s(M_Z^2)$ for a HERAPDF2.0Jets NNLO fits with fixed $\alpha _s(M_Z^2)$ with the standard $Q^2_\mathrm{min}$ for the inclusive data of 3.5 GeV$^2$ and $Q^2_\mathrm{min}$ set to 10 GeV$^2$ and 20 GeV$^2$. b For comparison, the situation for fits to only inclusive data, HERAPDF2.0 NNLO, is shown, taken from [2]

Fig. 4

The parton distribution functions $xu_v$, $xd_v$, xg and $xS=x(\bar{U}+\bar{D})$ of HERAPDF2.0Jets NNLO, with a $\alpha _s(M_Z^2)$ fixed to 0.1155 and b $\alpha _s(M_Z^2)$ fixed to 0.118, at the scale $\mu _\mathrm{f}^2 = 10$ GeV$^{2}$. The uncertainties are shown as differently shaded bands

Fig. 5

Comparison of the parton distribution functions a $xu_v$, b $xd_v$, c xg and d $xS=x(\bar{U}+\bar{D})$ of HERAPDF2.0Jets NNLO with fixed $\alpha _s(M_Z^2)= 0.1155$ and $\alpha _s(M_Z^2)= 0.118$, at the scale $\mu _\mathrm{f}^{2} = 10\,$GeV$^{2}$. The total uncertainties are shown as differently hatched bands

Fig. 6

Comparison of the parton distribution functions a $xu_v$, b $xd_v$, c xg and d $xS=x(\bar{U}+\bar{D})$ of HERAPDF2.0Jets NNLO with fixed $\alpha _s(M_Z^2)= 0.1155$ and $\alpha _s(M_Z^2)= 0.118$, at the scale $\mu _\mathrm{f}^{2} = M_Z^2$ with $M_Z=91.19$ GeV [38]. The total uncertainties are shown as differently hatched bands

Fig. 7

Comparison of the parton distribution functions $xu_v$, $xd_v$, xg and $xS=x(\bar{U}+\bar{D})$ of HERAPDF2.0Jets NNLO with HERAPDF2.0 NNLO based on inclusive data only, both with fixed $\alpha _s(M_Z^2)= 0.118$, at the scale $\mu _\mathrm{f}^{2} = 10\,$GeV$^{2}$. The uncertainties of HERAPDF2.0Jets NNLO are shown as differently shaded bands and the central value of HERAPDF2.0 NNLO is shown as a dotted line

Fig. 8

Comparison of the normalised uncertainties on the gluon PDFs of HERAPDF2.0Jets NNLO and HERAPDF2.0 NNLO, both for $\alpha _s(M_Z^2)= 0.118$ and at the scale $\mu _\mathrm{f}^{2} = 10\,$GeV$^{2}$, for a experimental (fit), b experimental plus model, c experimental plus parameterisation, d total uncertainties. The uncertainties on both gluon PDFs are shown as differently hatched bands

Fig. 9

Comparison of the normalised uncertainties on the gluon PDFs of HERAPDF2.0Jets NNLO and HERAPDF2.0 NNLO, both for $\alpha _s(M_Z^2)= 0.118$ and at the scale $\mu _\mathrm{f}^{2} = M_Z^{2}$, for a experimental (fit), b experimental plus model, c experimental plus parameterisation, d total uncertainties. The uncertainties on both gluon PDFs are shown as differently hatched bands

Fig. 10

Comparison of the normalised uncertainties on the gluon PDFs of HERAPDF2.0Jets NNLO for $\alpha _s(M_Z^2)= 0.1155$ and HERAPDF2.0 NNLO for $\alpha _s(M_Z^2)= 0.118$, both at the scale $\mu _\mathrm{f}^{2} = 10\,$GeV$^{2}$, for a experimental (fit), b experimental plus model, c experimental plus parameterisation, d total uncertainties. The uncertainties on both gluon PDFs are shown as differently hatched bands

Fig. 11

Comparison of the normalised uncertainties on the gluon PDFs of HERAPDF2.0Jets NNLO for $\alpha _s(M_Z^2)= 0.1155$ and HERAPDF2.0 NNLO for $\alpha _s(M_Z^2)= 0.118$, both at the scale $\mu _\mathrm{f}^{2} = M_Z^{2}$, for a experimental, i.e. fit, b experimental plus model, c) experimental plus parameterisation, d total uncertainties. The uncertainties on both gluon PDFs are shown as differently hatched bands

Fig. 12

Ratios of uncertainties relative to the total uncertainties of HERAPDF2.0 NNLO for $\alpha _s(M_Z^2)=0.118$ a total, b experimental, c experimental plus model, d experimental plus parameterisation uncertainties for HERAPDF2.0Jets NNLO for $\alpha _s(M_Z^2)=0.118$ and $\alpha _s(M_Z^2)=0.1155$, all at the scale $\mu _\mathrm{f}^{2} = 10$ GeV$^{2}$

Fig. 13

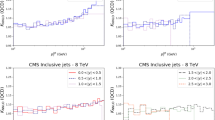
a Differential jet-cross-section predictions, $\mathrm{d}\sigma /\mathrm{d}p_\mathrm{T}$, based on HERAPDF2.0Jets NNLO with $\alpha _s(M_Z^2)= 0.1155$ in bins of $Q^2$ between 5 and 100 GeV$^2$ compared to H1 data [10]. Only data used in the fit are shown. b Measured cross sections divided by predictions based on HERAPDF2.0Jets NNLO. The bands represent the total uncertainties on the predictions excluding scale uncertainties; the bands are so narrow that they mostly appear as lines. Error bars indicate the full uncertainties on the data and are smaller than the symbols in (a). In b, the ratio of predictions based on HERAPDF2.0Jets NNLO with $\alpha _s(M_Z^2)= 0.118$ and $\alpha _s(M_Z^2)= 0.1155$ is also shown

Fig. 14

a Differential jet-cross-section predictions, $\mathrm{d}\sigma /\mathrm{d}p_\mathrm{T}$, based on HERAPDF2.0Jets NNLO with $\alpha _s(M_Z^2)= 0.1155$ in bins of $Q^2$ between 150 and 15,000 GeV$^2$ compared to H1 data normalised to neutral current (NC) inclusive cross sections [9]. Only data used in the fit are shown. b Measured normalised cross sections divided by predictions based on HERAPDF2.0Jets NNLO. The bands represent the total uncertainties on the predictions excluding scale uncertainties; the bands are so narrow that they mostly appear as lines. Error bars indicate the full uncertainties on the data and are smaller than the symbols for some bins in (a). In b, the ratio of predictions based on HERAPDF2.0Jets NNLO with $\alpha _s(M_Z^2)= 0.118$ and $\alpha _s(M_Z^2)= 0.1155$ is also shown

Fig. 15

a Differential jet-cross-section predictions, $\mathrm{d}\sigma /\mathrm{d}p_\mathrm{T}$, based on HERAPDF2.0Jets NNLO with $\alpha _s(M_Z^2)= 0.1155$ in bins of $Q^2$ between 5.5 and 80 GeV$^2$ compared to H1 data normalised to neutral current (NC) inclusive cross sections [14]. Only data used in the fit are shown. b Measured normalised cross sections divided by predictionst based on HERAPDF2.0Jets NNLO. The bands represent the total uncertainties on the predictions excluding scale uncertainties; the bands are so narrow that they mostly appear as lines. Error bars indicate the full uncertainties on the data and are mostly smaller than the symbols in (a). In b, the ratio of predictions based on HERAPDF2.0Jets NNLO with $\alpha _s(M_Z^2)= 0.118$ and $\alpha _s(M_Z^2)= 0.1155$ is also shown

Fig. 16

a Differential dijet-cross-section predictions, $\mathrm{d}\sigma /\mathrm{d}\langle p_\mathrm{T}\rangle _2$, based on HERAPDF2.0Jets NNLO with $\alpha _s(M_Z^2)= 0.1155$ in bins of $Q^2$ between 5.5 and 80 GeV$^2$ compared to H1 data normalised to neutral current (NC) inclusive cross sections [14]. The variable $\langle p_\mathrm{T}\rangle _2$ denotes the average $p_\mathrm{T}$ of the two jets. Only data used in the fit are shown. b Measured dijet cross sections divided by predictions based on HERAPDF2.0Jets NNLO. The bands represent the total uncertainties on the predictions excluding scale uncertainties; the bands are so narrow that they mostly appear as lines. Error bars indicate the full uncertainties on the data and are mostly smaller than the symbols in (a). In b, the ratio of predictions based on HERAPDF2.0Jets NNLO with $\alpha _s(M_Z^2)= 0.118$ and $\alpha _s(M_Z^2)= 0.1155$ is also shown

In the HERAPDF2.0Jets NLO analysis [2], hadronisation uncertainties were applied using the offset method, i.e. performing separate fits with the hadronisation corrections set to their maximal and minimal values. This resulted in a hadronisation uncertainty on $\alpha _s(M_Z^2)$ of $\pm 0.0012$ [2]. The current procedure improves upon this by including the uncertainties on the hadronisation corrections at the same level as the other systematic uncertainties. Thus, their contribution became part of the overall experimental (fit) uncertainties. They were treated as 50% correlated and 50% uncorrelated between bins and data sets. For fits with fixed $\alpha _s(M_Z^2)$, their contribution was negligible. For fits with free $\alpha _s(M_Z^2)$, their contribution to the experimental uncertainty on $\alpha _s(M_Z^2)$ was $\pm 0.0006$. This represents a significant reduction of the influence of the hadronisation uncertainties compared to previous analyses.

Fig. 17

a Differential jet-cross-section predictions, $\mathrm{d}\sigma /\mathrm{d}p_\mathrm{T}$, based on HERAPDF2.0Jets NNLO with $\alpha _s(M_Z^2)= 0.1155$ in bins of $Q^2$ between 150 and 15,000 GeV$^2$ compared to H1 data normalised to neutral current (NC) inclusive cross sections [13, 14]. Only data used in the fit are shown. b Measured normalised cross sections divided by predictions based on HERAPDF2.0Jets NNLO. The bands represent the total uncertainties on the predictions excluding scale uncertainties; the bands are so narrow that they mostly appear as lines. Error bars indicate the full uncertainties on the data and are smaller than the symbols for most bins in (a). In b, the ratio of predictions based on HERAPDF2.0Jets NNLO with $\alpha _s(M_Z^2)= 0.118$ and $\alpha _s(M_Z^2)= 0.1155$ is also shown

Fig. 18

a Differential dijet-cross-section predictions, $\mathrm{d}\sigma /\mathrm{d}\langle p_\mathrm{T}\rangle _2$, based on HERAPDF2.0Jets NNLO with $\alpha _s(M_Z^2)= 0.1155$ in bins of $Q^2$ between 150 and 15,000 GeV$^2$ compared to H1 data normalised to neutral current (NC) cross sections [13]. The variable $\langle p_\mathrm{T}\rangle _2$ denotes the average $p_\mathrm{T}$ of the two jets. Only data used in the fit are shown. b Measured dijet cross sections divided by predictions based on HERAPDF2.0Jets NNLO. The bands represent the total uncertainties on the predictions excluding scale uncertainties; the bands are so narrow that they mostly appear as lines. Error bars indicate the full uncertainties on the data and are mostly smaller than the symbols in (a). In b, the ratio of predictions based on HERAPDF2.0Jets NNLO with $\alpha _s(M_Z^2)= 0.118$ and $\alpha _s(M_Z^2)= 0.1155$ is also shown

Fig. 19

a Differential jet-cross-section predictions, $\mathrm{d}\sigma /\mathrm{d}p_\mathrm{T}$, based on HERAPDF2.0Jets NNLO with $\alpha _s(M_Z^2)= 0.1155$ in bins of $Q^2$ between 125 and 10,000 GeV$^2$ compared to ZEUS data [11]. Only data used in the fit are shown. b Measured cross sections divided by predictions based on HERAPDF2.0Jets NNLO. The bands represent the total uncertainties on the predictions excluding scale uncertainties; the bands are so narrow that they mostly appear as lines. Error bars indicate the full uncertainties on the data and are smaller than the symbols for most bins in (a). In b, the ratio of predictions based on HERAPDF2.0Jets NNLO with $\alpha _s(M_Z^2)= 0.118$ and $\alpha _s(M_Z^2)= 0.1155$ is also shown

Fig. 20

a Differential dijet-cross-section predictions, $\mathrm{d}\sigma /\mathrm{d}\langle p_\mathrm{T}\rangle _2$, based on HERAPDF2.0Jets NNLO with $\alpha _s(M_Z^2)= 0.1155$ in bins of $Q^2$ between 125 and 20000 GeV$^2$ compared to ZEUS data [12]. The variable $\langle p_\mathrm{T}\rangle _2$ denotes the average $p_\mathrm{T}$ of the two jets. Only data used in the fit are shown. b Measured dijet cross sections divided by predictions based on HERAPDF2.0Jets NNLO. The bands represent the total uncertainties on the predictions excluding scale uncertainties; the bands are so narrow that they mostly appear as lines. Error bars indicate the full uncertainties on the data and are smaller than the symbols in (a). In b, the ratio of predictions based on HERAPDF2.0Jets NNLO with $\alpha _s(M_Z^2)= 0.118$ and $\alpha _s(M_Z^2)= 0.1155$ is also shown

The total uncertainties on the PDFs were obtained by adding the experimental (fit), the model and the parameterisation uncertainties in quadrature.

4 HERAPDF2.0Jets NNLO – results

4.1 Simultaneous determination of $\alpha _s(M_Z^2)$ and PDFs

In pQCD fits to inclusive DIS data alone, the gluon PDF is only determined via the DGLAP equations, using the observed scaling violations. This results in a strong correlation between the shape of the gluon distribution and the value of $\alpha _s(M_Z^2)$. Data on jet-production cross sections provide an independent constraint on the gluon distribution and are also directly sensitive to $\alpha _s(M_Z^2)$. Thus, such data are essential for an accurate simultaneous determination of $\alpha _s(M_Z^2)$ and the gluon distribution.

When determining $\alpha _s(M_Z^2)$, it is necessary to consider so-called “scale uncertainties”, which serve as a proxy for the uncertainties due to the unknown higher-order contributions in the perturbation expansion. These uncertainties were evaluated by varying the renormalisation and factorisation scales by a factor of two, both separately and simultaneously.⁸ The maximum positive and negative deviations of the result were assigned as the scale uncertainties on $\alpha _s(M_Z^2)$. These were observed for the variations $(2.0\mu _{\mathrm{r}},1.0 \mu _{\mathrm{f}})$ and $(0.5\mu _{\mathrm{r}},1.0 \mu _{\mathrm{f}})$, respectively.

The HERAPDF2.0Jets NNLO fit with free $\alpha _s(M_Z^2)$ resulted in

$$\begin{aligned} \alpha _s(M_Z^2)&= 0.1156 \pm 0.0011~\mathrm{(exp)}\nonumber \\&\pm ^{ 0.0001}_{0.0002}~\mathrm{(model+parameterisation)} ~\nonumber \\&\pm 0.0029~\mathrm{(scale)}, \end{aligned}$$

(7)

where “exp” denotes the experimental uncertainty, which was taken as the fit uncertainty, including the contribution from hadronisation uncertainties. The value of $\alpha _s(M_Z^2)$ and the size of the experimental uncertainty were confirmed by a scan in $\alpha _s(M_Z^2)$, for which the resulting $\chi ^2$ values are shown in Fig. 2. The clear minimum observed in $\chi ^2$ coincides with the value of $\alpha _s(M_Z^2)$ listed in Eq. (7). The width of the minimum in $\chi ^2$ confirms the fit uncertainty. The small combined model and parameterisation uncertainty shown in Fig. 2 was determined by performing similar scans, for which the values of the model parameters and the parameterisation were varied as described in Sect. 3.1.

Figure 2 also shows the scale uncertainty, which dominates the total uncertainty. The scale uncertainty as listed in Eq. (7) was evaluated under the assumption of 100% correlated uncertainties between bins and data sets. The previously published result at NLO [2] had scale uncertainties calculated under the assumption of 50% correlated and 50% uncorrelated uncertainties between bins and data sets, owing to the inclusion of heavy-quark and trijet data. A strong motivation to determine $\alpha _s(M_Z^2)$ at NNLO was the expectation of a substantial reduction in the scale uncertainty. Therefore, the analysis was repeated for these assumptions in order to compare the NNLO to the NLO scale uncertainties. The re-evaluated NNLO scale uncertainty of ($\pm 0.0022$) is indeed significantly lower than the ($+0.0037,-0.0030$) previously observed in the HERAPDF2.0Jets NLO analysis.

The HERAPDF2.0Jets NNLO fit with free $\alpha _s(M_Z^2)$ was based on 1363 data points and had a $\chi ^2/$degree of freedom (d.o.f.) $= 1614/1348 = 1.197$. This can be compared to the $\chi ^2/$d.o.f. $= 1363/1131 = 1.205$ for HERAPDF2.0 NNLO based on inclusive data only [2]. The similarity of the $\chi ^2/$d.o.f. values indicates that the data on jet production do not introduce any additional tension into the fit and are fully consistent with the inclusive data.

The question of whether data at relatively low $Q^2$ bias the determination of $\alpha _s(M_Z^2)$ arose within the context of the HERAPDF2.0 analysis [2]. Figure 3a shows the result of $\alpha _s(M_Z^2)$ scans with $Q^2_{\mathrm{min}}$ for the inclusive data set to 3.5 GeV$^2$, 10 GeV$^2$ and 20 GeV$^2$. The positions of the minima are in good agreement, indicating that any anomalies at low $Q^2$ are small. Figure 3b shows the result of similar scans with only the inclusive data used as input [2]. The inclusive data alone cannot sufficiently constrain $\alpha _s(M_Z^2)$.

To verify that the use of the $A_g'$ term in the gluon parameterisation does not bias the determination of $\alpha _s(M_Z^2)$, cross-checks were made with two modified gluon parameterisations. These are $A_g'=0$ and $xg(x) = A_g x^{B_g} (1-x)^{C_g}$ as well as the alternative gluon parameterisation, AG [2], for which $A_g'=0$ and $xg(x) = A_g x^{B_g} (1-x)^{C_g} (1 + D_g x)$. A value of $\alpha _s(M_Z^2)= 0.1151 \pm 0.0010~\mathrm{(exp)}$ was obtained for both modifications of the parameterisation, which is in agreement with the result for the standard parameterisation. The value of $D_g$ in the AG parameterisation was consistent with zero. These results demonstrate that the present $\alpha _s(M_Z^2)$ determination is not very sensitive to the details of the gluon parameterisation.

Previous determinations of $\alpha _s(M_Z^2)$ at NNLO using jet data [28, 33] used predetermined PDFs. These analyses were performed with a cut $\mu > 2M_b$, which is quite similar to the $\mu > 10.0$ GeV cut used for this analysis. Thus, the scale uncertainties can be compared. The H1 result [33] is based on H1 data only and the quoted scale uncertainty is $\pm 0.0039$. The scale uncertainty published by NNLOjet [28] using only H1 and ZEUS inclusive jet data is $\pm 0.0033$. This can be compared to the $\pm 0.0029$ obtained for the analysis presented here. The H1 collaboration also provided one simultaneous fit of $\alpha _s(M_Z^2)$ and PDFs using a zero-mass variable-flavour-number scheme [33]. It was based on H1 inclusive and jet data with $Q^2_{\mathrm{min}} = 10$ GeV$^2$. For comparison, the analysis presented here was modified by also setting $Q^2_{\mathrm{min}} = 10$ GeV$^2$. The value of $\alpha _s(M_Z^2)$ published by H1 is $\alpha _s(M_Z^2)= 0.1147 \pm 0.0011~\mathrm{(exp)} \pm 0.0002~\mathrm{(model)} \pm 0.0003~\mathrm{(parameterisation)} \pm 0.0023~\mathrm{(scale)}$ while the current modified analysis resulted in $\alpha _s(M_Z^2)= 0.1156 \pm 0.0011~\mathrm{(exp)} \pm 0.0002~\mathrm{(model+parameterisation)} \pm 0.0021$ (scale). These values agree within uncertainties. Overall, the various determinations of $\alpha _s(M_Z^2)$ provide a very consistent picture up to NNLO.

4.2 The PDFs of HERAPDF2.0Jets NNLO obtained for fixed $\alpha _s(M_Z^2)$

Fixed values of $\alpha _s(M_Z^2)= 0.1155$ and $\alpha _s(M_Z^2)= 0.118$ were used for the determination of the two sets of PDFs released from the HERAPDF2.0Jets NNLO analysis, see Appendix A. The value of $\alpha _s(M_Z^2)= 0.1155$ corresponds⁹ to the determination of $\alpha _s(M_Z^2)$ presented in Sect. 4.1. The value of $\alpha _s(M_Z^2)= 0.118$ was the result of the HERAPDF2.0Jets NLO analysis and was used for the HERAPDF2.0 analyses at NNLO based on inclusive data only [2]. The PDFs of HERAPDF2.0Jets NNLO are shown in Fig. 4a, b for fixed $\alpha _s(M_Z^2)=0.1155$ and fixed $\alpha _s(M_Z^2)=0.118$, respectively, at the scale $\mu _{\mathrm{f}}^2=10$ GeV$^2$. The uncertainties shown are the experimental (fit) uncertainties as well as the model and parameterisation uncertainties defined in Sect. 3.2. The introduction of the parameter $D_{u_v}$ as a variation dominates the parameterisation uncertainty.

As the PDFs were derived with fixed $\alpha _s(M_Z^2)$ values, uncertainties on the PDFs from varying the scales in the fit procedure were not considered, since in this case, a quantification of the influence of higher orders by varying the renormalisation and factorisation scales in the fit becomes questionable. Any variation of the renormalisation scale effectively amounts, in its numerical effect, to a modification of the value of $\alpha _s(M_Z^2)$, since the compensation with the explicit scale-dependent terms in the NLO and NNLO coefficients is incomplete. If a fit is performed with a fixed value of $\alpha _s(M_Z^2)$, it might thus not reach a local minimum, which is required to estimate the influence of higher orders by varying the scales. Nevertheless, a cross-check with scale variations as described in Sect. 4.1 was made. The impact on the resulting PDFs was found to be negligible compared to the other uncertainties presented in Fig. 4.

A comparison between the PDFs obtained for $\alpha _s(M_Z^2)= 0.1155$ and $\alpha _s(M_Z^2)= 0.118$ is provided in Figs. 5 and 6 for the scales $\mu _{\mathrm{f}}^2=$10 GeV$^2$ and $\mu _{\mathrm{f}}^2=M_Z^2$, respectively. Here, only total uncertainties are shown. At the lower scale, a significant difference is observed between the gluon PDFs; the gluon PDF for $\alpha _s(M_Z^2)= 0.1155$ is above the gluon PDF for $\alpha _s(M_Z^2)= 0.118$ for x less than $\approx 10^{-2}$. This correlation between the value of $\alpha _s(M_Z^2)$ and the shape of the gluon PDF is as expected from QCD evolution. At the scale of $M_Z^2$, the differences become negligible in the visible range of x.

A comparison of the PDFs obtained for $\alpha _s(M_Z^2)= 0.118$ by HERAPDF2.0Jets NNLO to the PDFs of HERAPDF2.0 NNLO, based on inclusive data only, is provided in Fig. 7. These two sets of PDFs do not show any significant difference in the central values. However, the HERAPDF2.0Jets NNLO analysis results in a significant reduction of the uncertainties on the gluon PDFs as shown in Fig. 8 at the scale of $\mu _{\mathrm{f}}^2 = 10\,$GeV$^2$ and in Fig. 9 at the scale of $\mu _{\mathrm{f}}^2 = M_Z^2$. The reduction in the uncertainties for HERAPDF2.0Jets NNLO for $\alpha _s(M_Z^2)= 0.1155$ compared to $\alpha _s(M_Z^2)= 0.118$ is shown in Figs. 10 and 11. At high x and $\mu _{\mathrm{f}}^2 = M_Z^2$, the parameterisaton uncertainties become important, as can be seen by comparing Fig. 11b, c.

The reduction in model and parameterisation uncertainty for $x < 10^{-3}$ for HERAPDF2.0Jets NNLO compared to HERAPDF2.0 NNLO is mostly due to the improved procedure to estimate this uncertainty. The reduced ranges of variation of $M_c$ and $M_b$ had little effect. The major effect came from symmetrising the results of the variations of $\mu _{\mathrm{f0}}^2$ and $M_c^2$, as discussed in Sect. 3.3. This removed a double counting of sources of uncertainty that had been present in the orginal HERAPDF2.0 procedure. On the other hand, the reduction of experimental as well as model and parameterisation uncertainties for $x > 10^{-3}$ is due to the influence of the jet data. This is also demonstrated in Fig. 12, which shows ratios of the uncertainties with respect to the total uncertainties of HERAPDF2.0 NNLO based on inclusive data only. Shown are the experimental, the experimental plus model, and the experimental plus parameterisation uncertainties. Other selected ratio plots are provided in Appendix B.

4.3 Comparisons of HERAPDF2.0Jets NNLO predictions to jet data

Comparisons of the predictions based on the PDFs of HERAPDF2.0Jets NNLO with fixed $\alpha _s(M_Z^2)= 0.1155$ to the data on jet production used as input to the fit are shown in Figs. 13, 14, 15, 16, 17, 18, 19, and 20. Each figure presents a direct comparison of the cross sections and the respective ratios.

The uncertainties on the NNLO predictions as calculated by NNLOJET were taken into account in all HERAPDF2.0Jets NNLO fits. The predictions based on the PDFs of HERAPDF2.0Jets NNLO were computed using the assumption of massless jets, i.e. the transverse energy, $E_{\mathrm{T}}$, and the transverse momentum of a jet, $p_{\mathrm{T}}$, were assumed to be equivalent. For the inclusive-jet analyses, each jet $p_{\mathrm{T}}$ entered the cross-section calculation separately. For dijet analyses, the average of the transverse momenta of the two jets, $\langle p_{\mathrm{T}}\rangle _2$, was used. The factorisation and renormalisation scales were set accordingly for calculating predictions. Scale uncertainties were not considered [16] for the comparisons to data. The predictions based on the PDFs of HERAPDF2.0Jets NNLO describe the data on jet production well, demonstrating consistency of the inclusive and the jet-production data sets that were used in the current analysis.

5 Summary

The HERA DIS data set on inclusive ep scattering as published by the H1 and ZEUS collaborations [2], together with selected data on jet production, published separately by the two collaborations, have been used as input to a pQCD analysis at NNLO.

An analysis was performed where $\alpha _s(M_Z^2)$ and the PDFs were fitted simultaneously. This resulted in a value of $\alpha _s(M_Z^2)= 0.1156 \pm 0.0011~\mathrm{(exp)} ^{+0.0001} _{-0.0002}$ (model$+$ parameterisation) ± 0.0029 (scale). This result for $\alpha _s(M_Z^2)$ is compatible with the world average [38] and is competitive in comparison with other determinations at NNLO. The scale uncertainties were calculated under the assumption of fully correlated uncertainties between bins and data sets. They would decrease to $\pm 0.0022$ under the assumption of 50% correlated and 50% uncorrelated uncertainties, which is the value that can be directly compared to the previously published [2] scale uncertainties of ($+0.0037,-0.0030$) observed in the HERAPDF2.0Jets NLO analysis.

Two sets of PDFs were determined for HERAPDF2.0Jets NNLO for fixed $\alpha _s(M_Z^2)=0.1155$ and $\alpha _s(M_Z^2)=0.118$. They are available to the community [39]. Comparisons between the PDFs of HERAPDF2.0Jets NNLO obtained for the two values of $\alpha _s(M_Z^2)$ were shown, as well as comparisons to HERAPDF2.0 NNLO, for which jet data were not used as input to the fit. The PDFs of HERAPDF2.0Jets NNLO and HERAPDF2.0 NNLO are consistent over the whole kinematic range. This also demonstrates the consistency of the jet data and the inclusive data at NNLO level. The switch from NLO to NNLO led to a lower value of $\alpha _s(M_Z^2)$. The inclusion of the jet data reduced the uncertainty on the gluon PDF. Predictions based on the PDFs of HERAPDF2.0Jets NNLO give an excellent description of the jet-production data used as input.

The PDFs of HERAPDF2.0Jets NNLO complete the HERAPDF2.0 ensemble of parton distribution functions. This ensemble of PDFs, extracted from HERA data alone, presents a self-consistent picture in the framework of pQCD and is one of the major legacies of HERA.

Appendices

Appendix A: PDF sets released

Fig. 21

Ratios of uncertainties relative to the total uncertainties of HERAPDF2.0 NNLO with $\alpha _s(M_Z^2)=0.118$ for the total uncertainty of HERAPDF2.0Jets NNLO with $\alpha _s(M_Z^2)=0.1155$ and the a experimental, b experimental plus model, c experimental plus parameterisation uncertainty of HERAPDF2.0Jets NNLO with $\alpha _s(M_Z^2)=0.1155$ as well as HERAPDF2.0 NNLO with $\alpha _s(M_Z^2)=0.118$ at the scale $\mu _\mathrm{f}^{2} =10$ GeV$^{2}$

Fig. 22

Ratios of uncertainties relative to the total uncertainties of HERAPDF2.0 NNLO with $\alpha _s(M_Z^2)=0.118$ for the total uncertainty of HERAPDF2.0Jets NNLO with $\alpha _s(M_Z^2)=0.1155$ and the a experimental, b experimental plus model, c experimental plus parameterisation uncertainty of HERAPDF2.0Jets NNLO with $\alpha _s(M_Z^2)=0.1155$ as well as HERAPDF2.0 NNLO with $\alpha _s(M_Z^2)=0.118$ at the scale $\mu _\mathrm{f}^{2} = M_Z^{2}$

Fig. 23

Ratios of uncertainties relative to the total uncertainties of HERAPDF2.0 NNLO with $\alpha _s(M_Z^2)=0.118$ for the total uncertainty of HERAPDF2.0Jets NNLO with $\alpha _s(M_Z^2)=0.118$ and the a experimental, b experimental plus model, c experimental plus parameterisation uncertainty of HERAPDF2.0Jets NNLO with $\alpha _s(M_Z^2)=0.118$ as well as HERAPDF2.0 NNLO with $\alpha _s(M_Z^2)=0.118$ at the scale $\mu _\mathrm{f}^{2} =10$ GeV$^{2}$

Fig. 24

Ratios of uncertainties relative to the total uncertainties of HERAPDF2.0 NNLO with $\alpha _s(M_Z^2)=0.118$ for the total uncertainty of HERAPDF2.0Jets NNLO with $\alpha _s(M_Z^2)=0.118$ and the a experimental, b experimental plus model, c experimental plus parameterisation uncertainty of HERAPDF2.0Jets NNLO with $\alpha _s(M_Z^2)=0.118$ as well as HERAPDF2.0 NNLO with $\alpha _s(M_Z^2)=0.118$ at the scale $\mu _\mathrm{f}^{2} = M_Z^{2}$

The following two sets of PDFs are released [39] and available on LHAPDF:

(https://lhapdf.hepforge.org/pdfsets.html).

• HERAPDF2.0Jets NNLO

  • based on the combination of inclusive data from the H1 and ZEUS collaborations and selected data on jet production;

  • with $Q^2_\mathrm{min}=3.5\,$GeV$^2$;

  • using the RTOPT variable-flavour-number scheme;

    • with fixed value of $\alpha _s(M_Z^2)= 0.1155$;

    • with fixed value of $\alpha _s(M_Z^2)= 0.118$;

  • 14 eigenvector pairs give Hessian experimental (fit) uncertainties including hadronisation uncertainties;

  • grids of 14 variations are released to describe the model and parameterisation uncertainties.

Appendix B: Additional ratio plots on gluon PDF uncertainties

This appendix provides more plots in the style of Fig. 12. Figures 21 and 22 compare the uncertainties of HERAPDF2.0Jets NNLO $\alpha _s(M_Z^2)=0.1155$ to the uncertainties of HERAPDF2.0 NNLO $\alpha _s(M_Z^2)=0.118$ based on inclusive data only for the factorisation scale $\mu _\mathrm{f}^2=10$ GeV$^2$ and $\mu _\mathrm{f}^2=M_Z^2$, respectively. Figures 23 and 24 compare the uncertainties of HERAPDF2.0Jets NNLO $\alpha _s(M_Z^2)=0.118$ to the uncertainties of HERAPDF2.0 NNLO $\alpha _s(M_Z^2)=0.118$ for the factorisation scale $\mu _\mathrm{f}^2=10$ GeV$^2$ and $\mu _\mathrm{f}^2=M_Z^2$, respectively. These plots illustrate the influence of the jet data on the uncertainties.