1 Introduction

Despite the fact that the standard model of cosmology, a.k.a. the Big Bang model, provides a comprehensive explanation for a broad range of observed phenomena including the anisotropy of the cosmic microwave background (CMB) consisting of the small temperature fluctuations in the blackbody radiation left over from the Big Bang and a mechanism for generating the primordial energy density perturbations that are the seed for late time large-scale structure. However, there are some observations in which the traditional Big Bang model fails to explain. These cosmological problems are linked to the primordial universe. More concretely, the observed flatness, homogeneity, and the lack of relic monopoles posed severe problems in the standard Big Bang cosmology. In order to solve such fundamental problems, an inflationary scenario [1,2,3,4,5] is a well-established paradigm describing an early universe and posts an indispensable ingredient of modern cosmology.

In the standard picture, an accelerated expansion quickly erases all traces of any pre-inflationary matter or radiation density resulting the universe in the vacuum state. We explain the transition from inflation to the “hot Big Bang” state by requiring the nucleosynthesis and using the physics of recombination leading to the descriptions of the CMB temperature anisotropies we observed today. To this end, we need the interactions between the inflaton with other fields resulting the (partial) decay of the inflaton into ordinary matter and radiation. However, inflaton decay can only play a significant role at the end of the slow-roll regime, leading to the standard “(p)reheating” paradigm, see e.g. [6,7,8]. In standard cold inflation, any preexisting radiation is stretched and dispersed during a very short cosmic phase and no new radiation is produced. However, one can imagine an alternative scenario where dissipative effects and associated particle production can sustain a thermal bath concurrently with the accelerated expansion of the Universe during inflation. This alternative perspective was known as warm inflationary paradigm. The original proponent of warm inflation was proposed by Arjun Berera and his colleagues [9, 10]. As mentioned in Ref. [11], this alternative counterpart is proposed in which the radiation energy density smoothly decreases all during an inflation-like stage and with no discontinuity enters the subsequent radiation-dominated stage.

Beside, the Starobinsky \(R^2\) cosmic inflation model [1] and the non-minimal coupling Higgs inflation [12] are greatly received attention over decades. In particular, Those two models are very successful to explain the mechanisms of the inflationary universe and nicely fit with the observational data. However, these two models suffer from some fundamental problems per se. On the one hand, Higgs inflation encounters to the unitary problem if we consider single scalar Higgs field as the inflaton only and the Higgs field needs to large at the beginning of the inflationary phase [13]. On the other hand, the origin or mechanism to generate the \(R^2\) term in the Starobinsky model is still unclear. Fortunately, an attempt to combine and fulfill the Higgs with Starobinsky is successfully done by many authors of Refs. [14, 15]. This leads to a so-called Higgs–Starobinsky (HS) inflation model. The main idea of the HS model is that the Higgs field does couple to the graviton (Ricci scalar) at large coupling and this leads to the \(R^2\) emerging from the quantum correction between Higgs and graviton at least at one-loop level. As a result, this model does not suffer from all mentioned problems of the Higgs and Starobinsky inflationary models. Salient features of the HS are that there is no physics beyond standard model of particle physics and the higher curvature term \(R^2\) of the Starobinsky inflation is automatically generated by the quantum correction effect. In addition, the unitarity problem of the original Higgs inflation is solved. The HS inflation has been used to study in various aspects [16,17,18,19,20,21,22,23,24,25,26,27]. Moreover, there were some mixed Higgs–Starobinsky models in the Palatini formulation of gravity [28,29,30] as well as in the metric formulation of gravity [31]. Additionally, an extension of the scalaron-Higgs model by a non-minimal coupling of the Standard Model Higgs boson to the quadratic Ricci scalar was proposed by Ref. [32]. However, a study of the HS model in warm inflationary universe has not been reported yet and hence it is worth investigating it in the present work.

The structure of the present work is organized as follows. In Sect. 2, we set up the (warm) HS inflationary model and study it in the Einstein frame. We then derive the relevant cosmological observables in the warm inflation scenario. In Sect. 3 we compare the theoretical results in the warm HS inflation with the Planck 2018 data. Finally, We conclude our findings in the last section.

2 Model Set-up

2.1 The HS action

The gravitational action of the HS model with non-minimal coupling to the Ricci scalar and the self-interacting Higgs field is given by

$$\begin{aligned} S_J= & {} \int d^4x\sqrt{-g}\,\left[ -\frac{1}{2}\,M_p^2\, R - \frac{1}{2}\,\xi \,h^2\,R \right. \nonumber \\&\left. + \frac{1}{2}\,g^{\mu \nu }\partial _\mu h\,\partial _\nu h - \frac{\lambda }{4}\,h^4 - \alpha \,R^2 \,\right] , \end{aligned}$$
(2.1)

where the subscript \(S_J\) stands for the action in the Jordan frame and \(M_p^2 = 1/8\pi G\), \(\xi \) and \(\alpha \) are Planck mass, non-minimal Higgs and \(R^2\) Starobinsky term coupling constants, respectively, while the h field is the Higgs scalar field with the standard Higgs potential the self-interacting coupling constant \(\lambda \). In the HS model, the large coupling of the Higgs and graviton plays the role as the trigger of the Starobinsky inflation term \(R^2\) from the quantum correction [14, 15]. According to the RG analysis of the HS model at the one-loop level [26, 27], it was shown that the coupling of the \(R^2\) term, \(\alpha \), is proportional to \(\alpha (h) \propto (\xi +1/6)^2\ln (h/\mu )\) where the renormalization scale is set at the Planck mass, i.e., \(\mu \approx M_p\) and the Higgs field (h) is a sub-Planckian field as \(h \ll M_p\). This is the main mechanism behind the generation of the Starobinsky \(R^2\) inflation in the HS model. At the large values of non-minimal coupling \(\xi \) and the inflaton (scalaron, \(\phi \) see below) and in the slow-roll regime during inflation, we can drop kinetic term of the Higgs field. Then the HS gravity action is given by [18, 19, 23],

$$\begin{aligned} S_J = \int d^4x\sqrt{-g}\,\left[ -\frac{1}{2}\,M_p^2\, R - \frac{1}{2}\,\xi \,h^2\,R - \alpha \,R^2 - \frac{\lambda }{4}\,h^4 \,\right] . \nonumber \\ \end{aligned}$$
(2.2)

We can eliminate the non-minimal Higgs coupling term, \(\xi \,\sigma ^2\,R\)  via the equation of motion of h field. The Euler-Lagrange equation of the Higgs field, h is therefore written by

$$\begin{aligned} \frac{1}{2}\,\xi \,h^2\,R + \frac{\lambda }{4}\,h^4 = 0\,\quad \Longrightarrow \quad h^2 = -\,6\,\xi \,R/\lambda . \end{aligned}$$
(2.3)

Substituting the Higgs field in above equation, we find

$$\begin{aligned} S_J= & {} \int d^4x\sqrt{-g}\,M_p^2\left[ -\frac{1}{2}\, R - \frac{1}{12\,M^2} \,R^2 \right] , \end{aligned}$$
(2.4)
$$\begin{aligned} M^2= & {} \frac{M_p^2}{12\left( \alpha + 3\,\xi ^2/(2\,\lambda )\right) }. \end{aligned}$$
(2.5)

The above action is a standard form of the Starobinsky inflation action. We will see in the latter that the scalaron mass, \(M_\alpha \) of the pure Starobinsky inflaton field (for \(\xi = 0 =\lambda \)) is given by

$$\begin{aligned} M_\alpha ^2 = \frac{M_p^2}{12\,\alpha }, \end{aligned}$$
(2.6)

whereas the scalaron mass of the HS gravity is modified by [19, 23]

$$\begin{aligned} M^2 = \frac{M_\alpha ^2}{1+18\,(\xi ^2/\lambda )\,M_\alpha ^2/M_p^2}. \end{aligned}$$
(2.7)

According to the observational constraints of the amplitudes of the curvature perturbation, one finds \(M \approx 1.3\times 10^{-5}M_p\) [33]. By using the fixing M parameter, we obtain the relation between three parameters \(\xi \), \(\alpha \) and \(\lambda \) and we will employ action in Eq. (2.4) to work out relevant inflation parameters and fix the parameters from the HS model with the observational data in the next section.

It is very convenient to study the inflation dynamics in the Einstein frame which can be obtained via the conformal transformation. According to the HS action Eq. (2.1) in the Jordan frame, we can impose the conformal factor as

$$\begin{aligned} \Omega ^2&= \frac{2}{M_p^2}\,\frac{\partial }{\partial R}\left( \frac{1}{2}\,M_p^2\,R + \frac{M_p^2}{12\,M^2}\,R^2\right) = 1 + \frac{R}{3\,M^2} , \end{aligned}$$
(2.8)

where the definition of the effective mass M is given in Eq. (2.7). The conformal factor, \(\Omega ^2\), plays important role on transformation of the gravitational action from the Jordan frame to the Einstein frame. The relation between metric tensors of the Jordan and Einstein frames reads

$$\begin{aligned} g_{\mu \nu } = \Omega ^2\,\widetilde{g}_{\mu \nu }. \end{aligned}$$
(2.9)

We would like to mention that all quantities with “  \(\widetilde{~}\)  ” are represented quantities in the Einstein frame. The Ricci scalar in the Jordan frame is written in terms of quantities in the Einstein frame as

$$\begin{aligned} R = \Omega ^2\left( \widetilde{R} + 3\,\widetilde{g}^{\mu \nu }\partial _\mu \partial _\nu \ln \Omega ^2 - \frac{3}{2}\,\widetilde{g}^{\mu \nu }\partial _\mu \ln \Omega ^2\,\partial _\nu \ln \Omega ^2 \right) .\nonumber \\ \end{aligned}$$
(2.10)

More importantly, the scalaron field, \(\phi \), in the HS model is introduced via

$$\begin{aligned} \phi= & {} M_p\sqrt{\frac{3}{2}}\,\ln \Omega ^2 . \end{aligned}$$
(2.11)
$$\begin{aligned} S_E= & {} \int d^4x\,\sqrt{-\widetilde{g}}\,\left[ -\frac{1}{2}\,M_p^2\,\widetilde{R} + \frac{1}{2}\,\widetilde{g}^{\mu \nu }\,\partial _\mu \phi \,\partial _\nu \phi - V(\phi ) \right] , \nonumber \\ \end{aligned}$$
(2.12)

Using the definition of the scalaron field, one can write the effective potential of the scalaron in the Einstein frame as

$$\begin{aligned} V(\phi ) = \frac{3}{4}\,M_p^2\, M^2 \left( 1- e^{-\sqrt{\frac{2}{3}}\,\frac{\phi }{M_p}} \right) ^2 . \end{aligned}$$
(2.13)

This is the standard Starobinsky scalaron potential in the Einstein frame and we will employ this potential in the analysis of the warm inflation scenario throughout this work.

2.2 Cosmological equations in warm inflation scenario

Having used the HS action (2.12) in the Einstein frame with the flat FRW line element, the Friedmann equation of the warm inflation is written by,

$$\begin{aligned} H^2 = \frac{1}{3\,M_p^2}\left( \frac{1}{2}\,\dot{\phi }^2 + V(\phi ) + \rho _r\right) . \end{aligned}$$
(2.14)

The Klein–Gordon equation of the scalaron field (\(\phi \)) with the dissipative term (\(\Gamma \)) due to the warm inflation scenario is governed by

$$\begin{aligned} \ddot{\phi }+ 3H\,\dot{\phi }+ V' = -\Gamma \,\dot{\phi }, \end{aligned}$$
(2.15)

while the conservation of the radiation matter is read

$$\begin{aligned} \dot{\rho }_r + 4H\,\rho _r = \Gamma \,\dot{\phi }^2. \end{aligned}$$
(2.16)

According to the finite temperature field theory analysis in the supersymmetry models, one obtains the general form of the dissipative parameter as [34,35,36,37]

$$\begin{aligned} \Gamma = C_m\,\frac{T^m}{\phi ^{m-1}}. \end{aligned}$$
(2.17)

The dissipative parameter, \(\Gamma \), corresponds to the friction of the inflaton field in the thermal bath in the warm inflationary universe. In addition, \(C_m\) is a constant encoding the inflaton’s microscopic effect of the dissipative dynamics and the m is an integer. In particular, the high temperature supersymmetric model is governed by \(m=1\) whereas \(m=3\) is responded to the low temperature supersymmetric model [36]. The use of the general form of the dissipative parameter given in Eq. (2.17) can also be found in the context of warm inflation with power-law plateau potential [55]. In the following subsections, we will consider the dissipative parameter with the slow-roll approximation for \(m=1\) which corresponds to a so-called warm little inflation.

In warm inflationary universe with the slow-roll regime, we can re-write the Friedmann equation as well as the equations of motion for the scalaron (inflaton) and the radiation matter to obtain

$$\begin{aligned} H^2\approx & {} \frac{1}{3 M_p^2}\,V(\phi ), \end{aligned}$$
(2.18)
$$\begin{aligned} \dot{\phi }\approx & {} -\frac{V'(\phi )}{3H(1+Q)},\quad Q\equiv \frac{\Gamma }{3H}, \end{aligned}$$
(2.19)
$$\begin{aligned} \rho _r\approx & {} \frac{\Gamma \,\dot{\phi }}{4H},\quad \rho _r = C_r\,T^4, \end{aligned}$$
(2.20)

where Q is called a dissipative coefficient and \(C_r = g_*\,\pi ^2/30\). To obtain above equations, the following approximations have been used

$$\begin{aligned} \rho _r\ll & {} \rho _\phi ,\quad \rho _\phi = \frac{1}{2}\,\dot{\phi }^2 + V, \end{aligned}$$
(2.21)
$$\begin{aligned} \dot{\phi }^2\ll & {} V(\phi ), \end{aligned}$$
(2.22)
$$\begin{aligned} \ddot{\phi }\ll & {} 3H\left( 1 + Q\right) \dot{\phi }, \end{aligned}$$
(2.23)
$$\begin{aligned} \dot{\rho }_r\ll & {} 4H\,\rho _r, \end{aligned}$$
(2.24)

as usually done in the slow-roll scenario. It is more convenient to consider the warm inflation in two regimes as

$$\begin{aligned} Q\gg & {} 1,\quad \mathrm{strong~regime}, \end{aligned}$$
(2.25)
$$\begin{aligned} Q\ll & {} 1,\quad \mathrm{weak~regime}. \end{aligned}$$
(2.26)

More importantly, we can re-write the temperature in terms of the scalaron field, \(\phi \), by using the Eqs. (2.17)–(2.20) in the general m integer values. One finds

$$\begin{aligned} T= & {} \left( \frac{V'^{\,2}\,\phi ^{m-1}}{4H\,C_m\,C_r}\right) ^{\frac{1}{4+m}},\quad \mathrm{for}\,~Q\gg 1, \end{aligned}$$
(2.27)
$$\begin{aligned} T= & {} \left( \frac{C_m\,V'^{\,2}\,\phi ^{1-m}}{36H^3\,C_r}\right) ^{\frac{1}{4-m}},\quad \mathrm{for}\,~Q\ll 1. \end{aligned}$$
(2.28)

Next, we provide the slow-roll parameters in the warm inflation for general m and they read

$$\begin{aligned}&\varepsilon = \frac{M_p^2}{2}\left( \frac{V'}{V}\right) ^2,\quad \eta = M_p^2\,\frac{V''}{V},\nonumber \\&\beta = M_p^2\left( \frac{V'\,\Gamma '}{V\,\Gamma }\right) . \end{aligned}$$
(2.29)

The inflationary phase of the universe occurs under the following conditions

$$\begin{aligned} \varphi \ll 1 + Q,\quad \eta \ll 1 + Q,\quad \beta \ll 1 + Q. \end{aligned}$$
(2.30)

Moreover, the number of e-folds, N, can be written in two regimes as

$$\begin{aligned}&N = \int _{\phi _\mathrm{end}}^{\phi _N}\frac{Q\,V}{V'}\,d\phi ,\quad \mathrm{for}\ Q\gg 1,\quad \mathrm{and}\nonumber \\&N = \int _{\phi _\mathrm{end}}^{\phi _N}\frac{V}{V'}\,d\phi ,\quad \mathrm{for}\ Q\ll 1. \end{aligned}$$
(2.31)

The power spectrum of warm inflation has been calculated by the authors of Refs. [38,39,40,41,42,43,44,45] and it reads

$$\begin{aligned} \Delta _{\mathcal {R}} = \left( \frac{H_N^2}{2\pi \dot{\phi }_N}\right) ^2\left( \!1 + 2n_N \!+\!\left( \frac{T_N}{H_N}\right) \frac{2\sqrt{3}\,\pi \,Q_N}{\sqrt{3+4\pi \,Q_N}}\!\right) G(Q_N), \nonumber \\ \end{aligned}$$
(2.32)

where the subscript “N” is labeled for all quantities estimated at the Hubble horizon crossing and \(n = 1/\big ( \exp {H/T} - 1 \big )\) is the Bose–Einstein distribution function. More importantly, the function \(G(Q_N)\) encodes the coupling between the inflaton and the radiation in the heat bath which leads to a growing mode in the fluctuations of the inflaton field originally calculated in Ref. [38] and consequent implications [37, 40]. In contrast, however, if \(G(Q_N)=1\), the above expression for the amplitude of the primordial spectrum is only valid in the weak dissipative regime, as it has been stated in other studies of warm inflation, see for example Refs. [39, 46,47,48,49]. In addition, the scalar spectral index is defined by

$$\begin{aligned} n_s - 1 = \frac{d\ln \Delta _{\mathcal {R}}}{d\ln k}\Bigg |_{k=k_N} = \frac{d\ln \Delta _{\mathcal {R}}}{dN}, \end{aligned}$$
(2.33)

with \(\ln k\equiv a\,H =N\). The tensor-to-scalar ratio of the perturbation, r, can be calculated via the following formulae:

$$\begin{aligned} r = \frac{\Delta _T}{\Delta _{\mathcal {R}}}, \end{aligned}$$
(2.34)

where \(\Delta _T\) is the power spectrum of the tensor perturbation and it takes the same form as the standard (cold) inflation picture, i.e. \(\Delta _T = 2H^2/\pi ^2M_p^2 = 2V(\phi )/3\pi ^2 M_p^4\).

In the following, we will separately consider the amplitude of the power spectrum in Eq. (2.32) for the warm inflation with the HS theory in the weak regime (i.e., \(Q\ll 1\) and \(G(Q_N)=1\)) and the strong regime (\(Q\gg 1\) and \(G(Q_N)\ne 1\)) in the Sects. 2.2.1 and 2.2.2, respectively.

2.2.1 Weak regime: \(Q\ll 1\) and \(G(Q_N)=1\)

In this subsection, we will calculate observable quantities of the warm inflation by dropping the growing mode of the power spectrum in Eq. (2.32) which corresponds to \(Q\ll 1\) and \(G(Q_N)=1\) limit. In the warm inflationary universe, the parameter r has been determined and written in terms of the slow-roll parameters in the weak regimes for \(T\gg H\) limit by Refs. [41, 42] as

$$\begin{aligned} r = 16\,\varepsilon ,\quad \mathrm{for}~Q\ll 1. \end{aligned}$$
(2.35)

In this work, we consider up to the first order of the Q correction for r parameter. As results, we note that the dissipative coefficient Q does not play the role in the weak regime similar to the cold inflation scenario. Moreover, the \(n_s\) is evaluated in the simple analytical forms for the weak regime by Refs [41, 42]. Up to the first-order correction of the Q parameter, \(n_s\) are given by

$$\begin{aligned} n_s= & {} 1 -6\,\varepsilon + 2\,\eta + Q\left( 8\,\varepsilon - 2\,\beta \right) , \quad Q\ll 1. \end{aligned}$$
(2.36)

Next, we will compute all relevant inflationary observables by considering \(m=1\) dissipative parameter model. The dissipative parameter for \(m=1\) model reads

$$\begin{aligned} \Gamma = C_1\,T. \end{aligned}$$
(2.37)

As mentioned earlier, this model is related to the high temperature in supersymmetric models and also known as warm little inflation [46]. The coupling \(C_1\) in Eq. (2.37) is given by

$$\begin{aligned} C_1 \simeq \frac{3\,g^2}{h^2\big (1-0.34\log (h) \big )}, \end{aligned}$$
(2.38)

where g is the Yukawa couplings of the inflaton and heavy fermions in the warm little inflation scenario while the coupling h is used to determine decay widths of the heavy fermions decaying to light singlet scalar and other light fermion particles [46]. More interestingly, the inflaton in this scenario corresponds to the pseudo-Goldstone boson from the broken symmetry and it is analogy to the little Higgs mechanism in the electroweak symmetry breaking framework.

The slow-roll parameters of the \(\Gamma = C_1\,T\) model are given by,

$$\begin{aligned} \varepsilon= & {} \frac{4}{3\left[ e^{\sqrt{\frac{2}{3}}\,\frac{\phi }{M_p}} - 1\right] ^2},\quad \eta = \frac{4}{3}\,\frac{\left[ 2 - e^{\sqrt{\frac{2}{3}\,\frac{\phi }{M_p}}}\right] }{\left[ e^{\sqrt{\frac{2}{3}}\,\frac{\phi }{M_p}} - 1\right] ^2}, \nonumber \\ \beta= & {} \frac{4}{9}\,\frac{\left[ 1 - 2\,e^{\sqrt{\frac{2}{3}}\,\frac{\phi }{M_p}}\right] }{\left[ e^{\sqrt{\frac{2}{3}}\,\frac{\phi }{M_p}} - 1\right] ^2},\quad \mathrm{for}\ Q\ll 1. \nonumber \\ \beta= & {} \frac{4}{15}\,\frac{\left[ 2 - 3\,e^{\sqrt{\frac{2}{3}}\,\frac{\phi }{M_p}}\right] }{\left[ e^{\sqrt{\frac{2}{3}}\,\frac{\phi }{M_p}} - 1\right] ^2},\quad \mathrm{for}\ Q\gg 1. \end{aligned}$$
(2.39)

Before we proceed the theoretical results to be confronted with the data, we will determine the Q in the weak regime, \(Q\ll 1\). By using Eqs. (2.19), (2.28) and (2.37), the parameter Q is given by

$$\begin{aligned} Q = \frac{2}{3}\left[ \frac{\Theta \,e^{2\chi }}{3\left( e^{\chi } - 1 \right) ^4} \right] ^{\frac{1}{3}} \approx \frac{2}{3}\left[ \frac{\Theta }{3\,e^{2\chi }} \right] ^{\frac{1}{3}},\quad \mathrm{for}\ Q\ll 1, \nonumber \\ \end{aligned}$$
(2.40)

where we have defined a new parameter \(\Theta \equiv \left( C_1^4/C_r\right) \left( M_p^2/M^2\right) \) and \(\chi \equiv \sqrt{2/3}\,\phi /M_p\).

The warm inflation will stop when the following conditions are satisfied

$$\begin{aligned} \varepsilon = 1 + Q,\quad \eta = 1 + Q,\quad \beta = 1 + Q. \end{aligned}$$
(2.41)

In the latter, we will consider the end of the warm inflation for two cases, i.e., the strong \(Q\gg 1\) and weak \(Q\ll 1\) approximation. In this subsection, we start with the weak regime \(Q\ll 1\) and the end of inflation yields

$$\begin{aligned} \varepsilon _\mathrm{end}\approx & {} 1\,\quad \Longrightarrow \quad \phi _\mathrm{end} \approx 0.18\,M_p, \end{aligned}$$
(2.42)

while the number of e-folds in the weak regime is given by

$$\begin{aligned} N= & {} \frac{1}{M_p^2}\int _{\phi _\mathrm{end}}^{\phi _N}\frac{V}{V'}\,d\phi \nonumber \\\approx & {} \frac{3}{4}\,\left( e^{\sqrt{\frac{2}{3}}\,\frac{\phi _N}{M_p}} -e^{\sqrt{\frac{2}{3}}\,\frac{\phi _\mathrm{end}}{M_p}} \right) \nonumber \\\approx & {} \frac{3}{4}\,e^{\sqrt{\frac{2}{3}}\,\frac{\phi _N}{M_p}}=\frac{3}{4}\sqrt{\frac{4}{3\,\varepsilon }}, \end{aligned}$$
(2.43)

where approximations \(e^\chi \pm 1 \approx e^\chi \) and \(\phi _N\gg \phi _\mathrm{end}\) are once assumed. As a result, we find

$$\begin{aligned} \phi _N = \sqrt{\frac{3}{2}}\,M_p\,\ln \left( \frac{4}{3}\,N\right) . \end{aligned}$$
(2.44)

In addition, we also re-write the slow-roll parameters in terms of N in the weak regime, \(Q\ll 1\), as

$$\begin{aligned}&\varepsilon \approx \frac{3}{4\,N^2},\quad \eta \approx - \sqrt{\frac{4\,\varepsilon }{3}} = -\frac{1}{N},\nonumber \\&\beta \approx -\frac{2}{3}\,\sqrt{\frac{4\,\varepsilon }{3}} =-\frac{2}{3\,N}. \end{aligned}$$
(2.45)

Next section, we will evaluate the cosmological observables of the warm HS inflation in the strong regime limit.

2.2.2 Strong regime: \(Q\gg 1\) and \(G(Q_N)\ne 1\)

In the strong dissipative regime, the inflaton perturbations are non-trivially affected by the fluctuations of the thermal bath, and the amplitude of the spectrum may get a correction, generically called the “growing mode”, depending on the value of the dissipative ratio. This was originally computed by Graham and Moss [38], see also some relevant literature [50, 51]. In the present analysis, we will consider the warm inflation in the strong regime with the growing mode effect.

By using Eqs. (2.19), (2.27) and (2.37), we find Q for the strong limit as

$$\begin{aligned} Q = \left[ \frac{2^3}{3^4}\,\frac{\Theta \,e^{2\chi }}{\left( e^{\chi } - 1 \right) ^4} \right] ^{\frac{1}{5}} \approx \left[ \frac{2^3}{3^4}\,\frac{\Theta }{e^{2\chi } } \right] ^{\frac{1}{5}} ,\quad \mathrm{for}\ Q\gg 1, \nonumber \\ \end{aligned}$$
(2.46)

At the end of inflation in the strong regime, one finds from Eq. (2.41)

$$\begin{aligned} \varepsilon _\mathrm{end} \approx Q_\mathrm{end} \quad \Longrightarrow \quad \frac{4}{3\left( e^{\chi } - 1\right) ^2} \approx \left[ \frac{2^3}{3^4}\,\frac{\Theta \,e^{2\chi }}{\left( e^{\chi } - 1 \right) ^4} \right] ^{\frac{1}{5}}.\nonumber \\ \end{aligned}$$
(2.47)

From the above equality, we can solve to obtain the value of the inflaton field (scalaron) at the end of inflation:

$$\begin{aligned} \phi _\mathrm{end} \approx \sqrt{\frac{3}{2}}\frac{M_p}{8}\ln \left( \frac{2}{3}\,\frac{4^3}{\Theta }\right) , \end{aligned}$$
(2.48)

where the large field approximation has been done via \(e^\chi \pm 1 \approx e^\chi \) with \(\chi = \sqrt{2/3}\,\phi /M_p\). Moreover, the inflaton field at the Hubble horizon crossing in the strong regime, \(\phi _{N}\), can be determined to obtain

$$\begin{aligned} N= & {} \frac{1}{M_p^2}\int _{\phi _\mathrm{end}}^{\phi _N}\frac{Q\,V}{V'}\,d\phi \nonumber \\\approx & {} \frac{5}{2}\left( \frac{C_1^4\,M_p^2}{18^2\,C_r\,M^2}\right) ^{\frac{1}{5}}\left( e^{\frac{3}{5}\sqrt{\frac{2}{3}}\,\frac{\phi _N}{M_p}} -e^{\frac{3}{5}\sqrt{\frac{2}{3}}\,\frac{\phi _\mathrm{end}}{M_p}} \right) \nonumber \\\approx & {} \frac{5}{2}\,\left( \frac{\Theta }{18^2}\right) ^{\frac{1}{5}}\,e^{\frac{3}{5}\sqrt{\frac{2}{3}}\,\frac{\phi _N}{M_p}}=\frac{5}{4}\,\bigg [ \frac{2^3}{3^4}\,\Theta \bigg (\sqrt{\frac{4}{3\,\varepsilon }}\,\bigg )^{3}\,\Bigg ]^{\frac{1}{5}}, \nonumber \\ \end{aligned}$$
(2.49)

where \(\Theta \equiv \left( {C_1^4\,M_p^2}/{C_r\,M^2}\right) \) and the condition \(\phi _N\gg \phi _\mathrm{end}\) has been applied. This leads to

$$\begin{aligned} e^{\chi _N}= & {} \frac{12}{5}\left( \frac{6}{5^2}\,\frac{N^5}{\Theta }\right) ^{\frac{1}{3}},\quad \nonumber \\ \Longrightarrow \phi _N= & {} \sqrt{\frac{3}{2}}\,\frac{M_p}{3}\,\ln \left( 8\frac{6^4}{5^5}\, \frac{N^5}{\Theta }\right) , \end{aligned}$$
(2.50)

where \(\chi _N\equiv \sqrt{2/3}\,{\phi _N}/{M_p}\). As done above, we therefore can re-write the slow-roll parameters in terms of the number of e-folds, N, by using the large field approximation in the strong Q limit via

$$\begin{aligned} \varepsilon\approx & {} \frac{5^3}{4\cdot \,3^3}\left( \frac{5^2}{6}\,\frac{\Theta }{N^5}\right) ^{\frac{2}{3}},\nonumber \\ \eta\approx & {} - \sqrt{\frac{4\,\varepsilon }{3}} = -\frac{5\sqrt{5}}{9}\left( \frac{5^2}{6}\,\frac{\Theta }{N^5}\right) ^{\frac{1}{3}},\nonumber \\ \beta\approx & {} -\frac{2\,\sqrt{3\,\varepsilon }}{5} = -\frac{\sqrt{5}}{3}\left( \frac{5^2}{6}\,\frac{\Theta }{N^5}\right) ^{\frac{1}{3}}. \end{aligned}$$
(2.51)

Recalling the power spectrum in Eq. (2.32), we re-write the power spectrum as

$$\begin{aligned} \Delta _{\mathcal {R}}= & {} \frac{V(\phi _N) \big (1 + Q_N\big )^2}{24\,\pi ^2\,M_p^4\,\varepsilon }\nonumber \\&\times \left( 1 + 2\,n_N + \left( \frac{T_N}{H_N}\right) \frac{2\sqrt{3}\,\pi \,Q_N}{\sqrt{3+4\pi \,Q_N}}\right) G(Q_N),\nonumber \\ \end{aligned}$$
(2.52)

where the function \(G(Q_N)\) represents the growth rate of the inflaton field fluctuation from the coupling between the inflaton and the radiation fluid in the thermal bath [38]. Having solved the full set of the cosmological perturbation equations in the warm inflation scenario, the shape of the function \(G(Q_N)\) for the linear temperature of the dissipative parameter in Eq. (2.37) can be determined by performing a numerical fitting as done in Ref. [47]. For the Higgs-like and plateau-like potentials, the growing mode function has been proposed by Ref. [39] and is given by

$$\begin{aligned} G_1(Q_N) \simeq 1 + 0.18\,Q_N^{1.4} + 0.01\,Q_N^{1.8}, \end{aligned}$$
(2.53)

while the original growing mode function of the warm little inflation is written by [46]

$$\begin{aligned} G_2(Q_N) \simeq 1 + 0.335\,Q_N^{1.364} + 0.0185\,Q_N^{2.315}. \end{aligned}$$
(2.54)

In addition, at the thermalized inflaton fluctuation limit, \(1+ 2\,n_N \simeq 2\,T_N/H_N \) and \(T_N/H_N = 3\,Q_N/C_1\), one can re-write the power spectrum in the following form [39],

$$\begin{aligned} \Delta _{\mathcal {R}} \simeq \frac{5\,C_1^3}{12\,\pi ^4\,g_*\,Q_N^2} \left( 1+ \frac{\sqrt{3}\,\pi \,Q_N}{\sqrt{3+4\pi \,Q_N}}\right) G(Q_N)\, , \end{aligned}$$
(2.55)

where the relation \(\rho _r/V(\phi ) = \varepsilon \,Q/2(1+Q)^2\) is used to obtain above equation. We note that the above power spectrum in this limit is independent of the inflaton potential [39].

Then, the tensor-scalar ratio parameter r in this case can be obtained by using Eqs. (2.34) and (2.55). It reads

$$\begin{aligned} r \!=\! \frac{\Delta _T}{\Delta _{\mathcal {R}}} \!=\! 16\,\varepsilon \left[ \frac{6\,Q_N^3}{C_1}\left( 1+ \frac{\sqrt{3}\,\pi \,Q_N}{\sqrt{3+4\pi \,Q_N}}\right) G(Q_N)\right] ^{-1}. \nonumber \\ \end{aligned}$$
(2.56)

The spectral index of the power spectrum with the growing mode function in Eq. (2.53) is given by [39, 40, 47]

$$\begin{aligned}&n_s = 1 + \frac{Q_N}{3+5\,Q_N}\frac{\big (6\,\varepsilon - 2\,\eta \big )}{\Delta _{\mathcal {R}}}\,\frac{d\Delta _{\mathcal {R}}}{dQ_N}, \end{aligned}$$
(2.57)
$$\begin{aligned}&\frac{d\Delta _{\mathcal {R}}}{dQ_N} = \frac{5\,C_1^3}{12\,\pi ^4\,g_*}\Bigg [\frac{1}{Q_N^2}\left( 1+ \frac{\sqrt{3}\,\pi \,Q_N}{\sqrt{3+4\pi \,Q_N}}\right) \frac{dG(Q_N)}{dQ_N} \nonumber \\&\quad - \frac{1}{Q_N^3}\left( 2+ \frac{\sqrt{3}\,\pi \,Q_N}{ \sqrt{3+4 \pi \,Q_N}}+\frac{2 \,\sqrt{3}\, \pi ^2\,Q_N^2}{(3 + 4\,\pi \, Q_N)^{\frac{3}{2}}}\right) G(Q_N) \Bigg ]. \nonumber \\ \end{aligned}$$
(2.58)

In this section, we have derived all relevant equations of the warm inflation that will be used to confront with the observational data by considering two types of the growing mode functions, \(G_{1,2}(Q_N)\) as shown in Eqs. (2.53) and (2.54) in the next section.

3 Confrontation with the Planck 2018 data

In order to confront the results with the observational data, we need to compute the relevant observables, i.e., the tensor to scalar perturbation ratio, r, and the spectral index, \(n_s\), by using Eqs. (2.35) and (2.36), respectively. Moreover, we separate our investigations into two cases in the latter. The first one is the exclusion of the growing mode in the strong (\(Q\gg 1\)) and weak (\(Q\ll 1\)) limits. While in the second case, we will include the growing mode effects in the strong regime only.

We will constrain our scalaron potential with the COBE normalization condition [52] for fixing parameters in the Higgs–Starobinsky model. To generate the observed amplitude of the density perturbation (\(A_{s}\)), the potential must satisfy the COBE renormalization at horizon crossing \(\phi =\phi _{N}\):

$$\begin{aligned} \frac{V}{\varepsilon }\bigg |_{\phi =\phi _{N}} \simeq (0.0276\,M_{p})^{4}=\frac{3\mathcal{M}}{4}e^{2\chi _N}, \end{aligned}$$
(3.1)

where we have defined \(\mathcal{M}\equiv 3M^{2}_{p}M^{2}/4,\,\chi _N\equiv \sqrt{2/3}\,\phi _N/M_p\) and this is used to impose a constraint on the mass scale M given in Eq. (2.7).

3.1 Weak regime, \(Q\ll 1\)

The tensor to scalar perturbation ratio in the weak regime \(Q\ll 1\) is taken into the following form

$$\begin{aligned} r = 16\left[ \frac{4}{3\left( e^{\chi _N} - 1\right) ^2} \right] . \end{aligned}$$
(3.2)

According to the above equation, the parameter r has the same form as that of the standard (cold) inflation result. For the spectral index, \(n_s\), in the weak limit is written by

$$\begin{aligned} n_s= & {} 1 - \frac{24}{3\left( e^{\chi _N} - 1\right) ^2} + \frac{8}{3}\,\frac{\left( 2 - e^{\chi _N}\right) }{\left( e^{\chi _N} - 1\right) ^2}\nonumber \\&+ \frac{2}{3}\left[ \frac{\Theta \,e^{2\chi _N}}{3\left( e^{\chi _N} - 1 \right) ^4} \right] ^{\frac{1}{3}}\nonumber \\&\left[ \frac{32}{3\left( e^{\chi _N} - 1\right) ^2} - \frac{8}{9}\,\frac{\left( 1 - 2\,e^{\chi _N}\right) }{\left( e^{\chi _N} - 1\right) ^2}\right] .\nonumber \\ \end{aligned}$$
(3.3)

Again, it is more convenient to write r and \(n_{s}\) in terms of a number of e-folds N. For \(Q\ll 1\) case, with help of Eqs. (2.43) and (2.45), they read

$$\begin{aligned} r\approx & {} \frac{12}{N^{2}}, \end{aligned}$$
(3.4)
$$\begin{aligned} n_s\approx & {} 1-\frac{2}{N}-\frac{9}{2^2} +\frac{2}{3}\bigg (\frac{3 \left( 1.72 \times 10^6 C_{1}^4\right) }{2^4 C_{r}}\bigg )^{1/3}\nonumber \\&\left( \frac{6}{N^2}+\frac{3}{2 N}\right) . \end{aligned}$$
(3.5)

Here we write \(n_{s}\) in terms of parameters \(C_{1},\,C_{r}\) and N. Moreover, we solve Eq. (3.1) to obtain

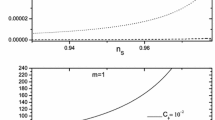
$$\begin{aligned} M^{2}=\frac{5.80\times 10^{-7}\,M_{p}^{2}}{N^{2}}. \end{aligned}$$
(3.6)

In Fig. 1, we compare our predictions given by Eqs. (3.4) and (3.5) for different values of N with Planck’18 results for TT, TE, EE, +lowE+lensing+BK15+BAO [53]. As an example, we use typical values of \(C_{r},\,C_{1}\) as given in Ref. [54]. In this weak limit, we also find that the results show very small values of r. In order to have the predictions fit well inside the \(1\,\sigma \) regions of the Planck 2018 data, values of \(C_r\) are constrained between \(55< N < 70\) using \(C_r=70,\,C_{1}=2.0\times 10^{-7}\). We discover for the weak limit that the thermal bath makes negligible effects to the inflationary observables r and \(n_{s}\) due to a very tiny values of \(C_{1}\) required.

For the weak limit, we can also use the scalaron mass parameter to constrain underlying parameters \(\alpha ,\,\lambda ,\,\xi \) using the relation:

$$\begin{aligned} M^2 = \frac{M_p^2}{12\left( \alpha + 3\,\xi ^2/(2\,\lambda )\right) }. \end{aligned}$$
(3.7)

Combining Eqs. (3.6) and (3.7), we find

$$\begin{aligned} \frac{M_p^2}{12\left( \alpha + 3\,\xi ^2/(2\,\lambda )\right) }\approx \frac{5.80\times 10^{-7}\,M_{p}^{2}}{N^{2}}, \end{aligned}$$
(3.8)

which yields

$$\begin{aligned} \lambda =\frac{1.04\times 10^{-5} \xi ^2}{N^2-6.96\times 10^{-6} \alpha }. \end{aligned}$$
(3.9)

We find for example using \(\lambda \approx 1044/\big (3600-6.96\times 10^{-6} \alpha \big )\) with \(N=60,\,\xi =10{,}000\). We find that values of underlying parameters \(\alpha ,\,\lambda ,\,\xi \) are not affected by the thermal bath counterpart.

Fig. 1
figure 1

We compare the theoretical predictions of the weak limit \(Q\ll 1\) given in Eqs. (3.4) and (3.5) in the \((r-n_{s})\) plane for different values of N using \(C_{r}=70\) and \(C_{1}=2.0\times 10^{-7}\) with Planck’18 results for TT, TE, EE, +lowE+lensing+BK15+BAO

Full size image

3.2 Strong regime, \(Q\gg 1\), with the growing mode effect

The power spectrum of the inflaton fluctuation with the growing mode provides more details about the coupling between inflaton and radiation fluid that we have calculated the relevant observables of the HS gravity in the warm inflation scenario. To confront with the Planck data 2018, it is convenient to re-write the tensor-scalar, r parameter and the spectral index, \(n_s\) in terms of the number of e-folds, N. More importantly, two forms of the growing mode functions \(G_{1,2}(Q_N)\) in Eqs. (2.53) and (2.54) will be used to compare to the data. We start with the r parameter. Recalling the result of the r parameter with the growing mode in Eq. (2.56), we find

Fig. 2
figure 2

We compare the theoretical predictions of \((r,\,n_s)\) in the strong limit \(Q>>1\) including the growing mode effect. In each contour, we consider two forms of \(G(Q_N)\) given in Eq. (3.12) for \(G_{1}(Q_N)\) (purple curve) and (3.13) for \(G_{2}(Q_N)\) (orange curve) with \(N=50\) (left panel) and \(N=55\) (right panel). We compare theoretical predictions of \((r,\,n_s)\) for different values of \(C_{r}\) and keep \(C_1\) fixed with \(C_{1}=8.0\times 10^{-1}\) with Planck’18 results for TT, TE, EE, +lowE+lensing+BK15+BAO

Full size image
$$\begin{aligned}&r_{1,2} =16\,\frac{5^3}{4\cdot \,3}\,Q^{2}_{N} \,\Bigg [\left( \frac{6}{C_1}\,\right) \,Q^{3}_{N} \mathcal {D}_N\,G_{1,2}(N)\Bigg ]^{-1}, \end{aligned}$$
(3.10)
$$\begin{aligned}&\mathcal {D}_N = 1+ \frac{\sqrt{3}\,\pi Q_{N}}{\sqrt{\left( 3 + 4\,\pi Q_{N}\right) }} , \end{aligned}$$
(3.11)
$$\begin{aligned}&G_1(N) = 1 + 0.18\,Q_{N}^{1.4} + 0.01\,Q_{N}^{1.8}, \end{aligned}$$
(3.12)
$$\begin{aligned}&G_2(N) = 1 + 0.335\,Q_{N}^{1.364} + 0.0185\,Q_{N}^{2.315}, \end{aligned}$$
(3.13)

with \(\Theta = \left( C_1^4/C_r\right) \left( M_p^2/M^2\right) \). In addition, Eqs. (2.46), (2.50) and (2.51) have been used to obtain above equation.

Substituting Eqs. (2.46), (2.50), (2.51) and (2.55) into Eq. (2.57), the spectral index with the growing mode in terms of the number of e-folds, N, is given by

$$\begin{aligned} n_s^{(1,2)}= & {} 1 + \frac{Q_{N}}{3+5\,Q_{N}}\left( \frac{5^3}{2}\,Q^{2}_{N} + \frac{10\sqrt{5}}{3}\,Q_{N}\right) \nonumber \\&\times \frac{1}{\Delta _{\mathcal {R}}^{(1,2)}(N)}\,\frac{d\Delta _{\mathcal {R}}^{(1,2)}(N)}{dQ_N},\end{aligned}$$
(3.14)
$$\begin{aligned} \Delta _{\mathcal {R}}^{(1,2)}(Q_{N})= & {} \frac{5\,C_1^3}{12\,\pi ^4\,g_*}\,\frac{\mathcal {D}_N\,G_{1,2}(Q_{N})}{Q_{N}^2}, \end{aligned}$$
(3.15)
$$\begin{aligned} \frac{d\Delta _{\mathcal {R}}^{(1,2)}}{dQ_N}= & {} \frac{5\,C_1^3}{12\,\pi ^4\,g_*}\Bigg (\frac{\mathcal {D}_N\,G'_{1,2}(Q_{N})}{Q_{N}^{2}} - \frac{\mathcal {D}'_Q\, G_{1,2}(Q_{N})}{\,Q_{N}^{3}}\Bigg ), \end{aligned}$$
(3.16)
$$\begin{aligned} \mathcal {D}'_Q= & {} 2+ \frac{\sqrt{3}\,\pi \,Q_{N}}{\left( 3 + 4\,\pi \,Q_{N}\right) ^{\frac{1}{2}}} +\frac{2 \,\sqrt{3}\, \pi ^2\,Q_{N}^2}{\left( 3 + 4\,\pi \,Q_{N}\right) ^{\frac{3}{2}}}, \end{aligned}$$
(3.17)
$$\begin{aligned} G'_1(Q_{N})= & {} 0.252\,Q_{N}^{0.4}+0.018\,Q_{N}^{0.8} \end{aligned}$$
(3.18)
$$\begin{aligned} G'_2(Q_{N})= & {} 0.457\,Q_{N}^{0.364}+ 0.0428\,Q_{N}^{1.315}, \end{aligned}$$
(3.19)

where \(Q_{N}\equiv \frac{1}{3}\left( \frac{5^2\,\Theta }{6\,N^2}\right) ^{\frac{1}{3}}\). Having used all variables defined above, we can write an explicit form of \(r_{1,2}\) and \(n_s^{(1,2)}\) written in terms of \(C_{r},\,C_{1}\) and N to obtain

$$\begin{aligned} r_1= & {} \frac{2.804 \left( C_{r} C_1\right) ^{1/5}}{N^2 X \left( 1+0.620 \left( \frac{C_{1}^{12/5}}{C_{r}^{3/5}}\right) ^{0.6}+4.462 \left( \frac{C_{1}^{12/5}}{C_{r}^{3/5}}\right) ^{0.47}\right) },\nonumber \\ \end{aligned}$$
(3.20)
$$\begin{aligned} r_2= & {} \frac{2.804 \left( C_{r} C_1\right) ^{1/5}}{N^2 X \left( 1+3.738 \left( \frac{C_{1}^{12/5}}{C_{r}^{3/5}}\right) ^{0.77}+7.646 \left( \frac{C_{1}^{12/5}}{C_{r}^{3/5}}\right) ^{0.455}\right) }, \nonumber \\ \end{aligned}$$
(3.21)
$$\begin{aligned} n_{s}^{(1)}= & {} 1+\frac{972.04 V \left( 0.0101909 W X\left( \frac{C_{1}^{12/5}}{C_{r}^{3/5}}\right) ^{1/3} - 0.00102877 Y Z\right) }{X Y \left( 3+49.5296 \left( \frac{C_{1}^{12/5}}{C_{r}^{3/5}}\right) ^{1/3}\right) }, \nonumber \\ \end{aligned}$$
(3.22)
$$\begin{aligned} n_{s}^{(2)}= & {} 1+\frac{972.039 V \left( 0.010191 XS \left( \frac{C_{1}^{12/5}}{C_{r}^{3/5}}\right) ^{1/3} - 0.00102876 U Z\right) }{U X \left( 3+49.5296 \left( \frac{C_{1}^{12/5}}{C_{r}^{3/5}}\right) ^{1/3}\right) }, \nonumber \\ \end{aligned}$$
(3.23)

where we have defined new variables as

$$\begin{aligned} X= & {} 1+\frac{53.902 \left( \frac{C_{1}^{12/5}}{C_{r}^{3/5}}\right) ^{1/3}}{\sqrt{3+124.481 \left( \frac{C_{1}^{12/5}}{C_{r}^{3/5}}\right) ^{1/3}}}, \nonumber \\ Y= & {} 1+0.620312 \left( \frac{C_{1}^{12/5}}{C_{r}^{3/5}}\right) ^{0.60}+4.462 \left( \frac{C_{1}^{12/5}}{C_{r}^{3/5}}\right) ^{0.47}, \nonumber \\ Z= & {} 1+X+\frac{3354.9 \left( \frac{C_{1}^{12/5}}{C_{r}^{3/5}}\right) ^{2/3}}{\left( 3+124.481 \left( \frac{C_{1}^{12/5}}{C_{r}^{3/5}}\right) ^{1/3}\right) ^{3/2}},\nonumber \\ W= & {} 0.112717 \left( \frac{C_{1}^{12/5}}{C_{r}^{3/5}}\right) ^{0.27}+0.630606 \left( \frac{C_{1}^{12/5}}{C_{r}^{3/5}}\right) ^{0.13},\nonumber \\ V= & {} 73.8343 \left( \frac{C_{1}^{12/5}}{C_{r}^{3/5}N^3}\right) ^{1/3} + 6132.95 \left( \frac{C_{1}^{12/5}}{C_{r}^{3/5}N^3}\right) ^{2/3},\nonumber \\ U= & {} 1+3.73825 \left( \frac{C_{1}^{12/5}}{C_{r}^{3/5}}\right) ^{0.77}+7.64619 \left( \frac{C_{1}^{12/5}}{C_{r}^{3/5}}\right) ^{0.45},\nonumber \\ S= & {} 0.873623 \left( \frac{C_{1}^{12/5}}{C_{r}^{3/5}}\right) ^{0.44}+1.05285 \left( \frac{C_{1}^{12/5}}{C_{r}^{3/5}}\right) ^{0.12}. \end{aligned}$$
(3.24)

Moreover, we solve Eq. (3.1) to obtain

$$\begin{aligned} M^{2}=0.0126\,\frac{M_p}{N}\left( \frac{C_1^4}{C_r}\right) ^{1/5}. \end{aligned}$$
(3.25)

Having compared with the weak regime case, the mass scale in the strong regime does also depend on the values of \(C_r\) and \(C_1\).

Fig. 3
figure 3

We compare the theoretical predictions of \((r,\,n_s)\) in the strong limit \(Q>>1\) including the growing mode effect. In each contour, we consider \(G_{1}(Q_N)\) (left panel) given in Eq. (3.12) with \(C_r=70\) (purple) and \(C_r=150\) (orange); whilst \(G_{2}(Q_N)\) (right panel) given in Eq. (3.13) with \(C_r=70\) (purple) and \(C_r=150\) (orange). We compare theoretical predictions of \((r,\,n_s)\) for different values of N ranging from \([40,\,100]\) and keep \(C_1\) fixed with \(C_{1}=8.0\times 10^{-1}\) with Planck’18 results for TT, TE, EE, +lowE+lensing+BK15+BAO

Full size image

We compare our predictions in the strong regime for different values of \(C_{r}\) with Planck’18 results for TT, TE, EE, +lowE+lensing+BK15+BAO illustrated in Fig. 2. Here we consider \(C_{1}=8.0\times 10^{-1}\) and keep a number of e-folds fixed at \(N=50\) (left panel) and \(N=55\) (right panel). On the left panel, we consider \(G_{1}(Q_N)\) (purple curve) and \(G_{2}(Q_N)\) (orange curve) and find that the predictions given by \(G_{1}(Q_N)\) are in excellent agreement with the \(1\,\sigma \) region of the Planck contour, while the results obtained from \(G_{2}(Q_N)\) fit in the \(2\,\sigma \) region of the Planck data only for large values of \(C_{r}\gtrsim 210\). Moreover, on the right panel, we display \(G_{1}(Q_N)\) (purple curve) and \(G_{2}(Q_N)\) (orange curve) and discover that the results given by \(G_{1}(Q_N)\) fit in the \(1\,\sigma \) region of the Planck contour for \(C_{r}\gtrsim 50\), while with the same values of input parameters, i.e., \(C_{1},\,N,\,C_{r}\), the results obtained from \(G_{2}(Q_N)\) lie outside the \(2\,\sigma \) region of the Planck data.

We further consider scenarios in which values of \(C_{1}\) and \(C_{r}\) are kept fixed for \(C_1=0.8\) and \(C_{r}=70,\,150\) for each \(G_{i}(Q_{N})\) displayed in Fig. 3. On the left panel, we show the results obtained from \(G_{1}(Q_{N})\) and find that the predictions when \(C_{r}=70\) (purple curve) and \(C_{r}=150\) (orange curve) fit in the \(1\,\sigma \) region of the Planck data for \(47\lesssim N\lesssim 57\) with \(C_{1}=0.8\), whilst on the right panel, we consider the predictions obtained from \(G_{2}(Q_{N})\) and notice that the results using \(C_{r}=70\) (purple curve) and \(C_{r}=150\) (orange curve) fit in the \(1\,\sigma \) region of the Planck data for \(N\lesssim 45\) and for \(N\lesssim 43\), respectively.

By using Eqs. (3.20) and (3.21) with \(r<0.07\), one may find the range of the possible \(C_1\) as function of \(C_r\). Moreover, the constraints on the coefficient \(C_{1}\) can be translated into constraints on the relation between Yukawa coupling g and h as follow. Let us consider Eq. (2.38) and choose \(C_{1}=0.8\) and \(N=50\) as an example. We then find from Eq. (2.38)

$$\begin{aligned} 0.8&\simeq \frac{3\,g^2}{h^2\big (1-0.34\log (h) \big )}\longrightarrow g\simeq 7.303\nonumber \\&\quad \times 10^{-2}\,\sqrt{50\,h^2-17\,h^2 \log (h)}. \end{aligned}$$
(3.26)

The above relation display the relation between the Yukawa coupling of the heavy fermions and the inflaton, g and the Yukawa coupling of heavy fermions, light singlet scalar and other light fermion particles, h. One may obtain the allowed values of the Yukawa couplings g and h by varying the h coupling with \(h^2/4\pi <1\) due to the validity of the perturbative expansion of the theory.

4 Conclusion

In this work, we have demonstrated a class of warm inflation scenario using HS gravity with a linear temperature of the dissipative parameter. We have studied the dynamics of the warm inflation in the Einstein frame and considered our analysis into two regimes, strong (\(Q\gg 1\)) and weak (\(Q\ll 1\)). In particular, the effect of the growing mode, i.e., the interaction between inflaton and radiation fluid, has been taken into account to the power spectrum amplitude. We have calculated relevant observables in the warm inflation in order to compare to the observational data. In the strong regime, we have discovered that inflationary parameters r and \(n_{s}\) can be written in terms of the parameters \(C_r\) and \(C_{1}\) and hence they are affected by having the thermal bath, while in the weak regime the inflationary parameters are very weakly affected by the thermal bath. Therefore the thermal bath effects are approximately negligible in this regime.

According to our analysis, we have found that the HS model in weak regime provides an excellent agreement with the data, whilst the thermal bath effects have played an significant role in the strong dissipative regime. The ranges of the parameters in HS model have been evaluated to make the predictions compatible with the Planck 2018 results. Consequently, we have also found that the Starobinsky gravitational coupling, \(\alpha \) is slightly modified by the dissipative parameters \(C_r\) and \(C_{1}\) present in warm inflation. Interestingly, in order to be satisfied with the Planck data, our results of \(C_1\) in the strong regime \(Q\gg 1\) exceed the upper bound of \(C_1\lesssim 0.02\) mentioned in the original model of warm little inflation [39, 46]. Additionally, when including the growing mode effect to the strong regime, we discovered that the dissipative parameters \(C_r\) also exceed the standard value, \(C_r = 70\) predicted by the minimal supersymmetric standard model [41]. Finally, with the sizeable number of e-folds and proper choices of parameters, we have also discovered for the strong regime that the predictions of warm HS model present in this work are in very good agreement with the latest Planck 2018 results.

In addition, more models of the different/same dissipative parameter are interesting for future investigation. More importantly, further studies on the dynamics of the universe after radiation-dominated era might shed some light on the Hubble tension problem. We wish to address this topic for future study.