New limits on double-beta decay of $^{190}$Pt and $^{198}$Pt

Abstract

A search for double-beta decay of $^{190}$Pt and $^{198}$Pt with emission of $\gamma$-ray quanta was realized at the HADES underground laboratory with a 148 g platinum sample measured by two ultralow-background HPGe detectors over 8946 h. The isotopic composition of the platinum sample has been measured with high precision using inductively coupled plasma mass spectrometry. New lower limits for the half-lives of $^{190}$Pt relative to different channels and modes of the decays were set on the level of $\lim T_{1/2}\sim 10^{14}$–$10^{16}$ year. A possible exact resonant $0\nu KN$ transition to the 1,2 1326.9 keV level of $^{190}$Os is limited for the first time as $T_{1/2} \ge 2.5 \times 10^{16}$ year. A new lower limit on the double-beta decay of $^{198}$Pt to the first excited level of $^{198}$Hg was set as $T_{1/2} \ge 3.2\times 10^{19}$ year, one order of magnitude higher than the limit obtained in the previous experiment.

1 Introduction

Double-beta decay was considered for the first time by Goeppert-Mayer in 1935 [1]. The neutrino accompanied mode of the decay with emission of electrons (two-neutrino double-beta decay, $2\nu 2\beta ^-$) is allowed in the Standard Model of particles and interactions (SM) and is already observed in eleven nuclei with measured half-lives in the range $T_{1/2}\sim (10^{19}$–$10^{24})$ year [2]. Another possibility could be $2\beta ^-$ decay without neutrino emission, neutrinoless double-beta decay ($0\nu 2\beta ^-$). However, this process violates the lepton number conservation and is only possible if neutrinos are massive Majorana particles [3]. Thus, the $0\nu 2\beta ^-$ decay is the most sensitive test of the lepton number conservation law and one of the most promising tools to study properties of the neutrino and the weak interaction. In general, the neutrinoless process can be mediated by many effects beyond the SM and is considered as one of the most powerful probes of the SM [4,5,6,7]. Despite the attempts, the $0\nu 2\beta ^-$ decay is still not observed: the most sensitive experiments give upper half-life limits in the range $\lim T_{1/2}\sim (10^{24}$–$10^{26})$ year. This allows to bound the effective Majorana neutrino mass at the level of $\lim \langle m_{\nu }\rangle \sim$ (0.1–0.5) eV (see, e.g., the reviews [6,7,8,9] and the recent original works [10,11,12,13,14,15,16]).

Fig. 1

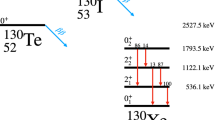
A simplified decay scheme of $^{190}$Pt [27]. The energies of the excited levels and of the emitted $\gamma$ quanta are in keV (the relative intensities of the $\gamma$ quanta are given in parentheses). $Q_{2\beta }$ and $Q_{\alpha }$ are the double-beta decay and alpha decay energies of $^{190}$Pt, respectively

Other channels of double-beta decay are “double-beta plus” decay processes: double-electron capture ($2\varepsilon$), electron capture with positron emission ($\varepsilon \beta ^+$), and double-positron decay ($2\beta ^+$). Although allowed in the SM, the two-neutrino mode of the $2\varepsilon$ process (theoretically the fastest decay channel due to the biggest values of the phase space factor) has yet to be indisputably discovered. There are indications of $2\nu 2K$ decay with $T_{1/2}\sim 10^{21}$ year in $^{130}$Ba [17,18,19] and $^{78}$Kr [20, 21]. However, the indications for $^{130}$Ba $2\nu 2K$ decay was obtained only in geochemical experiments by detection of an anomaly in the traces of xenon isotopic concentration in barite minerals. The results of the experiment [20, 21] with a proportional chamber need to be confirmed. Recently an observation of the $2\nu 2K$ decay of $^{124}$Xe with $T_{1/2}=(1.8 \pm 0.5) \times 10^{22}$ year was claimed by the XENON collaboration by using the XENON1T dark-matter detector [22]. As for the neutrinoless double-beta plus decay processes, their mechanisms are the same as for the decay with electrons emission. Moreover, there are some additional arguments to develop experimental methods to search for the $0\nu 2\varepsilon$, $0\nu \varepsilon \beta ^+$ and $0\nu 2\beta ^+$ decays, taking into account the potential to investigate the possible contribution of the right-handed currents to the $0\nu 2\beta ^-$ decay rate if observed [23], and an interesting possibility of a resonant $0\nu 2\varepsilon$ process (see [24] and references therein).

Two platinum isotopes are potentially unstable relative to the double-beta decay: $^{190}$Pt with the decay energy $Q_{2\beta }=1401.3(4)$ keV [25] and the isotopic abundance $\delta =0.012(2)\%$ [26], and $^{198}$Pt with the decay energy $Q_{2\beta }=1050.3(21)$ keV [25] and the isotopic abundance $\delta =7.356(130)\%$ [26]. A simplified decay scheme of $^{190}$Pt is shown in Fig. 1. The nuclide remains one of few nuclides with a possibility of exact resonant $0\nu 2\varepsilon$ decay. The resonant character of the process is expected in the $0\nu KN$ transition to the 1,2 1326.9(10) keV excited level of the daughter [24]. It should be stressed that the decay channel was not considered in the previous work [28] due to a rather poor accuracy of the $Q_{2\beta }$ value at the time of the experiment (in 2011 the recommended $Q_{2\beta }$ was 1383(6) keV [29]). A status of the decay as a potential resonance can be characterized by the resonance parameter $R_f$:

$$\begin{aligned} R_f = \Gamma _f/(\Delta ^2 + \Gamma _f^2/4), \end{aligned}$$

(1)

where $\Gamma _f = \Gamma _1 + \Gamma _2$ is the de-excitation width of the electron shell of the daughter nuclide. The degeneracy parameter $\Delta$ is equal to $Q_{2\beta }-E_{exc}-E_{b1}-E_{b2}$, where $E_{exc}$ is the energy of the daughter nucleus excited level, $E_{bi}$ are the binding energies of the captured electrons on the atomic shells of the daughter atom. Taking into account the presently recommended $Q_{2\beta }$ value [25] the resonance parameter for $^{190}$Pt (normalized on the value for the $0\nu 2\varepsilon$ decay $^{54}$Fe $\rightarrow$ $^{54}$Cr) can reach one of the biggest values $\approx 7.0\times 10^{8}$ among the possible resonant transitions [24].¹ The method of ultralow-background HPGe $\gamma$-ray spectrometry was applied in the present study to search for different channels and modes of $2\varepsilon$ and $\varepsilon \beta ^+$ processes in $^{190}$Pt, including the possible resonant transitions in the nuclide.

A simplified decay scheme of another possible $2\beta$ unstable isotope of platinum, $^{198}$Pt, is presented in Fig. 2. The $2\beta ^-$ transition of $^{198}$Pt to the first $2^+$ 411.8 keV excited level of $^{198}$Hg is expected to be accompanied by emission of a $\gamma$-ray quanta with energy 411.8 keV that can be detected by $\gamma$-spectrometry methods too.

Fig. 2

A simplified decay scheme of $^{198}$Pt [30]. The energies of the excited level and of the emitted $\gamma$ quantum are in keV. $Q_{2\beta }$ is the double-beta decay energy of $^{198}$Pt

In the next section we describe the high-purity platinum sample, precise measurements of its isotopic composition, and the ultralow background HPGe detector system used in the experiment. The data analysis and obtained limits on the $2\varepsilon$ and $\varepsilon \beta ^+$ processes in $^{190}$Pt and the $2\beta ^-$ decay of $^{198}$Pt to the first excited level of the daughter are presented in Sect. 3. A summary of the experiment is given in the Conclusions section.

2 Experiment

2.1 Platinum sample, isotopic composition of the material

A disk-shaped sample of metallic platinum with a diameter of 25.04(1) mm, a thickness of 14.07(2) mm, and with a mass of 148.122(1) g was used in the experiment. The purity grade of the platinum is 99.95%.² The representative isotopic abundance of $^{190}$Pt in normal terrestrial materials has a rather big uncertainty $\delta =0.012(2)\%$ [26]. Thus, special mass-spectrometry measurements of the sample were realized.

The Pt isotopic measurements were acquired using a sector field ICP-MS ELEMENT XR (ThermoScientific) at the John de Laeter Centre for Isotope Research, Curtin University. Measurements of masses $^{190}$Pt,$^{192}$Pt, $^{194}$Pt, $^{195}$Pt, $^{196}$Pt, and $^{198}$Pt were performed in low resolution mode using electrostatic scanning (e-scan, i.e., peak jumping) from a set magnet mass at $^{190}$Pt. Due to the drastically different abundances of Pt isotopes, the ELEMENT XR’s triple detection mode is advantageous for such analyses as isotopes such as $^{190}$Pt and $^{192}$Pt can be measured in a pulse-counting detection mode, while the remaining masses can be analysed in analogue mode all within the same analytical session. Prior to the analysis of each sample, a blank solution of 2% HNO$_{3}$ was measured to correct for background. A summary of the platinum isotopic composition, as well as numbers of nuclei of the isotopes in the sample are presented in Table 1.

Table 1 Isotopic composition ($\delta$) of the platinum sample measured in the present work and the numbers of nuclei of each isotope in the sample calculated by using the measured isotopic concentrations. The combined standard uncertainties of the isotopic abundances are given with a coverage factor $k=2$ (approximately 95% level of confidence). The representative isotopic abundances from [26] are given too

2.2 Ultra low-level gamma-ray spectrometry measurements

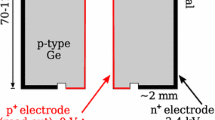
The platinum sample was measured in an ultralow-background HPGe-detector system located 225 m underground in the laboratory HADES (Belgium) [32, 33]. The detector system consists of two p-type Extended Range HPGe-detectors facing each other (see a schematic of the set-up in Fig. 3). Both the detectors were manufactured by Canberra semiconductor (Olen, Belgium). The detectors were shielded by 35 mm electrolytic copper (innermost) then 40 mm ultralow-level lead and on the outside 145 mm lead. The main characteristics of the HPGe detectors are presented in Table 2, more details of the detector system can be found in [34].

The data with the Pt sample were collected starting from February 6th, 2018 over a period of 805 days in 6 runs covering a live time of 8946 h (373 days). The measurements of background without sample were carried out for 674 h (28 days). The energy calibration and stability check was performed using reference point sources containing $^{60}$Co, $^{137}$Cs and $^{241}$Am.

3 Results and discussion

3.1 Radionuclides detected in the platinum sample

The sum energy spectra measured by the Ge7 and Ge15 detectors with the Pt sample and without sample (background) are shown in Fig. 4. The majority of the peaks can be assigned to $^{40}$K and nuclides of the $^{232}$Th, $^{235}$U and $^{238}$U decay families. There are also peaks of $^{22}$Na, $^{26}$Al, $^{54}$Mn, $^{60}$Co, $^{137}$Cs and $^{110m}$Ag. The traces of $^{22}$Na, $^{26}$Al and $^{110m}$Ag that were detected are presumingly reminiscence from neutron activation of minor impurities of the Pt-sample during the neutron experiment in Dresden and during air-transport. Radioactive $^{22}$Na and $^{26}$Al can be also cosmogenically generated in the aluminum details of the HPGe detectors [35]. $^{54}$Mn and $^{60}$Co are typical cosmogenic radionuclides that can be produced in Pt, copper and some other materials of the set-up. Presence of $^{137}$Cs can be a result of the set-up (sample) pollution after the Chernobyl or (and) Fukushima Daiichi nuclear disasters. In the Pt data there is a clear $\gamma$ peak with energy 137.2 keV due to the $\alpha$ decay of $^{190}$Pt to the 137.2 keV excited level of $^{186}$Os [36].³ Also peaks due to neutron-gamma reactions on the materials of the set-up were observed: in particular, a 139.7-keV peak of $^{75m}$Ge produced by neutron-gamma reaction on $^{74}$Ge, a 198.4-keV peak from $^{70}$Ge(n,$\gamma$)$^{71m}$Ge reaction, a 202.6-keV peak from $^{115}$In(n,$\gamma$)$^{116}$In reaction. There is also a peak of $^{41}$Ar with energy 1293.6 keV due to operation of the BR-1 nuclear reactor of the Belgian nuclear research centre. The peak is present on few specific days (approximately 15 days in total) during the measurements when air blows from the reactor towards the inlet of the ventilation for the HADES laboratory. We have decided to do not exclude the data with the $^{41}$Ar peak taking into account a rather mild effect of the radioactivity in the energy intervals of interest.

Fig. 3

Schematic of the experimental ultralow-background set-up with the HPGe detectors and the platinum sample

Table 2 Properties of the HPGe-detectors used in the present experiment. FWHM denotes the full width at half of maximum of $\gamma$-ray peak measured with a $^{60}$Co gamma-ray source

Fig. 4

Energy spectra in the energy intervals 20–800 keV (a) and 800–2700 keV (b) measured with the platinum sample over 8946 h (solid histogram) and without sample over 674 h (normalized to 8946 h, dots) by the ultralow-background HPGe-detector system. The energy of the $\gamma$ peaks is in keV

The energy dependence of the energy resolution in the sum energy spectrum measured with the Pt sample by the detectors Ge7 and Ge15 was determined for the low energy region (65–352 keV) by using intense X-ray and $\gamma$-ray peaks with energies 65.1 keV and 66.8 keV ($K_{\alpha 2}$ and $K_{\alpha 1}$ X-ray of Pt), 137.2 keV ($^{190}$Pt), 238.6 keV ($^{212}$Pb), 295.2 keV and 351.9 keV ($^{214}$Pb) as:

$$\begin{aligned} \text {FWHM \, (keV)}=1.08(12)+0.020(8)\sqrt{ E_{\gamma }}, \end{aligned}$$

(2)

where $E_\gamma$ is in keV. For the energies above 352 keV we use an approximation obtained by analysis of the $\gamma$ peaks 238.6 keV ($^{212}$Pb), 295.2 keV and 351.9 keV ($^{214}$Pb), 583.2 keV ($^{208}$Tl), 609.3 keV ($^{214}$Bi), 1173.2 keV and 1332.5 keV ($^{60}$Co) and 1460.8 keV ($^{40}$K):

$$\begin{aligned} \text {FWHM \, (keV)}=0.55(8)+0.049(4)\sqrt{ E_{\gamma }}. \end{aligned}$$

(3)

The specific activity⁴ of all detected radionuclides was calculated using the following formula:

$$\begin{aligned} A = (S_{sample}/t_{sample}-S_{bg}/t_{bg})/(\epsilon \cdot \eta \cdot m), \end{aligned}$$

(4)

where $S_{sample}$ ($S_{bg}$) is the area of a peak in the sample (background) spectrum; $t_{sample}$ ($t_{bg}$) is the time of the sample (background) measurement; $\epsilon$ is the $\gamma$-ray emission intensity of the corresponding transition; $\eta$ is the full energy peak efficiency; m is the sample mass. The detection efficiencies were calculated with the EGSnrc simulation package [37, 38], the events were generated homogeneously in the Pt sample. The Monte Carlo models of the two detectors have being validated through several participations in proficiency tests and an additional validation measurement was done using a $^{57}$Co point $\gamma$ source. The standard deviation of the relative difference between the simulations and the experimental data is $3.3\%$ for $\gamma$-ray peaks with energies 122.1 keV and 136.5 keV for the detectors Ge7 and Ge15. The estimated specific activities of radioactive impurities in the platinum are presented in Table 3.

Table 3 The specific activities of the detected radionuclides. The upper limits are given at 90% confidence level (C.L.), the reported uncertainties are the combined standard uncertainties calculated by summing the systematic and statistical uncertainties in quadrature. The reference date is the start of the measurement (February 6th, 2018)

3.2 Limits on the double-beta decay processes in $^{190}$Pt

No peculiarity was observed in the experimental energy spectra that could be ascribed to the $2\beta$ decay processes in $^{190}$Pt or $^{198}$Pt. Thus, we set limits on different modes and channels of the decays by using the following formula:

$$\begin{aligned} \lim T_{1/2} = N \cdot \eta \cdot t \cdot \ln 2 / \lim S, \end{aligned}$$

(5)

where N is the number of nuclei of interest in the sample (see Table 1), $\eta$ is the detection efficiency for the $\gamma$-ray (X-ray) quanta searched for, t is the measuring time, and $\lim S$ is the number of events of the effect which can be excluded at a given C.L. In the present work all the $\lim S$ values and the half-life limits are given with 90% C.L. The detection efficiencies of the detector system to the $\gamma$ (X-ray) quanta expected in different modes and channels of the double-beta processes in $^{190}$Pt and $^{198}$Pt were simulated with the EGSnrc simulation package [37, 38], the decay events were generated by the DECAY0 events generator [39].

A cascade of X-rays and Auger electrons due to deexcitation of Os electron shell with individual energies in the energy interval $\approx$ (61.5–73.4) keV is expected in the $2\nu 2K$ and $2\nu KL$ capture in $^{190}$Pt. However, the energies of the L X-rays are very low, (7.8–12.5) keV, and therefore heavily attenuated by the sample and also by the aluminium-windows of the HPGe-detectors. The Auger electrons avoid detection for the same reason. Thus, the response of the detector system to the $2\nu 2K$ and $2\nu KL$ decays of $^{190}$Pt was built assuming the following energies and intensities of X-rays from the K shell of Os atom (only the X-rays with the intensities higher than 0.5% were considered): 61.5 keV ($K_{\alpha 2}, 27.5\%$), 63.0 keV ($K_{\alpha 1}, 47.3\%$), 71.1 keV ($K_{\beta 3}, 5.45\%$), 71.4 keV ($K_{\beta 1}, 10.50\%$), 73.4 keV ($K_{\beta 2}, 3.69\%$) [40]. The detection efficiencies to the X-ray quanta were simulated by the EGSnrc code. To estimate $\lim S$ values for the $2\nu 2K$ and $2\nu KL$ decays, the energy spectrum taken with the Pt sample was fitted in the energy interval 49–86 keV by the $2\nu 2K$ ($2\nu KL$) distribution⁵ and a sum of several Gaussian functions to describe the 63.3-keV $\gamma$-ray peak of $^{234}$Th, X-ray peaks of Pt, Tl, Pb, Bi and Po present in the spectrum, plus a straight line to describe the continuous distribution. The result of the fit is shown in Fig. 5. Despite an empirical approach to build the background model, the quality of the fit is good: $\chi ^2$/n.d.f.$= 39.1/50=0.78$ (where n.d.f. is a number of degrees of freedom). The fit returned an area of the $2\nu 2K$ ($2\nu KL$) distribution $S=164\pm 125$ counts that indicates no evidence of the effect searched for. An excluded effect can be estimated by the simple Gaussian approach as $\lim S=369$ counts at 90% C.L. Taking into account the Monte-Carlo simulated detection efficiency for the whole $2\nu 2K$ ($2\nu KL$) effect $\eta =0.0092$ ($\eta =0.0047$), the following half-life limits were obtained for the $2\nu 2K$ and $2\nu KL$ capture in $^{190}$Pt:

$T_{1/2}^{2\nu 2K}~(^{190}$Pt, g.s.$~\rightarrow ~$g.s.) $\ge ~1.0\times 10^{15}$ year,

$T_{1/2}^{2\nu KL}~(^{190}$Pt, g.s.$~\rightarrow ~$g.s.) $\ge ~5.2\times 10^{14}$ year.

The half-life limits, the energies of the X-ray quanta ($E_{\gamma }$), which were used to set the $T_{1/2}$ limits, the detection efficiencies ($\eta$) and values of $\lim S$ are presented in Table 4,⁶ where also results of the previous experiment [28] are given for comparison. The limit for the $2\nu 2K$ decay half-life slightly exceeds the one reported in the previous work [28], while the limit for the $2\nu KL$ capture is obtained for the first time.

Fig. 5

The energy spectrum collected with the Pt sample by the HPGe detector system in the energy region where K X-ray quanta are expected for the $2\nu 2K$ and $2\nu KL$ decays of $^{190}$Pt. The fit of the data by the background model is shown by solid line, the peaks included in the model of the background are shown by dotted lines, while the excluded effect is presented by dashed line (the excluded distribution is multiplied by a factor 2 to improve visibility). Energy of $\gamma$ and X-ray quanta are in keV

Table 4 The half-life limits on $2\varepsilon$ and $\varepsilon \beta ^+$ processes in $^{190}$Pt and $2\beta ^-$ decay of $^{198}$Pt to the first excited level of $^{198}$Hg. The energies of the X-ray or $\gamma$ quanta ($E_{\gamma }$), which were used to set the $T_{1/2}$ limits, are listed with their corresponding detection efficiencies ($\eta$) and values of $\lim S$. The results of previous experiment [28] are given for comparison. Values of $\lim S$ and $T_{1/2}$ are given at 90% C.L. All the empirical fits from which the signal upper limits are derived describe the data well, with the goodness-of-fit values within $\chi ^2$/n.d.f. = (0.39–0.84)

The $2\nu$ double capture in $^{190}$Pt can undergo to several excited levels of $^{190}$Os (see Fig. 1). In this case, in addition to X-rays cascade, $\gamma$-peaks at the energy of the excited level (in the transition to the first $2^+$ 186.7 keV excited level) and also at the energies of the transitions between the initial and final levels of the daughter are expected. To estimate $\lim S$ value for a possible 186.7-keV peak area, the experimental spectrum was fitted in the energy interval 176–194 keV by a model consisting of a straight line, peaks of $^{235}$U and $^{226}$Ra with energies 185.7 keV and 186.2 keV, respectively, and a Gaussian peak at 186.7 keV with the width fixed according to the formula (2) to describe the effect searched for. The fit returns a 186.7-keV peak area $S=-28(39)$ counts, that corresponds to $\lim S=39$ counts following the recommendations [41]. A part of the energy spectrum gathered with the Pt sample in the vicinity of $\gamma$ peak 186.7 keV expected in the $2\varepsilon$ decay of $^{190}$Pt to the $2^+$ 186.7 keV excited level of $^{190}$Os is presented in Fig. 6. The half-life limits for the transitions to higher excited levels of $^{190}$Os were obtained in a similar way. The limits are presented in Table 4.

Fig. 6

The energy spectrum gathered with the Pt sample in the vicinity of $\gamma$ peak 186.7 keV expected in the $2\varepsilon$ decay of $^{190}$Pt to the $2^+$ 186.7 keV excited level of $^{190}$Os. The fit of the data is shown by solid line, while the excluded peak is presented by dashed line. The dotted lines show the peaks of $^{235}$U and $^{226}$Ra included in the background model. The energies of the background and expected $\gamma$ peaks are in keV

In the $0\nu$ double-electron capture in $^{190}$Pt the energy excess is assumed to be emitted by bremsstrahlung $\gamma$-ray quanta with an energy $E_{\gamma }=Q_{2\beta }-E_{b1}-E_{b2}-E_{exc}$. To estimate values of $\lim S$ for the $0\nu$ double-electron captures from K and L shells, the experimental spectrum was fitted in the regions of the expected peaks with energies (for the g.s. to g.s. transition) $1253.6 \pm 0.4$ keV, $1315.5 \pm 1.4$ keV and $1377.5 \pm 2.5$ keV for the $0\nu 2K$, $0\nu KL$, and $0\nu 2L$ captures, respectively. The variations of the expected peaks energy are due to the $Q_{2\beta }$ value uncertainty and different binding energies of the L atomic shells. Thus, the energy of a peak searched for was free parameter of the fits within the variations. A straight line was taken to describe the continuous background. The background model included background $\gamma$ peaks present in the energy intervals of the fits: 1238.1 keV of $^{214}$Bi (to estimate a $\lim S$ for the $0\nu 2K$ decay), and 1377.7 keV of $^{214}$Bi plus 1384.3 keV of $^{110m}$Ag (in the case of the $0\nu 2L$ capture). The results of the fits are shown in Fig. 7. The biggest peak areas were taken to derive the $\lim S$ values for the peaks searched for (see Table 4).

Fig. 7

The energy spectrum gathered with the Pt sample in the energy intervals where the $\gamma$ peaks from the $0\nu 2K$ (a), $0\nu KL$ (b), and $0\nu 2L$ (c) captures in $^{190}$Pt to the ground state of $^{190}$Os are expected. The fits of the data are shown by solid lines (see text for details of the background models), while the excluded peaks are presented by dashed lines. The horizontal lines (above the arrows labelling the energy of the peaks searched for) show the energy intervals corresponding to the uncertainties of the expected energies of the peaks. The energy of the $\gamma$ peaks are in keV

Limits on the neutrinoless $2\varepsilon$ transitions to the excited levels of the daughter were set by using the $\lim S$ values obtained to estimate the half-life limits for the two-neutrino processes. However, the detection efficiencies for the $0\nu$ modes are slightly smaller due to the energy transfer to the bremsstrahlung $\gamma$-ray quanta (absent in the $2\nu$ decay mode, where the energy is carried out by neutrinos).

The $0\nu KN$ transition in $^{190}$Pt to the 1,2 1326.9 keV excited level of $^{190}$Os is of special interest: the decay can be an exactly resonant, up to six orders of magnitude faster, if the degeneracy parameter $\Delta = Q_{2\beta }-E_{exc}-E_{b1}-E_{b2} \sim 10$ eV. However, with the uncertainties of the decay energy ($\pm 0.4$ keV [25]) and of the 1326.9-keV level energy ($\pm 1.0$ keV [27]) the degeneracy parameter lies in the interval from $-0.13$ keV to $+0.26$ keV with a combined uncertainty $\pm 1.1$ keV, that is too big to make a clear conclusion about resonance enhancement of the transition. Nevertheless, development of experimental techniques to study the decay at, as much as possible, high sensitivity level is an important task. The energy spectrum gathered with the Pt sample was fitted in the energy interval 1310–1357 keV to estimate a half-life limit on the decay. The background was described by a straight line and by a peak at 1332.5 keV ($\gamma$-peak of $^{60}$Co). The position of the peak searched for was bounded within $\pm 1$ keV, while the peak width was fixed as FWHM $=2.33$ keV according to the formula (3). The fit (with $\chi ^2/$n.d.f.$=41.4/88=0.47$) returned a peak area $S=29\pm 32$ counts.⁷ Considering the peculiarity as a statistical fluctuation we have obtained $\lim S=81$ counts. Taking into account the detection efficiency for $\gamma$-ray quanta with energy 1326.9 keV ($\eta =0.0488$), the resonant $0\nu KN$ transition in $^{190}$Pt to the 1,2 1326.9 keV excited level of $^{190}$Os is limited as:

$T_{1/2}^{0\nu KN}~(^{190}$Pt, g.s.$~\rightarrow ~1326.9$ keV$)~\ge ~2.5\times 10^{16}$ year.

The energy spectrum in the region of interest, the result of the fit and excluded peak for the possible resonant $0\nu KN$ transition in $^{190}$Pt to the 1,2 1326.9-keV excited level of $^{190}$Os is shown in Fig. 8a.

The bound on the transition to the 1326.9 keV level of $^{190}$Os is limited by $^{60}$Co background, that can be attributed entirely to the setup contamination (see Table 3) and not to the Pt sample. One can try to estimate a limit on the transition by analysis of the no-sample spectra subtracted from the data taken with the Pt sample, eliminating in such a way the $^{60}$Co background. A fit of the background-subtracted spectrum by a straight line (to describe the continuous background) plus a Gaussian peak with the bounded position and fixed width (the effect searched for) is shown in panel (b) of Fig. 8.⁸ However, statistical fluctuations in the background-subtracted spectrum are rather big due to a comparatively short time of the background measurement. As a result, the limit from the background-subtracted spectrum ($\lim S=109$ counts) is worse than the one from the sample-only spectrum. Nevertheless, the both approaches give comparable results providing a useful cross-check of the analysis.

Fig. 8

The energy spectra gathered with the Pt sample (with no sample) by the detector system where the $\gamma$ peak from possible resonant $0\nu KN$ transition to the 1,2 1326.9 keV level of $^{190}$Os is expected (a). The background-subtracted spectrum is shown in panel (b). The fits of the data are shown by solid lines (see text for details of the background models), while the excluded peaks are presented by dashed lines

The $0\nu LM$ transition of $^{190}$Pt to the $(0,1,2)^+$ 1382.4(2) keV level of $^{190}$Os can be characterized as “near” resonant one since the degeneracy parameter in this case is rather big $\Delta =$ (2.9–6.1) $\pm 0.6$ keV. The estimation of half-life limit for the decay was performed by analysis of the experimental data in the vicinity of $\gamma$ peak with energy 1195.7(2) keV emitted in the de-excitation of the 1382.4 keV level. The result of the data fit in the energy interval 1177–1220 keV by a simple model constructed from a straight line and a Gaussian peak at 1195.7(2) keV with a fixed width is presented in Fig. 9.

Fig. 9

The energy spectrum in the vicinity of $\gamma$ peak 1195.7 keV expected in the near resonant $0\nu LM$ transition of $^{190}$Pt to the $(0,1,2)^+$ 1382.4 keV level of $^{190}$Os (b). The fit of the data is shown by solid line, while the excluded peaks are presented by dashed line

The annihilation peaks at 511 keV were analyzed in the data with (without) the Pt sample to estimate half-life limits for the electron capture with positron emission in $^{190}$Pt to the energetically allowed transitions to the ground state and to the excited 186.7 keV level of the daughter. A fit of the data with (without) the Pt sample gives the 511-keV peak area $S=3143 \pm 71$ counts for measurement time 8946 h ($S=266 \pm 18$ counts for 674 h) that leads to the difference: $-\,388\pm 249$ counts that results in $\lim S=134$ counts. The energy spectrum taken with the Pt sample and the background spectrum in the vicinity of the 511 keV annihilation peak with the results of fits are shown in Fig. 10. The detection efficiencies are slightly different for the decays to the ground state and to the first 186.7 keV excited level of the daughter, as well as for the $2\nu$ and $0\nu$ modes of the decays. The obtained half-life limits are presented in Table 4.

Fig. 10

The energy spectrum measured with the Pt sample for 8946 h in the vicinity of the 511 keV annihilation peak. The background data (measured over 674 h, normalized on 8946 h) are shown by dots. The fit of the data obtained with the Pt sample is shown by solid line, the fit of the background spectrum is presented by dashed line

The obtained limits on the possible double-beta processes in $^{190}$Pt are higher up to an order of magnitude than the limits set in the previous study [28]. Moreover, the expected peaks positions for the $0\nu 2\varepsilon$ decays were far from the actual ones, taking into account a rather different $Q_{2\beta }$ value and much bigger uncertainty at the time when the experiment [28] was carried out. For this reason, the half-life limits for the $0\nu 2K$, $0\nu KL$ and $0\nu 2L$ captures can be considered as obtained for the first time.

However, the sensitivity of the present study is very far from theoretical estimations of the $^{190}$Pt decay probability. For instance, the calculations of the $^{190}$Pt half-life relative to the resonant $0\nu 2\varepsilon$ transitions to the 1326.2 keV [1382.4 keV] level of $^{190}$Os are in the interval $T_{1/2}\sim (3.3\times 10^{26}$–$1.6\times 10^{30})$ year [$T_{1/2}\sim (1.0\times 10^{30}$–$6.5\times 10^{30})$ year] (assuming the effective Majorana neutrino mass $\langle m_{\nu }\rangle =0.1$ eV and the weak axial-vector coupling constant $g_A=1.27$) (see Table IV in [24]). Nevertheless, achievement of the sensitivity on the level of $T_{1/2}\sim (10^{26}$–$10^{27})$ year looks realistic taking into account the great progress in the ultralow-background HPGe [14] and low-temperature bolometers [13, 15, 16, 42] detection techniques, the experimental approaches that look the most promising for possible large-scale searches for the resonant $0\nu 2\varepsilon$ decays.

3.3 Limit on the $2\beta ^-$ decay of $^{198}$Pt to the first excited level of $^{198}$Hg

A limit on the $2\beta ^-$ transition of $^{198}$Pt to the $2^+$ 411.8 keV excited level of $^{198}$Hg was set by analysis of the energy spectrum measured with the Pt sample. The spectrum was fit in the energy interval 390–430 keV by a straight line (to describe the continuous background) and a Gaussian function at 411.8 keV with the peak width determined by the formula (3) returning an effect area $S=-13\pm 26$ counts, that corresponds to $\lim S=31$ counts (the energy spectrum in the region of the fit is presented in Fig. 11). Taking into account the detection efficiency ($\eta = 0.0414$ both for the $2\nu$ and $0\nu$ modes of the decay), the following limit was obtained:

$T_{1/2}^{(2\nu +0\nu )2\beta ^{-}}(^{190}$Pt, g.s.$~\rightarrow ~411.8$ keV$)\ge ~3.2\times 10^{19}$ year.

Fig. 11

Part of the energy spectrum measured with the Pt sample where a peak with energy 411.8 keV after the $2\beta ^-$ decay of $^{198}$Pt to the first $2^+$ 411.8 keV excited level of $^{198}$Hg is expected. The fit of the data is presented by solid line, the excluded $\gamma$ peak is shown by dashed line

The limit is one order of magnitude higher than that set in the previous experiment [28]. Theoretical calculations for the $2\nu 2\beta ^-$ decay of $^{198}$Pt to the ground state of the daughter are in the interval $T_{1/2}\sim 5\times 10^{21}$–$5\times 10^{23}$ year [43, 44]. Similar estimations give semiempirical formulae: $T_{1/2}= (3.0\pm 1.5)\times 10^{23}$ year [45] and $T_{1/2}= 3.3\times 10^{22}$ year [46]. A probability of the $2\nu 2\beta ^-$ decay to the $2^+$ 411.8 keV excited level is expected to be several orders of magnitude lower due to a smaller value of the phase space factor and the spin change. The theoretical estimations of the $0\nu 2\beta ^-$ decay of $^{198}$Pt to the ground state of $^{198}$Hg are much higher: $T_{1/2}\sim 3\times 10^{26}$–$2\times 10^{28}$ year [43, 47,48,49],⁹ while the $0\nu 2\beta ^-$ transition to the $2^+$ 411.8 keV excited level of $^{198}$Hg is expected to be further suppressed. Thus, the sensitivity of the present experiment is rather far from the theoretical predictions for the two-neutrino mode of the decay, not to say for the neutrinoless process.

All the limits obtained in the present experiment are summarized in Table 4 where also results of the previous study [28] are given for comparison.

4 Summary and conclusions

A high-purity disk-shaped platinum sample with mass 148 g was measured in an ultralow background HPGe-detector $\gamma$-ray spectrometry system located 225 m underground at the HADES laboratory over 8946 hours aiming at searching for double-beta decay of $^{190}$Pt and $^{198}$Pt with emission of $\gamma$-ray quanta. The isotopic composition of the platinum sample has been measured with high precision using inductively coupled plasma mass spectrometry. No effect was observed but lower limits on the half-lives for the different channels and modes of the decays of $^{190}$Pt were set on the level of $\lim T_{1/2}\sim 10^{14}$–$10^{16}$ year. A possible exact resonant $0\nu KN$ transition to the 1,2 1326.9 keV level of $^{190}$Os is limited for the first time as $T_{1/2} \ge 2.5 \times 10^{16}$ year. A new improved limit is set for the $2\beta ^-$ transition of $^{198}$Pt to the $2^+$ 411.8 keV excited level of $^{198}$Hg as $T_{1/2} \ge 3.2 \times 10^{19}$ year. All the obtained limits exceed the previously obtained values up to one order of magnitude mainly thanks to a substantially bigger exposure (55.2 kg$\times$day in the present work and 3.2 kg $\times$ day in [28]). However, the sample geometry was not optimised since it was an existing sample foreseen for another project. Thus, a further improvement of the present experiment sensitivity can be achieved by decrease of the sample thickness by production of thin disk with a diameter comparable to the detectors size.

The sensitivity of the experiment to the $^{190}$Pt decays, particularly to the potentially resonant transition to the 1326.9 keV level of $^{190}$Os, could be advanced by using platinum enriched in the isotope $^{190}$Pt, increasing the exposure and detection efficiency by utilization of thin samples and multi-crystal system of HPGe $\gamma$-ray detectors or low-temperature bolometers. However, such an experiment could be considered after more accurate determination of the 1326.9-keV level energy (presently known with a rather big uncertainty $\pm 1.0$ keV). Nevertheless, we realize that implementation of such an experiment is practically a rather difficult task, first of all due to the inaccessibility of methods for enrichment of platinum isotopes in the hundreds kilograms scale requested for a competitive experiment (in terms of the Majorana neutrino mass) even in a case of an exact resonant transition.