1 Introduction

Quantifying the term “complexity” has been quite a fascinating challenge among researchers. Depending on various physical problems, the term complexity changes its notion. For example, a perfect crystal can be thought of as a system with zero complexity. Here, zero complexity means the crystal structure is perfectly ordered and periodic. In contrast, an isolated ideal gas is fully disordered and it contains maximum information as the system can be obtained in any accessible state with equal probability. Now, if we consider the concept of “disequilibrium” i.e. how a system deviates from the equilibrium, we find that the ideal gas has minimum disequilibrium while the perfect crystal has maximum disequilibrium. So the contrasting views of complexity while considering “information” and “disequilibrium” can be addressed by defining complexity as a product of these concepts [1]. So in this way, complexity is zero for both perfect crystal and ideal gas, as it should be. The work of Lopez-Ruiz and collaborators [1, 2] about complexity has been extended to self gravitating systems [3,4,5,6,7,8]. Recently, Carrasco-Hidalho and Contreras [9] proposed a polynomial complexity factor containing gravastar model [10] as a special case. Contreras and Fuenmayor [11] considered the complexity factor as a physical quantity containing anisotropy and gradients in the density. Herrera [12] proposed a new definition of complexity for self-gravitating, spherically symmetric systems, based on a specific parameter that arises in the orthogonal splitting of the Riemann tensor. Some more recent works in this regard can be found in [13,14,15,16].

It can be said, that fixing some value of the complexity factor for a specific scenario (example: a system having vanishing complexity) can act as an equation of state which may lead close approximation to Einstein’s field equations. But for these equations, it is very difficult to obtain analytical solutions. In this scenario, a recent well-known tool called Gravitational Decoupling (GD) by means of the minimal geometric deformation (MGD) [17] and its extension known as complete geometric deformation [18] formalism works perfectly to convert the isotropic solutions into anisotropic domain or can be even used to obtain new solutions. Moreover, it is well-known that the MGD tool is a transformation that is performed on the metric potential along with the radial component of the line element by introducing a decoupler function. As a consequence, the original system splits into two relatively simpler sets of equations. Another great advantage of MGD is that it can extend a simple solution to more generalized and complex cases by the addition of an extra source (\(\Theta ^i_j\)) with the original energy-momentum tensor via coupled with a dimensionless parameter. Later on, Ovalle and his collaborators found a drawback in the MGD approach, such as considering only radial transformation can’t explain a stable black hole with a well-defined horizon. In this regard, the MGD was extended to deform both radial and temporal metric functions [18]. Mathematically, in the extended case of MGD, the deformation acts in the following way:

$$\begin{aligned} \nu (r) \mapsto \xi (r) + \beta h(r),~~~~ \text {and}~~~~ \lambda (r) \mapsto - \ln [\mu (r) + \beta f(r)] \end{aligned}$$

It is noted here that the extended gravitational decoupling (EGD) demands the supposition of a seed solution, which allows reducing the number of free variables (or number of degrees of freedom). Due to this, we need only two extra conditions in order to close the system. There are many ways to solve the equation despite the appearance of the new degree of freedom h(r) in the \(\theta \)-sector, such as implementing the mimick approach with a particular form of h(r), or using the EoS approach together with the mimick approach [19,20,21] to solve the \(\Theta \)-sector. On the other hand, it must be noted that the hydrostatic balance gets severely modified because of the deformation. Therefore, it is very important to check the hydrostatic balance in order to assess the viability of the solution. Recently some interior solutions were generalized into the anisotropic domain using gravitational decoupling via MGD and CGD approaches in different contexts [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48].

In cases like extremely dense compact star solutions, the pressure can be broken down into radial and tangential components and which leads to pressure anisotropy. It can also be said, that considering anisotropic pressure components gives more realistic results, whereas, the pressure isotropy may be considered as an approximation in cases where the magnitude of pressure anisotropy is small enough for the general properties of a given model to remain unchanged. This is efficiently discussed by Herrera [49] and from the excerpt of that paper, we can see that due to the energy dissipation in stellar evolution, even if the initial configuration had isotropic pressure, it will disappear and the system will become anisotropic. And an already anisotropic system has no reason to lose its acquired anisotropy in the final stage of dynamic evolution. This dissipation happens due to the emission of massless particles like photons or neutrinos and it is one of the key features of the evolution of massive stars. In addition to that, neutrino emission is one of the reasonable explanations of the process of carrying away the bulk of the binding energy in collapsing stars which leads to the formation of neutron stars and black holes. The reason for this pressure anisotropy (radial and tangential components) can have several causes.

In fact, in both very high and very low-density systems, many factors can be the reason for the deviation from local isotropy. This has been discussed in detail by Herrera and Santos [50]. In extremely dense systems, the gravitational collapse may occur due to exotic phase transitions, with the most notable one of them being the pion condensed state. This pion condensed state releases a large amount of energy by softening the equation of state. This in turn has significant implications in the collapsing configurations. Sawyer and Scalapino [51] pointed out that pressure anisotropy can be one of the reasons for pion condensed phase because of the geometry of \(\pi ^-\) modes. While several researchers [52, 53] discussed that the anisotropic part of the stress tensor is related to the flux lines of a type-II superconductor and which is relevant to the neutron star configuration. The anisotropic factor is also associated with the existence of solid core [54, 55], boson stars [56, 57] and type-P superfluid as well. Viscosity is one of the potential sources of local anisotropy. But, in highly dense matter, where the Fermi energy is much higher than the temperature, the matter can be approximated to be isentropic as the dissipative processes are not taken into account during the relativistic calculation of gravitational collapse. This approximation is however not applicable in some specific stellar evolutionary scenarios. One such scenario is the event of neutrino trapping which can occur when the central density becomes of the order of \(10^{11} - 10^{12} g/cm^3\) [58]. These trapped neutrinos have high energy density and long mean free path and small radiative Reynolds number [59] and as a result, it makes the core fluid viscous [60, 61] and which in turn results in local anisotropy. In this connection, Ruderman [62] showed that for densities higher than \(10^{15} g/cm^3\), the two components of pressure don’t have the same magnitude and nuclear matter transforms into anisotropic distribution.In this regard, Herrera and Varela [63] have introduced a condition of the anisotropy parameter in the form \(P_t-P_r=g\,q^2\,r^2\) where g is a nonzero constant under a specific case of the electromagnetic mass model. Furthermore, Herrera and his collaborators have discussed the anisotropic polytropes in the context of the Newtonian [66] and the general relativistic regimes [64, 65].

On the other hand, the finding of the new physical viable anisotropic solution for a static self-gravitating system is easier than the isotropic solution of Einstein’s field equations. Till now, the researchers have obtained around 130 interior solutions of Einstein’s field equations (EFE) for perfect fluid matter distributions but only few of them are well-behaved that can be used for modeling the self-gravitating compact objects [67]. This is why it is still a challenge to obtain the new well-behaved isotropic solution of the Einstein field equations. Therefore, recently Casadio and his collaborators [68] have proposed is a very powerful methodology, known as isotropization techniques via gravitational decoupling using the MGD approach to find the new isotropic solutions for any known seed spacetime geometry corresponding to anisotropic matter distribution. In this work, they have investigated a new isotropic solution using the MGD approach as well as two other gravitationally decoupled anisotropic solutions corresponding to two systems with the same complexity factor, and zero complexity factor using Tolman IV solution. Some recent solutions on anisotropic stars with different complexity factor can be seen in the following works [9, 69,70,71,72].

In the current article, we develop a method of isotropization by employing a mathematical tool using gravitational decoupling in the framework of a complete geometric deformation (CGD) approach to find the new isotropic solutions from a known spacetime geometry for the anisotropic matter distribution. An example has been presented to validate this methodology. Moreover, we also discussed the complexity factor and the effect of the decoupling constant on the complexity factor for this isotropic solution. The present simple methodology has also been utilized to obtain the new anisotropic solutions by taking two systems with the same complexity factor as well as for zero complexity factor using the Karori-Barua solution.

The article is arranged as follows: Sect. 1 is the introduction, while in the Sect. 2, the Einstein field equation for two sources by gravitational decoupling has been discussed. Section 3 consists of the method of isotropization of the gravitationally decoupled system and new solution obtained by taking Tolman-Kuchowicz spacetime for seed solution. The complexity by gravitational decoupling has been analyzed in the Sect. 4. In this section, we also discussed the complexity factor for the isotropic solution obtained in Sect. 3. In Sect. 5, we have investigated new anisotropic EGD solutions generated by two systems with the same complexity factors and vanishing complexity factor using Karori-Barua seed solution, which are presented in Sects. 5.1 and 5.2. The last Sect. 6 contains the discussions and conclusions of the article.

2 Einstein’s field equation for two sources introduced by gravitational decoupling

We propose the brief review of Einstein’s field equations with two different sources,

$$\begin{aligned}&R_{ij}-\frac{1}{2}\,g_{ij}\,R= -8\pi (T_{ij}+\beta \,\Theta _{ij}) \end{aligned}$$
(1)

Now with \(G = c = 1\), the relativistic units are considered to express the field equations for the Ricci tensor denoted by \(R_{ij}\), and R is contracted Ricci scalar, and \(\beta \) is decoupling constant. Here, \(T_{ij}\) denote the energy-momentum tensor and the source \(\theta _{ij}\) may contain new fields, like scalar, vector and tensor fields. Since the Einstein tensor (1) satisfy the Bianchi identity, therefore the effective energy-momentum tensor \({\hat{T}}_{ij}=T_{ij}+\beta \,\Theta _{ij}\) must be conserved, that is,

$$\begin{aligned}&{\nabla _i}{\hat{T}}^{ij}=0. \end{aligned}$$
(2)

The following static spherically symmetric line element is taken for describing the space-time of the interior region of the stellar system as,

$$\begin{aligned} ds^2 = -e^ {\lambda (r)} dr^2 - r^2\big (d\theta ^2 + \sin ^2 \theta ~ d\phi ^2\big )~+ e^{\nu ( r)} dt^2 , \end{aligned}$$
(3)

where the metric potentials \(\nu \) and \(\lambda \) are only radially dependent. However, the effective energy-momentum tensor \({\hat{T}}_{ij}\) is considered for anisotropic matter distribution,

$$\begin{aligned}&{\hat{T}}_{ij} = \left( {\epsilon }+{P}_r\right) u_{i}u_{j}+{P}_\perp g_{ij}+({P}_r-{P}_\perp )\chi _{i}\,\chi _{j}, \end{aligned}$$
(4)

where \({P}_r\) and \({P}_\perp \) denote the radial and tangential pressures, respectively while \({\epsilon }\) is the energy density of matter. Moreover, \(u^{i}\) denotes a contravariant 4-velocity and \(\chi ^i=\sqrt{1/g_{rr}}\,\delta ^i_1\) is a unit space-like vector in the radial direction. Then under the line element (3), the Einstein field Eq. (1) with Eq. (4) provides the following differential equations,

$$\begin{aligned} 8\pi {\epsilon }= & {} T^0_0+\beta \,\Theta ^0_0=\frac{1}{r^2}-e^{-\lambda }\left( \frac{1}{r^2}-\frac{\lambda ^{\prime }}{r}\right) , \end{aligned}$$
(5)
$$\begin{aligned} 8\pi {P}_{r}= & {} -T^1_1-\beta \,\Theta ^1_1=-\frac{1}{r^2}+e^{-\lambda }\left( \frac{1}{r^2}+\frac{\nu ^{\prime }}{r}\right) , \end{aligned}$$
(6)
$$\begin{aligned} 8\pi {P}_{\perp }= & {} -T^2_2-\beta \,\Theta ^2_2\nonumber \\= & {} \frac{e^{-\lambda }}{4}\left( 2\nu ^{\prime \prime }+\nu ^{\prime 2}-\lambda ^{\prime }\nu ^{\prime }+2\frac{\nu ^{\prime }-\lambda ^{\prime }}{r}\right) , \end{aligned}$$
(7)

and, the conservation equation for system (5)–(7) will become,

$$\begin{aligned}&(P_r)^\prime + \frac{\nu ^\prime }{2} \big ( \epsilon + P_r \big ) - \frac{2}{r}(P_\perp -P_r) = -(T^1_1)^{\prime } \nonumber \\&\quad + \frac{\nu ^{\prime }}{2} \left( T^0_0 - T^1_1\right) +\frac{2(T^2_2-T^1_1)}{r}- \beta \, L(\Theta _i^i) =0, ~~ \end{aligned}$$
(8)

where the function \(L(\theta _i^i)\) is given by

$$\begin{aligned} L(\Theta _i^i) \equiv \left( \Theta ^{1}_{1} \right) ^{\prime } + \frac{\nu ^{\prime }}{2} \left( \Theta ^{0}_{0}-\Theta ^{1}_{1} \right) + \frac{2}{r} \left( \Theta ^{1}_{1}-\Theta ^{2}_{2}\right) . \end{aligned}$$
(9)

Now it is important to mention here that the source \(T_{ij}\) can describe perfect fluid or anisotropic fluid matter distribution. Suppose It describes an anisotropic fluid matter distribution then, the effective density and effective pressures can be read as,

$$\begin{aligned}&\epsilon = T^0_0+\beta \,\Theta ^0_0 =\rho +\beta \,\Theta ^0_0, \end{aligned}$$
(10)
$$\begin{aligned}&P_r= -T^1_1-\beta \,\Theta ^1_1=p_r-\beta \,\Theta ^1_1 , ~ \end{aligned}$$
(11)
$$\begin{aligned}&P_\perp = -T^2_2-\beta \,\Theta ^2_2=p_t-\beta \,\Theta ^2_2. \end{aligned}$$
(12)

where, \(\rho \), \(p_r\) and \(p_t\) denote the energy density, radial pressure and tangential pressure, respectively. Then the effective anisotropy can be given as,

$$\begin{aligned} {\hat{\Pi }}=P_\perp -P_r=\Pi +\beta \, \Pi _{\Theta } \end{aligned}$$
(13)

where,

$$\begin{aligned}&\Pi =p_t-p_r~~~ \text {and}~~~ \Pi _{\Theta }=(\Theta ^1_1-\Theta ^2_2). \end{aligned}$$
(14)

Here the anisotropy \(\Pi _{\Theta }\) is generated by second source \(\Theta _{ij}\), and Misner-Sharp mass function m(r) for the effective system can be calculated by the formula,

$$\begin{aligned} m(r)= & {} \frac{r}{2} [1-e^{-\lambda (r)}]=4\pi \int ^r_0 x^2 \epsilon (x) dx \nonumber \\= & {} \underbrace{4\pi \int ^r_0 x^2 \rho (x) dx}_{m_{GR}}+ \underbrace{4\pi \beta \int ^r_0 x^2 \Theta ^0_0(x) dx}_{m_{\Theta }}. \end{aligned}$$
(15)

The \(m_{GR}\) and \(m_{\Theta }\) represent the mass function due to matter distribution \(T_{ij}\) and \(\Theta _{ij}\), respectively.

Also, there is another definition in order to describe the energy content inside a fluid sphere which was proposed by Tolman many years before. The Tolman mass (\(m_T\)) for the spherically symmetric static spacetime (3) and energy-momentum tensor \({\hat{T}}_{ij}\) can be given by the formula [73]

$$\begin{aligned} m_T=4\pi \,\int ^r_0 x^2\,e^{(\lambda +\nu )/2} (\rho +P_r+2P_\perp ) dx. \end{aligned}$$
(16)

The above formula was proposed in order a measure the energy contained inside a fluid sphere of radius r. However, Tolman mass function \(m_T\) using the field Eqs. (5)–(7) under the spacetime (3) can be written as,

$$\begin{aligned} m_T=\frac{r^2\,\nu ^\prime }{2}\,e^{(\nu -\lambda )/2}. \end{aligned}$$
(17)

The above formula states about the physical meaning of \(m_T\) as the active gravitational mass. Since instantaneously at rest in a static gravitational field, the gravitational acceleration of a test particle is given by (see [12], for more details)

$$\begin{aligned} a=\frac{\nu ^\prime \,e^{-\lambda }}{2}=\frac{e^{-\nu /2}\, m_T}{r^2} \end{aligned}$$
(18)

Now we apply the extended gravitational decoupling by means of a complete geometric deformation (CGD) approach in order to see the general effects of the extra source \(\Theta \) on the energy-momentum tensor \(T_{ij}\). Under this, the metric functions \(e^{\lambda }\) and \(e^{\nu }\) undergone by the following transformation Ovalle [18] as,

$$\begin{aligned}&\xi (r) \mapsto \nu (r) = \xi (r) + \beta ~ h ( r ), \end{aligned}$$
(19)
$$\begin{aligned}&\mu (r) \mapsto e^{-\lambda (r)} = \mu (r) + \beta ~ f (r ). \end{aligned}$$
(20)

where, f(r) and h(r) denote the geometric deformation functions for the radial and temporal metric components, respectively. Since here we are considering the extended case therefore we need to set \(f(r)\ne 0\) and \(h(r)\ne 0\). Then the transformations (19) and (20) allow us to split the field Eqs. (5)–(7) into two sets of equations: (i) the standard Einstein field equations corresponding to energy-momentum tensor \(T_{ij}\) (same as at \(\beta \) = 0) as

$$\begin{aligned} 8\pi {\rho }&= \frac{1-\mu }{r^2} - \frac{\mu ^ \prime }{r}, \end{aligned}$$
(21)
$$\begin{aligned} 8\pi p_r&=\frac{\mu -1 }{r^2} - \frac{\mu ~~ \xi ^ \prime }{r} , \end{aligned}$$
(22)
$$\begin{aligned} 8\pi p_t&= \mu \bigg ( \frac{\xi ^{\prime \prime }}{2} + \frac{\xi ^{ \prime 2}}{4} + \frac{\xi ^\prime }{2r} \bigg ) + \bigg ( \frac{\xi ^ \prime \mu ^\prime }{4} + \frac{\mu ^\prime }{2r}\bigg ), \end{aligned}$$
(23)

with the conservation equation,

$$\begin{aligned} (p_r)^\prime + \frac{\xi ^\prime }{2} \big ( \rho + p_r \big ) = \frac{2\Pi }{r}. \end{aligned}$$
(24)

and the solution of this system can be described by the following spacetime,

$$\begin{aligned} ds^2 = -\mu dr^2 - r^2\big ( d\theta ^2 - \sin ^2 \theta d \phi ^2 \big ) + e^ \xi dt^2, \end{aligned}$$
(25)

with

$$\begin{aligned} \mu =1-\frac{2m_{GR}}{r}=4\pi \int ^r_0 x^2 \rho (x) dx. \end{aligned}$$
(26)

(ii) Now the second set of equations for the extra source is determined by turning on \(\beta \) as,

$$\begin{aligned} 8\pi \Theta ^0_0&=- ~~\bigg (\frac{f^\prime }{r} + \frac{f}{r^2}\bigg ), \end{aligned}$$
(27)
$$\begin{aligned} 8\pi \Theta ^1_1&= - f ~~\bigg ( \frac{\nu ^\prime }{r} + \frac{1}{r^2} \bigg ) - \frac{\mu h^\prime }{r} , \end{aligned}$$
(28)
$$\begin{aligned} 8\pi \Theta ^2_2&= - \frac{ f }{2} ~~\bigg ( \nu ^{\prime \prime } + \frac{\nu ^{\prime 2}}{2} + \frac{\nu ^\prime }{r} \bigg )\nonumber \\&\quad - \frac{\beta f^\prime }{2} ~~ \bigg (\frac{\nu ^\prime }{2} + \frac{1}{r}\bigg ) - \frac{\mu }{4}\big (2 h^{\prime \prime } + \beta h^{\prime 2} \nonumber \\&\quad + \frac{2~h^\prime }{r} + 2 \xi ^\prime h^\prime \big ) - \frac{\mu ^\prime ~h^\prime }{4}.~~~~~~ \end{aligned}$$
(29)

whose conservation equation read as,

$$\begin{aligned}&-\frac{\nu ^\prime }{2}\big (\theta ^0_0-\theta ^1_1\big ) +\big (\theta ^1_1 \big )^\prime -\frac{h^\prime }{2} \big (p_r + \rho \big )=\frac{2\Pi _{\Theta }}{r}. ~~~~~~~~ \end{aligned}$$
(30)

3 Isotropization of gravitationally decoupled system

In this section, we will adopt the systematic approach proposed by Casadio and his collaborators [68] to isotropize the decoupled system (5)–(7) under the EGD scenario. As we discussed previously, the effective anisotropy \({\hat{\Pi }}\) given by (13) may not be same as the anisotropy \(\Pi \) due to extra contribution \(\beta \,\Pi _{\Theta }\). Here, our aim is to isotropize the effective system, which can be obtained by setting \({\hat{\Pi }}=0\) with assuming \(\Pi \ne 0\) [see Ref.[68] for more details]. Therefore, \({\hat{\Pi }}=\Pi +\beta \,\Pi _{\Theta }=0\) leads

$$\begin{aligned} \Pi =-\beta \,\Pi _{\Theta }~~\Longrightarrow ~~ \Pi =-\beta (\Theta ^1_1-\Theta ^2_2). \end{aligned}$$
(31)

Now by plugging the Eqs. (28) and (29) in Eq. (31), we get the following non-linear differential equation,

$$\begin{aligned}&f^\prime (2 + \nu ^\prime r)+f (-4 - 2 \nu ^\prime r + 2 \nu ^{\prime \prime } r^2 + \nu ^{\prime 2} r^2) + r (-2 h^\prime \mu \nonumber \\&\quad + h^\prime \mu ^\prime r + 2 h^{\prime \prime } \mu r + b h^{\prime 2} \mu r + 2 h^\prime \nu ^\prime \mu r) + \frac{4r^2}{\beta }\,\Pi =0.~~~\nonumber \\ \end{aligned}$$
(32)

As we can see that the above Eq. (32) is a first-order linear ODE in f(r) while it is a second-order non-linear in h(r). Therefore, we solve the above differential for f(r) due to simplicity. Now we assume a spacetime corresponding energy-momentum tensor \(T_{ij}\) generated by Tolman-Kuchowicz metric functions \(\{\xi ,\,\mu \}\)

$$\begin{aligned} ds^2{=}-(1{+}Kr^2{+}Lr^4)\, dr^2{-} r^2 d\Omega _2^2 ~{+} e^{Ar^2+B} dt^2.~~~ \end{aligned}$$
(33)

together with temporal deformation function \(h(r)=Cr^2\) in order to isotropize the gravitationally decoupled system (5)–(7). Then, the metric functions \(\mu (r)=1/(1+Kr^2+Lr^4)\) and \(e^{\xi (r)}=e^{Ar^2+B}\) describe the anisotropic solution for the system (21)–(23). The constant parameters K, L, A, and B will be determined by matching of the seed spacetime (33) with exterior vacuum spacetime at surface \(r=R\), If we consider exterior vacuum spacetime is described by exterior Schwarzschild solution, then

$$\begin{aligned}&1-\frac{2M_s}{R}=e^{\xi (R)},~~~ \end{aligned}$$
(34)
$$\begin{aligned}&1-\frac{2M_s}{R}=\mu (R),~~~ \end{aligned}$$
(35)
$$\begin{aligned}&p_r(R)=0,~~~ \end{aligned}$$
(36)

where \(m_{GR}(R)=M_s\) is the total mass of the seed spacetime (33) related to the energy-momentum tensor \(T_{ij}\). Using the conditions (34)–(36), we find the constants A, B, and K

$$\begin{aligned}&A=\frac{M_s}{R^2 (R-2 M_s)}, \end{aligned}$$
(37)
$$\begin{aligned}&B=\frac{-4 M_s^2+5 M_s R-R^2}{(2 M_s-R) R}, \end{aligned}$$
(38)
$$\begin{aligned}&K=\frac{-2 M_s-2 L M_s R^4+L R^5}{(2 M_s-R) R^2}. \end{aligned}$$
(39)

By plugging of spacetime geometry (33) into Eq. (32) and using \(h=Cr^2\), we obtain the deformation function f(r) as

$$\begin{aligned} f(r)&= \frac{r^2 e^{-\left( r^2 (A+b C)\right) }}{\beta \sqrt{K^2-4 L} \left( K r^2+L r^4+1\right) \left( A^2+2 A \beta C-A K+\beta ^2 C^2-\beta C K+L\right) }\nonumber \\&\quad \times \Bigg [e^{-\frac{A K+\beta C K+L}{L}} \Bigg (e \Bigg \{\sqrt{K^2-4 L} \left( K+L r^2\right) \big (A^2+2 A \beta C-A K+\beta ^2 C^2-\beta C K+L\big ) \nonumber \\&\quad \times e^{\frac{(A+\beta C) \left( K+L r^2\right) }{L}}+\beta ^2 C^2 f_2(r) \left( K r^2+L r^4+1\right) \chi _1 +\beta ^2 C^2 f_3(r)\, \big (K r^2+L r^4+1\big ) \chi _2 \Bigg \}\nonumber \\&\quad -f_1(r) \sqrt{K^2-4 L} (A+\beta C) \left( K r^2+L r^4+1\right) e^{\frac{K (A+\beta C)}{L}} \nonumber \\&\quad \times \left( A^2+2 A \beta C-A K+3 \beta ^2 C^2-\beta C K+L\right) \Bigg )+F \Bigg ],~~~~~ \end{aligned}$$
(40)

where, F is a constant of integration, and then the solution of the system (5)–(7) can be described by the spacetime

$$\begin{aligned} ds^2&=-\frac{(1{+}Kr^2{+}Lr^4)}{1{+}\beta \,(1{+}Kr^2{+}Lr^4)\,f(r)} dr^2- r^2 d\Omega _2^2 \nonumber \\&\quad + \big (e^{Ar^2+B+\beta Cr^2}\big ) dt^2. \end{aligned}$$
(41)

However, the effective energy density and effective pressures can be given as,

$$\begin{aligned}&P_r(r,\,\beta )= \frac{1}{K r^4+L r^6+r^2}\Big [\beta f(r) \left( 2 A r^2+1\right) \nonumber \\&\quad \times \left( K r^2+L r^4+1\right) +r^2 \left( 2 A-K-L r^2\right) \nonumber \\&\quad +2 \beta ^2 Cr^2 f(r) \left( K r^2+L r^4+1\right) +2 \beta C r^2\Big ],~~~~ \end{aligned}$$
(42)
$$\begin{aligned}&P_\perp (r,\,\beta )=\frac{1}{2 r \left( K r^2+L r^4+1\right) ^2}\nonumber \\&\quad \times \Big [2 r \left( A^2 \left( K r^4+L r^6+r^2\right) \right. \nonumber \\&\quad \left. +A \left( K r^2+2\right) -K-2 L r^2\right) \nonumber \\&\quad +\beta ^2 C r \left( K r^2+L r^4+1\right) \Big (4 f(r) \left( A r^2+1\right) \nonumber \\&\quad \times \left( K r^2+L r^4+1\right) \nonumber \\&\quad +r \left( 6 C r+\Omega (r) K r^2+\Omega (r) L r^4+\Omega (r)\right) \Big )\nonumber \\&\quad +\beta \Big \{2 r \Big (C \left( 2 A \left( K r^4+L r^6+r^2\right) +K r^2+2\right) \nonumber \\&\quad +A f(r)\times \left( A r^2+2\right) \left( K r^2+L r^4+1\right) ^2\Big )\nonumber \\&\quad +\Omega (r) \left( A r^2+1\right) \left( K r^2+L r^4+1\right) ^2\Big \}\nonumber \\&\quad +2 \beta ^3 C^2 f(r) r^3 \left( K r^2+L r^4+1\right) ^2\Big ],~~~~~~~~~~ \end{aligned}$$
(43)
$$\begin{aligned}&\epsilon (r,\,\beta )=\frac{1}{\left( K r^3+L r^5+r\right) ^2}\left[ -\beta (\Omega (r) r+f) \right. \nonumber \\&\quad \left. \times \left( K r^2+L r^4+1\right) ^2\right. \nonumber \\&\quad \left. +K^2 r^4+K r^2 \left( 2 L r^4+3\right) +L r^4 \left( L r^4+5\right) \right] .~~~~~~~~~ \end{aligned}$$
(44)

The matching conditions (34)–(36) for new solution (41)–(44)

$$\begin{aligned}&e^{-\lambda (R)}=\frac{1}{1+KR^2+LR^4}+\beta \,f(R)=1-\frac{2 {M}}{R},~~~ \end{aligned}$$
(45)
$$\begin{aligned}&e^{\nu (R)}=e^{AR^2+B+\beta \,CR^2}=1-\frac{2 {M}}{R}, \end{aligned}$$
(46)
$$\begin{aligned}&P_r(R)=0, \end{aligned}$$
(47)

determine the constant B, total mass M, and integration constant F as

$$\begin{aligned}&B= \ln \Big [1-\frac{2M}{R}\Big ]-AR^2-\beta \,CR^2, \end{aligned}$$
(48)
$$\begin{aligned}&M=M_s-\frac{\beta \,R}{2}\,f(R) \end{aligned}$$
(49)

where \(m(R)=M\) is the total mass of the deformed compact object corresponding to energy-momentum tensor \({\hat{T}}_{ij}\) given by Eq. (4). However, we avoid writing the expression for F due to lengthy expression.

Fig. 1
figure 1

The behavior of radial pressure (\(P_r\times 10^4\))-top left, tangential pressures (\(P_\perp \times 10^4\))-top right, energy density (\(\epsilon \times 10^4\))-bottom left and anisotropy (\({\hat{\Pi }}\times 10^4\))-bottom right versus radial coordinate r/R for different coupling constant \(\beta \) with compactification factor \(\frac{M_s}{R}=0.2\) with \(C=0.0002\), and \(L= 1.5\times 10^{-8}\). The figures are plotted corresponding to the isotropic solution discussed in Sect. 3

Full size image

It is important to mention here that the expressions (42) and (43) given by \(P_r\) and \(P_\perp \) are the same at each point within the compact object for all \(\beta \) i.e. the effective anisotropy \({\hat{\Pi }}=0\) (see Fig. 1), which implies that the solution given by spacetime geometry (41) represents an isotropic solution of the decoupled system (5)–(7). Therefore, the gravitational decoupling not only extends the isotropic solution to anisotropic domain but also plays an important role to convert anisotropic solution to isotropic domain.

4 Complexity by gravitational decoupling

The definition of the complexity factor in static and spherically symmetric self-gravitating systems was initially proposed by Herrera, which is a scalar function denoted by \(Y_{TF}\) and it can be measured by anisotropy \(\Pi \) and energy density gradient \(\rho ^\prime \). Later on Herrara and his collaborators extended this complexity in the context of dynamical spherically symmetric dissipative self-gravitating fluid distributions. Based on the Herrera definition, we denote \({\hat{Y}}_{TF}\) as a complexity factor for the spherically symmetric static self-gravitating systems (5)–(7) which is given by,

$$\begin{aligned} {\hat{Y}}_{TF}= 8\pi {\hat{\Pi }} -\frac{4\pi }{r^3} \int ^r_0 x^3 \epsilon ^\prime (x) dx. \end{aligned}$$
(50)

As it is mentioned by Herrera that the complexity factor \({\hat{Y}}_{TF}\) represents the influence of local anisotropy of pressure and density inhomogeneity on the Tolman mass (\(m_T\)) Or, how the Tolman mass is changed by the above two factors defined in \({\hat{Y}}_{TF}\). In order to see the influence of \({\hat{Y}}_{TF}\) on the Tolman \(m_T\), we write the Eq. (16) in terms of complexity factor as,

$$\begin{aligned} m_T= M_T \Big (\frac{r}{R}\Big )^2+r^3\,\int ^R_r \frac{e^{(\nu +\lambda )/2}}{x}\,\hat{Y}_{TF} dx. \end{aligned}$$
(51)

Here, \(M_T\) denote the total Tolman mass of the fluid sphere of radius R.

According to Herrera [12] observations, it is worthwhile noting that

  1. (i)

    The complexity factor vanishes for not only isotropic fluid but also for all other configurations where both the terms in (50) identically vanish.

  2. (ii)

    From the abovementioned criteria, it is evident that there are plenty of configurations with vanishing complexity factors.

  3. (iii)

    It must also be noted that although the contribution of pressure anisotropy to \(\hat{Y}_{TF}\) is local in nature, this is not the case for density energy inhomogeneity.

In the context of MGD, Casadio et al. argued that the complexity factor satisfies the additive property and then the complexity factor for the gravitationally decoupled systems will be the sum of two existing complexity factors generated by the sources \(T_{ij}\) and \(\theta _{ij}\). Therefore, using the above facts, the complexity factor \({\hat{Y}}_{TF}\) given by Eq. (50) can be also written into the sum of two complexity factors corresponding to the source \(T_{ij}\) and \(\Theta _{ij}\) as,

$$\begin{aligned} {\hat{Y}}_{TF}= & {} 8\pi \,{\hat{\Pi }}-\frac{4\pi }{r^3} \int ^r_0 x^3 \epsilon ^\prime (x) dx,\nonumber \\= & {} 8\pi \,\Pi -\frac{4\pi }{r^3} \int ^r_0 x^3 \rho ^\prime (x) dx\nonumber \\&\quad + 8\pi \,\beta \,\Pi _{\Theta }-\frac{4\pi \,\beta }{r^3} \int ^r_0 x^3 \left[ \Theta ^0_0(x)\right] ^\prime dx, \end{aligned}$$
(52)

which is denoted as,

$$\begin{aligned}&{\hat{Y}}_{TF}= Y_{TF} + Y^{\Theta }_{TF}. \end{aligned}$$
(53)

Here, we denote the \( Y_{TF}\) is the complexity factor for the system (21)–(23) while \(Y^{\Theta }_{TF}\) for (27)–(29) corresponding to the sources \(T_{ij}\) and \(\Theta _{ij}\), respectively.

Now we will discuss two following cases: i. Complexity factor generated by the isotropic solution (40)–(44) for the energy-momentum tensor \({\hat{T}}_{ij}\), and ii. Some new solutions generated by the EGD approach for the systems having same or vanishing complexity factors.

4.1 Complexity factor generated by isotropic solution (41)–(44)

The complexity factor for the systems (5)–(7) corresponding to the energy-momentum tensor \({\hat{T}}_{ij}\) is

$$\begin{aligned} {\hat{Y}}_{TF}= & {} 8\pi \,{\hat{\Pi }}-\frac{4\pi }{r^3} \int ^r_0 x^3 \epsilon ^\prime (x) dx, \end{aligned}$$
(54)

Since the solution (41)–(44) is isotropic, then the effective anisotropy will be zero i.e. \({\hat{\Pi }}=0\), yields

$$\begin{aligned} {\hat{Y}}_{TF}= & {} -\frac{4\pi }{r^3} \int ^r_0 x^3 \epsilon ^\prime (x) dx, \end{aligned}$$
(55)

Using Eq. (5), we get

$$\begin{aligned} {\hat{Y}}_{TF}= & {} \frac{1}{r^2}-\frac{e^{-\lambda }}{r^2}-\frac{\lambda ^\prime \,e^{-\lambda }}{2r}, \end{aligned}$$
(56)

Now using the solution (41), we find expression for complexity factor \({\hat{Y}}_{TF}\)

$$\begin{aligned} {\hat{Y}}_{TF}= & {} \frac{r^2 \left( K^2+2 K L r^2+L \left( L r^4-1\right) \right) }{\left( K r^2+L r^4+1\right) ^2}\nonumber \\&\quad +\frac{\beta }{2r^2} \big [r\,\Omega (r) -2 f(r)\big ].~~~~ \end{aligned}$$
(57)
Fig. 2
figure 2

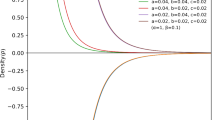
The behavior complexity factor \(({\hat{Y}}_{TF}\times 10^4)\) versus radial coordinate r/R for different coupling constant \(\beta \) with compactness factor \(\frac{M_s}{R}=0.2\) with \(C=0.0002\), and \(L= 1.5\times 10^{-8}\). This complexity figure is plotted for the isotropic solution obtained in Sect. 3

Full size image

It is noticed from Fig. 2, the decoupling constant \(\beta \) is influencing the complexity factor \({\hat{Y}}_{TF}\). The \({\hat{Y}}_{TF}\) increases when \(\beta \) increase, which implies that gravitational decoupling enhances the complexity of the self-gravitating isotropic models.

5 Some new solutions generated EGD approach for the systems having same or vanishing complexity factors

5.1 EGD solution for two systems with the same complexity factor

In this section, we will consider the situation where the complexity factor \(Y_{TF}\) related to energy-momentum tensor \(T_{ij}\) remains same after using gravitational decoupling via CGD, that is \({\hat{Y}}_{TF}=Y_{TF}\), which implies \(Y^{\Theta }_{TF}=0\) or

$$\begin{aligned}&\Pi _{\Theta }=\frac{1}{2r^3} \int ^r_0 x^3\, \big [ \Theta ^0_0(x) \big ]^\prime \, dx, \end{aligned}$$
(58)

where,

$$\begin{aligned}&\int ^r_0 x^3 \left[ \Theta ^0_0(x)\right] ^\prime dx= \frac{r^3}{4\pi }\Bigg (\frac{f}{r^2}-\frac{f^{\prime }}{2r}\Bigg ). \end{aligned}$$
(59)

Now using the Eqs. (27)–(29), the equation (58) yields,

$$\begin{aligned}&f^{\prime } (4r + \nu ^{\prime } r^2)+f (2 \nu ^{\prime \prime } r^2 + \nu ^{\prime 2} r^2-8 - 2 \nu ^{\prime } r) + r (-2 h^{\prime } \mu \nonumber \\&\quad + h^{\prime } \mu ^{\prime } r + 2 h^{\prime \prime } \mu r + \beta h^{\prime 2} \mu r + 2 h^{\prime } \nu ^{\prime } \mu r )=0,~~ \end{aligned}$$
(60)

It is clear that the new source \(\Theta _{ij}\) can be determined by any solution of the Eq. (60) which can be obtained through any known solution of the system (21)–(23) described by the metric functions \(\xi \) and \(\mu \) together with imposing any viable form of deformation function f(r) or h(r). For this purpose, we consider a well-known spacetime geometry proposed by Karori-Barau,

$$\begin{aligned}&e^{\xi (r)}=e^{Ar^2+B}, ~~~~\text {and}~~~\mu (r)=e^{-Dr^2}. \end{aligned}$$
(61)

where A, B, and D are constant parameters. Using above \(\xi \) and \(\mu \), the system (21)–(23) provides the energy density and pressures expressions for the energy-momentum tensor \(T_{ij}\) as,

$$\begin{aligned} p_r= & {} \frac{e^{-D r^2} \left( 1-e^{D r^2}+2 A r^2\right) }{r^2}, ~~~ \end{aligned}$$
(62)
$$\begin{aligned} p_t= & {} e^{-D r^2} \left[ A^2 r^2+A \left( 2-D r^2\right) -D\right] , ~~~ \end{aligned}$$
(63)
$$\begin{aligned} \rho= & {} \frac{e^{-D r^2} \left( -1+e^{D r^2}+2 D r^2\right) }{r^2}. ~~~ \end{aligned}$$
(64)

The constants involved in the solution are determined by the same matching conditions (34)–(36) for metric functions (61), which yields

$$\begin{aligned} D= & {} \frac{\ln R-\ln \left[ R-2M_{s}\right] }{R^2}, ~~~ \end{aligned}$$
(65)
$$\begin{aligned} A= & {} \frac{M_{s}}{(R-2 M_{s}) R^2}, ~~~ \end{aligned}$$
(66)
$$\begin{aligned} B= & {} -\frac{M_{s}}{R-2 M_{s}}+\ln \left[ 1-\frac{2 M_{s}}{R}\right] . ~~~ \end{aligned}$$
(67)

where \(m_{GR}(R)=M_s\) is the total mass of the object. Now we find the complexity factor \(Y_{TF}\) by using the definition (50) as,

$$\begin{aligned} Y_{TF}{=}\frac{e^{-D r^2} \left( -2{+}2 e^{D r^2}{+}A^2 r^4{-}D r^2 \left( 2{+}A r^2\right) \right) }{r^2},~~~ \end{aligned}$$
(68)

Using the spacetime geometry (61) together with the same form of temporal deformation function \(h(r)=Cr^2\) as used in previous Sect. 3, we find the radial deformation function by solving of the Eq. (60) as,

$$\begin{aligned} f(r)&=-\frac{C (2 A+3 \beta C-D) r^2 f_8(r)}{(A+\beta C)^2\,e^{\frac{2 (A+\beta C-D)}{A+\beta C}+(A+\beta C) r^2}}\nonumber \\&\quad +\frac{\left( 2+A r^2+\beta C r^2\right) \, r^2\,F}{e^{(A+\beta C) r^2}\,}, \end{aligned}$$
(69)

where F is a constant of integration with dimension \(length^{-2}\) and

$$\begin{aligned} f_8(r)&=-(A+\beta C) e^{\frac{(A+\beta C-D) \left( 2+A r^2+\beta C r^2\right) }{A+\beta C}} \\&\quad +(A+\beta C-D) \times \left( 2+A r^2+\beta C r^2\right) f_{9}(r),\\ f_9(r)&=\text {ExpIntegralEi}\\&\quad \times \left[ \frac{(A+\beta C-D) \left( 2+A r^2+\beta C r^2\right) }{A+\beta C}\right] , \end{aligned}$$

The deformation function f(r) given in Eq. (69) leads the same complexity factor \({\hat{Y}}_{TF}=Y_{TF}\) i.e. \(Y^{\Theta }_{TF}=0\) for all \(\beta \). Then the deformed metric functions can be read as,

$$\begin{aligned} e^{-\lambda (r)}= & {} e^{-Dr^2}+\beta \,\Bigg [-\frac{C (2 A+3 \beta C-D) r^2 f_8(r)}{(A+\beta C)^2\,e^{\frac{2 (A+\beta C-D)}{A+\beta C}+(A+\beta C) r^2}}\nonumber \\&\quad +\frac{\left( 2+A r^2+\beta C r^2\right) \, r^2\,F}{e^{(A+\beta C) r^2}\,}\Bigg ],~~~ \end{aligned}$$
(70)
$$\begin{aligned} e^{\nu (r)}= & {} e^{Ar^2+B+\beta \,Cr^2}. ~~~ \end{aligned}$$
(71)

The expressions for effective pressure and energy density,

$$\begin{aligned} P_r(r,\,\beta )&=\frac{e^{-D r^2}}{r^2}\, \Big [1+2 A r^2+2 \beta C r^2+e^{D r^2} \nonumber \\&\times \big (-1+2 \beta ^2 C \times f(r) r^2+\beta \,\nonumber \\&\times \big \{f(r)+2 A r^2\,f(r)\big \}\big )\Big ],~~~ \end{aligned}$$
(72)
$$\begin{aligned} P_\perp (r,\,\beta )= & {} \frac{e^{-D r^2}}{r^2} \Big [2+4 \beta C r^2+6 \beta ^2 C^2 r^4-2 \beta C D r^4+4 A \nonumber \\&\times (r^2{+}\beta C r^4){+}e^{D r^2} \big (-2{+}2 \beta ^3 C^2 f(r)\, r^4{+}\beta ^2 C r^2 \nonumber \\&\times \big [r\,\Psi (r)+4 f(r)\, \left( 1+A r^2\right) \big ]\nonumber \\&+\beta r [\Psi (r)+A \Psi (r) r^2\nonumber \\&+2 A f(r)\, r \times \left( 2+A r^2\right) ]\big )\Big ], ~~~ \end{aligned}$$
(73)
$$\begin{aligned} \epsilon (r,\,\beta )= & {} \frac{e^{-D r^2}}{r^2}\nonumber \\&\times \left( 2 D\, r^2-1+\frac{ \big (1-\beta \,[f(r)+\Psi (r)\, r]\big )}{e^{-D r^2}}\right) , ~~~ \end{aligned}$$
(74)

and effective anisotropy \({\hat{\Pi }}=P_{\perp }-P_r\) is

$$\begin{aligned}&{\hat{\Pi }} (r,\,\beta ) {=}\frac{e^{-D r^2}}{2 r^2} \Big [e^{D r^2} \Big (2{+}2 \beta ^3 C^2 f(r)\, r^4{+}\beta ^2 \,C\, r^3 \big (\Psi (r)\,\nonumber \\&\quad +4 A f(r)\, r\big )+\beta \left( 1+A r^2\right) \big \{-2 f(r)+\Psi (r) r\nonumber \\&\quad +2 A f(r) r^2\big \}\Big ) -2 \big (1-A^2 r^4-2 A \beta C r^4-3 \beta ^2 C^2\nonumber \\&\quad \times \, r^4 +D \left( r^2+(A+\beta C) r^4\right) \big )\Big ].~~~~~ \end{aligned}$$
(75)

where the expression \(\Psi (r)\) is mentioned in the Appendix. The metric functions (70) and (71) together with the Eqs. (72)–(75) represent the complete exact solution of the Einstein field equations (5)–(7), which is new a anisotropic form of Karori-Barua solution whose complexity factor \({\hat{Y}}_{TF}\) is same form as the complexity factor \(Y_{TF}\) given by Eq. (68). However, we impose the matching conditions (34)–(36) under the new solution (69)–(75) in order to determine the constant parameters F and B, and M,

$$\begin{aligned} F&=\Bigg [\frac{\beta C (2 A+3 \beta C-D)\,f_8(R)\, (2 AR^2+2 \beta CR^2+1) }{(A+\beta C)^2e^{\frac{2 (A+\beta C-D)}{A+\beta C}+(A+\beta C) R^2}}\nonumber \\&\quad +\frac{\left( -1+e^{D R^2}-2 A R^2\right) }{R^2e^{D R^2} }-2 \beta C e^{-D R^2}\Bigg ] F_{1}(R), \end{aligned}$$
(76)
$$\begin{aligned} B&= \frac{e^{-DR^2}+\beta \,f(R)}{e^{AR^2+\beta \,CR^2}}, \end{aligned}$$
(77)
$$\begin{aligned} M&=M_s-\frac{\beta \,R}{2}f(R). \end{aligned}$$
(78)

where \(M_s=\frac{R}{2}(1-e^{-Dr^2})\), while \(F_1(R)\) is mentioned in the Appendix.

Fig. 3
figure 3

The behavior of radial pressure (\(P_r\times 10^4\))-top left, tangential pressures (\(P_\perp \times 10^4\))-top right, energy density (\(\epsilon \times 10^4\))-bottom left and anisotropy (\({\hat{\Pi }}\times 10^4\))-bottom right versus radial coordinate r/R for different coupling constant \(\beta \) with compactification factor \(\frac{M_s}{R}=0.2\) with \(C=0.0002\). The above figures are plotted for EGD solution for the two systems with same complexity factor obtained in Sect. 5.1

Full size image

Figure 3 shows the behaviors of effective radial and tangential pressures, energy density, and anisotropy inside the self-gravitating anisotropic compact object. it can be observed that all the physical parameters \(P_r\), \(P_\perp \), and \(\epsilon \), and \({\hat{\Pi }}\) are satisfying the condition for a viable compact object, which implies that the CGD approach is also a very powerful technique to discover new physical viable gravitationally decoupled solution for two systems with same complexity factor.

For this anisotropic solution, the complexity factor \({\hat{Y}}_{TF}\) takes the form

$$\begin{aligned} {\hat{Y}}_{TF}= \frac{\big [2 e^{D r^2}-2+A^2 r^4-D\, r^2 \left( 2+A\, r^2\right) \big ]}{r^2\,e^{D r^2}}. \end{aligned}$$
(79)

Here we can generate the family of complexity factors by taking the different values of the compactness factor \(\frac{M_s}{R}\).

Since the complexity factor for the new anisotropic solution is same as the seed solution. Therefore \(\beta \) will not show any direct effect on the complexity. Therefore, we show the influence of the compactness on the complexity factor \({\hat{Y}}_{TF}\). As we can see from the Fig. 4, the complexity is increasing when the compactness factor \(\frac{M_s}{R}\) increases.

5.2 EGD solution generated by zero complexity factor

In this section, we discuss the gravitational decoupling solution via complete geometric deformation approach when the complexity factor is zero i.e. \({\hat{Y}}_{TF}=0\) with the condition \(Y_{TF}\ne 0\). Therefore, based on the Eq. (52), we can write

$$\begin{aligned}&{\hat{Y}}_{TF}= Y_{TF} +Y^{\Theta }_{TF} =0 \nonumber \\&\quad \Longrightarrow ~~ Y_{TF} =-8\pi \,\beta \,\Pi _{\Theta }+\frac{4\pi \,\beta }{r^3} \int ^r_0 x^3 \Theta ^0_0(x) dx. ~~~~ \end{aligned}$$
(80)

Plugging of the Eqs. (27)–(29) in condition (80), we determine the following differential equation in geometric deformation functions f(r) and h(r),

$$\begin{aligned}&(4 + \nu ^{\prime } r) r\,f^{\prime } - \big [ 2 \nu ^{\prime } r+8 r-2 \nu ^{\prime \prime } r^2 - \nu ^{\prime 2} r^2 \big ] \,f \nonumber \\&\quad +\big [ r\,\beta h^{\prime 2} \mu r-2 h^{\prime } \mu r + h^{\prime } \mu ^{\prime } r^2 + 2 h^{\prime \prime } \mu r^2 + 2 h^{\prime } \nu ^{\prime } \mu r^2 \big ]\nonumber \\&\quad + \frac{4 r^2}{\beta } Y_{TF}=0.~~ \end{aligned}$$
(81)

Now by considering again the Karori-Barua solution and the complexity factor given by Eqs. (61) and (68), respectively together with deformation function \(h(r)=Cr^2\), we get the following solution of the above differential equation,

$$\begin{aligned}&f(r)=\frac{r^2\,\left( 2+A r^2+\beta C r^2\right) }{e^{(A+\beta C) r^2}} \nonumber \\&\quad \times \Bigg [F-\frac{f_{12}(r)}{2 \beta }-f_{13}(r)\Bigg ],~~~~~ \end{aligned}$$
(82)

where F is a constant of integration and this above deformation f(r) provides the vanishing complexity factor i.e. \({\hat{Y}}_{TF}=0\). The expressions for effective radial and tangential pressures with effective energy density are given as,

$$\begin{aligned}&P_r(r,\,\beta ){=}\frac{\left( 1{-}e^{D r^2}{+}2 A r^2\right) }{r^2\,e^{D r^2}}{-}\beta \Bigg [\frac{\left( 2 Ar^2{+}2 \beta Cr^2+1\right) }{e^{(A{+}\beta C) r^2}}\nonumber \\&\quad \times \left( 2+A r^2+\beta C r^2\right) \nonumber \\&\quad \times \left( F-\frac{f_{12}(r)}{2 \beta }-f_{13}(r)\right) +\frac{2 C}{e^{D r^2}} \Bigg ], \end{aligned}$$
(83)
$$\begin{aligned}&P_\perp (r,\,\beta )=\frac{\left( 1-e^{D r^2}+2 A r^2\right) }{r^2\,e^{D r^2}}\nonumber \\&\quad +\beta \,\Bigg [\frac{\zeta (r) \left( 1+A r^2+\beta C r^2\right) }{2 r}\nonumber \\&\quad + \frac{C D \,r^2}{e^{D r^2}}+ \frac{\left( 2+2 A r^2+3 \beta C r^2\right) \,C}{e^{D r^2} } + e^{-(A+\beta C) r^2} r^2 \nonumber \\&\quad \times \left( 2+A r^2+\beta C r^2\right) \Big \{A^2 r^2+2 A \left( 1+\beta C r^2\right) +\beta C \nonumber \\&\quad \times \left( 2+\beta C r^2\right) \Big \} \left( F-\frac{f_{12}(r)}{2 \beta }-f_{13}(r)\right) \Bigg ], \end{aligned}$$
(84)
$$\begin{aligned}&\epsilon (r,\,\beta )=\frac{\left( e^{D r^2}+2 D r^2-1\right) }{r^2\,e^{D r^2}} \nonumber \\&\quad - \beta \, \Bigg [\frac{\zeta (r)}{r}+\frac{\left( 2+A r^2+b C r^2\right) }{e^{(A+b C) r^2} } \nonumber \\&\quad \times \left( F-\frac{f_{12}(r)}{2 \beta }-f_{13}(r)\right) \Bigg ]. \end{aligned}$$
(85)

where, \(\zeta (r)\) is given in the Appendix and the effective anisotropy factor read as,

$$\begin{aligned}&{\hat{\Pi }}(r,\,\beta )=\frac{e^{-D r^2} \left( -1+e^{D r^2}-2 A r^2\right) }{r^2}+\beta \Bigg (-2 C e^{-D r^2}\nonumber \\&\quad -\frac{\big [2 \beta (F-f_{13}(r))-f_{12}(r)\big ] (2 Ar^2+2 \beta Cr^2+1) }{2 \beta e^{(A+\beta C) r^2}(2+A r^2+\beta C r^2)^{-1}}\Bigg )\nonumber \\&\quad -\beta \Bigg [\frac{C Dr^2}{e^{D r^2}}-\frac{\zeta (r) \left( 1+A r^2+\beta C r^2\right) }{2 r}- \frac{(A+\beta C)}{e^{(A+\beta C) r^2}}\nonumber \\&\quad \times \frac{\big [2 \beta (F-f_{13}(r))-f_{12}(r)\big ] r^2 \left( 2+A r^2+\beta C r^2\right) ^2}{2 \beta }\nonumber \\&\quad - \frac{C \left( 2+2 A r^2+3 \beta C r^2\right) }{e^{D r^2}}\Bigg ]\nonumber \\&\quad - \frac{\left[ D-A^2 r^2+A (D r^2-2)\right] }{e^{D r^2}}.~~~ \end{aligned}$$
(86)
Fig. 4
figure 4

The behavior complexity factor \({\hat{Y}}_{TF}\) versus radial coordinate r/R for different compactification factor \(\left( u=\frac{M_s}{R}\right) \) with \(C=0.0002\). The above complexity figure is plotted corresponding to solution determined in Sect. 5.1

Full size image
Fig. 5
figure 5

The behavior of radial pressure (\(P_r\times 10^4\))-top left, tangential pressures (\(P_\perp \times 10^4\))-top right, energy density (\(\epsilon \times 10^4\))-bottom left and anisotropy (\({\hat{\Pi }}\times 10^4\))-bottom right versus radial coordinate r/R for different coupling constant \(\beta \) with compactification factor \(\frac{M_s}{R}=0.2\) with \(C=0.0002\). The above figures are plotted corresponding to EGD solution generated by zero complexity factor presented in in Sect. 5.2

Full size image

Now again use the boundary conditions (34)–(36) for present solution (82)–(86), we find the F, B and total mass M,

$$\begin{aligned}&F= \frac{e^{R^2 (A+\beta C)}}{\beta \left( 2 A R^2+2 \beta C R^2+1\right) \left( A R^2+\beta C R^2+2\right) } \Bigg [\frac{f_8(R)}{2} \nonumber \\&\quad \times \frac{\left( A R^2+\beta C R^2+2\right) }{e^{(A+\beta C) R^2}} \left( 2 AR^2+2 \beta CR^2+1\right) +\frac{f_{13}(R)}{2} \nonumber \\&\quad \times \frac{\left( 2 AR^2{+}2 \beta CR^2{+}1\right) }{R^2\,e^{\left( R^2 (A{+}\beta C)\right) {+}2}} {+}\frac{ \left( e^{D R^2} {-}2 A R^2-1\right) }{R^2 e^{D R^2}}{-}\frac{2 \beta C}{e^{D R^2}} \Bigg ],\nonumber \\ \end{aligned}$$
(87)
$$\begin{aligned} B&= \frac{e^{-DR^2}+\beta \,f(R)}{e^{AR^2+\beta \,CR^2}}, \end{aligned}$$
(88)
$$\begin{aligned} M&= M_s-\frac{\beta \,R}{2}f(R). \end{aligned}$$
(89)

where f(R) can be determined by Eq. (82) at \(r=R\) while the constant A and D will be same as given by Eqs. (65) and (66). Figure 5 has been plotted against the gravitationally decoupled solution obtained in the context of the zero complexity factor. It is observed that \(P_{r}\), \(P_\perp \), and \(\epsilon \) are monotonically decreasing towards the surface but the tangential pressure (\(P_\perp \)) is negative near the boundary. This happens due to stronger attractive force generated by the anisotropy, known as anisotropic force (\(F_a\)), near the surface of the object i.e. \(F_a=\frac{2{\hat{\Pi }}}{r}<0\). The same features also appear under the MGD scenario for Tolman IV solution as discussed by Casadio et al. [68]. Therefore, we can conclude that the gravitationally decoupled solution under zero complexity factor may not be suitable for modelling of the self-gravitating compact objects.

6 Discussions and conclusions

In the present article, we have used gravitational decoupling (GD) via complete geometric deformation (CGD) approach to isotropize the self-gravitating anisotropic matter distribution and discussed the complexity of this isotropic solution together with the effect of the decoupling parameter on the complexity. Furthermore, we also investigated two new gravitationally decoupled anisotropic solutions by imposing the condition of two systems with the same complexity factor as well as systems with zero complexity factor. As we know that most of the previous works, the new solutions were investigated by taking some particular procedures such as equations of state (EoS) for the extra sources added in the original energy-momentum tensor, mimick approaches, and particular ansatz for the deformation functions, etc. However, in this article we have adopted some different approaches to solve the systems by introducing the gravitational decoupling in the context of CGD. For simplicity, first we started with two energy-momentum tensors in which the first energy-momentum tensor corresponding to anisotropic matter distribution while the second one is an unknown source. As usual, the decoupled system is divided into two sets of equations through the CGD approach by introducing two unknown deformation functions f(r) and h(r) along the radial and temporal components of the metric function of the line element, respectively. After splitting the field equations, we have considered the following cases described in different sections as below:

In Sect. 3, we have investigated the isotropic solution for the gravitationally decoupled system. For this purpose, first we consider the spacetime geometry for the seed system corresponding the Tolman-Kuchowicz metric, which is necessary for GD system. After that we find the isotropic condition of the gravitationally decoupled systems by employing the effective anisotropy \({\hat{\Pi }}\) to be zero. In this way we get a differential equation containing two unknowns f(r) and h(r) and solved this equation for f(r) by assuming a particular viable form of \(h(r)=Cr^2\). The obtained solution for f(r) gives the vanishing effective anisotropy throughout the star which implies an isotropic solution of the gravitationally decoupled system.

In Sect. 4, we extended the definition of complexity proposed by Herrera [12] under gravitational decoupling. This section contains full details about the complexity of the gravitationally decoupled systems. Moreover, we also discussed the complexity factor and impact of decoupling constant \(\beta \) on complexity for the obtained isotropic solution in Sect. 3. We observe that the complexity is increasing when \(\beta \) increases.

Section 5 contains some new solutions generated by EGD approach for the systems having same or vanishing complexity factors which are divided into two Sects. 5.1 and 5.2:

(A). In the Sect. 5.1, we discover the anisotropic solution by imposing the condition of two systems with same complexity factor by using Krori-Barua seed solution. This said condition leads a vanishing complexity factor for extra source i.e. \(Y^{\Theta }_{TF}=0\), which governs a differential equation in f(r) and g(r). This differential equation has been again solved for f(r) by using the same ansatz \(h(r)=Cr^2\). Furthermore, we also discussed the complexity factor and the influence of the compactness on the complexity within the compact objects for the obtained GD anisotropic solution.

(B). The second Sect. 5.2 contains the GD anisotropic solution which is obtained by setting zero complexity factor corresponding to the gravitationally decoupled systems i.e. \({\hat{Y}}_{TF}=0\). The solution obtained in this section shows some drawbacks such that it gives a negative anisotropy throughout the configuration. Since this behavior of the anisotropy leads to an attractive force which may not much suitable for modeling the viable self-gravitating compact objects.

Finally, we would like to mention here that the gravitational decoupling via CGD approach is a very powerful and effective technique to generate new physically viable isotropic solutions from an anisotropic matter distribution. Moreover, this methodology is also useful to generate well-behaved anisotropic solutions by assuming of two systems with same complexity factors. In future projects, we will try to investigate some more conditions on complexity factor for generating the new solutions of Einstein’s field equations for static self-gravitating systems by using the gravitational decoupling technique.