Extended General Relativity: (3+1)-anyons in a preinflationary cosmological model

Abstract

We propose an extended General Relativistic formalism with boundary terms included, that describes the dynamics of quantum spinor fields, which can take intermediate values, named $(3+1)$-anyons. In the approach here worked, we use an extended manifold in which the $\left( 3+1\right)$-anyon fields can be expressed as a linear combination of bosons and fermions. We calculate the flow of these fields with self-interactions included in a preinflationary model that describes the birth of the universe from a null Hubble parameter, and we obtain the value of the cosmological parameter at this moment due to the flux of $(3+1)$-anyons through the 3d-closed hypersurface. The spectral indices at the end of preinflation are in very good agreement with observations. In particular the tensor to scalar ratio obtained at the end of preinflation is very small: $r(\phi _*) = 0.00336$.

1 Introduction

The pure spinor formalism [1, 2], has shown to be a powerful framework in the computation of scattering amplitudes and the quantization of the superstring [3,4,5,6] in curved backgrounds which can include Ramond–Ramond flux. The fact that manifolds with no-Euclidean geometry can help uncover new features of quantum matter makes it desirable to create manifolds of controllable shape and to develop the capability to add in synthetic gauge fields [7]. In the last years new physical possibilities, beyond the standard Dirac, Majorana and Weyl spinors, have been introduced and studied in a Minkowsky 4d-spacetime [8] and the Lounesto’s classification for Heisenberg spinors has been studied [9]. Once having established the classification of second quantized spinor fields into regular and singular classes in the four dimensional Minkowsky spacetime, an analogous second quantized classification on other kind of spaces has been considered [10, 11]. A generalizaton of the Lounesto’s classification was devised and discussed in [12]. In particular, symmetric curvature spinors with 2s indices that appear in twistors generalized Weyl curvature spinor can play an important role in the formulation of higher spin gauge theories extending Einstein [13] and Weyl [14, 15] gravity theories.

A very important question is how to construct a non-perturbative and covariant string formalism on a curved background which can be explained from a globally hyperbolic non-commutative quantum spacetime. With this aim, a few years ago was proposed unified spinor fields (USF), with the additament of including a quantization of the spacetime [16,17,18,19,20], and by taking into account also self-interactions of quantum spinor fields. The USF theory is developed in 8 dimensions, 4 of them related to the spacetime coordinates ($x^{\mu }$), and the other 4 related to the inner space ($\phi ^{\mu }$), which are compact coordinates that have spin components as canonical momentums: ($s_{\mu }$). To describe a non-commutative and globally hyperbolic spacetime, we consider unit vectors are $4\times 4$-matrices: $\bar{\gamma }^{\alpha }$. In the theory we use the Weyl representation of the Dirac matrices, which generate the background metric and we include the spinor information in the spacetime structure that can describe quantum effects in a relativistic framework [21]. An important fact in such description is that quantum spinor fields are considered on an extended manifold on which the variation of the metric tensor is nonzero, and therefore the norma associated to vector and tensor fields is not conserved. This is a key to can describe these fields in a background dynamical spacetime which can be expanding [20, 21] or collapsing.

In this work we shall extend a previous work [22], in which we have obtained the gluon field nonlinear dynamics by using a relativistic Ricci-flow defined on an extended manifold that is generated by a gluon field. The aim of this work consists to extend the manifold with connections that can take into account simultaneously, boson and fermion fields, in order to make possible the study of a more generic fermion-bosons interactions in the field’s dynamics. To make it, we shall consider the existence of a relativistic $\left( 3+1\right)$-anyon fields, which are some kind of quasi-particle that have properties less restrictive that bosons and fermions. In general, the operation of exchanging two identical particles can cause a global change of phase, which does not affect the observables. Anyones are generally classified as abelians or non-abelians (referring to their commutative and non-commutative behavior). Abelian anyons have been detected and play an important role in the fractional quantum Hall effect. The non-Abelian anyones have not been detected and their search is an active area of investigation [23]. In some recent works it is shown that the loop and string like excitations exist for topological orders in the $(3+1)$-dimensional spacetime, and their multi-loop/string-braiding statistics are the key signatures for identifying $(3+1)$-dimensional topological orders [24, 25].

The work is organized as follows: in Sect. 2 we describe the classical spacetime from a quantum origin. In Sect. 3 we review the background relativistic dynamics by taking into account the boundary conditions when we minimize the Einstein–Hilbert action, and we obtain the relevant quantum tensors, which we use to calculate the dynamics of the spinor fields. In Sect. 4 we analyse the flow at a quantum level and we normalize this flow with the parameter $\lambda (x)$. In Sect. 5 we introduce a new kind of connection $\hat{\delta \Gamma }^{\alpha }_{\beta \gamma } = b \,\hat{\Psi }^{\alpha } g_{\beta \gamma }$, which is generated by a $\left( 3+1\right)$-anyon field: $\hat{\Psi }^{\alpha }\equiv \alpha ^i\,\, _i\hat{\mathcal {B}}^{\alpha } + \beta ^i\,\,_i\hat{\mathcal {F}}^{\alpha }$ that takes into account bosons $_i\hat{\mathcal {B}}^{\alpha }$ and fermions $_i\hat{\mathcal {F}}^{\alpha }$. We describe the flow of $\hat{\Psi }^{\alpha }$, due to bosons and fermions and we obtain the wave equation that describe the dynamics of the $\left( 3+1\right)$-anyons $\hat{\Psi }^{\alpha }$ from the extended Einstein equations and strong interactions. In Sect. 6 we obtain the dynamic equations for the $(3+1)$-anyons in terms of boson and fermion fields for a particular gauge, for the extended Einstein equations and strong interactions. In Sect. 7 we calculate the time dependent cosmological parameter at the beginning of the universe in a preinflationary model, where the Hubble parameter is initially null, and increases until it reaches its maximum value. Finally, in Sect. 8, we develop some final comments.

2 Globally hyperbolic classical spacetime from a quantum spacetime

In order to can describe a globally hyperbolic 4d-spacetime with structure, from a quantum origin, we shall consider four spacetime operators $\delta \hat{X}^{\alpha }(x^{\nu })$ and four quantum operators which describe the inner space: $\delta \hat{\Phi }^{\alpha }(\phi ^{\nu })$, which are relevant to describe quantum spinor fields. These operators can be respectively represented by Fourier expansions

$$\begin{aligned} \delta \hat{X}^{\alpha }(x^{\nu })&= \frac{1}{(2\pi )^{2}} \int d^4 k \, \bar{\gamma }^{\alpha } \left[ b_k \, \hat{X}_k(x^{\nu }) + b^{\dagger }_k \, \hat{X}^*_k(x^{\nu })\right] , \end{aligned}$$

(1)

$$\begin{aligned} \delta \hat{\Phi }^{\alpha }(\phi ^{\nu })&= \frac{1}{(2\pi )^{2}} \int d^4 s \, \bar{\gamma }^{\alpha } \,\left[ c_s \, \hat{\Phi }_s(\phi ^{\nu }) + c^{\dagger }_s \, \hat{\Phi }^*_s(\phi ^{\nu })\right] . \end{aligned}$$

(2)

Here, $b^{\dagger }_k$ and $b_k$ act as creation and destruction operators of the coordinate spacetime and $c^{\dagger }_s$ and $c_s$ are respectively the creation and destruction operators in the inner space

$$\begin{aligned}&\langle B \left| \left( b_{k''}\,\hat{X}_k(x)\,\bar{\gamma }^{\mu } \right) \,\left( b^{\dagger }_{k''}\,\hat{X}^*_{k'}(x)\,\bar{\gamma }^{\nu }\right) \right| B' \rangle \nonumber \\&\quad = \left( dx\,\bar{\gamma }^{\mu }\right) \,\left( dx\,\bar{\gamma }^{\nu }\right) \,\delta ^{(4)}\left( {k}-{k''} \right) \,\delta ^{(4)}\left( {k'}-{k''} \right) \,\delta _{BB'}, \end{aligned}$$

(3)

$$\begin{aligned}&\langle B \left| \left( c_{s''}\,\hat{\Phi }_s(\phi ) \,\bar{\gamma }^{\mu }\right) \,\left( c^{\dagger }_{s''}\,\hat{\Phi }_{s'}(\phi )\,\bar{\gamma }^{\nu }\right) \right| B' \rangle \nonumber \\&\quad = \left( d\phi \,\bar{\gamma }^{\mu }\right) \,\left( d\phi \,\bar{\gamma }^{\nu }\right) \,\delta ^{(4)}\left( {s}-{s''} \right) \,\delta ^{(4)}\left( {s'}-{s''} \right) \,\delta _{BB'}. \end{aligned}$$

(4)

The generators of a globally hyperbolic spacetime are the unit vectors $4\times 4$-Weyl representation of the Dirac matrices: $\bar{\gamma }^{\alpha }$, with a non-commutative structure. In the Weyl representation of an global hyperbolic spacetime $\gamma _0$ commutes with $\gamma _i$: $\left[ \gamma _0, \gamma _i\right] =0$, and therefore this representation is the best to describe spacetime.

We shall use the Heisenberg representation for the quantum states $| B\rangle$, where operators are evolving and states are squeezed. The background representations of the 4-length dl and the 4-angle $d\phi$, are

$$\begin{aligned} dl^2 \delta _{BB'}= & {} \left<B\right| \delta \hat{X}^{\alpha } \delta \hat{X}_{\alpha } \left| B'\right> , \qquad d\phi ^2 \delta _{BB'}\nonumber \\= & {} \frac{1}{4}\, \left<B\right| \left( \delta \hat{\Phi }_{\alpha }\,\delta \hat{\Phi }_{\beta }\right) \,\left( \bar{\gamma }^{\alpha }\,\bar{\gamma }^{\beta }\right) \left| B'\right>, \end{aligned}$$

(5)

where the first equation in (5) describes a standard inner product

$$\begin{aligned}&\delta \hat{X}^{\alpha } \delta \hat{X}_{\alpha } = \frac{1}{4} \left\{ \delta \hat{X}_{\alpha },\delta \hat{X}_{\beta } \right\} \,\left\{ \bar{\gamma }^{\alpha } , \bar{\gamma }^{\beta } \right\} , \end{aligned}$$

(6)

and the second one in (5) represents the expectation value of a bi-vectorial product, such that

$$\begin{aligned} \delta \hat{\Phi }_{\alpha }\,\delta \hat{\Phi }_{\beta }= & {} \frac{1}{2} \left\{ \delta \hat{\Phi }_{\alpha }, \delta \hat{\Phi }_{\beta }\right\} + \frac{1}{2} \left[ \delta \hat{\Phi }_{\alpha }, \delta \hat{\Phi }_{\beta }\right] ,\nonumber \\ \bar{\gamma }_{\mu } \bar{\gamma }_{\nu }= & {} \frac{1}{2} \left\{ \bar{\gamma }_{\mu }, \bar{\gamma }_{\nu }\right\} + \frac{1}{2} \left[ \bar{\gamma }_{\mu }, \bar{\gamma }_{\nu }\right] , \nonumber \\ \bar{\gamma }^{\mu } \bar{\gamma }^{\nu }= & {} \frac{1}{2} \left\{ \bar{\gamma }^{\mu }, \bar{\gamma }^{\nu }\right\} - \frac{1}{2} \left[ \bar{\gamma }^{\mu }, \bar{\gamma }^{\nu }\right] . \end{aligned}$$

(7)

These matrices generate the background metric and we include the spinor information in the spacetime structure that can describe quantum effects in a relativistic framework. The interesting of this representation is that the structure of spacetime is included: $\bar{\gamma }^{\alpha }\,\bar{\gamma }_{\beta }= \delta ^{\alpha }_{\beta } \,\mathbb {I}_{4\times 4}+\frac{1}{2} \left[ \bar{\gamma }^{\alpha },\,\bar{\gamma }_{\beta }\right]$ so that they generate a non-commutative spacetime and comply with the transformation law

$$\begin{aligned} \bar{\gamma }^{\mu } = E^{\mu }_{\nu } \,\gamma ^{\nu }, \end{aligned}$$

(8)

where $E^{\mu }_{\nu }$ are the transformation matrices from a Minkowsky spacetime to an arbitrary curved spacetime generated by $\bar{\gamma }^{\mu }$. The components $\gamma ^{\mu }$ are described in the Weyl representation (quiral representation) for a Minkowsky spacetime.¹ We can use the fact that $\bar{\gamma }_{\mu }\bar{\gamma }^{\mu }= 4\,\mathbb {I}_{4\times 4}$, $\left\{ \bar{\gamma }_{\mu }\bar{\gamma }_{\nu }\right\} =2\,g_{\mu \nu }$ and $\bar{\gamma }_{\mu } \bar{\gamma }^{\nu }\bar{\gamma }^{\mu }= -2\,\bar{\gamma }^{\nu }$ to obtain the expression

$$\begin{aligned}&\frac{1}{4}\left( \bar{\gamma }_{\mu } \bar{\gamma }_{\nu }\right) \,\left( \bar{\gamma }^{\mu } \bar{\gamma }^{\nu }\right) \nonumber \\&\quad = \frac{1}{16} \left( \left\{ \bar{\gamma }_{\mu }, \bar{\gamma }_{\nu }\right\} \,\left\{ \bar{\gamma }^{\mu }, \bar{\gamma }^{\nu }\right\} - \left[ \bar{\gamma }_{\mu }, \bar{\gamma }_{\nu }\right] \,\left[ \bar{\gamma }^{\mu }, \bar{\gamma }^{\nu }\right] \right) \nonumber \\&\quad = \frac{1}{16} \left( 16\,\mathbb {I}_{4\times 4} - (-48)\,\mathbb {I}_{4\times 4}\right) = 4\,\mathbb {I}_{4\times 4}. \end{aligned}$$

(9)

Each component of spin $\hat{S}_{\mu }= s\,\bar{\gamma }_{\mu }$, is defined as the canonical momentum associated to the inner coordinate $\hat{\Phi }^{\mu }$, and therefore we can define the universal bi-vectorial invariant

$$\begin{aligned} \frac{1}{4} \left<B\left| \left( \hat{S}_{\mu } \hat{\Phi }_{\nu } \right) \left( \bar{\gamma }^{\mu } \bar{\gamma }^{\nu }\right) \right| B\right> =s \phi \, \mathbb {I}_{4\times 4} = (2\pi n \hbar ) \,\mathbb {I}_{4\times 4}, \end{aligned}$$

(10)

with n-integer.

3 Background dynamics with boundary conditions

With the aim to describe the background dynamics of an arbitrary system on a semi-Riemannian manifold, we shall consider the Einstein–Hilbert action

$$\begin{aligned} {{\mathcal {I}}} = \int d^4 x \sqrt{-g} \left[ \frac{R}{2\kappa } + {{\mathcal {L}}}_m\right] , \end{aligned}$$

(11)

where R is the background scalar curvature, $\kappa = 8 \pi \,G$ and ${{\mathcal {L}}}_m$ is the Lagrangian density that describes the physical fields that describes the background dynamics of the system under consideration. The varied action $\delta {{\mathcal {I}}}$, is

$$\begin{aligned} \delta {{\mathcal {I}}} = \int d^4 x \sqrt{-g} \left[ \delta g^{\alpha \beta } \left( G_{\alpha \beta } + \kappa T_{\alpha \beta }\right) + g^{\alpha \beta } \delta R_{\alpha \beta } \right] =0,\nonumber \\ \end{aligned}$$

(12)

where the background stress tensor ${{T}}_{\alpha \beta }$, is

$$\begin{aligned} {{T}}_{\alpha \beta } = 2 \frac{\delta {{{\mathcal {L}}}_m}}{\delta g^{\alpha \beta }} - g_{\alpha \beta } {{{\mathcal {L}}}_m}. \end{aligned}$$

(13)

The contribution $g^{\alpha \beta } \delta R_{\alpha \beta }$ takes into account the boundary terms given by the flow $\delta \Theta$ of the 4-vector field $\delta W^{\alpha }= \delta \Gamma ^{\epsilon }_{\beta \epsilon } {g}^{\beta \alpha }-\delta \Gamma ^{\alpha }_{\beta \gamma } {g}^{\beta \gamma }$, through the 3D-closed hypersurface. In the case that $\delta \Theta$ is nonzero, it alters the dynamics of the system, because acts as a source on the background equation of motion. We shall consider the particular case where this flow has a quantum nature. In this case one must consider the background contribution in (12), which is given by its expectation value

$$\begin{aligned} \left( g^{\alpha \beta } \delta R_{\alpha \beta }\right) \, \delta _{BB'}= \left<B\left| g^{\alpha \beta }\,\hat{\delta R}_{\alpha \beta }\right| B'\right>, \end{aligned}$$

(14)

where $|B\rangle$ describes a Fock space on the background curved space time. The background dynamics on the semi-Riemannian manifold are generated by the Levi–Civita connections $\left\{ \begin{array}{cc} \alpha \, \\ \beta \, \gamma \end{array} \right\}$ . However, we shall consider that boundary terms are on an extended manifold generated by the connections $\hat{\delta \Gamma }^{\alpha }_{\beta \gamma }$

$$\begin{aligned} \hat{\delta \Gamma }^{\alpha }_{\beta \gamma } = b \,\hat{\Psi }^{\alpha } g_{\beta \gamma }, \end{aligned}$$

(15)

such that $\hat{\Psi }^{\alpha }$ is a quantum spinor field and b is a parameter to be determined by the gauge we choose to describe its dynamics. Notice that $\hat{\delta \Gamma }^{\alpha }_{\beta \gamma }$ generates an extended manifold which is not a Riemann one. The extended manifold generated by (15) describes a quantum physical reality, meanwhile the Riemann one takes into account the background dynamics, generated by the fundamental metric tensor, with components: $g_{\alpha \beta }$, with which we describe the classical line element (5).

3.1 Quantum Ricci tensor and related tensors

We shall use the extended version of the Palatini identity [16, 17, 26] to define the variation of the Ricci tensor: $\delta {R}_{\beta \gamma }$, on the extended manifold.²

$$\begin{aligned} \hat{\delta {R}}^{\alpha }_{\beta \gamma \alpha }= \hat{\delta {R}}_{\beta \gamma }= \frac{1}{b}\,\left[ \left( \hat{\delta \Gamma }^{\alpha }_{\beta \alpha } \right) _{\Vert \gamma } - \left( \hat{\delta \Gamma }^{\alpha }_{\beta \gamma } \right) _{\Vert \alpha }\right] . \end{aligned}$$

(18)

The symmetric and anti-symmetric counterparts of $\hat{\delta {R}}_{\beta \gamma }$, with self-interactions included, are respectively given by [22]

$$\begin{aligned} \hat{\delta U}_{\mu \nu }= & {} -\left\{ \frac{1}{2} \left( \nabla _{\nu } \hat{\Psi }_{\mu }+ \nabla _{\mu } \hat{\Psi }_{\nu }\right) \nonumber \right. \\&\left. + \frac{1}{2} \left[ 2 b+(1-\xi ^2)\right] \left\{ \hat{\Psi }_{\mu }, \hat{\Psi }_{\nu }\right\} \nonumber \right. \\&\left. - g_{\mu \nu }\,\left[ \nabla _{\alpha }\,\hat{\Psi }^{\alpha } + \left[ 2b+\left( 1-\xi ^2\right) \right] \hat{\Psi }_{\alpha } \hat{\Psi }^{\alpha }\right] \right\} , \end{aligned}$$

(19)

$$\begin{aligned} \hat{\delta V}_{\mu \nu }= & {} - \frac{1}{2} \,\left\{ \left( \nabla _{\nu } \hat{\Psi }_{\mu }- \nabla _{\mu } \hat{\Psi }_{\nu }\right) \nonumber \right. \\&\left. + (1-\xi ^2) \,\left[ \hat{\Psi }_{\mu }, \hat{\Psi }_{\nu }\right] \right\} , \end{aligned}$$

(20)

where $\xi$ is the self-interaction dimensionless constant. As was demonstrated in [22], in the case that $\hat{\Psi }^{\alpha }$ has 1-spin, the quantum operator $\hat{\delta V}_{\mu \nu }$ give us the strength tensor: $\hat{\delta V}_{\mu \nu }\equiv {1\over 2}\hat{{{\mathcal {G}}}}_{\mu \nu }$, for $1-\xi ^2=i\,g_s$, such that $g_s=\sqrt{4\pi \alpha _s}$, and $\alpha _s$ is the coupling constant of the strong force. In such case, the eight matrices $\lambda ^a$, are the ($3\times 3$) Gell–Mann matrices in the SU(3) group representation and the components of the gluon field strength tensor comes from a linear combination with the Gell-Mann matrices

$$\begin{aligned} \hat{{{\mathcal {G}}}}_{\mu \nu }= \frac{\lambda _a}{2} \,\hat{{{\mathcal {G}}}}^a_{\mu \nu }. \end{aligned}$$

(21)

Furthermore, the gluon field strength tensor, written in terms of the gluon fields $\hat{A}^c_{\nu }$, is

$$\begin{aligned} \hat{{{\mathcal {G}}}}^a_{\mu \nu }= \nabla _{\mu } \hat{A}^a_{\nu } - \nabla _{\nu } \hat{A}^a_{\mu } + g_s\,f^a_{bc} \hat{A}^b_{\mu }\,\hat{A}^c_{\nu }, \end{aligned}$$

(22)

where $a,b,c=1,2,\ldots ,8$ enumerate the eight color charges and $f^a_{bc}$ are structure constants.

The quantum Einstein’s tensor, will be defined by taking into account the symmetric contribution of $\hat{\delta {R}}_{\mu \nu }$:

$$\begin{aligned} \hat{E}_{\mu \nu }= & {} \hat{\delta U}_{\mu \nu } - \frac{1}{2} \,\left[ g^{\mu \nu }\, \hat{\delta U}_{\mu \nu }\right] \nonumber \\= & {} -\frac{1}{2}\left\{ \left( \nabla _{\nu } \hat{\Psi }_{\mu }+ \nabla _{\mu } \hat{\Psi }_{\nu }\right) \nonumber \right. \\&\left. + \left[ 2 b+(1-\xi ^2)\right] \left\{ \hat{\Psi }_{\mu }, \hat{\Psi }_{\nu }\right\} \nonumber \right. \\&\left. + g_{\mu \nu }\,\left[ \nabla _{\alpha }\,\hat{\Psi }^{\alpha } + \left[ 2b+\left( 1-\xi ^2\right) \right] \hat{\Psi }_{\alpha } \hat{\Psi }^{\alpha }\right] \right\} . \end{aligned}$$

(16)

4 Back-reaction, normalization of the relativistic flow and dynamics

In order for describe back-reaction effects from USF, we shall consider the flow given by

$$\begin{aligned} \hat{\delta R}_{\alpha \beta }= \lambda (x)\,\hat{\delta g}_{\alpha \beta }, \end{aligned}$$

(23)

where $\lambda (x)$ is the called cosmological parameter, which in general can be dependent of the coordinates, ”$\Vert$” denotes the covariant derivative on the extended manifold with self-interactions included, ${U}^{\gamma }=\frac{\hat{d X}^{\gamma }}{\quad d l}$ are the components of the relativistic velocities on the Riemann manifold, and the variation of the metric tensor is³

$$\begin{aligned} \hat{\delta g}_{\alpha \beta }=\hat{g}_{\alpha \beta \Vert \gamma } \,{U}^{\gamma }. \end{aligned}$$

(24)

The flow through the 3D-closed hypersurface of a field $\hat{\delta W}^{\alpha }= \hat{\delta \Gamma }^{\alpha }_{\beta \gamma } {g}^{\beta \gamma }-\hat{\delta \Gamma }^{\epsilon }_{\beta \epsilon }{g}^{\beta \alpha }$. Therefore, if we require the minimized action equation that provides the dynamics of the system

$$\begin{aligned}&{\delta g}^{\alpha \beta } \left[ G_{\alpha \beta } + \kappa \,T_{\alpha \beta }\right] + g^{\alpha \beta }\,{\delta R}_{\alpha \beta }\nonumber \\&\quad \equiv \left<B\right| \hat{\delta g}^{\alpha \beta } \left[ G_{\alpha \beta } + \kappa \,T_{\alpha \beta }\right] + g^{\alpha \beta }\,\hat{\delta R}_{\alpha \beta }\left| B\right>=0, \end{aligned}$$

(25)

with (23), we obtain the expression for the flow [22]

$$\begin{aligned}&\nabla _{\alpha }\,\hat{\Psi }^{\alpha } + \left[ 2b+\left( 1-\xi ^2\right) \right] \nonumber \\&\hat{\Psi }_{\alpha } \hat{\Psi }^{\alpha }= \frac{2}{3}\,\lambda (x)\left[ 4\,\left( 1-\xi ^2\right) -b\right] \,\nonumber \\&\hat{\Psi }_{\alpha }\,U^{\alpha }. \end{aligned}$$

(26)

In this framework we can define the variation of the metric tensor on the extended manifold with self-interactions included

$$\begin{aligned} \hat{g}_{\beta \alpha \Vert \gamma } \,U^{\gamma } | B\rangle = \delta g_{\beta \alpha } | B\rangle , \end{aligned}$$

(27)

and the covariant derivative of the metric tensor on the extended manifold with self-interactions, is

$$\begin{aligned} \hat{g}_{\beta \alpha \Vert \nu }=\nabla _{\nu } g_{\beta \alpha } -b\, \left( g_{\beta \nu } \hat{\Psi }_{\alpha } + \hat{\Psi }_{\beta } g_{\alpha \nu } \right) + 2\left( 1-\xi ^2\right) \hat{\Psi }_{\nu } \, g_{\alpha \beta }, \nonumber \\ \end{aligned}$$

(28)

where we must consider the fact that the tensor metric is compatible with the Levi–Civita connections, so that its covariant derivative becomes zero: $\nabla _{\nu } g_{\beta \alpha }=0$. Therefore, the dynamics of the background system with boundary conditions included (25), will be given by the expression

$$\begin{aligned} \delta g^{\alpha \beta } \left[ G_{\alpha \beta } - \lambda \left( x\right) \,g_{\alpha \beta } + \kappa \,T_{\alpha \beta }\right] =0. \end{aligned}$$

(29)

Then, the redefined background Einstein equations with the boundary terms assimilated, take the form

$$\begin{aligned} G_{\alpha \beta } - \lambda \left( x\right) \,{g}_{\alpha \beta }=-\kappa \, T_{\alpha \beta }. \end{aligned}$$

(30)

It is important to notice that the Eq. (30) can be interpreted in two possible forms. The boundary terms with $\lambda (x)$ in (30) can be assimilated to the Einstein tensor, or the stress tensor. Therefore, the boundary additional terms in the Einstein’s equations should be considered of as geometrical sources, or terms of physical nature.

4.1 Boundary terms as geometrical sources

In this case the redefined Einstein’s tensor is given by

$$\begin{aligned} \bar{G}_{\alpha \beta } = {G}_{\alpha \beta } - \lambda (x)\, g_{\alpha \beta }, \end{aligned}$$

(31)

and the geometric dynamics is given by the equations

$$\begin{aligned} \nabla _{\beta }\,G^{\alpha \beta } = g^{\alpha \beta }\,\frac{\partial \lambda (x)}{\partial x^{\beta }}, \end{aligned}$$

(32)

and $\nabla _{\beta }\,T^{\alpha \beta }=0$. Therefore, in this case the right hand in the Eq. (32) must be considered of a geometric nature.

4.2 Boundary terms as physical sources and relativistic velocities $U^{\alpha }$

In this case the redefined stress tensor is given by

$$\begin{aligned} \bar{T}_{\alpha \beta } = {T}_{\alpha \beta } - \frac{1}{\kappa } \lambda (x)\, g_{\alpha \beta }, \end{aligned}$$

(33)

and the dynamics for the physical fields is given by the equations

$$\begin{aligned} \nabla _{\beta }\,T^{\alpha \beta } = \frac{1}{\kappa }\,g^{\alpha \beta }\,\frac{\partial \lambda (x)}{\partial x^{\beta }}, \end{aligned}$$

(34)

where $T_{\alpha \beta }$ is given by (13) and the geometric dynamics being given by the equation $\nabla _{\beta }\,G^{\alpha \beta }=0$. This means that the flux due to the boundary terms in the minimized action will be the source for the dynamics of the physical fields. In this work we shall consider that the sources are of physical nature. In this sense, one can enclose with a closed 3D-hypersurface an arbitrary region of the background Riemann spacetime, through of which there is a flow of the $\hat{\Psi }^{\alpha }$-field [see the Eq. (26)], which alters the background Riemannian dynamics of relativistic system. This mechanism is viewed through the spacetime-dependent cosmological parameter $\lambda (x)$, that is included in the background Einstein equations (30).

In order to describe the background relativistic velocities we can assume a stress tensor that describe a perfect fluid

$$\begin{aligned} T^{\alpha \beta } = \left( P + \rho \right) \,U^{\alpha }\,U^{\beta } - P \,g^{\alpha \beta }, \end{aligned}$$

(35)

where P is the background pressure and $\rho$ is the background energy density of the system. Hence, from (35) and (34), we obtain that the background velocities can be described by

$$\begin{aligned}&\left( P + \rho \right) \,\left[ U^{\beta }\nabla _{\beta }\,U^{\alpha } + U^{\alpha } \nabla _{\beta } U^{\beta }\right] \nonumber \\&\quad + \left( P+\rho \right) _{,\beta } \,U^{\alpha }\,U^{\beta } - P_{,\beta }\,g^{\alpha \beta } = \frac{1}{\kappa } \,g^{\alpha \beta } \,\lambda _{,\beta }, \end{aligned}$$

(36)

The Eq. (36) provides the geodesic equation for a perfect fluid with arbitrary P and $\rho$, when the flux along the 3d-hypersurface is given by

$$\begin{aligned} \delta \Theta = \lambda (x)\left<B\right| g^{\alpha \beta } \hat{\delta g}_{\alpha \beta } \left| B\right>, \end{aligned}$$

(37)

such that $P/\rho =\omega$ is not necessarily constant.

4.3 Fourier expansions, quantum spinor fields and normalized flow

The spinor fields with spin s, can be represented in a Fourier expansion, as the variation of the flow $\hat{\delta \Theta }$ with respect to the inner coordinates:⁴$\hat{\Psi }_{\alpha }=\frac{\hat{\delta \Theta }}{\hat{\delta {\Phi }}^{\alpha }}$

$$\begin{aligned} \hat{\Psi }_{\alpha }\left( x^{\beta }|\Phi ^{\alpha }\right)= & {} \frac{i\,s}{\hbar (2\pi )^4}\int d^4k \,\bar{\gamma }_{\alpha }\,\Bigg [ A_{s,k}\, \hat{\Theta }_{k,s}(x^{\beta }) \, e^{\frac{i}{\hbar } \underleftrightarrow {S} \overleftrightarrow {\Phi }} \nonumber \\&- B^{\dagger }_{s,k} \, \hat{\Theta }^*_{k,s}(x^{\beta }) \,e^{-\frac{i}{\hbar } \underleftrightarrow {S} \overleftrightarrow {\Phi }}\Bigg ], \end{aligned}$$

(40)

and therefore the flow $\hat{\delta \Theta }$ in (26), will be given by

$$\begin{aligned} \hat{\delta \Theta }\left( x^{\beta }|\Phi ^{\alpha }\right)= & {} -\frac{2\,\lambda (x)\,M_p\left[ 4\,\left( 1-\xi ^2\right) -b\right] \,i}{\hbar (2\pi )^4} \int d^4k \,\frac{1}{4}\, \nonumber \\&\times \left( \hat{S}_{\mu }\,U^{\mu }\right) \Bigg [ A_{s,k}\, \hat{\Theta }_{k,s}(x^{\beta }) e^{\frac{i}{\hbar } \underleftrightarrow {S} \overleftrightarrow {\Phi }}\nonumber \\&\quad - B^{\dagger }_{s,k} \, \hat{\Theta }^*_{k,s}(x^{\beta }) e^{-\frac{i}{\hbar } \underleftrightarrow {S} \overleftrightarrow {\Phi }}\Bigg ]. \end{aligned}$$

(41)

For massive and massless fields we respectively must require

$$\begin{aligned} U_{\mu }\,U^{\mu }=1, \quad U_{\mu }\,U^{\mu }=0. \end{aligned}$$

(42)

In order to avoid quantum divergences, we shall require that the expectation value of the flux on the background metric to be given by the parameter $\lambda (x)$:

$$\begin{aligned} \left<B\right| \hat{\delta \Theta }\left| B\right> = -\lambda (x)\,\mathbb {I}_{4\times 4}\,G^{-1/2}, \end{aligned}$$

(43)

where in natural units $G^{-1/2}\equiv M_p \simeq 1.2\times 10^{19}\,\mathrm{GeV}$. If we require the following normalization condition for the varied metric on the extended manifold

$$\begin{aligned} \left<B\right| g^{\alpha \beta }\hat{\delta g}_{\alpha \beta }\left| B\right>=-\left<B\right| g_{\alpha \beta } {\hat{\delta g}}^{\alpha \beta }\left| B\right>=-\mathbb {I}_{4\times 4}\,M_p, \end{aligned}$$

(38)

we obtain the following expectation value

$$\begin{aligned} \left<B\right| U^{\mu }\,\hat{\Psi }_{\mu }\left| B\right>=\frac{\mathbb {I}_{4\times 4}\,M_p}{2\,\left[ 4(1-\xi ^2)-b\right] }, \end{aligned}$$

(44)

and hence the expectation value for the inner product $U^{\mu }\,\hat{S}_{\mu }$, due to massive fields, results to be

$$\begin{aligned} \left<B\right| U^{\mu }\,\hat{S}_{\mu }\left| B\right>=\frac{4\,i\,\hbar \,\mathbb {I}_{4\times 4}}{2\,\left[ 4(1-\xi ^2)-b\right] }, \end{aligned}$$

(45)

with $4(1-\xi ^2)\ne b$.

5 Connections with $\left( 3+1\right)$-anyons

In this work we are interested to describe the quantum dynamics of quantum spinor fields with arbitrary spin in a relativistic context, which we shall call $\left( 3+1\right)$-anyon, with 4 components $\hat{\Psi }^{\alpha }$, given by a superposition of bosons $_i\hat{\mathcal {B}}^{\alpha }$, and fermions $_i\hat{\mathcal {F}}^{\alpha }$:

$$\begin{aligned} \hat{\Psi }^{\alpha } = \alpha ^i\,\, _i\hat{\mathcal {B}}^{\alpha } + \beta ^i\,\,_i\hat{\mathcal {F}}^{\alpha }, \end{aligned}$$

(46)

where we denote respectively by $_i\hat{\mathcal {B}}^{\alpha }$ and $_i\hat{\mathcal {F}}^{\alpha }$, the i-boson and i-fermion fields with spins $B_i$ and $F_i$. Here, $\alpha ^i$ and $\beta ^i$ are respectively the i-boson and i-fermion coupling constants. Because we are considering massive charged $(3+1)$-anyons with a spin $s=A\,\hbar$, due to the invariant (10), the operators $e^{\pm \frac{i}{\hbar } \underleftrightarrow {S} \overleftrightarrow {\Phi }}$ applied on the background state $|B\rangle$, will be invariant under $\phi = (2n/A)\,\pi$-rotations (n integer):

$$\begin{aligned} e^{\pm \frac{i}{\hbar } \underleftrightarrow {S} \overleftrightarrow {\Phi }}|B\rangle \,= \,e^{\pm \,{i} \,A\,\phi } \, |B\rangle , \end{aligned}$$

(47)

where we remember that we have adopted the Heisenberg representation for these states, such that the operators are evolving and states are squeezed. Because we are considering $(3+1)$-anyons given by a linear combination (46), the spin A will be given by the spin of bosons $B_i$, and fermions $F_i$ that compose the $\left( 3+1\right)$-anyon. Those bosons and fermions will describe respectively the following spinor algebra

$$\begin{aligned}&\bigg \langle B\left| \left[ \,^i\hat{\mathcal {B}}_{\mu }(\mathbf{x}, \mathbf{\phi }), \,^j\hat{\mathcal {B}}_{\nu }(\mathbf{x}', \mathbf{\phi }') \right] \right| B \bigg \rangle \nonumber \\&\quad = \frac{B_i\,B_j\ \,\delta ^{ij}}{2 \hbar ^2 }\left[ \bar{\gamma }_{\mu } , \bar{\gamma }_{\nu }\right] \, \sqrt{\frac{\eta }{g}} \,\,\delta ^{(4)} \left( \mathbf{x} - \mathbf{x}'\right) \,\delta ^{(4)} \left( \mathbf{\phi } - \mathbf{\phi }'\right) , \end{aligned}$$

(48)

$$\begin{aligned}&\bigg \langle B\left| \left\{ \,^i\hat{\mathcal {F}}_{\mu }(\mathbf{x}, \mathbf{\phi }), \,^j\hat{\mathcal {F}}_{\nu }(\mathbf{x}', \mathbf{\phi }') \right\} \right| B \bigg \rangle \nonumber \\&\quad = \frac{F_i\,F_j\,\delta ^{ij}}{2 \hbar ^2}\, \left\{ \bar{\gamma }_{\mu }, \bar{\gamma }_{\nu } \right\} \,\mathbb {I}_{4\times 4} \, \sqrt{\frac{\eta }{g}}\nonumber \\&\qquad \times \delta ^{(4)} \left( \mathbf{x} - \mathbf{x}'\right) \,\delta ^{(4)} \left( \mathbf{\phi } - \mathbf{\phi }'\right) , \end{aligned}$$

(49)

such that bosons and fermions will be invariant respectively under $\phi = (2n/B_i)\,\pi$-rotations (n integer), and $\phi = (2n/F_i)\,\pi$-rotations, for $B_i=0,\hbar ,2\,\hbar ,\ldots$ and $F_i=\hbar /2,3\hbar /2,\ldots$:

$$\begin{aligned}&e^{\pm \frac{i}{\hbar } \underleftrightarrow {S^{(B_i)}} \overleftrightarrow {\Phi }}|B\rangle = e^{\pm \,{i} \,B_i\,\phi } \, |B\rangle , \nonumber \\&e^{\pm \frac{i}{\hbar } \underleftrightarrow {S^{(F_i)}} \overleftrightarrow {\Phi }}|B\rangle = e^{\pm \,{i} \,F_i\,\phi } \, |B\rangle . \end{aligned}$$

(50)

Their Fourier’s representations for bosons and fermions will be

$$\begin{aligned} ^i\hat{\mathcal {B}}_{\alpha }\left( x^{\beta }|\Phi ^{\alpha }\right)&= \frac{i\,B_i}{\hbar (2\pi )^4} \int d^4k \,\bar{\gamma }_{\alpha }\nonumber \\&\quad \times \left[ A^{(B_i)}_{s,k}\, \left[ \hat{\Theta }^{(B_i)}\right] _{k,s}(x^{\beta }) \,e^{\frac{i}{\hbar }\underleftrightarrow {S^{(B_i)}} \overleftrightarrow {\Phi }}\right. \nonumber \\&\quad \left. - \left[ B^{(B_i)}\right] ^{\dagger }_{s,k} \, \left[ \hat{\Theta }^{(B_i)}\right] ^*_{k,s}(x^{\beta }) \,e^{-\frac{i}{\hbar } \underleftrightarrow {S^{(B_i)}} \overleftrightarrow {\Phi }}\right] , \end{aligned}$$

(51)

$$\begin{aligned} ^i\hat{\mathcal {F}}_{\alpha }\left( x^{\beta }|\Phi ^{\alpha }\right)&= \frac{i\,F_i}{\hbar (2\pi )^4} \int d^4k \,\bar{\gamma }_{\alpha }\nonumber \\&\quad \times \left[ A^{(F_i)}_{s,k}\, \left[ \hat{\Theta }^{(F_i)}\right] _{k,s}(x^{\beta })\, e^{\frac{i}{\hbar } \underleftrightarrow {S^{(F_i)}} \overleftrightarrow {\Phi }}\right. \nonumber \\&\quad \left. - \left[ B^{(F_i)}\right] ^{\dagger }_{s,k} \, \left[ \hat{\Theta }^{(F_i)}\right] ^*_{k,s}(x^{\beta })\, e^{-\frac{i}{\hbar } \underleftrightarrow {S^{(F_i)}} \overleftrightarrow {\Phi }}\right] . \end{aligned}$$

(52)

Therefore, for the connections (46), we obtain

$$\begin{aligned} \hat{\delta g}_{\beta \alpha }= & {} -b\,\Bigg \{ \Bigg [g_{\beta \nu } \left( \alpha _i\,\, ^i\hat{\mathcal {B}}_{\alpha } + \beta _i\,\,^i\hat{\mathcal {F}}_{\alpha }\right) \nonumber \\&\quad + \left( \alpha _i\,\, ^i\hat{\mathcal {B}}_{\beta } + \beta _i\,\,^i\hat{\mathcal {F}}_{\beta } \right) g_{\alpha \nu } \Bigg ]+ 2\left( 1-\xi ^2\right) \nonumber \\&\quad \times \left( \alpha _i\,\, ^i\hat{\mathcal {B}}_{\nu } + \beta _i\,\,^i\hat{\mathcal {F}}_{\nu }\right) \, g_{\alpha \beta }\Bigg \}\,U^{\nu }. \end{aligned}$$

(53)

With the particular connections (46), results to be the following equation for the flow

$$\begin{aligned}&\beta ^i\left( \nabla _{\alpha }\, _i\hat{\mathcal {F}}^{\alpha }\right) +\alpha ^i\left( \nabla _{\alpha }\, _i\hat{\mathcal {B}}^{\alpha }\right) + \beta _i\,\beta ^i\,\left[ 2b+\left( 1-\xi ^2\right) \right] \, ^i\hat{\mathcal {F}}_{\alpha }\, _i\hat{\mathcal {F}}^{\alpha }\nonumber \\&\quad = \frac{2}{3}\,\lambda (x)\left[ 4\,\left( 1-\xi ^2\right) -b\right] \,U_{\alpha }\,\left[ \beta ^i\, _i\hat{\mathcal {F}}^{\alpha }+\alpha ^i\, _i\hat{\mathcal {B}}^{\alpha } \right] . \end{aligned}$$

(54)

for $^i\hat{\mathcal {F}}_{\alpha }\, _i\hat{\mathcal {F}}^{\alpha }= \frac{1}{2} g_{\alpha \beta } \left\{ ^i\hat{\mathcal {F}}^{\alpha },\, _i\hat{\mathcal {F}}^{\beta }\right\}$. Notice that the right hand of (54) is the flow that crosses the 3D-hypersurface:

$$\begin{aligned} \hat{\delta \Theta } = -2\,\lambda (x)\left[ 4\,\left( 1-\xi ^2\right) -b\right] \,U_{\alpha }\,\left[ \beta ^i\, _i\hat{\mathcal {F}}^{\alpha }+\alpha ^i\, _i\hat{\mathcal {B}}^{\alpha } \right] . \end{aligned}$$

(55)

The Eq. (54) can be rewritten as two equations, one for fermions and the another for bosons:

$$\begin{aligned}&\nabla _{\alpha }\, _i\hat{\mathcal {F}}^{\alpha } + \beta _i\,\left[ 2b+\left( 1-\xi ^2\right) \right] \, ^i\hat{\mathcal {F}}_ {\alpha }\, _i\hat{\mathcal {F}}^{\alpha }\nonumber \\&\quad = \frac{2}{3}\,\lambda (x)\left[ 4\,\left( 1-\xi ^2\right) -b\right] \,U_{\alpha }\,\, _i\hat{\mathcal {F}}^{\alpha }, \end{aligned}$$

(56)

$$\begin{aligned}&\nabla _{\alpha }\, _i\hat{\mathcal {B}}^{\alpha } = \frac{2}{3}\,\lambda (x)\left[ 4\,\left( 1-\xi ^2\right) -b\right] \,U_{\alpha }\, _i\hat{\mathcal {B}}^{\alpha }. \end{aligned}$$

(57)

We shall consider massless bosons, so that $\left<B\right| U_{\alpha }\, _i\hat{\mathcal {B}}^{\alpha }\left| B\right>=0$. Therefore from the Eq. (44), we obtain that the contribution to the flow’s expectation value must be given only by the fermion fields and massive bosons

$$\begin{aligned} \left<B\right| \hat{\delta \Theta }\left| B\right>= & {} -2\,\lambda (x)\left[ 4\,\left( 1-\xi ^2\right) -b\right] \nonumber \\&\times \left<B\right| U_{\alpha }\,\left[ \alpha ^i\, _i\hat{\mathcal {B}}^{\alpha }+ \beta ^i\, _i\hat{\mathcal {F}}^{\alpha }\right] \left| B\right>\nonumber \\= & {} -\lambda (x)\,M_p\,\mathbb {I}_{4\times 4}. \end{aligned}$$

(58)

The Eq. (58) means that

$$\begin{aligned} \left<B\right| U_{\alpha }\,\left[ \alpha ^i\, _i\hat{\mathcal {B}}^{\alpha }+ \beta ^i\, _i\hat{\mathcal {F}}^{\alpha }\right] \left| B\right>= \frac{M_p\,\mathbb {I}_{4\times 4}}{2\,\left[ 4(1-\xi ^2)-b\right] } , \end{aligned}$$

(59)

so that the expectation value of the flux is independent of the choice for the parameters b and $\xi$.

Furthermore, using the fact that $\hat{\delta U}_{\mu \nu }$ is symmetric and $\hat{\delta V}_{\mu \nu }$ is antisymmetric, the Eqs. (18) and (19), with (54) included, take the form

$$\begin{aligned} \hat{\delta U}_{\mu \nu }= & {} - \left\{ \frac{1}{2}\Bigg [ \nabla _{\nu }\,\left( \alpha _i\,\, ^i\hat{\mathcal {B}}_{\mu } + \beta _i\,\,^i\hat{\mathcal {F}}_{\mu }\right) \right. \nonumber \\&\quad \left. + \nabla _{\mu } \left( \alpha _i\,\, ^i\hat{\mathcal {B}}_{\nu } + \beta _i\,\,^i\hat{\mathcal {F}}_{\nu }\right) \Bigg ]\nonumber \right. \\&\left. + \frac{\beta _i \beta _j}{2} \left[ 2 b+(1-\xi ^2)\right] \left\{ \,^i\hat{\mathcal {F}}_{\mu }, \,^j\hat{\mathcal {F}}_{\nu }\right\} \right. \nonumber \\&- \left. g_{\mu \nu }\frac{2}{3b}\,\lambda (x)\left[ 4\,\left( 1-\xi ^2\right) -b\right] \right. \nonumber \\&\quad \left. \times \,U_{\alpha }\,\left[ \beta ^i\, _i\hat{\mathcal {F}}^{\alpha }+\alpha ^i\, _i\hat{\mathcal {B}}^{\alpha } \right] \right\} , \end{aligned}$$

(60)

$$\begin{aligned} \hat{\delta V}_{\mu \nu }= & {} - \frac{1}{2} \,\Bigg \{ \Bigg [ \nabla _{\nu } \,\left( \alpha _i\,\, ^i\hat{\mathcal {B}}_{\mu } + \beta _i\,\,^i\hat{\mathcal {F}}_{\mu }\right) \nonumber \\&\quad - \nabla _{\mu } \,\left( \alpha _i\,\, ^i\hat{\mathcal {B}}_{\nu } + \beta _i\,\,^i\hat{\mathcal {F}}_{\nu }\right) \Bigg ]\nonumber \\&+ (1-\xi ^2) \,\alpha _i\,\alpha _j \left[ \,^i\hat{\mathcal {B}}_{\mu }, \,^j\hat{\mathcal {B}}_{\nu }\right] \Bigg \}, \end{aligned}$$

(61)

and the Einstein tensor (22), is

$$\begin{aligned} \hat{E}_{\mu \nu }= & {} -\frac{1}{2} \left\{ \Bigg [ \nabla _{\nu }\,\left( \alpha _i\,\, ^i\hat{\mathcal {B}}_{\mu } + \beta _i\,\,^i\hat{\mathcal {F}}_{\mu }\right) \right. \nonumber \\&\quad \left. + \nabla _{\mu } \left( \alpha _i\,\, ^i\hat{\mathcal {B}}_{\nu } + \beta _i\,\,^i\hat{\mathcal {F}}_{\nu }\right) \Bigg ] + \beta _i \beta _j\, \right. \nonumber \\&\quad \times \left. \left[ 2 b+(1-\xi ^2)\right] \left\{ \,^i\hat{\mathcal {F}}_{\mu }, \,^j\hat{\mathcal {F}}_{\nu }\right\} \right. \nonumber \\&+ \frac{2}{3b}\,\left. g_{\mu \nu }\,\lambda (x)\left[ 4\,\left( 1-\xi ^2\right) -b\right] \right. \nonumber \\&\left. \quad \times \,U_{\alpha }\,\left( \alpha ^i\, _i\hat{\mathcal {B}}^{\alpha }+\beta ^i\, _i\hat{\mathcal {F}}^{\alpha } \right) \right\} . \end{aligned}$$

(62)

The field equations on the extended manifold are given by

$$\begin{aligned} \left( \hat{E}^{\mu \nu }\right) _{\Vert \alpha } = 0, \quad \left( \delta \hat{V}^{\mu \nu }\right) _{\Vert \alpha } = 0. \end{aligned}$$

(63)

These equations can be expanded in terms of the covariant derivatives on the Riemann manifold

$$\begin{aligned}&\nabla _{\mu } \hat{{E}}^{\mu \nu } - \left( 1-\xi ^2\right) \,\left\{ \hat{{E}}^{\mu \nu },\hat{\Psi }_{\mu }\right\} + b\,\hat{\Psi }_{\mu }\,\hat{{E}}^{\mu \nu } \nonumber \\&\quad + b\,\hat{\Psi }^{\nu }\,g_{\alpha \mu }\hat{{E}}^{\alpha \mu }=0, \end{aligned}$$

(64)

$$\begin{aligned}&\nabla _{\mu } \delta \hat{{V}}^{\mu \nu } - \left( 1-\xi ^2\right) \,\left[ \delta \hat{{V}}^{\mu \nu },\hat{\Psi }_{\mu }\right] +b\, \hat{\Psi }_{\mu }\,\delta \hat{{V}}^{\mu \nu }=0, \end{aligned}$$

(65)

with (46). The Eq. (64) are the extended Einstein’s equations and describe the gravitational dynamics of $\left( 3+1\right)$-anyon fields that have a global fermionic behavior, on the extended manifold. On the other hand, the Eq. (65) can describe the dynamics of $\left( 3+1\right)$-anyon fields subject to strong interactions that have a global bosonic behavior. This dynamics was studied for 1-spin solitary gluon fields in a previous work [22], but without considering the coupling of fermion fields (quark fields) with the boson (gluon field) in the dynamics.

When we consider the Eqs. (64) with (62), we obtain the dynamic equations for the fields from the extended Einstein’s equations

$$\begin{aligned} \Box \hat{\Psi }^{\nu }= & {} -\nabla _{\mu } \nabla ^{\nu } \hat{\Psi }^{\mu } -\left[ 2b+ (1-\xi ^2)\right] \,\beta ^i \beta ^j \nabla _{\mu } \,\nonumber \\&\times \left\{ _i\hat{\mathcal {F}}^{\mu }, _j\hat{\mathcal {F}}^{\nu } \right\} - b\,\hat{\Psi }_{\mu }\left[ \nabla ^{\nu } \hat{\Psi }^{\mu } + \nabla ^{\mu } \hat{\Psi }^{\nu } \right] \nonumber \\&- \nabla ^{\nu } \,\left[ \nabla _{\alpha }\hat{\Psi }^{\alpha }+\left[ 2b+ (1-\xi ^2)\right] \beta _i\,\beta ^j \left( \,^i\hat{F}_{\alpha } \,_j\hat{F}^{\alpha }\right) \right] \nonumber \\&+\, \left( 1-\xi ^2\right) \,\left\{ \left[ \nabla ^{\nu } \hat{\Psi }^{\mu } + \nabla ^{\mu } \hat{\Psi }^{\nu } \right] ,\, \hat{\Psi }_{\mu }\right\} \nonumber \\&+ \, b\,\left[ 2b+ (1-\xi ^2)\right] \, \beta ^i \beta ^j \,\hat{\Psi }_{\mu }\,\nonumber \\&\times \left\{ _i\hat{\mathcal {F}}^{\mu }, _j\hat{\mathcal {F}}^{\nu } \right\} +\left( 1-\xi ^2\right) \,\left[ 2b+ (1-\xi ^2)\right] \beta _i\,\beta ^j\, \nonumber \\&\times \left\{ \left\{ _i\hat{\mathcal {F}}^{\mu }, _j\hat{\mathcal {F}}^{\nu } \right\} , \hat{\Psi }_{\mu }\right\} \nonumber \\&+ \left( 1-\xi ^2\right) \Bigg [ \left\{ \nabla _{\alpha }\hat{\Psi }^{\alpha }, \,\hat{\Psi }^{\nu }\right\} + \left[ 2b+ (1-\xi ^2)\right] \beta _i\,\beta ^j\, \nonumber \\&\left\{ \left( ^i\hat{\mathcal {F}}_{\alpha }\, _j\hat{\mathcal {F}}^{\alpha } \right) , \hat{\Psi }^{\nu }\right\} \Bigg ]- 7 b \,\hat{\Psi }^{\nu } \, \left[ \nabla _{\alpha }\hat{\Psi }^{\alpha }\nonumber \right. \\&\left. + \left[ 2b+ (1-\xi ^2)\right] \, \beta _i\,\beta ^j\,\left( ^i\hat{\mathcal {F}}_{\alpha }\, _j\hat{\mathcal {F}}^{\alpha } \right) \right] , \end{aligned}$$

(66)

where we remember that $\hat{\Psi }^{\nu }=\alpha ^i\,\, _i\hat{\mathcal {B}}^{\nu } + \beta ^i\,\,_i\hat{\mathcal {F}}^{\nu }$. Furthermore, for the Eq. (65), we obtain

$$\begin{aligned} \Box \hat{\Psi }^{\nu }= & {} \nabla _{\mu } \nabla ^{\nu } \hat{\Psi }^{\mu }+ (1-\xi ^2) \,\alpha ^i \alpha ^j \nabla _{\mu } \left[ _i\hat{\mathcal {B}}^{\mu }, _j\hat{\mathcal {B}}^{\nu } \right] \nonumber \\&+ b\,\hat{\Psi }_{\mu }\,\left[ \nabla ^{\nu } \hat{\Psi }^{\mu } - \nabla ^{\mu } \hat{\Psi }^{\nu } \right] + b\,(1-\xi ^2) \, \alpha ^i \alpha ^j \, \hat{\Psi }_{\mu }\, \nonumber \\&\times \left[ _i\hat{\mathcal {B}}^{\mu }, _j\hat{\mathcal {B}}^{\nu } \right] + (1-\xi ^2)\,\hat{\Psi }_{\mu }\,\left[ \nabla ^{\nu } \hat{\Psi }^{\mu } - \nabla ^{\mu } \hat{\Psi }^{\nu } \right] \,\nonumber \\&- \left( 1-\xi ^2\right) \left[ \nabla ^{\nu } \hat{\Psi }^{\mu }- \nabla ^{\mu } \hat{\Psi }^{\nu } \right] \, \hat{\Psi }_{\mu } + b\,(1-\xi ^2) \,\alpha ^i \alpha ^j \nonumber \\&\quad \times \left[ \hat{\Psi }_{\mu } ,\left[ _i\hat{\mathcal {B}}^{\mu }, _j\hat{\mathcal {B}}^{\nu } \right] \right] . \end{aligned}$$

(67)

The Eq. (66) describes the motion of $(3+1)$-anyons with fractional spin (or effective fermion fields), meanwhile the Eq. (26) is for $(3+1)$-anyons with integer spin (or effective boson fields). In both cases these fields can be a linear combination of bosons with fermions.

6 $\left( 3+1\right)$-anyon dynamics for the particular gauge $(1-\xi ^2)=-2b$

In the following we shall consider the particular gauge $(1-\xi ^2)=-2b$, in order to simplify the expression (66).

6.1 $\left( 3+1\right)$-anyon dynamics with global fermionic behavior from the Einstein’s equations, for $(1-\xi ^2)=-2b$

In that case we obtain that (66) takes the form

$$\begin{aligned} \Box \hat{\Psi }^{\nu }= & {} -\nabla _{\mu } \nabla ^{\nu } \hat{\Psi }^{\mu } -3\,b\,\hat{\Psi }_{\mu }\left[ \nabla ^{\nu }\hat{\Psi }^{\mu } + \nabla ^{\mu }\hat{\Psi }^{\nu }\right] \nonumber \\&+6 \nabla ^{\nu }\left[ \lambda (x) \left( U_{\alpha } \hat{\Psi }^{\alpha }\right) \right] \nonumber \\&- 2\,b\,\left[ \nabla ^{\nu }\hat{\Psi }^{\mu }+\nabla ^{\mu }\hat{\Psi }^{\nu }\right] \,\hat{\Psi }_{\mu }\nonumber \\&- 33\,b\,\lambda (x)\,\hat{\Psi }^{\nu }\,\left( U_{\alpha } \hat{\Psi }^{\alpha }\right) . \end{aligned}$$

(68)

Using the fact that, in absence of torsion (we remember that we are considering the Ricci tensor as the contraction of the contravariant index with the last covariant index: $R^{\mu }_{\beta \alpha \mu }= R_{\alpha \beta }$), we obtain that

$$\begin{aligned} \nabla _{\mu } \nabla _{\alpha } \,\hat{\Psi }^{\mu }= & {} R^{\mu }_{\beta \mu \alpha } \,\hat{\Psi }^{\mu }\,\nonumber \\ \hat{\Psi }^{\beta } + \nabla _{\alpha }\nabla _{\mu }\,\hat{\Psi }^{\mu }= & {} -R_{\beta \alpha } \,\hat{\Psi }^{\beta } + \nabla _{\alpha }\nabla _{\mu }\,\hat{\Psi }^{\mu }. \end{aligned}$$

(69)

Therefore, the Eq. (68) results

$$\begin{aligned} \Box \hat{\Psi }^{\nu }= & {} g^{\nu \alpha } \left[ R_{\beta \alpha } \,\hat{\Psi }^{\beta } + 6 \nabla _{\alpha }\left( \lambda (x) \,U_{\mu } \hat{\Psi }^{\mu }\right) \right] \nonumber \\&-3\,b\,\hat{\Psi }_{\mu }\left[ \nabla ^{\nu }\hat{\Psi }^{\mu } + \nabla ^{\mu }\hat{\Psi }^{\nu }\right] \nonumber \\&+ 6 \nabla ^{\nu }\left[ \lambda (x) \left( U_{\alpha } \hat{\Psi }^{\alpha }\right) \right] - 2\,b\,\left[ \nabla ^{\nu }\hat{\Psi }^{\mu } + \nabla ^{\mu }\hat{\Psi }^{\nu }\right] \nonumber \\&\,\hat{\Psi }_{\mu } - 33\,b\,\lambda (x)\,\hat{\Psi }^{\nu }\,\left( U_{\alpha } \hat{\Psi }^{\alpha }\right) , \end{aligned}$$

(70)

that are valid on a curved spacetime.

6.2 $\left( 3+1\right)$-anyon dynamics with global bosonic behavior for Strong interactions, for $(1-\xi ^2)=-2b$

The Eq. (67) can be simplified without loss of generality by using the particular gauge $(1-\xi ^2)=-2b$, and we obtain

$$\begin{aligned} \Box \hat{\Psi }^{\nu }= & {} \nabla _{\mu } \nabla ^{\nu } \hat{\Psi }^{\mu }- 2\,b \,\alpha ^i \alpha ^j \nabla _{\mu }\left[ _i\hat{\mathcal {B}}^{\mu }, _j\hat{\mathcal {B}}^{\nu } \right] \nonumber \\&+ b\,\hat{\Psi }_{\mu }\,\left[ \nabla ^{\nu } \hat{\Psi }^{\mu } - \nabla ^{\mu } \hat{\Psi }^{\nu } \right] - 2\,b^2 \, \alpha ^i \alpha ^j \,\nonumber \\&\times \hat{\Psi }_{\mu }\,\left[ _i\hat{\mathcal {B}}^{\mu }, _j\hat{\mathcal {B}}^{\nu } \right] - 2b\,\hat{\Psi }_{\mu }\,\left[ \nabla ^{\nu } \hat{\Psi }^{\mu } - \nabla ^{\mu } \hat{\Psi }^{\nu } \right] \nonumber \\&+ 2b\,\left[ \nabla ^{\nu } \hat{\Psi }^{\mu } - \nabla ^{\mu } \hat{\Psi }^{\nu } \right] \, \hat{\Psi }_{\mu } - 2\,b^2 \,\alpha ^i \alpha ^j\nonumber \\&\quad \times \left[ \hat{\Psi }_{\mu } ,\left[ _i\hat{\mathcal {B}}^{\mu }, _j\hat{\mathcal {B}}^{\nu } \right] \right] . \end{aligned}$$

(71)

Using the expression (69), we obtain

$$\begin{aligned} \Box \hat{\Psi }^{\nu }= & {} -g^{\nu \alpha } \left[ R_{\beta \alpha } \,\hat{\Psi }^{\beta } + 6 \nabla _{\alpha }\left( \lambda (x) \,U_{\mu } \hat{\Psi }^{\mu }\right) \right] \nonumber \\&- 2\,b \,\alpha ^i \alpha ^j \nabla _{\mu } \left[ _i\hat{\mathcal {B}}^{\mu }, _j\hat{\mathcal {B}}^{\nu } \right] \nonumber \\&\quad + b\,\hat{\Psi }_{\mu }\,\left[ \nabla ^{\nu } \hat{\Psi }^{\mu } - \nabla ^{\mu } \hat{\Psi }^{\nu } \right] \nonumber \\&- 2\,b^2 \, \alpha ^i \alpha ^j \,\hat{\Psi }_{\mu }\,\left[ _i\hat{\mathcal {B}}^{\mu }, _j\hat{\mathcal {B}}^{\nu } \right] \nonumber \\&- 2b\,\hat{\Psi }_{\mu }\,\left[ \nabla ^{\nu } \hat{\Psi }^{\mu } - \nabla ^{\mu } \hat{\Psi }^{\nu } \right] \nonumber \\&\quad + 2b\,\left[ \nabla ^{\nu } \hat{\Psi }^{\mu } - \nabla ^{\mu } \hat{\Psi }^{\nu } \right] \, \hat{\Psi }_{\mu } \nonumber \\&- 2\,b^2 \,\alpha ^i \alpha ^j \left[ \hat{\Psi }_{\mu } ,\left[ _i\hat{\mathcal {B}}^{\mu }, _j\hat{\mathcal {B}}^{\nu } \right] \right] , \end{aligned}$$

(72)

which are valid for an arbitrary curved spacetime.

7 Preinflation and the birth of the universe

To illustrate the formalism, we can consider an recently introduced model [27] that describes the birth of the universe. In that model the global expansion of the universe is driven by a single (and minimally coupled to gravity) scalar field $\phi$, in the Lagrangian ${{{\mathcal {L}}}}_{m}= -\left[ \frac{1}{2} g^{\alpha \beta } \phi _{,\alpha }\phi _{,\beta } - V(\phi )\right]$, of the action (11). In this work we shall consider natural units, so that $c=\hbar =1$. In order to describe the background dynamics with a variable time scale, we shall consider the line element [28]

$$\begin{aligned} dl^2 = e^{-2\int \gamma (t)\, \,dt}dt^2 - a_0^2 \,\, e^{2\int H(t) dt}\,\, {\delta }_{ij}\, \,d{x}^i d{x}^j, \end{aligned}$$

(73)

such that H(t) is the Hubble parameter on the background metric and $\gamma (t)$ describes the time scale of the background metric. This should be the case in an emergent accelerated universe in which the time scale can be considered variable with the expansion. The Weyl representation of the Dirac matrices for this metric are

$$\begin{aligned} \bar{\gamma }^0= \gamma ^0 \,e^{-\int \gamma (t)\,dt}, \qquad \bar{\gamma }^i= \gamma ^i\,e^{\int H(t) dt}. \end{aligned}$$

(74)

7.1 Einstein equations and background dynamics

The dynamics of the scalar field $\phi$ is given by

$$\begin{aligned} \ddot{\phi } + \left[ 3\,H+\gamma \right] \dot{\phi }+ \frac{\delta \bar{\Upsilon }}{\delta \phi }=0, \end{aligned}$$

(75)

where the redefined potential with back-reaction contributions due to the flow of $(3+1)$-anyons $\hat{\Psi }^{\mu }= \alpha ^i\, _i\hat{\mathcal {B}}^{\mu }+ \beta ^i\, _i\hat{\mathcal {F}}^{\mu }$, given by the Eq. (58), is

$$\begin{aligned} \bar{\Upsilon }(\phi )= & {} \left[ V(\phi )\,e^{-2\int \gamma (t)\,dt}+\frac{b\,\left<B\right| \hat{\delta \Theta }\left| B\right>}{(8\pi \,G)}\right] \nonumber \\= & {} \bar{V}(\phi ) + \frac{b\,\left<B\right| \hat{\delta \Theta }\left| B\right>}{(8\pi \,G)}, \end{aligned}$$

(76)

where we know from the Eq. (58) that the flow of $(3+1)$-anyons through the closed 3d-hypersurface is the responsible for the cosmological parameter: $b\,\left<B\right| \hat{\delta \Theta }\left| B\right>=-\lambda (t)$. For the particular gauge $(1-\xi ^2)=-2b$, we must require [see Eq. (59)]:

$$\begin{aligned} \left<B\right| U_{\mu }\,\left[ \alpha ^i\, _i\hat{\mathcal {B}}^{\mu }+ \beta ^i\, _i\hat{\mathcal {F}}^{\mu }\right] \left| B\right>= - \frac{M^2_p\,\mathbb {I}_{4\times 4}}{18}. \end{aligned}$$

(77)

The term $3H\,\dot{\phi }$ is due to the expansion of the universe, but the term $\gamma \,\dot{\phi }$, with $\gamma (t) <0$ describes a nontrivial time scale. When $\gamma >0$, it represents a friction parameter that produces (only when $\gamma > 3H$), the reheating of the universe. However, in our case, parameter $\gamma (t)$ is negative, and cannot be physically interpreted as a friction one, but as one that describes the energy that the quantum fields delivers to the universe, to fuel its initial expansion.

The background Einstein equations, are

$$\begin{aligned} 3 \,H^2&= 8\pi \,G\,\left[ \frac{{\dot{\phi }}^2}{2} +\bar{\Upsilon }(\phi )\right] = 8\pi \,G\,{\rho }, \end{aligned}$$

(78)

$$\begin{aligned} -\left( 3 \,H^2 +2 \dot{H} + 2\gamma \,H\right)&= 8\pi \,G\,\left[ \frac{\dot{\phi }^2}{2} -\bar{\Upsilon }(\phi )\right] = 8\pi \,G\,{P}. \end{aligned}$$

(79)

such that P and $\rho$ are respectively the pressure and the energy density on the action (11)

$$\begin{aligned} P\,e^{2\int \gamma (t)\, \,dt}\,\delta ^{i}_{\,\,j}=-\bar{T}^i_{\,\,\,j}, \quad \rho \,\, e^{2\int \gamma (t)\, \,dt}=\bar{T}^0_{\,\,\,0}, \end{aligned}$$

(80)

and the diagonal components of the stress tensor for a perfect fluid are $\bar{T}^{\mu }_{\,\,\,\nu }=diag(\bar{\rho },-\bar{P},-\bar{P},-\bar{P})$. Therefore, the effective equation of state

$$\begin{aligned} \omega = \bar{P}/\bar{\rho }= \frac{\frac{\dot{\phi }^2}{2} - \bar{\Upsilon }(\phi )}{\frac{\dot{\phi }^2}{2} + \bar{\Upsilon }(\phi )}. \end{aligned}$$

(81)

In order to describe an emergent universe which starts from a null Hubble parameter to reach its maximum value at the end of preinflation, we shall propose a Hubble parameter H, which is related with the parameter $\gamma$ by

$$\begin{aligned} 3\,H\left[ \phi (\tau )\right] + \gamma \left[ \phi (\tau )\right] = \epsilon \,H_0, \end{aligned}$$

(82)

where $H_0$ is constant and $\epsilon$ is a parameter to be determined. Using the Einstein Eqs. (78) and (79), we obtain that

$$\begin{aligned} 6\,H^2 + 2\left[ \dot{\phi }\, H' + \epsilon \,H_0-3\,H^2\right] - 16\pi \,G\,\bar{\Upsilon }\left[ \phi (t)\right] =0. \end{aligned}$$

(83)

One of the problems of inflationary models is that initially, the scalar field can take trans Planckian values. In order to avoid this kind of problems we shall consider a scalar field which is zero when the universe is created, and increases with time. To obtain the dynamics of the system we shall work in the opposite way to what is usually done, i.e., for a given dynamics of the scalar field $\phi (t)$, we shall look for the solution of the potential $\bar{\Upsilon }(\phi )$ by using the dynamical Eqs. (75), (78) and (79) with the constriction (82). Because we are aimed to describe the birth of the universe, we must consider that the Hubble parameter is initially null: $H(t=0)=0$. In other words, the theory must be able to explain how the universe began to expand from an initial state of stillness. For the choice $\phi (t) = N\,\phi _0\,\left[ 1-e^{-H_0\,t}\right]$, we obtain that $\dot{\phi }= H_0\,\left( N\,\phi _0 - \phi \right)$ and $\ddot{\phi }= -H^2_0\,\left( N\,\phi _0 - \phi \right)$, and from the Eq. (83) we obtain that the effective potential is

$$\begin{aligned} \bar{\Upsilon }\left[ \phi (t)\right]= & {} \frac{H_0^2}{8\pi \,G} \Bigg [\frac{1}{2(N+1)} \left( \frac{\phi (t)}{\phi _0}\right) ^2-\frac{N}{N+1}\left( \frac{\phi (t)}{\phi _0}\right) \nonumber \\&\quad +N\Bigg ]. \end{aligned}$$

(84)

Here, N is a dimensionless natural number that give us the scale of the energy for different epochs in the evolution of the universe. Furthermore, from the equation of motion (75), we obtain that

$$\begin{aligned} -H^2_0 \,\left( N\,\phi _0 - \phi \right) + 3\,\epsilon \,H^2_0\,\left( N\,\phi _0 - \phi \right) + \frac{\delta \bar{\Upsilon }}{\delta \,\phi }=0, \end{aligned}$$

(85)

where $\phi _0$ is asymptotic maximum value for $\phi (t)$, which is an increasing function of t and always takes sub-Planck values: $0 \le \phi (\tau )< N\,\phi _0 < M_p$, and $\bar{V}(\phi )$ is⁵

$$\begin{aligned} \bar{V}\left[ \phi (\tau )\right]= & {} \frac{H_0^2}{8\pi \,G}\left[ \frac{1}{2(N+1)} \left( \frac{\phi (t)}{\phi _0}\right) ^2\right. \nonumber \\&\left. -\frac{N}{N+1}\left( \frac{\phi (t)}{\phi _0}\right) +\frac{\left[ 6N(N+1)-1\right] }{6(N+1)}\right] , \end{aligned}$$

(92)

where the potentials $\bar{\Upsilon }(\phi )$ and $\bar{V}(\phi )$ are related by the expression

$$\begin{aligned} \bar{\Upsilon }(\phi )=\bar{V}(\phi ) + \frac{1}{48\,\pi \,G} \frac{\delta ^2 \bar{V}}{\delta \,\phi ^2}. \end{aligned}$$

(93)

In our model we shall chose $\epsilon ={2+N\over 1+N}$. Therefore, the cosmological parameter during preinflation, results to be constant $\lambda _0=\frac{1}{8\,\pi \,G} \frac{\delta ^2 \bar{V}}{\delta \,\phi ^2}$:

$$\begin{aligned} \lambda _0= \frac{H^2_0}{6(N+1)}, \end{aligned}$$

(94)

for $\phi _0^2={1\over 8\,\pi \,G}$ and $b={1 \over M_p}$. Notice that $\lambda _0 >0$ corresponds to a positive flow of $(3+1)$-anyons is due to back-reaction effects:

$$\begin{aligned} b\,\left<B\right| \hat{\delta \Theta }\left| B\right>= \lambda _0. \end{aligned}$$

(86)

Because $\lambda _0$ is a constant, the background geodesic dynamics described by (36) is given by

$$\begin{aligned} 2\,\rho \left( 1+\omega \right) \nabla _0 U^0 + \frac{\partial \left( \rho \left( 1+\omega \right) \right) }{\partial x^0} \,U^0 + \frac{\partial P}{\partial x^0}\,U^0=0, \end{aligned}$$

(87)

with $\omega$ given by (81). In the model here worked for preinflation $\omega \gtrsim -1$, and $\dot{\omega }<0$ along the evolution of this emergent stage of the universe. For a co-moving observer we must set $U^i=0$, so that the solution of the Eq. (93), results

$$\begin{aligned} U^0 = e^{\frac{1}{2} \int \left[ \frac{2\gamma \left[ \rho \left( 1+\omega \right) \right] -\dot{\rho }}{\rho \left( 1+\omega \right) }\right] \, dt}. \end{aligned}$$

(88)

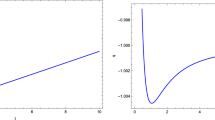
We must remember that we are considering natural unities $c=\hbar =1$. In the Fig. 1 we have plotted $U_0(t)$ for $G=1$, $N=9$ and $H_0=0.0005\, G^{-1/2}$. At the beginning $0<U_0 <1$, which means that the physical time $d\tau =U_0(t)\,dt$ is running slowly than in a non-inertial frame with $U_0=1$. However, after some Planckian times, $U_0$ accelerates and $U_0 >1$, so that the physical time runs faster than in a non-inertial frame. On the other hand $\gamma$, which is given by the Eq. (82), is positive at the beginning, but decreasing. Therefore it rapidly becomes negative and reach its minimum value at the end of preinflation.

7.2 Inflaton field fluctuations and spectral indices

The dynamics for the scalar fluctuations $\delta \varphi =\varphi - \left<\varphi \right> = \varphi - \phi (t)$, is given by

$$\begin{aligned}&\ddot{\delta \varphi } + \left[ 3\,H+\gamma \right] \dot{\delta \varphi }\nonumber \\&\quad - a^{-2}_0 e^{-2 \int \left[ H+\gamma \right] \,dt}\,\nabla ^2 \delta \varphi + \frac{\delta ^2 \bar{\Upsilon }}{\delta \phi ^2}\, \delta \varphi =0, \end{aligned}$$

(95)

where the effects of boundary conditions in the action are taking into account in the potential $\bar{\Upsilon }$ given by (89). During preinflation $\left[ 3\,H+\gamma \right] >0$. At the beginning $\gamma >0$ and $H\simeq 0$, but as the universe evolves the Hubble parameter increases $\dot{H}>0$, and $\gamma <0$ with $\dot{\gamma } <0$, but always in a such manner that $\left[ 3\,H+\gamma \right] >0$.

The scalar spectral index that characterizes the spectrum of $\delta \varphi$, is $n_s(\phi )=1-6\varepsilon (\phi ) + 2 \eta (\phi )$. Furthermore, the tensor index is given by $n_t(\phi )=-2\varepsilon (\phi )$ and can be defined the tensor to scalar index: $r(\phi )=-8\,n_t(\phi ) = 16\,\varepsilon (\phi )$. In particular, at the end of preinflation, when $\phi (t)\equiv \phi _*=\frac{N}{8\,\pi \,G}$, the values for the relevant spectral indices are:

$$\begin{aligned} 1-n_s(\phi _*)&=0.04, \quad n_t(\phi _*) = -0.0004, \quad r(\phi _*)\nonumber \\&= 0.00336, \end{aligned}$$

(96)

that agree with observational values [30].

8 Final comments

We have shown that boundary terms in General Relativity can be really important. In particular, we have introduced a quantum spinor field named $\left( 3+1\right)$-anyon, with a flow that is quantum in nature and is a superposition of boson and fermions: $\hat{\Psi }^{\alpha } = \alpha ^i\,\, _i\hat{\mathcal {B}}^{\alpha } + \beta ^i\,\,_i\hat{\mathcal {F}}^{\alpha }$. The relativistic flow modifies the background dynamics through the Einstein equations [see Eq. (30)]. We have required that the expectation value of the flow on the Riemannian background be the opposite value of the cosmological parameter [see Eq. (42)], which imposed the following constriction for trace of the varied tensor metric:

$$\begin{aligned} \left<B\right| g^{\alpha \beta }\hat{\delta g}_{\alpha \beta }\left| B\right>=-M_p\,\mathbb {I}_{4\times 4}. \end{aligned}$$

That expression is very important because avoid divergences for the metric fluctuations.

To illustrate the formalism, we have calculated the cosmological parameter in an emergent preinflationary universe which begins its expansion with a null Hubble parameter that increases with time, but after some Planck times, when $\phi (t_*)=N\,\phi _0$, H reaches its maximum. On the other hand $\gamma (t)$ becomes negative until reach its minimum value at $\phi _*=N\,\phi _0$, when the Hubble parameter takes the maximum value: $H_* \simeq \frac{N}{2}\,H_0$. In the model here worked, the flow due to $(3+1)$-anyon spinor fields results to be constant and positive [see Eqs. (91) and (92)]. Because these fields are self-interacting, back-reaction effects could have been responsible for the primordial expansion of the universe. In the Fig. 2 are plotted the indices $1-n_s(\phi )$, $n_t(\phi )$ and $r(\phi )$, for $G=1$, $N=9$ and $H_0=0.0005\, G^{-1/2}$ and $\phi _0 \simeq 0.2\, G^{-1/2}$. The inflaton field value where the Hubble parameter reaches its maximum value: $\phi _* \simeq 1.8\,G^{-1/2}$ that corresponds to the maximum: $H_* \simeq 0.00225\,G^{-1/2} \simeq 0.2745\times 10^{17}\,\mathrm{GeV}$. During preinflation, the scale factor increases as (for $e=2.718$)

$$\begin{aligned} a(t)=\left( \frac{a_0}{e}\right) \,e^{\frac{N}{2}H_0\,t + e^{-2H_0\,t}}, \end{aligned}$$

that describes a super exponential expansion of the universe from an initial value $a(t=0)=a_0$. We have adjusted the value of N in order to obtain the $n_s$-value according with observation [30]. Notice that at the end of preinflation, when $\phi \rightarrow \phi _*$, it is obtained that $1-n_s(\phi _*)\simeq 0.04$, and $|r(\phi _*)|\simeq |n_t(\phi _*)| < 0.01$ [see Eq. (96)]. Furthermore, the negative parameter $\gamma (t)$ along this model of preinflation cannot be physically interpreted as a friction one, but as one that describes the energy that the flow of $\hat{\Psi }^{\alpha }$ delivers to the universe. However, it would be interesting to study a model in which $\gamma$, takes initially negative values to later be positive. A model like this could be appropriate to describe the transition between the preinflation and fresh inflationary [31] stages. However, this issue go beyond the scope of this work.

Fig. 1

Plot of the covariant relativistic velocity $U_0(t)$, for $C=1$, $G=1$, $N=9$, and $H_0=0.0005\, G^{-1/2}$. Notice that $U_0 <1$ during the first stages of preinflation, but later increases and exceeds the unit

Fig. 2

Plot of indices $1-n_s(\phi )$, $n_t(\phi )$ and $r(\phi )$, for $G=1$, $N=9$ and $H_0=0.0005\, G^{-1/2}$ and $\phi _* \simeq 1.8\,G^{-1/2}$. Notice that $1-n_s(\phi _*) \simeq 0.034$ and $|r(\phi _*)|\simeq |n_t(\phi _*)| \ll 0.1$