1 Introduction

In 1948, Schwinger presented his result [1] for the “anomalous” magnetic moment of the electron, \(a_e \equiv (g_e - 2)/2\simeq \alpha /2\pi \). The observable has played one of the most important roles in establishing particle physics: consistency between prediction and experiment has established QED as the most accurate fundamental theory of Nature known to humankind. In the last two decades, with experiments able to perform ever precise measurements to expose the tiniest deviations, muon \(g-2\) has become a flagship observable in the search for New Physics (NP), or physics beyond the Standard Model (SM). Recent developments suggest a possible revival of muon (and tau) physics, as we illustrate.

The Fermilab Muon \(g-2\) experiment [2] reported recently its measurement of the \(g-2\) of the muon, confirming the previous result at Brookhaven [3]. Combining the two measurements [2] gives

$$\begin{aligned} a_\mu ^\mathrm{Exp} = 116 592 061(41) \times 10^{-11}. \end{aligned}$$
(1)

Compared with the community-wide theory consensus [4], \(a_\mu ^\mathrm{SM} = 116 591 810(43) \times 10^{-11}\), the difference

$$\begin{aligned} \Delta a_\mu = a_\mu ^\mathrm{Exp} - a_\mu ^\mathrm{SM} = (251 \pm 59) \times 10^{-11}, \end{aligned}$$
(2)

has a significance of \(4.2\sigma \) [2].

This large discrepancy has certainly attracted much attention. We refer the reader to Ref. [5] for a recent review of popular NP models that provide solutions to the muon \(g-2\) anomaly, whereas a slightly dated review can be found in Ref. [6]. One of the desired ingredients to ease the NP explanation is chiral enhancement. In this regard, the general two-Higgs doublet model (g2HDM), sometimes referred to as 2HDM Type-III [7], is one of the simplest extensions of SM which can do the job.

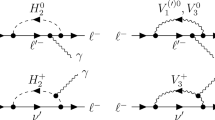
The usual 2HDM Type-II impose a \(Z_2\) symmetry to remove flavor violation from the Lagrangian [8]. In contrast, g2HDM does not adopt this symmetry, but one keeps all possible Yukawa coupling terms between fermions and both scalar doublets. Thus, there exists extra flavor changing neutral couplings (FCNC) such as \(\rho _{\tau \mu }\) (\(\rho _{\mu \tau }\)) that relate to lepton flavor violation (LFV) effects in the 32 sector. As illustrated in Fig. 1, these couplings can give rise to muon \(g-2\) via the one-loop diagram, with tau and heavy neutral scalars H and A in the loop. The diagram enjoys \(m_\tau /m_\mu \) chiral enhancement and can explain Eq. (2) for \(\rho _{\tau \mu }=\rho _{\mu \tau }\) at \(\mathcal{O}(20\lambda _\tau )\), where \(\lambda _\tau = \sqrt{2} m_\tau /v\), with sub-TeV but nondegenerate \(m_H\) and \(m_A\), as we showed recently in Ref. [9].

Fig. 1
figure 1

One-loop diagram for muon \(g-2\) (with \(\ell =\mu \)) and \(\mu \rightarrow e\gamma \) (with \(\ell = e\))

Full size image

The strength of \(\rho _{\tau \mu }\) and \(\rho _{\mu \tau }\) causes concern about LFV decay of the observed SM Higgs boson h, where [10]

$$\begin{aligned} \mathcal{B}(h\rightarrow \tau \mu ) < 0.15 \%, \end{aligned}$$
(3)

and is also warranted for other off-diagonal extra Yukawa couplings such as \(t \rightarrow ch\) [11, 12]. But this can be easily tackled by noting [11] that the strength of the \(h \bar{f}_i f_j\) vertex (\(i\ne j\)) is proportional to \(\rho _{ij} c_\gamma \), where \(c_\gamma \equiv \cos \gamma \) is the h–H mixing angle. Alignment, that \(c_\gamma \) seems quite small, emerged from detailed studies of h boson properties after its discovery [13,14,15]: the h boson resembles rather closely the SM Higgs. The smallness of \(c_\gamma \) suppresses [16] h boson FCNC naturally, and constraints such as Eq. (3) can be evaded.

We will take the alignment limit of \(c_\gamma \rightarrow 0\) in this work. This means the absence of flavor violating interactions of the h boson, while for the exotic H and A bosons they appear at full strength (i.e. \(\sin \gamma =1\)). The neutral exotic Yukawa couplings simplify to [17],

$$\begin{aligned}&\frac{1}{\sqrt{2}} \sum _{f = u, d, \ell } \bar{f}_{i} \,\rho ^f_{ij} \left[ H + i\,\mathrm{sgn}(Q_f) A \right] R\, f_{j} +\mathrm{h.c.}, \end{aligned}$$
(4)

where \(R=(1+\gamma _5)/2\) is the right-handed projection. The \(\rho _{ij}\) couplings are in general complex, where the phases can provide new sources of CP violation that can drive electroweak baryogengesis (EWBG) [18,19,20,21,22].

In this paper, we seek to explore charged LFV phenomena involving \(\mu \) and \(\tau \), with solving the muon \(g-2\) anomaly in the backdrop. This is especially salient in g2HDM, where the one-loop solution requires nonzero \(\tau \mu \) FCNC, therefore correlates directly with LFV. Previously, we highlighted [23, 24] the two-loop mechanism, with \(\rho _{tt}\simeq \mathcal{O}(\lambda _t)\) as the main driver of LFV. This was based on identifying two experimentally viable textures, viz. \(\rho _{3i} \lesssim \lambda _3\) \((i\ne 1)\) and \(\rho _{1j} \lesssim \lambda _1\). The one-loop solution to muon \(g-2\) anomaly requires large deviation from the first condition, which in turn suppresses \(\rho _{tt}\), hence the two-loop mechanism. But the second condition is not affected. With \(\rho _{\tau \mu }\rho _{\mu \tau }\) fixed by the one-loop solution to muon \(g-2\), we continue to adhere to

$$\begin{aligned} \rho _{1j} \lesssim \mathcal{O}(\lambda _1), \end{aligned}$$
(5)

as a working assumption. These modifications change the conclusion from Ref. [24] drastically. While we suggested that MEG II [25] would run into “diminished return” in its probe of \(\mu \rightarrow e \gamma \), the one-loop solution to muon \(g-2\), together with \(\rho _{\tau e}\lesssim \lambda _e\), Eq. (5), puts MEG II at the cusp of discovery, as we will show.

Many works have discussed charged LFV processes in g2HDM previously, in the context of the muon \(g-2\) anomaly [26,27,28,29,30,31]. In particular, Ref. [28] comes closest to this work. Let us therefore point out and contrast what is new in the present work. First, most other works were written in a time when there was a hint for \(h\rightarrow \tau \mu \) [32], and therefore necessarily required finite – and highly tuned – values of \(c_\gamma \). The hint quickly evaporated, however, and the latest CMS bound of Eq. (3) implies \(c_\gamma \lesssim 10^{-2}\) [9]. Second, we shall highlight \(\mu N\rightarrow e N\) as the ultimate probe of LFV in g2HDM. Both \(\mu e \gamma \) dipole and \(\mu eqq\) contact terms, as well as their interference, play important roles, and can be used to infer the sign of mass splitting, \(\Delta m = m_A - m_H\), which is important for the explanation of muon \(g-2\) in g2HDM. In a similar vein, Ref. [28] considered only tree level contributions to \(\mu \rightarrow 3e\) and \(\tau \rightarrow 3\mu \). Lastly, we avoid using any cosmetic cancellation mechanism between one- and two-loop contributions to \(\ell \rightarrow \ell ^\prime \gamma \) for sake of enlarging parameter space. We will lay out the reasons for this choice when we discuss the two-loop mechanism.

This paper is organized as follows. In Sect. 2 we discuss \(\mu \rightarrow e \gamma \) in g2HDM and highlight the interplay of LFV in 32 and 13 sectors. With the former couplings fixed by Eq. (2), the couplings associated with the latter, at \(\mathcal{O}(\lambda _e)\) or less, are shown to be well within the sensitivity of MEG II to probe. Implications for \(\mu \rightarrow 3 e\) are discussed. Turning to \(\mu N \rightarrow eN\) in Sect. 3, we discuss both dipole and contact contributions. In Sect. 4 we discuss \(\tau \rightarrow \mu \gamma \) and \(\tau \rightarrow 3\mu \) and their experimental prospects. Finally, we discuss in Sect. 5 other constraints and implications, and offer our conclusion.

2 \({{\varvec{\mu \rightarrow e \gamma }}}\)

The leading contribution to \(\mu \rightarrow e \gamma \) in g2HDM arises also through one-loop diagrams, as shown in Fig. 1. Only \(\tau \) is shown in the loop, as diagrams with muon and electron are chiral-suppressed and ignored. LFV in \(\mu \rightarrow e \gamma \) arises from \(\mu \tau \) and \(\tau e\) FCNC.

Defining the relevant effective Lagrangian as [33]

$$\begin{aligned} \begin{aligned} \mathcal {L}_{\mathrm {eff}}^\mathrm{\mu e\gamma }&= m_{\mu } \bigl (C_{T}^{R}\, \bar{e} \sigma _{\alpha \beta } L \mu + C_{T}^{L}\, \bar{e} \sigma _{\alpha \beta } R \mu \bigr ) F^{\alpha \beta } , \end{aligned} \end{aligned}$$
(6)

the \(\mu \rightarrow e \gamma \) branching fraction can be written in terms of the Wilson coefficients \(C_T^{L, R}\),

$$\begin{aligned} \mathcal{B}(\mu \rightarrow e\gamma ) = \frac{48\pi ^2}{G_F^2}\left( |C_T^{L}|^2+|C_T^{R}|^2\right) . \end{aligned}$$
(7)

The diagram in Fig. 1 gives

$$\begin{aligned} \begin{aligned} C_{T}^{R}|_{\phi = H, A} \simeq (\pm ) \frac{ \rho _{ \mu \tau }^{*}\rho _{\tau e}^{*} }{64 \pi ^{2}} \frac{em_\tau }{m_\mu m^2_\phi } \bigl [\log (m_\phi ^2/m_\tau ^2)- {3}/{2}\bigr ], \end{aligned}\end{aligned}$$
(8)

where \(+(-)\) sign is for the H(A) contribution, and some minor term has been dropped. To obtain \(C_T^{L}\), one replaces \(\rho _{ij}^*\rightarrow \rho _{ji}\). The diagram with \(H^+\) and neutrino in the loop is suppressed by neutrino mass. To further simplify our numerics, we treat \(\rho _{ij}\) as realFootnote 1 and, unless specified otherwise, take \(\rho _{ij}= \rho _{ji}\).

Before turning to numerical results for \(\mu \rightarrow e \gamma \), let us quickly recall the muon \(g-2\) solution in g2HDM [9]. This will provide a constraint on \(\rho _{\tau \mu }\) and help define benchmark masses for heavy scalars.

The one-loop formula for muon \(g-2\) is easily obtained from Eq. (8) by change of label from “e” to “\(\mu \)”,

$$\begin{aligned} \Delta a_\mu = \frac{4 m_\mu ^2}{e} \sum _{\phi =H, A} \mathrm{Re}\left[ C_T^{R}\right] _\phi \,, \end{aligned}$$
(9)

where H and A effects are opposite in sign. Thus, to have finite \(a_\mu \), H and A cannot be degenerate, or \(\Delta m = m_A - m_H \ne 0\). Choosing the sign of \(\Delta m\), i.e. to have H or A lighter, is a matter of taste. To keep consistency with our previous work [9], we take H lighter and fixed at \(m_H = 300\) GeV, and take \(\Delta m = 40\) and 200 GeV. The close to degenerate H and A case requires \(\rho _{\tau \mu }\simeq 30 \lambda _\tau \) for \(1\sigma \) solution of muon \(g-2\). For the large splitting case, the effect of A is damped with H dominant, and a smaller \(\rho _{\tau \mu }\simeq 20 \lambda _\tau \) suffices [9].

Fig. 2
figure 2

Parameter space in \(\rho _{\tau e}\)–\(\rho _{\tau \mu }\) plane which will be probed by three muon flavor violating processes. The dark (light) green shaded region is consistent with muon \(g-2\) within \(1\sigma \) (\(2\sigma \)). See text for details

Full size image

Returning to \(\mu \rightarrow e \gamma \), utilizing Eq. (8), we plot in Fig. 2 the region (red shaded) in the \(\rho _{\tau \mu }\)–\(\rho _{\tau e}\) plane to be probed by MEG II [25], for \(\Delta m = 40\) (200) GeV in the left (right) plot. The upper boundary corresponds to the MEG bound of \(\mathcal {B}(\mu \rightarrow e \gamma )_\mathrm{MEG}< 4.2 \times 10^{-13}\) [35], and the lower boundary is the projected reach of MEG II [25], \(\mathcal {B}(\mu \rightarrow e \gamma )_\mathrm{MEG ~II}< 6 \times 10^{-14}\). The parameter space consistent within \(1\sigma \) (\(2\sigma \)) range of muon \(g-2\), Eq. (2), is highlighted as the dark (light) green shaded area. As we continue to advocate Eq. (5) i.e. \(\rho _{\tau e}\lesssim \mathcal{O}(\lambda _e)\) as a natural choice for the electron-related off-diagonal coupling, we illustrate \(\rho _{\tau e}=\lambda _e\) and \(\rho _{\tau e}= 3\lambda _e, \, \lambda _e/3\) by horizontal solid and dashed lines, respectively. It is intriguing that \(\rho _{\tau e}= \lambda _e\) sits right in the middle of the region that MEG II would probe. One also sees that \(\rho _{\tau e}\gtrsim 3\lambda _e\) is already ruled out by MEG, while \(\rho _{\tau e}\lesssim \lambda _e/3\) or smaller will fall short of the MEG II range. However, if \(m_A\) is large compared to \(m_H\), as shown in Fig. 2(right), then MEG II can probe down to \(\rho _{\tau e}\simeq \lambda _e/3\).

Our working assumption of Eq. (5) therefore suggests that MEG II might well make a discovery.

2.1 Two-loop contributions

It is well-known that two-loop contributions, the so-called Barr–Zee diagrams, can dominate over one-loop contributions in certain parameter space of g2HDM. The corresponding formulae and loop functions for \(\mu \rightarrow e \gamma \) were originally calculated in Ref. [36], where it was shown that large extra top Yukawa coupling can drive these contributions well above the one-loop diagram just discussed. However, these Barr–Zee diagrams depend on \(\rho _{\mu e}\) and diagonal \(\rho _{ff}\) (\(f=t\) being the dominant loop contribution), which do not play any direct role in our NP interpretation of muon \(g-2\). Therefore, these diagrams provide constraint on the product of \(\rho _{\mu e}\rho _{tt}\). A more detailed phenomenological exploration of these contributions can be found in our previous work [24]. Numerically, the bound is \(\rho _{\mu e}\rho _{tt}\lesssim 0.4\, (0.5)\, \lambda _e \lambda _t\) for \(\Delta m = 40\) (200) GeV.

Since our focus is primarily on implications from NP in muon \(g-2\), we do not discuss combined result of one- and two-loop effects. The latter not only involves couplings inconsequential to muon \(g-2\), it also tends to cancel against the one-loop contribution, which will only bring uncertainty into our predictions of \(\mu \rightarrow e \gamma \) given in Fig. 2. One also needs to think about the complex phase of \(\rho _{tt}\), which is of interest for EWBG.

\({\varvec{\mu }}{\varvec{\rightarrow }} {\varvec{eee}}\). In g2HDM, neutral scalar exchange with couplings \(\rho _{\mu e}\) and \(\rho _{ee}\) can induce \(\mu \rightarrow 3e\), and the expression for the branching ratio can be found in Ref. [24]. Eq. (5) then implies that the contribution is very small [24]. For example, with \(m_{H\, (A)} = 300\) (340) GeV we find \(\mathcal{B}(\mu \rightarrow 3e)\simeq 3 \times 10^{-24}\), and even more suppressed for larger \(m_A\). This is far below the SINDRUM bound [37] of \(\mathcal{B}(\mu \rightarrow 3e) < 10^{-12}\). The Mu3e experiment plans to push the limit down to \(10^{-16}\) [38], which falls short by many orders of magnitude.

However, the \(\mu e \gamma \) dipole can generate sufficiently large contribution to \(\mu \rightarrow 3 e\) via [39]

$$\begin{aligned} \mathcal{B}(\mu \rightarrow 3e) \simeq \frac{\alpha }{3\pi } \left[ \mathrm{log}\left( \frac{m_\mu ^2}{m_{e}^2}\right) - \frac{11}{4} \right] \mathcal{B}(\mu \rightarrow e\gamma ). \end{aligned}$$
(10)

We plot in Fig. 2 the parameter space (blue shaded) probed by Mu3e, assuming Eq. (10). Note that the upper boundary does not correspond to the SINDRUM bound, as it is already ruled out by MEG. Furthermore, we show only the parameter space that lies beyond the reach of MEG II. This implies an important aspect of g2HDM: a discovery by MEG II means that Mu3e would observe \(\mu \rightarrow 3 e\) and confirm the dipole behavior. If MEG II does not see any hint, Mu3e can probe the dipole coupling further and find hints if \(\rho _{\tau e}\gtrsim \lambda _e/3\) for near-degeneracy \(\Delta m = 40\) GeV case. For larger \(\Delta m \), Mu3e can access smaller values of \(\rho _{\tau e}< \lambda _e/3\) (Fig. 2(right)).

3 \(\mu \rightarrow {\varvec{e}}\) conversion on nuclei

Concerning experimental prospects for muon flavor violation, it is the \(\mu N \rightarrow e N\) process where the ultimate progress would occur. The experimental bound is quoted in terms of the ratio, \(R_{\mu e}\), which is defined as the \(\mu \rightarrow e\) conversion rate normalized to the muon capture rate [39],

$$\begin{aligned} R_{\mu e} = \frac{\Gamma (\mu +(A, Z) \rightarrow e + (A, Z))}{\Gamma (\mu + (A, Z) \rightarrow \nu _\mu + (A, Z-1))}, \end{aligned}$$
(11)

with A and Z the mass and atomic numbers of the target nucleus, respectively. SINDRUM II gave the bound of \(R_{\mu e} < 7 \times 10^{-13}\) [40] using gold as target.

An array of experiments aim to improve the sensitivity in the near future. DeeMe [41] plans to reach a sensitivity of \(10^{-14}\) using thick silicon carbide (SiC) target. COMET [42] and Mu2e [43] aim at reaching \(\sim 10^{-17}\) using aluminum (Al) target, while PRISM [44] can push the sensitivity to \(10^{-18}\) with titanium (Ti) target. The experimental prospects seem quite promising.

In the context of g2HDM, the relevant effective Lagrangian for \(\mu \rightarrow e\) conversion is given by Eq. (6) plus Fermi contact terms [33, 45, 46],

$$\begin{aligned} \mathcal {L}_{\mathrm {eff}}^{\mu \rightarrow e} = \mathcal {L}_{\mathrm {eff}}^\mathrm{\mu e\gamma } + {\sum _q} \bigl (C_{q q}^{S R}\, \bar{e} L \mu + C_{q q}^{S L}\, \bar{e} R \mu \bigr )\, m_{\mu } m_{q} \bar{q} q, \end{aligned}$$
(12)

where \(C_{q q}^{S R(L)}\) arise from neutral scalar exchange [24]. Note that the Wilson coefficients in Eq. (12) are by definition invariant under one-loop QCD renormalization.Footnote 2 Therefore, the values of running quark masses and couplings \(\rho _{qq}\), which enter the expressions of \(C_{q q}^{S R(L)}\) (given in Ref. [24]), should be taken at the same scale. The conversion rate, \(\Gamma _{\mu \rightarrow e}\), is then defined as,

$$\begin{aligned} \begin{aligned} \Gamma _{\mu \rightarrow e}&= {m_{\mu }^{5}} \left| {1\over 2} C_{T}^{L} D + 2 \sum _q\Bigl (m_{\mu } m_{p}\, C_{qq}^{SL}f_q^p S^{p}{+} p {\rightarrow } n\Bigr )\right| ^{2}\\&\quad + (L \rightarrow R), \end{aligned} \end{aligned}$$
(13)

where the coefficients D and \(S^{p(n)}\) are related to lepton-nucleus overlap integrals, and \(f_q^{p(n)}\) are nucleon matrix elements. For gold nuclei, \(D = 0.189\), \(S^p = 0.0614\), \(S^n = 0.0918\) [51], while \(D=0.0362\), \(S^p=0.0155\), and \(S^n = 0.0167\) [51] for aluminum. The values of \(f^{p(n)}\)are taken from Ref. [45] for u and d quarks, from Ref. [52] for the s quark, and we use the relation [53] \(f_Q^{p(n)}= (2/27)(1-f_u^{p(n)}-f_d^{p(n)}-f_s^{p(n)})\) for the heavy quarks c, b, t.

3.1 Dipole dominance

In the absence of extra quark Yukawa couplings \(\rho _{qq}\), the conversion rate in Eq. (13) is governed by the \(\mu e \gamma \) dipole. In the dipole dominance scenario, Eq. (13) can be written in terms of the \(\mu \rightarrow e \gamma \) decay rate in a model independent way. For a given target nuclei with overlap integral coefficient D, one finds,

$$\begin{aligned} \Gamma _{\mu \rightarrow e} \simeq \pi D^2\,\Gamma (\mu \rightarrow e \gamma ). \end{aligned}$$
(14)

With the knowledge of the muon capture rate for a given nuclei, one can estimate the conversion ratio, \(R_{\mu e}\). For Au and Al, the muon capture rates are \(13.07 \times 10^6 \,s^{-1}\) and \(0.71 \times 10^{6}\, s^{-1}\), respectively [51, 54]. For other nuclei, the muon capture rates can be found in Ref. [51].

Taking Al as target nuclei, we illustrate in Fig. 2 the region (gray shaded) where the upcoming \(\mu N\rightarrow eN\) experiments will make further improvements in probing the g2HDM parameter space. The lower boundary shows the experimental sensitivity of \(10^{-17}\). It is no surprise that \(\mu N\rightarrow e N\) will be probing the \(\mu e \gamma \) dipole the furthest among all three processes, given the projected vast improvements in sensitivity. Even if \(\rho _{\tau e}\) turns out to be an order of magnitude smaller than our conservative suggestion of \(\rho _{\tau e}\simeq \mathcal{O}(\lambda _e)\), a discovery is still feasible.

Figure 2 also shows the possible interplay of different experiments. If MEG II finds hint of \(\mu \rightarrow e \gamma \), then Mu3e and Mu2e/COMET can confirm the dipole-only behavior, in accord with Eqs. (10) and (14). However, if MEG II does not see any hint, there is still window (blue shaded region) for Mu3e discovery, which again would likely be dipole-induced in g2HDM, and can help interpret any Mu2e/COMET confirmation. A discovery solely at Mu2e/COMET, however, leaves room for speculation on the nature of the interaction responsible for the hint – dipole-like or contact scalar interactions.

Fig. 3
figure 3

Parameter space in the \(\rho _{\tau \mu }\)–\(\rho _{\tau \tau }\) plane for \(\tau \rightarrow \mu \gamma \) to be probed by Belle II. See text for details

Full size image

3.2 Contact interactions

The \(\mu N\rightarrow e N\) process provides a distinct probe of charged LFV compared with \(\mu \rightarrow e \gamma \), because of scalar interactions in Eq. (12) that could be significant, due to diagonal extra \(\rho _{qq}\) couplings. Tree diagrams for \(\mu \rightarrow e\) conversion do not exhibit cancellation between H and A contributions. In fact, for real \(\rho _{ij}\), A does not contribute to coherent \(\mu N\rightarrow e N\). This unique feature of \(\mu N\rightarrow e N\) conversion can be exploited to probe the mass hierarchy of H and A, in the context of one-loop solution to muon \(g-2\) in g2HDM.

As mentioned in Sect. 2, muon \(g-2\) admits both \(m_A-m_H>0\) and \(m_A-m_H<0\), because one has freedom in the sign of the \(\rho _{\tau \mu }\rho _{\mu \tau }\) product to contribute positively to \(\Delta a _\mu \).Footnote 3 Since \(\mu N\rightarrow e N\) depends on the mass of H only (in case of real coupling), a lighter H will contribute significantly more. For example, taking \(\rho _{\mu e} = \lambda _e\), \(\rho _{qq} = \lambda _q\) for \(q\ne t\), and \(\rho _{tt} \sim 0.1\) (0), with Al as target we obtain \(R_{\mu e}|^\mathrm{contact} \simeq 1\, (0.95) \times 10^{-16}\) for \(m_H = 300\) GeV. Since \(R_{\mu e}|^\mathrm{contact}\) scales as \((1/m_H^4)\), it is quickly damped for heavier H. The tree level prediction in g2HDM is somewhat uncertain, given the large number of couplings involved. However, our estimate of \(\mathcal{O}(10^{-16})\), which lies well within experimental reach, is still a conservative estimate, as can be seen from our choice of \(\rho _{qq}\) values. This brings up another interesting aspect of \(\mu N\rightarrow e N\), which is the interference of dipole and contact interactions. If both contributions have comparable strength, constructive interference – the most optimistic case – can catapult the value of \(R_{\mu e}\) to be much larger than \(10^{-16}\). On the other hand, if A is the lighter one while H is heavy, the contact effect could be quite suppressed.

With results of MEG II, Mu3e, and COMET/Mu2e playing out and unfolding in the next decade, probing for flavor violation in muon decays look promising, if muon \(g-2\) is due to a large \(\rho _{\mu \tau }\) coupling.

4 \(\tau \rightarrow \mu \gamma \)

The Belle experiment updated recently the bound on \(\tau \rightarrow \mu \gamma \), giving \(\mathcal {B}(\tau \rightarrow \mu \gamma )_\mathrm{Belle} < 4.2 \times 10^{-8}\) [55]. The projected limit by Belle II is to push down to \(10^{-9}\) [56], and discovery is possible.

The physics of \(\tau \rightarrow \mu \gamma \) in g2HDM is similar to \(\mu \rightarrow e \gamma \) discussed in Sect. 2. One just replaces the label \(``\mu \)” with \(``\tau '' \) and set \(\ell =\mu \) for the one-loop diagram of Fig. 1, and corresponding expressions can be obtained from Eq. (8). Again, loops involving lighter leptons are chirally suppressed and neglected. We plot in Fig. 3 the region (red shaded) in the \(\rho _{\tau \mu }\)–\(\rho _{\tau \tau }\) plane probed by Belle II in g2HDM. The upper boundary is the Belle bound [55], while the lower boundary is the Belle II projection [56]. With large \(\rho _{\tau \mu }\) giving \(1\sigma \) solution to muon \(g-2\), the Belle limit already probes \(\rho _{\tau \tau }\simeq 6 \lambda _\tau \) for near-degenerate scalar masses (left plot). Belle II will continue to probe lower values and can push down to \(\rho _{\tau \tau }\simeq \lambda _\tau \) with full data. For large \(m_H-m_A\) mass difference (right plot), hence larger one-loop contribution, Belle II can probe smaller \(\rho _{\tau \tau }\) values. The Belle bound would already rule out \(\rho _{\tau \tau }> 3\lambda _\tau \) in regions allowed by muon \(g-2\), while Belle II can probe below \(\rho _{\tau \tau }\sim \lambda _\tau \).

It is interesting that one does not require a large value of extra \(\rho _{\tau \tau }\) coupling for \(\tau \rightarrow \mu \gamma \) to be discoverable at Belle II. Analogous to the \(\mu \rightarrow e\gamma \) discussion, a natural \(\rho _{\tau \tau }\simeq \mathcal{O}(\lambda _\tau )\) would suffice, so long that the one-loop mechanism is behind the muon \(g-2\) anomaly.

4.1 Two-loop mechanism

In contrast to the \(\mu \rightarrow e \gamma \) case, since the \(\rho _{\tau \mu }\) coupling enters the Barr–Zee diagrams for \(\tau \rightarrow \mu \gamma \) directly, the two-loop contributions have far more significant implications for extra top Yukawa coupling [23, 24], and for realizing EWBG in g2HDM [19,20,21]. We have discussed these contributions and the implications for muon \(g-2\) and at the LHC in Ref. [9]. For completeness, let us give a quick recount of the results.

For \(m_H,\, m_A =300\), 340 GeV, the dominant two-loop diagrams involving top give the strict bound of \(\rho _{tt}\lesssim 0.05\). For heavier pseudoscalar, \(m_A=500\) GeV, the bound gets slightly relaxed, \(\rho _{tt}\lesssim 0.1\). However, it turns out that the LHC search for \(gg \rightarrow H,A \rightarrow \tau \mu \) provides a stronger constraint [9] than \(\tau \rightarrow \mu \gamma \). Now, having \(\rho _{tt}\gtrsim 0.1 \) would make a more robust driver for EWBG in g2HDM [19]. One could then bring in another extra top Yukawa coupling, \(\rho _{tc}\), to dilute \(H, A\rightarrow \tau \mu \) and relax [9] the constraint on \(\rho _{tt}\). If \(\rho _{tt}\) is indeed very small in g2HDM, then \(\rho _{tc}\) can play the role of the EWBG driver [19]. Although it has nothing to do with muon \(g-2\), it could lead to interesting signals such as \(cg \rightarrow bH^+ \rightarrow \tau ^\pm \mu ^\mp b W^+, t\bar{c}bW^+\) at the LHC [9].

For real and positive values of extra Yukawa couplings, there is cancellation between one- and two-loop contributions, since the top loop of the latter brings in an extra minus sign. With \(\rho _{\tau \mu }\) fixed from one-loop solution to muon \(g-2\), the cancellation can enlarge the \(\rho _{\tau \tau }\) and \(\rho _{tt}\) parameter range, as pointed out in Ref. [28]. But this fine-tuned parameter space is not quite likely to survive. One reason could be the complex nature of \(\rho _{tt}\) that is needed for EWBG, making the two-loop amplitude complex, and e.g. for phase of \(\rho _{tt}\) at \(\pm \pi /2\) would make the cancellation mute. A second reason is experimental: the parameter space with \(\rho _{\tau \mu }\), \(\rho _{\tau \tau }\), and \(\rho _{tt}\) simultaneously large is actually under stress from LHC searches [9].

\({\varvec{\tau }}{\varvec{\rightarrow }} {\varvec{\mu }}{\varvec{\mu }}{\varvec{\mu }}\). This decay has been, and will be, searched for by several experiments. The current Belle limit [57] is \(\mathcal{B}(\tau \rightarrow 3\mu )|_\mathrm{Belle}< 2.1 \times 10^{-8}\). Both Belle II [56] and LHCb (Upgrade II) [58] plan to improve the sensitivity, with Belle II projecting a better reach of \(3.3 \times 10^{-10}\). There is also a new fixed-target proposal, TauFV [59], aiming to reach \(\sim 10^{-10}\) sensitivity. So the experimental prospect looks good.

Similar to \(\mu \rightarrow 3e\), this decay is induced at tree-level by H, A FCNC in g2HDM [24]. But unlike \(\mu \rightarrow 3e\), tree-level \(\tau \rightarrow 3\mu \) involves not only large \(\rho _{\tau \mu }\), but also the \(\rho _{\mu \mu }\) coupling, and \(\mathcal{B}(\tau \rightarrow 3 \mu )\) can be significant. For our benchmark cases of \(\Delta m = 40\) and 200 GeV, we find the current experimental bound only constrains \(\rho _{\tau \mu }\rho _{\mu \mu } \lesssim 260 \lambda _\tau \lambda _\mu \) and \(320 \lambda _\tau \lambda _\mu \), respectively. Taking the future sensitivity of Belle II, we get \(\rho _{\tau \mu }\rho _{\mu \mu } \lesssim 32 \lambda _\tau \lambda _\mu \) and \(40 \lambda _\tau \lambda _\mu \), respectively. This means that, for \(\rho _{\tau \mu }\simeq 30 \lambda _\tau \) (\(20\lambda _\tau \)) for \(\Delta m =40\) (200) GeV, discovery is projected in g2HDM even with \(\rho _{\mu \mu } \simeq \mathcal{O}(\lambda _\mu )\), which is again a “natural” strength in g2HDM.

If \(\rho _{\mu \mu } \ll \lambda _\mu \) turns out to be the case in Nature, then \(\tau \rightarrow 3\mu \) search will essentially be probing the \(\tau \mu \gamma \) dipole, which relates to \(\tau \rightarrow 3\mu \) by changing “\(\mu \)” to “\(\tau \)” and “e” to “\(\mu \)”in Eq. (10). This means that \(\mathcal{B}(\tau \rightarrow 3\mu )\) will be below \(\mathcal{B}(\tau \rightarrow \mu \gamma )\) by about \(2.3 \times 10^{-3}\). Therefore, as argued in Ref. [24], unless there is a hint of \(\tau \rightarrow \mu \gamma \) in the early data of Belle II, \(\mathcal{B}(\tau \rightarrow 3\mu )\) will be outside the sensitivity reach of planned experiments.

5 Discussion and summary

We find that \(\mu \rightarrow e \gamma \) can be enhanced in g2HDM to experimentally accessible values, even for exceptionally small extra Yukawa coupling \(\rho _{\tau e}= \mathcal{O}(\lambda _e)\). This is in context of using large \(\rho _{\tau \mu }\) coupling to explain the muon \(g-2\) anomaly. A diagram similar to Fig. 1 with \(\tau \) and \(H,\,A\) in the loop can contribute to electron \(g-2\), where recent measurements of \(\alpha \) suggest some tension [60]. But since large \(\rho _{\tau \mu }\) constrains \(\rho _{\tau e}\) (\(\rho _{e\tau }\)), through the MEG bound on \(\mu \rightarrow e\gamma \), to be consistent with Eq. (5), we find the contribution is negligible and the electron \(g-2\) remains SM-like. The \(\rho _{\tau e}\), \(\rho _{e\tau }\) couplings, together with \(\rho _{\tau \tau }\), induce \(\tau \rightarrow e\gamma \) decay. But again with Eq. (5) and with \(\rho _{\tau \tau }= \mathcal{O}(\lambda _\tau \)), the induced \(\mathcal{B}(\tau \rightarrow e\gamma )\) is very small. Putting it differently, the current bound of \(\mathcal{B}(\tau \rightarrow e\gamma ) < 3.3 \times 10^{-8}\) [61] sets only an extremely poor bound of \(\rho _{\tau e}\rho _{\tau \tau }\lesssim \mathcal{O}(10^4) \lambda _e \lambda _\tau \) for scalar masses considered in this work, and far from probing Eq. (5).

We mention some similarly weak constraints in passing. The \(Z\rightarrow \tau \tau \), \(\mu \mu \) partial widths and the leptonic \(\tau \rightarrow \mu \nu \bar{\nu }\), \(e \nu \bar{\nu }\) and \(\mu \rightarrow e \nu \bar{\nu }\) decays are easily compatible with Eq. (5) and \(\rho _{\tau \tau } \simeq \mathcal{O}(\lambda _\tau )\) [9] and even large \(\rho _{\tau \mu }\), and no serious constraint is set within our framework.

Because of the Fermilab confirmation of the muon \(g-2\) anomaly, we have taken the one-loop explanation in g2HDM seriously. We had not advocated this in our previous work [24], but it should be clear that Nature is entitled to this choice of a large \(\rho _{\tau \mu }\, (\simeq \rho _{\mu \tau })\), which has phenomenological consequences such as small \(\rho _{tt}\) and \(\rho _{\tau e} = \mathcal{O}(\lambda _e)\). We would still not advocate that Nature can whimsically dial up several extra Yukawa couplings, for it would seem hard to escape the exquisite flavor probes. Another curiosity worth emphasizing again is that, if it turns out that A is the lighter exotic scalar behind muon \(g-2\) and H is considerably heavier, since A exchange cannot be coherent over the nucleus, the contact interaction effects could be much subdued, hampering the \(\mu N \rightarrow eN\) program to study them.

In summary, in the general two Higgs doublet model, large LFV couplings \(\rho _{\tau \mu }\) and \(\rho _{\mu \tau }\), with inbuilt chiral enhancement, can explain the muon \(g-2\) anomaly. We cover LFV processes such as \(\mu \rightarrow e\gamma ,\, 3e\), \(\mu N\rightarrow e N\), \(\tau \rightarrow \mu \gamma ,\, 3\mu \). Taking \(\rho _{\tau e},\, \rho _{\mu e} = \mathcal{O}(\lambda _e)\) (Eq. (5)) and \(\rho _{\ell \ell } \simeq \mathcal{O}(\lambda _\ell )\) as reasonable, we find excellent chance for discovery of \(\mu e\gamma \) dipole effects with all three muon decay/transition experiments. Among these, \(\mu N\rightarrow e N\) conversion can ultimately determine or constrain the associated LFV couplings. If extra quark Yukawa couplings come into play, \(\mu N\rightarrow e N\) can probe the interference between dipole and contact interactions. By exploiting different nuclei and refined theory developments, the \(\rho _{qq}\) couplings might be unraveled. Prospects for \(\tau \rightarrow \mu \gamma \) and \(\tau \rightarrow 3\mu \) are also good, which probe the natural strengths of \(\rho _{\tau \tau } \sim \lambda _\tau \) and \(\rho _{\mu \mu } \sim \lambda _\mu \).

Let us hope that the muon \(g-2\) anomaly would usher in a new era of \(\mu /\tau \) discoveries.